Significance
Understanding how the variability of daily temperature may change with greenhouse gas emissions is important because it has been identified as a key factor in societal and economic well-being. Assessing historical changes to daily temperature variability in comparison with those from state-of-the-art climate models, we show that variability has changed with distinct global patterns over the past 65 years, changes which are attributable to rising concentrations of greenhouse gases. If these rises continue, temperature variability is projected to increase by up to 100% at low latitudes and decrease by 40% at northern high latitudes by the end of the century. We further show that these changes would be limited by mitigating emissions and will depend on the equilibrium climate sensitivity.
Keywords: climate change, atmospheric science, temperature variability
Abstract
Changes in mean climatic conditions will affect natural and societal systems profoundly under continued anthropogenic global warming. Changes in the high-frequency variability of temperature exert additional pressures, yet the effect of greenhouse forcing thereon has not been fully assessed or identified in observational data. Here, we show that the intramonthly variability of daily surface temperature changes with distinct global patterns as greenhouse gas concentrations rise. In both reanalyses of historical observations and state-of-the-art projections, variability increases at low to mid latitudes and decreases at northern mid to high latitudes with enhanced greenhouse forcing. These latitudinally polarized daily variability changes are identified from internal climate variability using a recently developed signal-to-noise-maximizing pattern-filtering technique. Analysis of a multimodel ensemble from the Coupled Model Intercomparison Project Phase 6 shows that these changes are attributable to enhanced greenhouse forcing. By the end of the century under a business-as-usual emissions scenario, daily temperature variability would continue to increase by up to a further 100% at low latitudes and decrease by 40% at northern high latitudes. Alternative scenarios demonstrate that these changes would be limited by mitigation of greenhouse gases. Moreover, global changes in daily variability exhibit strong covariation with warming across climate models, suggesting that the equilibrium climate sensitivity will also play a role in determining the extent of future variability changes. This global response of the high-frequency climate system to enhanced greenhouse forcing is likely to have strong and unequal effects on societies, economies, and ecosystems if mitigation and protection measures are not taken.
The effect of anthropogenic greenhouse gas emissions on mean climatic conditions is well understood. Theory, observational, and modeling work all demonstrate that average temperatures increase as a result of elevated greenhouse gas concentrations (1). However, it is also of considerable importance to natural and human systems whether changes in the temporal variability of climatic conditions have accompanied historical global warming and whether they will do so in the future (2–5). A more variable climate implies greater uncertainty and greater frequency of extremes, both of which constitute more damaging conditions.
The variability of climate from one year to the next has received considerable attention. Large-scale climatic oscillations, such as the El Niño Southern Oscillation and the Indian Ocean Dipole, are dominant determinants of interannual variability (6–8) and have been shown to exhibit more frequent extremes under enhanced greenhouse forcing within comprehensive climate models (9–11), results that are supported by paleoclimatic evidence (12). Identifying a response in interannual temperature variability has been less conclusive. Some studies have attributed recent summer temperature extremes to greater interannual variability, both regionally (13) and globally (14), but there is still debate as to the extent of the role of interannual variability (15–17). Some regional trends in interannual temperature variability have been identified (17–21), but there is no consensus between observations and climate models (22).
Here, we focus on variability of temperature at a higher frequency (daily), which a growing body of econometric literature has identified as an important determinant of societal outcomes, including human health (23–27), agriculture (28–30), and economic growth (31). The effect of enhanced greenhouse gas concentrations on the daily variability of temperature is therefore of wide societal importance and a critical component of the impact of anthropogenic climate change.
Decreases in daily temperature variability at northern mid to high latitudes have been detected in observations (32–34) and agree well with predictions from comprehensive climate models (34–36) and physical reasoning (34, 35). Previous generations of climate models have also suggested that daily variability may increase during European summer (37) and across the tropics (36, 38), but these predictions have not yet been detected in observations or confirmed in state-of-the art climate models. This paper unifies these works by presenting a global analysis of changes in subseasonal, daily temperature variability under enhanced greenhouse forcing in both reanalyses of historical observations (National Oceanographic and Atmospheric Administration [NOAA] 20th Century Reanalysis Version 3 and the European Centre for Medium-Range Weather Forecasts Reanalysis 5 [ERA-5]) and the latest generation of comprehensive climate models (Coupled Model Intercomparison Project phase 6 [CMIP-6]). Daily temperature variability refers to the intramonthly SD of daily surface temperature from hereon. We consider changes in daily variability in boreal winter (“DJF”), boreal summer (“JJA”), and across the year (“annual”) to both assess the season specific mechanisms identified in previous work and to provide an aggregated overview of variability changes.
Historical Changes in Daily Temperature Variability
Identifying externally forced signals in climate data is complicated by the internal multidecadal variability of the climate system. In order to identify possible forced signals in daily temperature variability, we use a pattern-recognition technique that has been recently developed to identify spatial patterns with coherent low-frequency temporal evolution (39, 40). Low-frequency component analysis (LFCA), an extension of traditional principal component analysis (PCA), identifies linearly independent modes that account for the greatest ratio of low frequency to total variance (see Materials and Methods for further details). Since climatic changes due to greenhouse forcing are slower to evolve than those due to internal variability, this approach can help to discriminate between them. LFCA has been shown to successfully separate externally forced climate signals from internal multidecadal variability, such as those of global warming and arctic amplification from El Niño Southern Oscillations and Pacific Decadal Oscillations in observations of monthly mean surface temperature (39, 40).
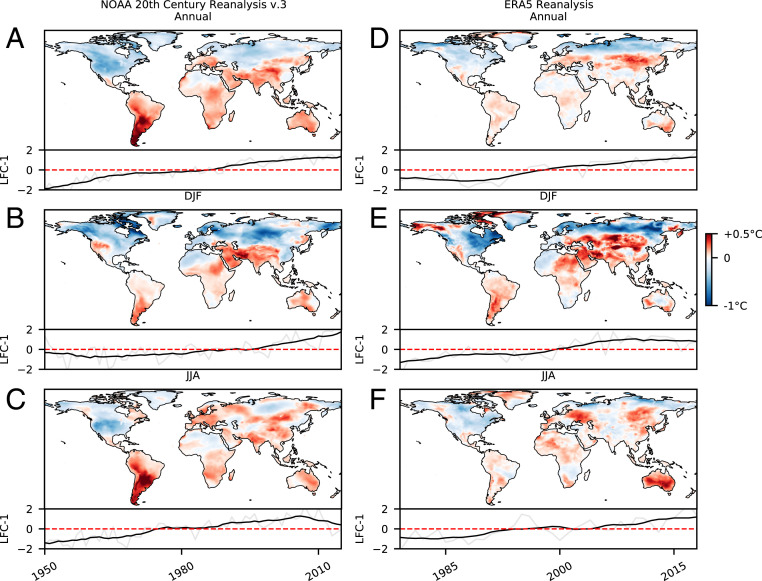
We apply LFCA to historical reanalyses of daily temperature variability (Materials and Methods). In each season and in the annual case, the lowest-frequency component identified by LFCA (LFC-1) has grown almost monotonically over the historical period (Fig. 1), separate from higher-frequency modes, which have not (SI Appendix, Fig. S1). In the NOAA 20th Century Reanalysis, the corresponding spatial patterns exhibit strong latitudinal polarization in both the annual and DJF cases: Reductions in daily temperature variability at northern mid to high latitudes are opposed by increases across the majority of the continental land mass elsewhere (Fig. 1 A and B). For JJA, the pattern consists of reductions across North America, the high Arctic, and parts of North Africa opposed by strong increases elsewhere (Fig. 1C). These latitudinally polarized components are responsible for increases and decreases of up to 40% and 20% over the past 65 y, with particularly strong percentage increases across the tropics (SI Appendix, Fig. S2 A–C).
Fig. 1.
Lowest-frequency patterns of change in daily temperature variability detected with LFCA from reanalyses of historical observations. Patterns of change in annual (A and D), boreal winter (DJF; B and E), and boreal summer (JJA; C and F) daily temperature variability, which have grown monotonically over the historical period, are identified. Results from the NOAA 20th Century Reanalysis version 3 are shown in A–C, and those from the shorter ERA-5 reanalysis are shown in D–F. Interdecadal changes (between the first and final decade) in daily temperature variability due to the lowest-frequency component are shown as colored maps, the time evolution of which is shown at the bottom in gray with a 10-y running mean in black.
Similar spatial patterns are detected in the ERA-5 reanalysis, Fig. 1 D–F. In particular, the latitudinal polarization in the annual and DJF cases and the increases across the tropics, Australia, Europe, and large parts of South America and Africa in boreal summer are distinct features in both. Regional discrepancies are present and are likely to occur due to the different temporal extent of the two reanalyses. We continue to use the NOAA 20th Century Reanalysis as our main specification, since we expect the longer time period to improve the separation of an externally forced response from internal climate variability.
The detection of these patterns of global change in daily temperature variability is robust to different specifications of the LFCA (SI Appendix, Fig. S3) and to alternative detection methods (SI Appendix, Fig. S4, grid-cell linear trends). This detection of historical increases in daily temperature variability in European summer and across the tropics and wider Southern Hemisphere confirms the predictions of previous generations of climate models (36–38).
Global Climate Projections from CMIP-6
We test whether the historical and monotonic growth of these global patterns in daily temperature variability is attributable to historically increasing concentrations of greenhouse gases with a multimodel ensemble of 10 bias-corrected Coupled Global Circulation Models (CGCMs) from CMIP-6 (refs. 41 and 42; see Materials and Methods for details). Daily temperature variability is calculated from the ensemble under historical (1950–2015) and future (2015–2100) greenhouse forcing. Future forcing is specified by the Shared Socioeconomic Pathway (SSP)-585, a business-as-usual emissions scenario under which greenhouse forcing continues to increase monotonically. Comparing daily temperature variability between the ensemble under historical forcing and the reanalysis data suggests that daily temperature variability is represented by the ensemble very well (SI Appendix, Fig. S5).
Multimodel ensembles, such as CMIP-6, encompass intermodel differences in both the representation of internal climate variability (due to variations in initial conditions) and in the representation of the forced response to greenhouse gases (due to structural differences). LFCA provides the opportunity to identify a forced response from internal climate variability within each individual ensemble member, thus retaining any biases in the modeling of the forced response. This allows a more nuanced estimate of the forced response to be made than would be possible with a simple multimodel average. Moreover, LFCA has been shown to identify externally forced signals from a single climate model with greater accuracy than ensemble averages with even 20 realizations (40). We therefore apply LFCA to calculations of daily temperature variability from individual ensemble members under historical and future forcing, covering the period 1950 to 2100.
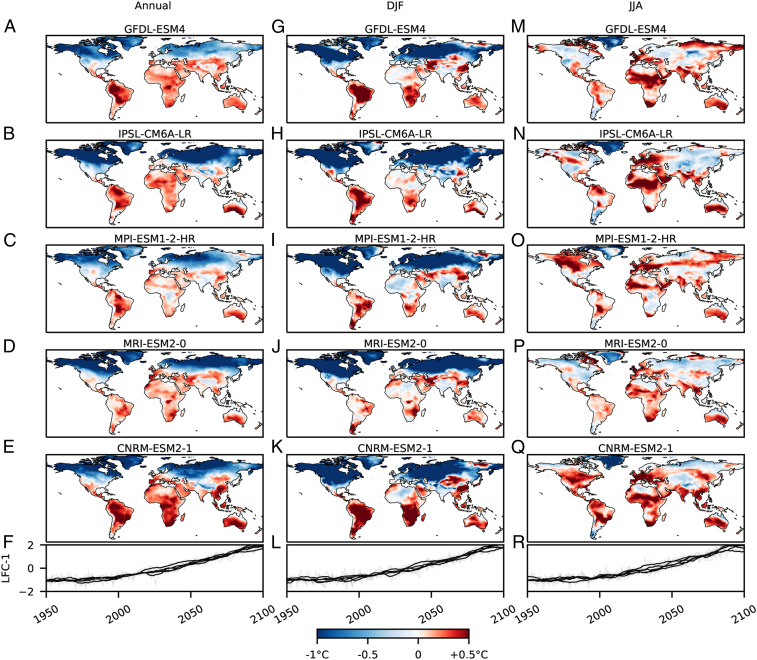
In each model and in each season, monotonically increasing patterns of change are identified from internal, multidecadal climate variability, which shows a high degree of consistency both between models and with those identified from the reanalysis of historical observations (Fig. 2 and SI Appendix, Fig. S6). In both the annual and DJF cases, strong latitudinal dependence in the response of daily temperature variability is noted. Most discrepancies between models are concentrated at the latitudinal boundary between decreasing and increasing variability or in North Africa (Figs. 2 and 3 D and E and SI Appendix, Fig. S6). In JJA, models consistently predict increasing variability across the tropics, Southern Hemisphere, and Europe, but show poor agreement on the signs of change at northern mid to high latitudes (with the exception of Greenland; Figs. 2 and 3F and SI Appendix, Fig. S6).
Fig. 2.
Lowest-frequency patterns of change in daily temperature variability from individual CMIP-6 climate models under greenhouse forcing (1950–2015: historical; 2015–2100: SSP-585), detected with LFCA. Results from 5 of the 10 models are shown for the annual (A–F), the boreal winter (DJF; G–L), and the boreal summer (JJA; M–R) response; see SI Appendix, Fig. S6 for the remaining 5 models. Interdecadal changes (1950–1960 to 2090–2100) due to the lowest-frequency component (Materials and Methods) are shown as colored maps, the time evolution of which are shown in the bottom panels in gray, with a 10-y running mean in black.
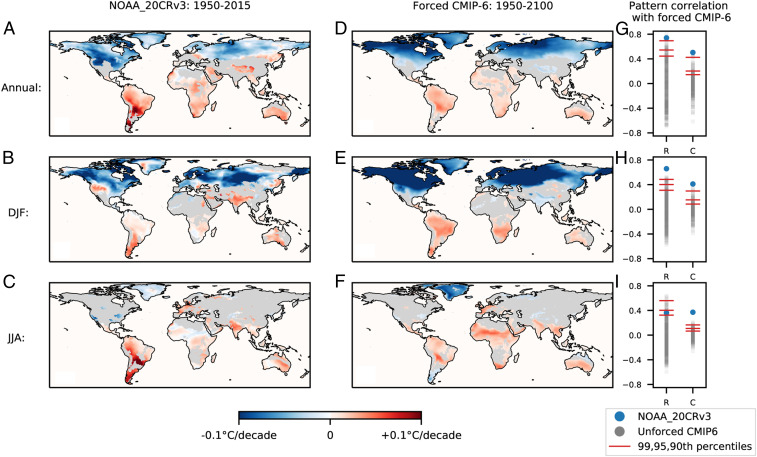
Fig. 3.
Attribution of historical changes in daily temperature variability to greenhouse forcing. (A–C) Historical patterns of change in daily temperature variability estimated with LFCA from the NOAA 20th Century Reanalysis of historical observations. (D–F) Simulated patterns of change in daily temperature variability estimated as the multimodel mean of the lowest-frequency component of each CMIP-6 ensemble member under historical and SSP-585 greenhouse forcing. Gray coloring indicates regions in which less than 90% of the models agree on the sign of change (see SI Appendix, Fig. S7 for results without this exclusion). (G–I) Centered (R) and uncentered (C) pattern-correlation statistics between the observed and simulated response of daily temperature variability to greenhouse forcing (blue) in comparison to those that could occur due to unforced internal climate variability (gray). Estimates of the distribution of changes due to unforced internal variability are obtained by applying LFCA to control runs of the CMIP-6 ensemble under constant preindustrial forcing (Materials and Methods). The 99th, 95th, and 90th percentiles of the distributions of pattern correlations between forced and unforced simulations are shown in red.
Attribution to Greenhouse Forcing
To attribute the observed historical changes identified in daily temperature variability to increasing greenhouse forcing requires two further steps. First is a formal assessment of the similarity between the historically observed changes and the expected response to greenhouse forcing identified from the CMIP-6 ensemble. We do so using two pattern-correlation statistics, following the work of previous detection-attribution studies (43). The uncentered pattern correlation (C) accounts for both the spatial similarity between and the magnitudes of the two patterns, whereas the centered pattern correlation (R) accounts only for their spatial similarity. The historically observed patterns of per-decadal change are taken as those identified with LFCA from the NOAA 20th Century Reanalysis (Fig. 3 A–C). The expected response to greenhouse forcing is estimated as the multimodel-ensemble average of the patterns of per-decadal change obtained from the lowest-frequency component of each individual model, detected with LFCA (Fig. 3 D–F). Second, the significance of the historically observed changes must be assessed with respect to those that could occur due to the natural internal variability of the climate system. We apply LFCA to control runs of the CMIP-6 ensemble under constant preindustrial greenhouse forcing to provide estimates of the distribution of interdecadal changes that can result from internal climate variability (Materials and Methods).
A high degree of spatial similarity between the historically observed and the forced response of daily temperature variability is noted in the case of the annual and DJF response (Fig. 3 G–I and SI Appendix, Fig. S7; centered pattern correlation R). A lesser degree of similarity is noted in JJA, likely due to the lesser degree of polarization in the response and the greater intermodel disagreement at northern mid to high latitudes. These assessments of spatial similarity are improved when regions in which less than 90% of climate models agree on the sign of change are excluded, as shown in Fig. 3. The uncentered pattern correlation (C), which assesses both spatial similarity and magnitude, is generally lower (with the exception of JJA). This is to be expected, given the weaker forcing in the historical period than in the SSP-585 scenario.
Most importantly, these assessments of similarity are significant with respect to those expected due to natural internal climate variability (Fig. 3 G–I and SI Appendix, Fig. S7 G–I). When considering only spatial similarity with the centered pattern-correlation statistic (R), the similarity of the historically observed response to the forced response is significant at least at the 1% level in the annual and DJF cases and at the 10% level in the JJA case. Moreover, when considering both spatial similarity and magnitude via the uncentered pattern-correlation statistic (C), the similarity is unmatched in the CMIP-6 control runs in all seasons and, therefore, significant at least at the 0.24% level.
We therefore conclude that the historically observed global patterns of change in daily temperature variability are extremely unlikely to occur due to natural internal variability and are consistent with the expected response to anthropogenic greenhouse forcing in the annual, DJF, and JJA cases.
Scaling between Variability Changes and Warming
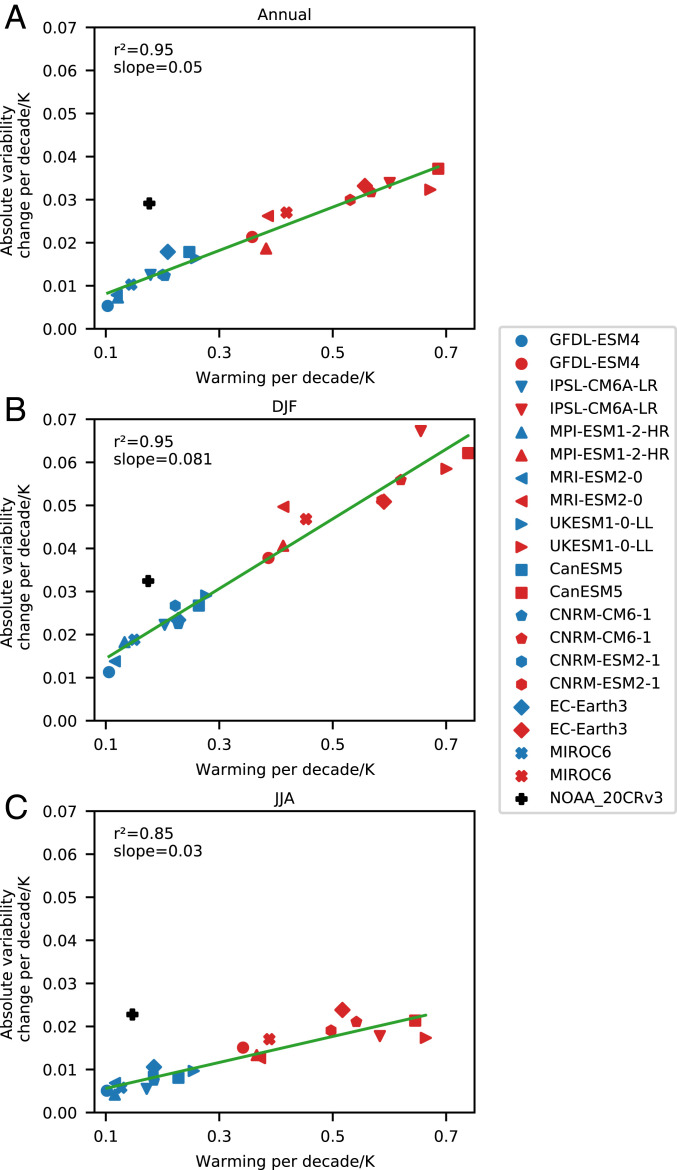
Mechanisms by which daily temperature variability may change have been linked to mean surface temperature changes (34, 35, 37), suggesting that daily variability changes may scale with warming. Such scaling has recently been identified in CMIP-5 models for interannual variability in European summer temperatures (21), but has not been considered for daily variability or at a global scale. We address this by assessing whether daily variability and mean temperature changes covary across CMIP-6 models and forcing scenarios.
Changes in both variables are estimated for each ensemble member from the lowest-frequency component identified with LFCA. Patterns of change are land-area averaged, after which strong linear covariation is noted across climate models and forcing scenarios (Fig. 4, SSP-126 shown in blue, SSP-585 shown in red). This scaling is also robustly identified for changes occurring over different 25-y periods within individual climate models (SI Appendix, Fig. S8). Furthermore, we find that the historically observed variability changes are considerably larger than those of the CMIP-6 ensemble, given the historical level of warming (Fig. 4, NOAA 20th Century Reanalysis shown in black).
Fig. 4.
Scaling between average continental warming and absolute variability changes estimated from CMIP-6 climate models and the NOAA 20th Century Reanalysis of historical observations for annual (A), boreal winter (“DJF,” B) and boreal summer (“JJA,” C) changes. Strong covariation is noted across climate models and forcing scenarios (SSP-126 shown in blue, SSP-585 in red). See SI Appendix, Fig. S8 for scaling between changes occurring over different 25-y periods within individual climate models.
These findings have two important implications. First, that future changes in daily temperature variability will depend not only on the extent of greenhouse gas forcing, but also on the true climate sensitivity, re-emphasizing the importance of providing constraints on its value. Second, that global climate models underpredict the extent to which daily variability changes in response to greenhouse forcing and surface warming, suggesting that CMIP-6 projections provide only a lower bound on how variability may change under future forcing scenarios.
Discussion and Conclusions
The present study has identified global patterns of change in daily temperature variability, which have grown monotonically over the past 65 y in reanalyses of historical observations. This provides evidence of increasing temperature variability across the tropics, Southern Hemisphere, and European summer in observational products and confirms the detection of decreasing variability at northern mid to high latitudes shown in previous work (32–35). The physical mechanisms behind these changes are well understood at northern mid to high latitudes, where Arctic amplification has reduced meridional temperature gradients, leading to reduced thermal advection (34, 35). The mechanisms behind the increases at lower latitudes found here are less clear, although modeling work on daily variability changes in Europe (37) and interannual variability changes across the tropics (22) suggests that soil drying and the resulting balance between sensible and latent heat fluxes may be a key driving process. The present demonstration of a robust scaling between surface warming and variability changes further suggests that the driving mechanisms will be closely related to surface warming.
Of further interest is the latitudinal boundary between increasing and decreasing temperature variability, which varies considerably between models (SI Appendix, Fig. S9) and with longitude (SI Appendix, Fig. S10). This is most clearly noted by the opposed increases across Europe and decreases across North America, as seen in the reanalyses (Fig. 1 A and D and SI Appendix, Fig. S10 D–F). This longitudinal dependence of the north to south transition persists in CMIP-6 (SI Appendix, Fig. S10 A–C), despite globally coherent shifts in the latitudinal boundary between models (e.g., compare Canadian Earth System Model Version 5 [CanESM5] and Centre National de Recherches Météorologiques Climate Model 6-1 [CNRM-CM6-1] in SI Appendix, Fig. S6 B and C). This effect may result from a longitudinally heterogeneous balance between the two mechanisms discussed above, which may be modulated by regionally dependent phenomena, such as geography, ocean currents (i.e., the Atlantic Meridional Overturning Current), aerosol loading, or greenhouse gas emissions. Distinguishing between these factors is beyond the scope of this work, but offers a promising avenue for future research.
The assessment of a multimodel ensemble of CMIP-6 climate models has shown that the historically observed global changes in daily temperature variability are very unlikely to have occurred due to natural internal climate variability and are highly consistent with the expected response to anthropogenic greenhouse forcing. Our assessment of the significance of these changes rests on the assumption that climate models accurately represent the internal variability of the real-world climate system, a common assumption of detection-attribution frameworks (44). In future work, this assumption could be complemented by adapting recent methods that estimate trend uncertainty due to internal variability directly from observations (45, 46). Furthermore, the CMIP-6 historical and SSP scenarios include additional forcing components (volcanic, solar, and aerosol) to greenhouse gases, which might undermine confidence that the detected response of daily temperature variability can be exclusively attributed to greenhouse gases. Nevertheless, a closer analysis of these forcings shows that only greenhouse gases can both explain the growth of the response across time and the two forcing scenarios (SI Appendix, SI Text and Fig. S11) and are physically consistent with the demonstrated scaling between variability changes and surface warming (SI Appendix, SI Text).
This global response of the high-frequency climate system has already caused changes in daily temperature variability of up to 40%, which are projected to change by a further 100% by the end of the century under a business-as-usual emission scenario. Analysis under an alternative future forcing scenario (SSP-126) (SI Appendix, Figs. S12 and S13) suggests that these changes would be limited considerably by mitigation of greenhouse gases. Furthermore, the observed scaling between warming and variability changes suggests that the Earth’s true climate sensitivity will also determine the future development of daily temperature variability and that future changes are likely to be larger than those projected by the CMIP-6 ensemble. These changes are likely to have strong impacts on human (23–31) and ecological (4, 5) systems across the globe, the full extent of which must be quantified in future multidisciplinary research efforts. Since the biggest increases in daily temperature variability are observed in and projected for low-latitude regions with typically low income and low historical emissions of greenhouse gases, regional inequalities and climate injustices are likely to be exacerbated.
Materials and Methods
Daily Temperature Variability.
Daily temperature variability is measured as the SD of daily surface temperature within a given month of a given year. Monthly values of daily temperature variability and of mean temperature are calculated from the daily 2-m surface temperature at each grid cell, and these values are mean averaged over months of a given season (for DJF and JJA) or year (for annual).
Reanalysis Data.
Daily 2-m surface temperature from the NOAA 20th Century Reanalysis Version 3 (1950–2015) (47) and from the ERA-5 reanalysis (1979–2019) are used. These reanalyses are chosen for their high temporal resolution (as is necessary to assess daily variability), global coverage, and long prior periods of reanalysis development. Data are obtained on regular grids at daily temporal resolution, 1 by 1 degree for NOAA 20th Century Reanalysis and 0.5 by 0.5 degree for ERA-5.
Comprehensive Climate Model Data.
Daily 2-m surface temperature from an ensemble of 10 bias-adjusted CGCMs from the CMIP-6 (41) are used. Bias adjustment is done by the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP) and is explicitly designed to preserve trends across different quantiles of daily climate variables (42); this feature makes it appropriate to assess trends in the variability of daily temperature. We use the models under preindustrial, historical, and future greenhouse forcing specified by SSP-126 and -585 (48). These represent a strong mitigation and business-as-usual emissions scenario, respectively. All data are obtained on a 0.5-by-0.5-degree grid at daily temporal resolution. A list of the CGCMs and their source institutions is given in SI Appendix, Table S1. Daily temperature variability is calculated on the original grid before linear interpolation to the grid of the NOAA 20th Century Reanalysis for further analysis.
LFCA
LFCA is a form of linear discriminant analysis that has been recently developed by the authors of refs. 39 and 40 to identify linearly independent modes that vary with the lowest frequency. It has been shown to be a powerful tool to isolate greenhouse-forced spatiotemporal signals from unforced multidecadal internal variability when only a single realization of the climate system is available. For a detailed description of the motivation for and development of the technique, see refs. 39 and 40. Here, we outline the method and our application of it to daily temperature variability. Anomalies of seasonal or annual daily temperature variability are calculated with respect to their mean values across the time period in question. The following procedures of LFCA are then applied. Empirical orthogonal functions (EOFs) are calculated with a traditional PCA. EOFs are the eigenvectors, , with eigenvalues, , of the covariance matrix, , of the -by- dimensional demeaned daily temperature variability data, :
| [1] |
Linear combinations of the first, , EOFs, , are then found that maximize the ratio, , of low frequency to total variance that their corresponding time series, , can explain:
| [2] |
Low-frequency variance is estimated by filtering departures from linear trends with a linear Lancoz low-pass filter, , with cutoff frequency, , and reflecting boundary conditions:
| [3] |
This procedure identifies low-frequency components (LFCs), , based on the frequency of their evolution. The corresponding low-frequency patterns (LFPs), , are obtained by projecting the unfiltered data onto these components:
| [4] |
LFCs describe the temporal evolution of their accompanying spatial pattern (LFP). The resultant LFCs are orthogonal to one another and are ordered by increasing frequency. The justification for this choice of variance maximization (maximizing the low-frequency to total variance ratio, rather than maximizing the total variance) is that spatiotemporal changes due to greenhouse forcing occur with a lower frequency than those due to most internal variability of the climate system.
The cutoff frequency used here is , and the number of leading EOFs retained in the linear combinations, N, is selected to maintain roughly 70% of the raw variance of . These choices follow previous work on the development of this method in the context of detecting anthropologically forced climate changes (39, 40). For the NOAA 20th Century Reanalysis, this corresponds to n = 15 for the annual and DJF cases and n = 20 for the JJA case. For the ERA-5 reanalysis data, this corresponds to n = 15, 12, and 16 for the annual, DJF, and JJA cases, respectively. For the CMIP-6 climate models, we use n = 15 for the annual and DJF case and n = 30 for the JJA case. Tests of the robustness of the results to these choices are shown in SI Appendix, Fig. S3.
LFCA is applied to daily temperature variability as calculated from the NOAA 20th Century and ERA-5 reanalyses and from individual climate models under historical and future forcing. The interdecadal changes due to a given component are calculated by multiplying the LFP by the difference between decadal averages of the corresponding LFC. LFCs are plotted both as raw data and after filtering with a 10-y running mean.
Attribution to Greenhouse Forcing.
We use pattern-correlation statistics as described in ref. 43 to estimate the similarity between the global patterns of change in daily temperature variability identified from the reanalyses and the CMIP-6 ensemble under greenhouse forcing. We use both the uncentered (C) and centered (R) pattern correlations to assess the spatial similarity with and without accounting for the magnitude of the patterns respectively. Given two spatial patterns, and , of dimension n, the uncentered pattern-correlation statistic (C) is given by:
| [5] |
and the centered pattern-correlation statistic (R) by:
| [6] |
where the hat denotes the spatial average over a pattern, the dot signifies a dot product, and , with defined equivalently.
The centered pattern correlation (R) ranges between −1 and 1, with much the same interpretation as a Pearson correlation coefficient; its value represents only the spatial similarity between the two patterns. The uncentered pattern correlation (C) is unbounded, and its value represents both the spatial similarity of to and the magnitude of as a proportion of that of .
These statistics are calculated between the responses identified from the reanalyses and the CMIP-6 ensemble under greenhouse forcing. To assess the significance of these correlations with respect to changes that could occur due to natural internal climate variability, we use CMIP-6 control runs under constant preindustrial greenhouse forcing. A total of 500 y of postspin-up control runs are available for each model, other than Centre National de Recherches Météorologiques Earth System Model 2-1 (CNRM-ESM2-1), for which 300 y are available. Daily temperature variability is calculated, and the data are interpolated to the reanalysis grid, as described above. The same detection method as applied to the reanalysis data (LFCA, with the same number of EOFs retained, ) is applied to calculate interdecadal differences between pairs of nonoverlapping decades. Decadal pairs are separated by 55 y to match the temporal period of the NOAA 20th Century Reanalysis, over which the observed changes in daily temperature variability are detected. Pooling these differences across models yields 420 interdecadal changes in daily temperature variability. Correlations between these changes and the expected forced response of the CMIP-6 ensemble under greenhouse forcing are calculated to provide a distribution of possible correlations, which could occur solely due to natural internal climate variability.
This approach differs from optimal fingerprinting, a commonly used detection-attribution framework, in two important ways. First, LFCA uses spatiotemporal covariance information to optimally separate low-frequency signals from internal climate variability. As such, these estimations of low-frequency changes are less obscured by internal variability than those based on linear trends and spatial or temporal averages (39, 40), which are commonly used in detection-attribution frameworks. Second, low-frequency patterns of change are here detected from observations and simulations separately before their similarity is assessed. This avoids assumptions regarding the accuracy with which climate models simulate the true response to greenhouse forcing, assumptions that are used to help detect a response in observations when projecting an optimal fingerprint, obtained from simulations, into the observational data.
Scaling between Variability Changes and Warming
Continental, area-weighted averages of changes in mean temperature and daily temperature variability are calculated from the interdecadal patterns of change identified with LFCA from the reanalysis and CMIP-6 data. In Fig. 4, the interdecadal changes are calculated between the first and final decades (1950–1960 to 2090–2100). In SI Appendix, Fig. S8, these changes are calculated between pairs of nonoverlapping decades separated by 25 y, yielding 12 changes per model per forcing scenario to assess the scaling within individual climate models. Least-squares, linear regression models are used to assess the covariance of the simulated per-decadal warming and variability changes across CMIP-6 models and forcing scenarios.
Supplementary Material
Acknowledgments
This work was supported by the Volkswagen Foundation. We thank Stefan Lange and the ISIMIP team for their work preparing the bias-corrected climate model data and the numerous teams of climate modelers, without whose efforts this study would not have been possible.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission. A.B. is a guest editor invited by the Editorial Board.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2103294118/-/DCSupplemental.
Data Availability
Previously published data were used for this work (CMIP-6; https://pcmdi.llnl.gov/CMIP6/, NOAA 20th Century Reanalysis; https://psl.noaa.gov/data/20thC_Rean/, and ERA5; https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era5/).
References
- 1.Intergovernmental Panel on Climate Change , Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (Cambridge University Press, Cambridge, UK, 2013). [Google Scholar]
- 2.Katz R. W., Brown B. G., Extreme events in a changing climate: Variability is more important than averages. Clim. Change 21, 289–302 (1992). [Google Scholar]
- 3.Rahmstorf S., Coumou D., Increase of extreme events in a warming world. Proc. Natl. Acad. Sci. U.S.A. 108, 17905–17909 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Vasseur D. A., et al., Increased temperature variation poses a greater risk to species than climate warming. Proc. Royal Soc. B. 281, 20132612 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Seddon A. W. R., Macias-Fauria M., Long P. R., Benz D., Willis K. J., Sensitivity of global terrestrial ecosystems to climate variability. Nature 531, 229–232 (2016). [DOI] [PubMed] [Google Scholar]
- 6.Ropelewski C., Halpert M. S., Global and regional scale precipitation patterns associated with the El Niño/Southern Oscillation. Mon. Weather Rev. 115, 1606–1626 (1987). [Google Scholar]
- 7.McPhaden M. J., Zebiak S. E., Glantz M. H., ENSO as an integrating concept in earth science. Science 314, 1740–1745 (2006). [DOI] [PubMed] [Google Scholar]
- 8.Cai W., et al., ENSO and greenhouse warming. Nat. Clim. Chang. 5, 849–859 (2015). [Google Scholar]
- 9.Cai W., et al., Increasing frequency of extreme El Niño events due to greenhouse warming. Nat. Clim. Chang. 4, 111–116 (2014). [Google Scholar]
- 10.Cai W., et al., Increased frequency of extreme Indian Ocean Dipole events due to greenhouse warming. Nature 510, 254–258 (2014). [DOI] [PubMed] [Google Scholar]
- 11.Cai W., et al., Increased frequency of extreme La Niña events under greenhouse warming. Nat. Clim. Chang.e 5, 132–137 (2015). [Google Scholar]
- 12.Grothe P. R., et al., Enhanced El Niño–Southern Oscillation variability in recent decades. Geophys. Res. Lett. 47, e2019GL083906 (2020). [Google Scholar]
- 13.Schär C., et al., The role of increasing temperature variability in European summer heatwaves. Nature 427, 332–336 (2004). [DOI] [PubMed] [Google Scholar]
- 14.Hansen J., Sato M., Ruedy R., Perception of climate change. Proc. Natl. Acad. Sci. U.S.A. 109, E2415–E2423 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rhines A., Huybers P., Frequent summer temperature extremes reflect changes in the mean, not the variance. Proc. Natl. Acad. Sci. U.S.A 110, E546–E546 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hansen J., Sato M., Ruedy R., Reply to Rhines and Huybers: Changes in the frequency of extreme summer heat. Proc. Natl. Acad. Sci. U.S.A. 110, E547–E548 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Huntingford C., Jones P. D., Livina V. N., Lenton T. M., Cox P. M., No increase in global temperature variability despite changing regional patterns. Nature 500, 327–330 (2013). [DOI] [PubMed] [Google Scholar]
- 18.Lenderink G., van Ulden A., van den Hurk B., van Meijgaard E., Summertime inter-annual temperature variability in an ensemble of regional model simulations: Analysis of the surface energy budget. Clim. Chang. 81, 233–247 (2007). [Google Scholar]
- 19.Fischer E. M., Schär C., Future changes in daily summer temperature variability: Driving processes and role for temperature extremes. Clim. Dyn. 33, 917 (2008). [Google Scholar]
- 20.Bathiany S., Dakos V., Scheffer M., Lenton T. M., Climate models predict increasing temperature variability in poor countries. Sci. Adv. 4, eaar5809 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chan D., et al., Summertime temperature variability increases with local warming in midlatitude regions. Geophys. Res. Lett. 47, e2020GL087624 (2020). [Google Scholar]
- 22.Lenton T. M., Dakos V., Bathiany S., Scheffer M., Observed trends in the magnitude and persistence of monthly temperature variability. Sci. Rep. 7, 5940 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Shi L., Kloog I., Zanobetti A., Liu P., Schwartz J. D., Impacts of temperature and its variability on mortality in New England. Nat. Clim. Chang. 5, 988–991 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zanobetti A., O’Neill M. S., Gronlund C. J., Schwartz J. D., Summer temperature variability and long-term survival among elderly people with chronic disease. Proc. Natl. Acad. Sci. U.S.A. 109, 6608–6613 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Yuming, et al., Temperature variability and mortality: A multi-country study. Environ. Health Perspect. 124 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yang J., et al., Vulnerability to the impact of temperature variability on mortality in 31 major Chinese cities. Environ. Pollut. 239, 631–637 (2018). [DOI] [PubMed] [Google Scholar]
- 27.Xue T., Zhu T., Zheng Y., Zhang Q., Declines in mental health associated with air pollution and temperature variability in China. Nat. Commun. 10, 2165 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wheeler T. R., Craufurd P. Q., Ellis R. H., Porter J. R., Prasad P. V., Temperature variability and the yield of annual crops. Agric. Ecosyst. Environ. 82, 159–167 (2000). [Google Scholar]
- 29.Rowhani P., Lobell D. B., Linderman M., Ramankutty N., Climate variability and crop production in Tanzania. Agric. For. Meteorol. 151, 449–460 (2011). [Google Scholar]
- 30.Ceglar A., Toreti A., Lecerf R., der Velde M. V., Dentener F.. Impact of meteorological drivers on regional inter-annual crop yield variability in France. Agric. For. Meteorol., 216, 58–67 (2016). [Google Scholar]
- 31.Kotz M., Wenz L., Stechemesser A., Kalkuhl M., Levermann A., Day-to-day temperature variability reduces economic growth. Nat. Clim. Chang. 11, 319–325 (2021). [Google Scholar]
- 32.Karl T. R., Knight R. W., Plummer N., Trends in high-frequency climate variability in the twentieth century. Nature 377, 217–220 (1995). [Google Scholar]
- 33.Michaels P. J., Balling R. C. Jr, Vose R. S., Knappenberger P. C., Analysis of trends in the variability of daily and monthly historical temperature measurements. Clim. Res. 10, 27–33 (1998). [Google Scholar]
- 34.Screen J. A., Arctic amplification decreases temperature variance in northern mid- to high-latitudes. Nat. Clim. Chang. 4, 577–582 (2014). [Google Scholar]
- 35.Schneider T., Bischoff T., Plstrokotka H.. Physics of changes in synoptic midlatitude temperature variability. J. Clim. 28, 2312–2331 (2015). [Google Scholar]
- 36.Kitoh A., Mukano T., Changes in daily and monthly surface air temperature variability by multi-model global warming experiments. J. Meteorol. Soc. Jpn. 87, 513–524 (2009). [Google Scholar]
- 37.Fischer E. M., Rajczak J., Schär C., Changes in European summer temperature variability revisited. Geophys. Res. Lett. 39, L19702 (2012). [Google Scholar]
- 38.Ylhäisi J. S., Räisänen J., Twenty-first century changes in daily temperature variability in CMIP3 climate models. Int. J. Climatol. 34, 1414–1428 (2014). [Google Scholar]
- 39.Wills R. C., Schneider T., Wallace J. M., Battisti D. S., Hartmann D. L., Disentangling global warming, multidecadal variability, and El Niño in Pacific temperatures. Geophys. Res. Lett. 45, 2487–2496 (2018). [Google Scholar]
- 40.Wills R. C., Battisti D. S., Armour K. C., Schneider T., Clara D., Pattern recognition methods to separate forced responses from internal variability in climate model ensembles and observations. J. Clim. 33, 8693–8719 (2020). [Google Scholar]
- 41.Eyring V., et al., Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 9, 1937–1958 (2016). [Google Scholar]
- 42.Lange S., Trend-preserving bias adjustment and statistical downscaling with ISIMIP3BASD (v1.0). Geosci. Model Dev. 12, 3055–3070 (2019). [Google Scholar]
- 43.Santer B. D., et al., Towards the detection and attribution of an anthropogenic effect on climate. Clim. Dyn. 12, 77–100 (1995). [Google Scholar]
- 44.Stott P. A., Allen M. R., Jones G. S., Estimating signal amplitudes in optimal fingerprinting. Part II: Application to general circulation models. Clim. Dyn. 21, 493–500 (2003). [Google Scholar]
- 45.McKinnon K. A., Poppick A., Dunn-Sigouin E., Deser C., An “observational large ensemble” to compare observed and modeled temperature trend uncertainty due to internal variability. J. Clim. 30, 7585–7598 (2017). [Google Scholar]
- 46.Thompson D. W. J., Barnes E. A., Deser C., Foust W. E., Phillips A. S., Quantifying the role of internal climate variability in future climate trends. J. Clim. 28, 6443–6456 (2015). [Google Scholar]
- 47.Slivinski L. C., et al., Towards a more reliable historical reanalysis: Improvements for version 3 of the Twentieth Century Reanalysis system. Q. J. R. Meteorol. Soc. 145, 2876–2908 (2019). [Google Scholar]
- 48.Riahi K., et al., The Shared Socioeconomic Pathways and their energy, land use, and greenhouse gas emissions implications: An overview. Glob. Environ. Chang. 42, 153–168 (2017). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Previously published data were used for this work (CMIP-6; https://pcmdi.llnl.gov/CMIP6/, NOAA 20th Century Reanalysis; https://psl.noaa.gov/data/20thC_Rean/, and ERA5; https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era5/).