Microscopic origins of the crystallographically preferred growth in evaporation-induced colloidal crystals

Significance

Self-assembly is one of the central themes in biologically controlled synthesis, and it also plays a pivotal role in fabricating a variety of advanced engineering materials. In particular, evaporation-induced self-assembly of colloidal particles enables versatile fabrication of highly ordered two- or three-dimensional nanostructures for optical, sensing, catalytic, and other applications. While it is well known that this process results in the formation of the face-centered cubic (fcc) lattice with the close-packed {111} plane parallel to the substrate, the crystallographic texture development of colloidal crystals is less understood. In this study, we show that the preferred <110> growth in the fcc colloidal crystals synthesized through evaporation-induced assembly is achieved through a gradual crystallographic rotation facilitated by mechanical stress-induced geometrically necessary dislocations.

Abstract

Unlike crystalline atomic and ionic solids, texture development due to crystallographically preferred growth in colloidal crystals is less studied. Here we investigate the underlying mechanisms of the texture evolution in an evaporation-induced colloidal assembly process through experiments, modeling, and theoretical analysis. In this widely used approach to obtain large-area colloidal crystals, the colloidal particles are driven to the meniscus via the evaporation of a solvent or matrix precursor solution where they close-pack to form a face-centered cubic colloidal assembly. Via two-dimensional large-area crystallographic mapping, we show that the initial crystal orientation is dominated by the interaction of particles with the meniscus, resulting in the expected coalignment of the close-packed direction with the local meniscus geometry. By combining with crystal structure analysis at a single-particle level, we further reveal that, at the later stage of self-assembly, however, the colloidal crystal undergoes a gradual rotation facilitated by geometrically necessary dislocations (GNDs) and achieves a large-area uniform crystallographic orientation with the close-packed direction perpendicular to the meniscus and parallel to the growth direction. Classical slip analysis, finite element-based mechanical simulation, computational colloidal assembly modeling, and continuum theory unequivocally show that these GNDs result from the tensile stress field along the meniscus direction due to the constrained shrinkage of the colloidal crystal during drying. The generation of GNDs with specific slip systems within individual grains leads to crystallographic rotation to accommodate the mechanical stress. The mechanistic understanding reported here can be utilized to control crystallographic features of colloidal assemblies, and may provide further insights into crystallographically preferred growth in synthetic, biological, and geological crystals.

As an analogy to atomic crystals, colloidal crystals are highly ordered structures formed by colloidal particles with sizes ranging from 100 nm to several micrometers (1–6). In addition to engineering applications such as photonics, sensing, and catalysis (4, 5, 7, 8), colloidal crystals have also been used as model systems to study some fundamental processes in statistical mechanics and mechanical behavior of crystalline solids (9–14). Depending on the nature of interparticle interactions, many equilibrium and nonequilibrium colloidal self-assembly processes have been explored and developed (1, 4). Among them, the evaporation-induced colloidal self-assembly presents a number of advantages, such as large-size fabrication, versatility, and cost and time efficiency (3–5, 15–18). In a typical synthesis where a substrate is immersed vertically or at an angle into a colloidal suspension, the colloidal particles are driven to the meniscus by the evaporation-induced fluid flow and subsequently self-assemble to form a colloidal crystal with the face-centered cubic (fcc) lattice structure and the close-packed {111} plane parallel to the substrate (2, 3, 19–23) (see Fig. 1A for a schematic diagram of the synthetic setup).

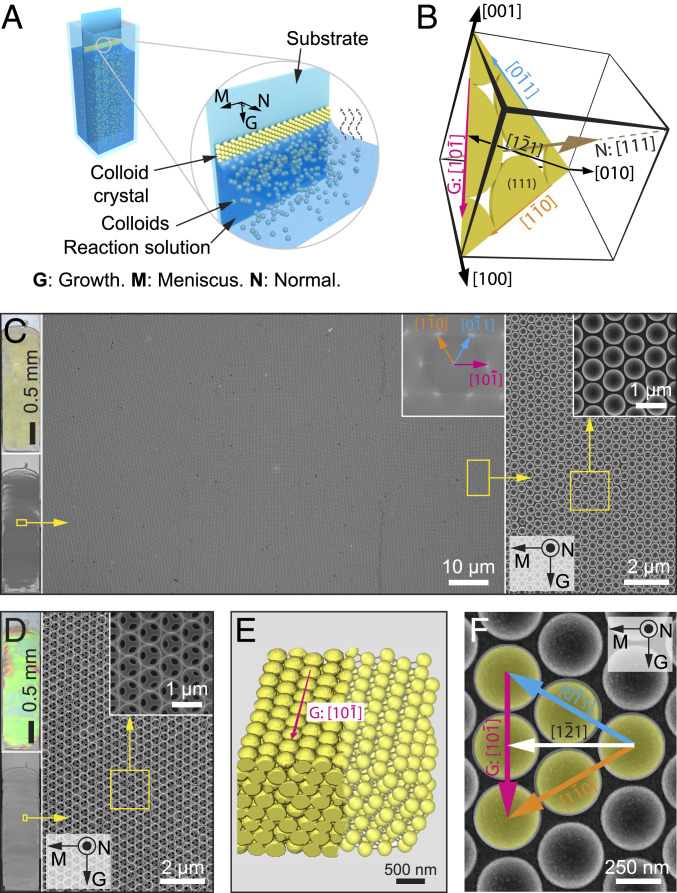
Fig. 1.

Evaporation-induced coassembly of colloidal crystals. (A) Schematic diagram of the evaporation-induced colloidal coassembly process. “G”, “M”, and “N” refer to “growth,” “meniscus,” and “normal” directions, respectively. The reaction solution contains silica matrix precursor (tetraethyl orthosilicate, TEOS) in addition to colloids. (B) Schematic diagram of the crystallographic system and orientations used in this work. (C and D) Optical image (Top Left) and scanning electron micrograph (SEM) (Bottom Left) of a typical large-area colloidal crystal film before (C) and after (D) calcination. (Right) SEM images of select areas (yellow rectangles) at different magnifications. Corresponding fast-Fourier transform (see Inset in Middle in C) shows the single-crystalline nature of the assembled structure. (E) The 3D reconstruction of the colloidal crystal (left) based on FIB tomography data and (right) after particle detection. (F) Top-view SEM image of the colloidal crystal with crystallographic orientations indicated.

While previous research has focused on utilizing the assembled colloidal structures for different applications (4, 5, 7, 8), considerably less effort is directed to understand the self-assembly mechanism itself in this process (17, 24). In particular, despite using the term “colloidal crystals” to highlight the microstructures’ long-range order, an analogy to atomic crystals, little is known regarding the crystallographic evolution of colloidal crystals in relation to the self-assembly process (3, 22, 25). The underlying mechanisms for the puzzling—yet commonly observed—phenomenon of the preferred growth along the close-packed <110> direction in evaporation-induced colloidal crystals are currently not understood (3, 25–29). The <110> growth direction has been observed in a number of processes with a variety of particle chemistries, evaporation rates, and matrix materials (3, 25–28, 30), hinting at a universal underlying mechanism. This behavior is particularly intriguing as the colloidal particles are expected to close-pack parallel to the meniscus, which should lead to the growth along the <112> direction and perpendicular to the <110> direction (16, 26, 31)^*.

Preferred growth along specific crystallographic orientations, also known as texture development, is commonly observed in crystalline atomic solids in synthetic systems, biominerals, and geological crystals. While current knowledge recognizes mechanisms such as the oriented nucleation that defines the future crystallographic orientation of the growing crystals and competitive growth in atomic crystals (32–34), the underlying principles for texture development in colloidal crystals remain elusive. Previous hypotheses based on orientation-dependent growth speed and solvent flow resistance are inadequate to provide a universal explanation for different evaporation-induced colloidal self-assembly processes (3, 25–29). A better understanding of the crystallographically preferred growth in colloidal self-assembly processes may shed new light on the crystal growth in atomic, ionic, and molecular systems (35–37). Moreover, mechanistic understanding of the self-assembly processes will allow more precise control of the lattice types, crystallography, and defects to improve the performance and functionality of colloidal assembly structures (38–40).

Results and Discussion

Evaporation-Induced Colloidal Self-assembly.

To study the crystallographic characteristics associated with the assembly process, we first utilized an evaporation-induced colloidal coassembly route as a model system (3, 15). Fluid flow drives the colloids to the meniscus, forming a colloidal crystal on the substrate as the solution slowly evaporates in the vertical direction (Fig. 1A). In the case of coassembly, the reaction solution contains, in addition to colloidal particles, the so-called matrix precursor, which can react and fill the space of the colloidal crystal. For example, in a typical coassembly process employed in this work, polystyrene (PS) particles (diameter 0.38 ± 0.01 μm; SI Appendix, Fig. S1) were coassembled with silica through the condensation of the silicate sol−gel precursor, tetraethyl orthosilicate (TEOS), during the assembly process. Fig. 1B presents a coordinate system used to describe the crystallography of the assembled particles. In this coordinate system, 1) the close-packed (111) plane is parallel to the substrate, and hence the [111] direction is parallel to the substrate normal N; and 2) the growth direction G is parallel to the close-packed direction $\left[10\overline{1}\right]$, which belongs to the <110> family, and the horizontal meniscus M is parallel to the $\left[1\overline{2}1\right]$ direction, which belongs to the <112> family.* As will be discussed extensively in later sections, this self-assembly process first nucleates a polycrystalline colloidal monolayer along the horizontal meniscus direction M with various crystal orientations of grains in which the close-packed direction is often parallel to the local meniscus orientation; then the number of layers increases depending on the concentration of colloidal particles; and, finally, the grains in multilayered colloidal crystal gradually rotate within several hundreds of micrometers until the close-packed direction coaligns with the growth direction G, after which the assembled cm-sized film remains uniformly <110>-oriented.

Fig. 1C shows a representative large area of a crack-free and uniformly crystallographically oriented colloidal crystal grown using evaporation-induced coassembly approach. Moreover, this method allows for facile formation of silica inverse opals after removing PS particles via either chemical etching or calcination (Fig. 1D). The inverse opals display strong blue-shifted photonic coloration due to the change from periodic polymer spheres to air spheres within the silica matrix (Fig. 1D). The resultant colloidal crystal can be clearly resolved at the single-particle level by three-dimensional (3D) reconstruction based on focused ion beam/scanning electron microscopy (FIB/SEM) tomography of a representative area, which confirmed the fcc lattice structure (Fig. 1E; see SI Appendix, Fig. S2). Crystallographic orientations in the colloidal crystal growing along the close-packed $\left[10\overline{1}\right]$ direction (hereafter denoted as <110> preferred growth direction) are indicated in Fig. 1F.

Meniscus-Induced <112> Growth at the Initial Assembly Stage.

To understand how the preferred growth along the <110> direction is achieved, we first performed structural analysis in the initiation region, where the colloidal crystal nucleates along the horizontal meniscus direction (Fig. 2). By combining large-area (1.6 mm × 0.2 mm) high-resolution imaging and quantitative image analysis based on 2D synchrosqueezed transform and variational regularization (41), we determined the crystal lattice types, crystallographic orientations, defects, and deformations in the top-most layer of the colloidal crystal (see Materials and Methods). As shown in a representative initiation region (Fig. 2 A, i; total length, 1.6 mm), the initiation line is approximately horizontal (parallel to the M direction), despite some local distortions. The number of layers in the colloidal crystal progressively increases from one to six within a vertical distance of ∼50 μm (shown by numbers in Fig. 2 A, ii). The calculated lattice types indicate that the assembly started with hexagonal packing and transitioned to square packing when an additional layer was added (Fig. 2 A, ii and B). This pattern can also be seen from the SEM images of the original as-grown and subsequently calcinated structure (Fig. 2F). This phenomenon has been observed previously in direct opal assemblies, possibly due to the confinement of the inclined meniscus during the assembly (20, 42, 43). As shown by the vertical thickness profile along the growth direction (Fig. 2D), a gradual increase in thickness is observed in the transition zones, leading to an overall wedge angle of ∼1.1° (Fig. 2E). As the number of layers becomes five or greater, the transition can proceed without the presence of square packing, although local packing imperfections may occur (Fig. 2 B and G).

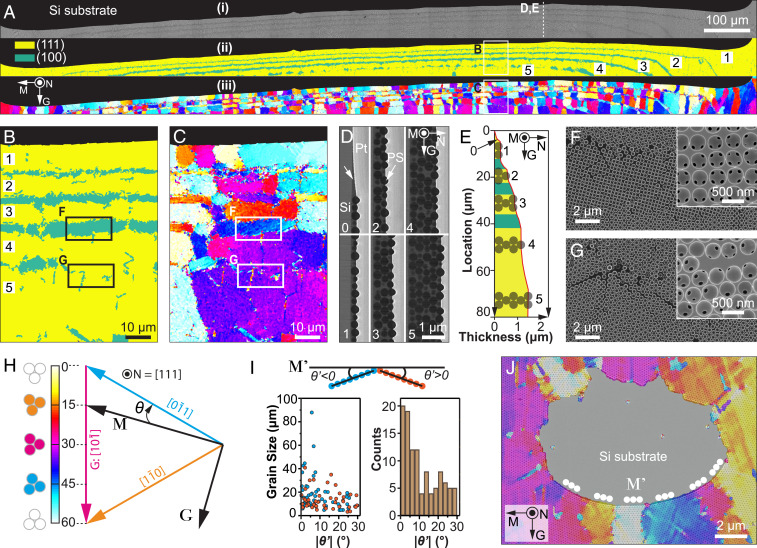
Fig. 2.

Morphological and crystallographic analysis of the initiation region. (A) (i) Original SEM image, (ii) corresponding lattice type map, and (iii) orientation map of a typical initiation region. The number of layers in the colloidal crystal gradually increases from one to five, as indicated in ii. (B and C) High-magnification maps of (B) lattice type and (C) orientation for a representative region indicated in A. (D) SEM images of FIB-milled cross-sections, demonstrating regions with a different number of layers: 0, submonolayer; 1, one layer; 2, two layers; etc. (E) The thickness profile of the colloidal crystal at the initiation region. (F) Transition zone from three-layer to four-layer region, demonstrating that the lattice type changes from a hexagonal to square to hexagonal packing. (G) Transition zone from four-layer to five-layer region, demonstrating that the crystal orientation is maintained. Insets in F and G show the corresponding structure after calcination. The regions of F and G were taken from B and C as indicated. (H) The color scheme used in orientation maps. The crystal angle, θ, is defined as the angle between the top left−bottom right−oriented [110] direction (i.e., $\left[0\overline{1}1\right]$ direction) and the global meniscus direction (M). (I) (Top) The local crystal misorientation angle, θ′, is defined as the angle between the local meniscus orientation (M′) and the nearest close-packed orientation, and the positive and negative signs are assigned according to the schematic diagram. (Bottom) The distribution of grain sizes and local crystal misorientation (θ′) based on statistical analysis of the orientation map shown in A. (J) An overlay of an original SEM image and orientation map shows an extreme example of a defect region with highly curved meniscus orientations, which are always aligned with the close-packed orientations locally (i.e., θ′ ≈ 0°). All orientation maps are based on the same color scheme, shown in H. All images except D and E were in the same sample orientation as in A.

In addition to lattice type, we mapped the distribution of the crystallographic orientations in the initiation region (Fig. 2 A, iii and C). As shown in Fig. 2H, the crystal orientation, θ, is defined as the angle between the global meniscus orientation (M) and the first close-packed direction (i.e., $\left[0\overline{1}1\right]$) in the clockwise direction. Due to the sixfold symmetry of the {111} plane, θ ranges from 0° to 60°, with θ = 30° corresponding to the case when $\left[10\overline{1}\right]$ is parallel to G. We also define a local mismatch angle, θ′, as the angle between the local meniscus orientation, M′, and the closest <110> direction (Fig. 2I; see SI Appendix, Fig. S3 for more examples). θ′ provides an intrinsic relationship between local meniscus and crystal orientations, since severe meniscus distortions can occur at substrate edges or defects. Fig. 2I summarizes the distribution of grain sizes and the magnitudes of θ′ for grains in the first layer mapped in Fig. 2A (average grain size 15.6 ± 12.1 μm, n = 106). The result clearly indicates that when the colloidal assembly first initiates, the close-packed orientation tends to align with the local meniscus (size-weighted average 9.2 ± 8.2°), leading to the $\left[1\overline{2}1\right]$ growth (<112> family) initially, as would be expected from the oriented nucleation induced by the particle pinning at the local meniscus line. In addition, grains with initial growth along the <112> orientation are usually larger in size (Fig. 2I). Fig. 2J shows an extreme example, where the meniscus is severely distorted locally; however, the close-packed direction is always parallel to the local meniscus orientation, leading to different θ values but similar θ′ values.

Crystallographic Rotation to the <110> Direction via Dislocations.

The analysis above indicates that the <110> direction is, indeed, initially parallel to the meniscus direction, contradicting the general observation that the <110> direction aligns with the growth direction in the assembled bulk crystal. To further explore this intriguing contradiction, we next conducted similar analysis along the growth direction to study the crystallographic evolution (Fig. 3). As shown in Fig. 3A, after reaching six or seven layers, the number of layers in the colloidal crystal becomes relatively constant, at which point large gradients are often visible in the crystal orientation within a single “grain” (Fig. 3 A, ii; see SI Appendix, Fig. S4 for a large-area map). The individual grains, regardless of their initial crystal orientations, gradually rotate toward the <110> direction (Fig. 3A, ii). The gradients in crystal rotation are not uniform, approaching the highest value of 0.3 °/μm for θ close to 15° and 45° (Fig. 3A; see SI Appendix, Fig. S5).

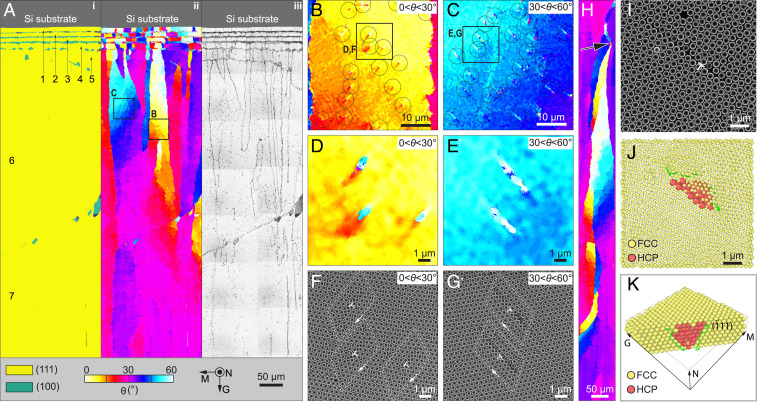
Fig. 3.

Evolution of crystallographic orientation during growth. (A) Large-area maps of (i) lattice type, (ii) corresponding orientation, and (iii) defects, demonstrating gradual rotation of crystallographic orientation along the growth direction. The number of layers is indicated, and a maximum of seven layers is observed at the lower portion of this region. (B and C) Enlarged orientation maps with local crystal orientation in the range of (B) 0° < θ < 30° and (C) 30° < θ < 60°, which are acquired in the regions as indicated in A. The circles highlight individual defects. (D and E) High-magnification of orientation map and (F and G) corresponding original SEM images showing the individual defects, which are acquired in the regions as indicated in B and C. In F and G, the dislocation cores are indicated by $\perp$ ; the white loops indicate Burgers circuits. (H) Orientation map acquired in a region where the preferred <110> growth has been achieved, showing a self-correction behavior. The crystallographic orientation rotates back to θ = 30° after a defect causes crystallographic misorientations (arrow). (I) Top-view SEM image of a region with a dislocation (indicated by $\perp$) selected for tomography analysis. (J) Top-view reconstruction of the same region. The red particles represent a stacking fault within the fcc lattice, which is represented with a smaller particle radius for ease of viewing. (K) Crystal reconstruction in a perspective view with front particles removed. All the orientation, phase, defect map, and SEM images are in the same orientation and color scheme as in A.

Close examination of the crystallographically rotating regions reveals the presence of localized coparallel defects with a spacing of ∼10 μm (Fig. 3 B and C). These defects align with the $\left[1\overline{1}0\right]$ and $\left[0\overline{1}1\right]$ directions for 0° < θ < 30° and 30° < θ < 60° regions, respectively. Notably, there occurs slight rotation toward θ = 30° after each defect (note yellow-to-orange transition and cyan-to-blue transition in Fig. 3 D and E, respectively). The original SEM images indicate that these defects exhibit classical dislocation structures similar to crystalline metals (Fig. 3 F and G and SI Appendix, Fig. S6). The Burgers circuits are illustrated by the white lines, exhibiting a closure failure around the dislocation core, which would otherwise close in a perfect lattice. The Burgers vectors b, which connect the starting and ending points of the Burgers circuit, are a/2$\left[1\overline{1}0\right]$ and a/2$\left[0\overline{1}1\right]$ for regions with 0° < θ < 30° and 30° < θ < 60°, respectively, where a is the lattice parameter of the fcc lattice. This rotation behavior is so powerful that, even when a local defect disrupts crystal continuity and generates a different crystal orientation, the crystal rotates back to the preferred growth orientation (3) (indicated by an arrow in Fig. 3H).

To further investigate the 3D structural characteristics of dislocations, FIB/SEM tomography was used to probe these crystal defects at the single-particle level. Fig. 3I shows a representative dislocation where the tomography data were acquired (θ = 45.2°), from which the positions of particles are determined (Fig. 3J). The subsurface defect structure can be visualized by representing particles in the normal fcc lattice with a smaller radius (Fig. 3J). Here the defect is detected by comparing the number of nearest opposing neighbor pairs, which changes from six in an fcc lattice to three in an hcp lattice. Therefore, the defect particles shown in red form a plane of stacking fault where the stacking order changes from ABCABC to ABCBCABC. By removing some fcc particles, we confirm that this stacking fault lies on the $\left(\overline{1}11\right)$ plane, and that its area gradually decreases in size from ∼10 to ∼3 particles from the top to bottom layers (Fig. 3K; also see SI Appendix, Fig. S7). The stacking fault is bounded by a pair of Shockley partial dislocations with Burgers vectors of a/6$\left[1\overline{1}2\right]$ and a/6$\left[\overline{1}\overline{2}1\right]$, which are also the most prominent dislocations observed in fcc metals (44). This analysis is consistent with the observation of the full edge dislocation from the top-view SEM image by the relationship $a/2\left[0\overline{1}1\right]=a/6\left[1\overline{1}2\right]+a/6\left[\overline{1}\overline{2}1\right]$, for the case of 30° < θ < 60°. FIB/SEM tomography measurements further confirm that the dislocations belong to the same slip system with similar size of stacking faults in regions where multiple dislocations are present within a short distance (SI Appendix, Fig. S8).

Origins of Dislocation Generation.

It is well known that evaporation-induced drying processes often produce a tensile stress field in the drying film parallel to substrates (45), which can be high enough to lead to the formation of cracks (for example, cracks in a drying muddy ground). In evaporation-induced colloidal crystals, the tensile stress primarily results from the mismatch between the shrinkage of the colloidal crystal film (including shrinkage of colloidal particles, capillary force-induced local readjustment, and shrinkage of the silica matrix for the case of coassembly here) and the constraint from the rigid substrate during the drying process (46–49). Quantification of the crack opening on a monolayer of PS particles after assembly and subsequent drying allow us to estimate the effective shrinkage as ca. 5% (SI Appendix, Fig. S9). We further note that, in the evaporation-induced assembly process, there exists a partially dried region at the assembly front [also known as the “gel” zone (48)], where the assembled particles can still undergo structural rearrangement before their positions are finally fixed in the fully dried stage (46–48) (Fig. 4A).

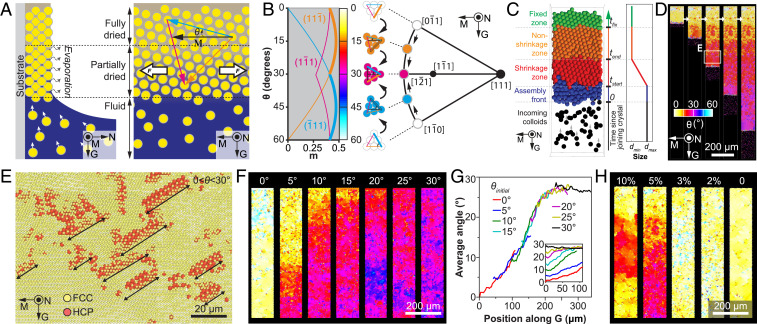
Fig. 4.

Mechanism of crystallographically preferred growth. (A) Schematic diagram of the evaporation and associated self-assembly process. A horizontal (i.e., along meniscus direction) tensile stress is generated during the drying process of the colloidal assemblies. (B) (Left) Determination of Schmid factor, m, as a function of colloidal crystal orientation, θ. Here only the three slip directions with the highest m values for the three close-packed planes ($\left(11\overline{1}\right)$, $\left(1\overline{1}1\right)$, and $\left(\overline{1}11\right)$) are displayed. (Right) A (111) stereographic projection showing the gradual crystal rotation toward the $\left[10\overline{1}\right]$ growth. (C–H) Results of the colloidal self-assembly modeling approach: (C) (Left) Schematic diagram of the evaporation-induced colloidal assembly modeling. (Right) The particle size profile used in the simulations; t_start and t_end specify the time range over which the particle size reduces from d_max to d_min; t_fix is the time when the particle becomes fixed. (D) A representative simulation result showing the gradual crystallographic rotation. (E) Detection of stacking faults due to the generation of dislocations at the growth front. The location of this volume is highlighted in D. (F) Effects of initial crystal orientation, θ_initial = 0°, 5°, 10°, 15°, 20°, 25°, and 30°. (G) Profile of average crystal angles along the growth direction, G. (H) Effects of particle shrinkage, s = 1 – d_min/d_max = 10%, 5%, 3%, 2%, and 0%.

In atomic crystals, dislocations can be generated by applying mechanical stresses beyond a critical level, which is one of the key mechanisms of plastic deformation for many materials (44). We, therefore, hypothesize that, similar to the stress-induced dislocations in atomic crystals, the drying-induced tensile stress field leads to the formation of dislocations in the partially dried colloidal crystal before the structure is fully dried and fixed. To validate our hypothesis, we determined the active slip system as a function of the crystal orientation, θ, under the tensile stress, by evaluating the Schmid factor (m) for the 12 equivalent slip systems in the fcc crystal following the classical analysis of single-crystal deformation via slips (SI Appendix, Fig. S10) (50). (Note here that the tensile stress is primarily along the M direction in the current directional drying setup, since the fluid at the bottom releases the stress in the vertical [growth] direction, unlike the equiaxial tensile field in uniformly drying films.) As summarized in Fig. 4B, the active slip systems are $\left[1\overline{1}0\right]\left(11\overline{1}\right)$ and $\left[0\overline{1}1\right]\left(\overline{1}11\right)$ for cases of 0° < θ < 30° and 30° < θ < 60°, respectively, consistent with experimental observations (Fig. 3 B–G).

Similar results have been obtained via finite element-based mechanical modeling at continuum level, indicating that the composite nature of the coassembled colloidal crystal does not affect the active slip systems (SI Appendix, Figs. S11–S14). The high density of dislocations observed in regions with θ close to 15° and 45° is simply due to their large m values, leading to greater resolved shear stresses for easier generation of dislocations. Moreover, the large width in the stacking fault area close to the crystal surface is also consistent with the fact that the drying-induced tensile stress is greater on the film surface than closer to the substrate (51). Since the (111) plane is always parallel to the substrate in the colloidal crystals formed by this self-assembly process, such preferred slip activation results in an in-plane rotation toward the <110> growth (Fig. 4B, Right). During this process, the slip direction gradually rotates toward the tensile axis, a well-known behavior in crystalline atomic materials (50, 52). When θ reaches 30°, m becomes the same for both $\left[1\overline{1}0\right]\left(11\overline{1}\right)$ and $\left[0\overline{1}1\right]\left(\overline{1}11\right)$ systems. At this point, any perturbations in the crystal orientation will result in rotation back, leading to stable <110> growth. It should be noted that the generation of dislocations is not induced by other defect types such as vacancies, which are uniformly distributed over the entire growth area (SI Appendix, Fig. S15). FIB/SEM tomography analysis also revealed that no local packing defects, such as large- or small-sized particles, interstitials, etc., are present close to dislocations. These observations further confirm that these dislocation defects are generated due to the mechanical stress with strong correlation of local crystallographic orientation during the assembly process.

Geometrically Necessary Dislocations: Continuum Analysis.

Crystallographic rotation has been observed in some atomic crystalline films obtained through direct electrodeposition (35) or thermal-induced phase transitions (36). Although this phenomenon has not been fully understood, the concept of geometrically necessary dislocations (GNDs) has been hypothesized as the possible mechanism (36), as an array of GNDs with the same Burgers vector can theoretically lead to a crystal orientation gradient within a grain (53, 54). However, the relationship between crystal rotation and the characteristics of GNDs was not well established in atomic crystals, mostly due to the fact that it requires structural analysis across the atomistic and grain level. The colloidal crystals formed through the evaporation-induced self-assembly process discussed here offer compelling experimental evidence that, indeed, the dislocations with the same Burgers vector within a grain, generated due to the drying-induced tensile stress, can result in a continuous crystallographic reorientation. Following the 2D model developed for atomic crystals (53), the GND density, ρ, can be estimated as ∼1.4 × 10¹⁰/m², by using the relationship ρ = θ/bd, where θ/d and b represent the rate of angular misorientation with position (0.3°/μm) and Burgers vector (0.38 μm for a full a/2 <110> dislocation), respectively. This corresponds to an inter-GND spacing of ∼9 μm (∼20 lattice parameters), agreeing with experimental observations (Fig. 3 B–G). A similar order of magnitude is estimated for GNDs in atomic crystals, despite a significant difference in the length scales of their lattice parameters (36), indicating that the effects of mechanical forces influence crystallization across more length scales than previously realized.

We can use the 1D model for the formation of misfit dislocations in strained epitaxial films (9, 55, 56) to estimate the critical thickness, h_c, at which the first dislocations form during the drying process. In this model, the colloidal crystal is treated as an isotropic, linear elastic continuum (Young’s modulus E, shear modulus µ, and Poisson ratio υ), and $h_c=\mu bln(R/r_c)/[4\pi E{\epsilon }_0\left(1-\upsilon \right)\cos \alpha ]$, where R and r_c are the outer and core radii of the strain field associated with the dislocation, ε₀ is the drying-induced tensile strain, and α is the angle between the Burgers vector and its projection onto the loading direction (see detailed analysis in SI Appendix). Here by taking ε₀ = 0.05, r_c = b/4 (9, 57, 58), υ = 1/3, and E/μ = 2(1+υ) (57), we find h_c = 1.24 µm, corresponding to 4.2 layers in the colloidal crystal. This prediction is consistent with our observations that the GND-induced crystallographic rotation usually occurs in regions with more than five layers whereas one- or two-layered colloidal crystals rarely exhibit any rotation.

Modeling of the Self-assembly Process.

We further developed a colloidal assembly modeling approach to investigate the effects of some important experimental parameters as well as the particle-level dislocation dynamics in this self-assembly process. Following our hypothesis of drying-induced tensile stress field governing the crystallographic rotation during assembly, this modeling approach considers a “shrinkage zone” after the particles are driven to the assembly front, in which they undergo self-assembly, rearrangement, and shrinkage (s = 1 – d_min/d_max) before finally fixing their positions (Fig. 4C; see SI Appendix, Figs. S16 and S17 and detailed descriptions of the modeling method). For simplification in this simulation scheme, we use the shrinkage of colloidal particles to represent the effective shrinkage of the colloidal crystal. By using experimental conditions (particle size = 0.38 µm, polydispersity = 2.8%, shrinkage s = 0.05, initial crystal orientation θ = 5°, and number of layers = 6), we successfully reproduced the gradual crystallographic rotation to the preferred <110> growth in the self-assembled colloidal crystals in silico, as shown in the series of snapshots at different stages of modeling (Fig. 4D and Movie S1). Remarkably, the length scale of the rotation region (200 μm to 300 µm along the G direction for θ rotating from ∼5° to 30°) is similar to experimental observations (Figs. 3A and 4G). Moreover, crystal structure analysis reveals that a perfect fcc crystal first forms in the assembly front, while dislocations are subsequently generated in the shrinkage zone. These dislocations exhibit the same slip system and similar spacing and sizes as observed in experiments (Fig. 4E).

We confirm that a consistent crystallographic rotation occurs regardless of the initial crystal orientation (Fig. 4F; see SI Appendix, Figs. S18 and S19 and Movie S2). In particular, the crystal angle profiles collapse onto a single master curve, which also reveals that the rotation gradient reaches the highest value of 0.3°/µm around 15°, matching the experimental observations (Fig. 4G; see SI Appendix, Fig. S5). Also note that, for the initial crystal orientation θ = 0°, it may take time for θ to fluctuate to a high enough value (∼5°) to induce the rotation, since, at θ = 0°, the system is symmetric with respect to the growth direction, which makes no preference for a particular slip system to operate (see the θ = 0° case in SI Appendix, Fig. S18). Moreover, by systematically varying the shrinkage of particles, we find that, when the shrinkage is smaller than 3%, no dislocations and hence no crystallographic rotation are observed in the current system, whereas a high shrinkage, for example, 10%, leads to occasional abrupt changes in crystal orientation (Fig. 4H; see SI Appendix, Figs. S20 and S21 and Movie S3). Lastly, previous work has shown that large polydispersity can suppress colloidal crystallization completely (59, 60). Here we observe the similar loss of close packing behavior when the polydispersity is greater than 10%, whereas consistent crystallographic rotation behavior can be achieved using particles with polydispersity smaller than 5%, including monosized particles (SI Appendix, Figs. S22 and S23 and Movie S4).

Conclusions and Outlook

We conclude that, by using a combination of comprehensive experimental, theoretical, and modeling analyses, we uncover the fundamental mechanism underlying the unique feature of the colloidal assemblies synthesized by an evaporation-induced approach to grow into large-area fcc crystals oriented in the <110> direction. Our results unequivocally show that, while the initial nucleation creates a polycrystalline area with domains close-packed parallel to the meniscus line, there occurs a gradual intragrain crystallographic rotation due to the presence of geometrically necessary dislocations (GNDs), which are generated as a result of the drying-induced mechanical stress field. While the GND characteristics can be well described by the continuum theory for atomic crystals, our findings also indicate that, unlike atomic crystals, the two main mechanisms for texture development, namely, epitaxial nucleation and orientation-dependent growth, are not the primary mechanisms for the <110> growth in evaporation-induced colloidal crystals. Since mechanical stresses are often present in evaporating systems, we expect that the mechanical stress-induced dislocations and the corresponding rotation of the crystal grains revealed here are a universal principle for crystallographically preferred growth in evaporation-driven colloidal assemblies (3, 25–28, 30). Indeed, we observed similar crystallographic rotation behavior for direct PS and inorganic silica colloidal assemblies (without the matrix material) (SI Appendix, Figs. S24–S28). It is worth mentioning that, as the thickness of the colloidal crystal is too high (∼20 layers for coassembled colloidal crystals), another form of strain release mechanism, namely, cracking, will occur in addition to dislocations (3, 4, 61). By taking advantage of the preferred <110> growth and directional cracking, one can precisely control the crack pattern formation in evaporation-induced colloidal crystals (49).

As mechanical stresses can also arise during the thin film growth of atomic and ionic crystals due to mechanisms such as substrate/film misfit and phase transformation, the mechanical stress-induced preferred growth via GNDs may provide further insights in understanding the texture development in these systems, in addition to colloidal crystals. Moreover, we further note that mechanical stress is generally considered to be present when amorphous biomineral precursors transform to oriented crystalline forms, which may contribute to the crystallographically preferred growth in biological crystalline structures, following a similar mechanism discussed here (62).

Materials and Methods

Synthesis of PS Colloids.

PS colloidal particles with diameters of 0.38 ± 0.1 μm and 0.54 ± 0.16 μm were prepared following a surfactant-free emulsion polymerization process (63). A typical synthesis procedure is described as follows. Styrene (20 mL, Aldrich) was purified to remove any inhibitors by column chromatograph (neutral aluminum oxide, 90-230 mesh, Aldrich). A three-necked, 300-mL round-bottomed flask with 170 mL of dionized (DI) water was deoxygenated by bubbling nitrogen gas for 30 min and heated to 70 °C. In a separate beaker, 0.0870 g of potassium persulfate initiator (Sigma-Aldrich) was added to 10 mL of water. The 10 mL of initiator solution and 20 mL of styrene were added to the round-bottomed flask. The solution was stirred at 300 rpm for 36 h at 70 ± 2 °C. The resulting latex spheres were filtered through glass wool to remove any large agglomerates. PS particles of 134 ± 5 nm (PC02006) and 277 ± 14 nm (PC02009) were purchased from Bangs Laboratories, Inc.

Synthesis of Monodisperse Silica Colloids (∼200 nm).

Four hundred milliliters of 95% ethanol, 20 mL of tetraethyl orthosilicate (TEOS, 98%, Sigma-Aldrich), 40 mL of 28% NH₄OH, and 40 mL of DI water were added to a 1,000-mL round-bottomed flask. The solution was stirred at 250 rpm at room temperature for 24 h. The obtained SiO₂ beads were collected through centrifugation, washed with ethanol three times, and finally dispersed in ethanol.

Colloidal Crystal via Evaporation-Induced Assembly Synthesis.

The method of evaporation-induced coassembly of colloidal crystals was described in detail in previous works (3, 15). Here a brief summary of the procedure is given. First, monodisperse PS colloids were diluted with deionized water (Milli-Q system) to 0.1% solid content for subsequent coassembly. A fresh stock solution of prehydrolyzed TEOS (Sigma-Aldrich) was prepared, which consisted of 1:1:1.5 ratio by weight of TEOS (98%, Sigma-Aldrich), HCl (0.1 M, Sigma-Aldrich), and ethanol (100%, Koptec). The TEOS stock solution was stirred for 1 h at room temperature, and then 140 µL was added to 20 mL of the 0.1% solid content colloidal solution in a scintillation vial. The mixture was briefly sonicated. After silicon substrates (∼1 × 4 cm) were cleaned in piranha solution, rinsed with ethanol, and fully dried, they were vertically suspended in the scintillation vial containing the colloid/TEOS solution. The solvent content was allowed to evaporate slowly over a period of 1 d to 2 d in an oven with a temperature of 65 °C (Memmert UF110 Oven). This process led to the deposition of a compound PS colloid−silica matrix colloidal crystal thin film (5 to 20 layers) onto silicon substrates (Wafer World, Inc.). To obtain inverse opals, the as-fabricated compound colloidal crystal was calcified at a maximum temperature of 500 °C for 2 h with a heating and cooling rate of 2 °C/min (Thermo Scientific). For the synthesis of direct PS opals, the procedure remained the same, except the TEOS and HCl mixture was not added to the final solution. For the synthesis of direct silica opals, 45 µL of 10 vol% “stock” SiO₂ colloidal suspension and 2 mL of absolute ethanol were added to a glass vial. A Si substrate (∼1 × 4 cm) precleaned in piranha solution was vertically suspended in the vial. The solvent was evaporated slowly in a 40 °C oven on a pneumatic vibration-free table, to allow the deposition of a thin film onto the suspended substrate.

Electron Microscopy.

Colloidal crystal films were coated with Pt/Pd (∼5 nm) to minimize charging effects, prior to imaging with a Helios Nanolab 660 Dual Beam (FEI) at an acceleration voltage of 2 kV and a working distance of ∼4 mm. The images used for quantitative crystallographic analysis were acquired in immersion mode with secondary electron mode with a beam current of 0.05 nA to 0.1 nA and a dwell time of 10 μs to 30 μs. The imaging conditions were maintained constant for each dataset to ensure consistency in image quality. The magnification was calibrated with a standard SEM calibration sample. The SEM images of the colloidal particles were imported into Fiji (64) and subsequently converted into eight-bit images for further processing. Preprocessing included background flattening and a Gaussian blur step to smooth the intensity distribution within individual particles. The images were next binarized, and a further watershed treatment was performed to separate any connected particles. Individual particles were then identified and registered, from which the particle area, radius, and circularity were determined for statistical analysis. The bin widths in the histogram plots were determined following the method proposed by Scott (65), where the optimal bin width h_n is given by 3.49sn^−1/3. Here s is the SD, and n is the sample size.

FIB/SEM Tomography.

The cross-sectional imaging and tomography of the colloidal crystals were obtained by using FIB milling and subsequent SEM imaging on a Helios Nanolab 660 Dual Beam (FEI) instrument. A typical protocol of FIB tomography based on the method of Slice and View is described as follows. The sample was first raised to the working distance of ∼4 mm and tilted to 52°. The region of interest was then aligned to the eucentric point where the electron beam and the ion beam were focused. A platinum protective layer (∼10 × 10 × 1 µm) was first deposited in situ on top of the rectangular region of interest at an ion beam condition of 30 keV and 0.28 nA. Three trenches on the side and front of the rectangular region (like a U shape) were milled by FIB (30 kV, 2.8 nA). The cross-section to be analyzed with the FIB Slice and View method was further polished with a lower ion beam current (30 keV, 93 pA). The electron imaging condition was first evaluated before Slice and View was started. Typically, the imaging was carried out in the “immersion” mode at 2 keV, 0.1 nA to 0.2 nA, 1,535 × 1,024 or 2,058 × 1,768 pixels per frame, 10 μs to 60 μs per pixel dwell time, and 5- to 10-nm pixel size. The imaging was performed in backscattered electron imaging mode. The automatic FIB tomography package (Slice & View G2, FEI) was used to perform data collection. Typical experimental parameters included a milling current of 80 pA and slice spacing of 5 nm to 20 nm. The collected 3D stacks of tomography images were first aligned by using Fiji/ImageJ (NIH). Volumetric rendering of the tomography data were performed using Avizo 7.1.0 (VSG).

Defect Analysis Based on Tomography Data.

The preprocessing of the original slices was performed on Fiji/ImageJ, which includes alignment, binary segmentation, inversion, and erosion. The preprocessed images were saved as an image stack to serve as an input file for the following procedure to identify the positions of individual particles. The method for particle detection used here was originally developed by John Crocker and David Grier (66) implemented in Matlab. The calculated particle positions were exported as an input file for the defect analysis by using Ovito (Open Visualization Tool, https://www.ovito.org/). The integrated algorithm Dislocation Extraction Algorithm was used to identify lattice types, dislocations, and Burgers vectors.

Quantitative 2D Crystallographic Analysis.

A synchrosqueezed transform technique was used for quantitative 2D imaging analysis to obtain information of crystal lattice type, defects, grain orientation, and deformation field (41, 67–69). Compared to the more commonly used windowed Fourier analysis, the synchrosqueezed transform technique offers several advantages, in particular, high resolution, which is crucial for the current work. Briefly, the Bravais lattice of the crystal image at a position x is encoded as a corresponding distribution of energy bumps in the frequency domain associated to x (SI Appendix, Fig. S29 A and B). Crystal deformation moves atoms away from their reference positions, and this is equivalent to moving the energy bumps away from their reference positions. The resolution of the windowed Fourier analysis is not high enough to reflect this deformation. The synchrosqueezed transform provides sharpened energy peaks in the frequency domain (see SI Appendix, Fig. S29C for an example), making it more feasible to compute the variation of these peaks away from their reference positions. By tracking the locations and energy concentration of these peaks, efficient algorithms have been proposed for crystal image analysis at the individual particle or atom scale, available as a MATLAB package called SynCrystal (41) (https://github.com/SynCrystal). For example, the peak positions in the angle coordinate indicate the grain orientation (SI Appendix, Fig. S29C); inside a grain, the synchrosqueezed transform reveals only a few well-concentrated energy peaks depending on the crystal lattice (SI Appendix, Fig. S29C). On the grain boundary or isolated defects, the synchrosqueezed transform provides irregular energy peaks spreading in the whole frequency domain (SI Appendix, Fig. S29D). Such characteristics can be used to identify defects and grain boundaries.

Schmid Factor Analysis.

By using the coordinate system shown in SI Appendix, Fig. S10, the slip planes that can be potentially activated under tensile loading along the M direction include $\left(11\overline{1}\right)$, $\left(1\overline{1}1\right)$, and $\left(\overline{1}11\right)$. The individual operating slip systems are 1) $\left[1\overline{1}0\right]\left(11\overline{1}\right)$, 2) $\left[0\overline{1}\overline{1}\right]\left(11\overline{1}\right)$, 3) $\left[\overline{1}0\overline{1}\right]\left(11\overline{1}\right)$, 4) $\left[10\overline{1}\right]\left(1\overline{1}1\right)$, 5) $\left[\overline{1}\overline{1}0\right]\left(1\overline{1}1\right)$, 6) $\left[0\overline{1}\overline{1}\right]\left(1\overline{1}1\right)$, 7) $\left[0\overline{1}1\right]\left(\overline{1}11\right)$, 8) $\left[\overline{1}0\overline{1}\right]\left(\overline{1}11\right)$, and 9) $\left[\overline{1}\overline{1}0\right]\left(\overline{1}11\right)$. The three slip systems on the (111) plane are not considered, because the plane normal is perpendicular to the loading axis. For a colloidal crystal with a given value of θ, the corresponding global meniscus direction, and hence the loading direction, can be represented as [A, −1, 1 − A], where A $\in$ [0,1] represents the length of the segment shown in SI Appendix, Fig. S10. In addition, the crystal orientation θ is related to A by $\tan \theta =\sqrt{3}A/(2-A)$. The Schmid factor, m, can be calculated by $m=\cos \lambda \cos \varphi$, where λ is the angle between the loading and slip direction, and ϕ is the angle between the loading direction and the normal direction of the slip plane. In cubic crystals, the cosine of the angle between two directions is given by the dot product of unit vectors in those directions. Therefore, we can calculate the angles of λ and ϕ as a function of A, and hence θ, for each slip system.

Finite Element Analysis.

Finite element simulations are performed on a representative volume element (RVE) with 4 × 4 spherical particles in the G−M plane and three layers of particles in the N direction. The microscopic deformation of the colloidal crystal under evaporation-induced tension is simulated by applying macroscopic stretches in the G−M plane with periodic boundary conditions in the G and M directions. Specifically, the effect of stretch direction, θ (with respect to the $\left[0\overline{1}1\right]$ direction), on the crystal deformation is studied by rotating the deformation gradient tensor F′=R^TFR while keeping the RVE unchanged. Note that R is the rotation tensor fully defined by θ. In the finite element implementation (commercial finite element package ABAQUS), the macroscopic deformation gradient F is assigned as the displacement components of three virtual nodes. The evaporation-induced tension is modeled as stretch F₁₁ = λ. Then, the principle of virtual work is used to capture the macroscopic mechanical response of the RVE. An elastic material model with Young’s modulus of 2.9 GPa and Poisson’s ratio of 0.4 is used for the PS particles, since their deformations are relatively small. Hyperelastic Neo Hooke model with G/2 = 0.1667 MPa and K = 1 GPa is used to capture the highly incompressible behavior of the matrix materials, where G and K are the shear and bulk modulus, respectively. Mesh convergence is verified, and the results are simulated from a finite element model with 3,457,387 C3D4 elements. After obtaining the stress and strain fields from the simulation (SI Appendix, Figs. S12–S14), the stresses are further projected to four close-packed planes, highlighting the shear components (SI Appendix, Fig. S11).

Data Availability

All data are available in the main text and SI Appendix. The synchrosqueezed transform technique for quantitative 2D crystal lattice analysis is available as a MATLAB package called SynCrystal (41) (https://github.com/SynCrystal). The computational colloidal assembly code implemented as a MATLAB code is available upon request.