Significance
The efficient utilization of electrical energy is an increasingly important challenge, especially as renewable energy sources become cheaper and demand increases. Electrochemical reactors utilizing flow-through electrodes (FTEs) provide an attractive path toward the efficient utilization of electrical energy. Their commercial viability and ultimate adoption hinge on attaining high current densities to drive cost competitiveness. There are limited opportunities for engineering FTE materials, as these are often random, disordered media. Alternatively, three-dimensional (3D)–printed FTEs provide the opportunity to quickly explore the impact of engineered electrode architectures on device performance. We demonstrate that 3D-printed FTEs have the potential to exceed the performance of conventional materials by using the expanded design freedom to engineer the internal flow.
Keywords: rapid prototyping, flow-through electrodes, 3D printing, mass transfer coefficients, computational fluid dynamics
Abstract
Electrochemical reactors utilizing flow-through electrodes (FTEs) provide an attractive path toward the efficient utilization of electrical energy, but their commercial viability and ultimate adoption hinge on attaining high currents to drive productivity and cost competitiveness. Conventional FTEs composed of random, porous media provide limited opportunity for architectural control and engineering of microscale transport. Alternatively, the design freedom engendered by additively manufacturing FTEs yields additional opportunities to further drive performance via flow engineering. Through experiment and validated continuum computation we analyze the mass transfer in three-dimensional (3D)–printed porous FTEs with periodic lattice structures and show that, in contrast to conventional electrodes, the mesoscopic length scales in 3D-printed electrodes lead to an increase in the mass correlation exponent as inertial flow effects dominate. The inertially enhanced mass transport yields mass transfer coefficients that exceed previously reported 3D-printed FTEs by 10 to 100 times, bringing 3D-printed FTE performance on par with conventional materials.
Electricity generated from renewable energy sources is becoming cheaper and more abundant, and deploying these resources to reduce or replace carbon-intensive processes is a crucial component of global decarbonization strategies (1–3). Industrial chemical manufacturing and refining are major consumers of global energy, and electrification of the industry is emerging as an especially attractive pathway for further progress (3–5). Beyond merely supplanting the traditional energy sources powering the reactors and auxiliary equipment, electrification of the chemical reactions themselves can completely avoid processes that otherwise generate carbon dioxide (4). Electrochemical synthesis reactors can use renewable electricity to directly drive chemical manufacturing of raw materials (5–8). An especially elegant embodiment of this idea creates fuel directly from carbon dioxide, simultaneously storing energy while reducing carbon emissions (2, 9, 10). Additionally, integration of these reactors with existing grid distribution systems can address known issues with intermittency and excess capacity as electricity that would otherwise be curtailed is instead shunted to the manufacture of valuable feedstocks (11).
High current densities at industrially relevant scales are a key driver for cost competitiveness and adoption (5, 8). An ubiquitous strategy to attain high current densities, and hence greater productivity, is to employ porous flow-through electrodes (FTEs) as the core reactive components (6). Porous FTEs find application across liquid-type electrochemical reactors including redox flow batteries (12, 13), microfluidic fuel cells (14), water purification cells (15), and electroorganic synthesis reactors (6, 7). Commonly used electrodes for these cells are carbon-fiber–based felts, foams, and papers consisting of microfibers (5 to 10 m in diameter) consolidated into disordered coherent freestanding layers with various types of microstructure depending on the manufacturing process. Although some structures perform better than others, the optimal geometries are not known nor are obvious criteria known to further increase performance (12, 16, 17).
FTEs are engineered to include high active surface area, high conductivity, and high permeability to minimize charge transfer resistance, ohmic losses, and concentration overpotential, respectively (17). At high currents the latter becomes especially evident as the system becomes mass transport limited, and the limiting current is dictated by the overall mass transfer coefficient (18–20). The adverse relationship between permeability and surface area prevents the straightforward engineering of the microstructure. The high permeability needed to increase mass transfer rates necessarily leads to a decrease in the hydrodynamically accessible surface area (12). Combined experimental and computational modeling approaches for finding an optimal electrode geometry are challenging because of the disordered nature of the fiber structures (12). Thus, modern strategies to increase mass transport performance have instead focused on assembly-level architectures and sophisticated fluid distribution through engineered flow-field plates (21, 22).
An emerging and powerful alternative approach employs additively manufactured FTEs to relieve these bottlenecks by creating controlled, deterministic structures. This enables precise tuning of the local reactive and hydrodynamic environment to attain greater mass transfer while simultaneously providing the versatility for integration/elimination of other cell components (e.g., current collector, flow field, etc.). Few studies of three-dimensional (3D)–printed FTEs manufactured by 3D-printing methods have been reported (23–25). Further, these were operated in “flow-by” mode (26). The 3D-printed nickel FTEs with simple cubic lattice and periodic structures fabricated by indirect 3D-printing techniques with 3.5 mm unit cell sizes showed overall mass transport coefficients close to those of perforated plate electrodes but significantly lower than those of reticulated vitreous carbon (RVC) electrodes (25). The 3D-printed stainless steel electrodes postcoated with Ni with smaller hexagonal lattices and unit cell sizes of 1.7 mm attained mass transport coefficients 10 times higher than those of 3D-printed nickel FTEs and comparable to those observed in typical RVC electrodes (23). Nevertheless, these values are far inferior (approximately one to three orders of magnitude lower) to typical FTEs employing Ni foam and carbon felt (23). Although performance will improve with increasing printing resolution, further advances are necessary to completely exploit the design flexibility of 3D-printed FTEs.
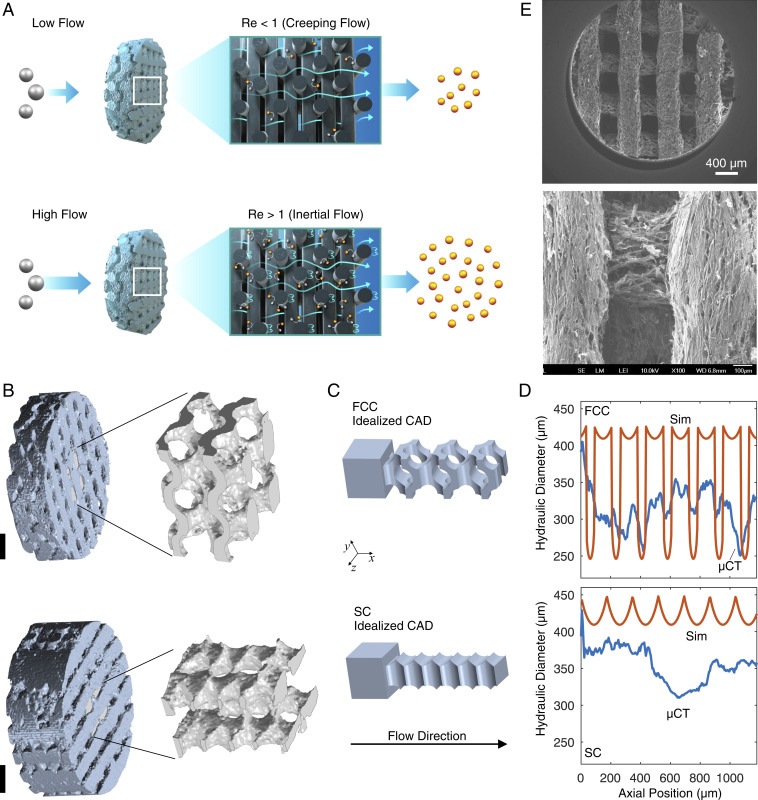
In this paper we focus on understanding the mass transport properties of ordered porous FTEs using both experimental studies and numerical simulations. We report the fabrication of 3D porous graphene FTEs. Direct ink writing is used to make ordered simple cubic (SC) and face-centered cubic (FCC) lattice structures with unit cells about two times smaller than previously reported printed FTEs (0.8 mm) (23). We demonstrate that our electrodes attain 10 to 100× larger mass transfer coefficients, rivaling some reported values of mass transfer coefficients in carbon felt electrodes and approaching the highest reported values. As summarized in Fig. 1A, our analysis reveals that this increased performance is due to operation in the inertial flow regime, thus activating secondary flows (e.g., wakes, recirculation, etc.) around electrode features that are otherwise absent in typical electrodes operated in the creeping flow regime (27). Heat transfer literature has recognized the potential to engineer inertial flow to enhance surface transport and overall heat transfer coefficients (28). However, although the impact of inertial and transitional flow on overall mass transfer coefficients has been previously reported, this effect has not been connected to the generation of secondary flow structures and there appears to have been no attempt to engineer the phenomena to improve performance (26).
Fig. 1.
Structure, morphology, and performance of 3D-printed flow-through electrodes. (A) Reactants are electrochemically converted at limiting current at higher rates when inertia induces secondary flows, as depicted by the recirculating streamlines. (B) Tomographic reconstruction of representative 3D-printed FCC (Top) and SC (Bottom) electrodes showing an expanded view of a section of the internal void region. (Scale bars, 1,000 m.) (C) Idealized CAD representation of the void region with an entrance region added to allow for simulation. (D) Hydraulic diameters of the tomographically reconstructed geometry (CT) and the idealized CAD geometry (Sim). (E) SEM of 3D-printed composite graphene aerogel/carbon filament electrodes.
We present an additional design dimension for engineering flow and mass transport in FTEs enabled by 3D printing. We generate reproducible structures with predictable mass transfer coefficients on par with commonly used electrode materials. We thus retain the advantages of 3D printing, including deterministic control of architectures, design flexibility to generate near arbitrary structures, and on-demand prototyping, without sacrificing performance. This work thus establishes 3D printing as a viable, versatile rapid-prototyping method for FTEs.
Results and Discussion
Characterization of the Electrode Structure.
We tomographically image the 3D-printed electrodes. In Fig. 1B we present the reconstructed surfaces for both the SC and FCC electrodes. For the SC structure, the void volume is composed of a large bundle of channels with corrugated surfaces all aligned in the axial direction ( direction, also the print and flow direction). Smaller channels (m) can occasionally connect the larger tubes, but the larger channels are otherwise hydrodynamically disconnected. If the printed filament were completely rigid, we would expect the final structure to more closely resemble a stack of fibers and that the interconnecting channels would be larger. However, the printed inks are soft and slump into one another, causing most of these channels to close. The tomography of the FCC structure reveals a markedly different geometry. The void paths are now interconnected throughout the electrode. In Fig. 1C the idealized representations, composed of constant diameter, overlapping cylinders for the SC and FCC electrode are shown. The computer-aided design (CAD) models of the void volumes serve as the input to our simulation (SI Appendix, Fig. S6). Tomography indicates that these structures are highly distorted FCC and SC lattices.
The hydraulic diameter ( = 4 void area/wetted perimeter) in planes perpendicular to the flow axis is presented in Fig. 1D and reveals the characteristic flow path length scale of the electrodes is 250 to 450 m, an order of magnitude larger than that of prevalently used electrode materials like carbon papers and felts (29, 30). The periodicity of the void region is evident in the CAD modeled structure, but the signal is weaker when measured for the experimental system.
Scanning electron micrographs of a representative 3D-printed FTE in Fig. 1E reveal that the surfaces of the electrodes are rough and composed of graphene sheets with embedded carbon fibers. The electrode has two porosity scales: a macroporous length scale controlled by the filament diameter and filament spacing and a microporous length scale internal to the filament. The tomographic images thus characterize the macroporous structure as if the filaments were considered solids. This is justified because the experiments in this paper are performed at limiting current conditions. Under these conditions the concentration of the reactant within the filament is negligible as the interior filament surfaces are at zero concentration (31). The filament behaves as though it were perfectly absorbing and the internal properties of the filament, those controlled by the microporosity, do not impact performance (nevertheless, these were measured and are reported in SI Appendix). Consistent with limiting current behavior, the performance of the electrode is thus controlled by the mass transport properties external to the filament as is demonstrated below.
The surface area per volume, , and porosity, , are computed from the tomography and CAD as presented in Table 1. The macroporous structures of the electrodes have lower porosity and have lower intrinsic surface area than conventional flow-through electrode materials (6). This is expected, as the printing length scale in this paper is an order of magnitude larger than the typical fiber length scales observed in carbon felts, foams, and papers (16, 30). The CAD model is in good agreement with the experimental FCC electrode and in reasonable agreement with the SC electrode.
Table 1.
Electrode structure characterization and comparison to CAD model
| SC | FCC | |||||
| Exp | CAD | Diff, % | Exp | CAD | Diff, % | |
| Area/volume, 1/m | 2,989 | 3,424 | 14.5 | 4,473 | 4,805 | 7.42 |
| Porosity | 0.223 | 0.305 | 36.8 | 0.245 | 0.278 | 13.5 |
CAD, value measured from the idealized CAD model; Diff, relative difference between the two values; Exp, experimentally measured value from analysis of the tomographic images.
Measurement of Limiting Currents.
Electrodes were tested in potassium hexacyanoferrate (II) solutions at concentrations from 1 to 50 mM in 1 M KCl supporting electrolyte. Cyclic voltammograms under no flow conditions for 3D-printed graphene electrodes show current peaks indicative of switching from the kinetically controlled regime to the mass transport-controlled regime under diffusional mass transport (SI Appendix, Fig. S1). Oxidation peak currents increase roughly linearly with solution concentration in agreement with first-order kinetics of one electron transfer ferrocyanide oxidation reaction: .
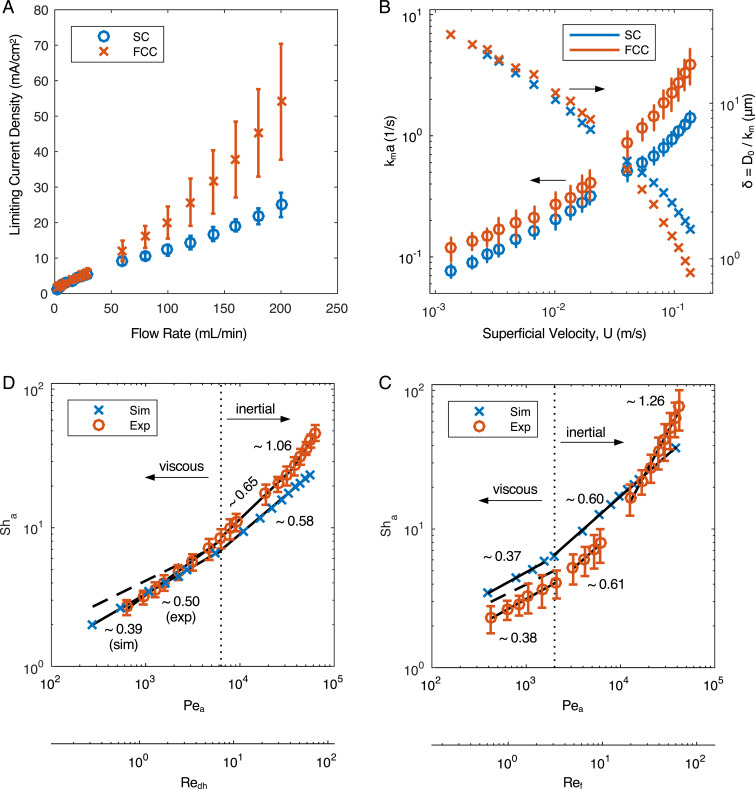
Steady-state voltammograms measured under the flow of solutions show current plateaus indicative of the mass transport limiting regime under diffusion–convection mass transport (examples of chronoamperometry data and voltammograms reconstructed by averaging chronoamperometry current over the last 10% of time interval for each voltage are shown in SI Appendix, Fig. S2 A and B, respectively). Limiting currents measured in solutions with different concentrations of potassium hexacyanoferrate were found to scale linearly with concentration (SI Appendix, Fig. S1B); therefore, mass transport properties were studied at one fixed reactant concentration chosen to be low to minimize the voltage drop from Ohmic losses. For the statistical analysis of mass flow performance two sets of identically made SC and FCC lattice electrodes ( electrodes for the FCC set and electrodes for the SC set) were prepared and measured at the same concentration [1 mM potassium hexacyanoferrate (II) solutions in 1 M KCl] under flow rates of 2 to 200 mL/min, and limiting current density plateau values are shown in Fig. 2A.
Fig. 2.
Mass transport in 3D-printed electrodes. (A) Limiting current density over the frontal area of the disk electrode represented as mean SEM in the SC and FCC electrodes against the imposed flow rate. Experiments were performed using mM. See SI Appendix, Fig. S9 for corresponding reactant conversion calculation. (B) The mass transfer coefficients (left axis) and boundary layer thickness estimate (right axis) for the FCC and SC electrodes are plotted as a function of superficial velocity. (C and D) The mass transfer coefficients are transformed into the Sherwood number experimental data for the (C) FCC and (D) SC. The solid lines are power-law fits to the data with the exponent as labeled in the plot. The dashed lines in and C and D are the correlations in Eqs. 4 and 5, respectively.
Analysis of Mass Transfer Coefficients.
Experimental results are compared to resolved simulation of the convection–diffusion equations, Eqs. 6 and 7, at the limiting current. In the simulations, a local mass transfer coefficient from the bulk to the surface at downstream position is defined by performing a differential species balance in the flow direction,
| [1] |
where is the velocity-weighted average concentration, , in planes perpendicular to the flow direction (i.e., directions); is the surface average along the intersection of the plane and filament surface (i.e., the filament–electrolyte interface); and is the diffusivity of (SI Appendix, Fig. S8). In the absence of dispersion, the local mass transfer coefficient is averaged to determine the overall or volumetrically averaged mass transfer coefficient (18–20)
| [2] |
where is measured limiting current, is the number of electrons transferred in the reaction, is Faraday’s constant, is the imposed flow rate (i.e., superficial velocity frontal area ), and is the length of the electrode. This expression reveals the expected linear scaling of the limiting current with bulk concentration, as experimentally reinforced in SI Appendix, Fig. S1B.
The mass transport properties of the electrode are most directly determined by operating under mass transport limited conditions: The operating current needs to approach the limiting current. Since the latter scales linearly with concentration, this condition can be more easily met using low-concentration solutions, and this work thus devised a setup specifically to meet this condition and extract the mass transfer coefficient. Fortunately, because the mass transfer coefficient is independent of concentration, it can nevertheless be used to determine the limiting current in the electrodes at much higher concentrations (18–20). Generally, when engineering a full device, the mass transport in the electrodes should be maximized regardless of the application, as this maximizes the limiting current in the system (17). For a system running at high concentration, the larger limiting currents ensure low-concentration overpotentials over a greater range of operating currents. Alternatively, for an electrochemical reactor the limiting current controls the maximal productivity (6). Of course, the flow-through electrode is only a single component of a full device, and the key requirement is to ensure that it is optimally engineered to maximize device performance without introducing unnecessary cost or losses.
Scaling Analysis Reveals Operational Regimes with Enhanced Mass Transport.
Using Eq. 2, the limiting current density data in Fig. 2A is transformed into the overall mass transfer coefficient, , and plotted as a function of the superficial velocity in Fig. 2B. The mass transfer coefficient is extracted using the tomographically determined values of the surface area per volume in Table 1. The ratio of the diffusivity to the mass transfer coefficient () provides an estimate of the mass transfer length scales, yielding a range from m at high flow rates to m at lower flow rates as shown in Fig. 2B. As expected for high Schmidt number () flows, the mass transfer boundary layers are generally much thinner than the geometric features. This implies that architected features above these lengths will negligibly impact the mass transfer coefficients. However, this inherently assumes slow flow predominantly parallel to the filament surface. As explored below, higher flow rates and larger features increase the fluid inertia and dramatically alter the flow field in the vicinity of the surface, strongly disrupting the very thin mass transport boundary layers.
In Fig. 2 C and D the mass transfer coefficients are scaled using the porous electrode Sherwood number (32),
| [3] |
and plotted for both the experiment and computation. Using the Péclet number , the data are fitted to power-law functions of the form . Larger exponents lead to enhanced mass transport and transitions between exponents demarcate operational regimes. Three distinct mass transport regimes, characterized by increasing exponent, are observed as the flow rate is increased (equivalently or an appropriately defined Reynolds number, ) for both the SC electrode, where increases from 0.50 to 1.06, and the FCC electrode, where increases from 0.38 to 1.26. These slope changes are due to a change in the underlying transport mechanism driven by the system hydrodynamics. Most importantly, this reveals an underutilized opportunity to engineer flow-through electrodes for improved mass transfer performance.
Inertially Driven Secondary Flows Enhance Mass Transport in FCC Electrodes.
From Fig. 1 B and C it is evident that the flow paths in the FCC electrodes are interconnected and result from flow around overlapping filaments. The hydrodynamic behavior is thus characterized using the filament length scale. For the FCC system, the Reynolds number is defined as .
The first mass transfer regime in Fig. 2C is characterized by an experimentally determined value of for . The agreement between simulation and experiment is excellent. These results are compared to a commonly used correlation for the mass transfer coefficient in porous media (18, 32, 33),
| [4] |
and found to be in close agreement with the data even though this correlation is expected to be accurate only for . The exponent is typical of mass transfer in viscous, creeping flow including fibers in porous media (34, 35). The observed exponent is in near agreement with recent simulations for mass transfer in the viscous regime () for carbon felts () and papers () (36).
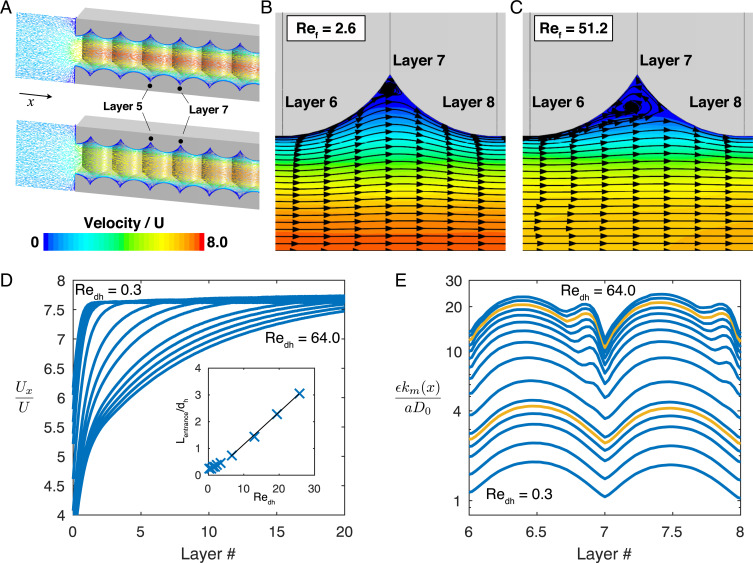
At higher flow rates, the power-law exponent increases to and for the simulation and experiment, respectively, and they are again nearly identical. The increase in power-law exponent signals a change in the underlying transport mechanism and coincides with , revealing that fluid inertia is important. The transition to inertial flow coincides with the expected transition for a single cylinder in cross flow (i.e., ) (37). As with a single filament, comparison of Fig. 3 B and C shows that for flow rates where , secondary flows, defined as flows that strongly deviate from the expected parallel flow paths that are expected for creeping or potential flows, emerge in the interior of the electrode. Larger wakes, recirculation bubbles, and corresponding surface stagnation lines appear in the inertial flow regime, and the location of these regions coincides with the position of new local maxima in , as seen in Fig. 3D. Note that entrance effects are minimally important, as even at the highest simulated flow rate, , the flow is fully developed after ∼2.5 layers as shown in Fig. 3E.
Fig. 3.
Local analysis of FCC electrode. (A) Symmetry is used to simulate a quarter of the FCC domain. The solid is gray. The velocity magnitude is shown at (Top) and (Bottom), and a detailed view of the streamlines is shown in B and C, respectively. The arrows show the emergence of surface stagnation lines. The color bar shows the velocity magnitude normalized by the superficial velocity. (D) The local mass transfer coefficient from Eq. 1 is plotted in the axial direction. The curves correspond to the simulation points from Fig. 2C and are in ascending 0.6 to 24.3. The dashed line corresponds to , the first curve in the inertial regime. The orange curves correspond to (top) and (bottom). (E) The velocity in the axial direction along a line down the center of the quarter domain in the axial direction at the extremes of the simulated .
The enhanced mass transfer seen in FCC electrodes is engineered by controlling the secondary flows and is accessible only when . The secondary flows lead to the emergence of surface stagnation lines and increased surface strain rates in the adjacent regions, a principal driver of increased mass transfer for very thin boundary layers (38–40). The flow near the stagnation lines now has a significant component perpendicular to the filament surface and convection becomes a dominant transport mechanism orthogonal to the surface. Inertial flows are difficult, if not impossible, to realize in conventional, fibrous electrode materials like carbon felts due both to the small lengths scale, which preclude operation at large , and to the random arrangement of the fibers (29, 30). In the viscous flow regime, the impact from the random orientation is small (34, 35), but in the inertial regime any flow along the fiber axis will diminish the occurrence of secondary flow. In contrast, the FCC electrodes orient all filament axes orthogonal to the incoming flow, allowing for maximal wake formation behind the filament, and are ordered, preventing filaments from overly shielding incoming flow and thus maximizing the prevalence of secondary flows around the filaments (SI Appendix, Fig. S4).
The experimental data in Fig. 2C reveal a third mass transport regime beyond . This deviates significantly from the simulation data, despite the good agreement at lower values. Turbulence in the electrodes is not a factor, as , but the flow can become unsteady. We thus performed one time-dependent simulation, over an extended periodic domain, and found that the flow becomes unsteady at . This value is in approximate agreement with the onset for vortex shedding for a single cylinder in cross-flow (37). Although the flow is unsteady, there is no observed impact on the power-law exponent of the simulation, and mixing due to unsteady flow is ruled out as a mechanism for increasing mass transfer to the surface. Mixing induced by unsteadiness may become more important when enhancing mass transfer in systems that undergo high reactant conversion since this will significantly increase flow-induced dispersion. Alternatively, at the highest flow rates the boundary layers are expected to be m, and this may approach the surface roughness of the filaments (Fig. 1E). The boundary layer thickness, however, would need to be significantly smaller than the surface roughness length scale to impact mass transfer. Given that simulation reveals no mechanism for enhanced transfer from the interior of the electrode, the further enhancement in the third regime is hypothesized to arise from transfer on the front of the electrode. Indeed, larger are often observed for impinging flow (41).
Inertially Driven Developing Flow Enhances Mass Transport in SC Electrodes.
As seen in Fig. 1 B and C, the geometry of the SC electrode is equivalent to a nonhydrodynamically communicating tube bundle of irregular cross-section embedded in a solid matrix. A model for the mass transfer in the bundle is constructed by geometrically scaling the analytical results for the average mass transfer coefficient for completely developed flow in a single tube (42):
| [5] |
where the SC CAD data from Fig. 1D are used to determine the average value for the hydraulic diameter . For flows in tube-like structures the Reynolds number is defined, (43).
The experimental data in Fig. 2D show that undergoes three slope changes, with increases from to at and then to at . In the first region, where , the experiment and simulation are both in close agreement with the correlation, as expected since the correlation applies for fully developed flow. There is some expected disparity between the power-law slopes of the experiment, correlation, and simulation, as the geometry deviates slightly between the three domains. In this regime, the mass transfer behavior of the SC electrodes is closest to low , creeping flow mass transfer, as additionally reflected by an exponent near and in agreement with the predicted values from Eq. 5. The SC electrode offers no mass transport enhancement in this regime.
Alternatively, the experimental and simulation data both show an increase in the power-law exponent at , signaling a mass transfer enhancement and a change in the underlying transport mechanism. Fig. 4A shows that as the flow rate is increased, the flow field develops over a greater distance. The latter is evident in the plot of the centerline velocity magnitude of the flow field as shown in Fig. 4D. The position at which the centerline velocity reaches 95% of its plateau value is defined as the entrance length and plotted against . The linear dependence of entrance length with is analogous to the same phenomenon in circular tubes (43) and it is observed that the flow is fully developed throughout the SC electrode when the entrance length is smaller than the hydraulic diameter, .
Fig. 4.
Local analysis of SC electrode. (A) Visualization of the modeled SC domain with solid in gray. The velocity vectors are shown for developed flow at (Top) and developing flow at (Bottom), and a detailed view of the streamlines is shown in B and C, respectively. The color bar shows the velocity magnitude normalized by the superficial velocity. (D) The velocity in the axial direction along a line down the center of the domain for all simulated . Inset shows the flow development entrance length dependence on . (E) The local mass transfer coefficient from Eq. 1 is plotted in the axial direction. The curves correspond to the simulation points from Fig. 2D and are in ascending to 64.0. The orange curves correspond to = 51.2 (top) and (bottom).
The emergence of the momentum boundary layer provides a mechanism to explain the improved mass transport. The surface velocity gradients are greatest, equivalently the momentum boundary layer is the thinnest, when the flow first enters the electrode and slowly decay as the flow develops. In analogy with the FCC electrodes, the increased surface strain rate in the developing region leads to greater local mass transport. This also explains the observed transition in the overall mass transfer coefficient data in Fig. 2D. As the momentum and mass transfer boundary layers begin to coevolve with position in the tube, we expect to see high mass transfer rates. Indeed, the simulation and experimental transition coincide with the emergence of the entrance length exceeding hydraulic diameter at .
Beyond the experimental data show a further increase of the power-law exponent to . As with the FCC data, the increased mass transfer is hypothesized to arise from reaction on the front face of the electrode. Interestingly secondary flows, also driven by fluid inertia, emerge in the interior of the electrode as the flow rate is increased as shown in the increased recirculation of the streamlines in Fig. 4 B and C. These lead to new local maxima in the local mass transfer coefficient as presented in Fig. 4E.
Comparing Mass Transfer Coefficients across Systems.
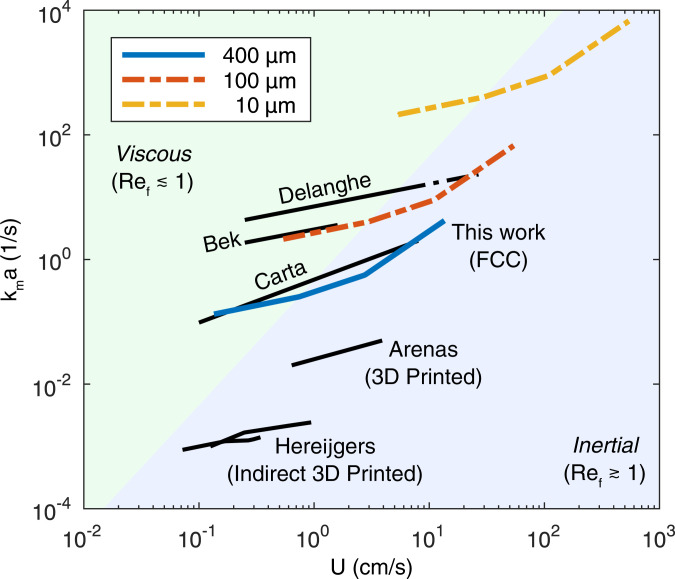
To enable comparison to a broad set of literature, in Fig. 5 the overall mass transfer coefficients, , of the FCC electrode are compared to those in previous studies that employed the same chemistry, as the dimensional will depend on the transport properties of the electrolyte and reactive species. The mass transport coefficients of the FCC and SC electrodes are comparable (Fig. 2) but we focus on the FCC structure since its inertially enhanced properties are not principally driven by the electrode thickness.
Fig. 5.
Volumetrically averaged mass transfer coefficient across systems and length scales as a function of the superficial velocity. The FCC experimental data are redimensionalized and scaled using similitude to determine the expected performance of the electrodes as they are manufactured with filament diameters of 100 m and 10 m. The 400-m data correspond to power-law fits to the experimental FCC data. As the FCC electrode is made smaller, the transition from the viscous to the inertial regime occurs at greater velocities but the mass transfer coefficient increases. The black curves are a comparison to correlations developed by experiments with in carbon felt by Bek and Zamyatin (45), Carta et al. (46), and Delanghe et al. (20); in 3D-printed Ni/SS electrodes by Arenas et al. (23); and the indirect 3D-printed electrodes of Hereijgers et al. (25). The work of Delanghe et al. (20) is extrapolated using a dashed line to the velocity at which the flow transitions from viscous flow to inertial flow (i.e., ). The shaded region shows where the FCC electrodes will operate in the inertial regime. All extrapolations are represented using dashed lines.
At limiting current conditions controls the electrochemical reactor performance and serves as the metric for comparison while still normalizing for the size of the reactor (6, 32). In Fig. 5 the FCC electrode mass transfer is compared to measurements in several carbon felt FTEs as these are commercially available, high-performance materials that have seen pervasive adoption (44). The experimental curves in Fig. 5 are representative of several studies of ferrocyanide redox reaction in high-porosity carbon felts with -m fiber diameter (20, 45–48). Even at length scales that are >40× the carbon felt, the FCC electrode shows comparable performance to the work of Carta et al. (46).
As the flow rate is increased, the FCC electrode crosses into the inertial regime before the carbon felt, leading to a stronger flow dependence for the mass transfer coefficient, and the performance gap relative to the highest observed from literature is reduced to 4×. The carbon felt may also transition to the inertial regime, provided enough of the fibers are oriented orthogonal to the flow and do not suffer from excessive wake interference between the fibers, but this transition will occur at much larger flow rates as shown by the extrapolation in the dashed line in Fig. 5. This transition has been previously observed in the fluorescence microscopy of carbon papers (49). Indeed, the flow in any electrode can transition to the inertial regime, and for larger internal-feature length-scale electrodes like foam and RVC electrodes the transition will occur at lower flow speeds. Here too, however, the random arrangement of the structures in the electrode may not fully exploit the enhancement expected from secondary flow generation.
To understand how the FCC FTEs will perform as printing resolution is increased, dynamic similarity is used to redimensionalize the experimental data in Fig. 2C for smaller length scales as shown in Fig. 5. Mass transfer coefficients for FCC electrodes with 100-m filaments, merely 4× smaller than what has been produced in this paper, will rival the performance of carbon felts and even exceed it as the FCC electrode enters the inertial regime. At the same filament length scale as the carbon felts (10 m) the FCC electrodes are expected to greatly outperform these materials.
There is limited work on porous electrodes generated using additive manufacturing techniques (23–25). The electrodes in this work exceed the value of for previously developed 3D-printed Ni/SS electrodes (23) by an order of magnitude and for 3D electrodes formed using an indirect 3D-printing method by two orders of magnitude (25). These 3D-printed electrodes contain internal feature sizes that could lead to inertial flows at the operational flow rates; however, the obstacle arrangement in these studies may not have maximized this effect.
Conclusions
This work reveals that engineered flows enabled by 3D printing can dramatically enhance mass transfer in flow-through electrodes. The key to this high performance is the strong dependence of the mass transport properties on the flow when operating in the inertial regime over the creeping flow regime. Ordered features aligned orthogonal to the flow can be used to induce secondary flows driven by fluid inertia. The near wall flow changes and induced stagnation lines locally increase the surface stain rate and lead to inertially enhanced mass transfer even for a very thin concentration boundary layer. Indeed, the mass transfer coefficients reported here exceed those from previous work on 3D-printed electrodes by one to two orders of magnitude and approach the mass transfer coefficients for electrodes composed of internal features that are 40× smaller. Greater print resolution will continue to increase the performance of 3D-printed electrodes, but here we note that appropriate design of larger features can nevertheless lead to superior performance by enabling greater limiting currents. By demonstrating mass transfer performance on par with commonly used electrode materials, we establish 3D printing as a viable rapid-prototyping method for FTEs, enabling rapid exploration of novel FTE architectures without requiring the expensive development of industrialized manufacturing techniques. Engineered flow in FTEs can be leveraged to significantly boost the performance of electrochemical devices and help make them more attractive solutions to the global energy crisis.
Materials and Methods
Preparation of FTE.
Three-dimensional–printed carbon-based graphene aerogel electrodes were used for the flow tests performed in this work. A schematic of the overall fabrication process is shown in SI Appendix, Fig. S5. A thixotropic aqueous graphene oxide ink was formulated for direct ink writing (DIW). DIW is an extrusion process by means of which a thixotropic ink is deposited onto a substrate to fabricate 3D structures. For SC lattices, multiple orthogonal layers of parallel cylindrical rods were printed alternately. Whereas, for FCC lattices an offset of 400 m was introduced in and directions such that every odd layer will cover the gap of an even layer. The printed samples were later freeze dried and carbonized under inert atmosphere to obtain 3D-printed graphene aerogels. A more detailed explanation of the ink formulation, print, and other process parameters can be found in SI Appendix.
For the actual flow test, circular discs of 5.6-mm diameter were cut using a commercial laser cutter (Universal Laser Systems VLS 3.50; CO2 laser, 50 W) under inert atmosphere. After cutting, electrode thicknesses ranged from 1.90 to 2.00 mm for SC electrodes and 1.50 to 1.65 mm for FCC electrodes. To make an electrical contact to an FTE, a platinum wire (99.99% purity, diameter 0.127 mm; Sigma Aldrich) was hooked to an edge of the glass pipette (5.6-mm inner diameter on average) and conductive carbon epoxy (product AA-CARB 61LP of Atom Adhesives) was distributed as a ring over the edge of the tube. A laser cut disk was placed on top of the tube and the edges were coated with conductive epoxy to improve electrical contact. After drying in an oven at C for 15 to 20 min, the edges of the electrode, the gap between electrode and glass tube, and surrounding Pt wire were coated with nonconductive epoxy (Loctite 9462 Hysol) and dried for another 30 min at C.
Tomography Characterization and Analysis of 3D Geometry.
Samples were exposed to iodine prior to tomography measurements to increase contrast of low-absorbing carbon materials. Tomography scans were carried out on a Xradia 510 Versa (Carl Zeiss X-ray Microscopy Inc.) 3D X-ray microscope machine with the X-ray source tuned to 80 kV, 7 W without filter. Samples were placed 120 mm from the source and 30 mm from the detector. X-ray radiographies were collected using a 4× objective lens, yielding a pixel size resolution of 5.44 m per pixel. A series of 2,400 projections was obtained over a range with 5 s exposure time.
Tomography reconstructions were performed using XMReconstructor version 5 (Carl Zeiss X-ray Microscopy Inc.), and output volumes were cropped and converted to .tiff format using Avizo Lite v9.5.0. Volumes were rotated and 2D morphological filtering was performed using a dilation disk with two-pixel radius and resliced from top and left stacks of reconstructed images using MorphololibJ (50). The two filtered stacks of image were combined using the “max” calculator and resulting volume of filtered using the 2D median algorithm. Manual thresholding was performed to differentiate sample from background. The volume was further processed by removing closed pores using the 3D fill holes algorithm. Channels were analyzed by measuring particles ranging from 1,000 to 300,000 on each slice of the volume. Image processing and analysis were done using Fiji v.1.52p (51).
SEM Analysis.
Scanning characterization of 3D-printed electrodes was obtained with a JEOL7401-F SEM at a 5-kV accelerating voltage.
Electrochemical Measurement Setup.
Electrodes were tested for potassium hexacyanoferrate (II) oxidation under flow-through conditions inside a custom two-compartment cell separated by a Nafion membrane to avoid reoxidation of species electrochemically generated at the counterelectrode (SI Appendix, Fig. S3). A large surface area coiled platinum electrode served as a counterelectrode and a standard Ag/AgCl electrode was used as a reference electrode. Fresh solutions for tests were prepared daily by dissolving potassium hexacyanoferrate (II) trihydrate (99.0% min purity; Sigma Aldrich) in 1 M KCl supporting electrolyte. A syringe pump (KDS200; KD Scientific) with a 50-mL glass syringe and polytetrafluoroethylene (PTFE) tip plunger was used for mass flow control at low flow rates of 2 to 55 mL/min. A peristaltic pump with an Iridium liquid flow control system (McMillan Flow Products) was used at high flow rates of 60 to 200 mL/min. Solutions were forced through a glass tube (inner diameter 5.6 mm) with a porous electrode glued at the end with the help of a syringe pump or a peristaltic pump with an Iridium liquid flow control system. Parts in contact with solution were made of chemically resistive materials: glass, PTFE, and Viton. Electrochemical measurements were performed by an SP-300 Potentiostat (Bio-Logic Science Instruments). To obtain steady-state voltammograms chronoamperometry the following experiments were performed: The potential was changed stepwise and the current at each potential was monitored until steady current was recorded. For limiting current measurement, the potential was increased stepwise with 50-mV steps until the steady-state current value became insensitive to a potential increase. Potential limits were kept within the water stability window to avoid contribution to the current due to water electrolysis.
Conductivity Measurement.
Discs with 5.6-mm diameters were extracted from 3D-printed SC and FCC samples using a commercial laser cutter (Universal Laser Systems VLS 3.50; CO2 laser, 50 W) for conductivity measurements. Silver epoxy paste was applied on the sample to ensure electrical contact and conductivity measurements were performed using a multimeter. The conductivity, , of electrodes was calculated from resistance as , where is sample thickness and is surface area. The resistance of leads was negligible compared to the resistance of the samples.
Printed structures were characterized for electrical conductivity. The conductivity of 3D-printed graphene samples was 2.2 0.3 S/cm independent of lattice type. It is well within the range of the conductivities of the typical carbon-based FTEs and for comparison just 1.7× lower than the conductivity of Segracet 29AA. Carbon paper is 3.8 S/cm commonly used in various electrochemical reactors (http://www.fuelcellstore.com).
Simulations.
High-resolution, continuum, computational fluid dynamics are used to simulate the flow and mass transport in the lattice geometries and enable direct comparison to the experimentally studied systems. At the limiting current, the surface concentration of the lone reactive species (i.e., for oxidation of ferrocyanide) is zero and the electrochemical and electrostatic problems are decoupled. The complete, steady mass transport behavior can be described by two, one-way coupled partial differential equations for the fluid flow field, , and species concentration, . To enable comparison across species and geometries, lengths are made dimensionless with the filament diameter (), timescales with the ratio of the filament diameter to the inlet flow velocity (), and concentration with the inlet concentration, :
| [6] |
| [7] |
where is the dynamic pressure field (determined from the continuity equation, ). Dimensionless scalars are denoted () and dimensionless vectors using (). The behavior of the system is controlled by two dimensionless parameters, the Reynolds number, , and the Péclet number, . Here = 997.6 kg/m3 is the electrolyte density, = 0.889 mPa-s is the electrolyte viscosity, and = 7.2 × /s is the molecular diffusivity of the species. The simulations are run at fixed . Boundary conditions were chosen to match experimental testing conditions. For more detail see SI Appendix.
Supplementary Material
Acknowledgments
This work was performed under the auspices of the US Department of Energy by Lawrence Livermore National Laboratory (LLNL) under Contract DE-AC52-07-NA27344 and was supported by the LLNL–Laboratory Directed Research and Development program under Projects 16-ERD-051 and 19-SI-005, LLNL Release no. LLNL-JRNL-815948.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2025562118/-/DCSupplemental.
Data Availability
All study data are included in this article and/or SI Appendix.
References
- 1.Denholm P., Clark K., O’Connell M., “On the path to SunShot: Emerging issues and challenges in integrating high levels of solar into the electrical generation and transmission system” (NREL/TP-6A20-65800, National Renewable Energy Laboratory, Golden, CO, 2016).
- 2.Oleksandr S., et al., What should we make with CO2 and how can we make it? Joule 2, 825–832 (2018). [Google Scholar]
- 3.Schmidt T. S., Spurring low-carbon electrosynthesis through energy and innovation policy. iScience 24, 102045 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Schiffer Z. J., Manthiram K., Electrification and decarbonization of the chemical industry. Joule 1, 10–14 (2017). [Google Scholar]
- 5.Stankiewicz A. I., Nigar H., Beyond electrolysis: Old challenges and new concepts of electricity-driven chemical reactors. React. Chem. Eng. 5, 1005–1016 (2020). [Google Scholar]
- 6.Kim M. J., Seo Y., Cruz M. A., Wiley B. J., Metal nanowire felt as a flow-through electrode for high-productivity electrochemistry. ACS Nano 13, 6998–7009 (2019). [DOI] [PubMed] [Google Scholar]
- 7.Shatskiy A., Lundberg H., Kärkäs M. D., Organic electrosynthesis: Applications in complex molecule synthesis. ChemElectroChem 6, 4067–4092 (2019). [Google Scholar]
- 8.Leow W. R., et al., Chloride-mediated selective electrosynthesis of ethylene and propylene oxides at high current density. Science 368, 1228–1233 (2020). [DOI] [PubMed] [Google Scholar]
- 9.Montoya J. H., et al., Materials for solar fuels and chemicals. Nat. Mater. 16, 70–81 (2017). [DOI] [PubMed] [Google Scholar]
- 10.Vedharathinam V., et al., Using a 3D porous flow-through electrode geometry for high-rate electrochemical reduction of CO2 to CO in ionic liquid. ACS Catal. 9, 10605–10611 (2019). [Google Scholar]
- 11.Gür T. M., Review of electrical energy storage technologies, materials and systems: Challenges and prospects for large-scale grid storage. Energy Environ. Sci. 11, 2696–2767 (2018). [Google Scholar]
- 12.Weber A. Z., et al., Redox flow batteries: A review. J. Appl. Electrochem. 41, 1137–1164 (2011). [Google Scholar]
- 13.Soloveichik G. L., Flow batteries: Current status and trends. Chem. Rev. 115, 11533–11558 (2015). [DOI] [PubMed] [Google Scholar]
- 14.Kjeang E., Djilali N., Sinton D., Microfluidic fuel cells: A review. J. Power Sources 186, 353–369 (2009). [Google Scholar]
- 15.Suss M. E., et al., Capacitive desalination with flow-through electrodes. Energy Environ. Sci. 5, 9511–9519 (2012). [Google Scholar]
- 16.Castañeda L. F.Walsh F. C., Nava J. L., de León C. P., Graphite felt as a versatile electrode material: Properties, reaction environment, performance and applications. Electrochim. Acta 258, 1115–1139 (2017). [Google Scholar]
- 17.Forner-Cuenca A., Brushett F. R., Engineering porous electrodes for next-generation redox flow batteries: Recent progress and opportunities. Curr. Opin. Electrochem. 18, 113–122 (2019). [Google Scholar]
- 18.Wilson E. J., Geankoplis C. J., Liquid mass transfer at very low Reynolds numbers in packed beds. Ind. Eng. Chem. Fundam. 5, 9–14 (1966). [Google Scholar]
- 19.Fedkiw P. S., Newman J., Mass-transfer coefficients in packed beds at very low Reynolds numbers. Int. J. Heat Mass Transf. 25, 935–943 (1982). [Google Scholar]
- 20.Delanghe B., Tellier S., Astruc M., Mass transfer to a carbon or graphite felt electrode. Electrochim. Acta 35, 1369–1376 (1990). [Google Scholar]
- 21.Milshtein J. D., et al., Quantifying mass transfer rates in redox flow batteries. J. Electrochem. Soc. 164, E3265–E3275 (2017). [Google Scholar]
- 22.Ke X., et al., Rechargeable redox flow batteries: Flow fields, stacks and design considerations. Chem. Soc. Rev. 47, 8721–8743 (2018). [DOI] [PubMed] [Google Scholar]
- 23.Arenas L. F., de León C. P., Walsh F. C., 3D-printed porous electrodes for advanced electrochemical flow reactors: A Ni/stainless steel electrode and its mass transport characteristics. Electrochem. Commun. 77, 133–137 (2017). [Google Scholar]
- 24.Lölsberg J., et al., 3D-printed electrodes with improved mass transport properties. ChemElectroChem 4, 3309–3313 (2017). [Google Scholar]
- 25.Hereijgers J., Schalck J., Lölsberg J., Wessling M., Breugelmans T., Indirect 3D printed electrode mixers. ChemElectroChem 6, 378–382 (2019). [Google Scholar]
- 26.Langlois S., Coeuret F., Flow-through and flow-by porous-electrodes of nickel foam. 2. Diffusion convective mass-transfer between the electrolyte and the foam. J. Appl. Electrochem. 19, 51–60 (1989). [Google Scholar]
- 27.Lange C. F., Durst F., Breuer M., Momentum and heat transfer from cylinders in laminar crossflow at 10−4 ≤ Re ≤ 200. Int. J. Heat Mass Transf. 41, 3409–3430 (1998). [Google Scholar]
- 28.Alam T., Kim M.-H., A comprehensive review on single phase heat transfer enhancement techniques in heat exchanger applications. Renew. Sustain. Energy Rev. 81, 813–839 (2018). [Google Scholar]
- 29.Banerjee R., et al., Carbon felt electrodes for redox flow battery: Impact of compression on transport properties. J. Energy Storage 26, 100997 (2019). [Google Scholar]
- 30.Zenyuk I. V., Parkinson D. Y., Connolly L. G., Weber A. Z., Gas-diffusion-layer structural properties under compression via X-ray tomography. J. Power Sources 328, 364–376 (2016). [Google Scholar]
- 31.Newman J., Thomas-Alyea K. E., Electrochemical Systems (John Wiley & Sons, Hoboken, NJ, 2012). [Google Scholar]
- 32.Trainham J. A., Newman J., A flow-through porous electrode model: Application to metal-ion removal from dilute streams. J. Electrochem. Soc. 124, 1528–1540 (1977). [Google Scholar]
- 33.Darling R. M., Perry M. L., The influence of electrode and channel configurations on flow battery performance. J. Electrochem. Soc. 161, A1381–A1387 (2014). [Google Scholar]
- 34.Spielman L., Goren S. L., Model for predicting pressure drop and filtration efficiency in fibrous media. Environ. Sci. Technol. 2, 279–287 (1968). [Google Scholar]
- 35.Lee K. W., Liu B. Y. H., Theoretical study of aerosol filtration by fibrous filters. Aerosol Sci. Technol. 1, 147–161 (1982). [Google Scholar]
- 36.Kok M. D. R., et al., Mass transfer in fibrous media with varying anisotropy for flow battery electrodes: Direct numerical simulations with 3D X-ray computed tomography. Chem. Eng. Sci. 196, 104–115 (2019). [Google Scholar]
- 37.Kundu P. K., Cohen I. M.. Fluid Mechanics (Academic Press, San Diego, CA, 2002). [Google Scholar]
- 38.Acrivos A., On the solution of the convection equation in laminar boundary layer flows. Chem. Eng. Sci. 17, 457–465 (1962). [Google Scholar]
- 39.Stewart W. E., Forced convection in three-dimensional flows: I. Asymptotic solutions for fixed interfaces. AIChE J. 9, 528–535 (1963). [Google Scholar]
- 40.Baier G., Grateful T. M., Graham M. D., Lightfoot E. N., Prediction of mass transfer rates in spatially periodic flows. Chem. Eng. Sci. 54, 343–355 (1999). [Google Scholar]
- 41.Ingenieure V. D., VDI Heat Atlas (Springer-Verlag, Berlin, Germany, 2006). [Google Scholar]
- 42.Levich V. G., Physicochemical Hydrodynamics (Prentice-Hall, Englewood Cliffs, NJ, 1962). [Google Scholar]
- 43.Deen W. M., Analysis of Transport Phenomena (Oxford University Press, Oxford, UK, 1998). [Google Scholar]
- 44.Thi X. H. L., Bechelany M., Cretin M., Carbon felt based-electrodes for energy and environmental applications: A review. Carbon 122, 564–591 (2017). [Google Scholar]
- 45.Bek R. Y., Zamyatin A. P., Mass transfer coefficient and area accessible to electrolysis in flow-through graphitic-carbon-fiber electrodes. Soviet Electrochem. 14, 1034–1039 (1978). [Google Scholar]
- 46.Carta R., Palmas S., Polcaro A. M., Tola G., Behaviour of a carbon felt flow by electrode Part I: Mass transfer characteristics. J. Appl. Electrochem. 21, 793–798 (1991). [Google Scholar]
- 47.Schmal D., Van Erkel J., Van Duin P. J., Mass transfer at carbon fibre electrodes. J. Appl. Electrochem. 16, 422–430 (1986). [Google Scholar]
- 48.Vatistas N., Marconi P. F., Bartolozzi M., Mass-transfer study of the carbon felt electrode. Electrochim. Acta 36, 339–343 (1991). [Google Scholar]
- 49.Wong A. A., Aziz M. J., Rubinstein S. M.. Direct visualization of electrochemical reactions and comparison of commercial carbon papers in operando by fluorescence microscopy using a quinone-based flow cell. ECS Trans. 77, 153 (2017). [Google Scholar]
- 50.Legland D., Arganda-Carreras I., Andrey P., MorphoLibJ: Integrated library and plugins for mathematical morphology with ImageJ. Bioinformatics 32, 3532–3534 (2016). [DOI] [PubMed] [Google Scholar]
- 51.Schindelin J., et al., Fiji: An open-source platform for biological-image analysis. Nat. Methods 9, 676–682 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in this article and/or SI Appendix.