Ion correlations drive charge overscreening and heterogeneous nucleation at solid–aqueous electrolyte interfaces

Significance

Ion distributions at charged solid–water interfaces, referred to as the electrical double layer (EDL), are poorly understood at high ion concentrations, in part due to the lack of molecular-scale descriptions of the interactions between adsorbed hydrated ions. Here, direct visualization of the salinity-dependent evolution of EDL structure reveals molecular origins of nonclassical transformation of the EDL, in which charge overscreening and heterogeneous nucleation are driven by ion–ion correlations at the interfaces. This manifestation of the atomistic basis of nonclassical behaviors provides a much-needed understanding of the impact of ion cooperativity at charged interfaces for the development of predictive models for element transport in natural environments and advanced technologies for material growth and synthesis in saline environments.

Abstract

Classical electrical double layer (EDL) models are foundational to the representation of atomistic structure and reactivity at charged interfaces. An important limitation to these models is their dependence on a mean-field approximation that is strictly valid for dilute aqueous solutions. Theoretical efforts to overcome this limitation are severely impeded by the lack of visualization of the structure over a wide range of ion concentration. Here, we report the salinity-dependent evolution of EDL structure at negatively charged mica–water interfaces, revealing transition from the Langmuir-type charge compensation in dilute salt solutions to nonclassical charge overscreening in highly concentrated solutions. The EDL structure in this overcharging regime is characterized by the development of both lateral positional correlation between adsorbed ions and vertical layering of alternating cations and anions reminiscent of the structures of strongly correlated ionic liquids. These EDL ions can spontaneously grow into nanocrystalline nuclei of ionic compounds at threshold ion concentrations that are significantly lower than the bulk solubility limit. These results shed light on the impact of ion cooperativity that drives heterogeneous nonclassical behaviors of the EDL in high-salinity conditions.

Our understanding of the behavior of ions at charged solid–water interfaces is based on electrical double layer (EDL) theories, which represent charge screening as occurring through two phenomena: ion interaction with specific surface sites in a Stern (or inner Helmholtz) layer and ion interaction with the mean electrostatic field in a diffuse (or outer Helmholtz) layer (i.e., using the linearized Poisson–Boltzmann equation) (1). A well-known weakness of these classical theories is that they explicitly ignore energetic contributions from the interactions between adsorbed ions (2–4) and effects of hydration (5–8). Therefore, they often fail in describing various interfacial phenomena occurring at high salinities that commonly exist in geological and biological systems (9–11) and chemical and engineering processes (12–15). For example, recent interest in the use of solvate melt electrolytes in electrochemical energy storage systems is motivated by enhancement in the electrolyte stability window, which is speculated to be related to the formation of the solid electrolyte interphase on electrodes, but the detailed mechanism has not been fully understood (16–18). These gaps in our molecular-scale understanding have been bottlenecks in the development of predictive models for environmental remediation and advanced technologies for material growth and synthesis.

Here, we present in situ observations of the atomistic details of EDL structure at a charged solid–aqueous electrolyte interface to visualize molecular origins of nonclassical behaviors as a function of salinity. The distribution of ions adsorbed on the negatively charged basal surface of muscovite mica, a well-defined interfacial system with a fixed charged density (8, 19, 20), is studied using in situ high-resolution X-ray reflectivity (XR) (21) to determine the atomic-scale structure (i.e., electron-density distribution) as a function of distance from the interface (22, 23). Our study focuses on the simple Rb⁺-based aqueous electrolytes (i.e., RbCl and RbI solutions) in which the distribution of Rb⁺ adsorbed at the mica–water interface is probed directly by element-specific resonant anomalous XR (RAXR) (24, 25). These structures are compared with those derived from molecular dynamics (MD) simulations carried out using a methodology previously developed for alkali-metal halide systems (26). This combination of experimental and computational approaches delivers unexpected insights that impact how we view and understand the nonclassical interfacial phenomena associated with ion–ion correlation (2–4) and ion hydration (5–8) near the charged interface. Specifically, the results shed light on the manner in which surface structure and charge distribution control ion adsorption at high salinities, in which specific interactions between adsorbed ions give rise to strong deviations from classical EDL models, including charge overscreening, multilayer ion adsorption, and, eventually, heterogeneous nucleation and growth of ionic crystals.

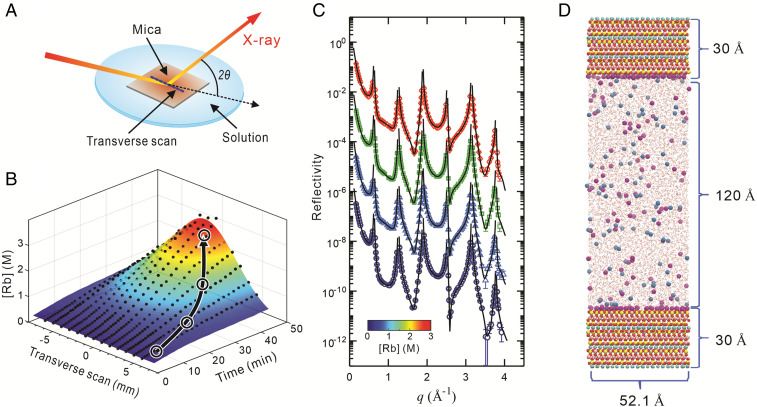
Samples for the XR measurements were prepared using freshly cleaved muscovite mica crystals in contact with either RbCl or RbI solution in a thin-film cell (22) (Fig. 1A, SI Appendix, Fig. S1). All solutions were prepared at near-neutral pH (∼6) to minimize the impact of hydronium and hydroxyl ions in the systems. XR signals, defined as the ratio of the reflected to incident X-ray intensities (21), were collected as a function of momentum transfer (q) along the surface normal direction, where q is defined as 4πsin(2θ/2)/λ with 2θ, the angle between incident and reflected X-rays, and λ = 0.689 Å, the X-ray wavelength at 18.0 keV (Materials and Methods). RAXR spectra were measured as a function of photon energy, E, near the X-ray K-absorption edge energy of Rb at a series of fixed q values. As described previously (27), the ion concentration in the thin-film cell increases with time because of slow evaporation of water through the permeable Kapton membrane. The fluorescence yield (FY) of Rb K_α measured as a function of time (t) and position (x) transverse to the scattering plane shows the largest enhancement in ion concentration at the center of the sample surface (Fig. 1B). To the best of our knowledge, this chemical variation has been ignored in the majority of previous XR studies: otherwise, its impact is mitigated by either measuring data on a location far from the center of the substrate surface or frequently flushing the solutions in the cell. In this study, we took advantage of this temporal change in solution composition to obtain a robust understanding of the relationship between the solution chemistry and interfacial structure. That is, we continuously monitored the compositional variations of dissolved ions, specifically Rb⁺, using Rb K_α FY, while optimizing the measurement scheme (i.e., angular range and counting time) so as to complete one XR scan within a substantially shorter time period (∼3 min instead of typical time of >30 min) and thereby minimize the change in ion concentration within each scan. This method allowed us to obtain multiple XR datasets (Fig. 1C) spanning a wide range of Rb concentrations during a single experiment. The reproducibility of the XR data were tested and confirmed by repeating the measurements using eight different mica crystals (purchased from Asheville-Shoonmaker Mica Company) (SI Appendix, Table S1).

Fig. 1.

Observation of EDL structure at the muscovite mica (001)–saline solution interface using in situ high-resolution X-ray reflectivity and MD simulation. (A) Experimental setup for X-ray reflectivity. A single-crystal muscovite mica in contact with either RbCl or RbI solution is encapsulated in a thin-film X-ray cell (22). (B) Position-dependent evolution of Rb concentration ([Rb]) in the cell recorded as a function of time. The data (with the initial [Rb] of 0.3 M) were collected by translating the mica sample transverse to the X-ray scattering plane. The black arrow with four circles schematically shows a pathway along which a series of XR datasets are collected during evolution of the solution composition in the cell. (C) A series of XR datasets as a function of [Rb]. The data at average [Rb] of 0.36, 0.76, 1.6, and 2.6 M were collected as a function of momentum transfer (q) along the surface normal direction and are plotted after scaling by factors of 10⁻², 1, 10², and 10⁴, respectively, for clarity. (D) Snapshot of the MD simulation at [Rb] = 0.5 M (yellow = Si; pink = Al; red = O; white = H; cyan = K; purple = Rb; blue = Cl). Water molecules are displayed using stick models.

Results and Discussion

A series of XR datasets measured at various RbCl compositions are shown in Fig. 2A and SI Appendix, Figs. S2–S4. These data are plotted after normalization to the generic crystal truncation rod shape (22) to visually enhance fine details associated with changes in interfacial structure. The most prominent changes are observed in the q range of 0.8 to 1.7 Å^–1, in which a single concave pattern at [Rb] ≤ ∼0.05 M progressively transforms into a doublet pattern with increasing [Rb] (Fig. 2A). This concentration-dependent change differs from our previous results at lower [Rb] (i.e., 0.001 to 0.020 M), in which the XR data are largely invariant with salinity (22, 28, 29). Within this lower concentration range, the maximum Rb⁺ surface coverage matches the cationic charge density required to compensate the negative charge density of the mica surface. Compared to these observations, our observations at higher [Rb] reveal the onset of a secondary evolution of EDL structure beyond the dilute electrolyte regime.

Fig. 2.

Structural change at the muscovite mica (001)–RbCl interface measured by X-ray reflectivity and MD simulation. (A) Normalized XR as a function of [Rb] (0.022, 0.050, 0.090, 0.36, 0.49, 0.76, 0.84, 1.3, 2.1, 2.6, 3.7, and 6.7 M). These datasets are scaled by factors of 10^n–1, where n (= 1, 2, 3, …) increases from Bottom to Top, following the sequence of increasing [Rb]. (B) Total electron-density profiles derived from the best-fit models of the XR data. Results are normalized to the density of bulk water and broadened by the spatial resolution of the data (π/q_max = ∼0.8 Å, where q_max is the maximum q of each XR dataset). Line thickness reflects the two-standard-deviation uncertainty. The profile at the lowest [Rb] (= 0.022 M) is offset by three, and each of the subsequent profiles is offset by one from the previous profile. The Rb-specific profiles derived from RAXR data in [Rb] = 0.003 and 0.4 M (ρ_Rb0.003 and ρ_Rb0.4) are plotted without vertical offset. (C) Total electron-density profiles derived from MD simulations as a function of [RbCl] (= 0.1, 0.2, 0.5, 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, and 7.0 M). Results are calculated from the density profiles of the atomic nuclei weighted by the number of electrons associated with each nucleus and broadened by the spatial resolution of the corresponding XR data. The profile at [Rb] = 0.1 M is offset by five to match the offset for the profile determined experimentally at a similar [Rb] (= 0.09 M), and each of the subsequent profiles is offset by one from the previous profile. The Rb profiles determined by MD in the lowest [RbCl] limit and at 3.0 M (ρ_Rb0.0 and ρ_Rb3.0) are plotted without vertical offset, while the Cl profiles determined by MD in the same solutions (ρ_Cl0.0 and ρ_Cl3.0) are plotted as dotted lines with a vertical offset of four. Black and green open arrows indicate the locations of Cl⁻ and secondary Rb⁺ adsorbed at the mica (001)–water interface, respectively.

The best-fit models of the XR data (SI Appendix, Tables S2–S4) attribute this unexpected change in reflectivity pattern to excess adsorption of Rb⁺ at the mica–water interface. Each total electron-density profile derived from the best-fit model has a protruding peak of solution species adsorbed at a height (z) of ∼2 Å (measured from the top oxygen plane of the mica surface) (Fig. 2B and SI Appendix, Figs. S2–S4). This peak has an electron density that is substantially higher than that of bulk water and a height that matches the height for inner-sphere (IS) Rb⁺ adsorbed in a ditrigonal cavity site of the mica surface (25). With increasing [Rb], the integrated area under the peak (hereafter referred to as the occupancy factor) increases, indicating enhanced adsorption of IS Rb⁺. Additional changes in the interfacial structure beyond the IS Rb⁺ uptake include the emergence and growth of electron-density peaks at z ∼ 4 and 6.5 Å (indicated with black and green open arrows, respectively, in Fig. 2B).

Salinity-dependent variations in the exact distribution of Rb⁺ adsorbed at the mica–water interface were determined using RAXR measured in 0.003- and 0.4-M RbCl solutions (Fig. 2B, SI Appendix, Figs. S5 and S6). In the 0.003-M solution, the derived Rb-specific profile (ρ_Rb0.003) contains IS Rb⁺ at z ∼ 2 Å, consistent with the location of the highest electron-density peak of the solution profile. The coverage of IS Rb⁺ (${\text{Γ}}_{{\text{Rb}}_{\text{IS}}}$) is ∼0.8 Rb⁺/A_UC, where A_UC = 46.72 Ų is the area of the unit cell in mica’s (001) plane. The profile also has a minor fraction of Rb⁺ (with a coverage of ∼0.1 Rb⁺/A_UC) adsorbed farther (centered at ∼6.5 Å, indicated with a green arrow at the bottom in Fig. 2B) from the surface. These two adsorbed Rb⁺ species compensate ∼90% of the negative charge of the mica surface (∼1e⁻/A_UC) (22), consistent with the expectation from classical EDL theories. In a solution with a higher ion concentration (i.e., [Rb] = 0.4 M, Fig. 2B and SI Appendix, Table S5), the derived Rb profile (ρ_Rb0.4) shows a substantial enhancement in IS Rb⁺ coverage compared with that in 0.003-M RbCl (ρ_Rb0.003). The coverage of IS Rb⁺ for ρ_Rb0.4 was ∼1.5 Rb⁺/A_UC, nearly twice as high as that for ρ_Rb0.003. This element-specific analysis also shows two additional Rb⁺ species that are located farther from the surface (at ∼6.5 and 11 Å) and have smaller coverages (∼0.5 and 0.3 Rb⁺/A_UC, respectively) than IS Rb⁺ (SI Appendix, Table S5). Overall, the total coverage of Rb⁺ adsorbed at the mica surface (∼2.3 Rb⁺/A_UC) far exceeds the amount needed for the charge compensation of the mica surface (∼1 Rb⁺/A_UC), indicating the occurrence of charge overscreening that significantly deviates from classical EDL models.

MD simulations were applied to validate the salinity-dependent changes in EDL structure observed by XR and RAXR. Briefly, the simulation represents a slab of muscovite mica, the 2M₁ structure with unit cell formula KAl₂(Si₃Al)O₁₀(OH)₂ based on Catti et al. (30), in contact with solutions of various concentrations in a 52.1 × 45.2 × 180.0 ų periodically replicated simulation cell (Fig. 1D and SI Appendix, Fig. S7; Materials and Methods). Interatomic interactions were described using well-established force fields (31–34) selected based on our previous work (26) and additional validation (Materials and Methods and SI Appendix, Fig. S8). Each system was equilibrated for 1 ns and then simulated for 30 ns at 298 K in the canonical ensemble with fixed number of atoms, N, volume, V, and temperature, T (NVT), with a 1-fs time step.

The electron-density profiles derived from the MD simulations in RbCl solutions are generally consistent with the experimental observations by our XR measurements (e.g., Fig. 2C in comparison with Fig. 2B). The simulations confirm that the electron-density enhancement at z ∼ 2 Å is due to IS Rb⁺ adsorption (as shown in ${\rho }_{Rb0.0}$ and ${\rho }_{Rb3.0}$, obtained from the Rb atomic density profiles weighted by the number of electrons). They also show that the electron-density peak at 4 Å, which is not seen by Rb-RAXR, stems from adsorption of Cl⁻ above the plane of IS Rb⁺ (indicated with black arrows in Fig. 2 B and C). Finally, they predict the existence of additional Rb⁺ species at heights of ∼6.3 Å and ∼10 Å (shown at the bottom of Fig. 2C), yet only at significantly higher concentrations (i.e., [RbCl] ≥ 2 M and 5 M, respectively) than that for RAXR (i.e., [RbCl] = 0.4 M; Fig. 2B). We note that this alternating layer structure is similar to the oscillatory structure of ionic liquids observed at charged interfaces (35, 36), where the formation of discrete layers of charge is controlled by the balance between steric and electrostatic forces between ionic species (37, 38).

We also explore the role of anions through the comparison between the XR data measured in RbCl and RbI aqueous solutions (SI Appendix, Figs. S9 and S10 and Tables S6 and S7). At ∼0.02 ≤ [Rb] < ∼1 M, IS Rb⁺ coverages in RbI solutions increase with increasing [Rb] beyond the level needed for charge compensation, consistent with the overcharging phenomenon observed in RbCl solutions (Fig. 3A). In RbI solutions, the electron-density peak at z ∼ 4 Å, which is attributed to coadsorbed anions by MD simulations (Fig. 2C), has greater occupancy factor and height, consistent with adsorption of more electron-dense and larger I⁻ than Cl⁻ (Fig. 3 B and C and SI Appendix, Fig. S9). When [Rb] ≥ ∼1 M, however, the profiles in RbI solutions show a distinct atomic layering that extends beyond z = 10 Å (SI Appendix, Fig. S10), in stark contrast to those in RbCl solutions, which only show general enhancement in overall electron density in the same height range without any discernible changes in fine structure. These complex interfacial structures in RbI are due to the heterogeneous nucleation and growth of RbI crystals on the mica surface (39, 40). When [RbI] ≥ ∼1 M, the XR data show the growth of new Bragg peaks at q = 2.24 and 4.48 Å⁻¹, corresponding to the (111) and (222) reflections of cubic RbI crystals (SI Appendix, Fig. S10). Specifically, these scattering signals, such as that of RbI (111), appear as well-defined peaks rather than arcs (the latter of which is the X-ray diffraction (XRD) pattern of randomly oriented salt powder), indicative of the structural alignment of these secondary crystals with respect to the mica’s (001) plane (SI Appendix, Fig. S11). It is noteworthy that these solutions were undersaturated with respect to the solid phase (SI Appendix), implying that this nucleation was promoted by the structural similarity (i.e., epitaxy) between the (001) plane of the mica surface and the (111) plane of the RbI crystal. Heterogeneous nucleation of RbI crystals on the mica surface has been observed previously (39, 40) and interpreted to be promoted by the epitaxy, consistent with our interpretation. In contrast, a similar behavior was not observed for RbCl, presumably because the lattice spacings within the RbCl (111) plane are ∼10% smaller than those in the mica surface (SI Appendix, Fig. S11).

Fig. 3.

Control of ion cooperativity over interfacial energetics and structures at the muscovite mica–saline solution interface. (A) [Rb]-dependent changes in the coverage of IS Rb (Γ_RbIS) in RbCl and RbI from XR. The black solid line through the data points is derived from a two-K isotherm model (SI Appendix). The deviation of the data from the classical Langmuir isotherm (green solid line) is due to overcharging. The theoretical limit associated with the formal charge of the mica surface is also shown for comparison. The variation in the coverage of IS Rb obtained from MD simulations is also plotted (open circles). The simulated data show similar trends to the experimental data. However, the adsorption edge is shifted by ∼10 toward higher [Rb], indicating that the simulated adsorption of Rb during overcharging is weaker than that determined by experiment. (B and C) Comparison of the interfacial electron-density profiles between RbCl and RbI solutions. The total electron-density profiles measured in solutions containing [Rb] = ∼0.05, ∼0.5, and ∼1 M are shown in dotted, dashed, and solid lines, respectively. Additional layering is observed in RbI solutions when [Rb] ≥ ∼1 M (i.e., below the saturation concentration of the ionic crystal [shown as a yellow area in A]) (SI Appendix, Figs. S10 and S11). (D and E) Snapshots of the mica–saline solution interface at [RbI] = 3 M at 1 and 20 ns, respectively, showing IS Rb and the first layer of the coadsorbed anions. (F–H) Large-scale simulation of the mica–RbI solution interface at 3 M. Side-view snapshots taken at 1, 18, and 30 ns displaying the evolution of heterogeneous nucleation events. Note the abundance of heterogeneously nucleated crystals in an earlier time (i.e., 18 ns) in contrast to the rare occurrence of homogeneous nucleation (blue arrow, single event observed during a 30-ns-long simulation; Movie S2).

The systematic variation in the Rb uptake behavior provides a window through which to observe atomistic details of the overcharging phenomenon at the mica–water interface (Fig. 3A). In [RbCl] solutions containing [Rb] ≤ 0.02 M, ${\text{Γ}}_{{\text{Rb}}_{\text{IS}}}$ increases with increasing [Rb] until it reaches a plateau at ∼0.9 Rb/A_UC [which is ∼10% higher than ${\text{Γ}}_{{\text{Rb}}_{\text{IS}}}$ determined by RAXR at [Rb] = 0.003 M (22)]. For [Rb] > 0.02 M (for both RbCl and RbI solution systems), the Rb coverage progressively increases beyond this plateau, indicating overcharging. This overcharging occurs at significantly lower salinities (Fig. 3A; with the adsorption edge concentration = 0.48 ± 0.11 M for Rb⁺; SI Appendix) than expected, based on previous analyses (41). For example, the transition from classical to nonclassical charge screening in RbCl or RbI bulk aqueous electrolytes is expected to occur at [Rb] ∼ 3 M (41). The discrepancy between this theoretical calculation and our experimental observation suggests that the mica surface plays a key role in promoting the emergence of nonclassical effects. For [Rb] ≥ 1 M, the Rb⁺ coverage approaches the number density of ditrigonal cavity sites (= 2 sites/A_UC) on the mica surface. Compared to these XR results, the MD simulations, which independently predict the same overcharging phenomenon, underestimate the IS Rb coverage at a given [Rb]. This underestimation indicates that charge overscreening is sensitive to one or several phenomena that are incompletely or indirectly represented in our simulations, which may include atomic polarization effects, mica surface structural relaxation, or the details of mica structural charge distribution (Materials and Methods and SI Appendix, Fig. S7).

To elucidate atomic details of these nonclassical phenomena at the mica–water interface, we simulated the temporal evolution of the RbI system at 3 M with a laterally extended cell (260.5 Å × 225.0 Å in Fig. 3 D–H and SI Appendix, Fig. S12 and Movie S1). In early stages of the simulation (<∼2 ns, Movie S1), the coverage of IS Rb⁺ progressively increases beyond the amount needed for full compensation of the negative charge of the mica surface, indicating the onset of overcharging. In this stage, the simulation trajectories show that the excess Rb⁺ adsorption occurs in the ditrigonal cavity sites that have at least one preexisting adsorbed Rb⁺ in neighbor cavity sites, followed by subsequent adsorption of anions (i.e., I⁻) (Fig. 3D). These adsorbed anions are generally located near the centerline between two adjacent IS Rb⁺ (Fig. 3D and Movie S1), and this adsorbed <Rb···I···Rb>⁺ across two adjacent cavity sites balances the local charge density of the mica surface. With increasing simulation time, the coverage of IS Rb⁺ increases, leading to the increasingly frequent occurrence of IS Rb⁺ ions in three adjacent cavity sites in a triangular configuration. In this geometry, coadsorbed anions are stabilized above the center of the triangle formed by three IS Rb⁺ (Fig. 3E and Movie S1). These simulations clearly show that cooperativity between adsorbed cations and anions, as well as transformation of this correlated ion structure, drives a stepwise evolution in the arrangement of adsorbed ions within the Stern layer.

Our simulations also show additional adsorption of Rb⁺ on the plane of the preestablished adsorbed anions (i.e., beyond what is expected from the classical Stern layer structure). In the RbI system, this secondary Rb⁺ adsorption occurs exclusively in a single site (SI Appendix, Fig. S13), resulting in the layered structure of alternating Rb⁺ and I⁻, which eventually evolves into the nucleation and growth of crystalline structures at multiple locations of the surface (Fig. 3 F–H and Movie S2). With the set of force fields used in this study, despite the existence of metastable RbI and RbCl ion pairs at [Rb] ≥ 1 M (SI Appendix, Fig. S12 and SI Appendix), growth occurs primarily via the ion-by-ion attachment mode described in classical nucleation models (42, 43). The resulting crystalline structures are in the form of cubic RbI crystals whose (111) planes are aligned parallel to the (001) plane of the mica substrate, as confirmed by our in situ observation of the Bragg peaks at elevated RbI concentrations (SI Appendix, Figs. S10 and S11). In contrast, MD simulations in the RbCl system reveal that the secondary Rb⁺ ions dynamically exchange their positions between two distinct states that are energetically equivalent, while no heterogeneous nucleation of RbCl crystals is observed until [RbCl] is close to the salt saturation level (SI Appendix, Fig. S13 and SI Appendix).

Our combined use of experimental and computational approaches visualizes atomic-scale details during the evolution of EDL structure at the negatively charged basal surface of muscovite mica in contact with concentrated saline solutions. The observed transition from classical Langmuir-type full charge compensation by adsorbed ions to nonclassical charge overscreening is controlled by positional correlations between adsorbed ions rather than chemical complexations (e.g., ion pair formation) that are generally assumed in current physicochemical theories. Charge overscreening at the mica–saline aqueous solution interface is described by the formation of discrete atomic layers formed by alternating monovalent cations and anions. This observation is unexpected from ion–ion correlation theories (2–4) for aqueous solutions in which positional correlations between monovalent ions are typically assumed to be negligible. The observed multilayer structure is analogous to the oscillatory structure of ionic liquids developed at charged interfaces in solvent-free systems (35–38). Here, the correlations between monovalent ions is enhanced at elevated ion concentration (i.e., low water content) near the highly charged surface. In natural waters, these ion–ion correlations are expected to be influenced by the presence of other ions, including hydronium and hydroxyl ions in acidic and alkaline solutions, via either competition for sorption sites on the mica surface or changes in ion speciation (e.g., ion pair formation and hydrolysis) in solutions (28, 29, 44). These interactions are expected to be more pronounced and more complex for multivalent cations due to stronger ion–ion correlations (2–4) and the increased role of ion hydration (5–8). In the RbI system, ions adsorbed in this multilayer structure continuously undergo rearrangements in their two-dimensional lattice structure, promoted by epitaxy, and eventually evolve into the nucleation and growth of ionic crystals even from solutions that are undersaturated with respect to the solid phases. These results shed light on the manner in which surface structure and charge distribution control specific interactions of adsorbed ions beyond the Stern layer. More generally, manifestation of the atomistic basis of nonclassical behaviors in the EDL provides a much-needed understanding on the impact of ion cooperativity at charged interfaces in the development of predictive models for element transport in natural environments, including nutrients and heavy metals, and advanced technologies for material growth and synthesis, including energy storage materials.

Materials and Methods

Sample Preparation.

Experimental solutions were prepared by dissolving RbCl (99.8% from Sigma-Aldrich) and RbI (99.9% from Sigma-Aldrich) salts in deionized water (DIW) (18.2 MΩ·cm). Each salt solution was prepared in a series of Rb concentration, [Rb], ranging from 0.01 to 3.0 M (molarity, mol/L). The prepared solutions were stored in high-density polyethylene (HDPE) bottles prior to usage. A gem-quality single-crystal muscovite from Asheville-Schoonmaker Mica Company was cleaved to expose a fresh (001) cleavage surface and rinsed with DIW. The wet crystal was mounted in an X-ray thin-film cell (21) before injection of a Rb-containing solution.

XR Measurements.

X-ray data were collected at the beamline 33-ID-D of the Advanced Photon Source. The monochromatic incident X-ray beam at 18.00 keV (i.e., wavelength, λ, of 0.689 Å) was focused vertically by a Kirkpatrick–Baez mirror. The focused beam had a size of 0.03 mm (v) × 1.0 mm (h) with a flux of ∼5 × 10¹² photons/s at the sample position. In situ crystal truncation rod (CTR) data were collected in the specular geometry as a function of momentum transfer q, defined as 4πsin(2θ/2)/λ = 2πL/d, where 2θ is the angle between the incident and reflected X-rays, L is the Bragg index of the muscovite mica (001) reflection, and d of ∼19.96 Å is the (001) layer spacing (45). Each dataset was collected in the q range from ∼0.15 to ∼4.0 Å⁻¹. During this measurement, the change in [Rb] was monitored by measuring Rb K_a FY at a constant angle of incidence (α = 1.6°, corresponding to the momentum transfer q = 0.48 Å⁻¹). At this angle, the X-ray beam illuminates ∼1.0 mm × 1.0 mm of the mica surface. The CTR data were analyzed using a least-squares regression algorithm described in SI Appendix, Supplementary Methods.

In situ RAXR spectra were collected by scanning photon energy (E) around the X-ray K-absorption edge energies of Rb (E_Rb = ∼15.2 keV) at a series of fixed q. The evolution of [Rb] was also monitored by measuring Rb K_a FY. When [Rb] > 0.6 M, we flushed the cell with a fresh 0.1-M RbCl solution, and excess solution was drained by gravity out of the cell. At the beginning of and during a series of data collection in one setup, the stability of the interfacial structure was monitored by periodically measuring RAXR spectra at q = 0.48 Å⁻¹, where the RAXR signals are sensitive to the coverage and average height of adsorbed cations (46). Only data that were measured within 0.2 M ≤ [Rb] ≤ 0.6 M were included for the analyses. Details of the RAXR data analysis are described in SI Appendix, Supplementary Methods.

MD Simulations.

Simulation setup.

The muscovite structure was simulated as a rigid body except for the structural H atoms of the hydroxyl groups and the interlayer K ions, and the SHAKE algorithm (47) was employed for the water molecules to keep them rigid. Interatomic interactions were solved up to 12 Å in real space. Long-range Coulomb interactions beyond 12.0 Å were solved in k-space using the particle–particle particle–mesh (PPPM) technique with an accuracy of 99.99%. All MD simulations were carried out on the supercomputers at the National Energy Research Scientific Computing Center (NERSC) using the code Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) (48).

Isomorphic substitution.

In accordance with the ideal muscovite unit cell chemical formula, KAl₂(Si₃Al)O₁₀(OH)₂ (30), one out of four Si atoms was substituted by Al following Löwenstein’s avoidance rule (i.e., no neighboring isomorphic Al substitution), in which the substitution sites were randomly determined for each tetrahedral sheet. The resulting heterogeneity of Al distribution (i.e., charge distribution) in the mica model created patches with higher or lower surface charge density (SI Appendix, Fig. S7). We note that the ideal formula of the simulated muscovite likely does not exactly match the unit cell formula of the natural muscovite used in the XR experiments, which may explain the small difference in predicted versus measured IS Rb⁺ coverage.

Selection of force fields for saline conditions.

For both RbCl and RbI systems, we performed 1-ns-long bulk liquid water simulations for a wide range of concentrations. The simulations were run in the isothermal-isobaric ensemble with fixed number of atoms, N, pressure, P = 1 bar, and temperature, T = 298 K (NPT), in a 31 × 31 × 50 ų cell with periodic boundary conditions. The resulting density was plotted as a function of ion concentration (in units of molality, mol/kg) and compared against experimental data (SI Appendix, Fig. S8 A and B). Experimental data for RbI solutions were limited, and therefore the selection of force fields was informed mostly by the RbCl system. Results showed that the parameters of Dang (33) and Dang and Garrett (32), in combination with the extended simple point-charge (SPC/E) water model (31), underestimate the salinity dependence of water density by about 2 to 10% from the experimental data (49, 50). Interaction parameters proposed more recently by Joung and Cheatham (51) yield improved predictions of the RbCl density. Unfortunately, the compatibility of the Joung and Cheatham parameters with the CLAYFF force field (34) is unsatisfactory with respect to our XR data as shown in SI Appendix, Fig. S8C, in which the density enhancement due to the IS Rb⁺ adsorption is predicted at 1.7 Å (offset of 0.3 Å) and the second and the third density peaks tend to shift away from the mica surface as the concentration increases.

Data Availability

All study data are included in the article and/or supporting information.