Abstract
The COVID-19 epidemic, in which millions of people suffer, has affected the whole world in a short time. This virus, which has a high rate of transmission, directly affects the respiratory system of people. While symptoms such as difficulty in breathing, cough, and fever are common, hospitalization and fatal consequences can be seen in progressive situations. For this reason, the most important issue in combating the epidemic is to detect COVID-19(+) early and isolate those with COVID-19(+) from other people. In addition to the RT-PCR test, those with COVID-19(+) can be detected with imaging methods. In this study, it was aimed to detect COVID-19(+) patients with cough acoustic data, which is one of the important symptoms. Based on these data, features were obtained from traditional feature extraction methods using empirical mode decomposition (EMD) and discrete wavelet transform (DWT). Deep features were also obtained using pre-trained ResNet50 and pre-trained MobileNet models. Feature selection was applied to all obtained features with the ReliefF algorithm. In this case, the highest 98.4% accuracy and 98.6% F1-score values were obtained by selecting the EMD + DWT features using ReliefF. In another study in which deep features were used, features obtained from ResNet50 and MobileNet using scalogram images were used. For the features selected using the ReliefF algorithm, the highest performance was found with support vector machines-cubic as 97.8% accuracy and 98.0% F1-score. It has been determined that the features obtained by traditional feature approaches show higher performance than deep features. Among the chaotic measurements, the approximate entropy measurement was determined to be the highest distinguishing feature. According to the results, a highly successful study is presented with cough acoustic data that can easily be obtained from mobile and computer-based applications. We anticipate that this study will be useful as a decision support system in this epidemic period, when it is important to correctly identify even one person.
Keywords: COVID-19, Cough, Deep features, Empirical mode decomposition, Discrete wavelet transform, ReliefF
1. Introduction
The new coronavirus disease, declared as a pandemic by the World Health Organization (WHO), first appeared in Wuhan, China. It spread throughout China and other countries in the world in a short time [1,2]. The name of the virus that causes the epidemic, popularly known as COVID-19, is severe acute respiratory syndrome coronavirus-2 (SARS-CoV-2) [3]. This virus causes severe respiratory infections with very high mortality and poses a serious threat to humans. The most common symptoms of the COVID-19 outbreak are severe fever, dry cough, and difficulty in breathing [4]. In addition, it is known to be seen in symptoms such as low back pain, weakness, diarrhea, nausea, headache and dizziness [5]. Acute Respiratory Distress Syndrome (ARDS) may occur after a while in people with severe illness. In addition to all these symptoms, a series of tests are performed to detect COVID-19 patients. The “reverse transcription polymerase chain reaction (RT-PCR)” test, known as the gold standard, is performed with the recommendation of WHO [6]. This test is time-consuming and costly, and results are obtained late [7]. Therefore, medical imaging methods are used to detect COVID-19 patients in addition to this test [8]. Among these, the most used are Computed tomography (CT), and chest radiography (X-ray) images. Another helpful method is approaches based on the analysis of cough acoustic sounds produced by the respiratory system [9]. There are many studies in the literature using CT and X-ray images in the detection of COVID-19 [10,11]. Deep learning techniques that can work directly on data are widely used [12,13]. State-of-art models were used frequently in these studies. These include pre-trained models and transfer learning models in abundance. There are many studies done with another approach called deep feature extraction [14,15]. Traditional feature extraction methods are among the most used methods in detecting COVID-19 patients [16,17]. Studies conducted with cough acoustic data analysis, which is one of the remarkable approaches, has recently taken its place in the literature. Approaches based on cough acoustic data for detecting COVID-19 patients are as follows: Laguarta et al. proposed a study based on analysis of cough audio recordings taken from a mobile phone. They obtained the cough audio recordings through the website they set up. They proposed a high-performance model with Mel Frequency Cepstral Coefficients (MFCCs) conversion and three pre-trained parallel ResNet50 models to these signals. The highest recall and specificity score achieved were 98.5% and 94.2%, respectively [18]. Alsabek et al. proposed a study using cough sound, breathing sound, and voice data from COVID-19 patients and non-COVID-19 people. In their work, they obtained the features using the MFCCs method and conducted a study on Pearson's Correlation coefficient values [19]. Sharma et al. worked with a data set called “Coswara”, which includes data for cough, breath, and voice. They proposed a study with 28 spectral measurements and random forest classifiers. The overall accuracy rate obtained was 67.7% [20] Mouawad et al. have developed a model that can detect coughs and other vocal sounds with high sensitivity and, provides fast and reliable scanning. They used MFCCs from spectral approaches and recurrence quantification analysis methods from nonlinear statistical approaches. They reported that they achieved high performance with five different classification algorithms. Their performance was calculated to have an accuracy value of 97.0% and F1-score value of 62.0% [21]. Pal and Sankarasubbu proposed a study based on four classes of cough signals: COVID-19, asthma, bronchitis, and healthy. They obtained results of working with time, frequency and nonlinear features such as MFCCs, log energy, zero crossing rate, skewness, entropy, formant frequencies, and kurtosis. The highest accuracy score and F1-score achieved were 97.0% and 97.3%, respectively [22]. In another study, Imran et al. aimed to identify COVID-19 patients by looking at cough sound signals with a study they called AI4COVID-19. They obtained mel-spectrogram images for CNN models. For the classical machine learning approach, they used MFCC and principal component analysis based on feature extraction and support vector machines (SVM) classification algorithm. As a result, they achieved 95.6% accuracy and 95.6% F1-score [23].
In the mentioned studies, researches conducted with various sound data, especially cough sound data, were included. In almost all studies, they have carried out research using the MFCCs method. In this study, different from the others, time domain and nonlinear features were obtained by using 5-level empirical mode decomposition (EMD) and 5-level discrete wavelet transform (DWT) methods. The entire study using cough acoustic signals from people with COVID-19(+) and COVID-19(−) is shown in Fig. 1 . In addition to this study, deep features obtained from scalogram images obtained by continuous wavelet transform were also used. Deep features have been obtained over the ResNet50 and MobileNet models. Using the ReliefF feature selection method, it has been investigated how the results will change with fewer features. SVM (linear, quadratic, cubic) algorithms were used to determine performances in the traditional machine learning approach and deep feature extraction approach.
Fig. 1.
The schematic of the whole proposed hybrid method.
2. Materials and methods
2.1. Dataset
Cough acoustic data on COVID-19(+) and COVID-19(−) have been obtained from the free access site https://virufy.org/. The data was provided by a mobile application developed by Stanford University. The data belong to a total of 1187 people. All data were determined as positive and negative according to the results obtained from the RT-PCR test. As a result of the test, data of 595 COVID-19(+) and 592 COVID-19(−) people were labeled. All data were removed from the noise. In addition, all data were normalized with the z-normalization method before the study carried out.
2.2. Z-normalization
Z-normalization is a type of standard deviation that allows us to find the probability of a value occurring in a normal distribution, or to compare two samples from different populations. Z-normalization can take a positive or negative value; minus or plus indicates whether our value is above or below the arithmetic value.
Z-normalization can be expressed by the following formula:
| (1) |
Where x is any point, mean is the mean of the population, and std is the standard deviation of the population.
2.3. Empirical mode decomposition
EMD is a method used to analyze non-linear and non-stationary data. This method was introduced by Huang in 1998 [[24], [25], [26]]. In EMD, the starting signal is cyclically decomposed into intrinsic mode functions (IMFs) from high frequency to low frequency. IMFs are based on two important principles [24]. These:
-
1)
The number of local extreme points and zero crossings in the whole data set must be equal or differ by at most 1 point.
-
2)
At any point, the mean value of the envelope defined by the local maximums and local minimums is zero.
EMD operation is applied to a given x(t) signal as follows:
-
1)
All local extreme points of the original x(t) signal are defined.
-
2)
The upper and lower envelopes of the x(t) signal are created by interpolating the cubic splines.
-
3)
Calculate the average m(t) value at each point from the upper and lower envelopes.
-
4)
The difference signal is calculated by subtracting the average value from the original signal. d(t) = x(t)-m(t)
-
5)
If d(t) is an IMF, it is assigned c(t) = d(t) and if d(t) is not an IMF, d(t) is considered the original signal and the first 4 steps d(t) value is an IMF is repeated until.
-
6)
After finding the first component, it is subtracted from the original signal and the residue is obtained as r(t) = x(t)-c(t).
-
7)
In the last step, r(t) is considered the original data and the first 6 steps are repeated. EMD, the process is stopped when residue r(t) is a monotonic function or a constant from which no more IMF components can be removed.
The 5-level IMF signals obtained from the COVID-19(+) and COVID-19(−) acoustic cough data used in the study are shown in Fig. 2 . Standard deviation, mean and root mean square were used from time domain measurements on each IMF signal. From non-linear chaotic measurements, Shannon entropy, log energy, threshold, time, norm and approximate entropy measurements were used. A total of 45 features obtained are shown in Table 1 .
Fig. 2.
COVID-19(+) and COVID-19(−) acoustic cough data and 5-level IMF signals.
Table 1.
Description of obtained features on IMF signals.
| Features | Description | Number of Features |
|---|---|---|
| Standard Deviation | Standard deviation of all IMFs | 5 |
| Mean | Mean of all IMFs | 5 |
| Root Mean Square | The square root of the mean of all IMFs | 5 |
| Shannon | Shannon entropy of all IMFs | 5 |
| Log Energy | Log energy entropy of all IMFs | 5 |
| Threshold | Threshold entropy of all IMFs | 5 |
| Time | Time entropy of all IMFs | 5 |
| Norm | Norm entropy of all IMFs | 5 |
| Approximate | Approximate entropy of all IMFs | 5 |
| Total Number of Features | 45 |
2.4. Discrete wavelet transform
Continuous wavelet transform (CWT) results in the formation of very large data stacks. Studying all of these data poses great difficulties. As a result of the wavelet transform, wavelet coefficients are found depending on the scale and position. If scaling and shifting are chosen as powers of two (2n), the solutions are more effective than the CWT. This process, called DWT, is as accurate as the CWT. Wavelet can be expressed as a small part of the wave. In this context, wavelet is a time-limited vibration signal [27]. Daubechies, Morlet, Haar, Mexican hat are the main types of wavelet that are most frequently utilized in the wavelet transform. Wavelets separate the data according to different frequency components. In addition, wavelets match the data to their scales. Calculation of wavelet coefficients at scale value causes the occurrence of a large number of coefficients and excessive processing load. Therefore, calculating these coefficients only in the selected scales and time period provides many advantages. In this way, a smaller number of coefficients are obtained, which still give the variation of the frequency scale information of the signal over time. These coefficients form a time series and these time series can be used for various goals. In the discrete wavelet transform process, binary scale and time step are used very often. In other words, each element obtained in this way gives the time series or wavelet coefficients of the scale values in the form of two and multiples of two. The wavelet function used for DWT is as follows:
| (2) |
Here m and n are integer values. These values are the shifting parameters of the wavelet in scale and time axis, respectively. s 0 indicates a fixed shifting step and is taken as 2 in this study. τ indicates the shifting interval in the time axis and its value is used as 1. These values were chosen by considering the most frequently used values in the literature. The wavelet equation created using multiples of two can be expressed as:
| (3) |
Spectral analysis of non-stationary cough acoustic signals of COVID-19 patients were performed using a small-sized window at high frequencies and a large-sized window at low frequencies. With the wavelet transform, 5-level detail and approximate coefficients were obtained. In this study, the highest results were obtained with the Daubechies-6 (db6) main wavelet. Therefore db6 was used. The 5-level Detail (D1, D2, D3, D4, D5) and Approximate (A5) coefficients obtained from cough acoustic signals are shown in Fig. 3 . Standard deviation, mean and root mean square from time domain measurements were used for each coefficient. From non-linear chaotic measurements, Shannon entropy, log energy, threshold, time, norm and approximate entropy measurements were used. A total of 54 features obtained are shown in Table 2 .
Fig. 3.
COVID-19(+) and COVID-19(−) cough data and 5-level DWT coefficients.
Table 2.
Description of obtained features on DWT approximate (A) and detailed (D) coefficients (coef) signals.
| Features | Description | Number of Features |
|---|---|---|
| Standard Deviation | Standard deviation of D1,D2,D3,D4,D5, A5 coef. | 6 |
| Mean | Mean of D1,D2,D3,D4,D5, A5 coef. | 6 |
| Root Mean Square | The square root of D1,D2,D3,D4,D5, A5 coef. | 6 |
| Shannon | Shannon entropy of D1,D2,D3,D4,D5, A5 coef. | 6 |
| Log Energy | Log energy entropy of D1,D2,D3,D4,D5, A5 coef. | 6 |
| Threshold | Threshold entropy of D1,D2,D3,D4,D5, A5 coef. | 6 |
| Time | Time entropy of D1,D2,D3,D4,D5, A5 coef. | 6 |
| Norm | Norm entropy of D1,D2,D3,D4,D5, A5 coef. | 6 |
| Approximate | Approximate entropy of D1,D2,D3,D4,D5, A5 coef. | 6 |
| Total Number of Features | 54 |
2.5. Obtaining scalogram images
In this study, deep features were obtained from pre-trained models in which scalogram images were given as input. Scalogram images are obtained from one-dimensional cough acoustic signals with the help of continuous time wavelet transform. For detailed information, refer to the relevant references [28,29]. Continuous Daubechies-6 (db6) main wavelet was used in the study. The scalogram images of the COVID-19(+) and COVID-19(−) signals are shown in Fig. 4 .
Fig. 4.
2D scalogram images obtained over 1D dimensional cough signals a) for COVID-19(+) b) for COVID-19(−).
2.6. Deep feature extraction
Convolutional neural network (CNN) is one of the deep learning models consisting of feature extraction and classification parts [30]. It exhibits high performance with end-to-end approaches using raw data. Likewise, the use of the extracted features in hybrid systems also yields high results. Convolution processes, pooling processes, normalization processes and dilution processes performed with filters of different sizes within it provide the creation of a map specific to each pattern. There are many studies in the literature using various pre-trained CNN models [7,31]. In this study, deep features were obtained over two different architectures, ResNet50 and MobileNet. The ResNet50 model is among the models commonly used in the literature. It has a structure consisting of blocks of residual values that feed the next layers. The ResNet50 model consists of 25.6 million parameters [32]. Another lighter and less computationally complex model used in feature extraction is the pre-trained MobileNet CNN architecture [33]. MobileNet model consists of 3.5 million parameters. In deep learning models, feature extraction can be from all layers. However, generally, the features obtained from the layer just before the classification step are used over the fully connected layer. In this study, deep features were obtained over the fully connected layers “fc1000” for ResNet50 and ‘Logits’ for MobileNet. Feature maps of 1 × 1 × 1000 size were obtained on the layers where features were extracted. Feature map images in different layers obtained only for the pre-trained ResNet50 model are given in Fig. 5 . The mini-batch size value was chosen as 10 for the ResNet50 and MobileNet models. The epoch value was set to 30. The learning rate was chosen as 0.0001.
Fig. 5.
Outputs of the input sample image on some layers.
2.7. Feature selection using ReliefF algorithm
ReliefF algorithm is a feature selection method developed by Kira et al., in 1992. The main purpose of this method is to weigh the features according to the correlation between them [34]. ReliefF algorithm gives successful results on the data of two classes. However, it did not yield successful results for data sets containing more than two classes. To eliminate this problem, Kononenko developed the ReliefF algorithm, which works in data sets with more than two classes, in 1994 [35]. The ReliefF method is a method used in multi-class pattern recognition problems, especially when classifying features [36].
2.8. Support vector machines
SVM is a highly effective and easy supervised learning method used in machine learning, especially in classification. SVM was introduced by Vapnik [37]. SVM aims to find the boundary where classes are separated from each other, a function that can draw an optimum hyperplane. For each class, a hyperplane is drawn that passes over the elements closest to this limit. Therefore, because the drawn hyperplanes provide support, they are also called support vectors. A plurality of optimal hyperplanes can be drawn equidistant from these support planes. However, this gives optimum hyperplane solution where the separation between classes is farthest from optimum hyperplanes. There are no class members on this optimum hyperplane as shown in Fig. 6 . This method is often used for linearly separable data. However, for data that cannot be separated linearly, a solution is found by making the data linearly decomposable through kernel functions shown in Table 3 . The parameter of C was tested from 0.01 to 50 with 0.1 increments. The kernel scale was set to 1 and the box constraint set to 1.
Fig. 6.
General procedure of SVM algorithm.
Table 3.
Polynomial (Poly) kernel functions.
| Kernel Function | Mathematical Expression | Parameter |
|---|---|---|
| Poly. Kernel | K(x, y) = ((x.y) + 1)d | Poly. Degree(d) |
| Normalized Poly. Kernel | K(x,y) = | Poly. Degree(d) |
2.9. Performance metrics
The results were evaluated using five different performance metrics in this study [38,39].
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
TP = True Positive, FP = False Positive, TN = True Negative, FN = False Negative. The number of what the classifier actually identified as COVID-19(+) and COVID-19(+) is TP, the number of people mistaking it as COVID-19(−) is FN, actually COVID-19(−) and the number of what the classifier identified as COVID-19(−) is TN, FP is when those with COVID-19(−) are mistakenly classified as COVID-19(+) [40].
While determining the classifier performances, the data were divided into test and training datasets by using the 5-fold cross validation method. In the k-fold evaluation method, the dataset is divided into k parts. While the k-1 piece is used for training, one of them is used for testing. This process is repeated until all parts are used for testing. Classifier performance is calculated as classifier training and test performance by taking averages separately for training and testing [41,42].
3. Experimental results
In this study, the pre-processing of the cough acoustic signals obtained, the features obtained by traditional and deep learning approaches, the feature selection process, and the determination of all performance metrics were carried out with the help of MATLAB2020a software. In the first study, traditional machine learning approaches were used. From the signals obtained as a result of z-normalization, 45 features for EMD and 54 features for DWT were extracted. All these features were obtained separately for each data. The contribution of the best distinguishing features to success was investigated with the help of the ReliefF algorithm. All these results are given in Table 4 .
Table 4.
Performance comparison of all EMD and all DWT based features and selected features by ReliefF algorithm. Performances in the left column are all features, performances in the right column are selected features by ReliefF.
(Acc, accuracy, Rec, recall, Spe, specificity, Pre, precision, F1, F1-score).
| Methods/Algorithm | Performances(%) for all features |
Performances(%) for selected features |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Acc | Rec | Spe | Pre | F1 | Acc | Rec | Spe | Pre | F1 | |
| EMD/SVM Linear | 86.0 | 88.9 | 83.2 | 84.0 | 86.4 | 89.5 | 91.6 | 87.4 | 87.8 | 89.7 |
| EMD/SVM Quadratic | 84.7 | 87.5 | 81.8 | 82.7 | 85.1 | 87.3 | 89.2 | 85.4 | 85.9 | 87.5 |
| EMD/SVM Cubic |
83.7 |
86.5 |
80.8 |
81.8 |
84.1 |
86.5 |
89.0 |
84.0 |
84.7 |
86.8 |
| DWT/SVM Linear | 96.5 | 97.5 | 95.5 | 95.5 | 96.5 | 97.2 | 98.3 | 96.1 | 96.2 | 97.2 |
| DWT/SVM Quadratic | 94.4 | 96.3 | 92.6 | 92.8 | 94.5 | 98.1 | 99.0 | 97.3 | 97.3 | 98.2 |
| DWT/SVM Cubic |
93.9 |
95.8 |
91.9 |
92.2 |
94.0 |
97.0 |
98.0 |
96.0 |
96.0 |
97.0 |
| EMD + DWT/SVM Linear | 97.6 | 98.6 | 96.5 | 96.5 | 97.6 | 98.4 | 99.5 | 97.3 | 97.4 | 98.6 |
| EMD + DWT/SVM Quadratic | 96.2 | 97.5 | 95.0 | 95.1 | 96.2 | 98.1 | 99.3 | 97.0 | 97.1 | 98.2 |
| EMD + DWT/SVM Cubic | 95.3 | 96.6 | 93.9 | 94.1 | 95.3 | 98.0 | 99.2 | 96.8 | 96.9 | 98.1 |
According to this table, the performances obtained through EMD and DWT were compared in determining the COVID-19(+) and COVID-19(−) classes, which were tried to be determined by three different SVM approaches. At the same time, performances were obtained by combining both approaches. The results obtained with the EMD have the lowest performance among the results obtained with the traditional approach. It has been observed that the performance is slightly increased for the features selected with ReliefF. The same is not the case with the features obtained with DWT. Very high results were obtained even without feature selection. At the same time, performances were obtained by combining both approaches. In SVM quadratic and SVM cubic algorithms, the performance of the features selected with ReliefF has increased significantly. The results are obtained very high by using EMD and DWT features together. In the research, the highest performance values were obtained with these features. For SVM linear 98.4% accuracy, 99.5% recall, 97.3% specificity, 97.4% precision and 98.6% F1-score values were obtained. Three high-performance features among the EMD and DWT features selected with ReliefF are given in Fig. 7 . Here, approximation entropy (IMF1, IMF3, IMF4, D1, D2), Log Energy (D1) measurements are the features with the highest distinctiveness selected with ReliefF. It is clear that approximate entropy measurement, one of the nonlinear chaotic approaches, can be said to be a very effective method for distinguishing COVID-19(+)/(−) states for EMD and DWT features.
Fig. 7.
Boxplot representation of features with high distinctiveness for EMD (upper) and DWT (bottom) (p < 0.001).
In the second study, deep features obtained from CNN models, in which 2D scalogram images are given as input, are used. 1000 deep features were obtained separately for each of the ResNet50 and MobileNet CNN models. The performance results obtained from these features and the features selected with the help of the ReliefF method are presented in detail in Table 5 .
Table 5.
Performance comparison of deep features and deep features selected by ReliefF algorithm. Performances in the left column are all deep features, performances in the right column are selected deep features by ReliefF.
(Acc, accuracy, Rec, recall, Spe, specificity, Pre, precision, F1, F1-score).
| Methods/Algorithm | Performances(%) for all features |
Performances(%) for selected features |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Acc | Rec | Spe | Pre | F1 | Acc | Rec | Spe | Pre | F1 | |
| MobileNet/SVM Linear | 82.5 | 85.6 | 79.3 | 80.5 | 83.0 | 85.0 | 88.2 | 81.8 | 82.9 | 85.4 |
| MobileNet/SVM Quadratic | 80.6 | 84.0 | 77.3 | 78.6 | 81.2 | 86.0 | 89.4 | 82.7 | 83.7 | 86.4 |
| MobileNet/SVM Cubic |
80.1 |
84.0 |
76.3 |
77.9 |
80.8 |
87.3 |
89.9 |
84.7 |
85.4 |
87.6 |
| ResNet50/SVM Linear | 78.3 | 81.6 | 75.1 | 76.5 | 79.0 | 85.2 | 87.2 | 83.2 | 83.8 | 85.4 |
| ResNet50/SVM Quadratic | 86.1 | 88.2 | 84.0 | 84.6 | 86.4 | 97.4 | 97.6 | 97.1 | 97.2 | 97.5 |
| ResNet50/SVM Cubic | 84.0 | 86.1 | 81.9 | 82.5 | 84.3 | 97.8 | 98.5 | 97.3 | 97.4 | 98.0 |
According to this table, it is seen that the performances increase significantly because of feature selection in deep features. It has been concluded that the features obtained through ResNet50 have higher success compared to the features obtained from MobileNet. The highest performance value was obtained from the selection of ResNet50 deep features with ReliefF. These performances were determined as 97.8% accuracy, 98.5% recall, 97.3% specificity, 97.4% precision and 98.0% F1-score values.
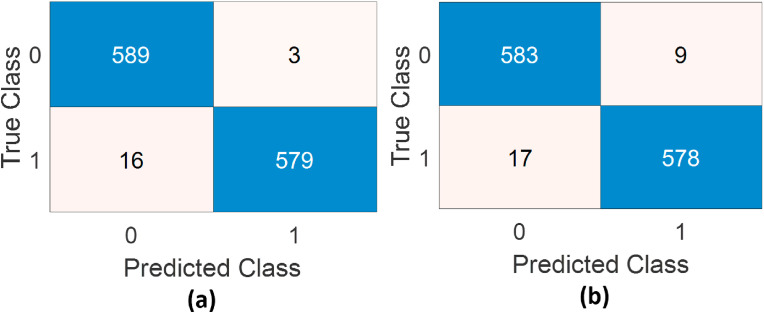
The confusion matrix for the highest performance result from the results obtained with traditional machine learning approaches is given in Fig. 8 -(a). It is clear that while 16 of those in the COVID-19(+) were detected incorrectly, only 3 of those in the COVID-19(−) class were detected incorrectly. The confusion matrix with the highest performance in the study using deep features is given in Fig. 8-(b). It can be said that while 17 of those in the COVID-19(+) class were detected incorrectly, 9 of those in the COVID-19(−) class were detected incorrectly.
Fig. 8.
Confusion matrices belonging to the highest performances a) from traditional features b)from deep features. (0, COVID-19(−), 1, COVID-19(+)).
4. Discussion
One of the most talked about topics of recent years is undoubtedly COVID-19 case. The most important stage of getting rid of this epidemic is the correct detection process. For this reason, there are many machine learning-based studies in the literature [9,10]. Detection of COVID-19(+) cases with cough acoustic signals, which offer a different approach, are among the current alternative approaches. The comparisons of the studies in this field are given in Table 6 . In these studies, mostly traditional machine learning approaches are used.
Table 6.
COVID-19 detection using acoustic signals in the literature. (CV, cross validation, Acc, accuracy, Spe, specificity, Rec, recall, F1, F1-score).
| Authors | Methods | Number of Data | Performance(%) |
|---|---|---|---|
| Pahar et al. (2020) [43] | MFCCs, log energy, zero-crossing rate | 1171 | Rec = 93.0 Spe = 95.0 |
| and kurtosis/ResNet50 | Acc = 98.0 | ||
| Laguarta et al. (2020) [18] | MFCCs/3 parallel ResNet50 | 5320 | Rec = 98.5 Spe = 94.2 |
| Sharma et al. (2020) [20] | MFCCs, and other spectral measurements/ | 941 | Acc = 67.7 |
| random forest | |||
| Mouawad et al. (2020) [21] | MFCCs and RQA/XGBoost | 1927 | Acc = 97.0 F1 = 62.0 |
| Pal ve Sankarasubbu (2020) [22] | MFCCs, time domain and, | 150 | Rec = 96.9 Spe = 96.8 |
| non-linear measurements/TabNet network | Acc = 97.0 F1 = 97.3 | ||
| Imran et al. (2020) [23] | MFCC and PCA/SVM | 543 | Rec = 96.0 Spe = 95.2 |
| Acc = 95.6 F1 = 95.6 | |||
| This study | IMF and DWT based features+ | 1187 | Rec=99.5 Spe=97.3 |
| ReliefF feature selection/SVM | Acc=98.4 F1=98.6 | ||
| This study | ResNet50 based deep features+ | 1187 | Rec=98.5 Spe=97.3 |
| ReliefF feature selection/SVM | Acc=97.8 F1=98.0 |
Pahar et al. achieved 95% accuracy with the ResNet50 CNN model. Laguarta et al. obtained a sensitivity value of 98.5% and a specificity value of 94.2% using 3 pre-trained parallel ResNet50 model. Sharma et al. determined the overall accuracy value of 66.74% for random forest classifier test data from a data set called Coswara. Mouawad et al. reported that they achieved high performance with 5 different classification algorithms. They obtained an average accuracy of 97% from the cough signals. Pal and Sankarasubbu achieved 95.04 ± 0.18% specificity and 96.83 ± 0.18% accuracy with the method called TabNet with 4 classes (COVID-19, Asthma, Bronchitis, and Healthy). Imran et al. obtained 95.6% overall accuracy using SVM classification algorithm. In all these studies, the features and images obtained by using the Mel Frequency Cepstral Coefficients (MFCCs) method were used.
In this study, feature extraction was performed with 5-level empirical mode decomposition and 5-level discrete wavelet transform to distinguish between COVID-19(+) and COVID-19(−) classes. 9 measurements were obtained from the signals at each level. The performances were analyzed by making the feature selection with the ReliefF method. The highest 98.4% Accuracy and 98.6% F1-score values were obtained by using SVM (linear) with EMD and DWT measurements and ReliefF feature selection. In our other research where deep features were used, the performances were analyzed using the features obtained from ResNet50 and MobileNet using scalogram images and the features selected by ReliefF. As a result, the highest 97.8% Accuracy and 98.0% F1-score values were obtained in this study. It can clearly be stated that the features obtained by traditional feature approaches show higher performance than deep features. In addition, approximate entropy measurements are among the features with the highest discrimination from nonlinear measurements. The issues that distinguish the study from other studies can be summarized as follows:
1) Detection of COVID-19(+) patients based on cough acoustic signals has been realized with traditional machine learning approaches and deep learning approaches. 2) The performances of EMD and DWT methods were analyzed. 3) The performances of the deep features obtained from 2D Scalogram images were investigated. 4) Feature selection was made with the ReliefF method. The features with the highest discrimination were determined. 5) A decision support system has been proposed to experts for identifying COVID-19(+) people with an alternative hybrid approach that works with very high accuracy.
As an alternative to imaging techniques, it is essential that the detection of COVID-19(+) patients can be based on cough acoustic signals. This method can easily be integrated as a smartphone application and a computer application. In this way, it can become easier to control the epidemic. As a result, being able to protect even one person from the epidemic is one of the most beneficial tasks in this epidemic process. In this epidemic affecting the whole world, we believe that such systems with high accuracy will make a significant contribution. One of the reasons why deep features show lower performance than traditional methods is the limited number of data. The limited number of data is one of the disadvantages of the study. Increasing the number of data received from different centers will provide more stable systems.
In our future studies, the number of nonlinear measurements will be increased. Meta-heuristic feature selection methods will be applied. Analyzes of the performances will be made with a large number of classification algorithms.
5. Conclusion
In the detection of COVID-19(+) patients, a computer-assisted automatic diagnosis system working with high accuracy by a hybrid model has been proposed. The study was conducted with the traditional feature extraction approach and deep feature extraction obtained through EMD and DWT. Feature selection was made with ReliefF in order to increase the performance with less features. It has been determined that the features obtained with DWT from traditional machine learning methods can distinguish COVID-19(+) ones with high performance. We think that alternative automatic detection systems with such high performance will be useful in the evaluation of COVID-19(+) cases.
Funding
There is no funding source for this article.
Ethical approval
This article does not contain any data, or other information from studies or experimentation, with the involvement of human or animal subjects.
Declaration of competing interest
The authors declare that there is no conflict to interest related to this paper.
References
- 1.Liu W., Yue X.G., Tchounwou P.B. Vol. 17. Int J Environ Res Public Health; 2020. Response to the COVID-19 Epidemic : The Chinese Experience and Implications for Other Countries; pp. 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Guan W.J., Liang W.H., Zhao Y., Liang H.R., Chen Z.S., Li Y.M., Liu X.Q., Chen R.C., Tang C.I., Wang T., Ou C.Q., Li L., Chen P.Y., Sang L., Wang W., Li J.F., Li C.C., Ou L.M., Cheng B., Xiong S., Ni Z.Y. Eur Respir J.; 2020. Comorbidity and its impact on 1590 patients with COVID-19 in China: a nationwide analysis. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lai C.C., Shih T.P., Ko W.C., Tang H.J., Hsueh P.R. Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) and coronavirus disease-2019 (COVID-19): The epidemic and the challenges. Int J Antimicrob Agents. 2020;55(3):105924. doi: 10.1016/j.ijantimicag.2020.105924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Menni C., Sudre C.H., Steves C.J., Ourselin S., Spector T.D. Correspondence Quantifying additional will save lives. Lancet. 2020;395:e107–e108. doi: 10.1016/S0140-6736(20)31281-2. 10241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhang L.-b., Pang R.-r., Qiao Q.-h., Wang Z.-h., Xia X.-y., Wang C.-j., Xu X.-l. 2020. Successful Recovery of COVID-19-Associated Recurrent Diarrhea and Gastrointestinal Hemorrhage Using Convalescent Plasma; pp. 5–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lim J., Lee J. Current laboratory diagnosis of coronavirus disease. Korean J Intern Med. 2020;2019:741–748. doi: 10.3904/kjim.2020.257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ardakani A.A., Kanafi A.R., Acharya U.R., Khadem N., Mohammadi A. Application of deep learning technique to manage COVID-19 in routine clinical practice using CT images: results of 10 convolutional neural networks. Comput. Biol. Med. 2020;121(March) doi: 10.1016/j.compbiomed.2020.103795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.He C., Wang D.-q., Sun J.-l., Gan W.-n., Lu J.-y. 2020. The Role of Imaging Techniques in Management of COVID-19 in China : from Diagnosis to Monitoring and Follow-Up; pp. 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hariri W., Narin A. 2012. Deep Neural Networks for COVID-19 Detection and Diagnosis Using Images and Acoustic-Based Techniques: A Recent Review, arXivarXiv.http://arxiv.org/abs/2012.07655 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shoeibi A., Khodatars M., Alizadehsani R., Ghassemi N., Jafari M., Moridian P., Khadem A., Sadeghi D., Hussain S., Zare A., Sani Z.A., Bazeli J., Khozeimeh F., Khosravi A., Nahavandi S., Acharya U.R., Shi P. 2007. Automated Detection and Forecasting of COVID-19 Using Deep Learning Techniques: A Review, arXivarXiv; p. 10785.http://arxiv.org/abs/2007.10785 [Google Scholar]
- 11.Swapnarekha H., Sekhar H., Nayak J., Naik B. Role of intelligent computing in COVID-19 prognosis : a state-of-the-art review. Chaos, Solit. Fractals. 2020;138 doi: 10.1016/j.chaos.2020.109947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ranjan S., Ranjan D., Sinha U., Arora V. Biomedical Signal Processing and Control Application of deep learning techniques for detection of COVID-19 cases using chest X-ray images : a comprehensive study. Biomed. Signal Process Contr. 2021;64(October 2020) doi: 10.1016/j.bspc.2020.102365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Islam M.M., Karray F., Alhajj R., Zeng J. A review on deep learning techniques for the diagnosis of novel coronavirus (COVID-19) IEEE Acc. 2021;9:30551–30572. doi: 10.1109/ACCESS.2021.3058537. arXiv:2008.04815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Attique M., Kadry S., Zhang Y.-d., Akram T., Sharif M., Rehman A., Saba T. Prediction of COVID-19 - pneumonia based on selected deep features and one class kernel extreme learning machine. Comput. Electr. Eng. 2021;90(December 2020):106960. doi: 10.1016/j.compeleceng.2020.106960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Turkoglu M. Covidetectionet: covid-19 diagnosis system based on x-ray images using features selected from pre-learned deep features ensemble. Appl. Intell. 2020:1–14. doi: 10.1007/s10489-020-01888-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Shiri I., Sorouri M., Geramifar P., Nazari M., Abdollahi M., Salimi Y., Khosravi B., Askari D., Aghaghazvini L., Hajianfar G., Kasaeian A., Abdollahi H., Arabi H., Rahmim A., Reza A., Zaidi H. Machine learning-based prognostic modeling using clinical data and quantitative radiomic features from chest CT images in COVID-19 patients. Comput. Biol. Med. 2021;132 doi: 10.1016/j.compbiomed.2021.104304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Xu W., Sun N.N., Gao H.N., Chen Z.Y., Yang Y., Ju B. Risk factors analysis of COVID- 19 patients with ARDS and prediction based on machine learning. Sci. Rep. 2021:1–12. doi: 10.1038/s41598-021-82492-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Laguarta J., Hueto F., Subirana B. COVID-19 artificial intelligence diagnosis using only cough recordings. IEEE Open J. Eng. Med. Biol. 2020;1:275–281. doi: 10.1109/OJEMB.2020.3026928. https://ieeexplore.ieee.org/document/9208795/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Alsabek M.B., Shahin I., Hassan A. 2020 International Conference on Communications, Computing, Cybersecurity, and Informatics (CCCI) IEEE; 2020. Studying the similarity of COVID-19 sounds based on correlation analysis of MFCC; pp. 1–5.https://ieeexplore.ieee.org/document/9256700/ [DOI] [Google Scholar]
- 20.Sharma N., Krishnan P., Kumar R., Ramoji S., Chetupalli S.R., R N., Ghosh P.K., Ganapathy S. Proceedings of the Annual Conference of the International Speech Communication Association, INTERSPEECH 2020-Octob. 2020. Coswara – a database of breathing, cough, and voice sounds for COVID-19 diagnosis; pp. 4811–4815.http://arxiv.org/abs/2005.10548 arXiv:2005.10548. [DOI] [Google Scholar]
- 21.Mouawad P., Dubnov T., Dubnov S. Robust detection of COVID-19 in cough sounds. SN Comput. Sci. 2021;2(1):34. doi: 10.1007/s42979-020-00422-6. http://link.springer.com/10.1007/s42979-020-00422-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Pal A., Sankarasubbu M. 2010. Pay Attention to the Cough: Early Diagnosis of COVID-19 Using Interpretable Symptoms Embeddings with Cough Sound Signal Processing, arXivarXiv.http://arxiv.org/abs/2010.02417 02417. [Google Scholar]
- 23.Imran A., Posokhova I., Qureshi H.N., Masood U., Riaz M.S., Ali K., John C.N., Hussain M.I., Nabeel M. AI4COVID-19: AI enabled preliminary diagnosis for COVID-19 from cough samples via an app. Inform. Med. Unlocked. 2020;20:100378. doi: 10.1016/j.imu.2020.100378. http://arxiv.org/abs/2004.01275 arXiv:2004.01275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Huang N.E., Shen Z., Long S.R., Wu M.C., Snin H.H., Zheng Q., Yen N.C., Tung C.C., Liu H.H. The empirical mode decomposition and the Hubert spectrum for nonlinear and non-stationary time series analysis. Proc. Math. Phys. Eng. Sci. 1971;454:903–995. doi: 10.1098/rspa.1998.0193. 1998. [DOI] [Google Scholar]
- 25.Melillo P., Izzo R., Orrico A., Scala P., Attanasio M., Mirra M., De Luca N., Pecchia L. Automatic prediction of cardiovascular and cerebrovascular events using heart rate variability analysis. PloS One. 2015;10(3):1–14. doi: 10.1371/journal.pone.0118504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kaya C., Erkaymaz O., Ayar O., Özer M. Impact of hybrid neural network on the early diagnosis of diabetic retinopathy disease from video-oculography signals. Chaos, Solit. Fractals. 2018;114:164–174. doi: 10.1016/j.chaos.2018.06.034. [DOI] [Google Scholar]
- 27.Daubechies I. Where do wavelets come from? a personal point of view. Proc. IEEE. 1996;84(4):510–513. [Google Scholar]
- 28.Narin A. Detection of focal and non-focal epileptic seizure using continuous wavelet transform-based scalogram images and pre-trained deep neural networks. Irbm. 2020;1:1–10. doi: 10.1016/j.irbm.2020.11.002. [DOI] [Google Scholar]
- 29.Jadhav P., Rajguru G., Datta D. ScienceDirect Automatic sleep stage classification using time – frequency images of CWT and transfer learning using convolution neural network. Integr. Med. Res. 2020;40(1):494–504. doi: 10.1016/j.bbe.2020.01.010. [DOI] [Google Scholar]
- 30.Lecun Y., Kavukcuoglu K. 2010. Convolutional Networks and Applications in Vision; pp. 253–256. [Google Scholar]
- 31.Narin A., Kaya C., Pamuk Z. Automatic detection of coronavirus disease ( COVID - 19 ) using X - ray images and deep convolutional neural networks. Pattern Anal. Appl. 2021;24(3):1207–1220. doi: 10.1007/s10044-021-00984-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wu Z., Shen C., van den Hengel A. Wider or deeper: revisiting the ResNet model for visual recognition. Pattern Recogn. 2019;90:119–133. doi: 10.1016/j.patcog.2019.01.006. arXiv:1611.10080. [DOI] [Google Scholar]
- 33.A. G. Howard, M. Zhu, B. Chen, D. Kalenichenko, W. Wang, T. Weyand, M. Andreetto, H. Adam, Mobilenets: Efficient Convolutional Neural Networks for Mobile Vision Applications, arXiv Preprint arXiv:1704.04861.
- 34.Kira K., Rendell L. A., A Practical Approach to Feature Selection, Morgan Kaufmann Publishers, Inc, doi:10.1016/B978-1-55860-247-2.50037-1.
- 35.Kononenko I. European Conference on Machine Learning. Springer; 1994. Estimating attributes: analysis and extensions of relief; pp. 171–182. [Google Scholar]
- 36.Stańczyk U., Jain L.C. Springer; 2015. Feature Selection for Data and Pattern Recognition. [DOI] [Google Scholar]
- 37.Vapnik V.N. An overview of statistical learning theory. 1999;10(5):988–999. doi: 10.1109/72.788640. [DOI] [PubMed] [Google Scholar]
- 38.Duda R.O., Hart P.E., Stork D.G. second ed. 2001. PATTERN; p. 654.https://cds.cern.ch/record/683166/files/0471056693_TOC.pdf URL. [Google Scholar]
- 39.Erdoğan Y.E., Narin A. 29th Signal Processing and Communications Applications Conference. SIU; 2021. Performance of emprical mode decomposition in automated detection of hypertension using electrocardiography.https://ieeexplore.ieee.org/document/9477887 [DOI] [Google Scholar]
- 40.Isler Y., Narin A., Ozer M., Perc M. Chaos , Solitons and Fractals Multi-stage classification of congestive heart failure based on short-term heart rate variability. Chaos, Solit. Fractals: Interdisciplinary J. Nonlinear Sci. Nonequilibrium and Complex Phenomena. 2019;118:145–151. doi: 10.1016/j.chaos.2018.11.020. [DOI] [Google Scholar]
- 41.Rodríguez J.D., Pérez A., Lozano J.A. Sensitivity analysis of k-fold cross validation in prediction error estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2010;32(3):569–575. doi: 10.1109/TPAMI.2009.187. [DOI] [PubMed] [Google Scholar]
- 42.Y. Isler, A. Narin, M. Ozer, Comparison of the effects of cross-validation methods on determining performances of classifiers used in diagnosing congestive heart failure, Meas. Sci. Rev. 15 (4). doi:10.1515/msr-2015-0027.
- 43.Pahar M., Klopper M., Warren R., Niesler T. 2012. COVID-19 Cough Classification Using Machine Learning and Global Smartphone Recordings, arXiv (2020) 1–10arXiv.http://arxiv.org/abs/2012.01926 01926. [DOI] [PMC free article] [PubMed] [Google Scholar]