Epidemic mitigation by statistical inference from contact tracing data

Significance

Contact tracing mobile applications are clear candidates for enabling us to slow down an epidemic and keep society running while holding the health risks down. Currently used mobile applications aim to notify individuals who were recently in significant contact with an individual who tested COVID-19 positive. In our work, we aim to quantify the epidemiological gain one would obtain if, additionally, individuals who were recently in contact could exchange messages of information. With such a message-passing addition, the risk of contracting COVID-19 could be estimated with much better accuracy than simple contact tracing. We conclude that probabilistic risk estimation is capable of enhancing performance of digital contact tracing and should be considered in the mobile tracing applications.

Abstract

Contact tracing is an essential tool to mitigate the impact of a pandemic, such as the COVID-19 pandemic. In order to achieve efficient and scalable contact tracing in real time, digital devices can play an important role. While a lot of attention has been paid to analyzing the privacy and ethical risks of the associated mobile applications, so far much less research has been devoted to optimizing their performance and assessing their impact on the mitigation of the epidemic. We develop Bayesian inference methods to estimate the risk that an individual is infected. This inference is based on the list of his recent contacts and their own risk levels, as well as personal information such as results of tests or presence of syndromes. We propose to use probabilistic risk estimation to optimize testing and quarantining strategies for the control of an epidemic. Our results show that in some range of epidemic spreading (typically when the manual tracing of all contacts of infected people becomes practically impossible but before the fraction of infected people reaches the scale where a lockdown becomes unavoidable), this inference of individuals at risk could be an efficient way to mitigate the epidemic. Our approaches translate into fully distributed algorithms that only require communication between individuals who have recently been in contact. Such communication may be encrypted and anonymized, and thus, it is compatible with privacy-preserving standards. We conclude that probabilistic risk estimation is capable of enhancing the performance of digital contact tracing and should be considered in the mobile applications.

One of the main tools public health authorities use to mitigate the spread of a pandemic, such as COVID-19, is the trace–test–isolate strategy. Identifying, calling, testing, and if needed, quarantining the recent contacts of an individual who has just been tested positive are the standard route for limiting the transmission of a highly contagious virus. This standard strategy proves its efficacy at early stages of the epidemic, when the number of newly infected individuals is small enough to be manageable by manual contact tracing infrastructures. However, it cannot be applied as such when the epidemic starts to spread faster because the average number of contacts of a typical individual in the few days before he tests positive can be large, not all contacts are with people known to the individual, and manual tracing incurs delays during which infected contacts keep on spreading the virus.

For these reasons and taking into account the properties and parameters of the COVID-19 epidemic, digital contact tracing was convincingly argued to be a viable route to mitigation of COVID-19 and other similar epidemics (1). Current mobile-phone technology indeed enables automated, real-time proximity tracing between individuals, and much work in this direction was initiated and deployed in the past months (2–6). With currently developed mobile applications, the distance and duration of a contact between two individuals can be estimated. Furthermore, contextual or health information about individuals can be included as well. This tracing can be used while preserving the privacy of each individual’s information, and the level of privacy protection depends on the protocol. While many works have been devoted to the compatibility of privacy and tracing (e.g., refs. 2, 4, and 6–8), much less work is available concerning the assessment of the best use of digital tracing and its possible efficacy to mitigate a pandemic.

So far, most digital applications use the tracing data simply as a fast and scalable device to identify all recent contacts. The information that they provide is of binary nature (I have been in contact with someone infected or not). In this paper, we show that probabilistic inference techniques allow for a smarter use of the data exchanged by the tracing applications: They can provide accurate estimates of the probability that any given individual is infected, hereafter called “risk.” This risk information is more refined than the binary one. For instance, the risk of an individual can increase if he has met many persons who all have a moderate risk, a process that is not currently taken into account. The risk estimate can then be used in order to focus the tests and other interventions on the group of individuals who have the largest probabilities of being infected, even if they do not show symptoms. The proposed contact tracing protocols require individuals who are in contact, or have been in contact in the recent past, to be able to exchange small amounts of information about their risk. Probabilistic inference then concatenates this information from all past contacts locally on the individuals’ phones and sends updates of the status to their contacts.

While the advantage of digital over manual contact tracing in detecting secondary cases and interrupting chains of contagion remains disputed in general (9, 10), digital tracing has been proposed in the case of COVID-19 due to the fundamental role of presymptomatic and asymptomatic individuals in the spreading dynamics (1, 11). To this end, a number of smartphone applications have been released (12–17) that leverage proximity signals to provide a fast and scalable approach for identifying all recent contacts. Recent results suggest that current contact tracing apps help in reducing the spread of COVID-19 (18–20).

In the face of exponential epidemic growth, the limited availability of tests and personnel substantially reduces the ability to break chains of contagion. In such a regime, the reasonable strategy of isolating individuals who have been in recent contact with positive cases would result in quarantining a large portion of the population (21). Assessing the individual infection risk can, in this case, help improve testing and quarantine strategies.

In a scenario in which adoption of the digital tracing instruments is not compulsory, the use and storage of individual-level data in a centralized way raise privacy concerns (22, 23) that could result in limited app adoption. For this reason, decentralized communication and storage protocols have been developed to enable privacy-preserving contact tracing mobile apps (2, 3, 6–8). Recent works showed how, in a privacy-preserving regime, information from users such as age or neighborhood census data (24) can be used to estimate the risk of infection.

Overall, despite the growing volume of literature on contact tracing and its value in epidemic control, only a few studies focus on the design of actual algorithms combining information from the network of contacts with prior assumption on the epidemic propagation to assess individual risk in a fully decentralized, highly scalable, and robust manner.

Three concurrent works in progress share the same aim as ours (i.e., inference of infection risk from contact tracing data) (SI Appendix). The work in ref. 5 tackles the problem of infection risk estimation with a machine learning strategy based on amortized variational inference, under strict privacy constraints. The works in refs. 25 and 26 propose to estimate the individual infection risk from tracing data via Monte Carlo sampling on compartmental epidemic models. In ref. 25, the authors evaluate an inference procedure based on a Bayesian probabilistic formulation similar to ours on systems up to 10,000 individuals.

A key aspect of our work is that our inference algorithms are tested against data coming from a much more complex propagation model (27). We believe this point to be crucial to the eventual validation on real-world contact data.

Methods

Bayesian Approach.

Algorithms proposed in this work rely on a Bayesian probabilistic approach for the description of the infection state in a population at the individual level. In this approach, an epidemic propagation model assigns a prior probability $\mathbb{P}\left[q\right]$ to any collective “trajectory” $q\left(t\right)=\left(q_1\left(t\right),\dots ,q_N\left(t\right)\right)$ of the infection states of $N$ individuals in a population, for $t$ in a given time interval. The evidence $\mathcal{O}$ is provided by the set of observations gathered from individuals in the population, including their reported symptoms and the results of tests, which could indicate infection or acquired immunity. Given a trajectory $q$, the probability of obtaining evidence $\mathcal{O}$ is modeled as a likelihood $\mathbb{P}\left[\mathcal{O}|q\right]$. These quantities are simply related to the posterior distribution of infection states $\mathbb{P}\left[q|\mathcal{O}\right]$ through Bayes’ formula

$$\mathbb{P}\left[q|\mathcal{O}\right]=\frac{1}{\mathbb{P}\left[\mathcal{O}\right]}\mathbb{P}\left[\mathcal{O}|q\right]\mathbb{P}\left[q\right],$$ [1]

where $\mathbb{P}\left[\mathcal{O}\right]={\sum }_{q^{\prime }}\mathbb{P}\left[\mathcal{O}|q^{\prime }\right]\mathbb{P}\left[q^{\prime }\right]$ is a normalization constant. The scope of this work is to exploit information from the posterior to estimate individual infective risks (i.e., our best knowledge of their probability of being infective). The estimated risk $r_i$ of individual $i$ can be measured from the marginal posterior probability $\mathbb{P}\left[q_i\left(t\right)|\mathcal{O}\right]$, where

$$\mathbb{P}\left[q_i\left(t\right)|\mathcal{O}\right]=\sum _{\left\{q_j\left(t^{\prime }\right):\left(j,t^{\prime }\right)\ne \left(i,t\right)\right\}}\mathbb{P}\left[q|\mathcal{O}\right].$$ [2]

Using $r_i$, appropriate sanitary protocols can be implemented, typically implying higher-risk individuals to be tested and subsequently isolated in case of a positive result.

Propagation Model.

It is crucial for the propagation model not only to be able to represent the epidemic propagation reasonably well but also, to be robust with respect to unknown details of the real epidemic process. Here, we adopt a simple agent-based susceptible–infected–recovered (SIR) model, serving as the prior model $\mathbb{P}\left[q\right]$ in our Bayesian approach. Our method could easily be adapted to richer propagation models (e.g., including additional individual states). It should be emphasized that any propagation model will be at best a rough approximation of the natural diffusive phenomenon. For this reason, we carefully evaluated our results (employing the simple SIR propagation prior) against data generated by much richer and complicated propagation models.

In the SIR agent-based model, each individual $i$ can be in one of the three states: susceptible, infected, removed $\equiv \left\{S,I,R\right\}$. The category $R$ includes all of the individuals who recovered (and developed immunity) or died, such that they do not transmit the infection. In our notation, $q_i\left(t\right)\in \left\{S,I,R\right\}$, $\forall t$, and the individual risk is estimated as $r_i\left(t\right)=\mathbb{P}\left[q_i\left(t\right)=I|\mathcal{O}\right]$. For the sake of concreteness and simplicity, we describe here the dynamics of the infection process in discrete time and take the time step to be 1 d. This choice is well suited to updating information and exchanging messages between individuals. A different time discretization, or continuous time evolution, could also be used. When going from time $t$ to time $t+1$ (day $t$ to day $t+1$), the following events can take place.

• •An infected individual $i$ [i.e., $q_i\left(t\right)=I$] can recover/die with probability ${\mu }_i$. In that case, $q_i\left(t+1\right)=R$.
• •A susceptible individual $i$ [i.e., $q_i\left(t\right)=S$] can be independently infected by any infected individual $j$ with probability ${\lambda }_{j\to i}\left(t\right)$. In that case, $q_i\left(t+1\right)=I$.

Individuals not affected by these events retain their state [i.e., $q_i\left(t+1\right)=q_i\left(t\right)$]. In particular, individuals in state $R$ will always remain in state $R$. The probability that a susceptible $i$ will be infected results in $1-{\prod }_{j\ne i}\left(1-{\lambda }_{j\to i}\left(t\right)\delta \left(q_j\left(t\right),I\right)\right)$ [here, $\delta \left(\cdot ,\cdot \right)$ is a Kronecker delta function]. The probability of transmission ${\lambda }_{j\to i}\left(t\right)$ takes into account the duration and the distance of the contact as well as any protective measure, if the information is available. In particular, ${\lambda }_{j\to i}\left(t\right)=0$ if $j$ has not been in contact with $i$ at time $t$.

To best reflect the characteristics of typical clinical recovery and time-dependent infectiousness, ${\mu }_i$ and ${\lambda }_{i\to j}$ will in general depend on the time elapsed since infection of individual $i$. In this case, the propagation model is not Markovian [i.e., $q\left(t+1\right)$ will also depend on the state at times before $t$].

The SIR agent-based model thus defines a transition probability $\mathbb{P}\left[q\left(t+1\right)|q\left(t_0\right),\dots ,q\left(t\right)\right]$. The prior probability of an epidemic evolution $q\left(t_0\right),\dots ,q\left(t\right)$ between an initial time $t_0$ and a final time $t$ can be expressed as

$$\mathbb{P}\left[q\left(t_0\right),\dots ,q\left(t\right)\right]=\mathbb{P}\left[q\left(t_0\right)\right]\prod _{t^{\prime }=t_0}^{t-1}\mathbb{P}\left[q\left(t^{\prime }+1\right)|q\left(t_0\right),\dots ,q\left(t^{\prime }\right)\right].$$ [3]

Considering propagation properties of COVID-19, it is reasonable to consider a time window $\left[t_0,t\right]$ as small as 2 or 3 wk. In practice, we take $\mathbb{P}\left[q\left(t_0\right)\right]$ to be a simple i.i.d. distribution, based on a rough estimation of the ratios of $S,I$, and $R$ in the population at time $t_0$. Note that, when ${\mu }_i$ and ${\lambda }_{j\to i}$ do not depend on the time since infection (Markovian case), $\mathbb{P}\left[q\left(t^{\prime }+1\right)|q\left(t_0\right),\dots ,q\left(t^{\prime }\right)\right]$ can be replaced by $\mathbb{P}\left[q\left(t^{\prime }+1\right)|q\left(t^{\prime }\right)\right]$ in Eq. 3.

Observations.

Given a set of independent observations $\mathcal{O}=\left\{{\mathcal{O}}_r\right\}$, where each observation ${\mathcal{O}}_r$ provides some information on the state of an individual at a given time, $\mathbb{P}\left[\mathcal{O}|q\right]$ takes the factorized form

$$\mathbb{P}\left[\mathcal{O}|q\right]=\prod _r\mathbb{P}\left[{\mathcal{O}}_r|q\right]\hspace{0.17em}.$$ [4]

Observations can include reported symptoms or test results. For instance, if observation ${\mathcal{O}}_r$ is that individual $i$ tested positive at time $t$, then $\mathbb{P}\left[{\mathcal{O}}_r|q\right]=\left(1-p_{FNR}\right){\delta }_{q_i\left(t\right),I}+p_{FPR}\left(1-{\delta }_{q_i\left(t\right),I}\right)$ where $p_{FNR}$ and $p_{FPR}$ are the false-negative and -positive rates (i.e., the probability of testing negative while being infected and the probability that the test results are positive for noninfected individuals, respectively).

Mean-Field Approximations.

Putting together Eqs. 1–4, we are left with the mathematical challenge of computing the marginal posterior probability $\mathbb{P}\left[q_i\left(t\right)|\mathcal{O}\right]$ for the state of each individual $i$ at time $t$ defined in Eq. 2. The computational problem resides in the sum over an exponential number of terms [i.e., all combinations of $q_j\left(t^{\prime }\right)$ according to the sum in Eq. 2]. We will attempt to compute it approximately using two schemes based on the mean-field approach of statistical physics, namely the simple mean-field (SMF) algorithm and the belief propagation (BP) algorithm.

There are two main advantages of mean-field methods in this context. First, they are based on systems of equations for the marginals of interests defined in Eq. 2 (or similar related quantities), so they can directly provide the individual risks. Second, these systems can be (and typically are) efficiently solved iteratively, which fits well with a distributed approach in which computation is performed on individuals’ cell phones, with a relatively small, although regular, exchange of information between individuals who have been in a contact.

BP is a well-known message-passing approach (28) that can be employed to compute marginal distributions of probabilistic models. This method has been recently employed in the analysis of the large deviation properties in a class of dynamical processes on networks, including applications to epidemics (29–33), in particular the patient zero problem and the inference of causality chains of infection. BP can be used directly to compute marginals of the posterior in Eq. 2.

SMF is a simpler algorithmic scheme to compute approximate marginal probabilities ${\mathbb{P}}_{MF}\left[q_j\left(t\right)=S\right]$, ${\mathbb{P}}_{MF}\left[q_j\left(t\right)=I\right]$, and ${\mathbb{P}}_{MF}\left[q_j\left(t\right)=R\right]$ for the prior [3] in the case of Markovian dynamics. The probability of individual $j$ receiving the infection from her contact $k$ at time $t$ depends on ${\lambda }_{k\to j}\left(t\right)$ and on the joint probability of $j$ being $S$ and $k$ being $I$ at time $t$. The mean-field approximation estimates this joint probability by the product ${\mathbb{P}}_{MF}\left[q_j\left(t\right)=S\right]\hspace{0.17em}{\mathbb{P}}_{MF}\left[q_k\left(t\right)=I\right]$, leading to a closed set of equations. To approximate the posterior [2], we developed a heuristic procedure that enforces the following constraints on the probabilities for individual $i$.

• •If $i$ is tested $S$ at time $t_{\text{obs}}$, it has been $S$ for all $t\le t_{\text{obs}}$.
• •If $i$ is tested $R$ at time $t_{\text{obs}}$, it will be $R$ for all $t\ge t_{\text{obs}}$
• •If $i$ is tested $I$ at time $t_{\text{obs}}$, the heuristic assumes that he has been $I$ at times $\left[t_{\text{obs}}-\tau ,t_{\text{obs}}\right]$, where $\tau$, the typical time between infection and observation, is a parameter of the algorithm.

The full BP and SMF algorithms are described in SI Appendix.

As we will see, BP is more accurate than SMF, but it is relatively more complex and requires the exchange of a larger amount of information between individuals (roughly around 1 megabyte (MB) per user/d against 2 kilobyte (KB) per user/d). Information exchange could be in principle exploited to identify individuals and their risks, so it must be reduced as much as possible. The choice between SMF and BP must thus be based on the trade-off between simplicity and privacy vs. efficacy.

Setting of the Numerical Experiments.

Our algorithms are based of two main steps of modeling: the mathematical model and the mean-field approximations. Both will be validated on two epidemic spreading simulators.

Geometric contact model.

The epidemic is a simple SIR model–based propagation in a population of $N$ individuals, where the graph of contact is updated dynamically at each step as follows. The individuals are distributed uniformly in a square of side $\sqrt{N}$, and at each time step, a contact can be established between two individuals $i$ and $j$ with a probability $e^{-d_{ij}/\ell }$, where $d_{ij}$ is the Euclidean distance between the points and $\ell$ is a parameter that controls the density of the contact graph. In this case, our prior corresponds to the true dynamics of the epidemic, and the simulations test the accuracy of the two mean field–based algorithms.

Oxford OpenABM model.

Accurate agent-based models are based on a detailed description where, at each time, a given individual is in a state that belongs to a finite set of possible states, including susceptible, exposed, infected–asymptomatic, infected–symptomatic, in intensive care unit (ICU), recovered, or dead. In these models, infected individuals are not immediately contagious upon infection and may be asymptomatic or develop mild/severe symptoms with some delay, and the ages, households, and workplaces are also taken into account. They also include nontrivial distributions of incubation and recovery times and time-dependent viral transmission capacity (34–38), as well the time-varying contact network over which viral transmissions occur, some including real-world mobility data (39) or computer-generated synthetic surrogates (1, 27). In this paper, we shall use the epidemic spread model of ref. 1, which is aimed at capturing some of the essential features of the contacts in real populations as well as the real epidemiology of COVID-19 (SI Appendix has details). In the absence of sufficiently detailed real-world data, we view the data from this OpenABM model as “realistic.” In this case, our simple agent-based SIR prior is far from capturing the details and complexity of the “true” epidemic dynamics. Despite this use of a crude prior and of the mean-field approximation, our two risk inference algorithms still work and provide a large improvement over competing current contact tracing methods.

Another important issue for risk inference methods concerns their robustness. Some important sources of performance degradation will be tested: the partial adoption of the application among the individuals, the imperfect detection of contacts even for full coverage of the population, and the diagnostic errors associated with the medical test results.

Results

Risk inference is tested on the two epidemic spreading models described above. In both cases, the simulation starts at time 0 with every individual in the susceptible state $S$ except for a small number in the infected state. The number of these “patients zero” will be specified in the following for each case.

In order to investigate how contact tracing can be used to mitigate the epidemic, the following testing–intervention protocols are considered. Interventions start after a fixed number of days ($t_{\text{start}}$). Every day, a fixed number $n_r$ of individuals, among those not previously tested positive, are tested. These are the individuals with the largest risk of being infected according to four different risk estimation strategies. Results of the test are assumed to be available on the same time step (day) and are included in the observations used to adjust the probabilities of risk on the next time step (day). The new tested-positive individuals are then confined (slightly different strategies will be specified case by case). The following ranking strategies are considered.

• •Random guessing (RG): Individuals are ranked randomly.
• •Contact Tracing (CT): Individuals are ranked according to the number of contacts with confirmed positive individuals during the time interval $\left[t-\tau ,t\right[$. This is what would be possible to implement with the currently deployed mobile applications. A more advanced contact tracing technique is instead presented in SI Appendix.
• •SMF: Individuals are ranked according to their risk ${\mathbb{P}}_{MF}\left(q_i\left(t\right)=I\right)$ as estimated by SMF ran over a time window [$t-t_{\text{SMF}},\hspace{0.17em}t$].
• •BP: Individuals are ranked according to the probability of infection in the last ${\delta }_{\text{rank}}$ days as estimated by BP. Prioritizing recent infections can be more effective as it helps contain the “boundary” of an ongoing outbreak.

Results show that BP- and SMF-based methods are able to control the epidemic considerably more successfully than the classic contact tracing strategy. Implementation of the SMF and BP risk estimation algorithms and all of the tests that follow can be found in ref. 40.

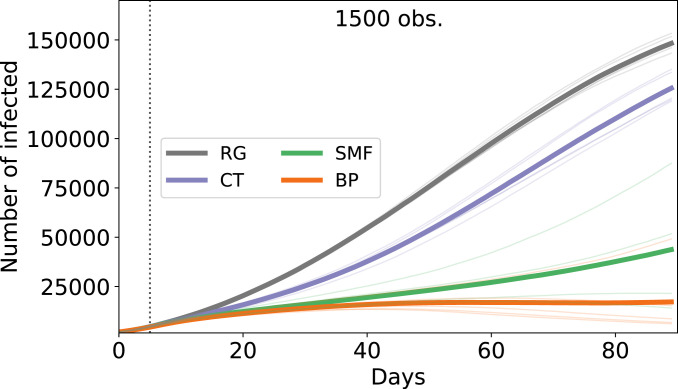
For the geometric contact model, the development of the epidemic over 3 mo in a population of $\mathrm{5,00,000}$ individuals is subject to large fluctuations across runs (Fig. 1). Nevertheless, one sees a very clear signal indicating that the proposed inference methods, SMF and BP, largely improve upon the usual contact tracing, itself better than RG. The best inference method is clearly BP, but the simpler SMF is also quite successful. Even in this pessimistic regime (i.e., where a large fraction of the population gets infected), both risk inference methods significantly slow down the epidemic spread, when compared with classic contact tracing.

Fig. 1.

SIR model on proximity-based random network with six contacts on average per day and $\mathrm{5,00,000}$ individuals. The epidemic parameters are the same as those used by the inference algorithms: $\lambda =0.05,\mu =0.02$. In the plot, we show the average numbers (bold lines) of infected individuals vs. time among three different realizations (thin lines) of the epidemics with 200 patients zero. The system freely evolves for the first 10 d, and then, interventions start. We consider $50\%$ of the infected individuals each day as severely symptomatic. These individuals are observed as infected 5 d after their infection. Then, 1,500 tests are performed daily according to the ranking given by the algorithms. The observed infected individuals are quarantined. The parameters used for these simulations are $\tau =5$ for both SMF and CT and $t_{\text{SMF}}=15$ for SMF. obs., observations.

This first test shows that the mean-field approximations are very effective in the case where our prior description accurately represents the underlying epidemic propagation. In fact, as reported in SI Appendix, these results are considerably robust in cases where the inference procedure has only partial knowledge about the spreading parameters and the contact networks.

Still, a much more stringent test can be performed by generating epidemics through the more realistic OpenABM COVID-19 model. A post lockdown scenario is mimicked where only a small number of individuals are initially infected (i.e., a few tens of patients zero in a population of 500,000 individuals who all employ a contact tracing application). The epidemic dynamics freely evolve according to the OpenABM model (27) for 10 d, and then, a number of individuals with the highest infection risk, assessed by RG, CT, SMF, or BP, are tested on a daily basis. The original contact dynamics are then modified: An individual who is tested positive is confined and can have contacts only with the individual’s cohabitants. Results obtained from a more restrictive intervention scenario, in which all of the households are confined, are reported in SI Appendix.

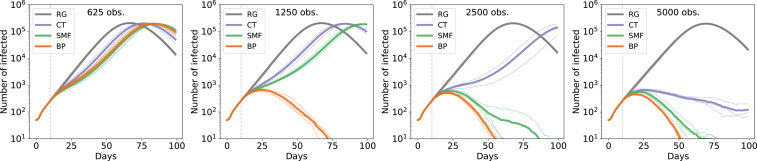
Fig. 2 shows the number of infected individuals in a time interval of 100 d when the number of initial infections is 50 and the intervention starts after 10 d (additional details on the OpenABM dynamics are in the figure). The number of available tests per day increases from 625 to 5,000 (shown in the panels from left to right), while the lines are colored according to the adopted ranking strategy. Results for three independent realizations of the epidemics are shown (thick lines indicate the mean number of infected individuals). The results suggest that for both the inference strategies, the size of the epidemic is significantly reduced if compared with random testing and also, with classic contact tracing, even when few tests are available. When only 1,250 medical tests are performed daily, the confinement of the people inferred by BP suffices to stop the epidemic in 75 d. The SMF-based strategy performs notably better than contact tracing, and it achieves similar performance to BP when the number of daily observations is large.

Fig. 2.

Effect of the control strategy on the epidemic spreading, according to the OpenABM model, in a population of 500,000 individuals. Each infected individual can either be asymptomatic or show symptoms of various degree (mild or severe). Individuals who show severe symptoms are immediately quarantined or hospitalized when symptoms emerge. In addition, half of the mildly symptomatic individuals are assumed to self-report and self-isolate as well. No direct information is available on asymptomatic (or presymptomatic) infected individuals. The number of tests based on suggestions by the inference method is fixed, while there is no limitation on tests used for symptomatic individuals. In all panels, we show the number of infected individuals in a time window of 100 d when interventions are applied starting from day 10. The number of patients zero is set to 50. Thin lines represent the results for single instances of the epidemics, while the thick lines are the averages among the different realizations. We compare the effect of an increasing number of available medical tests per day, from $\left[\mathrm{625,5000}\right]$, performed on the individuals at highest risk as evaluated by the corresponding strategy (RG, CT, SMF, and BP). We show here four selected cases to stress the qualitative differences among the methods. Here, only tested-positive individuals, and not their cohabitants, are confined. The SMF algorithm fixes the parameters $\lambda =0.02$, $\mu =1/12$, $\tau =5$, and $t_{\text{SMF}}=10$. SI Appendix has details on the parameters used in BP. obs., observations.

Robustness of the Inference.

The previous section investigated how intervention protocols control realistic epidemics when paired to the considered risk assessment strategies (RG, CT, MF, and BP). However, some of the conditions assumed in that section are not realistic. In reality, the sensitivity of medical tests is not 100%, and it is to be expected that only a fraction of the population will adopt the app, so that not all contacts are detectable. These two issues will be addressed in this section, focusing on the more realistic OpenABM model.

A first test of robustness that is considered concerns the case in which the results of the medical tests are inaccurate, and therefore, a fraction of the tested individuals are incorrectly identified as uninfected or infected. Concerning the fraction of false-positive tests, this simply puts a small additional fraction of individuals in isolation but does not lead to deterioration of the epidemic control. Our analysis hence focuses on the influence of false negatives and how the performance depends on the false-negative rate (FNR) of the medical tests. Within the Bayesian framework, it is possible to correctly include this information as described in Observations: This Bayesian protocol is implemented within the BP algorithm but not for the SMF in order to keep it as simple as possible and test its robustness. In Fig. 3, results for several simulations are shown (three different realizations of the dynamics) when the FNR spans the range $\left[0.09,0.40\right]$. All of the control strategies present good robustness with respect to the false-negative tests. Contact tracing and SMF control the spreading up to FNR 0.19, while the intervention based on BP completely stops the spreading even for large values of the FNR, up to 0.31.

Fig. 3.

Effect of test inaccuracy on the evolution of the controlled epidemics. The intervention protocol is the same as Fig. 2 when 2,500 daily observations are available, only differing in the treatment of the households. The cohabitants of the tested-positive individuals are also confined. The effects of a nonnegligible FNR of the results of the medical tests are considered, ranging from 0.09 to 0.40. Four representative regimes to underline the different behavior of the risk assessment methods are shown.

In order to study the effects of partial adoption of the mobile application, the contacts of a fraction of individuals are made invisible to the inference algorithm: These hidden contacts are associated with individuals who either do not have the application or do not own a smartphone. Fig. 4 shows the result of the mitigation, in the OpenABM model, with AF (the fraction of individuals who have adopted the app) ranging between 0.6 and 0.9. Let us stress that the fraction of hidden contacts is remarkably large (from 19 to 64% for the considered AF range). Although performance is severely affected, one observes that even at AF equal to 0.6, the use of inference algorithms allows for a delay of the spreading of the epidemic and helps to flatten the peak of infected individuals, way more efficiently than the classical contact tracing strategy. Furthermore, it should be noted that application utilization may be positively correlated to the number of contacts of individuals. Including more detailed information about mobile application utilization (e.g., in population age classes) may greatly reduce the impact of low adoption.

Fig. 4.

Effect of a poor AF of the mobile application on the number of infected individuals. The same intervention protocol of Fig. 2 is used here for 5,000 daily observations and the quarantine of the households. Only a fraction AF of the population, from 90 to 60%, uses the mobile application.

Discussion

The above results show that, in the regime where the epidemic is growing and exhaustive testing of all contacts is unfeasible, inference methods allow us to contain the epidemics more efficiently than the classical tracing of contacts. Both inference schemes require exchange of information between individuals during a limited time window after they have been in contact and could be implemented in contact tracing smartphone applications in a distributed way. Additionally, numerical tests show that the approach is robust to false negatives in the test results as well as to partial adoption of the mobile tracing applications, although the adoption rate required for efficient control of the epidemic (with the number of daily tests considered here) is larger than the one of the currently deployed applications.

Using the good estimate of posterior probability of being infected in time, as provided by these mean-field algorithms, a series of threshold values could be put in place so as to suggest actions of individuals, including reduction of contacts, self-isolation, and testing.

Future work should include testing the proposed risk inference methods in real-world settings. This would require contact tracing applications that allow communication between individuals who have recently been in contact. These are currently not supported by the protocols employed to contain the spread of COVID-19 (12–17). As far as we can see, currently existing data for COVID-19 do not allow us to test the results, both due to the unavailability of concurrent contact and infection data and more importantly, because the intervention strategy would modify the dynamics itself. It is, however, clear that the looming possibility of future pandemics should motivate trials where volunteers use a contact tracing application with a virtual epidemic being run on their contact networks, and different contact tracing methods can then be evaluated and compared. An interesting possibility for such a test could be the Operation Outbreak project (41), which is a platform for science, technology, engineering, and math (STEM) education on infectious diseases and outbreak preparedness.

With regard to privacy, it is worth emphasizing that the proposed inference methods are in principle more protective than manual tracing. On the one hand, both can be implemented in a fully distributed way using point-to-point cryptography without fully centralized processing and storage of information on infections or contacts. On the other hand, by identifying individuals who have the largest probability of being infected through a cumulative process by which information is integrated, the direct attribution of potential infection events to a given individual is made much harder. Details of such fully privacy-preserving implementation, along the lines of ref. 4, are left for future work.

Data Availability

All study data are included in the article and/or SI Appendix.