Propagation of the pure-cubic optical solitons and stability analysis in the absence of chromatic dispersion

Abstract

The main concentration of this article is to extract pure-cubic optical solitons in nonlinear optical fiber modeled by nonlinear Schrödinger equation (NLSE). The governing model is discussed the with the effect of third-order dispersion, Kerr law of nonlinearity and without chromatic dispersion. We extract the solutions in different forms like, Jacobi’s elliptic, hyperbolic, periodic, exponential function solutions including a class of solitary wave solutions such that bright, dark, singular, kink-shape, multiple-optical soliton, and mixed complex soliton solutions. Recently developed integration tools known as ${\Phi }^6$-model expansion method, generalized exponential rational function method (GERFM) and generalized Kudryashov method are applied to analyze the governing model. The studied model is also discussed by the concept of modulation instability (MI) analysis. The constraints conditions are explicitly presented for the resulting solutions and singular periodic wave solutions are recovered. Furthermore, for explaining the solutions in physical phenomena, the three dimensional, two dimensional, and their related contours graphs are plotted under the selection of appropriate parameters. The accomplished results show that the applied computational system is direct, productive, reliable and can be carried out in more complicated phenomena. The results show that the studied equation theoretically has extremely rich pure-cubic optical structures of nonlinear fiber relevance.

Introduction

In the science and technology fields like engineering, circuit analysis, chemical physics, plasma physics, geochemistry, optical fiber, fluid mechanics, and many others, NLPDEs are utilized as a governing equation to discuss the complications of the physical phenomena. To know the behavior of intricate physical occurrence, to calculate the solutions of the governing NLPDEs is necessary. Generally, the solutions of the NLPDEs are categorized into three types as exact solutions, analytic solutions and numerical solutions. Exact solutions to NLPDEs play a significant part in nonlinear science, since they can give a lot of physical data and more knowledge of the actual parts of the issue and accordingly lead to additional applications. Wave phenomena in dissipation , dispersion, reaction, diffusion and convection are very much important (Younas and Ren 2021; Bilal et al. 2021; Inc et al. 2016; Inc and Kilic 2017; Osman et al. 2020; Tchier et al. 2016; Jhangeer et al. 2021; Kilic and Inc 2017; Tchier et al. 2016a; Bilal et al. 2021a; Tchier et al. 2017; Bilal et al. 2021b).

Moreover, over the past few years, it has been observed the extraordinary progress in the theory of soliton. The fundamental perception about a soliton was shaped by Russell in 1844, attributable to a serendipitous idea in 1834 on the Edinburgh–Glasgow Canal. He named it the “great wave of translation”. In acknowledgment of its single pulse form, this phenomenon was later named as a solitary wave. In this way, Boussinesq and Rayleigh, were between the preeminent specialists who executed hypothetical contemplations of a solitary wave. From that point forward, the Solitary wave’s examination has mounted to a prime field of examinations of solitary waves. The stable, powerful, self-restricted and enduring solitary waves which do not scatter and maintain their uniqueness as they travel in a medium- are ubiquitous in nature are refereed to solitons and nonlinear wave excitations. Solitons in fact the result between non-linearity (trend to increase the wave slope) and dispersion (the wave attentive tendency). They emerge in numerous crucial areas of technology and physics from high-piece rate media communications and controllable soliton supercontinuum generation in ultrafast photonics, condensed matter, and plasma physical science to elementary particle physics, cosmology, and oceanic monster (rogue) waves as well as Bose–Einstein condensates. Due to its Galilean symmetry the soliton is characterized by its own de Broglie wavelength analogue as the self-localized wave entity. On the other hand, the soliton as an extended particle-like entity, due to nonlinear self-interaction, becomes a bound state in its own self-induced trapping potential and as a result, possesses negative self-interaction (binding) energy. Ones may obtain the information about the form and the shape of the solitons. The structural stability of the solitons and in the same way as nuclear binding energy, the degree to which the quasiparticles that make up the soliton are tightly bound together can be considered (Russell 1844; Nguepjouo et al. 2014). The telecommunications engineering splits into wired communications that make use of underground communications cables and wireless communications that involve the transmission of information over a distance without help of wires. Fiber optics clarifies nonlinear reaction of properties like recurrence, polarization, phase of incident light. These nonlinear cooperations bring about a large group of optical phenomenas. Recently, numerous new ways have been proposed for improved nonlinearity and light control, including contorted chromospheres, joining rich thickness of states with bond shift, minute falling of second-request nonlinearity, etc. Therefore, sub-atomic nonlinear optics has been broadly utilized in the biophotonics field, containing bioimaging, phototherapy, biosensing, and so forth. The theory of optical solitons has made remarkable and far-reaching advances during the past few decades (Biswas et al. 2020; Wang et al. 2021; Triki et al. 2021; Daoui et al. 2021; Biswas et al. 2020a; Tchier et al. 2021a; Biswas et al. 2020b; Aslan and Inc 2017; Wang et al. 2021a; Ates and Inc 2017; Aslan et al. 2017; Inc 2017; Tchier et al. 2017a; Shehata et al. 2019; Talarposhti et al. 2020; Sabiu et al. 2020; Tchier et al. 2017b; Alquran et al. 2021; Bilal et al. 2021c; Younis et al. 2017). There are a wide variety of new concepts that have been introduced to bring about performance enhancement in this field with regards to telecommunications industry. There are two key ingredients that constitute the soliton propagation dynamics. These are chromatic dispersion (CD) and nonlinear refractive index of the optical fiber. The arising problem for pure-quartic soliton related to the governing nonlinear Schrödinger equation can be nonintegrable one, for this reason we will propose the concept of cubic-quartic solitons in which the chromatic dispersion is replaced by the third order dispersion and fourth order dispersion together (Yıldırım et al. 2020; Blanco-Redondo et al. 2016; Zayed et al. 2020; Al-Kalbani et al. 2020; Zayed et al. 2021; Bansal et al. 2018; Biswas et al. 2017; Das et al. 2019; Gaxiola et al. 2020; Biswas et al. 2017a; Kohl et al. 2019; Yıldırım et al. 2020a; Biswas and Arshed 2018; Yıldırım et al. 2020b; Hosseini et al. 2020; Kodama and Hasegawa 1995).

However, in this study, we successfully apply the proposed methods (Zayed et al. 2018; Ghanbari et al. 2019; Mahmuda et al. 2017) to find the different forms of pur-cubic optical solitons such as bright, dark, singular, kink and combined forms of the soltions.

This article is arranged as: In Sect. 2, governing model and the summary of the methods in Sect. 3. Section 4 consists of extraction of solutions with graphical representation, and MI analysis is presented in Sect. 5. Finally paper comes to concluding remarks in Sect. 6.

The model

The studied equation for cubic optical solitons is written as (Yıldırım et al. 2020)

$$\begin{array}{c}\hfill i{\psi }_t+i\alpha {\psi }_{\mathit{xxx}}+{F(|\psi |}^2{)\psi =i[\lambda (|\psi |}^{2m}{\psi )}_x+{\theta |\psi |}^{2m}{\psi }_x+{\sigma (|\psi |}^{2m}{)}_x\psi ,\end{array}$$ 1

where $\psi (x,t)$ is a complex-valued function that represents the wave profile. The independent variables x and t are spatial and temporal Co-ordinates respectively and $i=\sqrt{-1}$. $\alpha$ represents the coefficient of third-order dispersion (3OD) while $\lambda$ is the coefficient of selfsteepening nonlinearity. Next, $\theta$ and $\sigma$ account for the higher-order dispersion effects. Also, m is the full nonlinearity parameter. Finally, the functional F accounts for the nonlinear form of refractive index where

$$\begin{array}{c}\hfill {F(|\psi |}^2)\psi \in {\cup }_{m,n=1}^{\infty }{C}^k((-n,n)\times (-m,m);R^2)\end{array}$$

Overview of the methods

We present brief description of the proposed methods in this section,.

Suppose a NLPDE,

$$\begin{array}{c}\hfill \Delta (\varpi ,{\varpi }_t,{\pi }_x,{\varpi }_{\mathit{tt}},{\varpi }_{\mathit{xt}},{\varpi }_{\mathit{xx}},\cdots )=0,\end{array}$$ 2

where $\Delta$ is a polynomial in its arguments. We start with hypothesis as:

$$\begin{array}{c}\hfill \varpi (x,t)=\Pi (\xi )\text{and}\xi =B(x-ct).\end{array}$$ 3

Here B is amplitude component and c denotes the velocity. On solving the Eqs. (2) and (3), yields NODE as:

$$\begin{array}{c}\hfill \Lambda (\Pi ,{\Pi }^{\prime },{\Pi }^{″},{\Pi }^{″\prime },\cdots )=0,\end{array}$$ 4

where ${}^{\prime }$ represents the derivative w.r.t $\xi$.

${\Phi }^6$-model expansion method (Zayed et al. 2018)

This technique incorporates the following steps.

Step 1 The solution of (4) is written as

$$\begin{array}{c}\hfill \Pi (\xi )=\sum _{j=0}^{2n}{\chi }_j{\phi }^j(\xi ),\end{array}$$ 5

where constants ${\chi }_j$ $(j=0,\cdots ,2n)$ are determined later, while $\phi (\eta )$ satisfies the following NODE

$$\begin{array}{c}\hfill {\phi }^{{\prime }^2}(\xi )=h_0+h_2{\phi }^2(\xi )+h_4{\phi }^4(\xi )+h_6{\phi }^6(\xi ),\\ \hfill {\phi }^{″}(\xi )=h_2\phi (\xi )+2h_4{\phi }^3(\xi )+3h_6{\phi }^5(\xi ).\end{array}$$ 6

Step 2 On the utilization of the homogeneous balance principle, the n in Eq. (4) is calculated. For detail, if $deg[\Pi (\xi )]=n$ then the degree of the other terms will be expressed as follows

$$\begin{array}{cc}& deg[{\displaystyle \frac{d^k\Pi }{d{\xi }^k}}]=n+k,\hfill \\ \hfill & deg[{(\Pi (\xi ))}^p({\displaystyle \frac{d^k\Pi }{d{\xi }^k}}{)}^s]=np+s(n+k).\hfill \end{array}$$ 7

Step 3 The solution of Eq. (6) is expressed as

$$\begin{array}{c}\hfill \phi (\xi )=\frac{\tau (\xi )}{\sqrt{{\varsigma }_1{\tau }^2(\xi )+{\varsigma }_2}},\end{array}$$ 8

where $({\varsigma }_1{\tau }^2(\xi )+{\varsigma }_2)>0$ and $\tau (\xi )$ is the solution of the Jacobian elliptic equation

$$\begin{array}{c}\hfill {\tau }^{{\prime }^2}(\xi )=l_0+l_2{\tau }^2(\xi )+l_4{\tau }^4(\xi ),\end{array}$$ 9

and $l_k(k=0,2,4)$ are real constant, while ${\varsigma }_1$ and ${\varsigma }_2$ are given by

$$\begin{array}{cc}\hfill {\varsigma }_1& =\frac{h_4(l_2-h_2)}{{(l_2-h_2)}^2+3l_0{l}_4-2l_2(l_2-h_2)},\hfill \\ \hfill {\varsigma }_2& =\frac{3l_0{h}_4}{{(l_2-h_2)}^2+3l_0{l}_4-2l_2(l_2-h_2)},\hfill \end{array}$$

under the constraints condition

$$\begin{array}{c}\hfill h_4^2(l_2-h_2)[9l_0{l}_4-(l_2-h_2)(2l_2+h_2)]+3h_6{[3l_0{l}_4-(l_2^2-h_2^2)]}^2=0.\end{array}$$ 10

Step 4 Eq. (9) has solutions in the form of JEFs as in Zayed et al. (2018). On solving Eqs. (9), (8) and (4) together. A set of algebraic system is extracted on the comparison of specific terms. On solving the obtained algebraic equations, we get the solutions of Eq. (2).

GERFM (Ghanbari et al. 2019)

Step 1 Consider the solution of Eq. (4) is represented as:

$$\begin{array}{c}\hfill \Pi (\xi )=d_0+\sum _{k=1}^n{d}_k\Omega {(\xi )}^k+\sum _{k=1}^n{f}_k\Omega {(\xi )}^{-k},\end{array}$$ 11

where

$$\begin{array}{c}\hfill \Omega (\xi )=\frac{r_1{e}^{s_1\xi }+r_2{e}^{s_2\xi }}{r_3{e}^{s_3\xi }+r_4{e}^{s_4\xi }}.\end{array}$$ 12

The unknown coefficients $d_0$, $d_k$, $f_k$ $(1\le k\le n)$ and constants $r_i$, $s_i$ $(1\le i\le 4)$ are determined and homogeneous balance principle is used to find n.

Step 2 We get a cluster of algebraic equations on putting Eq. (11) in Eq. (4).

Step 3 On solving the cluster of equations, we get the unknown terms and consequently, the required solutions are achieved.

The generalized Kudryashov method (Mahmuda et al. 2017)

Step 1 Suppose that Eq. (4) has the solution in the following form.

$$\begin{array}{c}\hfill \Pi (\xi )=\frac{{\sum }_{i=0}^T{a}_i{G}^i(\xi )}{{\sum }_{j=0}^H{b}_j{G}^j(\xi )},\end{array}$$ 13

where, $a_i(i=1,2,3,\cdots ,T)$ and $b_J(j=1,2,3,\cdots ,H)$ are constants to be determined after ward such that $a_T\ne 0$ and $b_H\ne 0$.

Now, next consider NODE in the following shape

$$\begin{array}{c}\hfill G^{\prime }(\xi )=G^2(\xi )-G(\xi ).\end{array}$$ 14

Moreover,the solution of Eq. (14) has the structure like

$$\begin{array}{c}\hfill G(\xi )=\frac{1}{1+S{e}^{\xi }}.\end{array}$$ 15

Here, S is constant of integration.

Step 2 The values of T and H are evaluated by using homogeneous balance principle in Eq. (4).

Step 3 We obtain a polynomial in $G(\eta )$, after putting Eqs. (13) and (14) into Eq. (4). We get a cluster of an algebraic equations on equating the same powers of $G(\xi )$ to zero, and we secure the values of $a_i(i=1,2,3,\cdots ,T)$ and $b_J(j=1,2,3,\cdots ,H)$. On the utilization of the obtained values in Eq. (13) with the usage of Eq. (15), we finally find the exact solution of Eq. (2).

Extraction of soliton solutions

This section deals the application of the applied method and we secure the different forms of the solutions to the under consideration model with Kerr law of nonlinearity.

For Kerr law the governing model is described as:

$$\begin{array}{c}\hfill i{\psi }_t+i\alpha {\psi }_{\mathit{xxx}}+{b|\psi |}^2\psi ={i[\lambda (|\psi |}^{2m}{\psi )}_x+{\theta |\psi |}^{2m}{\psi }_x+{\sigma (|\psi |}^{2m}{)}_x\psi ,\end{array}$$ 16

Now, we have to discuss the Eq. (16). For proceeding, we use the transformation as follows:

$$\begin{array}{c}\hfill \psi (x,t)=H(\xi )e^{i\phi (x,t)},\xi =\eta (x-\nu t),\phi (x,t)=-\kappa x+\omega t+{\theta }_0\end{array}$$ 17

where $\nu ,\kappa ,\omega$ and ${\theta }_0$ represent the speed, frequency, wave number and phase constant of the wave, respectively. Replacing Eq. (17) into Eq. (16). We get the real and imaginary parts, respectively

Real part

$$\begin{array}{c}\hfill 3\alpha \kappa {\eta }^2{H}^{{}^{\prime \prime }}-(\omega +\alpha {\kappa }^3)H+b{H}^3-\kappa (\lambda +\theta )H^{2m+1}=0\end{array}$$ 18

Imaginary part

$$\begin{array}{c}\hfill \alpha \kappa {\eta }^2{H}^{{}^{\prime \prime }}-(\nu +3\alpha {\kappa }^2)H-\frac{(\lambda +\theta +2\sigma m+2\lambda m)H^{2m+1}}{2m+1}=0\end{array}$$ 19

For integrability of this model, by using of $m=1$, the Eqs. (18) and (19) are reduced to

$$\begin{array}{c}\hfill 3a\kappa {\eta }^2{H}^{{}^{\prime \prime }}-(\omega +a{\kappa }^3)H+(b-\kappa (\lambda +\theta ))H^3=0\end{array}$$ 20

and

$$\begin{array}{c}\hfill \alpha \kappa {\eta }^2{H}^{{}^{\prime \prime }}-(\nu +3\alpha {\kappa }^2)H-\frac{(\theta +2\sigma +3\lambda )H^3}{3}=0\end{array}$$ 21

As the amplitude component holds Eqs. (20) and (21), we have

$$\begin{array}{c}\hfill 3\kappa =\frac{\omega +a{\kappa }^3}{\nu +3a{\kappa }^2}=-\frac{(3(b-\kappa \lambda -\kappa \theta )}{\theta +2\sigma +3\lambda }\end{array}$$ 22

which gives rise to

$$\begin{array}{c}\hfill \nu =\frac{\omega +\alpha {\kappa }^3-9\alpha {\kappa }^2}{3\kappa },\sigma =-\frac{2\kappa \lambda +b}{2\kappa }\end{array}$$ 23

Solutions via ${\Phi }^6$-model expansion method

By using balance principle in Eq. (20), we get $n=1$. Thus, the solution of Eq. (20) takes the following form

$$\begin{array}{c}\hfill H(\xi )={\chi }_0+{\chi }_1\phi +{\chi }_2{\phi }^2,\end{array}$$ 24

where ${\chi }_0,{\chi }_1,{\chi }_2$ are constants to be determined later. Solving Eqs. (24) and (20) together and following the steps of method with the aid of Mathematica, we have solutions sets as

Family-1:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\chi }_0\to 0,{\chi }_1\to \eta \sqrt{\frac{6\alpha h_{4}k}{-b+\theta k+k\lambda }},{\chi }_2\to 0,\hfill \\ h_0\to h_0,h_2\to \frac{\alpha k^3+\omega }{3\alpha {\eta }^{2}k},h_4\to h_4,h_6\to 0.\hfill \end{array}\right)\end{array}$$

Family-2:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\chi }_0\to 0,{\chi }_1\to -\eta \sqrt{\frac{6\alpha h_{4}k}{-b+\theta k+k\lambda }},{\chi }_2\to 0,\omega \to 3\alpha {\eta }^2{h}_{2}k-\alpha k^3,\hfill \\ h_0\to h_0,h_2\to \frac{\alpha k^3+\omega }{3\alpha {\eta }^{2}k},h_4\to h_4,h_6\to 0.\hfill \end{array}\right)\end{array}$$

The resulting solutions of Eq. (16) crosspounding to Family-1 are summarized as under

1. If $l_0=1$, $l_2=-(1+m^2)$, $l_4=m^2$, $0<m<1$, then $\tau (\xi )=\mathrm{sn}(\xi ,m)$ or $\tau (\xi )=\mathrm{cd}(\xi ,m)$, then we retrieve Jacobi elliptic function solutions

$$\begin{array}{c}\hfill {\psi }_1(x,t)=\left\{\frac{\sqrt{6}\eta \sqrt{\frac{\alpha h_{4}k}{k(\theta +\lambda )-b}}\text{sn}\left(\eta ,\left(x,-,\frac{t\left(\alpha ,(k-9),k^2,+,\omega \right)}{3k}\right),,,m\right)}{\sqrt{{\varsigma }_1\text{sn}{\left(\eta ,\left(x,-,\frac{t\left(\alpha ,(k-9),k^2,+,\omega \right)}{3k}\right),,,m\right)}^2+{\varsigma }_2}}\right\}\times e^{i\left({\theta }_0,-,k,x,+,t,\omega \right)},\end{array}$$ 25

or

$$\begin{array}{c}\hfill {\psi }_2(x,t)=\left\{\frac{\sqrt{6}\eta \sqrt{\frac{\alpha h_{4}k}{k(\theta +\lambda )-b}}\text{cd}\left(\eta ,\left(x,-,\frac{t\left(\alpha ,(k-9),k^2,+,\omega \right)}{3k}\right),,,m\right)}{\sqrt{{\varsigma }_1\text{cd}{\left(\eta ,\left(x,-,\frac{t\left(\alpha ,(k-9),k^2,+,\omega \right)}{3k}\right),,,m\right)}^2+{\varsigma }_2}}\right\}\times e^{i\left({\theta }_0,-,k,x,+,t,\omega \right)},\end{array}$$ 26

where

$$\begin{array}{c}\hfill {\varsigma }_1=-\frac{3\alpha {\eta }^2{h}_{4}k\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,\left(m^2,+,1\right),+,\omega \right)}{2\alpha k^3\omega +{\alpha }^2{k}^2\left(k^4,-,9,{\eta }^4,\left(m^4,-,m^2,+,1\right)\right)+{\omega }^2},\\ \hfill {\varsigma }_2=\frac{27{\alpha }^2{\eta }^4{h}_4{k}^2}{2\alpha k^3\omega +{\alpha }^2{k}^2\left(k^4,-,9,{\eta }^4,\left(m^4,-,m^2,+,1\right)\right)+{\omega }^2},\end{array}$$

under the constraint condition

$$\begin{array}{cc}& \left[-,\frac{h_4^2\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,\left(1,-,2,m^2\right),+,\omega \right)\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,\left(m^2,-,2\right),+,\omega \right)\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,\left(m^2,+,1\right),+,\omega \right)}{27{\alpha }^3{\eta }^6{k}^3}\right]\hfill \\ \hfill & +30{\left[-,\frac{{\left(\alpha ,k^3,+,\omega \right)}^2}{9{\alpha }^2{\eta }^4{k}^2},-,3,m^2,+,{\left(m^2,+,1\right)}^2\right]}^2=0,\hfill \end{array}$$

provided that $(\alpha h_{4}k)(k(\theta +\lambda )-b)>0$.

$\bullet$ On selecting $m\to 1$ in Eq. (25), dark optical soliton solution falls out

$$\begin{array}{c}\hfill {\psi }_{1,1}(x,t)=\left\{\frac{\sqrt{2}\eta \sqrt{\frac{\alpha h_{4}k}{k(\theta +\lambda )-b}}tanh\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)\right)}{\sqrt{\frac{\alpha {\eta }^2{h}_{4}k\left(9,\alpha ,{\eta }^2,k,-,\left(\alpha ,k^3,+,6,\alpha ,{\eta }^2,k,+,\omega \right),{tanh}^2,\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)\right)\right)}{2\alpha k^3\omega +{\alpha }^2{k}^2\left(k^4,-,9,{\eta }^4\right)+{\omega }^2}}}\right\}\times e^{i\left({\theta }_0,-,k,x,+,t,\omega \right)},\end{array}$$ 27

under the constraint condition

$$\begin{array}{c}\hfill 30{\left[1,-,\frac{{\left(\alpha ,k^3,+,\omega \right)}^2}{9{\alpha }^2{\eta }^4{k}^2}\right]}^2-\left[\frac{h_4^2{\left(\alpha ,k^3,-,3,\alpha ,{\eta }^2,k,+,\omega \right)}^2\left(\alpha ,k^3,+,6,\alpha ,{\eta }^2,k,+,\omega \right)}{27{\alpha }^3{\eta }^6{k}^3}\right]=0.\end{array}$$

and if $m\to 0$ in Eq. (26), the explicit periodic wave solution is extracted as

$$\begin{array}{c}\hfill {\psi }_{2,1}(x,t)=\left\{\frac{\sqrt{2}\eta \sqrt{\frac{\alpha h_{4}k}{k(\theta +\lambda )-b}}cos\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)\right)}{\sqrt{-\frac{\alpha {\eta }^2{h}_{4}k\left(\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,+,\omega \right),{cos}^2,\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)\right),-,9,\alpha ,{\eta }^2,k\right)}{2\alpha k^3\omega +{\alpha }^2{k}^2\left(k^4,-,9,{\eta }^4\right)+{\omega }^2}}}\right\}\times e^{i\left({\theta }_0,-,k,x,+,t,\omega \right)},\end{array}$$ 28

under the constraint condition

$$\begin{array}{c}\hfill 30{\left[1,-,\frac{{\left(\alpha ,k^3,+,\omega \right)}^2}{9{\alpha }^2{\eta }^4{k}^2}\right]}^2-\left[\frac{h_4^2\left(\alpha ,k^3,-,6,\alpha ,{\eta }^2,k,+,\omega \right){\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,+,\omega \right)}^2}{27{\alpha }^3{\eta }^6{k}^3}\right]=0.\end{array}$$

2. If $l_0=1-m^2$, $l_2=2m^2-1$, $l_4=-m^2$, $0<m<1$, then $\tau (\xi )=\mathrm{cn}(\xi ,m)$, then Jacobi elliptic function solution emerges

$$\begin{array}{c}\hfill {\psi }_3(x,t)=\left\{\frac{\sqrt{2}\eta \sqrt{\frac{\alpha h_{4}k}{k(\theta +\lambda )-b}}\text{cn}\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right),,,m\right)}{\sqrt{-\frac{\alpha {\eta }^2{h}_{4}k\left(\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,\left(1,-,2,m^2\right),+,\omega \right),\text{cn},{\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right),,,m\right)}^2,+,9,\alpha ,{\eta }^2,k,\left(m^2,-,1\right)\right)}{2\alpha k^3\omega +{\alpha }^2{k}^2\left(k^4,-,9,{\eta }^4,\left(m^4,-,m^2,+,1\right)\right)+{\omega }^2}}}\right\}\times e^{i\left({\theta }_0,-,k,x,+,t,\omega \right)},\end{array}$$ 29

The above solution is valid under the condition

$$\begin{array}{cc}& \left[-,\frac{h_4^2\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,\left(1,-,2,m^2\right),+,\omega \right)\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,\left(m^2,-,2\right),+,\omega \right)\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,\left(m^2,+,1\right),+,\omega \right)}{27{\alpha }^3{\eta }^6{k}^3}\right]\hfill \\ \hfill & +30{\left[-,\frac{{\left(\alpha ,k^3,+,\omega \right)}^2}{9{\alpha }^2{\eta }^4{k}^2},+,m^4,-,m^2,+,1\right]}^2=0.\hfill \end{array}$$

$\bullet$ On selecting $m\to 1$ in Eq. (29), bright optical soliton solution is extracted as

$$\begin{array}{c}\hfill {\psi }_{3,1}(x,t)=\left\{\frac{\sqrt{2}\eta \sqrt{\frac{\alpha h_{4}k}{k(\theta +\lambda )-b}}\text{sech}\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)\right)}{\sqrt{-\frac{\alpha {\eta }^2{h}_{4}k\left(\alpha ,k^3,-,3,\alpha ,{\eta }^2,k,+,\omega \right){\text{sech}}^2\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)\right)}{2\alpha k^3\omega +{\alpha }^2{k}^2\left(k^4,-,9,{\eta }^4\right)+{\omega }^2}}}\right\}\times e^{i\left({\theta }_0,-,k,x,+,t,\omega \right)},\end{array}$$ 30

under the constraint condition

$$\begin{array}{c}\hfill 30{\left[1,-,\frac{{\left(\alpha ,k^3,+,\omega \right)}^2}{9{\alpha }^2{\eta }^4{k}^2}\right]}^2-\left[\frac{h_4^2{\left(\alpha ,k^3,-,3,\alpha ,{\eta }^2,k,+,\omega \right)}^2\left(\alpha ,k^3,+,6,\alpha ,{\eta }^2,k,+,\omega \right)}{27{\alpha }^3{\eta }^6{k}^3}\right]=0.\end{array}$$

while on choosing $m\to 0$ in Eq. (29), the following solution is expressed

$$\begin{array}{c}\hfill {\psi }_{3,2}(x,t)=\left\{\frac{\sqrt{2}\eta \sqrt{\frac{\alpha h_{4}k}{k(\theta +\lambda )-b}}cos\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)\right)}{\sqrt{-\frac{\alpha {\eta }^2{h}_{4}k\left(\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,+,\omega \right),{cos}^2,\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)\right),-,9,\alpha ,{\eta }^2,k\right)}{2\alpha k^3\omega +{\alpha }^2{k}^2\left(k^4,-,9,{\eta }^4\right)+{\omega }^2}}}\right\}\times e^{i\left({\theta }_0,-,k,x,+,t,\omega \right)},\end{array}$$ 31

under the constraint condition

$$\begin{array}{c}\hfill 30{\left[1,-,\frac{{\left(\alpha ,k^3,+,\omega \right)}^2}{9{\alpha }^2{\eta }^4{k}^2}\right]}^2-\left[\frac{h_4^2\left(\alpha ,k^3,-,6,\alpha ,{\eta }^2,k,+,\omega \right){\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,+,\omega \right)}^2}{27{\alpha }^3{\eta }^6{k}^3}\right]=0.\end{array}$$

3. If $l_0=m^2$, $l_2=-(1+m^2)$, $l_4=1$, $0<m<1$, then $\tau (\xi )=\mathrm{ns}(\xi ,m)$ or $\tau (\xi )=\mathrm{dc}(\xi ,m)$, then Jacobi elliptic function solution is written as

$$\begin{array}{c}\hfill {\psi }_4(x,t)=\left\{\frac{\sqrt{2}\eta \sqrt{\frac{\alpha h_{4}k}{k(\theta +\lambda )-b}}\text{ns}\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right),,,m\right)}{\sqrt{-\frac{\alpha {\eta }^2{h}_{4}k\left(\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,\left(m^2,+,1\right),+,\omega \right),\text{ns},{\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right),,,m\right)}^2,-,9,\alpha ,{\eta }^2,k,m^2\right)}{2\alpha k^3\omega +{\alpha }^2{k}^2\left(k^4,-,9,{\eta }^4,\left(m^4,-,m^2,+,1\right)\right)+{\omega }^2}}}\right\}\times e^{i\left({\theta }_0,-,k,x,+,t,\omega \right)},\end{array}$$ 32

or

$$\begin{array}{c}\hfill {\psi }_5(x,t)=\left\{\frac{\sqrt{2}\eta \sqrt{\frac{\alpha h_{4}k}{k(\theta +\lambda )-b}}\text{dc}\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right),,,m\right)}{\sqrt{-\frac{\alpha {\eta }^2{h}_{4}k\left(\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,\left(m^2,+,1\right),+,\omega \right),\text{dc},{\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right),,,m\right)}^2,-,9,\alpha ,{\eta }^2,k,m^2\right)}{2\alpha k^3\omega +{\alpha }^2{k}^2\left(k^4,-,9,{\eta }^4,\left(m^4,-,m^2,+,1\right)\right)+{\omega }^2}}}\right\}\times e^{i\left({\theta }_0,-,k,x,+,t,\omega \right)},\end{array}$$ 33

The validity condition for solution (32) and (33) is defined as

$$\begin{array}{c}\hfill \left[-,\frac{h_4^2\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,\left(1,-,2,m^2\right),+,\omega \right)\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,\left(m^2,-,2\right),+,\omega \right)\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,\left(m^2,+,1\right),+,\omega \right)}{27{\alpha }^3{\eta }^6{k}^3}\right]\\ \hfill +30{\left[-,\frac{{\left(\alpha ,k^3,+,\omega \right)}^2}{9{\alpha }^2{\eta }^4{k}^2},-,3,m^2,+,{\left(m^2,+,1\right)}^2\right]}^2=0.\end{array}$$

$\bullet$ On taking $m\to 1$ in Eq. (32), we get explicitly hyperbolic solitary wave solution as

$$\begin{array}{c}\hfill {\psi }_{4,1}(x,t)=\left\{\frac{\sqrt{2}\eta \sqrt{\frac{\alpha h_{4}k}{k(\theta +\lambda )-b}}coth\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)\right)}{\sqrt{-\frac{\alpha {\eta }^2{h}_{4}k\left(\left(\alpha ,k^3,+,6,\alpha ,{\eta }^2,k,+,\omega \right),{coth}^2,\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)\right),-,9,\alpha ,{\eta }^2,k\right)}{2\alpha k^3\omega +{\alpha }^2{k}^2\left(k^4,-,9,{\eta }^4\right)+{\omega }^2}}}\right\}\times e^{i\left({\theta }_0,-,k,x,+,t,\omega \right)},\end{array}$$ 34

and on considering $m\to 0$ in Eq. (33), the following combined trigonometric solution is expressed

$$\begin{array}{c}\hfill {\psi }_{5,1}(x,t)=\left\{\frac{\sqrt{2}\eta \sqrt{\frac{\alpha h_{4}k}{k(\theta +\lambda )-b}}csc\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)\right)}{\sqrt{-\frac{\alpha {\eta }^2{h}_{4}k\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,+,\omega \right){csc}^2\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)\right)}{2\alpha k^3\omega +{\alpha }^2{k}^2\left(k^4,-,9,{\eta }^4\right)+{\omega }^2}}}\right\}\times e^{i\left({\theta }_0,-,k,x,+,t,\omega \right)},\end{array}$$ 35

The solutions (34) and (35) hold under the constraint conditions, respectively

$$\begin{array}{cc}& 30{\left[1,-,\frac{{\left(\alpha ,k^3,+,\omega \right)}^2}{9{\alpha }^2{\eta }^4{k}^2}\right]}^2-\left[\frac{h_4^2{\left(\alpha ,k^3,-,3,\alpha ,{\eta }^2,k,+,\omega \right)}^2\left(\alpha ,k^3,+,6,\alpha ,{\eta }^2,k,+,\omega \right)}{27{\alpha }^3{\eta }^6{k}^3}\right]=0.\hfill \\ \hfill & 30{\left[1,-,\frac{{\left(\alpha ,k^3,+,\omega \right)}^2}{9{\alpha }^2{\eta }^4{k}^2}\right]}^2-\left[\frac{h_4^2\left(\alpha ,k^3,-,6,\alpha ,{\eta }^2,k,+,\omega \right){\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,+,\omega \right)}^2}{27{\alpha }^3{\eta }^6{k}^3}\right]=0.\hfill \end{array}$$

4. If $l_0=-m^2$, $l_2=-1+2m^2$, $l_4=1-m^2$, $0<m<1$, then $\tau (\xi )=\mathrm{nc}(\xi ,m)$, reveals Jacobi elliptic function solution

$$\begin{array}{c}\hfill {\psi }_6(x,t)=\left\{\frac{\sqrt{6}\eta \sqrt{\frac{\alpha h_{4}k}{k(\theta +\lambda )-b}}\text{nc}\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right),,,m\right)}{\sqrt{{\varsigma }_1\text{nc}{\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right),,,m\right)}^2+{\varsigma }_2}}\right\}\times e^{i\left({\theta }_0,-,k,x,+,t,\omega \right)},\end{array}$$ 36

where

$$\begin{array}{cc}& {\varsigma }_1=-\frac{3\alpha {\eta }^2{h}_{4}k\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,\left(1,-,2,m^2\right),+,\omega \right)}{2\alpha k^3\omega +{\alpha }^2{k}^2\left(k^4,-,9,{\eta }^4,\left(m^4,-,m^2,+,1\right)\right)+{\omega }^2},\hfill \\ \hfill & {\varsigma }_2=-\frac{27{\alpha }^2{\eta }^4{h}_4{k}^2{m}^2}{2\alpha k^3\omega +{\alpha }^2{k}^2\left(k^4,-,9,{\eta }^4,\left(m^4,-,m^2,+,1\right)\right)+{\omega }^2},\hfill \end{array}$$

under the constraint condition

$$\begin{array}{cc}& \left[-,\frac{h_4^2\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,\left(1,-,2,m^2\right),+,\omega \right)\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,\left(m^2,-,2\right),+,\omega \right)\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,\left(m^2,+,1\right),+,\omega \right)}{27{\alpha }^3{\eta }^6{k}^3}\right]\hfill \\ \hfill & +30{\left[-,\frac{{\left(\alpha ,k^3,+,\omega \right)}^2}{9{\alpha }^2{\eta }^4{k}^2},+,m^4,-,m^2,+,1\right]}^2=0.\hfill \end{array}$$

provided that $(\alpha h_{4}k)(k(\theta +\lambda )-b)>0$.

$\bullet$ In particular, on considering $m\to 1$ in Eq. (36), we get explicit solitary wave solution

$$\begin{array}{c}\hfill {\psi }_{6,1}(x,t)=\left\{\frac{\sqrt{2}\eta \sqrt{\frac{\alpha h_{4}k}{k(\theta +\lambda )-b}}cosh\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)\right)}{\sqrt{-\frac{\alpha {\eta }^2{h}_{4}k\left(\left(\alpha ,k^3,-,3,\alpha ,{\eta }^2,k,+,\omega \right),{cosh}^2,\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)\right),+,9,\alpha ,{\eta }^2,k\right)}{2\alpha k^3\omega +{\alpha }^2{k}^2\left(k^4,-,9,{\eta }^4\right)+{\omega }^2}}}\right\}\times e^{i\left({\theta }_0,-,k,x,+,t,\omega \right)},\end{array}$$ 37

under the constraint condition

$$\begin{array}{c}\hfill 30{\left[1,-,\frac{{\left(\alpha ,k^3,+,\omega \right)}^2}{9{\alpha }^2{\eta }^4{k}^2}\right]}^2-\left[\frac{h_4^2{\left(\alpha ,k^3,-,3,\alpha ,{\eta }^2,k,+,\omega \right)}^2\left(\alpha ,k^3,+,6,\alpha ,{\eta }^2,k,+,\omega \right)}{27{\alpha }^3{\eta }^6{k}^3}\right]=0.\end{array}$$

while on taking $m\to 0$ in Eq. (36), the singular periodic wave solution is mentioned as

$$\begin{array}{c}\hfill {\psi }_{6,2}(x,t)=\left\{\frac{\sqrt{2}\eta \sqrt{\frac{\alpha h_{4}k}{-b+\theta k+k\lambda }}sec\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)\right)}{\sqrt{-\frac{\alpha {\eta }^2{h}_{4}k\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,+,\omega \right){sec}^2\left(\eta ,\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)\right)}{2\alpha k^3\omega +{\alpha }^2{k}^2\left(k^4,-,9,{\eta }^4\right)+{\omega }^2}}}\right\}\times e^{i\left({\theta }_0,-,k,x,+,t,\omega \right)},\end{array}$$ 38

The solution (38) holds with the condition

$$\begin{array}{c}\hfill 30{\left[1,-,\frac{{\left(\alpha ,k^3,+,\omega \right)}^2}{9{\alpha }^2{\eta }^4{k}^2}\right]}^2-\left[\frac{h_4^2\left(\alpha ,k^3,-,6,\alpha ,{\eta }^2,k,+,\omega \right){\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,+,\omega \right)}^2}{27{\alpha }^3{\eta }^6{k}^3}\right]=0.\end{array}$$

5. If $l_0=\frac{1}{4}$, $l_2=\frac{1-2m^2}{2}$, $l_4=\frac{1}{4}$, $0<m<1$, then $\tau (\xi )=\frac{\mathrm{sn}(\xi ,m)}{1\pm \mathrm{cn}(\xi ,m)}$, gives JEFs

$$\begin{array}{c}\hfill {\psi }_7(x,t)=\left\{\frac{\eta \text{sn}(\xi ,m)\sqrt{\frac{\alpha h_{4}k}{k(\theta +\lambda )-b}}}{\sqrt{2}(\text{cn}(\xi ,m)\pm 1)\sqrt{\frac{\alpha {\eta }^2{h}_{4}k\left(9,\alpha ,{\eta }^2,k,{(\text{cn}(\xi ,m)\pm 1)}^2,-,2,\text{sn},{(\xi ,m)}^2,\left(2,\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,\left(2,m^2,-,1\right),+,2,\omega \right)\right)}{{(\text{cn}(\xi ,m)\pm 1)}^2\left(32,\alpha ,k^3,\omega ,+,{\alpha }^2,k^2,\left(16,k^4,-,9,{\eta }^4,\left(16,m^4,-,16,m^2,+,1\right)\right),+,16,{\omega }^2\right)}}}\right\}\times e^{i\left({\theta }_0,-,k,x,+,t,\omega \right)},\end{array}$$ 39

Solution (39) holds under the condition

$$\begin{array}{cc}& h_4^2\left[-,\frac{\alpha k^3+\omega }{3\alpha {\eta }^{2}k},-,m^2,+,\frac{1}{2}\right]\left[\frac{\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,\left(1,-,2,m^2\right),+,\omega \right)\left(2,\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,\left(2,m^2,-,1\right),+,2,\omega \right)}{18{\alpha }^2{\eta }^4{k}^2},+,\frac{9}{16}\right]\hfill \\ \hfill & +30{\left[-,\frac{{\left(\alpha ,k^3,+,\omega \right)}^2}{9{\alpha }^2{\eta }^4{k}^2},+,m^4,-,m^2,+,\frac{1}{16}\right]}^2=0.\hfill \end{array}$$

$\bullet$ On selecting $m\to 1$ in Eq. (39), we get explicit solitary wave solution in combined form as

$$\begin{array}{c}\hfill {\psi }_{7,1}(x,t)=\left\{\frac{\eta tanh\left(\frac{\xi }{2}\right)\sqrt{\frac{\alpha h_{4}k}{k(\theta +\lambda )-b}}}{\sqrt{2}\sqrt{\frac{\alpha {\eta }^2{h}_{4}k\left(9,\alpha ,{\eta }^2,k,{(\text{sech}(\xi )+1)}^2,-,2,{tanh}^2,(\xi ),\left(2,\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,+,2,\omega \right)\right)}{{(\text{sech}(\xi )+1)}^2\left(32,\alpha ,k^3,\omega ,+,{\alpha }^2,k^2,\left(16,k^4,-,9,{\eta }^4\right),+,16,{\omega }^2\right)}}}\right\}\times e^{i\left({\theta }_0,-,k,x,+,t,\omega \right)},\end{array}$$ 40

under the constraint condition

$$\begin{array}{cc}& h_4^2\left[-,\frac{\alpha k^3+\omega }{3\alpha {\eta }^{2}k},-,\frac{1}{2}\right]\left[\frac{\left(\alpha ,k^3,-,3,\alpha ,{\eta }^2,k,+,\omega \right)\left(2,\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,+,2,\omega \right)}{18{\alpha }^2{\eta }^4{k}^2},+,\frac{9}{16}\right]\hfill \\ \hfill & +30{\left[\frac{1}{16},-,\frac{{\left(\alpha ,k^3,+,\omega \right)}^2}{9{\alpha }^2{\eta }^4{k}^2}\right]}^2=0.\hfill \end{array}$$

and on choosing$m\to 0$ in Eq. (39), we extract the following solution

$$\begin{array}{c}\hfill {\psi }_{7,2}(x,t)=\left\{\frac{\eta sin(\xi )\sqrt{\frac{\alpha h_{4}k}{k(\theta +\lambda )-b}}}{(cos(\xi )+1)\sqrt{\frac{\alpha {\eta }^2{h}_{4}k{sec}^2\left(\frac{\xi }{2}\right)\left(cos,(\xi ),\left(4,\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,+,4,\omega \right),-,4,\alpha ,k^3,+,15,\alpha ,{\eta }^2,k,-,4,\omega \right)}{32\alpha k^3\omega +{\alpha }^2{k}^2\left(16,k^4,-,9,{\eta }^4\right)+16{\omega }^2}}}\right\}\times e^{i\left({\theta }_0,-,k,x,+,t,\omega \right)},\end{array}$$ 41

The solution (41) holds with the condition

$$\begin{array}{cc}& h_4^2\left[\frac{1}{2},-,\frac{\alpha k^3+\omega }{3\alpha {\eta }^{2}k}\right]\left[\frac{\left(\alpha ,k^3,+,3,\alpha ,{\eta }^2,k,+,\omega \right)\left(2,\alpha ,k^3,-,3,\alpha ,{\eta }^2,k,+,2,\omega \right)}{18{\alpha }^2{\eta }^4{k}^2},+,\frac{9}{16}\right]\hfill \\ \hfill & +30{\left[\frac{1}{16},-,\frac{{\left(\alpha ,k^3,+,\omega \right)}^2}{9{\alpha }^2{\eta }^4{k}^2}\right]}^2=0.\hfill \end{array}$$

where $\xi =\eta (x-\nu t)$ and $\nu =\frac{\alpha k^3-9\alpha k^2+\omega }{3k}$. For details see reference (Zayed et al. 2018). The physical appearance of the gained results are depicted below under the suitable selection of variables.

Solutions via GERFM

The solution of Eq. (20) based on $n=1$ is expressed as

$$\begin{array}{c}\hfill H(\xi )=d_0+d_1\Omega (\xi )+f_1\Omega {(\xi )}^{-1}.\end{array}$$ 42

Family-1: For $r=[1,1,1,1]$ and $s=[0,0,1,-1]$, Eq. (12) gives

$$\begin{array}{c}\hfill \Omega (\xi )=\frac{2}{e^{\xi }+e^{-\xi }}.\end{array}$$ 43

Inserting Eq. (42) and Eq. (43) in Eq. (20), we secure solution set as follows:

Set-1:

$$\begin{array}{c}\hfill d_0=0,d_1=\frac{\sqrt{2}\sqrt{\alpha k^3+\omega }}{\sqrt{b-k(\theta +\lambda )}},f_1=0,\eta =\frac{\sqrt{\alpha k^3+\omega }}{\sqrt{3\alpha k}}.\end{array}$$

For set-1, the bright optical soliton emerges as

$$\begin{array}{c}\hfill {\psi }_1(x,t)=\left\{\frac{\sqrt{2}\sqrt{\alpha k^3+\omega }\text{sech}\left(\frac{\sqrt{\alpha k^3+\omega }\left(\alpha ,k^3,t,-,9,\alpha ,k^2,t,-,3,k,x,+,t,\omega \right)}{3k\sqrt{3}\sqrt{\alpha k}}\right)}{\sqrt{b-k(\theta +\lambda )}}\right\}\times e^{i(-kx+\omega t+{\theta }_0)}.\end{array}$$ 44

Here, $(\alpha k^3+\omega )(b-k(\theta +\lambda ))>0$ and $(\alpha k^3+\omega )\alpha k>0$ are considered as the validity conditions for the above solution.

Family-2: For $r=[-1,-1,1,-1]$ and $s=[1,-1,1,-1]$, then Eq. (12) gives

$$\begin{array}{c}\hfill \Omega (\xi )=-\frac{cosh(\xi )}{sinh(\xi )}.\end{array}$$ 45

Putting Eq. (42) and Eq. (45) in Eq. (20), the solution sets and their crossponding solutions are extracted as follows:

Set-1:

$$\begin{array}{c}\hfill d_0=0,d_1=0,f_1=-\frac{\sqrt{\alpha k^3+\omega }}{\sqrt{b-k(\theta +\lambda )}},\eta =\sqrt{\frac{-\alpha k^3-\omega }{6\alpha k}}.\end{array}$$

Inserting set-1 and Eq. (45) in Eq. (42), one may get

Dark soliton solution

$$\begin{array}{c}\hfill {\psi }_2(x,t)=\left\{\frac{\sqrt{\alpha k^3+\omega }tanh\left(\frac{\sqrt{-\alpha k^3-\omega }\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)}{\sqrt{6}\sqrt{\alpha }\sqrt{k}}\right)}{\sqrt{b-k(\theta +\lambda )}}\right\}\times e^{i(-kx+\omega t+{\theta }_0)}.\end{array}$$ 46

Set-2:

$$\begin{array}{c}\hfill d_0=0,d_1=-\frac{\sqrt{\alpha k^3+\omega }}{\sqrt{b-k(\theta +\lambda )}},f_1=0,\eta =\sqrt{\frac{-\alpha k^3-\omega }{6\alpha k}}.\end{array}$$

Substituting set-2 and Eq. (45) in Eq. (42), we get

Singular soliton solution

$$\begin{array}{c}\hfill {\psi }_3(x,t)=\left\{\frac{\sqrt{\alpha k^3+\omega }coth\left(\frac{\sqrt{-\alpha k^3-\omega }\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)}{\sqrt{6\alpha k}}\right)}{\sqrt{b-k(\theta +\lambda )}}\right\}\times e^{i(-kx+\omega t+{\theta }_0)}.\end{array}$$ 47

Set-3:

$$\begin{array}{c}\hfill d_0=0,d_1=\frac{\sqrt{\alpha k^3+\omega }}{2\sqrt{b-k(\theta +\lambda )}},f_1=\frac{\sqrt{\alpha k^3+\omega }}{2\sqrt{b-k(\theta +\lambda )}},\eta =\frac{1}{2}\sqrt{\frac{-\alpha k^3-\omega }{6\alpha k}}.\end{array}$$

Substituting set-3 and Eq. (45) in Eq. (42), we get

Dark-singular soliton solution

$$\begin{array}{cc}\hfill {\psi }_4(x,t)& =e^{i(-kx+\omega t+{\theta }_0)}\hfill \\ \hfill & \times \left\{\frac{\sqrt{\alpha k^3+\omega }tanh\left(\frac{\sqrt{-\alpha k^3-\omega }\left(\alpha ,k^3,t,-,9,\alpha ,k^2,t,-,3,k,x,+,t,\omega \right)}{6k\sqrt{6\alpha k}}\right)\left({coth}^2,\left(\frac{\sqrt{-\alpha k^3-\omega }\left(\alpha ,k^3,t,-,9,\alpha ,k^2,t,-,3,k,x,+,t,\omega \right)}{6k\sqrt{6k\alpha }}\right),+,1\right)}{2\sqrt{b-k(\theta +\lambda )}}\right\}.\hfill \end{array}$$ 48

The solutions (46), (47) and (48) are valid with the conditions $(\alpha k^3+\omega )(b-k(\theta +\lambda ))>0$ and $(-\alpha k^3-\omega )\alpha k>0$.

Family-3: For $r=[-2-i,-2+i,1,1]$ and $s=[i,-i,i,-i]$, then Eq. (12) gives

$$\begin{array}{c}\hfill \Omega (\xi )=\frac{sin(\xi )-2cos(\xi )}{cos(\xi )}.\end{array}$$ 49

Replacing Eq. (42) and Eq. (49) in Eq. (20), we establish solution sets given below.

Set-1:

$$\begin{array}{c}\hfill d_0=-\frac{2\sqrt{-\alpha k^3-\omega }}{\sqrt{b-k(\theta +\lambda )}},d_1=0,f_1=-\frac{5\sqrt{-\alpha k^3-\omega }}{\sqrt{b-k(\theta +\lambda )}},\eta =\sqrt{\frac{\alpha k^3+\omega }{6\alpha k}}.\end{array}$$

Using set-1 and Eq. (49) in Eq. (42), we get explicitly periodic wave solutions in combined form

$$\begin{array}{cc}\hfill {\psi }_5(x,t)& =e^{i(-kx+\omega t+{\theta }_0)}\hfill \\ \hfill & \times \left\{\frac{\sqrt{\alpha \left(-,k^3\right)-\omega }}{\sqrt{b-k(\theta +\lambda )}},\left(-,\frac{5cos\left(\frac{\sqrt{\alpha k^3+\omega }\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)}{\sqrt{6}\sqrt{\alpha }\sqrt{k}}\right)}{sin\left(\frac{\sqrt{\alpha k^3+\omega }\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)}{\sqrt{6}\sqrt{\alpha }\sqrt{k}}\right)-2cos\left(\frac{\sqrt{\alpha k^3+\omega }\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)}{\sqrt{6}\sqrt{\alpha }\sqrt{k}}\right)},-,2\right)\right\}.\hfill \end{array}$$ 50

Set-2:

$$\begin{array}{c}\hfill d_0=\frac{2\sqrt{\alpha \left(-,k^3\right)-\omega }}{\sqrt{b-k(\theta +\lambda )}},d_1=\frac{\sqrt{-\alpha k^3-\omega }}{\sqrt{b-k(\theta +\lambda )}},f_1=0,\eta =\frac{\sqrt{\alpha k^3+\omega }}{\sqrt{6\alpha k}}.\end{array}$$

Using set-2 and Eq. (49) in Eq. (42), we get singular periodic wave solution

$$\begin{array}{c}\hfill {\psi }_6(x,t)=\left\{\frac{\sqrt{-\alpha k^3-\omega }tan\left(\frac{\sqrt{\alpha k^3+\omega }\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)}{\sqrt{6}\sqrt{\alpha }\sqrt{k}}\right)}{\sqrt{b-k(\theta +\lambda )}}\right\}\times e^{i(-kx+\omega t+{\theta }_0)}.\end{array}$$ 51

${\psi }_5(x,t)$ and ${\psi }_6(x,t)$ hold under the constraint conditions $(\alpha k^3+\omega )(b-k(\theta +\lambda ))>0$ and $-(\alpha k^3\omega )\alpha k<0$.

Family-4: For $r=[-3,-1,1,1]]$ and $s=[1,-1,1,-1]$, then Eq. (12) gives

$$\begin{array}{c}\hfill \Omega (\xi )=\frac{-sinh(\xi )-2cosh(\xi )}{cosh(\xi )}.\end{array}$$ 52

Solving Eqs. (42), (52) and (20) together, we obtain the following solution sets..

Set-1:

$$\begin{array}{c}\hfill d_0=\frac{2\sqrt{\alpha k^3+\omega }}{\sqrt{b-k(\theta +\lambda )}},d_1=0,f_1=\frac{3\sqrt{\alpha k^3+\omega }}{\sqrt{b-k(\theta +\lambda )}},\eta =\sqrt{\frac{-(\alpha k^3+\omega )}{6\alpha k}}.\end{array}$$

For set-1, combo soliton solution is written as

$$\begin{array}{cc}\hfill {\psi }_7(x,t)=& e^{i(-kx+\omega t+{\theta }_0)}\hfill \\ \hfill & \times \left\{\frac{\sqrt{\alpha k^3+\omega }}{\sqrt{b-k(\theta +\lambda )}},\left(2,-,\frac{3cosh\left(\frac{\sqrt{\alpha \left(-,k^3\right)-\omega }\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)}{\sqrt{6}\sqrt{\alpha }\sqrt{k}}\right)}{sinh\left(\frac{\sqrt{\alpha \left(-,k^3\right)-\omega }\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)}{\sqrt{6}\sqrt{\alpha }\sqrt{k}}\right)+2cosh\left(\frac{\sqrt{\alpha \left(-,k^3\right)-\omega }\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)}{\sqrt{6}\sqrt{\alpha }\sqrt{k}}\right)}\right)\right\}.\hfill \end{array}$$ 53

Set-2:

$$\begin{array}{c}\hfill d_0=-\frac{2\sqrt{\alpha k^3+\omega }}{\sqrt{b-k(\theta +\lambda )}},d_1=-\frac{\sqrt{\alpha k^3+\omega }}{\sqrt{b-k(\theta +\lambda )}},f_1=0,\eta =\sqrt{\frac{-(\alpha k^3+\omega )}{6\alpha k}}.\end{array}$$

For set-2, teh dark soliton solution falls out

$$\begin{array}{c}\hfill {\psi }_8(x,t)=\left\{\frac{\sqrt{\alpha k^3+\omega }tanh\left(\frac{\sqrt{-\alpha k^3-\omega }\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)}{\sqrt{6}\sqrt{\alpha }\sqrt{k}}\right)}{\sqrt{b-k(\theta +\lambda )}}\right\}\times e^{i(-kx+\omega t+{\theta }_0)}.\end{array}$$ 54

The above solutions hold under $(\alpha k^3+\omega )(b-k(\theta +\lambda ))>0$ and $(\alpha k^3+\omega )\alpha k<0$.

Family-5: For $r=[-1,0,1,1]$ and $s=[0,1,0,1]$, then Eq. (12) gives

$$\begin{array}{c}\hfill \Omega (\xi )=-\frac{1}{e^{\xi }+1}.\end{array}$$ 55

Set-1:

$$\begin{array}{c}\hfill d_0=\frac{\sqrt{\alpha k^3+\omega }}{\sqrt{b-k(\theta +\lambda )}},d_1=\frac{2\sqrt{\alpha k^3+\omega }}{\sqrt{b-k(\theta +\lambda )}},f_1=0,\eta =\sqrt{\frac{-2(\alpha k^3+\omega )}{3\alpha k}}.\end{array}$$

We get exponential solution on solving Eqs. (42), (55) and set 1 as

$$\begin{array}{c}\hfill {\psi }_9(x,t)=\left\{\frac{\sqrt{\alpha k^3+\omega }\left(1,-,\frac{2}{exp\left(\frac{\sqrt{\frac{2}{3}}\sqrt{\alpha \left(-,k^3\right)-\omega }\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)}{\sqrt{\alpha }\sqrt{k}}\right)+1}\right)}{\sqrt{b-k(\theta +\lambda )}}\right\}\times e^{i(-kx+\omega t+{\theta }_0)}.\end{array}$$ 56

The above solutions hold under $(\alpha k^3+\omega )(b-k(\theta +\lambda ))>0$ and $(\alpha k^3+\omega )\alpha k<0$.

The graphical view of the earned solutions are sketched below with the choice of appropriate parameters.

Solutions via generalized Kudryashov method

The generalized Kudryashov method is utilized to analyze a variety of solution to the considered model. Take the homogeneous balance between $H^3$ and $H^{{}^{\prime \prime }}$ provides the relation $T=H+1$. Particularly, for $H=1$, we have $T=2$. Therefore, the Eq. (20) takes the solution in following form

$$\begin{array}{c}\hfill \varphi (\xi )=\frac{a_0+a_{1}G(\xi )+a_2{G}^2(\xi )}{b_0+b_{1}G(\xi )},\end{array}$$ 57

where $a_0,a_1,a_2,b_0$ and $b_1$ are to be determined. Now, solving Eqs. (20) and (57), and following the step 3 of the method, the following system of equations is obtained as:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}-\alpha a_0{b}_0^2{k}^3-a_0{b}_0^2\omega +a_0^{3}b-a_0^3\theta k-a_0^3\lambda k=0\hfill & \hfill \\ -\alpha a_1{b}_0^2{k}^3-2\alpha a_0{b}_0{b}_1{k}^3+3\alpha a_1{b}_0^2{\eta }^{2}k-3\alpha a_0{b}_0{b}_1{\eta }^{2}k-a_1{b}_0^2\omega -2a_0{b}_0{b}_1\omega +3a_0^2{a}_{1}b-3a_0^2{a}_1\theta k-3a_0^2{a}_1\lambda k=0\hfill & \hfill \\ 3a_0{a}_1^{2}b-3a_0{a}_1^2\theta k-3a_0{a}_1^{2}k\lambda +3a_0^2{a}_{2}b-3a_0^2{a}_2\theta k-3a_0^2{a}_{2}k\lambda -9\alpha a_1{b}_0^2{\eta }^{2}k-\alpha a_2{b}_0^2{k}^3+12\alpha a_2{b}_0^2{\eta }^{2}k\hfill \\ -\alpha a_0{b}_1^2{k}^3-2\alpha a_1{b}_0{b}_1{k}^3+3\alpha a_0{b}_1^2{\eta }^{2}k+9\alpha a_0{b}_0{b}_1{\eta }^{2}k-3\alpha a_1{b}_0{b}_1{\eta }^{2}k+a_2{b}_0^2\omega -a_0{b}_1^2\omega -2a_1{b}_0{b}_1\omega =0\hfill & \hfill \\ 6\alpha a_1{b}_0^2{\eta }^{2}k-30\alpha a_2{b}_0^2{\eta }^{2}k-6\alpha a_0{b}_0{b}_1{\eta }^{2}k+a_1^{3}b+6a_0{a}_2{a}_{1}b-a_1^3\theta k-6a_0{a}_2{a}_1\theta k-a_1^{3}k\lambda -6a_0{a}_2{a}_{1}k\lambda \hfill \\ -\alpha a_1{b}_1^2{k}^3-2\alpha a_2{b}_0{b}_1{k}^3-3\alpha a_0{b}_1^2{\eta }^{2}k++3\alpha a_1{b}_0{b}_1{\eta }^{2}k+9\alpha a_2{b}_0{b}_1{\eta }^{2}k-a_1{b}_1^2\omega -2a_2{b}_0{b}_1\omega =0\hfill & \hfill \\ -9\alpha a_2{b}_1^2{\eta }^{2}k+18\alpha a_2{b}_0{b}_1{\eta }^{2}k+3a_1{a}_2^{2}b-3a_1{a}_2^2\theta k-3a_1{a}_2^{2}k\lambda =0\hfill & \hfill \\ 6\alpha a_2{b}_1^2{\eta }^{2}k+a_2^{3}b-a_2^3\theta k-a_2^{3}k\lambda =0\hfill & \hfill \\ -\alpha a_2{b}_1^2{k}^3+18\alpha a_2{b}_0^2{\eta }^{2}k+3\alpha a_2{b}_1^2{\eta }^{2}k-27\alpha a_2{b}_0{b}_1{\eta }^{2}k-a_2{b}_1^2\omega +3a_0{a}_2^{2}b+3a_1^2{a}_{2}b-3a_0{a}_2^2\theta k-3a_1^2{a}_2\theta k-3a_0{a}_2^2\lambda k\hfill \\ -3a_1^2{a}_2\lambda k=0\hfill \end{array}\right)\end{array}$$ 58

The system (58) is manipulated with the aid of of computational packages like Mathematica, we get the solution sets as

Set-1:

$$\begin{array}{cc}\hfill a_0=& \frac{i{b}_0\sqrt{\alpha k^3+\omega }}{\sqrt{k(\theta +\lambda )-b}},a_1=-\frac{i\left(2,b_0,-,b_1\right)\sqrt{\alpha k^3+\omega }}{\sqrt{k(\theta +\lambda )-b}},a_2=-\frac{2i{b}_1\sqrt{\alpha k^3+\omega }}{\sqrt{k(\theta +\lambda )-b}},\hfill \\ \hfill \eta =& \sqrt{-\frac{2\left(\alpha ,k^3,+,\omega \right)}{3\alpha k}},b_0=b_0,b_1=b_1.\hfill \end{array}$$

On substituting the above values of parameters in Eq. (57) and with the assistance of Eq. (15), and on setting $S=1$, we secure the general soliton solution in terms of hyperbolic functions.

$$\begin{array}{c}\hfill {\psi }_1(x,t)=\left\{\frac{i\sqrt{\alpha k^3+\omega }\left(1,-,2,tanh,\left(\frac{\sqrt{-\frac{\alpha k^3+\omega }{\alpha k}}\left(x,-,\frac{t\left(\alpha ,(k-9),k^2,+,\omega \right)}{3k}\right)}{\sqrt{6}}\right)\right)}{\sqrt{k(\theta +\lambda )-b}}\right\}\times e^{i(-kx+\omega t+{\theta }_0)}.\end{array}$$ 59

$(\alpha k^3+\omega )(b-k(\theta +\lambda ))>0$ and $(\alpha k^3+\omega )\alpha k<0$ are the constraint conditions for the existence of the above secured solution.

Set-2:

$$\begin{array}{cc}\hfill a_0& =-\frac{i{b}_0\sqrt{\alpha k^3+\omega }}{\sqrt{k(\theta +\lambda )-b}},a_1=\frac{i\left(2,b_0,+,b_1\right)\sqrt{\alpha k^3+\omega }}{\sqrt{k(\theta +\lambda )-b}},a_2=0,\eta =\sqrt{-\frac{2\left(\alpha ,k^3,+,\omega \right)}{3\alpha k}},\hfill \\ \hfill b_0& =b_0,b_1=b_1.\hfill \end{array}$$

By taking $S=1$ and solving Eqs. (57) and (15) together, we get combine soliton solution as follows

$$\begin{array}{cc}\hfill {\psi }_2(x,t)=& e^{i(-kx+\omega t+{\theta }_0)}\hfill \\ \hfill & \times \left\{\frac{i\sqrt{\alpha k^3+\omega }\left(1,-,\frac{2\left(b_0,+,b_1\right)}{b_0\left(sinh,\left(\sqrt{\frac{2}{3}},\sqrt{-\frac{\alpha k^3+\omega }{\alpha k}},\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)\right),+,cosh,\left(\sqrt{\frac{2}{3}},\sqrt{-\frac{\alpha k^3+\omega }{\alpha k}},\left(x,-,\frac{t\left(\alpha ,k^3,-,9,\alpha ,k^2,+,\omega \right)}{3k}\right)\right),+,1\right)+b_1}\right)}{\sqrt{k(\theta +\lambda )-b}}\right\}.\hfill \end{array}$$ 60

with the constraint conditions $(\alpha k^3+\omega )(b-k(\theta +\lambda ))>0$ and $(\alpha k^3+\omega )\alpha k<0$.

Set-3:

$$\begin{array}{c}\hfill a_0=b_0\eta \sqrt{\frac{3\alpha k}{2(k(\theta +\lambda )-b)}},a_1=2b_0\eta \sqrt{\frac{6\alpha k}{k(\theta +\lambda )-b}},a_2=0,b_0=b_0,b_1=2b_0,\omega =-\frac{1}{2}\alpha k\left(3,{\eta }^2,+,2,k^2\right).\end{array}$$

By selecting $S=1$ and solving Eqs. (57) and (15) together, we get bright-dark soliton solution as follows

$$\begin{array}{cc}\hfill {\psi }_3(x,t)=& exp\left(i,\left({\theta }_0,-,\frac{1}{2},\alpha ,k,t,\left(3,{\eta }^2,+,2,k^2\right),-,k,x\right)\right)\hfill \\ \hfill & \times \left\{\frac{\sqrt{\frac{3}{2}}\eta \sqrt{\frac{\alpha k}{k(\theta +\lambda )-b}}\left(tanh,\left(\frac{1}{2},\alpha ,\eta ,t,\left({\eta }^2,+,6,k\right),+,\eta ,x\right),+,4,\text{sech},\left(\frac{1}{2},\alpha ,\eta ,t,\left({\eta }^2,+,6,k\right),+,\eta ,x\right),+,1\right)}{tanh\left(\frac{1}{2},\alpha ,\eta ,t,\left({\eta }^2,+,6,k\right),+,\eta ,x\right)+3\text{sech}\left(\frac{1}{2},\alpha ,\eta ,t,\left({\eta }^2,+,6,k\right),+,\eta ,x\right)+1}\right\}.\hfill \end{array}$$ 61

under constraint condition $(\alpha k^3+\omega )(b-k(\theta +\lambda ))>0$.

Set-4:

$$\begin{array}{c}\hfill b_1=\left(\frac{a_1}{a_0},+,2\right)b_0,a_2=-2\left(2,a_0,+,a_1\right),\omega =\frac{a_0^2\left(3,{\eta }^2,+,2,k^2\right)(b-k(\theta +\lambda ))}{3b_0^2{\eta }^2},\alpha =\frac{2a_0^2(k(\theta +\lambda )-b)}{3b_0^2{\eta }^{2}k}.\end{array}$$

For $S=1$, we get the kink-type soliton solution

$$\begin{array}{cc}\hfill {\psi }_4(x,t)=& exp\left(i,\left(\frac{a_0^{2}t\left(3,{\eta }^2,+,2,k^2\right)(b-k(\theta +\lambda ))}{3b_0^2{\eta }^2},+,{\theta }_0,-,k,x\right)\right)\hfill \\ \hfill & \times \left\{\frac{a_{0}tanh\left(\frac{1}{2},\eta ,\left(\frac{a_0^{2}t\left(3,{\eta }^2,+,2,k^2\right)(k(\theta +\lambda )-b)}{9b_0^2{\eta }^{2}k},-,\frac{1}{3},\alpha ,(k-9),k,t,+,x\right)\right)}{b_0}\right\}.\hfill \end{array}$$ 62

Set-5:

$$\begin{array}{c}\hfill b_0=\frac{i\sqrt{\frac{b-k(\theta +\lambda )}{6\alpha k}}}{\eta },b_1=-\frac{{\text{ia}}_0\sqrt{\frac{2(b-k(\theta +\lambda ))}{3\alpha k}}}{\eta },a_2=2a_0,a_1=-2a_0,\omega =\alpha (-k)\left(6,{\eta }^2,+,k^2\right).\end{array}$$

In particular, on $S=1$, we get the following solitary wave solution

$$\begin{array}{c}\hfill {\psi }_5(x,t)=\left\{coth,\left(\eta ,\left(\alpha ,t,\left(2,{\eta }^2,+,3,k\right),+,x\right)\right)\right\}\times e^{i\left({\theta }_0,-,\alpha ,k,t,\left(6,{\eta }^2,+,k^2\right),-,k,x\right)}.\end{array}$$ 63

MI Analysis

In this, we use the concept of standard linear stability analysis (Younas and Ren 2021; Bilal et al. 2021) to observed the MI analysis Eq. (16) on considering $m=1$. The starting hypothesis for finding the MI analysis for Eq. (16) is defined as:

$$\begin{array}{c}\hfill \psi (x,t)=e^{i\chi x}\left(P,(x,t),+,\sqrt{\chi }\right),\end{array}$$ 64

where $\chi$ is the steady state solution for Eq. (16). Putting Eq. (64) into Eq. (16) and linearizing, provides

$$\begin{array}{c}\hfill i{P}_t+(\alpha {\chi }^3+3b\chi +3\theta {\chi }^2+3\lambda {\chi }^2)(P+P^{\ast })-\left(3,i,\alpha ,{\chi }^2,+,i,\theta ,\chi ,+,3,i,\lambda ,\chi ,+,2,i,\sigma ,\chi \right)P_x-3\alpha \chi P_{\mathit{xx}}+i\alpha P_{\mathit{xxx}}=0,\end{array}$$ 65

where $\ast$ indicates the conjugate of complex function. For proceeding, we take the solution of Eq. (65) as:

$$\begin{array}{c}\hfill P(x,t)=f_1{e}^{i(lx-t\varpi )}+f_2{e}^{-i(lx-t\varpi )},\end{array}$$ 66

where l and $\varpi$ are the normalized wave number and frequency of perturbation, respectively. On solving the Eqs. (66) and (65) together, and splitting the coefficients of $e^{i(xl-\varpi t)}$ and $e^{-i(xl-\varpi t)}$ yields, the dispersion relation:

$$\begin{array}{cc}& 18\alpha b{l}^2{\chi }^2-{\alpha }^2{l}^6+3{\alpha }^2{l}^4{\chi }^2-2\alpha \theta l^4\chi -6\alpha \lambda l^4\chi -4\alpha l^4\sigma \chi -2\alpha l^3\varpi -3{\alpha }^2{l}^2{\chi }^4+12\alpha \theta l^2{\chi }^3\hfill \\ \hfill & -12\alpha l^2\sigma {\chi }^3-{\theta }^2{l}^2{\chi }^2-6\theta \lambda l^2{\chi }^2-4\theta l^2\sigma {\chi }^2-9{\lambda }^2{l}^2{\chi }^2-12\lambda l^2\sigma {\chi }^2-4l^2{\sigma }^2{\chi }^2\hfill \\ \hfill & -6\alpha l{\chi }^2\varpi -2\theta l\chi \varpi -6\lambda l\chi \varpi -4l\sigma \chi \varpi -{\varpi }^2=0,\hfill \end{array}$$ 67

Solving the dispersion relation of Eq. (67) for $\varpi$ provides

$$\begin{array}{c}\hfill \varpi =-\alpha l^3-3\alpha l{\chi }^2-\theta l\chi -3\lambda l\chi -2l\sigma \chi \pm \sqrt{3}\sqrt{6\alpha b{l}^2{\chi }^2+3{\alpha }^2{l}^4{\chi }^2+2{\alpha }^2{l}^2{\chi }^4+6\alpha \theta l^2{\chi }^3+6\alpha \lambda l^2{\chi }^3}.\end{array}$$ 68

We discuss the steady-state stability with the assistant of above dispersion relation. If the wave number $\varpi$ has a real part then the steady-state turn to stable against small perturbations. Moreover, if the wave number $\varpi$ is imaginary then the steady-state solution turns unstable since the perturbation grows exponentially. Therefore, the steady-state solution is unstable if, $6\alpha b{l}^2{\chi }^2+3{\alpha }^2{l}^4{\chi }^2+2{\alpha }^2{l}^2{\chi }^4+6\alpha \theta l^2{\chi }^3+6\alpha \lambda l^2{\chi }^3<0$. Finally, the MI gain spectrum $G(\chi )$ is achieved as:

$$\begin{array}{cc}\hfill G(\chi )=& 2Im(\varpi )=2Im(-\alpha l^3-3\alpha l{\chi }^2-\theta l\chi -3\lambda l\chi \hfill \\ \hfill & -2l\sigma \chi \sqrt{3}\sqrt{6\alpha b{l}^2{\chi }^2+3{\alpha }^2{l}^4{\chi }^2+2{\alpha }^2{l}^2{\chi }^4+6\alpha \theta l^2{\chi }^3+6\alpha \lambda l^2{\chi }^3}).\hfill \end{array}$$ 69

Concluding remarks

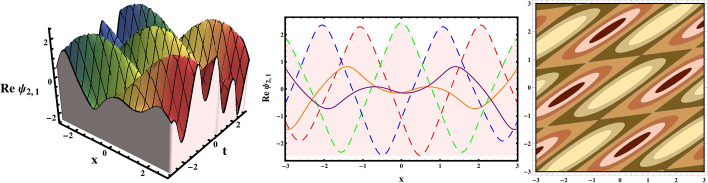
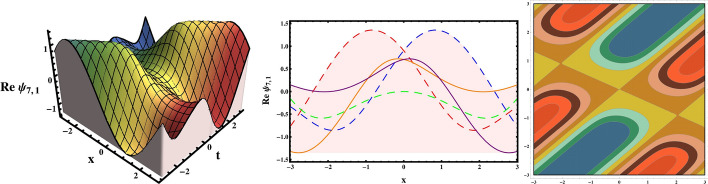
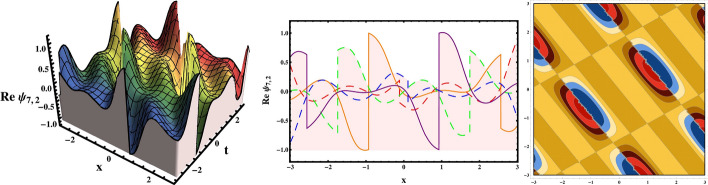
In this manuscript, we have discussed the pure-cubic optical solitons with Kerr law of nonlinearity. The nonlinear Schrödinger equation with effects of chromatic dispersion and third order dispersion is studied as a governing model. With the assistant of three sound integration computational tools, namely, ${\Phi }^6$-model expansion method and GERFM and generalized Kudryashov method, the results are expressed in the forms of hyperbolic, periodic, exponential, Jacobi elliptic function, bright, dark, combo, singular, kink and multiple soliton solutions The accomplished outcomes are remarkable and new from the current results in available writing. The principle achievement of these procedures lie in the manner that, we have prevailing in a single move to extricate most extreme results which can vary it from different methods. We encountered that the results presented in this article could be helpful in explaining the genuine meaning of various nonlinear advancement conditions arising in the different fields of nonlinear sciences. For example, hyperbolic functions shows up in various regions like, in the computation and speed of special relativity, in the Langevin function for attractive polarization, in the gravitational capability of a chamber and the estimation of as far as possible, in the profile of a laminar jet. Moreover, the bright soliton solutions will be a big asset in controlling the soliton clutter as mentioned in the introduction section. This means that the solitons can be converted to a state of separation from a state of attraction which would mean clearing the clutter. The bright soliton solutions will be a major resource in controlling the soliton mess as referenced in the presentation area. This implies that the solitons can be changed over to a condition of partition from a condition of fascination which would mean clearing the messiness. Thusly, this would bring a factor of "ease" to the Internet bottleneck that is a developing issue to the cutting edge media communications industry where the Internet is a day by day fundamental for endurance. During the current COVID-19 pandemic period, where all business activities are conducted online, it is critical to have a smooth and uninterrupted flow of pulses for uninterrupted Internet communications. Similarly, when a background wave is present, dark solitons can aid soliton transmission. Three dimensional, two dimensional and contour graphs are sketched in Figs. (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12) for explaining the physical appearance to the earned solution for the suitable selection of parameters. The results are fascinating not just from a hypothetical perspective yet in addition from a practical perspective, especially regarding the conduct of optical gadgets.

Fig. 1.

3D, 2D and contour graphical representations of solution (27)

Fig. 2.

3D, 2D and contour graphical representations of solution (28)

Fig. 3.

3D, 2D and contour graphical representations of solution (34)

Fig. 4.

3D, 2D and contour graphical representations of solution (35)

Fig. 5.

3D, 2D and contour graphical representations of solution (40)

Fig. 6.

3D, 2D and contour graphical representations of solution (41)

Fig. 7.

3D, 2D and contour graphical representations of solution (44)

Fig. 8.

3D, 2D and contour graphical representations of solution (50)

Fig. 9.

3D, 2D and contour graphical representations of solution (53)

Fig. 10.

3D, 2D and contour graphical representations of solution (60)

Fig. 11.

3D, 2D and contour graphical representations of solution (61)

Fig. 12.

MI gain spectrum for Eq. (69)

Declarations

Conflict of interest

The authors declare that they have no conflict of interest.