Modelling multiregional brain activity

Abstract

The dynamics of multiregional brain networks in response to temporally varying patterns of ongoing direct electrical stimulation can be predicted by modelling, with variabilities in prediction accuracy explained by at-rest functional connectivity.

For some patients with Parkinson’s disease, epilepsy and other neurological disorders who are not treatable with pharmacologic interventions, direct electrical stimulation (DES) of their brain has provided relief from tremors. In DES, electrodes implanted in the brain modulate ongoing neural activity by stimulating the surface of the brain or structures deep into it. The success of DES for some clinical applications has raised the possibility that it may be a powerful tool for modulating neural circuits relevant for higher-order cognitive function. For example, recent clinical trials suggest that DES may be effective for treating neuropsychiatric disorders such as treatment-resistant depression and chronic pain¹. However, the effects of DES, including how its amplitude and frequency can modulate ongoing activity in large-scale multiregional brain networks, remains poorly understood. This has led to conflicting reports of whether DES can be optimized to improve memory and other complex thinking^2,3.

Ideally, effective therapeutic stimulation would be informed by a detailed understanding of the effects of electrical stimulation on ongoing large-scale neuronal activity. However, current computational models are limited in their ability to predict the outcome of brain stimulation. First, DES of the brain leads to complex responses both in local tissue — that is, tissue closest to the electrode — and in distributed large-scale networks farther away from the electrode⁴. Furthermore, biophysical models of the brain have traditionally focused on spiking neurons, which requires nonlinear modelling. Therefore, although biophysical spiking-neuron models have provided valuable insights into the relationship between stimulation and neural response, they often include a large number of parameters that must be fit using large datasets captured through experimental protocols. Acquiring these data in humans is often difficult, and limits the use of such models to real-time closed-loop settings. And more broadly, it is difficult to infer the effects of stimulation on large-scale distributed networks with heterogenous neuronal populations. Reporting in Nature Biomedical Engineering, Maryam Shanechi and colleagues now show that the responses of large-scale multiregional brain networks to temporally varying stimulation can be predicted by a dynamic linear-state space model⁵.

By using microelectrodes implanted in the brains of two rhesus monkeys, Shanechi and co-authors analysed recordings of local field potentials (LFPs) while simultaneously applying microstimulation. The authors constructed a dynamic input–output model that captures the effects of stimulation on ongoing large-scale brain activity by manipulating the amplitude and frequency of input stimulation and by analysing the model’s LFP outputs. They analysed the output of four frequency bands (1–8 Hz, 8–12 Hz, 12–30 Hz and 30–50 Hz; these include the typical rhythms relevant for brain function and dysfunction) in several brain regions, and defined each combination of brain region and power-spectrum feature of the LFP as a network node, with the objective of the model being to predict the activity in the network as a function of the stimulation parameters. In contrast to simple linear regression, the model is dynamic — that is, the output of the model is a function of a latent (unobserved, yet inferred) state that depends on its own past LFP-power-spectrum features. To produce input signals with a white spectrum (that is, a signal that has equal intensity at different frequencies and that allows for the identification of the model’s parameters), the authors stochastically switched stimulation amplitude and frequency between multiple discrete levels (Fig. 1a). They also used an experimental design allowing for the input-driven dynamics to be dissociated from the overall ongoing network activity being measured, and quantified model performance as the ability of the model to predict the input-driven dynamics using only past stimulation inputs (Fig. 1b).

Fig. 1 |. Predicting network responses to DES by using a dynamic input–output model.

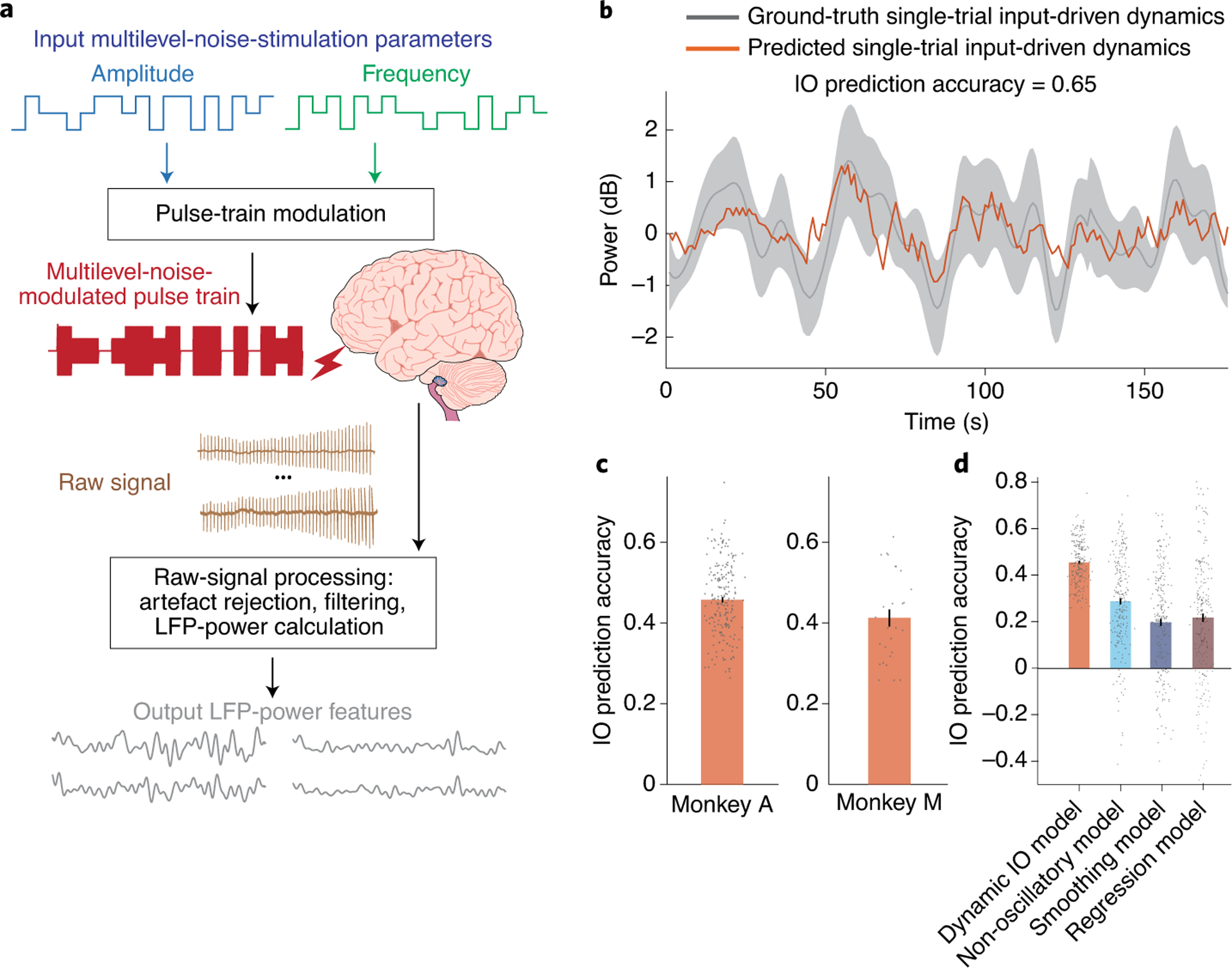
a, Microstimulation pulse-trains are modulated by independently generated amplitude and frequency time series that change stochastically between multiple levels. b, Example of a forward-prediction trace from the superior frontal gyrus in response to orbitofrontal cortex stimulation (orange). The grey solid line represents the ground-truth single-trial input-driven dynamics, and the grey area provides the standard error of the mean (s.e.m.) of the ground truth, which was computed from the measured LFP-power-spectrum features across trials. c, Prediction accuracies for predictable power-spectrum features for two monkeys. d, Forward-prediction accuracy of predictable power features for the dynamic model compared to non-oscillatory, smoothing and regression models across the two monkeys. In c and d, the error bars denote the mean and the s.e.m. The dots are the individual input–output (IO) prediction accuracies. Figure adapted with permission from ref.⁵, Springer Nature Ltd.

Because, to predict outputs, forward prediction uses only past stimulation inputs rather than past network activity, it is a strong test of the performance of input–output models. To assess the statistical significance of the predictions of the model, Shanechi and colleagues applied it to artificially generated datasets generated by fixing the outputs and randomly generating the inputs, or by fixing the inputs and using baseline network activity as the outputs. Features with a forward prediction that was statistically significant for both tests were defined as predictable power-spectrum features (Fig. 1c). Across both monkeys, over 70% of the brain regions contained at least one predictable power-spectrum feature, suggesting a distributed network response to electrical stimulation. The forward-prediction accuracy when using only one of the two inputs (stimulation amplitude or frequency) was significantly smaller than the accuracy when using both inputs, indicating that the dynamics of the network depend on both stimulation amplitude and frequency.

Shanechi and co-authors also show that the inclusion of dynamics into the model via latent states was necessary to obtain accurate predictions. This is supported by three comparisons. First, the authors compared the performance of the model with (static) linear regression, and with two constrained dynamical models: a smoothing model characterizing the effect of input stimulation at each time point as simply a smoothed average of past inputs with equal weights on how they affect the current state, and a non-oscillatory model that explicitly constrained the original model so that it cannot include oscillatory dynamics. The full dynamical model performed significantly better than each of the three alternative models (Fig. 1d). Although prediction accuracies were high on average, there was variability at the level of individual network nodes. The authors show that some of this variability can be explained by resting-state functional connectivity to the stimulation site. They quantified functional connectivity between nodes using a measure of controllability drawn from control theory. Specifically, they calculated controllability by quantifying the energy needed to change the neural activity at a network node when stimulating at a particular site. High controllability indicated that a stimulation node was effective at driving a particular network node, and therefore that it was related to the connectivity between the two sites. By focusing on stimulation from the site with the highest overall controllability (the orbitofrontal cortex in their case), the authors show that both prediction accuracy and the estimated strength of the neural response were significantly correlated with the resting-state functional connectivity with the stimulation site. The correlations were significant not only at the level of brain regions, but also for individual nodes and thus for the power-spectrum features.

To show that the model could enable closed-loop control of an internal brain state, Shanechi and colleagues analysed the performance of the models in a synthetic study of closed-loop control of mood. They show that model-based closed-loop control outperformed model-free closed-loop control with neural feedback. The dynamic input–output model identified stimulation parameters for driving the brain out of the simulated depressive state and into a clinically reasonable mood state, and could be maintained at this target state.

By establishing that the response of large-scale networks to ongoing stimulation can be predicted from a dynamic input–output model, Shanechi and colleagues provide a principled approach for designing stimulation protocols. Specific stimulation patterns can be constructed in order to most efficiently modulate neural activity toward specified patterns. Casting the problem of predicting responses to stimulation as a control-theory problem takes advantage of well-established tools developed for control systems engineering while also providing intuition for the parameters of the model. The linearity of the model allows for these parameters to be learned quickly and robustly. These are critical requirements for closed-loop systems that aim to operate in real time.

For clinical applications, stimulation amplitudes and frequencies must be chosen carefully to ensure patient safety. Thus, the allowable stimulation parameters are often a subset of those that are available through the stimulating device. Shanechi and colleagues’ dynamic modelling offers an efficient approach for selecting the optimal stimulation parameters from this subset. Similarly, the number of potential stimulation sites may be limited by safety and hardware considerations. The strong correlation of both prediction accuracy and the estimated strength of the response to resting-state functional connectivity suggests that functional-connectivity maps can be used as priors to select stimulation sites that may achieve maximal control of the network. This relationship between stimulation responses and functional connectivity reflects the constraints that the underlying neural network places on the possible patterns of activity. Combining the predictions of dynamic models with what is known about synaptic connectivity may therefore open up possibilities for paradigms that causally manipulate synaptic connectivity in large-scale cortical networks, for more effective neuromodulation treatments.