Graphical abstract
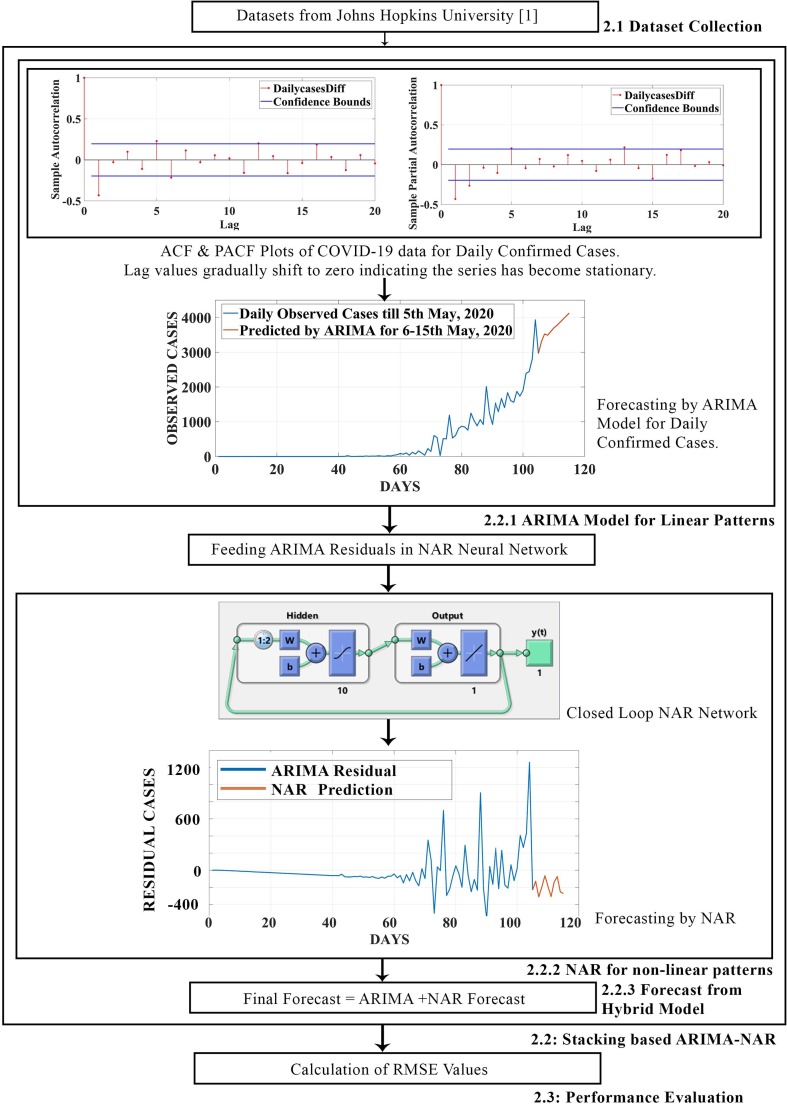
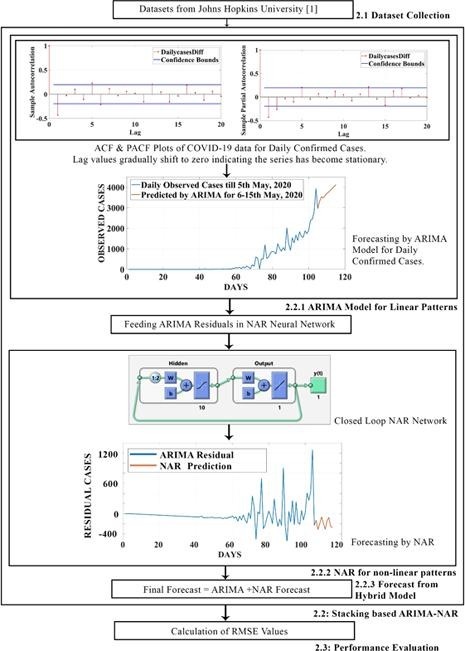
Fig. 2: Pictorial description of the stack based ensemble ARIMA model.
Keywords: Hybrid model, Forecasting, COVID-19, ARIMA, NAR
Abbreviations: ACF, Auto-Correlation Function; ADF, Augmented Dickey-Fuller; AIC, Akaike's Information Criterion; ANFIS, Adaptive Neuro-Fuzzy Inference System; ANN, Artificial Neural Networks; AR, Auto-Regressive; ARIMA, Autoregressive Integrated Moving Average; BIC, Bayesian Information Criterion; COVID-19, Coronavirus Disease -2019; DNN, Deep Neural Network; GROOMS, Group of Optimized and Multisource Selection; IoT, Internet of Things; KNN, K-Nearest Neighbors; MA, Moving Average; MAE, Mean Absolute Error; MAPE, Mean Absolute Percentage Error; MERS, Middle East Respiratory Syndrome; ML, Machine Learning; NAR, Nonlinear Autoregressive; PACF, Partial Auto-Correlation Function; PR, Polynomial Regression; RMSE, Root Mean Square Error; SARS, Severe Acute Respiratory Syndrome; SARS, CoV-2 –Severe Acute Respiratory Syndrome Coronavirus 2; SEIR, Susceptible–Exposed–Infectious–Resistant; SES, Single Exponential Smoothing; SIRD, Suspected-Infected-Recovered-Dead); SVR, Support Vector Regression; WHO, World Health Organization; WMA, Weighted Moving Average
Abstract
Background
Time-series forecasting has a critical role during pandemics as it provides essential information that can lead to abstaining from the spread of the disease. The novel coronavirus disease, COVID-19, is spreading rapidly all over the world. The countries with dense populations, in particular, such as India, await imminent risk in tackling the epidemic. Different forecasting models are being used to predict future cases of COVID-19. The predicament for most of them is that they are not able to capture both the linear and nonlinear features of the data solely.
Methods
We propose an ensemble model integrating an autoregressive integrated moving average model (ARIMA) and a nonlinear autoregressive neural network (NAR). ARIMA models are used to extract the linear correlations and the NAR neural network for modeling the residuals of ARIMA containing nonlinear components of the data.
Comparison: Single ARIMA model, ARIMA-NAR model and few other existing models which have been applied on the COVID-19 data in different countries are compared based on performance evaluation parameters.
Result
The hybrid combination displayed significant reduction in RMSE (16.23%), MAE (37.89%) and MAPE (39.53%) values when compared with single ARIMA model for daily observed cases. Similar results with reduced error percentages were found for daily reported deaths and cases of recovery as well. RMSE value of our hybrid model was lesser in comparison to other models used for forecasting COVID-19 in different countries.
Conclusion
Results suggested the effectiveness of the new hybrid model over a single ARIMA model in capturing the linear as well as nonlinear patterns of the COVID-19 data.
1. Introduction
The novel coronavirus, COVID-19 (SARS-CoV-2), which was first reported in Wuhan, China, after the outbreak of exceptional pneumonia in late 2019, has already infected over 5.6 million people and caused more than three fifty thousand deaths worldwide [1]. Surpassing the fatalities caused by previous outbreaks such as severe acute respiratory syndrome coronavirus (SARS) [2], [3], and middle east respiratory syndrome (MERS) [4], [5], COVID-19 has been characterized by the world health organization (WHO) as a global pandemic [6]. The virus, which is assumed to be of zoonotic origin [7], [8], has spread rapidly with a transmission rate of around 1.4 to 2.5 [9].
Therefore, to curb the outbreak, the nationwide lockdown has been observed in more than two hundred countries and in India. Table 1 shows the phases of lockdown conducted in India.
Table 1.
Depiction of lockdown phases.
| Lock down phases | Dates | Number of cases | Days | Increase percentage |
|---|---|---|---|---|
| Phase 0 | 22/01/2020, 24/03/2020 | 2872 | 58 | – |
| Phase 1 | 25/03/2020–14/04/2020 | 10,951 | 21 | 281.3% |
| Phase 2 | 15/03/2020 – 02/05/2020 | 31,118 | 19 | 184.16% |
| Phase 3 | 03/05/2020–17/05/2020 | 53,193 | 12 | 70.93% |
COVID-19 first appeared in India in Kerala back in late January, where the patient had a recent travel record to Wuhan, China. Initially, the transmission was slow, and the virus could infect very few people within Kerala only. However, the number of cases started rising again in mid-march after the pandemic hit western Europe, and after that, strict lockdown measures were observed throughout the nation.
India is the second-most populous country in the world after China. A slight negligence in constraining the pandemic can lead to unprecedented panic and widespread loss of trade, economy, outsourcing workforce, manufacturing, and other services all over the world. For all these, it is essential to have a proper strategy for combating the epidemic. In the current situation of unavailability of an adequate cure of the disease, having short term forecasts of the spread can provide state authorities with a realistic estimate of the magnitude of the outbreak for the coming weeks.
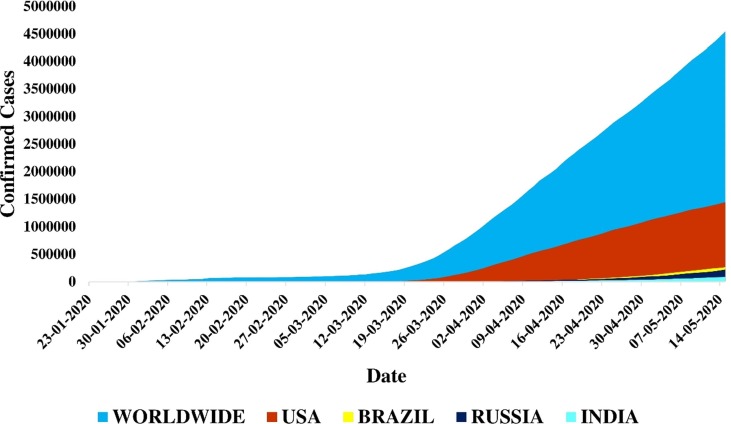
However, despite all the intervention strategies implemented by state authorities, the curve has jumped exponentially (Fig. 1 ). Presently, the highest no of cases is observed in the United States; however, the curve is abruptly rising in Russia, India, and South American countries like Brazil.
Fig. 1.
Total Confirmed cases of COVID-19 Worldwide from Jan 22 to May 15, 2020 [1].
Time-series forecasting during epidemics has been regarded as an essential tool in the past for containing the spread of contagious diseases like ebola, influenza, etc. [10], [11], [12], [13], [14], [15], [16]. Timing plays a critical role in an epidemic, and from the very beginning, an exceptional level of monitoring is required to curb the spread. Several studies have shown that proper analysis of such outbreaks can contribute substantially in devising the right course of action in due time [17], [18]. In this connection, a standard model often used for analyzing the trend of an epidemic, 'susceptible–exposed–infectious–resistant' (SEIR), has been applied recently for analyzing COVID-19 cases in various countries [19], [20], [21], [22], [23], [24], [25], [26], [27].
Researchers have subsequently proposed alternate forecasting models involving machine learning algorithms like LSTM, SVR, ARIMA, and few others for forecasting COVID-19 cases in different countries [28], [29], [30], [31], [32], [33], [34], [35], [36], [37], [38], [39], [40], [41], [42], [43]. Some of the relevant work is presented in Table 2 .
Table 2.
Existing models over COVID-19 data in different countries.
| Author | Dataset duration | Country |
Results |
||
|---|---|---|---|---|---|
| Methods | RMSE (Daily Confirmed Cases) | RMSE (Total Confirmed Cases) | |||
| Al-Qaness et al. [41] | 30 days | China | ANN | 8750 | NA |
| KNN | 12,100 | ||||
| SVR | 7822 | ||||
| ANFIS | 7375 | ||||
| PSO | 6842 | ||||
| GA | 7194 | ||||
| ABC | 8327 | ||||
| FPA | 6059 | ||||
| FPASSA | 5779 | ||||
| Ceylan et al. [42] | 45 days | France | ARIMA | NA | 971.9250 |
| Italy | 1654.6600 | ||||
| Spain | 2031.1200 | ||||
| Punn et al. [32] | 71 days | Worldwide | SVR | NA | 27456.47 |
| DNN | 163335.65 | ||||
| LSTM | 15647.64 | ||||
| PR | 455.92 | ||||
| Moftakhar et al. [43] | 71 days | Iran | ANN | 746.60 | NA |
| ARIMA | 1539.43 | ||||
(ABC – Artificial Bee Colony; KNN – K-Nearest Neighbors; Support Vector Regression (SVR); ANFIS – Adaptive Neuro-Fuzzy Inference System; PSO – Particle Swarm Optimization; GA – Genetic Algorithm; FPA – Flower Pollination Algorithm; FPASSA – Flower pollination algorithm Salp Swarm Algorithm; ARIMA – Auto -Regressive Integrated Moving Average; DNN – Deep Neural Network; LSTM – Long short-term memory; PR- Polynomial Regression; ANN – Artificial Neural Networks).
However, among all these forecasting models, ARIMA is most popular [44], [45], [46]. ARIMA works with an underlying assumption that the present data is linearly related to past observed values and errors. However, previous pandemics have often shown complex and nonlinear patterns with time, and therefore a linear approach might not yield the best results. Artificial Neural Networks (ANN) have emerged as one of the most successful methods to overcome this limitation of non-linearity [47], [48], [49], [50]. However, ANN models are not capable of capturing both linear as well as nonlinear features of the time series equally well [51], and thus several hybrid methodologies have been developed [52], [53], [54], [55]. Zhang [56] proposed a combination of ARIMA and NAR (Non-linear Auto-Regressive) Neural Network on some well-known datasets. Wang et al. [57] also implemented a similar model for forecasting tuberculosis cases in China. The same approach was opted by Benmouiza et al. in [58] for small-scale solar radiation forecasting. Most of the hybrid models were successful in improving the prediction accuracy as compared to the individual alternatives of those models. Therefore, the study of a hybrid model having capabilities of modeling both linear and nonlinear time-series for COVID-19 could be capable of better forecasting.
With this motivation, we develop an ensemble model combining ARIMA and NAR models for predicting future cases of COVID-19 in India and then compare the results produced by the hybrid model with the regular one.
The organization of the rest of the paper is as follows: In Section 2, we discuss the methods for forecasting future COVID-19 cases along with the overall flow of the work. The implementation of these methods, along with a comparative analysis, is described in Section 3. Section 4 holds a discussion, and Section 5 depicts the conclusion.
2. System description
In Section 2.1, COVID-19 time-series data sources are mentioned. Section 2.2 describes our proposed ensemble model. A pictorial description of the same is presented in Fig. 2 . First we implement ARIMA model and analyze its results. Then to further improvise its results, a hybrid combination of ARIMA-NAR was developed. A comparison is made using performance evaluation parameters amongst these models. The section ends with a brief description of the accuracy estimation parameters in 2.3. All the ARIMA and NAR models are built in MATLAB v. 9.4.0.813654 (R2018a) using the Econometric Modeller Toolbox and Neural Net Time Series Toolbox respectively.
Fig. 2.
Pictorial description of the stack based ensemble ARIMA model.
2.1. Data set collection
The cumulative count of confirmed cases, reported deaths and recovered cases of COVID-19 were taken from the official COVID-19 Data Repository of the Jhon Hopkins University [1] and for our study, we formulated the data in Microsoft Excel to obtain the respective cases on a daily basis for three phases, between may 6–15, July 21–30 and Aug 1–10. The starting point however is fixed at 22nd January.
2.2. Stacking based ARIMA-NAR model
Stacking based models basically use predictions from multiple models to build a new one. In this study, we utilize ARIMA models for extracting the linear relationships of the data and NAR neural network for the non linear patterns. Fig. 4 gives a step wise explanation for the ARIMA-NAR ensemble model. First in 2.2.1, we describe the working of the ARIMA model. Next, Section 2.2.2 talks about the NAR neural network and finally the contribution of both the models in making the final forecast is realized in Section 2.2.3.
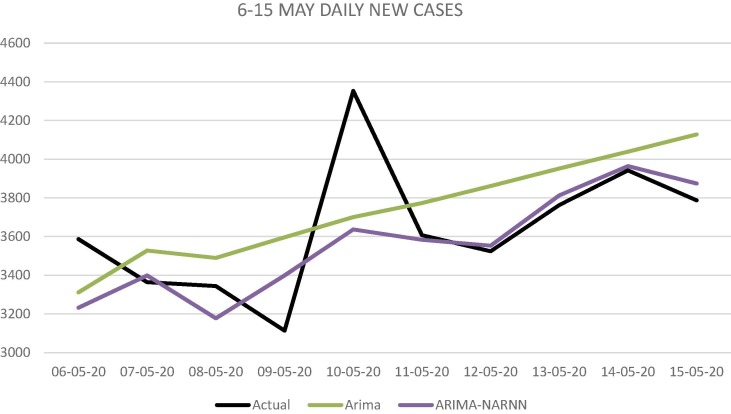
Fig. 4.
Prediction by ARIMA, ARIMA-NAR Model for daily new cases of COVID-19 in India between May 6–15, 2020.
2.2.1. ARIMA model for linear patterns
The econometric model, ARIMA was first presented by Box & Jenkins in 1970 [59]. The model is generally favored for its flexibility to various types of time-series data and its predicting accuracy.
ARIMA is a combination of A.R. and M.A. models, along with differencing. In Autoregressive models (A.R.), predictions are based on past values of the time-series data, and in Moving Average models (MA), prior residuals are considered for forecasting future values. The underlying process could be written as:
| (1) |
Here, is the actual observed value at time and is random error. and are model parameters where and denote order of the model. Random errors are generally independent and identically distributed with zero mean and constant variance.
In simpler terms, it represented as ARIMA (a, b, c) where 'a' denotes the order of A.R. model, 'b' is the differencing degree, 'c' is the order of the M.A. model. All these mentioned parameters of ARIMA model are determined in three iterative steps of model recognition, parameter selection and model verification.Since ARIMA models are generally suitable for stationary time series, so firstly in the identification step, stationarity of the time series is checked. If the series is not stationary, then differencing can be applied to make it stationary. After stationary tests, in the second step, appropriate parameters for the A.R. Snd M.A. models are selected for fitting based on Autocorrelation function (ACF) and Partial Autocorrelation Function (PACF) plots of the stationary data. In the final step, the goodness of the fit is verified by Akaike's Information Criterion (AIC) and Bayesian information criterion (BIC). These three steps are repeated untill a satisfactory model is achieved which is then used for forecasting.
2.2.2. NAR neural network for nonlinear patterns
An artificial neural network (ANN) is an intuitive mapping structure represented by a mathematical model simulated around the biological nervous system. It is equipped with the ability to comprehend dynamic nonlinear time series patterns and arbitrary functions of all sorts. An ANN processes information by combining various neurons connected in a network of weighted links and then gives the output by computing certain activation functions that can be expressed in mathematical terms as mentioned:
| (2) |
where is the activation function, is the bias of neuron, represents the weight, input, and is the output.
Nonlinear autoregressive neural network (NAR) is a well-known ANN for modeling dynamic systems and predicting future values in a nonlinear time series [56], [57], [58]. It is based on the architecture of a recurrent neural network having embedded memory with feedback connections. The general equation of a NAR model could be defined as:
| (3) |
Here, represents the nonlinear function, and the previous output values determine the future values.
Among multiple architectures in a NAR model, the close loop network is widely used for multi-step ahead forecasting.
| (4) |
Here, denotes number of future points.
2.2.3. Forecast from ANN, NAR combined hybrid model
Although ARIMA and ANN both are potent methods for time-series forecasting, they have their own limitations. ARIMA models have achieved success in linear problems, whereas NAR models are more suitable for nonlinear domains [56], [57], [58]. While dealing with a real-world problem, it is challenging to ascertain all the characteristics of data, and therefore they study of a hybrid model having capabilities of modeling both linear and nonlinear time-series is essential.
In general, a time-series contains both linear autocorrelation structure as well as nonlinear components, and it could be written as:
| (5) |
where, is the original time-series data, denotes the linear component, and the nonlinear part at time . The hybrid methodology is carried out in two steps. First, the linear component is modeled using ARIMA such that the residuals left after modeling will contain only the nonlinear relationship. If we can denote the residuals left by ARIMA at time as , then we get,
| (6) |
where, denotes forecasted valuesat time by the ARIMA model.
Residual diagnosis plays a vital role in checking the sufficiency of ARIMA models. Although an ARIMA model is considered sufficient if the residuals left after fitting display no linear correlation structures, residual analysis cannot detect the presence of any significant nonlinear patterns in the data. Thus, by modeling the residuals using ANNs, nonlinear patterns can be realized. So, for the second step, the residuals are modeled to a NAR neural network with input nodes as follows:
| (7) |
where, represents the nonlinear function evaluated by the NAR model and the leftover error is denoted by such that the final prediction can be equated as:
| (8) |
where, denotes the final predicted values at time , and Eq. is represented as , the forecast value of residuals.
The ARIMA-NAR combination thus exploits the strength of ARIMA as well as ANN models for capturing linear as well as nonlinear patterns.
Zhang [56] and Granger [60] have further pointed out the importance of the subjective selection of component models while building a hybrid model, as sometimes a combination of sub-optimal models can yield better forecasts for the hybrid model than that of the optimal ones.
3. Constructing the hybrid model in MATLAB
Data is first divided into training, testing and validation randomly on multiple iterations. Several weight optimising algorithms are then used for adjusting the weight values, and the 'Neural Net Time Series Toolbox' in MATLAB provides three sets of such algorithms, namely Levemberg–Marquardt [61], Bayesian Regularization [62] and scaled conjugate gradient [63]. Low MSE and higher R values account for selection the optimum NAR model. The error autocorrelation plot is also used for verifying the adequacy of the model. After the training is finished, all the synaptic weights are saved, and the model is ready for prediction.
3.1. Performance evaluation measures
In general, the performance of any forecasting model is determined by comparing the actual values with the predicted ones, and three standard methods for evaluation are:mean absolute percentage error (MAPE), root mean square error (RMSE) and mean absolute error (MAE). The optimum prediction model can thus beselected based on these performance measures.
| (9) |
| (10) |
| (11) |
4. Results
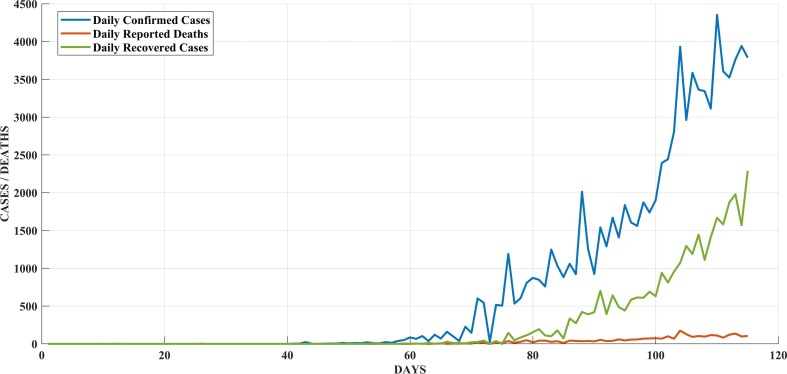
A total of 85,784 cases of novel coronavirus were reported throughout India along with 2,753 deaths and 30,258 cases of recovery till May 15, 2020. Fig. 5 shows the number of cases observed on a daily basis, daily reported deaths and daily recovered cases in India between January 22 and May 15, 2020. We utilize the data from Jan 22 to May 5, 2020 for training purpose and then test the respective models for 6–15 May 2020 for all three datasets and additionally for 21–30 July and 1–10 Aug for cumulative cases in India. We also compare the results with LSTM and SIR model.
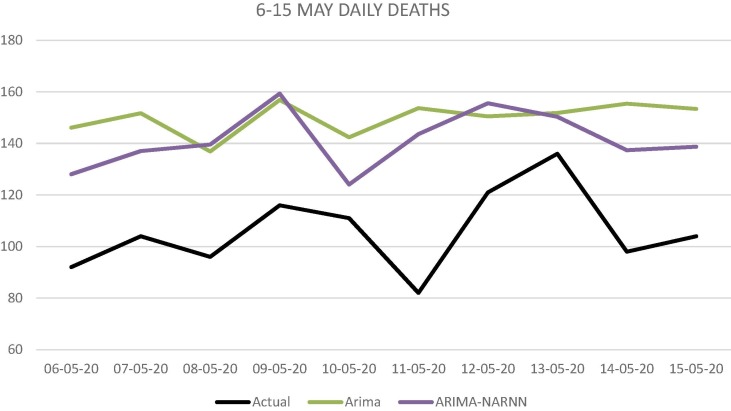
Fig. 5.
Prediction by ARIMA, ARIMA-NAR Model for daily new reports of death due to COVID-19 in India between May 6–15, 2020.
The final forecasting is done by combining the separate prediction values of ARIMA and NAR models. Fig. 4, Fig. 5, Fig. 6 respectively show the prediction of future cases by the ARIMA and NAR neural network for daily observed cases, reported deaths, and daily recovered cases between May 6–15, 2020. RMSE, MAE and MAPE values are calculated for the predictions made by single ARIMA model and the ARIMA-NAR combined model for all the three datasets (Table 3a, Table 3b, Table 3c ). Fig. 7, Fig. 8, Fig. 9 further draw a comparision between three different models, ARIMA, Hybrid ARIMA and LSTM for cumulative cases of covid-19 in India for three different phases, respectively 6–15 May, 21–30 July, 1–10 Aug. Additionally, we also draw comparision with the compartmental model, SIR in Fig. 10 and Table 4 . Finally, we also present long term forecast of covid-19 cases with the hybrid model (Fig. 11 ) and Table 5 .
Fig. 6.
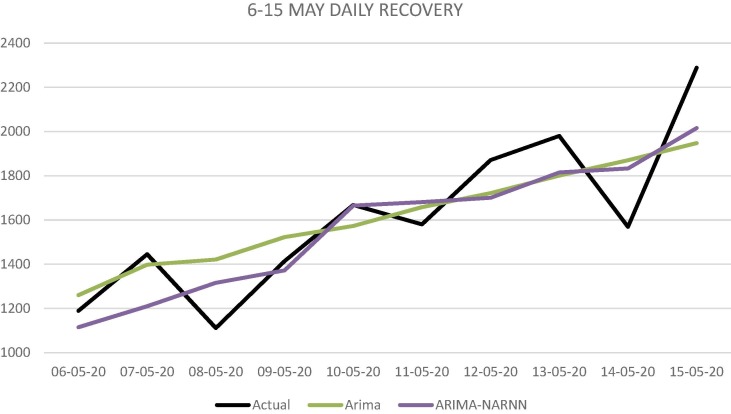
Prediction by ARIMA, ARIMA-NAR Model for daily new cases of recovery from COVID-19 in India between May 6–15, 2020.
Table 3a.
Prediction accuracy evaluation for daily observed cases in India between 6th and 15th May 2020.
| Model | RMSE | MAE | MAPE |
|---|---|---|---|
| Single arima | 329.4373 | 284.9 | 7.8% |
| Hybrid arima | 275.9648 | 176.9298 | 4.7% |
Table 3b.
Prediction accuracy evaluation for daily reported deaths in India between 6th and 15th May, 2020.
| Model | RMSE | MAE | MAPE |
|---|---|---|---|
| Single arima | 46.3923 | 43.8708 | 44.02% |
| Hybrid arima | 37.79482 | 35.3597 | 35.32% |
Table 3c.
Prediction accuracy evaluation for daily recovered cases in India between 6th and 15th May, 2020.
| Model | RMSE | MAE | MAPE |
|---|---|---|---|
| Single Arima | 198.0642 | 168.1494 | 10.66% |
| Hybrid Arima | 177.6032 | 153.3469 | 9.67% |
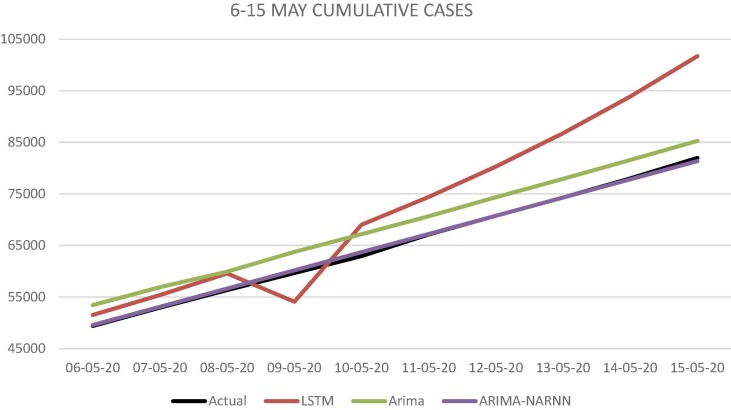
Fig. 7.
Prediction by ARIMA, ARIMA-NAR and LSTM Model for cumulative new cases of COVID-19 in India between May 6–15, 2020.
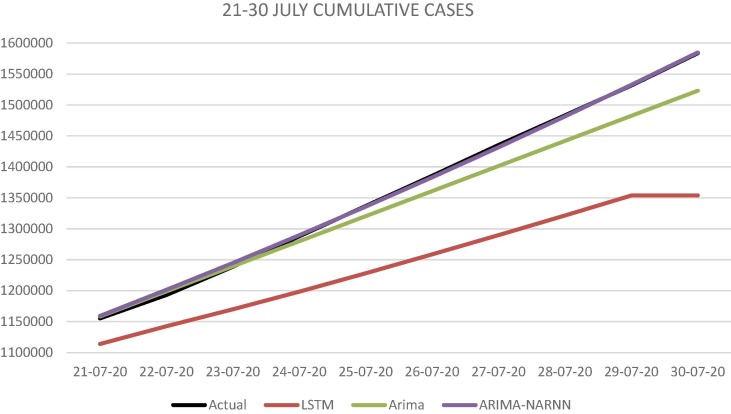
Fig. 8.
Prediction by ARIMA, ARIMA-NAR and LSTM Model for cumulative new cases of COVID-19 in India between July 21–30, 2020.
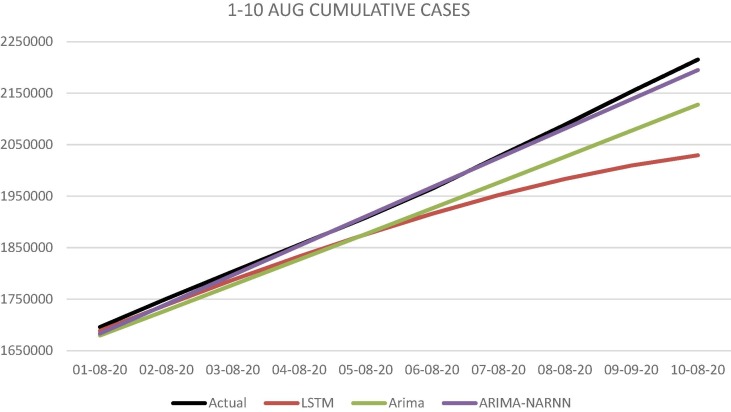
Fig. 9.
Prediction by ARIMA, ARIMA-NAR and LSTM Model for cumulative new cases of COVID-19 in India between Aug 1–10, 2020.
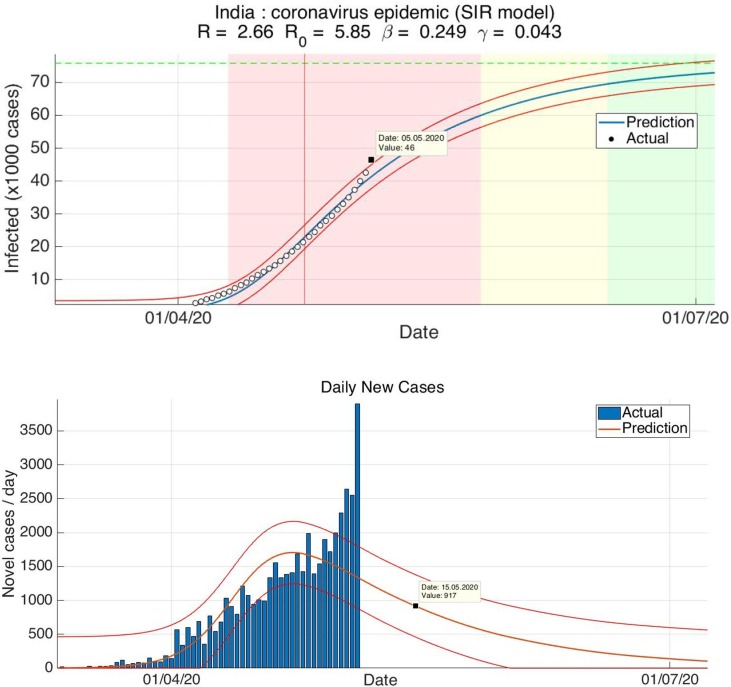
Fig. 10.
Predictions using the SIR model. Top panel with white, red, yellow and green regions indicate initial exponential growth, fast growth (with positive and negative phase separated by red vertical line), asymptotic slow growth and curve flattening, respectively. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Table 4.
Accuracy comparison of SIR model and Hybrid Arima model for daily new cases in India between 6th and 15th May 2020.
| SIR model | Hybrid model | ||
|---|---|---|---|
| RMSE | 2499.233 | 275.9648 |
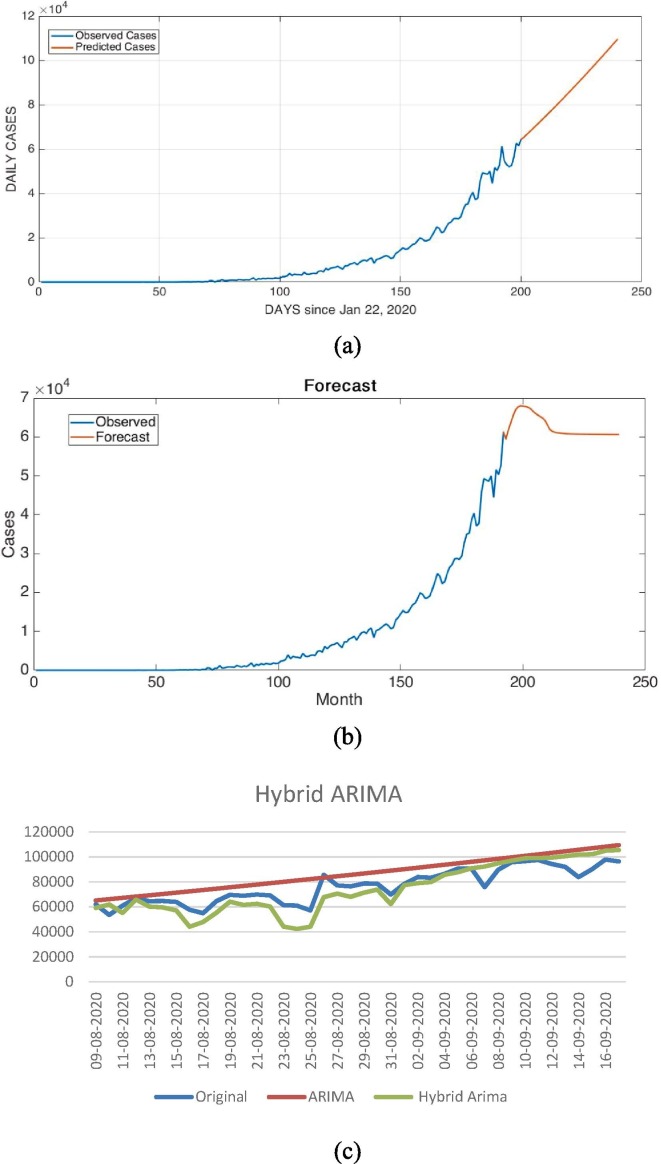
Fig. 11.
Forecast for a duration of 40 days using (a) ARIMA; (b) LSTM; (c) Hybrid ARIMA.
Table 5.
Accuracy comparison of ARIMA model and Hybrid Arima model for a duration of 40 days.
| ARIMA model | Hybrid model | ||
|---|---|---|---|
| RMSE | 11759.72517 | 8908.786344 |
As seen in Table 3a, Table 3b, Table 3c, hybrid ARIMA's performance provide more adequate results. The RMSE, MAE and MAPE value of the hybrid combination for daily observed cases are 275.9648 (16.23% reduction), 176.9298 (37.89% reduction), 4.7% (39.53% reduction). Regarding daily reported deaths, cases of recovery and cumulative confirmed cases similar results were found with reduced error percentages. Further, it is evident from Fig. 4, Fig. 5, Fig. 6, Fig. 7, Fig. 8, Fig. 9 that Hybrid ARIMA has consistently performed better on all occasions.
Prediction with SIR model-
The well known compartmental model, Susceptible-Infectious-Recovered (SIR) model deals with the number of susceptibles ‘S’; number of infectious ‘I’; and the number of recovered or deceased individuals ‘R’. Details of the implementation including selection of R0 (basic reproduction number), β (transmission rate) and γ (average recovery rate) can be found in Batista [64] and Ranjan [65].
After carrying out the overall prediction, we particularly noted the predicted values of daily new cases from 6th May 2020 to 15th May 2020 in order to calculate rmse and do the required comparison with the hybrid model (Table 4).
To check the validity of the model on a longer duration, we trained the data for 200 days and predicted it for next 40 days. Since Arima is a linear model, we see that for the testing data, the graph just rises linearly up in Fig. 11.(a); similarly in 11.(b) we see the lstm model also settling down in the long run. But when the residual corrections are added in the hybrid arima, the graph shows some non linear variations in Fig. 11.(c). However, the non-linear variations also become constant over a period of time which goes to show that the error values captured in the training data more or start repeating over a period of time which is unlikely to happen in a real life scenario. Thus, to forecast for a longer duration, we may need to make proper adjustments in the model. Still compared to the single ARIMA and LSTM model, the hybrid model is more reliable (Table 5).
5. Discussion
The current COVID-19 outbreak has brought forward a major challenge for healthcare sector all over the world. After witnessing a catastrophic rise in the number of COVID-19 cases in USA and western Europe, a proper strategy for epidemic control in a densely populated country like India has become priority and to implement control measures in due time, forecasting of future cases is certainly essential. Several forecasting models have been proposed in recent months for predicting future cases of COVID-19 in different countries. Most of the forecasting work has been done using standard ARIMA models which are popular for their statistical properties in building models.
Generally, a time series compromises of linear as well as nonlinear patterns and the existing trend of COVID-19 over last few months clearly depicted nonlinear patterns (Fig. 3). While ARIMA models have proven quite useful for linear time-series, they cannot extract nonlinear patterns sufficiently. On the other hand, NAR, a powerful class of ANN has displayed favourable characteristics for modelling nonlinear time-series. However, ANN models have their own limitations in equally capturing both the linear and nonlinear patterns. Therefore, a hybrid approach that utilizes ARIMA and ANN models together is proposed in the present study.
Fig. 3.
Daily observed cases, reported deaths and recovered cases of COVID-19 in India till May 15, 2020.
Our study highlighted the key point of analysing linear and nonlinear patterns using separate models in context of a time series forecasting. Three separate datasets of daily confirmed cases of COVID-19 in India, reported deaths and cases of recovery were respectively trained on both the models for a duration of over hundred days between January 22 to May 5, 2020. First, the best model was selected for training the respective datasets on ARIMA and subsequently the fitting curve and residual plot of all the three datasets were generated.
Further, for extracting the nonlinear patterns, the residuals left from the ARIMA models were fitted to the NAR neural network. Both the models, ARIMA and NAR were then used to predict the future cases and residuals respectively. The combination of prediction results from both these models were used as the final results for the hybrid model.
Our hybrid ARIMA model was able to capture the nonlinear patterns quite well which were left as residuals by the ARIMA model. On the basis of RMSE, MAE, and MAPE measures (Eqs. (9), (10), (11)), we evaluated the prediction accuracy of both the models for all the three datasets. Reduced error as seen in Table 3a, Table 3b, Table 3c clearly advocate for the superiority of the proposed hybrid ARIMA model over a single ARIMA model. We have also compared the model with LSTM, SIR model and the hybrid ARIMA outperformes that as well.
Although our model has shown better performance compared to LSTM, SIR and ARIMA, the difference between the results however starts to reduce as days increase for cumulative cases with larger dataset. This goes to show the limitation of our model to forecast on longer horizon of months. In addition to current covid transfer rate and prevention policies, uncertain behavioural patterns, and mitigation schemes also account for forecasting accuracy at longer intervals.
Still, our model is particularly suited for quick short term forecasts in an epidemic. This is in line with previous studies where a combination of ARIMA and NAR model has been explored as a possibility for producing better time-series forecasting results. Hence, the present study can be regarded as an authentic approach for time-series forecasting during pandemics.
6. Conclusion
In this paper, we presented a new hybrid model for COVID-19 time-series forecasting by combining an Auto-Regressive Integrated Moving Average (ARIMA) model with a Nonlinear Auto-Regressive (NAR) neural network. ARIMA models were used to capture the linear relationship from the time-series, and the residuals of the ARIMA model containing the nonlinear components were fitted by the NAR Model. The prediction accuracy of both the models were measured on the basis of Root Mean Squared Error, Mean Absolute Error, and Mean Absolute Percentage Error. With low values of RMSE, MAE, and MAPE, the combination of ARIMA-NAR models produced better prediction results as compared to the single ARIMA, model. Our model also outperforms SIR and LSTM model for short term forecasts. Therefore, the new hybrid model can be considered as a reliable tool for policymakers in predicting short term forecasts of COVID-19 and devising proper strategies in due time.
However, for longer intervals, the difference of results between models reduces owing to the uncertainities of data, mitigation policies and behavioural patterns.
Ethical approval: This article does not contain any studies with human participants or animals performed by any of the authors.
CRediT authorship contribution statement
Aman Swaraj: Methodology, Software. Karan Verma: Conceptualization. Arshpreet Kaur: Writing– original draft. Ghanshyam Singh: Visualization. Ashok Kumar: Investigation. Leandro Melo Sales: Writing – review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work is under the project “DEVELOPMENT OF ENSEMBLE MODEL FOR PREDICTING TRENDS OF COVID-19”. We thank Jhon Hopkins University [1] for publicly providing respective time-series data of confirmed cases, deaths and recovery for our research work.
References
- 1.https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data/csse_covid_19_time_series, 2019.
- 2.World Health Organization. 2004. Available at: https://www.who.int/ith/diseases/sars/en/ (accessed January 2020).
- 3.Centres for Disease Control and Prevention. 2017. Available at: https://www.cdc.gov/sars/about/fs-sars.html (accessed January 2020).
- 4.World Health Organization. 2019. Available at: https://www.who.int/emergencies/mers-cov/en/ (accessed January 2020).
- 5.Oboho I.K., et al. 2014 MERS-CoV outbreak in Jeddah—a link to health care facilities. N. Engl. J. Med. 2015;372(9):846–854. doi: 10.1056/NEJMoa1408636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.World Health Organization, 2020. Coronavirus disease 2019 (COVID-19): situation report, 51.
- 7.Zhou P., Yang X.L., Wang X.G., et al. A pneumonia outbreak associated with a new coronavirus of probable bat origin. Nature. 2020 doi: 10.1038/s41586-020-2012-7. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Li Q., Guan X., Wu P., et al. Early transmission dynamics in wuhan, china, of novel coronavirus-infected pneumonia. N. Engl. J. Med. 2020 doi: 10.1056/NEJMoa2001316. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mahase, Elisabeth, “China coronavirus: what do we know so far?,” 2020. [DOI] [PubMed]
- 10.W. Jia, X. Li, K. Tan, G. Xie, Predicting the outbreak of the hand-foot- mouth diseases in china using recurrent neural network, in: 2019 IEEE International Conference on Healthcare Informatics (ICHI), IEEE, 2019, pp. 1–4.
- 11.Shashvat, Kumar, RikmantraBasu, Amol P. Bhondekar, Application of time series methods for dengue cases in North India (Chandigarh), J. Public Health (2019): 1-9.
- 12.Forna A., Nouvellet P., Dorigatti I., Donnelly C. Case fatality ratio estimates for the 2013–2016 west African Ebola epidemic: application of boosted regression trees for imputation. Int. J. Infect. Dis. 2019;79:128. doi: 10.1093/cid/ciz678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shashvat Kumar, et al. Comparison of time series models predicting trends in typhoid cases in northern India. Southeast Asian J. Trop. Med. Public Health. 2019;50(2):347–356. [Google Scholar]
- 14.S.-L. Jhuo, M.-T. Hsieh, T.-C. Weng, M.-J. Chen, C.-M. Yang, C.H. Yeh, Trend prediction of influenza and the associated pneumonia in Taiwan using machine learning, in 2019 International Symposium on Intelligent Signal Processing.
- 15.Machado G., Vilalta C., Recamonde-Mendoza M., Corzo C., Torremorell M., Perez A., VanderWaal K. Identifying outbreaks of porcine epidemic diarrhoea virus through animal movements and spatial neighbourhoods. Sci. Rep. 2019;9(1):1–12. doi: 10.1038/s41598-018-36934-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.G. Kalipe, V. Gautham, R.K. Behera, Predicting malarial outbreak using Machine Learning and Deep Learning approach: A review and analysis. In 2018 International Conference on Information Technology (ICIT) (pp. 33-38). IEEE, 2018, December.
- 17.Singh R., Singh R., Bhatia A. Sentiment analysis using Machine Learning technique to predict outbreaks and epidemics. Int. J. Adv. Sci. Res. 2018;3(2):19–24. [Google Scholar]
- 18.S.A. Abdulkareem, E.-W. Augustijn, T. Filatova, K. Musial, Y.T. Mustafa, “Risk perception and behavioural change during epidemics: Comparing models of individual and collective learning,”PloS one, 2020. [DOI] [PMC free article] [PubMed]
- 19.T. Kuniya, Prediction of the Epidemic Peak of Coronavirus Disease in Japan, 2020, J. Clin. Med. 2020; 9 (3): E789. Published 2020 March 13. doi:10.3390/jcm9030789. [DOI] [PMC free article] [PubMed]
- 20.Gupta, Rajan, et al., SEIR and Regression Model based COVID-19 outbreak predictions in India, medRxiv, 2020.
- 21.Yuan, George Xianzhi, et al., The framework for the prediction of the critical turning period for outbreak of COVID-19 spread in China based on the iSEIR model, Available at SSRN 3568776, 2020.
- 22.C. Anastassopoulou, L. Russo, A. Tsakris, C. Siettos, Data-based analysis, modelling and forecasting of the novel coronavirus (2019-nCoV) outbreak, medRxiv, no. February, p. 2020.02.11.20022186, 2020, doi: 10.1101/2020.02.11.20022186. [DOI] [PMC free article] [PubMed]
- 23.Joseph T. Wu, Kathy Leung, Mary Bushman, Nishant Kishore, Rene Niehus, Pablo M. de Salazar, Benjamin J. Cowling, Marc Lipsitch& Gabriel M. Leung. Estimating clinical severity of COVID-19 from the transmission dynamics in Wuhan, China. Nature Medicine (2020), March 19 2020.https://doi.org/10.1038/s41591-020-0822-7. [DOI] [PMC free article] [PubMed]
- 24.Wu J.T., Leung K., Leung G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020;395:689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kiesha Prem, Yang Liu, Timothy W. Russell, Adam J. Kucharski, Rosalind M. Eggo, Nicholas Davies, The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: a modelling study. Lancet Public Health 2020. Published Online March 25, 2020, https://www.thelancet.com/journals/lanpub/article/PIIS2468-2667(20)30072-4/fulltext. [DOI] [PMC free article] [PubMed]
- 26.X. Liu, Geoffrey Hewings, Shouyang Wang, Minghui Qin, Xin Xiang, Shan Zheng, Xuefeng Li, Modelling the situation of COVID-19 and effects of different containment strategies in China with dynamic differential equations and parameters estimation. medRxiv preprint doi: https://doi.org/10.1101/2020.03.09.20033498, 2020.
- 27.Qianying Lin, Shi Zhao, Daozhou Gao, Yijun Lou, Shu Yang, Salihu S. Musa, Maggie H. Wang, Yongli Cai, Weiming Wang, Lin Yang, Daihai He. A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action, Int. J. Infect. Dis. (93) (2020), 211-216. [DOI] [PMC free article] [PubMed]
- 28.J.L. Murray, Forecasting COVID-19 impact on hospital bed-days, ICU-days, ventilator days and deaths by U.S. state in the next 4 months. MedRxiv. March 26 2020. doi:10.1101/2020.03.27.20043752.
- 29.H.H. Elmousalami, A.E. Hassanien, Day Level Forecasting for Coronavirus Disease (COVID-19) Spread: Analysis, Modelling and Recommendations. ArXiv preprint arXiv:2003.07778, 2020.
- 30.Pal, Ratnabali, et al., Neural network-based country wise risk prediction of COVID-19, arXiv preprint arXiv:2004.00959, 2020.
- 31.Bandyopadhyay, Samir Kumar, Shawni Dutta, Machine learning approach for confirmation of COVID-19 cases: positive, negative, death and release, medRxiv, 2020.
- 32.Punn, Narinder Singh, Sanjay Kumar Sonbhadra, Sonali Agarwal, COVID-19 Epidemic Analysis using Machine Learning and Deep Learning Algorithms, medRxiv, 2020.
- 33.D. Benvenuto, M. Giovanetti, L. Vassallo, S. Angeletti, M. Ciccozzi, Application of the ARIMA model on the COVID-2019 epidemic dataset, Data Brief. 2020; 29: 105340. Published 2020 Feb 26. doi: 10.1016 / j .dib.2020.105340. [DOI] [PMC free article] [PubMed]
- 34.Ding, Guorong, et al., Brief Analysis of the ARIMA model on the COVID-19 in Italy, medRxiv, 2020.
- 35.Perone, Gaetano, An ARIMA model to forecast the spread and the final size of COVID-2019 epidemic in Italy. No. 20/07. HEDG, c/o Department of Economics, University of York, 2020.
- 36.Dehesh T., Mardani-Fard H.A., Dehesh P. Forecasting of COVID-19 Confirmed Cases in Different Countries with ARIMA Models. MedRxiv. 2020 [Google Scholar]
- 37.Gupta, Rajan, Saibal Kumar Pal, Trend Analysis and Forecasting of COVID-19 outbreak in India, medRxiv, 2020.
- 38.Tandon, Hiteshi, et al., Coronavirus (COVID-19): ARIMA based time-series analysis to forecast near future, arXiv preprint arXiv:2004.07859, 2020.
- 39.Kumar, Pavan, et al., Forecasting the dynamics of COVID-19 Pandemic in Top 15 countries in April 2020: ARIMA Model with Machine Learning Approach, medRxiv, 2020.
- 40.Shi Z., Fang Y. Temporal relationship between outbound traffic from Wuhan and the 2019 coronavirus disease (COVID-19) incidence in China. MedRxiv. 2020 [Google Scholar]
- 41.Al-Qaness Mohammed A.A., et al. Optimization method for forecasting confirmed cases of COVID-19 in China. J. Clin. Med. 2020;9(3):674. doi: 10.3390/jcm9030674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ceylan Zeynep. Estimation of COVID-19 prevalence in Italy, Spain, and France. Sci. Total Environ. 2020;138817 doi: 10.1016/j.scitotenv.2020.138817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Moftakhar Leila, Mozhgan S.E.I.F., Safe Marziyeh Sadat. Exponentially Increasing Trend of Infected Patients with COVID-19 in Iran: A Comparison of Neural Network and ARIMA Forecasting Models. Iranian J. Public Health. 2020;49:92–100. doi: 10.18502/ijph.v49iS1.3675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Zhang Y., Yang H., Cui H., Chen Q. Comparison of the Ability of ARIMA, WNN and SVM Models for Drought Forecasting in the Sanjiang Plain. China. Nat. Resour. Res. 2019;29:1447. [Google Scholar]
- 45.Zhang X., et al. Applications and comparisons of four time series models in epidemiological surveillance data. PLoS ONE. 2014;9 doi: 10.1371/journal.pone.0088075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Li Q., et al. Application of an autoregressive integrated moving average model for predicting the incidence of haemorrhagic fever with renal syndrome. Am. J. Trop. Med. Hyg. 2012;87:364–370. doi: 10.4269/ajtmh.2012.11-0472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Adly A.A., et al. Utilizing neural networks in magnetic media modelling and field computation: a review. J. Adv. Res. 2014;5:615–627. doi: 10.1016/j.jare.2013.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Haykin S. 2nd ed. Prentice Hall; 1998. Neural networks: a comprehensive foundation. [Google Scholar]
- 49.Ljung L. 2nd ed. Prentice Hall PTR; 1998. System identification: theory for the user. [Google Scholar]
- 50.Connor J.T., Martin R.D., Atlas L.E. Recurrent neural networks and robust time series prediction. IEEE Trans. Neural Networks. 1994;5(2):240–254. doi: 10.1109/72.279188. [DOI] [PubMed] [Google Scholar]
- 51.Taskaya-Temizel Tugba, Casey Matthew C. A comparative study of autoregressive neural network hybrids. Neural Networks. 2005;18(5-6):781–789. doi: 10.1016/j.neunet.2005.06.003. [DOI] [PubMed] [Google Scholar]
- 52.Philemon M.D., Ismail Z., Dare J. A review of epidemic forecasting using artificial neural networks. Int. J. Epidemiologic Res. 2019;6(3):132–143. [Google Scholar]
- 53.Aslanargun Atilla, Mammadov Mammadagha, Yazici Berna, Yolacan Senay. Comparison of ARIMA, neural networks and hybrid models in time series: tourist arrival forecasting. J. Stat. Comput. Simul. 2007;77(1):29–53. [Google Scholar]
- 54.Jain Ashu, Kumar Avadhnam Madhav. Hybrid neural network models for hydrologic time series forecasting. Appl. Soft Comput. 2007;7(2):585–592. [Google Scholar]
- 55.Yu L., et al. Application of a new hybrid model with seasonal auto-regressive integrated moving average (ARIMA) and nonlinear auto-regressive neural network (NARNN) in forecasting incidence cases of HFMD in Shenzhen, China. PLoS ONE. 2014;9 doi: 10.1371/journal.pone.0098241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Zhang G.Peter. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing. 2003;50:159–175. [Google Scholar]
- 57.Wang K.W., et al. Hybrid methodology for tuberculosis incidence time-series forecasting based on ARIMA and a NAR neural network. Epidemiol. Infect. 2017;145(6):1118–1129. doi: 10.1017/S0950268816003216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Benmouiza Khalil, Cheknane Ali. Small-scale solar radiation forecasting using ARMA and nonlinear autoregressive neural network models. Theor. Appl. Climatol. 2016;124(3-4):945–958. [Google Scholar]
- 59.Box G.E.P., Jenkins G. Holden-Day; San Francisco, CA: 1970. Time Series Analysis, Forecasting and Control. [Google Scholar]
- 60.Granger C.W.J. Combining forecasts—Twenty years later. J. Forecasting. 1989;8:167–173. [Google Scholar]
- 61.Levenberg K. A method for the solution of certain problems in least squares. Q. Appl. Math. 1944;5:164–168. [Google Scholar]
- 62.D.J.C. MacKay, Bayesian interpolation, Neural Comput. 1992;4(3):415–47.
- 63.Møller Martin Fodslette. A scaled conjugate gradient algorithm for fast supervised learning. Neural Networks. 1993;6(4):525–533. [Google Scholar]
- 64.Milan Batista, Estimation of the final size of the covid-19 epidemic, medRxiv, doi, 10(2020.02):16–20023606, 2020.
- 65.Ranjan, Rajesh, Predictions for COVID-19 outbreak in India using epidemiological models, MedRxiv, 2020.