Uncovering structured responses of neural populations recorded from macaque monkeys with linear support vector machines

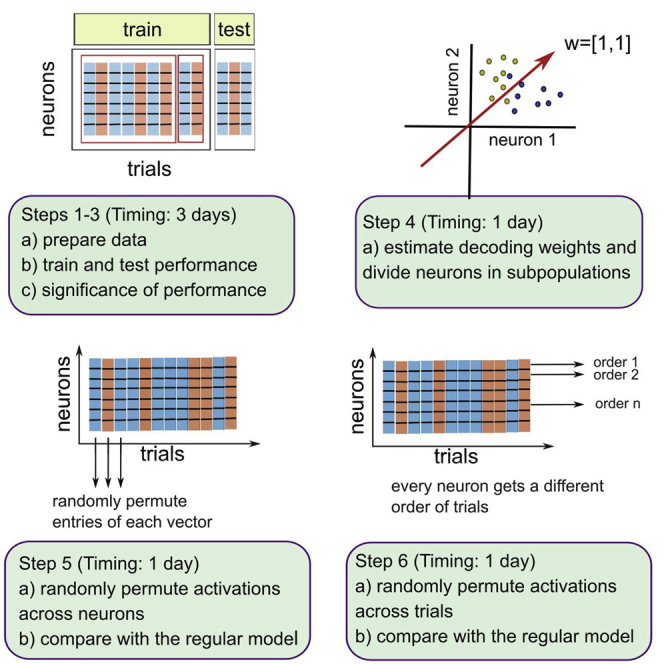
Summary

When a mammal, such as a macaque monkey, sees a complex natural image, many neurons in its visual cortex respond simultaneously. Here, we provide a protocol for studying the structure of population responses in laminar recordings with a machine learning model, the linear support vector machine. To unravel the role of single neurons in population responses and the structure of noise correlations, we use a multivariate decoding technique on time-averaged responses.

For complete details on the use and execution of this protocol, please refer to Koren et al. (2020a).

Graphical abstract

Highlights

• •Linear support vector machine (SVM) is an efficient model for decoding from neural data
• •Permutation test is a rigorous method for testing the significance of results
• •Neural responses along the cortical depth are heterogeneous
• •Decoding weights and noise correlations share a similar structure

When a mammal, such as a macaque monkey, sees a complex natural image, many neurons in its visual cortex respond simultaneously. Here, we provide a protocol for studying the structure of population responses in laminar recordings with a machine learning model, the linear support vector machine. To unravel the role of single neurons in population responses and the structure of noise correlations, we use a multivariate decoding technique on time-averaged responses.

Before you begin

The protocol below describes a method to analyze parallel recordings from V1 and V4 visual areas of two adult macaque monkeys (macaca mulatta), performing a match-to-sample visual task on complex visual stimuli. However, the protocol is generally applicable on parallel recordings of neural activity in any species and any brain area, as long as these recordings are accompanied by the measurement of a binary variable, related to either an external stimulus or an observed animal’s behavior.

Here, we decode binary categories “match” and “non-match” of the external visual stimulus through a multivariate analysis of the population activity of simultaneously-recorded neurons. The animal views two consecutive stimuli, interleaved with a delay period. The two stimuli can be either identical (condition “match”) or different (condition “non-match”). In terms of the classification variable, other applications of our protocol include decoding a specific sensory feature of the stimulus, the choice of the animal, or any other behavioral feature that quantifies the animal’s behavior.

Classification protocols are nowadays being increasingly automatized (Molnar, 2019). While automatization of protocols eases comparison of models and modeling results, there is the danger of misuse due to the lack of understanding of the underlying methods.

Training for the task and setting the experimental protocol

Timing: >12 months

• 1.
  Training of the animal subjects for the task.

  • a.
    The animal is placed in front of a screen and learns to fixate in the middle of the screen.
  • b.
    As the fixation is stable, the trial is initiated automatically. The animal views two consecutive stimuli, the target and the test, interleaved with a delay period. The two stimuli, each lasting 300 milliseconds (ms), can be either identical (condition “match”) or different (condition “non-match”). In non-matching trials, the only difference between the target and the test stimulus is the rotation of the test stimulus with respect to the target. The task of the animal is to report the decision “same” by releasing the bar and the decision “different” by holding the bar. The delay period lasts between 800 to 1000 ms. A variable duration of the delay prevents the animal from expecting the timing of arrival of the test stimulus. Stimuli are complex naturalistic black-and white images depicting an outdoor scene.
  • c.
    The animal is trained until it reaches the performance of 70% correct on non-matching stimuli. The non-matching stimuli are randomly rotated in a range between 3 and 10 degrees.
• 2.Implantation of a head post-device and of recording chambers over V1 and V4.

Parallel recordings, spike sorting, and inclusion criteria

Timing: >3 months

• 3.
  Multi-unit signal is recorded with two laminar electrodes, one in V1 and one in V4, while the animal is performing the task.

  • a.
    Laminar electrodes are inserted perpendicularly to the cortical surface.
  • b.
    Laminar electrodes have 16 recording channels each, with 0.1 mm spacing between contacts.
• 4.Spike sorting of the multiunit signal is performed, in order to assign neuron’s identity to each spike.
• 5.We include in the analysis all neurons that respond to the stimulus with at least a 4-fold increase in the firing rate compared to the baseline. Moreover, we only utilize trials with correct behavioral outcome.

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Experimental models: Organisms/Strains
Macaca mulatta (male, 7 years old)	Oregon Primate Research Center	22993
Macaca mulatta (male, 11 years old)	New Iberia Research Center	605
Software and algorithms
MATLAB	MathWorks Inc 2019b	N/A
Custom code (Git repository)	(Koren et al., 2020a)	https://github.com/VeronikaKoren/struct_pop_public
Other
Laminar electrodes	Plexon Inc.	https://plexon.com/products/plexon-s-probe/

Step-by-step method details

Preparation of the data

Timing: 4 h

As a first step, we choose the classification method and prepare the data for classification. Correct pre-processing and the choice of the classification method have an important influence on the results and the quality of analysis. These choices should be led by the scientific question to be answered, and by considering the dataset constraints.

Note that the indicated Timings are a rough estimation of the computational time needed to perform computations on a server with 10 cores. Timings do not include the time needed for implementation of the source code.

• 1.
  Choose the classification method.

  • a.
    Our choice of the classifier is the linear Support Vector Machine (SVM). The SVM is used for binary classification and regression problems on multivariate data (i.e., data with multiple variables). The SVM is particularly efficient on datasets with many variables and a limited number of samples, since it has optimal generalization performance, and achieves good performance also on non-Gaussian distributions (Belousov et al., 2002; Meyer et al., 2003). These are precisely the properties of neural data that we typically obtain from in-vivo experiments. In in-vivo experiments, the number of samples (corresponding to the number of trials) in a recording session is typically low (<100) and the number of variables (corresponding to the number of neurons recorded in parallel) can be moderate to high, typically on the order of tens to hundreds of units. Moreover, distributions of spike counts across neurons are often not Gaussian. Another reason why the linear SVM is an attractive choice for the analysis of electrophysiological data is its ability to associate the activity of each neuron with its weight in the classification task in a straightforward manner.

Note, however, that the choice of a linear model is not always appropriate. A linear classification model is searching for a linear separation of data points belonging to classes A and B, and a linear separation might not always be optimal. Troubleshooting 1

• 2.
  Choose which conditions to decode.

  • a.
    We decode conditions match vs. non-match, using only trials with correct behavioral performance. Since these conditions differ in both the stimulus presented and the subsequent choice of the animal, we are decoding a mixed variable “stimulus+choice” (see Koren et al., 2020a).
• 3.
  Choose a relevant time window for averaging neural responses.

  • a.
    In the dataset considered here, the information about matching and non-matching of the target and the test stimuli only becomes available when the test stimulus is shown. We therefore expect that the neural activity contains class-related information during and after the presentation of the test stimulus, and not before. We use a time window of 0–500 ms after the onset of the test stimulus. This time window covers the entire presentation of the test stimulus (0–300 ms), and, in addition, 200 ms after the offset of the test stimulus, when potential choice-related information is expected to unfold. Troubleshooting 2
• 4.
  Set binary labels for the two classes.

  • a.
    We can choose arbitrary labels, for example y_j = 1 for trials in condition match and y_j = −1 for trials in condition non-match.
• 5.
  Decide for a cross-validation (CV) method and split the data samples and the class labels into training and validation sets. We use Monte-Carlo CV, where the data is randomly split into non-overlapping training and test sets. Troubleshooting 3

  • a.
    For each Monte-Carlo CV set, the order of trials is randomly permuted, without repetition. The new trial order is applied to data samples $x_j$ and to labels $y_j$.
  • b.
    Trials are then split into the training set (80%) and the test set (the remaining 20%). This is again relevant to both data samples and labels.
  • c.
    Steps in 6.a and 6.b are iterated N^CV-times. We use N^CV=100 cross-validations in every recording session.

• 6.
  Compute z-scored spike counts in the chosen time window. Troubleshooting 4

  • a.
    Compute the spike count in the chosen time window. For the neuron $n$ in trial $j$, the spike count is the following:

    $$S_{nj}=\sum _k{f}_{nj}\left(t_k\right)$$

    where $f_{nj}\left(t_k\right)$ is a binary vector of zeros and ones (the spike train) of the neuron n in trial j.
  • b.
    Compute the Z-scored spike counts for each neuron individually. For each neuron, compute the mean and the standard deviation of the spike count across trials, using only trials from the training set. Then, z-score the spike counts in the training as well as in the test set as follows:

    $$x_{nj}=\frac{S_{nj}-{\overline{S}}_n}{STD\left(S_n\right)}$$
    If N is the number of neurons in the recording session, the vector of N z-scored spike counts in trial $j$ is one sample for the classifier (Figure 1A) and can be written as follows:

    $$x_j=\left[x_{1j},x_{2j},\dots x_{Nj}\right]$$

    where $T$denotes the transpose.

CRITICAL: For a control, it is important to repeat the analysis for additional time windows where we expect that no significant effect occurs, for example the target and/or the delay period. This increases the validity of the chosen method and the credibility of results.

Note: The purpose of the decoding model here is to extract from the data information that is useful for classification, and not to build a generative model of the neural activity. See Part 4 and Troubleshooting 6 for further information and discussion on this topic.

Note: As we use all the available trials in the experiment, the number of trials in each condition is imbalanced. The cross-validation does not change this since it merely permutes the order of trials. However, the imbalance in the number of trials, unless extreme, is not a problem if we use a performance measure that takes into account this bias (see Part 2).

Alternatives: There are many alternative classification models that can be applied to neuroscience data, such as logistic regression (Alkan et al., 2005) or Generalized Linear Models (GLMs, see Pillow et al., 2011). For an introduction into explainable machine learning methods and some more examples, see Molnar (2019).

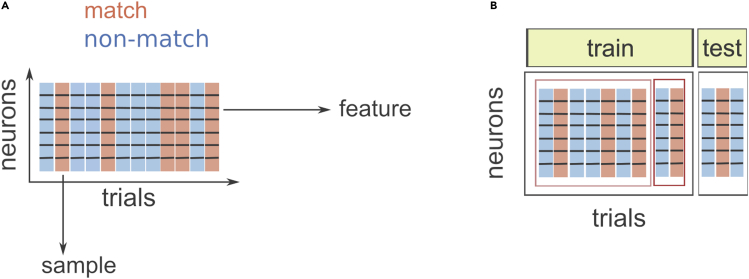
Figure 1.

Preparing the data for binary classification

(A) Schema of a dataset from one recording session. We measure the z-scored spike count of multiple neurons in many trials. Each trial belongs to one of the two binary classes, “match” or “non-match”. For the classifier, trials are samples, and neurons are features.

(B) Schema of the division of the dataset in the training set and the test set (gray rectangles). Within the training set, another division of the data is done for the selection of the C-parameter (red rectangles).

Computation of the classification model and its performance

Timing: 6 h

When working with linear SVMs, we utilize neurons as features and trials as samples for the classifier (Figure 1A). While features can be correlated, samples are required to be independent and therefore uncorrelated. Troubleshooting 5

• 7.
  Compute the parameters of the classification model on the training set.

  • a.
    The linear SVM has one hyperparameter, the regularizer, also commonly referred to as the C-parameter. The C-parameter must be optimized, utilizing exclusively the training set (Figure 1B). First, define a range of C parameters to be tested, for example, C = [0.001, 0.01, 0.1, 1, 10, 100, 1000]. If most of the data is best fit with one of suggested C-parameters, we may refine the range around plausible values. However, once the range is defined, it cannot be changed anymore. In particular, the same range should be used for all recording sessions.
  • b.
    Choose the optimal C-parameter with 10-fold cross-validation (CV). Split the training data into 10 folds. 9 folds are used to compute the classification model while the remaining fold (the validation set for the C-parameter) is used to compute the performance of the model (Figure 1B). Iterate the procedure such that every fold is the validation set, and average across iterations. By testing the entire range of C-parameters, we can choose the C-parameter that gives the highest performance (optimal C-parameter).
  • c.
    Now, all the training data is gathered to compute a new classification model, utilizing the optimal C-parameter.

• 8
  Test the performance of the model on the test set.

  • a.
    After the classification model has been trained, we assess its performance on yet unseen samples, the test set. As a performance measure, we use the balanced accuracy (BAC), which corrects for the imbalance in the number of trials (samples) across the two categories (“match” and “non-match”). The balanced accuracy is defined as follows:

    $$BAC=\frac{1}{2}\left(\frac{TP}{TP+FN}+\frac{TN}{TN+FP}\right)$$
    where TP, TN, FP and FN are the number of true positive, true negative, false positive and false negative test samples, respectively. Let us think of the condition “match” as “positive” and “non-match” as a “negative”. We can see that the balanced accuracy computes the proportion of correct classifications of the condition “match” among all classifications that are “match” (first term in the parenthesis on the right-hand-side), and the proportion of correct classifications of “non-match” among all classifications that are “non-match” (second term on the right-hand side).
  • b.
    Balanced accuracy, which is a single number between 0 and 1, is calculated in each cross-validation run. After collecting results across cross-validation runs, we report the balanced accuracy that is averaged across cross-validations.

CRITICAL: It is crucial that the model is tested on yet unseen data. Testing the performance on the training set will usually give much higher performance than on a held-out test set. Testing on a held-out test set is putting to the test the capability of the classification model to generalize to yet unseen samples.

Note: In a binary classification task, the balanced accuracy of 0.5 is the chance level performance, meaning that test samples have been classified correctly as often as incorrectly. The balanced accuracy of 1, on the other hand, indicates that all test samples have been classified correctly.

Alternatives: We opted for the 10-fold CV method for determining the C-parameter because it is faster than the Monte-Carlo CV. Computation of the optimal C-parameter is nested in the training set/validation set CV and is for this reason computationally expensive. With small datasets, however, Monte-Carlo CV is an alternative method for the selection of the C-parameter.

Alternatives: We chose to measure the classification performance with balanced accuracy, a measure that accounts for the imbalance for the data classes. As an alternative, one can balance the classes with stratified k-fold cross-validation, a method that ensures equal participation of classes in each fold (Zeng and Martinez, 2000).

Assessment of significance of classification performance

Timing: 24 h

Significance of classification performance is assessed with a permutation test. The permutation test is a non-parametric test that does not make any assumption on data, but instead creates the distribution of results of random models from the data itself, against which the true result is tested.

• 9.
  Compute the performance of models trained on randomly permuted class labels.

  • a.
    Gather class labels of the training data in a vector $y$. Randomly permute the entries of the vector $y$, without repetition.
  • b.
    Train and test the classification model as in steps 7 and 8 but utilizing permuted class labels. The permutation of class labels is iterated N^perm-times, giving N^perm values for the balanced accuracy (BAC^perm). We used N^perm=1000.
• 10.
  Compute the p-value by ranking the balanced accuracy among the distribution of balanced accuracies of models with permuted class labels.

  • a.
    The p-value is the proportion of the BAC^perm that are bigger than the BAC. Note that this is a one-sided test. If the p-value is smaller than the significance level α, the BAC is significant. We used a significance level α=0.05.
  • b.
    When performing more than one permutation test, the significance level must be corrected for multiple testing. We used the Bonferroni correction, where the significance level is divided by the number of tests, α ^corrected=α/N^test.

CRITICAL: The precision of the p-value depends on the number of permutations we use. If we use N^perm=1000 permutations, and if one instance of BAC^perm is larger than the BAC, our result is significant with the p-value of p=0.001. If no instance of BAC^perm is larger than the BAC, our p-value is p<0.001. The precision of the p-value is therefore limited by the number of permutations, more precisely, with the p-value of p<1/ N^perm. Even if all BAC^perm are larger than BAC, stating that the p-value is zero is incorrect.

Note: As we randomly permute class labels, the classification model cannot find the underlying structure of the data, since the association between data samples and class label has been randomized by the permutation. However, due to the limited number of samples, the BAC^perm will not be exactly 0.5, but will take values around 0.5 in different permutation cycles (Figure 2A).

Alternatives: The permutation test is a very rigorous way of testing the significance of an effect. On the down side, the permutation test takes a long time to run, since it requires that the entire model is re-computed and re-evaluated N^perm - times. An alternative significance test can be performed with a parametric test, where one needs to be careful that the criteria of the parametric test are met.

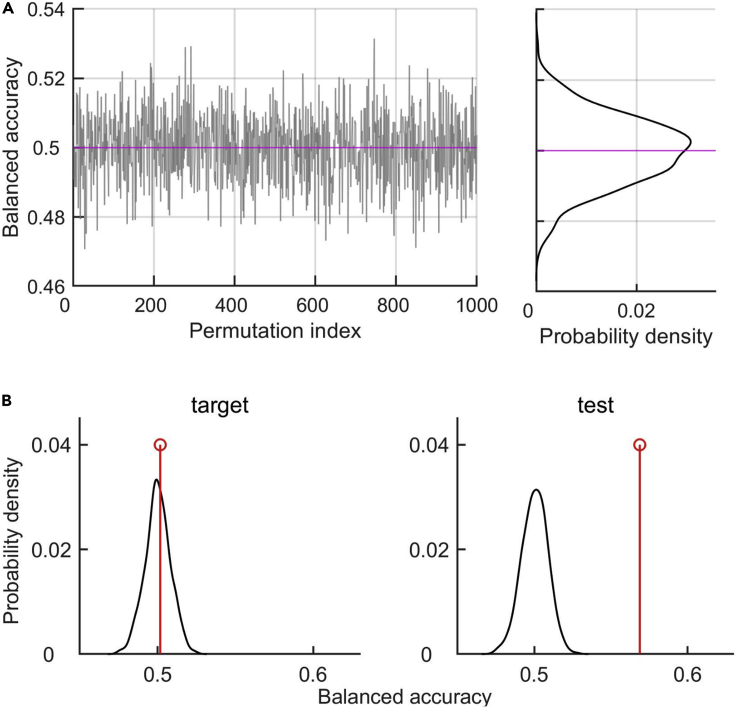
Figure 2.

Balanced accuracy of models with permuted class labels

(A) Left: BAC of models with permutation of class labels (BAC^perm) in one recording session. We used 1000 random permutations. Right: Distribution of BAC shown on the left. The magenta line marks the mean of the distribution.

(B) Left: Distribution of BAC^perm (black) and the BAC of the regular model (red) during target. The p-value is p=0.418. Right: Same as on the left, but during test. The p-value is p<0.001, since none of the BAC^perm is bigger than the BAC.

Decoding weights and functionally relevant subgroups

Timing: 6 h

If the balanced accuracy is significant, we can proceed to study the role of single neurons in the classification task. With the linear SVM, neurons are features of the model (Figure 1A), and the activity of each neuron is associated with one feature weight. Considering feature weights of N neurons observed in parallel, we define a weight vector $w$. The weight vector determines the orientation of the separating boundary that separates data points in conditions A and B (Figure 3). Troubleshooting 6

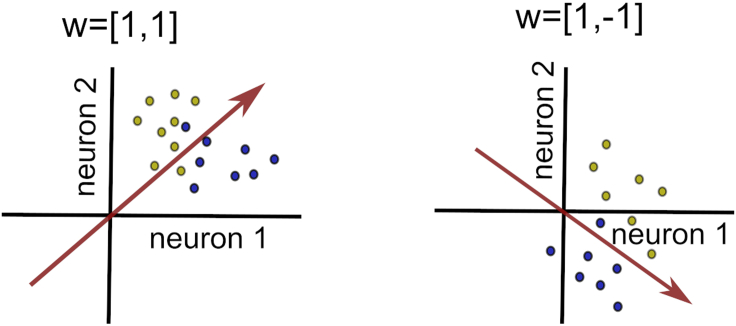
Figure 3.

Schema of the separating boundary in a toy model with two neurons

The separating boundary is an (N-1)-dimensional plane (a hyperplane) in the space of inputs of N neurons. In case of N=2 neurons, the separating boundary is a line. The separating boundary optimally divides the space of inputs from category A and B (yellow and blue circles). The separating boundary is fully determined by the offset from the origin (here the offset is 0), and the weight vector w that determines its orientation. The weight vector has N entries, one for each neuron. The change in sign of the weight of a particular neuron changes the orientation of the separating boundary.

The weight vector can easily be calculated numerically from the classification model. To calculate the weight vector, we utilize a subset of data points that are the most informative for the classification task, the so-called “support vectors” (hence the name of the classifier). A support vector is a data point in the N-dimensional data space (in a particular trial) that the classifier has used for determining the separation boundary. Support vectors are data points that lie on or close to the separation boundary.

• 11.
  Gather all data and compute the classification model.

  • a.
    When estimating feature weights of the model, no training/validation is required. Apply steps 6 and 7 on the complete dataset.

• 12.
  Compute feature weights of the model.

  • a.
    As we compute the classification model, the classification function has several available outputs. We call the following outputs from the classification function: support vectors ${\alpha }_j$, indices of support vectors, and Lagrange multipliers ${\lambda }_j$.
  • b.
    Compute weights according to the following expression:

    $$w=\sum _{j=1}^Q{\lambda }_j{y}_j{x}_j$$

    where $y_j$ is the class label in trial $j$ and $x_j$ is the vector of z-scored spike counts in trial $j$. $Q$ is the number of support vectors, and it is smaller than the number of trials.
  • c.
    Repeat the procedure for every cross-validation run. Average weights across cross-validations.

• 13.
  Normalize weight vectors and gather results across recording sessions.

  • a.
    Normalize the weight vector in every recording session as follows:

    $$\tilde{w}=w/\Vert w\Vert$$

    where $\Vert w\Vert =\sqrt{w_1^2+w_2^2+\dots ,w_N^2}$ is the L2 norm.
  • b.
    Gather results across recording sessions.

• 14.
  Using properties of weights, define functional subgroups.

  • a.
    An important property of the weight is its sign. Neurons with positive and negative weights have the opposite effect on the separation boundary, as they are pulling the separation boundary in opposite directions (Figure 3). Another important property is the amplitude of the weight. The larger the amplitude of the weight of a particular neuron, the higher the importance of the neuron for classification is.

Note: The range of weights depends on the C-parameter, and the C-parameter differs across recording sessions. If we want to compare the amplitude of weights across neurons from different recording sessions, we are required to normalize the weight vector.

Note: If all samples are correctly separated by the separation boundary, we say that the data is linearly separable. However, the model can function even in the absence of linear separability. In neural recordings, linear separability is unlikely. even samples in the training data can sometimes lie on the wrong side of the separating boundary. Such samples are called “slack points." The C-parameter determines how strongly slack points are considered in the computation of the separating boundary (see Belousov et al., 2002; Vapnik and Vapnik, 1998).

Alternatives: There are alternative ways of determining effects of a particular feature, one example of which is a Shapely value (see Molnar, 2019). The Shapley value is the average marginal contribution of a feature (or set of features) across all possible sets of features. Unfortunately, the computation of the Shapley value is computationally expensive, to the point that it is only feasible if the number of simultaneously recorded units is small. We need to account for all possible subpopulations of neurons, which quickly leads to a combinatorial explosion. In the case of our data with up to 17 parallel units, systematic computation of Shapley values for single neurons was not feasible. However, computing the Shapley value might be feasible in datasets with a small number of parallel units (e.g., 5 units).

The effect of heterogeneity across neurons on performance

Timing: 12 h

If all neurons contribute the same quantity of information to the classifier and respond to the stimulus class the same way (e.g., by increasing in the firing rate for the stimulus “match”), we can call the observed population homogeneous. Within such a population, and assuming no correlations in the data, all neurons would have the same decoding weight. A homogeneous network is an abstract concept that would hardly ever happen in the real-world scenarios, where we rather expect that neurons differ in the way they activate for a given class (e.g., some neurons increase the firing rate for the class “match” while others decrease the firing rate for the class “non-match”). We also expect that neurons differ in the quantity of information that they convey to the classifier. In such a case, every neuron has a different weight, and we call the population heterogeneous.

Here, we inquire how the heterogeneity across neurons contributes to the performance of the classification model. To this end, we compute the performance of the model that is homogeneous across neurons (Figure 4A) and compare it to the performance of the regular model. We remove the heterogeneity across neurons by permuting the activity across neurons, independently in each trial. Such a procedure destroys the activation patterns that are a source of information for the classifier, and we therefore expect a decrease in classification performance.

• 15.
  Assess the effect of heterogeneity across neurons.

  • a.
    Randomly permute, without repetition, the elements of the vector of activations $x_j$ across all simultaneously recorded neurons. The vector of activations is permuted independently in every trial (Figure 4B), so that the identity of neurons is mixed differently across trials. Note that the class labels do not change.
  • b.
    Repeat steps 5–8. In step 8, we get the balanced accuracy of the homogeneous model, BAC^h.
  • c.
    Compare BAC^h with BAC by computing the difference, Δ^h = BAC-BAC^h, in every recording session.
• 16.
  Assess the effect of heterogeneity within functional subpopulations. A population is defined by the same sign of the weight.

  • a.
    Randomly permute, without repetition, the vector of activations $x_j$, but only across units with the same sign of the weight. As in step 15.a, the permutation is done on every trial independently, while labels stay untouched.
  • b.
    Repeat steps 5–8. In step 8, we get the balanced accuracy of the model that is homogeneous within groups, BAC^h.groups.
  • c.
    Compare BAC^h,groups with BAC by computing the difference,

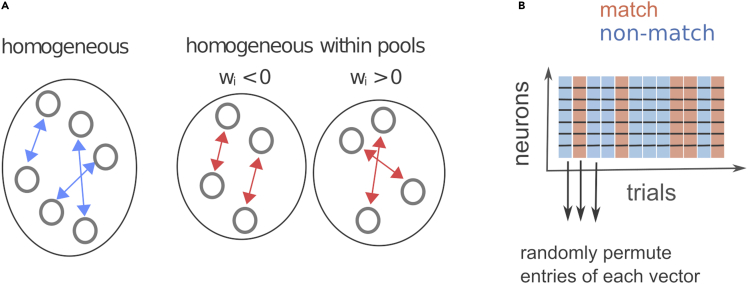
Figure 4.

Creating homogeneous neural ensembles

(A) By swapping the activity across all the neurons from the population (left) or between neurons with the same sign of the weight (right), we create homogeneous neural ensembles. Figure reprinted with permission from Koren et al., 2020a.

(B) Homogeneous ensembles are created by randomly permuting the neural activity across neurons in the same group, independently in each trial.

Δ^{h, groups} = BAC-BAC^{h, groups}, in every recording session.

CRITICAL: It is crucial that all the steps are performed on the data from the same recording session. Gathering data from different recording sessions before we start with the step 14 will create artificial assemblies with artificial covariance and will give misleading results. However, we can evaluate the general effect of heterogeneity by gathering across recording sessions final results, Δ^h and Δ^{h, groups.}.

Note: Comparing the performance of the homogeneous models with the regular model, we assess how much the heterogeneity across neurons contributes to the performance of the regular model. Note that removing heterogeneity is always expected to decrease the performance of the model. However, it is interesting to consider how much of the prediction accuracy of the regular model is due to heterogeneity across neurons, and to compare results from steps 15 and 16 (see Expected Outcomes).

The effect of noise correlations on classification performance

Timing: 12 h

Neural responses are often correlated, in particular within local neural ensembles (Cohen and Kohn, 2011). Measuring the co-variability of responses between a pair of neurons, we can distinguish the signal correlation and the noise correlation. The signal correlation measures the similarity of tuning curves of the two neurons across a range of stimuli. We measure the signal correlation by varying the stimulus and measuring the correlation of responses. However, neuronal responses also vary upon the repeated presentation of the same stimulus. If we repeatedly show the same stimulus and measure neural responses in many trials, the correlation among neuronal responses across the two neurons is termed noise correlation (Averbeck et al., 2006).

Noise correlations can, in principle, increase or decrease the transfer of information (Averbeck et al., 2006), and here, we are interested in the effect of noise correlations on the classification performance. We tackle the effect of noise correlations on the performance by removing noise correlations from the data, computing the balanced accuracy, and comparing the results with the regular model where correlations are intact. Theoretical studies have shown that positive correlations among neurons with similar tuning decrease the information transfer (Averbeck et al., 2006; Moreno-Bote et al., 2014). In our data, if neurons with similar weight are positively correlated, we therefore expect that the removal of correlations will increase the performance of the classifier.

• 17.
  Assess the effect of noise correlations across all units (Figure 5A, left).

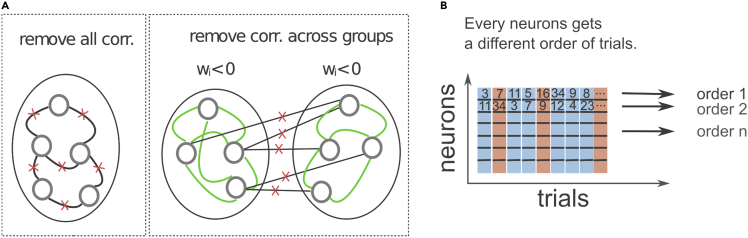
  • a.
    Remove noise correlations across all simultaneously recorded units by permuting the order of trials of each neuron. In order to keep correct labels, the permutation is limited to trials within a given condition (match and non-match). The permutation of the trial order is done independently across neurons (Figure 5B).
  • b.
    Repeat steps 6–8. In step 8, we get the balanced accuracy of the uncorrelated ensemble, BAC^uncorr.
  • c.
    Compare BAC^uncorr with BAC, in a similar fashion as in step 15c.
• 18.
  Assess the effect of noise correlation within functional subgroups (Figure 5A, right).

  • a.
    Proceed the same way as in step17.a but remove noise correlations only between neurons within a functional subpopulation (e.g., the same sign of the weight).
  • b.
    Repeat steps 6–8. In step 8, we get BAC^{uncorr, groups}.
  • c.
    Compare BAC^{uncorr, groups} with BAC, in a similar fashion as in step 15c.

CRITICAL: In order to address real effects that are present in the data, it is again crucial that all the steps are performed on the data from the same recording session.

Note: It is important to permute the trial order only for trials within the same condition. Otherwise, labels are wrongly assigned, leading to chance level performance.

Figure 5.

Removing of noise correlations

(A) We are testing the effect of removing correlations between all neuronal pairs (case 1, left), and across the groups of neurons with the same sign of the weight (case 2, right). Note that for the case 2, correlations within each group remain intact (right). Figure reprinted with permission from Koren et al., 2020a.

(B) Noise correlations are correlations that arise in the same trial. We remove them by randomly permuting the trial order. In the case 1 (remove all correlations), we permute the order of trials for every neuron independently. In the case 2 (remove correlations across groups), we assign a different trial order to each group of neurons, while neurons from the same group maintain the same order of trials. In all cases, the permutation of trial order is limited to trials within a given condition.

Comparison of noise correlations across functional subgroups

Timing: 16 h

As we divided neurons into functional subgroups, we can now verify if these subgroups differ in the strength of noise correlations.

• 19.
  Compare the strength of noise correlations between pairs of neurons with the same sign and the opposite sign of the weight.

  • a.
    Group neurons into those with positive and negative weight.
  • b.
    Compute noise correlations between neurons with the same sign of the weight (“correlations same”; green links in Figure 5A, right), using only neurons in the same recording sessions.
  • c.
    Gather “correlations same” across the two groups.
  • d.
    Compute correlations for pairs with the opposite weights (“correlations different”; black links in Figure 5A, right).
  • e.
    Gather “correlations same” and “correlations different” across recording sessions.

• 20.
  Test if the difference of “correlations same” and “correlations different” is significant using the permutation test.

  • a.
    The test statistics is the mean difference of correlations,

    $$d^{same,different}=⟨{\mathrm{r}}^{same}⟩-⟨{\mathrm{r}}^{different}⟩$$

    where $⟨r⟩$ is the empirical mean across pairs.
  • b.
    To construct the null model, assign randomly the sign of the weight to neurons in each recording session.
  • c.
    Repeat steps 19a–19e and 20a for neurons with randomly assigned sign of the weight.
  • d.
    Repeat the whole procedure N^{perm –} times, getting N^perm instances of the statistics with randomly assigned sign of the weight, ${d_p}^{same,different}$.
  • e.
    Rank the difference $d^{same,different}$ among analogous results on data with permuted sign of the weight, ${d_p}^{same,different}$, and compute the p-value as in 10a.

• 21.
  Compare the strength of correlations between neurons with strong and weak weights.

  • a.
    Categories for strong and weak weights are defined with respect to the absolute value of the normalized weight. We distinguish neurons with strong and weak weights by ranking the absolute value of the weight among the same result of models with permuted class labels. If the strength of the weight is ranked among the first 25% of models with permuted labels, we categorize the weight as strong, and weak otherwise.
• 22.
  Compute pairwise correlations for neurons with strong weights and for neurons with weak weights.

  • a.
    Gather results across recording sessions.
  • b.
    Test the two distributions with the permutation test, as in step 20.

Note: Depending on the data, the number of pairs within and across groups might be imbalanced. This is however not a problem if we test the difference between “correlations same” and “correlations different” with a permutation test.

Expected outcomes

When should classification work and why?

The primary source of information for a classification model is the difference in patterns of activation between conditions A and B. Note that patterns or activation are high-dimensional (N-dimensional if we have N neurons). It is not necessary that all neurons change their activity between conditions A and B, but the change in activity of at least some neurons is required for a better-than-chance prediction. As an example, let us have 3 neurons, all responding strongly to the stimulus, and let us observe the change in the spike count with respect to the baseline of these neurons in single trials. Let us say that neuron 1 increases its spike count and neuron 2 decreases its spike count in condition A, while the opposite happens in condition B (neuron A decreases and neuron B increases the spike count). Such a combination of activation patterns is informative for the classifier, and neurons 1 and 2 will have strong weights with the opposite sign. Neuron 3, on the contrary, does not change the spike count between the two conditions. Activity of the neuron 3 is not informative for the classification task and its weight will be close to zero. Neuron 3 is likely responding to a feature of the visual stimulus that is unrelated to the classification task, while neurons 1 and 2 are responding to the classification variable, or at least a variable that is correlated with it. In the case of the present dataset with matching and non-matching stimuli, neuron 3 could, for example, be responding to the color of the stimuli, which does not change between conditions, while neurons 1 and 2 are responding to stimulus classes “match” and “non-match”.

In what time window do we expect the classification to be above chance?

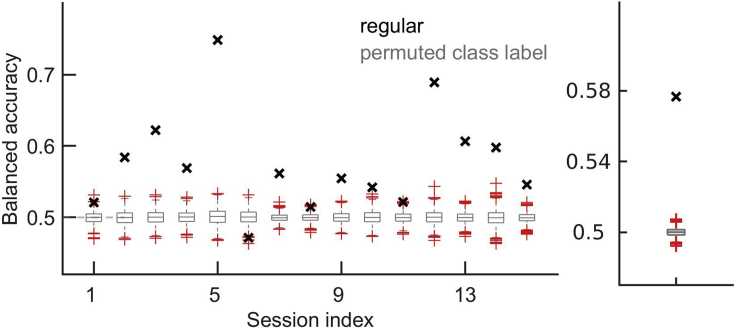
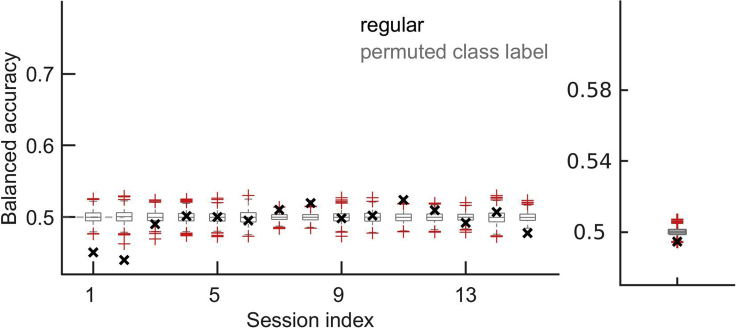
In our specific classification problem, we can predict stimulus classes “match” vs. “non-match” from neural responses in V1 during the test stimulus (Figure 6), but not during the target stimulus (Figure 7). This is expected since the information about the matching and non-matching of the target and the test stimuli is only available after the two stimuli have been seen. Applying our protocol to the neural responses during the target stimulus is, however, a good control of the method and of our hypotheses. If prediction accuracy during target was above chance, this would put into question the interpretation of results during test, since it would invalidate our hypothesis that sensory evidence drives patterns of activations that are predictive of the stimulus class. We would have to think about alternative explanations, such as neural responses being driven by a strong internal bias that could drive neuronal responses before sensory evidence is presented.

Figure 6.

Balanced accuracy during the test time window

Left: balanced accuracy in recording sessions (black crosses) and distribution of same results for models with permuted class labels (gray boxplots). Red crosses are outliers of the distribution in gray. An outlier is a value that is more than 1.5 times away from bottom or top of the box, where the top and the bottom of the box indicate the 25th and the 75th percentile of the data sample, respectively. Right: Session-averaged results of the regular model and of models with permuted class labels. Figure reprinted with permission from Koren et al., 2020a.

Figure 7.

Same as in Figure 6, but for the target time window

Correlation or causality between the neural activity and the classification variable?

Are observed neurons responding directly to the binary classification variable (e.g., the match and non-match of two consecutive stimuli) or are they responding to some confounding variable that is merely correlated with the classification variable? In the case of the present dataset, for example, we might ask whether patterns of neural activity predict the match/non-match of the stimuli, or perhaps some low-level sensory feature that systematically differs between these two conditions and has escaped the attention of experimentalists. In the present behavioral task, the identity of the stimulus is constant within the recording session (but changes from one recording session to another). To prevent the decision-making from relying on some low-level feature, we could change the identity of the stimulus in every trial. Also, to see how general is the coding of categories “match” vs. “non-match” by the observed neural activity, we could enlarge the dataset and test how the activity of observed neurons predicts matching and non-matching stimuli of different kinds.

It must be emphasized that the prediction accuracy does not tell us anything about the causal relation between the neural activity and the classification variable. Testing classifiers, we assess the correlation between the patterns in the data and the classification variable, but we cannot be informed about the causal role of the neural activity for the classification task. Even a perfect classification with prediction accuracy of 1 does not guarantee a causal relation. Up to now, methods of causal inference on observational neuroscience data are still in early stages of development. To assess causal relations, manipulative experimental approaches are required, such as perturbation of neural circuits (Panzeri et al., 2017) or pharmacological manipulation. Other methods for inferring causal relations in the neuroscience data have been suggested (Marinescu et al., 2018), but their validity remains to be confirmed.

How to address confounding variables?

It is precisely the absence of causality between patterns in the data and the classification variable that makes classification results prone to confounding variables. Besides changing the dataset or applying causality methods, we can address confounding variables with appropriate methods. We might try to disentangle the importance of the variable “stimulus class” from the variable “choice” with a linear regression model that searches for the contribution of each of the two explanatory variables to variations in the data (Turner et al., 2017). Alternatively, we might use the transfer of learning. In the current classification task, we were studying the predictability of binary variables stimulus+choice and obtained a better-than-chance prediction accuracy. This leaves us uninformed whether the information that underlies successful prediction comes from the stimulus class, the choice of the animal, or a combination of both. With the “transfer of learning” decoding scheme, we train the classifier on trials that differ in both stimulus and choice but test the model on trials that only differ in choice, but not in stimuli (e.g., conditions with choice “same” and “different on non-matching stimuli; see Koren et al., 2020b). If such a classification scheme has a chance level accuracy, we can conclude that the classifier is predicting the stimulus class, and not the choice. A better-than-chance accuracy, meanwhile, implies that the information about the choice is important for the classifier.

Yet it remains unclear whether variables such as the stimulus class and the choice of the animal are disentangled in the brain. A new line of research has convincingly demonstrated that neural populations in the cortex encode highly mixed set of variables, including stimulus features, variables related to the internal state (Stringer et al., 2019a), and to spontaneous movement of the animal (Musall et al., 2019). These analyses have also suggested that highly mixed representations might serve an important function of binding together different types of information (Stringer et al., 2019a, 2019b) perhaps to form objects that are instrumental to the information processing in the brain.

A nontrivial question: The effect of heterogeneity of neural responses

We investigated the effect of heterogeneity of neural populations for the classification performance of the model. This is not a trivial question since successful classification does not necessarily require heterogeneous neural ensembles. Imagine, for example, that the experimenter shows to the animal two stimuli with orthogonal orientation while recording the activity of nearby neurons in a single cortical column of V1. We would expect neurons from the same column to have the same orientation preference and therefore a largely homogeneous response pattern. If all neurons fire with an increase in firing rate for the stimulus A and are silent for the stimulus B, we could easily predict the stimulus class from such a homogeneous ensemble.

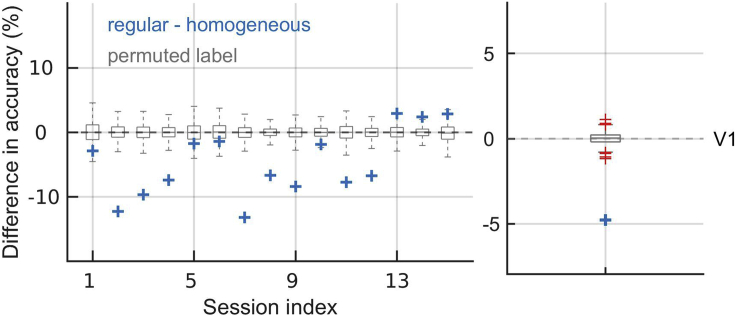
In the present dataset, interestingly, making neural responses homogeneous strongly decreased the balanced accuracy (Figure 8). Permuting the activity across all neurons decreased the prediction accuracy in V1 by 4.8 and in V4 by 3.5% with respect to the regular model (Koren et al., 2020a). Since the accuracy of the regular model is about 7% above chance, heterogeneity thus accounted for a big proportion of the predictive power of the regular model. Heterogeneity across neurons accounted for 92 (V1) and 94% (V4) of prediction accuracy of the regular model. This implies that neural responses are heterogeneous, and heterogeneity is an important source of information for the classification task. This result suggests that some neurons prefer (or fire more for) the stimulus class “match” while others prefer the stimulus class “non-match”. Shuffling the activity across these two functional subpopulations, we destroyed those activity patterns that are the most informative for the classification model, hence a significant drop in balanced accuracy.

Figure 8.

Difference in accuracy between the regular model and the homogeneous model

We show results in recording sessions (left), and average across sessions (right). Gray box plots mark distributions of models’ results with permuted class labels. Red crosses mark outliers. Making neural responses homogeneous across neurons decreases classification performance. Figure reprinted with permission from Koren et al., 2020a.

As a cautionary note, consider that shuffling the data across neurons could potentially decrease the performance also in the case where all neurons respond in the same way to the stimulus class (e.g., by increasing the firing rate for “match”). Even though all neurons respond in the same way to the stimulus class, they likely contain different levels of trial-to-trial variability. In the regular model, neurons with strong variability might get a weaker weight while more reliable neurons would get a stronger weight. Shuffling the activities across neurons also homogenizes the variability, potentially contributing to a decrease in classification performance.

While the permutation of neural indexes is always expected to decrease the performance, this is not necessarily the case of the subgroup-permuted model. We expect that the permutation limited to subgroups has smaller or even no effect on the performance compared to the regular model. In the present dataset, permutation of neural indexes within subgroups has decreased the performance for 4.0% (V1) and 0.7% (V4) with respect to the regular model. If the performance of the subgroup-permuted model is on the same level as the regular model (i.e., not significantly different), we may conclude that within the subgroup of neurons with the same sign of weight, neural populations can be described as homogeneous without loss of information for the classification task. This result might be useful for reductionist approaches to neural dynamics such as mean-field models. In the present dataset, the model “homogeneous within groups” accounts for 48% (V1) and 89% (V4) of the prediction accuracy of the regular model, and in V4, the BAC of the model “homogeneous within groups” is not significantly different than the BAC of the regular model. This suggests that the neural activity in V4 can be reduced to two homogeneous ensembles without a significant loss of information.

Noise correlations between neurons with the same sign of the weight are expected to decrease the performance

With steps 19 and 20, we investigated the effect of noise correlations on the performance of the model. What is the expected outcome? Theoretical studies have shown that correlations can enhance or harm discrimination depending on the relation between the sign of the correlation and the similarity of neuronal selectivity (Moreno-Bote et al., 2014). The effect of positive noise correlations is the most relevant in practice since negative correlations are only rarely observed in neural data. Positive noise correlations between neurons with similar selectivity are harmful for discrimination (Averbeck et al., 2006). In our setting, neuronal selectivity is estimated by the neuron’s weight, and due to the binary classification task, we can divide neurons in two groups, a group with positive and a group with negative weights. Neurons with the same sign of the weight can therefore be thought of as having similar selectivity, and the theory predicts that correlations among these neurons (we call them “correlations same”) are harmful for the performance. Note also that correlations can be divided in two non-overlapping groups of “correlations same” and “correlations different” (Figure 5A)

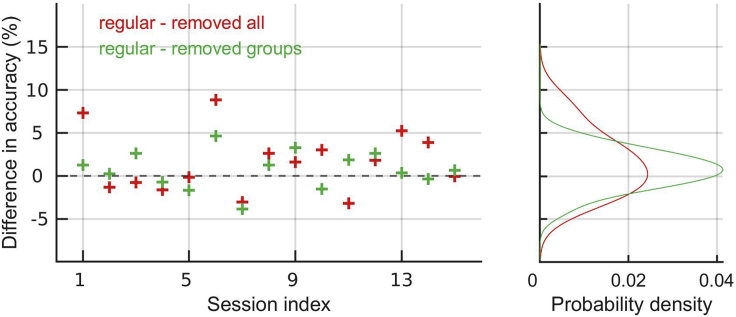
As we remove “correlations different” from neural activity, the classification performance does not change significantly (Figure 9, green). As we now remove all correlations, performance slightly increases (Figure 9, red). This implies that removing “correlations same” provoked the increase in performance. We conclude that removing noise correlations between neurons with the same sign of the weight increases the performance.

Figure 9.

Difference in balanced accuracy between the regular model and models with removed correlations

Left: Results in recording sessions. Right: Distribution of results on the left.

How can removing correlations help the classifier? Let us consider two neurons that are perfectly positively correlated (correlation coefficient of 1). Clearly, it is sufficient to observe one of the neurons to know the response of both. Observing both neurons therefore does not bring more information than observing one of them. If responses of the two neurons are uncorrelated, however, observing the two neurons brings us more information than observing only one of them. Removing correlations among neurons with similar selectivity therefore makes more neurons informative for the classification task, potentially raising the classification performance.

Limitations

Time-averaged data

One of the major limitations of our protocol is that decoding is applied to time-averaged neural responses. In cortical neurons, firing probability may change rapidly over time (Shadlen and Newsome, 1998), implying possible rapid changes in the firing rate over the course of the trial. The SVM assumes uncorrelated samples, meaning that instantaneous firing rate samples cannot be used for classification, since such samples are likely to be strongly temporally correlated. The present protocol is therefore limited to time-averaged responses. To increase the temporal precision of decoding with the SVM, the averaging time window can be shortened (for example, to 300 or 250 milliseconds). However, we cannot decrease the length of the time-window ad libitum. In the present data, going below 200 milliseconds was problematic since some neurons would never spike in such a short time window. We can calibrate the length of the time window also by computing the autocorrelation function on population responses. The autocorrelation will show at which timescales the firing-rate responses are correlated.

If the evolution of a low-dimensional, class-related signal over the course of the trial is the focus of the analysis, we suggest using a decoding protocol that is designed for time-resolved signals (see Nirenberg and Latham, 2003, and Pillow et al., 2011, for methodological reviews, and Koren et al., 2019, for decoding of spike trains from the present dataset without temporal averaging). Classification with the linear SVM is surprisingly successful in the case where we can expect the neural code to be based on the firing rate, and when the change in the firing rate from the baseline is consistent within the averaging time window. With an appropriate choice of the time window, and if a linear model is a suitable choice given the data, a linear SVM might extract from the neural system a large amount of the information that is relevant for the classification task, and give robust and deterministic results (Belousov et al., 2002).

A systematic approach for assessing the classification performance in different time windows over the course of the trial is to use a sliding window. We predetermine the length of the window (e.g., 300 ms) and the step size (e.g., 20 ms). We compute the prediction accuracy of the SVM in the first time window, slide the window for the step size forward, recompute, slide forward, etc. To assess the significance of results, we must correct for multiple testing. Standard correction methods, such as the Bonferroni correction, are not applicable due to correlations of the data in overlapping time windows, however, the method of cluster-based permutation test has been designed to deal with such cases (Sassenhagen and Draschkow, 2019).

Incorrect trials

Caution is required if we want to apply the present protocol to conditions with incorrect behavior. First, incorrect behavior can have different causes, such as the fluctuation of attention (Cohen and Maunsell, 2010), noise in the incoming sensory evidence (Brunton et al., 2013) or error in transmission of the neural signal from one cortical area to another (Shahidi et al., 2019), to mention just a few. If different causes dominate a different subset of incorrect trials, lumping together all incorrect trials will give a diverse set of responses, making it difficult for the classifier to extract any relevant patterns in the data. In case of correct behavior, we expect the correct choice to be largely due to correct interpretation of the sensory evidence by the brain. Even though the correct choice might not always be due to successful sensory processing (in two-alternative forced choice setups in particular), the causes of correct choice seem to be less and less diverse than causes for incorrect choice.

As the second cautionary note, one should consider that major changes in response patterns can take place during an incorrect trial. Since our protocol requires time-averaging of neural responses, rapid and major changes in activity patterns within the averaging window will most likely result in chance level performance, particularly if we use a long averaging window. If we decide to use the SVM on incorrect trials, it might be advisable to apply the sliding-window method.

Binary classification task

Since the SVM is a binary classifier, the current protocol is best suited for the study of neural responses on binary classification tasks. Experimental designs with more than two classes are therefore not suitable for the present protocol.

Extracellular recordings of neural activities recorded in parallel

The present protocol was designed for studying extracellular recordings where the activity of multiple neurons is acquired in parallel. Since one of the interests of multivariate methods is to account for the covariance in the data, it is misleading to gather activities of single neurons that are not recorded simultaneously and treat them as a population. Moreover, the preset protocol cannot be safely extrapolated to whole-brain recordings, such as the functional magnetic resonance imaging (fMRI) data or electroencephalography (EEG) data because these datasets are expected to contain additional sources of measurement noise (see Troubleshooting 6).

Troubleshooting

Problem 1

Classes A and B might be better separable with a non-linear rather than with a linear function (step 1).

Potential solution

To test if this is the case, we can run a non-linear SVM (Vapnik and Vapnik, 1998), for example, the SVM with the Radial Basis Function kernel. If the performance of the non-linear model is superior to the performance of the linear model, it might be more appropriate to work with the non-linear model. Note however that the non-linear SVM cannot be interpreted in the manner we have shown here.

Problem 2

Different choices of the time window result in different model performances (step 2).

Potential solution

To find the time window that maximizes prediction accuracy, one can pre-determine starting points and possible lengths of the time window and test the performance systematically. To interpret the results, it is important to consider the way the experimental task unfolds in time and the expected timing of neural responses. For example, if we want to compare different time windows to show that the prediction accuracy during a particular time window is significantly higher than in another one, we must take care to correct for multiple testing and for a possible overlap between the time windows.

Problem 3

Is it better to use Monte Carlo cross-validation or k-fold cross-validation (step 5)?

Potential solution

Cross-validation (CV) is a method of model validation. A specific partitioning choice of the data into training and validation sets is arbitrary, hence, we must sample different partitions to get close to the true performance. A common cross-validation scheme is k-fold CV. With k-fold CV, the data is subdivided into k (usually 10) parts or folds. The model is trained on (k-1) - folds and tested on the remaining fold. This procedure is iterated, such that each of the k-folds is once the test fold once. With Monte-Carlo CV, the order of trials is randomly permuted, without repetition, and then subdivided into the training/test set. This procedure can be repeated ad libitum. When running classification models on neural responses, we have found Monte-Carlo cross-validation to be superior to k-fold cross-validation, due to the strong trial-to-trial variability.

With k-fold CV, the number of partitions is limited to k, while the number of partitions with the Monte-Carlo method is not prescribed and we can run as many repetitions as we can afford. Due to strong trial-to-trial variability, it is relatively easy to find an “unlucky” partition of the training/test data. If the number of partitions is small (as with k-fold CV), this can have a substantial effect on the prediction accuracy. We have found it beneficial to compute classification results from many partitions of the training/validation set, which is achieved with Monte-Carlo sub-sampling. Still, the k-fold cross-validation has the advantage of being faster and might be a viable option with large datasets, in particular if the number of samples per class is balanced within each fold. To have an overview of these two and other alternative methods of cross-validation, see Bishop, 2006.

Problem 4

Is z-scoring of data a necessary step (step 6)?

Potential solution

While z-scoring does not increase the quantity of the information in the dataset, it prevents our classification model from being biased by the activity of neurons with a strong firing rate. Without z-scoring, the classification model might rely excessively on neurons with strong firing rate, instead of searching for the difference in patterns of activity between conditions A and B. Z-scoring is also necessary for interpretation of weights (Molnar, 2019).

Problem 5

The SVM requires independent data samples. However, it can happen that trials are correlated, due to the presence of a global variable that changes on a slow time scale. For example, the animal might be engaged at the beginning of the recording session and become progressively less engaged towards the end of the session. In such cases, the behavioral state of the animal might influence the neural activity (step 7).

Potential solution

To verify the presence of a slow variable that systematically influences the neural activity across trials, we can verify if the firing rates and other statistics systematically change within the recording session. In addition, we can test if the classification performance is stable within the session by comparing the classification performance on trials from the beginning and from the end of the recording session. If such analyses reveal slow autocorrelation of the data samples, we can examine the timescale of the autocorrelation and subsample the data on that characteristic timescale. Note however that this procedure could potentially lead to a substantial reduction of the dataset size.

Problem 6

When analyzing whole-brain recordings, such as fMRI and EEG data, weights of decoding models are not guaranteed to convey class-related directions in the data, as they do not necessarily reveal the patterns that are predictive of the class labels (Haufe et al., 2014). Weights of decoding models are rather interpreted as the most suitable combinations of data channels that maximize discrimination. Neural noise and correlations among recording channels are the main reasons why weights of decoding models do not necessarily convey class-related information in whole-brain recordings.

Potential solution

Compared to fMRI voxels or EEG channels, spike trains, obtained from laminar extracellular recordings, are much less prone to measurement noise. Spike sorting and selection criteria for inclusion in the analysis (in our case, increase of the firing rate with the stimulus at least 4-fold with respect to the baseline) make sure that the observed neural activity is related to the stimulus class and/or to the decision variable, or at least to correlated confounding variables (see “How to address confounding variables? in Expected Outcomes). While fMRI and EEG datasets comprise time- and space-averaged data from the entire brain, laminar extracellular recordings capture the neural activity on a much more local scale. Instead of billions of neurons, we only dispose of a handful of neurons, and interpreting local information with decoding models as activity patterns is indeed justified (Kriegeskorte et al., 2006; Etzel et al. 2013). Whether trial-to-trial variability of the spiking signal is “useless noise” or a signature of a clever neural code that we cannot decipher yet is an open question in neuroscience (see Chapter 7 in Gerstner et al., 2014; Boerlin et al., 2013; Koren and Denève, 2017).

Weights of encoding and decoding models are nevertheless expected to differ due to correlations between neurons. For example, if the activity of neurons 1 and 2 has a strong positive correlation with the class A, and these two neurons are also positively correlated, only one of the two neurons might have a large positive weight, while the other neuron might have a small weight. Even though correlations in cortical networks are typically weak to moderate, they are often significant (Cohen and Kohn, 2011) and are likely to influence the weights.

In Koren et al., 2020a, we have shown extensive evidence of how decoding weights are useful to study the structure of correlations in our particular dataset. However, the relation between decoding weights and correlations is not true in general. A likely explanation for the sign of decoding weight being informative about the structure of noise correlations in Koren et al., 2020a is a top-down input that drives patterns of spike counts as well as noise correlations. A correlated top-down input can simultaneously drive changes in firing patterns from one trial to another, and influence noise correlations (Bondy et al., 2018). Such a correlated top-down input that specifically targets neurons with positive weights in trials with the stimulus class “match” (decision “same”) and neurons with negative weights in trials with the stimulus class “non-match” (decision “different”) can explain why decoding weights and noise correlations in our dataset are inter-related.

Weights of a decoding model reflect the influence of single neurons for the classification task and are not meant to describe a generative model of neural activity. The relation between decoding and encoding weights is an interesting question that, however, goes beyond the scope of the present protocol. Briefly, the relation between encoding and decoding weights can be addressed in several ways. If we are interested in a generative model of the data, we can turn the backward model into a forward model (Haufe et al., 2014). Furthermore, the effect of correlations on a decoding model can be studied by comparing weights of the regular model with weights of a correlation-free model (see Part 6). Finally, we might be interested in how single neurons alone predict the classes, without taking into account their covariance. In this case, we could use methods of univariate analysis of neural activity, such as the Receiver-Operating Curve (ROC) analysis (Britten et al., 1992).

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Veronika Koren (koren@math.tu-berlin.de).

Materials availability

This study did not generate new unique reagents.

Data and code availability

The code generated during this study is available in a public repository https://github.com/VeronikaKoren/struct_pop_public