Combining data assimilation and machine learning to build data‐driven models for unknown long time dynamics—Applications in cardiovascular modeling

Abstract

We propose a method to discover differential equations describing the long‐term dynamics of phenomena featuring a multiscale behavior in time, starting from measurements taken at the fast‐scale. Our methodology is based on a synergetic combination of data assimilation (DA), used to estimate the parameters associated with the known fast‐scale dynamics, and machine learning (ML), used to infer the laws underlying the slow‐scale dynamics. Specifically, by exploiting the scale separation between the fast and the slow dynamics, we propose a decoupling of time scales that allows to drastically lower the computational burden. Then, we propose a ML algorithm that learns a parametric mathematical model from a collection of time series coming from the phenomenon to be modeled. Moreover, we study the interpretability of the data‐driven models obtained within the black‐box learning framework proposed in this paper. In particular, we show that every model can be rewritten in infinitely many different equivalent ways, thus making intrinsically ill‐posed the problem of learning a parametric differential equation starting from time series. Hence, we propose a strategy that allows to select a unique representative model in each equivalence class, thus enhancing the interpretability of the results. We demonstrate the effectiveness and noise‐robustness of the proposed methods through several test cases, in which we reconstruct several differential models starting from time series generated through the models themselves. Finally, we show the results obtained for a test case in the cardiovascular modeling context, which sheds light on a promising field of application of the proposed methods.

We propose a method to discover differential equations describing the long‐term dynamics of phenomena featuring a multiscale behavior in time, starting from measurements taken at the fast‐scale. Our methodology is based on a synergetic combination of data assimilation, used to estimate the parameters associated with the known fast‐scale dynamics, and machine learning, used to infer the laws underlying the slow‐scale dynamics. By exploiting the scale separation between the fast and the slow dynamics, we propose a decoupling of time scales that allows to drastically lower the computational burden.

1. INTRODUCTION

Mathematical models are built upon two types of sources, namely a priori information (physics principles, simplifying assumptions, empirical laws, etc.) and experimental data. The relative weight of the two sources should be properly balanced: the fewer data are available, the stronger a priori assumptions are needed. By moving towards the Big Data era, mathematical models are fed with more and more data, reducing the necessity of strong a priori assumptions. The asymptote of this process is data‐driven modeling, that is to say the construction of a mathematical model for a given phenomenon solely on the basis of experimental data, as opposed to physics‐based modeling, that on the other hand makes use of data only to tune the parameters appearing in equations written on the basis of a detailed study of the phenomenon by the modeler. Between pure physics or pure data, hybrid approaches allow to circumvent the uncertainties inherent to physics‐based models by making full use of the data available on the system. This is particularly the case when developing estimation strategies of dynamical models,¹, ² with a particular concern in identification—that is, parameter estimation—of such systems.³, ⁴, ⁵, ⁶ Note that these strategies are also known as data assimilation (DA) approaches in the engineering community since their introduction in environmental sciences in the late 70s.⁷

Data‐driven modeling appears particularly advantageous when traditional modeling encounters limitations. A representative case is given by systems whose behavior is well understood and accurately modeled, but for which the model parameters themselves feature a long‐term evolution that is difficult to predict because the underlying mechanisms are not fully elucidated. This motivates the idea of resorting to a data‐driven approach to apprehend the slow‐scale parameter evolution, while still relying on the mathematical model at the fast scale. This is the specific focus of this paper. Examples are given by the long‐term remodeling of biological systems and by the development of diseases under the influence of factors such as lifestyle or environmental conditions that are hardly within reach of mathematical modeling. In Section 1.3 we consider an example model inspired by the development of hypertension.

Data‐driven modeling poses the problem of finding the laws governing the evolution of a given phenomenon (a natural phenomenon, an engineering process, a system of agents, etc.) starting from its observation. Here comes the challenge of leveraging the information contained in large amounts of data to extract knowledge, by finding the principles hidden in data.

In the past few years, several algorithms have been proposed to automate the process—historically a human prerogative—of discovering the laws hidden in experimental data. In this paper we consider data‐driven modeling of time‐dependent phenomena. With respect to most machine learning (ML) techniques that are designed to learn the steady‐state relationship between two quantities, the introduction of the time variable dramatically increases the complexity of the problem since the object to be learned is not a function, but, typically, a differential equation.

1.1. Learning time‐dependent models from data

Data‐driven algorithms capable of building black‐box time‐dependent models have been developed with the two following goals:

• Data‐driven modeling: in this case data come from experimental measurements of a given phenomenon that one wants to understand and possibly predict (this is the case considered in this paper).

• Data‐driven model order reduction (MOR): in this case data are generated by an high‐fidelity model and the goal is to obtain a different model (hopefully with fewer variables and with a lower computational complexity) reproducing—up to some error—the same input–output map.⁸, ⁹, ¹⁰, ¹¹

In most cases, the algorithms developed for one goal are also suited for the other one. Hence, in this section, we review the algorithms proposed in the literature for either goal.

Symbolic regression¹², ¹³, ¹⁴ is a technique to find a model, written as a differential equation in symbolic form, by means of an iterative process consisting in the generation of candidate symbolic differential equations and in the selection of the best ones.

In Peherstorfer et al.¹⁵ the authors propose a data‐driven MOR technique for systems with linear state dependence, based on the idea of inferring the frequency‐domain response of the linear system from a collection of trajectories and to apply the Loewner framework¹⁶ to interpolate the transfer function measurements at a collection of interpolation points.

Sparse Identification of Nonlinear Dynamics (SINDy, see Brunton et al¹⁷) is an algorithm that infers a dynamical system from a collection of measurements on the system—the state, the time derivative of the state and the input at different times—under the assumption that the right‐hand side of the model depends on a few combination of predetermined functions of the input and the state (linear combinations, products and trigonometric functions). In Costello and Martin¹⁸ a similar ML technique is employed to predict metabolic pathway dynamics from time series multiomics data. In Wang et al.¹⁹ a nonlinear differential equation is learned from data, by assuming a polynomial form with sparse coefficients by compressive sensing. In Bocquet et al.²⁰ the authors proposed a method to infer an ODE (ordinary differential equation) representation of a model from time‐dependent output data. The right‐hand side of the ODE is represented as a linear combination of multivariate polynomials of (at most) quadratic order in each state variable.

In Daniels and Nemenman²¹ an S‐system (a class of models inspired by the mass‐action kinetics) is trained by Bayesian model selection to learn a time‐dependent dynamics.

Dynamic mapping Kriging (DMK, see Hernandez and Gallivan²²) is an extension to the time‐dependent case of Kriging²³ or Gaussian process (GP) regression.²⁴, ²⁵ Kriging is a regression method that uses a GP, with a covariance function dependent on hyper‐parameters to be tuned from data, as prior for the outcome of a function. DMK consists in performing Kriging on a difference equation, where the independent variables are the state and the input of a system at the current time step, and the dependent variable is the state at the next time step.

In Regazzoni et al.²⁶ a technique based on artificial neural networks (ANNs) to learn a time‐dependent differential equation from a collection of input–output pairs has been proposed. The authors also provided a universal approximation result stating that these ANN models can approximate any time‐dependent model with arbitrary accuracy. In Regazzoni et al.²⁷ this method has been extended by informing the learning machine with some a priori knowledge on the system to learn, moving from a purely black‐box framework to a semi‐physical (or gray‐box) one. A similar ANN model is proposed in Chen et al.,²⁸ where an efficient algorithm for sensitivities computation is discussed.

Learning algorithms for data‐driven discovery of PDEs, either based on ANNs (see, e.g., Raissi et al.²⁹, ³⁰, ³¹) or GP³², ³³ have been proposed. Those methods require the knowledge of the form of the equations and are thus better suited for the identification of parameters. In Raissi et al.³⁴ the authors proposed an ANN‐based algorithm to discover nonlinear time‐dependent models from a collection of snapshots of the state of the system, by minimizing the residual of some given multi‐step time‐stepping scheme. In Zhu et al.³⁵ the authors proposed an ANN‐based method to build a surrogate model, using the physical knowledge as a constraint. In Tartakovsky et al.³⁶ the method of Raissi et al.³¹ has been applied to the identification of the constitutive relationship underlying a PDE, starting from snapshots of the solution.

1.2. Accounting for inter‐individual variability

The above mentioned methods seek a unique model capable of describing the evolution of some quantities, based on a training set composed of observed trajectories. In many applications, however, each trajectory is referred to a different individual of some group (e.g., human beings). Since each individual is different, one should thus look for a family of models, rather than a unique model; or, from another perspective, for a single model dependent on some parameters, accounting for inter‐individual variability.

Whereas parametric models are widely used in traditional physics‐based modeling, the introduction of parameters raises conceptual difficulties when dealing with data‐driven modeling since, in a black‐box framework, parameters cannot be measured. Moreover, assuming that the learning algorithm is capable of assigning to each training individual a parameter value, then the problem of interpretability comes into play. What is the physical meaning of such learned parameters? The lack of interpretability also hampers the use of the learned models for predictive purposes since, without a clear physical meaning of the parameters, one cannot easily determine the parameters associated with an individual not included in the training set.

In this paper we show how a wise interplay between ML and DA techniques can help to deal with those issues. We define in such a way a framework to perform data‐driven modeling of phenomena featuring inter‐individual variability, without renouncing to interpretability and predictivity of the learned model.

1.3. A motivating example: arterial network remodeling

To motivate the approach and to help fix the ideas with the notation, we provide in this section an example that can be treated with the framework proposed in this paper. In Section 3.4 we consider again this example, by showing some numerical results. Specifically, we consider the slow development of diseases related to the remodeling of the arterial network (such as hypertension). Even if the dynamics at the fast scale (order of seconds) of the circulation of blood through the network has been deeply studied and relatively well understood (different mathematical models, from lumped‐parameters models³⁷ to complex three‐dimensional fluid–structure interaction models³⁸, ³⁹ are available), the mechanisms driving the long‐term evolution of the arterial network are not fully elucidated. Indeed, in spite of some important steps towards the understanding of the determinants of vascular remodeling,⁴⁰, ⁴¹ a comprehensive mathematical model capable of predicting the development and evolution of this phenomenon is still missing.

For the sake of simplicity, we consider a simple model to describe the evolution in the fast‐scale dynamics, namely the two‐stage Windkessel model (see Figure 1), which reads³⁷

$$\left\{\begin{array}{ll}\frac{\mathrm{d}}{\mathrm{d}t}{P}_{\mathrm{p}}\left(t\right)=\frac{P_{\mathrm{d}}\left(t\right)-P_{\mathrm{p}}\left(t\right)}{R_{\mathrm{p}}{C}_{\mathrm{p}}}+\frac{Q\left(t\right)}{C_{\mathrm{p}}}& t\in \left(0,T\right],\\ \frac{\mathrm{d}}{\mathrm{d}t}{P}_{\mathrm{d}}\left(t\right)=\frac{P_{\mathrm{p}}\left(t\right)-P_{\mathrm{d}}\left(t\right)}{R_{\mathrm{p}}{C}_{\mathrm{d}}}+\frac{P_{\mathrm{vs}}-P_{\mathrm{d}}\left(t\right)}{R_{\mathrm{d}}{C}_{\mathrm{d}}}& t\in \left(0,T\right],\\ P_{\mathrm{p}}\left(0\right)=P_{\mathrm{p},0},& \\ P_{\mathrm{d}}\left(0\right)=P_{\mathrm{d},0},& \end{array}\right.$$ (1)

where we denote by x(t) = (P _p(t), P _d(t)) the state of the model, given by the proximal and distal pressures; we denote the parameters of the fast‐scale model by θ = (R _p, C _p, R _d, C _d), respectively, the proximal and distal resistance and compliance; Q(t) is the blood flux. We suppose then to be able to measure the proximal pressure at a collection of time instants (t ₁, …, t _K) and we collect all the measurements into the observation vector z = (P _p(t ₁), …, P _p(t _K)).

FIGURE 1.

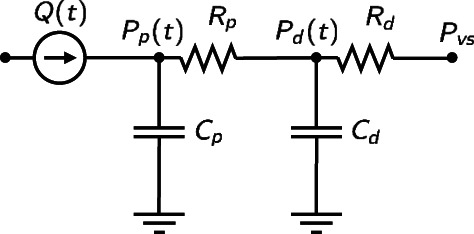
Visual representation of the two‐stage Windkessel model of Equation (1). In this electrical analogy, current represents blood flux, while voltage represents blood pressure. The heart is represented as a current generator, while the arterial network comprises dissipative and compliant elements, represented by resistances and capacitors, respectively

When considering the fast time scale (i.e., the typical time scale of a heartbeat), the value of θ, describing the properties of the arterial network, is fixed. However, if we consider a longer time scale (days and above), θ may evolve, possibly associated with some disease. For instance, hypertension is linked to an increase of the arterial resistance R _d, which requires a higher systolic pressure to preserve the cardiac output. We thus introduce a slow time variable τ and we write θ(τ), assuming that the fast‐scale parameters are in fact functions of the slow‐scale time variable.

We consider the following scenario. Suppose that we have a set of N _P patients, periodically monitored over the long‐term horizon at times $\left({\tau }_1<{\tau }_2<\dots <{\tau }_{N_S}\right)$. At each time τ _j (for j = 1, …, N _S), the arterial pressure of the i‐th patient (for i = 1, …, N _P) is measured for a few seconds, collecting the observation vector $z_j^i$. More precisely, we denote the measured observation vector by ${\tilde{z}}_j^i=z_j^i+{\chi }_j^i$, where ${\chi }_j^i$ is the measurement error. The measurement ${\tilde{z}}_j^i$ reflects the value of the fast‐scale parameters of the i‐th patient at the slow‐scale time τ _j, which we define as ${\theta }_j^i≔{\theta }^i\left({\tau }_j\right)$, where θ ⁱ(τ) denotes the slowly evolving i‐th patient's parameters of the fast‐scale model.

The goal is to learn a model for the slow‐scale evolution of θ(τ) from the collection of noisy measurements ${\left\{{\tilde{z}}_j^i\right\}}_{j=1,\dots ,N_S}^{i=1,\dots ,N_P}$. As mentioned before, all patients are different, and thus inter‐individual variability must be taken into account.

1.4. Paper outline

The paper is organized as follows. In Section 2, we state in mathematical terms the problem that we deal with in this paper and we introduce the associated notation. Then, we present the methods that we propose to solve such a problem, based on a decoupling of the time scales. In Section 3, we show the effectiveness and the noise‐robustness of the proposed methods by means of several numerical test cases. Finally, in Section 4, we critically discuss the results obtained and we draw our conclusions.

2. PROBLEM STATEMENT AND PROPOSED METHODS

In this section, motivated by the example of Section 1.3, we state the setting of the problem that we consider in this paper, in which the example of Section 1.3 can be recast, before introducing and analyzing our proposed methods.

We consider a collection of N _P individuals, such that the i‐th individual is associated with ${\theta }^i\left(\tau \right)\in \mathcal{P}\subset {\mathrm{ℝ}}^{N_{\theta }}$, which evolves with a slow dynamics driven by an equation of the form

$$\left\{\begin{array}{l}\frac{\mathrm{d}}{\mathrm{d}\tau }{\theta }^i\left(\tau \right)=g\left({\theta }^i\left(\tau \right),{\alpha }^i\right)\tau \in \left(0,\mathcal{T}\right],\\ {\theta }^i\left(0\right)={\theta }_0^i,\end{array}\right.$$ (2)

where ${\alpha }^i\in \mathcal{A}\subset {\mathrm{ℝ}}^{N_{\alpha }}$ are parameters characterizing the i‐th individual at the slow‐scale, accounting for inter‐individual variability. In this paper, we always assume that

$$g\in \mathcal{G}≔\left\{g\in {\mathcal{C}}^0\left({\mathrm{ℝ}}^{N_{\theta }\times N_{\alpha }};{\mathrm{ℝ}}^{N_{\theta }}\right),\text{Lipschitz continuous in}\theta \right\},$$

so that the models admit a unique solution for each initial state and parameter.

This slow‐scale model is coupled with a fast‐scale dynamics, for which θ ⁱ(τ) can be considered as a constant. Specifically, we consider a collection of times $\left({\tau }_1<{\tau }_2<\dots <{\tau }_{N_S}\right)$ over the long‐term horizon, and we write ${\theta }_j^i≔{\theta }^i\left({\tau }_j\right)$, for j = 1, …, N _S and i = 1, …, N _P. We consider a model for the fast‐scale dynamics with the following form

$$\left\{\begin{array}{l}\frac{\mathrm{d}}{\mathrm{d}t}{x}_j^i\left(t\right)=f\left(x_j^i\left(t\right),{\theta }_j^i,t\right)t\in \left(0,T\right),\\ x_j^i\left(0\right)=x_{j,0}^i,\end{array}\right.$$ (3)

where $x_j^i\left(t\right)\in \mathcal{X}\subset {\mathrm{ℝ}}^{N_x}$ is the fast‐scale state. We recall that ${\theta }_j^i$ are considered as constant parameters at this scale (we assume T ≪ τ _j − τ _j − 1). On this system, we consider an observation process given at the fast scale, namely

$$z_j^i={\int }_0^{T}h\left(x_j^i,t\right)\mathrm{d}t,$$ (4)

where $z_j^i\in \mathcal{Z}\subset {\mathrm{ℝ}}^{N_z}$ and we define the measured observations as ${\tilde{z}}_j^i=z_j^i+{\chi }_j^i$, where ${\chi }_j^i\sim \mathcal{N}\left(0,W\right)$ are the measurement errors that we assume to be i.i.d. and Gaussian with covariance matrix W. In the example of Section 1.3, the observation vector contains direct measurements of the first entry of the state x at a collection of discrete times t _k, for k = 1, …, K. This can be written in the form of Equation (4) by defining the observation map as $h\left(x,t\right)≔{\sum }_{k=1}^{K}x\cdot e_1\delta \left(t-t_k\right)e_k$, where e _k denotes the k‐th element of the canonical basis of ℝⁿ and where δ denotes the Dirac delta function (in fact, given a function f(t), we have ${\int }_0^{T}f\left(t\right)\delta \left(t-t_k\right)\mathrm{d}t=f\left(t_k\right)$).

We assume that we have perfect knowledge about the equation driving the fast‐scale evolution and that we want to identify a model to describe the slow‐scale evolution. Specifically, we assume that we know:

(K1): f, h: the fast‐scale evolution and observation laws.

(K2): ${\left\{{\tilde{z}}_j^i\right\}}_{j=1,\dots ,N_S}^{i=1,\dots ,N_P}$: the fast‐scale measurements.

Whereas we do not know:

(U1): g: the slow‐scale evolution law.

(U2): ${\left\{{\alpha }^i\right\}}^{i=1,\dots ,N_P}$: the slow‐scale parameters of individuals.

(U3): ${\left\{{\theta }_0^i\right\}}^{i=1,\dots ,N_P}$: the slow‐scale initial states of individuals, for which we assume a prior distribution $\mathcal{N}\left(\overline{\theta },{\mathrm{\Pi }}_{\theta }\right)$.

(U4): ${\left\{x_{j,0}^i\right\}}_{j=1,\dots ,N_S}^{i=1,\dots ,N_P}$: the fast‐scale initial states of individuals, for which we assume a prior distribution $\mathcal{N}\left(\overline{x},{\mathrm{\Pi }}_x\right)$.

The goal is to identify the unknown objects (U1)–(U4) from the known ones (K1)–(K2). We notice that this task is situated in an intermediate position between the fields of DA, as we here seek to identify the parameters and the state for a known dynamics, and ML, as we seek to discover the law driving the slow‐scale (unknown) dynamics. We remark that the setting considered in this paper differs from that of a standard parameters identification problem, in which one aims to identify unknown parameters of a known model from time series data (see, e.g., Yu et al.³, ⁴, ⁴²), for two main reasons. First, the observations ${\tilde{z}}_j^i$ are taken at the fast‐scale, while we are interested in inferring knowledge at the slow‐scale. Secondly, we assume that we are agnostic of the model whose parameters we aim to identify. As a matter of fact, we aim at simultaneously learning the parameters α ⁱ and the differential Equation (2).

2.1. General strategy

In this paper we propose to combine ML and DA concepts in order to address the problem presented above. Specifically, concerning the task of learning the law g given the measurements ${\left\{{\tilde{z}}_j^i\right\}}_{j=1,\dots ,N_S}^{i=1,\dots ,N_P}$, we extend the strategy proposed in Regazzoni et al.²⁶ Hence, we select a set of candidate laws ${\mathcal{G}}_n$ (where n indicates that the set is parameterized by a finite number of parameters), such that ${\mathcal{G}}_n\subset \mathcal{G}$, and we look for the model, inside the family ${\mathcal{G}}_n$, that best fits the available data. This can be interpreted, by assuming Gaussian distribution of the measurement errors, as the maximum‐likelihood estimation of the evolution law g inside the family ${\mathcal{G}}_n$. This formalism allows to write the problem of identifying/learning the objects (U1)–(U4) in a unified minimization framework, as we show in the next section.

2.1.1. A unified minimization framework

The maximum likelihood estimation of the unknown objects is found by minimizing the negative log‐likelihood

$$\left(\widehat{g},{\left\{{\widehat{\alpha }}^i\right\}}^i,{\left\{{\widehat{\theta }}_0^i\right\}}^i,{\left\{{\widehat{x}}_{j,0}^i\right\}}_j^i\right)=\underset{\begin{array}{c}g\in {\mathcal{G}}_n\\ {\left\{{\alpha }^i\right\}}^i\in {\mathcal{A}}^{N_P}\\ {\left\{{\theta }_0^i\right\}}^i\in {\mathcal{P}}^{N_P}\\ {\left\{x_{j,0}^i\right\}}_j^i\in {\mathcal{X}}^{N_P{N}_S}\end{array}}{\text{argmin}}=\sum _{i=1}^{N_P}\left(\sum _{j=1}^{N_S}\left(\frac{1}{2}{\left|z_j^i-{\tilde{z}}_j^i\right|}_{W^{-1}}^2+\frac{1}{2}{\left|x_{j,0}^i-\overline{x}\right|}_{{\Pi }_x^{-1}}^2\right)+\frac{1}{2}{\left|{\theta }_0^i-\overline{\theta }\right|}_{{\Pi }_{\theta }^{-1}}^2\right),$$ (5)

such that (2), (3) and (4) hold true. Here and in what follows, given a vector w ∈ ℝⁿ and a symmetric positive‐definite matrix Q ∈ ℝ^n × n , we denote by |w|_Q ≔ (w ^T Qw)^1/2 the energy norm. Moreover, for the sake of brevity, we denote by ${\left\{\cdot \right\}}_j^i$ and {⋅}ⁱ sets indexed by j = 1, …, N _S and i = 1, …, N _P, where the values taken by the indexes j and i are left implicit.

Problem (5) can be interpreted as that of finding the slow‐scale law, the slow‐scale parameter for each individual, and the initial state at both scales such that the resulting outputs $z_j^i$ best approximate the measured outputs ${\tilde{z}}_j^i$. The last two terms of the loss functional can be regarded as regularization terms.

2.1.2. Decoupling the two scales

Despite its solid foundation, the solution of Problem (5) may be unaffordable in practice, because of the huge number of differential equations that serve as constraints for the minimization problem. Indeed, Problem (5) is constrained by the N _P slow‐scale differential Equations (2) and the N _P × N _S differential Equations (3). Moreover, Problem (5) attempts to simultaneously identify objects related to both the slow scale and the fast scale for each j = 1, …, N _S and i = 1, …, N _P.

To lower the complexity of Problem (5), we propose to exploit the scale separation between the fast and the slow dynamics, and to split the problem into two steps:

(P1): The first step consists in finding an estimate for ${\theta }_j^i$, for each j = 1, …, N _S and i = 1, …, N _P, on the basis of the measurements ${\tilde{z}}_j^i$, by solving the problem

$$\left({\widehat{\theta }}_j^i,{\widehat{x}}_{j,0}^i\right)=\underset{\begin{array}{c}{\theta }_j^i\in \mathcal{P}\\ x_{j,0}^i\in \mathcal{X}\end{array}}{\text{argmin}}\left(\frac{1}{2}{\left|z_j^i-{\tilde{z}}_j^i\right|}_{W^{-1}}^2+\frac{1}{2}{\left|x_{j,0}^i-\overline{x}\right|}_{{\Pi }_x^{-1}}^2+\frac{1}{2}{\left|{\theta }_j^i-\overline{\theta }\right|}_{{\Pi }_{\theta }^{-1}}^2\right),$$ (6)

such that (3) and (4) hold true.

(P2): Once the estimates ${\left\{{\widehat{\theta }}_j^i\right\}}_{j=1,\dots ,N_S}^{i=1,\dots ,N_P}$ are available, we consider the problem

$$\left(\widehat{g},{\left\{{\widehat{\alpha }}^i\right\}}^i,{\left\{{\widehat{\theta }}_0^i\right\}}^i\right)=\underset{\begin{array}{c}g\in {\mathcal{G}}_n\\ {\left\{{\alpha }^i\right\}}^i\in {\mathcal{A}}^{N_P}\\ {\left\{{\theta }_0^i\right\}}^i\in {\mathcal{P}}^{N_P}\end{array}}{\text{argmin}}\sum _{i=1}^{N_P}\sum _{j=1}^{N_S}\frac{1}{2}{\left|{\theta }^i\left({\tau }_j\right)-{\widehat{\theta }}_j^i\right|}_{{\Pi }_{\theta }^{-1}}^2,$$ (7)

such that (2) holds true.

We notice that (P1) involves only the fast‐scale dynamics, whereas (P2) only the slow‐dynamics. Indeed, the two scales have been decoupled. As a consequence, in (P1), each individual and each slow‐scale instant τ _j can be treated separately; the problem can be solved for each j = 1, …, N _S and i = 1, …, N _P independently of each other. This allows for a possibly parallel solution of (P1). Moreover, differently from Problem (5), in Problems (P1) and (P2) objects related to the fast and slow scales are never simultaneously identified. In other words, the complex Problem (5) has been split into (N _P  N _S + 1) simpler problems.

A further effect of splitting Problem (5) into two steps, is that Problems (P1) and (P2) feature different natures. While the former is a purely DA problem, as it consists in the identification of the state and the parameters for System (3), the latter is a learning problem, as the laws governing the slow‐scale dynamics need to be discovered. This is a consequence of the decoupling between the fast‐scale, driven by a known dynamics, from the slow‐scale, whose dynamics is governed by unknown laws.

Several identifications procedures are available in the literature for the solution of problems written in the form of (P1) (see, e.g., Yu et al.³, ⁴, ⁵, ⁶). In this paper, we restrict our scope to measurements sampled in time, instead of continuous signals, and we consider a state and parameter sequential estimation strategy², ⁶, ⁴³ based on the extended Kalman filter (EKF), an extension of the Kalman filter (KF) algorithm to nonlinear systems, performed at each step, of Equation (3).⁷, ⁴³ We recall that whereas KF is equivalent to least square estimation for linear dynamics, EKF only gives an approximation of the least square estimation (P1) with, however, the benefit of being “on the fly.” This is particularly adapted to the fast‐scale dynamics where we can typically face real‐time monitoring constraints.

2.1.3. Interpretation of the learned model

Before presenting an algorithm for the solution of Problem (P2) (which is treated in Section 2.2), we deal with the problem of interpreting the solution of Problem (P2) itself. This is instrumental to the presentation of the proposed methods. Therefore, in this section we assume the existence of an algorithm capable of solving Problem (P2) and we speculate about the interpretation of its solution. Solving Problem (P2) serves indeed different purposes, which we list in what follows.

Understanding

First, the function $\widehat{g}$ provides insight into the phenomenon under exam. Indeed, $\widehat{g}$ yields a description of the underlying laws written in mathematical terms and as such it can provide understanding of the phenomenology. Moreover, an analysis of the features of the function $\widehat{g}$ may reveal properties such as states of equilibrium, symmetry properties and relationships among the variables that may not be immediately identifiable from the observation of the experimental data.

Classification of training individuals

By solving Problem (P2), a (possibly vector‐valued) parameter ${\widehat{\alpha }}^i$ is assigned to each individual. However, the physical meaning of such parameters is not clear, as they are learned in a black‐box manner. Moreover, the value of such parameters in the solution of Problem (P2) is not unique: given a solution of Problem (P2), one can always find an equivalent solution with different values of the parameters (we will deal extensively with this issue in Section 2.3).

Nonetheless, even if we cannot interpret such parameters in physical terms, we know that they characterize the variability among the individuals. Indeed, one may be tempted to conclude that similar parameters reveal similarities among individuals (that is to say, if ${\widehat{\alpha }}^i\simeq {\widehat{\alpha }}^k$, then the i‐th and the k‐th individuals are similar). In Section 2.3 we will show under which conditions this conclusion is licit. In that case, the learned parameters ${\left\{{\widehat{\alpha }}^i\right\}}^i$ allow to classify the individuals.

For instance, in the example of Section 1.3, the parameter α may describe how the arterial network of a given patient remodels in time, and thus it can be regarded as an indication of the severity of related pathologies.

Predictions

The ultimate aim of mathematical models is making predictions. However, the lack of physical meaning of the parameter α apparently undermines this possibility for the learned model $\widehat{g}$. In fact, let us consider a new individual (i.e. not employed to train the model), which we denote as the (N _P + 1) − th individual; to solve Problem (P2) with the learned model $\widehat{g}$, in order to predict the evolution of ${\theta }^{N_P+1}\left(\tau \right)$, one needs to know ${\alpha }^{N_P+1}$. However, unlike the parameters of physics‐based models that, having a physical meaning, can be measured in practice, the parameters of data‐driven models cannot be measured.

This inconvenience can be overcome by combining once again ML with DA (the latter acting this time at the slow‐scale). All we need is to observe the (N _P + 1) − th individual for a (short) interval of time, on the slow‐scale, $\tau \in \left[0,{\mathcal{T}}^{\mathrm{obs}}\right]$, with ${\mathcal{T}}^{\mathrm{obs}}<\mathcal{T}$. During this observation time interval, we collect the observations ${\tilde{z}}_j^{N_P+1}$, associated with the slow‐scale time instants $0={\tau }_1<{\tau }_2<\dots {\tau }_{N_S^{\mathrm{obs}}}={\mathcal{T}}^{\mathrm{obs}}$, and we find the estimates, by solving (P1), for the associated fast‐scale parameters ${\widehat{\theta }}_j^{N_P+1}$. Then, by the slow‐scale evolution of such parameters, we estimate the value of ${\widehat{\alpha }}^{N_P+1}$, by solving the following DA problem

$$\left({\widehat{\alpha }}^{N_P+1},{\widehat{\theta }}_0^{N_P+1}\right)=\underset{\begin{array}{c}{\alpha }^{N_P+1}\in \mathcal{A}\\ {\theta }_0^{N_P+1}\in \mathcal{P}\end{array}}{\text{argmin}}\left(\sum _{j=1}^{N_S^{\mathrm{obs}}}\frac{1}{2}{\left|{\theta }^{N_P+1}\left({\tau }_j\right)-{\widehat{\theta }}_j^{N_P+1}\right|}_{U^{-1}}^2+\frac{1}{2}{\left|{\theta }_0^{N_P+1}-\overline{\theta }\right|}_{{\mathrm{\Pi }}_{\theta }^{-1}}^2+\frac{1}{2}{\left|{\alpha }^{N_P+1}-\overline{\alpha }\right|}_{{\mathrm{\Pi }}_{\alpha }^{-1}}^2\right),$$ (8)

subject to the constraint

$$\left\{\begin{array}{l}\frac{\mathrm{d}}{\mathrm{d}\tau }{\theta }^{N_P+1}\left(\tau \right)=\widehat{g}\left({\theta }^{N_P+1}\left(\tau \right),{\alpha }^{N_P+1}\right),\tau \in \left(0,{\mathcal{T}}^{\mathrm{obs}}\right]\\ {\theta }^{N_P+1}\left(0\right)={\theta }_0^{N_P+1}.\end{array}\right.$$ (9)

In Equation (8), U denotes the covariance matrix associated with the error introduced during the resolution of the DA Problem (P1). We remark that U can be estimated whenever Problem (P1) is solved, for example, by an algorithm of the Kalman Filter family. Alternatively, assuming that the error introduced by the DA algorithm can be considered as a white noise of magnitude $\sigma \frac{\mathit{dB}\left(\tau \right)}{\mathit{d\tau }}$ (B(τ) being a Wiener process), we set U = σ ²/Δτ I, where I is the N _θ × N _θ identity matrix. On the other hand, $\overline{\alpha }$ and Π _α respectively denote the expected value and the covariance matrix associated with the slow‐scale parameter α, estimated from the parameters ${\left\{{\alpha }^i\right\}}^{i=1,\dots ,N_P}$ learned during the step (P2). Specifically, we set $\overline{\alpha }$ equal to the arithmetic mean of these parameters and Π _α equal to their sample covariance.

We can finally employ the estimated slow‐scale parameter ${\widehat{\alpha }}^{N_P+1}$ to predict the evolution of ${\theta }^{N_P+1}\left(\tau \right)$ in the time interval $\left({\mathcal{T}}^{\mathrm{obs}},\mathcal{T}\right]$, by solving

$$\left\{\begin{array}{l}\frac{\mathrm{d}}{\mathrm{d}\tau }{\widehat{\theta }}^{N_P+1}\left(\tau \right)=\widehat{g}\left({\theta }^{N_P+1}\left(\tau \right),{\widehat{\alpha }}^{N_P+1}\right),\tau \in \left({\mathcal{T}}^{\mathrm{obs}},\mathcal{T}\right]\\ {\widehat{\theta }}^{N_P+1}\left({\mathcal{T}}^{\mathrm{obs}}\right)={\widehat{\theta }}_{N_S^{\mathrm{obs}}}^{N_P+1}.\end{array}\right.$$ (10)

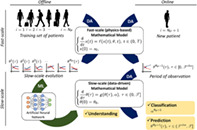
To summarize, in a preliminary offline phase, we learn Model (2) from the observation of a set of training individuals, by combining DA at the fast‐scale with ML at the slow‐scale. Then, in the online phase, we employ DA on both the fast‐scale and, for a short interval, on the slow‐scale $\left[0,{\mathcal{T}}^{\mathrm{obs}}\right]$ to characterize the features of a new individual, so that the previously learned model can be used to predict the evolution of this individual. The interplay that takes place, at different levels, between DA and ML is summarized in Figure 2.

FIGURE 2.

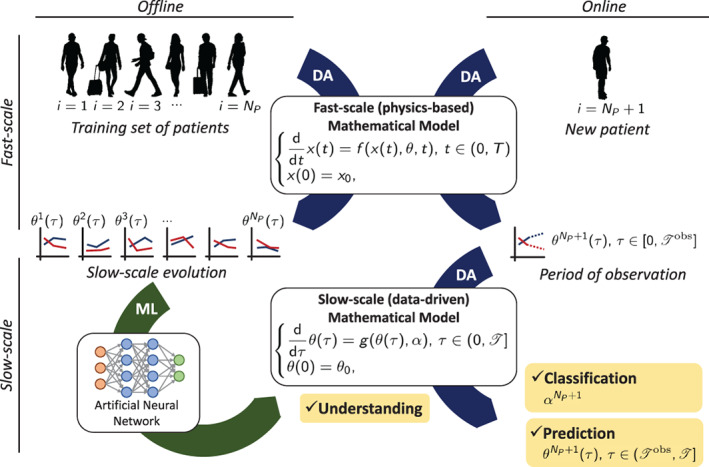
Interplay between ML (green arrow) and DA (blue arrows)

2.2. Learning a differential equation from data

In this section we present an algorithm to numerically solve Problem (P2). The algorithm presented in this paper represents an extension of the algorithm presented in Regazzoni et al.,²⁶ whose goal is learning a (possibly parametric) time‐dependent differential equation from a collection of input–output time‐series. However, in Regazzoni et al.,²⁶ the parameters associated with the training data are assumed to be known, while in this paper we need to learn them simultaneously to learning the model. The backbone of the algorithm proposed in this paper is based on that presented in Regazzoni et al.²⁶ Therefore we recall here the main ideas and we highlight the differences, while we refer to Regazzoni et al.²⁶ for the details common to both algorithms. The algorithm is based on a ANN‐based representation of the function g, which is trained by computing sensitivities through the adjoint method.⁴⁴ A similar approach is presented in Chen et al.²⁸ under the name of Neural ODEs, in which the state equation is discretized by means of a Runge–Kutta method.⁴⁵ Our algorithm represents a generalization of this method to some extent, as it learns a parametric differential equation with unknown parameters, rather than assuming that all the samples share the same dynamics.

2.2.1. Solution strategy

Following,²⁶ we parameterize g by a finite number of real parameters μ ∈ ℝⁿ and we define the set of candidate laws as ${\mathcal{G}}_n=\left\{\left(\theta ,\alpha \right)\mapsto g\left(\theta ,\alpha ;\mu \right):\mu \in {\mathrm{ℝ}}^n\right\}$. For the moment, we do not detail how this parameterization is performed, in order to not restrict ourselves to a specific case. To fix ideas, the reader can think of g as a polynomial in θ and α, where μ are the coefficients of the polynomial.

Problem (P2) can thus be rewritten as the following discrete constrained optimization problem

$$\left\{\begin{array}{ll}\underset{\begin{array}{c}\mu \in {\mathrm{ℝ}}^n\\ {\left\{{\alpha }^i\right\}}^i\in {\mathcal{A}}^{N_P}\\ {\left\{{\theta }_0^i\right\}}^i\in {\mathcal{P}}^{N_P}\end{array}}{\min }& \sum _{i=1}^{N_P}\sum _{j=1}^{N_S}\frac{1}{2}{\left|{\theta }^i\left({\tau }_j\right)-{\widehat{\theta }}_j^i\right|}_{{\mathrm{\Pi }}_{\theta }^{-1}}^2\\ \begin{array}{l}\mathrm{s}.\mathrm{t}.\\ \end{array}& \begin{array}{l}\frac{\mathrm{d}}{\mathrm{d}\tau }{\theta }^i\left(\tau \right)=g\left({\theta }^i\left(\tau \right),{\alpha }^i;\mu \right),\tau \in \left(0,\mathcal{T}\right],i=1,\dots ,N_P\\ {\theta }^i\left(0\right)={\theta }_0^i,i=1,\dots ,N_P,\end{array}\end{array}\right.$$ (11)

where ${\left\{{\widehat{\theta }}_j^i\right\}}_{j=1,\dots ,N_S}^{i=1,\dots ,N_P}$ are given. To derive the gradient of the cost functional $\mathcal{J}={\sum }_{i=1}^{N_P}{\sum }_{j=1}^{N_S}\frac{1}{2}{\left|{\theta }^i\left({\tau }_j\right)-{\widehat{\theta }}_j^i\right|}_{{\mathrm{\Pi }}_{\theta }^{-1}}^2$ under the constraint given by Equation (2), we introduce a family of Lagrange multipliers ${\sigma }^i\in {\mathcal{C}}^0\left(\left[0,\mathcal{T}\right];\mathcal{P}\right)$ and we write the Lagrangian associated with Problem (11).

$$\begin{array}{l}\mathrm{ℒ}\left(\mu ,{\left\{{\alpha }^i\right\}}^i,{\left\{{\theta }_0^i\right\}}^i,{\left\{{\theta }^i\right\}}^i,{\left\{{\sigma }^i\right\}}^i\right)\\ =\sum _{i=1}^{N_P}\sum _{j=1}^{N_S}\frac{1}{2}{\left|{\theta }^i\left({\tau }_j\right)-{\widehat{\theta }}_j^i\right|}_{{\mathrm{\Pi }}_{\theta }^{-1}}^2-\sum _{i=1}^{N_P}{\int }_0^{\mathcal{T}}\left(\frac{\mathrm{d}}{\mathrm{d}\tau }{\theta }^i\left(\tau \right)-g({\theta }^i\left(\tau \right),{\alpha }^i;\mu )\right)\cdot {\sigma }^i\left(\tau \right)\mathit{d\tau }-\sum _{i=1}^{N_P}\left({\theta }^i\left(0\right)-{\theta }_0^i\right)\cdot {\sigma }^i\left(0\right)\\ =\sum _{i=1}^{N_P}\sum _{j=1}^{N_S}\frac{1}{2}{\left|{\theta }^i\left({\tau }_j\right)-{\widehat{\theta }}_j^i\right|}_{{\mathrm{\Pi }}_{\theta }^{-1}}^2+\sum _{i=1}^{N_P}{\int }_0^{\mathcal{T}}{\theta }^i\left(\tau \right)\cdot \frac{\mathrm{d}}{\mathrm{d}\tau }{\sigma }^i\left(\tau \right)\mathit{d\tau }+\sum _{i=1}^{N_P}{\int }_0^{\mathcal{T}}g\left({\theta }^i\left(\tau \right),{\alpha }^i;\mu \right)\cdot {\sigma }^i\left(\tau \right)\mathit{d\tau }-\sum _{i=1}^{N_P}{\theta }^i\left(\mathcal{T}\right)\cdot {\sigma }^i\left(\mathcal{T}\right)+\sum _{i=1}^{N_P}{\theta }_0^i\cdot {\sigma }^i\left(0\right),\end{array}$$

where the last inequality is obtained by integrating by parts the time integral. By setting to zero the variation of the Lagrangian with respect to the variables {θ ⁱ}ⁱ we get the adjoint equations, valid for i = 1, …, N _P

$$\left\{\begin{array}{l}-\frac{\mathrm{d}}{\mathrm{d}\tau }{\sigma }^i\left(\tau \right)={\nabla }_{\theta }^{T}g\left({\theta }^i\left(\tau \right),{\alpha }^i;\mu \right)+\sum _{j=1}^{N_S}{\mathrm{\Pi }}_{\theta }^{-1}\left({\widehat{\theta }}_j^i-{\theta }^i\left(\tau \right)\right){\delta }_{{\tau }_j}\left(\tau \right),\tau \in \left[0,\mathcal{T}\right)\\ {\sigma }^i\left(\mathcal{T}\right)=0,\end{array}\right.$$ (12)

Finally, by computing the variation of the Lagrangian with respect to the design variables we get the gradient of the cost functional with respect to the design variables themselves

$${\nabla }_{\mu }\mathcal{J}=\sum _{i=1}^{N_P}\underset{0}{\overset{\mathcal{T}}{\int }}{\nabla }_{\mu }^{T}g\left({\theta }^i\left(\tau \right),{\alpha }^i;\mu \right){\sigma }^i\left(\tau \right)\mathit{d\tau };{\nabla }_{{\alpha }^i}\mathcal{J}=\underset{0}{\overset{\mathcal{T}}{\int }}{\nabla }_{\alpha }^{T}g\left({\theta }^i\left(\tau \right),{\alpha }^i;\mu \right){\sigma }^i\left(\tau \right)\mathit{d\tau };{\nabla }_{{\theta }_0^i}\mathcal{J}={\sigma }^i\left(0\right).$$ (13)

Given the gradient of the cost functional, any gradient‐based optimization (or training) algorithm can be used to find an approximate solution of Problem (11). To produce the results shown in this paper, we employed the Levenberg–Marquardt algorithm (see, e.g., Nocedal and Wright⁴⁶), which is specifically designed for least‐squares problems, coupled with a line‐search for the step length, as illustrated in Regazzoni et al.²⁶

Following,²⁶ we discretize the state equations in (11) by means of the Forward Euler scheme. The choice of an explicit scheme is aimed at lowering the computational cost of the training phase. To find the discrete version of the adjoint Equations (12), we write the Lagrangian associated with the fully discretized version of Problem (11) and we proceed as above (see Regazzoni et al.²⁶ for further details).

2.2.2. Choice of the space of candidate models

The only missing ingredient to define the algorithm for the numerical solution of Problem (P2) is the definition of the set of candidate laws ${\mathcal{G}}_n$. This choice is driven by the trade‐off between two different desired features: on the one hand, the space ${\mathcal{G}}_n$ should be rich enough to contain a law that can accurately explain the training data; on the other hand, a too rich space would lead to overfitting, that is to say the learned law would fit very accurately the training data, while featuring bad generalization properties in new cases (see Regazzoni et al.²⁶ for a detailed discussion on this topic).

A class of function approximators that accomplishes a good trade‐off between the accuracy in fitting data and the generalization capability is that of ANNs.⁴⁷ As a matter of fact, ANNs are universal approximators in several function spaces, including that of continuous functions (see, e.g., the density results contained in Cybenko⁴⁸, ⁴⁹, ⁵⁰). Moreover, ANNs provide an effective way of tuning the richness of the space ${\mathcal{G}}_n$ by suitably selecting the number of layers and of neurons.

Hence, we define ${\mathcal{G}}_n=\left\{\left(\theta ,\alpha \right)\mapsto g\left(\theta ,\alpha ;\mu \right):\mu \in {\mathrm{ℝ}}^n\right\}$ where g(θ, α; μ) denotes an ANN where the input is given by (θ, α) and μ ∈ ℝⁿ represents the vector of ANN parameters, that is, weights and biases.⁴⁷ The gradients ∇_θ g(θ, α; μ), ∇_α g(θ, α; μ) and ∇_μ g(θ, α; μ), needed in Equations (12) and (13), are computed through the backward‐propagation formulas, as given in Yegnanarayana.⁴⁷

2.3. Learning an interpretable slow‐scale dynamics

In Section 2.2 we have presented an algorithm for the solution of Problem (P2). In this section, we discuss the interpretation of the solution of such a problem. We recall that, as mentioned Section 2.1.3, the solution of Problem (P2) serves three different purposes, namely understanding the phenomenon though its mathematical description, classifying individuals and predicting the evolution of new (not yet observed) individuals. The discussion is conducted through two test cases. In all the tests presented in this paper, fully connected ANNs with hyperbolic tangent activation functions are employed.

2.3.1. Test Case 1: Non‐uniqueness of representation of models

In order to assess the possibility of accomplishing the above mentioned purposes, we consider the following idealized situation. We consider only the slow‐scale equation, given by

$$\left\{\begin{array}{l}\frac{\mathrm{d}}{\mathrm{d}\tau }\theta \left(\tau \right)=g\left(\theta \left(\tau \right),\alpha \right)\tau \in \left(0,\mathcal{T}\right],\\ \theta \left(0\right)={\theta }_0.\end{array}\right.$$ (14)

Hence, in this section we will simply denote θ as the state and α as the parameter, without specifying the scale on which the dynamics occur. Moreover, we assume that we are in a maximal information situation: namely, we assume that we have a population of individuals (that we denote by Ω) such that all the possible values of initial condition and parameter are covered (i.e., ${\left\{\left({\theta }_0\left(\omega \right),\alpha \left(\omega \right)\right)\right\}}_{\omega \in \mathrm{\Omega }}=\mathcal{P}\times \mathcal{A}$) and that we observe the evolution of θ(τ, ω) for each ω ∈ Ω and $\tau \in \left[0,\mathcal{T}\right]$, without noise (we denote the observed data as θ ^obs(τ, ω)). Finally, we assume that we are able to solve the following problem

$$\left(\widehat{g},{\left\{\widehat{\alpha }\left(\omega \right)\right\}}_{\omega \in \mathrm{\Omega }},{\left\{{\widehat{\theta }}_0\left(\omega \right)\right\}}_{\omega \in \mathrm{\Omega }}\right)=\underset{\begin{array}{c}g\in \mathcal{G}\\ {\left\{\alpha \left(\omega \right)\right\}}_{\omega }\in {\mathcal{A}}^{\mathrm{\Omega }}\\ {\left\{{\theta }_0\left(\omega \right)\right\}}_{\omega }\in {\mathcal{P}}^{\mathrm{\Omega }}\end{array}}{\text{argmin}}\underset{0}{\overset{\mathcal{T}}{\int }}\underset{\omega \in \mathrm{\Omega }}{\int }\frac{1}{2}{\left|\theta \left(\tau ,\omega \right)-{\theta }^{\mathrm{obs}}(\tau ,\omega )\right|}_{{\Pi }_{\theta }^{-1}}^2\mathit{d\omega }\mathit{d\tau },$$ (15)

subject to

$$\left\{\begin{array}{l}\frac{\mathrm{d}}{\mathrm{d}\tau }\theta \left(\tau ,\omega \right)=g\left(\theta \left(\tau ,\omega \right),\alpha \left(\omega \right)\right)\tau \in \left(0,\mathcal{T}\right],\omega \in \mathrm{\Omega }\\ \theta \left(0,\omega \right)={\theta }_0\left(\omega \right).\end{array}\right.$$ (16)

More precisely, we assume that we are able to find a triplet $\left(\widehat{g},{\left\{\widehat{\alpha }\left(\omega \right)\right\}}_{\omega \in \mathrm{\Omega }},{\left\{{\widehat{\theta }}_0\left(\omega \right)\right\}}_{\omega \in \mathrm{\Omega }}\right)$ that is a global minimum of the loss functional of Problem (15). We notice that, indeed, this problem admits global minimizers, as the loss functional is bounded from below by the value zero, which is attained by the triplet (g, {α(ω)}_{ω ∈ Ω}, {θ ₀(ω)}_{ω ∈ Ω}) itself (namely, the exact solution).

The idealized situation above described is visually represented in Figure 3. The triplet (g, {α(ω)}_{ω ∈ Ω}, {θ ₀(ω)}_{ω ∈ Ω}) generates the collection of data ${\left\{{\theta }^{\mathrm{obs}}\left(\tau ,\omega \right)\right\}}_{\tau \in \left[0,\mathcal{T}\right],\omega \in \mathrm{\Omega }}$, from which the triplet $\left(\widehat{g},{\left\{\widehat{\alpha }\left(\omega \right)\right\}}_{\omega \in \mathrm{\Omega }},{\left\{{\widehat{\theta }}_0\left(\omega \right)\right\}}_{\omega \in \mathrm{\Omega }}\right)$ is inferred. Hence, one may tempted to conclude that we have $g\equiv \widehat{g}$, $\alpha \left(\omega \right)\equiv \widehat{\alpha }\left(\omega \right)$, ${\theta }_0\left(\omega \right)\equiv {\widehat{\theta }}_0\left(\omega \right)$ for any ω ∈ Ω. However, while the latter conclusion is clearly true (since θ ₀(ω) = θ(0, ω) is part of the training dataset), the first two conclusions may be wrong. Consider, for instance, the following toy model

$$\left\{\begin{array}{l}\frac{\mathrm{d}}{\mathrm{d}\tau }\theta \left(\tau \right)=\alpha \theta \left(\tau \right)\tau \in \left(0,\mathcal{T}\right],\\ \theta \left(0\right)={\theta }_0,\end{array}\right.$$ (17)

where we have g(θ, α) = α θ and we set $\mathcal{P}=\mathcal{A}=\mathrm{ℝ}$. The data generated by Model (17) are given by θ ^obs(τ, ω) = θ ₀(ω)e ^α(ω)τ for any ω and τ. Consider now the following model

$$\left\{\begin{array}{l}\frac{\mathrm{d}}{\mathrm{d}\tau }\theta \left(\tau \right)=\frac{1}{2}\tilde{\alpha }\theta \left(\tau \right)\tau \in \left(0,\mathcal{T}\right],\\ \theta \left(0\right)={\tilde{\theta }}_0,\end{array}\right.$$ (18)

where we have $\tilde{g}\left(\theta ,\tilde{\alpha }\right)=\frac{1}{2}\tilde{\alpha }\theta$ and $\tilde{\alpha }\in \tilde{\mathcal{A}}=\mathrm{ℝ}$. If we set $\tilde{\alpha }\left(\omega \right)=2\alpha \left(\omega \right)$ and ${\tilde{\theta }}_0\left(\omega \right)={\theta }_0\left(\omega \right)$ for any ω ∈ Ω, then the data generated by Model (18) are given by ${\theta }^{\mathrm{obs}}\left(\tau ,\omega \right)={\tilde{\theta }}_0\left(\omega \right)e^{\frac{1}{2}\tilde{\alpha }\left(\omega \right)\tau }={\theta }_0\left(\omega \right)e^{\alpha \left(\omega \right)\tau }$ for any ω and τ. Therefore, the triplet $\left(\tilde{g},{\left\{\tilde{\alpha }\left(\omega \right)\right\}}_{\omega \in \mathrm{\Omega }},{\left\{{\tilde{\theta }}_0\left(\omega \right)\right\}}_{\omega \in \mathrm{\Omega }}\right)$ and the triplet (g, {α(ω)}_{ω ∈ Ω}, {θ ₀(ω)}_{ω ∈ Ω}) generate the same data.

FIGURE 3.

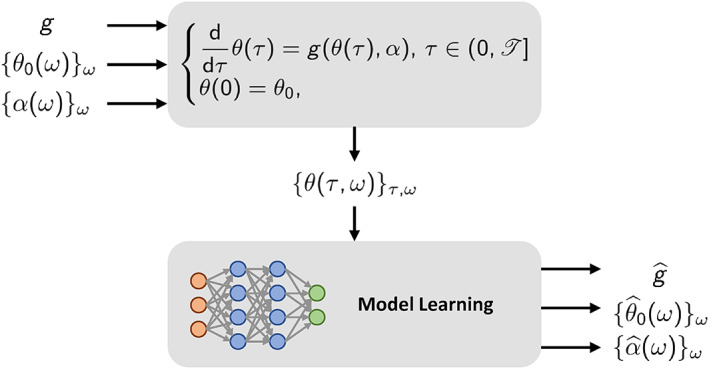
Visual representation of the idealized situation considered in Section 2.3

More generally, given any invertible and sufficiently regular function $\psi :\mathcal{A}\to \tilde{\mathcal{A}}$, and by setting $\tilde{g}\left(\theta ,\tilde{\alpha }\right)=g\left(\theta ,{\psi }^{-1}\left(\tilde{\alpha }\right)\right)$, $\tilde{\alpha }\left(\omega \right)=\psi \left(\alpha \left(\omega \right)\right)$ and ${\tilde{\theta }}_0\left(\omega \right)={\theta }_0\left(\omega \right)$ for any ω ∈ Ω, the two triplets generate the same data. Hence, the two models g and $\tilde{g}$ are indistinguishable solely on the basis on their output. This entails that Problem (15) (and, thus, Problem (P2)) is intrinsically ill‐posed, as it features many solutions. In other terms, even in the idealized case considered in this section, we do not have any guarantee that the learned model $\tilde{g}$ and the learned parameters $\tilde{\alpha }\left(\omega \right)$ coincide with the original ones (g and α(ω)). We remark that this is a more subtle issue than the case when different combinations of parameters lead to the same dynamics, which makes the parameters identification problem ill‐posed. In the case considered here, indeed, different combinations of models and parameters lead to the same dynamics. This makes the problem of learning the model itself ill‐posed.

Nonetheless, we remark that, in the previous example, Model (17) and Model (18) are both valid mathematical descriptions of the phenomenon and there is no apparent reason why the former should be preferable to the latter. As a matter of fact, due to the black‐box nature of Problem (15), the solution is totally transparent to the specific representation of the parameters α. Indeed, the reformulation obtained through the invertible map ψ is associated with a mere change of variables and the underlying model is essentially the same. Hence, we say that model $\tilde{g}$ is a trivial reformulation of model g, as it does not represent a substantially different model. In Section 2.3.3, we will give a more rigorous definition of this concept.

To illustrate the practical implications of the existence of trivial reformulations, we consider again the Problem (17), which we denote as Test Case 1. We consider N _P = 20 training individuals, for which we randomly generate an initial state ${\theta }_0^i\in \left(\mathrm{1,1.1}\right)$ and a parameter α ⁱ ∈ (0, 1) by sampling from the two intervals with uniform probability, for i = 1, …, N _P. Then, for each individual, we synthetically generate the evolution θ ⁱ(τ) for $\tau \in \left(0,\mathcal{T}\right]$ (with $\mathcal{T}=1$), by numerically approximating the solution of (17). The obtained transients are represented in Figure 4. Then, we subdivide the time interval $\left[0,\mathcal{T}\right]$ into equally distributed time instants $\left({\tau }_1<{\tau }_2<\dots <{\tau }_{N_S}\right)$ with a time step of Δτ = 1e − 2, and we apply the algorithm of Section 2.2 in order to solve Problem (P2), where we set ${\widehat{\theta }}_j^i={\theta }^i\left({\tau }_j\right)$ (i.e., we assume, for simplicity, that the slow‐scale states can be estimated without error). Specifically, we train an ANN (endowed with a single hidden layer with three neurons) starting from the collection of observations ${\left\{{\widehat{\theta }}_j^i\right\}}_{j=1,\dots ,N_S}^{i=1,\dots ,N_P}$, which, in this case, are not affected by noise. In this manner, we obtain a model $\widehat{g}$ and a parameter ${\widehat{\alpha }}^i$ for each of the training individuals. We remark that the proposed method is not restricted to single‐layer ANNs, but more complex ANN architectures can be employed.

FIGURE 4.

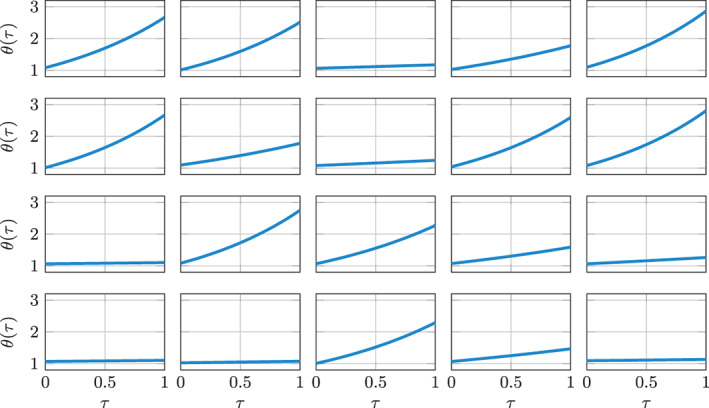
Test Case 1: training data. Each plot represents a training individual, characterized by a given pair (θ ₀, α)

In Figure 5(A) we plot the value of the original parameter α ⁱ against the value of the corresponding learned parameter ${\widehat{\alpha }}^i$, for each of the N _P = 20 training individuals (colored circles). We notice that, even if we do not have ${\widehat{\alpha }}^i={\alpha }^i$, a one‐to‐one relationship between the two classes of parameters is easily detectable. Hence, we can conclude that the ANN‐based model, learned from the data, is based on a different (but, possibly, equivalent) parameterization of the space of parameters.

FIGURE 5.

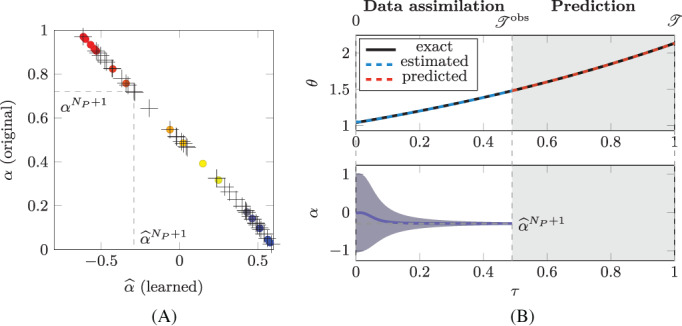
Test Case 1. In (A), the colored circles represent the original parameters α ⁱ plotted against the corresponding learned parameters ${\widehat{\alpha }}^i$ for the training individuals (i = 1, …, N _P). Conversely, the black crosses represent the original parameters ${\alpha }^{N_P+k}$ plotted against the corresponding estimated parameters ${\widehat{\alpha }}^{N_P+k}$ for the testing individuals. In the first row of (B) we show the evolution of ${\theta }^{N_P+1}\left(\tau \right)$ (blue solid line), while the black dashed line represent the value of ${\widehat{\theta }}^{N_P+1}\left(\tau \right)$ estimated by means of the EKF algorithm (for $\tau \in \left[0,{\mathcal{T}}^{\mathrm{obs}}\right]$) and its predicted value (for $\tau \in \left({\mathcal{T}}^{\mathrm{obs}},\mathcal{T}\right]$). In the second row of (B), we show the evolution of the estimation of the value of ${\widehat{\alpha }}^{N_P+1}$, with the ±3σ bands, where σ denotes the standard deviation of the estimate

In order to test the capabilities of the learned model to be used for classification and prediction purposes, we apply the procedure introduced in Section 2.1.3. Specifically, we consider a new individual, for which we randomly generate an initial state ${\theta }_0^{N_P+1}$ and a parameter ${\alpha }^{N_P+1}$. Similarly to what was done for the training individuals, we synthetically generate the evolution of the state ${\theta }^{N_P+1}\left(\tau \right)$, for $\tau \in \left(0,\mathcal{T}\right]$ by means of the original model (17). Then, we introduce an intermediate time instant ${\mathcal{T}}^{\mathrm{obs}}=0.5$ s and we imagine to observe the evolution of the new individual in the interval $\left[0,{\mathcal{T}}^{\mathrm{obs}}\right]$. In this time interval, we apply the EKF algorithm through the learned model $\widehat{g}$: more precisely, we solve Problem (8), in order to estimate the value of the parameter ${\widehat{\alpha }}^{N_P+1}$ and of the state ${\theta }^{N_P+1}\left(\tau \right)$ (see Figure 5(B)). We repeat the same protocol multiple times: we generate a random initial state ${\theta }_0^{N_P+k}$ and a random parameter ${\alpha }^{N_P+k}$, for k = 1, …, we generate the corresponding synthetic data, from which, by means of DA, we estimate the values of ${\widehat{\alpha }}^{N_P+k}$. In Figure 5(A), we plot the obtained pairs $\left({\widehat{\alpha }}^{N_P+k},{\alpha }^{N_P+k}\right)$. We notice that the estimated values of $\widehat{\alpha }$ are compliant with the one‐to‐one relationship between the parameters α and the parameters $\widehat{\alpha }$ that emerged in the training phase. Therefore, since in practical applications one cannot observe ${\alpha }^{N_P+k}$, while ${\widehat{\alpha }}^{N_P+k}$ can be estimated, this provides a way of classifying the new individual. Indeed, the mere observation ${\widehat{\alpha }}^{N_P+k}$ allows to conclude that the (N _P + k)‐th individual features characteristics similar to those of the individuals with a similar $\widehat{\alpha }$.

As mentioned in Section 2.1.3, by exploiting the estimated value of ${\widehat{\alpha }}^{N_P+1}$, the model $\widehat{g}$ can be exploited to predict the evolution of ${\theta }^{N_P+1}\left(\tau \right)$ for $\tau \in \left({\mathcal{T}}^{\mathrm{obs}},\mathcal{T}\right]$. In Figure 5(B) we report the prediction of ${\theta }^{N_P+1}\left(\tau \right)$ obtained by numerically approximating the solution of Problem (10). We repeat the same protocol for 1000 synthetically generated testing individuals, obtaining an overall normalized L ² error between the prediction and the exact solutions of 3.8e − 3.

In conclusion, even if the learned model does not coincide with the original one (it is indeed a trivial reformulation of it), thanks to the interplay between ML and DA, it can still be employed to classify individuals and to make predictions. In Section 2.3.4 we will deal with the problem of unequivocally selecting a unique representative model within a class of trivially reformulations of the same underlying model. However, before dealing with this topic, we show that something more subtle than a trivial reformulation may hinder the interpretability of the results.

2.3.2. Test Case 2: Non‐trivial reformulations

Let us consider the following model, which we denote as Test Case 2, where the state is given by the two‐dimensional vector θ = (θ ₁, θ ₂) ∈ ℝ², while the parameter is one‐dimensional

$$\left\{\begin{array}{ll}\frac{\mathrm{d}}{\mathrm{d}\tau }{\theta }_1\left(\tau \right)=\alpha {\theta }_1\left(\tau \right)& \tau \in \left(0,\mathcal{T}\right],\\ \frac{\mathrm{d}}{\mathrm{d}\tau }{\theta }_2\left(\tau \right)=0& \tau \in \left(0,\mathcal{T}\right],\\ {\theta }_1\left(0\right)={\theta }_{1,0},{\theta }_2\left(0\right)={\theta }_{2,0}.& \end{array}\right.$$ (19)

Test Case 2 is obtained from Test Case 1 by introducing a further state variable, with a trivial dynamics (θ ₂ is clearly constant in τ). However, even if the modification is only minimal, the results (shown in Figure 6(A)) are significantly different from those obtained for the Test Case 1 (see Figure 5(A)). Indeed, for Test Case 2 the parameters of the original model g are not related with those of the learned one $\widehat{g}$ by a one‐to‐one relationship.

FIGURE 6.

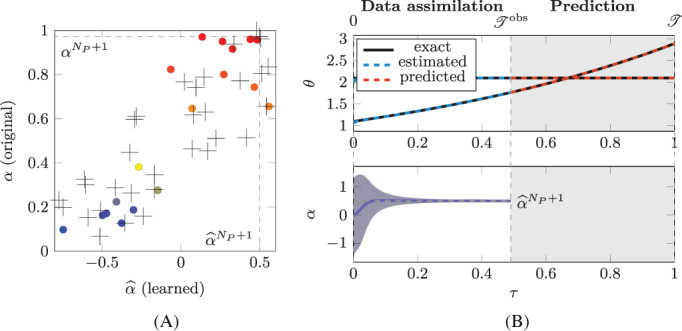
Test Case 2: (A) original parameters α ⁱ plotted against the corresponding learned parameters ${\widehat{\alpha }}^i$ and (B) evolution of ${\theta }^{N_P+1}\left(\tau \right)$, of ${\widehat{\theta }}^{N_P+1}\left(\tau \right)$ and of the estimation of ${\widehat{\alpha }}^{N_P+1}$. See caption of Figure 5 for the notation

At first sight, we are tempted to conclude that the algorithm of Section 2.2 failed its goal of finding a good description of the training individuals. However, if we employ the learned model, as for Test Case 1, to predict the evolution of a new individual (by observing it over the time interval $\left[0,{\mathcal{T}}^{\mathrm{obs}}\right]$, where ${\mathcal{T}}^{\mathrm{obs}}=0.5$, and by estimating the parameter ${\widehat{\alpha }}^{N_P+1}$ through the EKF algorithm), we still obtain good results (see Figure 6(B)). As a matter of fact, by repeating the above mentioned protocol for 1000 synthetically generated individuals, we obtain an overall relative error of 3.7 × 10⁻³.

Since the obtained error is similar to that obtained for Test Case 1, we conclude that also for Test Case 2 the learned model is a faithful mathematical description of the original one. However, the model learned in Test Case 2 cannot be obtained from the original one simply by a change of variable in α. Hence, we say that model $\tilde{g}$ is a non‐trivial reformulation of model g.

To provide an example that shows how a non‐trivial reformulation of Model (19) can be obtained, we consider the following model

$$\left\{\begin{array}{ll}\frac{\mathrm{d}}{\mathrm{d}\tau }{\theta }_1\left(\tau \right)=\left(\tilde{\alpha }+{\theta }_2\left(\tau \right)\right){\theta }_1\left(\tau \right)& \tau \in \left(0,\mathcal{T}\right],\\ \frac{\mathrm{d}}{\mathrm{d}\tau }{\theta }_2\left(\tau \right)=0& \tau \in \left(0,\mathcal{T}\right],\\ {\theta }_1\left(0\right)={\tilde{\theta }}_{1,0},{\theta }_2\left(0\right)={\tilde{\theta }}_{2,0}.& \end{array}\right.$$ (20)

If we set $\tilde{\alpha }\left(\omega \right)=\alpha \left(\omega \right)-{\theta }_{2,0}\left(\omega \right)$, ${\tilde{\theta }}_{1,0}\left(\omega \right)={\theta }_{1,0}\left(\omega \right)$ and ${\tilde{\theta }}_{2,0}\left(\omega \right)={\theta }_{2,0}\left(\omega \right)$ for any ω ∈ Ω, then it follows that Models (19) and (20) generate the same data (i.e., θ ₁(τ, ω) = θ _1,0(ω)e ^α(ω)τ and θ ₁(τ, ω) = 0).

A less trivial example, where we do not have a constant state as in Model (19), is given by the following model

$$\left\{\begin{array}{ll}\frac{\mathrm{d}}{\mathrm{d}\tau }{\theta }_1\left(\tau \right)=\alpha {\theta }_1\left(\tau \right)& \tau \in \left(0,\mathcal{T}\right],\\ \frac{\mathrm{d}}{\mathrm{d}\tau }{\theta }_2\left(\tau \right)=-\alpha {\theta }_2\left(\tau \right)& \tau \in \left(0,\mathcal{T}\right],\\ {\theta }_1\left(0\right)={\theta }_{1,0},{\theta }_2\left(0\right)={\theta }_{2,0}.& \end{array}\right.$$ (21)

A non‐trivial reformulation of Model (21) is given by

$$\left\{\begin{array}{ll}\frac{\mathrm{d}}{\mathrm{d}\tau }{\theta }_1\left(\tau \right)=\left(\tilde{\alpha }+{\theta }_1\left(\tau \right){\theta }_2\left(\tau \right)\right){\theta }_1\left(\tau \right)& \tau \in \left(0,\mathcal{T}\right],\\ \frac{\mathrm{d}}{\mathrm{d}\tau }{\theta }_2\left(\tau \right)=-\left(\tilde{\alpha }+{\theta }_1\left(\tau \right){\theta }_2\left(\tau \right)\right){\theta }_2\left(\tau \right)& \tau \in \left(0,\mathcal{T}\right],\\ {\theta }_1\left(0\right)={\tilde{\theta }}_{1,0},{\theta }_2\left(0\right)={\tilde{\theta }}_{2,0},& \end{array}\right.$$ (22)

and by setting $\tilde{\alpha }\left(\omega \right)=\alpha \left(\omega \right)-{\theta }_{1,0}\left(\omega \right){\theta }_{2,0}\left(\omega \right)$, ${\tilde{\theta }}_{1,0}\left(\omega \right)={\theta }_{1,0}\left(\omega \right)$ and ${\tilde{\theta }}_{2,0}\left(\omega \right)={\theta }_{2,0}\left(\omega \right)$ for any ω ∈ Ω. It easy to check that, due to the fact that the product θ ₁(τ)θ ₂(τ) is constant in time, the two models produce the same data.

We notice that in both cases (Models (19) and (21)) there is a quantity C(θ) that is constant in time (we have C(θ) = θ ₂ and C(θ) = θ ₁ θ ₂, respectively). This quantity is a constant value characterizing individuals, as much as the parameters α: in both the above considered examples, indeed, the map between (α, C(θ ₀)) and $\left(\tilde{\alpha },C\left({\tilde{\theta }}_0\right)\right)$ is one‐to‐one. Conversely, in the formulations considered above, the constant C(θ) is embedded into the state, which could be reduced to a single variable. In other words, we are trying to model more than necessary: the state could be reduced to the first variable θ ₁(τ), and the second variable θ ₂(τ) can be obtained by solving C(θ(τ)) = C(θ ₀). For this reason, we say that a model that admits (respectively, does not admit) a non‐trivial reformulation is non‐minimal (respectively, minimal). In Section 2.3.3 we state rigorous definitions of these concepts.

To motivate the importance of model minimality, we recall that the parameter ${\widehat{\alpha }}^{N_P+1}$ estimated through a non‐trivial reformulation g of a model $\widehat{g}$ is not related to the original parameter ${\alpha }^{N_P+1}$ by a one‐to‐one relationship. Hence, it cannot be employed to infer knowledge on the N _P + 1 individual (classification purposes) and it hampers the interpretability of the learned model.

2.3.3. Definition of reformulation

In what follows, we identify a model written in the form of Equation (14) with the triplet $\left(g,\mathcal{P},\mathcal{A}\right)$. Moreover, we denote the solution map associated with such a model as $s_g:\mathcal{P}\times \mathcal{A}\times \left[0,+\infty \right)\to \mathcal{P}$, defined as s _g(θ ₀, α, τ) = θ(τ), where θ(τ) is the solution of Equation (14). We introduce the following definitions.

Definition 1

We say that a function $\tilde{A}:\mathcal{P}\times \mathcal{A}\to \tilde{\mathcal{A}}$ is:

• trivial, if it is constant in its first argument; non‐trivial, otherwise;

• non‐pathological, if $\left\{\tilde{A}\left({\theta }_0,\alpha \right):\alpha \in \mathcal{A}\right\}=\tilde{\mathcal{A}}$ for any ${\theta }_0\in \mathcal{P}$; pathological, otherwise.

Definition 2

We say that $\left(\tilde{g},\mathcal{P},\tilde{\mathcal{A}}\right)$ is a reformulation of $\left(g,\mathcal{P},\mathcal{A}\right)$ if there exists a non‐pathological function $\tilde{A}:\mathcal{P}\times \mathcal{A}\to \tilde{\mathcal{A}}$ such that:

$$g\left(s_g\left({\theta }_0,\alpha ,\tau \right),\alpha \right)=\tilde{g}\left(s_g\left({\theta }_0,\alpha ,\tau \right),\tilde{A}\left({\theta }_0,\alpha \right)\right)\forall {\theta }_0\in \mathcal{P},\alpha \in \mathcal{A},\tau \ge 0.$$ (23)

Moreover, we say that $\left(\tilde{g},\mathcal{P},\tilde{\mathcal{A}}\right)$ is a

• non‐trivial reformulation of $\left(g,\mathcal{P},\mathcal{A}\right)$, if (23) holds for some non‐trivial non‐pathological function $\tilde{A}$;

• trivial reformulation if all the non‐pathological functions $\tilde{A}$ satisfying (23) are trivial.

Definition 3

A model $\left(g,\mathcal{P},\mathcal{A}\right)$ is minimal if it does not admit any non‐trivial reformulation.

We remark that the hypothesis that the function $\tilde{A}$ be non‐pathological is needed to avoid pathological situations, such as the case when a reformulation if obtained by a mere piece‐wise redefinition of the coefficient. Moreover, we remark that the definition of reformulation is motivated by the following result, for which the proof is given in A.

Proposition 1

Let $\left(\tilde{g},\mathcal{P},\tilde{\mathcal{A}}\right)$ be a reformulation of $\left(g,\mathcal{P},\mathcal{A}\right)$ through the map $\tilde{A}:\mathcal{P}\times \mathcal{A}\to \tilde{\mathcal{A}}$. Then we have

$$s_g\left({\theta }_0,\alpha ,\tau \right)=s_{\tilde{g}}\left({\theta }_0,\tilde{A}\left({\theta }_0,\alpha \right),\tau \right)\forall {\theta }_0\in \mathcal{P},\alpha \in \mathcal{A},\tau \ge 0.$$ (24)

We remark that minimality is an intrinsic property of models: it is not affected, for instance, by invertible transformations of either the inputs, the outputs or the parameters (such as scaling or nondimensionalization). Even if, as shown in Test Case 2, the methods proposed in this paper can be applied to any model (minimal and non‐minimal ones), working with minimal models enhances the quantity of information that can be extracted from the learned model. This leads to the issue of devising tests to check minimality of models. Clearly, since the original model is not known in practical applications, the minimality of the model to be learned cannot in practice be analytically checked through the Definition 3. In the case that some a priori knowledge about the physical phenomenon is available, minimality could be deduced by means of physics‐based considerations. The development of a posteriori numerical tests aimed at checking model minimality will be the subject of future works.

We recall an important concept, that is identifiability of models.⁵¹, ⁵²

Definition 4

Two parameters ${\alpha }_1,{\alpha }_2\in \mathcal{A}$ are said indistinguishable for the model $\left(g,\mathcal{P},\mathcal{A}\right)$ if

$$\exists {\theta }_0\in \mathcal{P}\forall \tau \ge 0s_g\left({\theta }_0,{\alpha }_1,\tau \right)=s_g\left({\theta }_0,{\alpha }_2,\tau \right).$$ (25)

Moreover, we define I(α) = {α ^* s. t. α and α * are indistinguishable}.

Definition 5

We say that a model $\left(g,\mathcal{P},\mathcal{A}\right)$ is identifiable if I(α) = {α} for any $\alpha \in \mathcal{A}$, that is

$$\forall {\theta }_0\in \mathcal{P},{\alpha }_1\ne {\alpha }_2\in \mathcal{A}\exists {\tau }^{*}>0s_g\left({\theta }_0,{\alpha }_1,{\tau }^{*}\right)\ne s_g\left({\theta }_0,{\alpha }_2,{\tau }^{*}\right)$$ (26)

In fact, if a model is identifiable, then the map from the parameter‐trajectory map α ↦ {s _g(θ ₀, α, τ)}_τ ≥ 0 is one‐to‐one, for each ${\theta }_0\in \mathcal{P}$. Conversely, if a model is not identifiable, then, for some choices of the initial condition ${\theta }_0\in \mathcal{P}$ the DA assimilation problem of identifying the parameter α from the trajectory {s _g(θ ₀, α, τ)}_τ ≥ 0 is ill‐posed. Hence, in this paper we assume that we work with identifiable models. We remark that for linear models identifiability can be assessed by standard criteria (e.g., by studying the spectral properties of the observability matrix⁴³). Nonetheless, in this paper we consider the more general case of nonlinear parametric dynamical models.

2.3.4. Uniqueness of representation of models

Clearly, every model (even the minimal ones) admit trivial reformulations. Indeed, the parameter α is never measured and so it is subject to changes of variables. This is linked to the black‐box structure of the model learning Problem (P2). As a consequence, the solution of Problem (P2) is not unique. In order to transform such a problem into a problem with a unique solution, we need to select a representative model inside each class of trivial reformulations. In this section, we suggest a strategy to accomplish this goal. Specifically, we restrict the space of candidate models ${\mathcal{G}}_n$ by imposing some a priori constraints on the dependence of g on α.

Let us suppose that there exists a function, Γ{g(⋅, α)}(α), expressed as a combination of g and of its derivatives in θ (of any order) evaluated at some given points of $\mathcal{P}$, invertible in α. Then, we perform learning by restricting the search space to functions g satisfying the constraint Γ{g}(α) = α. In what follows we will show that, in this way, the solution of the model learning problem is unique.

This strategy can be interpreted as that of giving a physical meaning to the parameter α, which would be otherwise a black‐box object. As a matter of fact, the constraint Γ{g}(α) = α provides a definition of the parameter α. Let us consider the following example.

Example 1

Select some ${\theta }^{*}\in \mathcal{P}$, and set Γ{g}(α) = g(θ ^*, α). In this case, performing optimization under the constraint g(θ ^*, α) = α is equivalent to defining the parameter as the time rate of change of the state at θ ^*.

The effectiveness of the proposed strategy is supported by the following proposition (the proof is given in A).

Proposition 2

Let $\left(g,\mathcal{P},\mathcal{A}\right)$ be an identifiable model. Suppose that there exists an operator Γ{g(⋅, α)}(α), which acts on g as a function of θ, which is injective in α. Then, there exists a unique trivial reformulation of $\left(g,\mathcal{P},\mathcal{A}\right)$ (that we denote by $\left(\tilde{g},\mathcal{P},\tilde{\mathcal{A}}\right)$) such that $\mathrm{\Gamma }\left\{\tilde{g}\right\}\left(\tilde{\alpha }\right)=\tilde{\alpha }$ for any $\tilde{\alpha }\in \tilde{\mathcal{A}}$.

From an implementative viewpoint, the constraint can be imposed in two alternative ways. The first (that we denote as weak constraint) consists in adding to the loss function of Problem (P2) the following penalization term

$$\frac{w^2}{2}{\int }_{\mathcal{A}}{\left|\alpha -\mathrm{\Gamma }\left\{g\right\}\left(\alpha \right)\right|}^2\mathit{d\alpha },$$ (27)

where w denotes a weighting constant. From a numerical viewpoint, we evaluate the integral by Latin Hypercube Sampling⁵³ of the parameters space $\mathcal{A}$. When computing the gradients of the loss function (see Equation 13), the gradient of the penalization term with respect to μ is added to ${\nabla }_{\mu }\mathcal{J}$.

The second strategy (that we denote as strong constraint) consists in a manipulation of the ANN architecture, such that the constraint is exactly satisfied. Let us consider for instance Example 1. In this case, we define the space ${\mathcal{G}}_n$ as

$${\mathcal{G}}_n=\left\{\left(\theta ,\alpha \right)\mapsto \mathrm{\mathscr{H}}\left(\theta ,\alpha ;\mu \right)-\mathrm{\mathscr{H}}\left({\theta }^{*},\alpha ;\mu \right)+\alpha :\mu \in {\mathrm{ℝ}}^n\right\},$$

where ℋ(θ, α; μ) denotes an ANN, whose input is given by (θ, α) and where μ ∈ ℝⁿ represents the vector of ANN weights and biases. In this manner, the constraint α = Γ{g}(α) = g(θ ^*, α) for any $\alpha \in \mathcal{A}$ is automatically satisfied by any function $g\in {\mathcal{G}}_n$. We notice that, in this case, the last layer of biases can be removed from the ANN since its action in canceled by construction.

We remark that, while the weak constraint strategy is always feasible, the strong constraint feasibility depends on the specific form of the function Γ.

3. NUMERICAL ILLUSTRATIONS

In this section, we present the results of several numerical test cases, showing the effectiveness and the noise‐robustness of the proposed methods. All the results shown in this paper were produced within the matlab library model‐learning (publicly available in a GitHub repository¹), which was suitably extended with the implementation of the methods proposed here.

3.1. Test Case 1: Gaining a unique solution

In order to assess the effectiveness of the strategy proposed in Section 2.3.4 to identify a unique representative model among a class of trivial reformulations, we consider again Test Case 1, already considered in Section 2.3.1 (see Equation (17)). Since this model is minimal (in the sense of Definition 3), when learning from its data we obtain one of its infinitely many trivial reformulations. As a matter of fact, by running the learning algorithm several times, with different random initialization of the ANN parameters, we obtain a different model every time, as testified by Figure 7(A)–(C), which show, for three different models learned from the same dataset, the values of the original parameters α ⁱ against the value of the corresponding learned parameters ${\widehat{\alpha }}^i$. Even if in each case an underlying one‐to‐one relationship linking α to $\widehat{\alpha }$ can be easily detected, this relationship is different in each case.

FIGURE 7.

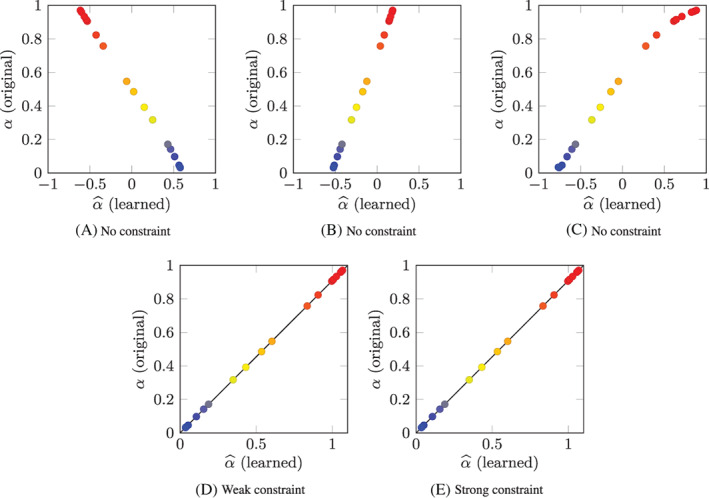
Test Case 1: original parameters α ⁱ plotted against the corresponding learned parameters ${\widehat{\alpha }}^i$ for the training individuals (i = 1, …, N _P). The models considered in (A), (B) and (C) are obtained with the non‐constrained strategy, the model of (D) and (E) are obtained with the weak and the strong strategies, respectively. In (D) and (E), the black line represents the analytical solution $\alpha ={\psi }^{-1}\left(\tilde{\alpha }\right)$

In order to obtain a unique solution, we consider the constraint $\mathrm{\Gamma }\left\{\tilde{g}\right\}\left(\tilde{\alpha }\right)=\tilde{\alpha }$ for $\mathrm{\Gamma }\left\{\tilde{g}\right\}\left(\tilde{\alpha }\right)=\tilde{g}\left({\theta }^{*},\tilde{\alpha }\right)$, by setting θ ^* = 1.1. By Proposition 2, we know that there is a unique model $\left(\tilde{g},\mathcal{P},\tilde{\mathcal{A}}\right)$, trivial reformulation of the model of Equation (17), such that $\tilde{g}\left({\theta }^{*},\tilde{\alpha }\right)=\tilde{\alpha }$. It is easy to check that this model has a right‐hand side defined as $\tilde{g}\left(\theta ,\tilde{\alpha }\right)=\tilde{\alpha }\theta /{\theta }^{*}$ and that the parameters of such model are related to those of the original one by the relationship $\tilde{\alpha }\left(\omega \right)=\psi \left(\alpha \left(\omega \right)\right)={\theta }^{*}\alpha \left(\omega \right)$.

We perform several runs of the learning algorithm of Section 2.2 with different random initialization of the ANN parameters, both with the weak and with the strong constraint approach. Unlike the non‐constrained case, this time (with both approaches) we obtain the same model in every run (up to numerical errors). In Figure 7(D),(E) we show the α ⁱ versus ${\widehat{\alpha }}^i$ plot obtained with the weak and the strong constraint strategies, respectively. In both figures we superimpose (black line) the relationship $\alpha ={\psi }^{-1}\left(\tilde{\alpha }\right)=\tilde{\alpha }/{\theta }^{*}$, corresponding to the analytical exact solution of the learning problem. The remarkably good agreement between the analytical solution and the learned parameters demonstrates the performance of the learning algorithm and of the strategy proposed in Section 2.3.4 to select a unique representative model.

As noticed in Section 2.3.1, the original and the learned model right‐hand sides are related by the relationship $g\left(\theta ,\alpha \right)=\tilde{g}\left(\theta ,\mathrm{\Gamma }\left\{g\right\}\left(\alpha \right)\right)=\tilde{g}\left(\theta ,{\theta }^{*}\alpha \right)$ for any $\theta \in \mathcal{P}$ and $\alpha \in \mathcal{A}$. In order to check that the learned models are consistent with this relationship, we show in Figure 8 a comparison between the functions g(θ, α) and $\widehat{g}\left(\theta ,\mathrm{\Gamma }\left\{g\right\}\left(\alpha \right)\right)$ (where $\widehat{g}$ denotes the learned model) in the portion of the state‐parameter plane $\mathcal{P}\times \mathcal{A}$ spanned by the training dataset. We can see that, with both the weak and the strong constraint strategies, the results are consistent with the analytical solution, except for the region of the state‐parameter plane corresponding to low α and large θ. The reason for this discrepancy lies in the fact that, when α ⁱ is low, the state of the i‐th individual never reaches the region where θ ⁱ is large. Hence, the training dataset does not contain any information about the behavior of the phenomenon in this region of the state‐parameter plane and we cannot expect the data‐driven apparatus to learn anything that is associated with this region (extrapolation effect). Nonetheless, if the training dataset contains a sufficiently representative collection of the possible behaviors of the phenomenon to be modeled, spanning the values of parameters and initial conditions of interest and the time horizon of interest, even if the learned model is not reliable outside the state‐parameter region spanned by the training dataset, in practical applications the complementary of this region is never reached. Hence, in this case, the risks associated with extrapolation do not represent a threat. However, it is important to be aware of this limitation. A good practice would be to check a posteriori, when the learned model is used for prediction purposes, that the state‐parameter pair does not move “too far” from the region spanned by the training dataset (i.e., ${\left\{\left({\widehat{\theta }}_j^i,{\widehat{\alpha }}^i\right)\right\}}_{j=1,\dots ,N_S}^{i=1,\dots ,N_P}$).

FIGURE 8.

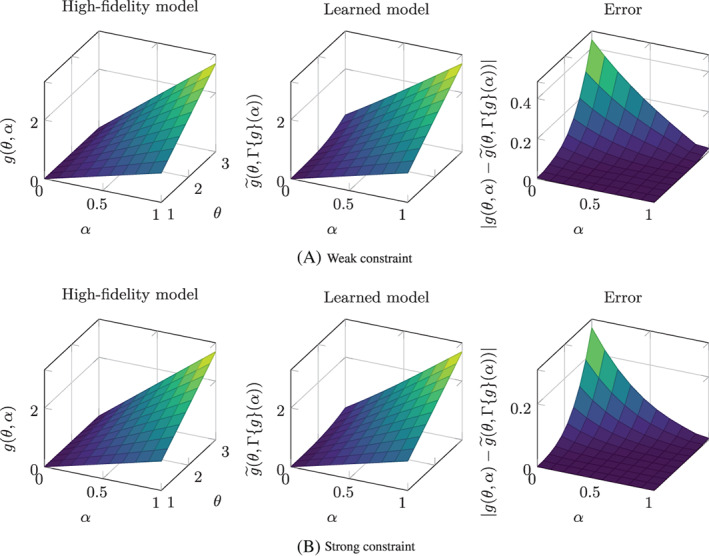
Test Case 1: comparison between the original model right‐hand side g(θ, α) with the learned model right‐hand side, mapped back to the state‐parameter plane of the original model (i.e., $\tilde{g}\left(\theta ,\mathrm{\Gamma }\left\{g\right\}\left(\alpha \right)\right)$). The last column shows the absolute error between the two functions. (A) Weak constraint. (B) Strong constraint

3.2. Test Case 1: Noise robustness of the learning algorithm

In the numerical tests considered so far, we have considered the case when measurements of the variables θ ⁱ(τ) are available without error. However, in practical applications, measurements are never error‐free. Moreover, in case the variables ${\widehat{\theta }}_j^i$ are obtained as results of a DA algorithm (as in the framework proposed in Section 2.1), their values are affected by the error introduced by the DA procedure. Hence, it is of utmost importance to investigate how much the proposed learning algorithm is robust to noise.

With this aim, we consider again Test Case 1, this time by assuming that the available measurements are affected by noise. Specifically, we set ${\widehat{\theta }}_j^i={\theta }^i\left({\tau }_j\right)+{\epsilon }_j^i$, where the observation errors ${\epsilon }_j^i\sim \mathcal{N}\left(0,U\right)$ are independent and identically distributed. By assuming that the stochastic variables ${\epsilon }_j^i$ are the result of a discrete sampling of the white noise $\sigma \frac{\mathit{dB}\left(\tau \right)}{\mathit{d\tau }}$ (where B(τ) is a Wiener process and σ is the noise magnitude), we set U = σ ²/Δτ. In particular, we set σ = σ _offline to generate the training data (offline noise) and σ = σ _online to generate the data to test the learned model (online noise). In all the test cases presented in this paper, we assumed the noise magnitude as given. A possible future development could be using suitable algorithms to automatically estimate the noise magnitude (see, e.g., Bavdekar et al.⁵⁴).

We add a random noise to the dataset used in Sections 2.3.1 and 3.1 for Test Case 1, with different magnitudes of σ _offline, and we run the learning algorithm. For the sake of brevity in this section we only consider the strong constraint strategy, but similar results are obtained with the weak constraint strategy too. In Figure 9(A) we show the α ⁱ versus ${\widehat{\alpha }}^i$ plot obtained for σ _offline ranging between 10⁻²s^1/2 and 10⁻⁵s^1/2. We notice that, as the noise decreases, the accuracy in the attribution of the parameters ${\widehat{\alpha }}^i$ increases.

FIGURE 9.

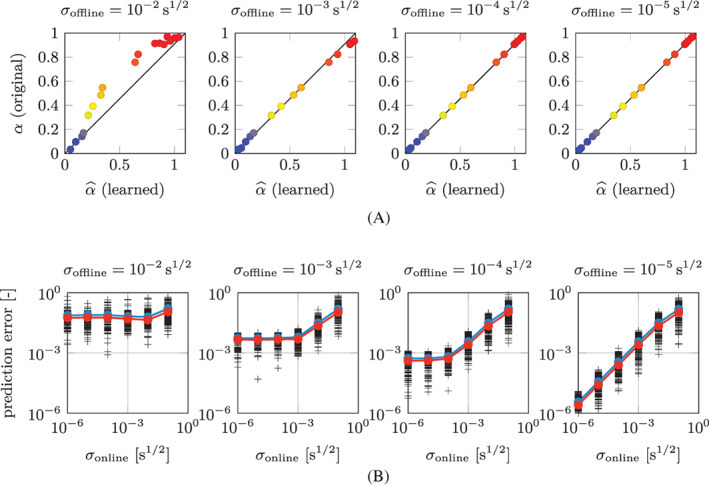
Test Case 1: (A) original parameters α ⁱ plotted against the corresponding learned parameters ${\widehat{\alpha }}^i$ for the training individuals (i = 1, …, N _P), for different noise magnitudes σ _offline and (B) overall L ² relative prediction errors obtained for different values of σ _offline and σ _online. In (B), each black cross represent a testing individual, the blue curve represent the arithmetic mean, the red curve the geometric mean

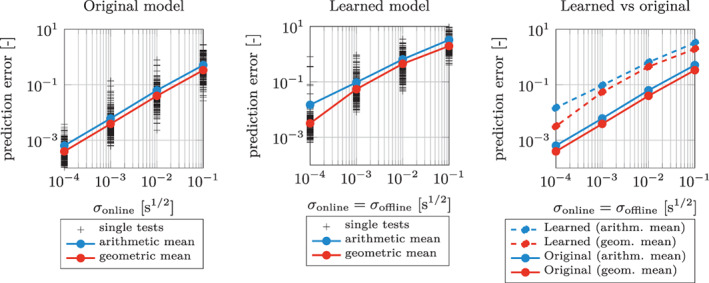
To quantitatively assess the noise‐robustness of the method, we generate 1000 random test individuals and we add a random noise (with different levels of magnitude σ _online), we apply the EKF algorithm in the time interval $\left[0,{\mathcal{T}}^{\mathrm{obs}}\right]$, in order to estimate the parameters ${\widehat{\alpha }}^i$ associated with those individuals, and finally we predict their evolution in the interval $\left({\mathcal{T}}^{\mathrm{obs}},\mathcal{T}\right]$. In Figure 8 we show the overall normalized L ² error between the predictions and the exact solutions, for the different values of σ _offline and σ _online. We notice that, when σ _online is large compared to σ _offline, the prediction error has a trend which is proportional to σ _online. However, for low values of σ _online, the prediction error saturates to a level that depends on σ _offline. Indeed, the learned model $\widehat{g}$ is an approximate surrogate for the laws governing the phenomenon (represented in this example by the original model g). As such, the learned model is affected by a model error, that is to say it is endowed with a limited capability of describing and predicting the behavior of the phenomenon. In conclusion, when σ _online ≫ σ _offline, the error introduced by the online noise prevails over the model error, which explains the linear trend between σ _online and the prediction error. Conversely, when σ _online < σ _offline, the model error comes into play and the decreasing trend of the prediction error ends.

We notice that in most practical applications, measurements are available with the same quality in the online and the offline stage. Hence, we repeat the test performed in Figure 9(B), by setting σ _online = σ _offline, that is by simultaneously decreasing the offline and the online error. In order to provide a benchmark value for the errors obtained in this manner, we perform the same test, this time by employing the original model g itself in the DA and in the prediction stage. The prediction errors so obtained are reported in Figure 10. Such errors represent the minimum error that can be attained for a given level of noise. Indeed, they are obtained in the idealized case of absence of any model error (they are only affected by the online noise). In Figure 9 we also report the prediction errors obtained by replacing the ground‐truth model g with its data‐driven surrogates. The closeness of the error curve obtained with the ANN‐based model to that obtained with the original one demonstrates that the effect of the model error introduced by replacing the original model with its surrogate is small compared to the error due to the noise. Hence, we conclude that the learned model can be reliably used to interpret data and to make predictions for the phenomenon.

FIGURE 10.

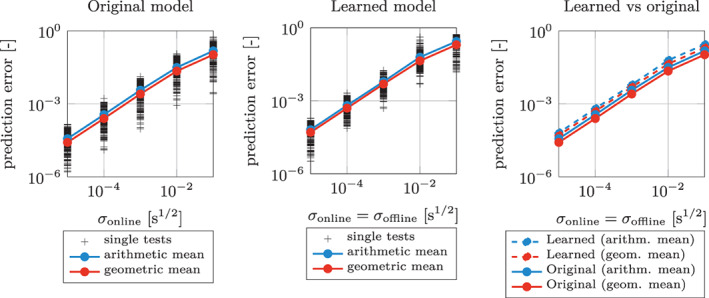
Test Case 1: overall L ² relative prediction errors for different values of σ _online obtained by employing the original model (left) and the learned models (center), by setting σ _offline = σ _online (we use the same conventions of Figure 9(B)). Finally, we show a comparison of the arithmetic and the geometric means of the prediction errors, for the original and the learned models (right)

3.3. Test Case 3: Nonlinear second‐order dynamics

In order to test the capabilities of the proposed method to deal with more complex test cases than the linear first‐order dynamics considered in the previous sections, we consider the following second‐order nonlinear model

$$\left\{\begin{array}{l}\frac{d^2}{d{\tau }^2}\omega \left(\tau \right)+\beta \sin \left(\omega \left(\tau \right)-{\alpha }_1\right)+{\alpha }_2\frac{d}{\mathit{d\tau }}\omega \left(\tau \right)=0\tau \in \left(0,\mathcal{T}\right],\\ \omega \left(0\right)={\omega }_0,\\ \frac{d}{\mathit{d\tau }}\omega \left(0\right)={\psi }_0,\end{array}\right.$$ (28)

describing the dynamics of a nonlinear oscillator. The state of the model is given by $\theta \left(\tau \right)=\left(\omega \left(\tau \right),\frac{d}{\mathit{d\tau }}\omega \left(\tau \right)\right)$. The two parameters α ₁ and α ₂ represent the steady‐state value of the variable ω and the damping coefficient, respectively, while β = 5 s⁻² is a constant. We generate N _P = 20 training samples, by randomly sampling the state space θ ₀ ∈ [−1, 1] × [−0.1 s⁻¹,0.1 s⁻¹] and the parameters space α ∈ [−0.2,0.2] × [0.5 s⁻¹,1.5 s⁻¹] and by setting $\mathcal{T}=10\mathrm{s}$. For the time discretization we set Δτ = 1 ⋅ 10⁻² s.

As in Section 3.2, we build several data‐driven models with different values of σ _offline. For each model, we set a single hidden layer with eight neurons. Then, we randomly generate several test samples; we add noise to the model output; we perform DA in the time interval $\left[0,{\mathcal{T}}^{\mathrm{obs}}\right]$, for ${\mathcal{T}}^{\mathrm{obs}}=4\mathrm{s}$; finally, we predict the evolution in the time interval $\left({\mathcal{T}}^{\mathrm{obs}},\mathcal{T}\right]$, for $\mathcal{T}=10\mathrm{s}$.

We report in Figure 11 the predicted evolution of the system state for a random sample, in the case σ _offline = σ _online = 10⁻⁴ s^1/2. Then, in Figure 12, we compare the overall L ² relative prediction errors obtained, for different noise levels, by employing the data‐driven models and the exact model of Equation (28). Even if the errors obtained with the data‐driven models are larger than those obtained with the exact model, compared to Test Case 1, the error still converges to zero when the noise decreases.

FIGURE 11.

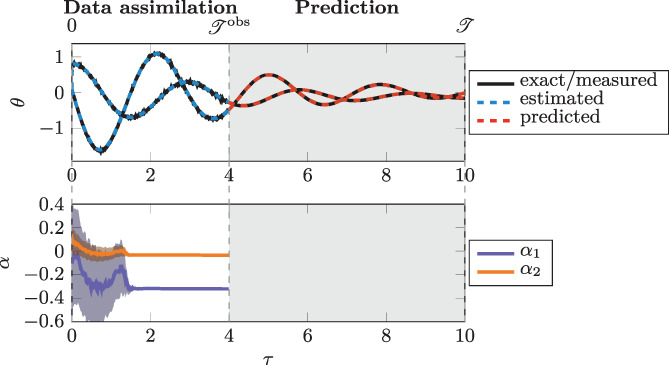
Test Case 3: evolution of ${\theta }^{N_P+1}\left(\tau \right)$, of ${\widehat{\theta }}^{N_P+1}\left(\tau \right)$ and of the estimation of ${\widehat{\alpha }}^{N_P+1}$. See caption of Figure 5 for the notation

FIGURE 12.

Test Case 3: overall L ² relative prediction errors for different values of σ _online obtained by employing the original model (left) and the learned models (center), by setting σ _offline = σ _online (we use the same conventions of Figure 9(B)). Finally, we show a comparison of the arithmetic and the geometric means of the prediction errors, for the original and the learned models (right)

3.4. Test Case 4: A synthetic test case of hypertension evolution

As a final test case (Test Case 3) we consider the example introduced in Section 1.3 as a motivation for the methods proposed in this paper. In this test case, the fast‐scale phenomenon is the blood circulation, which we here describe by means of the two‐stage Windkessel model of Equation (1). The evolution of the fast‐scale variables x(t) = (P _p(t), P _d(t)) is conditioned by the four parameters θ = (R _p, C _p, R _d, C _d), which evolve on a slower time scale τ. In order to test the proposed methods, we synthetically generate data that we use in place of experimental measurements. With this aim, we consider the following model for the slow scale evolution of the parameters θ

$$\left\{\begin{array}{ll}\frac{\mathrm{d}}{\mathrm{d}\tau }{R}_{\mathrm{p}}\left(\tau \right)=0& \tau \in \left(0,\mathcal{T}\right],\\ \frac{\mathrm{d}}{\mathrm{d}\tau }{C}_{\mathrm{p}}\left(\tau \right)=0& \tau \in \left(0,\mathcal{T}\right],\\ \frac{\mathrm{d}}{\mathrm{d}\tau }{R}_{\mathrm{d}}\left(\tau \right)=\alpha R_{\mathrm{d}}& \tau \in \left(0,\mathcal{T}\right],\\ \frac{\mathrm{d}}{\mathrm{d}\tau }{C}_{\mathrm{d}}\left(\tau \right)=-\alpha C_{\mathrm{d}}& \tau \in \left(0,\mathcal{T}\right],\\ R_{\mathrm{p}}\left(0\right)=R_{\mathrm{p},0},C_{\mathrm{p}}\left(0\right)=C_{\mathrm{p},0},R_{\mathrm{d}}\left(0\right)=R_{\mathrm{d},0},C_{\mathrm{d}}\left(0\right)=C_{\mathrm{d},0}.& \end{array}\right.$$ (29)

Model (29) describes the evolution of hypertension due to a progressive increase of the distal arterial resistance R _d, while the distal arterial capacitance C _d accordingly decreases so that the characteristic time constant of the arterial system (corresponding to the product R _d C _d) is preserved. On the other hand, the properties of the proximal arterial system (i.e., R _p and C _p) are not subject to long‐term variations. The slow‐scale coefficient $\alpha \in \mathcal{A}≔\left[0,1\times {10}^{-2}{\text{week}}^{-1}\right]$ represents the disease severity (more precisely, we have $\alpha =\log \left(2\right)/{\mathcal{T}}_{\text{double}}$, where ${\mathcal{T}}_{\text{double}}$ is the doubling time of R _d).

3.4.1. Synthetic data generation

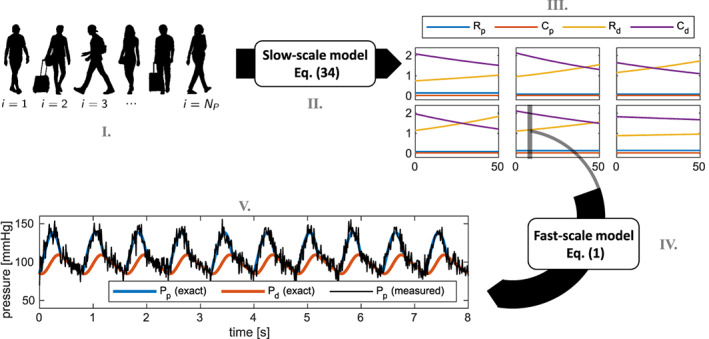
We generate the data needed to test the methods proposed in this paper alongside the following steps, visually represented in Figure 13.

1. We generate 100 synthetic patients, each one characterized by an initial state θ ₀ = (R _p,0, C _p,0, R _d,0, C _d,0) and by a degree of disease severity α. Specifically, the i‐th patient initial state ${\theta }_0^i$ and α ⁱ are randomly selected by sampling with uniform probability the sets $\left[R_{\mathrm{p}}^{\min },R_{\mathrm{p}}^{\max }\right]\times \left[C_{\mathrm{p}}^{\min },C_{\mathrm{p}}^{\max }\right]\times \left[R_{\mathrm{d}}^{\min },R_{\mathrm{d}}^{\max }\right]\times \left[C_{\mathrm{d}}^{\min },C_{\mathrm{d}}^{\max }\right]$ (see Table 1) and $\mathcal{A}$.

2. For each patient, we solve the slow‐time model of Equation (29), obtaining θ ⁱ(τ) for $\tau \in \left(0,\mathcal{T}\right]$, with $\mathcal{T}=50$ weeks.

3. We suppose that we monitor each patient with a period of Δτ = 1 week. Hence, we subdivide the interval $\left(0,\mathcal{T}\right]$ into the time instants $0={\tau }_1<{\tau }_2<\dots <{\tau }_{N_S}=\mathcal{T}$, such that τ _j + 1 = τ _j + Δτ.

4. At each time τ _j (for j = 1, …, N _S) and for each patient i, we simulate the fast‐scale patient circulation, by solving the Windkessel model (1) by setting θ = θ ⁱ(τ _j). We simulate 10 heartbeats, in order to let the dynamical system reach a limit cycle, and then we record the result of the following 10 heartbeats. In this manner, we obtain $z_j^i$, namely the observation associated with the i‐th patient at the j‐th discrete slow‐time. We recall that, in this test case, the observation vector z collects the measurements of the proximal arterial pressure at a discrete collection of time instants (t ₁, …, t _K), with t _k + 1 − t _k = Δt = 1e − 2 (i.e., we have z = (P _p(t ₁), …, P _p(t _K)).

5. In order to mimic the measurement error that unavoidably comes with any experimental measurement, we define the measured observation as ${\tilde{z}}_j^i=z_j^i+{\chi }_j^i$, where ${\chi }_j^i\sim \mathcal{N}\left(0,W\right)$ are independent and identically distributed observation errors. Similarly to what we have done in Section 3.2, we assume that the observation errors derive from a white noise of magnitude ρ = 0.75 mmHgs^−1/2. Hence, we set W = ρ ²/Δt = (7.5 mmHg)². This means that any pointwise measurement is affected by a relative error of the order of 10%.

Among the quantities generated through the above mentioned steps, the unique information available to the learning algorithm consists in the noisy observations ${\left\{{\tilde{z}}_j^i\right\}}_j^i$. The goal is that of climbing back those steps, in order to obtain the initial state of each patient, their degree of disease severity, and the laws governing the slow‐scale arterial network remodeling. Although the data employed for this test case are synthetically generated, the assumptions made here are consistent with an hypothetical clinical use of the proposed procedure; indeed this type of measurements can be available, for patients with specific indications, with the accuracy assumed above.⁵⁵

FIGURE 13.

Test Case 4: visual representation of the five steps followed to generate synthetic data (see Section 3.4.1)

TABLE 1.

Test Case 4: Lower and upper bounds of the initial values of the slow‐scale variables

Parameter	Value	Parameter	Value	Units
$R_{\mathrm{p}}^{\min }$	8.1757 × 10−2	$R_{\mathrm{p}}^{\max }$	1.7326 × 10−1	mmHg s mL−1
$C_{\mathrm{p}}^{\min }$	3.1197 × 10−2	$C_{\mathrm{p}}^{\max }$	3.1464 × 10−2	mL mmHg−1
$R_{\mathrm{d}}^{\min }$	6.9006 × 10−1	$R_{\mathrm{d}}^{\max }$	1.1599	mmHg s mL−1
$C_{\mathrm{d}}^{\min }$	1.1851	$C_{\mathrm{d}}^{\max }$	2.1731	mL mmHg−1

3.4.2. Data‐driven model for hypertension development

Starting from the noisy observation ${\left\{{\tilde{z}}_j^i\right\}}_j^i$, we build a data‐driven model by following the procedure proposed in Section 2.1 and visually represented in Figure 14.

FIGURE 14.

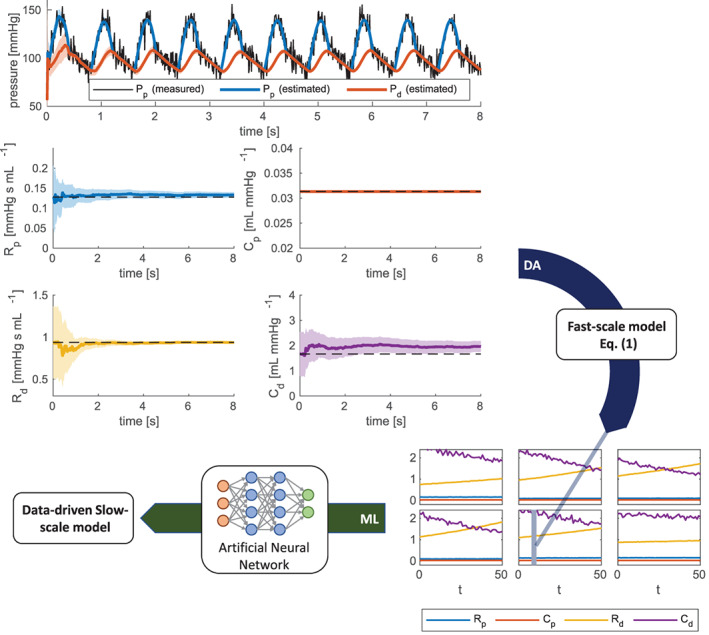
Test Case 4: visual representation of the procedure followed to generate a data‐driven model for hypertension development (see Section 3.4.2). In the top part of the figure we represent in black the noisy measurement of P _p associated with a given patient i and a to given slow‐time instant τ _j. The colored line represent the time evolution of estimated values of the system state (P _p and P _d) and of the four parameters (R _p, C _p, R _d and C _d). The shadowed areas represent the ±3σ bands, where σ denotes the standard deviation of the estimate. By combining the estimated values of the parameters obtained for all patients and for all the slow‐time instants, we obtain an estimate of their slow‐scale evolution, represented in the bottom‐right part of the figure

Specifically, we select N _P = 25 training patients. For each of them and for each slow‐scale time instant τ _j, we consider the noisy observation ${\tilde{z}}_j^i$, collecting the proximal arterial pressure measurements along 10 heartbeats. By solving Problem (P1) by means of the EKF algorithm, we obtain an estimate of the slow‐scale parameter vector for the i‐th patient at time τ _j, denoted by ${\widehat{\theta }}_j^i$. By collecting the estimated parameters for all i and j, we obtain the slow‐scale training dataset, a subset of which is displayed in Figure 14.

Next, we employ this dataset to train a data‐driven model. Specifically, since hypertension is related to an increase of the peripheral system resistance, we focus on the variable R _d. Hence, we solve Problem (P2) for θ(τ) ≔ R _d(τ) by means of the algorithm proposed in Section 2.2. In order to guarantee the uniqueness of the solution for Problem (P2) and to enhance the interpretability of the results, we adopt the constraint of Example 1, for ${\theta }^{*}=R_{\mathrm{d}}^{*}≔0.75\text{mmHg}\mathrm{s}{\mathrm{mL}}^{-1}$, by following the strong constraint strategy. We set N _α = 1, and we train an ANN with a single three‐neurons hidden layer. In this manner, we obtain the data‐driven model $\widehat{g}$ and the slow‐scale parameters ${\left\{{\widehat{\alpha }}^i\right\}}^i$.

In order to a posteriori check the quality of the obtained results, in Figure 15 we show the learned parameters ${\widehat{\alpha }}^i$, plotted against the ground‐truth parameters of the original model α ⁱ, used to the generate the data. We can see that, thanks to the proposed methodologies, we have successfully classified patients, by ranking them according to the disease severity.

FIGURE 15.

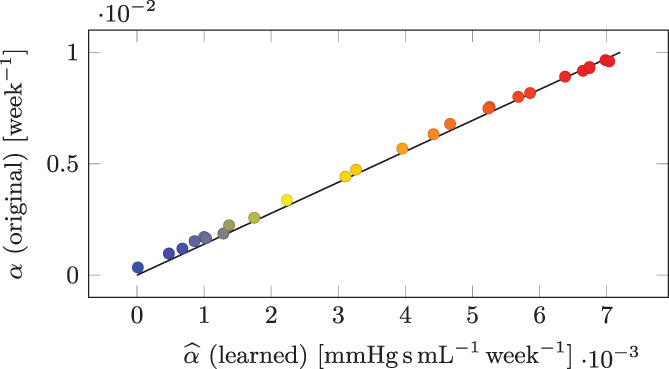
Test Case 4: original parameters α ⁱ plotted against the corresponding learned parameters ${\widehat{\alpha }}^i$ for the training individuals (i = 1, …, N _P)

Then, we consider the 75 synthetic patients generated in Section 3.4.1 but not included in the training set, in order to check the capability of the learned model to interpret unseen data and to make predictions. Hence, we apply the EKF algorithm in the time interval $\left[0,{\mathcal{T}}^{\mathrm{obs}}\right]$, with ${\mathcal{T}}^{\mathrm{obs}}=25$ weeks, to estimate the value of the parameter $\widehat{\alpha }$ for the testing patients. Then, we use the estimated parameter to predict the future evolution of the patient state in the time interval $\left({\mathcal{T}}^{\mathrm{obs}},\mathcal{T}\right]$. In this manner, we obtain an overall relative L ² error between the prediction and the exact solutions equal to 1.06 × 10⁻².

The computations were run on a standard laptop (single core Intel i7‐6500U). The execution of the EKF algorithm took nearly 140 ms for each run, for a total of nearly 7 s for each patient (as we have N _S = 50 checkpoints per patient). Therefore, preprocessing the 25 patients used to train the ANN required less than 3 min. The ANN training took instead 160 s. In conclusion, the whole offline phase took nearly 5 min. Concerning the online phase, for each patient the EKF algorithm needs to be run on the fast scale model up to ${\mathcal{T}}^{\mathrm{obs}}$, taking nearly 3.5 s; then the EKF algorithm is run on the slow scale model, which is then used to forecast the evolution of the patient. These steps only took 20 ms for each patient.

Finally, we notice that thanks to the application of the constraint of Example 1, the otherwise black‐box parameter $\widehat{\alpha }$ is endowed with a physical meaning. In particular, it owns a measure unit (arterial resistance per time unit) and it corresponds to the time rate of change of arterial resistance when its value is equal to $R_{\mathrm{d}}^{*}$. This allows to provide a practical definition of the parameter: its numerical value (expressed as mmHg s mL⁻¹ week⁻¹) can be estimated as the increase of arterial resistance occurring in 1 week, when the patient has resistance equal to $R_{\mathrm{d}}^{*}$. Thanks to the enhanced interpretability, this will facilitate the use of such data‐driven models in clinical practice.

4. CONCLUSIONS

In this paper we considered the problem of discovering differential equations describing the long‐term evolution of phenomena featuring two temporal scales, starting from experimental measurements related to the fast‐scale dynamics. We proposed to split the problem into two steps. The first step deals uniquely with the fast scale, and consists in estimating the fast‐scale parameters by means of DA methods. Then, in the second step, we employ the reconstructed slow‐scale evolution of these parameters to build a data‐driven model for the dynamics occurring at this slow time scale.

With this aim, we proposed a ML algorithm that builds a data‐driven model starting from time series data of a phenomenon featuring inter‐individual variability. In practice, this algorithm discovers a differential equation, depending on one parameter or more, that approximates the time evolution of the individuals belonging to the training set. Moreover, this algorithm also learns the most likely value of such parameters for each of the training individual. We remark that this algorithm can be easily generalized to the case when the slow‐scale phenomenon features a time‐dependent input, similarly to what was done in Regazzoni et al.²⁶

Then, we investigated the issue of interpretability of the learned model. In particular, we have highlighted that the problem of learning from time series a differential equation featuring one parameter or more never has a unique solution. Indeed, since the parameters are not directly measured, each model is associated with an equivalence class of models that can be obtained from the original one by an invertible transformation of the parameters into a new parameterization of the parameters themselves (we call such models trivial reformulations of the original one). Motivated by this, we have proposed a strategy to select a unique representative model inside each class of trivial reformulations of a given model. This is obtained by adding a constraint to the candidate class of models, either in weak or in strong form.

Moreover, we have shown that models can be split into two categories: minimal and non‐minimal. Models belonging to the second class feature a disadvantage when one tries to build a data‐driven model for the underlying phenomenon. In fact, non‐minimal models admit, besides trivial reformulations, what we call non‐trivial reformulations. Non‐trivial reformulations are mathematical models, written as parametric differential equations, that can produce the same output of the original model, but that cannot be obtained from it simply by an invertible transformation of the parameters. For this reason, it is preferable to work with minimal models. Although minimality is an intrinsic property of a model, we recall that a non‐minimal model can typically be reduced to a minimal one by removing variables that can be obtained as a combination of other variables. In other words, one should try not to learn a model with more variables than necessary; otherwise the dynamics would occur on trivial manifolds in the state space, leading to the existence of non‐trivial reformulations. The development of criteria that allow to check the minimality of a model will be the subject of future works.

Once the training phase (offline phase) is accomplished, the learned model serves multiple purposes. First, it provides understanding of the phenomenon to be modeled. Secondly, by performing DA through the learned model, one can estimate the values of the parameters associated with an individual not included in the training set (online phase). In case the model is minimal, then the parameters obtained in this manner allow to classify the individual, as their values may be used to detect patients that have similar features. Thirdly, once an estimate of the parameters associated with an unseen individual is available, then the learned model can be used to predict the future evolution of such individual. We remark that, while classification is only possible when working with minimal models, the learned model can be employed to predict the future evolution of unseen individuals both when working with minimal and with non‐minimal models.

Finally, we considered several test cases to show the effectiveness of the proposed methods and algorithms. Specifically, we synthetically generated time series by numerically approximating the solution of various differential models, including linear and nonlinear, first‐order and second‐order dynamics. Then, we employed our algorithm to learn parametric differential equations describing the measured data. We showed that, by suitably employing DA on the learned models in order to estimate the associated parameters, the future evolution of individuals not included in the training set can be accurately predicted. Moreover, numerical tests demonstrate that, when the noise added in the online and in the offline phases decreases, the prediction accuracy increases. Finally, we have shown that the strategy proposed to make the model learning problem well‐posed succeeds in selecting a unique model among the equivalence class of trivial reformulations of the original model, thus enhancing the interpretability of the learned model. Moreover, this strategy also provides a physical meaning to the parameters associated with the learned model, which would otherwise be a black‐box object without any clear physical interpretation.

A PROOFS OF THE PRESENTED RESULTS

We give in this appendix the Proofs of Propositions 1 and 2.

Proof of Proposition 1

Let us consider a generic ${\theta }_0\in \mathcal{P}$ and $\alpha \in \mathcal{A}$. Let us denote θ(τ) ≔ s _g(θ ₀, α, τ). In virtue of Equation (23), we have

$$\frac{\mathrm{d}}{\mathrm{d}\tau }\theta \left(\tau \right)=g\left(\theta \left(\tau \right),\alpha \right)=\tilde{g}\left(\theta \left(\tau \right),\tilde{A}\left({\theta }_0,\alpha \right)\right),\tau \ge 0.$$ (A1)

By the uniqueness of the solution of this ODE system, if follows that $s_{\tilde{g}}\left({\theta }_0,\tilde{A}\left({\theta }_0,\alpha \right),\tau \right)=\theta \left(\tau \right)$ for any τ ≥ 0.

Proof of Proposition 2

Let us define

$$\tilde{A}\left({\theta }_0,\alpha \right)≔\mathrm{\Gamma }\left\{g\right\}\left(\alpha \right),\tilde{g}\left(\theta ,\tilde{\alpha }\right)≔g\left(\theta ,\mathrm{\Gamma }{\left\{g\right\}}^{-1}\left(\tilde{\alpha }\right)\right)\forall \theta \in \mathcal{P},\alpha \in \mathcal{A}$$ (A2)

and let $\tilde{\mathcal{A}}$ be the image of $\tilde{A}$. Clearly, the model $\left(\tilde{g},\mathcal{P},\tilde{\mathcal{A}}\right)$ is a trivial reformulation of $\left(g,\mathcal{P},\mathcal{A}\right)$.

Let us suppose that $\left(g,\mathcal{P},\mathcal{A}\right)$ admits another trivial reformulation, which we denote by $\left(\overline{g},\mathcal{P},\overline{\mathcal{A}}\right)$, satisfying $\mathrm{\Gamma }\left\{\overline{g}\right\}\left(\overline{\alpha }\right)=\overline{\alpha }$ for any $\overline{\alpha }\in \overline{\mathcal{A}}$. Then, by Equation (23), there exists a function $B:\mathcal{A}\to \overline{\mathcal{A}}$ such that

$$g\left(\theta ,\alpha \right)=\overline{g}\left(\theta ,B\left(\alpha \right)\right)\forall \theta \in \mathcal{P},\alpha \in \mathcal{A}.$$ (A3)

By definition of identifiability, there exists a function h such that, for any ${\theta }_0\in \mathcal{P}$ and $\alpha \in \mathcal{A}$

$$\alpha =h\left({\left\{s_g\left({\theta }_0,\alpha ,\tau \right)\right\}}_{\tau \ge 0}\right)=h\left({\left\{s_{\overline{g}}\left({\theta }_0,B\left(\alpha \right),\tau \right)\right\}}_{\tau \ge 0}\right),$$

where the second equality follows from Proposition 1. The function B is thus invertible (in particular, we have $B^{-1}\left(\overline{\alpha }\right)=h\left({\left\{s_{\overline{g}}\left({\theta }_0,\overline{\alpha },\tau \right)\right\}}_{\tau \ge 0}\right)$).

By combining Equation (A2) with Equation (A3), we obtain

$$\tilde{g}\left(\theta ,\tilde{\alpha }\right)=\overline{g}\left(\theta ,B\left(\mathrm{\Gamma }{\left\{g\right\}}^{-1}\left(\tilde{\alpha }\right)\right)\right)\forall \theta \in \mathcal{P},\tilde{\alpha }\in \tilde{\mathcal{A}}.$$ (A4)

Therefore, we have $\tilde{\alpha }=\mathrm{\Gamma }\left\{\tilde{g}\right\}\left(\tilde{\alpha }\right)=\mathrm{\Gamma }\left\{\overline{g}\right\}\left(B\left(\mathrm{\Gamma }{\left\{g\right\}}^{-1}\left(\tilde{\alpha }\right)\right)\right)=B\left(\mathrm{\Gamma }{\left\{g\right\}}^{-1}\left(\tilde{\alpha }\right)\right)$, for each $\tilde{\alpha }\in \tilde{\mathcal{A}}$. By applying the function B ⁻¹(⋅) at both sides, we get $B^{-1}\left(\tilde{\alpha }\right)=\mathrm{\Gamma }{\left\{g\right\}}^{-1}\left(\tilde{\alpha }\right)$, which entails B(⋅) ≡ Γ{g}(⋅). Moreover, the sets $\overline{\mathcal{A}}$ and $\tilde{\mathcal{A}}$ coincide, being defined as the image of the maps B(⋅) and Γ{g}(⋅), respectively. Finally, by setting $B\left(\mathrm{\Gamma }{\left\{g\right\}}^{-1}\left(\tilde{\alpha }\right)\right)=\tilde{\alpha }$ in Equation (A4), we get $\tilde{g}\equiv \overline{g}$.

Regazzoni F, Chapelle D, Moireau P. Combining data assimilation and machine learning to build data‐driven models for unknown long time dynamics—Applications in cardiovascular modeling. Int J Numer Meth Biomed Engng. 2021;37(7):e3471. 10.1002/cnm.3471