Abstract
We present and discuss the use of a high‐dimensional computational method for atmospheric inversions that incorporates the space‐time structure of transport and dispersion errors. In urban environments, transport and dispersion errors are largely the result of our inability to capture the true underlying transport of greenhouse gas (GHG) emissions to observational sites. Motivated by the impact of transport model error on estimates of fluxes of GHGs using in situ tower‐based mole‐fraction observations, we specifically address the need to characterize transport error structures in high‐resolution large‐scale inversion models. We do this using parametric covariance functions combined with shrinkage‐based regularization methods within an Ensemble Transform Kalman Filter inversion setup. We devise a synthetic data experiment to compare the impact of transport and dispersion error component of the model‐data mismatch covariance choices on flux retrievals and study the robustness of the method with respect to fewer observational constraints. We demonstrate the analysis in the context of inferring CO2 fluxes starting with a hypothesized prior in the Washington D.C. /Baltimore area constrained by a synthetic set of tower‐based CO2 measurements within an observing system simulation experiment framework. This study demonstrates the ability of these simple covariance structures to substantially improve the estimation of fluxes over standard covariance models in flux estimation from urban regions.
Keywords: error covariance, regularization, inversion, Ensemble Transform Kalman Filter, green house gases
Key Points
Urban‐scale transport errors are correlated in space and time, which should be included in atmospheric inversions that estimate greenhouse gas emissions
In a synthetic data study, multiple methods to characterize correlated errors with model‐data covariance matrices demonstrate a better performance
Overall, dynamically adaptive covariance structures perform better than standard parametric models in both recovering total fluxes and their spatial distributions
1. Introduction
Historically, Bayesian inversions have been used at various spatial and temporal scales to study the carbon cycle (e.g., Gurney et al., 2002; Kirschke et al., 2013; Lauvaux et al., 2016; Yadav et al., 2019). Inversions involve the use of an atmospheric transport and dispersion model, coupled to atmospheric observations of greenhouse gases (GHGs), along with a prior estimate of the sources and sinks of the GHG of interest (e.g., carbon dioxide, CO2). Inversions also require a choice of various assumptions including the structure and quantification of errors associated with the representation of (a) the temporal and spatial distribution of prior information and (b) those of measurement, aggregation, representation, incoming air flow, and atmospheric transport/dispersion. Errors associated with the prior are associated with the characterizations of the GHG fluxes while those related to atmospheric transport/dispersion model, background and so on are associated with the atmospheric observations. In an inversion, the former is known as the prior error and the latter is referred to as model‐data mismatch error.
One of the most important challenges in characterizing the model‐data mismatch error is the lack of understanding of the atmospheric transport and dispersion component in the observational error. Often, these errors are assumed to be independent (or uncorrelated for the non‐Gaussian case) and identically distributed (i.i.d). This assumption may be sufficient for inverse studies that use surface measurements from a sparse, continental network for example, (Alden et al., 2016; Chatterjee et al., 2012; Gourdji et al., 2010, 2011). However, it may not be suitable for studies at the urban scale where networks are denser and the resolution of estimated fluxes much finer (e.g., spatially 1–10 km and temporally sub‐weekly Lauvaux et al., 2016; Yadav et al., 2019), or in aircraft‐based inverse modeling, where the observations are densely spaced along a flight track, and some satellite‐based inverse models, where the observations are also densely distributed along a satellite flight track. Thus, a violation of the assumption of i.i.d. errors, especially due to the difficulty of modeling atmospheric dynamics at finer resolution, could have a large impact, both in terms of both the bias and spatial correlation, on estimated fluxes.
Some papers have discussed the impact of transport model choices on inferred flux estimates (e.g., Baker et al., 2006; Gurney et al., 2002). For example, in a regional study, Peylin et al. (2002) showed that the choice of transport models, along with other factors, had a significant impact on the spread of estimated sources and sinks. Various studies thereafter (e.g., Berchet et al., 2013; Chevallier, 2007; Cressot et al., 2014) also demonstrated that the constructed observation error, when correlations are not considered, can have a large influence on flux estimates. Recently, the importance of transport errors in estimating urban emissions has also been noted, for example, Deng et al. (2017) and Lauvaux et al. (2016).
Other statistical applications that account for correlated errors have been used with GHG observations to yield improved flux estimates in an observing system simulation experiment (OSSE). For example, Mukherjee et al. (2011) outlined a statistical approach that models the spatial model‐data mismatch structures within an inversion framework. This study demonstrated that model‐data mismatch structures, through conditional autoregressive (CAR) models in a complete conjugate Bayesian inverse framework, can effectively recover true sources within a synthetic data experiment. Mukherjee et al. (2011) used this approach with MOPITT satellite CO retrievals to estimate global CO fluxes. Although appealing, this method assumes that the mismatches are purely attributed to the misrepresentation of spatial processes rather than temporal dynamics. Urban inversions at finer spatial and temporal resolutions result in a numerically large problem and thus, representing the model‐data mismatch error as well as the prior error in space and time can be challenging. As such, these challenges render implementation of CAR within a complete conjugate Bayesian inverse framework not only complex but also computationally expensive.
Motivated by this previous work, here we use an OSSE for the month of February 2016 to explore the impact of spatially and temporally correlated atmospheric transport and dispersion errors associated with the estimates of urban GHG emissions using a variation of the Ensemble Kalman Filter model. As Peylin et al. (2002) noted, it is important to discern the impact of mischaracterizing the transport and dispersion error component of the model‐data mismatch on both the magnitudes and uncertainties of emission estimates. We postulate that observations from a dense network that are used within an inverse model have associated atmospheric transport and dispersion errors that are inherently spatio‐temporal in nature. Thus, it is logical to ask how much do these errors vary spatially compared to temporally, and whether accounting for this variability within model‐data mismatch significantly impacts inferred flux estimates. Another question to ask is how reasonable is the common assumption of exponentially decaying smoothness of correlations in the presence of spatial dependencies? This study explores these questions through an OSSE that uses an ensemble of influence functions derived from several atmospheric transport model configurations.
This work is part of the Northeast Corridor (NEC) project, which was established in 2015 by the National Institute of Standards and Technology. The goals for the NEC project are to demonstrate the utility of atmospheric inversion methods in an urban domain that is complicated by many upwind and nearby emissions sources and surrounded by other cities and suburban areas. The NEC project has a current focus on the urban areas of Washington, D.C. and Baltimore, Maryland, U.S.A. (BW), with a network of tower‐based, in situ carbon dioxide (CO2) measurement sites in and surrounding these two cities. Because of the region's dense observational network (12 sites), the area provides a good case study for assessing correlated transport errors on flux estimates.
In this experiment, we explore a standard representation of transport error, that is, errors that are Gaussian in nature. A handful of studies also model the transport errors using a temporal decay function which we also consider in the OSSE. Here, we present a nonparametric way to model atmospheric transport and dispersion error correlations that is also dynamic. To do this, we employ a shrinkage‐based estimator (Schäfer & Strimmer, 2005) that is remarkably simple to implement yet very effective in capturing the underlying temporal and spatial error dependencies. Finally, we combine the commonly adopted exponential correlated error structure with the nonparametric approach. To understand the methods' dependency on the number and location of measurements, we vary the size of the measurement network as well. Note that this work focuses on CO2 fluxes. However, it is expected that our conclusions could be translated to any forms of Bayesian inversions that involve other trace gases such as methane (CH4).
2. Method Motivation
The basic concept of this study is to use several atmospheric transport models coupled with a dispersion model to create simulated CO2 observations within an OSSE to explore the key question of how spatial and temporal errors impact estimated fluxes if misrepresented within an Ensemble Transform Kalman Filter (ETKF) inversion framework. In Section 2.1, we describe how we construct the “true emission,” a prior emission, and an ensemble of observations using different transport and dispersion models and prior, while in Section 2.2 we use this ensemble to explore how the transport and dispersion errors are correlated.
2.1. Methodology for Generating Ensemble of Observations
To construct model‐data mismatch variances that represent expected variability in atmospheric transport and dispersion error, five different variations of Weather Research Forecast (WRF) configuration model simulations were generated for this study (see Figure 2). The model allows for two‐way nesting strategy (with feedback). Over the study domain, the spatial resolution is 1 km and the time‐step of the iteration was defined dynamically to ensure model stability. Other details of the base WRF model configuration are provided in Lopez‐Coto et al. (2017).
Figure 2.
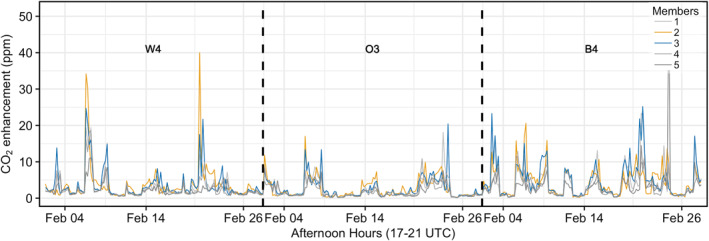
Time series of the five ensemble members after convolving the different transport model runs (Table 1) with the prior for three towers in the BW domain. The synthetic observations at these locations are the least correlated among the other towers. The sites are W4 in Washington D.C., O3 in outer‐urban area, and B4 in Baltimore. The transport model corresponding to the ensemble member in blue is used to generate the synthetic data and the transport model related to the orange member is used in the inversion model (see Section 3.1).
The WRF model was slightly modified from Lopez‐Coto et al. (2017) to create the five ensemble members used in this study. Specifically, we vary planetary boundary layer (PBL) schemes using three common choices and use two different initial boundaries conditions (North America Reanalysis Runs [NARR] and High‐Resolution Rapid Refresh [HRRR]). Initial boundary condition is one of the key components because it directly impacts wind fields, and boundary layer height among many other parameters driving discernible differences in transport and dispersion.
Another important factor is the planetary boundary layer (PBL) scheme that parametrizes atmospheric turbulence and interaction between atmosphere and land surface (Lopez‐Coto et al., 2020; Sarmiento et al., 2017). Domains with dominant urban land cover also pose an extra layer of complexity. One parametrization for urban land cover is the Building Energy Parametrization (BEP) (a multilayer urban canopy model) that allows complex interaction between urban environments and atmosphere (e.g., Liao et al., 2014). Given our urban domain, we have included an ensemble member using an additional WRF simulation generated using the HRRR PBL scheme with the inclusion of a multi‐layer urban canopy model (BEP).
Overall, we chose five configurations previously used for urban transport simulations in the literature (e.g., Lopez‐Coto et al., 2020; Sarmiento et al., 2017) that provided a reasonable representation of transport uncertainty. These atmospheric models (Table 1) coupled with the Stochastic Time Inverted Lagrangian Transport (STILT) model (Lin et al., 2003), were used to generate influence functions (Figure 1a), that is, footprints, that represent the relationship between a CO2 flux and an observation of CO2 at a measurement tower location. This results in sets of footprints from these different models which provides several plausible representations of atmospheric transport and dispersion. The STILT footprints were carried out at 0.01 × 0.01° (approximately 1 km2) which is consistent with spatial resolution of WRF for this domain.
Table 1.
Different Flavors of WRF Model Simulations Employed to Simulate the CO2 Observation Ensemble
| Name | Transport model | Boundary condition | PBL scheme | Other parametrizations |
|---|---|---|---|---|
| Member 1 (H1) | WRF + STILT | HRRR | BouLac | |
| Member 2 (H2) | WRF + STILT | NARR | YSU | |
| Member 3 (H3) | WRF + STILT | HRRR | YSU | |
| Member 4 (H4) | WRF + STILT | HRRR | QNSE | |
| Member 5 (H5) | WRF + STILT | HRRR | BouLac | BEP |
Notes. Abbreviations used for two different boundary conditions, three PBL schemes, and one multi‐layer urban canopy models are as follows: HRRR, High‐Resolution Rapid Refresh; NARR, North America Reanalysis Runs; BouLac, Bougeault‐Lacarr‘ere; YSU, Yonsei University; QNSE, Quasi‐normal scale elimination; and BEP, Building Energy Parametrization respectively. For other model parameterization details see Lopez‐Coto et al. (2017).
Abbreviations: PBL, planetary boundary layer; WRF, Weather Research Forecast.
Figure 1.
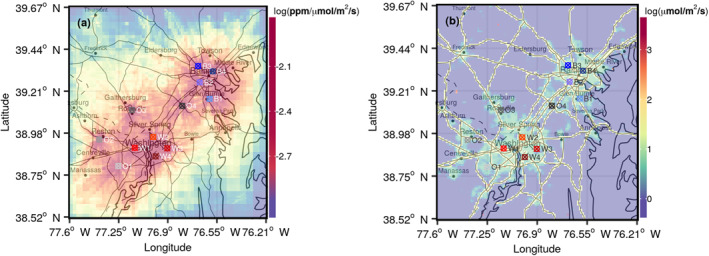
Left panel (a) shows the average afternoon hour sensitivities of all the 12 sites combined over the BW region. Right panel (b) is the map of true emission for the observing system simulation experiment over BW region. Observing sites are colored by the cities; shades of red are for the sites near or in Washington D.C. (W1–W4), shades of gray for the outer urban sites (O1–O4), and shades of blue for the Baltimore‐area sites (B1–B4).
For this OSSE, all inversions use the same prior fluxes in the region. The fluxes are positive (i.e., only emission), constructed as described in Lopez‐Coto et al. (2017). This inventory is a combination of emissions from four sectors: roads, urban, point sources and nonurban sectors. In short, emissions from urban areas are the urban fraction from MODIS‐IGBP land cover times 5 μmolm2s−1, emissions from roads are assumed to be 30 μmolm2s−1, point source emissions are from the EPA GHG reporting program (GHGRP), normalized by the area of one grid cell. To create our simulated “true” observations, we use CO2 fluxes that are a realistic perturbation of the prior fluxes described above; we create these true fluxes as described below, and refer to them as the “truth” henceforward. Except for the point sources, for each sector we specify an exponential covariance kernel of the log Gaussian Process (GP). The exponential kernel can be expressed as the following
| (1) |
where and are the standard deviations of the emission from grid cells s i and s j respectively, while d(.,.) is Euclidean distance between grid s i and s j and L represents the correlation length scale of the spatial field. c is a multiplicative constant. We choose to be 50% of the grid's prior emission in log‐scale. We simulate three spatial fields from three separate log GPs with length scales and multiplicative factors being 5, 5, 10 and 1.5, 2, and 0.5 representing roads, urban, and the rest respectively. Then we consider three radial basis functions (Nychka et al., 2015, Section 2.3) centered on the cities of Washington, D.C., Baltimore, MD and Frederick, MD with radii approximately 55, 55, and 30 km respectively. We use these three masks to rescale emissions for each sector around those cities. For roads, this rescaling factor ranges from 0.5 to 1.5 and for urban areas, it ranges from 1 to 2.5 based on emission intensities. Although we do not rescale the nonurban areas, we scale the point sources slightly with the scaling factor ranging from 0.8 to 1.2. What we get through this process is a realistic perturbation of a prior emission that is more like a snapshot of mean emissions of the afternoon hours. We have constructed the “truth” in such a way that the true flux from any grid cell is not simply a product of multiplying the prior flux by a scaling factor. Thus, unless we capture the true underlying transport and associate uncertainties, the areas constrained by the observations simulated using the “true” emission described above would be hard to update in the right direction.
We convolve the prior CO2 emission field s (based on the inventory described above and in Lopez‐Coto et al., 2017) with the five sets of footprints generated by the transport models listed in Table 1 for each of the 12 tower locations. This results in an ensemble spread of simulated hourly CO2 observations at each of the 12 in situ tower locations for the month of February 2016. The width of the ensemble (i.e., standard deviations of the simulated CO2 observations) provides a measure of the atmospheric transport and dispersion modeling error. We note that these methods for constructing the transport and dispersion error component of the model‐data mismatch are dependent on the ensemble spread being representative of the true transport model error. If it is not, the methods will not be able to correct the error. For this investigation, we assume that our ensemble provides a realistic spread and more ensemble members can be used if deemed appropriate in a real‐world application.
Finally, we use the “true” fluxes instead of the prior to simulate the “true” observations so that our ensemble spread (which was generated using the prior fluxes) includes some measure of error associated with the prior. Thus, we convolve the true fluxes with footprints from one of the atmospheric and dispersion models (Figure 1a) to generate our hourly observations at each of the 12 towers within the BW. Note that both the prior fluxes and “true” prior are static in time but vary in space.
2.2. Characterization of Transport and Dispersion Errors
Before we employ the inversion method, we first evaluate how atmospheric transport and dispersion errors vary in time and space by examining the standard deviation of hourly simulated CO2 observations at each tower throughout February. As shown in Figure 3a), the standard deviations vary significantly in time. This variability is mainly due to different types of synoptic events as shown in (Martin et al., 2019). Overall, standard deviations of the nearby or within‐city towers (i.e., those represented with the same line color) look more similar than those between different city towers. However, there appear to be some periods of convergence. Thus, when we look more closely, even among the most extreme sites, we see from Figure 3b that there are certain times when the standard deviations tend to loosely group together in three regions across the BW domain, that is, those in or near Washington DC (W4, shaded red in Figure 1), those between Washington DC and Baltimore (O3, shaded gray in Figure 1), and those from Baltimore (B4, shaded blue in Figure 1). Similar groupings were shown in an OSSE by K. Mueller et al. (2018). Regardless, the dominant variability is temporal in nature. Figure 3 provides us further evidence to the fact that atmospheric transport and dispersion errors should not be assumed to be constant in time even across measurement sites. It also hints that the pattern of error variability in time interacts (i.e., changes) with spatial proximity of the sites.
Figure 3.
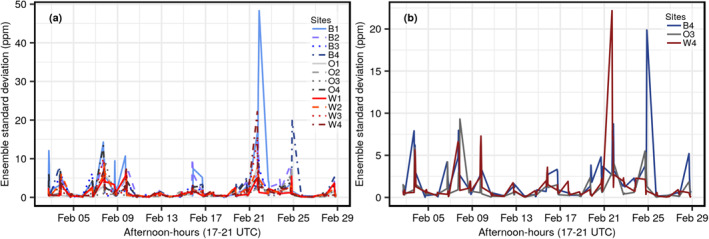
Left panel (a) is the time series of ensemble standard deviations for all the 12 sites. The colors of the sites from Figure 1 have been used here to represent the time series for each site; Baltimore (blue shades), Washington D.C. (red shades), and sites outside the cities or outer‐urban (gray shades) as shown in the legend. Right panel (b) shows the same relationship for the W4, O3, and B4 sites.
We further explore the extent of the spatial and temporal correlations of the errors by plotting their empirical semi‐variances (black, red, gray, and blue dots in Figures 4a–4d respectively) against distance (a) and time (b–d) with fitted exponential variogram models. The semi‐variances in Figure 4a indicate that there is scant structured spatial correlation; they are largely random. This may be because atmospheric dynamics is not spatially stationary. This nonstationarity explains why the convolutions in Figure 3b show some grouping into three classifications (those observations from towers in Washington DC, Baltimore and in between) that is not clear in Figure 3a.
Figure 4.
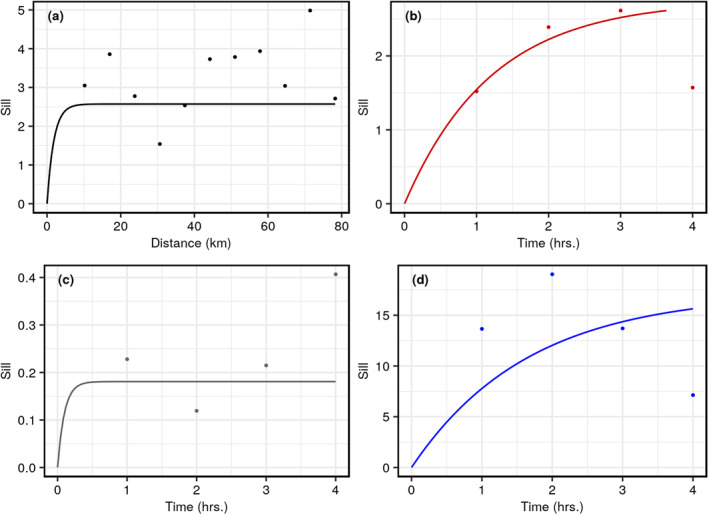
Top left panel (a) is the empirical marginal spatial (averaging over the variogram values along temporal bins for each spatial bin in the empirical spatio‐temporal variogram) semi‐variogram for the BW region for a randomly chosen member from the ensemble. For the same member, panels (b–d) show examples of empirical marginal temporal semi‐variograms grouped by sites from (b) Washington D.C., (c) outer‐urban, and (d) Baltimore areas (as indicated by different colors in Figure 1) over all five afternoon hour observations from a randomly chosen day for each group. Colored lines show the respective fitted exponential theoretical variogram models.
However, temporal correlations are reflected in the empirical variograms grouped by tower (Figure 4b, Washington DC, Figure 4c, outer‐urban, and Figure 4d, Baltimore). The fitted variogram models suggest that an exponential model can be a reasonable assumption for the model‐data mismatch error's temporal component at certain times. However, there may be possible nonstationarity or other patterns (e.g., the dip in empirical variogram in Figure 4d), or poor exponential fit in Figure 4c) that cannot be adequately represented by an exponential decay. Generally, Figure 4 demonstrates that the model‐data mismatch errors may benefit from temporally correlated errors in urban inversions.
Now that we have an idea of how transport and dispersion errors are structured in space and time separately, we further explore whether there are dependencies between these errors. Spatio‐temporal interaction between errors can be detected through error clusters. Space‐time clusters are often seen through plots like the Hovmoller diagram that is a visualization technique showing the spatial evolution of the atmospheric transport and dispersion errors over time. Since we have an ensemble of observations, it is easier to find patterns from a Hovmoller diagram of the standard deviations than from the individual members. When the errors in space and time are correlated their standard deviations form clusters. In Figure 5, we can see clusters of standard deviations on February 2nd and 3rd and between the seventh through the ninth over the first 10 days of February which may be due to synoptic conditions. This is consistent with (Martin et al., 2019), who showed that atmospheric transport and dispersion errors in the BW area are greater during the cold or warm frontal passages over the BW area (Martin et al., 2019) because it is more difficult to model these specific events. As a result, these time windows in the Hovmoller diagrams (Figure 5) show larger spatio‐temporally interacting standard deviations associated with the simulated observations. Further evidence of the structure of spatial and temporal correlations in the model‐data error from the OSSE is shown in Figure S1.
Figure 5.
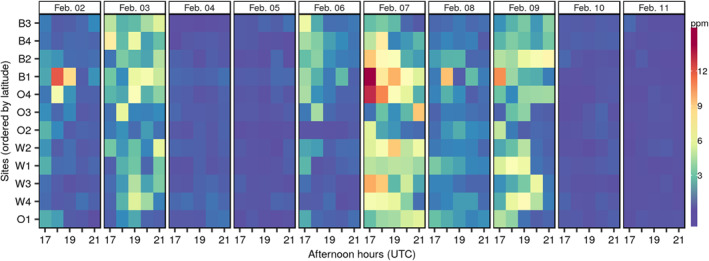
Hovmoller diagram of the ensemble standard deviations as a function of the tower sites (space) and time from February 2nd to 11th, 2016. In the Y‐axis, towers are ordered based on their latitude.
The exploratory analysis above provides motivation to model the temporal and spatial correlation of the observational error within the inversion using a covariance function that not only captures variability in time but also accounts for possible nonexponential and space‐time interacting behavior. This motivates the method that we propose to model transport and dispersion error within our urban OSSE inversion framework.
3. Methods
The following two subsections describe the OSSE study, and the error covariance quantification respectively.
3.1. Observing System Simulation Experiment (OSSE) and Inversion Method
The goal of the OSSE is to explore different ways of modeling atmospheric transport and dispersion error to improve estimation of CO2 emissions. For the OSSE, we employ an estimation domain of 120 × 129 km which encompasses Washington D.C. and Baltimore, Maryland (Figure 1). For the sake of simplicity, we assume emissions to be temporally constant throughout the entire month of February and we estimate emissions spatially resolved at 0.01 × 0.01° (approximately 1 km2). Thus, our resulting state‐vector (or total number of estimates, p) is 15,480. The number of observations (n) depends on the total number of sites and the number of the observational hours used in the OSSE. We only consider five afternoon hours (i.e., 12–4 p.m. local time) when it is considered to have nearly stationary transport. Thus, the number of observations (n) used within the OSSE is 1,680. Note that this spatial resolution of OSSE inversion is the same as the footprint resolution.
We use the “true” emission (s ∗: a 15,480 × 1 vector) and a sensitivity matrix (H), or Jacobian (dimension 1,680 × 15,480), which is comprised of one of the atmospheric transport and dispersion set of footprints (H 3: third member from ensemble Table 1) to generate the “true” synthetic observations (y ∗: a 1,680 × 1 vector)
| (2) |
We use a different ensemble member (H 2: second member from the ensemble Table 1) in the inversion model. This approach introduces transport error into the inversion framework. It mimics a real atmospheric transport and dispersion scenario where we do not know the underlying transport completely, although we can reproduce the atmospheric dynamics well. Note, these two particular ensemble members are neither the most nor least correlated.
The synthetic observations are then used to update a priori CO2 emission (Rodgers, 2000) in a statistically optimal way using the Ensemble Transform Kalman Filter (ETKF) method, which is fast and scalable for high‐dimensional spatial fields. This enables us to test a variety of model parameter estimation strategies (such as parameterizing an exponential decay function in the model‐data mismatch) that can be used with ETKF (see Figure 6 for the flowchart of the OSSE).
Figure 6.
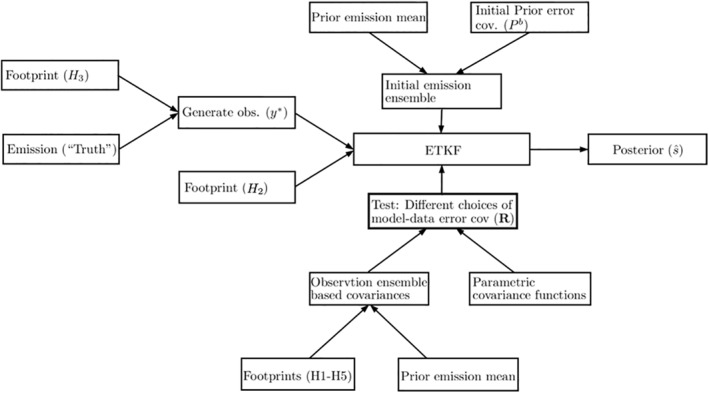
Schematic of the entire flow of the experiment. First, we generate the synthetic observations. Second, we simulate an ensemble from the Gaussian process (see Equation 1) to start Ensemble Transform Kalman Filter (ETKF). Third, we create the model‐data mismatch covariance R using a number of methods including proposed observational ensemble‐based techniques and traditional parametric exponential covariance models. In this study, R represents only one error component that is the error associated with misspecifying the atmospheric transport and dispersion. Once we have a triplet {y*, X b, R} and a footprint H 2, we run ETKF several times to obtain the MLEs of the parameters in R. Finally ETKF is run again with all the parameter estimates to obtain posterior ensemble X a and hence the ensemble mean . Details of the steps are described in this section.
Ensemble Kalman Filter (EnKF) (in particular, ETKF) approximates the Kalman filter by representing the distribution of the state vector with an ensemble of draws from an initial a priori distribution of the states. The ensemble members are then updated based on newly available observation. Ensemble representation in ETKF can be thought as a dimension reduction where only a small number of members are propagated instead of the full joint distribution. We follow the Harlim and Hunt (2005) ETKF construction in this study. The analysis mean and it's ensemble perturbation matrix are connected with the corresponding background mean and the background ensemble by the following Equations 3 and 4. Equation 5 evolves the analysis ensemble at time step t according to a nonlinear (stochastic) model to obtain a forecast ensemble () for the next time step t + 1. However, since we assume temporally constant fluxes, the nonlinear operator M becomes an identity transformation here. This means the analysis ensemble at any time step directly becomes the forecast ensemble for the next time step (Equation 6). The forecast ensemble is also often termed as the background ensemble in data assimilation (DA) literature, including Harlim and Hunt (2005). For simplicity and consistency, over the rest of the article (on or after Equation 6) we drop the subscript t, unless we perform any operation involving successive time steps and denote the forecast ensemble as background ensemble.
| (3) |
| (4) |
| (5) |
| (6) |
Columns of perturbation matrices X (b,a) are of the form for each ensemble member where K is the ensemble size.; y ∗ is the vector of “true” simulated synthetic observations; is the background ensemble mean in observation space or background observations (), where H 2 is the Jacobian matrix (note that H 2 is different from the one used in simulating y ∗ i.e., H 3);
is the analysis error covariance matrix in observational space. R is the model‐data error covariance matrix (or observational error covariance matrix in the DA literature) that characterizes the structure and magnitude of the atmospheric transport and dispersion model errors. Clearly is a function of the background ensemble mean (), background observation ensemble (Y b), mismatch error covariance R, and with being the Kalman Gain Lorenc (1986) analogue.
Although, there is a large body of literature (e.g., J. L. Anderson, 2007a, 2007b; Wang & Bishop, 2003) dedicated to inferences on the covariance inflation parameter for EnKF, we did not employ covariance inflation in this study. First, we tested various inflation parameters and found that the results were insensitive to small deviations from one. Additionally, there have been recent studies that have not used covariance inflation so as to focus on the comparison between methods or to measure impact of different statistical choices relative to one another rather than retrieving most realistic approximation of the emissions (see Liu et al., 2016; Stroud et al., 2018). We adopt their approach given the nature and scope of our study.
Performance of ETKF relies on the initial ensemble choice in a high‐dimensional flux estimation problem where observations are extremely limited in space. To incorporate spatial structure and introduce spatial correlation in the initial ensemble, we create the initial background state vector ensemble X b by sampling from the initial distribution of the prior error with a specified covariance. This is also termed as initial background covariance P 0 or initial prior error covariance. This is similar to the prior covariance matrix employed in traditional Bayesian inversion approaches. In ETKF, the constructed prior error covariance enters the inversion system only at the beginning to create an ensemble of the state vectors.
| (7) |
In ETKF, this initial distribution is assumed to follow a Gaussian distribution with an exponential covariance kernel (Lopez‐Coto et al., 2017; K. L. Mueller et al., 2008; Shiga et al., 2013) described in Equation 1 which is kept fixed over the entire experiment. The components in Equation 7 are defined in Equation 1 of Section 2. We assume background uncertainty of the emission from grid cell i (i.e., ) to be 100% of grid cell i's prior emission. Based on an exploratory variogram analysis of the prior emission excluding the high emitters, we choose and fix the decay length scale L (see Equation 1) of the spatial correlation to be 25 km throughout the experiment. We simulate an ensemble of size 150 from the described Gaussian process with exponential covariance kernel and add the prior emission vector s (described in Section 2.1) to obtain the initial background ensemble X b.
We apply ETKF forwards in time (Equations 3 and 4) with a window of five hours. We shift the window forward by one hour in each iteration starting with the state vector ensemble generated from the prior distribution. We run ETKF in this manner and find maximum likelihood estimates (MLE) of the parameters of the proposed covariances for R (see Section 3.2.1). We find the MLE estimates by maximizing the approximate ETKF likelihood function described in Section 3.2.2. Then, we run ETKF (Equations 3 and 4) again using the estimated covariance parameters and compare the estimated ensemble mean at each time period with the “truth” to evaluate the impact of the proposed covariances on the posterior. While running the ETKF, in the state‐space or flux space, we evaluate the bias and standard deviation (sd) of the differences between the retrieved analysis ensemble mean and the “truth." In the observational space, we compute the correlation coefficient (r) between the “true” synthetic observations (Equation 2) and predicted observations using the posterior ensemble mean. The correlation coefficient facilitates the comparison between the predicted and the true synthetic observations. We also track the evolution of the Bayesian Information Criterion (BIC) over the iterations since we have the log‐likelihood function. Given a fixed set of observational content, BIC ranks the proposed covariance models for R and provides a measure for selecting the best candidate.
We run five different ETKF inversions using various representations of the model‐data error (see Equations 10 and 11, Section 3.2.1). Throughout the experiment, we keep the initial prior error covariance fixed (see Section 4 for the specified values of the covariance parameters) for simplicity. In our final analysis, we compare performance of the overall retrieval under different network settings (12‐, six‐, and two‐tower networks) by using the final bias, standard deviation (sd), and BIC.
3.2. Error Covariances and Estimation of Parameters
For the purpose of comparison and the evaluation of the performance of the proposed methods under a dense and sparse network of observations settings, we consider five ways of constructing the model‐data mismatch error covariance matrix, R. First, we consider two commonly adopted structures of R, which are diagonally constant (R a) and spatially and temporally exponential (R b) (Hu et al., 2015). For the third option, R c, we consider a diagonally varying R coming from the ensemble spread (Equation 8) with no correlations. The fourth and fifth are semi‐parametric structures described in the next section. Table 2 provides a list of the five different types of R considered in this study.
| (8) |
Table 2.
Five Different Types of Model‐Data Mismatch Covariance Matrices R That are Being Considered for the Experiment
| Name | Type |
|---|---|
| R a | Diagonal R with constant |
| R b | Exponentially decaying R in space and time with constant diagonal |
| R c | Diagonal R with ensemble variance |
| R d | Shrinkage based full R from ensemble |
| R e | Regularized (by an exponential taper cov.) sample covariance based full R |
Note. The last three types are proposed transport ensemble‐based error covariances.
Parameter α is a multiplicative constant. The D s and D t are spatial and temporal distance matrices respectively. Symbol ⊗ denotes the Kronecker product. Parameters L s and L t are the spatial and temporal decay lengths respectively.
3.2.1. A Family of Semi‐Parametric Model‐Data Mismatch Covariance R
In addition to R a, R b and R c, we construct a covariance (R d) that is dynamic and spatio‐temporally interacting. Sample covariances (can also be called as ensemble variance) are natural candidates in such cases. The idea of estimating transport and dispersion error covariance from an ensemble of transport models dates back to Engelen et al. (2002). However, Engelen et al. (2002) did not consider the fact that errors could be correlated. The diagnostics proposed in Desroziers et al. (2005) showed usage of ensembles using Kalman Filter error statistics as an unbiased estimator of R. The diagnostics proposed in that work provide correct estimates only when the model is exact. Desroziers et al. (2005) did not explicitly exploit the error correlations either. Methods proposed in this study are in the spirit of previous work but here we extend the concept to accurately incorporate error correlations.
All the flux inversion methods using linear models (e.g., Kalman Filter, Batch Bayesian, Geostatistical inverse method etc.) assume the observation y to be linked with surface flux through a linear operator H (aka the transport operator or footprints) plus error (see Equation 2). Suppose {E 1, …, E n} is a random sample from N p(0, Σ) then the corresponding sample covariance is . It follows that, under the Gaussian assumption on the distribution of errors, the sample covariance is the Maximum Likelihood estimate of this error covariance matrix (T. Anderson, 2003). Although unbiased (with divisor n−1), it is well known (Johnstone, 2001; Stein, 1956, 1975) that sample covariance S n behaves poorly when becomes large (Schäfer & Strimmer, 2005). This is due to distortion in the Eigen structure stemming from spurious correlations. In this study we consider a transport model ensemble of size 5 to represent the model‐data error covariance matrix R which is far less than the total number of observations (here p = number of towers × time‐steps per iteration and the dimension of R is p × p) in each iteration of ETKF. In order to avoid these small sample consequences, we utilize the two‐way shrinkage method proposed by Schäfer and Strimmer (2005) and Opgen‐Rhein and Strimmer (2007). Shrinkage‐based regularized covariances are more efficient than empirical covariances in the mean square error sense, well‐conditioned, and positive‐definite having no problems being inverted and at the same time do not assume an underlying distribution. Schäfer and Strimmer (2005)'s estimator in our context can be written as the following
| (9) |
where s ii, s median, and r ij denote empirical variance, median of the variances and correlation, respectively. Shrinkage coefficients and are estimated from the ensemble (see Opgen‐Rhein & Strimmer, 2007). Typically, unlike ML methods, regularization parameters, like λs, are estimated using different types of loss functions. In this case, it is an expected square error loss (see Schäfer & Strimmer, 2005) on the ensemble covariance at each iteration. We use the R package corpcor associated with the Schäfer and Strimmer (2005) study. This has been applied in many other peer‐reviewed studies (see e.g., Hauser & Demirov, 2013; Nino‐Ruiz & Sandu, 2019; Ogle et al., 2015). Here is the shrinkage reconstruction of . Intuitively, it shrinks the diagonal toward the variances and then shrinks the correlations toward zero, that is, it shrinks toward a diagonal target. We choose this particular shrinkage because we have assumed the ensemble spread to be representative of the spread in transport and dispersion error that constitutes R diagonals. This implies that we have reasonable evidence to construct a diagonal R using the ensemble spread that is representative of the true R diagonal (see Desroziers et al., 2005; Engelen et al., 2002). Shrinkage‐based covariance as described above penalizes the data likelihood. It does not necessarily maximize the posterior likelihood of the fluxes. We introduce a multiplicative scaling factor α on to account for this. We estimate α by maximizing the ETKF posterior likelihood. We do not cite corresponding values of the λs at each iteration here, as they do not add significantly to the interpretation of results.
| (10) |
In order to explore the effect of exponential smoothing as a regularization operation on the empirical covariance we also consider an empirical covariance that is smoothed by a theoretical exponential correlation function. The smoothed is:
| (11) |
where ◦ is the element‐wise Hadamard product between the two matrices, D s, D t, L s, and L t are defined after Equation 8. We adopt this idea from a commonly used technique called “localization." Many of the localization techniques can be cast as a form of “tapering” from a statistical point of view. Furrer and Bengtsson (2007) showed “tapering” as a form of regularization on the covariance matrix that is gradually shrinking the off‐diagonal elements toward zero. However, instead of using the common taper functions (Gaspari & Cohn, 1999; Wendland, 1995, 1998), we use an exponential correlation function for smoothing or tapering the off‐diagonals. Then we estimate the parameters α, L s, L t by maximizing the posterior likelihood. We call the proposed estimators of R as semi‐parametric estimators since they are partly parametric. Clearly, both R d and R e can model error correlations that are spatio‐temporally interacting adaptively based on the underlying error structures.
3.2.2. Likelihood Function and Parameter Estimation
Estimating the covariance parameters involved in EnKF (in particular ETKF) has not been common in the data assimilation or flux inversion community until the last decade (Frei & Künsch, 2013; Stroud et al., 2010). One approach of parameter estimation is to construct the approximate likelihood function constructed with EnKF outputs or Bayesian methods. Let Σ t(θ) = + R t(θ) be the innovation covariance matrix, and ( and both depend on θ implicitly) the innovation vector at time step t where θ is the vector of unknown parameters in R. For a linear Gaussian state space model, the log‐likelihood can be written as (see Shumway & Stoffer, 2017)
| (12) |
Generally, in ENKF, or Σ t(θ) are not known analytically and are approximated using the propagated ensemble. In particular, in ETKF, is never computed explicitly and neither is Σ t(θ). At every time step t, there are K innovation vectors from the background ensemble Y b (see Section 3.1). Therefore, to approximate the likelihood function L(θ) we replace the innovation vector and its covariance by their ensemble analogue as and . Here T is the innovation covariance‐tapering matrix. For T, we use the Wendland1 (Furrer & Bengtsson, 2007) taper covariance with a cutoff radius of 10 based on a grid‐search. We find that beyond the cutoff radius of size 10, the likelihood increment is marginal. The negative log‐likelihood obtained in this way can be minimized (i.e., the likelihood function is maximized) numerically using an optimization method (see Shumway & Stoffer, 2017, Section 6.3 for details) that is suitable for non‐smooth high‐dimensional models (for example the Spectral Gradient Method or Generalized Simulated Annealing). However, to save computational time, we utilize the technique of smoothing the likelihood surface by using common random numbers over each likelihood evaluation (Pitt, 2002; Stroud et al., 2010) and apply a standard quasi Gauss‐Newton algorithm that uses empirical gradients to minimize the negative log likelihood.
4. Results
The results from this analysis include estimating the covariance parameters that are used in constructing the different R configurations outlined in Section 4.1, performance of the proposed R configurations in retrieving the “truth” in Section 4.2, and estimation of total and grid‐scale level emissions in Section 4.3.
4.1. Estimated Covariance Parameters
To evaluate the performance of the different configurations of R, we need to estimate the covariance parameters that are used in their construction. To do this, we employ a box‐constrained quasi‐Newton method (nlminb) to obtain the maximum likelihood estimates of the parameters θ = (α, L s, L t) under three different network configurations. Table 3 shows all of the MLEs with respect to different network configurations. We run ETKF again using these estimated values to obtain state‐vector estimates at every time step.
Table 3.
Maximum Likelihood Estimates (MLE) of the Parameters for the Proposed Covariance Models (See Table 2) Under the Three Different Network Scenarios
| # Towers = 12 | # Towers = 6 | # Towers = 2 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|||||||||
| R a | 20.19 (6E‐2) | 15.27 (6E‐2) | 09.71 (9E‐2) | ||||||||||||||
| R b | 18.54 (5E‐2) | 6.77 | 1 | 14.40 (6E‐2) | 7.95 | 1 | 10.01 (1E‐1) | 31.59 | 1 | ||||||||
| R c | 04.52 (3E‐3) | 03.65 (4E‐3) | 02.71 (6E‐3) | ||||||||||||||
| R d | 01.36 (2E‐4) | 01.39 (5E‐4) | 01.01 (3E‐3) | ||||||||||||||
| R e | 00.87 (1E‐4) | 60 | 20 | 01.01 (3E‐4) | 60 | 20 | 01.69 (3E‐3) | 60 | 20 | ||||||||
Note. Quantities in the parentheses after denote variance of the ML estimator (aka the uncertainty) from the inverse hessian at MLE.
The physical significance of the scaling factor α in Table 3 is not the same across all of the different constructions of R. In the fully parametric cases R a and R b, α represents the model error spread and hence their values are higher and more similar than cases R c through R e. In cases R c through R e, α is a scaling factor on the error covariance matrix estimated offline using the model ensemble. In these cases, α is simply a scaling parameter that adjusts the entire error covariance up or down according to which α value maximizes the posterior likelihood (see Equations 10 and 11). For these cases, a scaling factor of one means that the error covariance will not be adjusted. Consequently, is similar between R d and R e across the network. However, the same estimate indicates over‐dispersiveness for R c across the network which means that transport errors are inflated more than what is expected. This can happen if the error correlations are not accounted for, especially when the error correlations are related to standard deviations.
Overall, when R is either fully parametric (R a, R b) or diagonally varying (R c), we notice the estimated scaling factor decreases as the network becomes sparser. Due to the loss of observational information content in the system, the ML based method—being driven by the likelihood, tries to put more weight onto the priors especially when the transport model is not correctly specified. The parameter estimates become more inconsistent with sparse observational constraints in this setup. This is also reflected by the consistent increase in uncertainty estimates as the network, and hence the observational constraint, becomes more sparse. However, when we have full information about how the errors are interacting in space and time, the semi‐parametric estimators adapt dynamically according to the information content provided by the data. Consequently, the ML estimates of the scaling factors for the proposed cases, being close to one, show the adequacy of the constructed ensemble and the method to represent the magnitude of the true model error variability. The proposed R d constructed this way provides near optimal magnitude even without scaling.
The space‐ and time‐decay parameters {L s, L t} in R b represent the length‐scales of space and time decorrelations present in the model errors. As the network becomes sparser, the estimated spatial decorrelations also increase (second row of Table 3). Estimated time‐decay lengths indicate an absence of time correlation or poor performance of the exponential covariance function. This is consistent with the evidence provided by marginal temporal variograms of the ensemble errors (see Figure 4 and Section 3 for discussion). The decay parameters in R e work as smoothness parameters on the off‐diagonal elements. We choose the upper bound of the spatial decay to be 60 km as this is approximately half of the domain size which is generally the maximum effective spatial correlation length considered in practice. Albeit more than the length of the time window considered here, we fix the upper limit of the time‐decay at 20 h based on the decorrelation length obtained from the variogram analysis. In this case, ML estimates of the decay parameters approach the respective upper bounds regardless of the network configuration. This demonstrates the need of having a flat and smooth exponential function as a regularizer. Note that the taper function works as a smoothing operator on the sample covariance.
4.2. Performance of the Different Covariance Configurations
Figure 7 demonstrates the performance of the different choices of R mentioned in Section 3.2.1 with respect to the bias and SD of the difference between the posterior mean and the truth for the three different network settings (i.e., 12, 6, and 2 towers). Overall, for the dense network case (12‐tower networks; Figures 7a and 7b) both the bias and SD decrease steadily after approximately the 40th iteration (i.e., close to February 9th) except for three big jumps that seem to have destabilized the filter's performance. These phenomena are observed at the 6th, 36th, and 101th iterations (i.e., on the 3rd, 8th, and 22nd days of February). We find that the time series of ensemble spreads in Figure 3 have the greatest difference on those days. As mentioned previously, the Hovmoller plot in Figure 5 also shows large variability in the ensemble perturbations on those days. Parametric R a (diagonal R) and R b (exponential R), being fixed over the entire iterative period, cannot adapt to the bias introduced by the sudden surge in error. This result also indicates that a longer assimilation time period may be needed to help the fixed parametric R a and R b to converge in such cases. Since the R c (varying diagonal R) through R e (regularized R) are semi‐parametric, they dynamically adapt and do not reflect the same types of destabilizing jumps in the flux retrieval. Overall, we see the comparable performance of the shrinkage‐based R d (shrinkage‐based R) and R e in recovering the total flux. Although, the shrinkage‐based R d recovers the total flux better than R e, it is the smoothed semi‐parametric R e that shows lower SD (i.e., better precision) under a sparse observational regime (Figure 7f). Figure 9 confirms the general finding as we see smaller residuals over space with less structure over the roads, when method R d and R e are used.
Figure 7.
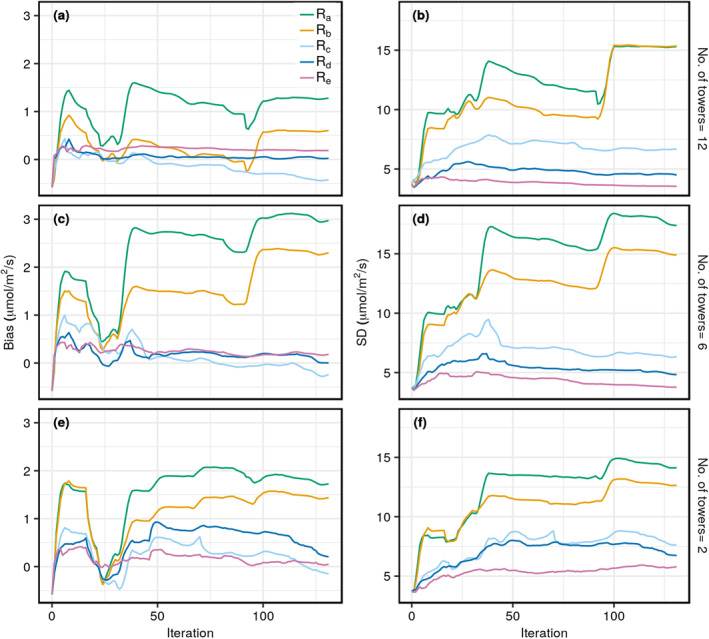
The bias (left panels) and standard deviation (SD, right panels) evolution of the CO2 flux retrieval as a function of the ETKF iteration number. Three different rows correspond to three different network configurations, as indicated to the right of each row. Colored lines correspond to different choices (see Table 2) of the model‐data mismatch covariance R.
Figure 9.
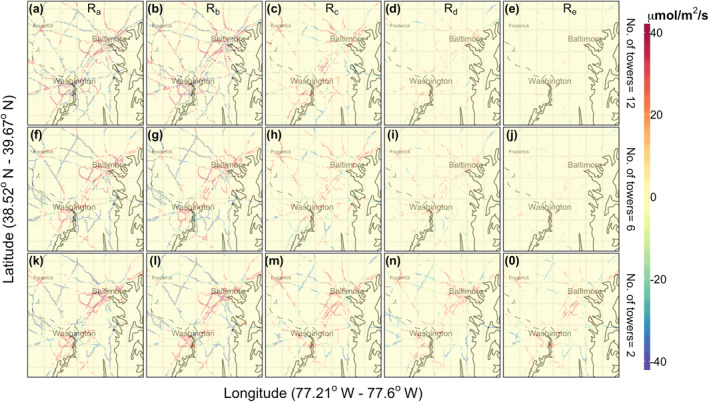
Residual plots of the “truth” minus the finalized retrieved fluxes. Three different rows correspond to three different networks (with number of towers indicated to the right of the rows). The columns represent residual plots with respect to model‐data mismatch covariance R a–R e (see Table 2) as indicated at the top of each column.).
The performance of the flux retrieval using R a through R e changes when there are fewer observations. The same jumps occur on the 6th, 36th, and 101th iterations with the six‐ and two‐tower networks (Figures 7c and 7e). However, these jumps are more pronounced especially for the six‐tower network case. This case is more susceptible to prior and transport error because it has fewer observations than the 12‐tower case shown earlier. At some point, as the observational information content decreases, the model assumptions drive the flux retrieval performance which can, on appearance, look more stable. This is demonstrated in the two‐tower network case results (Figure 7e). Clearly, proper quantification of the space‐time error correlations is crucial in times when the atmospheric transport and dispersion are difficult to model.
4.3. Estimation of Whole‐Domain and Grid‐Scale Emissions
Box plots of the posterior totals in Figure 8 show how well the inversion, using the different covariance matrices (Rs), is able to retrieve the “true” total monthly flux aggregated across the entire flux estimation domain. Although, with a slight negative bias, posterior totals are closer to the truth for R c than the simplistic diagonal constant R a and R b. This is consistent with the bias evolution pattern (sky blue line) shown in Figure 7. This could be due to the larger in the absence of the error correlations that overestimates the true spread of the error (the over‐dispersiveness described earlier). The R d and R e cases clearly show the importance of having the error correlations, that is, the off‐diagonals, in R. Overall, the box‐plots for R d encompass the truth with an uncertainty slightly higher than case R e. The R d, is considerably the best‐performing case from the perspective of accuracy.
Figure 8.
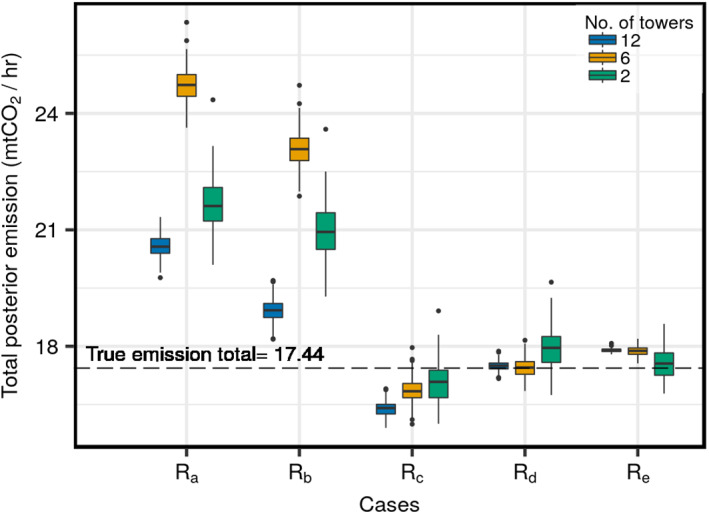
Side by side box and whisker plot of the total posterior emission and respective variability for the five cases (R a−R e) grouped by network. Three colors represent three different networks of different sizes, as indicated in the legend. The dashed black line is the true emission total for the OSSE. Units of emissions have been converted to mtCO2/hr for better readability.
We see that R d and R e recover the “true” grid‐scale fluxes (Figure 9) better than R a through R c. When the observational constraint decreases, as with the six‐tower case, R e (Figures 9i and 9j) yields fluxes that are closer to the “truth” at the grid scale. In the six‐tower network case, although R e performs better, fluxes estimated using all covariances (Rs) result in large grid‐scale residuals. Note, in the two‐tower case, at the aggregated level, the differences between the posterior and the truth using R d are slightly larger than when using R c (see Figure 8). As mentioned earlier, a sparse network of only two towers has very little information to inform the full correlation matrix in space and time. This results in spurious correlations in off‐diagonal entries. However, R e performs better for the two‐tower network case than the other methods because the exponential smoothing provides an additional constraint that diminishes spuriousness.
The performance of R e, in this case is likely not a result of the way the “truth” was constructed which we explain herein. First, the existence of correlation in the “truth” does not clearly translate into the true transport errors. This is because, when emissions are transported into observation space through the transport operator (also known as H), the spatial correlations of both the emissions and atmospheric transport and dispersion become conflated. Second, as shown in Figures 4 and 5, the ensembles have more variability in correlation in time rather than space. This is also true of the synthetic observations (variogram analysis not shown). Since the “truth” was constructed with an exponential structure but with no temporal variability, we assume that the temporal correlation in the synthetic data is mostly due to the atmospheric transport. Therefore, the exponential tapering in R e is helping to constrain mostly the error due to the variability in atmospheric transport rather than the errors due to the exponential spatial structure in the “true” emissions.
5. Discussion
Table 4 summarizes comparative summary statistics, which include the overall bias and SD from Figure 7 as well as the correlation coefficient between the “true” synthetic observations and the transported a posteriori fluxes and BIC values. It is clear from the correlation coefficient (r) that the inversion using the semi‐parametric covariances (i.e., R c through R e) yield fluxes that are in better linear agreement with true observations when convolved with H3. As noted earlier, the standard deviation and bias all improve with the parameterization of the model‐data mismatch, which is further confirmed by the BIC values. Note, that the BIC values cannot be compared across the different network configurations since the informational content in the system (i.e., the set of dependent values) changes.
Table 4.
Summary Table of the Performance Metrics Under Different Choices of Model‐Data Mismatch Covariance and Network Size That are Considered (See Section 3.1) for This Experiment
| # Towers = 12 | # Towers = 6 | # Towers = 2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | SD | r | BIC | Bias | SD | r | BIC | Bias | SD | r | BIC | |
| R a | 1.27 | 15.27 | 0.927 | 79,093 | 2.97 | 17.53 | 0.961 | 31,365 | 1.73 | 14.18 | 0.949 | 9,852 |
| R b | 0.59 | 15.32 | 0.930 | 80,564 | 2.28 | 14.99 | 0.961 | 31,051 | 1.43 | 12.68 | 0.950 | 9,802 |
| R c | −0.43 | 6.65 | 0.986 | 28,570 | −0.25 | 6.34 | 0.993 | 13,881 | −0.11 | 7.74 | 0.988 | 4,190 |
| R d | 0.03 | 4.56 | 0.996 | 13,242 | 0.02 | 4.90 | 0.997 | 8,624 | 0.26 | 6.85 | 0.993 | 3,811 |
| R e | 0.19 | 3.56 | 0.999 | 3,050 | 0.17 | 3.79 | 0.999 | 3,997 | 0.05 | 5.74 | 0.996 | 2,841 |
There are certain characteristics that we observe in this study. Shrinkage‐based R d and R e provide similar small biases, although their spatial pattern recovery is best (especially in the case of R e) as the observational constraint decreases. In addition, the ensemble case (R c) provides biases and uncertainties of aggregated a posteriori fluxes to the full BW domain that are similar to R d. However, they do not spatially recover the emissions as well as R d and R e, suggesting that the choice of the representation of transport and dispersion model error should coincide with the overall goals of a particular study. Although in all three cases, multiple ensemble members are required, the parametrization of R d, and R e is more complex than R c. If the goal is to recover a full domain flux estimate, an R c may be suitable.
The analysis presented herein clearly demonstrates that accounting for space‐time error correlations is crucial during periods with significant synoptic meteorological events. The typical representation of transport and dispersion errors within urban studies, that is, R a and to a lesser extent, R b, may result in large biases because the emission residuals during periods with large transport errors along with prior error can skew the final posterior emission estimates. These error representations show evidence of large standard deviations in the residuals themselves suggesting that R c, R d, and R e are also better able to capture the true emission estimates at the native estimation scale (1 km2 in this study). The semiparametric covariances adaptively model the space‐time interaction and assign a better model‐data mismatch uncertainty to these time periods. Hence, the inversion using these configurations of the model‐data mismatch covariance matrices do not manifest large instability.
We note that the results of this experiment may be sensitive to the choice of the transport models used to create the synthetic observations as well as the one used as the Jacobian in the inversion. However, given that the members used in this study neither represent the extremes of the spread nor are too similar (per Section 3.1), it is unlikely that the conclusions from this study would change significantly. In addition, throughout the study we assume that the errors represented by the ensemble spread represents the true model‐error. We note that the performance of the methods presented herein could be impacted by an ensemble member that is significantly extreme, as explained in the previous section, as well as the size of the ensemble. Given that this study demonstrates methods, the choice of the number of ensembles, the inclusion of an extreme ensemble, or the experimentation on bounds of noise magnitude are left for future investigation.
This study does not account for transport error due to variation at a finer resolution than the transport model. In real‐world application, this is manifested in the representation error when a user averages sub‐hourly observations which smoothes out any fine‐scale variation. Most often, this is regarded as another independent component of the model‐data mismatch and thus appears as the nugget or unexplained variability when distance (in space and/or time) is zero (Cressie, 2015).
Although we perform the experiment for February when fossil fuel emissions dominate the total observational signal, the same approach can be used during the summer months when there is significant biological activity. This is dependent, however, on how the biological fluxes are considered within the inversion. If the biological fluxes are considered well known and subtracted from the observations so that the estimates only include those from anthropogenic sources, R can have another component that stems from errors in the transported bio‐fluxes in the observational space. Otherwise, any errors associated with the modeling of biological fluxes should be considered in the initial background covariance matrix. If this is the former case, one can apply the same methods to compute both the fossil and bio‐component of R in the presence of multiple transport and/or multiple bio‐flux models. However, irrespective of whether R includes the bio‐component or not, proposed approaches to model R will be equally benefited from having dynamic adaptation based on summer months' footprints and leverage this structure over fixed parametric Rs.
In this study, we demonstrate that the dynamically adapted R configurations (R c to R e) outperform other constructions (R a, and R b). This study focused on characterizing the errors associated with atmospheric transport and dispersion. We used a time invariant prior to isolate the errors associated with this component as it has been shown to dominate other error components (e.g., aggregation error, etc.) A direct application of the proposed approaches in presence of time varying fluxes would likely yield a noisier estimate and the relative skill of the proposed choices of R may differ. However, we think that the performance of dynamic R's will hold so long as the ensemble approach captures the underlying variability (see last part of Section 2.1).
Of note here is that the proposed approaches are not reliant on any particular inversion type. In fact, they can be easily adopted within many other legacy inversion frameworks including traditional Bayesian inversions due to their simple structure. Except for the shrinkage parameters that are estimated offline at each iteration, all other parameters in the proposed approaches admit easy derivatives. Therefore, it can be easily incorporated in the traditional Bayesian frameworks.
Finally, we note that our conclusions may be dependent on other choices made herein. We chose plausible representations of all elements (e.g., atmospheric transport, tower locations, emission priors etc.) rather than the most realistic representation of any single element. For example, there may be better representations of the transport model that we could have used as the Jacobian in the inversion. Additionally, other emissions maps, which also include temporally varying fluxes, may represent true emissions in the BW better than the “truth” used herein. However, due to the scope and nature of this study, our goal is to demonstrate the value of these methods, for example, dynamic adaptation of the proposed model‐data mismatch covariance matrices, for a real‐world application. Future investigation should explore the methods' skill using real data.
6. Conclusions
Accounting for temporally and spatially correlated atmospheric transport and dispersion error is important for minimizing bias and recovering spatially resolved emission estimates. We demonstrate that ensemble‐based approaches outperform the traditional choices of modeling transport error correlations that are often too simplistic and ignore complex dynamic behavior. Although the shrinkage‐based regularized ensemble covariance (R d) helps recover the total flux better than the exponentially smoothed ensemble covariance (R e) when the measurement network is dense, the latter method recovers the spatial structures better. In particular, exponentially smoothed ensemble covariance (R e) recovers both the total flux and spatial features better under sparser networks. The effect of the space‐time correlations in the model‐data mismatch covariance matrix decreases when the number of measurement towers decreases. In this case, the representation of the transport and dispersion errors can be reasonably approximated by a diagonal matrix constructed using the ensemble spread of simulated observations based on different transport and dispersion models.
The analysis presented here is intended to provide the first proof of concept that provides an example of how spatio‐temporal structures due to transport and dispersion errors can be incorporated in urban flux inversions leveraging an ensemble of model predictions. In this study, we demonstrate the ability of simple ensemble based, regularized model‐data covariances to significantly improve GHG emission estimates over the standard choices using Bayesian inversion methods at urban scales.
Supporting information
Supporting Information S1
Acknowledgments
The authors thank Israel Lopez‐Coto from National Institute of Standards and technology (NIST) for providing the influence functions and the prior emission inventory; Adam Pinter, Anna Karion, and Sharon Goudji from NIST for their valuable comments. This research was supported by the National Institute of Standards and Technology's Green House Gas Measurement Program (University of Notre Dame, #70NANB19H132).
Ghosh, S., Mueller, K., Prasad, K., & Whetstone, J. (2021). Accounting for transport error in inversions: An urban synthetic data experiment. Earth and Space Science, 8, e2020EA001272. 10.1029/2020EA001272
Data Availability Statement
All data used in this analysis are available at https://doi.org/10.7274/r0-ncf7-4852.
References
- Alden, C. B., Miller, J. B., Gatti, L. V., Gloor, M. M., Guan, K., Michalak, A. M., et al. (2016). Regional atmospheric CO2 inversion reveals seasonal and geographic differences in amazon net biome exchange. Global Change Biology, 22(10), 3427–3443. 10.1111/gcb.13305 [DOI] [PubMed] [Google Scholar]
- Anderson, J. L. (2007a). An adaptive covariance inflation error correction algorithm for ensemble filters. Tellus A: Dynamic Meteorology and Oceanography, 59(2), 210–224. 10.1111/j.1600-0870.2006.00216.x [DOI] [Google Scholar]
- Anderson, J. L. (2007b). Exploring the need for localization in ensemble data assimilation using a hierarchical ensemble filter. Physica D: Nonlinear Phenomena, 230(1–2), 99–111. 10.1016/j.physd.2006.02.011 [DOI] [Google Scholar]
- Anderson, T. (2003). An introduction to multivariate statistical analysis (Wiley series in probability and statistics). [Google Scholar]
- Baker, D., Law, R. M., Gurney, K., Rayner, P., Peylin, P., Denning, A., et al. (2006). Transcom 3 inversion intercomparison: Impact of transport model errors on the interannual variability of regional CO2 fluxes, 1988–2003. Global Biogeochemical Cycles, 20(1). 10.1029/2004gb002439 [DOI] [Google Scholar]
- Berchet, A., Pison, I., Chevallier, F., Bousquet, P., Conil, S., Geever, M., et al. (2013). Toward better error statistics for atmospheric inversions of methane surface fluxes. Atmospheric Chemistry and Physics, 13(14), 7115–7132. 10.5194/acp-13-7115-2013 [DOI] [Google Scholar]
- Chatterjee, A., Michalak, A. M., Anderson, J. L., Mueller, K. L., & Yadav, V. (2012). Toward reliable ensemble Kalman filter estimates of CO2 fluxes. Journal of Geophysical Research, 117(D22). 10.1029/2012jd018176 [DOI] [Google Scholar]
- Chevallier, F. (2007). Impact of correlated observation errors on inverted CO2 surface fluxes from OCO measurements. Geophysical Research Letters, 34(24). 10.1029/2007gl030463 [DOI] [Google Scholar]
- Cressie, N. (2015). Statistics for spatial data. John Wiley & Sons. [Google Scholar]
- Cressot, C., Chevallier, F., Bousquet, P., Crevoisier, C., Dlugokencky, E., Fortems‐Cheiney, A., et al. (2014). On the consistency between global and regional methane emissions inferred from SCIAMACHY, TANSO‐FTS, IASI and surface measurements. Atmospheric Chemistry and Physics, 14(2), 577–592. 10.5194/acp-14-577-2014 [DOI] [Google Scholar]
- Deng, A., Lauvaux, T., Davis, K. J., Gaudet, B. J., Miles, N., Richardson, S. J., et al. (2017). Toward reduced transport errors in a high resolution urban CO2 inversion system. Elementa: Science of the Anthropocene, 5. 10.1525/elementa.133 [DOI] [Google Scholar]
- Desroziers, G., Berre, L., Chapnik, B., & Poli, P. (2005). Diagnosis of observation, background and analysis‐error statistics in observation space. Quarterly Journal of the Royal Meteorological Society, 131(613), 3385–3396. 10.1256/qj.05.108 [DOI] [Google Scholar]
- Engelen, R. J., Denning, A. S., & Gurney, K. R. (2002). On error estimation in atmospheric CO2 inversions. Journal of Geophysical Research, 107(D22). 10.1029/2002jd002195 [DOI] [Google Scholar]
- Frei, M., & Künsch, H. R. (2013). Bridging the ensemble Kalman and particle filters. Biometrika, 100(4), 781–800. 10.1093/biomet/ast020 [DOI] [Google Scholar]
- Furrer, R., & Bengtsson, T. (2007). Estimation of high‐dimensional prior and posterior covariance matrices in Kalman filter variants. Journal of Multivariate Analysis, 98(2), 227–255. 10.1016/j.jmva.2006.08.003 [DOI] [Google Scholar]
- Gaspari, G., & Cohn, S. E. (1999). Construction of correlation functions in two and three dimensions. Quarterly Journal of the Royal Meteorological Society, 125(554), 723–757. 10.1002/qj.49712555417 [DOI] [Google Scholar]
- Gourdji, S., Hirsch, A., Mueller, K., Yadav, V., Andrews, A., & Michalak, A. (2010). Regional‐scale geostatistical inverse modeling of North American CO2 fluxes: A synthetic data study. Atmospheric Chemistry and Physics, 10(13), 6151–6167. 10.5194/acp-10-6151-2010 [DOI] [Google Scholar]
- Gourdji, S., Mueller, K., Yadav, V., Huntzinger, D., Andrews, A., Trudeau, M., et al. (2011). North American CO2 exchange: Intercomparison of modeled estimates with results from a fine‐scale atmospheric inversion. Biogeosciences Discussions, 8(4), 6775. 10.5194/bgd-8-6775-2011 [DOI] [Google Scholar]
- Gurney, K. R., Law, R. M., Denning, A. S., Rayner, P. J., Baker, D., Bousquet, P., et al. (2002). Toward robust regional estimates of CO2 sources and sinks using atmospheric transport models. Nature, 415(6872), 626. 10.1038/415626a [DOI] [PubMed] [Google Scholar]
- Harlim, J., & Hunt, B. R. (2005). Local ensemble transform Kalman filter: An efficient scheme for assimilating atmospheric data. [Google Scholar]
- Hauser, T., & Demirov, E. (2013). Development of a stochastic weather generator for the sub‐polar north atlantic. Stochastic Environmental Research and Risk Assessment, 27(7), 1533–1551. 10.1007/s00477-013-0688-z [DOI] [Google Scholar]
- Hu, L., Montzka, S. A., Miller, J. B., Andrews, A. E., Lehman, S. J., Miller, B. R., et al. (2015). US emissions of HFC‐134a derived for 2008–2012 from an extensive flask‐air sampling network. Journal of Geophysical Research: Atmospheres, 120(2), 801–825. 10.1002/2014jd022617 [DOI] [Google Scholar]
- Johnstone, I. M. (2001). On the distribution of the largest eigenvalue in principal components analysis. Annals of Statistics, 29(2), 295–327. 10.1214/aos/1009210544 [DOI] [Google Scholar]
- Kirschke, S., Bousquet, P., Ciais, P., Saunois, M., Canadell, J. G., Dlugokencky, E. J., et al. (2013). Three decades of global methane sources and sinks. Nature Geoscience, 6(10), 813. 10.1038/ngeo1955 [DOI] [Google Scholar]
- Lauvaux, T., Miles, N. L., Deng, A., Richardson, S. J., Cambaliza, M. O., Davis, K. J., et al. (2016). High‐resolution atmospheric inversion of urban CO2 emissions during the dormant season of the Indianapolis flux experiment (influx). Journal of Geophysical Research: Atmospheres, 121(10), 5213–5236. 10.1002/2015jd024473 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao, J., Wang, T., Wang, X., Xie, M., Jiang, Z., Huang, X., & Zhu, J. (2014). Impacts of different urban canopy schemes in WRF/chem on regional climate and air quality in Yangtze River delta, China. Atmospheric Research, 145, 226–243. 10.1016/j.atmosres.2014.04.005 [DOI] [Google Scholar]
- Lin, J., Gerbig, C., Wofsy, S., Andrews, A., Daube, B., Davis, K. J., & Grainger, C. (2003). A near‐field tool for simulating the upstream influence of atmospheric observations: The stochastic time‐inverted Lagrangian transport (stilt) model. Journal of Geophysical Research: Atmospheres, 108(D16). 10.1029/2002jd003161 [DOI] [Google Scholar]
- Liu, J., Bowman, K. W., & Lee, M. (2016). Comparison between the local ensemble transform Kalman filter (LETKF) and 4d‐var in atmospheric CO2 flux inversion with the goddard earth observing system‐chem model and the observation impact diagnostics from the LETKF. Journal of Geophysical Research: Atmospheres, 121(21), 13–066. 10.1002/2016jd025100 [DOI] [Google Scholar]
- Lopez‐Coto, I., Ghosh, S., Prasad, K., & Whetstone, J. (2017). Tower‐based greenhouse gas measurement network design—The national institute of standards and technology North East corridor testbed. Advances in Atmospheric Sciences, 34(9), 1095–1105. 10.1007/s00376-017-6094-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez‐Coto, I., Ren, X., Salmon, O. E., Karion, A., Shepson, P. B., Dickerson, R. R., et al. (2020). Wintertime CO2, CH4, and CO emissions estimation for the Washington, DC—Baltimore metropolitan area using an inverse modeling technique. Environmental Science & Technology, 54(5), 2606–2614. 10.1021/acs.est.9b06619 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenc, A. C. (1986). Analysis methods for numerical weather prediction. Quarterly Journal of the Royal Meteorological Society, 112(474), 1177–1194. 10.1002/qj.49711247414 [DOI] [Google Scholar]
- Martin, C. R., Zeng, N., Karion, A., Mueller, K., Ghosh, S., Lopez‐Coto, I., et al. (2019). Investigating sources of variability and error in simulations of carbon dioxide in an urban region. Atmospheric Environment, 199, 55–69. 10.1016/j.atmosenv.2018.11.013 [DOI] [Google Scholar]
- Mueller, K., Yadav, V., Lopez‐Coto, I., Karion, A., Gourdji, S., Martin, C., & Whetstone, J. (2018). Siting background towers to characterize incoming air for urban greenhouse gas estimation: A case study in the Washington, DC/Baltimore area. Journal of Geophysical Research: Atmospheres, 123(5), 2910–2926. 10.1002/2017jd027364 [DOI] [Google Scholar]
- Mueller, K. L., Gourdji, S. M., & Michalak, A. M. (2008). Global monthly averaged CO2 fluxes recovered using a geostatistical inverse modeling approach: 1. Results using atmospheric measurements. Journal of Geophysical Research, 113(D21). 10.1029/2007jd009734 [DOI] [Google Scholar]
- Mukherjee, C., Kasibhatla, P., & West, M. (2011). Bayesian statistical modeling of spatially correlated error structure in atmospheric tracer inverse analysis. Atmospheric Chemistry and Physics, 11(11), 5365. 10.5194/acp-11-5365-2011 [DOI] [Google Scholar]
- Nino‐Ruiz, E. D., & Sandu, A. (2019). Efficient parallel implementation of DDDAS inference using an ensemble Kalman filter with shrinkage covariance matrix estimation. Cluster Computing, 22(1), 2211–2221. 10.1007/s10586-017-1407-1 [DOI] [Google Scholar]
- Nychka, D., Bandyopadhyay, S., Hammerling, D., Lindgren, F., & Sain, S. (2015). A multiresolution Gaussian process model for the analysis of large spatial datasets. Journal of Computational & Graphical Statistics, 24(2), 579–599. 10.1080/10618600.2014.914946 [DOI] [Google Scholar]
- Ogle, S. M., Davis, K., Lauvaux, T., Schuh, A., Cooley, D., West, T. O., et al. (2015). An approach for verifying biogenic greenhouse gas emissions inventories with atmospheric CO2 concentration data. Environmental Research Letters, 10(3), 034012. 10.1088/1748-9326/10/3/034012 [DOI] [Google Scholar]
- Opgen‐Rhein, R., & Strimmer, K. (2007). Accurate ranking of differentially expressed genes by a distribution‐free shrinkage approach. Statistical Applications in Genetics and Molecular Biology, 6(1). 10.2202/1544-6115.1252 [DOI] [PubMed] [Google Scholar]
- Peylin, P., Baker, D., Sarmiento, J., Ciais, P., & Bousquet, P. (2002). Influence of transport uncertainty on annual mean and seasonal inversions of atmospheric CO2 data. Journal of Geophysical Research, 107(D19). 10.1029/2001jd000857 [DOI] [Google Scholar]
- Pitt, M. K. (2002). Smooth particle filters for likelihood evaluation and maximization (Technical Report). [Google Scholar]
- Rodgers, C. D. (2000). Inverse methods for atmospheric sounding: Theory and practice (Vol. 2). World Scientific. [Google Scholar]
- Sarmiento, D. P., Davis, K. J., Deng, A., Lauvaux, T., Brewer, A., Hardesty, M., & Palmer, P. (2017). A comprehensive assessment of land surface‐atmosphere interactions in a WRF/urban modeling system for Indianapolis. Elementa: Science of the Anthropocene, 5. 10.1525/elementa.132 [DOI] [Google Scholar]
- Schäfer, J., & Strimmer, K. (2005). A shrinkage approach to large‐scale covariance matrix estimation and implications for functional genomics. Statistical Applications in Genetics and Molecular Biology, 4(1). 10.2202/1544-6115.1175 [DOI] [PubMed] [Google Scholar]
- Shiga, Y. P., Michalak, A. M., Randolph Kawa, S., & Engelen, R. J. (2013). In‐situ CO2 monitoring network evaluation and design: A criterion based on atmospheric CO2 variability. Journal of Geophysical Research: Atmospheres, 118(4), 2007–2018. 10.1002/jgrd.50168 [DOI] [Google Scholar]
- Shumway, R. H., & Stoffer, D. S. (2017). Time series analysis and its applications: With r examples. Springer. [Google Scholar]
- Stein, C. (1956). Inadmissibility of the usual estimator for the mean of a multivariate normal distribution (Technical Report). Stanford University Stanford United States. [Google Scholar]
- Stein, C. (1975). Estimation of a covariance matrix. In 39th Annual Meeting IMS. [Google Scholar]
- Stroud, J. R., Katzfuss, M., & Wikle, C. K. (2018). A Bayesian adaptive ensemble Kalman filter for sequential state and parameter estimation. Monthly Weather Review, 146(1), 373–386. 10.1175/mwr-d-16-0427.1 [DOI] [Google Scholar]
- Stroud, J. R., Stein, M. L., Lesht, B. M., Schwab, D. J., & Beletsky, D. (2010). An ensemble Kalman filter and smoother for satellite data assimilation. Journal of the American Statistical Association, 105(491), 978–990. 10.1198/jasa.2010.ap07636 [DOI] [Google Scholar]
- Wang, X., & Bishop, C. H. (2003). A comparison of breeding and ensemble transform Kalman filter ensemble forecast schemes. Journal of the Atmospheric Sciences, 60(9), 1140–1158. [DOI] [Google Scholar]
- Wendland, H. (1995). Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Advances in Computational Mathematics, 4(1), 389–396. 10.1007/bf02123482 [DOI] [Google Scholar]
- Wendland, H. (1998). Error estimates for interpolation by compactly supported radial basis functions of minimal degree. Journal of Approximation Theory, 93(2), 258–272. 10.1006/jath.1997.3137 [DOI] [Google Scholar]
- Yadav, V., Duren, R., Mueller, K., Verhulst, K. R., Nehrkorn, T., Kim, J., et al. (2019). Spatio‐temporally resolved methane fluxes from the Los Angeles megacity. Journal of Geophysical Research: Atmospheres, 124(9), 5131–5148. 10.1029/2018jd030062 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information S1
Data Availability Statement
All data used in this analysis are available at https://doi.org/10.7274/r0-ncf7-4852.


