Uncertainty quantification of years of potential life lost—based estimates from mortality data summarized as death counts within age intervals

Introduction

Disease burden is often encapsulated in mortality rates. However, given the connection between age and death, mortality rates typically are most influenced by deaths among older adults. Alternative epidemiologic measures of mortality burden have been proposed that explicitly weight deaths at younger ages more heavily [1–3]. One such measure is years of potential life lost [4] (YPLL), which has been used in diverse contexts to quantify premature mortality burden [5,6]. YPLL for an individual fatality i is defined to be an upper reference age $\mathcal{A}$—typically close to a broadly applicable life expectancy—minus age at death a_i if the difference is positive and zero otherwise.

$${\mathrm{YPLL}}_i=\max \{\mathcal{A}-a_i,0\}$$ (1)

Mortality data are often summarized as death counts within age intervals because of privacy issues, such as national death counts from the coronavirus disease 2019 (COVID-19) pandemic [7], precluding exact calculation of YPLL values. In such settings, the standard approach is to operationally replace each individual’s age at death with its interval midpoint for the purpose of calculating aggregate YPLL, a method that implicitly assumes that ages at death within intervals are uniformly distributed [8]. However, no attempt is typically made in applied epidemiologic studies using this “midpoint method” to quantify the uncertainty in YPLL-based estimates because of the administrative interval censoring of ages at death [9–12]. To address this limitation, we propose a straightforward and easily implementable Monte Carlo (MC) simulation procedure that yields point estimates of YPLL-based quantities with associated uncertainty quantification consistent with the assumption of uniformly distributed ages at death within intervals.

Proposed Monte Carlo simulation procedure

Suppose we wish to estimate a scalar quantity θ that is a function F of individual YPLL values. Let d₁, d₂, …, d_K denote the death counts in K mutually exclusive, collectively exhaustive, and chronologically ordered age intervals (L₁ = 0, U₁), (L₂, U₂)…,(L_K, U_K = ∞), respectively, from the study population. The proposed procedure simulates plausible ages at death for each individual at each MC iteration, and an estimate of θ is obtained from their corresponding YPLL values. The collection of MC estimates of θ is then summarized as an overall point and interval estimate of θ, reflecting the uncertainty in the true ages at death. Observe that choosing $\mathcal{A}$ such that $\mathcal{A}\le L_K$ obviates the need to simulate ages at death from (L_K, ∞). The proposed procedure can be described as follows:

1. Let {(L₁, U₁), (L₂, U₂),…, (L_r, U_r)} denote the maximal set of intervals such that L₁ < L₂ < ⋯ < L_r < $\mathcal{A}$, and r < K. For each death i in interval (L_j, U_j), j = 1,2,…,r, independently simulate an age at death a_ij from a continuous uniform distribution corresponding to the interval:

   $${\tilde{a}}_{ij}\stackrel{ind}{\sim }\mathcal{U}(L_j,U_j),i=1,2,\dots ,d_j.$$ (2)
2. Compute a point estimate of θ from the ${\sum }_{j=1}^r{d}_j$ simulated ages:

   $$\widehat{\theta }=F\left({\left\{\max \left\{\mathcal{A}-{\tilde{a}}_{ij},0\right\}\right\}}_{j=1,i=1}^{r,d_j}\right).$$ (3)
3. Repeat steps 1 and 2 to obtain $\mathcal{B}$ point estimates of θ, denoted $\{{\widehat{\theta }}^{(1)},{\widehat{\theta }}^{(2)},\cdots ,{\widehat{\theta }}^{(\mathcal{B})}\}$. The overall point estimate of θ is given by the following equation:

   $$\widehat{\theta }=\frac{1}{\mathcal{B}}\sum _{b=1}^{\mathcal{B}}{\widehat{\theta }}^{(b)}.$$ (4)

Furthermore, a (1 –α) × 100% interval estimate of θ is given by the $\frac{\alpha }{2}$ and $1-\frac{\alpha }{2}$ quantiles of $\{{\widehat{\theta }}^{(1)},{\widehat{\theta }}^{(2)},\dots ,{\widehat{\theta }}^{(\mathcal{B})}\}$:

$${\mathcal{I}}_{1-\alpha }=\left({\widehat{\theta }}_{\frac{\alpha }{2}},{\widehat{\theta }}_{1-\frac{\alpha }{2}}\right),$$ (5)

where ${\widehat{\theta }}_q$ denotes the q ∈ (0, 1) quantile of $\{{\widehat{\theta }}^{(1)},{\widehat{\theta }}^{(2)},\dots ,{\widehat{\theta }}^{(\mathcal{B})}\}$.

The proposed procedure and the midpoint method yield estimates of total YPLL equal in expectation, but challenges can arise when using the midpoint method to estimate age-standardized YPLL rates. The midpoint method requires the age intervals in the mortality data to be aligned with those in the study and standard population—which may require combining age intervals—to calculate age-specific YPLL rates in the study population that are then applied to the standard population. If analyses are based on a coarser representation of the mortality data, study population, or standard population in order to align age intervals, it is expected that resulting estimates will be less accurate. If the age intervals cannot be aligned by combining age intervals, it is not straightforward how to proceed with the midpoint method. A key advantage of the proposed procedure is its flexibility; because simulated ages are continuous, their corresponding YPLL values can be aggregated with respect to an arbitrary collection of age intervals for which age-specific YPLL rates can be calculated and subsequently applied to the standard population.

Illustrative data example

We demonstrate the proposed procedure on COVID-19 death counts by age and sex from the Directorate General of Health in Portugal [13], calculating a point and 95% interval estimate of the age-adjusted male-to-female YPLL rate ratio (RR). The cumulative death counts by age and sex as of July 30, 2020, are presented in the July 31, 2020, daily Directorate General of Health epidemiologic report (pg. 4), included as Supplementary File 1. Although the number of male (n = 867) and female (n = 868) deaths are almost equal, a greater concentration of male deaths occurs at earlier ages, which will be reflected in YPLL calculations.

We use 2020 estimates of the sex-stratified age distribution of Portugal from PopulationPyramid.net [14] (summarized in 5-year intervals up to age 100 years) to calculate sex- and age-specific YPLL rates, and we use their combined overall age distribution as the standard population (see Supplementary File 2 for the corresponding data). Direct age adjustment [15] is used to calculate the male and female age-adjusted YPLL rates, and their quotient is the age-adjusted male-to-female YPLL RR. Consistent with the Organisation for Economic Co-operation and Development Health Statistics standard [16], we use an upper reference age of $\mathcal{A}=70\text{years}$, and we perform $\mathcal{B}=1000$ MC iterations.

Figure 1 displays a boxplot of the 1000 MC estimates of the age-adjusted male-to-female YPLL RR along with the midpoint method estimate for comparison. The overall point estimate of the age-adjusted male-to-female YPLL RR is 1.77 with an associated 95% interval estimate of (1.65, 1.90), meaning that after accounting for differences in the male and female population age distributions, males experienced COVID-19-attributable YPLL before age 70 at a rate estimated to be 77% higher than females with a 95% interval estimate of the true relative increase of 65%—90%. The midpoint method, which requires the Portugal population age intervals to be combined into 10-year intervals, yields an estimate of 1.78 with no uncertainty quantification. R code implementing this reproducible illustrative data example is provided as Supplementary File 3.

Fig. 1.

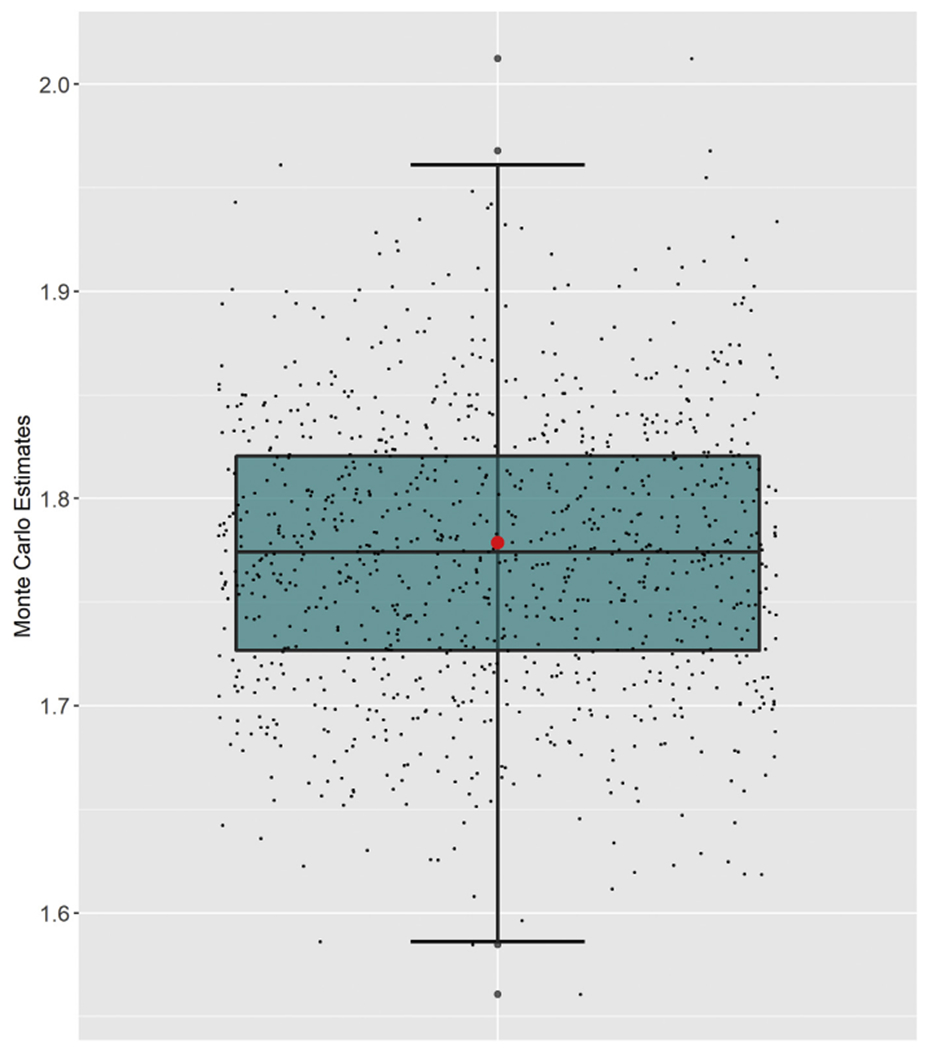
Boxplot of the 1000 Monte Carlo estimates of the age-adjusted male-to-female YPLL rate ratio with respect to cumulative COVID-19 deaths in Portugal as of July 30, 2020, accompanied by jittered points denoting the individual Monte Carlo estimates. The red dot represents the estimate obtained from the midpoint method. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

Conclusions

In summary, we developed a straightforward and easily implementable MC simulation procedure to quantify the uncertainty of YPLL-based estimates from mortality data summarized as death counts within age intervals. We demonstrated the procedure on COVID-19 mortality data from Portugal, calculating a point and 95% interval estimate for the age-adjusted male-to-female YPLL RR with respect to cumulative deaths as of July 30, 2020. We encourage future applied epidemiologic research quantifying the mortality burden of public health problems in terms of YPLL to quantify the uncertainty of their estimates.