Abstract
The COVID-19 pandemic has accelerated the study of the potential of multi-target drugs (MTDs). The mixture of homologues called ivermectin (avermectin-B1a + avermectin-B1b) has been shown to be a MTD with potential antiviral activity against SARS-CoV-2 in vitro. However, there are few reports on the effect of each homologue on the flexibility and stiffness of proteins associated with COVID-19, described as ivermectin targets. We observed that each homologue was stably bound to the proteins studied and was able to induce detectable changes with Elastic Network Models (ENM). The perturbations induced by each homologue were characteristic of each compound and, in turn, were represented by a disruption of native intramolecular networks (interactions between residues). The homologues were able to slightly modify the conformation and stability of the connection points between the Cα atoms of the residues that make up the structural network of proteins (nodes), compared to free proteins. Each homologue was able to modified differently the distribution of quasi-rigid regions of the proteins, which could theoretically alter their biological activities. These results could provide a biophysical-computational view of the potential MTD mechanism that has been reported for ivermectin.
Abbreviations: ENM, Elastic Network Models; NMA, Normal Mode Analysis; CG, Coarse-Grained; GNM, Gaussian Network Model; ANM, Anisotropic Network Models; PSN, Protein Structure Network; SPECTRUS, SPECTral-based Rigid Units Subdivision; SWAXS, Small- and Wide-Angle X-ray Scattering curves
Keywords: SARS-CoV-2, ENM, ANM, GNM, NMA
Table of symbols
- Rg
Radius of gyration
- 〈δ〉
main chain deformability
β-factor (temperature factor)
- 〈ε〉
motion stiffness
- Nf
number of flexible fragment
- Nn
number of connection point or set of vertices between the Cα atoms of the residues that make up the structural network of proteins (nodes)
- Nlk
number of links in path (communication route or structural interaction in the considered system)
- 〈Σ〉
average path force (kcal/mol*Å2)
- 〈Ω〉
average path force correlation
- Ξ
average path (%) of the effective network center (hubs)
- 〈Φ〉
average (%) of correlation of nodes
1. Introduction
COVID-19 is a respiratory infection caused by the SARS-CoV-2 virus, which as of July 2021 has claimed over 4 million lives worldwide (https://www.who.int/emergencies/diseases/novel-coronavirus-2019). This pandemic has been exacerbated by the lack of panviral agents or other effective treatments to limit spread, reduce hospital admissions and prevent death or long-term health complications. To date much of the literature has focused on repurposing marketed drugs, such as hydroxychloroquine and remdesivir, to allow quick clinical adoption [1]. However, despite promising data from in vitro studies many of these compounds have failed to show efficacy in human clinical trails [2]. Faced with these problems, new computational approaches offer attractive alternatives to large-scale in vitro drug screening by using tiered network pharmacology to identify targets and subsequent ligands of interest. Multi-Target Drugs (MTDs) have the potential of binding to two or more targets, enabling the control of complex diseases [3]. Multi-Target Drugs (MTDs) have increasing market value - an estimated 20% of approved drugs are MTDs [4]. Multiple studies have revealed a wide range of antiviral effects of the antihelminthic drug ivermectin, including against SARS-CoV-2 [5], [6], [7]. Interest has been building around the use of ivermectin as a MTD, however, more trials are needed to evaluate the potential efficacy of ivermectin in the clinical setting [5].
Similarly, a wide variety of computational studies have been carried out to determine the multitarget capacity of ivermectin against SARS-CoV-2 [8], [9], [10], [11], [12]. Ivermectin is composed of an approximately 80:20 mixture of two homologues, avermectin B1a (AVM-B1a) and avermectin B1b (AVM-B1b), which differ both in stereochemistry and in the presence of a sec-butyl and isopropyl group, in the position C25, respectively (Fig. 1 ). However, there are few reports on the effect of each homologue on the flexibility and stiffness of proteins associated with COVID-19, described as ivermectin targets Importin α1 (IMPα1), Importin β1 (IMPβ1), Helicase and Mpro, in terms of flexibility and structural and conformational rigidity using methods based on elastic network models (ENMs) coupled to molecular dynamics. In this study, ligand–protein complexes were built by molecular docking using the DockThor-VS web server optimized for the reuse of drugs focused on SARS-CoV-2 (see Fig. 2, Fig. 3, Fig. 4, Fig. 5).
Fig. 1.
Molecular structure of the two homologues considered in this study obtained from PubChem. A) Avermectin B1a (AVM-B1a), and B) Avermectin B1b (AVM-B1b). The differential chemical group of each structure is indicated.
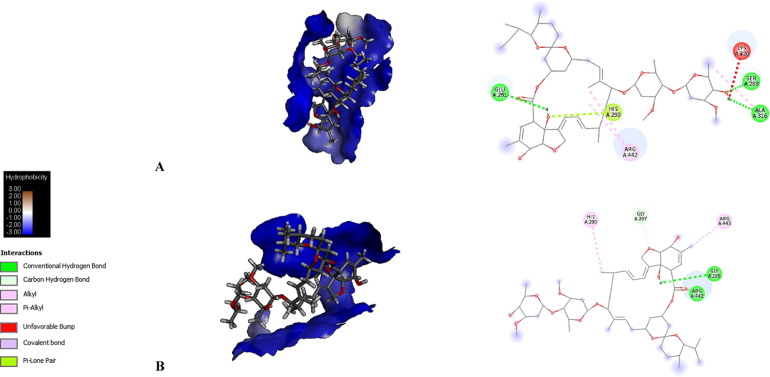
Fig. 2.
Molecular docking is shown in a topological plot of the hydrophobicity of the binding pocket regions of each protein with each avermectin homologue. Typical interactions found with residues in the binding pocket are also shown. A, IMPα1 + AVM-B1a; B, IMPα1 + AVM-B1b.
Fig. 3.
Molecular docking is shown in a topological plot of the hydrophobicity of the binding pocket regions of each protein with each avermectin homologue. Typical interactions found with residues in the binding pocket are also shown. A, IMPβ1 + AVM-B1a; B, IMPβ1 + AVM-B1b.
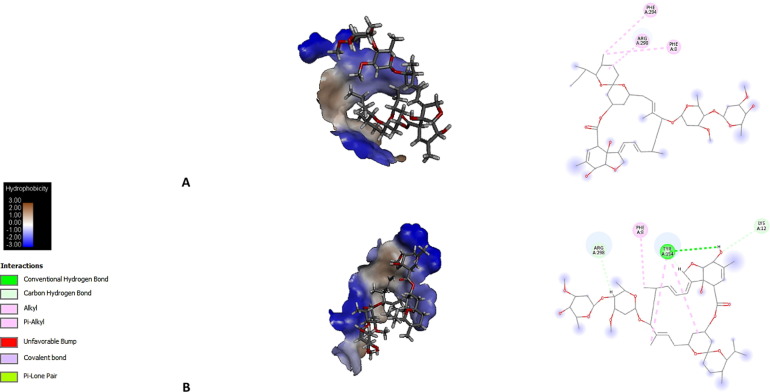
Fig. 4.
Molecular docking is shown in a topological plot of the hydrophobicity of the binding pocket regions of each protein with each avermectin homologue. Typical interactions found with residues in the binding pocket are also shown. A, Helicase + AVM-B1a; B, Helicase + AVM-B1b.
Fig. 5.
Molecular docking is shown in a topological plot of the hydrophobicity of the binding pocket regions of each protein with each avermectin homologue. Typical interactions found with residues in the binding pocket are also shown. A, Mpro + AVM-B1a; B, Mpro + AVM-B1b.
The most favorable complexes obtained under the conditions of this study (they are ligand–protein complexes in the probabilistically most feasible and thermodynamically most favorable positions, with the relatively lower free binding energy generated by the docking simulations) were subjected to molecular dynamics simulations in an explicit water system equivalent to a physiological environment to predict minimum energy structures that were analyzed using Elastic Network Models (ENMs) such as the Gaussian Network (GNM), Anisotropic Network (ANM), Normal mode analysis (NMA), Protein Structure Network (PSN) and spectrum-based quasi-rigid domain decomposition of complexes (SPECTRUS) simulations. These models and their theoretical foundations described below, and allowed us to analyze the perturbations in terms of structural and conformational deformability that may be induced by each homologue of ivermectin in a group of previously identified proteins of interest as a target for ivermectin and associated with COVID-19.
2. Theory
The employment of atomistic Molecular Dynamics (MD) trajectories instead of a single structure provides a dynamic description of the network as links break and form with atomic fluctuations. Dynamic networks can be inferred by employing time averages of the interaction strength cutoff for protein structure graph building, time averages of the interaction energy for edge weighting, frequency cutoffs for link formation and hub definition, and cross-correlation of atomic motions to search for the shortest interaction pathways [13].
The low-frequency modes from Elastic Network Model (ENM) agree well with essential dynamics modes from MD simulations, both in terms of directions and relative amplitudes of motions. The calculation of modes by ENM approaches only takes seconds, consequently, several approaches have already made use of such directional information, e.g., for steering MD simulations, incorporating receptor flexibility in docking approaches, flexible fitting of molecular structures, and efficient generation of pathways of conformational changes [14].
2.1. Elastic network models (ENM)
ENM is a coarse-grained (CG) normal mode analysis (NMA) technique able to describe the vibrational dynamics of protein systems around an energy minimum. Within this technique, the protein structure is described by a reduced subset of atoms (usually Cα-atoms), whose coordinates can be derived either from structure determinations (X-ray crystallography, NMR, etc.) or from molecular simulations. The interactions between particle pairs are given by a single term Hookean harmonic potential. The total energy of the system is thus described by the simple Hamiltonian:
| (1) |
where and are the instantaneous and equilibrium distances between Cα-atoms and , respectively, whereas is a force constant, whose definition varies depending on the type of ENM used. The second derivatives of the harmonic potential are stored in a 3 N × 3 N Hessian matrix (H), whose diagonalization gives a set of 3 N-6 nonzero-frequency eigenvectors and associated eigenvalues.
Two alternative versions of ENM have been implemented. In the first version, termed “linear cutoff-ENM,” the force constant is equal to 1 for pairwise interactions between the Cα-atoms lying within a cutoff distance chosen by the user, and adjacent Cα-atoms are assigned a force constant equal to 10. In the second one, termed “Kovacs-ENM,” the force constant depends on the distance of the interacting particles:
| (2) |
where is constant (with a default value of 40 kcal/mol*Å2). The structural perturbation method (SPM) has been recently described as a technique useful to characterize allosteric wiring diagrams in the context of the ENM lowest frequency modes. According to this methodology, amino acid positions that are relevant to protein dynamics are searched by perturbing systematically all the springs that connect the Cα-atoms and then measuring the residue-specific response of such perturbations in the context of a given mode . The perturbation response is computed as:
| (3) |
where is the eigenvector of mode , is its transpose, and is the Hessian matrix of the perturbation to the energy of the elastic network:
| (4) |
The response is proportional to the elastic energy of the springs that are connected to the residue when they are perturbed by an arbitrary value (0.1), thus defining the most critical nodes for the dynamics of a given mode. A node represents a connection point or a set of vertices within the network, or protein structure graph, typically each protein node is the Cα atom of a residue [15], [16]. The number of modes used for the computation is specified by the user (from 1 up to 3 N-6). It is also possible to generate, for each analyzed mode, a pdb file containing the values of in the β-factor field.
Thermal B-factors from normal modes or thermal B-factor (Debye–Waller factor) of atoms in a protein describe the average squared displacements of the atoms in the protein away from their equilibrium positions at a temperature . They are a useful measure of a protein’s flexibility or rigidity. Normal modes can be used to estimate the B-factors. Theoretical β-factors can be computed inside the ENM module, by the formula:
| (5) |
where νmn is the n th element of eigenvector m, λm is the associated eigenvalue, k is the Boltzmann constant, and T is the temperature in K. Cross correlations between theoretical and experimental β-factors can be also computed according to the following equation:
| (6) |
where and are the theoretical and experimental β-factors, and and are the theoretical and experimental β-factor average over all atoms, respectively. The number of modes used for the computation is specified by the user (from 1 up to 3 N-6). Moreover, involvement coefficients I between the ENM modes and the displacement vector between a given structure/frame T and a reference structure R can be computed according to the following equation:
where and is the coordinate in the two conformers and is the element of eigenvector . By default, the computation is done for all 3 N-6 modes, and only the values of greater than an arbitrary threshold (i.e., 0.2) are output. The cumulative square overlap (CSO) between all modes and the displacement vector is computed according to the following equation:
| (8) |
Finally, residue correlation is computed as:
| (9) |
For further detail, see [13], [17], [18], [19]. The evidence that functional dynamics of proteins relies on highly cooperative, low frequency, global/essential modes caused the diffusion of methods like the NMA able to infer such collective modes. The observed robustness of global modes with respect to details in atomic coordinates or specific interatomic interactions and their insensitivity to the specific energy functions and parameters that define the force field provided support to the development of simplified, i.e. CG, descriptions of protein structures such as the ENM. The latter relies on the fact that the property that dominates the shape of global modes is the network of inter-residue contacts, which is a purely geometric quantity defined by the overall shape or native contact topology of the protein. In recent years, the ENM-based NMA (ENM-NMA) contributed significantly to improving our understanding of the collective dynamics of proteins. For further details, see [13].
2.2. Normal mode analysis (NMA)
NMA is a popular approach to describe the collective functional movements of macromolecules. Each normal mode comprises both a strain vector and a frequency. The first encodes a direction of atomic displacement and the second is related to the relative amplitude of the motion. NMA in Cartesian coordinates is used in online modeling of protein flexibility [20]. NMA is a technique to investigate the vibrational motion of a harmonic oscillating system in the immediate vicinity of its equilibrium. The motions studied are of small amplitude in a potential well and they cannot cross energy barriers. A system is defined to be in equilibrium, or in the bottom of the well (region surrounding a local minimum of potential energy), when the generalized forces acting on the system are equal to zero. At this minimum , the potential energy can be expanded in a Taylor series, yielding a quadratic approximation , to the potential energy , with respect to the generalized coordinates :
| (10) |
where is the deviation from the equilibrium . Similarly the kinetic energy, , is also approximated as a quadratic function. The Lagrangian is given by , which leads to the linear differential equations of motion:
| (11) |
By assuming an oscillatory solution, and substituting it in Eq. (2), one obtains an eigenvalue problem:
| (12) |
where is the matrix of the amplitudes, and is the matrix of the second derivatives of the potential energy and is referred to as the Hessian. is a diagonal matrix, and . The pattern of motions is fully specified by the vibrational normal modes, i.e. the eigenvectors () and their associated eigenvalues (). The normal mode vectors describe in which direction each particle moves, and how far it moves relative to the other particles. Hence, it does not give an absolute amount of displacement for each particle. All particles in each normal mode vibrate with the same frequency. For details, see [21]. ENM-NMA is the basis for web servers (iMODS, WEBnma and webPSN) and algorithms using the alternative approaches Gaussian Network Model (GNM) (HingeProt), Anisotropic Network Model (ANM) (HingeProt) and Protein Structure Network (PSN) (webPSN) [13], [19], [20], [21], [22].
2.3. Gaussian network model (GNM)
GNM predicts the relative magnitudes of fluctuations, describing a protein as a network of connected by springs of uniform force constant if they are located within a cutoff distance (10 Å in this study). In GNM, the interaction potential for a protein of residues is:
| (13) |
where and are the equilibrium and instantaneous distance between residues and , and is Kirchhoff matrix, which is written as follows:
| (14) |
Then, square fluctuations are given by
| (15) |
The NMA are extracted by eigenvalue decomposition: , where is the orthogonal matrix whose kth column is kth mode eigenvector. is the diagonal matrix of eigenvalues, can be written in terms of the sum of the contribution of each mode as follows:
| (16) |
Thus, the cross-correlation can be calculated by
| (17) |
The cross-correlation value ranges from −1 to 1: positive values mean that two residues have correlated motions (motions in the same directions), while the negative values mean that they have anticorrelated motions (motions toward each other).
2.4. Anisotropic network model (ANM)
ANM predicts the directionalities of the collective motions in addition to their magnitudes. ANM in an extension of the GNM, both are coarse-grained residue level elastic network models. In ANM, the interaction potential for a protein of residues is;
| (18) |
The motion of the ANM mode of proteins is determined by 3 N × 3 N Hessian matrix H, whose generic element is given as follows:
| (19) |
where , , and represent the Cartesian components of residues and is the potential energy of the system. used here is 18 Å. Accordingly, ANMs provide the information not only about the amplitudes but also about the direction of residue fluctuations. For details, see [18], [19].
GNM is used to calculate mean-square fluctuations and correlation between the fluctuations of residues, and ANM to generate the conformations that describe the fluctuations of residues from the average X-ray structure in the principal directions of motion. GNM results are more reproducible, and thus are preferentially used for evaluating square displacements in low frequency modes [19].
2.5. Protein structure network (PSN)
PSN gives more insights into the global properties of protein structures. The representation of protein structures as networks of interactions between amino acids has proven to be useful in a number of studies, such as protein folding, residue contribution to the protein–protein binding free energy in given complexes, and prediction of functionally important residues in enzyme families [23]. All these aspects pertain to the issue of intra-molecular and inter-molecular interaction.
PSN is constructed from the atomic coordinates of residues, which represent the nodes of the network. Two nodes are connected by an edge if the percentage of interaction between them is greater than or equal to a given Interaction Strength cutoff;
| (20) |
where is the interaction percentage of nodes and , is the number of side-chain atom pairs within a given distance cutoff (4.5 Å as a default), and and are, respectively, the normalization factors (NF) for residues and , which take into account the differences in size of the different nodes and their propensity to make the maximum number of contacts with other nodes in protein structures.
The are calculated for all node pairs excluding , where n is a given neighbour cutoff (2 as default), and each node pair with an value greater than or equal to a given cutoff is connected by an edge. Different networks can be achieved by probing a range of I min cutoffs. At high cutoffs, only nodes with high number of interacting atom pairs will be connected by edges, indicative of stronger inter-residue interactions. At a given cutoff, those nodes that realize more than a given number of edges (4 as default) are called hubs. The percentage of interaction of a hub node is;
| (21) |
where is the hub interaction percentage of node , is the number of side-chain atom pairs within a given distance cutoff and is the normalization factor of residue . Node inter-connectivity is finally used to highlight cluster-forming nodes, where a cluster is a set of connected amino acids in a graph. For details, see [13], [17], [24].
3. Materials and methods
3.1. Building of complexes with molecular docking
The crystal structure of protein complexes speculated as possible mechanistic pathways for ivermectin in the in vitro inhibition of SARS-CoV-2 were considered (Fig. 2). As the nuclear import for macromolecules is facilitated by importins, the structures of importin α1 subunit (PDB: 5KLR) from Mus musculus and importin β1 subunit (PDB: 2P8Q) from Homo sapiens were used as a model for the members of the nuclear import superfamily. The host nuclear import system can be bound and sequestered by pathogens such as SARS-CoV-2 allowing transportation of viral proteins to the host nucleus leading to increased viral replication [25], [26], [27], [28], [29]. Additionally, we also consider the multi-functional helicase (nsp13) of SARS-CoV-2 responsible for viral replication (PDB: 6ZSL) [30], [31], [32], and the main protease (Mpro) of SARS-CoV-2 (PDB: 6LU7) as it is a key enzyme of coronaviruses and has a fundamental role in mediating viral replication and transcription, making it an attractive target for drugs [33], [34], [35], [36], [37]. All structures were obtained in PDB format from the RCSB Protein Data Bank (https://www.rcsb.org/). The homologues structures of avermectin B1a (AVM-B1a, CID_6321424) and avermectin B1b (AVM-B1b, CID_6321425) that make up ivermectin were obtained from PubChem (https://pubchem.ncbi.nlm.nih.gov/) in SDF format and converted to a PDB format using the OpenBabel-3.0 converter [38].
The complexes were built in the DockThor-VS web server (https://dockthor.lncc.br/v2/) optimized for the design and reuse of drugs focused on SARS-CoV-2 [39]. The DockThor program is a phenotypic multiple solution steady-state stochastic genetic algorithm (SSGA), which uses crowding as a search method. Crowding method is a technique used in genetic algorithms to preserve diversity in the population and to prevent premature convergence to local optima. It consists of pairing each offspring with a similar individual in the current population (pairing phase) and deciding which of the two will remain in the population (replacement phase). This genetic algorithm is able to handle a wide and diverse set of data as the variables to be optimized are called genes and the chains that contain the genes are known as chromosomes, allowing for analysis of other macromolecules including proteins. It differs from the simple genetic algorithm in that the tournament selection does not replace the selected individuals in the population and, instead of adding the children of the selected parents to the next generation, the best two individuals from the two parents and the two children are added back to the population so that the population size remains constant, and therefore has multiple phenotypic solutions [40], [41], [42].
The DockThor-VS platform utilizes a topology file for the ligand and a specific input file for the protein containing the atom types and partial charges from the MMFF94S force field, and both are generated using the in-house tools MMFF Ligand and PdbThorBox. The file of the ligand is generated by the MMFF Ligand program, which utilizes the facilities of the Open Babel chemical toolbox for deriving partial charges and atom types with the MMFF94S force field, defining the rotatable bonds and the terminal hydroxyl groups, and calculating the properties necessary for computing the intramolecular interactions. The PdbThorBox program is used to set the protein atom types and the partial charges from the MMFF94S force field. Thus, in the DockThor program, both protein and ligand are treated with the same force field in the docking experiment. Subsequently, the results are analyzed using DTStatistics.
The Web server utilizes the computational facilities of the Brazilian highperformance platform (SINAPAD, https://www.lncc.br/sinapad/) and the supercomputer SDumont (https://sdumont.lncc.br/). The complexes were built using the flexibility algorithm and blind docking. The affinity prediction and ranking of distinct ligands are performed with the linear model (mathematical algorithms that make it possible to determine the location of an active segment of protein from an analysis of the potential energy matrix of the electrostatic interaction between various segment) and DockTScore GenLin scoring function [39], [43]. To increase accuracy 30 runs were made with 106 evaluations per run. As is usually done, all the water molecules were removed and the PDB files were separated into two different files, one containing the protein and the other containing the ligand structure. All the molecular force field parameterisations are performed automatically by the programs cited. The remaining settings, conditions and parameters offered by the program were used in the default mode.
To validate the docking results, the Pose&Rank server (https://modbase.compbio.ucsf.edu/poseandrank/) was used to score the protein–ligand complexes, using the statistical scoring function dependent on the atomic distance RankScore. RankScore is a method that has been optimized to distinguish ligands from molecules that do not bind. Again, all the water molecules were removed and the PDB files were separated into two different files, one containing the protein and the other containing the ligand structure. Only the three runs with the most favorable berth were considered in the sampling of the probabilistically most feasible and thermodynamically most favorable positions in the complexes. A thermodynamically stable ligand–protein complex is represented by the system with the relatively lower free binding energy generated by the docking simulations [44]. This criterion was used to discriminate the complexes that would be subjected to further analysis.
3.2. Preparation of complexes with molecular dynamics (MD) simulations
Simulations for a docking were carried out to sample the minimum energy conformations and study the structural and conformational alteration of the complexes through the subsequent analysis of the elastic network. For a protein–ligand complex, the MD system was first relaxed through a series of minimization procedures. There were three phases for a MD simulation: the relaxation phase, the equilibrium phase, and the sampling phase, as recommended. The MD simulation of the crystal structures was carried out in an explicit water system. Specifically, the solvation of the system was carried out in a solvation box of 8.0 Å [45]. Our MD system also consisted of one copy of each protein system and one copy of the docking ligand. An Amber99SB-ILDN force field was applied to the complex, with TIP3P water model including ion particles of Cl– in order to neutralize the total charge of the system. For this, the system simulates the diffusion of salts between the solution and the crystalline phases (for a ligand–protein system with a net charge, the counter ions are usually modeled in a slight excess over the co-ions in the crystalline phase and close to the chain side charged amino acids to maintain overall charge neutrality) [45], [46], [47]. In protein systems, TIP3P water is suitable for the Particle Mesh Ewald method (PME). Water plays an important role in almost all biological simulations that have an explicit solvent and typically represents more than 80% of the particles in the simulations. Water-water interactions dominate both computational cost and surrounding properties. In this sense, and although there are several water models, we used TIP3P, since it is an important water model widely used in various biological simulations [45], [46], [48].
Periodic boundary conditions were applied and the Berendsen algorithm was adopted to carry out molecular docking at constant temperature and pressure (300 K and 1 atm, respectively). After initially applying the steepest descent-based simulation method (5000 steps) and then the conjugate gradient energy minimization method (5000 steps) with position constraints on the atoms of the protein–ligand complex, modeling was carried out at an initial simulation of 100 ps with the positions of the atoms of the protein–ligand complex constrained by a force constant of 10 kcal/(mol Å2) to allow water molecules to diffuse around the protein and achieve equilibrium with the protein–ligand system. All model water molecules were treated as rigid bodies, thus allowing a simulation time step of 2 fs. The PME was used to calculate the electrostatic contribution to nonbonded interactions with a cutoff of 14.0 Å and a time step of 1 fs [46]. The cutoff distance of the Van der Waals interaction was 14.0 Å. After this equilibration run, the NVT (canonical set model where quantity of substance (N), volume (V) and temperature (T) are conserved) production run at 300 K was performed with the cell size remaining the same [45], [46]. The SHAKE algorithm (algorithm used to satisfy link geometry constraints) was applied to the system [45], [46], and the time step was set to 2 fs. The minimized energy structures were obtained in PDB format every 10 ns as target structures extracted from a 100 ns trajectory to be used in the following analyzes. Finally, we obtained a minimized energy structure at 100 ns and 10 instantaneous structures every 10 ns. All MD simulations and additional adjustments were performed using cosgene/myPresto [8], [36], [49]. Cosgene/myPresto is available at http://presto.protein.osaka-u.ac.jp/myPresto4/index_e.html.
3.3. Comparative study of the conformational fluctuations of the ligand–protein complexes
The WAXSiS method is an alternative method of molecular dynamics that was used to analyze the two SARS-CoV-2 proteins and two human proteins investigated in this study. Small- and Wide-Angle X-ray Scattering (SWAXS) curves based on explicit-solvent all-atom MD simulations were calculated on WAXSiS server (http://waxsis.uni-goettingen.de). SWAXS is used to detect global parameters of biomolecules, such as the radius of gyration. All settings, conditions and parameters offered by the program were used in the default mode. In all cases the simulations considered the number of atoms in the envelope, the frames per simulation, the simulation time and the equilibrium time, the number of solute atoms and water molecules, as well as the neutralization of the simulation cell [4].
We used the HullRad (http://52.14.70.9/index_test.html) method to predict the hydrodynamic properties of the molecular structures accurately and quickly. This method uses a convex hull model to estimate the hydrodynamic volume of the molecule and the Radius of gyration (Rg). It works well for both folded proteins and ensembles of conformationally heterogeneous proteins. The convex hull method is implemented in a Python script [50].
Tools from the energy-based Bhageerath package (http://www.scfbio-iitd.res.in/software/proteomics/rgnew1.jsp) were used to narrow the search space for tertiary structures of small globular proteins and predict the Rg. The protocol comprises eight different computational modules that form an automated filtering system that combines physics-based potentials with biophysical filters to arrive at 10 plausible candidate structures from sequence and secondary structure information [51]. To evaluate the conformational quality of each structure, ProSA-web (https://prosa.services.came.sbg.ac.at/prosa.php) was used. ProSA-web is used to calculate the z-score of a specific model and correlate this score to those calculated scores from all publicly available structures on PDB website [52].
3.4. Comparative study of structural deformation of complexes
Molecular flexibility was determined by Normal Mode Analysis (NMA) combined with coarse-grained (CG) on iMOD server (http://imods.chaconlab.org/) in an advance mode using sigmoid Elastic Network Model (ENM). iMOD provides Normal Mode Analysis (NMA) combined with Coarse-Grained (CG) and describes molecular flexibility based on localized displacements or collective conformational changes by diagonalizing the Hessian and kinetic energy matrices for solving the Lagrangian equations of motion of macromolecular complexes at extended timescales [4]. Tools were used to predict parts of rigid protein complexes and the flexible regions connecting them in the native topology of protein chains using ENM.
HingeProt (http://www.prc.boun.edu.tr/appserv/prc/hingeprot/index.html) was used to apply both the Gaussian Network Model (GNM) and the Anisotropic Network Model (ANM). GNM and its extension ANM are coarse-grained residue level ENMs. GNM predicts the relative magnitudes of the fluctuations, whereas ANM predicts the directionalities of the collective motions in addition to their magnitudes. GNM results are more reproducible, and thus are preferentially used for evaluating square displacements in low frequency modes. Here GNM is used to calculate mean-square fluctuations and correlation between the fluctuations of residues, and ANM to generate the conformations that describe the fluctuations of residues from the average X-ray structure in the principal directions of motion [16], [19].
To explore the collective movements of the protein complexes, the NMA template was also used considering the internal coordinates (torsion space). NMA in internal (dihedral) coordinates naturally reproduces the collective functional motions of biological macromolecules. For this, the iMODS server was used (http://imods.chaconlab.org.) [20] and WEBnma v2.0. In WEBnma, the force field used for computing the normal modes is the C-α force field. It uses only the C-α atoms of the protein which are assigned the masses of the whole residue they represent. Since it uses a coarse-grained model, frequencies and energies are predicted on relative scales and, therefore, normalized and unitless [22], [53].
The webPSN (http://webpsn.hpc.unimo.it/wpsn.php) was used for its high-performance investigation of allosterism in biological systems, which uses a mixed protein structure network (PSN) and an ENM-NMA (PSN-ENM), strategy to predict the interaction structure between residues in proteins (structural communication) [13]. Finally, the SPECTRUS (http://spectrus.sissa.it/#home) server was used, which performs a decomposition into quasi-rigid domains of proteins or protein complexes, based on the analysis of the distance fluctuations between pairs of amino acids. For this, the MD trajectories treated under the previous conditions are used to compare the functional dynamics of protein complexes with different degrees of structural similarity. Similarly, this method uses ENM that, thanks to the specific properties of each protein complex and its free energy landscape, can reliably reproduce structural fluctuations [54].
4. Results and discussion
4.1. Comparative study between conformational fluctuations of protein-avermectin complexes
The protein–ligand complexes presented a thermodynamically favorable and differential docking between each homologue with each of the tested structures (see Fig. 2, Fig. 3, Fig. 4, Fig. 5 ). The genetic algorithm used predicted a docking of AVM-B1b with Mpro with ΔG = -10.2 kcal/mol, and of AVM-B1a with ΔG = − 9.6 kcal/mol. For the helicase, the free binding energies were ΔG = -10.2 kcal/mol and ΔG = − 9.1 kcal/mol for AVM-B1b and AVM-B1a, respectively. For IMPα it was ΔG = -8.9 kcal/mol and ΔG = − 8.7 kcal/mol for AVM-B1b and AVM-B1a, respectively. And for the IMPβ of ΔG = − 8.4 kcal/mol and ΔG = -8.9 kcal/mol for AVM-B1b and AVM-B1a, respectively (see Table 1 ).
Table 1.
Comparative analysis of the molecular docking of each homologue (AVM-B1a and AVM-B1b) obtained with each of the proteins using the different affinity and scoring methods.
| Target | ΔG (kcal/mol) |
Ki (10-7 M) |
MMPBSA (kcal/mol) |
INTERACTIONS |
||||
|---|---|---|---|---|---|---|---|---|
| HB1a | HB1b | HB1a | HB1b | HB1a | HB1b | HB1a | HB1b | |
| IMPα1 | −8.9 | −8.7 | 3.3 | 4.6 | −70.9 | −100.1 | N-188HB, W-184HB, N-228H, E-266H, R-227H, W-184H, W-231H, N-188H, N-146H, D-270H, S-149H, A-269H, L-307H, T-311H, P-308H, W-273H | S-149HB, N-228HB, R-238HB, E-266HB, S-149H, D-270H, N-235H, G-191H, R-238H, G-150H, D-192H, W-231H, N-188H, E-266H, G-187H, A-148H, G-224H, N-228H, R-227H, W-184H |
| IMPβ1 | −8.4 | −8.9 | 7.5 | 3.0 | −36.8 | −59.1 | K-62HB, K-60H, M−61H, K-62H, R-53H, L-64H, I-54H, D-63H, R-52H | K-62HB, K-60H, M−61H, K-62H, R-53H, L-64H, I-54H, D-63H, R-52H |
| Helicase | −9.1 | −10.2 | 2.3 | 0.4 | −83.1 | −79.6 | S-289HB, A-316HB, H-290HB, E-261HB, R-442HB, E-319H, L-317H, A-316H, S-289H, R-443H, E-540H, G-285H, G-538H, S-264H, D-260H, R-442H, H-290H, F-262H, G-287H, T-286H, E-261H, K-323H, Y-324H, K-320H | E-261HB, S-289HB, A-316HB, T-286H, G-285H, G-538H, G-287H, R-443H, E-540H, E-319H, S-289H, L-317H, H-290H, A-316H, S-264H, D-260H, R-442H, F-262H, E-261H, K-320H, Y-324H, K-323H |
| Mpro | −9.6 | −10.2 | 1.0 | 0.4 | −73.1 | −67.9 | R-298HB, Y-154HB, F-8H, I-152H, F-294H, V-297H, D-153H, G-302H, E-299H, S-301H, R-298H, Y-154H, K-12H, D-155H, P-9H | Y-154H, D-153H, I-152H, F-264H, F-8H, R-298H |
Binding energy values reported using complexes and similar algorithms are shown. These are indicated in superscript against the values in this study highlighted in black. Ki, inhibition constant for binding of ligand to proteins in units of M; HB1a, Avermectin B1a; HB1b, Avermectin B1b. HB, Hydrogen Bonds; H, Hydrophobic Interactions; A, Alanine; R, Arginine; N, Asparagine; D, Aspartic Acid; E, Glutaminic Acid; Q, Glutamine; G, Glycine; H, Histidine; I, Isoleucine; L, Leucine; K, Lysine; M, Methionine; F, Phenylalanine; P, Proline; S, Serine; T, Threonine; W, Tryptophan; Y, Tyrosine; V, Valine.
AVM-B1a bound multiple W and N-type residues, while AVM-B1b bound both W and N-type residues, as well as D192 and G150 residues in IMPα (see Table 1). These interactions are important because part of nuclear import involves the recognition of IMPα from nuclear localization signals (NLS). NLS are recognized by an IMPα linker, which, when bound by IMPβ1, can mediate transport across the nuclear pore complex. IMPα retains an IMPβ-binding domain (IBB) responsible for binding to IMPβ1 and ten Armadillo tandem repeat motifs (ARM), the efficiency of nuclear transport depends on the binding affinity to NLS-IMPα, the basis for recognition of IMPα-NLS lies in the structure of the ARM repeats, rich in conserved residues of type W and N, described as part of the main binding site, while residues D192 and G150 are key for the affinity of IMPα to NLS. It has been reported that the disturbance in the interaction with residues D192 and G150 alter the binding of NLS to IMPα with a decrease of up to 3 kcal / mol in the free binding energy [27].
Both homologues at IMPβ1 bound to residues within the 52–64 region (see Table 1), which is important because similar to IMPα, snurportin 1 (SNP1) transport adapter-mediated nuclear import uses an IMPβ binding domain (IBB) to recruit the IMPβ receptor and gain access to the nucleus, and the IBB domain has been reported to contain binding determinants for IMPβ spanning residues 25–65 and includes the IMPα IBB homology region (αIBB) [55]. Both homologues bound to residue S-289 and to residues within the 523–542 region, which are part of putative functional sites in helicase (see Table 1). In helicase, residue S-289 is part of the active site of ATP hydrolysis reported in SARS-CoV and SARS-CoV-2. In addition, the segment of residues 523–542 has also been determined as part of the dsDNA binding site [56]. It was found that both homologues interact with the residue R-298 (see Table 1), which has been reported as key in the catalytic activity of the enzyme. This residue has been described to be involved in dimerization of this protein and plays a key role in the catalytically active conformation of Mpro [57], [58].
The Z-Score showed conformational fluctuations between free protein and low-energy ligand–protein complexes. Starting from this model, it was observed that all the Avermectins-Protein complexes presented differences in the distances of their Cα atoms, as well as in their energetics at 100 ns of simulation and with respect to their corresponding free protein subjected to the same dynamic conditions. In ProSA-web, the most extreme Z-Score values were related to more dynamic and distant conformations of the free protein. This applies both for very negative values and for values very close to 0, since they tend to fall outside the Z-Score obtained from all the protein chains determined experimentally in the Protein Data Bank (PDB). In fact, the Z-Score for proteins such as the Multidrug ABC transporter (PDB: 2HYD) has been reported to be −8.29, which is in the range of native conformations. Whereas according to the ProSA-web results obtained for the homologous ABC transporter protein of multiple drugs (PDB: 1JSQ), the Z-Score of this model is − 0.60, a value too high for a typical native structure [52].
In IMPα1, the complexes with the homologues presented the most distant conformational fluctuation from the free protein one with a Z-Score more negative than that obtained for the ligand-free protein, which suggests unfolding of this protein with both stereoisomers. On the contrary, although a similar trend towards unfolding against Mpro was predicted, especially with compound B1b, the results are not very significant in terms of the Z-Score. In contrast, the results obtained for IMPβ1 suggest refolding or compactation of structure in all cases. While for the case of the helicase, the results indicate that only with AVM-B1a induced conformational changes of this protein (Table 2 ).
Table 2.
Comparison between Z-score, radius of gyration and hydrodynamic radius in relation to the minimum energy structure at 100 ns MD simulation for each complex.
| Complexes | Simulation time (100 ns) |
|||||
|---|---|---|---|---|---|---|
| Z_Score | Rga | Rgb | Rgc | Rhd | Rhe | |
| IMPα1 | −8.50 | 21.94 | 21.89 | 21.93 | 22.06 | 23.92 |
| IMPα1 + AVM-B1a | −12.20 | 28.16 | 28.12 | 23.92 | 28.53 | 28.16 |
| IMPα1 + AVM-B1b | −10.38 | 28.78 | 28.64 | 23.92 | 28.91 | 28.78 |
| IMPβ1 | −5.93 | 15.61 | 14.92 | 14.92 | 15.31 | 16.33 |
| IMPβ1 + AVM-B1a | −4.87 | 14.73 | 15.48 | 14.72 | 15.55 | 16.33 |
| IMPβ1 + AVM-B1b | −4.72 | 14.68 | 15.17 | 14.67 | 15.16 | 16.33 |
| Helicase | −5.27 | 32.07 | 32.02 | 31.97 | 32.51 | 33.51 |
| Helicase + AVM-B1a | −5.03 | 31.91 | 31.34 | 31.32 | 31.67 | 33.51 |
| Helicase + AVM-B1b | −5.24 | 32.78 | 32.14 | 32.09 | 32.54 | 33.51 |
| Mpro | −6.17 | 21.65 | 21.56 | 21.62 | 21.55 | 21.41 |
| Mpro + AVM-B1a | −6.50 | 21.76 | 21.71 | 21.72 | 21.86 | 21.41 |
| Mpro + AVM-B1b | −6.28 | 22.13 | 22.02 | 22.09 | 21.95 | 21.41 |
, radius of gyration (Rg) (Jayaram et al., 2006).
, radius of gyration (Rg) with WAXSiS server.
, radius of gyration (Rg) with HullRad.
, radius hydrodynamic (Rh) with WAXSiS server.
, radius hydrodynamic (Rh) with HullRad. Units for all radii are in Angstroms (Å).
The scores obtained by the ProSA server for all structures, validate that most of the predicted complexes differ from free protein and show slight conformational changes after simulations, with values within those reported [59], [60], [61], a phenomenon that was observed more consistently in the AVM-B1a-bound complexes.
The radius of gyration (Rg) can be used as a measure of the compactness of a protein which allows understanding of its folding properties. Small Rg values indicate a folding whereas high Rg values show an unfolding for a protein under perturbation. A relative constant Rg value through time indicates that the ligands hold the folding behavior of the protein whereas abrupt fluctuations of the Rg values denote protein folding instability [11]. In Table 2, no statistically significant differences can be observed between all Rg values calculated from the Avermectins-Protein complexes at 100 ns of simulation with the different methods considered (p ˃ 0.001). The methods predicted conformational fluctuations in the studied complexes oriented towards the folding or unfolding of the complexes without important differences in relation to the ligand-free proteins, indicative of stable ligand–protein complexes. Observations dependent on both the type of protein system and the homologue were considered (Table 2). It is very important to note that the analysis of Rh data allows conclusions to be drawn similarly to those obtained using the parameter Rg by showing results without significant differences (Table 2).
For IMPα1, AVM-B1a and AVM-B1b specifically, an unfolded conformation of the protein is induced, with an average difference between both homologues and the free protein of Rg ≈ 5 Å. With mean values for each homologue of Rg ≈ 4.8 ± 2.4 Å and Rg ≈ 5.2 ± 2.8 Å, for complex with AVM-B1a and AVM-B1b, respectively (Table 2). Results that would allow us to infer, together with those of the atomic distance in terms of RMSD and the graphs thrown by WAXSiS server, that IMPα1 presents an almost “sphero-cylindrical” folded structural state (Supplementary material Fig.S1). Starting from the same criteria we can indicate that the IMPβ1 protein showed a slight refolding with fluctuating values between each homologue. The mean difference between both complexes and the free protein was Rg ≈ 0.24 Å. With mean values Rg for the complex with AVM-B1a and AVM-B1b of −0.2 ± 0.7 Å and −0.3 ± 0.6 Å, respectively (Table 2). Although it is an important signal, observations at the RMSD level show that none of the homologues was able to induce significant differential perturbations compared to the free protein, showing stability in the systems. These results show a slightly greater effect of unfolding AVM-B1b on IMPα1 and folding on IMPβ1, compared to AVM-B1a. As well as a differential behavior of each homologue against each type of Importin tested in terms of induction of conformational changes.
In the helicase, AVM-B1b induced a slightly unfolded conformation, whereas the AVM-B1a induced slight refolding of this protein (Table 2). This is related to the atomic distance values which show important and differential variations between these compounds compared to the free protein of the helicase, inducing a globular folded conformational state with both avermectin homologues. While for Mpro the effect of both homologues was oriented towards conformational unfolding. The mean difference between both homologues and the free protein was Rg ≈ 0.29 Å. Specifically, the mean values of the difference between each homologue were Rg ≈ − 0.5 ± 0.3 Å and 0.3 ± 0.3 Å, for AVM-B1a and AVM-B1b, respectively. In this sense, although there is a differential behavior of each homologue in terms of Rg, they were not able to induce important perturbations compared to the free protein. Similarly, although the greatest effect of Mpro unfolding was by AVM-B1b compared to AVM-B1a, the compounds were unable to induce significant perturbations compared to the free protein, which would allow inferring that the ligand–protein complexes are stable. The presentation in graphical mode of the results shown in Table 2 of the WAXSiS server model can be seen in supplementary material such as Fig.S1.
4.2. Comparative analysis between structural deformation of complexes using the ENM-based approaches of normal mode analysis (NMA), anisotropic network models (ANM) and gaussian network model (GNM) for each complexes
The analyzes carried out using the models NMA, ANM and GNM were Deformation () and B-factor () (measures of the ability of a given molecule to deform in each of its residues (Table 3 ). In these models, the regions of high deformability usually have values ≥ 0.2 and the higher the value, the greater the deformability. The value is a comparison between the NMA field and the PDB field of the portein-ligand complex in terms of deformability, for which, experimental is taken from the corresponding PDB field and the calculated NMA is obtained by multiplying the mobility of NMA by 8π2. The Eigenvalue () associated to each normal mode represents the motion stiffness. Its value is directly related to the energy required to deform the structure, and the lower the 〈ε〉, the easier it will be to deform the biomolecular structure. The use of ENM-based methods for the study of inhibitors has already been suggested, and it has been observed that each type of ligand could, of course, show a different behavior in the corresponding structures and show different “hot spots” of union depending on the nature of each studied complex and product of the typical general properties that emerge from each elastic structure global [20], [21], [22]. In addition, protein residue fluctuations have already been accurately predicted using this type of model in SARS-CoV-2 [62].
Table 3.
Values of deformation and flexibility of complexes using the normal mode analysis (NMA), Anisotropic Network models (ANM) and Gaussian Network Model (GNM) approach for each complex. The predictions correspond to the minimum energy structure at 100 ns MD simulation.
| Complexes | NMA/MD-ANM/GNM (simulation time 100 ns) |
||||||
|---|---|---|---|---|---|---|---|
| 〈δ〉a,* | b,* | Def. Frag.c,* | d,* | SM1** | Scorese,** | Nf.f,** | |
| IMPα1 | 0.4 | 0.2 – 0.4 | 1–400 | 3.7 | 72–278; 279–497 | 0.93; 0.93 | 7 |
| IMPα1 + AVM-B1a | 0.6 | 0.4 – 0.8 | 1–50; ≈400 | 1.0 | 72–281; 282–497 | 0.94; 0.94 | 15 |
| IMPα1 + AVM-B1b | 0.6 | 0.2 – 0.6 | ≈400 | 7.5 | 72–282; 283–497 | 0.95; 0.96 | 17 |
| IMPβ1 | 0.4 | 0.4 | 1–20; 60–80 | 2.0 | 1–68; 69–140 | 0.96; 0.61 | 6 |
| IMPβ1 + AVM-B1a | 0.6 | 0.4 | 1–50; 100–120; 350 | 3.4 | 1–69; 128–140 | 0.89; 0.55 | 9 |
| IMPβ1 + AVM-B1b | 0.6 | 0.4 | 1–40; 100–140; 400 | 3.0 | 1–68; 69–140 | 0.95; 0.55 | 9 |
| Helicase | 0.6 | 0.4 | 1–200; 400–500 | 4.7 | 2–141; 142–203 | 0.99; 0.96 | 3 |
| Helicase + AVM-B1a | 0.6 | 0.4 | 50–100; 500 | 6.3 | 2–142; 143–203 | 0.99; 0.96 | 5 |
| Helicase + AVM-B1b | 0.6 | 0.4 | 50–100; 200–500 | 4.3 | 2–141; 142–203 | 0.99; 0.96 | 4 |
| Mpro | 0.6 | 0.4 | 1–50; 200–300 | 6.7 | 1–196; 197–306 | 0.94; 0.89 | 12 |
| Mpro + AVM-B1a | 0.4 | 0.6 | 1–50; 100–150; 200–300 | 7.9 | 1–196; 197–306 | 0.94; 0.89 | 11 |
| Mpro + AVM-B1b | 0.4 | 0.6 | 1–100; 150–200; 250–300 | 8.5 | 1–196; 197–306 | 0.95; 0.90 | 13 |
SM1 = Slowest mode predicted from the ANM/GNM.
, = Deformation (Regions of high deformability typically have values ≥ 0.2. The higher the value, the greater the deformability).
, = Beta Factors (Regions of high deformability typically have values ≥ 0.2. The higher the value, the greater the deformability). Beta Factors is taken from the corresponding PDB field and from the calculated NMA that is obtained by multiplying the mobility of NMA by 8π2.
, Deformable Fragment.
, = Eigenvalue, value is directly related to the energy required to deform the structure. The lower, the easier the deformation. All values are in 10-6.
, Score to Slowest mode.
, number of Flexible Fragment.
, predicted from the NMA.
, predicted from the ANM/GNM.
In the complexes, low fluctuation regions were observed with a significant propensity to deform, specifically, the NMA predicted a greater relative amplitude of atomic shifts in terms of 〈δ〉 for IMPα1 and IMPβ1 in the presence of AVM-B1a and AVM-B1b ≥ 0.6 in all cases, and with respect to the free protein (≥0.4) (see Table 3). An atomic shift of between 0.4 and 0.8 and 0.2 – 0.6 was also predicted for IMPα1 in the presence of AVM-B1a and AVM-B1b in terms of calculated 〈β〉, respectively, in contrast to the values of the free protein (0.2 – 0.4). Although these values show greater fluctuation and structural deformation of IMPα1 induced by AVM-B1a, compared to AVM-B1b, the differences are not statistically significant, and show stable complexes. This corresponds to the most favorable values of binding energy of AVM-B1a by IMPα1, which could in turn be related to the conformational changes at the folding level described above.
A similar trend in relation to 〈δ〉 was predicted with each homologue against IMPβ1, with a similar atomic shift between each avermectin in terms of ≥ 0.4, as was observed at the level of conformational changes predicted with the models Rg for each compound. The two homologues caused in both Importins a level of 〈δ〉 of ≥ 0.2 with respect to the free protein, especially in the region of residue ≈ 400 of the chain of IMPα1, which coincides with the low mobility regions with the most favorable scores (Scores = 0.94–0.96) predicted in IMPα1 by the integrated ANM / GNM models, which are located around the residuals 282–497. While for IMPβ1 the fluctuations predicted could be related to the favoring of a greater number of regions with a greater propensity to deformation. Establishing low mobility conformations between residues 1–140 as predicted by all ENM approaches tested here (NMA, ANM and GNM) with a score of 0.89 and 0.95, for AVM-B1a and AVM-B1b, respectively (Table 3).
These results show that avermectin homologues caused only slight conformational changes in Importins represented by positional fluctuations as a result of atomic shift in deformed regions, and are related to the stability calculated with MD. However, the ligands caused the appearance of a greater number of adjacent short regions to be theoretically favored in both Importins characterized by having greater flexibility in the appearance of each homologue, a phenomenon associated with an important conformational and structural disturbance in terms of rigidity and flexibility, observed especially between IMPα1 and AVM-B1a. These observations correspond to the mechanism of action described for ivermectin in this context, which has been determined as a direct binding to IMPα, leading to structural changes that result in greater flexibility. These changes in IMPα1 have been reported to prevent interaction with the virus, as well as IMPβ1, and that the IMPα-dependent mode of action of ivermectin explains the wide range of viruses for which ivermectin has demonstrated antiviral effects both in vitro and in vivo [29].
In the helicase, the NMA approach predicted a relative amplitude of atomic shifts in terms of similar 〈δ〉 for the protein in the presence and absence of ligands (≥0.6), even in terms of the calculated ≥ 0.4 (Table 3). The propensity to deformation was therefore similar between each complex with the same scores for the prediction of low mobility regions. All ENM-based models used predicted similar regions of low mobility and high propensity to be deformed regardless of the absence or presence of the ligands. An interesting result because it allows us to infer that none of the homologues caused important structural changes on this protein in terms of deformation and stiffness, according to the approaches tested here by NMA, ANM and GNM. However, it is important to note that the differential activity was predicted in terms of the generation of short fragments of maximum flexibility, specifically, AVM-B1a and AVM-B1b caused an increase of 5 and 4 fragments of maximum flexibility, respectively; compared to the 3 flexible fragments predicted for the free protein. In this sense, although regions of low mobility were not predicted due to the effect of homologues on helicase, both compounds caused an increase in structural flexibility in a similar manner, especially due to the action of AVM-B1a, which is related to the lower number of regions determined as rigid in the helicase in the presence of this avermectin (Table 3).
As shown in Table 3 the relative amplitude of the atomic displacements in terms of 〈δ〉 for Mpro varied both in terms of deformation and with respect to the free protein, but they were similar between the two homologues. Specifically, the fluctuations in terms of deformation were score ≥ 0.4 in each complex as opposed to a score ≥ 0.6 deformation in the free protein, with a similar atomic shift between each avermectin in terms of ≥ 0.6 which was higher than the prediction without ligands (≥0.4). The propensity to deformation was more favorable in the presence of AVM-B1b ( = 8.5x10-6)) in contrast to AVM-B1a ( = 7.95x10-6)) and in comparison, with the control ( = 6.75x10-6)), therefore, the ANM and GNM approaches show a greater deformation of Mpro in the presence of both homologues, especially due to the effect of AVM-B1b. Observations that are related to the higher number of predicted flexible short regions Nf in the AVM-B1b + Mpro complex of 13, as opposed to the Nf = 11 predicted flexible fragments for AVM-B1a. The regions of low mobility with preference to deform were predicted in a similar way in each complex by all the elastic network approaches considered, and exhibited greater diversity in the complexed Mpro models compared to the protein without ligand (Table 3).
The ability of ENMs to efficiently assess intrinsically favored global movements, as well as the relevance of these predictions to the dominant changes in structure observed for a given protein in the presence of different ligands suggest that intrinsic dynamics play a role in the mediation of ligand–protein complex interactions, and could be comparable to MD measurements [63], [64]. However, there are few reports on the use of ENM for the study of conformational perturbations in SARS-CoV-2, in this direction, our results show that the complexed structures have a stable interaction movement with each other after the molecular union, in addition, the complexes presented a greater deformation than those reported [65]. The presentation in graphical mode of the results shown in Table 3 of the NMA model can be seen in supplementary material such as Fig. S2–S4.
It has already been reported that calculations based on ENM templates can identify the location of new sites with particular local dynamics, and, simulations based on ENM-type methods have proven to be powerful in locating candidates for susceptible binding sites, so they are complemented with docking studies and MD, in fact, it has been found that experimental free energies are normally arranged in the same sequence as ENM values, although they cannot deliver predicted values for total free binding energies. Finally, these analyzes are important because the recognition of stiffness and flexibility control regions on the surface of proteins has a pharmacological application and raises other general questions in the biophysics of the elasticity of fluctuation in proteins [62].
4.3. Study of the structural interaction of the protein regions in complexes using the ENM-based approaches of normal mode analysis (NMA) and protein structure network analysis (PSN)
Based on what was discussed in the previous section, the minimum energy structures of each Avermectin-Importin complex obtained with MD at 100 ns were analyzed with the integrated PSN-ENM/NMA approach (Table 4 ). The parameters considered were number of nodes (Nn) and links (Nlk) in MetaPath, average path force () and correlation (), average % of correlation of nodes () and average path hubs percent (). The above parameters allow the calculation of the shortest path in the structural regions of the protein interaction, and the increase or decrease of these values are related to the increase or decrease of the intramolecular interactions. Values with a ≥ 0.60 represent complexes that contain at least one correlated residue, and this usually allows only the shortest paths to be retained. The highest average correlation of the routes between each node for each of the homologues against IMPα1 was 0.96 (a slightly higher correlation than the free protein 0.94), with a percentage in the correlation of the nodes of 54.26 %, which represents 53.24% and 55.28% for the complex with AVM-B1a and AVM-B1b, correspondingly, and they are more favorable correlations than those calculated for this Importin without ligands.
Table 4.
Comparison between the complexes using the Elastic Network Models (ENM), Normal Mode Analysis (NMA), Protein Structure Network (PSN) and SPECTRUS approach for each complex. The predictions correspond to the minimum energy structure at 100 ns MD simulation.
| Complexes | PSN/MD-ENM/NMA-SPECTRUS (simulation time 100 ns) |
|||||||
|---|---|---|---|---|---|---|---|---|
| Nna | Nlkb | c | d | e | f | NDQg | Scoreh | |
| IMPα1 | 68 | 67 | 7.51 | 0.94 | 46.42 | 38.22 | 11 | 2.42 |
| IMPα1 + AVM-B1a | 108 | 107 | 6.98 | 0.96 | 53.24 | 38.14 | 5 | 2.81 |
| IMPα1 + AVM-B1b | 84 | 83 | 6.40 | 0.96 | 55.28 | 41.48 | 10 | 3.12 |
| IMPβ1 | 44 | 43 | 7.64 | 0.91 | 47.40 | 36.89 | 4/70 | 3.21/3.61 |
| IMPβ1 + AVM-B1a | 55 | 54 | 7.43 | 0.91 | 50.57 | 30.71 | 4 71 | 2.81/5.18 |
| IMPβ1 + AVM-B1b | 69 | 68 | 7.86 | 0.89 | 40.20 | 29.69 | 6/70 | 2.74/2.94 |
| Helicase | 211 | 210 | 7.98 | 0.98 | 39.81 | 41.34 | 7 | 5.94 |
| Helicase + AVM-B1a | 173 | 172 | 8.47 | 0.98 | 34.31 | 34.96 | 9 | 4.54 |
| Helicase + AVM-B1b | 221 | 220 | 7.62 | 0.97 | 44.02 | 29.28 | 8 | 5.78 |
| Mpro | 70 | 69 | 6.42 | 0.93 | 43.84 | 33.25 | 12 | 2.76 |
| Mpro + AVM-B1a | 63 | 62 | 6.83 | 0.93 | 35.60 | 35.72 | 12 | 2.70 |
| Mpro + AVM-B1b | 70 | 69 | 7.10 | 0.94 | 51.95 | 31.74 | 6 | 3.04 |
, Nn = Number of nodes in MetaPath.
, Nlk = Number of links MetaPath.
, Average path force.
, Average path correlation.
, Average % of correlation of Nodes.
, Average path hubs percent. The increase or decrease of all these values (Nn, Nlk, 〈Σ〉, 〈Ω〉, 〈Φ〉 and Ξ) is related to the increase or decrease of intramolecular interactions. Values with a 〈Ω〉 ≥ 0.60 represent complexes that contain at least one correlated residue.
, NDQ = Number of Domains Q (subdivision). Represents the position of the subdivision of the quasi-rigid domain.
, Score to NDQ.
The average percentage of hub nodes present in the global peer group was 39.81% (38.14% and 41.48% for AVM-B1a and AVM-B1b respectively). Furthermore, the average of the interaction strength between the links present in the global group was 6.69, represented by a bond strength of 6.98 for complex with AVM-B1a and 6.40 with AVM-B1b. These interaction forces were lower than those found in the structure without ligand. The meta pathway generated Nn from the interactions of each of the avermectins revealed 108 and 84 nodes, for complex with AVM-B1a and AVM-B1b respectively. The strength of the interactions, as well as the number of nodes Nn and predicted links Nlk in the trajectories show that both homologues are capable of altering the conformation and stability of the free protein. AVM-B1a induced the formation of a greater number of amino acid rearrangements, disrupting native intra-molecular networks and interactions (Table 4).
For IMPβ1, the highest average correlation of the routes between each node for the AVM-B1a and AVM-B1b was 0.91 and 0.89 respectively. A percentage in the correlation of the nodes of 45.39% was predicted, represented by 50.57 % and 40.20% for complex with AVM-B1a and AVM-B1b, correspondingly. The average percentage of hub nodes present in the global peer group was 30.20 %, with 30.71% and 29.69% for the complex with the AVM-B1a and AVM-B1b respectively. Likewise, the average of the interaction strength between the links present in the global group was 7.65, represented by a binding force of 7.43 for complex with AVM-B1a and 7.86 for complex with AVM-B1b. The meta pathway Nn generated from the interactions of each of the homologues revealed Nn 55 and 69 nodes, for complex with AVM-B1a and AVM-B1b respectively. The results calculated above show that the ligands may be capable of modifying the conformation and stability of the nodes of the free protein. The observations on the effect of AVM-B1b against IMPβ1 in terms of strength of interactions, number of nodes and bonds generated correspond to what has been previously described, highlighting that both compounds affect this Importin, but AVM-B1b has a slightly higher propensity to disrupt the native intra-molecular networks and interactions of IMPβ1 (Table 4).
The highest average correlation of the routes between each node for each of the homologues against Helicase was 0.98 and 0.97 for the AVM-B1a and AVM-B1b, respectively, with a percentage in the correlation of the nodes of 39.17 %, represented by 34.31% and 44.02% for the complex with AVM-B1a and AVM-B1b correspondingly. The average percentage of hub nodes present in the global peer group was 32.12% (34.96% and 29.28% for the complex with the AVM-B1a and AVM-B1b respectively). Furthermore, the average of the interaction strength between the links present in the global group was 8.05, represented by a binding force of 8.47 for complex with AVM-B1a and 7.62 for AVM-B1b. The meta pathway Nn generated from the interactions of each of the avermectins revealed 173 and 221 nodes, for AVM-B1a and AVM-B1b, respectively. The number of nodes observed, as well as the links and the correlation between them show that the AVM-B1b is capable of inducing the greatest number of perturbations in the intramolecular interactions in helicase, and this corresponds to the most favorable values of binding energy of AVM-B1b predicted against this protein. Although the greater strength in these interactions may be mediated by the AVM-B1a, but with a lower number of nodes linked and correlated at the energy level compared to the free protein. All these observations show that both homologues are able to affect the natural interactions of this protein in a differential way, with an increase or decrease in the number of these predicted by the AVM-B1b and AVM-B1a complexes, respectively (Table 4).
The highest average correlation of the interactions between each node for the complexes with avermectin homologues versus Mpro was 0.94 and 0.93 for the the complex with AVM-B1a and AVM-B1b, respectively, with a percentage in the correlation of the nodes of 43.78%, represented by = 35.60% and 51.95% for the complex with AVM-B1a and AVM-B1b, correspondingly. The average percentage of main nodes was 33.73%, being 35.72% and 31.74% for the complex with AVM-B1a and AVM-B1b, comparatively. In addition, the average interaction force between the links was 6.97, represented by a force in the interaction of 6.83 for the complex with AVM-B1a and 7.10 for the complex with AVM-B1b. Additionally, it was observed that the meta-path generated revealed Nn = 63 and 70 nodes, for the complex with AVM-B1a and AVM-B1b, respectively. These predictions show that the highest correlation between nodes occurred between the AVM-B1b and Mpro (51.95%) as opposed to its homologue (35.60%) and the protein without ligand (43.84%), generating the highest strength in the bonds and interactions calculated (7.10) compared to the complex with the ligand B1a (6.83) and the free protein (6.42), with a number of nodes and links similar to the free protein but greater than those predicted for AVM-B1a. Therefore, these observations indicate that both compounds affect the intramolecular interaction pathways of the complexed Mpro, being the AVM-B1b the compound capable of affecting to a greater extent the stability and native interactions of the viral protease according to the PSN-ENM/NMA approach (Table 4). The presentation in graphical mode of the results shown in Table 4 of the PSN model can be seen in supplementary material such as Fig. S5–S9.
4.4. Comparison of structural rigidity between complexes using the ENM-based approach of SPECTRUS for each complex
The rigidity of the minimum energy structure was studied by means of the decomposition approach in quasi-rigid domains of the simulated complexes, based on the analysis of the fluctuations of distance between pairs of amino acids with ENM. This so-called SPECTRUS approach is based on the notion that, for genuinely rigid systems, the distances between any two constitutive points are strictly conserved during movement in space during simulation (Table 4 and Fig. 6 ), and the parameter considered were the NDQ = Number of Q domains (subdivision), which represents the position of the subdivision of the quasi-rigid domain. Variations in native NDQ can indicate the relative shift of the domains, a dynamic phenomenon that can alter the biological functionality in proteins [54].
Fig. 6.
Comparison between the spectrum-based quasi-rigid domain decomposition of complexes using SPECTRUS. A, IMPα with and without Avermectin B1a (AVM-B1a) and Avermectin B1b (AVM-B1b); B, IMPβ with and without Avermectins, C, Helicase with and without Avermectins; D, Mpro with and without Avermectins. The predictions correspond to the minimum energy structure at 100 ns MD simulation.
Very favorable quasi-rigid regions were predicted for IMPα1 (Score = 2.81 for complex with AVM-B1a and Score = 3.12 with AVM-B1b) with respect to the free protein one (Score = 2.42) and that correspond to the fragments with a greater propensity to be deformed and to adopt low mobility conformations previously predicted by the NMA, ANM and GNM approaches. The scores of these regions show that both homologues were able to generate regions with greater stiffness than those present in free protein. AVM-B1a displaced the quasi-rigid domain from the native NDQ = 11 subdivision to the NDQ = 5 subdivision, this represents a significant conformational fluctuation in terms of local stiffness. The fluctuations caused by the AVM-B1b on IMPα1 oscillated in subdivisions close to the free protein, but with scores that show a very favorable quasi-rigid region generated, more stable than in the non-complexed form (Fig. 6).
Similar results were obtained between the SPECTRUS model and the remaining ENM-type approaches used to predict the flexibility and rigidity of the Avermectins-IMPβ1 systems, specifically, the regions of lower mobility previously reported by NMA, ANM and GNM correspond to the quasi-rigid domains determined with the decomposition into domains. All systems predicted 2 quasi-rigid domains in this protein, and the score for the first region of the complexed systems was less favorable compared to the free protein. This shows a stiffer NDQ = 4 first subdivision in the free protein (Score = 3.21) compared to the complexed ones, indicating that AVM-B1b caused the displacement of the first domain (NDQ = 4, Score = 2.81 for the complex with AVM-B1a; and NDQ = 6, Score = 2.74 for the complex AVM-B1b). The same trend was maintained in the second quasi-rigid subdivision between the free protein and the AVM-B1b complex, while the AVM-B1a complex showed a more favorable quasi-rigid conformation and shifted towards the NDQ = 71 domain, unlike the NDQ = 70 domain of the AVM-B1b complex and the free protein, these results show a clear variation in the distribution of quasi-rigid regions with favorable predictive scores in Importins (see Table 4 and Fig. 6). What validates that these homologues are capable of affecting the global and local conformation and structural stability of these protein systems, altering the native intramolecular interactions once the complexes have been established and modifying the regions and their constitutive fluctuations.
It is important to note that despite all the observations related to the effect of AVM-B1a on IMPα1 are discriminatory, at the energy level, AVM-B1b can also alter the structure of this Importin, exerting a similar effect, although our results show that AVM-B1a is capable of inducing a marked conformational folding, as well as a structural deformation, promoting the formation of fluctuating regions of greater rigidity. This close activity on IMPα1 is also reflected against IMPβ1 before which the results do not show a clear tendency or inclination towards any of the homologues in relation to the primary variables considered in this study (Table 4 and Fig. 6).
Less favorable quasi-rigid regions were predicted for helicase (Score = 4.54 for complex with AVM-B1a and Score = 5.78 for complex with AVM-B1b) with respect to the free protein (Score = 5.94) and they correspond to the fragments with greater propensity to be deformed and to adopt conformations previously predicted low mobility (Table 4 and Fig. 6). The scores of these regions show that both homologues were able to generate regions with a stiffness that differs from those present in the free protein, specifically, homologue B1a displaced the quasi-rigid domain from the native NDQ = 7 subdivision to the NDQ = 9 subdivision (Fig. 6), this represents a significant conformational fluctuation in terms of local stiffness, while the fluctuations caused by the AVM-B1b counterpart on Helicase oscillated in the subdivision NDQ = 8 (Table 4). Observations show that homologues can generate changes at the distribution level of the initial quasi-rigid regions in this viral protein.
In addition, compared to Mpro, the SPECTRUS model predicted quasi-rigid regions similar to those previously described by the NMA, ANM and GNM models, the most favorable was the subdivision NDQ = 6 with a score of 3.04 generated by AVM-B1b, followed by AVM-B1a with a domain NDQ = 12 (similar to free protein) with a score of 2.70 (Table 4). The predicted regions correspond to the fragments with the highest propensity to be deformed and to adopt low mobility conformations (Fig. 6), and these observations show that the AVM-B1b was able to displace the quasi-rigid domain maintained in the complex established by the B1a homologue and in the free protein. Therefore, AVM-B1b can affect rigidity, and therefore the stability and native interactions of the viral protease, with a greater propensity than that exhibited by AVM-B1a, as predicted by the PSN-ENM/NMA approaches (Table 4 and Fig. 6). Importantly, the SPECTRUS method based on domain decomposition does not consider the structural properties of the protein, but it allows the study of the variations in the clustering of protein residues in terms of dynamically correlated domain networks, based on the effective correlation times of the pair distance correlation functions [66], it has also been shown to be a useful approach to identify dynamic domains in complex proteins [67], [68].
These theoretical predictions could guide the possibility of deriving formulations or analogues that can be administered to achieve relevant therapeutic concentrations, as it has been suggested necessary to do in the particular case of ivermectin [5], [69]. It is important to say that these predictions based on theoretical models are not without interest as they show the possible structural distortion that ivermectin homologues induce in both cellular and viral sites, which in some way may be a reflection of the remarkable and controversial clinical benefits noted very recently by different groups worldwide [70], [71]. The novel approach of ENM-based models showed a possible multidirectional activity of ivermectin, and an orientation towards cellular structures (AVM-B1a), and also towards viral proteins (AVM-B1b) associated with COVID-19, because homologues can generate changes at the distribution level of the initial quasi-rigid regions in this proteins, what could affect biological activity. However, these results should not be taken as final, and it is recommended to study a greater number of possible targets under the same conditions of this study.
5. Conclusions
In this study, given that a wide diversity of possible targets for ivermectin has been reported whilst there are few reports that compare the behavior of its homologues components, our objective was to investigate from a biophysical and computational chemical perspective the effect of the interactions of each homologue on the flexibility and stiffness of the predicted complexes with IMPα1, IMPβ1, helicase and Mpro.
We observed that each homologue was stably bound to the proteins studied, and were able to induce detectable changes with ENMs, specifically, in IMPα1 and IMPβ1, the homologues induced slightly unfolded and folded conformations, respectively, whilst the helicase underwent slight unfolding and refolding by AVM-B1b and AVM-B1a, respectively. The effect of avermectin binding to Mpro was oriented towards the slight conformational unfolding.
The NMA, ANM and GNM models showed behaviors that correspond to the stability calculated with MD, and in a strict sense, the perturbations induced were characteristic to each compound, and were predicted more clearly with the PSN and SPECTRUS models. In this sense, and in view of the fact that are currently looking for drugs to screen in vitro, in vivo or for clinical trials, our data should be taken seriously because the calculated perturbations were represented by a disruption of the interactions between amino acids, causing the modification of the conformation and stability of the proteins studied, with an impact on the distribution of the quasi-rigid regions of said structures, which could affect the biological activity of the protein systems analyzed.
Funding sources
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sector.
CRediT authorship contribution statement
Lenin González-Paz: Conceptualization, Methodology, Investigation, Writing – review & editing. Laura Jeffreys: Reviewing and Editing. María Laura Hurtado-León: Investigation. Carla Lossada: Investigation. Francelys V. Fernández-Materán: Investigation. Joan Vera-Villalobos: . Marcos Loroño: Writing – original draft. J.L. Paz: Writing – original draft. Laura Jeffreys: . Ysaias J. Alvarado: Conceptualization, Methodology, Investigation, Writing – review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.molliq.2021.117284.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
References
- 1.Ng Y.L., Salim C.K., Chu J.J.H. Drug repurposing for COVID-19: Approaches, challenges and promising candidates. Pharmacology & Therapeutics. 2021;1(228) doi: 10.1016/j.pharmthera.2021.107930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lewis, K., Chaudhuri, D., Alshamsi, F., Carayannopoulos, L., Dearness, K., Chagla, Z., Alhazzani, W. & GUIDE Group. (2021). The efficacy and safety of hydroxychloroquine for COVID-19 prophylaxis: A systematic review and meta-analysis of randomized trials. PloS one, 16(1), e0244778. DOI: https://doi.org/10.1371/journal.pone.0244778. [DOI] [PMC free article] [PubMed]
- 3.Sánchez-Tejeda J.F., Sánchez-Ruiz J.F., Salazar J.R., Loza-Mejía M.A. A definition of “multitargeticity”: identifying potential multitarget and selective ligands through a vector analysis. Front. Chem. 2020;8(176) doi: 10.3389/fchem.2020.00176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fatoki, T. H., Ibraheem, O., Ogunyemi, I. O., Akinmoladun, A. C., Ugboko, H. U., Adeseko, C. J., Awofisayo, O., Olusegun, S., & Enibukun, J. (2020). Network analysis, sequence and structure dynamics of key proteins of coronavirus and human host, and molecular docking of selected phytochemicals of nine medicinal plants. Journal of Biomolecular Structure and Dynamics, 20, 1-23. DOI: https://doi.org/10.1080/07391102.2020.1794971. [DOI] [PubMed]
- 5.Heidary F., Gharebaghi R. Ivermectin: a systematic review from antiviral effects to COVID-19 complementary regimen. The Journal of Antibiotics. 2020;73(9):593–602. doi: 10.1038/s41429-020-0336-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Heidary F., Gharebaghi R., Lateef M., Mohammed M.Z.A., Alshmailawi S.F.H., Alkhafaji K., Thamer R., Khalaf H., Fazil N., Alkhshaymee M. Antiviral Vector Effects of Ivermectin on COVID-19: An Update. Journal of Cellular & Molecular Anesthesia. 2021;6(1):101–103. doi: 10.22037/jcma.v6i1.33827. [DOI] [Google Scholar]
- 7.Yesilbag K., Toker E.B., Ates O. Ivermectin also inhibits the replication of bovine respiratory viruses (BRSV, BPIV-3, BoHV-1, BCoV and BVDV) in vitro. Virus Res. 2021;297:198384. doi: 10.1016/j.virusres.2021.198384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.González-Paz L.A., Lossada C.A., Moncayo L.S., Romero F., Paz J.L., Vera-Villalobos J., Pérez A.E., Portillo E., San-Blas E., Alvarado Y.J. A Bioinformatics Study of Structural Perturbation of 3CL-Protease and the HR2-Domain of SARS-CoV-2 Induced by Synergistic Interaction with Ivermectins. Biointerface Research in Applied Chemistry. 2021;11(2) doi: 10.33263/BRIAC112.98139826. DOI. [DOI] [Google Scholar]
- 9.Azam, F., Taban, I.M., Eid, E.E.M., Iqbal, M., Alam, O., Khan, S., Mahmood, D., Anwar, M.J., Khalilullah, H., Khan, M.U. (2020). An in-silico analysis of ivermectin interaction with potential SARS-CoV-2 targets and host nuclear importin α. Journal of Biomolecular Structure and Dynamics, Nov 2:1-14. DOI: https://doi.org/10.1080/07391102.2020.1841028. [DOI] [PMC free article] [PubMed]
- 10.de Oliveira O.V., Rocha G.B., Paluch A.S., Costa L.T. Repurposing approved drugs as inhibitors of SARS-CoV-2 S-protein from molecular modeling and virtual screening. J. Biomol. Struct. Dyn. 2020;1–10 doi: 10.1080/07391102.2020.1772885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mosquera-Yuqui F., Lopez-Guerra N., Moncayo-Palacio E.A. Targeting the 3CLpro and RdRp of SARS-CoV-2 with phytochemicals from medicinal plants of the Andean Region: molecular docking and molecular dynamics simulations. J. Biomol. Struct. Dyn. 2020;1–14 doi: 10.1080/07391102.2020.1835716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hosseini, M., Chen, W., Xiao, D., & Wang, C. (2020). Computational molecular docking and virtual screening revealed promising SARS-CoV-2 drugs. Precision Clinical Medicine, pbab001. DOI: https://doi.org/10.1093/pcmedi/pbab001. [DOI] [PMC free article] [PubMed]
- 13.Felline A., Seeber M., Fanelli F. webPSN v2. 0: a webserver to infer fingerprints of structural communication in biomacromolecules. Nucleic Acids Res. 2020;48(W1):W94–W103. doi: 10.1093/nar/gkaa397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ahmed A., Rippmann F., Barnickel G., Gohlke H. A normal mode-based geometric simulation approach for exploring biologically relevant conformational transitions in proteins. J. Chem. Inf. Model. 2011;51(7):1604–1622. doi: 10.1021/ci100461k. [DOI] [PubMed] [Google Scholar]
- 15.Doruker P., Atilgan A.R., Bahar I. Dynamics of proteins predicted by molecular dynamics simulations and analytical approaches: application to alpha-amylase inhibitor. Proteins. 2000;40(3):512–524. doi: 10.1002/1097-0134(20000815)40:3<512::AID-PROT180>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
- 16.Atilgan A.R., Durrell S.R., Jernigan R.L., Demirel M.C., Keskin O., Bahar I. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J . 2001;80(1):505–515. doi: 10.1016/S0006-3495(01)76033-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Seeber M., Felline A., Raimondi F., Muff S., Friedman R., Rao F., Caflisch A., Fanelli F. Wordom: a user-friendly program for the analysis of molecular structures, trajectories, and free energy surfaces. J. Comput. Chem. 2011;32(6):1183–1194. doi: 10.1002/jcc.21688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dykeman E.C., Sankey O.F. Normal mode analysis and applications in biological physics. J. Phys.: Condens. Matter. 2010;22(42):423202. doi: 10.1088/0953-8984/22/42/423202. [DOI] [PubMed] [Google Scholar]
- 19.Emekli U., Schneidman-Duhovny D., Wolfson H.J., Nussinov R., Haliloglu T. HingeProt: automated prediction of hinges in protein structures. Proteins Struct. Funct. Bioinf. 2008;70(4):1219–1227. doi: 10.1002/prot.21613. [DOI] [PubMed] [Google Scholar]
- 20.López-Blanco J.R., Aliaga J.I., Quintana-Ortí E.S., Chacón P. iMODS: internal coordinates normal mode analysis server. Nucleic Acids Res. 2014;42(W1):W271–W276. doi: 10.1093/nar/gku339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Skjaerven L., Hollup S.M., Reuter N. Normal mode analysis for proteins. J. Mol. Struct. (Thoechem) 2009;898(1–3):42–48. doi: 10.1016/j.theochem.2008.09.024. [DOI] [Google Scholar]
- 22.Hollup S.M., Sælensminde G., Reuter N. WEBnm@: a web application for normal mode analysis of proteins. BMC Bioinf. 2005;6(52) doi: 10.1186/1471-2105-6-52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Greene L.H. Protein structure networks. Briefings in Functional Genomics. 2012;11(6):469–478. doi: 10.1093/bfgp/els039. [DOI] [PubMed] [Google Scholar]
- 24.Hu G., Di Paola L., Liang Z., Giuliani A. Comparative study of elastic network model and protein contact network for protein complexes: the hemoglobin case. Biomed Res. Int. 2017;2017:1–15. doi: 10.1155/2017/2483264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tu W.J., McCuaig R.D., Melino M., Rawle D.J., Le T.T., Yan K., Suhrbier A., Johnston R.L., Koufariotis L.T., Waddell N., Cross E.M., Tsimbalyuk S., Bain A., Ahern E., Collinson N., Phipps S., Forwood J.K., Seddiki N., Rao S. Targeting novel LSD1-dependent ACE2 demethylation domains inhibits SARS-CoV-2 replication. Cell Discovery. 2021;7:37. doi: 10.1038/s41421-021-00279-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Halder K., Dölker N., Van Q., Gregor I., Dickmanns A., Baade I., Kehlenbach R.H., Ficner R., Enderlein J., Grubmüller H., Neumann H. MD simulations and FRET reveal an environment-sensitive conformational plasticity of importin-β. Biophys. J . 2015;109(2):277–286. doi: 10.1016/j.bpj.2015.06.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Smith K.M., Di Antonio V., Bellucci L., Thomas D.R., Caporuscio F., Ciccarese F., Ghassabian H., Wagstaff K.M., Forwood J.K., Jans D.A., Palù G., Alvisi G. Contribution of the residue at position 4 within classical nuclear localization signals to modulating interaction with importins and nuclear targeting. Biochim. Biophys. Acta, Mol. Cell. Res. 2018;1865(8):1114–1129. doi: 10.1016/j.bbamcr.2018.05.006. [DOI] [PubMed] [Google Scholar]
- 28.Bernardes N.E., Fukuda C.A., da Silva T.D., de Oliveira H.C., de Barros A.C., Dreyer T.R., Bertolini M.C., Fontes M.R.M. Comparative study of the interactions between fungal transcription factor nuclear localization sequences with mammalian and fungal importin-alpha. Sci. Rep. 2020;10(1):1458. doi: 10.1038/s41598-020-58316-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Martin A.J., Jans D.A. Antivirals that target the host IMPα/β1-virus interface. Biochem. Soc. Trans. 2021;9(1):281–295. doi: 10.1042/BST20200568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Thurakkal L., Singh S., Roy R., Kar P., Sadhukhan S., Porel M. An in-silico study on selected organosulfur compounds as potential drugs for SARS-CoV-2 infection via binding multiple drug targets. Chem. Phys. Lett. 2021;763:138193. doi: 10.1016/j.cplett.2020.138193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Culletta G., Gulotta M.R., Perricone U., Zappalà M., Almerico A.M., Tutone M. Exploring the SARS-CoV-2 Proteome in the Search of Potential Inhibitors via Structure-Based Pharmacophore Modeling/Docking Approach. Computation. 2020;8(3):77. doi: 10.3390/computation8030077. [DOI] [Google Scholar]
- 32.Kapoor N., Ghorai S.M., Kushwaha P.K., Shukla R., Aggarwal C., Bandichhor R. Plausible mechanisms explaining the role of cucurbitacins as potential therapeutic drugs against coronavirus 2019. Inf. Med. Unlocked. 2020;21:100484. doi: 10.1016/j.imu.2020.100484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Shah S., Chaple D., Arora S., Yende S., Mehta C., Nayak U. Prospecting for Cressa cretica to treat COVID-19 via in silico molecular docking models of the SARS-CoV-2. Journal of Biomolecular Structure and Dynamics. 2021;15:1–9. doi: 10.1080/07391102.2021.1872419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Panikar S., Shoba G., Arun M., Sahayarayan J.J., Usha Raja Nanthini A., Chinnathambi A., Alharbi S.A., Nasif O., Kim H.-J. Essential oils as an effective alternative for the treatment of COVID-19: Molecular interaction analysis of protease (Mpro) with pharmacokinetics and toxicological properties. Journal of Infection and Public Health. 2021;14(5):601–610. doi: 10.1016/j.jiph.2020.12.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chhetri A., Chettri S., Rai P., Sinha B., Brahman D. Exploration of inhibitory action of Azo imidazole derivatives against COVID-19 main protease (Mpro): A computational study. J. Mol. Struct. 2021;1224:129178. doi: 10.1016/j.molstruc.2020.129178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.González-Paz L.A., Lossada C.A., Fernández-Materán F.V., Paz J.L., Vera-Villalobos J., Alvarado Y.J. Can Non-Steroidal Anti-inflammatory Drugs Affect the Interaction Between Receptor Binding Domain of SARS-COV-2 Spike and the Human ACE2 Receptor? A Computational Biophysical Study. Front. Phys. 2020;8:526. doi: 10.3389/fphy.2020.587606. [DOI] [Google Scholar]
- 37.Neupane N.P., Karn A.K., Mukeri I.H., Pathak P., Kumar P., Singh S., Qureshi I.A., Jha T., Verma A. Molecular dynamics analysis of phytochemicals from Ageratina adenophora against COVID-19 main protease (Mpro) and human angiotensin-converting enzyme 2 (ACE2) Biocatalysis and Agricultural Biotechnology. 2021;32:101924. doi: 10.1016/j.bcab.2021.101924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.O'Boyle N.M., Banck M., James C.A., Morley C., Vandermeersch T., Hutchison G.R. Open babel: an open chemical toolbox. J. Chem. 2011;3(33):1–14. doi: 10.1186/1758-2946-3-33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Guedes I.A., Costa L.S., Dos Santos K.B., Karl A.L., Rocha G.K., Teixeira I.M., Galheigo M.M., Medeiros V., Krempser E., Custódio F.L., Barbosa H.J., Nicolás M.F., Dardenne L.E. Drug Design and Repurposing with DockThor-VS Web Server: Virtual Screening focusing on SARS-CoV-2 Therapeutic Targets and their Non-Synonym Variants. Sci. Rep. 2020;11(1):5543. doi: 10.1038/s41598-021-84700-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Rawal K., Khurana T., Sharma H., Verma S., Gupta S., Kubba C., Strych U., Hotez P.J., Bottazzi M.E. An extensive survey of molecular docking tools and their applications using text mining and deep curation strategies. PeerJ Preprints. 2019;7:e27538v1. doi: 10.7287/peerj.preprints.27538v1. [DOI] [Google Scholar]
- 41.Santos K.B., Guedes I.A., Karl A.L.M., Dardenne L.E. Highly flexible ligand docking: benchmarking of the DockThor program on the LEADS-PEP protein–peptide data set. Journal of Chemical Information and Modeling. 2020;60(2):667–683. doi: 10.1021/acs.jcim.9b00905. [DOI] [PubMed] [Google Scholar]
- 42.Magalhães C.S.D., Barbosa H.J., Dardenne L.E. A genetic algorithm for the ligand-protein docking problem. Genetics and Molecular Biology. 2004;27(4):605–610. doi: 10.1590/S1415-47572004000400022. [DOI] [Google Scholar]
- 43.Guedes I.A., Barreto A.M., Marinho D., Krempser E., Kuenemann M.A., Sperandio O., Dardenne L.E., Miteva M.A. New machine learning and physics-based scoring functions for drug discovery. Sci. Rep. 2021;11(3198):1–19. doi: 10.1038/s41598-021-82410-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Verkhivker G.M., Bouzida D., Gehlhaar D.K., Rejto P.A., Arthurs S., Colson A.B., Freer S.T., Larson V., Luty B.A., Marrone T., Rose P.W. Deciphering common failures in molecular docking of ligand-protein complexes. J. Comput. Aided Mol. Des. 2000;14(8):731–751. doi: 10.1023/a:1008158231558. [DOI] [PubMed] [Google Scholar]
- 45.Wahedi H.M., Ahmad S., Abbasi S.W. Stilbene-based natural compounds as promising drug candidates against COVID-19. J. Biomol. Struct. Dyn. 2021;39(9):3225–3234. doi: 10.1080/07391102.2020.1762743. [DOI] [PubMed] [Google Scholar]
- 46.Wada M., Kanamori E., Nakamura H., Fukunishi Y. Selection of in silico drug screening results for G-protein-coupled receptors by using universal active probes. J. Chem. Inf. Model. 2011;51(9):2398–2407. doi: 10.1021/ci200236x. [DOI] [PubMed] [Google Scholar]
- 47.Zhou H.X., Pang X. Electrostatic interactions in protein structure, folding, binding, and condensation. Chem. Rev. 2018;118(4):1691–1741. doi: 10.1021/acs.chemrev.7b00305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Yonezawa Y. Electrostatic properties of water models evaluated by a long-range potential based solely on the Wolf charge-neutral condition. Chem. Phys. Lett. 2013;556:308–314. doi: 10.1016/j.cplett.2012.12.028. [DOI] [Google Scholar]
- 49.Kasahara K., Terazawa H., Itaya H., Goto S., Nakamura H., Takahashi T., Higo J. myPresto/omegagene 2020: a molecular dynamics simulation engine for virtual-system coupled sampling. Biophysics and Physicobiology. 2020;17(0):140–146. doi: 10.2142/biophysico.BSJ-2020013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Fleming P.J., Fleming K.G. HullRad: Fast calculations of folded and disordered protein and nucleic acid hydrodynamic properties. Biophys. J . 2018;114(4):856–869. doi: 10.1016/j.bpj.2018.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Jayaram B., Bhushan K., Shenoy S.R., Narang P., Bose S., Agrawal P., Sahu D., Pandey V. Bhageerath: an energy based web enabled computer software suite for limiting the search space of tertiary structures of small globular proteins. Nucleic Acids Res. 2006;34(21):6195–6204. doi: 10.1093/nar/gkl789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Elmezayen A.D., Al-Obaidi A., Şahin A.T., Yelekçi K. Drug repurposing for coronavirus (COVID-19): in silico screening of known drugs against coronavirus 3CL hydrolase and protease enzymes. J. Biomol. Struct. Dyn. 2021;39(8):2980–2992. doi: 10.1080/07391102.2020.1758791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Tiwari S.P., Fuglebakk E., Hollup S.M., Skjærven L., Cragnolini T., Grindhaug S.H., Tekle K., Reuter N. WEBnm@ v2. 0: Web server and services for comparing protein flexibility. BMC Bioinf. 2014;15(1):1–12. doi: 10.1186/s12859-014-0427-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ponzoni L., Polles G., Carnevale V., Micheletti C. SPECTRUS: A dimensionality reduction approach for identifying dynamical domains in protein complexes from limited structural datasets. Structure. 2015;23(8):1516–1525. doi: 10.1016/j.str.2015.05.022. [DOI] [PubMed] [Google Scholar]
- 55.Mitrousis G., Olia A.S., Walker-Kopp N., Cingolani G. Molecular basis for the recognition of snurportin 1 by importin β. J. Biol. Chem. 2008;283(12):7877–7884. doi: 10.1074/jbc.M709093200. [DOI] [PubMed] [Google Scholar]
- 56.Jia Z., Yan L., Ren Z., Wu L., Wang J., Guo J., Zheng L., Ming Z., Zhang L., Lou Z., Rao Z. Delicate structural coordination of the Severe Acute Respiratory Syndrome coronavirus Nsp13 upon ATP hydrolysis. Nucleic Acids Res. 2019;47(12):6538–6550. doi: 10.1093/nar/gkz409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Goyal B., Goyal D. Targeting the dimerization of the main protease of coronaviruses: a potential broad-spectrum therapeutic strategy. ACS Comb. Sci. 2020;22(6):297–305. doi: 10.1021/acscombsci.0c00058. [DOI] [PubMed] [Google Scholar]
- 58.Lin P.Y., Chou C.Y., Chang H.C., Hsu W.C., Chang G.G. Correlation between dissociation and catalysis of SARS-CoV main protease. Arch. Biochem. Biophys. 2008;472(1):34–42. doi: 10.1016/j.abb.2008.01.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Oany A.R., Pervin T., Moni M.A. Pharmacoinformatics based elucidation and designing of potential inhibitors against Plasmodium falciparum to target importin α/β mediated nuclear importation. Infection, Genetics and Evolution. 2021;88:104699. doi: 10.1016/j.meegid.2020.104699. [DOI] [PubMed] [Google Scholar]
- 60.Yadav R., Choudhury C., Kumar Y., Bhatia A. Virtual repurposing of ursodeoxycholate and chenodeoxycholate as lead candidates against SARS-Cov2-Envelope protein: A molecular dynamics investigation. J. Biomol. Struct. Dyn. 2020;1–12 doi: 10.1080/07391102.2020.1868339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Gurung A.B. In silico structure modelling of SARS-CoV-2 Nsp13 helicase and Nsp14 and repurposing of FDA approved antiviral drugs as dual inhibitors. Gene Reports. 2020;21:100860. doi: 10.1016/j.genrep.2020.100860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Dubanevics I., McLeish T.C. Computational analysis of dynamic allostery and control in the SARS-CoV-2 main protease. J. R. Soc. Interface. 2021;18(174):20200591. doi: 10.1098/rsif.2020.0591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Bahar I., Cheng M.H., Lee J.Y., Kaya C., Zhang S. Structure-encoded global motions and their role in mediating protein-substrate interactions. Biophys. J . 2015;109(6):1101–1109. doi: 10.1016/j.bpj.2015.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Bope C.D., Tong D., Li X., Lu L. Fluctuation matching approach for elastic network model and structure-based model of biomacromolecules. Prog. Biophys. Mol. Biol. 2017;128:100–112. doi: 10.1016/j.pbiomolbio.2016.12.006. [DOI] [PubMed] [Google Scholar]
- 65.Bhattacharya M., Sharma A.R., Patra P., Ghosh P., Sharma G., Patra B.C., Saha R.P., Lee S.-S., Chakraborty C. A SARS-CoV-2 vaccine candidate: In-silico cloning and validation. Inf. Med. Unlocked. 2020;20:100394. doi: 10.1016/j.imu.2020.100394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Calligari P., Gerolin M., Abergel D., Polimeno A. Decomposition of proteins into dynamic units from atomic cross-correlation functions. J. Chem. Theory Comput. 2017;13(1):309–319. doi: 10.1021/acs.jctc.6b00702. [DOI] [PubMed] [Google Scholar]
- 67.Lakhani B., Thayer K.M., Black E., Beveridge D.L. Spectral analysis of molecular dynamics simulations on PDZ: MD sectors. J. Biomol. Struct. Dyn. 2020;38(3):781–790. doi: 10.1080/07391102.2019.1588169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Mirza M.U., Froeyen M. Structural elucidation of SARS-CoV-2 vital proteins: Computational methods reveal potential drug candidates against main protease, Nsp12 polymerase and Nsp13 helicase. J. Pharm. Anal. 2020;10(4):320–328. doi: 10.1016/j.jpha.2020.04.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Schmith, V. D., Zhou, J., & Lohmer, L. R. (2020). The approved dose of ivermectin alone is not the ideal dose for the treatment of COVID‐19. Clinical Pharmacology & Therapeutics, 108(4), 762-765. DOI: https://doi.org/10.1002/cpt.1889. [DOI] [PMC free article] [PubMed]
- 70.Kow C.S., Merchant H.A., Mustafa Z.U., Hasan S.S. The association between the use of ivermectin and mortality in patients with COVID-19: a meta-analysis. Pharmacol. Rep. 2021;29:1–7. doi: 10.1007/s43440-021-00245-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Pott-Junior H., Bastos M., Constantino A., da Cunha A., de Melo C., Neves F., da Silva L., Roscani M., Dos Santos S., Chachá S. Use of ivermectin in the treatment of Covid-19: A pilot trial. Toxicol. Rep. 2021;8:505–510. doi: 10.1016/j.toxrep.2021.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.