A hybrid thermal management system for high power lithium-ion capacitors combining heat pipe with phase change materials

Abstract

Lithium-ion capacitor (LiC) technology is an energy storage system (ESS) that combines the working mechanism of electric double-layer capacitors (EDLC) and lithium-ion batteries (LiB). When LiC is supposed to work under high power applications, the inevitable heat loss threatens the cell's performance and lifetime. Therefore, a proper thermal management system (TMS) can remove the generated heat of the LiC during high cycling conditions. In this paper, a hybrid TMS (HTMS) using phase change materials (PCM) and six flat heat pipes is proposed to maintain the temperature profile below 40 °C under a high current rate of 150 A for 1400 s profile without any pause. Two K-type thermocouples (T1 & T2) are responsible for monitoring the experiments' temperature evolution in the experiments. Numerical analysis is also performed and verified with experimental results to analyze the temperature profile numerically. The experimental and numerical simulation comprises three case studies, including the cell's temperature under natural convection, temperature distribution when using the heat pipe TMS, and temperature distribution when using HTMS. The results reveal that the HTMS is an exceptionally robust cooling system since it reduces the T₁ temperature by 35% compared to the natural convection case study, while the heat pipe TMS can reduce the T₁ temperature by 15% compared to the same case study.

Lithium-ion capacitor (LiC), Hybrid thermal management system (HTMS), Heat pipe, Phase change material (PCM), Computational fluid dynamics (CFD).

1. Introduction

Fossil fuels are the major global warming player since they are responsible for over 65% of greenhouse gasses (Masson-Delmotte et al., 2018). Therefore, finding the best energy substitute would be a massive challenge (Ajuria et al., 2017). Within this frame, renewable energies are infinite power supply to protect the environment and for long-term sustainability. Energy storage systems (ESS) are flexible carbon-free systems that can provide energy to the electrical network (Denholm et al., 2011). Besides, increasing the number of electric vehicles (EV) is a promising way to lower environmental pollution, which can be reached by developing efficient and cost-effective ESSs (Soltani et al., 2020; Khaleghi et al., 2021).

Lithium-ion batteries (LiB) and electric double-layer capacitors (EDLC) are amongst the two main ESSs. LiBs are being used for EVs and electronic devices due to their high energy density and low self-discharge. However, low power density and limited lifespan are their main drawbacks (Hoog et al., 2017; Karimi et al., 2021). In contrast, EDLCs have high power density and high lifetime but suffer from low energy density (Parvini et al., 2016). In this regard, combining the LiBs and EDLCs would result in a hybrid system that benefits from high energy and high power capabilities over a long life span (Miller, 2016). Based on this combination, lithium-ion capacitors (LiC) came into existence, comprising EDLCs cathode and LiBs anode (Zuo et al., 2017). LiCs have advantages like higher energy density and higher voltage than the EDLCs, and higher power density and longer lifetime than the LiBs (JSR Micro, 2009). However, despite these advantages, when LiCs are employed in high fast charge/discharge applications, generate excessive heat, which may decrease the lifetime of the LiCs (Soltani et al., 2018). Hence, there is an essential need to propose a thermal management system (TMS) to remove the generated heat. In general, the typical TMS classifies into active and passive cooling systems.

The active cooling system is an effecting TMS due to its high performance, which includes an air-cooling system, liquid cooling system and refrigerant cooling system (Karimi et al., 2020a, 2020b). Air cooling is a straightforward system due to its cost-effective scheme and simple structure (Giuliano et al., 2012; Behi et al., 2020b). Nevertheless, air cooling systems suffer from low heat transfer and low thermal conductivity (Rao and Wang, 2011). Therefore, the air-cooling system would be pretty ineffective for high charge/discharge applications. The liquid cooling system is another active cooling system with more cooling capacity but is heavy with high maintenance costs (Karimi et al., 2019; Jaguemont and Van Mierlo, 2020). In comparison, passive cooling system energy consumption is negligible compared to the active cooling system (Behi et al., 2021c).

Phase change materials (PCM) are among the passive cooling system that absorbs and release high amounts of generated heat thanks to their phase change process (Behi, 2015; Behi et al., 2018). The first idea of using PCMs as vehicle's TMS was proposed by Hallaj (Hallaj and Selman, 2000). The advantages of PCMs for vehicle TMS were revealed gradually (Ianniciello et al., 2018; Karimi et al., 2020c). The cooling performance of the PCM and air for battery cycle life was numerically considered in which the outcome of the air velocity, phase change, and ambient temperature on the degradation process of the battery cell was studied (Chen et al., 2020). However, PCMs suffer from low thermal conductivity (Karimi et al., 2020c), limiting their performance during the absorbed heat rejection. Hence, several techniques like adding nanomaterial, meshes, and heat pipes are used to increase the thermal conductivity of PCMs (Jaguemont et al., 2019; Behi et al., 2020e). The performance of a paraffin PCM surrounded by aluminum mesh grid foil for a dual-cell LiC module was experimentally considered in which the combination of PCM and aluminum mesh grid foil would reduce the maximum module temperature by 20% and 13% in comparison with forced-convection and pure PCM, respectively (Karimi et al., 2020d).

In contrast, heat pipes are passive TMS that benefit from high thermal conductivity. Heat pipes as a passive cooling system are extremely under the attention due to their high thermal conductivity, low cost and maintenance, and lightweight (Behi et al., 2020a; Gandoman et al., 2021). A heat pipe consists of a container, wick structure, and working fluid transport. Since heat pipes benefit from marvelous features, they have been used in many cooling and heat transfer applications (Behi et al., 2017; Karimi et al., 2021). The heat pipe and air cooling effect on the cylindrical battery module was numerically studied in which the maximum module temperature decreased by 42.1% using an air-based heat pipe cooling system (Behi et al., 2020c). The heat pipe's cooling performance for high current applications was experimentally and numerically analyzed in which the cooling capability of the liquid cooling system and liquid cooling system embedded heat pipe (LCHP) was investigated. Also, the battery module's maximum temperature reduced by 29.9% and 32.6% for the liquid cooling system and LCHP, respectively (Behi et al., 2020d). A sandwich heat pipe cooling system (SHCS) configuration for fast discharging was built, and the cooling effect of the heat pipes in three different scenarios was studied. The results showed a 13.7%, 31.6%, and 33.4% temperature drop for discharging the LTO cell by the cooling strategy using natural convection, forced convection, and forced convection for cell and SHCS (Behi et al., 2020). The heat pipe and evaporative cooling impact for the cell and module level were numerically considered in which a reduction of maximum temperature for the cell and module was seen by 35.8% and 23.8%, respectively (Behi et al., 2021b).

Although several researchers combined heat pipe cooling systems with PCM to control batteries' temperature, none have assessed such a hybrid TMS for LiC in high power applications. PCM-assisted heat pipe TMS was investigated for an LTO cell in a high current discharging process, in which 40.7% enhancement was seen compared to the natural convection scenario (Behi et al., 2021a). Thermal performance analysis of compact-type simulative battery module with flat plate heat pipe and PCM was developed to keep the maximum temperature and uniformity for continuous operation (Abbas et al., 2021). In another research, a TMS based on PCM and heat pipe was designed that reduced the temperature by 30% without increasing system investment. Also, a strategy was developed to optimize the thickness distribution of PCM in the TMS (Chen et al., 2021). Performance of PCM and heat pipe as passive TMS for electric vehicles was investigated to identify the optimal PCM for a temperature range of 25–55 °C and control the maximum temperature under a 60 W heat load (Putra et al., 2020). PCM's thermal performance coupled with heat pipe was experimentally investigated to study the melting time and thermal balance temperature of two systems (Qu et al., 2019). Heat transfer enhancement of PCM using three combined methods based on heat pipe-fins-copper foam (HP-Fin-CF) was numerically studied using the evolution of the melting rates in which the total cycle time of the PCM with the HP-Fin-CF is decreased by 93.34% (Zhang et al., 2020).

According to the authors' best knowledge, no comprehensive work was dedicated to the TMS using heat pipe or PCM for the LiC technology. Especially hybrid TMS (HTMS) combining PCM and flat heat pipes has never been investigated for LiC technology with a fast 150 A charge/discharge current rate. Such a hybrid TMS topology was investigated for LiB batteries in the literature, which in the harshest scenario they only fast charge the batteries for one charging period. Therefore, it is sensible to investigate the HTMS using heat pipe and PCM to improve the PCM's low thermal conductivity employing the flat heat pipes to realize the full potential of the PCM and control the maximum temperature as well as the temperature uniformity for high power applications.

The remainder of the work is organized as follows: First, the experimental methodology is introduced. Then, numerical analysis is described. Validation of the results and discussion are presented in the next section. Finally, the last section concludes the main points of the work.

2. Experimental methodology

In this work, a hybrid thermal management system (HTMS) combining heat pipe with phase change materials (PCM) is designed to study the performance of the proposed method for a commercial prismatic 2300 F LiC cell as the energy storage system (ESS).

2.1. LiC cell description

A fresh LiC cell is used to investigate its heat loss under a discharge rate of 150 A. Figure 1 illustrates the LiC technology's schematic. This cell has nominal voltage and nominal capacity of 3 V and 1 Ah, respectively. Although LiC cell has a low nominal capacity, it shows a high-power capability. Compared to the other high-power ESSs and supercapacitors (SC), the LiC can deliver energy at the current of 1100 A for less than a second. This is the highest delivered energy by the LiC, according to the manufacturer. The LiC specifications are listed in Table 1.

Figure 1.

The commercial prismatic 2300 F LiC cell.

Table 1.

Specifications of the LiC cell.

Parameters	Value	Unit
Capacitance	2300	F
Operating voltage range	2.2 to 3.8	V
Cell weight	355	grams
Current rate	1–1100	A
Energy density	8	Wh/kg
Dimensions	150 × 93 × 15.5	mm3
Operating temperature	-30 to +70	ºC
DC-IR	0.7	mΩ

2.2. Heat pipe description

The used heat pipe in the designed TMS is flat in which distilled water is its working media, and its wick structure is sintered. Figure 2 shows the heat pipe and its sections. Since the flat heat pipe's thermal contact resistance is lower than the other types, they are better candidates for thermal management applications. Table 2 shows the parameters of the heat pipe used in the HTMS.

Figure 2.

Schematic of the flat heat pipe with its sections and dimensions.

Table 2.

Parameters of the flat heat pipe.

Parameters	Value	Unit
Length	250	mm
Width	11.2	mm
Height	3.5	mm
Thermal conductivity	8212	W/m K
cooling power	100	W
Operating temperature	+30 to +120	ºC
Cross sectional area	38.3	mm2
Leff	125	mm

2.3. Phase change material description

The LiC cell with all the six heat pipes is embedded inside the Polyvinyl chloride (PVC) casing. The length, width, and height of the PVC casing are 265 mm, 39 mm, and 105 mm, respectively. Then, PCM was melted by putting it inside a 30 °C chamber and was poured inside the PVC casing. The 30 °C melting temperature is quite optimal and effective for the recommended working temperature limit of the LiC cell. The main idea of adding the PCM to the heat pipes is the PCM's low thermal conductivity compensation. The specifications of the PCM are listed in Table 3. Figure 3 illustrates the schematic of the LiC and the heat pipes which are immersed in the PCM container.

Table 3.

Specifications of the used PCM.

Parameters	Value	Unit
Max. working temperature	210	ºC
Melting point	25 to 32	ºC
Thermal conductivity	0.25 to 0.4	W/m K
Density	0.8	kg/lit
Specific heat capacity	2500	J/kg K
Heat storage capacity	220	kJ/kg

Figure 3.

The schematic of the LiC and the heat pipes that are immersed in the PCM container.

2.4. Experimental test bench

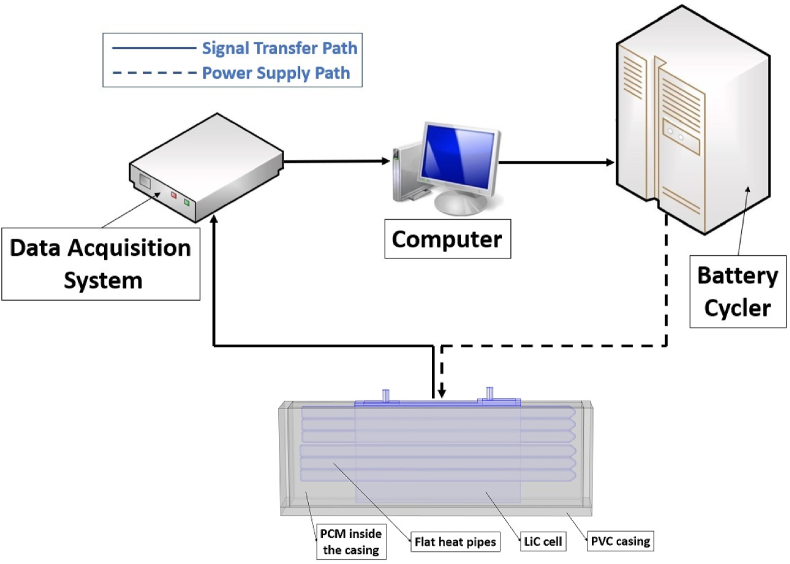
In this work, the cooling performance of the HTMS using six horizontal heat pipes and a PCM is studied on the prismatic 2300 F LiC cell in three cases. The first case study is to investigate the temperature profile of the cell under natural convection. In the second case study, six horizontal heat pipes are attached to the cell to monitor the heat pipe cooling system's performance. In the third case, the LiC with the attached heat pipes is immersed in the PCM container. Figure 2 shows the second case study, where Figure 3 demonstrates the third case study. The experimental test bench includes the LiC cell, six horizontal heat pipes, the PEC battery tester, and battery cycler, a PCM, two K-type thermocouples, and a data logger. The precision of the K-type thermocouples is ±0.2 °C, in which they measure the surface temperature of the cell. The flow diagram of the experimental test bench is exhibited in Figure 4. As can be seen, a computer is connected to the data acquisition system to monitor the cell temperature during the cycling test. The battery cycler duty is monitoring the voltage and the current of the cell using the computer. The cycling of the LiC cell is performed under the rate of 150 A at 1400 s. The LiC is cycled (charged/discharged) by connecting the voltage and current cables to the battery cycler and the data logger.

Figure 4.

The flow diagram of the experimental test bench.

The first and the most vital step to start the cycling and also to develop the numerical analysis is the LiC cell's characterization. Therefore, characterization tests should be performed to imagine how the cell would behave under different conditions. The current, voltage and resistance of the cell would be identified in this step. Besides, the generated heat of the cell would be calculated using these specified parameters. The ACT0550 battery cycler, PEC SBT05250L, and climate chambers were employed to extract the LiC parameters fed into the numerical model.

The uncertainty analysis is also calculated for the current test. Based on Eq. (1), Schultz and Cole method (Sheikholeslami and Ganji, 2016) is used, in which U_VI represents the error for individual factors, and U_R shows the total number of errors.

$$U_R={\left(\sum _{i=1}^n{\left(\frac{\partial R}{\partial V_I}{U}_{VI}\right)}^2\right)}^{0.5}$$ (1)

For this test bench, the uncertainty for current, voltage, thermocouples, and data logger are ±0.005%, ±0.005%, ±0.2%, and ±0.025%, respectively. Therefore, based on the parameters’ uncertainty and Eq. (1), the maximum uncertainty analysis shows less than 2.01% error.

3. Experimental results and discussion

The first case study of this work investigates the LiC cell's temperature evolution under natural convection. This case study aims to find the cell's heat generation's outcome on the transient thermal characteristics when the cell is charged/discharged by 150 A current rate. Since there is no TMS or any cooling system in this case study, the results of this case would be beneficial to compare the cell's temperature profile with a case with a cooling system. Figure 5 illustrates the position of the K-type thermocouples and different domains of the cell. The computer-aided modeling (CAD) of the LiC cell, as well as the HTMS CAD models, are designed employing Autodesk Inventor® software.

Figure 5.

The position of the thermocouples on the LiC cell (left) and the cell domains (right).

The temperature evolution of all three use cases can be seen in Figure 6. As is evident, the thermocouples' temperature trend is almost the same for the first case study, but the temperature difference of the T₁ and T₂ thermocouples is 3.6 °C. However, the maximum temperature reaches more than 55 °C, far beyond the safe working limit that the manufacturer announced. The maximum temperature monitored by the T₁ and T₂ thermocouples is 55.3 °C and 51.7 °C, respectively. Since the heat transfer coefficient between the cell surface and the environment is low, the LiC cell's temperature increases during the cycling test. It can be concluded that natural convection is insufficient to keep the cell's temperature in the desired range. Hence, there is a crucial need for a proper TMS to obtain an acceptable cooling performance and to control the cell's temperature.

Figure 6.

Heat generation of the LiC cell for the three use cases.

In this work, the first step to cool down the cell is employing six horizontal flat heat pipes due to their high thermal conductivity. During the cycling, the generated heat of the cell would be absorbed rapidly and transferred to the environment thanks to the heat pipes' high thermal conductivity. As is evident in Figure 6, heat pipes help remove the cell's heat loss so as the temperature of the T₁ and T₂ thermocouples decreases to 46.8 °C and 44.4 °C, which is 15% and 14% temperature reduction compared to the first case study. However, the cell's maximum temperature is still higher than the safe limit. Therefore, a more robust system should be designed to control the temperature profile.

Designing a hybrid TMS employing a PCM and six flat heat pipes is the last case study, which in this work is investigated. The heat pipes' high thermal conductivity would be beneficial for the HTMS design since the most significant problem of PCMs is low thermal conductivity. As Figure 6 illustrates, the LiC cell's temperature under 150 A intense current rate is entirely controlled using the HTMS, which shows the heat pipe assisted PCM strategy's performance. The T1 and T2 thermocouples' maximum monitored temperatures are 35.8 °C and 35.2 °C, respectively, far lower than the previous case studies. The reason for this perfect performance lies behind the heat exchange phenomenon in which the PCM and the heat pipes conduct the cell's heat loss simultaneously. That is why the cooling performance of the HTMS is around 35% better than the natural convection and 23% better than the heat pipe TMS. The figure's most crucial point is the temperature difference between the T₁ and T₂ thermocouples, which for the first and the second case studies are 3.6 °C and 2.4 °C, respectively. But in the HTMS (the third case study), the temperature difference on the cell surface is around 0.5 °C, which shows that the HTMS is an exceptionally robust cooling system to make the temperature distribution of the cell more uniform.

To understand how the HTMS can make uniform the temperature distribution of the cell, the heat transfer process of the HTMS can be explained as follows:

• 1)During the cell cycle, the flat heat pipes absorb the cell's generated heat by conduction and then transfer the heat to the PCM.
• 2)The PCM receives the heat from the heat pipes through sensible heat storage and latent heat during the phase change.
• 3)The HTMS dissipates the heat to the environment. The high performance of the designed HTMS stems from the high heat storage capacity of the PCM as well as the high thermal conductivity of the heat pipes.

The maximum temperature of the cell that T₁ and T₂ thermocouples sensed is compared in Table 4. Also, the temperature difference between T₁ and T₂ monitored temperatures is an excellent way to understand the cooling system's effectiveness because it shows how the cooling system can uniformly distribute the temperature. Generally, temperature uniformity impacts the charging and discharging power of the cell due to the electrical imbalance of the cell (Kuper et al., 2009). Therefore, the performance of the HTMS was compared to the heat pipe TMS and natural convection without a cooling system in Table 4. The results prove that HTMS reduced the temperature difference by 86%, which is far beyond the heat pipe TMS, reducing the temperature difference by 33%. Therefore, it can be claimed that HTMS can enhance the temperature uniformity of the LiC, which is vital to avoid hot spots that diminish the performance of the LiC cell. Also, A temperature difference between 10 to 15 °C leads to 30%–50% degradation of batteries (Saw et al., 2016). Hence, a robust cooling system like the HTMS is essential for optimum performance of the LiC.

Table 4.

Comparison of the maximum monitored temperature of the cell for three use cases.

Case studies	T1 temperature	T2 temperature	Temperature difference
1st: natural convection	55.3 °C	51.7 °C	3.6 °C
2nd: TMS using heat pipe	46.8 °C	44.4 °C	2.4 °C
3rd: Hybrid TMS (HTMS)	35.8 °C	35.2 °C	0.5 °C
Comparison: 1st & 2nd cases	15%	14%	33%
Comparison: 1st & 3rd cases	35%	32%	86%

4. Numerical analysis

4.1. Geometric construction

Designing the HTMS has been performed using 1D MATLAB SIMULINK® software for the electro-thermal modeling, 3D Autodesk Inventor software for the CAD design, and 3D COMSOL Multiphysics software for the computational fluid dynamics (CFD) analysis. The model's geometry can be seen in Figure 7, in which six flat heat pipes surround the prismatic 2300 F LiC cell, where they are immersed into the PVC casing full of PCM. All the materials and initial conditions of the system and the boundaries were set in the CFD model to investigate the performance of the proposed HTMS and achieve the numerical analysis results. The system's mentioned initial conditions and boundaries include heat sources, heat transfer coefficient, initial temperature, volume reference temperature, heat conduction parameters for the heat transfer module, including thermal conductivity, density, and heat capacity at constant pressure. The thermo-physical parameters of the model are listed in Table 5.

Figure 7.

Geometry of the HTMS.

Table 5.

Thermo-physical parameters of the model.

Data information	Electrode domain	Negative tab	Positive tab	Unit
Density	1627	8960	2700	kg/m3
Electrical resistance	7e-4	5.9e-6	9.9e-6	Ω
Thermal conductivity	λy = λz = 5; λx = 0.36	400	238	W/m K
Specific heat capacity	1271	385	900	J/kg K

4.2. Governing equations

The heat generation of the LiC cell can be calculated using the extracted parameters of current, voltage, and cell resistance. The heat generation of the cell contains the electrochemical reaction loss, the side loss, and the Joule loss, which is explained as follows (Bernardi, 1985):

$${\dot{q}}_{gen}={\dot{q}}_{irr}+{\dot{q}}_{rev}=I\left(U-V\right)-IT\frac{\partial U}{\partial T}$$ (2)

The Bernardi equation for heat generation consists of reversible heat from the entropy change and irreversible heat from the internal resistances (Panchal et al., 2016). In the mentioned equation, I [A], U [V], V [V], and ∂U/∂T [V K⁻¹] denote the current, open-circuit voltage (OCV), terminal voltage, and the entropy coefficient. The side reaction loss is neglected because the cell would work at a reasonable temperature limit (Zhang et al., 2014). In this work, the cell's heat sources are divided into two parts: the LiC cell domain and the tab domain. The heat generation for the LiC cell domain is explained in Eq. (2). The heat equation for the tab domain is as follows (Karimi et al., 2021):

$${\dot{q}}_{gen}=\frac{R{I}^2}{V_{tab}}$$ (3)

$$R={\rho }^{\prime }\frac{l}{S}$$ (4)

Where R [Ω], I [A], V_tab [V], ${\rho }^{\prime }$[Ωm], l [m], and S [m³] represent the tab resistance, current, volume, resistivity, length, and cross-sectional area. Besides the heat generation equations, the energy balance equation is vital to explain the transient thermal distribution that occurs inside the LiC, which can be expressed as follows (Soltani et al., 2019):

$$m{C}_p\frac{\partial T}{\partial t}+q_{conv}=k\left[\frac{{\partial }^{2}T}{\partial x^2}+\frac{{\partial }^{2}T}{\partial y^2}+\frac{{\partial }^{2}T}{\partial z^2}\right]+{\dot{q}}_{gen}$$ (5)

In the energy balance equation, $m$, $C_p$, $k$, and $T$ denote the mass, the specific heat capacity, the thermal conductivity, and the temperature, respectively. Also, $q_{conv}$ represents the heat transfer of the cell to the ambient, which is expressed as follows (Jaguemont et al., 2016):

$$q_{conv}=hS(T_{amb}-T)$$ (6)

Where $h$, $S$, $T_{amb}$, and $T$ represent the heat transfer coefficient of the cell, cross-sectional area, ambient temperature, and the LiC cell temperature.

For the electro-thermal model of the numerical analysis, 1D simulation software MATLAB/SIMULINK® is employed. A second-order electro-thermal model that uses the voltage governing equations is used to characterize the electrical parameters. Based on the electrical parameters, the cell's heat generation can be modeled, which will then be used in the 3D thermal model. Figure 8 shows the relation between the 1D-3D models and the modeling methodology. The second-order electro-thermal model would not be explained in this work because it has already been published in our previous work (Hosen et al., 2020). Figure 9 exhibits the heat generation of the LiC cell during the cycling regime.

Figure 8.

The modeling methodology to show the relation between 1D and 3D models.

Figure 9.

The heat generation of the LiC cell during the cycling regime.

4.3. Generation of the mesh and grid independence of the thermal model

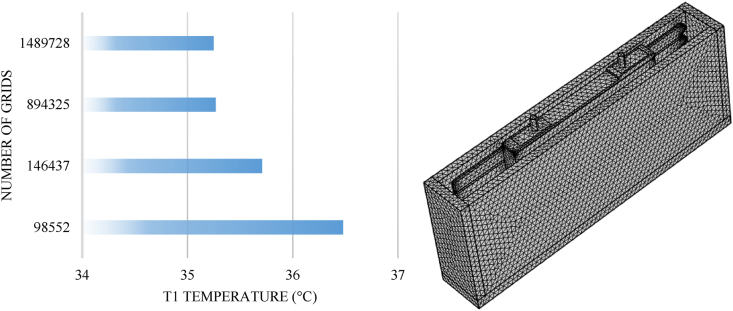
The generation of mesh elements is the next step after geometry construction since the solver, and chosen mesh highly impacts the precision of the results. For the HTMS, the selected mesh is tetrahedral, while the thermal model's grid independence is performed under 23 °C inlet temperature for all three case studies to verify the simulation results against experimental test results. The simulation analysis is time-consuming due to the different geometrical scales of the HTMS model. The T₁ thermocouple temperature is employed for the grid independence analysis. The model's generated mesh is illustrated in Figure 10, showing the model's grid independence for the T1 thermocouple.

Figure 10.

The generated mesh of the HTMS (right) and grid independency analysis (left).

As Figure 10 shows, when the grid number increases from 894,325 to 1,489,728 elements, the temperature difference is 0.2 °C, which is negligible. Besides, to converge the T₁ thermocouple temperature, the time step of 1 s was selected. Based on what the figure demonstrates, 894,325 mesh elements with 1 s time step are chosen for the numerical analysis. Moreover, the radiation was neglected during the simulation (National Renewable Energy Laboratory (NREL), 2014), and the heat transfer coefficient is 13 W m⁻². K⁻¹ for the heat flux.

5. Validation results and discussion

In this section, the developed 3D CFD thermal model is analyzed to validate against the experiments. The CFD model uses the heat generation of the cell that is obtained from the 1D electro-thermal model. The validation of the experiments is carried out for the mentioned three case studies, including:

• 1)The LiC cell's temperature when no TMS is attached to the cell to investigate the natural convection effect.
• 2)The temperature of the LiC cell when six flat heat pipes are surrounded both sides of the cell (three heat pipes in each side of the cell) to investigate the simple TMS performance.
• 3)The LiC cell's temperature when the previous case study with six heat pipes is immersed into the PVC casing, which is full of melted PCM to investigate the hybrid TMS's robustness.

In this section, only the temperature of the thermocouple T₁ is selected for the three case studies to facilitate the verification of the results and show the robustness of the numerical analysis. Figure 11 exhibits the validation results for all three use cases, in which there is a perfect match between the numerical and experimental results.

Figure 11.

Verification of the numerical and experimental results: Exp = experimental, Sim = simulation, NC = natural convection, HP = heat pipe, PCM-HP = PCM with heat pipe.

5.1. 1st case study: the temperature profile of the LiC cell under natural convection

This section deals with the temperature evolution of the LiC cell when the cell is under natural convection under 150 A current rate at 1400 s. The initial temperature is set to a constant 23 °C, and the temperature distribution of the investigated to see the cell's thermal response when no cooling system is attached. In the numerical analysis, solving the governing equations would produce the simulation results using the finite elements method (FEM) in the CFD software. Thermal parameters and initial and boundary conditions impact the simulation results. Two thermocouples and the data acquisition system monitor the temperature at 1400 s at 23 °C room-controlled temperature. As Figure 12 shows, the cell's temperature increases sharply under natural convection, which working at such a high temperature would decrease the lifetime of the cell (Pesaran, 2002). Therefore, proposing a proper TMS is inevitable for the LiC cell to operate within a safe working limit.

Figure 12.

The temperature profile of the LiC cell under natural convection at 1400 s.

5.2. 2nd case study: the temperature profile of the LiC cell using six flat heat pipes

In this section, six flat heat pipes were added to the LiC cell to reduce the maximum temperature and enhance temperature uniformity. Figure 13 demonstrates the transient simulation analysis of this model, which is in good accordance with the experiment results. In the CFD model, a solid region of flat heat pipes is utilized, taking into account the heat pipes' effective thermal conductivity in the numerical analysis (Behi et al., 2020).

Figure 13.

The temperature profile of the LiC cell using six flat heat pipes.

5.3. 3rd case study: the temperature profile of the LiC cell using PCM and six flat heat pipes

The proposed cooling system is the HTMS that uses six heat pipes and PCM to control the temperature contour of the LiC cell during 1400 s of the high charge/discharge current rate. In this regard, the CFD model of the HTMS is analyzed to validate the numerical model and investigate the performance of the designed cooling system. Figure 14 shows the Fluke thermal camera's image to insight the temperature distribution on the LiC cell. Besides, the figure depicts the CFD software's simulation results, which are verified against the experiments. As can be seen, PCM surrounds the cell and the heat pipes from the beginning of the test, where it is in the solid state till the end of the test, where it is in the liquid state.

Figure 14.

The temperature profile of the LiC cell using PCM and six flat heat pipes.

At the beginning of the cycling test, the flat heat pipes absorb the generated heat immediately and transfer the absorbed heat to the PCM, which is solid in this phase. The solid PCM achieves the heat from the heat pipes and the cell thanks to the PCM's sensible heat until the PCM's temperature reaches the phase change temperature. Then, a PCM layer that is in direct contact with the cell and the heat pipes is melted. The melting zone increases by absorbing more heat thanks to its latent heat. The significant problem of PCMs is their low thermal conductivity, which should be compensated to reject the absorbed heat. In this work, heat pipes help the PCM to receive and release the heat much faster.

Moreover, Figure 15 shows the entire process of absorption and rejection of the LiC cell's heat generation during the fast charge/discharge cycling test. Figure 15 (a) shows the thermal image of the HTMS starting from the initial temperature of 23 °C Figure 15 (b) verifies that the numerical simulations are in perfect accordance with the experimental results. Phase change temperatures are exhibited in Figure 15 (c), in which the solid form is zero and the liquid form is one. In the middle of the solid and the liquid forms, phase change would happen in the mushy zone. Figure 15 (d) depicts the front view and back view of the cooling system showing the solid form of the PCM at the beginning of the test, half solid-half liquid when 700 s pass, and the liquid form of the PCM at the end of the cycling test.

Figure 15.

(d) Thermal images of the HTMS equipped with PCM and sex flat heat pipes, (b) maximum temperature of the LiC cell, (c) phase change contours in which “zero” depicts fully solid, and “one” represents the fully liquid zones (d) PCM state from the solid form at the beginning of the test to liquid zone at the end of the cycling test.

6. Conclusion

In this paper, a hybrid thermal management system (HTMS), including six flat heat pipes and a PCM, was proposed for a commercial prismatic 2300 F LiC technology. When the LiC is operating in high charge/discharge applications, the generated heat diminishes the cell's life span, and in the worst scenario, thermal runaway would happen. Hence, designing a thermal management system (TMS) is vital to absorb and remove the cell's heat loss during the cycle test. The performance of the HTMS has been compared to natural convection case study and heat pipe TMS case study. The cycling of the LiC was performed under 150 A high current rate at 1400 s without any pause during the cycling. Numerical simulations were also carried out for validation of the experimental results. The simulation and experimental tests comprise three case studies: temperature of the cell under natural convection, temperature distribution when using the heat pipe TMS, and temperature distribution when using HTMS.

The results reveal that for the first case study (natural convection), T1 and T2 thermocouples' maximum monitored temperatures are 55.3 °C and 51.7 °C, respectively. For the heat pipe TMS (second case study), T₁ and T₂ temperatures show 46.8 °C and 44.4 °C, which reduces the temperature by 15% and 14% compared to the first case study. For the HTMS (the third case study), the T₁ and T₂ thermocouples exhibit 35.8 °C and 35.2 °C, respectively, which improve the heat rejection by 35% and 32 %, respectively. Besides, the temperature uniformity of the cell was improved by the HTMS. The results prove that although passive TMS using heat pipes is an effective system for the overheating problem of the LiC but combining PCM to this cooling system would control the temperature profile. This method is also beneficial for the PCM to enhance its thermal conductivity problem. Therefore, the HTMS is quite robust to maintain the maximum cell temperature and to enhance the temperature uniformity.

6.1. Limitations of the study

All the developed 1D-3D models can be utilized as an effective tool to investigate the LiC technology. However, the developed method is verified for a single cell. Applying the same methodology and verification of the models for a module or a pack would be a challenge, which is in the authors' next plan to investigate the HTMS for a LiC module/pack. Then, the system's validation and optimization would be the future work to enhance the numerical simulations' robustness and effectiveness.

Declarations

Author contribution statement

Danial Karimi: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Md Sazzad Hosen & Hamidreza Behi: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Sahar Khaleghi, Mohsen Akbarzadeh, Joeri Van Mierlo & Maitane Berecibar: Contributed reagents, materials, analysis tools or data.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

The data that has been used is confidential.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.