Deep-Learning-Assisted Volume Visualization

Abstract

Designing volume visualizations showing various structures of interest is critical to the exploratory analysis of volumetric data. The last few years have witnessed dramatic advances in the use of convolutional neural networks for identification of objects in large image collections. Whereas such machine learning methods have shown superior performance in a number of applications, their direct use in volume visualization has not yet been explored. In this paper, we present a deep-learning-assisted volume visualization to depict complex structures, which are otherwise challenging for conventional approaches. A significant challenge in designing volume visualizations based on the high-dimensional deep features lies in efficiently handling the immense amount of information that deep-learning methods provide. In this paper, we present a new technique that uses spectral methods to facilitate user interactions with high-dimensional features. We also present a new deep-learning-assisted technique for hierarchically exploring a volumetric dataset. We have validated our approach on two electron microscopy volumes and one magnetic resonance imaging dataset.

1. Introduction

Deep learning and, more specifically, convolutional neural networks (CNNs) have received much attention in image classification [1], face recognition [2], [3], and segmentation [4], [5]. Given raw images as input, a CNN progressively builds its final outcome by sequentially propagating responses from one neural network layer to the next. The hierarchical architecture of CNNs resembles the multiscale process of human visual system that aggregates lower-level signals into higher-level concepts. A CNN can learn, by iteratively fitting the network to the data, useful application-dependent representations [2], [6] that facilitate the search for solutions to complex problems.

Volume visualization typically involves three steps. First, users define the criteria (e.g., intensity and texture) that distinguish the structures of interest (e.g., soft tissue and bone). Second, based on these user-defined criteria, users choose an appropriate set of per-voxel features that span the low-dimensional subspace in which one can look for desirable solutions (i.e., visualizations). Finally, users interact with the visualization tool to create and modify the solutions. In the past, handcrafted features that correspond to specific user-defined criteria (e.g., size [7], [8], texture [9], and visibility [10]) have been successfully used as volumetric features for the second step. Nevertheless, as the complexity of the user-desired criteria grows, finding features that precisely describe the characteristics of the target structures becomes increasingly challenging. Conventional handcrafted features no longer suffice because they are defined locally without addressing the relationships among voxels in the global context, often crucial to characterizing complex structures.

Although the high structural complexity significantly hinders the manual search for suitable feature spaces in the second step of the current visualization workflow, users can still provide valuable domain knowledge in a different way. From a machine learning point of view, the criteria that distinguish different structures can be implicitly defined by a large number of examples that include as many structural variants as possible. In this paper, we present our approach in which we train a CNN as if we were solving a classification problem based on a given set of examples. After training, the CNN automatically derives a high-level data representation, thus creating a feasible feature space for visualizing complex structures. Despite improvements in user interfaces [11], [12], [13], [14] and semi-automatic techniques [15], [16], current methods proceed with the assumption that a suitable feature space is explicitly defined, not automatically learned. In contrast, the proposed deep-learning-assisted approach automatically creates a high-dimensional feature space in a data-driven way without an explicit specification from the user.

In the derived feature space, voxels with similar characteristics are in close proximity. These similar voxels can therefore be selected for visualization based on a representative feature vector, which we call characteristic feature vector throughout this paper. However, the characteristic feature vector becomes complicated to modify as its dimensionality grows. Previous work alleviates this problem by designing visualizations in a reduced space with manageable complexity [12], [17]. In this work, we present two techniques for this usability problem. The first one reorders the features with respect to their similarity. With this improved, similarity-aware feature layout, the conventional design widget can select groups of similar voxels in the original space without dimensionality reduction. This is complementary to the dimension-reduction-based techniques. The second one is a semi-automatic technique that generates a hierarchy of volume visualizations for users to choose from, thus providing another layer of abstraction on top of the high-dimensional feature space.

Although modern rendering techniques and hardware can now render volumetric data interactively, we still need a suitable feature space that facilitates natural differentiation of target structures and an intuitive and interactive way of designing visualizations. This paper presents our initial explorations in using deep learning methods to assist the design of volume visualizations. We expect that the techniques presented in this work will be useful in many visual computing tools that require informative visualizations.

The contributions of this work are:

• A deep-learning-assisted approach to automatically derive high-level features based on information extracted from a larger context than conventional local features.

• A feature reordering technique that groups similar features together to facilitate manual visualization design and a semi-automatic technique for hierarchical exploration.

• A method that converts a high-dimensional feature space to a binary field that can be used as an input to the conventional marching cubes algorithm.

2. Related Work

2.1. Convolutional Neural Networks

The basic components of a conventional feedforward CNN include convolutional layers, spatial pooling layers, and fully-connected layers. A convolutional layer filters an input tensor with trainable kernels, which combine neurons in a fixed receptive field. The size of receptive fields directly affects the number of trainable parameters. A spatial pooling layer outputs an aggregation of nearby neurons with a predefined operator. For example, a max-pooling layer outputs the maximum value within a small neighborhood. A fully-connected layer connects every input neuron with the output neurons, disregarding their spatial proximity. The raw output values of neurons in convolution layers and fully-connected layers are usually transformed by an activation function (usually non-linearly) into the result signals, representing the activation level of neurons.

AlexNet [1] is one of the most recognized contributions in image classification and has become the standard benchmark algorithm. AlexNet contains five convolutional layers followed by two fully-connected layers, and three max-pooling layers mixed in between. The last fully-connected layer then connects to the output consisting of 1,000 neurons, one for each target class.

Most ordinary CNN architectures more or less resemble the basic construct of AlexNet but differ in depth. For example, GoogLeNet [18] has 22 trainable layers, much deeper than AlexNet, which has seven trainable layers. At this scale of depth, kernel sizes have to be kept small to maintain a manageable model complexity. This limitation in kernel size does not restrict the power of deep CNNs. In fact, deliberately stacking multiple convolutional layers with small kernels leads to a large receptive field, which is comparable to that of a large kernel but with fewer parameters [19]. Although research in complex problems tends to create deeper networks, simply stacking convolutional layers in a CNN does not always lead to better performance because of the increased model complexity. Addressing the deficiency of conventional CNNs, a 152-layer residual network [20] shows significant improvement over the state-of-the-art architectures.

Given a sequence of training examples, the training procedure starts with a forward pass through the network, calculates a loss value with respect to certain criteria, and then adjusts the weights associated with the neurons in the network accordingly by the backpropagation algorithm. Training a CNN appropriately can be challenging because of problems such as overfitting and premature convergence, which deteriorate performance significantly. Dropping connections between random neurons (i.e., removing them from the network temporarily) avoids co-adaptations among them [21], thereby reducing the chance of overfitting but also slowing down convergence. The slow convergence of CNNs is partly due to the frequent changes in the distribution of a layer’s input during training. Batch normalization [22] addresses this problem by normalizing each feature independently to have a zero sum and unit variance distribution.

2.2. Volume Visualization

Typical volume rendering techniques can be grouped into two categories: direct and indirect volume rendering. Direct volume rendering (DVR) techniques, such as volume ray-casting [23], compose a result image by aggregating the colors and opacities of relevant voxels calculated using a user-defined transfer function [24]. Indirect volume rendering (IVR) techniques first generate geometric primitives as an intermediate representation and then render those primitives using conventional 3D computer graphics. For example, the marching cubes algorithm [25] extracts a triangular mesh that represents an isosurface in a structured grid.

Despite different ways of composing result images, DVR and IVR techniques all require a feature space suitable for the visualization criteria. Simple structures that are distinguishable by intensity values can be extracted and visualized as corresponding isosurfaces [25] following the IVR framework. In many applications, however, the complex structures and their surroundings are indistinguishable based on a single isovalue. In these cases, the target structures may be better extracted as subvolumes composed of voxels with intensity values lay between an interval [26], [27].

Whereas typical IVR techniques extract geometric primitives from a scalar field formed by intensity values, DVR techniques rely on a transfer function, sometimes defined in an alternative feature space derived from the intensity, to assign distinct colors and opacities to different structures. Common features such as gradient magnitude [11] and curvature [28] allow distinguishing regions with significant local changes in intensity. Other specialized features are used for structures with specific characteristics. For example, twenty texture features were used to identify voxels with texture differences [9]. Evaluating the size of structures in scale-space at each voxel creates a scale field that distinguishes structures of different sizes [7]. An alternative way to assess structure sizes is by searching in all directions for neighboring voxels with similar intensities [8].

Whereas most volume visualizations are done manually, semi-automatic techniques automate specific time-consuming procedures to accelerate the design. Candidate isosurfaces that correspond to meaningful structure boundaries can be selected automatically based on gradient magnitudes [29]. Exploiting the proximity of voxels in the feature space, many semi-automatic techniques use clustering algorithms to group similar voxels, thus reducing the complexity of visualization design [15], [16].

A prerequisite of successful volume visualizations, including those created by semi-automatic techniques, is that the selected feature space must differentiate the target structures. Finding such a feature space is therefore critical for volume visualization design. Nevertheless, existing feature spaces, including those formed by texture features, are too local to reliably differentiate complex structures when given only limited context around each voxel. In this work, we address this limitation by automatically forming a feature space based on high-level features extracted from a trained CNN. Based on the CNN-derived feature space, we then create visualizations following the IVR framework.

3. Methodology

3.1. Motivation

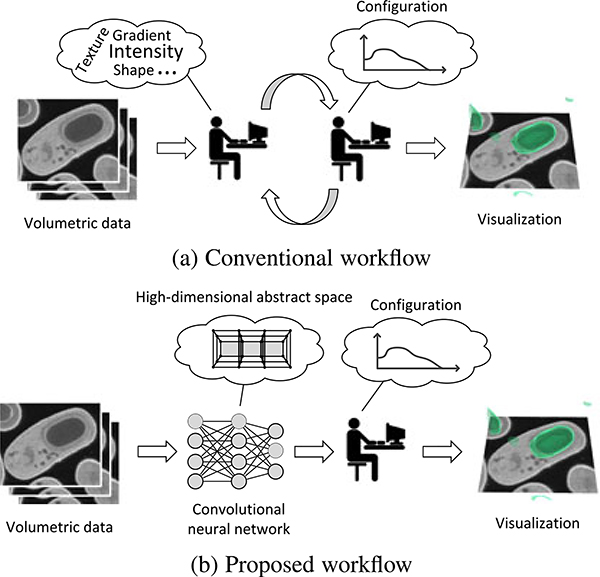
Visualization is crucial to the analysis of volumetric data, for example the diagnosis of brain injuries [30], [31], yet its design remains labor intensive. Conventional visualization workflow assumes a feature space in which users, after some trial and error, find a transfer function configuration suitable for the target structures. Typically the feature space is handcrafted with respect to specific application-dependent criteria. This manual procedure limits the feature space to incorporate only local features because of the limited human capacity to comprehend and integrate non-local properties defined in high-dimensional spaces. As structural complexity grows, the assumption of having a user-manipulable feature space becomes increasingly unrealistic. When the visualization results are not satisfactory, users are faced with the hard choices of modifying the feature space, the transfer function configuration, or both (Fig. 1a).

Fig. 1.

(a) Conventional workflow requires users to adjust both the feature space and the configuration. (b) Our deep-learning-assisted approach derives from labeled examples a feasible feature space automatically instead of relying on a user-defined feature space.

This observation motivates our deep-learning-assisted approach that learns a feasible feature space automatically when provided enough examples of the target structures. This approach adopts a workflow that effectively replaces the manual search for a feasible feature space by labeling of samples followed by deep learning (Fig. 1b). In contrast to crafting features in a high-dimensional abstract space, the labeling task is much easier for typical users, who are domain experts familiar with the data but have limited knowledge of computational techniques.

3.1.1. Conventional Volume Visualization Design

With imaging modalities such as X-Ray and computed tomography, structures of different intrinsic material densities (e.g., soft tissue and bone) are distinguishable by their distinct intensity values. This characteristic allows conventional intensity-based feature spaces to separate these structures effectively. For example, the boundaries of bone may correspond well to a specific isosurface. With other modalities, such as electron microscopy, the type of structures to which a voxel belongs is seldom decided solely by the voxel’s intensity value without consulting the arrangement of the neighboring voxels. Large intra-class variations further complicate the decision. In addition, gradient only describes local changes in intensity values and lacks the capability of depicting the boundary of complex structures. As a result, intensity and gradient do not provide enough information for designing comprehensive visualizations for complex structures.

For example in Fig. 2, we compare the mesh generated from the ground truth labels of mitochondria (Fig. 2b) with the meshes generated using the conventional marching cubes algorithm (Fig. 2c) and our deep-learning-assisted approach (Fig. 2d) for the hippocampus dataset (cf. Section 4.2). Although the mitochondria are typically low in intensity, many non-mitochondria voxels (e.g., those of the membranes) are also low in intensity (Fig. 2a). As a result, the isosurface of isovalue 112, which is close to the average intensity value of mitochondria, does not map precisely to boundaries of mitochondria, thus creating an incomprehensible visualization with severe occlusions of various structures. In contrast, our method creates a visualization of mitochondria comparable to the ground truth labels.

Fig. 2.

(a) In the hippocampus dataset, we find it challenging to differentiate mitochondrial regions (orange) from non-mitochondrial regions using conventional intensity-based feature spaces. (b) The ground truth mitochondria. (c) The isosurface of isovalue 112, which is the average intensity value of mitochondria, does not correspond well to the boundary of mitochondria. In fact, no single isovalue would be suitable for differentiating the mitochondria (cf. Fig. 3a). (d) Our visualization result is comparable to the ground truth because it is based on a feasible feature space derived automatically.

The previous example shows the deficiency of conventional feature spaces in depicting complex structures. In fact, a significant overlap of the two types of voxels (i.e., mitochondria and non-mitochondria) in the intensity histogram confirms that we cannot obtain clear boundaries using a single isovalue (Fig. 3a). Adding gradient magnitude as a second dimension does not improve separation in the density plot either (Fig. 3b). Besides intensity and gradient magnitude, Haralick features [32], a set of texture features calculated from a small local neighborhood, also lack the power of isolating mitochondria although they have been successful for other structures in computed tomography and magnetic resonance images [9]. Here we calculate seven Haralick features (i.e., energy, inertia, inverse difference moment, entropy, correlation, contrast, and sum of entropy) with the same configuration [9]. After projecting the voxels in two dimensions using principal component analysis, the large overlap near the center shows that the selected Haralick features do not separate the mitochondria from the rest of the image (Fig. 3c).

Fig. 3.

(a) The overlap in the intensity histogram shows that we cannot extract the mitochondria precisely using a single isovalue. The density plots, in which higher saturation indicates higher density, show that (b) intensity and gradient, and (c) seven selected Haralick features do not help isolate the mitochondria either. The seven Haralick features are projected onto the first two principal components, “PC 1” and “PC 2”, obtained using principal component analysis.

3.1.2. Deep-Learning-Assisted Visualization Design

Previous studies on the hippocampus dataset have shown that features depicting both the complex shape of the mitochondria and the contextual information around voxels perform better in segmentation [33]. If we were to apply the conventional design workflow to visualize mitochondria and other complex structures presented in this paper, users would need to define such sophisticated features themselves. Although there may exist a combination of novel and established features suitable for specific targets, searching manually for that combination is time-consuming and challenging. On the contrary, our proposed approach uses a CNN to perform that search effectively and automatically. Users can therefore focus on creating comprehensive volume visualizations based on the derived feature space.

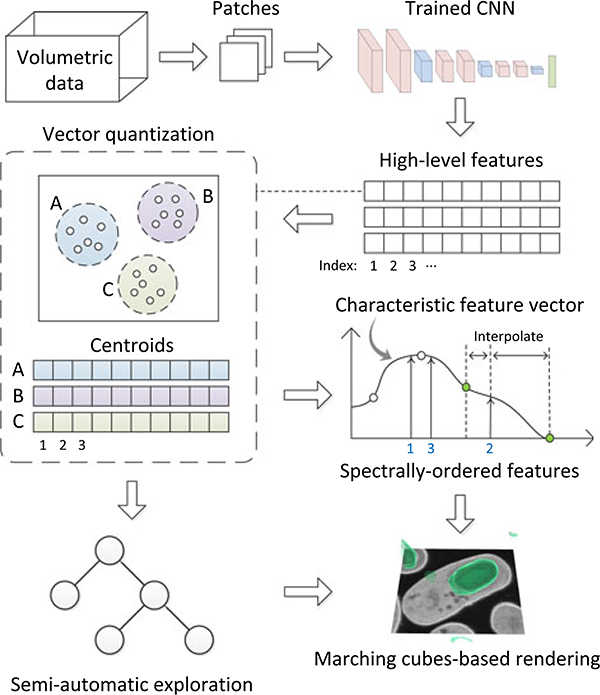
Our deep-learning-assisted approach extracts high-level features (i.e., deep features) from a trained CNN (top of Fig. 4). We first train the CNN as if we were solving a voxel-wise classification problem. Because CNNs are powerful in finding suitable application-dependent features, we use those features to distinguish voxels that belong to various complex structures during rendering. The extracted deep features correspond to much higher level concepts when compared with local features such as gradient magnitude or textures, thus improving their capability in discerning complex structures.

Fig. 4.

Our proposed deep-learning-assisted approach first extracts high-level features from a trained CNN. We then use vector quantization to encode the extracted high-dimensional features of each voxel by the nearest centroid found using k-means clustering. Users modify the visualization result, which is generated by a marching cubes-based rendering, either by editing the characteristic feature vector or exploring a pre-generated subvolume hierarchy semi-automatically.

Based on the derived feature space, we address practical issues when creating volume visualizations using deep features (bottom of Fig. 4). Even for moderate-sized volumetric data, the high dimensionality of features could be overwhelming because of the limited memory available to a GPU. Therefore, we use vector quantization to compress the features to a manageable size. Furthermore, because the derived features are not independent, we apply a spectral method to reorder them. After feature reordering, users can easily create visualizations by modifying a characteristic feature vector through a simple design widget. We also use a semi-automatic method to accelerate the design of volume visualization by pre-generating a tree of visualizations, with which users can explore the volumetric data hierarchically and interactively.

3.2. Learning High-Level Features

3.2.1. CNN Model

The high-level features are extracted from a CNN, which contains three groups of convolutional layers (Table 1). In each group, we stack two convolutional layers with 3 × 3 kernels to resemble the reception field of a 5 × 5 kernel but with fewer trainable parameters. We perform batch normalization [22] for all the convolutional layers. We use dropout [21] with a probability of 0.5 for the first fully-connected layer. The first fully-connected layer contains 200 neurons, which connect to neurons in the second fully-connected layer. Each neuron in the second fully-connected layer corresponds to an individual class in the data. After training the CNN, we extract 200-dimensional voxel representation from the first fully-connected layer.

TABLE 1.

The Architecture of Our Proposed CNN

Layer	#channels	#neurons	Kernel	stride
Convolutional	64	32 × 32	3 × 3	2
Convolutional	64	32 × 32	3 × 3	1
Max-pooling	64	16 × 16	2 × 2	2
Convolutional	64	16 × 16	3 × 3	1
Convolutional	64	16 × 16	3 × 3	1
Max-pooling	64	8 × 8	2 × 2	2
Convolutional	64	8 × 8	3 × 3	1
Convolutional	64	8 × 8	3 × 3	1
Max-pooling	64	4 × 4	2 × 2	2
Fully-connected		200	1 × 1
Fully-connected		#classes	1 × 1

We chose the values of parameters based on the results of our preliminary study conducted using the target datasets. We applied a random search strategy, which is often used for designing CNNs, to determine the parameters based on the observed loss values and the convergence of the network. For other datasets, we may need to adjust these parameters depending on the complexity of target classes for better performance. A more systematic but time-consuming approach is through automatic hyperparameter optimization [34].

A convolutional layer slides k trainable kernels W_m,k over the input 3D tensor U of size x × y × m, where x and y correspond to the spatial dimensions, and m denotes the number of input feature maps (or, channels). The layer outputs a 3D tensor V, which is connected to the next layer. The ith output feature map V_i is calculated as $V_i={\sum }_m{W}_{m,i*}{U}_m+b_i$, where b_i denotes the associated bias term. The convolution can be selectively applied to neurons separated by a predefined distance referred to as stride. Here the first convolution uses a stride of two, resulting in a reduction in spatial dimension by half (first row, Table 1).

The output of a convolutional layer is always subjected to an activation function that transforms the values in the ith feature map V_i into corresponding activation signals. For all convolutional layers and the first fully-connected layer, we use Parametric Rectified Linear Unit (PReLU) [35]. For the second fully-connected layer, we apply the soft-max function to calculate the predicted probability of voxel classes.

Max-pooling layers scan and output the maximum neuron within a local window. We use max-pooling with a 2 × 2 window and a stride of two to reduce the spatial dimension by half after each group of two convolutions.

3.2.2. Training

The training data contain 65 × 65 patches centered at a voxel samples selected at random. We choose the same patch size used in a previous study [4] with tissue sample and resolution similar to the hippocampus dataset (cf. Section 4.2.3). We draw 400,000 voxels divided equally among the classes to avoid the majority class from dominating other classes during training. We use a batch size of 200 and train a total of 60,000 iterations. After 2,000 iterations the training set is resampled to learn from diverse examples. We use ADA-DELTA solver [36] with a momentum of 0.9 and a decay of 5 × 10⁻⁴ during training.

The input volume is padded with reflection about the edges before generating patches to take into account cases where the sampled voxels are near an edge. Because we only have incomplete context information to predict voxel class in these boundary cases, the padding essentially fills the incomplete region with information extrapolated from the neighborhood.

3.2.3. Class Imbalance

The CNN trained with balanced classes tends to overestimate the probability of the minority class in the testing stage because of the significant disparity in abundance between the training data, which contain equal amounts of samples among voxel classes, and the testing data, which would have the actual class distribution. Such a class imbalance is increasingly problematic as the disparity grows.

Because the degree of class imbalance in the datasets we used is moderate, a simple way to address this problem is by multiplying the predicted probability of each class by the corresponding prior probability, thereby scaling down the predicted probability of the minority class. We have also implemented the fitted transform postprocessing [4], which finds a monotonic cubic polynomial to match the predicted probability and the prior probability based on the training samples. Instead of having a constant scaling factor (i.e., the class prior), this technique transforms the predicted probability in a data-driven way that allows the setting of variable scaling factors with respect to the probability values.

3.3. Depicting Multiscalar Volumes

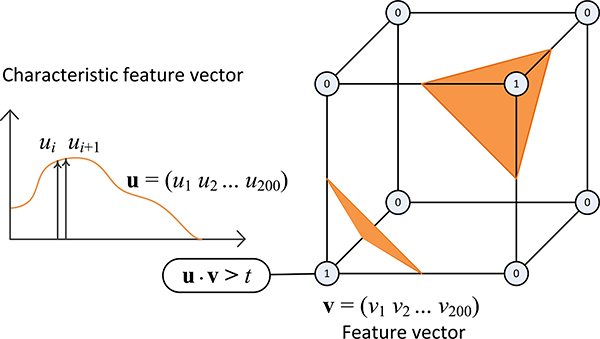
We apply the conventional marching cubes algorithm [25] to extract boundaries that separate dissimilar voxels based on high-dimensional features. For each cube, the marching cubes algorithm determines the triangles given the eight bits defined at the bounding voxels. Because in this work the input is a multiscalar field formed by the high-dimensional feature space, we describe in the following a method that converts the input multiscalar field to a binary field with which the marching cubes algorithm can extract surfaces as usual (Fig. 5).

Fig. 5.

After feature extraction, we generate a binary field by comparing the dot product of the characteristic feature vector u and the feature vector v of each voxel with a threshold t. We then apply the conventional marching cubes algorithm on the binarized volume.

Assuming that each voxel is represented by a 200-dimensional feature vector v = (v₁ v₂ . . . v₂₀₀), we can decide whether two voxels belong to the same structure by comparing their dot product with a threshold t. Following the same intuition, we can also decide whether a voxel belongs to a user-defined structure, which is specified by a characteristic feature vector u = (u₁ u₂ . . . u₂₀₀). The value of a voxel v in the binary field, used as the input for the marching cubes algorithm, is calculated as

$$f(\mathbf{u},\mathbf{v})=\{\begin{array}{ll}0,\hfill & \text{if}\mathbf{u}\cdot \mathbf{v}\le t\hfill \\ 1,\hfill & \text{otherwise}.\hfill \end{array}$$ (1)

The extracted surface changes with the (binary) value of f(u, v), which is controlled by the characteristic feature vector u and the value of threshold t. Users can interact with the design widget to configure u and t as well as the color and opacity of the corresponding surface (used for blending multiple semi-transparent surfaces).

The marching cubes algorithm is highly parallelizable because each cube can be processed independently. Our GPU-based parallel implementation uses the histogram pyramid data structure [37] to facilitate the query of a triangle’s location in the volume and the query of the triangle indices (if any) inside of a specific cube. In a histogram pyramid, each space-partitioning square cell stores the number of triangles in the corresponding partition. The levels from the bottom to the top of the pyramid represent the volumetric data at increasingly lower spatial resolutions. When constructing the pyramid, a cell stores the sum of eight (2 × 2 × 2) corresponding cells in the previous (lower) level. Both queries require a top-down pyramid traversal, which only takes a time logarithmic to the size of spatial dimension (or linear to the height of pyramid). For visual appeal, we smooth the extracted triangular mesh by moving each vertex to the average location of its adjacent vertices in the mesh. During mesh smoothing, the query of adjacent vertices is done by first fetching a list of triangles in the current cube and its neighboring cubes (through the second type of queries) and then inspecting each edge of the fetched triangles. We use two vertex buffers to store vertex positions before and after the smoothing. After each smoothing iteration, we swap the two vertex buffers to avoid expensive data movement.

3.4. Reordering High-Dimensional Features

The order of features in conventional volume visualization designs is usually straightforward and less of a concern because of the low dimensionality of feature spaces. Nevertheless, the high-level features extracted from the CNN are 200-dimensional. Further, some, but not all, of the extracted features could be closely related to each other. When features are in arbitrary order along the x-axis of the design widget (left of Fig. 5), assigning a meaningful characteristic feature vector may require numerous control points, explicitly defining the value of each dimension. Although the reordering of features does not add to the possible visualizations that can be generated using the deep-learning-assisted approach, the usability issue must be addressed to benefit from the power of high-dimensional representations.

We address the relationships among features by rearranging them using spectral ordering, which sorts the features by the eigenvector of the second smallest eigenvalue of a graph Laplacian [38]. First, the normalized Laplacian matrix is generated based on feature-to-feature similarity; then, the eigenvector associated with the second smallest non-negative eigenvalue (the Fiedler vector) is calculated; finally, the features are sorted based on their values in the Fiedler vector. The result is an ordering of features where neighboring features are similar. The Fiedler vector and other eigenvectors associated with small eigenvalues also form the basis of spectral clustering [39].

We use the following example to show the effect of rearranging deep features into the spectral order (Fig. 6). A bright pixel in the 200 × 200 similarity matrix marks a pair of highly correlated features (Fig. 6a). Many pairs of the 200 features are indeed highly correlated because many pixels are bright. Nevertheless, an arbitrary order of features does not take advantage of such correlations, resulting in a disorganized similarity matrix (left of Fig. 6a). The spectrally ordered similarity matrix puts similar features closer together, resulting in large bright blocks of various sizes along the diagonal (right of Fig. 6a). An accessible feature order therefore allows selecting similar voxels using fewer control points in the design widget.

Fig. 6.

(a) Before spectral ordering, the similarity matrix, in which a bright pixel represents a pair of highly correlated features, does not show any apparent pattern. After spectral ordering, highly correlated features are closer to each other. (b) A simple characteristic feature vector. (c) The arbitrary order of features does not exploit the correlation among features, thus leading to broken surfaces. The spectrally ordered features allow creating a visualization that reveals interesting structures using the same, simple characteristic feature vector in (b).

Reordering features into this accessible form is a crucial step. In this example, we use the same characteristic feature vector, which simply specifies an increasing weight from the first (leftmost) to the last (rightmost) feature (Fig. 6b), and compare the visualization results obtained before and after reordering features. An arbitrary feature order does not exploit the similarity among features and creates surfaces that are broken into small pieces, which do not correspond well to specific structures (left of Fig. 6c). In contrast, the spectrally ordered features are highly structured such that even a simple characteristic feature vector can reveal some interesting structure (right of Fig. 6c).

3.5. Feature Compression

Interactive rendering of volumetric data based on high-dimensional voxel representations can be prohibitive because the inflated data size may exceed the memory size on modern GPUs. Although directly using 20-dimensional texture features has been shown to be effective previously on small datasets (less than 8.4 million voxels) [9], in this paper we use 200-dimensional features and validate our technique on much larger datasets (over one hundred million voxels). Suppose each feature is stored as a four-byte floating point number, loading all 200 features would require 80 gigabytes of memory per hundred million voxels. The high storage demand far exceeds the capability of modern consumer-level graphic cards.

Possible solutions to this problem are out-of-core rendering and data compression. For simplicity, we use vector quantization (VQ) to compress the high-dimensional feature vector v. We use an incremental k-means algorithm [40] to find N_c voxel clusters (i.e., code words in the codebook). Each voxel is encoded by the index of the nearest cluster centroid based on L² distance. During rendering, voxels are decoded by referencing the codebook.

Reconstruction using VQ, which is a lossy compression technique, inevitably introduces information loss. The codebook size N_c is closely related to the reconstruction error of VQ. Choosing too small a value for N_c leads to excessive information loss such that the reconstructed feature vectors (i.e., the cluster centroids found by k-means) do not well approximate the actual feature vectors. On the other hand, choosing too large a value for N_c inflates the size of the codebook and requires much more computation. A similar information loss introduced by dimension reduction techniques has been shown to be tolerable when simplifying the feature space of volume rendering [12], [17]. In the following, we will evaluate how information loss affects the quality of visualizations created using our deep-learning-assisted approach.

In Fig. 7, we visually evaluate the quality of the visualization results with various codebook sizes N_c. In this example, we use a subvolume containing a sporulating bacterium of the bacteria dataset (Fig. 7a). By comparing the results shown in Figs. 7b, 7c, 7d, and 7e, the only visually apparent difference is in the small region near the center of the spore (black box in Fig. 7b) when N_c = 64; the other three results are comparable despite the difference in N_c (Figs. 7c, 7d, and 7e).

Fig. 7.

The size of codebook N_c in VQ controls the amount of information loss. The zoom-in views shown in (b–e) are generated from the same subvolume (red box in (a)) in the bacteria dataset with N_c ranges from 64 to 512. When N_c = 64, the view shows a noticeable disparity near the center of the spore (black box in (b)). The results in (c–e) are comparable without significant visual differences.

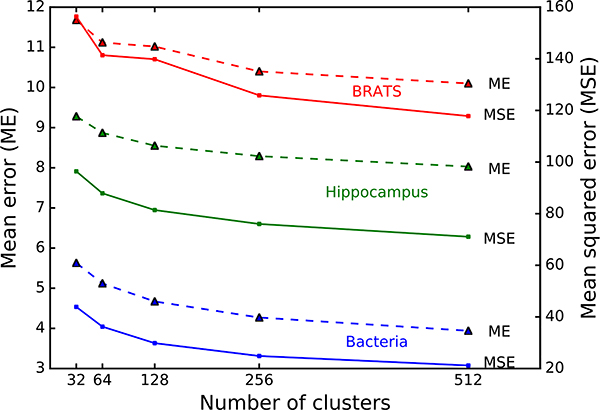
Fig. 8 shows the mean and mean squared error with N_c ranging from 32 to 512 for the three datasets we used (Sections 4.2.2, 4.2.3, and 4.2.4). Here we measure error as the L² distance between the actual and reconstructed vectors. As the value of N_c increases, both errors decrease exponentially, whereas the running time increases linearly (cf. Fig. 18). The reconstruction error for the BRATS dataset is larger than the other two datasets possibly because the BRATS dataset is multimodal with large intra-class variations. Larger N_c requires more storage for the code, thus limiting the size of volume that can be loaded on a GPU. Therefore, throughout this work, we choose N_c = 256 so that we can conveniently store the code in one byte without incurring size limitation.

Fig. 8.

The reconstruction error of vector quantization decreases as the size of codebook (i.e., number of clusters) increases.

Fig. 18.

The run time of k-means and VQ grows linearly with N_c.

In some cases where an outlier voxel is replaced by the centroid of the assigned cluster, calculated as the representative for the majority voxels in that cluster, the error leads to an effect similar to a low-pass filter. The errors introduced in such cases are troublesome if those outliers, possibly anomalies or infrequent cases in the data, should be presented (instead of filtered out) in the visualization. In our applications that focus on creating a general view of the data, the low-pass filtering effect does not obstruct the understanding and interpretation of the visualization results.

3.6. Semi-Automatic Exploration

The extraction of surfaces based on a user-defined characteristic feature vector is flexible in identifying various groups of voxels. Nevertheless, even after reordering features, configuring the characteristic feature vector can still be tedious and time consuming. In the past, we have used recursive segmentation of intensity-gradient 2D histogram to group similar voxels into a hierarchy [16]. Here we develop a similar semi-automatic method to explore volumetric data by exploiting voxel similarities in high-dimensional feature spaces. This method enables users to efficiently explore a set of surfaces sequentially following a pre-calculated hierarchy.

The hierarchy is generated as follows. Given the N_c centroids obtained by VQ, we calculate the adjacency matrix based on the L² distance between two centroids. Based on the adjacency matrix, we then subdivide the N_c centroids into two groups of centroids using spectral clustering [39]. In the next iteration, the same subdivision procedure is applied to both generated groups, further subdividing them into smaller groups. The subdivision is repeated until the group contains only one centroids and cannot be further subdivided. We organize the result of subdivision into a binary tree, in which a subdivision is represented by a parent node and two child nodes. Each node corresponds to a subset of codes grouped together during subdivision. Given that the membership of voxels in that subset defines a binary field, we can extract for each node the corresponding surface using the marching cubes algorithm.

During interaction, the user traverses the binary tree to hierarchically explore surfaces generated from the volumetric data. For example, by switching from a parent node to its child node, the surface shrinks from the one represented by the parent node to the one represented by the child node. The user can also select two child surfaces to visualize the subdivision of the parent surface.

4. Experiments

4.1. Implementation

We implemented the CNN using Caffe framework [41]. The GPU-based parallel implementation of the marching cubes-based volume rendering is implemented using OpenGL and OpenCL.¹ The feature reordering and compression are implemented in MATLAB and Python, respectively.

4.2. Results

High-resolution 3D imaging has become an important tool to study minute changes in morphology and geometry [42], [43]. Visualization of large high-resolution volumes is essential to the analysis of complex structures that are inaccessible by conventional methods. In this section, we focus on two imaging modalities: focused ion-beam scanning electron microscopy (FIB-SEM) and magnetic resonance imaging (MRI). FIB-SEM is a high-resolution (up to few nanometers) imaging technique for 3D reconstruction. MRI is clinically used for diagnosis of brain tumor and traumatic brain injury. We present visualization results generated with two FIB-SEM images and one MRI dataset of human brain using the deep-learning-assisted approach. In addition, we evaluate the power of CNN-derived features by comparing segmentation performance.

4.2.1. Segmentation Performance Measures

The segmentation performance is evaluated by the VOC score [44], which is calculated as $\text{VOC}=\frac{\text{TP}}{\text{TP}+\text{FP}+\text{FN}}$, where TP, FP, and FN denote the number of true positives, false positives, and false negatives, respectively. By penalizing classifiers with high FP rates, the VOC score can distinguish reasonable classifiers from classifiers that predict the same (majority) class all the time. We calculate class-wise VOC to evaluate segmentation quality for each class individually.

4.2.2. Dataset 1: Bacteria

The first dataset contains one volume of size 1,150 × 450× 400 at resolution 12 nm × 12 nm × 12 nm. The original anisotropic volume resolution is 3 nm × 3 nm × 6 nm [45]. With this dataset researchers study the sporulation of B. subtilis [46], a common rod-shaped gram-positive bacterium. Sporulation (i.e., formation of an endospore) is a unique survival mechanism triggered by certain bacteria in response to environmental stressors such as nutrient depletion. Once initiated, the process of sporulation includes a series of events that are tightly regulated both genetically and temporally. This temporal process results in a sequence of well-defined and replicable morphological states [46]. The course of cell development is of great interest to biologists.

This dataset is manually labeled with four classes: Resin, cell wall, spore, and others.

1. Resin: The dark region in the background.

2. Cell wall: The bright thin layer separating the interior of a bacterium and the surrounding resin.

3. Spore: The large dark oval-shaped structure inside of a sporulating bacterium. The intensity value and shape of a spore change over time, depending on the life cycle stage of the bacterium. In this dataset, about 20 percent of the bacteria are sporulating.

4. Others: All the other unlabeled subcellular features (e.g., vesicles and cytoplasm).

Fig. 9 shows an example of two bacterial cells with the four structures of interest. Because the cells are oriented arbitrarily in 3D, the appearance of these structures can be significantly different in 2D projections; this observation also applies to the hippocampus dataset (Section 4.2.3). We divide the original image stack into two sets of equal size 575 × 450 × 400, one for training and validation, and the other for testing.

Fig. 9.

(left) The bacteria dataset is divided into the left and right halves for training and testing. (right) Both the spores (green) and the vesicles (yellow arrow) in the two sporulating bacteria are low in intensity. Because the difference in intensity between a spore and other structures (e.g., vesicle and cytoplasm) can be small, conventional intensity-based feature spaces will not differentiate them well.

In the following, we evaluate the quality of the segmentation results and compare the effectiveness of the two postprocessing techniques that address the class imbalance problem (Section 3.2.3). In the training volume of the bacteria dataset, the proportion of (resin, cell wall, spore, others) is (0.472, 0.119, 0.034, 0.374), respectively. Because of the scarcity of the spores (0.034), we expect an overestimation of the abundance of spores in the testing stage.

Interestingly, the result shows that simple postprocessing using class prior can actually deteriorate segmentation performance. Fig. 10 compares the precision and recall obtained with and without postprocessing. For the bacteria dataset, scaling the predicted probability by class prior overestimated the effect of class imbalance and scaled down the predicted probability of minority classes (i.e., spore) too much, resulting in a significant drop in recall for the spore class (from 0.881 to 0.718; blue hexagon to green hexagon, Fig. 10). In contrast, the result generated by the fitted transformation (red hexagon, Fig. 10) has a better balance between precision and recall and lies near the diagonal line, where precision and recall are the same.

Fig. 10.

Left: The fitted transform postprocessing (red) generates results along the diagonal of the precision-recall plot; the results are better than those obtained with scaling by class prior (green) and without postprocessing (blue). Right: The same conclusion can be drawn by comparing class-wise VOC scores.

Fig. 11 shows a concrete example comparing the segmentation results (Figs. 11c, 11d, and 11e) of the input image (Fig. 11a) with the ground truth (Fig. 11b). For the spore class, scaling by class prior resulted in significantly more false negatives (Fig. 11d) than before postprocessing (Fig. 11c). The VOC score of the spore class decreases from 0.733 to 0.690 (right, Fig. 10). Scaling by the fitted transformation is more robust for diverse classes because the scaling factors are derived in a data-driven way. In fact, the fitted transformation increased the VOC scores of all four classes in the bacteria dataset and both classes in the hippocampus dataset (right, Fig. 10).

Fig. 11.

This example shows the spore (green) in (b) the ground truth labels and the segmentation results (c) generated without postprocessing, and postprocessed with (d) class prior and (e) fitted transform for the raw image in (a). Simply scaling the predicted probability by class prior resulted in many false negatives for the spore class. In contrast, the data-driven fitted transformation of probability is more robust and generates a result comparable to the ground truth.

Having validated the segmentation results, we next present our visualization results using the deep-learning-assisted approach in Fig. 12. The two characteristic feature vectors shown in Fig. 12e correspond to the surfaces extracted for the spores (Figs. 12a and 12b) and the cell walls (Fig. 12c), respectively. Combining the two extracted surfaces leads to a composite visualization showing both structures (Fig. 12d). The close relationships between the semantics and the derived deep features are attributed to the semantic information users provide (in the form of the voxel labels) to the CNN in the training stage. Grouping semantically-related features together in the design widget with spectral ordering facilitates the editing of characteristic feature vectors to target voxels with specific semantics. Further studies are needed to examine the constituents of these semantically-coherent features and whether they can be reused for building visualizations for different structures.

Fig. 12.

(a) The visualization of the spores in the bacteria dataset generated using the deep-learning-assisted approach. We show in the next two figures (b) the spore and (c) the cell wall of a bacterial cell. (d) By rendering two semi-transparent surfaces, the composite result shows both the spore and the cell wall. (e) The green and orange characteristic feature vectors generate the green (t = 0.36) and orange (t = 0.46) surfaces.

4.2.3. Dataset 2: Hippocampus

The second dataset² [33], [47] contains two volumes of hippocampus, each of size 1,024 × 768 × 165 at resolution 5 nm × 5 nm × 5 nm. Abnormal changes in morphology and spatial distribution of mitochondria are known to be related to cancer and neurodegenerative diseases such as Parkinson’s disease. Better visualization and segmentation of mitochondria are crucial to the study of these diseases. The mitochondria in both volumes are manually labeled; all the other structures are considered as non-mitochondria (Fig. 13). We use the first volume for training and validation, and the second volume for testing. The first volume is divided into the training and the validation sets of size 768 × 768 × 165 and 256 × 768 × 165, respectively.

Fig. 13.

(left) The hippocampus dataset consists of two volumes for training and testing (not shown here), both of the same size. (right) Both the mitochondria (orange) and membranes (yellow arrow) are low in intensity; therefore, they are inseparable using intensity-based features.

Previous studies have shown that contextual features improve segmentation quality over standard features including intensity histogram, gradient magnitude, and texture-related features calculated locally [33]. Similar to the high-level features derived by CNNs, the contextual features describe relationships among voxels in a large neighborhood, thus allowing them to depict more precisely the structures of mitochondria. Nevertheless, the contextual features are handcrafted instead of automatically learned.

Fig. 10 shows that the postprocessing affects segmentation performance significantly for the hippocampus dataset, where the mitochondria occupy about four percent of the total voxels in the training volume. After applying the two postprocessing techniques, the precision of mitochondria increased significantly whereas the recall decreased moderately (blue plus symbol to green and red plus symbols in Fig. 10). The postprocessing has a large impact on performance because more voxels have similar predicted probabilities for both classes in the hippocampus dataset. After adjusting the predicted probabilities, more voxels in the hippocampus dataset change their predicted class from mitochondria (minority class) to non-mitochondria (majority class). The postprocessing increased the VOC scores of mitochondria from 0.566 to 0.752 (class prior) and 0.754 (fitted transformation); both scores are higher than 0.741, which is the state-of-the-art previously reported [33].

We have shown that the visualization results of the bacteria dataset (cf. Fig. 12) indicate that the derived deep features are semantically meaningful. In that example, the features align closely with the classes assigned by users. For a voxel class with large intra-class variations, the derived deep features may each detect specific variants of the same class. For solving a classification problem, the CNN aggregates those deep features (using the last fully-connected layer) to detect that voxel class as a whole. For creating interesting visualizations, we can use these diverse deep features to show subclasses within a user-assigned voxel class.

For example in Fig. 14b, the mitochondria (orange) and the non-mitochondria regions in the left (blue) correspond to the orange and blue characteristic feature vectors (Fig. 14c). Although the same (non-mitochondria) class is assigned to both non-mitochondria regions in the left and right during training, the CNN derived different features for them because of their distinct appearance. In the left, the single largest non-mitochondria region is bright and uniform, whereas the non-mitochondria regions in the right consist of small bright regions separated by dark membranes. As a result, the blue characteristic feature vector generates the surface that separates the left region from the right region.

Fig. 14.

(a) Within the non-mitochondria region (outside of the orange regions), subregions with noticeably different characteristics can be identified. (b) The extracted deep features enable the visualization of the non-mitochondria regions without membranes (blue subvolumes in the left). (c) The two characteristic feature vectors correspond to the mitochondria (orange, t = 0.63), and the non-mitochondria regions without membranes (blue, t = 0.49) in the composite visualization.

4.2.4. Dataset 3: Multimodal Brain Tumor Image Segmentation Benchmark (BRATS)

The Multimodal Brain Tumor Image Segmentation Benchmark (BRATS) [48] contains MRI images taken with glioma patients. Here we report results generated with the dataset released with the MICCAI 2013 data challenge.³ In this dataset, each sample volume consists of four channels, namely the T1, T1c, T2, and Flair channels. The abnormal tissues, edema, necrosis, non-enhancing tumor, and enhancing tumor, are manually labeled by experts. The boundaries between abnormal tissues and normal tissues (e.g., the gray matter, the white matter and the cerebrospinal fluid) are usually ambiguous. Fig. 15 shows an example of the four channels and the four types of abnormal tissues. Typical volumes are cube-shaped, composed of about six to eight million voxels, resampled and registered into 1 mm isotropic resolution.

Fig. 15.

A slice in the volume for the (a) T1, (b) T1c, (c) T2, and (d) Flair channels. (e) The ground truth labels of the necrosis (red), edema (green), non-enhancing tumor (blue), and enhancing tumor (yellow).

Here we report the visualization results based on the deep features extracted from a recently published CNN-based method [5], which is designed specifically for the BRATS dataset. Instead of training from scratch, we use the trained CNN model provided by the authors of the original study as a feature extractor that generates 256 deep features⁴ for each voxel. We focus on showcasing the semi-automatic exploration of our visualization design given an alternative high-dimensional feature space, which in this case is also derived by a trained CNN model.

The visualizations presented in Fig. 16 are created with a sample of high-grade gliomas (i.e., HG_0011) in the BRATS dataset. Following the hierarchical exploration procedure from the top to the bottom of the tree, the final four surfaces correspond to four leaf nodes in the binary partition tree (Fig. 16c). Comparing the composite result (Fig. 16b) created with the four surfaces obtained using the semi-automatic method with the ground truth (Fig. 16a), we can see some inconsistencies near the center of the tumorous region. For example, the yellow region (enhancing tumor) that wraps around the red region (necrosis) is more apparent in our visualization. These inconsistencies are due to the difficulty in precisely identifying the ambiguous boundaries between abnormal tissues of different types. In fact, the BRATS dataset is so challenging that the evaluation of segmentation performance is done after merging multiple voxel classes (e.g., complete tumor that consists of all four classes and core tumor that consists of the three classes excluding edema [48]). Our semi-automatic exploration method enables users to visualize the complete tumor by selecting the purple node (top left corner of Fig. 16c), which represents the union of the four child subvolumes represented by the leaf nodes.

Fig. 16.

(a) The visualization of ground truth labels. (b) The composite result generated using the semi-automatic method. (c) The binary tree allows hierarchical exploration of the volume. The four child subvolumes (represented by the leaf nodes) are created by partitioning the parent subvolume (represented by the purple node).

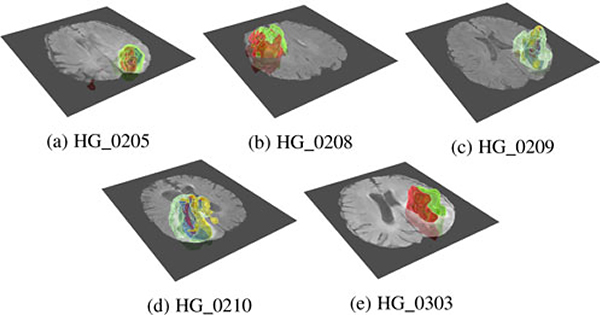
Fig. 17 shows five visualization results generated from images in the testing set of BRATS, which are not used during the training of the CNN. By applying the semi-automatic exploration method, we can visually distinguish diverse subvolumes with pseudo colors. The ground truth labels for images in the testing set are, however, not available to the public. These subvolumes need to be further validated by experts to ensure that they belong to tumorous tissues.

Fig. 17.

The visualization results generated by the semi-automatic approach reveal subvolumes inside of the brain; these subvolumes could correspond to tumorous tissues in the high-grade gliomas samples. The cut plane shows the Flair channel.

As research using CNN-based methods on this dataset increases (from three in 2014 to nine in 2016), we expect the derived high-level features to grow more powerful in the future. Our deep-learning-assisted visualization approach can continually leverage the advances in deep learning methods. Another interesting observation in applying our deep-learning-assisted approach to multimodal data is that the interactions among the four different channels are addressed by the first convolution layer. Therefore, the final deep features we extracted are derived both from a larger context and across various channels. Combining information across channels is crucial to effectively visualize multimodal data. In particular for MRI, using the joint histogram of multiple channels as the feature space has been shown to be effective in showing normal tissues such as cerebrospinal fluid and gray matter [49]. For tumorous tissues, deep features may be more descriptive, thus leading to better visualizations.

4.3. Rendering Speed and Computation Time

Compared with the conventional marching cubes algorithm, our deep-learning-assisted volume visualization introduces extra steps to 1) decode a voxel to its corresponding feature vector and 2) update the binary field whenever the characteristic feature vector or the threshold changes. In our implementation, decoding is a simple texture look-up. Updating the binary field requires re-evaluating Equation (1), which can be done efficiently and in parallel using vector arithmetic on the GPU.

We measure the rendering speed with an NVIDIA Quadro K6000 GPU. For a volume with 43 million voxels, our GPU-based volume renderer can render surfaces of similar size (470k triangles) at a speed of 45 and 40 frames per second using the conventional marching cubes algorithm and our deep-learning-assisted approach, respectively. Five iterations of smoothing of the mesh with 470k triangles took about 0.26 second, which is too slow if we perform smoothing every time the mesh changes when users interact with the widget. Consequently, we perform mesh smoothing optionally.

The processing time reported in the following is based on a computer with an Intel Xeon E3–1230 V2 3.3 GHz CPU, 16 GB of RAM, and an NVIDIA GTX 970 GPU. Fig. 18 shows the time to perform k-means clustering and VQ with N_c ranging from 32 to 512; the computation time grows linearly with N_c. The training of the CNN took about 2.5 hours; the training needs to be done only once for the training dataset. After training the CNN, the extraction of deep features for new data (i.e., forward pass of a trained CNN) took 3.4 minutes per million voxels. The extraction is voxel-independent and can be parallelized to multiple GPUs.

4.4. Discussion

In the previous sections, we have shown that the proposed deep-learning-assisted volume visualization is powerful in discerning complex structures using high-level features extracted from a trained CNN. Ideally, we would want to know the corresponding high-level concept each individual feature represents. Understanding these derived features is an ongoing pursuit in the deep learning community [6], [50]. As of now the limited interpretability of deep features indeed causes difficulties in establishing the connections between a deep-feature-based characteristic feature vector and the corresponding visualization result. Interestingly, by organizing features using spectral ordering, users can still design useful volume visualizations without directly interpreting each feature dimension that defines the feature space. An alternative strategy, used in our semi-automatic method, is to circumvent the interpretability problem by providing another layer of abstraction and hide the underlying features from users. This strategy is also used by many other semi-automatic methods.

Although the choice of features evolves from intensity to locally-derived features (e.g., texture) and, as introduced in this paper, deep features, volume visualization design remains a manual and trial-and-error process. A distinct line of research focuses on minimizing human involvement by creating volume visualizations automatically [51]. These automatic techniques can also be adapted to search for solutions in the CNN-derived feature space used in this paper.

4.5. Limitation

Our current supervised-learning-based approach requires labeled data for training the CNN; this limitation could be mitigated by applying semi-supervised or unsupervised learning. For example, instead of training a CNN for classification, train an autoencoder [52] that learns to reconstruct voxels from intermediate codes without supervision. These intermediate codes then serve as the high-level features that can be used in volume rendering and other visualization applications [53]. The other techniques used in our deep-learning-assisted approach still apply to these derived abstract features regardless of the way they are generated. Unsupervised techniques, while not relying on user inputs, at the same time eliminate valuable supplementary domain knowledge from the learning process. Further studies are needed to understand whether and how unsupervised learning can help visualize complex volumetric data.

All the images used in this paper are isotropic such that the rendering results can be easily interpreted visually (with a 1:1:1 aspect ratio). Some imaging modalities, such as FIB-SEM, produce anisotropic raw images with a lower resolution along the imaging axis (e.g., z-axis for the bacteria dataset, Section 4.2.2). In that regard, simple binning or other sophisticated reconstruction methods [54] can be applied.

5. Conclusions and Future Work

Designing volume visualizations is challenging because the current workflow requires users to explicitly define a feasible feature space for the target structures. Existing studies have focused on visualizing structures based on specific handcrafted local features. As the complexity of structures increases, the difficulty of defining a suitable feature space also increases significantly.

In this work, instead of relying on handcrafted features, we use convolutional neural networks to automatically derive useful features from the data. In contrast to the local features that have been used in the past, the features extracted from the CNNs depict high-level concepts that are difficult to describe by local features. We rearrange the extracted high-dimensional abstract features by spectral ordering such that similar abstract features are close together in the design widget, thus facilitating interactive exploratory visualization. In addition, we present a semi-automatic volume exploration technique that enables users to traverse a tree of volume visualizations.

In the future, we plan to apply fully-convolutional network to accelerate the time-consuming voxel-wise prediction [55], and 3D convolutions to further address the spatial relationships among voxels [56]. We also plan to examine the differences in features derived by different CNN models. Another possible extension is integrating features from different layers in the CNN to design visualizations at various granularities, possibly showing substructures within a structure.

Biographies

Hsueh-Chien Cheng received the BS degree in computer science from National Tsing Hua University, the MS degree in computer science and information engineering from National Taiwan University, and the PhD degree in computer science from the University of Maryland. His research interests include computer graphics and data visualization with biomedical applications.

Antonio Cardone received the PhD degree in mechanical engineering from the University of Maryland, College Park, in 2005. He is a research associate in the National Institute of Standards and Technology (NIST) and a research scientist for the Institute for Advanced Computer Studies, University of Maryland. His research focuses on computational geometry, image processing and CAD/CAM with application in bioinformatics, material science, and engineering design.

Somay Jain received the BTech (Honors) degree in computer science from the International Institute of Information Technology, Hyderabad, in 2015 and the MS degree in computer science from the University of Maryland, College Park, in 2017. His research interests include computer graphics, computer vision, and using them in biomedical applications.

Eric Krokos received the BS and master’s degrees in computer science from the University of Maryland at College Park. He is currently working toward the PhD degree in the Department of Computer Science, University of Maryland at College Park. His research interests include understanding the psychological effects of virtual reality and developing effective data visualization and interaction.

Kedar Narayan received the PhD degree in immunology and a background in chemistry, pathology, and biophysics. He is a group leader in the Center for Molecular Microscopy, Frederick National Lab. His work focuses on the use of emerging technologies, including FIB-SEM, electron tomography and correlative imaging approaches to explore cellular processes at nanoscale resolutions.

Sriram Subramaniam is a senior investigator in the NIH, and the founding director of both the Center for Molecular Microscopy, and the National Cryo-EM Facility at the National Cancer Institute, NIH. He holds visiting faculty appointments with the Johns Hopkins University School of Medicine and the Institute for Advanced Computer Studies, University of Maryland, College Park. His current work is focused on the development of advanced technologies for imaging macromolecular assemblies using 3D electron microscopy, and their application to address fundamental problems in infectious disease, cancer, and neuroscience.

Amitabh Varshney received the BTech degree in computer science from IIT Delhi and the PhD degree in computer science from UNC Chapel Hill. He is the director of the Institute for Advanced Computer Studies (UMIACS) and professor of computer science with the University of Maryland at College Park. His research is on exploring large data visualization and interaction including spatial and temporal summarization, multiresolution hierarchies, gesture recognition for virtual environments, and visual interaction with wall-sized tiled displays. He is the director of the NVIDIA CUDA Center of Excellence at Maryland. He received a NSF CAREER Award and the IEEE Visualization Technical Achievement Award in 2004. He served as the chair of the IEEE Visualization and Graphics Technical Committee 2008–2011. He is a fellow of the IEEE.