Abstract
We propose a data-driven approach for modelling an organism's behaviour instead of conventional model-based strategies in chemical plume tracing (CPT). CPT models based on this approach show promise in faithfully reproducing organisms’ CPT behaviour. To construct the data-driven CPT model, a training dataset of the odour stimuli input toward the organism is needed, along with an output of the organism’s CPT behaviour. To this end, we constructed a measurement system comprising an array of alcohol sensors for the measurement of the input and a camera for tracking the output in a real scenario. Then, we determined a transfer function describing the input–output relationship as a stochastic process by applying Gaussian process regression, and established the data-driven CPT model based on measurements of the organism’s CPT behaviour. Through CPT experiments in simulations and a real environment, we evaluated the performance of the data-driven CPT model and compared its success rate with those obtained from conventional model-based strategies. As a result, the proposed data-driven CPT model demonstrated a better success rate than those obtained from conventional model-based strategies. Moreover, we considered that the data-driven CPT model could reflect the aspect of an organism’s adaptability that modulated its behaviour with respect to the surrounding environment. However, these useful results came from the CPT experiments conducted in simple settings of simulations and a real environment. If making the condition of the CPT experiments more complex, we confirmed that the data-driven CPT model would be less effective for locating an odour source. In this way, this paper not only poses major contributions toward the development of a novel framework based on a data-driven approach for modelling an organism’s CPT behaviour, but also displays a research limitation of a data-driven approach at this stage.
Keywords: chemical plume tracing, data-driven model, sensor array, wind tunnel, Gaussian process regression
1. Introduction
Chemical plume tracing (CPT) consists of locating an odour source from traces of the corresponding chemical substance in the air. Many living organisms use this ability for activities such as food foraging and mate selection. As CPT can be applied to search for victims in disaster sites and find drugs at airports and other places, its development in engineering is valuable. Although various types of organisms have directly been used for CPT (e.g. [1]), they have limited action spans due to fatigue and can be difficult to deploy in harsh conditions, such as environments polluted by fire smoke and toxic gases. Therefore, using animals for CPT may be challenging and infeasible in some situations.
Several studies have focused on CPT performed by autonomous robots to overcome the limitations of using living organisms [2–4]. However, as chemical plumes are intermittent and change their shape due to airflow [5,6], it is difficult to locate the odour source by simply following a concentration gradient. Instead, two approaches have been widely used: biomimetics and statistical methods. The biomimetic methods involve modelling the CPT behaviour of an organism in real time [7–9]. Statistical methods involve a lot of variations of estimation algorithms such as Bayes estimation [10,11], kernel methods [12,13] and probabilistic and map-based algorithms [14,15]. In this study, we adopted biomimetic methods and focused on the silkworm moth, an organism with high CPT capability.
Almost all existing biomimetic methods use model-based strategies [16–18] which are based on an organism’s characteristic behaviour. Although these strategies may lead a CPT agent to the source of the odour, the adaptability of organisms modulating their behaviour depending on the surrounding environment (such as [19]) may be lost through these strategies. Thus, their performance depends upon environmental conditions and an effective CPT model should take into account an organism’s adaptability. However, due to limited understanding of the mechanism in question, it remains difficult to extract information about an organism’s adaptability. Therefore, in this study, we propose a novel framework based on a data-driven approach for modelling the CPT behaviour of living organisms that may effectively reflect organisms’ adaptability in their CPT behaviour, instead of using the conventional model-based strategies. To obtain the CPT model based on data-driven approach, we simultaneously measured the odour stimuli input toward a silkworm moth and the CPT behaviour output in a real scenario. To this end, we used an array of alcohol sensors in a wind tunnel to measure the odour distribution and determine the corresponding response. Moreover, we tracked the moth trajectory during CPT by using a camera system. Finally, we modelled the moth CPT behaviour as a stochastic process based on the measured input–output data, and verified that the data-driven CPT model demonstrated a better performance than conventional model-based strategies through CPT experiments in simulations and a real environment.
2. Problem statement
We determine the CPT model using the data-driven approach and verify its performance through CPT experiments. First, we install an array of alcohol sensors and a camera in a wind tunnel to simultaneously measure the odour stimuli input and CPT behaviour output of silkworm moths in a real scenario. Then, we apply Gaussian process regression to the measurements to determine the odour distribution and obtain the corresponding input–output relationship. Subsequently, we express the data-driven CPT model according to the moth CPT behaviour as a stochastic process using Gaussian process regression. Finally, we conduct CPT experiments in simulations and a real environment using the obtained data-driven CPT model and confirm that it provides better success rates than conventional model-based strategies.
In our study, we chose Gaussian process regression [20–23] for modelling the CPT behaviour of silkworm moths. Gaussian process regression is a non-parametric, Bayesian approach that makes it possible to handle nonlinear problems. Moreover, Gaussian process regression is able to provide the measurement uncertainty for predictions. These would be of benefit for modelling the CPT behaviour because silkworm moths demonstrate the adaptability of behaviour modulation in response to the surrounding environment, meaning their behaviour (e.g. movement velocity) varies during CPT. However, as mentioned previously, we still only have a small understanding of the mechanism of such adaptive behaviour. Therefore, we expect that Gaussian process regression for modelling CPT behaviour has the advantage of reflecting an adaptability hidden in CPT behaviour with measurement uncertainty. In addition, Gaussian process regression works well even on small datasets, which is of particular merit in biological experiments that cannot be conducted repeatedly.
We used the male silkworm moth (Bombyx mori) as the target organism (figure 1a). Its body is approximately 30 mm long and 10 mm wide, and it has two antennae of approximately 6 mm in length that are used to detect female sex pheromones [28]. Usually, the moth does not exhibit spontaneous actions, including drinking water, and its only action is searching for a female when it perceives sex pheromones with its antennae (figure 1b). After detecting sex pheromones, the moth exhibits a surge action by moving forward toward the source of sex pheromones. When the moth loses the pheromone track, it moves in zigzags by turning its body from side to side and in loops by rotating. The moth restarts the search sequence from the surge action once it perceives a sex pheromone again. This simple search behaviour provides a high CPT performance [24,25], and it is able to be implemented into the autonomous robot as the programmed-moth (P-Moth) strategy [26,27] (figure 1c).
Figure 1.
Searching behaviour of male silkworm moth for female mate. (a) Male silkworm moth. (b) Action transition diagram [24,25]. (c) Flowchart of programmed-moth (P-Moth) strategy inspired by the silkworm moth [26,27]. The detail parameters (e.g. duration time (s)) were determined based on biological experimental data [25].
As the relationship between odour stimuli and response CPT behaviour is clear, we consider the moth as a suitable organism for system identification. However, the output of CPT behaviour, such as movement velocity and timing of switching action phases, varies depending on the environmental situation. Although a CPT model reflecting this adaptability may further improve the CPT performance, the mechanism remains unclear [19]. Therefore, we expect that a data-driven CPT model can reflect the underlying adaptability of the moth, possibly outperforming existing model-based CPT models. In addition, as a result of millennia of selective breeding by humans, the silkworm moth has lost the ability to fly and can only search for females by walking (electronic supplementary material, video S1). As the two antennae on its head are in a low position from the ground while walking, we expect that the input stimuli coming toward a moth could be emulated through the response of sensors embedded in the ground in a wind tunnel.
To induce the CPT behaviour of the silkworm moth, the main component of the female sex pheromones, bombykol, has been commonly used as an odour stimulus [29]. As the effectiveness of bombykol has been demonstrated [30,31], we used this component as the odour stimuli in our study. In addition, we employed a mixture with ethanol to measure the odour distribution using an array of alcohol sensors in the wind tunnel. The output of the alcohol sensors (MiCS5524 gas sensor breakout; Adafruit Industries, New York, NY, USA) was stabilized by aging them for more than 24 h [32] and we evaluated the dynamics homogeneity across sensors in the array.
The estimation of bombykol stimuli input toward the silkworm moths should satisfy the following two conditions between the sensor responses and the bombykol stimuli output of the silkworm moth:
-
(a)
Similar temporal response.
-
(b)
Similar spatial distribution characteristics.
To measure the bombykol stimuli toward the silkworm moth, we employed the electroantennogram (EAG) method [33]. This method allows detection of an odour substance by measuring the voltage variation induced by an odour substance received on antennae. By comparing the sensor and EAG responses toward a discharge of bombykol and ethanol mixture, we confirmed the similarity between both responses, and the EAG response can be estimated from the alcohol sensor measurements.
3. Input–output data acquisition
3.1. Measurement system
The measurement system simultaneously measures the input of odour stimuli toward the silkworm moth and the resulting CPT behaviour to obtain the corresponding input–output relationship. The implemented measurement system is illustrated in figure 2 and comprises the sensor array in a wind tunnel for measuring the odour stimuli to the silkworm moth and a camera for tracking the moth trajectory during CPT experiments. The source of the odour from which both ethanol and bombykol are discharged is defined as the origin of the x–y coordinate system in the wind tunnel. The wind generated by a fan passes through a flow rectifier made of plastic straws. The wind speed is controlled at approximately 0.68 m s−1 at the odour source, and odour stimuli are diffused with the wind along the positive x-axis. As for capturing the entire wind condition in the wind tunnel, we measured the wind speed using an anemometer (testo 405i; Testo SE & Co. KGaA, Titisee-Neustadt, Germany) at each sensor position at 1 Hz for 30 s. Average wind speeds and standard deviations at each sensor position were connected by linear interpolation to be displayed as a map (figure 2b,c). Odour stimuli were measured by the sensor array in the wind tunnel from 27 points at 50 mm intervals in a . The sensor sampling rate was 100 Hz using data acquisition devices (NI-DAQ USB-6218, USB-6215; National Instruments, Austin, TX, USA) which were placed as close as possible to sensors and connected to them via shielded cables to reduce the noise effect. The initial position of the silkworm moth for CPT experiments was 500 mm from the odour source, and the moth trajectory was measured by a camera mounted on top of the wind tunnel recording at 15 Hz. The size of the wind tunnel was set at 550 × 200 mm following the conventional biological reports [25,30,34].
Figure 2.
Overview of measurement system to obtain input–output data for data-driven CPT model. (a) Wind tunnel composed of sensor array, camera and control unit. (b) Average wind speed map of 30 s. (c) Standard deviation map of wind speed.
To acquire sensor measurements and stimulate the silkworm moth, we simultaneously discharged ethanol and bombykol using the system shown in figure 3. The odour discharge was generated by injecting air from an air compressor (MAS-1; AS ONE, Osaka, Japan). The compressed air passed through a gas washing bottle containing absorbent cotton, activated carbon, and distilled water and adjusted to a flow rate of 1.0 l min−1 as measured by a flowmeter. By controlling the opening and closing of a solenoid valve via a microcontroller (Arduino Uno R3; Arduino, Milan, Italy), compressed air was discharged every 1 s (open for 200 ms and closed for 800 ms) to resemble the pheromone emission frequency of female silkworm moths [35]. The conditioned air was discharged into a 99.5% ethanol solution, and the air then flowed into a glass tube. A filter paper with 1000 ng of bombykol was placed at the tip of the glass tube to release air containing the mixture into the wind tunnel.
Figure 3.
System to discharge compressed air containing ethanol and bombykol (DW, distilled water).
3.2. Dynamics homogeneity across sensors
To evaluate dynamics homogeneity across sensors in an array, we checked the sensor response toward the mixed odour stimuli. We used four randomly picked alcohol sensors and placed one of them at the position of 20 mm from the mixed odour discharge port to ensure the odour reaches it (figure 4a). One shot (open valve duration: 200 ms) was discharged using the same odour discharge system of figure 3. We conducted the experiments three times per sensor.
Figure 4.
Confirmation experiments of dynamics homogeneity across sensors. (a) Overview of the experimental set-up. (b) Each sensor response toward the mixture odour. The green area represents the solenoid valve aperture to discharge the odour. (c) Values obtained by DTW across sensors.
The responses of each sensor are shown in figure 4b. The coloured lines respectively represent the average values of the four sensors, and the shaded areas represent the corresponding standard deviations. The green area represents the solenoid valve aperture to discharge the mixed odour. For checking the dynamics homogeneity across the sensors, we applied the Dynamic Time Warping (DTW) [36] algorithm which outputs the remaining cumulative distance between the two responses. When the two responses are the same, the value obtained from DTW becomes 0. According to the examples in [37], the waveform clustering can be realized with the DTW value of around one digit. Following that criterion, we regard the two responses as being similar in the case where the DTW value is under 10. Figure 4c shows the values obtained by applying DTW to the responses of each sensor, all of which were less than 5.50. Therefore, we confirmed that the sensors used in the wind tunnel demonstrated the similarity in the response toward the mixed odour stimuli, and we concluded the dynamics homogeneity across sensors.
3.3. Effect of ethanol on silkworm moth
As for demonstrating the motor and sensory effects of ethanol upon silkworm moths, we compared the EAG responses and moth behaviour toward bombykol with those toward the mixture of bombykol and ethanol. Firstly, we constructed the EAG unit shown in figure 5a to measure the bombykol stimuli. The unit is composed of a pin header gluing the antennae removed from a silkworm moth and an amplifier with a bandpass filter in 0.1–300 Hz with an amplification factor of 1000. We placed it at the position of 20 mm from an odour discharge port. We compared the EAG responses toward two types of odour discharging: bombykol, and a mixture of bombykol and ethanol. The experimental set-up was the same as figure 4a. When discharging only bombykol, the ethanol bottle (shown as dotted box coloured in red in figure 5a) was removed. We conducted the experiments three times per odour type.
Figure 5.
Confirmation experiments regarding the effect of ethanol on silkworm moth. (a) Overview of the experimental set-up. EAG unit is placed 20 mm from odour discharge port. (b) EAG response toward bombykol and mixture of bombykol and ethanol. The green area represents the solenoid valve aperture to discharge the odour. (c) Measurement of heading angle θ and angular velocity . (d) Time sequence of heading angle θ of silkworm moth after discharging one-shot odour stimulus which is represented as the green area. (e) Average angular velocity calculated from the heading angle θ.
The results of EAG responses are shown in figure 5b. EAG responses passed 10 Hz lowpass filtering to avoid the hum noise in the biological signal. The red line represents the average value of the EAG response toward bombykol and the black line represents that toward the mixture of bombykol and ethanol. The shaded areas represent the corresponding standard deviations. The green area represents the solenoid valve aperture to discharge the odour. We evaluated the similarity between the EAG responses toward bombykol and the mixture of bombykol and ethanol by applying the DTW, whose obtained value was 3.36. Therefore, it implies that the EAG response toward bombykol is quite similar to that toward mixture odour. In other words, there is no effect on sensing bombykol for silkworm moth even if discharging the mixture odour. However, the effect of the mixture odour on the silkworm moths’ behaviour is unclear; we compare the velocity of silkworm moth after discharging bombykol and a mixture of bombykol and ethanol.
According to [38], CPT behaviour of the male silkworm moth is induced only by pheromone molecules and not other compounds. As for the confirmation, we discharged bombykol and the mixture of bombykol and ethanol toward the silkworm moth. Since silkworm moth normally shows the rotational movements that change the head angle from side to side in response to a one-shot odour stimulus, we measured heading angle θ (rad) and angular velocity (rad s−1) of silkworm moth as quantitative evaluation (figure 5c). The result of time sequence of measured heading angle θ toward each odour discharging is shown in figure 5d, and the average angular velocity with standard deviation in figure 5e. From figure 5d, it is obvious that the silkworm moth shows CPT behaviour of zigzag by turning its body from side to side toward the mixture odour as well. In addition from figure 5e, there is no significant difference of angular velocity between two types of odour discharging according to the Wilcoxon rank sum test (p = 0.063). Therefore, we confirmed that mixing ethanol with bombykol had no effect on the behaviour of silkworm moth as on sensing bombykol, and we concluded to use the mixture odour as the target odour.
3.4. Comparison of sensor and electroantennogram responses toward odour stimuli
To confirm that the bombykol stimuli input toward the silkworm moth can be estimated by the alcohol sensor measurements, we evaluated the following two conditions:
-
(a)
Similar temporal response.
-
(b)
Similar spatial distribution characteristics.
For condition (a), we verified that the sensor and EAG responses in rising terms were similar and that the sensor responses could capture the timing of odour reaching the EAG. For condition (b), we evaluated that the characteristics of the spatial distribution of the odour measured by EAG was similar to that of the odour measured by sensors by comparing the odour detection rate at each sensor position.
Experimental set-up is shown in figure 6a. By placing the EAG unit at each sensor position, we simultaneously measure the sensor and EAG responses. The same odour discharging system of figure 3 is used so that the discharge of the bombykol and ethanol mixture is controlled at 1 Hz and proceeds for 10 s: the mixture odour is discharged 10 times.
Figure 6.
Results of temporal and spatial analysis of EAG and alcohol sensor. (a) Experimental set-up. (b) Sensor and EAG responses at position . (c) Comparison of odour detection rate at each sensor position.
The sensor and EAG responses at sensor position are shown in figure 6b to indicate the responses measured in the wind tunnel in general. To avoid the hum noise in the biological signal, EAG response passed 10 Hz lowpass filtering. Then, the average values of the sensor and EAG response were normalized to compare and are represented by the blue and red lines respectively. The blue and red shaded areas represent the corresponding standard deviations. The green area represents the solenoid valve aperture to discharge the odour stimuli. The delay at rise time between sensor response t′b and EAG response tb was 0.04 s, being below the sampling rate of the camera of 15 Hz (0.07 s/frame). In addition, we applied the DTW to the responses until the peak time t′u of sensor response and tu of EAG response, whose obtained value was 0.46. Hence, both responses in the rising term were quite similar and the effect of delay at the rising time can be negligible for the measurement system. Finally, condition (a) was satisfied.
The odour detection rates at each sensor position are mapped in figure 6c. As for the determination of the odour detection from each response, we counted the number of the rising edge of the response by setting the threshold the same as in [3]. Therefore, odour detection rate was calculated by (the number of odour detection)/10. To ensure that the spatial distribution of the odour measured by EAG was similar to that of the odour measured by the sensors, we used the Kullback–Leibler Divergence (K-L Divergence) [39] to the odour detection rates of sensor and EAG responses. K-L Divergence is a way of measuring the similarity between the two probability distributions. When comparing the same probability distributions, the value obtained from K-L Divergence becomes 0. K-L Divergence is functioned through logarithmic calculation; the value obtained from K-L Divergence increases rapidly from zero when the probability distributions start to shift [40]. Hence, we define the value of close to zero as being small enough for similarity. Following that criterion, the values obtained from K-L Divergence were 0.06 in Forward and 0.08 in Reverse, which were quite close to zero. Therefore, we concluded the target distributions as being similar, and condition (b) was satisfied.
4. Data-driven chemical plume tracing model based on Gaussian process regression
4.1. Estimation of odour stimulus at silkworm moth position
The proposed measurement system allows to obtain the relationship between the odour stimuli input and CPT behaviour of the silkworm moth to construct a dataset by associating the sensor response with the moth trajectory during CPT. As the sensors have discrete positions, intermediate measurement values should be determined through interpolation. We estimate the sensor value at an arbitrary position by using Gaussian process regression. The process of odour stimulus estimation at silkworm moth position is shown in figure 7 and appendix A. First, we define the two-dimensional sensor coordinates psensor = {(50, − 50), (50, 0), …, (450, 50)} as the input and sensor measurements csensor = (c(50,−50), c(50,0), …, c(450,50)) as the output. Then, the estimated sensor value, cmoth, at moth position pmoth can be obtained from a new dataset, p′sensor and c′sensor , by Gaussian process regression. From these values, the estimated odour stimuli input at the moth position provided by the camera recording can be obtained over time. We use the scikit-learn library in Python 3.8.0 to implement Gaussian process regression. The radial basis function serves as kernel function k(xi, xj) [41,42]:
| 4.1 |
Here, xi and xj are the two samples from the inputs of psensor, and θ is a free parameter which is optimized via the L-BFGS-B method [43]. When using Gaussian process regression from now on, the same kernel function and hyperparameter optimization are used.
Figure 7.

Diagram of odour stimulus estimation at silkworm moth position.
4.2. Measurement of input and output data from the silkworm moth
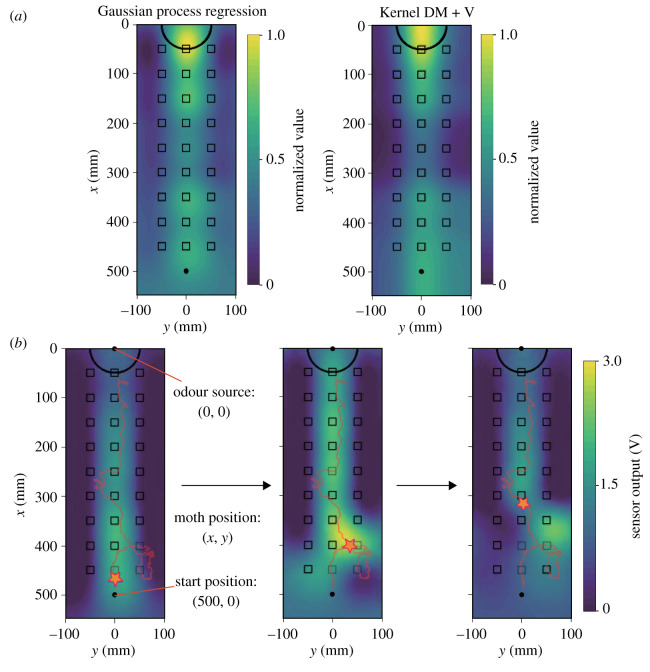
We conducted CPT experiments on a silkworm moth to measure the input odour stimuli toward it and its output CPT behaviour. The results obtained using Gaussian process regression on these data are shown in figure 8. Figure 8a shows the results of preliminary experiments that measured the average value of each sensor response over 300 s toward mixed odour discharging in the wind tunnel. In terms of implementation, we determined using Gaussian process regression both in an estimation of odour stimulus and the modelling of moths’ behaviour (described in the next section) as being reasonable. To demonstrate Gaussian process regression applicable to the estimation of odour distribution, we compared the odour distribution map made of Gaussian process regression with that made of another interpolation method: Kernel DM + V [12]. For the Kernel DM + V, we set the parameter of kernel width to 30 mm. Between both odour distribution maps, we applied K-L Divergence to each estimated sensor value at the points of 5 mm intervals in the whole field, whose obtained values were 0.06 in Forward and 0.07 in Reverse. Hence, we confirmed that the performance of Gaussian process regression for the estimation of odour distribution could be comparable to another method. Figure 8b shows a sequence of odour distributions and moth positions during CPT in the measurement system. Therefore, by using Gaussian process regression, we obtained the relationship between the input odour stimuli toward the silkworm moth and the output CPT behaviour as a dataset (electronic supplementary material, video S2).
Figure 8.
Results of CPT experiments on silkworm moth within wind tunnel. (a) Odour distribution made of Gaussian process regression and Kernel DM+V [12] from average sensor values over 300 s. (b) Sequence showing odour distribution and moth position during CPT.
4.3. Data-driven chemical plume tracing model
We model the CPT behaviour of the silkworm moth as a stochastic process using Gaussian process regression to obtain the corresponding transfer function. The training data were obtained from CPT experiments on silkworm moths within a wind tunnel. Specifically, 10 silkworm moths of 3–5 days of age were used to conduct two trials per moth, obtaining 20 trials. When a moth was 50 mm from the odour source position, the CPT trial was considered successful. If the moth failed to complete a CPT trial over 300 s, it was considered as a failure. During the CPT experiments, we controlled the room temperature and humidity at 23–25°C and 50–60%. From the CPT experiments, we obtained a success rate of 80% (16/20). Then, we randomly selected several successful trials to be half the amount of all datasets for the training data of the data-driven CPT model, to reduce the effect of high computational complexity in the kernel matrix calculation [44].
We obtained estimated sensor values cmoth = (c1, c2, …, cT) at moth positions pmoth = {(x1, y1), (x2, y2), …, (xT, yT)} from all the time steps over trials (same process as figure 7). Then, (T − 3) rows and four columns of data containing the time series of odour stimuli received by the moth were regarded as the input of the data-driven CPT model:
| 4.2 |
Then, the moth displacements over four steps were obtained as Δpx(t) = (xt − xt−3), Δpy(t) = (yt − yt−3), and data groups Δpx = (Δpx(4), Δpx(5), …, Δpx(T)), Δpy = (Δpy(4), Δpy(5), …, Δpy(T)) were regarded as the output of the data-driven CPT model. We modelled the corresponding transfer function as a stochastic process by applying Gaussian process regression, establishing the proposed data-driven CPT model (figure 9).
Figure 9.
Schematic of data-driven CPT model.
For the design of the data-driven CPT model, we focused on time step data in line with the biological reports:
-
(A)
Silkworm moths began to move about 0.3 s after an odour stimulation [45].
-
(B)
Silkworm moths walked in a straight line for less than 0.5 s continuously in response to an odour stimulation [25].
-
(C)
Average speeds of silkworm moths during the free walking were around 11 mm s−1 [46].
Statement (A) implies that the response of moths toward odour stimuli appears after the corresponding time delay. Considering such characteristics, capturing 4 steps’ data at 15 Hz (0.07 s/frame), which covers the input–output data in the range of 0.28 s (approximately the same time delay as 0.3 s), has an important role for the inclusion of the effect of time delay. In addition, we focused on the moth displacement over four steps: Δpx(t) = (xt − xt−3), Δpy(t) = (yt − yt−3) as the output of the data-driven CPT model. As statement (B) implies that moths put a priority to a consistent straight movement in a short term, we regarded that the moth displacement during four steps does not change significantly. From statement (C), the displacement of the silkworm moth between each time step is quite small so that focusing on the displacement over 4 steps could be reasonable for avoiding the measurement noise.
We evaluate the performance of the data-driven CPT model through CPT experiments in simulations and a real environment. As depicted in figure 10, we first consider estimated sensor values Cagent = (Ct, Ct−1, Ct−2, Ct−3) at the position of CPT agent Pagent = (Xt, Yt) at time t as the input to the data-driven CPT model. The expected value and variance of the predicted CPT agent’s displacement are generated from the data-driven CPT model:
| 4.3 |
and
| 4.4 |
where K is the kernel matrix, k* is the vector of the inner product between the training data and new input Cagent, and k∗∗ is the inner product between new inputs Cagent. Then, the data-driven CPT model randomly generates x- and y-axes displacements Δpx(t) and Δpy(t) from distributions N(μx, σx) and N(μy, σy), respectively, to determine the next position of the CPT agent:
| 4.5 |
Figure 10.
Diagram of data-driven CPT model by CPT agent. GPR, Gaussian process regression.
By performing this process iteratively, performance of the data-driven CPT model can be evaluated (details in appendix B).
5. Performance evaluation of data-driven chemical plume tracing model in simulation
5.1. Experimental set-up
We conducted simulation experiments to evaluate the performance of the data-driven CPT model. The simulation environments shown in figure 11 include:
-
(A)
Open-field environment.
-
(B)
Environment with an obstacle.
Figure 11.
Odour distribution in simulations based on measured sensor values in real environment. (a) Open-field environment (left); odour distribution map in simulation based on average sensor values over 300 s measured in open-field environment (right). (b) Environment with an obstacle (left); odour distribution map in simulation based on average sensor values over 300 s measured in environment with an obstacle (right).
The environments were set as in the wind tunnel, with the origin of the x–y coordinate system being the odour source and a rectangular area of 0 ≤ x ≤ 550 mm and −100 ≤ y ≤ 100 mm. In addition, we placed a cylindrical obstacle in the middle of the sensor array (x = 250, y = 0) mm for environment (B). Regarding the odour distribution in the simulation environments (figure 11-right), we used the sensor values measured in figure 11-left over 300 s from a 9 × 5 sensor array, in which additional sensors were installed under the walls for the CPT agent’s initial positions (described later). Again, a trial was considered successful when the agent was within 50 mm from the odour source position. If the CPT agent failed to locate the source over 300 s, the trial was considered as a failure. To evaluate the performance of the data-driven CPT model, we prepared three initial agent positions, (x = 500, y = −100), (x = 500, y = 0) and , with two of them being different from the initial position of the training data.
For comparison with the data-driven CPT model, we chose conventional model-based strategies: P-Moth strategy (figure 1c) and Casting strategy [47]. The P-Moth strategy was based on the characteristic behaviour of our target organism, the silkworm moth. The detail parameters of the P-Moth strategy (e.g. duration time at each state in figure 1c) were determined based on biological experimental data [25]. Casting strategy was inspired by the characteristic behaviour of flying moths. The CPT agent moves upwind with a casting angle β until it loses the plume for a certain distance dlost. Then, the CPT agent turns and moves cross-wind until it hits an odour plume, and moves upwind with angle β again. As it performs different behaviour from the P-Moth strategy when losing the odour plume, it is a suitable model for comparison. We set a casting angle β of and the plume lost distance dlost of 12 mm as referring to [47]. By the data-driven CPT model and these model-based strategies, 100 trials in each experimental environment were simulated per initial position.
5.2. Results
Figure 12 shows the simulation results using the data-driven CPT model, P-Moth strategy, and Casting strategy in environment (A) and result of CPT experiments on a silkworm moth starting at the initial position . Figure 12a shows the success rates of each model at the initial position and that of the silkworm moth in CPT experiments which had been conducted for acquiring the training data. The success rate of the data-driven CPT model reaches 96%, being much higher than that of the P-Moth strategy of 78%, Casting strategy of 75%, and silkworm moth CPT experiments of 80% (electronic supplementary material, video S3). Likewise, in figure 12b, the success rates of the data-driven CPT model at the other two initial positions are superior to those obtained from P-Moth strategy and Casting strategy.
Figure 12.
Results of simulation experiments in the environment (A). Fisher’s exact test was applied to the results of success rate and Student’s t test was applied to the results of sinuosity index. (a) Success rate at initial position . (b) Success rates at the other two initial positions. (c) Sinuosity index at initial position . (d) Sinuosity index at the other two initial positions. (e) Example trajectories obtained from data-driven CPT model.
For a comparison of the trajectories of each strategy, we apply a sinuosity index [47] calculated by
| 5.1 |
Here, the sinuosity index equals one if the CPT agent moves straight toward an odour source without any tortuosity. Figure 12c shows the results of sinuosity index at the initial position . The sinuosity index of the data-driven CPT model was very similar to that of CPT experiments on silkworm moths, and much higher than those of the P-Moth and Casting strategies. Likewise, in figure 12d, the results of the sinuosity index at the other two initial positions displayed the same tendency. It is obvious that the P-Moth strategy has a low sinuosity index due to the programmed behavioural pattern which keeps rotating at that location, in order to reacquire the odour information when losing it. Although it may lead a CPT agent to the odour source, it tends to take much more time to reacquire the odour information at the area where there is little odour, and then results in a failure. In regards to Casting strategy, the CPT agent could reach an odour source by chance because of the simple algorithm moving upwind reflexively in response to odour stimuli. In other words, the performance of Casting strategy depends on environmental conditions. If the CPT agent obtains an odour information successfully, it goes straight to the odour source, but if not, it fails to catch an odour information and easily results in a failure. By contrast, silkworm moths modulate their behaviour depending on the surrounding environment to acquire the odour information, it tends to become a high sinuosity index. The same tendency of high sinuosity index is also shown in the data-driven CPT model, it moved actively as well during the CPT experiments (figure 12e), and finally resulted in high success rate. Thus, it implies the data-driven CPT model demonstrated the adaptability of silkworm moths modulating their behaviour with respect to the surrounding environment.
Figure 13 shows the simulation results in environment (B). Like for environment (A), the data-driven CPT model provided a higher success rate than the P-Moth and Casting strategies (figure 13a; electronic supplementary material, video S4), and the sinuosity indexes of the data-driven CPT model were higher than those of P-Moth and Casting strategies (figure 13b) at the three initial positions. The Casting strategy could not get any success at and . As shown in figure 13c, the data-driven CPT model moved actively to acquire the odour information, and resulted in success even in the environment with obstacle.
Figure 13.
Results of simulation experiments in the environment (B). Fisher’s exact test was applied to the results of success rate and Student’s t-test was applied to the results of sinuosity index. (a) Success rate at three initial positions. (b) Sinuosity index at three initial positions. (c) Example trajectories obtained from data-driven CPT model.
The simulation results indicate that the data-driven CPT model can achieve the high CPT performance of the silkworm moth. In addition, the data-driven CPT model outperforms conventional model-based CPT strategies and shows applicability to different environments from the training data. However, it remains unclear whether the data-driven CPT model is applicable to a real environment. Thus, we verified the implementation effectiveness of the data-driven CPT model on an autonomous robot, as reported in the next section.
6. Performance evaluation of data-driven chemical plume tracing model in real environment
6.1. Experimental set-up
To apply CPT in a real environment, we implemented the proposed data-driven CPT model into the autonomous robot shown in figure 14a. A gas sensor attached in front of the robot measured the ethanol concentration. By using the Mecanum omnidirectional wheels, the robot could directly move to the odour source while keeping its posture constant. An Arduino Mega board (Arduino, Torino, Italy) with a Bluetooth module was used as controller, and 3.7 V batteries were used as power source. As for the inner loop laws for the robot’s control, we employed feedforward control because the notion that insects use a sensitive feedback control might be unrealistic [48]. We used DC-to-DC converter to avoid the effect of voltage fluctuation of a battery to motor outputs and keep the voltage applied to the motor driver constant. The relationship between PWM and movement speed was calibrated before the CPT experiments.
Figure 14.
CPT experimental set-up in real environment. (a) Communication diagram between desktop PC and robot equipped with Arduino Mega board, motor drivers, Bluetooth module, battery, and gas sensor. (b) Rectangular search field of 1800 × 1350 mm.
At first, the robot starts with random walk until a four-step concentration is sampled. The sensor response values were measured at the sampling period of 0.1 s and transmitted via the Bluetooth module to a desktop PC to predict the x- and y-axes displacements of the robot by the data-driven CPT model, and the robot performed the corresponding motion. The robot’s control period is set at 0.4 s, which is longer than the simulation’s one of 0.07 s to allow the robot to move smoothly. Every control period of 0.4 s that the robot receives a displacement command, the robot goes to the target position by setting a movement speed according to that displacement. During the process of one displacement for 0.4 s, the robot measures an odour concentration every 0.1 s to obtain the time series of odour stimuli, then uses it as the input of the data-driven CPT model. By iterating this process, we evaluated the CPT performance of the data-driven CPT model in a real environment.
In regards to the latency in software system of the robot, the Bluetooth communication delay was around 0.02 s, which was sufficiently faster than the sampling period of 0.1 s. In addition, the model optimization was done before the CPT experiments so that matrix calculation was only required to obtain the displacement command, which did not take any time. Therefore, the latency in software system of the robot could be dealt with in the sampling period of 0.1 s. The x- and y-axes displacements of the robot were quite small for application in the large environment due to the low average speed of silkworm moths during free walking [46], as mentioned previously. Therefore, the x- and y-axes displacements of the robot were scaled according to the real environment.
The search field for this environment was an indoor environment with a rectangular area of 1800 × 1350 mm, and the robot started the CPT experiment 1500 mm away from the odour source position (figure 14b). If the robot moved 250 mm from the odour source position, the CPT trial was considered successful. If the robot left the search field, the trial was considered as a failure. Like in the wind tunnel, ethanol was discharged in the field every 1 s under airflow at 0.85 m s−1 generated by a fan. From the results of simulation experiments, we determined the Casting strategy as being a limited applicability strategy and it did not work well under the odour discharging of 1 Hz. Therefore, for the CPT experiments in a real environment, we conducted 20 CPT trials with the robot implementing the data-driven CPT model and P-Moth strategy for comparison.
6.2. Results and discussion
Figure 15 shows the experimental CPT results obtained from the autonomous robot in the real environment. The success rate of the data-driven CPT model is 60%, performing better than the P-Moth strategy with success rate of 40% (figure 15a). Likewise, in simulation experiments, the sinuosity index of the data-driven CPT model is higher than that of the P-Moth strategy (figure 15b).
Figure 15.
Experimental results of CPT performed by autonomous robot in real environment. Fisher’s exact test was applied to the results of success rate and Student’s t test was applied to the results of sinuosity index. (a) Success rates of data-driven CPT model and P-Moth strategy. (b) Sinuosity index of data-driven CPT model and P-Moth strategy. (c) Example trajectories obtained from data-driven CPT model and P-Moth strategy.
Figure 15c shows the example trajectory of data-driven CPT model and P-Moth strategy. In the data-driven CPT model, the robot first moves upwind staying on the centre line of the search field (location in figure 15c), but gradually deviates off the centre line (location ). After not locating the odour information for a period, the robot repeatedly moves backward perhaps elicited by the historical input of four time steps’ data for odour stimuli, eventually returning to the centre line of the search field (location ; electronic supplementary material, video S5). By contrast, once the robot implementing the P-Moth strategy moves away from the centre line, it cannot return and rotates indefinitely (location in figure 15c). These trajectories show the difference of the CPT behaviours between each model when it loses the odour information. The P-Moth strategy makes the robot rotate until recovering an odour trace. Although this strategy may lead to identifying the direction of the source of odour, it depends on the environmental situation, as shown in figure 15c. In contrast, the data-driven CPT model could modulate the behaviour depending on the environmental situation by eliciting unexpected but effective behaviours such as moving away from the odour source like a Lévy walk [49].
However, here a question arose: why could the robot represent an adaptability like the silkworm moths when even fundamental properties of the robot were different from those of silkworm moths? Obviously, the robot has different sensing and actuation capabilities from silkworm moths, that causes odour information obtained to differ between robots and moths. While there are several researches fighting for such difference (e.g. [50]), it is far from closing the gap between robots and organisms. Thus, Hernandez Bennetts et al. [51] present arguments against the general applicability of biomimetic approaches because of such differences. Nonetheless, the robot performed well and demonstrated elements of adaptability modulating its behaviour depending on the environmental situation. One possible answer to this is that we modelled the moth CPT behaviour by regarding the sensor voltages as the real input of the silkworm moth, wherein the robot also used the same sensor for the robot’s sensory component. From a first stage of modelling CPT behaviour, we translated odour stimuli input toward the moths into sensor voltages, with the hope that it might reduce the difference in sensing capability.
In this way, this framework modelling the CPT behaviour by a data-driven approach could potentially close the gap between robots and organisms by improving the input–output data of the model. For example, an animal-in-the-loop system [52] is a system wherein organisms manipulate a robot remotely to achieve the search for a female. This system allows measurement of the dataset of an organism’s behaviour, including the underlying adaptability of the organism toward the difference of sensing and actuation capabilities. By using these obtained data as input–output data, the data-driven CPT model on an autonomous robot may be more applicable in the CPT problem.
In addition, considering the other information for the input data is also important because silkworm moths may use an integrated information of odour as well as others (e.g. wind direction [27]). In this study, we only used the odour information for the input as a first step for modelling CPT behaviour. Although the data-driven CPT model performed well at this earlier stage, this has been due to the CPT experiments being performed under simple environments. All the CPT experiments in this paper placed the odour source at the origin of the x–y coordinate system and placed the robot on an positive area of x-axis. Since the data-driven CPT model was established on the hypothesis that an upwind direction was the negative direction of x-axis, the data-driven CPT model tends to produce the output of displacement toward the negative direction of x-axis. If the CPT experiment in simulation is conducted in an environment vertically flipped from figure 11, namely the odour source is placed at (x = 500, y = 0), the initial position of the robot is at (x = 0, y = 0), and the wind direction also flips, from x = 600 to x = 0 along the negative x-axis, the data-driven CPT model does not locate an odour source at all due to the tendency of moving away from the odour source rather than approaching it. That is a research limitation at this stage.
When trying to apply the data-driven CPT model into these variety of environments, the calibration of upwind direction before searching an odour source is vital for x–y coordinate transformation. However, as a wind direction changes intermittently in a real scenario, the initial calibration of upwind direction is prone to be inaccurate. Therefore, introducing additional information (e.g. a wind direction or a direction of odour detection) into the input of the data-driven CPT model would be the next step to extend the model’s generalization ability.
7. Conclusion
We proposed a novel framework for modelling CPT behaviour of silkworm moth using a data-driven approach. To obtain the data-driven CPT model, we constructed a measurement system to simultaneously obtain the odour stimuli input and CPT behaviour output of silkworm moths. A transfer function described the input–output relationship as a stochastic process by applying Gaussian process regression, and the data-driven CPT model was constructed using measurements from CPT experiments on silkworm moths. From the results of CPT experiments in simulations as well as real environments, the proposed data-driven CPT model demonstrated a better success rate than conventional methods. In addition, the data-driven CPT model demonstrated elements of silkworm moths’ adaptability, such as moving away from the odour source in response to the environmental situation. In this way, our study contributes to creation of a novel framework for modelling CPT behaviour using a data-driven approach that could reproduce an organism’s CPT behaviour.
However, it was only applied to a limited number of environments and there remains room for improvement in terms of practicality. To apply the model in more general usage, we need to further consider the dataset of the data-driven CPT model in future works. We are therefore in the process of conducting CPT experiments on silkworm moths in an obstacle environment to obtain more general and diverse training data. As the airflow in the obstacle environment tends to be turbulent and strongly affects the shape of chemical plumes, we expect to observe more clearly the relevance of wind information on silkworm moths during CPT than in the current normal environment. Hence, combining such elicited information into the data-driven CPT model would be our next step for improving the current model.
Acknowledgements
The silkworm strains used in this study were provided by the National Bio-Resource Project (NBRP) of MEXT, Japan. We thank Dr Takeshi Sakurai (Tokyo University of Agriculture) for providing the purified bombykol.
Appendix A
This is to describe the detail of Gaussian process regression for the section ‘Estimation of odour stimulus at silkworm moth position’.
We defined the two-dimensional sensor coordinates psensor = {(50, − 50), (50, 0), …, (450, 50)} as the input and sensor measurements csensor = (c(50,−50), c(50,0), …, c(450,50)) as the output. To simplify these, we describe psensor as p = {p1, p2, …, p27} and csensor as c = (c1, c2, …, c27), and associate these data with a data group:
| A 1 |
In the data group D, there is a relationship: c = f(p) between p, c, which the function f is generated from a Gaussian process with an average of 0:
| A 2 |
Here, c follows a Gaussian distribution and is described by using kernel matrix K which is composed of kernel function k(p, p′) about all pairs of inputs (pn, pn′):
| A 3 |
The estimated sensor value c* at moth position p* can be described by using kernel matrix K′ which is based on a new dataset p′ = {p1, p2, …, p27, p*}, c′ = (c1, c2, …, c27, c*):
| A 4 |
| A 5 |
| A 6 |
| A 7 |
In this way, c* can be obtained as conditional probability premised on c:
| A 8 |
Appendix B
This is to describe the detail of Gaussian process regression of the section ‘Data-driven CPT model’.
We defined rows and four columns of data containing the time series of odour stimuli cmoth = (c1, c2, …, cT) at moth positions pmoth = {(x1, y1), (x2, y2), …, (xT, yT)} as the input of the data-driven CPT model. Aside from this, the moth displacements over four steps were obtained as Δpx(t) = (xt − xt−3), Δpy(t) = (yt − yt−3), and data groups Δpx = (Δpx(4), Δpx(5), …, Δpx(T)), Δpy = (Δpy(4), Δpy(5), …, Δpy(T)) were regarded as the output of the data-driven CPT model. To simplify these, we describe and Δpx (or Δpy) as Δp = (Δp4, Δp5, …, ΔpT), and associate these data with a data group:
| B 1 |
In the data group D, there is a relationship of between , Δp, which the function f is generated from a Gaussian process with an average of 0:
| B 2 |
Here, Δp follows a Gaussian distribution and is described by using kernel matrix K which is composed of kernel function about all pairs of inputs :
| B 3 |
The predicted agent displacement Δp* on odour stimuli history c* can be described by using kernel matrix K′ which is based on a new dataset , Δp′ = (Δp4, Δp5, …, ΔpT, Δp*):
| B 4 |
| B 5 |
| B 6 |
| B 7 |
In this way, Δp* can be obtained as conditional probability premised on Δp:
| B 8 |
Data accessibility
Additional data are provided in the electronic supplementary material.
Authors' contributions
K.O. conceived and designed the experiments, implemented the measurement system, and wrote the paper. K.O., T.S., D.N.R. and C.H.R. implemented the Gaussian process regression. K.O. and S.S. obtained the biological data through experiments. K.S. and D.K. analysed and evaluated the results. S.S., K.S. and D.K. contributed to manuscript revision.
Competing interests
We declare we have no competing interests.
Funding
This work was supported by JKA through its promotion funds from AUTORACE and JSPS KAKENHI under grant nos. JP19K14943 and JP19H02104.
References
- 1.Komori Y, Ohno K, Fujieda T, Suzuki T, Tadokoro S. 2015Detection of continuous barking actions from search and rescue dogs’ activities data. In 2015 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015, pp. 630–635. [Google Scholar]
- 2.Rozas R, Morales J, Vega D. 1991Artificial smell detection for robotic navigation. In 5th Int. Conf. on Advanced Robotics’ Robots in Unstructured Environments, Pisa, Italy, 19–22 June 1991, pp. 1730–1733. [Google Scholar]
- 3.Shigaki S, Fikri MR, Kurabayashi D. 2018Design and experimental evaluation of an odor sensing method for a pocket-sized quadcopter. Sensors 18, 3720. ( 10.3390/s18113720) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jatmiko W, Sekiyama K, Fukuda T. 2007A pso-based mobile robot for odor source localization in dynamic advection-diffusion with obstacles environment: theory, simulation and measurement. IEEE Comput. Intell. Mag. 2, 37-51. ( 10.1109/MCI.2007.353419) [DOI] [Google Scholar]
- 5.Chen XX, Huang J. 2019Odor source localization algorithms on mobile robots: a review and future outlook. Rob. Auton. Syst. 112, 123-136. ( 10.1016/j.robot.2018.11.014) [DOI] [Google Scholar]
- 6.Shraiman BI, Siggia ED. 2000Scalar turbulence. Nature 405, 639. ( 10.1038/35015000) [DOI] [PubMed] [Google Scholar]
- 7.Harvey DJ, Lu TF, Keller MA. 2008Comparing insect-inspired chemical plume tracking algorithms using a mobile robot. IEEE Trans. Rob. 24, 307-317. ( 10.1109/TRO.2007.912090) [DOI] [Google Scholar]
- 8.Ishida H, Wada Y, Matsukura H. 2012Chemical sensing in robotic applications: a review. IEEE Sensors J. 12, 3163-3173. ( 10.1109/JSEN.2012.2208740) [DOI] [Google Scholar]
- 9.Lochmatter T, Martinoli A. 2008Simulation experiments with bio-inspired algorithms for odor source localization in laminar wind flow. In 2008 7th Int. Conf. on Machine Learning and Applications, San Diego, CA, USA, 11–13 December 2008, pp. 437–443.
- 10.Hutchinson M, Liu C, Chen WH. 2018Information-based search for an atmospheric release using a mobile robot: algorithm and experiments. IEEE Trans. Control Syst. Technol. 27, 2388-2402. ( 10.1109/TCST.2018.2860548) [DOI] [Google Scholar]
- 11.Vergassola M, Villermaux E, Shraiman BI. 2007‘Infotaxis’ as a strategy for searching without gradients. Nature 445, 406-409. ( 10.1038/nature05464) [DOI] [PubMed] [Google Scholar]
- 12.Lilienthal AJ, Reggente M, Trincavelli M, Blanco JL, Gonzalez J. 2009A statistical approach to gas distribution modelling with mobile robots-the kernel DM + V algorithm. In 2009 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, St Louis, MO, USA, 10–15 October 2009, pp. 570–576.
- 13.Reggente M, Lilienthal AJ. 2010The 3D-kernel DM + V/W algorithm: using wind information in three dimensional gas distribution modelling with a mobile robot. In SENSORS, Waikoloa, HI, USA, 1–4 November 2010, pp. 999–1004.
- 14.Hayes AT, Martinoli A, Goodman RM. 2002Distributed odor source localization. IEEE Sensors J. 2, 260-271. ( 10.1109/JSEN.2002.800682) [DOI] [Google Scholar]
- 15.Ferri G, Jakuba MV, Mondini A, Mattoli V, Mazzolai B, Yoerger DR, Dario P. 2011Mapping multiple gas/odor sources in an uncontrolled indoor environment using a Bayesian occupancy grid mapping based method. Rob. Auton. Syst. 59, 988-1000. ( 10.1016/j.robot.2011.06.007) [DOI] [Google Scholar]
- 16.Li W, Farrell JA, Pang S, Arrieta RM. 2006Moth-inspired chemical plume tracing on an autonomous underwater vehicle. IEEE Trans. Rob. 22, 292-307. ( 10.1109/TRO.2006.870627) [DOI] [Google Scholar]
- 17.Russell RA, Bab-Hadiashar A, Shepherd RL, Wallace GG. 2003A comparison of reactive robot chemotaxis algorithms. Rob. Auton. Syst. 45, 83-97. ( 10.1016/S0921-8890(03)00120-9) [DOI] [Google Scholar]
- 18.Yang Y, Feng Q, Cai H, Xu J, Li F, Deng Z, Yan C, Li X. 2019Experimental study on three single-robot active olfaction algorithms for locating contaminant sources in indoor environments with no strong airflow. Build. Environ. 155, 320-333. ( 10.1016/j.buildenv.2019.03.043) [DOI] [Google Scholar]
- 19.Shigaki S, Shiota Y, Kurabayashi D, Kanzaki R. 2019Modeling of adaptive chemical plume tracing algorithm of insect using fuzzy inference. IEEE Trans. Fuzzy Syst. 28, 72-84. ( 10.1109/TFUZZ.2019.2915187) [DOI] [Google Scholar]
- 20.Bishop CM. 2006Pattern recognition and machine learning. Berlin, Germany: Springer. [Google Scholar]
- 21.Rasmussen CE, Williams CKI. 2006Gaussian processes for machine learning. Cambridge, MA: The MIT Press. [Google Scholar]
- 22.Kanagawa M, Hennig P, Sejdinovic D, Sriperumbudur BK. 2018Gaussian processes and kernel methods: a review on connections and equivalences. (http://arxiv.org/abs/1807.02582)
- 23.MacKay DJ. 1998Introduction to Gaussian processes. NATO ASI Ser. F Comput. Syst. Sci. 168, 133-166. [Google Scholar]
- 24.Obara Y. 1979Bombyx mori mating dance: an essential in locating the female. Appl. Entomol. Zool. 14, 130-132. ( 10.1303/aez.14.130) [DOI] [Google Scholar]
- 25.Kanzaki R, Sugi N, Shibuya T. 1992Self-generated zigzag turning of Bombyx mori males during pheromone-mediated upwind walking. Zool. Sci. 9, 515-527. [Google Scholar]
- 26.Lilienthal A, Reimann D, Zell A. 2003Gas source tracing with a mobile robot using an adapted moth strategy. In Autonome mobile systeme (ed. H Numata), pp. 150–160. Berlin, Germany: Springer.
- 27.Shigaki S, Haigo S, Reyes CH, Sakurai T, Kanzaki R, Kurabayashi D, Sezutsu H. 2019Analysis of the role of wind information for efficient chemical plume tracing based on optogenetic silkworm moth behavior. Bioinspir. Biomim. 14, 046006. ( 10.1088/1748-3190/ab1d34) [DOI] [PubMed] [Google Scholar]
- 28.Loudon C, Koehl MA. 2000Sniffing by a silkworm moth: wing fanning enhances air penetration through and pheromone interception by antennae. J. Exp. Biol. 203, 2977-2990. ( 10.1242/jeb.203.19.2977) [DOI] [PubMed] [Google Scholar]
- 29.Butenandt A, Beckmann R, Hecker E. 1961Über den sexuallockstoff des seidenspinners, I. Der biologische test und die isolierung des reinen sexuallockstoffes bombykol. Hoppe-Seyler s Zeitschrift für Physiologische Chemie 324, 71-83. ( 10.1515/bchm2.1961.324.1.71) [DOI] [PubMed] [Google Scholar]
- 30.Minegishi R, Takashima A, Kurabayashi D, Kanzaki R. 2012Construction of a brain-machine hybrid system to evaluate adaptability of an insect. Rob. Auton. Syst. 60, 692-699. ( 10.1016/j.robot.2011.06.012) [DOI] [Google Scholar]
- 31.Takasaki T, Namiki S, Kanzaki R. 2012Use of bilateral information to determine the walking direction during orientation to a pheromone source in the silkmoth Bombyx mori. J. Comp. Physiol. A 198, 295-307. ( 10.1007/s00359-011-0708-8) [DOI] [PubMed] [Google Scholar]
- 32.Adafruit MiCS5524 CO / Alcohol / VOC Gas Sensor Breakout (cited 27 October 2020). See https://www.mouser.jp/datasheet/2/737/adafruit-mics5524-gas-sensor-breakout-1396484.pdf.
- 33.Schneider D. 1957Elektrophysiologische Untersuchungen von Chemound Mechanorezetoren der Antenne des Seidenspinners Bombyx mori L. Z. Ver. Physiol. 40, 8-41. ( 10.1007/BF00298148) [DOI] [Google Scholar]
- 34.Ando N, Emoto S, Kanzaki R. 2013Odour-tracking capability of a silkmoth driving a mobile robot with turning bias and time delay. Bioinspir. Biomim. 8, 016008. ( 10.1088/1748-3182/8/1/016008) [DOI] [PubMed] [Google Scholar]
- 35.Fujiwara T, Kazawa T, Sakurai T, Fukushima R, Uchino K, Yamagata T, Namiki S, Haupt SS, Kanzaki R. 2014Odorant concentration differentiator for intermittent olfactory signals. J. Neurosci. 34, 16 581-16 593. ( 10.1523/JNEUROSCI.2319-14.2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Salvador S, Chan P. 2007Toward accurate dynamic time warping in linear time and space. Intell. Data Anal. 11, 561-580. ( 10.3233/IDA-2007-11508) [DOI] [Google Scholar]
- 37.Keogh E, Ratanamahatana CA. 2005Exact indexing of dynamic time warping. Knowl. Inf. Syst. 7, 358-386. ( 10.1007/s10115-004-0154-9) [DOI] [Google Scholar]
- 38.Schneider D. 1969Insect olfaction: deciphering system for chemical messages. Science 163, 1031-1037. ( 10.1126/science.163.3871.1031) [DOI] [PubMed] [Google Scholar]
- 39.Marsh C. 2013Introduction to continuous entropy. Princeton, NJ: Princeton University Press. [Google Scholar]
- 40.Bazan E, Doklädal P, Dokladalova E. 2019Quantitative analysis of similarity measures of distributions. In Proc. British Machine Vision Conf., Cardiff, UK, 9–12 September 2019.
- 41.Vert JP, Tsuda K, Schölkopf B. 2004A primer on kernel methods. Kernel Methods Comput. Biol. 47, 35-70. ( 10.7551/mitpress/4057.001.0001) [DOI] [Google Scholar]
- 42.Wendland H. 2005Scattered data approximation. Cambridge Monographs on Applied and Computational Mathematics, vol. 17. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 43.Byrd RH, Lu P, Nocedal J, Zhu C. 1995A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 16, 1190-1208. ( 10.1137/0916069) [DOI] [Google Scholar]
- 44.Hayashi K, Imaizumi M, Yoshida Y. 2020On random subsampling of Gaussian process regression: a graphon-based analysis. In Int. Conf. on Artificial Intelligence and Statistics, Palermo, Italy, 26–28 August 2020, pp. 2055–2065.
- 45.Mishima T, Kanzaki R. 1998Coordination of flipflopping neural signals and head turning during pheromone-mediated walking in a male silkworm moth Bombyx mori. J. Comp. Physiol. A 183, 273-282. ( 10.1007/s003590050255) [DOI] [Google Scholar]
- 46.Shigaki S, Fukushima S, Kurabayashi D, Sakurai T, Kanzaki R. 2016A novel method for full locomotion compensation of an untethered walking insect. Bioinspir. Biomim. 12, 016005. ( 10.1088/1748-3190/12/1/016005) [DOI] [PubMed] [Google Scholar]
- 47.Lochmatter T, Raemy X, Matthey L, Indra S, Martinoli A. 2008A comparison of casting and spiraling algorithms for odor source localization in laminar flow. In 2008 IEEE Int. Conf. on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008, pp. 1138–1143..
- 48.Kanzaki R, Nagasawa S, Shimoyama I. 2004Neural basis of odor-source searching behavior in insect microbrain systems evaluated with a mobile robot. In Bio-mechanisms of swimming and flying (eds N Kato, S Kamimura), pp. 155–170. Tokyo, Japan: Springer.
- 49.Kareiva PM, Shigesada N. 1983Analyzing insect movement as a correlated random walk. Oecologia 56, 234-238. ( 10.1007/BF00379695) [DOI] [PubMed] [Google Scholar]
- 50.Okajima K, Shigaki S, Reyes CH, Sanada K, Kurabayashi D. 2020Analysis of the effect of sampling strategy: flicking for chemical plume tracing by an autonomous robot. In 2020 IEEE/SICE Int. Symp. on System Integration (SII), Honolulu, HI, USA, 12–15 January 2020, pp. 542–545.
- 51.Hernandez Bennetts V, Lilienthal AJ, Neumann P, Trincavelli M. 2012Mobile robots for localizing gas emission sources on landfill sites: is bio-inspiration the way to go? Front. Neuroeng. 4, 20. ( 10.3389/fneng.2011.00020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Shigaki S, Fikri MR, Hernandez Reyes C, Sakurai T, Ando N, Kurabayashi D, Kanzaki R, Sezutsu H. 2018Animal-in-the-loop system to investigate adaptive behavior. Adv. Rob. 32, 945-953. ( 10.1080/01691864.2018.1511473) [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Additional data are provided in the electronic supplementary material.