Combining Measurements from Mobile Monitoring and a Reference Site To Develop Models of Ambient Ultrafine Particle Number Concentration at Residences

Abstract

Significant spatial and temporal variation in ultrafine particle (UFP; <100 nm in diameter) concentrations creates challenges in developing predictive models for epidemiological investigations. We compared the performance of land-use regression models built by combining mobile and stationary measurements (hybrid model) with a regression model built using mobile measurements only (mobile model) in Chelsea and Boston, MA (USA). In each study area, particle number concentration (PNC; a proxy for UFP) was measured at a stationary reference site and with a mobile laboratory driven along a fixed route during an ~1-year monitoring period. In comparing PNC measured at 20 residences and PNC estimates from hybrid and mobile models, the hybrid model showed higher Pearson correlations of natural log-transformed PNC (r = 0.73 vs 0.51 in Chelsea; r = 0.74 vs 0.47 in Boston) and lower root-mean-square error in Chelsea (0.61 vs 0.72) but no benefit in Boston (0.72 vs 0.71). All models overpredicted log-transformed PNC by 3–6% at residences, yet the hybrid model reduced the standard deviation of the residuals by 15% in Chelsea and 31% in Boston with better tracking of overnight decreases in PNC. Overall, the hybrid model considerably outperformed the mobile model and could offer reduced exposure error for UFP epidemiology.

Graphical Abstract

1. INTRODUCTION

Ultrafine particles (UFPs; <100 nm in aerodynamic diameter) in urban air derive mainly from combustion processes and photochemical oxidative pathways.^1,2 UFPs are a health concern because they have been shown to be toxic in in vitro and in vivo assays, and due to their small size, they can penetrate deep into the lungs, cross into the circulatory system, and become widely dispersed in the body.^3–6 UFP epidemiology studies have shown increased cardiovascular disease risk and mortality with increasing UFP concentrations,^7–9 albeit the effect estimates are often either weakly significant or only suggestive of associations. Because ambient UFP concentrations vary significantly in both space and time (with the highest concentrations occurring near sources and attenuation patterns depending on wind speed and direction, atmospheric stability, and other variables),^10–15 accurately characterizing exposure is a central challenge in UFP epidemiology.

The two most common strategies used to inform UFP model development are stationary monitoring and mobile monitoring. Data from stationary monitoring, where UFP is measured continuously for days, weeks, months, or even years at fixed sites in a study area,^16–24 is used to develop spatial regression models based on covariates such as land use and distance to major roadways. Such models (referred to as land-use regression models) have typically been used to generate long-term (e.g., annual average) UFP concentration estimates and generally show good agreement with UFP measurements (adjusted-R² = ~0.30–0.60 for hourly measurements and 0.87–0.89 for biannual and annual measurements).^16–24 Data from mobile monitoring, where UFP monitors mounted on mobile platforms are driven, biked, or walked along prescribed routes through a study area for multiple hours a day on multiple days, is used to characterize fine-scale spatial and/or short-term temporal variation.^20,25–30 These models have incorporated temporal (e.g., temperature, wind speed, and wind direction) as well as spatial (e.g., distances to roadways and land-use characteristics) covariates. Mobile-monitoring models have performed moderately well with adjusted-R² values ranging from 0.18 to 0.68.^20,25–30 In addition, some studies have incorporated reference sites along with stationary or mobile monitoring to account for temporal variability.^19,22,25 For example, Hoek et al.¹⁹ and Hankey and Marshall²⁵ used UFP measurements from background sites to adjust for temporal variation in the development of land-use regression models, while Rivera et al.²² adjusted for temporal variation by scaling UFP levels based on daily mean concentrations of nitrogen oxides at a background site.

We were interested in evaluating the benefits of combining stationary and mobile-monitoring data in developing regression models for UFP in urban study areas. To our knowledge, no studies have investigated combining mobile and stationary monitoring data together in a single model for the purpose of making highly temporally (i.e., 1 h) and spatially resolved (i.e., <100 m²) UFP estimates. We hypothesized that combining data from a long-term stationary monitor with data collected using a mobile-monitoring platform would substantially improve model predictions compared to only using data from mobile monitoring. Our objectives were to (1) build and evaluate separate models of ambient particle number concentration (PNC; a proxy for UFP) based on mobile-monitoring-only and combined mobile-and-stationary-monitoring data sets collected in two urban study areas and (2) compare PNC estimated by the two models with PNC measured at residences in the study. This work was part of a study examining associations between traffic-related air pollutants and cardiovascular disease risk in the Boston Puerto Rican Health Study (BPRHS) cohort.³¹

2. MATERIALS AND METHODS

2.1. Study Areas.

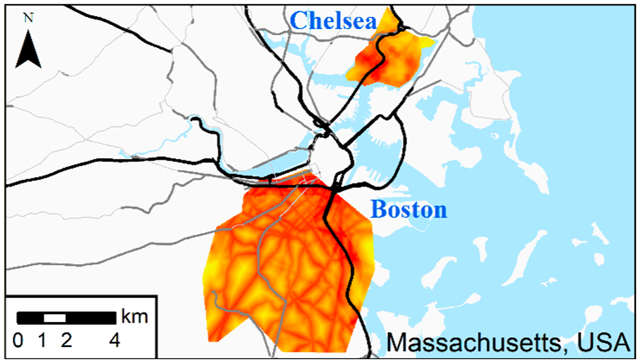
PNC monitoring was conducted in study areas in Chelsea and Boston, Massachusetts (Figure 1). A total of 159 BPRHS participants live the Chelsea study area and 814 live in the Boston study area. The Chelsea study area is 6 km² and has two highways: U.S. Route 1 (US-1; 83 000 vehicles/day) and Massachusetts Route 16 (40 000 vehicles/day).³² Twenty-six percent of all roads in Chelsea are classified as major roads (4.5 km road/km²) with an average of 16 400 vehicles/day/road. Major roads are defined by functional classification and vehicle access: limited-access highway (Interstate and U.S. highways; Class 1); nonlimited-access multilane highway (state highways; Class 2); other major roads, arterials, and collectors (Class 3 and 4) (see Figure 1). Approximately 27% of the land is classified as residential.³³ Logan International Airport (~1000 flight operations/day; not shown in Figure 1) is 2.3 km southeast from the nearest edge of the Chelsea study area.

Figure 1.

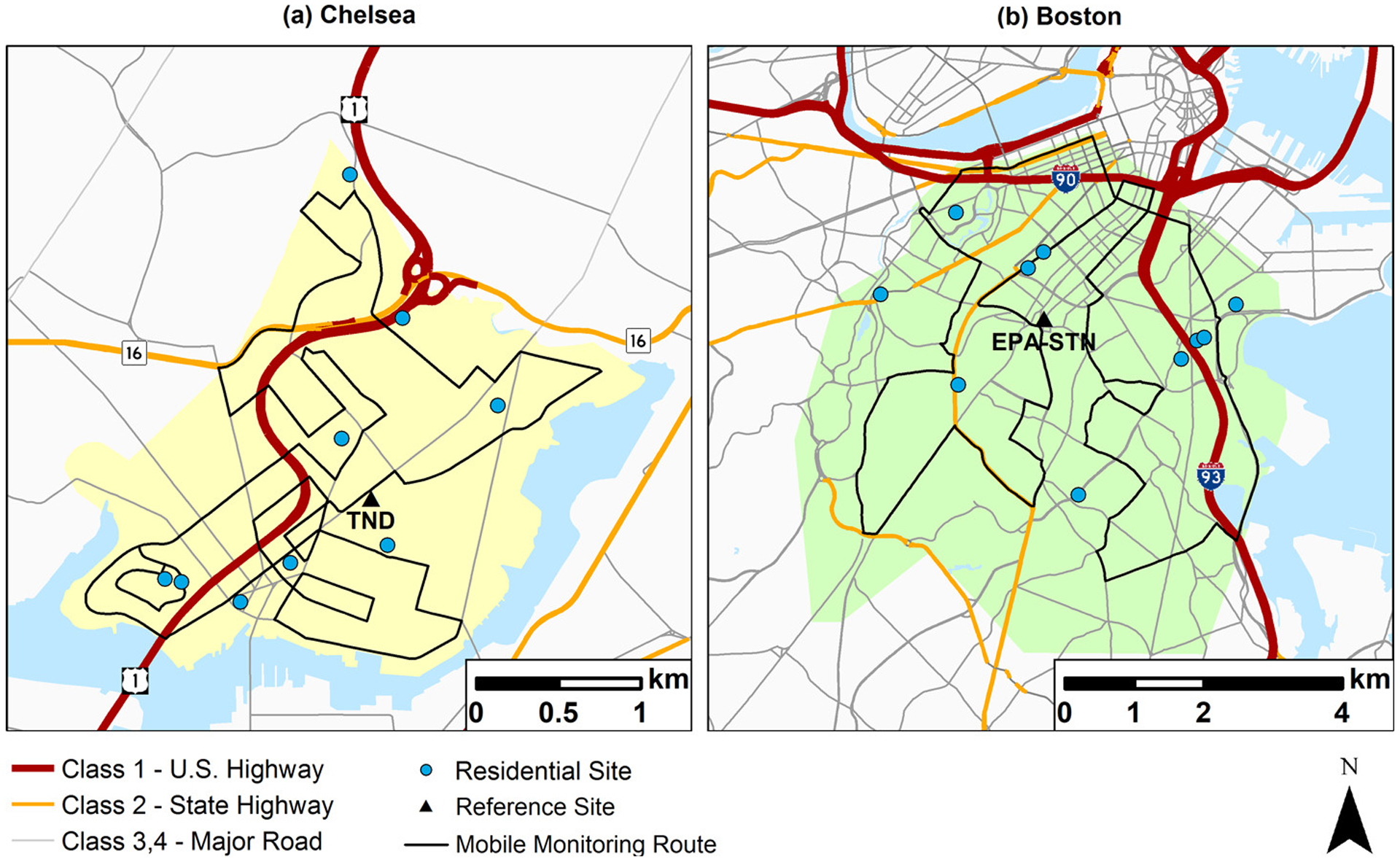
Chelsea (a) and Boston (b) study areas with road classes 1–4 highlighted. Chelsea monitoring period was from Dec 2013–May 2015; Boston monitoring period was from Dec 2011–Nov 2013.

The Boston study area is 40 km² and contains two highways: Interstates 90 and 93 (110 000 and 195 000 vehicles/weekday, respectively).³² Thirty-four percent of all roads in the Boston study area are classified as major roads (6.5 km road/km²) with an average of 17 600 vehicles/day/road. Approximately 40% of the land in the Boston study area is classified as residential.³³ Logan Airport is 4.4 km northeast from the nearest edge of the Boston study area.

2.2. Monitoring Sites and Periods.

PNC was measured via three different monitoring strategies (i.e., reference-site, mobile, and residential monitoring) in both study areas.³⁴ Monitoring in Chelsea was conducted between December 2013 and May 2015, while monitoring in Boston was conducted between December 2011 and November 2013. At the stationary reference sites, PNC was measured continuously (24 h/day, 7 days/week) throughout the study period. There was one stationary reference site in each study area: the Chelsea stationary reference monitor was located on the roof of a three-story building in a mixed residential/commercial area within the city; the Boston stationary reference monitor was located at the U.S. Environmental Protection Agency Speciation Trend Network site (EPA-STN; ID: 25-025-0042). Mobile monitoring was conducted with the Tufts Air Pollution Monitoring Laboratory (TAPL), a converted gasoline-powered recreational vehicle,¹³ by driving along fixed routes in each study area (Figure 1). Mobile monitoring was performed on 46 days in the Chelsea study area and 48 days in the Boston study area; monitoring was performed in 4–6-h shifts, between 05:00 and 21:00 h (local time) on all days of the week and in all seasons. Residential monitoring was conducted at 9 homes in Chelsea and 11 homes in Boston for six consecutive weeks per home (Figure 1). Up to two homes in the same study area were monitored concurrently. At each residence, both outdoor and indoor PNCs were measured at alternating 15-min intervals using a solenoid valve that switched between the two environments. Only outdoor data were used to evaluate model performance; indoor data are discussed in Brugge et al.³⁵

2.3. Instrumentation and Data Processing.

Water-based condensation particle counters (CPC; Model 3783, TSI, Shoreview, MN; 7–3000 nm; 30-s averaging, 1-min averaging prior to May 2013) were used at the two stationary reference sites and in all the residences; a butanol-based CPC (Model 3775, TSI, Shoreview, MN; 4–3000 nm; 1-s averaging) was used in the mobile laboratory. Timestamps of PNC measured with the mobile laboratory were adjusted by three seconds to account for travel time from the TAPL inlet to the CPC. To minimize the risk of self-sampling, we removed on-road data when the TAPL was moving at <5 km/h for >10 s and we continued to remove data until the TAPL speed increased to >5 km/h for >10 s. All CPC data were reviewed for instrument-reported errors (i.e., faults related to pulse height, nozzle pressure, vacuum pressure, temperature, and laser malfunction); impacted data were removed (<1% of total data). The hour-to-hour variability in regional PNC was estimated as the hourly fifth percentile of stationary reference-site measurements.^36,37 Outdoor PNCs at each residence were aggregated to the hourly median. We determined that the butanol-based CPC measured ~14% higher PNC (presumably due to the lower particle size detection limit) compared to the water-based CPC (Figure S1);^38,39 therefore, butanol-based CPC measurements were adjusted downward by 14% prior to all analyses for better agreement with stationary reference-site and residential measurements. To preserve spatial information, no averaging was performed on the mobile-monitoring measurements.

Covariate data included meteorology and traffic. Hourly solar radiation data were obtained from three different EPA monitoring stations in Boston (Long Island, ID: 25-025-0041, EPA-STN, and Von Hillern St., ID: 25-025-0044).⁴⁰ Upper-air temperature profiles (0–16 km; ~20 vertical soundings every 12-h) were obtained from the U.S. National Weather Service (NWS) station in Chatham, MA (KCQX). Other meteorological data were obtained from the NWS station at Logan International Airport (KBOS) at 1-min resolution. Hourly wind speed and direction were calculated using EPA AERMINUTE (version 15272), while hourly mixing height, based on upper-air data, was calculated using AERMET (version 15181).⁴¹ Hourly solar radiation was based on the mean of the three Boston-area solar radiation monitors. All other meteorology and traffic measurements were also averaged to the hour. Hourly meteorological data and stationary reference-site PNC were assigned to each second of mobile-monitoring data for a given hour. Five-minute average traffic volume and speed along Interstates 90 and 93 (I-90 and I-93) reported by Massachusetts Department of Transportation microwave sensors were obtained via the HERE web interface.⁴² Hourly traffic data were not available for other roadways within the study areas. Bus schedules for both study areas were obtained from the Massachusetts Bay Transportation Authority (MBTA; www.mbta.com). The number of buses in each study area was calculated by first identifying bus routes in the study areas using data layers obtained from the Massachusetts Office of Geographic Information⁴³ and then counting the number of departure times for both ends of the bus route. All data sets were merged by timestamp using R (version 3.4).

2.4. Development of Models.

Two linear multivariable regression models were developed for each study area: one used data acquired via mobile monitoring only (designated as Mobile-C for Chelsea and Mobile-B for Boston), while the other used both mobile and stationary monitoring data (designated as Hybrid-C and Hybrid-B). Meteorology data, traffic data, and distances to different land uses (i.e., the straight-line distance to the nearest point classified with that land use) were tested as explanatory variables in all models (Table S1). Model building was performed in a supervised forward stepwise approach using the univariate model with the highest R² as the starting point. All remaining potential independent variables were then tested in univariate models of the model residuals, and the variable with the highest R² was then selected and added to the multivariable model and so on. Variables continued to be added to the model as long as the adjusted-R² increased by ≥0.001. Variables were retained in the model if (1) they had statistically significant associations with the natural-log of PNC (ln(PNC)) (p < 0.05), (2) their inclusion could be justified by known physical processes, and (3) collinearity among model covariates was low, i.e., collinearity value <2 as given by eq 1:

$$\text{collineaity value}={\sqrt{\text{VIF}}}^{1/\text{DF}}$$ (1)

where VIF is the variance inflation factor and DF is the degrees of freedom for a variable of interest.⁴⁴ Model residuals were tested for normality and homoscedasticity. All models were fitted using the statistical package R (version 3.4). ArcGIS 10.4 was used to generate maps and spatial variables.

2.4.1. Mobile-Monitoring Models.

Mobile-C and Mobile-B were based on the natural log of PNC measured with the mobile laboratory. The models were developed using the same approach as previous PNC mobile-monitoring models for other Boston-area neighborhoods.^26,27 The form of the models is shown in eq 2:

$$\text{ln}{\left(\text{PNC}\right)}_{{\text{mod}}_{x,y,h}}={\beta }_0+\sum {\beta }_i{u}_{i_{x,y,h}}+{\epsilon }_{x,y,h}$$ (2)

where variables (u_i) were functions of space (i.e., spatial coordinates (x,y)) and/or time (h, the hour of the day), β_i was the regression coefficient, β₀ was the model intercept, and ε was the random error term. One-second ln(PNC) values were used to develop the model to retain a high degree of spatial resolution, but temporal and spatiotemporal variables were at an hourly resolution; thus, the model estimated the average ln(PNC) for a given hour.

2.4.2. Spatial Factor and Hybrid Models.

Hybrid-C and Hybrid-B were based on PNC measurements collected with both the mobile laboratory and the stationary reference-site monitors. We combined these data streams by calculating ratios between mobile measurements and reference-site measurements. Specifically, we calculated the ratio of one-second PNC measurements made with the mobile laboratory to the hourly fifth percentile of PNC measured at the reference site (eq 3). We refer to this ratio as the measured spatial factor (SF_meas). We calculated ratios instead of concentration differences to simplify interpretability (e.g., it is possible to get negative values for differences if PNC at the reference site is not always the lowest concentration in the study area). SF_meas values represent the location-specific deviation of PNC measured with the mobile laboratory to PNC measured concurrently at the reference site. To minimize local impacts and to better represent the hour-to-hour regional variability, we used the hourly fifth percentile of PNC at the reference site when calculating spatial factors:

$${\left({\text{SF}}_{\text{meas}}\right)}_{x,y,t}=\frac{{\left({\text{PNC}}_{\text{mobile}}\right)}_{x,y,t}}{{\left({\text{PNC}}_{\text{reference},\text{hourly}5\text{thpercentile}}\right)}_h}$$ (3)

where x and y represent the spatial coordinates of the mobile laboratory at time, t, to the nearest second; h represents the hour of the day. This ratio is similar to one described by Cordioli et al.,⁴⁵ who normalized nitrogen dioxide concentrations measured with a network of passive samplers to reference-site measurements in the same study area.

As shown in eq 4, the spatial factors were an integral part of the hybrid models:

$${\text{PNC}}_{\text{mod}x,y,h}={\text{SF}}_{{\text{mod}}_{x,y,h}}\times {\left({\text{PNC}}_{\text{reference},\text{hourlyfifthpercentile}}\right)}_h$$ (4)

where SF_mod was the modeled spatial factor. Spatial factors were modeled to be able to estimate spatial factor values for all times during which reference-site measurements were available and at any location within the study areas. SF_mod was estimated using the same multivariable linear regression procedure used to build the mobile models (see eq 2 for model form). Specifically, natural-log transformed values of the measured spatial factors (SF_meas) were regressed against spatial covariates (e.g., distance from highways, distance from intersections, and distance from various land uses; see Table S1) to create spatial factor models. Finally, PN concentrations were estimated by multiplying SF_mod values corresponding to locations of interest by the hourly fifth percentile PNC measured at the reference site during the hour of interest.

2.4.3. Model Assessment and Sensitivity Analyses.

Mobile and spatial factor models were evaluated on the basis of adjusted-R² and root-mean-square error (RMSE). Model performance was assessed by training the models on a random 50% subset of the data set and by testing model predictions against the 50% of PNC measurements not used for model building. This process was repeated 50 times and the results were averaged (2-fold, 50-repeat cross-validation).⁴⁶ We conducted a sensitivity analysis of Mobile-B by removing all of the mobile-monitoring data collected on 28 January 2013 from the model. This analysis was performed because the average measured PNC on this day was >3-fold higher than the next highest monitoring-day average in Boston. In contrast, the highest average measured PNC day in Chelsea was only 3% higher than the next highest day; thus, a similar sensitivity analysis was not performed for the Chelsea study area. In addition, sensitivity analyses were conducted with the hybrid models by (1) regressing spatial factor values against temporal and spatiotemporal covariates and (2) comparing Hybrid-B models with and without data from 28 January 2013. To assess the effect of autocorrelation in our data sets, we tested all models by including a first-order autoregressive (AR-1) term using SAS 9.4.

2.5. Modeled PNC Values at Residences.

To test their performance, the mobile and hybrid models, the models were used to predict hourly ln(PNC) for 20 residences. Values for the spatial variables used in the models were calculated for each residence using ArcMap 10.4 and data layers from MassGIS.⁴⁷ Temporal variables were calculated on the basis of the local meteorology corresponding to the monitoring period for each home. The mobile-model and hybrid-model estimates were compared to ambient PNC measured at the residences using Pearson linear correlation coefficients (r), Spearman rank correlation coefficients, RMSE, and Bland-Altman statistics. Pearson and Spearman coefficients were used to assess the consistency of temporal patterns; RMSE was used to measure how well models predicted measured concentrations, and Bland-Altman statistics were used to quantify systematic differences between predicted and measured concentrations at homes (i.e., systematic error) as well as to quantify the variability of predictions (i.e., random error or, specifically, the standard deviation of the absolute residuals).⁴⁸ Modeled and measured PNCs were natural-log transformed prior to analysis to minimize the influence of extreme values on the calculated statistics.

3. RESULTS AND DISCUSSION

3.1. Particle Number Concentration and Spatial Factor Measurements.

Temporal and spatial differences in PNC measurements in Chelsea and Boston, as observed in mobile-monitoring and stationary reference-site data, are described in detail elsewhere.³⁴ Briefly, PNC in the two study areas was generally highest during the winter and lowest in the summer, higher during periods of greater atmospheric stability (Figure S2),⁴⁹ and correlated with traffic congestion on I-93 (Figure S3). Additionally, PNC was higher near major roadways and bus routes than on minor roads and areas farther from bus routes. These results are consistent with the findings of other studies.^{26,28,50–53} Measured spatial factors (SF_meas) also decreased with increasing distance from highways and major roadways and were lower in residential than in industrial and commercial areas (Figures S4 and S5). In addition, as mixing heights decreased SF_meas values generally trended toward unity because of reduced differences between the mobile laboratory and the reference-site measurements.

3.2. Particle Number Concentration Models.

3.2.1. Mobile-Monitoring Models.

The hourly PNC models built with only mobile-monitoring data for Chelsea (Mobile-C) and Boston (Mobile-B) had adjusted-R² of 0.46 and 0.43, respectively, and RMSE of 0.56 and 0.72, respectively. These results are comparable to other hourly PNC models built from mobile-monitoring data sets,^25,54,55 including those from other Boston neighborhoods.²⁶ Mobile-C and Mobile-B had similar covariates, and temporal variables (i.e., temperature, wind speed and direction, solar radiation, time of day, and I-93 traffic) accounted for most of the variability captured by the models (Table 1). Cross validation indicated that both models were stable: the hold-out validation R² was 0.46 in Chelsea and 0.43 in Boston.

Table 1.

Summary of Chelsea and Boston Mobile-Monitoring Models^a

	Chelsea (adj. R2 = 0.46) (n = 508 871)b		Boston (adj. R2 = 0.43) (n = 293 475)b
variable	β coefficient	std. error	β coefficient	std. error
(intercept)	11.28	0.011	9.894	0.019
temperature (per °C)	−0.0331	0.0001	−0.0652	0.0002
wind speed (per m/s)	−0.1183	0.0006	−0.1270	0.0008
relative humidity (per %)	−0.0047	0.0001	n/a	n/a
pressure (per mb difference from 1013.25 mb)c	−0.0171	0.0001	n/a	n/a
cloud cover (1–10 scale; 1 = clear, 10 = overcast)	n/a	n/a	0.0467	0.0007
solar radiation (per kW/m2)	0.316	0.005	n/a	n/a
solar radiation, lagged 1 h (per kW/m2)	n/a	n/a	1.787	0.010
wind direction (rel. to no wind)
NNE (0–45°)	−0.670	0.011	0.398	0.015
ENE (45–90°)	−0.711	0.011	0.386	0.014
ESE (90–135°)	−0.281	0.011	0.184	0.015
SSE (135–180°)	−0.009d	0.011	0.563	0.017
SSW (180–225°)	−0.081	0.011	0.731	0.015
WSW (225–270°)	−0.297	0.011	0.483	0.015
WNW (270–315°)	−0.522	0.010	0.332	0.015
NNW (315–360°)	−0.613	0.011	0.375	0.015
downwind of Logan Airport (±15°; binary)	n/a	n/a	0.254	0.006
type of hour/day (rel. to weekdays 18:00–06:00)
weekday morning rush (06:00–09:00)	0.110	0.003	0.167	0.006
weekday midday (09:00–15:00)	−0.055	0.003	−0.360	0.006
weekday evening rush (15:00–18:00)	−0.263	0.003	−0.135	0.007
Saturday or Sunday (all hours)	−0.437	0.003	−0.306	0.007
I-93 traffic (hourly ln(vehicles/km/h))	0.221	0.002	0.376	0.007
distance from bus route (per km)	n/a	n/a	−0.974	0.012
distance from road classes 1–4 (per km)e	−0.457	0.008	−0.875	0.021
near major-road intersection (<150 m; binary)	0.080	0.002	n/a	n/a
near interstate (<100 m; binary)	n/a	n/a	0.191	0.007
near interstate (<300 m; binary)	n/a	n/a	0.082	0.005
distance from elevated US-1 (per km)	−0.157	0.001	n/a	n/a
near US-1 (<200 m; binary)	0.077	0.002	n/a	n/a
distance from residential land use (per km)	0.557	0.015	0.833	0.024
distance from transportation land use (per km)	n/a	n/a	−0.181	0.006
distance from open spaces (any size; per km)	n/a	n/a	0.310	0.011
distance from open spaces (>5000 m2; per km)	0.443	0.009	n/a	n/a

^aModels predict ln(PNC), where PNC is in units of particles/cm³. Variables are significant at p < 0.05 unless specified otherwise.

^bNumber of 1-sec data points used to build the model.

^cPressure was adjusted from the absolute scale to be the arithmetic difference from 1013.25 mb (standard atmosphere) to improve interpretability of the β coefficient. For example, a measured pressure of 1005 mb was expressed in the model as −8.25 mb.

^dNot significant at p < 0.05.

^eRoad classes are defined by functional classification and vehicle access: limited-access highway (Class 1), nonlimited-access multilane highway (Class 2), other numbered routes (Class 3), and major arterials and collectors (Class 4). For reference, Class 5 and 6 roads are minor streets and roads.

Terms for traffic volume and traffic speed on I-93 and I-90 did not account for enough of the PNC variability (ΔR² < 0.001) to be included as independent covariates in Mobile-C and Mobile-B. Instead, we used the natural-log transform of the ratio of hourly traffic volume (vph) to hourly average traffic speed (km/h) for traffic along I-93 in the models (n.b., natural-log transform of ratios <1 yield negative numbers). The values of this derived variable ranged from −0.68 (no traffic congestion) to 2.5 (heavy congestion) in the two models and was correlated with increased ambient PNC (Table 1). This is consistent with other studies, which have reported that the highest PNCs occur during periods of high traffic volume and low traffic speed, while the lowest PNCs occur during periods of low traffic volume and high traffic speed.^26,27,56 Solar radiation was also correlated with an increase in ambient PNC after accounting for temperature in the models, likely due to increased secondary particle formation during the summer months.⁵⁷ Although day of the week was a significant predictor of PNC, it was not included in the models because the association was likely impacted by the mobile-monitoring schedule and was not representative of actual trends. For example, a disproportionate number of monitoring hours during the morning rush hour on the same day each week (Wednesdays in Chelsea, Thursdays in Boston) could have led to a significantly higher or lower β coefficient for that day as compared to other days of the week. To capture general traffic patterns throughout the day, we tested a time-of-day categorical term based on time cutoffs used in the Boston Region Metropolitan Planning Organization’s traffic model (i.e., weekday morning rush hour (06:00–09:00), weekday midday (09:00–15:00), weekday evening rush hour (15:00–18:00), weekday overnight (18:00–06:00), and weekends (Saturday and Sunday, all hours)). As expected, the weekday morning rush hour period was the most strongly correlated with PNC.

Proximity to traffic was also correlated with increased PNC indicating that the models identified gradients near major roadways, which compares well to the monitoring data (Figure S6). We tested both linear and inverse distance variables, although none of the inverse distance variables were included in the final models. Distance from bus routes was a significant predictor (p < 0.05) in both the Boston study area (70 bus routes; ~5880 buses/day) and Chelsea study area (7 bus routes; ~790 buses/day),⁴³ but this factor only increased the adjusted-R² by ≥0.001 in Mobile-B and was not included in Mobile-C. The downwind-of-airport term met the acceptance criteria to be included in the Mobile-B model, but not in Mobile-C; however, wind direction may have served as a proxy for airport impacts in Mobile-C.⁵⁸ Removing 28 January 2013 resulted in a reduced adjusted-R² of 0.31 in Mobile-B (vs 0.43 when this data was retained). Data from this day were retained in the final model (see Figure S7 for more detail).⁵⁹ After adding the AR-1 term into Mobile-C and Mobile-B models, all variables remained significant (p < 0.05) except for the categorical time-of-day variable in Mobile-B and the distance to residential land use and the 200-m buffer around US-1 in Mobile-C. The loss of significance of these terms likely occurred because they were serving as a proxy for a temporal autocorrelation structure (time-of-day variable) and an interlinked spatial structure (proximity variables) in the data. Therefore, we kept the time-of-day and proximity variables in the models rather than use the AR-1 term.

3.2.2. Spatial Factor Models and Hybrid Models.

The spatial factor models, which were based on spatial covariates only, had low adjusted-R²: 0.09 in Chelsea and 0.06 in Boston (RMSEs were 0.57 and 0.80, respectively) (Table 2), likely resulting from the high resolution of the mobile-monitoring data (i.e., one second). Cross-validation indicated the spatial factor models were stable for both study areas: the hold-out validation R² was 0.09 in Chelsea and 0.06 in Boston. Adding an AR-1 term to the spatial models resulted in no change of significance for any of the variables. Figure 2 illustrates the spatial contrasts predicted with the spatial factor models for the two study areas. The vein-like structure in the Boston model (Figure 2b) is due to the greater number of major roads throughout the study area and the larger β coefficient for the distance from major roadway term, as compared to the Chelsea model. Circular patterns around intersections in Chelsea (Figure 2a) are due to the binary “major intersection” term; this term only met the acceptance criteria for inclusion in the Chelsea model. The two spatial factor models included all spatial variables used in Mobile-C and Mobile-B (Table 1). The reference-site measurements may have served as a proxy for Logan Airport impacts in the hybrid models since PNC measured at the two reference sites have previously been shown to be associated with being downwind from the airport.⁵⁸

Table 2.

Summary of Chelsea and Boston Spatial Factor Models^a

	Chelsea (adj. R2 = 0.09) (n = 513 976)b		Boston (adj. R2 = 0.06) (n = 224 129)b
variable	β coefficient	std. error	β coefficient	std. error
(intercept)	0.580	0.003	0.671	0.004
distance from road classes 1–4 (per km)	−0.458	0.008	−0.813	0.052
distance from bus routes (per km)	n/a	n/a	−1.011	0.016
distance from US-1 (elevated section; per km)	−0.167	0.001	n/a	n/a
near US-1 (<200 m; binary)	0.080	0.002	n/a	n/a
near interstate (<400 m; binary)	n/a	n/a	0.077	0.005
near interstate (<100 m; binary)	n/a	n/a	0.142	0.008
distance from open spaces (any size; per km)	n/a	n/a	0.278	0.014
distance from open spaces (>5000 m2; per km)	0.430	0.009	n/a	n/a
distance from residential land use (per km)	0.558	0.015	0.787	0.003
distance from transportation land use (per km)	n/a	n/a	−0.211	0.008
near major-road intersection (<150 m; binary)	0.081	0.002	n/a	n/a

^aModels predict ln(SF), where SF is the unitless spatial factor. Variables are significant at p < 0.05.

^bNumber of 1-sec data points used to build the model.

Figure 2.

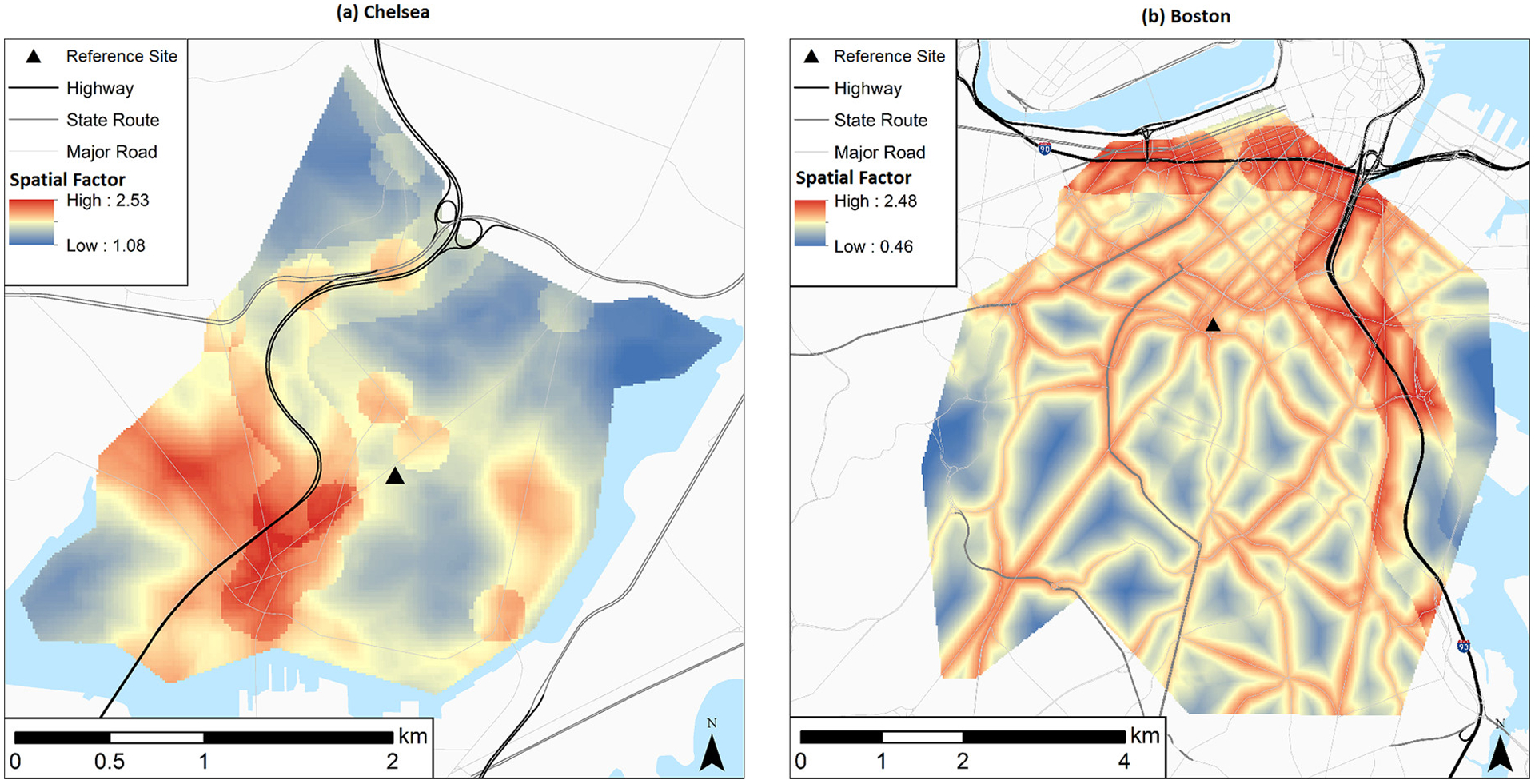
Predicted spatial factor values (20 m × 20 m grid) for the (a) Chelsea and (b) Boston study areas; spatial factor values range from 1.08 to 2.53 in Chelsea and 0.46 to 2.48 in Boston. Predicted values are based on the models described in Table 2.

Sensitivity tests indicated that the spatial factor models were sensitive to the inclusion of temporal and spatiotemporal covariates (Hybrid_temporal; Table S2). Including temporal terms for wind direction, time of day, and Monin-Obukhov length improved the adjusted-R² for spatial factor models in both study areas: 0.21 in Chelsea and 0.17 in Boston (RMSEs were 0.53 and 0.76, respectively). Nonetheless, the improved adjusted-R² did not correspond to improvements in model predictions when comparing modeled to measured PNC at homes (Tables S3). Given the form of the hybrid model, it is possible that including temporal and spatiotemporal variables as spatial factor predictors led to an overfit hybrid model. Since meteorology impacts the reference site and meteorological terms were also used as spatial factor predictors, when the reference-site PNC and spatial factor are multiplied together in the hybrid model, meteorology may be accounted for twice. Therefore, we chose to use the spatial factor model with spatial variables only in the hybrid model. Removing the 28 January 2013 mobile-monitoring data from the Boston study area SF_meas data set resulted in no change in the adjusted-R² or loss of significance for any of the variables; therefore, data from this day were retained in Hybrid-B.

3.3. Modeled Versus Measured PNC at Residences.

In both study areas, the hybrid model significantly outperformed the mobile model in terms of accuracy and precision as well as capturing the spatial and temporal trends in the measurements. Pearson correlations (r) between hybrid-model predictions and ln(PNC) measured at all residences in both study areas were higher than those between mobile-model predictions and ln(PNC) measured at all residences (r_{all homes} was 0.73 for the hybrid model vs 0.51 for the mobile-monitoring model in Chelsea and 0.74 vs 0.47 in Boston) (Tables 3 and S4). Results were similar using Spearman rank correlations (Tables 3 and S5). Time series of both hybrid- and mobile-model predictions of ln(PNC) were consistent with measured ln(PNC); however, the hybrid models predicted overnight concentrations substantially better than the mobile models (Figures 3 and S8). Additionally, the hybrid models had greater precision than the mobile models, as reflected by the lower standard deviation of the residuals for the hybrid-model predictions in both study areas (15% lower in Chelsea; 31% lower in Boston) and at 18 out of the 20 individual residential sites (Table S6 and Figures S9–S12).

Table 3.

Summary Statistics Comparing Modeled to Measured ln(PNC) at All Homes Combined

	Chelsea		Boston
statistica	Mobile-C (n = 8469)	Hybrid-C (n = 8805)	Mobile-B (n = 10 162)	Hybrid-B (n = 10 161)
Pearson correlation	0.51	0.73	0.47	0.74
Spearman correlation	0.50	0.73	0.48	0.73
mean differenceb	0.37	0.30	0.24	0.56
standard deviation of mean difference	1.22	1.04	1.31	0.90
RMSE	0.72	0.61	0.71	0.72

^aStatistics are based on all study-area homes grouped into one large data set.

^bThe mean difference between modeled and measured PNC at all homes combined.

Figure 3.

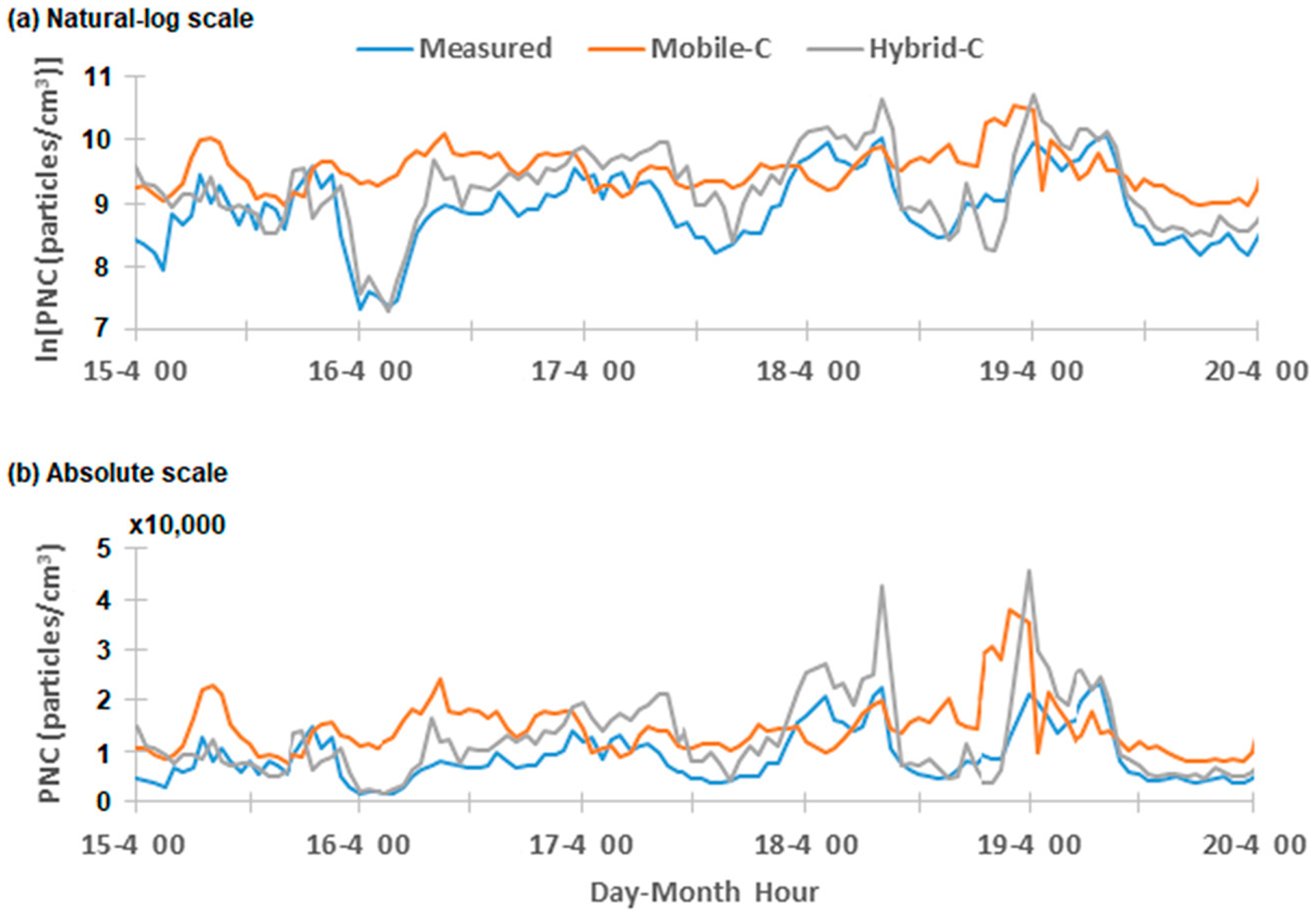
Comparisons of Mobile-C and Hybrid-C predictions versus measured (a) ln(PNC) and (b) PNC at Home 13 in Chelsea from 15 to 20 Apr 2014.

Overprediction, defined as the median hourly percent difference between predicted and measured ln(PNC) at each residential site, ranged between 3% and 6% for all models (corresponding to a 36–76% overprediction on a nonlog-transformed scale). In the Chelsea study area, overprediction was reduced after including the reference monitor, whereas in the Boston study area overprediction increased. Hybrid models had lower overall RMSE than mobile models; the difference was more pronounced in Chelsea (0.61 vs 0.72) whereas in Boston there was no appreciable difference (0.72 vs 0.71) (Tables 3 and S7). The greater overprediction and larger RMSE with Hybrid-B were likely due in part to the location of the stationary reference site since the reference site accounts for a large portion of the estimated PNC at the residential sites. In Boston, the reference site was located at ground level in a heavily-trafficked residential/commercial area (average traffic was 4300 vehicle-hours per km² per weekday),⁶⁰ 75 m from a bus station. In contrast, the Chelsea reference site was located on a third-story roof in a more residential area (700 vehicle-hours per km² per weekday),⁶⁰ which reduced the potential for nearby source impacts.

Hybrid-model predictions of ambient residential PNC at the lower (<5000 particles/cm³) and higher (>50 000 particles/cm³) end of the concentration range were improved over the mobile models. At the lower end of the measured PNC range, mobile models tended to overpredict ambient concentrations while the hybrid-model predictions were generally consistent with the measured concentrations. These trends were more pronounced with the Chelsea model (Figure 4) than with the Boston model (Figure S13). Hybrid-model predictions at the higher end of the PNC range were similarly improved over the mobile models. In the 5000 to 50 000 particles/cm³ range, the differences between the hybrid-model and mobile-model predictions were less apparent, but hybrid models still maintained greater precision as indicated in the Bland-Altman statistics (Table S6). The improvement in hybrid-model predictions was observable at individual residences (Figures S9–S12).

Figure 4.

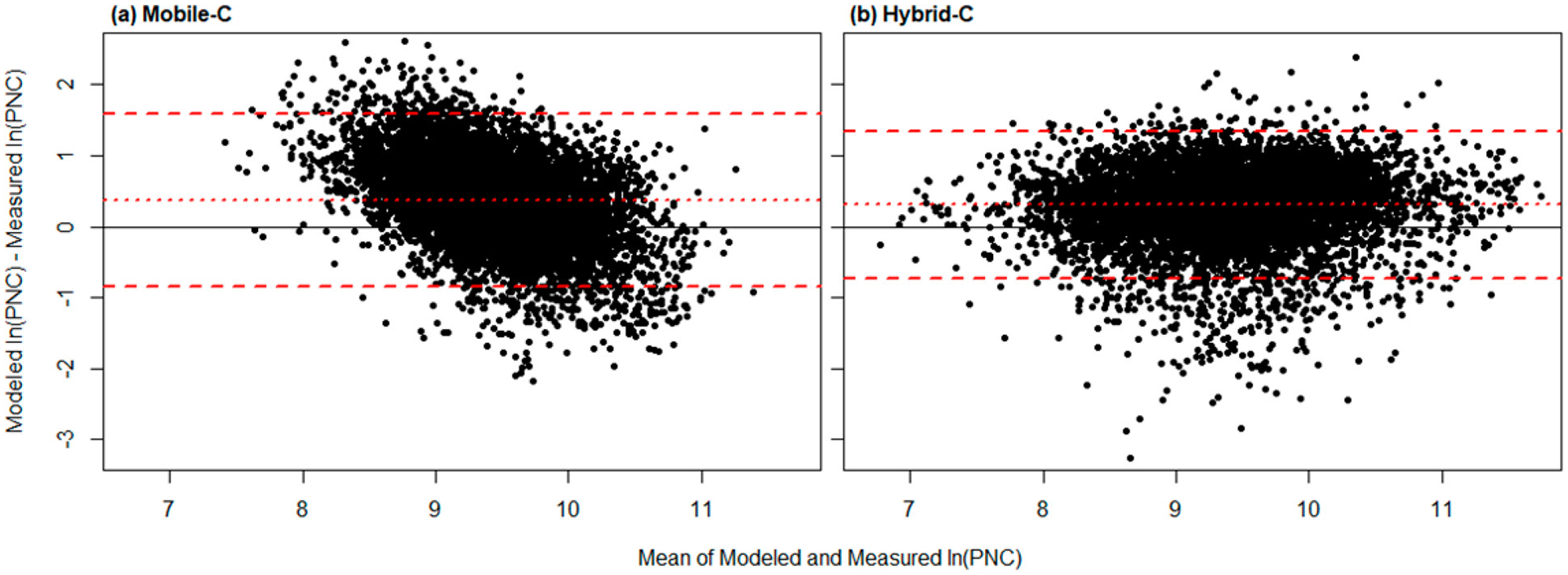
Bland-Altman plot comparing modeled to measured hourly ln(PNC) at all residential sites in the Chelsea study area using (a) Mobile-C and (b) Hybrid-C. The y-axis represents the difference between hourly modeled and measured ln(PNC), and the x-axis represents the mean of hourly modeled and measured ln(PNC). Mean differences (dotted red lines) indicate systematic positive differences of modeled ln(PNC) relative to measured ln(PNC). The solid black (reference) line represents a mean difference of zero. Outer dashed red lines represent ± two standard deviations from the mean difference.

3.4. Limitations.

Our study had three main limitations. First, because mobile monitoring was only conducted between 05:00 and 21:00, overnight measurements were not included in the spatial factor or mobile-monitoring models. The lack of overnight measurements may introduce error into the predictions; however, some variables in the models adjusted for this, such as traffic and solar radiation, which were both higher during the day and associated with higher PNC. Second, to minimize self-sampling of TAPL exhaust, we excluded PNC data when TAPL speeds were <5 km/h for >10 s, which typically occurred at intersections. While this may have introduced error in characterizing the near-intersection environment, we drove through >65% of intersections without having to remove data; therefore, data from intersections were generally well represented in the models. Third, the mobile and hybrid models will have limited transferability to other study areas due to the use of study-area specific variables. Even with generalizing PNC regression models, we have shown transferability to be low;²⁶ however, our model-building methodology is likely transferable to other study areas and other pollutants. Additional studies could be performed to test this.

3.5. Implications of Exposure Model Error.

Exposure assignments for epidemiology can result in systematic error (inaccuracy) and random error (imprecision). Systematic error is the consistent over- or underprediction by models relative to measured PNC, while random error is the random divergence of individual modeled PNC estimates relative to measured PNC. One or both errors may be present in the exposure assignment at any time. We found that systematic error was not substantially reduced by the hybrid models relative to the mobile models as indicated by consistent overprediction at residences with all models. The systematic difference observed by the mobile laboratory over stationary sites (i.e., higher PNC) is likely the main reason for the overpredictions by the hybrid models.³⁴

Since the spatial factor models were based on on-road data, the models will be biased by the overall trends observed on the roads, which in this case were higher concentrations. Systematic overprediction of PNC has also been observed in other studies involving mobile (on-road) measurements. Both Sabaliauskas et al.²⁸ and Kerckhoffs et al.²⁰ observed that predictions from a mobile-monitoring PNC model systematically overpredicted concentrations at stationary sites. In both of these studies, mobile models estimated PNC at stationary sites to be ~1.3 times higher on average (~5000 particles/cm³) than the measured values. Similarly, Kerckhoffs et al.⁶¹ observed that modeled PNC (24-h average) were on average 1.27-fold higher (~4100 particles/cm³) than at homes, which is similar to what we observed with Hybrid-C and -B for hourly concentrations. The overprediction with the Hybrid-B was the highest among the four models we compared. Future studies should consider the potential impact the location of the stationary reference site can have on model predictions when using this methodology. Ultimately, systematic error will have limited influence on direction or strength of association or statistical significance in epidemiological studies, but it will be important to address to facilitate interpretation of model outputs (i.e., understanding the magnitude of biological effects relative to exposure). Model corrections could be used to reduce systematic error if other reference sites were available to compare modeled and measured PNC.

By incorporating stationary-site data into the hybrid models, random error was reduced (i.e., model precision increased) relative to Mobile-B and Mobile-C, as evidenced by a decrease in the standard deviation of the residuals (Table 3). This was apparent in the time series of modeled and measured ln(PNC) where the hybrid models more closely followed residential-site trends in PNC (Figures 3 and S8). Minimizing this type of classical error reduces potential model bias, especially for studies interested in exposures over short time periods (e.g., days) that do not have the benefit of time to dampen out short-term errors as might occur when calculating an annual average. Mobile models may also overpredict nighttime concentrations (since data are usually not collected at night when concentrations are typically lowest), which would affect annual average assignments. Understanding how these model improvements translate to increased ability to detect associations in epidemiological studies warrants further investigation, such as comparing the epidemiological study outcomes from using these two different model formulations. Many different exposure assessments are used for epidemiological studies;⁶² our results highlight the benefits of combining mobile and reference-site monitoring strategies to better inform model development, especially for studies interested in highly temporally and spatially resolved UFP exposure estimates.