A comparison of multiple neighborhood matrix specifications for spatio-temporal model fitting: a case study on COVID-19 data

Abstract

Establishing proper neighbor relations between a set of spatial units under analysis is essential when carrying out a spatial or spatio-temporal analysis. However, it is usual that researchers choose some of the most typical (and simple) neighborhood structures, such as the first-order contiguity matrix, without exploring other options. In this paper, we compare the performance of different neighborhood matrices in the context of modeling the weekly relative risk of COVID-19 over small areas located in or near Valencia, Spain. Specifically, we construct contiguity-based, distance-based, covariate-based (considering mobility flows and sociodemographic characteristics), and hybrid neighborhood matrices. We evaluate the goodness of fit, the overall predictive quality, the ability to detect high-risk spatio-temporal units, the capability to capture the spatio-temporal autocorrelation in the data, and the goodness of smoothing for a set of spatio-temporal models based on each of the neighborhood matrices. The results show that contiguity-based matrices, some of the distance-based matrices, and those based on sociodemographic characteristics perform better than the matrices based on k-nearest neighbors and those involving mobility flows. In addition, we test the linear combination of some of the constructed neighborhood matrices and the reweighting of these matrices after eliminating weak neighbor relations, without any model improvement.

Introduction

In the field of disease mapping, the use of spatial or spatio-temporal models is essential to estimate the distribution in space and time of the risk of suffering from a disease, or of dying from it, among others. These models make it possible to obtain reliable estimates even in the context of small areas or, in general, low case counts for the spatial or spatio-temporal units considered. From the spatial point of view, the key lies in borrowing strength across the surrounding spatial units, which helps to smooth the modeled variable and eases the interpretability of the estimates. Under the Bayesian framework, this is done by defining autoregressive spatial random effects based on the average corresponding to those units that are considered nearby, usually called neighbors (Lawson 2018). Thus, depending on how neighbor relations are defined, or the magnitude of such relations, the modeling may be affected in terms of goodness of fit, smoothing, or even interpretation. Although this fact is generally known, there is not much literature devoted to testing the possible effects of varying the neighborhood matrix. Even less provides guidelines on what might be the optimal way to define it. Indeed, since the seminal work of Cliff and Ord (1981) on neighborhood matrix specifications, few studies have provided such recommendations, and many of them have specifically focused on the case of spatial econometric models. In particular, choosing a rather small number of neighbors (Florax and Rey 1995; Griffith 1996; Getis and Aldstadt 2004), using data-driven methodologies for selecting the weights of the neighborhood matrix (Stakhovych and Bijmolt 2009; Kostov 2010), or simply employing the typically used contiguity matrix (Stakhovych and Bijmolt 2009) are some advised strategies. Besides, other extensive comparative studies have been carried out in the context of disease mapping to assess how the choice of the neighborhood matrix when fitting a spatial model can influence the results. For instance, Earnest et al. (2007) studied the spatial distribution of birth defects in New South Wales, Australia, and found that distance-based neighborhood matrices might outperform contiguity-based matrices in terms of the agreement between observed and predicted relative risks. In contrast, in the context of analyzing the incidence of lip cancer across Scotland, Duncan et al. (2017) noticed that using a first-order contiguity matrix could produce a better model fit than other alternatives such as distance-based or covariate-based neighborhood matrices. Finally, Corpas-Burgos and Martinez-Beneito (2020) have recently proposed a methodology to define adaptive conditional autoregressive distributions in which the entries of the neighborhood matrix are treated as random variables to be modeled. These authors show that models based on these adaptive neighborhood matrices can provide a better fit than those based on contiguity matrices in a multivariate disease mapping context considering mortality data.

In this paper, the objective is to assess the suitability of different neighborhood matrix specifications in the context of modeling the spatio-temporal incidence of COVID-19 at a small-area scale, considering the cases recorded by a public hospital in Valencia, Spain, during the first months of the COVID-19 pandemic.

The paper is structured as follows. In Sect. 2, the data used to conduct the study is described. Section 3 provides an overview of the spatio-temporal model considered for the analysis, the different neighborhood matrices constructed for the comparison, and multiple model assessment tools. Next, Sect. 4 summarizes the main results found. Finally, some concluding remarks are provided in Sect. 5.

Data

Study settings

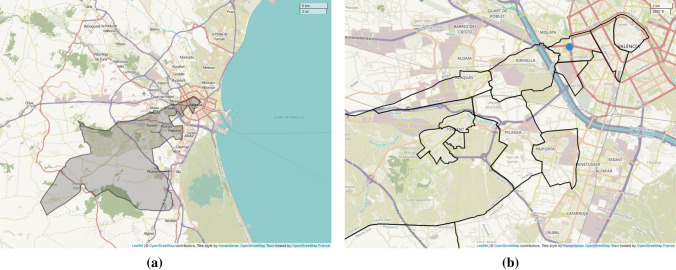
The study locations correspond to 14 municipal districts under the responsibility of the Consorcio Hospital General Universitario (CHGUV) of Valencia, Spain, which is the third most populated city in the country. This public hospital provides services to approximately 350,000 people. In some cases, the mentioned municipal districts constitute an entire municipality, so we will generally refer to the districts as areas in the remainder of this paper. Fig. 1a shows the overall study settings and Fig. 1b a closer look at the districts near the central area of Valencia. Both maps have been obtained from OpenStreetMap (OpenStreetMap contributors 2020).

Fig. 1.

Map of the study area, which corresponds to the Consorcio Hospital General Universitario (CHGUV) of Valencia, Spain, reference area a. In b, the closest districts to the center of Valencia among those considered for the study are displayed. The blue point indicates the location of the hospital

COVID-19 data

The home addresses of COVID-19 patients treated in the hospital from February 19, 2020, to August 31, 2020 (spanning 29 weeks) were geocoded in a double-stage process, including an automatic and manual assignation of the coordinates. Specifically, starting from a set of 2778 patients, 2725 were finally geocoded at the municipal district level, resulting in a 98% geocoding hit rate, which exceeds the minimum acceptable geocoding hit rate suggested by recent research (Andresen et al. 2020; Briz-Redón et al. 2020).

Human mobility data

Human mobility data is helpful for gaining insights into the spread of COVID-19 across space (Kraemer et al. 2020). The Spanish Statistical Office (Instituto Nacional de Estadística) has estimated the daily number of people that moved from their home area to a different area from 10 am to 4 pm within the first months of the COVID-19 pandemic. The locations of the mobile phones linked to the three main mobile companies in Spain (which provide service to more than 80% of mobile phone users in the country) were tracked to derive these estimates. An exploratory temporal analysis of the data at the area level allowed us to confirm that the magnitude of human flows on weekdays was higher than on weekend days during this period, while the variation between the different weekdays was relatively small. For this reason, we decided to average the data corresponding to six Wednesdays between April and June 2020 (April 1, April 15, April 29, May 13, May 27, and June 10) to estimate the flow matrix between the analyzed areas (we also tested other weekdays but hardly noticed any difference).

Sociodemographic data

In order to account for the sociodemographic characteristics of the areas under study, the following three widely used covariates have been considered given their potential role on COVID-19 propagation (Carella et al. 2020; Dowd et al. 2020; Kodera et al. 2020; Whittle and Diaz-Artiles 2020; Coşkun et al. 2021): population density (inhab/${\text{km}}^2$), average household income (euros), and the proportion of the population aged 65 years and over (percentage). These three covariates have also been obtained from the Spanish Statistical Office.

Methodology

Model definition

The number of new daily COVID-19 cases observed in area i ($i=1,\dots ,14$) on week t ($t=1,\dots ,29$), denoted by $O_{\mathit{it}}$, is assumed to follow a Poisson distribution with mean ${\mu }_{\mathit{it}}=E_i{r}_{\mathit{it}}$, where $E_i$ denotes the number of cases per week expected in area i, and $r_{\mathit{it}}$ the relative risk for area i and week t. If $R={\sum }_i{\sum }_t{O}_{\mathit{it}}/{\sum }_{i}po{p}_i$ represents the average COVID-19 incidence rate for the set of areas of interest during the period under study (where $po{p}_i$ is the population of area i), the number of expected cases is set to $E_i=po{p}_{i}R/29$. Thus, ${\mu }_{\mathit{it}}$ is specified according to the following spatio-temporal structure

$$\begin{array}{c}\hfill log({\mu }_{\mathit{it}})=\alpha +log(E_i)+u_i+v_i+{\gamma }_t+{\varphi }_t+{\delta }_{\mathit{it}}\end{array}$$

where $\alpha$ denotes the intercept of the model, $u_i$ and $v_i$ represent, respectively, the structured and unstructured spatial random effect of the model, ${\gamma }_t$ and ${\varphi }_t$ are, respectively, the structured and unstructured temporal random effect, and ${\delta }_{\mathit{it}}$ is the random spatio-temporal effect. Regarding the spatial random effects, the Besag–York–Mollié (BYM) model has been considered (Besag et al. 1991), which establishes that the conditional distribution of the spatially-structured effect on area i, $u_i$, is

$$\begin{array}{c}\hfill u_i|u_{j\ne i}\sim Normal(\sum _{j\ne i=1}^n{w}_{\mathit{ij}}{u}_j,\frac{{\sigma }_u^2}{N_i})\end{array}$$

where $N_i$ is the number of neighbors for area i, $w_{\mathit{ij}}$ is the (i,j) element of the row-normalized neighborhood matrix, and ${\sigma }_u^2$ represents the variance of this random effect. The spatially-unstructured effect over the areas, denoted by $v_i$, follows a Gaussian distribution, $v_i\sim Normal(0,{\sigma }_v^2)$, where ${\sigma }_v^2$ is the variance of the effect. Regarding the two temporal effects, on the one hand, the temporally-structured effect, ${\gamma }_t$, is specified through a second-order random walk ${\gamma }_t|{\gamma }_{t-1},{\gamma }_{t-2}\sim Normal(2{\gamma }_{t-1}+{\gamma }_{t-2},{\sigma }_{\gamma }^2)$, where ${\sigma }_{\gamma }^2$ is the variance component. On the other hand, an independent and identically distributed Gaussian prior is chosen for ${\varphi }_t\sim Normal(0,{\sigma }_{\varphi }^2)$. Finally, a Gaussian structure is also assumed for the spatio-temporal interaction term, ${\delta }_{\mathit{it}}$, with variance ${\sigma }_{\delta }^2$.

The spatio-temporal model described above has been fitted by using the Integrated Nested Laplace Approximation (INLA), proposed by Rue et al. (2009). The implementation of the model has required to add specific constraints on the random effects to avoid identifiability issues (Goicoa et al. 2018).

Neighborhood matrix specifications

In the remaining of the section, $w_{\mathit{ij}}$ represents the (i, j) entry of any of the defined neighborhood matrices (in general, before applying row normalization), and $d_{\mathit{ij}}$ denotes the physical distance (in decimal degrees) between the centroids of the i and j areas. In all cases, the elements of the diagonal, $w_{\mathit{ii}}$, are set to 0.

Contiguity-based neighbors

Neighborhood matrices based on contiguity relations are possibly the most widely used in spatial statistics and related fields. Under the contiguity criterion, two areas are first-order neighbors if they share a common edge or vertex (“queen” criterion). In general, two areas are kth-order neighbors if they have a ($k-1$)th-order neighbor in common. Hence, a kth-order contiguity matrix is defined by $w_{\mathit{ij}}=1$ if areas i and j are kth-order neighbors, and 0 otherwise. In the present comparative analysis, $C_k$, for $k\in \{1,2,3\}$, denotes the corresponding kth-order contiguity matrix.

Distance-based neighbors

Several distance-based neighborhood matrices have been considered, including k-nearest neighborhood matrices for $k\in \{1,3,5,7\}$, according to which $w_{\mathit{ij}}=1$ if the centroid of area j is among the k nearest area centroids from the centroid of area i, and 0 otherwise. These four matrices are denoted by $D_1$, $D_2$, $D_3$, and $D_4$, respectively. As there are only 14 spatial units within our study window, we decided to limit the analysis to $k\le 7$. We have included only the odd values of k in this interval for slightly reducing the set of matrices under comparison since the results for intermediate (even) values of k turn out to be very similar.

Besides, the inverse distance neighborhood matrix ($D_5$) given by $w_{\mathit{ij}}=1/d_{\mathit{ij}}$, and the “Gravity” ($D_6$) and “Entropy” ($D_7$) neighborhood matrices (Earnest et al. 2007) are also considered. The “Gravity” matrix is defined by $w_{\mathit{ij}}=po{p}_{i}po{p}_j/d_{\mathit{ij}}$, while the “Entropy” matrix is given by $w_{\mathit{ij}}=exp(-50d_{\mathit{ij}})$. The “Gravity” neighborhood matrix allows assigning greater weights on highly populated areas (in other words, it reduces the influence of sparsely populated areas), whereas the “Entropy” matrix drastically reduces the weights corresponding to distant areas. In this regard, while Earnest et al. (2007) chose $w_{\mathit{ij}}=exp(-10d_{\mathit{ij}})$ for defining the “Entropy” neighborhood matrix, we found more suitable in our case to use $w_{\mathit{ij}}=exp(-50d_{\mathit{ij}})$. Indeed, if $w_{\mathit{ij}}=exp(-a{d}_{\mathit{ij}})$, with $a>0$, increasing the value of a favors that the weights corresponding to distant areas get closer to 0 more quickly. For the set of spatial units analyzed in this paper, choosing $a=10$, as in Earnest et al. (2007), leads to an uninformative neighborhood matrix in which all the weights are too similar. In contrast, increasing the value of a to 50 allowed us to obtain the desired decaying effect on the weights for the most distant areas (we increased a from 10 to 50 in intervals of 10, until we considered that the matrix was informative enough).

Covariate-based neighbors

The estimate of the number of people moving from area i to area j, denoted as $flo{w}_{\mathit{ij}}$, has been used to construct the neighborhood matrix F by defining $w_{\mathit{ij}}=flo{w}_{\mathit{ji}}$. Hence, the influence of the observations corresponding to area j on the observations of area i is set to be proportional to the average number of people that area i receives from area j during the morning of a working day.

Besides, the three considered sociodemographic covariates have been used to compute a “sociodemographic distance” between each pair of areas under analysis. Specifically, this distance is defined as $d_{\mathit{ij}}^S={\Vert {\mathit{x}}_i-{\mathit{x}}_j\Vert }_2$, where ${\mathit{x}}_i$ denotes a three-dimensional vector including the standardized values of the chosen sociodemographic covariates for area i, and ${\Vert ·\Vert }_2$ the Euclidean distance. Therefore, the sociodemography-based neighborhood matrix, S, is characterized by $w_{\mathit{ij}}=1/d_{\mathit{ij}}^S$.

Hybrid neighbors

Covariate and spatial information have been combined following previous research (Earnest et al. 2007; Duncan et al. 2017), leading to what we refer to as hybrid neighbors. Specifically, a neighborhood matrix accounting for mobility flows and physical distances ($H_1$) is defined by $w_{\mathit{ij}}=flo{w}_{\mathit{ji}}/d_{\mathit{ij}}$, and a matrix considering physical and sociodemographic distances simultaneously ($H_2$) is determined by setting $w_{\mathit{ij}}=1/(d_{\mathit{ij}}{d}_{\mathit{ij}}^S)$. Finally, a neighborhood matrix including information on mobility flows, sociodemographic characteristics, and physical distances ($H_3$) has been constructed by choosing $w_{\mathit{ij}}=flo{w}_{\mathit{ji}}/(d_{\mathit{ij}}{d}_{\mathit{ij}}^S)$. The definition of hybrid neighborhood structures enables us to establish that the dependency relationship between two areas will only be strong if both are close in space and similar according to some covariate or set of covariates.

Combined neighborhood matrices and negligible neighbors

In addition to constructing the previously defined matrices, the possibility of obtaining linear combinations of the matrices has also been explored, inspired by the recent work of Ejigu and Wencheko (2020) to account for the spatio-environmental dependence between regions, along with the reweighting of these matrices after the elimination of weak neighbor relations (negligible neighbors), according to some prespecified threshold. Specifically, if $w_{\mathit{ij}}^{M_1}$ and $w_{\mathit{ij}}^{M_2}$ denote the row-normalized entries of two of the above-defined neighborhood matrices, a combined matrix can be obtained by defining $w_{\mathit{ij}}^C=s{w}_{\mathit{ij}}^{M_1}+(1-s)w_{\mathit{ij}}^{M_2}$. For simplicity, we can denote this combined matrix as $M_1+M_2$. Besides, those entries such as $w_{\mathit{ij}}^C<u$, for a given (small) $u\in [0,1]$, can be set to 0 to remove the influence of negligible neighbors (row normalization is then applied again). The usual way to proceed would be to choose different values of u and observe their effect on the quality of the model. Increasing the value of u will lead to a larger number of neighbors considered as negligible and, therefore, to more sparse neighborhood matrices.

Edge effects

The existence of edge effects (Griffith 1983; Dreassi and Biggeri 1998) at the areas located in the boundary of the study window is an issue that is often overlooked in disease mapping analyses. Edge effects arise as a consequence of data incompleteness (missing data for some neighboring areas), potentially affecting model estimates (Rodeiro and Lawson 2005). The study window considered in this paper might also suffer from edge effects, as the data from areas corresponding to other hospitals was not available for the analysis.

Therefore, we followed Lawson et al. (1999) to take edge effects into account. If $\mathcal{B}$ denotes the set of areas that constitute the boundary of the study window, the following edge effect correction factor, $c_j$, was defined for a given area j

$$\begin{array}{c}\hfill c_j=\left\{\begin{array}{cc}1,\hfill & j\notin \mathcal{B}\hfill \\ 1-(\frac{{\ell }_j^{\mathcal{B}}}{{\ell }_j}{)}^k,\hfill & j\in \mathcal{B}\hfill \end{array}\right)\end{array}$$ 1

where ${\ell }_j$ denotes the length of the perimeter of area j and ${\ell }_j^{\mathcal{B}}$ the length of the perimeter of the intersection between area j and the external boundary of the study window. Hence, the edge-corrected entries of a neighborhood matrix defined as ${(w_{\mathit{ij}})}_{n\times n}$ are $w_{\mathit{ij}}^{\ast }=c_j{w}_{\mathit{ij}}$ (although row normalization is applied again as a final step). In this way, the weight of a boundary area is reduced according to the length of perimeter lying outside the interior of the study area. The parameter $k\ge 1$ allows controlling the level of reduction to be applied, as the reduction decays as the value of k is increased. Figure 2 shows the values of $c_j$ that are obtained for our study window, considering $k=1$ (Fig. 2a) and $k=2$ (Fig. 2b). In this case, only the three small areas located in the central part of the study window are not contained in $\mathcal{B}$ (for these areas it holds that $c_j=1$). It can also be seen that using $k=1$ strongly reduces the weight of some of the areas, so it has been preferred to use $k=2$ for all the neighborhood matrices under analysis.

Fig. 2.

Edge effect correction factors, computed according to (1), considering $k=1$ a and $k=2$ b, for the areas under analysis. The external boundary of the study window is represented by a thicker line

Summary

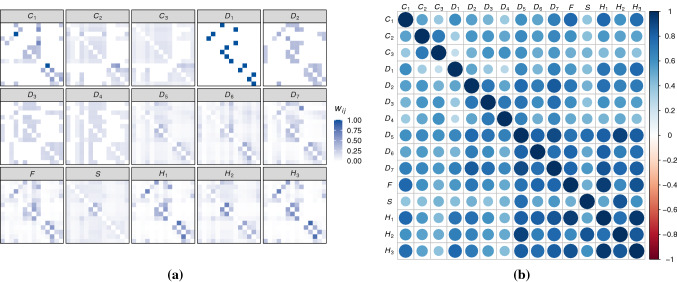
To summarize the information provided in this section, Fig.  3 displays the structure of the fifteen types of neighborhood matrices described above. Despite the particularities of each matrix specification, some of them are quite similar, as suggested by Fig. 3a, and especially Fig. 3b, which shows the correlation coefficients across matrices, computed as the Pearson’s correlation of their vectorized forms (if $A={(a_{\mathit{ij}})}_{m\times n}$, its vectorization is ${(a_{11},\dots ,a_{m1},\dots ,a_{1n},\dots ,a_{\mathit{mn}})}^{\mathsf{T}}$). Moreover, Table 1 shows some basic properties of the neighborhood matrices under comparison, which allow distinguishing those sparse matrices containing only a few neighbor relations (such as the contiguity-based or the k-nearest neighborhood matrices) from those dense matrices where every area under study has some influence on the rest.

Fig. 3.

Graphical description of the main fifteen neighborhood matrices (of size $14\times 14$) considered for the comparative analysis a. The entries of the matrices ($w_{\mathit{ij}}$) have been row-normalized to allow for comparison ($w_{\mathit{ij}}$ always lies between 0 and 1). The correlation between each pair of matrices, computed as the correlation between the vectorizations of the matrices, are shown in b

Table 1.

Average number of neighbors, percentage of non-zero entries, and average value of the non-zero entries (${\overline{w}}_{\mathit{ij}}$) for the main fifteen neighborhood matrices considered for the analysis. The percentage of non-zeros is computed with respect to the number of off-diagonal entries, as $w_{\mathit{ii}}=0$ by definition

	$C_1$	$C_2$	$C_3$	$D_1$	$D_2$	$D_3$	$D_4$	$D_5$	$D_6$	$D_7$	F	S	$H_1$	$H_2$	$H_3$
No. of neighbors	2.86	6.71	9.29	1.00	3.00	5.00	7.00	13.00	13.00	13.00	11.50	13.00	11.50	13.00	11.50
Non-zeros (%)	21.98	51.65	71.43	7.69	23.08	38.46	53.85	100.00	100.00	100.00	88.46	100.00	88.46	100.00	88.46
${\overline{w}}_{\mathit{ij}}$ (non-zeros)	0.35	0.15	0.11	1.00	0.33	0.20	0.14	0.08	0.08	0.08	0.09	0.08	0.09	0.08	0.09

In the remainder of the paper, the spatio-temporal models considered are referred to following the same notation used for the matrices (for instance, Model $C_1$ will correspond to the spatio-temporal model based on matrix $C_1$).

Model comparison

Model quality has been assessed through multiple statistical tools, allowing us to perform a comprehensive comparison across models. First, the Deviance Information Criterion (DIC) introduced by Spiegelhalter et al. (2002) and the Watanabe–Akaike Information Criterion (WAIC) proposed by Watanabe and Opper (2010) have been used for measuring the goodness-of-fit of the models.

The overall predictive performance of the models has been evaluated with two Bayesian diagnostics: the conditional predictive ordinate (CPO) (Pettit 1990) and the probability integral transform (PIT) (Dawid 1984). On the one hand, the CPO corresponding to a specific spatio-temporal unit is defined as ${\mathrm{CPO}}_{\mathit{it}}=P(y_{\mathit{it}}^{\mathit{obs}}|{\mathit{y}}_{-it})$, where $y_{\mathit{it}}^{\mathit{obs}}$ is the value observed on spatio-temporal unit (i,t), and ${\mathit{y}}_{-it}$ is the vector containing all observations except the one corresponding to unit (i,t). A small value of ${\mathrm{CPO}}_{\mathit{it}}$ suggests that the observation on (i, t) is surprising (an outlier) based on the rest of observations (Pettit 1990). Besides, the Log Pseudo-Marginal Likelihood (LPML) computed as ${\sum }_i{\sum }_{t}log({\mathrm{CPO}}_{\mathit{it}})$ can be used for model choice (Held et al. 2010). On the other hand, the PIT is another leave-one-out cross-validation score defined as ${\mathrm{PIT}}_{\mathit{it}}=P(Y_{\mathit{it}}<y_{\mathit{it}}^{\mathit{obs}}|{\mathit{y}}_{-it})$, where $Y_{\mathit{it}}$ represents a random variable generated from the posterior distribution of the model being evaluated. If the PIT scores are uniformly distributed, the model is well calibrated (Czado et al. 2009), whereas deviations from uniformity indicate that the predictive distribution of the model is either underdispersed (U-shaped distribution), overdispersed (inverse-U shape distribution), or biased (skewed distribution).

Furthermore, the ability of the models to detect high-risk spatio-temporal units has also been studied. Specifically, high-risk units have been defined as those satisfying $P(r_{\mathit{it}}>1)>c$, choosing a cutoff probability $c=0.7$, as suggested by Richardson et al. (2004). According to this decision rule, several measures of the performance of the classification test are computed for each of the models, including the sensitivity, the specificity, and the Matthews correlation coefficient (MCC) introduced in Matthews (1975), which is more informative to analyze a classification problem as claimed by recent research (Chicco and Jurman 2020).

Finally, the degree of spatio-temporal autocorrelation remaining in model residuals has been assessed by using an extension of Moran’s I (Moran 1950a, b) for spatio-temporal data (Lee and Li 2017), hereinafter denoted by $I_{\mathit{st}}$. The fact that $I_{\mathit{st}}$ is significantly greater than 0 indicates that model residuals are spatio-temporally correlated, which suggests that the model is misspecified. To compute $I_{\mathit{st}}$, it has been considered that two spatio-temporal units are neighbors if they are neighbors in space (considering the corresponding neighborhood matrix) and only one week apart.

Software

The R programming language (Core Team 2020) has been used to carry out the present study. In particular, the R packages caRtociudad (Gil Bellosta and Frías 2018), corrplot (Wei and Simko 2017), ggplot2 (Wickham 2016), INLA (Rue et al. 2009; Lindgren and Rue 2015), rgdal (Bivand et al. 2019), rgeos (Bivand and Rundel 2020), and spdep (Bivand et al. 2008) have been used.

Results

Model assessment and comparison

This section shows the performance of the different models tested, taking into account the different metrics described in Sect. 3.3. Thus, Table 2 shows several indicators related to the goodness of fit, the overall predictive quality, the ability to detect high-risk units, and the capability to capture the spatio-temporal autocorrelation inherent to the type of data being modeled. In summary, the set of the fifteen defined matrices can be split into two groups based on their performance, as indicated in Table 2. The contiguity-based matrices, the inverse distance matrix, the “Gravity” and “Entropy” matrices, and the matrices based on sociodemographic characteristics (both in their pure and hybrid forms), performed similarly and noticeably better than the rest of the neighborhood matrices considered in the analysis, namely the k-nearest neighborhood matrices and the matrices based on population flows. The following paragraphs detail some of the discrepancies found in terms of performance for the set of matrices studied. As both sets of matrices present practically identical results within each group, we usually highlight the differences observed between specific members of each of the groups.

Table 2.

Summary of the main metrics considered for the assessment and comparison of the spatio-temporal models fitted, each one based on a different neighborhood matrix (a brief description of each of the matrices is provided). Two groups of matrices are identified according to the distinct performance of the models

Group	Matrix	DIC	WAIC	LPML	Sensitivity	Specificity	MCC	$I_{\mathit{st}}$ (p-value)
1	$C_1$ (first-order contiguity)	1666.625	1632.306	0.209	0.729	0.997	0.808	0.013 (0.357)
1	$C_2$ (second-order contiguity)	1666.710	1633.549	0.209	0.729	0.997	0.808	0.012 (0.359)
1	$C_3$ (third-order contiguity)	1666.811	1634.228	0.209	0.729	0.997	0.808	0.012 (0.359)
1	$D_5$ (inverse distance)	1666.250	1631.888	0.209	0.729	0.997	0.808	0.015 (0.342)
1	$D_6$ (“Gravity”)	1666.250	1631.888	0.209	0.729	0.997	0.808	0.015 (0.342)
1	$D_7$ (“Entropy”)	1666.250	1631.888	0.209	0.729	0.997	0.808	0.015 (0.342)
1	S (sociodemography)	1666.250	1631.888	0.209	0.729	0.997	0.808	0.015 (0.342)
1	$H_2$ (hybrid between $D_5$ and S)	1666.250	1631.888	0.209	0.729	0.997	0.808	0.015 (0.342)
2	$D_1$ (1-nearest neighbors)	2102.532	2233.515	0.101	0.757	0.983	0.798	0.192 (0.000)
2	$D_2$ (3-nearest neighbors)	3770.938	3851.917	0.073	0.738	0.930	0.683	0.331 (0.000)
2	$D_3$ (5-nearest neighbors)	3739.163	3875.593	0.073	0.729	0.940	0.693	0.334 (0.000)
2	$D_4$ (7-nearest neighbors)	3673.010	3861.366	0.072	0.738	0.953	0.725	0.340 (0.000)
2	F (mobility flows)	3766.721	3866.660	0.072	0.738	0.933	0.689	0.332 (0.000)
2	$H_1$ (hybrid between $D_5$ and F)	3766.721	3866.660	0.072	0.738	0.933	0.689	0.332 (0.000)
2	$H_3$ (hybrid between $D_5$, F and S)	3766.721	3866.660	0.072	0.738	0.933	0.689	0.332 (0.000)

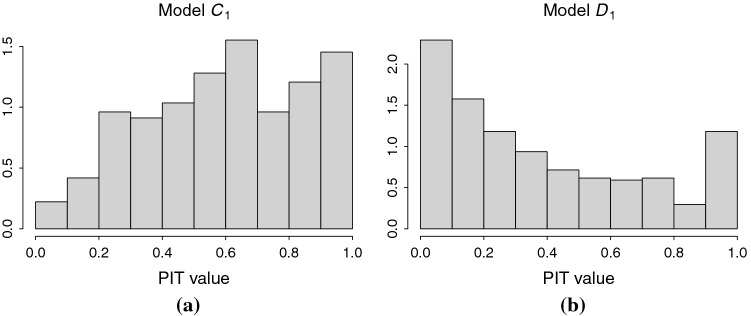
First, Table 2 confirms that both the goodness of fit (according to both the DIC and the WAIC) and the overall predictive quality (indicated by the LPML) are widely superior in the first group of matrices mentioned above. However, a visual inspection of the distribution of the PIT scores reveals that all the models considered still have room for improvement, as shown in Fig. 4 for models $C_1$ (the predictive distribution is moderately biased) and $D_1$ (the predictive distribution is heavily biased and underdispersed). Nevertheless, the distribution of the PIT scores is closer to uniform among the matrices belonging to the first group, which reflects their superior performance.

Fig. 4.

Histograms of the PIT scores obtained for the models based on neighborhood matrices $C_1$ a and $D_1$ b

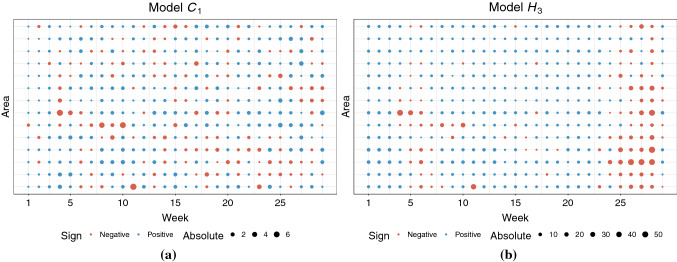
Furthermore, the neighborhood matrices of group 1 are more suitable to detect high-risk spatio-temporal units with a higher level of accuracy, as indicated by the sensitivity, specificity, and MCC values shown in Table 2. The inferior performance of the matrices in group 2 in this regard could also be related to the inability of these models to adequately capture the spatial-temporal autocorrelation inherent in the data under study, as indicated by the values of $I_{\mathit{st}}$ (Table 2). Thus, as can be seen in Fig. 5, while the residuals of Model $C_1$ show a random spatio-temporal structure, the residuals generated by Model $H_3$ are considerably greater in magnitude during the last weeks studied, and their sign is markedly dependent on the temporal unit considered.

Fig. 5.

Graphical summary of the residuals yielded by the fitted spatio-temporal models based on neighborhood matrices $C_1$ a and $H_3$ b. The size of each point is proportional to the absolute value of the residual, whereas the color of the point indicates the sign of the residual. Note that two different scales have been used for representing the absolute values of the residuals given the large differences observed between the two models under comparison

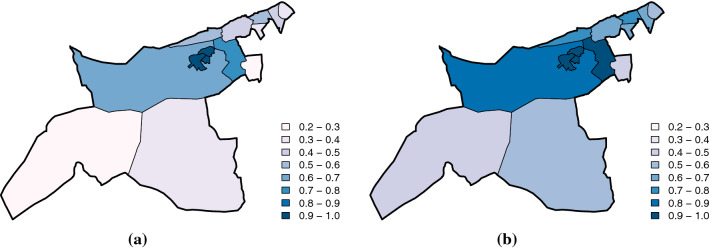
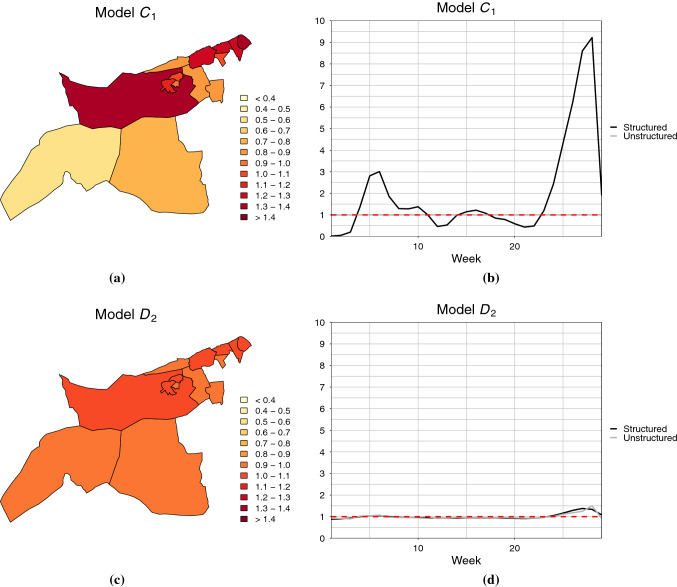
Regarding the goodness of smoothing achieved by the models, although none of the specific metrics available (Duncan and Mengersen 2020) has been employed, the visualization of the estimates of relative risks by spatial (area) or temporal (week) unit allows verifying that the matrices from group 1 also perform better in this respect. In particular, Fig. 6 shows the estimates of these relative risks corresponding to matrices $C_1$ and $D_2$. While the model based on $C_1$ shows how the relative risk varies considerably across the different areas studied (Fig. 6a), distinguishing areas of high risk from others of low risk, the estimates of the relative risks in the case of $D_2$ are oversmoothed, as they all fluctuate around 1 (Fig. 6c). Similarly, the weekly relative risk estimates provided by Model $D_2$ are uninformative (Fig. 6d), suffering from the same problem, whereas Model $C_1$ is indeed able to capture the evolution of the overall relative risk over the months considered, which peaked at the beginning of April (around week number 6) and by the end of August (Fig. 6b).

Fig. 6.

Area-specific relative risks, computed as $exp(u_i+v_i)$, and week-specific relative risks, computed as either $exp({\gamma }_t)$ (structured component) or $exp({\varphi }_t)$ (unstructured component), obtained with the fitted spatio-temporal models based on neighborhood matrices $C_1$ and $D_2$. In (b) and (d), the red dashed line represents a relative risk of 1

Some tests on matrix combinations and negligible neighbors

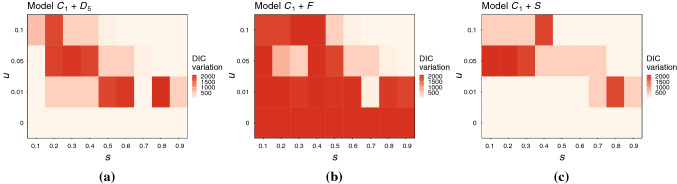
We have conducted several experiments following the procedure described in Sect. 3.2.5. In particular, we have combined matrices $C_1$ with $D_5$, $C_1$ with F, and $C_1$ with S, varying s in the range [0.1, 0.9]. We have chosen these specific combinations to account for two different forms of geographic information (contiguity-based and distance-based) and to combine geographic information with both sociodemographic and mobility information. We have only considered the combination of $C_1$ with F and S (and not $D_5$ with F and S) to limit the number of comparisons and reduce the computational burden. To eliminate the effect of negligible neighbor relations, we have set to 0 those elements of the combined matrix lower than u, considering $u\in \{0,0.01,0.05,0.10\}$, where $u=0$ corresponds to not performing any elimination.

However, as shown in Fig. 7, no improvements have been observed in terms of DIC variations with respect to the optimal DIC value yielded by the main fifteen matrices considered in the analysis (${\mathrm{DIC}}_{\mathit{opt}}=1666.25$, as shown in Table 2). In all cases, the combined matrix gives rise to a model with a worse (higher) DIC value, although it depends strongly on the choice of s and u. More specifically, the effect of s and u is similar in the case of Models $C_1+D_5$ and $C_1+S$, since increasing u (which implies considering more neighbors as negligible), or reducing s (which means giving more weight to $C_1$ in this case), usually produces combined matrices that result in models of higher DIC (although the pattern is not entirely consistent). In combining matrices $C_1$ and F, almost any combination of s and u is very detrimental in terms of the DIC. Unlike what happened with the two combinations mentioned above, in the case of $C_1$ and F, it is convenient to take a value of s close to 1 and favor eliminating negligible neighbor relations. The poor performance of the F matrix has probably led to these results.

Fig. 7.

DIC variations with respect to the optimal DIC value (${\mathrm{DIC}}_{\mathit{opt}}=1666.25$), yielded by different combinations of the neighborhood matrices $C_1$ and $D_5$ a, $C_1$ and F b, and $C_1$ and S c, considering different values of the weight s (from 0.1 to 0.9, in intervals of 0.1), and several thresholds of u (0, 0.01, 0.05, and 0.10) for determining the negligible neighbors

In short, combining the selected matrices and eliminating some weak neighbor relations have not improved model fitting, at least for the experiments performed (testing all possible combinations of matrices is computationally very expensive). Despite this, the results achieved indicate that small variations in the neighborhood matrix can be considerably detrimental to the fit, as reflected in Fig. 7. The low number of areas under analysis may be the cause of this fact, but it is difficult to determine to what degree each neighbor relation improves/worsens the fit.

Model selection and application

As highlighted in Sect. 1, the appropriate use of spatio-temporal models enables the estimation and prediction of the distribution of diseases such as the COVID-19 and, therefore, the establishment of epidemiological surveillance methods for the benefit of public health. In light of the comparative analysis carried out, Model $C_1$, which could be regarded as the best model given the metrics of performance considered and because of the simplicity of its associated neighborhood matrix (although any of the models of group 1 leads to similar conclusions), allows us to reach the following conclusions.

First, Model $C_1$ indicates that the areas closer to the center of Valencia experienced higher relative risks during the study period, even though other more distant areas also presented relative risks above 1 (Fig. 6a). Nevertheless, although Figure 6a might suggest that the spatial distribution of the relative risks is moderately to highly structured, the computation of the amount of variance explained by the spatially-structured effect (Blangiardo and Cameletti 2015) has revealed that the spatially-unstructured component, $v_i$, captures around 95% of the spatial variability of the data. Therefore, most of the spatial variability cannot be explained through neighbor relations in this particular case study.

With regard to the estimated temporal effects, it is worth noting that the (structured) week-specific relative risk reached a maximum value above 9 at the end of August (Fig. 6b). Moreover, it can be observed that the temporal variability of the data is markedly structured, in contrast to the spatial variability. Indeed, the estimation of the spatio-temporal relative risks for the complete set of areas under study suggests that all of them followed a similar pattern during the study period, as shown in Fig. 8.

Fig. 8.

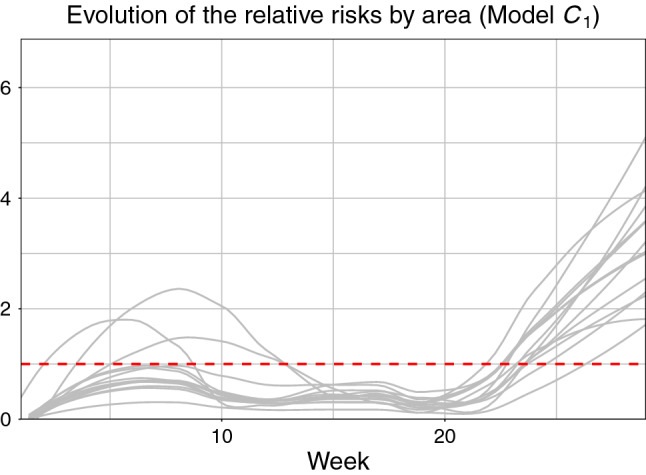
Evolution of the relative risks ($r_{\mathit{it}}$), according to the estimates provided by Model $C_1$ in the fourteen areas under analysis. The relative risks have been smoothed through a locally estimated scatterplot smoothing (LOESS) regression (Fox and Weisberg 2018) for ease of visualisation. The red dashed line represents a relative risk of 1

Besides the capability of Model $C_1$ to capture spatial, temporal, and spatio-temporal effects, this model also allows performing short-term predictions. The biased distribution of the PIT scores yielded by Model $C_1$ (Fig. 4a) suggests that the model shows a tendency to underestimate the number of weekly COVID-19 cases for some of the areas. This could be attributed to the common presence of extreme values in COVID-19 datasets, especially in the context of analyzing small areas. Using a generalization of the Poisson distribution could be helpful in this regard (Jalilian and Mateu 2021).

Conclusions

Using the right neighborhood matrix when conducting a spatial or spatio-temporal analysis is an essential but rarely addressed issue. According to our results, some classical and non-sophisticated choices such as the first-order contiguity matrix or the inverse distance matrix are still the most suitable. However, more research would be needed to better assess the performance of some of the neighborhood matrices considered (especially those that include covariate information) to reach more definite conclusions. The results also suggest that even though two neighborhood matrices may be highly similar in structure, slight differences in their definition can lead to significantly different model performances. For example, although the flow-based matrix turned out to be quite similar to the first-order contiguity matrix, the attenuation of certain neighbor relations between some contiguous areas causes a noticeable detriment in terms of performance. Furthermore, it is worth noting that, even though some previous studies suggest that a smaller average number of neighbors per spatial unit is beneficial for model fitting, some neighborhood structures only based on a few neighbors (such as k-nearest neighborhood matrices) performed worse than other alternatives accounting for more neighbor relations.

Therefore, testing multiple sensible specifications of the neighborhood matrix is highly advisable. Otherwise, an unsuitable choice of this matrix can lead to poor models in terms of explanatory and forecasting capability. Given the inconvenience of having to fit numerous models, a good strategy might be to test a fairly general neighborhood matrix of each of the main types available (contiguity-based, distance-based, etc.), select the one that gives the overall best results, and then assess the performance of multiple variations of such typology of matrix selected. In this regard, neither the combination of neighborhood matrices nor the elimination of weaker neighbor relations have improved the performance of the models for the matrices tested. Anyhow, we believe that the employment of both strategies in an attempt to obtain a more informative neighborhood matrix, which more adequately represents the connections between the areas under analysis, deserves consideration. The low number of areas available in our study window, together with the dominance of the unstructured component of the estimated spatial variability, may have made it more challenging to see such improvements, so further case studies or even simulation studies would be necessary to better assess the potential benefits of this methodology. Finally, it is also necessary to point out that considering edge effects is highly convenient if there is missing information for some surrounding areas. The method proposed by Lawson et al. (1999), which we chose, is easily implementable, but there are other alternatives available. In our case study, we have verified that not accounting for edge effects would not have caused any change in model fitting. Nonetheless, more applied and theoretical research would be required in this direction to better assess the possible impact of edge effects on a spatial/spatio-temporal analysis.

Compliance with ethical standards

Funding

This study has received funding from the Innovation, University, Science and Digital Society Council through the Valencia Innovation Agency (AVI).

Conflict of interest

The authors declare no conflict of interest in this study.

Availability of data and material

The authors are not allowed to share the COVID-19 data used to conduct this study.

Code availability

The R code created to carry out this study is available upon reasonable request from the authors.