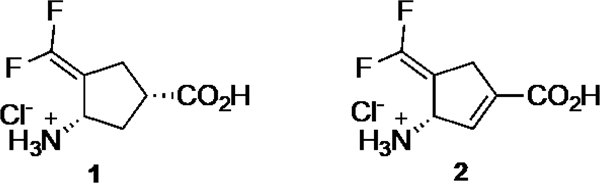Theoretical and Mechanistic Validation of Global Kinetic Parameters of the Inactivation of GABA Aminotransferase by OV329 and CPP-115

Abstract

((S)-3-Amino-(difluoromethylenyl)cyclopent-1-ene-1-carboxylic acid (OV329) is a recently discovered inactivator of γ-aminobutyric acid aminotransferase (GABA-AT), which has 10 times better inactivation efficiency than its predecessor, CPP-115, despite the only structural difference being an endocyclic double bond in OV329. Both compounds are mechanism-based enzyme inactivators (MBEI), which inactivate GABA-AT by a similar mechanism. Here, a combination of a variety of computational chemistry tools and experimental methods, including quantum mechanical (QM) calculations, molecular dynamic simulations, progress curve analysis, and deuterium kinetic isotope effect (KIE) experiments, are utilized to comprehensively study the mechanism of inactivation of GABA-AT by CPP-115 and OV329 and account for their experimentally obtained global kinetic parameters k_inact and K_I. Our first key finding is that the rate-limiting step of the inactivation mechanism is the deprotonation step, and, according to QM calculations and the KIE experiments, k_inact accurately represents the enhancement of the rate-limiting step for the given mechanism. Secondly, the present study shows that the widely-used simple QM models do not accurately represent the geometric criteria that are present in the enzyme for the deprotonation step. In contrast, QM cluster models successfully represent both the ground state destabilization and the transition state stabilization, as revealed by natural bond orbital analysis. Furthermore, the globally derived K_I values for both of the inactivators represent the inhibitor constants for the initial binding complexes (K_d) and indicate the inactivator competition with the substrate according to progress curve analysis and the observed binding isotope effect. The configurational entropy loss accounts for the difference in K_I values between the inactivators. The approach we describe in this work can be employed to determine the validity of globally-derived parameters in the process of MBEI optimization for given inactivation mechanisms.

Graphical Abstract

INTRODUCTION

We recently reported the design, synthesis, and evaluation of (1S,3S)-3-amino-4-difluoromethylenyl-1-cyclopentanoic acid (CPP-115, 1)¹ and (S)-3-amino-(difluoromethylenyl)cyclopent-1-ene-1-carboxylic acid (OV329, 2),² highly potent γ-aminobutyric acid aminotransferase (GABA-AT) inactivators (Figure 1).

Figure 1.

Chemical structures of CPP-115 (1) and OV329 (2)

GABA-AT is a pyridoxal 5’-phosphate (PLP)-dependent enzyme that catalyzes the conversion of GABA, the major inhibitory neurotransmitter in the central nervous system into succinic semialdehyde. OV329 blocks the release of dopamine in the corpus striatum and is targeted as a treatment for both epilepsy and addiction. It contains a wide margin of safety as indicated by a lack of activity against alanine- and aspartate aminotransferases, the hERG potassium ion channel, various microsomal cytochrome P450 enzymes, and the Cerep SpectrumScreen³ panel of 176 pharmacological targets. Additionally, a negative Ames test and promising in vivo pharmacokinetics and toxicology make OV329 a very promising drug candidate.

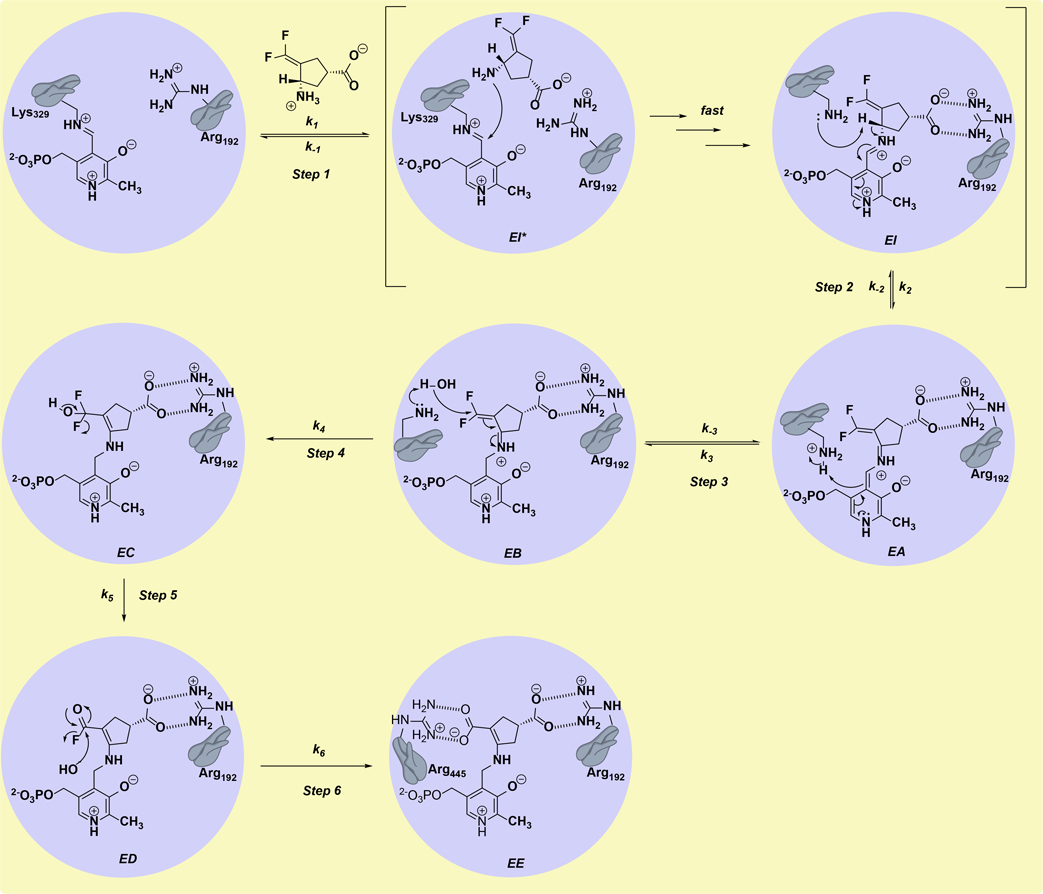
OV329 was developed from CPP-115 (1) and was found to be almost 10 times more efficient at inactivation of GABA-AT than CPP-115.¹ Both OV329 and CPP-115 are mechanism-based enzyme inactivators (MBEIs), unreactive compounds that undergo activation by the target enzyme’s catalytic mechanism; the proposed mechanism of inactivation is shown in Scheme 1.⁴ The first step of the mechanism (Step 1) is attack by the amino group of the inactivator at C₄^’ of the internal PLP-Lys329 aldimine to give the productive Michaelis complex, also known as the external aldimine (EI), which is characteristic of all PLP-dependent enzymes. The conversion of EI* to EI with release of Lys329 as a free base occurs rapidly because transimination is more facile than imine formation from its corresponding aldehyde and amine, and, therefore, does not contribute to rate limitation and kinetically can be modeled as a single step.^5,6 The second step of the inactivation mechanism is the deprotonation of C_α-H of the external aldimine by Lys329 to form the quinonoid (EA), with delocalization of the C_α-H electrons onto the pyridinium nitrogen. Step 3 is the re-protonation of the C₄’ of the quinonoid to give the ketimine intermediate (EB). The ketimine is attacked by the Lys329-activated water molecule at the CF₂ group of EB (Step 4), leading first to EC, then to ED by elimination of HF (Step 5), and finally by water attack on ED to give the final adduct (Step 6, EE), which causes inactivation of the enzyme as a result of the formation of a tight-binding complex between the newly generated carboxylate on the inactivator and Arg445, which is an important residue for binding to a-ketoglutarate in the second half of the enzyme-catalyzed reaction with substrates.

Scheme 1.

Mechanism of inactivation of GABA-AT by OV329/CPP-115; CPP-115 (1) is shown.

The optimization of MBEIs is somewhat different from simple reversible inhibitors, where the latter involves enhancing the favorable enthalpic and entropic contributions to the binding free energy (∆G) via chemical structure modifications, which lower the dissociation constant (K_d) of the enzyme-inhibitor complex.⁷ In contrast, MBEI optimization targets two global kinetic parameters, k_inact, which represents the maximum rate of inactivation of the enzyme by the inactivator, and K_I, which is the concentration of the inactivator at which half-maximum inactivation is observed.⁸ The K_I represents how well the inhibitor binds to the enzyme active site and competes with the substrate, but only if it correlates well with K_d. For a simple inactivation mechanism with two steps, where the initial step is rapid and reversible, k_inact becomes the rate of formation of the fully inactivated complex and K_I becomes the dissociation constant (K_d) of the initial enzyme-inhibitor complex, which is more consistent with how the inhibitor competes with the substrate.⁹ However, for an inactivation mechanism that involves many steps, K_I and k_inact will become complex expressions of the microscopic rate constants and will take the following form for the OV329/CPP-115 mechanism (see Supporting Information for derivation).¹⁰

$$k_{\mathrm{inact}}=\frac{k_6{k}_5{k}_4{k}_3{k}_2}{k_6{k}_5{k}_4\left(k_{-2}+k_3\right)+k_6{k}_5{k}_3\left(k_{-3}+k_2\right)+k_4{k}_3{k}_2\left(k_6+k_5\right)}$$ (1)

$$K_I=\frac{k_6{k}_5{k}_4\left(k_3{k}_{-1}+k_2{k}_{-2}\right)+k_6{k}_5{k}_3\left(k_2{k}_{-3}+k_4{k}_2\right)}{k_1[k_6{k}_5{k}_4\left(k_{-2}+k_3\right)+k_6{k}_5{k}_3\left(k_{-3}+k_2\right)+k_4{k}_3{k}_2\left(k_6+k_5\right)]}$$ (2)

As depicted in the above equations, the presence of reversible steps beyond the initial binding step makes the expressions more complex and completely decouples the k_inact from the microscopic rate constant of the rate-limiting step of the mechanism; consequently, K_I does not correlate well with K_d. However, if Step 2 (deprotonation), Step 3 (re-protonation at C₄’), and Step 4 (water-mediated nucleophilic attack on CF₂) have insignificant reversibilities, the above expressions can be simplified as follows,

$$k_{\mathrm{inact}}=\frac{1}{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$k_2$}\right.+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$k_4$}\right.+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$k_5$}\right.+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$k_6$}\right.}$$ (3)

$$K_I=\frac{\left(k_{-1}+k_2\right)}{k_1}\times \frac{1}{1+\raisebox{1ex}{$k_2$}\!\left/ \!\raisebox{-1ex}{$k_4$}\right.+\raisebox{1ex}{$k_2$}\!\left/ \!\raisebox{-1ex}{$k_5$}\right.+\raisebox{1ex}{$k_2$}\!\left/ \!\raisebox{-1ex}{$k_6$}\right.}=K_{\text{d}}^{}\times F$$ (4)

where K_d is the dissociation constant of the initial binding constant, and F is a constant. The simplified expression for k_inact(equation 3), with the assumptions mentioned above, indicates a clear correlation of the microscopic rate constant of the rate-limiting step with k_inact, and the enhancement of the rate-limiting step would be reflected in the k_inact value. The deprotonation step is known to be the rate-limiting step for GABA-AT with respect to its substrate GABA, whereas the covalent modification step, which is complementary to the water-mediated nucleophilic attack step (Step 4), is known to be the rate-limiting step for inactivators such as γ-vinyl GABA.^11,12 Therefore, in the proposed inactivation mechanism, the rate-limiting step could be either the deprotonation step (Step 2) or the water-mediated nucleophilic attack step (Step 4), given the intramolecular nature of both steps. As we point out below, it is crucial to determine the rate-limiting step of the inactivation mechanism to understand the origin of the efficient inactivation of GABA-AT by OV329 compared to that by CPP-115. Quantum mechanical (QM) calculations of active-site models and kinetic isotope effect (KIE) studies have proven to be compelling tools in the study of enzymatic reaction mechanisms as well as in the determination of rate-limiting steps, both theoretically and experimentally.^12–14

In the simplified expression for K_I (equation 4), the quantity denoted by (k_-1+k₂)/k₁ closely resembles the K_d of the initial binding complex (k_-1+k₁) under rapid equilibrium conditions whenk₂ becomes significantly smaller than k_-1. Then, the rest of the equation becomes a constant (F), whose value is governed by the rate-limiting step. If the deprotonation step becomes rate-limiting (smallerk₂), the above constant (F) approaches unity; consequently, the K_I approaches the K_d of the initial binding complex, and both quantities correlate well. Also, a change in the rate-limiting step does not have any effect on the K_I value (see the Supporting Information for a further explanation) and entirely depends on the K_d of the initial binding complex. In this scenario, the K_I value is very informative and indicates how well the inhibitor competes with the substrate for the active site.

If the water-mediated nucleophilic attack step becomes rate limiting (smaller k₄), the aforementioned constant (F) becomes significantly smaller than one (deviates from unity), and the K_I does not correlate with the K_d value. In fact, enhancement of the microscopic rate constant of the rate-limiting step would increase the K_I value and does not provide an accurate assessment of how well the inhibitor binds to the active site and compete with the substrate (see the Supporting Information for a further explanation). In the past, a Kitz and Wilson plot has been widely used to determine the K_I values of MBEIs.¹⁵ However, with the momentous advancement in statistical software packages, the progress curve analysis method has become popular among scientists, which has significant advantages over a Kitz and Wilson plot.⁸ In addition to the K_I of the inactivator, the progress curve analysis method allows for the determination of the inhibitor constant ${(K}_{\mathrm{i}}^{*})$ of the reversible part of the inactivation mechanism, which resembles the dissociation constant of the initial binding complex of the inactivator with the enzyme. Therefore, K_I and K_d values can be directly compared for the inactivator and establish a correlation between them without considerable effort.

Herein, we report the use of density functional theory (DFT) calculations to study the two important reaction steps of the inactivation mechanism of GABA-AT by OV329 and CPP-115 in detail, namely, deprotonation and the water-mediated nucleophilic attack steps, to determine the theoretical rate-limiting step. Initially, DFT calculations were performed on a simplified QM model followed by a large cluster model, which includes essential active site residues that interact with the PLP bound inactivators. Our findings suggest that the cluster model accurately represents the crucial geometric criteria unique to PLP-dependent enzymatic reactions, and the rate-determining step of the inactivation mechanism is the deprotonation step. Subsequently, classical molecular dynamics (MD) simulations and natural bond orbital (NBO) analysis were employed to investigate the deprotonation step exclusively, to probe the magnitude of the ground-state (GS) destabilization, and the transition state (TS) stabilization in the external aldimine. These studies provided insights into the underlying factors that govern the activation free energy barrier of the deprotonation step, which ultimately accounts for the similarity between the k_inact values of OV329 and CPP-115. Furthermore, to establish a correlation between the K_I and the K_d, progress curve analysis was employed, and the findings revealed that the inhibitor constants of OV329 and CPP-115 closely resemble the dissociation constants of the initial binding complex. To further reckon the origin of the K_d difference between OV329 and CPP-115, interaction energies of the initial binding complexes and the configurational entropy loss of the inactivators upon binding to the enzyme active site were estimated using MD simulations. Finally, [3-²H]OV329 was synthesized, and KIE studies were carried out to verify the inferences obtained from theoretical studies. The methodology and the findings of the current work are important to the further optimization of mechanism-based enzyme inactivators of GABA-AT that follow a similar mechanism to that of OV329 or CPP-115 and can validate the use of global kinetic parameters in the optimization process. Furthermore, this methodology can be expanded to optimize MBEIs of other enzymes where the mechanism is known.

RESULTS AND DISCUSSION

QM Calculations on a Simplified Model

A simplified model, consisting of PLP-bound inactivator and methylamine to mimic Lys329, was used to carry out the initial QM calculations with the aid of density functional theory (DFT) to study the deprotonation step (Step 2) and the water-mediated nucleophilic attack step (Step 4). The methylamine was placed on the si face of the PLP ring according to X-ray crystallographic evidence (Supporting Information Figure S1).^1,2 Furthermore, the X-ray crystal structure of the inactivator complex formed by OV329 and CPP-115 with GABA-AT shows that the endogenous carboxyl groups of the inhibitors are held fixed via the salt-bridge interaction with the side chain of Arg192. Therefore, to stabilize the carboxyl groups, to prevent the negatively-charged oxygen atoms from twisting toward the ring, and to avoid charge delocalization problems, the carboxyl groups were protonated. The phosphate group of the PLP ring also has been replaced by a methyl group because it does not play a crucial role in the catalytic mechanism. Also, the X-ray crystallographic data suggest that the PLP phenolic oxygen is hydrogen-bonded to the nearby Gln301 residue; to mimic this effect, the phenolic oxygen of the simplified model was protonated. These types of simplifications are widely used in QM calculations of PLP-dependent enzymatic reactions to simplify the model and reduce the calculation cost.^13,16 Most importantly, the pyridine nitrogen of the PLP ring was considered protonated because it stabilizes the charge neutralized quinonoid resonance form, which has been widely recognized as one of the most crucial sources of the catalytic power as well as reaction specificity of PLP-dependent enzymes.¹⁷ In PLP-dependent aminotransferases, the pyridine nitrogen is known to be in the protonated state and hydrogen-bonded to a nearby glutamate or aspartate residue (Asp298 in GABA-AT). The protonated state of the pyridine nitrogen stabilizes the quinonoid species upon deprotonation at the C_α position and facilitate the re-protonation at the C₄’ position of the PLP ring, thereby generating auspicious conditions for the aminotransferase activity over racemase activity. In PLP-dependent racemases, the pyridine nitrogen is in the deprotonated state and hydrogen bonded to a nearby arginine residue, causing destabilization of the quinonoid species, which promotes racemase activity via re-protonation at the C_α position instead of the C₄’ position.¹⁸

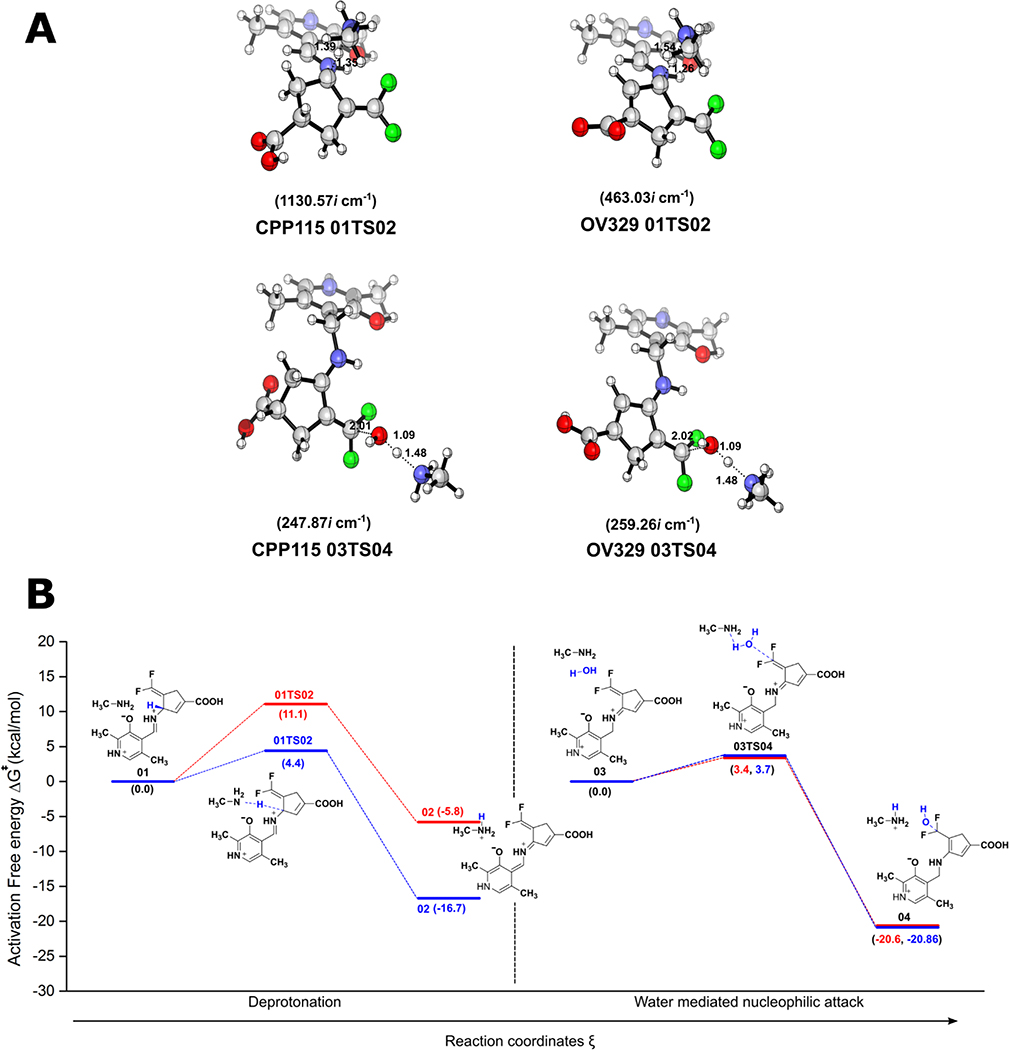
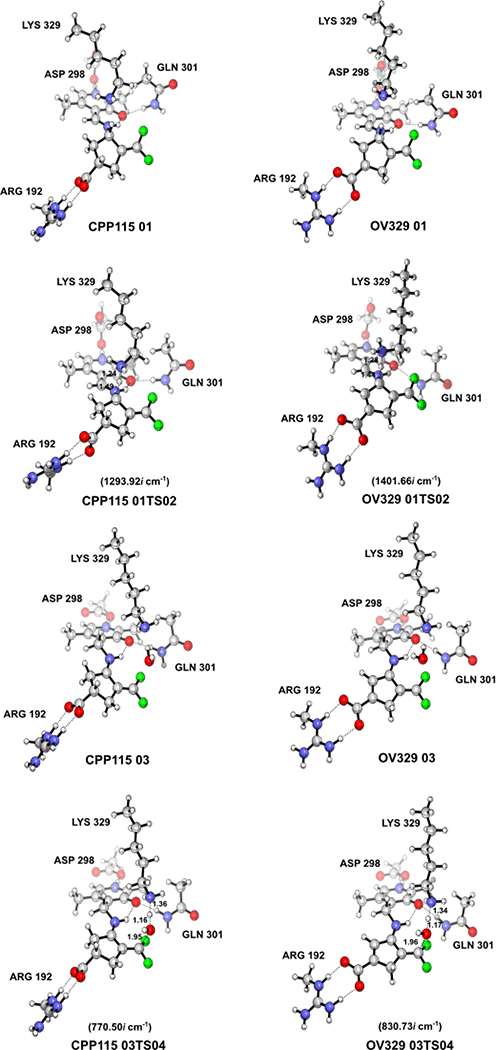
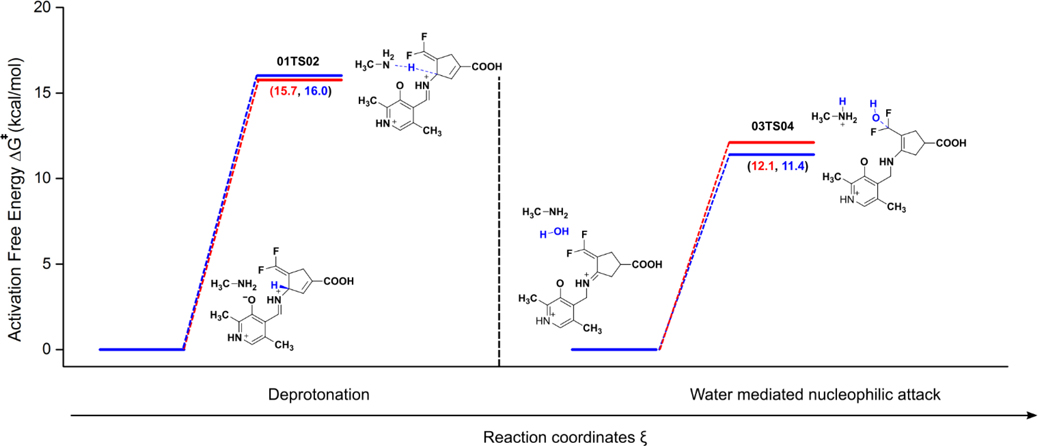
The geometries of the gas phase optimized structures of the transition states (TS), their frequencies, and specific distances, along with calculated relative free energy barriers, are given in Figure 2 (see Supporting Information for a full list of optimized geometries for reactants and products). According to these calculations, the gas-phase free energy barriers for the formation of the transition state structure (01TS02) corresponding to the deprotonation steps (Step 2) for CPP-115 and OV329 are 11.1 kcal/mol and 4.4 kcal/mol, respectively. These data suggest that the deprotonation step for CPP-115 is significantly slower than that for OV329. Furthermore, the free energy barrier for the deprotonation step of CPP-115 is much greater than the free energy barrier for the water-mediated nucleophilic attack step (3.4 kcal/mol) (Step 4), which makes the deprotonation step rate-limiting for CPP-115. However, for OV329 the free energy barrier for the deprotonation step (4.4 kcal/mol) is only slightly higher than the free energy barrier for the water-mediated nucleophilic attack step (3.7 kcal/mol), making both steps partially rate-limiting.

Figure 2.

Results of the QM calculations on the simplified model. (A) Optimized geometries of the TS, their frequencies, and important distances (in angstroms) (B) Calculated energy profiles for the deprotonation and the water-mediated nucleophilic attack steps in the simplified model (CPP-115, green lines; OV329, blue lines)

Out of the two reaction steps, the deprotonation step is mostly affected by the geometry of the reactants and TS. According to Dunathan’s hypothesis regarding PLP-dependent enzymatic reaction specificity, the enzyme aligns the C_α-H scissile bond perpendicular to the plane of the PLP ring (parallel to the p orbitals of the conjugated π-system of the PLP ring), causing the stabilization of the burgeoning charge on the C_α atom of the TS, which leads to the TS stabilization.¹⁹ Furthermore, this alignment allows hyperconjugation of the σ(C_α-H) bond in the ground state with the π-system of the PLP ring that weakens the σ bond; this is referred to as ground state (GS) destabilization. Careful observation of the optimized geometries of the reactants and TS of the deprotonation step revealed that the specific geometric criteria for the GS destabilization are completely diminished relative to the reactants. At the same time, it is somewhat conserved in the TS structure for TS stabilization.

In the gas phase optimized TS structures, the dihedral angles between the C_α-H bond and the PLP ring are 94.94⁰ and 98.88⁰ for CPP-115 and OV329, respectively, which is closer to the optimum value of 90⁰. However, in the reactants, these dihedral angles deviate significantly from 90⁰ (107.86⁰ for CPP-115 and 135.21⁰ for OV329), making the simplified model incapable of comprehensively portraying the GS destabilization, which is crucial for the accurate estimation of the free energy barrier of the deprotonation step. Therefore, a descriptive cluster model with important active site residues that maintain the required geometric criteria became necessary to accurately model the deprotonation step. First, to observe the behavior of CPP-115 and OV329 in the external aldimine complex with GABA-AT (complex EA in Scheme 1), as well as to quantify the specific geometric criteria, classical MD simulations were carried out. Finally, based on the MD simulation results, a descriptive cluster model was constructed to recalculate the QM calculations for deprotonation and the water-mediated nucleophilic attack steps.

Classical MD Simulations of the External Aldimine of CPP-115 and OV329 with GABA-AT

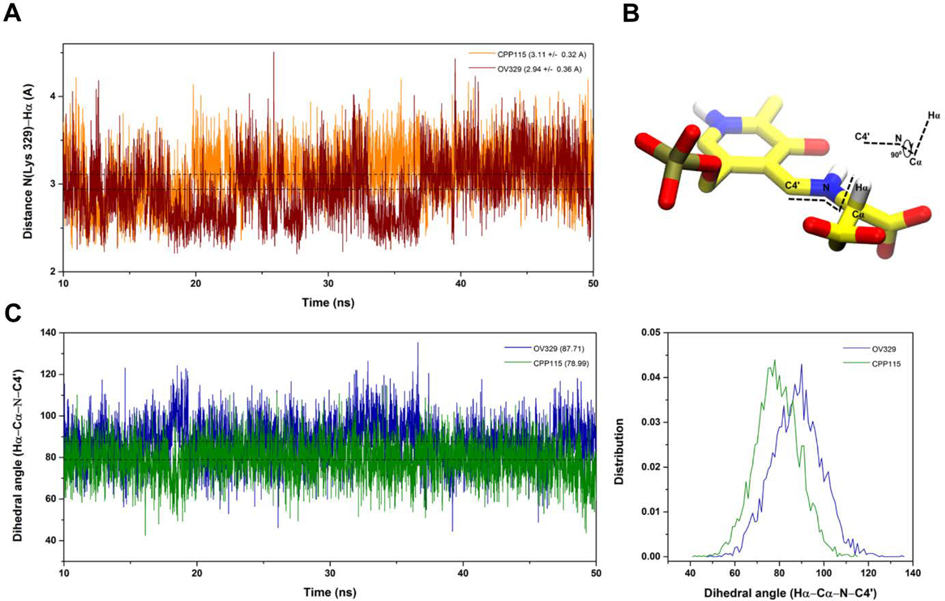
The 50 ns classical MD simulations were started from the docking poses of the PLP-bound inactivators with GABA-AT. The trajectories were analyzed to monitor the distance between the catalytic Lys329 nitrogen and H_α as well as the dihedral angle between the C_α-H bond and the PLP ring plane. As shown in Figure 3A, the catalytic Lys329 nitrogen and the H_α distance of the inactivators in the external aldimine complex are similar (3.11 A and 2.94 A for CPP-115 and OV329, respectively). Also, the average dihedral angle between the C_α-H bond and the PLP ring plane varies slightly between CPP-115 and OV329. In the OV329 model, the above dihedral angle is 89.9^o, whereas, in the CPP-115 model, it is 78.8^o, which makes ground state destabilization of the C_α-H bond slightly more probable for OV329 compared to CPP-115. However, as seen in Figure 3B, the dynamic nature of the complex makes both inactivators able to attain the required geometry at specific time points. Overall, the classical MD simulations revealed that the necessary geometric criteria for GS destabilization was present in both CPP-115 and OV329 but was absent in our simplified QM model. With this information in hand, we moved on to the cluster model to further refine the QM calculations for accurate estimation of the activation free energy barriers for the deprotonation and water-mediated nucleophilic attack steps.

Figure 3.

Classical MD simulation. (A) Distance between the Lys329 N and the H_α atom of the inactivators; (B) Definition of the dihedral angle between the C_α-H bond and the PLP ring plane; (C) Fluctuation of the dihedral angle between the C_α-H bond and the PLP ring plane during the MD simulation

QM Calculations on a Cluster Model

A cluster model of the active site of GABA-AT with PLP bound inhibitors in the external aldimine complex (EI) was constructed from the appropriate time frames of the MD simulations with the C_α-H bond perpendicular to the PLP ring plane. The cluster model for the water-mediated nucleophilic attack step (EB) was constructed in a similar fashion from our previous MD simulation of this complex.² In both modules, all of the interacting residues of the active sites, which include Arg192, Gln301, Asp298, and Lys329, were incorporated and truncated at the C_δ, C_γ, C_β, and C_α atoms, respectively (Supporting Figure S2). The atoms at the truncated points of the active site residues were frozen and held fixed with respect to each other during the optimization using redundant coordinates to prevent the deformation of the active site and to maintain the correct geometry. The PLP bound inactivators were allowed to freely optimize within the active site cage without any restraints. We used this cluster model to study the forward reactions of both steps to estimate the activation free energy barrier and accurately determine the rate-limiting step of the inactivation mechanism. Frequency analysis of the optimized geometries indicated few (<3) imaginary frequencies, all below 30i cm⁻¹, as a result of the presence of frozen atoms. However, the contribution of these small frequencies to the zero-point energy was negligible, and the free energy values were unaffected. The optimized geometries of the reactants and the TS of the two reaction steps and the frequencies of the TS are given in Figure 4. Similar activation free energy barriers for the deprotonation steps in the cluster model are shown for CPP-115 and OV329 (15.7 kcal/mol and 16.0 kcal/mol, respectively) in Figure 5. The activation free energy barrier for the water-mediated nucleophilic attack was noticeably lower for both inactivators (12.1 kcal/mol for CPP-115 and 11.4 kcal/mol for OV329) compared to the deprotonation step. This clearly makes the deprotonation step the rate-limiting step of the inactivation mechanism for both compounds. In fact, lysine is known to be used as a catalyst for Michael addition reactions of α,β-unsaturated ketones with water, which also coincides with the lower activation free energy barrier obtained for the water-mediated nucleophilic attack step.² Observation of the reactants and TS geometries of the deprotonation step revealed that the σ(C_α-H)-bond is perpendicular to the PLP π-ring plane with both of the inactivators, which facilitates GS destabilization and TS stabilization. The pK_a calculations of the free inactivators using the thermodynamic cycle technique demonstrated a weak acidity associated with the H_α atoms. Even though the acidity is weak, there is a significant pK_a difference between CPP-115 (pKa 33.04) and OV329 (pKa 17.93) (Supporting Information Table S4), partly because of the additional stability of the OV329 conjugated base as a result of the endocyclic π* (C_β1-C_γ1) bond.

Figure 4.

Optimized geometries of the reactants and the TS in the cluster model

Figure 5.

Calculated energy profile for the forward reactions of the deprotonation and the water-mediated nucleophilic attack steps in the cluster model (CPP-115 red lines, OV329 blue lines)

In the PLP-bound inactivators, H_α becomes more acidic, and the pK_a difference between the two inactivators dramatically drops because of the stabilization of the conjugated base of both inactivators by the PLP π-ring system (CPP-115 pK_a 11.48 and OV329 pK_a 4.65). These calculated pKa values agree with the literature values for the PLP bound aminoacids.²⁰ Furthermore, this also demonstrates that the endocyclic double bond’s influence on the pKa difference is diminished by the PLP. PLP is known to be an excellent electron sink for stabilization of anions and is the primary stabilizing driving force of PLP-dependent enzymes. However, in the enzyme active site, GS destabilization of the reactants (which is absent in the free PLP-bound inactivator outside the active site and in the simple model) makes the C_α-H sigma bond much weaker, and the endocyclic double bond’s influence on the pKa difference to be further diminished, which might bring the acidity further up and make the acidity difference between the inactivators insignificant. This might cause the deprotonation step of OV329 and CPP-115 to be somewhat easier inside the active site and equally feasible.

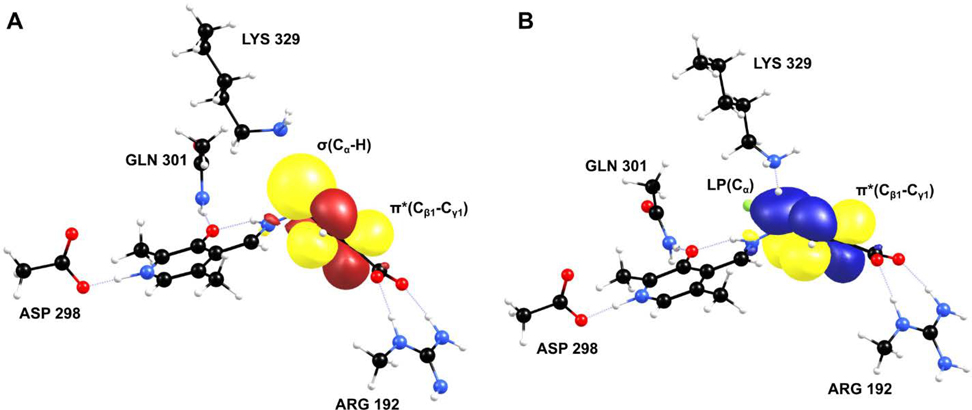
To further investigate the GS destabilization and the TS stabilization that occur in the deprotonation step, we have conducted NBO analysis on the reactants and the TS structures derived from the cluster model. The origin of the GS destabilization and the TS stabilization is the hyperconjugation of the p-orbitals of the PLP π-ring system with the σ(C_α-H)-bond of the reactants and the developing negative charge (lone pair) on C_α of the TS, respectively. The NBO approach is widely used to study the hyperconjugation effect and provides information about the interactions between the filled (bonding or lone pair) Lewis type NBOs (donor) and the empty (antibonding or Rydberg) non-Lewis NBOs (acceptor); the energetic importance is estimated by second-order perturbation theory.²¹ The stabilization energy (E₂) of these interactions as a result of delocalization from i (donor) to j (acceptor) is given by the following equation,

$$E^2={∆E}_{ij}=q_i\frac{F_{ij}^2}{{\epsilon }_i-{\epsilon }_j}$$ (5)

where F_IJ is the Fock matrix elements between the NBO i and j, q_i is the donor orbital occupancy, and ε_i and ε_j are the orbital energies. Stabilization energy greater than 1 kcal/mol is an indication of the presence of hyperconjugation between the donor and the acceptor. The NBO analysis results are shown in Figure 6, and the stabilization energies of each species are given in Table 2. According to the stabilization energy values, it is evident that the hyperconjugation of the lone pair on C_α of the TS state is significant for both OV329 and CPP-115 compared to the reactants. Also, there is additional stabilization coming from the hyperconjugation of the C_α lone pair with the endocyclic π* (C_β1-C_γ1)-bond of OV329 (Figure 6B). Nevertheless, the total stabilization energy difference between CPP-115 and OV329 is only 1.89 kcal/mol, which is not that significant compared to the magnitude of the total stabilization energy. The hyperconjugation of the σ(C_α-H) bond with the PLP π-ring system in the reactants is smaller than the TS hyperconjugation of the C_α lone pair with the PLP π-ring system. However, there still is substantial hyperconjugation, as is evident from the total stabilization energies of 6.20 kcal/mol and 7.87 kcal/mol for CPP-115 and OV329, respectively. The additional hyperconjugation observed in the TS, which involves the endocyclic π* (C_β1-C_γ1)-bond of OV329, can still be seen in the reactants (Figure 6A), which contributes to the GS destabilization. Overall, NBO analysis provided a useful insight into the origin of the GS destabilization and TS stabilization of CPP-115 and OV329, which makes the deprotonation step of the inactivators equally feasible in the active site both experimentally and in the cluster model compared to the simple model, where GS destabilization is absent.

Figure 6.

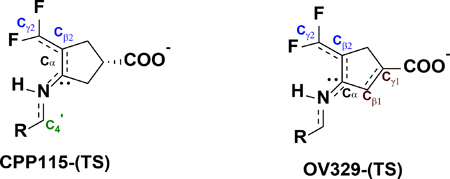
NBO analysis of the cluster model to illustrate the extra stability coming from the endocyclic double bond of OV329 in reactants (A) and TS (B)

Table 2.

Second-order perturbation energies of donor-acceptor NBO interactions for reactants and TS with CPP-115 and OV329

State	Inactivator	Donor NBO (i)	Acceptor NBO (j)	E2 (kcal/mol)	Total (kcal/mol)
Reactants	CPP-115	σ(Cα-H)	π*(C4’-N)(2)	3.17	6.20
		σ(Cα-H)	π*(Cβ2-Cγ2)(2)	3.03
	OV329	σ(Cα-H)	π*(C4’-N)(1)	1.00	7.87
		σ(Cα-H)	π*(C4’-N)(2)	2.90
		σ(Cα-H)	π*(Cβ2-Cγ2)(2)	1.92
		σ(Cα-H)	π* (Cβ1-Cγ1)(2)	2.05
TS	CPP-115	LP(Cα)	π*(C4’-N)(2)	59.70	90.11
		LP(Cα)	π*(Cβ2-Cγ2)(2)	30.41
	OV329	LP(Cα)	π*(C4’-N)(2)	44.61	92.00
		LP(Cα)	π*(Cβ2-Cγ2)(2)	26.55
		LP(Cα)	π* (Cβ1-Cγ1)(2)	2084

The activation free energy values obtained for the deprotonation step were used to estimate the rate constants for the forward reactions of the deprotonation steps for both inactivators. The calculations were done at 298.15 K using transition state theory,²²

$$k\left(T\right)={\rm X}\frac{k_{B}T}{h{c}^0}{e}^{-{∆G}^{‡}/RT}$$ (6)

where Χ is the transmission coefficient (taken to be unity), k_B is the Boltzmann constant, T is the temperature, h is the Planck’s constant, c⁰ is the standard-state concentration (taken to be 1.0 M), R is the universal gas constant, and ΔG^‡ is the activation free energy barrier for the forward reaction. The estimated rate constants for the deprotonation step with CPP-115 and OV329 are 17.09 s⁻¹ (1.0 × 10³ min⁻¹) and 11.21 s⁻¹ (0.67 × 10³ min⁻¹), respectively. According to equation 3 discussed in the introduction, which shows the simplified relationship between k_inact and the microscopic rate constants of the inactivation mechanism, the above-estimated rate constants for the deprotonation step can be translated into the k_inact values of 17.09 s⁻¹ (1.0 × 10³ min⁻¹) and 11.21 s⁻¹ (0.67 × 10³ min⁻¹) for CPP-115 and OV329, respectively. These estimated values are significantly higher compared to the experimental k_inact values obtained for the inactivators (2.05 min⁻¹ for CPP-115 and 3.25 min⁻¹ for OV329). One of the main reasons for the overestimated reaction rate constants might be because the calculations were performed in aqueous medium. The aqueous environment could stabilize the developing charge on the TS compared to the reactants, which makes the activation free energy barrier lower compared to the actual protein environment, where the dielectric constant is significantly lower than water. Also, the experimental k_inact value for OV329 is slightly higher than that for CPP-115, whereas, in the estimated values, the order is reversed. The estimated k_inact value difference between CPP-115 and OV329 is 0.33 × 10³ min⁻¹, which corresponds to a relative free energy value difference of 0.25 kcal/mol. This error in estimation is associated with the level of theory used for the DFT calculations. According to a recent study that benchmarked the QM methods for calculating energetics of enzymatic reactions, the mean absolute error (MAE) of the B3LYP/6–31+(d) level of theory for calculating a proton transfer reaction is closer to 3.0 kcal/mol.²³ This error value is greater than the estimated activation free energy difference we obtained for the deprotonation step between CPP-115 and OV329. Therefore, under the current level of theory used in this study, it is difficult to distinguish the activation free energy barriers for the deprotonation step between the two inactivators, and the estimated activation free energy barrier difference between the deprotonation step and the water-mediated nucleophilic attack step is above the MAE for both CPP-115 and OV329. Consequently, the current level of theory employed in the study confidently identifies the deprotonation step as the rate-limiting step in the inactivation mechanism. We then moved on to a progress curve analysis to find out the correlation between the inhibitor constant K_I and the dissociation constant of the initial binding complex for each inactivator ($K_{\mathrm{d}}/K_{\mathrm{i}}^{*}$). The above correlation will provide useful information about the rate-limiting step of the inactivation mechanism that can be used to validate the DFT calculation findings.

Progress Curve Analysis and Inhibitor Constants (K_I and ${\mathit{K}}_{\mathit{i}}^{*}$) Correlation

Progress curve analysis is a powerful tool to identify slow binding inhibitors. Most of the time, inhibitors with mechanisms that involve covalent bond formation (reversible or irreversible) with the enzyme active site or enzyme isomerization upon formation of the initial binding complex tend to display slow binding behavior. Reversible, slow-binding inhibitors with two steps, where the second step is the slower step, have a unique shape to their progress curves, which can be fitted to the following equation,⁸

$$\left[P\right]=v_{s}t+\frac{v_i-v_s}{k_{\mathrm{obs}}}\left[1-e^{-{(k}_{\mathrm{obs}}t)}\right]$$ (7)

where [P] is the product concentration, v_s is the steady-state velocity, v_i is the initial velocity, and k_obs is the observed rate of inactivation. At first, the inhibitor competes with the substrate for the enzyme active site by forming the initial binding complex and reaches its equilibrium fast, which is known as the initial velocity (v_i) (Supporting Information Figure S3). After some period of time the inhibitor starts establishing its second equilibrium slowly, and the v_i gradually decreases to achieve its steady-state velocity (v_s). This phase is known as the steady-state velocity phase. The rate at which the initial velocity phase converts to the steady-state velocity is the k_obs.

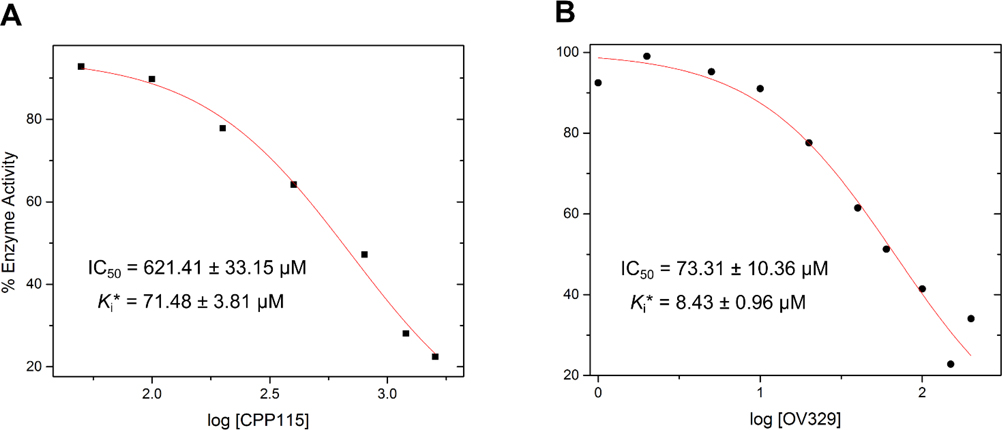
The progress curve of a MBEI closely resembles the aforementioned progress curve (reversible and two steps), except for a lack of a steady-state velocity phase. MBEIs are irreversible (covalent or tight binding) inhibitors so that after the initial velocity phase, the v_i gradually decreases until it becomes zero without reaching a steady-state phase, where the enzyme is completely inactive. Therefore, fitting a progress curve of a MBEI to equation 7 will always result in v_s values close to zero (even at lower inhibitor concentrations). As discussed in the introduction, at the initial velocity phase, the irreversible inhibition is absent, and v_i can be used to calculate the inhibitor constant of the reversible part of the inhibition, which also represents the dissociation constant K_d of the initial binding complex of the inactivator. We have also shown from our derivations that in the simplified expression for the K_I (inhibitor concentration at which the half maximum k_inact is achieved) (equation 4), the K_I becomes equal to the K_d times a constant (F), where the constant approaches unity if the deprotonation step (k₂) is the rate-limiting step. In other words, the K_I of the inactivator becomes the inhibitor constant of the reversible part of the mechanism, which also represents the dissociation constant of the initial binding complex (K_d). If the water-mediated nucleophilic attack step (k₄) becomes rate limiting, the outcome will be completely different; the constant would become significantly smaller than 1 and the K_I would become inversely proportional to the K_d. Therefore, the correlation between K_I and K_d, as well as the magnitude of constant F, are powerful ways of confirming our DFT finding that the deprotonation step is the rate-limiting step. To achieve this goal we took our previous progress curve analysis data for CPP-115 and OV329 and re-analyzed them by fitting them to equation 7, where we obtained values for v_i and v_s.² Those values were converted into percent inactivation of the enzyme (Supporting Information Table S4), from which we estimated the IC₅₀ values and K_d of the reversible part of the inactivation (Figure 7).

Figure 7.

Estimated IC₅₀ values of the reversible part of the inactivation mechanism (initial binding complex formation) for (A) CPP-115 (B) OV329 (K_d values were determined from IC₅₀ values using the Cheng-Prusoff equation)

According to the percent inactivation values, the enzyme was inactive at the end of the experimental time (v_s is close to zero) for both of the inactivators. This is strong evidence that both inactivators act as irreversible inactivators of GABA-AT, which we had not investigated during the previous progress curve analysis. The estimated values of IC₅₀, K_d,K_I and constant F are given in Table 3. According to these estimations, constant F has values of 0.82 ± 0.13 and 1.15 ± 0.19 for CPP-115 and OV329, respectively. These findings suggest that the mechanism of the inactivation agrees with the simplified version of the equation, where it is assumed that the deprotonation and the nucleophilic water attack steps have insignificant reversiblities. Furthermore values of constant F closer to 1 confirm that the deprotonation step is indeed the rate-limiting step, as predicted from our DFT calculations, and the observed K_I difference arises from the formation of the initial binding complex rather than differences in the rate-limiting step between CPP-115 and OV329. Therefore, to further investigate the origin of the K_I difference, we performed classical MD simulations of the initial binding complexes (EI^*) for CPP-115 and OV329 and the free inactivators in water.

Table 3.

Progress curve analysis data

Compound	IC50 (μM)	Kd (μM)	KI (μM)	Factor (KI/Kd)
CPP-115	621.41 ± 33.15	71.48 ± 3.81	58.8	0.82 ± 0.13
OV329	73.31 ± 10.36	8.43 ± 0.96	9.69	1.15 ± 0.19

Linear Interaction Energy (LIE) Estimation of the Initial Binding Complex

The linear interaction energy (LIE) technique was enforced on the MD simulation trajectories of the EI^* complexes and the free inactivators to estimate and compare the binding free energies of CPP-115 and OV329. The LIE equation for the estimation of binding free energy (∆G_binding) takes the following form,²⁴

$${∆G}_{binding}=\beta 〈∆U_{elec}〉+\alpha 〈∆U_{vdw}〉+\gamma$$ (8)

where ∆U_elec and ∆U_vdw are the differences in the averaged inactivator-environment electrostatic and van der Waals energies, which are collected for the free (inactivator solvated in water) and the bound (inactivator bound with GABA-AT in water) states of the ligand. The α values are scaling factors, and 0.18 and 0.5 were selected for α and β respectively, according to the literature.²⁴ The offset factor γ was considered to be zero because we are estimating the relative binding free energies for comparison, rather than the absolute free energies, to account for the observed experimental K_I difference. The calculations resulted in similar ∆G_binding values for CPP-115 and OV329, which did not explain the origin of the experimental K_I. On the other hand, these values are acceptable given the fact that the inactivators have identical structures and interacting functional groups, except for the endocyclic double bond in OV329, which should lead to similar interaction energies ((-59.034 +/- 14.632 kJ/mol and -64.072 +/- 19.157 kJ/mol for CPP-115 and OV329, respectively). However, the above LIE calculation does not include the configurational entropy loss of the inactivator during the initial binding complex formation, which might be the origin of the K_I difference. To estimate the configurational entropy loss, we performed principal component analysis (PCA) on the inactivators in both the free and enzyme-bound forms, and the quasi-harmonic approximation (QHA) technique was used to estimate the configurational entropy.

Configurational Entropy Loss of the Inactivators During Initial Binding Complex Formation

The configurational entropy is the sum of the conformational and vibrational entropy, two of the main unfavorable contributions to the entropic component of the binding free energy.²⁵ Most of the free energy estimation methods, including the LIE technique, do not account for the above contribution; therefore, they overestimate the binding free energy. The QHA method is a widely used technique to estimate the configurational entropy associated with protein folding as well as small molecules binding with biomolecules.²⁶ In this method, MD simulation trajectories are used to perform the conformational sampling in which the structures visit multiple potential minima. The configurational entropies are estimated from the PCA analysis, which employs a mass-weighted variance-covariance matrix calculation from the MD trajectory after the overall translations and rotations of the desired molecules are removed using least-squares fits followed by diagonalization of the covariance matrix to obtain the required modes and frequencies.

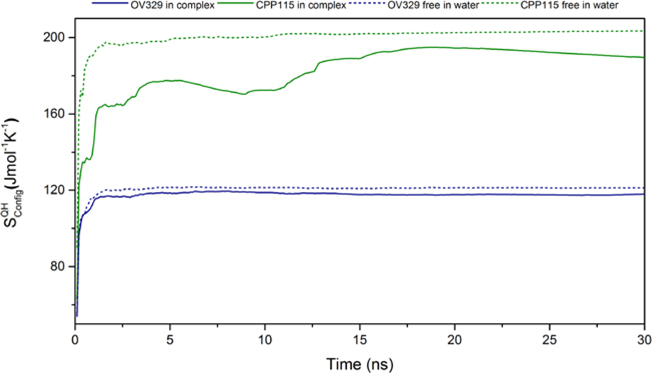
First, we performed PCA analysis on the heavy atoms of the five-membered ring of both free inactivators simulated in water to find out if there is any significant conformational difference between them. Interestingly, the free energy landscapes constructed via projecting the original trajectories on the common subspace defined by the first two principal components suggest that OV329 exists as a single conformation, whereas CPP-115 exists as two major conformations in water (Figure 8). The average structures corresponding to the two-energy minimum of the free energy landscape of CPP-115 in water reveal the presence of an axial-equatorial equilibrium, which is absent in the enzyme-bound form. In the enzyme-bound form, CPP-115 exists predominantly as a single equatorial conformation. The DFT calculations of the two conformations in the gas phase revealed that the energy difference is only 0.092 kcal/mol. Even though there is a clear conformational difference between CPP-115 and OV329, the conformational contribution to the configurational entropy is known to be smaller compared to the vibrational contribution for small molecule drug binding.²⁷ Therefore, we performed PCA analysis on all of the heavy atoms of both inactivators in water and the complex form to estimate the configurational entropy, which includes both conformational and vibrational components. The evolution of the configurational entropy of the inactivators using the quasi-harmonic approximation technique in both free and bound form over time is shown in Figure 9. According to the estimations, CPP-115 has a significantly higher configurational entropy compared to OV329 in both free and complex forms. This indicates that the endocyclic double bond makes OV329 more rigid compared to CPP-115, which is more flexible. The estimated configurational entropy losses ($T{∆S}_{Config}^{QH}$) at 310 K for CPP-115 and OV329 are −4.14 ± 0.09 kJ/mol and −1.09 ± 0.05 kJ/mol, respectively (average over last 2 ns). The difference in the configurational entropy loss between CPP-115 and OV329 (3.05 ± 0.10 kJ/mol) accounts for the significant fraction of the binding free energy difference between the inactivators (4.647 kJ/mol) derived from the following equation,

$$∆G=-RTln{K}_I$$

where ∆G is the binding free energy, R is the universal gas constant, T is the temperature, and K_I is the inhibitor constant. Overall, these calculations imply that the configurational entropy is the major contributing factor for the observed experimental K_I difference between CPP-115 and OV329. With the above findings, we attempted to experimentally validate the theoretical findings by KIE experiments.

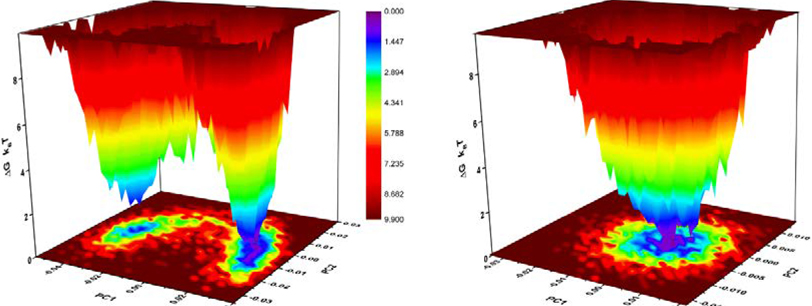
Figure 8.

Free energy landscape of (A) CPP-115 and (B) OV329 in water constructed via PCA analysis. OV329 exists as a single conformation while CPP-115 clearly shows two distinct conformations (axial and equatorial).

Figure 9.

Evolution of the configurational entropy throughout the 30 ns MD simulation

KIE Experiments and the Determination of the Rate-Limiting Step

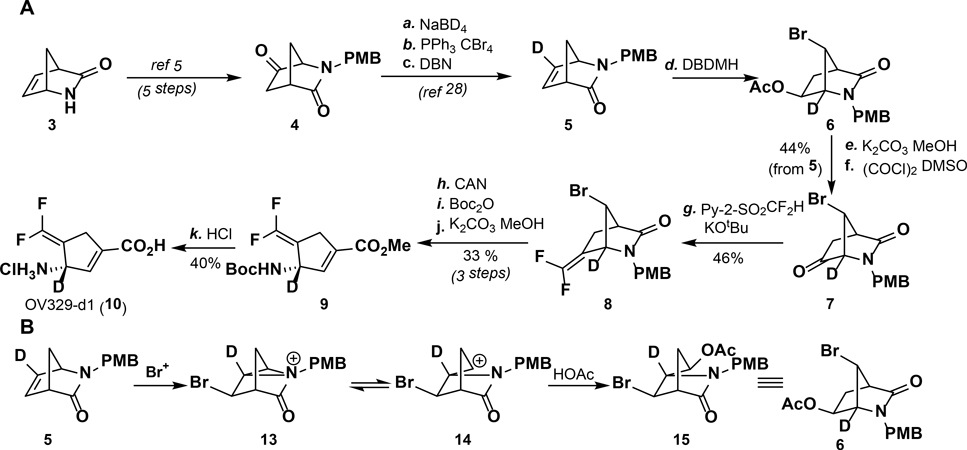
The KIE experiments started with the synthesis of [3-²H]-OV329 (Scheme 2A, 10) from the Vince lactam (3). The deuteron was installed in the proper position through a bromonium ion-catalyzed rearrangement of 5, resulting in the deuterium at the α-nitrogen position in 6 (Scheme 2B).²⁸ The remainder of the synthesis is identical to the synthesis of OV329.² Compound 5 was obtained from the corresponding ketone via a known NaBD₄ reduction and elimination sequence.²⁹ Ketone 4 was accessed from 3 in five steps.³⁰ Because the synthesis proceeds through a double inversion of stereochemistry (two bromonium ion-catalyzed rearrangements result in retention of stereochemistry from the starting lactam), (1S,4R)-2-azabicyclo[2.2.1]hept-5-en-3-one (3) is required as the starting material. As 3 is quite expensive, the synthesis was run with the racemate. Rac-[3-²H]-OV329 (10) was isolated in 17 steps overall.

Scheme 2.

(A) Synthesis of rac-[3-²H]-OV329 and (B) mechanism of bromonium ion-catalyzed rearrangement of 5 to 6

As noted above, we employed the progress curve analysis method to determine the K_I and k_inact values for the inactivators (Figure 10). rac-[3-²H]-OV329 was determined to have a similar K_Ito that of rac-OV329 (K_I= 36 ± 8.0 μM for rac-[3-²H]-OV329, K_I = 45 ± 11 μM for rac-OV329). k_inact however, was affected as expected with a k_inact-H/k_inact-D of 4.5 ± 0.36 (k_inact = 1.5 ± 0.5 min⁻¹ for rac-[3-²H]- OV329; k_inact = 6.7 ± 1.0 min⁻¹ for rac-OV329). The efficiency of inactivation (k_inact/K_I) was found to be 36 ± 8 and 146 ± 13 mM⁻¹min⁻¹ for rac-[3-²H]-OV329 and rac-OV329, respectively, indicating that there is a primary kinetic isotope effect, specifically with respect to k_inact, of 4.5 ± 0.36. These experimental observations coincide well with our theoretical findings. First, the apparent primary KIE value associated with k_inact supports our theoretical finding that the deprotonation step is the rate-limiting step; this rate deceleration should be reflected in the k_inact only if the deprotonation step is rate-limiting according to equation 3. Secondly, the magnitude of the primary KIE associated with the k_inact value supports our hypothesis that the deprotonation step takes place in a stepwise fashion rather than concerted. The KIE gives important insights into the changes in the vibrational frequencies between the reactant and the TS, which are also connected to force constant changes. For a given reaction, the variation in the TS frequencies is greater than the corresponding reactant changes. Therefore, the KIE has been used to study the geometries of the TS.³¹ Linear TSs, mostly with higher stretching frequencies, give rise to larger primary KIE values, while non-linear TSs with smaller bending frequencies give rise to smaller primary KIE values. A concerted mechanism for the deprotonation step would yield a non-linear TS, while a stepwise mechanism gives rise to a linear TS. Since k_inact reflects the enhancement of the rate-limiting step (deprotonation step), the higher primary KIE value (4.5) associated with the k_inact indicates a linear TS for the deprotonation step, which support a stepwise mechanism.

Figure 10.

Inhibitor versus k_obs plot of rac-OV329 (black) and rac-[3-²H]-OV329 (red) and their corresponding inactivation constants and kinetic isotope ratio

As we have previously shown for our inactivation mechanism, the K_I is entirely governed by the formation of the initial binding complex, and there is no effect from the rate-limiting step (equation 4). This is further evident by the absence of a larger primary kinetic isotope effect in the K_I value. Interestingly the primary kinetic isotope effect of 1.25 ± 0.33 associated with the K_I is an indication of the probable presence of a binding isotope effect (BIE), which has been used in the literature to demonstrate the GS destabilization associated with PLP-dependent enzymes).^32,33 The observed deuterium BIE results from the hyperconjugation of the σ(C_α-H)-bond of the external aldimine (initial productive binding complex) with the π-system of the PLP ring, which we have also seen in the NBO analysis of the cluster model. It should be noted that the BIE can only be observed in the external aldimine complex, which is the effective initial binding complex of PLP-dependent enzymes.³² Therefore, the observed BIE strongly supports our theoretical and progress curve analysis findings of K_I being the inhibitor constant (K_d) of the initial binding complex, which reflects the competition of the inactivator with substrate to the enzyme active site. BIE experiments for substrate binding were reported in the literature for alanine racemase and aspartate aminotransferase.^17,34 Those experiments either involved the determination of the complete set of microscopic rate constants associated with the mechanism or a modification of the enzyme to isolate the initial binding step. The current study demonstrates the capability of using simple progress curve analysis to determine the BIE of mechanism-based inactivators when the global kinetic parameter K_I represents the inhibitor constant of the initial binding complex (K_d).

CONCLUSION

A combination of various computational chemistry tools, including MD simulations, QM (DFT) calculations, and NBO analysis, as well as experimental methods, including progress curve analysis and KIE experiments, were utilized to comprehensively study the mechanism of inactivation of GABA-AT by CPP-115 and OV329. Furthermore, we established the validity of the global kinetic parameters associated with the inactivation mechanism (k_inact and K_I). We also showed that they accurately reflect the enhancement of the rate-limiting step and the competition of the inactivator with the substrate for the enzyme active site; therefore, they serve as reliable parameters to optimize MBEIs for a given mechanism.

Theoretical findings coincided well with the experimental findings, supporting the effectiveness of these methods as a combination to study and optimize MBEIs. For the proposed mechanism of inactivation of GABA-AT by CPP-115 and OV329, the rate-limiting step was found to be the deprotonation step, which also is the rate-limiting step with the substrate of the enzyme (GABA). The above finding was initially predicted from DFT calculations of energy profiles of the key steps in the inactivation mechanism and were later confirmed by progress curve analysis and KIE studies. The simplified expressions for k_inact (equation 3) and K_I(equation 4) in terms of the microscopic rate constants of the inactivation mechanism tend to correlate well with the experimental values and can be employed to predict the outcome of the structural modifications toward the mechanism in this work. Furthermore, for the given mechanism, the globally estimated inhibitor constant K_I correlates well with the inhibitor constant for the initial binding complex K_d based on the progress curve analysis results and the observed BIE. In fact, the K_I is only governed by the formation of the initial binding complex and well reflects the competition of the inactivators with the substrate for the active site. The observed K_I difference between CPP-115 and OV329 arises from the differences in the configurational entropy loss of the initial binding event. Most importantly, we have successfully demonstrated the use of progress curve analysis to compare the K_I with K_d values and determine the importance and reliability of the K_I value as an optimization parameter for a MBEI. The K_I value of a MBEI is only meaningful if it accurately reflects the enhancement of the rate-limiting step and correlates with competition of the inactivator with the substrate for the active site.⁸ The traditional tedious way of establishing this relationship has involved a complete kinetic characterization of the MBEI via the transient kinetic approach.⁸ As we have shown in this study, progress curve analysis can alone establish this correlation, which requires less effort compared to the transient kinetic approach. Also, the current study demonstrates an alternative use of the progress curve analysis method beyond its traditional use of determining the global kinetic parameters of MBEIs. We believe that the method presented here will be valuable for guiding MBEI optimizations in a meaningful way and establishing the validity of global kinetic parameters in the optimization process when the mechanism of inactivation is known.

EXPERIMENTAL SECTION

General Procedures

Unless otherwise noted, all of the reagents were obtained from commercial sources and used as received without further purification. All solvents were distilled and stored under an argon or nitrogen atmosphere before use. All of the syntheses were carried out under an atmosphere of argon using flame-dried glassware. ¹H NMR and ¹³C NMR spectra were recorded on a Bruker AVANCE III 500 spectrometer at 26 °C using DMSO-d₆ or CDCl₃ as solvents. Chemical shifts are reported in parts per million (ppm, δ) and referenced to DMSO-d₆ (2.50 ppm for ¹H NMR and 39.52 ppm for ¹³C NMR) or CDCl₃ (7.26 ppm for ¹H NMR and 77.2 ppm for ¹³C NMR). Coupling constants (J) are reported in Hz, and spin multiplicities are described as s (singlet), br (broad singlet), d (doublet), t (triplet), q (quartet), and m (multiplet). High-resolution mass spectra (HRMS) were measured with an Agilent 6210 LC-TOF (ESI,APCI, APPI) mass spectrometer. Purities of the final deuterated compounds were greater than 95%, as determined by reverse-phase HPLC analysis.

Compounds 4 and 5 were prepared according to literature procedures.^29,30

7-Bromo-2-(4-methoxybenzyl)-2-azabicyclo[2.2.1]heptane-3,6-dione-1-d (7).

Compound 5 (2.66 g, 11.55 mmol) was dissolved in AcOH (57.0 mL), and 1,3-dibromo-5,5-dimethylhydantoin (1.91 g, 6.93 mmol, 0.6 equiv) was added. The reaction mixture was stirred for 6 h and then diluted with water (200 mL). The aqueous layer was extracted with diethyl ether (2 × 100 mL), and the organic layers were washed with 1 M NaOH (50 mL), dried over Na₂SO₄, and concentrated to give compound 6 as an oil, which was used in the next step without further purification. The above compound was dissolved in 57 mL of methanol, and K₂CO₃ (5.38 g, 34.5 mmol, 3 equiv) was added. The reaction mixture was stirred for 1 h, filtered, and concentrated. The solid was suspended in EtOAc (150 mL) and washed with water (50 mL). After being dried over Na₂SO₄ and concentrated, a white solid (2.1 g, 6.42 mmol) of the corresponding alcohol was obtained and used without further purification.

Oxalyl chloride (0.71 mL, 8.34 mmol, 1.3 equiv) was added to CH₂Cl₂ (16 mL) and cooled to −78 °C. DMSO (0.59 mL, 8.34, 1.3 equiv) was then added dropwise via an addition funnel, and the reaction was stirred for 10 min. The above alcohol compound (2.1 g, 6.42 mmol) was dissolved in CH₂Cl₂ (16 mL) and added dropwise to the flask at −78 °C. After being stirred for 10 min, Et₃N (4.47 mL, 32.1 mmol, 5 equiv) was added, and the reaction was further stirred for 10 min, warmed to room temperature, and quenched with 1 M HCl. The layers were separated, and the organic layer was dried over Na₂SO₄ and concentrated. Flash chromatography yielded 7 (1.66 g, 5.1 mmol, 44% over three steps) as a white solid. ¹H NMR (500 MHz, CDCl₃) δ 7.2 (m, 1H), 7.0 (m, 1H), 4.8 (dd, J = 14.5, 11.1 Hz, 1H), 4.4 (m, 1H), 4.0 (m, 1H), 3.9 (s, 1H), 3.3 (m, 1H), 2.8 (dt, J = 17.8, 4.5 Hz, 1H), 2.3 (dd, J = 17.7, 2.7 Hz, 1H).¹³C NMR (126 MHz, CDCl₃) δ 202.9, 172.6, 159.6, 129.8, 127.0, 114.4, f (t, J = 26.6 Hz), 55.3, 48.9, 48.2, 45.3, 32.1. HRMS (ACPI⁺) calc’d for C₁₄H₁₄DBrNO₃: 325.03; found 324.34.

7-Bromo-6-(difluoromethylene)-2-(4-methoxybenzyl)-2-azabicyclo[2.2.1]heptan-3-one-1-d (8).

7 (300 mg, 0.92 mmol) and 2-((difluoromethyl)sulfinyl)pyridine (232 mg, 1.2 mmol, 1.3 equiv) were added to a round bottom flask and purged with argon. DMF (5 mL) was then added, and the reaction was cooled to between −55 and −65 °C. KO^tBu (166 mg, 1.5 mmol, 1.6 equiv, 0.5 M in DMF) was added via syringe pump over 1 h. The temperature was maintained between −55 and −65 °C. After addition was complete, the reaction mixture was further stirred for 30 min at −60 °C. Saturated NH₄Cl (1.00 mL) was then added, and the reaction mixture was stirred for 5 min at −60 °C before 6 M HCl (1.00 mL) was added. After 5 min of stirring at −60 °C, the reaction mixture was warmed to room temp and then to 65 °C for 1 h. After being cooled, the reaction mixture was diluted with brine, extracted (2 × 15 mL) with ethyl acetate, and washed with brine (10 mL). Upon drying over Na₂SO₄ and concentrating, an oil was obtained, which was purified via flash chromatography to yield 8 as a white solid (150 mg, 0.42 mmol, 46% yield). ¹H NMR (500 MHz, CDCl₃) δ 7.2 (d, J = 8.5 Hz, 1H), 7.0 (d, J = 8.6 Hz, 1H), 4.7 (d, J = 14.7 Hz, 1H), 4.3 (m, 1H), 4.0 (d, J = 14.7 Hz, 1H), 3.9 (s, 2H), 3.1 (td, J = 3.7, 1.7 Hz, 1H), 2.9 (dd, J = 15.3, 3.4 Hz, 0H), 2.4 (dq, J = 15.2, 2.2 Hz, 1H). ¹³C NMR (126 MHz, CDCl₃) δ 173.0, 153.9 (t, J = 290 Hz), 129.7, 127.5, 114.3, 87.0 (t, J = 24 Hz), 63.1 (m), 55.3, 50.9, 50.7, 44.6, 24.8. HRMS (ESI^-) calc’d for C₇H₇F₂NO₂-H: 174.0372; found 174.0369.

Methyl 3-((tert-butoxycarbonyl)amino)-4-(difluoromethylene)cyclopent-1-ene-1-carboxylate-1-d (9).

Intermediate 7-bromo-6-(difluoromethylene)-2-azabicyclo[2.2.1]heptan-3-one-1-d was prepared from 8 (150 mg, 0.42 mmol), which was added to MeCN (2.0 mL) and cooled to 0 °C. Ceric ammonium nitrate (686.5 mg, 1.25 mmol, 3 equiv) in 0.70 mL of H₂O was added dropwise. The reaction mixture was allowed to warm to room temp and stirred for 2 h. After completion, water was added, and the solution was extracted with ethyl acetate (2 × 10 mL). The organic layers were dried over Na₂SO₄ and concentrated under reduced pressure. Flash chromatography yielded 7-Bromo-6-(difluoromethylene)-2-azabicyclo[2.2.1]heptan-3-one-1-d as a white solid (60 mg, 0.25 mmol, 60% yield). ¹H NMR (500 MHz, CDCl₃) δ 6.6 (s, 1H), 4.3 (d, J = 2.8 Hz, 1H), 2.9 (d, J = 3.8 Hz, 1H), 2.9 (dq, J = 15.3, 3.4 Hz, 1H), 2.3 (dd, J = 15.4, 2.0 Hz, 1H). ¹³C NMR (126 MHz, CDCl₃ δ 175.5, 153.4 (t, J = 285 Hz), 88.6 (t, J = 24.1 Hz), 60.5 (m), 51.5, 50.4, 24.2. HRMS (ESI⁺) calc’d for C₇H₆DBrF₂NO: 238.9742; found 238.9740.

The 7-bromo-6-(difluoromethylene)-2-azabicyclo[2.2.1]heptan-3-one-1-d (60.0 mg, 0.25 mmol) prepared above was added to dichloromethane (1.5 mL) followed by the addition of Boc₂O (65 mg, 0.30 mmol, 1.2 equiv), DMAP (3 mg, 0.03 mmol, 0.1 equiv), and Et₃N (0.07 mL, 0.5 mmol, 2 equiv). The reaction mixture was stirred for 2 h and then was washed with 1 M HCl (5 mL), dried over Na₂SO₄, and concentrated. The resulting oil was dissolved in methanol (1.5 mL), then K₂CO₃ (104 mg, 0.73 mmol, 3.0 equiv) was added, and the reaction mixture was stirred for 6 h. The reaction mixture was diluted with brine and extracted with ethyl acetate (3 × 20 mL). After being dried over Na₂SO₄, concentrated, and purified by flash chromatography, 9 was obtained as a white solid (40 mg, 0.14 mmol, 55% yield; ¹H NMR (500 MHz, CDCl₃) δ 6.6 (m, 1H), 4.6 (s, 1H), 3.7 (s, 3H), 3.3 (dq, J = 20.3, 2.7 Hz, 1H), 3.2 (dq, J = 20.3, 2.7 Hz, 1H), 1.4 (s, 9H). ¹³C NMR (126 MHz, CDCl₃) δ 164.3, 154.6, 152.4 (t, J = 289.4 Hz), 140.6, 135.6, 88.8 (t, J = 22.2, 20.8 Hz), 80.1, 55.0 (m), 51.9, 31.1 (d, J = 2.5 Hz), 28.3. HRMS (ESI⁺) calc’d for C₁₃H₁₆DF₂NO₄ + Na: 313.1086, found 313.1077.

3-Amino-4-(difluoromethylene)cyclopent-1-ene-1-carboxylic acid hydrochloride-1-d (10).

9 (40.0 mg, 0.14 mmol) was dissolved in dioxane (0.5 mL), and 6 M HCl (0.5 mL) was added. After being heated at 80 °C for 2 h, the reaction mixture was concentrated to yield 10 as a light brown powder. Crystallization from ethanol/diethyl ether yielded pure 10 as an off-white powder (12 mg, 0.06 mmol, 40%). ¹H NMR (500 MHz, D₂O) δ 6.4 (s, 1H), 3.4 (dd, J = 20.4, 2.9 Hz, 1H), 3.3 (d, J = 20.4 Hz, 2H). ¹³C NMR (126 MHz, D₂O) δ 168.3, 152.9 (t, J = 293.9, 290.1 Hz), 143.2, 133.0, 86.3, 54.6, 31.3. HRMS (ESI⁺) calc’d for C₇H₇DF₂NO₂ 177.0586; found 177.0587.

Determination of k_inact and K_I Values and the KIE

The activity of GABA-AT was measured in the presence of different concentrations of rac-OV329 (deuterated and non-deuterated); the detailed procedure can be found elsewhere.² The progress curve analysis was carried out by fitting the obtained data into equation 7 to obtain k_obs values at different inactivator concentrations. Then these values were fitted into the following equation to obtain the k_inact and K_I values,⁸

$$k_{\mathrm{o}\mathrm{b}\mathrm{s}}=\frac{k_{\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{c}\mathrm{t}}\left[I\right]}{K_{\mathrm{I}}^{\mathrm{a}\mathrm{p}\mathrm{p}}\times \left[I\right]}$$

where [I] is the inhibitor concentration and the $K_{\mathrm{I}}^{\mathrm{a}\mathrm{p}\mathrm{p}}$ is the apparent inhibitor constant of the inactivator. From the above $K_{\mathrm{I}}^{\mathrm{a}\mathrm{p}\mathrm{p}}$ value K_I of the inactivator was derived according to the following equation,

$$K_{\mathrm{I}}^{\mathrm{a}\mathrm{p}\mathrm{p}}=K_{\mathrm{I}}(1+\raisebox{1ex}{$\left[S\right]$}\!\left/ \!\raisebox{-1ex}{$K_{\mathrm{M}}$}\right.)$$

where [S] is the substrate concentration and K_M is the Michaelis constant of the substrate (GABA) of the enzyme (GABA-AT). The KIE associated with each global kinetic parameter was estimated as the ratio of the non-deuterated and deuterated rac-OV329.

The progress curve analysis data obtained for CPP-115 and OV329 in our previous study were re-analyzed to obtain the v_i and v_s values (initial and steady-state velocity values, respectively).³⁵ The v_i values were used to estimate the percent inhibition of the enzyme, from which the IC₅₀ values were calculated for the reversible part of the enzyme inhibition, which also corresponds to the initial binding complex formation. The calculated IC₅₀ values were converted to $K_{\mathrm{I}}^{*}$ values (inhibitor constant of the reversible part of the mechanism) using the Cheng-Prusoff equation.³⁶ GraphPad Prism 6 software was used for the analysis.

Quantum Mechanical Calculation Details

All of the geometry optimizations and frequency calculations of the species involved in the two reaction steps (deprotonation and the water-mediated nucleophilic attack) were performed by DFT at the B3LYP/6–31+G(d,p) level of theory using Gaussian09 software³⁷. The polarization functions on the hydrogen atoms were utilized to provide a more accurate description, especially for the deprotonation step. The optimizations and the evaluation of free energy values for the simplified model were performed in the gas phase, while for the cluster model, the optimizations and the calculations were done in aqueous phase using a conductor-like polarizable continuum model. All of the free energy values include zero-point energy corrections and thermal free energy corrections at 298 K and 1 atm. The characterizations of minima and saddle points were done by performing frequency analysis on the optimized geometries. Intrinsic Reaction Coordinate calculations were performed to further confirm the TS. The activation free energy values were calculated as the difference of the free energies between the TS and the reactants. The estimation of the forward reaction rate constants for the deprotonation step was done according to equation 6.

In the simplified model, methylamine was used to model Lys329. The carboxylic group of the inactivators, the hydroxyl group, imine, and the pyridine nitrogen of the PLP were considered as protonated. The phosphate group of the PLP was replaced by a methyl group. In the cluster model, all of the residues that interact with the PLP bound inactivators, which include Arg192, Gln301, Asp298, and Lys329, were incorporated and truncated at C_δ, C_γ, C_β, and C_α atoms, respectively. The atoms at the truncated points (C_δ, C_γ, C_β, and C_α) of the amino acid residues were frozen and held fixed during the optimization using redundant coordinates. The initial coordinates for the cluster model were taken from the MD simulations of the EI complex performed in the current study and from our previous MD simulations of the EB complex. The NBO analysis of the reactants and the TS of CPP-115 and OV329 were carried out at the same level of theory as used in the cluster model to determine the GS destabilization and the TS stabilization in the deprotonation step.

The pK_a values of the free inactivators and the PLP bound inactivators in water were calculated using the thermodynamic cycle approach according to a previously published procedure.³⁸ The details of the calculations, including equations, the thermodynamic cycle scheme, and the energy values, are given in the Supporting Information.

Molecular Dynamics Simulations

All of the MD simulations were carried out using the GROMACS 5.1.2 software package³⁹ according to our previously published protocol.² The MD simulation time for the EI complex was 50 ns, and for the free inactivators in water and the EI* complex the simulation time was 30 ns. To determine the important distance and angle measurements of the EI complex mentioned in the manuscript, the distance, mindist, and angle tools available in the GROMACS software package were used.

Principal component analysis (PCA) was performed on the five-membered ring heavy atoms of CPP-115 and OV329 in water to investigate their flexibilities and the conformational differences. A detailed procedure can be found elsewhere.^35,40 In addition, the configurational entropy of the free and bound form of the inactivators was estimated using a quasi-harmonic approximation (QHA) with the PCA analysis on all the heavy atoms of the inactivators. The configurational entropy loss was calculated as the configurational entropy difference between the bound and the free forms of the inactivators at 310 K. To perform the above tasks, the covar (for PCA), anaeig (for PCA/QHA) and sharm (for free energy landscape) tools available in the GROMACS software package and in-house python scripts were utilized.