Sparse Coding in Temporal Association Cortex Improves Complex Sound Discriminability

Abstract

The mouse auditory cortex is comprised of several auditory fields spanning the dorsoventral axis of the temporal lobe. The ventral most auditory field is the temporal association cortex (TeA), which remains largely unstudied. Using Neuropixels probes, we simultaneously recorded from primary auditory cortex (AUDp), secondary auditory cortex (AUDv), and TeA, characterizing neuronal responses to pure tones and frequency modulated (FM) sweeps in awake head-restrained female mice. As compared with AUDp and AUDv, single-unit (SU) responses to pure tones in TeA were sparser, delayed, and prolonged. Responses to FMs were also sparser. Population analysis showed that the sparser responses in TeA render it less sensitive to pure tones, yet more sensitive to FMs. When characterizing responses to pure tones under anesthesia, the distinct signature of TeA was changed considerably as compared with that in awake mice, implying that responses in TeA are strongly modulated by non-feedforward connections. Together, these findings provide a basic electrophysiological description of TeA as an integral part of sound processing along the cortical hierarchy.

SIGNIFICANCE STATEMENT This is the first comprehensive characterization of the auditory responses in the awake mouse auditory temporal association cortex (TeA). The study provides the foundations for further investigation of TeA and its involvement in auditory learning, plasticity, auditory driven behaviors etc. The study was conducted using state of the art data collection tools, allowing for simultaneous recording from multiple cortical regions and numerous neurons.

Introduction

The mouse auditory cortex is comprised of several auditory fields, the definition of which may vary between parcellation methodologies (Geissler et al., 2016; Tsukano et al., 2016). The most ventral region of these fields is the auditory temporal association cortex (TeA). While both primary (AUDp) and secondary/ventral (AUDv) auditory fields were subject to significant research over several decades and in several species (Rothschild et al., 2010; Issa et al. 2014, 2017; Maor et al., 2016; Ohga et al., 2018), TeA remained largely unexplored.

In the rodent brain, TeA is a narrow and elongated cortical field, located below somatosensory, auditory and visual cortices. TeA is subdivided to these sensory modalities according to its corresponding positions along the rostro-caudal axis (Zingg et al., 2014; Ramesh et al., 2018; Yamashita et al., 2018). The auditory TeA region in the mouse or analogous fields in the rat were shown to be tonotopically organized and involved in auditory fear-conditioning (Quirk et al., 1997; Polley et al., 2007; Dalmay et al., 2019; Romero et al., 2020). Recently, the auditory TeA was shown to play a key role in maternal behavior in the context of the mother's processing of pup ultrasonic vocalizations (Tasaka et al., 2020). Otherwise, to the best of our knowledge, little is known about the function or physiology of TeA.

Here, we set out to study basic response profiles of single neurons and populations in auditory TeA (hereafter, called TeA) of awake head-restrained mice. Using Neuropixels probes (Jun et al., 2017), we recorded single-unit (SU) activity from multiple neurons and cortical regions simultaneously. We used both pure tones and frequency-modulated (FM) sounds as auditory stimuli, while simultaneously recording responses in AUDp, AUDv, and TeA. We describe the activity in TeA with respect to its upstream primary cortices. We found that, as compared with more primary stations, TeA exhibits sparser auditory-driven activity with more complex late activity that is likely modulated by non-feed-forward signals. As compared with AUDp, TeA shows lower discriminability to simple tones, and better discriminability to the more complex FM sweeps. We also compared the response profile of AUDp and TeA under two physiological states, wakefulness and anesthesia. We show that anesthesia has distinct effects in these brain regions.

Materials and Methods

Extracellular recordings using Neuropixels

Ten- to 13-week-old TRAP2;TB double heterozygous females (F1 hybrid of C57BL/6 and FVB strain; Tasaka et al., 2020, 2018 n = 5 awake mice, n = 5 anesthetized mice) were used for electrophysiological recordings. The data set is the same as the naive animal dataset used in Tasaka et al., 2020. Before the recording, a custom-made metal bar was implanted on the mouse skull, and a small craniotomy was made on the left hemisphere (coordinates relative to bregma: anterior −2.5, lateral 4.2 mm). The craniotomy was protected by a wall of dental cement and covered with a silicone elastomer (WPI; Kwik-Cast catalog #KWIK-CAST). The surgery was done under ketamine medetomidine anesthesia (0.80 and 0.65 mg/kg, respectively) and a subcutaneous injection of carprofen (0.004 mg/g). For awake recordings, mice were given 1–2 d to recover, after which they were head-fixed for ∼30 min to habituate to the recording setup. Recordings were performed 1–2 d posthabituation. On the day of the recording, animals were head-fixed and the craniotomy was exposed. Then, a Neuropixels probe (IMEC, phase 3A) was inserted through the craniotomy in a 20-degree tilt (from vertical position) and lowered down ∼3 mm deep. Penetration and probe depth were performed and monitored using a micromanipulator (Scientifica PatchStar micromanipulator). Probes were covered with a fluorescent dye [DiI (Invitrogen catalog #V22885) or DiO (Invitrogen catalog #V22886)] before penetration, to enable reconstruction of penetration sites in high resolution. For anesthetized recordings, the procedure was the same but followed the surgery directly, under continuous anesthesia. In each mouse, we performed up to three consecutive probe penetrations. Probe trajectories were reconstructed from consecutive coronal slices (for histological methods, see Tasaka et al., 2020) using an open source software (Shamash et al., 2018; Fig. 1D). Following the reconstruction, probe channels were annotated with corresponding brain regions they were recording from.

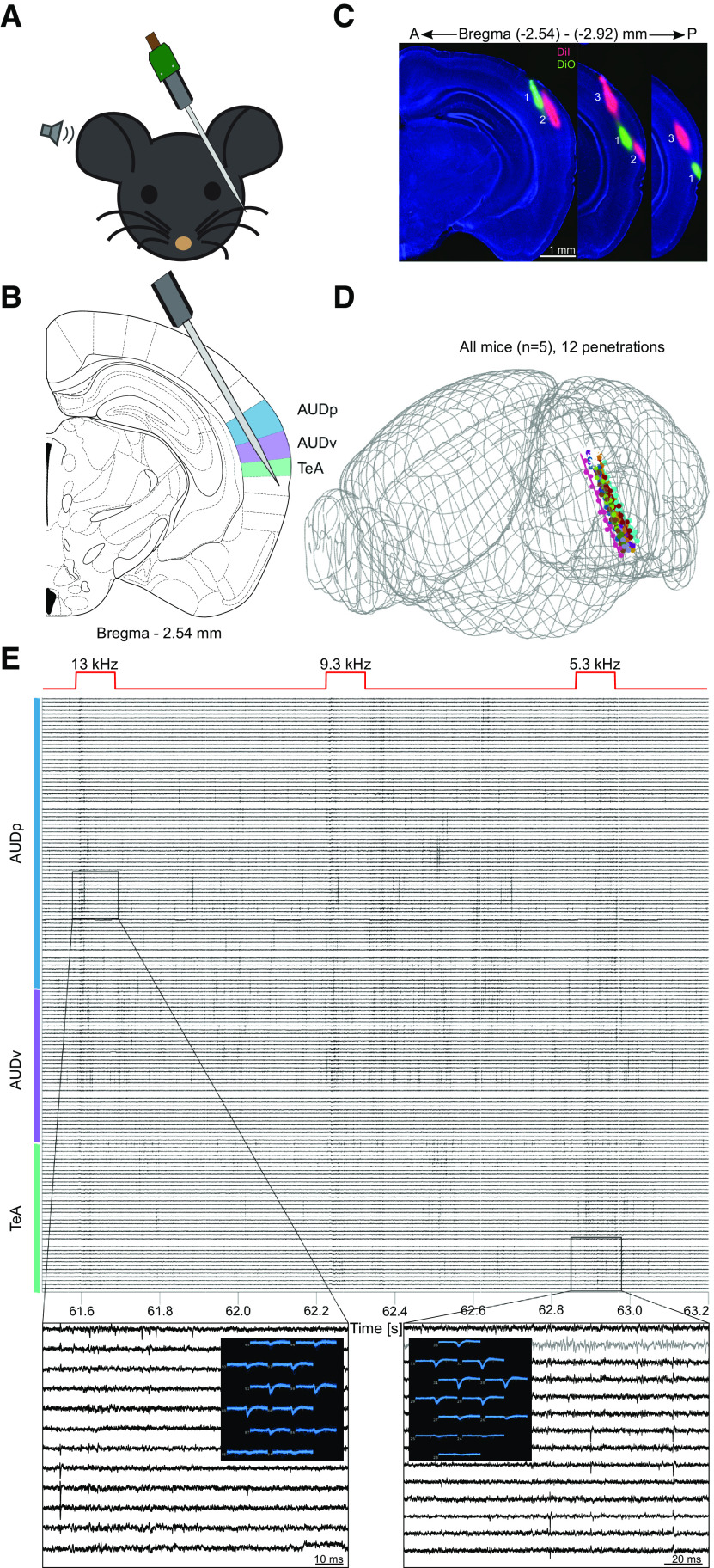
Figure 1.

Simultaneous recording from three auditory cortices in awake mice. A, Schematic representation of the experimental setup. B, Probe penetration setting enabling simultaneous recording of activity from three auditory cortices (AUDp, AUDv, and TeA; highlighted in color). C, Three consecutive fluorescent images of coronal brain slices showing three probe tracks in one mouse. D, Reconstructed trajectories of all probe tracks (12 penetrations, n = 5 mice). E, A 1.7-s snippet of the raw voltage traces recorded during pure tone presentation (total of 156 contacts shown). Top red trace shows the delivered sound stimuli, with captions indicating frequency in kHz. Color bar shows annotated regions according to channel and depth. Two activity snippets are shown in zoomed-in version (gray trace, internal reference channel). A snapshot shows how the activity of one unit is captured by several nearby channels within the snippet.

All recordings were acquired using Neuropixels phase 3A probes (IMEC), a base-station connector (IMEC) and a commercially available FPGA board (KC705, Xilinx). An external reference electrode (Ag/AgCl wire) was positioned on the skull and covered with saline solution. Data were sampled at 30 kHz, with action potential band filtered to contain 0.3- to 10-kHz frequencies. Action potential band gain was set to 500. All recordings from the same animal and position were concatenated, and automatically sorted using Kilosort/Kilosort2 (anesthetized and awake correspondingly) open source software (Pachitariu et al., 2016; https://github.com/MouseLand/Kilosort2). Following automatic sorting, manual sorting was performed using the “Phy” open-source GUI (UCL; https://github.com/cortex-lab/phy). During manual sorting, spike clusters were merged based on assessment of waveform similarity and the appearance of drift patterns. Finally, each spike cluster was assessed in criteria of waveform size, consistency, and the presence of short-latency interspike intervals (ISIs). If and only if a cluster was classified by Kilosort2 as a well isolated SU with minimal contamination (based on violations of the expected refractory period, see https://github.com/MouseLand/Kilosort/wiki) and the manual inspection showed it to be satisfactory on all abovementioned accounts, it was tagged as a SU implying it corresponds to a single neuron. If a cluster did not meet the above criteria but was clearly reflecting neuronal activity (and not noise) it was tagged as a multi-unit (MU), corresponding to a group of neurons clustered together. A more detailed explanation for the manual sorting guidelines can be found in https://phy.readthedocs.io/en/latest/sorting_user_guide. Figures 1D was generated using the Allen CCF software (UCL; https://github.com/cortex-lab/allenCCF). Figure 1E was generated using the Neuropixels-utils software kit, developed by Dan O'shea (https://github.com/djoshea/neuropixel-utils).

Auditory stimuli

The pure tone protocol was comprised of 30 pure tones (100 ms in duration, 5 ms on and off linear ramps) logarithmically spaced between 3 and 80 kHz, presented at four sound pressure levels (72, 62, 52, and 42 dB SPLs). Each frequency x attenuation combination was presented 12 times. Pure tones were presented in a random order, with 600-ms intervals between tone onsets.

The FM protocol was comprised of 10 stimuli, spanning the range between 4 and 64 kHz either in a positive (“rising”) of negative (“falling”) FM (1 ms on and off linear ramps). The stimuli had five different logarithmic slopes that generated stimuli with varying durations (±2 octaves/s 2 s, ±5.32 octaves/s 752 ms, ±14.14 octaves/s 283 ms, ±37.61 octaves/s 106 ms, ±100 octaves/s 40 ms). All stimuli were presented in 62 dB SPL for 12 repetitions. Stimuli were presented at 0.37 Hz in randomized order.

Pure tone data analysis

Data analysis and statistics were performed using a custom written code in MATLAB (MathWorks). Before analysis, MUs and SUs firing <10 spikes during the entire protocol were eliminated. Spontaneous firing rates (FRs) are the mean of the baseline activity (100 ms) preceding all trials (n = 1440). To detect auditory units, we looked for 50-ms maximal and minimal response windows in the time between 0 and 200 ms poststimulus onset. The maximal and minimal response windows were then compared with 50 ms of baseline (one-sided two-sample t test, p < 0.05). According to test results, units were considered as excited and or suppressed. If no significant window was found, the unit was considered non-auditory and excluded from further analysis. Based on these response windows, frequency-response areas (FRAs) were extracted, and the best frequency (BF) of excited units was identified as the frequency evoking the maximal response (in a single attenuation). Evoked FRs were considered as FRs in response to a units' BF during the maximal response window, subtracted with the units' spontaneous FR.

To determine the significance of responses to individual frequency x attenuation combinations, response during the optimal (excited) windows was compared with baseline activity in the relevant trials via one-tailed Wilcoxon rank-sum tests. Bandwidth of excited units was calculated as the number of frequencies played at 62 dB SPL which elicited a significant response, subtracted with the number of expected false positives based on the number of performed comparisons and the required significance level (30 frequencies, p < 0.05; expected FP 30 × 0.05 = 1.5). Population sparseness was then calculated as the fraction of units in each region exhibiting a significant excitatory response to each one of the stimuli played at 62 dB SPL. Lifetime sparseness was calculated for excited units from FRs to all tones in a given attenuation (chosen to be the attenuation of the BF) using the following formula:

$$S=\left(1-\left[\frac{{\left(\frac{\text{Σ}{r}_i}{n}\right)}^2}{\frac{\text{Σ}{r}_i^2}{n}}\right]\right)/\left[1-\frac{1}{n}\right].$$

The values $r_i$ are the FRs in response to each frequency, and n = 30 is the number of pure tones presented. Values of S near 0 correspond to a dense code and values near 1 correspond to a sparse code (Vinje and Gallant, 2000).

Latency to peak was calculated as the time poststimulus in which the units' PSTH (smoothed with a 9-ms window) is maximal. A similar approach was applied for time to minima of suppressed units. To calculate minimal latency, we first screened for units having a significant early excitatory response window, by looking for a significant 50-ms excitatory response window within 0–110 ms poststimulus onset (similarly to what was described above). We calculated FRAs for the early response windows and extracted the “early BF.” The trials corresponding to the early BF were isolated (only trials from the best attenuation), and the latency of the first poststimulus spike in each trial was detected. The minimal latency of a unit was considered the early BFs' median latency to first spike.

Population response was calculated by averaging the trials of all units in a given region to each one of the pure tone stimuli (frequency x attenuation combination). After averaging, the mean baseline response (100 ms prestimulus onset) was subtracted from the trace, and the response was smoothed (9-ms window). Finally, the population responses to all stimuli were averaged together to obtain mean and SEM of the population response to pure tones. To assess deviation from baseline, the population response at every given 1-ms time bin was compared via a two-sample t test to the mean baseline population response (average of the activity during 100 ms prestimulus). Required significance level was corrected for multiple comparisons by requiring p < 0.05/# compared time bins (p < 0.05/700).

FM analysis

Here too, data analysis and statistics were performed using a custom written code in MATLAB (MathWorks). Before analysis, MUs and SUs firing <10 spikes during the entire protocol were eliminated. First, and similarly to pure tones, maximal and minimal 50-ms response windows were detected in response to each one of the FM stimuli. For each such window, the FR within the window was calculated, and the response was compared with 50 ms of baseline in a one-tailed Wilcoxon rank-sum test. This determined whether a unit was significantly excited/suppressed by each FM stimulus (total of 10 stimuli). Units were considered responsive to FMs if at least one FM stimulus elicited a significant excitatory/suppressive response. A unit was considered excited if it had a significant excitatory window to at least one FM stimulus, and suppressed if the same was true for suppressive windows. If both types of windows were significant for at least one stimulus, the unit was considered both excited and suppressed. FM bandwidth was considered the number of FM stimuli (out of total 10) eliciting a significant excitatory response. Population sparseness and lifetime sparseness were calculated similarly to pure tones based on responses to all FM stimuli.

Direction selectivity index (DSI) was calculating using $DSI=\frac{FR\uparrow -FR\downarrow }{FR\uparrow +FR\downarrow }$, where $FR\uparrow$ refers to the summed FR for all rising FMs, and $FR\downarrow$ is the summed FR for all falling FMs. FRs were calculated based on maximal 50-ms response window to each FM stimulus. To calculate population speed selectivity, each unit's response to FMs with the same slope and different directions was summed (responses calculated based on maximal response windows for each FM as mentioned before). All units within each region were pooled, and the population response to different FM speeds was pairwise compared via a two-sampled t test; p value significance level was Bonferroni corrected to the number of performed comparisons (0.05/10).

FM minimal latency and latency to peak were calculated similarly to pure tones, only using FM stimuli trials and PSTHs.

Correlation analysis

Pairwise signal correlations (SCs) were calculated by computing the Pearson correlation of FRAs between every pair of simultaneously recorded units. Note that since FRAs were calculated based on response windows unique to each unit, correlated variability (noise correlation; NC) should not contribute to the calculated SCs. FRAs were constructed based on excitatory response windows for units having them and based on suppressive response windows for units lacking excitatory responses. Shuffled distributions were calculated by correlating shuffled FRAs and repeating this for n = 500 iterations. To calculate NCs, data were binned into 20-ms bins. For each pure tone stimulus (frequency x attenuation combination) the mean response in all time bins was calculated and subtracted from all individual trials to obtain “trial-fluctuation-vectors.” For each unit, fluctuations from 0 to 200 ms (10 time bins) poststimulus (from all stimulus trials) were concatenated to form a long fluctuation vector. Pairwise NCs were calculated via Pearson correlating between the concatenated fluctuation vectors. Shuffled NCs were calculated by randomizing the time bins in each units' fluctuation vector and calculating the resulting Pearson correlation. This procedure was repeated for n = 500 iterations.

d Prime analysis

In order to estimate the ability of a network to discriminate between two given pure tones or FM sweeps, we calculated pairwise d primes based on the activity of the entire SU population recorded in each region (calculation similar to that in Shani-Narkiss et al., 2020). For two given auditory stimuli (either two pure tones or two FM sweeps), p and q, d primes were calculated according to the formula:

$$d^{\prime }=\frac{Distance\left(mean\left(p\right),mean\left(q\right)\right)}{Mean\left(inner-distanc{e}_p,inner-distanc{e}_q\right)},$$

where p/q is a matrix with 12 columns (one column for each repetition) and n rows (n = number of SUs in each cortical region), in which each entry contains the response of a specific SU to a specific stimulus at a specific trial; mean(p)/mean(q) are vectors with n entries representing the mean coordinates (averaged over the individual trials) in n-dimensional space for stimuli p/q. The difference between these vectors was assessed as a scalar by Euclidean distance, i.e., $\sqrt{{\text{Σ}}_{i=1}^n{\left(\widehat{p_i}-\widehat{q_i}\right)}^2}$. Inner-distance_p and inner-distance_q were similarly assessed as two scalars, by calculating the Euclidean distance between each one of the 12 single trials with the stimulus average representation, and then averaging over the 12 resulting measures. Since the d prime is the ratio of two Euclidean distances in the same n-dimensional space, the end result is not dependent on the size n and is comparable between populations of different sizes.

Experimental design and statistical analysis

All statistical analyses were performed with MATLAB (MathWorks). Comparison between AUDp, AUDv, and TeA for pure tone response properties such as spontaneous FR, responsivity, BFs, evoked firing rated, bandwidth, population sparseness, and lifetime sparseness (Fig. 2, all sections aside of 2 h) were conducted using Kruskal–Wallis (KW) test, followed up with post hoc Tuckey–Davies HSD (TK HSD). BF differences between nearby units originating from the same or different cortical regions (2 h) were compared using Wilcoxon rank-sum test. Pure tone response latencies (Fig. 3B–D) of different cortices were compared using KW followed by TD HSD. Sparseness metrics for FM responses (Fig. 4D–F) as well as DSIs (Fig. 5A) were compared between regions using KW followed by TD HSD. Correlation magnitudes were compared between regions using Wilcoxon rank-sum tests, and compared with shuffled distributions using the Kolmogorov–Smirnoff (KS) test. Comparison between pure tone response properties under anesthesia of AUDp and TeA were conducted between regions and between conscious states using Wilcoxon rank-sum tests. Testing FR distributions for normality (spontaneous and evoked FRs) was performed using Lilliefors test.

Figure 2.

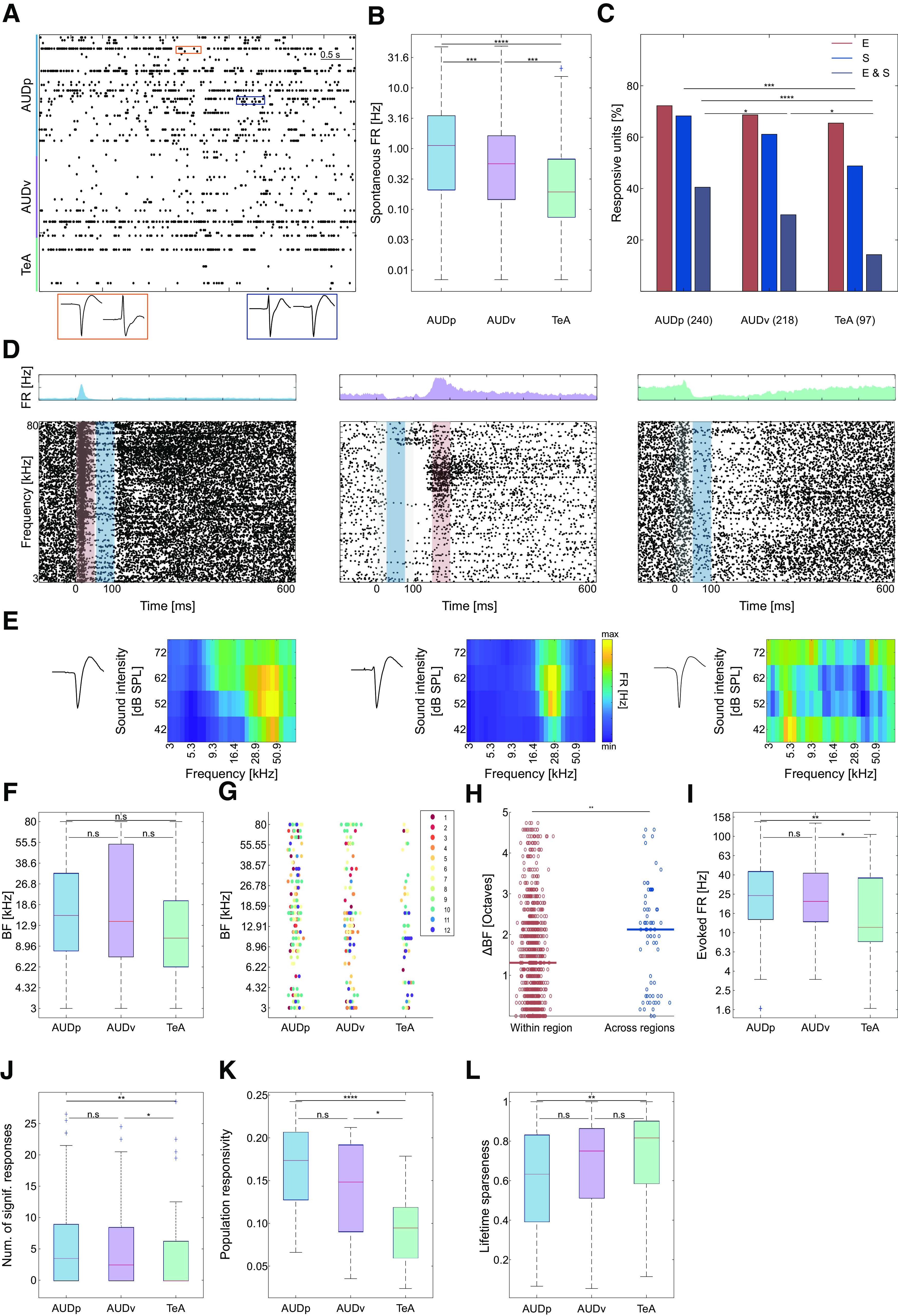
Pure tone response properties in TeA, AUDp, and AUDv. A, Raster plot showing 5 s of spontaneous activity. Color bar shows annotated regions according to channel and depth. Examples of waveforms from two pairs of SUs recorded from the same channel are shown at the bottom (orange pair, channel 173; blue pair, channel 130). B, Spontaneous FRs (log-scaled) of SUs in the three cortices [median (IQR): AUDp, 1.13 (0.21–3.48) n = 240; AUDv, 0.56 (0.14–1.63) n = 218; TeA, 0.19 (0.07–0.67) n = 97]. Spontaneous FRs decrease along the auditory D-V axis (H₍₂₎ = 35.85, p < 1e-4; Kruskal–Wallis), are highest in AUDp, and lowest in TeA (AUDp vs AUDv p = 0.003, AUDp vs TeA p < 1e-4, AUDv vs TeA p = 0.003; TK HSD test). C, Bar graph showing the distribution of response types to pure tones (E, excitatory; S, suppressive, E&S, both) in all cortical regions. Percentage computed out of all responsive units (number of SUs shown in parentheses). Excitatory responses are abundant and their fraction is maintained high in all three cortices (H₍₂₎ = 1.5, p = 0.47; Kruskal–Wallis), while abundance of suppressed units (H₍₂₎ = 10.06, p = 0.006; Kruskal–Wallis; AUDp vs AUDv, p = 0.28 n.s.; AUDp vs TeA p < 0.005; AUDv vs TeA p = 0.12 n.s.; TK HSD test) as well as units showing both response types decreases from AUDp to TeA (H₍₂₎ = 20.1, p < 1e-4; Kruskal–Wallis; AUDp vs AUDv, p = 0.048; AUDp vs TeA, p < 1e-4; AUDv vs TeA, p = 0.03 TK HSD test). D, Three examples of SU responses to pure tones recorded in AUDp (left), AUDv (center), and TeA (right). Above each raster is the unit's PSTH (scale adjusted per unit). Stimulus is presented between 0 and 100 ms (gray shaded region), and each units' maximal or minimal response window is marked by a red and/or blue bar, respectively. The units are categorized as excitatory and suppressed (left and center) and suppressed (right). E, FRAs corresponding to the three SUs shown in D. FRAs pixel values correspond to the excitatory (left and center) or suppressive (right) response window. To the left of the FRAs, spike waveform templates of the corresponding units are shown. F, SU BFs across brain regions [median (IQR): AUDp, 15.5 (8.3–32.3) kHz, n = 164 SUs; AUDv, 13.8 (7.4–53.9) kHz, n = 136 SUs; TeA, 10.4 (6.3–20.0) kHz, n = 55 SUs]. We found no effect of brain region over BF (H₍₂₎ = 3.07, p = 0.21; Kruskal–Wallis), as well as no difference between BF medians (AUDp vs AUDv, U = 2.470e4, p = 0.98 n.s.; AUDp vs TeA U = 1.875e4, p = 0.08 n.s.; AUDv vs TeA U = 1.357e4, p = 0.14 n.s.; Wilcoxon rank-sum test). G, SU BF distribution by recorded region and probe penetration. Each point represents the BF of one SU, with colors corresponding to unique probe penetrations (units sharing color were simultaneously recorded). BF distribution in all regions do not vary across penetrations (H₍₁₁₎ = 18.92, p = 0.06; Kruskal–Wallis); however, within region one, AUDv recording (#7) was biased toward high BF ranges (AUDp, H₍₁₁₎ = 9.97, p = 0.53 n.s.; AUDv, H₍₁₁₎ = 32.74, p = 0.0006; TeA, H₍₁₁₎ = 10.46, p = 0.23 n.s.; Kruskal–Wallis). H, BFs difference in octaves of adjacent SUs (⩽8 contacts apart or up to ∼80-μm distance) originating from the same or different (“within region”/“across regions”) brain regions [median (IQR): within region, 1.31 (0.49–2.29) octaves, n = 880 pairs; across regions, 2.12 (0.49–2.87), n = 69 pairs]. Transition between auditory cortices shows increased shifts in units' BFs (U = 4.110e5, p = 0.0013; Wilcoxon rank-sum test). I, Evoked FRs at BFs [median (IQR): AUDp, 24.5 (13.9–43.3) Hz, n = 164 SUs; AUDv, 21.2 (13.1–41.7) Hz, n = 136 SUs; TeA, 11.4 (8.2–37.2) Hz, n = 55 SUs]. SUs in TeA had lower FRs compared with units from both AUDp and AUDv (H₍₂₎ = 11.13, p = 0.004; Kruskal–Wallis; AUDp vs AUDv, p = 0.63 n.s.; AUDp vs TeA, p = 0.002; AUDv vs TeA, p = 0.03; TK HSD test). J, Bandwidth of SUs assessed as the number of frequencies at 62 dB SPL evoking a significant response [median (IQR): AUDp, 3.5 (0–9), n = 164 SUs; AUDv, 2.5 (0–8.5), n = 136 SUs; TeA, 0 (0–6.25), n = 55 SUs]. Bandwidth in TeA was smaller than in AUDp and AUDv (H₍₂₎ = 10.08, p = 0.006; Kruskal–Wallis; AUDp vs AUDv, p = 0.6 n.s.; AUDp vs TeA, p = 0.004; AUDv vs TeA, p = 0.04; TK HSD test). K, Population sparseness quantified as response probabilities of SUs in each region to all frequencies played at 62 dB SPL [median (IQR): AUDp, 0.17 (0.12–0.21), AUDv, 0.15 (0.09–0.19), TeA, 0.09 (0.06–0.12)]. Response probability is highest in AUDp and lowest in TeA (H₍₂₎ = 21.86 p < 1e-4; Kruskal–Wallis; AUDp vs AUDv, 0.2 n.s.; AUDp vs TeA, p < 1e-4; AUDv vs TeA, p = 0.01; TK HSD test). L, Lifetime sparseness of SUs [median (IQR): AUDp, 0.64 (0.39–0.83), AUDv, 0.75 (0.51–0.87), TeA, 0.82 (0.59–0.90)]. Sparseness was larger in TeA compared with AUDp (H₍₂₎ = 11.32, p = 0.003; Kruskal–Wallis; AUDp vs AUDv, p = 0.08 n.s.; AUDp vs TeA, p = 0.004; AUDv vs TeA, p = 0.3 n.s.; TK HSD test).

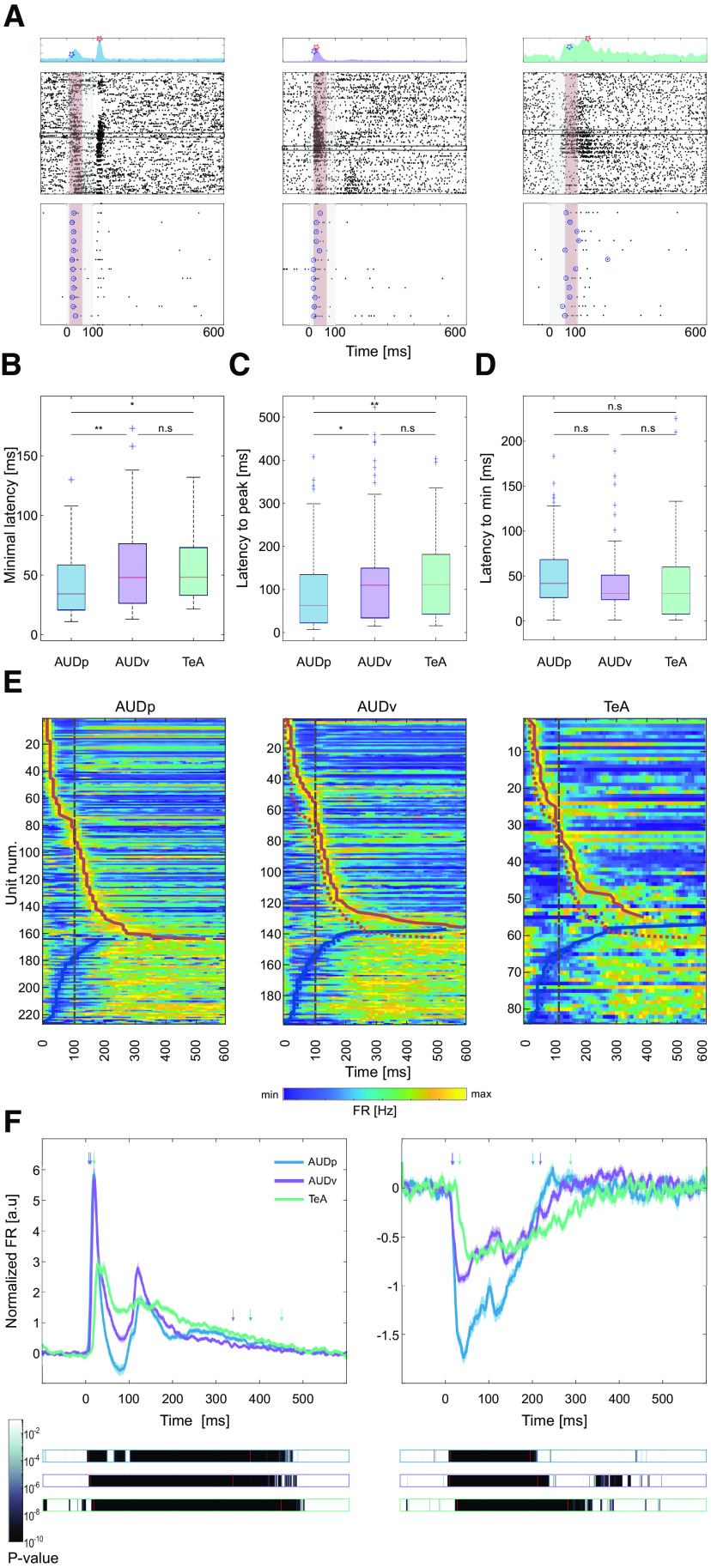
Figure 3.

Temporal response profile of SUs in TeA, AUDp, and AUDv. A, Three representative example SUs from AUDp (left), AUDv (center), and TeA (right). Top, PSTHs showing the units' minimal latency (blue marker) and latency to peak (red marker). Center, Raster plots (details as in Fig. 2D). Red shaded regions mark the 50-ms maximal early response windows of each unit, and black rectangles mark the units' early BF trials. Bottom, Magnification of early BF trials with circles surrounding the first spike in each trial. B, Minimal latency across brain regions [median (IQR): AUDp, 34 (21–59) ms n = 123; AUDv, 48 (26–76) ms n = 101; TeA, 48 (33–73) ms n = 38]. Minimal latency in AUDp was shorter compared with both other auditory cortices (H₍₂₎ = 12.43, p = 0.002; Kruskal–Wallis; AUDp vs AUDv, p = 0.007; AUDp vs TeA, p = 0.02; AUDv vs TeA, p = 0.9 n.s.; TK HSD test). C, Latency to peak across brain regions [median (IQR): AUDp, 63 (23–135) ms n = 164; AUDv, 110 (34–149) ms n = 136; TeA, 112 (43–181) ms n = 55]. TeA units' latency to peak was larger than that of AUDp units (H₍₂₎ = 12.48, p = 0.002; Kruskal–Wallis; AUDp vs AUDv, p = 0.01; AUDp vs TeA, p = 0.007; AUDv vs TeA, p = 0.6 n.s.; TK HSD test). D, Latency to minima across brain regions [median (IQR): AUDp, 42 (26–68) ms n = 63; AUDv, 31 (24–51) ms n = 62; TeA, 31 (8–60) ms n = 29]. Time to minima was similar across cortices (H₍₂₎ = 1.78, p = 0.4 n.s.; Kruskal–Wallis). E, Heat maps of SU FRs in AUDp (left), AUDv (center), and TeA (right) sorted by latency to peak for excited units (top to bottom) and latency to minima for suppressed units (bottom up). Thick red and blue lines mark times to peak and to minima, respectively. The trajectory of AUDp is overlaid on top of the heat maps of AUDv and TeA (dashed colored lines). Time of stimulus offset is marked with gray dashed lines. F, Normalized population response averaged across pure tone stimuli for excited (left) and suppressed (right) SUs. Bold lines and shaded regions mark mean response and SEM, respectively (blue, AUDp; purple, AUDv; green, TeA). Bars (bottom) show the p value of the instantaneous activity versus baseline for each region. The time of deviation from baseline was larger for TeA (excited: AUDp, 5 ms; AUDv, 8 ms; TeA, 16 ms; suppressed: AUDp, 15 ms; AUDv, 13 ms; TeA, 30 ms; t test Bonferroni corrected for multiple comparisons over time bins to such that p_(thresh) = 7.1e-5). Duration of responses in TeA was >69 ms longer than in other regions (time to return to baseline, excited: AUDp, 375 ms; AUDv, 335 ms; TeA, 446 ms; suppressed: AUDp, 198 ms; AUDv, 215 ms; TeA, 284 ms; paired t test corrected for multiple comparisons such that p_(thresh) = 7.1e-5). Time to deviate and return to baseline is marked by red lines and colored arrows.

Figure 4.

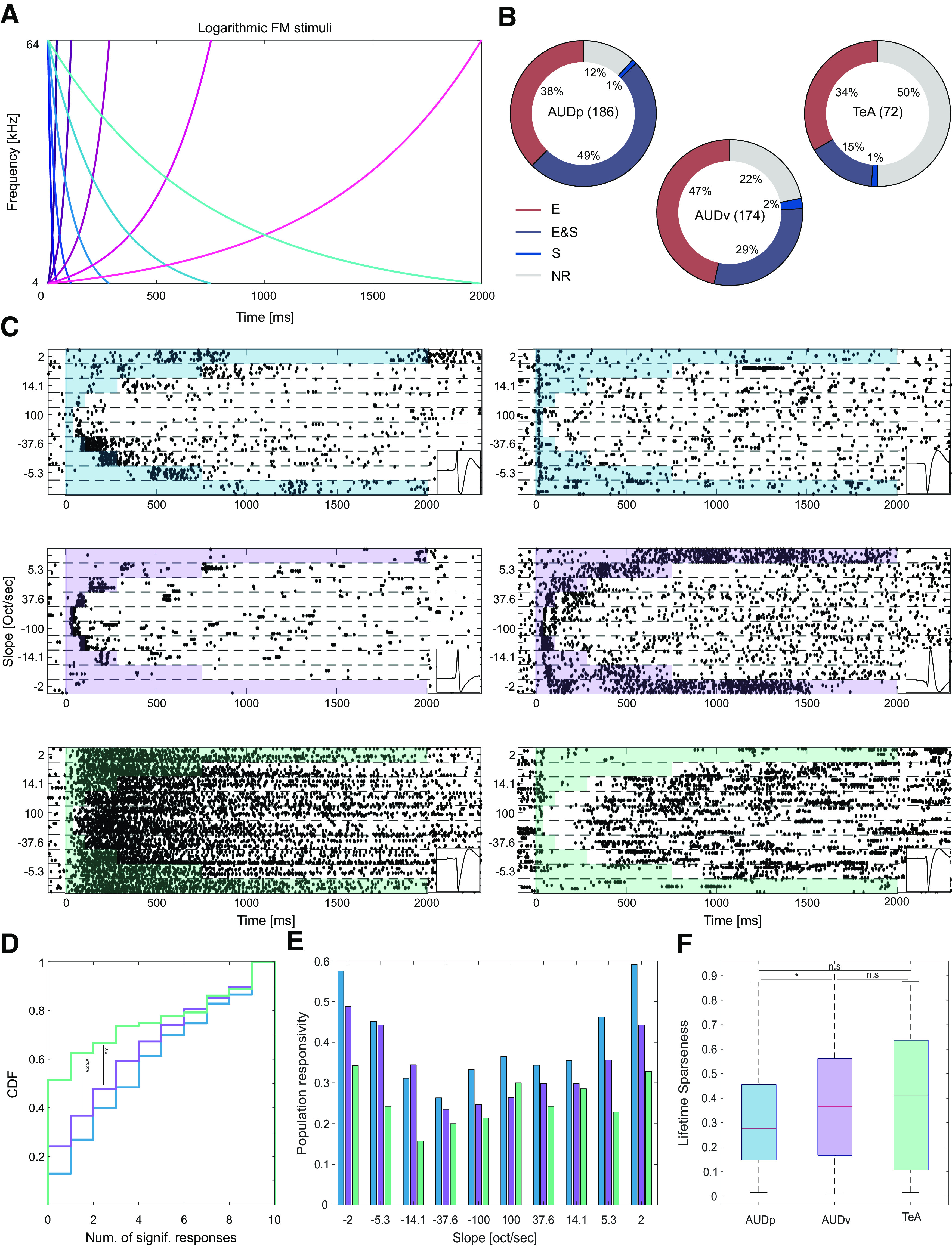
Basic response to FMs in TeA, AUDp, and AUDv. A, FM stimulus set. Frequency versus time representations of rising (pink palette) and falling (blue palette) logarithmic FM sweeps. Darker colors correspond to larger modulation speeds and shorter stimuli. B, Donut plots summarizing FM response types. E (excited), E and S (excited and suppressed), S (suppressed), and NR (not responding). The numbers of SUs recorded in region are shown in parentheses. In all regions, at least half of the SUs exhibit excitatory responses, with the fraction of excited SUs decreasing along the D-V axis of the cortex (fraction excited SUs: AUDp, 162/186 = 0.87; AUDv, 132/174 = 0.76; TeA, 35/72 = 0.49; H₍₂₎ = 42.57 p < 1e-4; Kruskal–Wallis; AUDp vs AUDv p = 0.03, AUDp vs TeA p < 1e-4; AUDv vs TeA p = 0.009; TK HSD test). C, Representative examples of SU FM responses from AUDp (top row), AUDv (central row), and TeA (bottom row). Shaded regions mark the stimulus durations. Panels on the right bottom of each example show the units template waveform. D, CDF showing the number of FM stimuli evoking significant excitatory response [median (IQR): AUDp, 4 (1–7) n = 186, AUDv, 3 (1–6) n = 174, TeA, 0 (0–4.5) n = 72] in SUs of AUDp (blue) AUDv (purple) and TeA (green). Responsivity was lower in TeA compared with both AUDp and AUDv (H₍₂₎ = 21.74 p < 1e-4, Kruskal–Wallis; AUDp vs AUDv, p = 0.08 n.s.; AUDp vs TeA, p < 1e-4; AUDv vs TeA, p = 0.008; TK HSD test). E, Population sparseness presented as the response probability of SUs in each region to logarithmic FMs. F, Lifetime sparseness calculated for FM responses [median (IQR): AUDp, 0.28(0.15–0.46) n = 162, AUDv, 0.37 (0.17–0.56) n = 132, TeA, 0.41 (0.11–0.64) n = 35]. Sparseness was lower in AUDp compared with AUDv (H₍₂₎ = 6.90 p = 0.03; Kruskal–Wallis; AUDp vs AUDv, p = 0.04, AUDp vs TeA, p = 0.2 n.s.; AUDv vs TeA p = 0.9 n.s.; TK HSD test).

Figure 5.

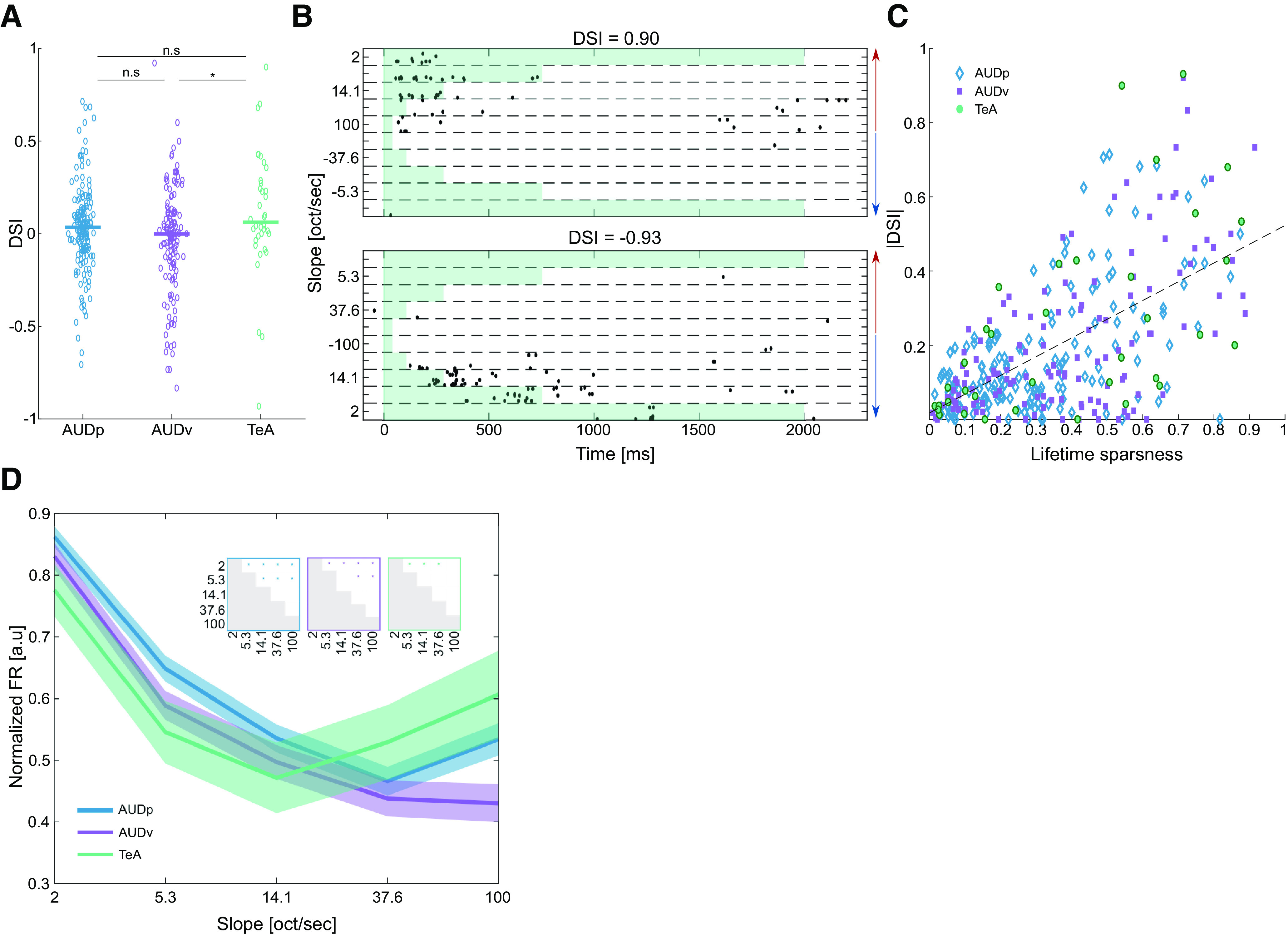
Selectivity to FMs in TeA, AUDp, and AUDv. A, Scatter plot of DSI values. Median values marked by bold lines [median (IQR): AUDp, 0.035 (−0.082–0.137) n = 164; AUDv, −0.002 (−0.165–0.109) n = 136; TeA, 0.062 (−0.025–0.280 n = 36)]. DSI was different from zero in AUDp and TeA (AUDp, z = 2.10, p = 0.04; AUDv, z = −1.29, p = 0.2; TeA, z = 2.26, p = 0.024; Wilcoxon signed-rank test), with TeA SUs showing a greater preference toward rising FMs (H₍₂₎ = 9.85 p = 0.007, Kruskal–Wallis; AUDp vs AUDv, p = 0.07 n.s.; AUDp vs TeA, p = 0.3 n.s.; AUDv vs TeA, p = 0.01; TK HSD test). B, Raster plots of two SUs from TeA exhibiting high selectivity to rising (top) and falling (bottom) FM stimuli, respectively. Red and blue arrows mark FM direction (rising and falling, respectively). Each unit's DSI is noted above the raster. C, Scatter plot of absolute DSI values versus lifetime sparseness. Units are “color and shape-coded” according to their cortical origin. Black dashed line shows fitted regression line between the two parameters (|DSI| = 0.50*LS + 0.02, R² = 0.374). D, Normalized population FRs for different logarithmic FM slopes (AUDp, n = 162 SUs; AUDv, n = 132 SUs; TeA, n = 35 SUs). Bold lines and shaded regions mark mean response and SEM, respectively (blue, AUDp; purple, AUDv; green, TeA). Insets show statistical comparisons of within population responses to different FM speeds (two-sample t-tests, with significance level Bonferroni corrected for multiple comparisons by setting p < 0.005).

Code accessibility

Codes used for data analysis are available from the corresponding author on request or in https://github.com/LibiF/Neuropixels-Scripts. The analyzed data can be found in https://github.com/MizrahiTeam.

Results

Simultaneous recording from three auditory cortices in awake mice

To study the nature of auditory responses in TeA, we recorded extracellular spiking activity in response to sounds using the high-density probe, Neuropixels (Fig. 1A; Jun et al., 2017). We assessed responses in TeA, in head-fixed awake mice, with reference to auditory responses in two well-studied auditory cortices: AUDp and AUDv. To do so, we penetrated the brain with a single probe such that it diagonally traversed all three cortical regions; from dorsal to ventral (D-V): AUDp →AUDv→TeA (Fig. 1B). To validate the locations of our recordings we reconstructed (postmortem) the probe tracts, which were coated with a fluorescent lipophilic dye. We used DiI-coated and/or DiO-coated probes for multiple (up to three) sequential penetrations in each mouse (Fig. 1C; Materials and Methods). All probe trajectories were aligned to the Allen Brain Atlas coordinate framework validating the exact positions of our recordings in all mice (Fig. 1D; Shamash et al., 2018). In this manner, we obtained simultaneous recordings from all three auditory cortices in all mice. A representative 1.7-s snippet of raw data recorded from AUDp →AUDv→TeA is shown in Figure 1E. Following spike sorting, we obtained both well-isolated SUs and MUs. In total, we recorded from 12 probe penetrations in five mice, obtaining 1006 units (555 SUs and 451 MUs). Throughout the paper we present data from the well isolated SUs (AUDp, n = 240 SU; AUDv, n = 218 SU; TeA, n = 97 SU; Tables 1, 2; for details of layer distribution, see Table 3). Results from the MU data were pooled separately, and used only for supplementary analyses (Tables 3, 4, 5).

Table 1.

SU Recording statistics

	Pure tone protocol		FM protocol
	#Num recorded units	Responding to PTs	#Num recorded units	Responding to logarithmic FMs
AUDp	240	227 (95%)	186	164 (88%)
AUDv	218	198 (91%)	174	136 (78%)
TeA	97	84 (87%)	72	36 (50%)

Numbers of SUs recorded in our dataset responding to pure tones or FMs.

Table 2.

SU Pure tone response statistics

	Spont. FR (Hz)	Bandwidth (#num)	Lifetime sparseness	BF (kHz)	Evoked FR (Hz)	Minimal latency (ms)	Latency to peak (ms)
AUDp	1.1 (0.2–3.5)	3.5 (0–9)	0.63 (0.39–0.83)	15.5 (8.3–32.3)	24.5 (13.9–43.3)	34 (21–59)	63 (23–135)
AUDv	0.6 (0.1–1.6)	2.5 (0–8.5)	0.75 (0.51–0.87)	13.8 (7.4–53.9)	21.2 (13.1–41.7)	48 (26–76)	110 (34–149)
TeA	0.2 (0.1–0.7)	0 (0–6.2)	0.82 (0.59–0.90)	10.4 (6.3–20.0)	11.4 (8.2–37.2)	48 (33–73)	112 (43–181)

Response properties of SUs to pure tones.

Table 3.

Unit layer distributions

	Unit type	Pure Tone protocol				FM protocol
		Number of recorded units	Units per layer		Percent of total units (%)	Number of recorded units	Units per layer		Percent of total units (%)
AUDp	SU	240	1	—	—	186	1	—	—
			2/3	—	—		2/3	—	—
			4	2	0.8		4	2	1
			5	238	99.2		5	184	99
			6	—	—		6	—	—
	MU	190	1	—	—	158	1	—	—
			2/3	—	—		2/3	—	—
			4	2	1		4	3	2
			5	188	99		5	155	98
			6	—	—		6	—	—
AUDv	SU	218	1	—	—	174	1	—	—
			2/3	2	0.9		2/3	2	1.1
			4	69	31.7		4	69	39.7
			5	147	67.4		5	103	59.2
			6	—	—		6	—	—
	MU	165	1	—	—	129	1	—	—
			2/3	8	4.8		2/3	8	6.2
			4	39	23.6		4	37	28.7
			5	118	71.5		5	84	65.1
			6	—	—		6	—	—
TeA	SU	97	1	8	8.2	72	1	6	8.3
			2/3	27	27.8		2/3	26	36.1
			4	17	17.5		4	14	19.5
			5	45	46.4		5	26	36.1
			6	—	—		6	—	—
	MU	96	1	13	13.5	80	1	12	15
			2/3	41	42.7		2/3	38	47.5
			4	12	12.5		4	14	17.5
			5	30	31.3		5	16	20
			6	—	—		6	—	—

Cortical layer distributions for SUs and MUs recorded in our dataset.

Table 4.

MU Recording statistics

	Pure tone protocol		FM protocol
	Number of recorded units	Responding to PTs	Number of recorded units	Responding to logarithmic FMs
AUDp	190	185 (97%)	158	151 (96%)
AUDv	165	152 (92%)	128	107 (84%)
TeA	96	87 (91%)	80	55 (69%)

Numbers of MUs recorded in our dataset responding to pure tones or FMs.

Table 5.

MU Pure tone response statistics

	Spont. FR (Hz)	Bandwidth (number)	Lifetime sparseness	BF (kHz)	Evoked FR (Hz)	Minimal latency (ms)	Latency to peak (ms)
AUDp	1.4 (0.3–3.2)	3.5 (0.2–7)	0.61 (0.36–0.80)	16.4 (7.9–28.9)	19.6 (12.2–32.7)	34 (23–61)	98 (22–148)
AUDv	0.7 (0.2–2.3)	2.5 (0–4.7)	0.68 (0.49–0.85)	16.4 (10.4–35.6)	19.6 (11.4–33.1)	40 (27–80)	100 (25–142)
TeA	0.4 (0.2–1.2)	0.5 (0–5.5)	0.72 (0.52–0.81)	13.1 (7.6–63.8)	19.6 (13.1–40.0)	42 (28–60)	114 (32–154)

Basic response properties of MUs to pure tones in our dataset.

Auditory responses to pure tones in TeA become sparser

As expected from cortical responses in awake mice, spiking activity was highly heterogeneous in all of the three auditory regions (Fig. 2; Zhan and Luo, 2010; Montijn et al., 2015; Tao et al., 2017; Cembrowski and Spruston, 2019). The first striking difference between TeA and the two other cortices was its sparser spiking activity which was evident in several different measurements. Spontaneous FRs decreased along the D-V cortical axis (Fig. 2A,B). Spontaneous FRs were distributed log-normally (AUDp, K₍₂₄₀₎ = 0.058, p = 0.03 n.s.; AUDv, K₍₂₁₈₎ = 0.04, p = 0.5 n.s.; TeA, K₍₉₇₎ = 0.073, p = 0.23 n.s.; Lilliefors test for normality with Bonferroni correction). To characterize evoked auditory responses to pure tones, we presented thirty 100-ms pure tones with frequencies ranging between 3 and 80 kHz, each at four different attenuations (between 72 and 42 dB SPL). The vast majority of SUs in all three auditory cortices were significantly responsive to pure tones (Table 1), with responses being either excitatory or suppressive (for defining excitatory and suppressive responses, see Materials and Methods). Excitatory responses to pure tones were more dominant than suppressive responses (Fig. 2C). However, while the fraction of excited units (out of all auditory units) remained high and consistent across all cortices, the fraction of units undergoing significant suppression decreased along the auditory D-V axis (Fig. 2C, from 68% to 49%). The rich nature of pure tone responses is poorly captured when being described as excitatory or suppressive alone. For example, some SUs responded by interleaved excitation and suppression (Fig. 2D, left and center), while others responded to different frequency bands with “on” or “off” or both response types. Excitatory responses were highly diverse; from being transient and time-locked to the stimulus, through jittery spiking responses, and up to strong and long-lasting activity. Suppressive responses were as rich and heterogenous as the excitatory responses (Fig. 2D). FRAs were heterogeneous in all regions, ranging from V-shaped FRAs (Fig. 2E, left), I-shaped (Fig. 2E, center), or having more complex tuning properties (Fig. 2E, right). This observation is consistent with previous reports on AUDp response heterogeneity, extending it to both TeA and AUDv (Bandyopadhyay et al., 2010; Rothschild et al., 2010; Bowen et al., 2020). In all cortices, the span of BFs in our recordings was similarly widespread (Fig. 2F,G). Nonetheless, cross-region transitions (e.g., AUDp to AUDv or AUDv to TeA) were characterized by larger BF differences between neighboring SUs compared with neighboring units within a single region, as expected from crossing anatomically-defined boundaries (Fig. 2H). Evoked FRs were significantly higher in AUDp and AUDv as compared with TeA (Fig. 2I), all of which were also distributed log-normally (AUDp, K₍₁₆₄₎ = 0.073, p = 0.03 n.s.; AUDv, K₍₁₃₆₎ = 0.057, p = 0.33 n.s.; TeA, K₍₅₅₎ = 0.127, p = 0.03 n.s.; Lilliefors test for normality with Bonferroni correction).

Next, we examined the breadth of excitatory response profiles in more detail employing three parameters of sparseness – broadness of tuning, population sparseness and lifetime sparseness. For assessing the broadness of tuning of each unit we examined the number of frequencies at a constant sound level (62 dB SPL) evoking a statistically significant response (Fig. 2J). The average broadness in the units of TeA was narrower as compared with units of AUDp and AUDv (Fig. 2J). In fact, the majority of SUs in TeA were only weakly responsive and not strongly tuned (e.g., 56% of SUs had no significant responses in their FRA). We estimated population sparseness (also referred to as activity sparseness by Willmore and Tolhurst, 2001), by calculating the fraction of SUs responsive to each stimulus. In TeA, the response of the population was sparser as compared with AUDp and AUDv (Fig. 2K). Finally, we calculated lifetime sparseness, a statistic describing how dispersed is a neurons' firing across different stimuli. Lifetime sparseness was significantly larger in TeA as compared with AUDp (Fig. 2L). To validate that our results were not influenced by the different layer distribution of TeA SUs compared with AUDp and AUDv, we performed the same analysis on SUs originating solely from layer (L)5 of the three cortices. L5 units of TeA were sparser in all three metrics tested compared with AUDp, and sparser than or equally sparse as AUDv. (Table 6). Our data, therefore, show that representation of frequency in awake mice becomes sparser along the dorsoventral axis of the auditory cortex.

Table 6.

PT Sparseness results and statistics of L5 SUs

	PT bandwidth (#Sig. responses)	Population sparseness	Lifetime sparseness
AUDp	3.5 (0–9.5)	0.17 (0.13–0.21)	0.63 (0.39–0.83)
AUDv	1.5 (0–10.5)	0.14 (0.08–0.18)	0.74 (0.47–0.89)
TeA	0 (0–5.5)	0.07 (0.05–0.10)	0.84 (0.78–0.89)
Cross-region difference statistics (Kruskal–Wallis)	p = 0.047 (H = 6.08)	p < 1e-4 (H = 32.15)	p = 0.002 (H = 12.28)
AUDp vs AUDv (TK HSD)	p = 0.6 n.s.	p = 0.07 n.s	p = 0.2 n.s.
AUDp vs TeA (TK HSD)	p = 0.04	p < 1e-4	p = 0.003
AUDv vs TeA (TK HSD)	p = 0.2 n.s.	p = 0.002	p = 0.1 n.s.

Top, Comparison of response properties SUs from L5 only. Bottom, Cross-region difference statics using Kruskal–Wallis test, followed up with post hoc TK HSD.

TeA responses to pure tones are delayed and protracted

Recently, using monosynaptic rabies tracing, we showed that TeA is one synapse downstream of AUDp (Tasaka et al., 2020). We, therefore, expected that auditory responses in TeA will lag behind AUDp by several milliseconds. A units' latency can be estimated in several different ways, each of which capturing different aspects of the neuronal response. Thus, we used two separate measures for describing unit latency, “minimal latency” and “latency to peak” (Fig. 3A). To calculate minimal latency, we isolated solely excited units with response windows that were detected up to 110 ms from stimulus onset (and effectively 10 ms poststimulus offset, to avoid offset responses). In these units, we calculated the median latency to the first spike in the response window at the unit's BF. As we anticipated, the minimal latency in TeA was larger as compared with AUDp (Fig. 3B; Δ = 14 ms). To calculate latency to peak, we measured the latency to the extremum of each units' response. This statistic was measured for units that were excited (as latency to peak) as well as for units that were suppressed (as latency to minima). Latency to peak, but not to minima, was 49 ms higher in TeA as compared with AUDp (Fig. 3C,D, respectively). The time to peak of individual units was diverse, tiling a wide temporal window (from 7 to 523 ms; Fig. 3E). As compared with AUDp, the distribution of peak times in TeA was shifted to slower values (Fig. 3E). Notably, and in agreement with previous reports (Mormann et al., 2008), latency and sparseness were positively correlated (r = 0.215, p < 1e-4).

The normalized population response of all excited units (n: AUDp = 164 SUs, AUDv = 132 SUs, TeA = 55 SUs) across all stimuli further shows that TeA activity arises later than both AUDp and AUDv (Fig. 3F). Moreover, population activity in TeA was not only delayed, but was also more persistent and decayed with slower time scales as compared with AUDp and AUDv. It takes the population response in TeA at least 70 ms longer than in AUDp and AUDv to return to baseline (Fig. 3F). We conclude, therefore, that TeA exhibits delayed and prolonged auditory evoked responses as compared with both AUDp and AUDv.

TeA responses to FMs are excitatory and sparse

While pure tones are the fundamental elements of any sound, they lack the rich spectro-temporal attributes of more natural sounds. To obtain a more complete characterization of basic auditory responses in TeA, we used FM sounds. Specifically, we used 10 logarithmic FM sweeps, all spanning the range between 4 and 64 kHz at varying slopes, and presented at a sound intensity of 62 dB SPL. Five of the FM stimuli were rising (from 4 to 64, gradually) and five were falling in the exact opposite direction. Different stimuli had different durations (range: 40 ms to 2 s; Fig. 4A).

At least half of the units in all regions exhibited significant responses to at least one FM stimulus (fraction non-responsive SUs: AUDp, 22/186 = 0.12; AUDv, 38/174 = 0.22; TeA, 36/72 = 0.5; Fig. 4B). We focused our FM analysis almost exclusively on SU responses that were excitatory since these were the vast majority (Fig. 4B). SU responses to FMs were diverse in their nature in all three cortical regions (Fig. 4C). Some units had excitatory responses during specific time windows along the sweep, corresponding to the units preferred frequency range (Fig. 4C, center left and right). Other response types could be suppressed during all or most sound duration, with potential excitatory overshoots at specific stimulus times (Fig. 4C, left: top, right: bottom). Some units responded to sound onset, independent of the FM type and direction (Fig. 4C, right, top), and a small fraction of the SUs was characterized by persistent firing (Fig. 4C, left, bottom).

Next, we examined the sparseness of FM responses with similar measures to those we used for the analysis of pure tone responses, broadness, population sparseness, and lifetime sparseness. We assessed the broadness of each SU by counting the number of FM stimuli evoking a significant response. Compared with both AUDp and AUDv, TeA SUs were sparser and, on a per-unit basis, responded to fewer FM stimuli (Fig. 4D). To assess population sparseness, we counted the fraction of SUs in each region having a significant response to each FM stimulus. Here, again, the number of TeA units being activated by FM stimuli was consistently smaller compared with AUDp and AUDv (fraction of population responsive: TeA<AUDp, 10/10 FM stimuli; TeA<AUDv, 9/10 FM stimuli; AUDv<AUDp, 9/10 FM stimuli; Fig. 4E). Finally, we calculated the lifetime sparseness of FM responses. Sparseness was qualitatively larger for TeA and AUDv units compared with AUDp, however TeA units exhibited a relatively wide distribution of sparseness values which rendered the finding statistically insignificant (Fig. 4F). Therefore, and qualitatively similar to the pure tone analysis, TeA responses to FMs become sparser along the D-V cortical axis.

FM-direction and FM-speed selectivity are reduced in TeA

One way to characterize FM responses is to assess direction and speed selectivity (Nelken and Versnel, 2000; Zhang et al., 2003; Trujillo et al. 2013; Sollini et al., 2018). We calculated DSI per SU as $DSI=\frac{FR\uparrow -FR\downarrow }{FR\uparrow +FR\downarrow }$ (see Materials and Methods). A DSI of 1 indicates that the unit's response it strictly to the rising FMs and vice versa for a DSI of −1. A DSI of 0 indicates no direction selectivity. AUDp and TeA had an average DSI different and larger than zero, indicating a slight preference for rising FMs. This preference was stronger in TeA which exhibited higher DSIs (Fig. 5A). In some SUs, it was evident that response sparseness was accompanied by strong FM direction selectivity (Fig. 5B shows two such examples). Indeed, DSI and lifetime sparseness were strongly and significantly correlated (r = 0.612, p < 1e-4; Fig. 5C), suggesting that TeA's sparseness may contribute to its FM selectivity.

To examine speed-selectivity we plotted response magnitudes to the different FM slopes (Fig. 5D). In AUDp and AUDv, response magnitudes were highest for low speed FMs and decreased as speeds grew (Fig. 5D, blue and magenta). In TeA, this monotonic effect was attenuated (Fig. 5D, green). Since responses were calculated based on optimal response windows per FM which were all the same size (50 ms), we presume different FM durations were not the source of these variations. Thus, TeA's speed selectivity is “bimodal.”

Population responses in TeA differ in discriminability for pure tones and FM sweeps

While single neurons are the fundamental building blocks of sensory coding, sensory codes are likely read as a population. Moreover, correlations among neurons have been suggested as key features of the population neural code (Nirenberg and Latham, 2003; Averbeck et al., 2006; Cohen and Kohn, 2011). Thus, we next characterized pairwise correlations of simultaneously recorded SUs. For simplicity, we focus on two brain regions only, AUDp and TeA, and only responses to pure tones. First, we assessed pairwise signal correlations (SCs), which describes the similarity in FRA tuning (Gawne and Richmond, 1993; Cohen and Kohn, 2011). The mean SC within regions were generally low in both regions (Fig. 6A), yet significantly larger than expected from shuffled data (p < 1e-4 for all comparisons of shuffled vs data; Kolmogorov–Smirnoff test). Cross region correlations were even lower which is expected because correlations are known to decay with increasing distance (Fig. 6A; Smith and Kohn, 2008; Rothschild et al., 2010). Nonetheless, highly correlated pairs were evident in all distributions (Fig. 6A, see positive “tails” in all distributions). Second, we measured noise correlations (NCs), the trial-to-trial tendency of units FRs to fluctuate together (Averbeck et al., 2006; Cohen and Kohn, 2011). Mean NC were centered around 0, although within-region correlations were significantly higher than cross region correlations (Fig. 6B). Positive tails of higher correlated units were evident for NC as well (Fig. 6B). Finally, we tested the relationship between SC and NC (Smith and Kohn, 2008; Rothschild et al., 2010). SC and NC were positively correlated, with a higher interaction within regions as compared with among cortical regions (AUDp, r = 0.396 p < 1e-4; TeA, r = 0.444 p < 1e-4; AUDp-TeA, r = 0.227 p < 1e-4; Fig. 6C). These data show that SC and NC behave largely similarly along the auditory cortical hierarchy. Notably, the same trends were evident when restricting the correlation analysis to units recorded solely from L5 (data not shown).

Figure 6.

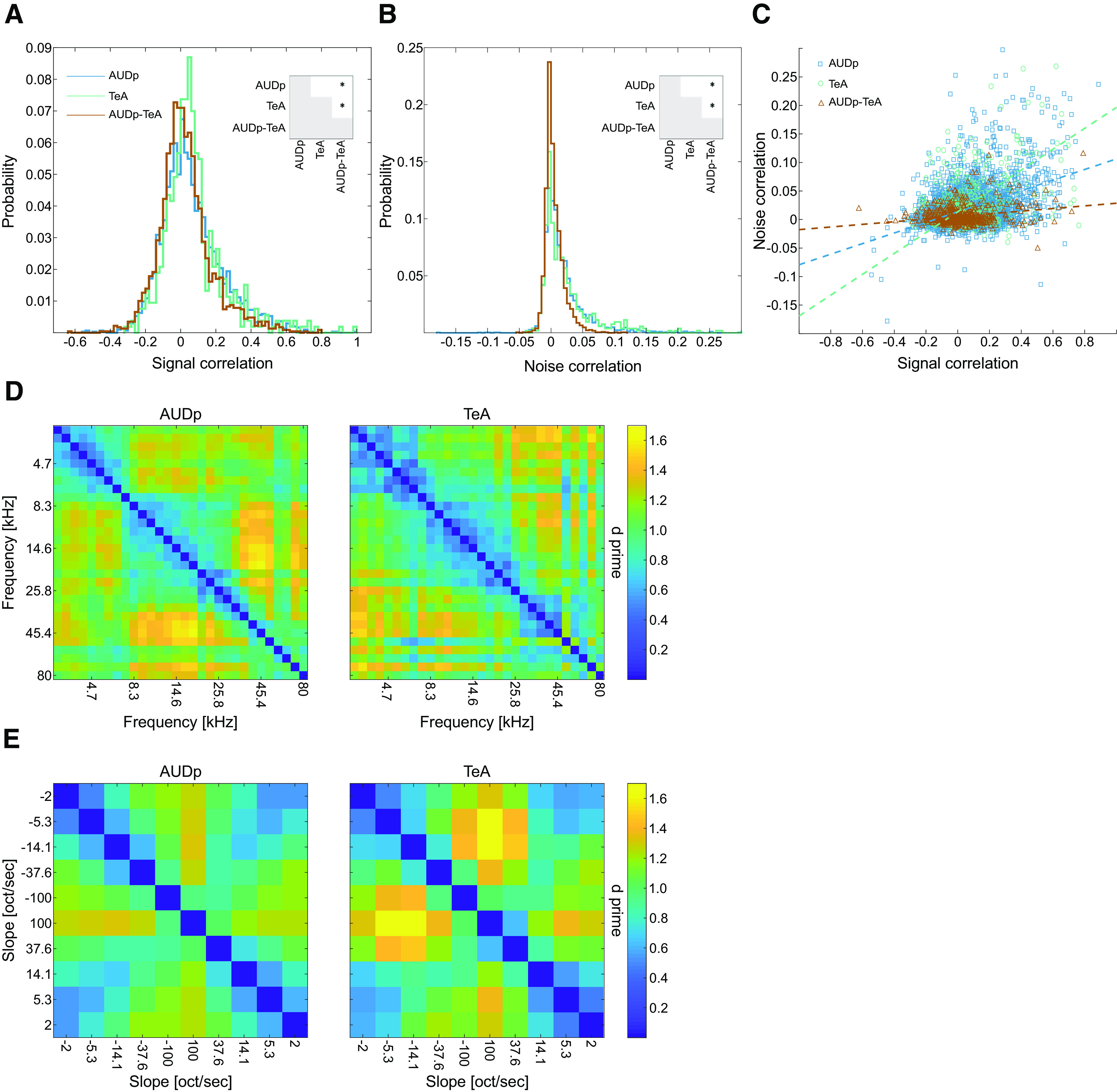
Population analysis of pure tones and FMs in AUDp and TeA. A, Pairwise signal correlations (SCs) in AUDp (blue), TeA (green), and between both regions [AUDp-TeA, brown; median (IQR): AUDp, 0.04 (−0.05–0.16) n = 3042; TeA, 0.05 (−0.02–0.13) n = 529; AUDp-TeA, 0.01 (−0.06–0.09) n = 2296]. Correlation in AUDp and TeA were similar and larger than the cross region correlations (AUDp vs TeA, U_(3042,529) = 5.406e6 p = 0.2 n.s.; AUDp vs cross-region, U_(3042,2296) = 8.549e6 p < 1e-4; TeA vs cross-region, U_(529,2296) = 8.494e5 p < 1e-4; Wilcoxon rank-sum test; significant comparisons shown in inset). All distributions were different from shuffled (p < 1e-4 for all comparisons, Kolmogorov–Smirnoff test). B, Same as A for noise correlations (NCs) [median (IQR): AUDp, 0.009 (−0.001–0.028) n = 3042; TeA, 0.011 (−0.001–0.034) n = 529; AUDp-TeA, 0.001 (−0.004–0.011) n = 2296]. Here, too, correlations were indistinguishable between AUDp and TeA and larger in both than cross region correlations (AUDp vs TeA, U_(3042,529) = 5.406e6 p = 0.2 n.s.; AUDp vs cross-reg, U_(3042,2296) = 9.016e6 p < 1e-4; TeA vs cross-region, U_(529,2296) = 9.128e5 p < 1e-4; Wilcoxon rank-sum test). All distributions were different from shuffled (p < 1e-4 for all comparisons, Kolmogorov–Smirnoff test). C, Scatter plot showing relationship between NCs and SCs. Dashed lines show linear fits for each individual population. Linear correlation between the two was strongest for TeA and weakest for cross region correlations (linear fit, R²: AUDp, NC = 0.09*SC + 0.01 R² = 0.157; TeA, NC = 0.18*SC + 0.01 R² = 0.198; TeA-AUDp, NC = 0.02*SC + 0.005 R² = 0.052). D, Matrices of d primes for all pure tone pairs (62 dB SPL) calculated based on the activity of all SUs in AUDp (left, n = 240 SUs) and TeA (right, n = 97 SUs). Pairwise pure tone discriminability was larger in AUDp compared with TeA (mean ± std: AUDp, 1.06 ± 0.23, TeA, 0.98 ± 0.26; t₍₄₃₄₎ = 7.75 p < 1e-4, paired sample t test). E, Matrices of d primes for logarithmic FM sweep pairs calculated based on the activity of all SUs in AUDp (left, n = 186 SUs) and TeA (right, n = 72 SUs). Pairwise FM sweep discriminability was larger in TeA compared with AUDp (mean ± std: AUDp, 0.93 ± 0.23, TeA, 1.01 ± 0.32; t₍₄₅₎ = 2.83 p = 0.007, paired sample t test).

Next, we tested whether the neuronal populations in AUDp and TeA exhibit differences in their discriminability for both types of sounds we presented. We calculated pairwise d primes for population responses (see Materials and Methods) to all the individual pure tones presented at 62 dB SPL (Fig. 6D) and the logarithmic FM sweeps (Fig. 6E). d Prime measures the discriminability of two distributions by calculating the ratio of mean differences to the mean noise level in the distributions. A higher d prime indicates better discriminability. The population of neurons in AUDp showed significantly higher discriminability between pure tone pairs (t₍₄₃₄₎ = 7.74 p < 1e-4, paired t test), as compared with TeA. This result was opposite for FM sweeps. In TeA, d prime values were significantly higher than in AUDp (t₍₄₄₎ = 2.83 p = 0.007, paired t test). These data suggest that neurons in TeA are more prone to dissociate more complex auditory stimuli as compared with more primary cortices.

Distinct effects of anesthesia on TeA and AUDp

Accumulating evidence suggest that anesthesia has a stronger effect on higher order cortices as compared with primary cortices (Jordan et al., 2013; Mashour, 2014). Thus, since TeA is downstream of AUDp, we hypothesized it will be more strongly affected by anesthesia. To this end, we conducted a separate experiment, where we recorded in Ketamine-Medetomidine anesthetized mice, and assessed SU responses to pure tones (six probe penetrations in five anesthetized mice, obtaining 199 SUs from both regions; AUDp, n = 151; TeA, n = 48). Responsivity was significantly larger in the anesthetized compared with the awake state in both regions (AUDp, 150/151 = 99% responsive SUs; TeA, 47/48 = 98% responsive SUs; F_{(conscious state)} = 10.78 p = 0.0011, F_{(brain region)} = 7.18 p = 0.008; two-way ANOVA). Anesthesia had a distinct signature on AUDp as compared with TeA. Spontaneous activity in TeA significantly increased, leveling up with spontaneous activity in AUDp, which did not change (Fig. 7A). Under anesthesia, evoked FRs were significantly lower in AUDp, but higher in TeA, such that responses were now stronger in TeA (Fig. 7B). Furthermore, the sparseness which was a prominent characteristic of TeA was strongly affected, resulting in similar levels of sparseness in both regions under anesthesia (Fig. 7C,D).

Figure 7.

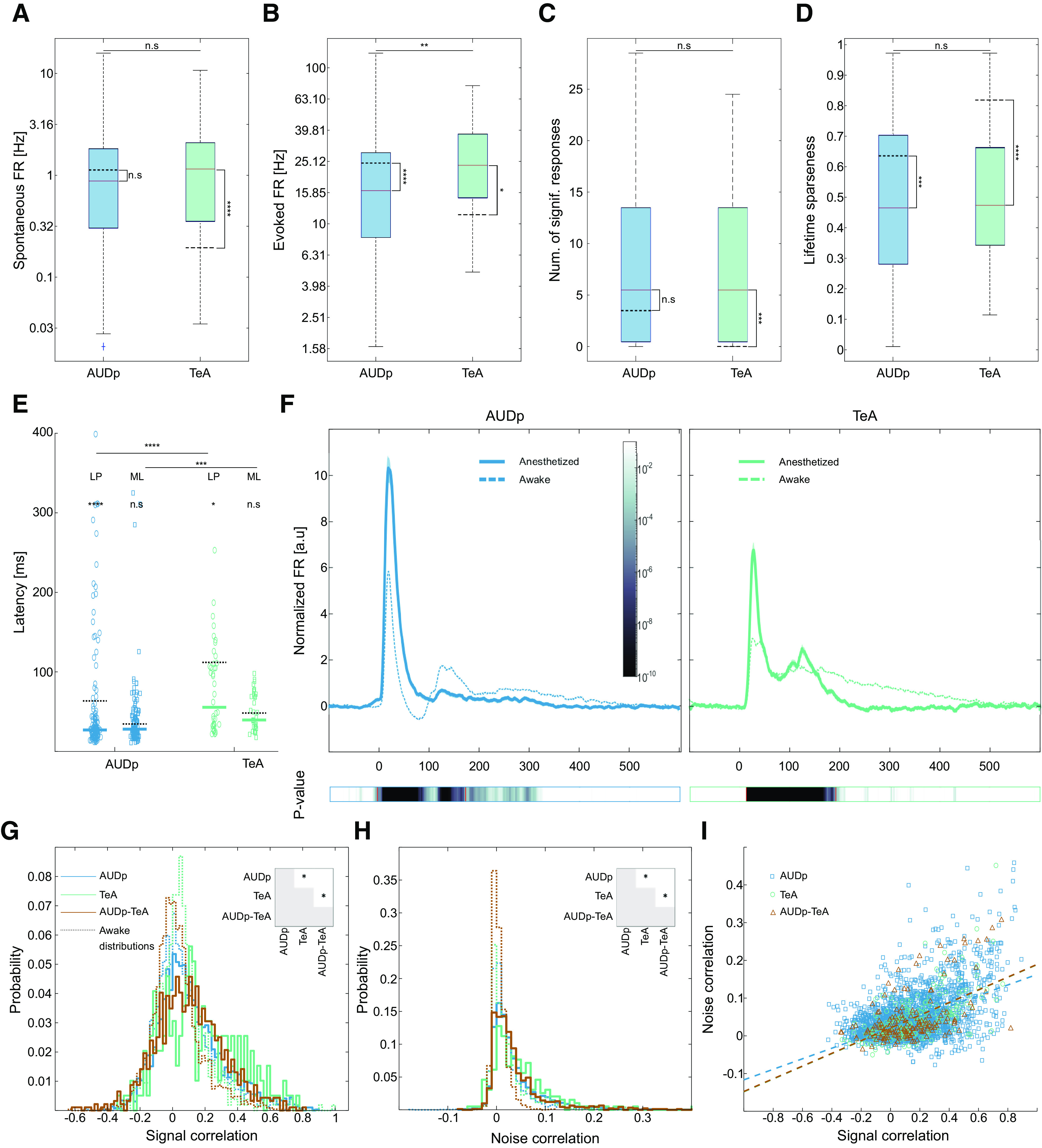
Anesthesia affects TeA and AUDp in distinct ways. A, Spontaneous FRs in anesthetized AUDp and TeA [median (IQR): AUDp, 0.88 (0.30–1.83) Hz n = 151; TeA, 1.15 (0.35–2.09) Hz n = 48) are not significantly different (U_(151,48) = 14 704 p = 0.2 n.s.; Wilcoxon rank-sum test]. Anesthesia induces a significant increase in TeA spontaneous FR (AUDp, U_(240,151) = 49 169 p = 0.05 n.s.; TeA, U_(97,48) = 6011 p < 1e-4; Wilcoxon rank-sum test Bonferroni corrected for MC). Dashed black lines mark awake population medians, adjacent asterisks mark within region anesthetized versus awake comparisons. B, Evoked FRs in response to BFs [median (IQR): 16.34 (8.17–28.59) Hz n = 132; TeA, 23.69 (14.70–37.58) Hz n = 42]. Evoked FRs in the anesthetized cortex are higher in TeA compared with AUDp (U_(132,42) = 10 752 p = 0.005; Wilcoxon rank-sum test). Anesthesia reduced evoked activity in AUDp and raised it in TeA (AUDp, U_(164,132) = 27 472 p < 1e-4; TeA, U_(55,42) = 2378 p = 0.02; Wilcoxon rank-sum test Bonferroni corrected for MC). C, Bandwidth of SUs in the anesthetized cortex assessed as the number of frequencies at 62 dB SPL evoking a significant response [median (IQR): AUDp, 5.5 (0.5–13.5) n = 132; TeA, 5.5 (0.5–13.5) n = 42]. TeA bandwidth is larger under anesthesia compared with the awake state (AUDp, U_(164,132) = 22 784 p = 0.03 n.s.; TeA, U_(55,44) = 2188 p = 0.0001; Wilcoxon rank-sum test Bonferroni corrected for MC), and is comparable with bandwidth in AUDp (U_(132,42) = 11 507 p = 0.9 n.s.; Wilcoxon rank-sum test). D, Lifetime sparseness of SUs in the anesthetized cortex [median (IQR): AUDp, 0.46 (0.28–0.70) n = 132; TeA, 0.47 (0.34–0.66) n = 42]). Sparseness was similar across regions (U_(132,42) = 11,423 p = 0.6 n.s.; Wilcoxon rank-sum test) and lower compared with the awake state (AUDp, U_(164,132) = 27,026 p = 0.0003; TeA, U_(55,42) = 3298 p < 1e-4; Wilcoxon rank-sum test Bonferroni corrected for MC). E, SU minimal latencies [ML, right column, squares; median (IQR): AUDp, 28 (20–45) ms n = 121; TeA, 39 (30–70) ms n = 37] and latencies to peak [LP, left column, circles; median (IQR): AUDp, 27 (21–42) ms n = 132; TeA, 55 (33–110) ms n = 42] in the anesthetized state. Median values are marked with thick lines. Awake median values are marked with dashed black lines. Both latency parameters were larger in TeA (minimal latency: U_(121,37) = 8785 p = 0.0006; latency to peak: U_(132,42) = 10 294 p < 1e-4; Wilcoxon rank-sum test); however, on a per region basis, tended to be shorter than for the awake condition (minimal latency: AUDp, U_(123,121) = 15 955 p = 0.1 n.s., TeA, U_(38,37) = 1518 p = 0.4 n.s.; latency to peak: AUDp, U_(164,132) = 27 445 p < 1e-4; TeA, U_(55,42) = 3047 p = 0.01; Wilcoxon rank-sum test Bonferroni corrected for MC). F, Normalized population response averaged across pure tone stimuli for excited SUs (AUDp, n = 132; TeA = 42) under anesthesia. Bold lines and shaded regions mark mean response and SEM, respectively (left, blue, AUDp; right, green, TeA). Population responses from the awake condition are shown as dashed lines for comparison. Bottom color bars show p value for comparisons of instantaneous activity to baseline, red lines marking beginning (left) and end (right) of deviation from baseline. Return to baseline activity (AUDp, 171 ms; TeA, 192 ms; paired t test corrected for MC over time bins) was shorter than during wakefulness for both cortices. G, Pairwise SCs in AUDp (blue), TeA (green), and between both regions (AUDp-TeA, brown) under ketamine-domitor anesthesia [median (IQR): AUDp, 0.077 (−0.025−0.220) n = 2915; TeA, 0.133 (−0.018–0.327) n = 196; AUDp-TeA, 0.097 (−0.034–0.238) n = 918]. Correlations were highest in TeA (AUDp vs TeA, U_(2915,196) = 4.495e6 p = 0.0009; AUDp vs cross-region, U_(2915,918) = 5.572e6 p = 0. 7 n.s.; TeA vs cross-region, U_(196,918) = 1.215e5 p = 0.003; Wilcoxon rank-sum test; significant comparisons shown in inset). All distributions were higher than their parallels during wakefulness (shown as dashed histograms; AUDp, U_(3042,2915) = 8.491e6 p < 1e-4; TeA, U_(529,196) = 1.79e5 p < 1e-4; AUDp-TeA, U_(2296,918) = 3.427e6 p < 1e-4; Wilcoxon rank-sum test). All distributions were different from shuffled (p < 1e-4 for all comparisons, Kolmogorov–Smirnoff test). H, Same as G for NCs [median (IQR): AUDp, 0.021 (0.005–0.052) n = 2915; TeA, 0.033 (0.007–0.071) n = 196; AUDp-TeA, 0.022 (0.004−0.051) n = 918]. Correlations were highest in TeA (AUDp vs TeA, U_(2915,196) = 4.502e6 p = 0.006; AUDp vs cross-region, U_(2915,918) = 5.598e6 p = 0.7 n.s.; TeA vs cross-region, U_(196,918) = 1.207e5 p = 0.005; Wilcoxon rank-sum test; significant comparisons shown in inset), and generally larger than in the awake recordings (AUDp, U_(3042,2915) = 8.001e6 p < 1e-4; TeA, U_(529,196) = 1.771e5 p < 1e-4; AUDp-TeA, U_(2296,918) = 3.188e6 p < 1e-4; Wilcoxon rank-sum test). All distributions were different from shuffled (p < 1e-4 for all comparisons, Wilcoxon rank-sum test). I, Scatter plot showing relationship between NCs and SCs. Dashed lines show linear fits for each individual population. Linear correlation between the two was strongest for TeA and for cross region correlations (linear fit, R²: AUDp, NC = 0.14*SC + 0.02 R² = 0.257; TeA, NC = 0.17*SC + 0.02 R² = 0.380; TeA-AUDp, NC = 0.17*SC + 0.02 R² = 0.302).

The temporal aspects of the neural response were also changed in the anesthetized state. Latency was decreased in both AUDp and TeA, although the hierarchical gradient was maintained (minimal latency in TeA follows A1 by 11.5 ms, and latency to peak by 28.5 ms; Fig. 7E). Moreover, the temporal aspects of the late responses were particularly affected, such that the population response under anesthesia was considerably shorter. AUDp and TeA retuned to baseline ∼110 and ∼254 ms earlier as compared with the awake state, respectively (Fig. 7F). Suppressive population response were modulated as well, becoming weaker and generally more sluggish. However, the small number of SUs exhibiting suppressive responses under anesthesia in our dataset precluded a statistical validation of this qualitative impression (data not shown).

Finally, we examined how anesthesia changes the interactions within and between neurons in AUDp and TeA. We expected that within-region correlations will be higher under anesthesia (Harris and Thiele, 2011; Ecker et al., 2014). Indeed, both SCs and NCS were higher under anesthesia as compared with the awake state (Fig. 7G,H). While all correlations increased under anesthesia, the effect was larger in TeA and across-regions, making TeA SC and NC larger than their AUDp counterparts and cross-region correlations indistinguishable from AUDp correlations. Linear correlations between SC and NC increased as well (Fig. 7I). Together, the more prominent effects of anesthesia on TeA further suggests that TeA is a higher order auditory cortex.

Discussion

The rodent's TeA was recognized as an auditory field approximately 30 years ago. Initial anatomic studies of regions akin to TeA in the rat cortex showed feed-forward connectivity from AUDp, distinct connectivity patterns from the non-leminiscal auditory thalamus, and strong projections to the amygdala and striatum (Arnault and Roger, 1990; LeDoux et al., 1991; Romanski and LeDoux, 1993). Recently, using trans-synaptic rabies tracing we found that TeA receives most of its inputs (∼45%) from AUDp, as well as inputs from dorsal/medial thalamus that surpass those from ventral thalamus. In addition, TeA receives direct inputs from numerous other (>100) cortical and sub-cortical structures (Tasaka et al., 2020). Aside from describing its connectivity, physiological studies of TeA are scarce. Basic response profiles to pure tones have been documented in anesthetized rats with MU recordings (Polley et al., 2007) and recently using surface imaging of the cortical sheet in mice (Romero et al., 2020). Here, using electrophysiology, we characterized how SUs in TeA represent pure tones and FMs in awake mice, and characterized interactions between TeA and its main upstream region, the AUDp. We suggest that TeA, by virtue of its physiological sparseness, temporal sluggishness, and improved representation of FMs is a high-order auditory processing station. Despite strong feed-forward connectivity evident from the anatomy (Tasaka et al., 2020), AUDp and TeA units exhibit weak functional correlations during wakefulness, suggesting TeA activity is strongly shaped by inputs from other regions, and/or within region computations.

Extracellular recordings using Neuropixels probes

Neuropixels is a novel extracellular recording method that allows the collection of dozens of well isolated SUs. Exploiting the long shank of the Neuropixels probe (Jun et al., 2017), we were able to measure auditory responses along several stations of the cortical hierarchy, simultaneously. Notably, however, all methods have biases. Such biases must be recognized because they can be the reason for numerous discrepancies among studies. One such bias of extracellular recording methods is their tendency to capture specific cell types and particularly highly-active neurons (Barth and Poulet, 2012). Indeed, comparing our data with previous reports where an unbiased recording method, like loose-patch recordings, was used, we found that both spontaneous FRs and evoked responses tended to be larger for measurements with Neuropixels, in both awake and anesthetized preparations (Hromádka et al., 2008; Cohen and Mizrahi, 2015; Maor et al., 2020). Another major source of variation is layer specificity. In our experiments, we penetrated the cortex to record from L5 in AUDp, and from various layers (albeit still dominated by L2/3 and L5) in TeA. Such layer biases were a result of our probe penetration constellation, and the geometry of the probe restricting the recording to nearby units usually originating from the same layer. Previous studies in rodents showed that AUDp L5 neurons are the least sparse along the cortical column, exhibiting broad tuning and short latencies competing and even preceding those of L4 neurons, which are classically considered the main recipients of lemniscal thalamic inputs (Wallace and Palmer, 2008; Sakata and Harris, 2009; Intskirveli et al., 2016). Studies in cat AUDp showed that feedback from auditory association areas is transmitted to all AUDp layers (Mitani and Shimokouchi, 1985). Our own recent tracing experiments in mice showed that the input from AUDp to TeA is dominated by L5 (three times higher compared with L2/3), and feedback connections from TeA to AUDp were also dominated by L5-to-L5 projections (Tasaka et al., 2020). Thus, our recording setup is particularly prone to record from putatively interconnected neuronal populations in AUDp and TeA. Finally, we find it worth mentioning that our current recording setup was restricted to head-restrained mice which is not suitable for chronic long-term recording using electrophysiology. As a result, we were limited in our ability to track spiking responses over long periods of time. Such a setup, therefore, captures only “snapshots” of neural activity. Long-term variability of neurons can be considerable and was not taken into account in our observations.

Sparse activity in TeA

The most striking difference between the responses in TeA as compared with AUDp and AUDv was the increase in neural sparseness along the hierarchy. Both spontaneous and evoked activities were attenuated for all stimuli we presented, and sparseness increased in all the metrics we tested, i.e., bandwidth, population sparseness and lifetime sparseness (Figs. 2, 4). Notably, these findings also hold when restricting the compared populations to L5 alone, implying that layer differences could not underlie this observation (Table 6). Sparse coding is a guiding principle in neural coding. Theoretically, sparse coding has been suggested to have many advantages such as being energetically efficient, having a high memory and representational capacity, and facilitating efficient feature extraction from natural stimuli (Lewicki, 2002; Laughlin and Sejnowski, 2003; Olshausen and Field, 2004). It has been widely reported that primary sensory cortices, auditory cortex included, are sparse in their nature (Vinje and Gallant, 2000; Hromádka et al., 2008; Barth and Poulet, 2012). While evidence from humans and primates showed that sparseness and responses to abstract features increase in higher-order sensory cortices (Quiroga et al., 2005; Waydo et al., 2006; Freiwald et al., 2009; Wolfe et al., 2010), the few previous characterization of putative TeA actually showed that it was more broadly tuned as compared with AUDp (Polley et al., 2007; Romero et al., 2020). Our data from awake mice shows a different picture, and if anything, an opposite trend. We show that tuning in TeA narrows down and becomes more specific as compared with AUDp. Obvious differences between the studies which may underlie the observed differences are that we recorded in awake mice (see Fig. 7, for effects of anesthesia on sparseness and tuning bandwidth), and the recording methods. Here, we measured from SU while others measured from MUs or widefield imaging. In support of this claim, some metrics of sparseness that we tested on our MU data did not show statistically significant differences between AUDp and TeA (Table 5; statistics not shown).

While the increase in sparseness along the cortical hierarchy is a well-documented phenomenon in other senses, the mechanisms underlying it are poorly understood. The most common suggested mechanisms argue that sparseness is a result of inhibition. For example, strong feed-forward or recurrent inhibition (Silberberg and Markram, 2007; Kapfer et al., 2007), temporal dynamics between excitation and inhibition (Wehr and Zador, 2003), and asymmetry between broadly-tuned inhibition and narrowly tuned excitation (Poo and Isaacson, 2009; Haider et al., 2013), have all been argued to underlie sparser responses. In our data, suppressive responses were abundant in all cortical regions and in response to all presented stimuli (Figs. 2B, 4B), but not limited to TeA. Nevertheless, spontaneous and evoked activity were smaller in TeA (Fig. 2B,G), suggesting higher baseline levels of inhibition. While we do not fully understand how inhibition shapes responses in auditory cortex, it is clearly a prominent feature of the cortical response (Wehr and Zador, 2003; Haider et al., 2013; Froemke, 2015). Future characterization of inhibitory populations in TeA may provide a more mechanistic explanation to the source of sparseness in this brain region.

TeA as a high-order auditory processing station

Previous work studying higher-order sensory cortices involved characterization of receptive fields, identification of neuronal feature selectivity profiles, and examination of activity during task engagement (Marshel et al., 2011; Andermann et al., 2011; Elgueda et al., 2019; Gilad et al., 2020). Here, we studied auditory responses in passively listening mice, and identified two distinct features of FM responses in TeA, higher selectivity to FM direction (Fig. 5A) and decreased selectivity to FM speeds (Fig. 5D). The lower selectivity to FM speed is possibly in agreement with previous reports of invariance to spectro-temporal modulations of sounds in the rat SRAF (presumably the equivalent of mouse TeA; Carruthers et al., 2015). Alongside the SU response features to FMs, population discriminability for FM stimuli was larger in TeA compared with AUDp, and opposite to the trend observed for pure tones. Increased selectivity and discriminability for complex sensory stimuli is a prominent feature of higher-order visual cortices (Freiwald et al., 2009; Marshel et al., 2011), supporting a similar role for TeA in audition.

Classically, longer response latencies are associated with higher-order processing (Bullier and Nowak, 1995; Capalbo et al., 2008), but latencies were also suggested to underlie a neural latency code (Shriki et al., 2012; Storchi et al., 2012; Paoli et al., 2018) or even be correlated with the degree of conscious perception (Reber et al., 2017) and stimulus selectivity (Mormann et al., 2008). Since TeA receives the vast majority of its inputs directly from AUDp, and particularly from L5, we expected an order of ∼15-ms difference in response latency between the two regions (London et al., 2010). Indeed, the minimal latencies of SUs in both regions showed just that (Δmedians = 14 ms; Fig. 3B). Aside from minimal latency, the “time to peak” of responses and the overall response duration are larger in TeA (Fig. 3C,F). This temporal profile of responses is also compatible with TeA being a higher-order auditory processing station, directly downstream of AUDp (Elgueda et al., 2019).

To the best of our knowledge, only two studies causally manipulated TeA to test its function in behaving animals. TeA was shown to be necessary for auditory fear conditioning (Dalmay et al., 2019), and for maternal recognition of pup calls (Tasaka et al., 2020). Both these functions of TeA may supervene, at least partially, on strong bi-lateral projections between TeA and the amygdala (LeDoux et al., 1991; Dalmay et al., 2019; Tsukano et al., 2019; Tasaka et al., 2020). We postulate that TeA's unique connectivity profile (Tasaka et al., 2020), and physiological signature as a high-order station, enables it to take a more central part in computations that integrate auditory information with other cues, which may be experience dependent. Characterization of TeA's activity during auditory-task performance and its manipulation in additional behavioral contexts and following learning will shed further light on its functional role and the specific computations it contributes to.

Functional connectivity between AUDp and TeA

Ketamine-domitor anesthesia affected both AUDp and TeA. However, TeA's activity was significantly more modulated by anesthesia. Specifically, activity in TeA increased, sparseness decreased, and auditory responses were faster and lasted for shorter durations (Fig. 7). Ketamine anesthesia is known to leave primary sensory representations intact, affecting mostly activity in frontal regions and top-down functional connectivity (Blain-Moraes et al., 2014; Mashour, 2014; Schroeder et al., 2016). One of the prominent changes induced by anesthesia is the decrease in late post-stimulus activity and shortening of the auditory response (Fig. 7F). Accumulating evidence show that late sensory-evoked activity is associated with conscious perception of stimuli and behavioral outputs (Del-Cul et al., 2007; Sachidhanandam et al., 2013). In addition, it was demonstrated that late post-stimulus dendritic spikes and bursting activity in L5 pyramidal cells in somatosensory cortex are induced via top-down excitatory connections targeting the apical tuft (Manita et al., 2015). We, therefore, suggest that a decrease in top-down inputs is the main cause of response shortening in auditory cortex. This hypothesis is in agreement with reports showing that late but not early activity is abolished by general anesthesia (Hudetz et al., 2009). Thus, anesthesia likely shuts down much of the rich input landscape to TeA leaving mainly early feed-forward signals intact.