The maturation and cognitive relevance of structural brain network organization from early infancy to childhood

Abstract

The interactions of brain regions with other regions at the network level likely provide the infrastructure necessary for cognitive processes to develop. Specifically, it has been theorized that in infancy brain networks become more modular, or segregated, to support early cognitive specialization, before integration across networks increases to support the emergence of higher-order cognition. The present study examined the maturation of structural covariance networks (SCNs) derived from longitudinal cortical thickness data collected between infancy and childhood (0–6 years). We assessed modularity as a measure of network segregation and global efficiency as a measure of network integration. At the group level, we observed trajectories of increasing modularity and decreasing global efficiency between early infancy and six years. We further examined subject-based maturational coupling networks (sbMCNs) in a subset of this cohort with cognitive outcome data at 8–10 years, which allowed us to relate the network organization of longitudinal cortical thickness maturation to cognitive outcomes in middle childhood. We found that lower global efficiency of sbMCNs throughout early development (across the first year) related to greater motor learning at 8–10 years. Together, these results provide novel evidence characterizing the maturation of brain network segregation and integration across the first six years of life, and suggest that specific trajectories of brain network maturation contribute to later cognitive outcomes.

1. Introduction

Multiple theoretical frameworks have been proposed to explain how neurodevelopment underlies the emergence of cognitive ability in childhood. Traditionally, maturational frameworks of brain development have proposed that through the maturation of individual brain regions, related cognitive abilities emerge (for a review, see: Johnson, 2001). For example, early sensory cortex maturation leads to early sensory abilities, while later association cortex maturation supports the gradual emergence of more complex cognition, such as executive functions – a set of higher order skills needed for goal-oriented behavior (Best and Miller, 2010; Girault et al., 2020; Huttenlocher, 1990; Johnson, 2001, 2011). However, individual brain regions are highly interconnected, and recent literature has begun to characterize the maturation of interactions across brain regions at the network level (Cao et al., 2017; Geng et al., 2017; Grayson and Fair, 2017; Morgan et al., 2018; Zhao et al., 2019). Thus, focusing on the maturation of individual brain regions without taking network structure into account likely limits our ability to fully understand the complex relationship between brain and cognitive development.

Extant literature supports the premise that cognitive development relies on brain network development. Brain network organization is hypothesized to develop first with increases in network segregation – the strength of local connections within networks – followed by increases in integration – the strength of long-range connections that span discrete brain networks (Cao et al., 2017; Johnson and Munakata, 2005; Zhao et al., 2019). Cognitive development is thought to proceed in parallel to this pattern of neurodevelopment (Johnson and Munakata, 2005). Specifically, fundamental work across several cognitive domains (e.g., sensorimotor, language, working memory) has revealed specialization, or the dissociation and refinement of specific cognitive processes, early in development, followed by improvement of cognitive abilities that require integrated processing of multiple sensory and cognitive domains (D’Souza et al., 2017; for reviews, see Johnson 2001; Johnson and Munakata, 2005). This pattern of increased specialization, followed by increased integration, is evident for both sensorimotor processes and for executive functions, albeit on different timeframes (e.g., sensorimotor development occurs over the first years of life, while the development of executive functions is more protracted and extends throughout childhood and adolescence; D’Souza et al., 2017; Johnson and Munakata, 2005; Luna et al., 2015; Marrus et al., 2018; Metcalfe et al., 2005).

1.1. Structural covariance and maturational coupling during early childhood

Brain networks derived from cortical thickness data, commonly referred to as structural covariance networks (SCNs), are well-suited to study early structural brain development, a time during which rapid changes in cortical thickness occur (Gilmore et al., 2018; Li et al., 2014, 2015a). SCNs are obtained by correlating the cortical thickness of pairs of regions across subjects (for a review, see: Alexander-Bloch et al., 2013a). SCNs thus measure how cortical regions covary in thickness at the group level. Accordingly, SCN network segregation represents how regions cluster into distinct networks whose regions have similar levels of cortical thickness across subjects, whereas SCN network integration represents the similarity of cortical thickness levels across subjects for regions distributed more widely across the brain. SCNs quantify coordinated cortical growth at the group level, therefore reflecting group-level neurodevelopmental processes underlying coordination across groups of brain regions (i.e., networks), with a focus on gray matter networks. This is in contrast to structural brain networks based on tractography data, which assess network organization based on white matter tracts at the individual level. Therefore, SCNs provide information that is complementary to that obtained via other structural brain networks. Prior work relating SCNs and tractography networks has revealed similar values of network organization between these two types of structural networks at 1 and 2 years (Nie et al., 2014). In adults, positive, but not negative, cortical thickness correlations have been shown to correspond to tractography connections (Gong et al., 2012). Finally, there are strong similarities between SCNs and brain networks derived from functional connectivity estimates (Alexander-Bloch et al., 2013b; Smith et al., 2019) that become more similar across infant development (Geng et al., 2017), thus it has been proposed that similarity in cortical thickness across regions may reflect coordinated development through synchronized brain function and functional connectivity (Alexander-Bloch et al., 2013a,b; Geng et al., 2017). Together, this work suggests that SCNs partly reflect underlying functional and structural connectivity and provide additional information about coordinated cortical maturation.

Similar to both infant tractography networks (Ratnarajah et al., 2013; Yap et al., 2011) and resting-state networks of the fetal (Turk et al., 2019) and infant brain (De Asis-Cruz et al., 2015; Gao et al., 2011; van den Heuvel et al., 2015), small world topology of SCNs has been found to be present at birth, with dense clusters of local connections and sparser, long-range connections across clusters (Fan et al., 2011). When assessed at 0, 1, and 2 years, both segregation and integration of SCNs have been shown to increase over the first two years of life (Fan et al., 2011). While on the surface this appears to contradict the theory that early segregation is followed by later integration (Cao et al., 2017; Johnson and Munakata, 2005; Zhao et al., 2019), there are two possibilities for these findings. First, these annual intervals may miss rapid changes within the first year of life. Second, the divergence may occur later in childhood. Thus, densely-sampled intervals during infancy that extend through childhood are needed to investigate how the trajectories of network segregation and network integration may differ across this time frame.

Since SCNs are constructed on the group level, they cannot assess how structural network organization relates to individual differences in cognitive functioning. However, two previous cross-sectional studies have observed on the group level that children and adolescents (aged 6–18) with higher intelligence quotient (IQ) had more integrated SCN organization (i.e., higher global efficiency) as compared to those with lower IQ (Khundrakpam et al., 2017; Solé-Casals et al., 2019), although results were inconsistent regarding whether the higher IQ group was more modular (Khundrakpam et al., 2017) or less modular (Solé-Casals et al., 2019). This is mostly consistent with studies observing that both greater integration and greater segregation of resting state (Sherman et al., 2014; Wu et al., 2013) and tractography networks (Keunen et al., 2017; Kim et al., 2016) are related to higher IQ in children.

A recent methodological advancement allows for subject-level analysis of change across time in structural brain features, such as cortical thickness, to quantify how pairs of brain regions mature in tandem within an individual. This approach is referred to as subject-based maturational coupling (Khundrakpam et al., 2019). If two brain regions have strong maturational coupling, this indicates that their cortical thickness varies similarly across time (e.g., increases or decreases at the same rate). In contrast, if two brain regions have weak maturational coupling, this indicates that changes in cortical thickness across time are not related (e.g., the cortical thickness of one may increase rapidly while the cortical thickness of the other may remain stable, increase slowly, or decrease). Subject-based maturational coupling networks (sbMCNs), therefore, describe the coupling of cortical thickness maturation on a network level for a given subject. When comparing the average of individual sbMCN matrices in typically developing subjects aged 5–25 to a single group-level SCN matrix of the same subjects, regions with similar within-subject maturational trajectories also had similar group-level structural covariance (Khundrakpam et al., 2019). This suggests that regions that mature similarly lead to similar levels of cortical thickness. No study has yet to quantify sbMCNs across early development (i.e., before age 5), nor have any studies assessed how sbMCNs relate to cognition.

The goals of the current study are two-fold. First, we aim to characterize trajectories of early structural brain network development using group-level SCNs from infancy to childhood using a densely-sampled design (i.e., six timepoints within the first two years of life). The design of the dataset allows us to quantify the rapid changes in gray matter observed over the first two years of life in addition to more protracted development into childhood (Gilmore et al., 2018). Previous literature characterizing processes of change in cognitive and brain development (Cao et al., 2017; Johnson and Munakata, 2005; Luna et al., 2015; Zhao et al., 2019) cover infancy and childhood separately, not together. Our unique dataset, with six timepoints within the first two years of life and additional annual timepoints extending to age six, allows us to characterize network segregation and integration with higher temporal resolution and across a longer time frame than prior studies. Using the metrics of modularity to index network segregation and global efficiency to index network integration, we predict that across the first six years of life we will observe early increases in network segregation followed by later network integration increases.

Second, we aim to relate individual differences in structural network maturation to cognitive outcomes in middle childhood using sbMCNs. Based on previous research that has documented earlier motor specialization and protracted development of higher order cognitive processes such as working memory (D’Souza et al., 2017; Best and Miller, 2010), in addition to literature in functional and tractography networks observing relationships between network organization and both motor ability and working memory (Bassett et al., 2015; Cohen and D’Esposito, 2016; Murphy et al., 2020), we hypothesized that early maturational trajectories across the first year of life that have a segregated network structure (i.e., high modularity) would be related to increased motor learning performance, while protracted maturational trajectories across the first six years of life that have an integrated network structure (i.e., high global efficiency) would be related to increased working memory performance.

2. Materials and methods

2.1. Participants

The Institutional Review Board of the University of North Carolina (UNC) School of Medicine approved this study. Pregnant mothers were recruited during their second trimester of pregnancy from the UNC hospitals registry to enroll their infants in a longitudinal MR imaging study of early brain development. Informed consent was obtained from both parents. As described in a previous paper with this sample (Gao et al., 2015), inclusion criteria required birth between gestational age of 35 and 42 weeks, appropriate weight for gestational age, and the absence of major pregnancy and delivery complications. Exclusion criteria included prenatal or congenital anomalies, or presence of any major medical or mental illness in the mother. 93 healthy infants (45 females) were recruited. 5 subjects with neuroimaging data that could not successfully be processed with the imaging pipeline described below were excluded from analyses, leaving a total of 88 subjects (43 females). Sample demographics include the following ethnicities (2010 U.S. Census estimates of North Carolina demographics reported for comparison): 97.7% non-Hispanic (90.2%), 2.3% Hispanic (9.8%); and the following races: 64.8% White (70.6%), 25.0% Black (22.2%), 2.3% Asian (3.2%), 1.1% Native American (1.6%), and 6.8% multiple races or other (2.4%).

2.2. Study procedure

Neuroimaging sessions occurred every 3 months between 2 weeks to 12 months (0, 3, 6, 9, and 12 months), at 18 months, and then annually between 2 and 6 years. This resulted in a total of 11 possible timepoints (i.e., 0, 3, 6, 9, 12, 18, 24, 36, 48, 60, and 72 months). Not all subjects participated in all timepoints due to subject dropout or unavailability when scheduling a visit. See Fig. 1 and Table 1 for the distribution of and specific ages during existing subject timepoints. The mean number of timepoints per subject was 5.14 (SD = 2.87, range: 1–11). All subjects were imaged during natural sleep without the use of sedation when they were infants and toddlers (ages 0–2). The protocol for conducting asleep scans was similar to that of other infant neuroimaging studies (Dean et al., 2014). When subjects returned for later timepoints at age three and beyond, subjects underwent scans either asleep or awake.¹ During awake scans, subjects watched a video inside the MRI scanner.

Fig. 1.

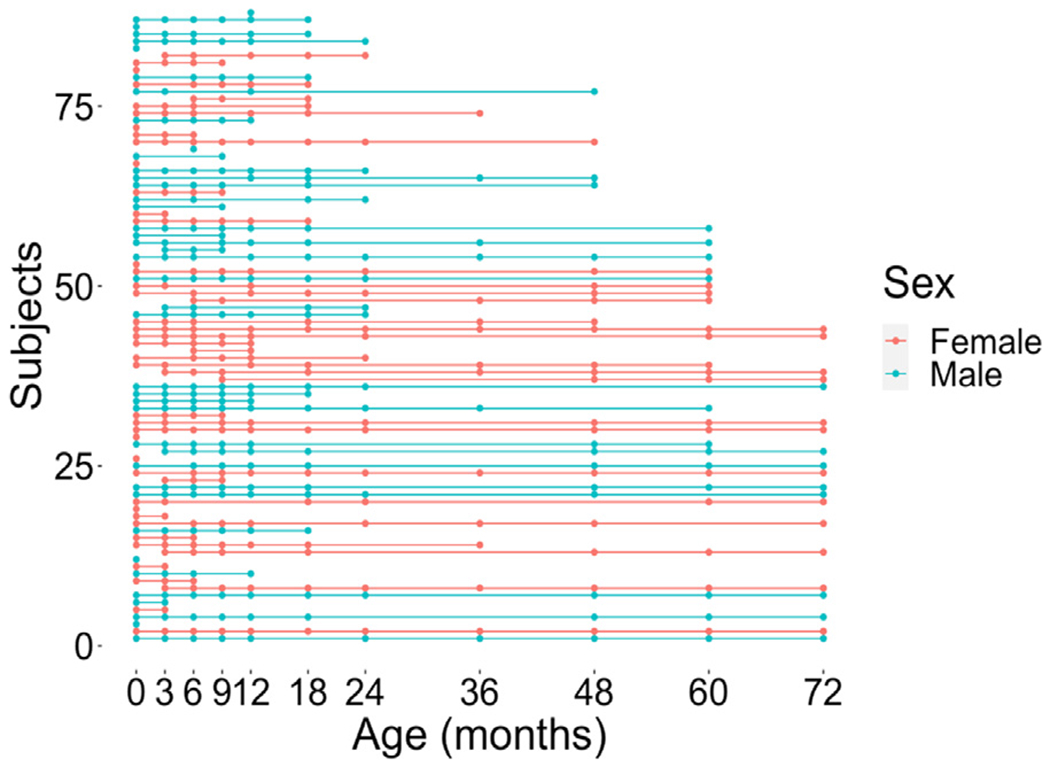
A longitudinal plot demonstrating the distribution of timepoints per subject labeled by sex. Additional information regarding specific age in days for each timepoint is presented in Table 1.

Table 1.

Number of subjects, sex distribution, and specific age (mean, SD, and range) at each timepoint.

Timepoint in months	0	3	6	9	12	18	24	36	48	60	72
N (F/M)	74 (38/36)	58 (30/28)	60 (31/29)	50 (23/27)	49 (21/28)	42 (19/23)	26 (14/12)	16 (11/5)	29 (17/12)	28 (16/12)	20 (12/8)
Mean age in days (SD)	25.8 (9.5)	94.5 (8.8)	187.6 (17.6)	278.1 (14.3)	376.8 (15.4)	556.4 (20.2)	737.7 (26.0)	1099.1 (18.4)	1475.6 (22.0)	1861.6 (42.2)	2212.3 (25.9)
Age range in days	2–48	75–116	116–225	240–312	352–418	507–613	666–797	1073–1147	1438–1530	1816–2009	2180–2285

2.3. Behavioral measures

39 of the 88 subjects returned for an additional timepoint between the ages of 8 and 10 years old (mean age = 9.3, SD = 0.56, range: 8.2–10.6, 22 females). During the additional timepoint, subjects completed two behavioral tasks as part of a larger study: a serial reaction time (SRT) task that probed motor learning and an n-back task that probed working memory. The behavioral data was acquired during fMRI scanning; the fMRI data collection is still ongoing and will not be discussed here. As no prior research has examined maturation of cortical thickness networks across this entire age range, nor related sbMCNs to outcome measures, our initial goal is to relate sbMCNs to behavior. Future studies will report the results from the fMRI data after data collection is complete.

2.3.1. Serial reaction time (SRT) task

For the SRT task, subjects were told to indicate the location of an ‘X’ presented on the screen by a button press using the index through pinkie fingers of their right hand (Fig. 2a). There were two conditions in this task: 1) a sequence condition, which consisted of a repeating 12-item pattern (i.e. 1-2-3-1-4-3-4-2-1-3-2-4); and 2) a random condition, which consisted of items in a pseudorandom order. The pseudorandom order was constrained such that items could not be a repeat of the previous item, nor could a random block begin or end with the same item with which the sequence block began or ended. For each trial, the letter ‘X’ was presented for 1000 milliseconds with an inter-stimulus interval of 250 milliseconds. This trial timing is consistent with prior work (Cohen and Poldrack, 2008) and this task has successfully been administered to children of this age range (Hodel et al., 2014; Thomas and Nelson, 2001; Thomas et al., 2004). Each block contained 24 trials. Each run contained 4 blocks each of sequence and random conditions in an interleaved order for a total of 8 blocks. Across subjects, the interleaved order was counterbalanced. A 24 s crosshair was presented at the start, middle and end of each run. Two runs of 5.2 min each of the SRT task were collected.

Fig. 2.

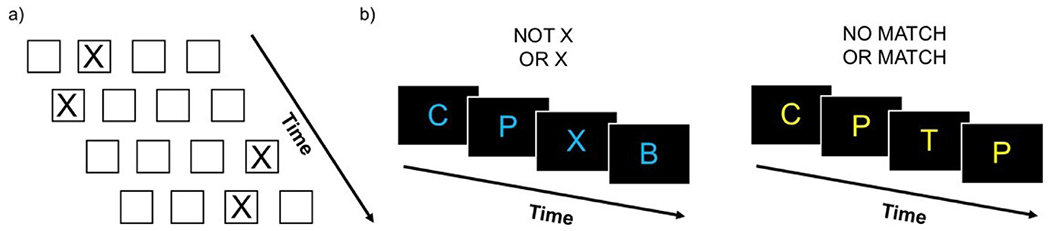
Behavioral task design. a) Serial reaction time (SRT) task. Subjects were told to indicate the location of an ‘X’ presented on the screen by a button press. Trial stimuli were presented for 1000 ms, followed by an inter-stimulus interval consisting of a blank grid for 250 ms. b) An illustration of the paradigm used for the n-back task with 0-back (in blue) and 2-back (in yellow) conditions. Subjects were told to respond with a button press whether the current stimulus was the same as (a ‘match’) or different from (a ‘non-match’) the stimulus seen n previously. For the 0-back condition, ‘X’ was used as a ‘match’ and any other letter was a ‘non-match’. For the 2-back condition, subjects responded whether the current stimulus was a ‘match’ or a ‘non-match’ to the letter presented two previously. Block instruction text was presented for 6 s. Trial stimuli were presented for 1000 ms, followed by an inter-stimulus interval consisting of a fixation cross for 1000 ms.

Prior to the MRI scan, subjects completed an initial practice session of 12 trials to ensure that they could correctly map stimulus locations to the correct buttons, and then a second practice session of the same length inside an MRI simulator.

The SRT task probes motor sequence learning such that subjects become faster on sequence trials as compared to random trials with practice (Cohen and Poldrack, 2008; Robertson, 2007; Thomas et al., 2004). Average response time (RT) on correct trials for the sequence condition, as well as the average RT difference between sequence and random conditions (average correct random RT – average correct sequence RT), were used as measures of motor learning. Paired t-tests comparing performance on run 1 versus run 2 assessed learning on the SRT task using the behavioral measures of interest. T-tests were corrected for two comparisons using the false discovery rate (FDR) correction. 12 subjects were excluded based on poor task performance inside the MRI machine (less than 50% accuracy on all responded trials), which resulted in 27 subjects (18 females) for subsequent behavioral analysis of the SRT task.

2.3.2. N-back task

For the n-back task, subjects were told to respond with a button press using the index and middle fingers of their right hand whether the current stimulus was the same as (a ‘match’; index finger) or different from (a ‘non-match’; middle finger) the stimulus seen n previously (Fig. 2b). 0- and 2-back conditions of the n-back task were administered to examine low and high working memory loads respectively. For the 0-back condition, ‘X’ was used as a ‘match’ and any other letter was a ‘non-match’. For the 2-back condition, subjects responded whether the current stimulus was a ‘match’ or a ‘non-match’ to the letter presented two previously. For each trial, a letter stimulus was presented for 1000 milliseconds with an inter-stimulus interval of 1000 milliseconds. Each block contained 20 trials that included 4 match trials and 16 non-match trials. There were 5 null event trials lasting 2000 ms each that were randomly interspersed throughout each block. Each task block began with a 6 s presentation of instructions (‘Not X or X’ for 0-back blocks or ‘No Match or Match’ for 2-back blocks). Jittered intervals lasting either 2 (50%), 3 (25%), or 4 (25%) seconds were presented between the block instruction text and the start of trials, and again at the end of each block of trials. A 10 s crosshair was presented at the start of each run. Each run contained four task blocks (two each of 0- and 2-back conditions) in a randomized order. Rest blocks were presented after every two task blocks. Rest blocks consisted of a 6 s presentation of ‘REST’ followed by 24 s of crosshair presentation. Two runs lasting 5.2 min each were acquired.

Prior to the MRI scan, subjects completed an initial practice session of 10 trials that progressed when they pressed the correct button, followed by 24 trials that progressed with the same timing as the actual task. They then completed a second, identical practice session inside an MRI simulator.

Accuracy on 2-back target trials and d’ were used as measures of n-back performance, which is consistent with previous literature administering the n-back task to children (Roussotte et al., 2011; Schleepen and Jonkman, 2009; Stollstorff et al., 2010). D’ was calculated as the difference between z-transformed hit rate (correct matches) and z-transformed false alarm rate (incorrect non-matches). Paired t-tests were used to test for differences of these behavioral measures between 0-back and 2-back conditions. T-tests were corrected for two comparisons using the FDR correction. 14 subjects were excluded based on poor task performance inside the MRI machine (responding to fewer than 50% of 0-back trials and accuracy less than 50% on 2-back trials), which resulted in 25 subjects (16 females) for subsequent behavioral analysis of the n-back task.

2.3.3. Effects of age on task performance

Given the potential contribution of age to performance on the SRT task (Hodel et al., 2014; Thomas and Nelson, 2001; Thomas et al., 2004) and the n-back task (Schleepen and Jonkman, 2009), we also correlated age with task performance. For the SRT task, sequence RT and RT difference of the second run were correlated with age to focus on when motor sequences should be most learned. For the n-back task, 2-back target accuracy and d’ were correlated with age. Correlations between age and task performance were corrected for 4 comparisons using the FDR correction (4 behavioral metrics [SRT task: sequence RT, RT difference; n-back task: 2-back target accuracy, 2-back d’]).

2.4. Image acquisition

For each timepoint in this study from 0 to 6 years, T1-weighted (T1w) and T2-weighted (T2w) images were acquired at the UNC Biomedical Research Imaging Center using a 3T Siemens scanner (TIM TRIO) with a 32-channel head coil. The two structural brain images were acquired for optimal distinction of gray and white matter throughout infancy and early childhood. The tissue boundaries during this age range are not as clear when using intensity-based segmentation, thus both structural images are needed for optimal processing (Shi et al., 2010). T1w images were acquired with the following parameters: 144 sagittal slices, repetition time (TR) = 1900 ms, echo time (TE) = 4.38 ms, flip angle = 7°, acquisition matrix = 256 × 192, and voxel size = 1 × 1 × 1 mm³. T2w images were acquired with the following parameters: 64 axial slices, TR = 7380 ms, TE = 119 ms, flip angle = 150°, acquisition matrix = 256 × 128, and voxel size = 1.25 × 1.25 × 1.95 mm³ . Additionally, in a subset of subjects, resting-state fMRI data was acquired. For the purposes of this study, resting-state data was used to calculate motion during the scanning session to ensure that results were not due to changes in subject motion with age. See Supplementary Material for data acquisition parameters.

2.5. Image processing and cortical surface construction

Structural brain images were processed with the infant Brain Extraction and Analysis Toolbox (iBEAT; Dai et al., 2013; Li et al., 2015b) for volume-based and cortical surface-based analysis that was specifically developed for pediatric MRI scans matching the data acquisition parameters used in this study. First, the intensity inhomogeneities of both the T1w and T2w images were corrected using the nonparametric nonuniform intensity normalization (N3) method (Sled et al., 1998). Second, the T2w image was linearly aligned onto the T1w image for each subject and then resampled with the T1w resolution using FLIRT (Smith et al., 2004). The skull, brainstem, and cerebellum of the aligned images were further removed based on a learning-based infant-specific method (Shi et al., 2012). Third, the cortex was further segmented into white matter, gray matter and cerebrospinal fluid (CSF) based on T1w and T2w structural images using a learning-based infant-specific method (Wang et al., 2015). Fourth, the segmented cortex was further separated into the left and right hemispheres; non-cortical structures were removed and filled with white matter. To correct the topological defects in tissue segmentation images, a topologically-preserving surface method was utilized (Han et al., 2004). Fifth, the topologically correct and geometrically accurate inner cortical surface was reconstructed, which was further smoothed and deformed to the interface between the gray matter and CSF for reconstructing the outer cortical surface (Li et al., 2012, 2014). Based on the reconstructed cortical surfaces, for each vertex we computed the cortical thickness as the minimum distance between the reconstructed inner and outer cortical surfaces (Fischl and Dale, 2000; Li et al., 2015a). To construct the structural brain network, we used the 146 regions of interest (ROIs) from the Destrieux atlas (Destrieux et al., 2010). To register the atlas to each subject’s and each timepoint’s cortical surface, we first mapped the inner cortical surface onto a sphere using FreeSurfer (Fischl, 2012), then aligned the mapped spherical cortical surface onto the UNC 4D Infant Cortical Surface Atlas (Wu et al., 2019; https://www.nitrc.org/projects/infantsurfatlas/) using Spherical Demons (Yeo et al., 2010). This established the vertex-wise correspondence between the individual surface and the Destrieux ROI labels in the infant surface atlas space. Finally, each ROI’s cortical thickness was computed by averaging the cortical thickness for all vertices within that region. To guarantee the quality of the reconstructed cortical surfaces for the subsequent analysis, an expert rater manually checked two aspects of each surface: a) whether the reconstructed cortical surface was accurately located at the gray/white matter tissue interfaces; and b) whether the reconstructed cortical surface was accurately parcellated. Any surfaces with inaccurate locations or inaccurate parcellations were removed, since they may introduce bias for the network construction (33 scans from 5 subjects). Cortical surfaces were also removed from subsequent analysis if they were beyond two standard deviations from the overall mean thickness of that timepoint (21 scans from 10 subjects). Therefore, a total of 50 subjects (24 females) with 318 good quality longitudinal cortical surfaces were used for analysis in this study based on the criterion that each subject has at least three timepoints of good quality data.

2.6. Structural covariance networks

For group level SCNs, each of the 11 timepoints was considered separately. For each timepoint, correlation matrices were constructed based on the across-subject correlations of cortical thickness between all pairs of regions (Fig. 3a). Similar to previous work (Fan et al., 2011; Khundrakpam et al., 2013), linear regression was used to remove effects of sex, age in days from birth, and mean overall cortical thickness. Permutation tests were used to investigate the differences between two contiguous timepoints, for a total of 10 tests. Each permutation sample was obtained by randomly assigning each subject’s 1 × 146 vector of data (residuals of cortical thickness of each region) from the two contiguous age groups to one or the other without replacement, resulting in a permutation sample with the same sample size as the original group. If a subject had data from both timepoints, the two data series were assigned to different timepoints. For each permutation test, 1000 permutation samples were obtained for each timepoint. Each permutation sample was used to calculate across-subject correlations, again controlling for sex, age in days, and mean cortical thickness between each pair of brain regions, which resulted in a 146 × 146 structural covariance matrix for subsequent graph metric calculation.

Fig. 3.

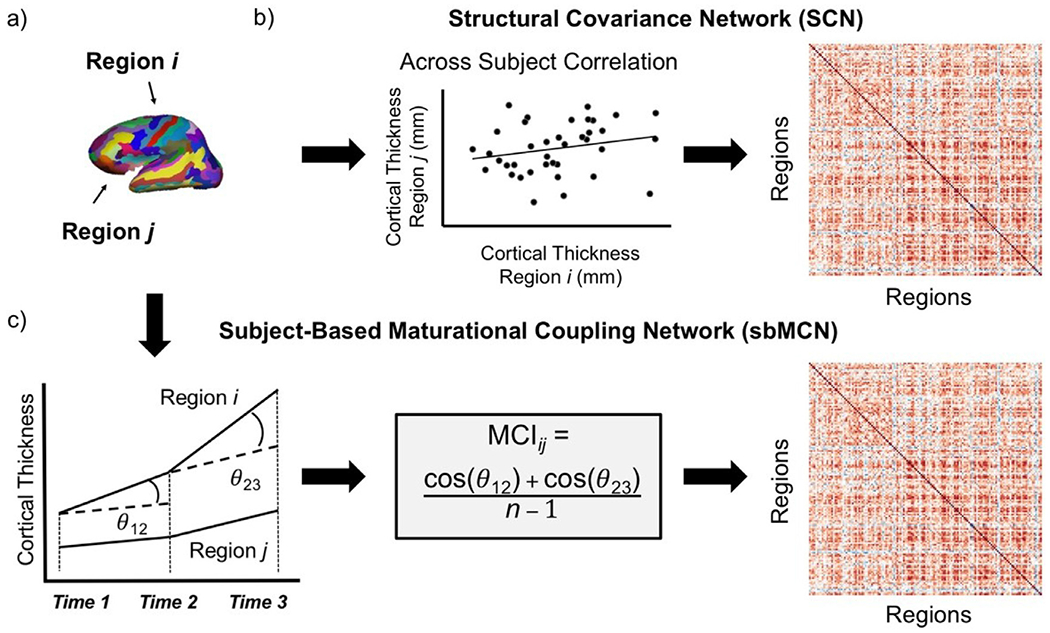
Steps to construct cortical thickness matrices both across and within subjects. a) Regions of interest (ROIs) from the Destrieux brain atlas (Destrieux et al., 2010). b) The construction of a structural covariance network (SCN), which estimates edge strength between nodes as the correlation of cortical thickness across subjects. The resulting matrix used for SCN analysis is a correlation matrix with correlation coefficients as the cells representing the edge strength between each pair of regions. c) The construction of a subject-based maturational coupling network (sbMCN), which estimates edge strength between nodes as the maturational coupling index (MCI) for a subject with available number of timepoints n. Steps to construct an sbMCN depicted here for a subject with 3 timepoints. The resulting matrix used for sbMCN analysis is a maturational coupling matrix with the MCI for a pair of regions as the cells representing the edge strength between each pair of regions. Panel C adapted from Khundrakpam et al. (2019) with permission.

Network segregation and network integration were quantified from each structural covariance matrix for each of the 10 permutation tests using the Brain Connectivity Toolbox, a MATLAB-based toolbox for structural and functional MRI network analysis (brain-connectivity-toolbox.net; Rubinov and Sporns, 2010). We calculated modularity as our measure of network segregation and global efficiency as our measure of network integration. The graph metrics were calculated with weighted and undirected correlation matrices using the below equations (Rubinov and Sporns, 2010, 2011). Only positive weights were included.

Modularity is a measure of the number of intra-network connections as compared to the number of intra-network connections expected in a random graph, and quantifies the strength of segregation into distinct networks. Higher modularity values represent stronger network segregation. Modularity of positive edges only (Q⁺) is defined as follows:

$$Q^{+}=\frac{1}{{\upsilon }^{+}}\sum _{ij}\left({\omega }_{ij}^{+}-\frac{s_i^{+}{s}_j^{+}}{{\upsilon }^{+}}\right)\delta m_i{m}_j$$

where v⁺ is the sum of all the graph’s positive edge weights, ${\omega }_{ij}^{+}$ is the positive edge weight between two nodes i and j, $s_i^{+}$ and $s_j^{+}$ are the sums of positive edge weights connected to nodes i and j respectively, and δ m_i m_j = 1 if i and j are in the same module and δ m_i m_j = 0 if i and j are in different modules.

Global efficiency is the average inverse of the weighted shortest path length of each node to all other nodes. Higher global efficiency is indicative of faster information transfer, or greater network integration. Weighted global efficiency $\left(E_{global}^w\right)$ is defined as follows:

$$E_{global}^w=\frac{1}{n}\sum _{i\in N}\frac{{\sum }_{j\in N,j\ne i}{\left(d_{ij}^w\right)}^{-1}}{n-1}$$

where n is the number of nodes in the graph, N is the set of all nodes in the graph, and $d_{\mathit{ij}}^w$ is the weighted shortest path length between nodes i and j. The weighted shortest path length is the smallest sum of the weights of the edges across all possible paths between nodes i and j.

Trajectories of these graph metrics were plotted to qualitatively depict changes in network organization from infancy to childhood. For timepoints that were included in two permutations tests (i.e., the 3 month timepoint was included in the 0–3 month and the 3–6 month comparisons), their distributions were combined and plotted for visualization purposes for a total of 2000 observations. For modularity and global efficiency, two-tailed two-sample t-tests were used for each contiguous pair of age groups for the 10 permutation tests and were corrected for 10 comparisons using the FDR correction, similar to previous SCN studies (Fan et al., 2011; Khundrakpam et al., 2013). To examine the nonrandom modular organization of SCNs, 1000 random graphs with the same degree distributions as actual non-permuted SCNs were generated for each timepoint (Maslov and Sneppen, 2002), and the means of the graph metrics for the random graphs were calculated and plotted for comparison.

2.7. Subject-based maturational coupling

For each individual subject, the similarity of cortical thickness trajectories across pairs of regions was quantified by adapting the maturational coupling index introduced by Khundrakpam et al. (2019). Only subjects with at least three timepoints were included in this analysis to be consistent with the measurement of longitudinal change by Khundrakpam et al. (2019). All timepoints with good quality data for each subject were used, thus the number of timepoints and which specific timepoints were included varied across subjects. Thus, the original maturational coupling index, calculated as the product of cosines across time, was adapted to be calculated as the average of cosines across time for the current study (Fig. 3c). Here, the maturational coupling index for each subject is defined as follows:

$$MC{I}_{ij}=\frac{\cos \left(\text{θ}12\right)+\cos \left(\text{θ}23\right)+\dots +\cos \left({\theta }_{\left(n-1\right)\left(n\right)}\right)}{n-1}$$

where i and j are two nodes, n is the number of timepoints available for a given subject, and cos(θ_t1t2) is the cosine of the angle of maturational slopes between each pair of adjacent timepoints (i.e., between timepoints 1 and 2, then between timepoints 2 and 3, and so on for all possible timeframes for a given subject). Two sets of analyses were conducted. First, maturation across the first year of life (0, 3, 6, 9, and 12 months), during which the largest developmental changes occur, was assessed (Gilmore et al., 2018; Li et al., 2014, 2015a). 48 subjects had at least three timepoints, including a first timepoint at either 0 or 3 months and a final first-year timepoint at either 9 or 12 months, and were thus included in this analysis (mean number of timepoints = 4.06, SD = 0.73, range: 3–5). Next, maturation across all 6 years (0, 3, 6, 9, 12, 18, 24, 36, 48, 60, 72 months) was assessed, to characterize more prolonged maturation. 32 subjects had at least three timepoints, including a first timepoint at either 0 or 3 months and a final timepoint at either 60 or 72 months, and were thus included in this analysis (mean number of timepoints = 7.34, SD = 1.84, range: 4–10). These two sets of sbMCN analyses were used to determine the relevance of early brain development (first year) versus more protracted brain development through childhood (first six years) to cognitive outcomes. For each set of sbMCN analyses, a 146 × 146 maturational coupling matrix for each subject was constructed. Following the method used by Khundrakpam et al. (2019), we applied a cumulative distribution function kernel to each individual maturational coupling matrix to distinguish real and spurious connections between regions, essentially normalizing each individual sbMCN. As described above, modularity and global efficiency were calculated from each sbMCN to assess network segregation and network integration respectively.

Task performance measures on the SRT and n-back tasks at 8–10 years were correlated with modularity and global efficiency from sbMCNs. These task performance measures included sequence RT and RT difference from the SRT task, and 2-back target accuracy and 2-back d’ from the n-back task. Of those included in the early development sbMCN analyses, 22 subjects had SRT task data of sufficient quality and 19 subjects had n-back task data of sufficient quality. Of those included in the protracted development sbMCN analyses, 20 subjects had SRT task data of sufficient quality and 18 subjects had n-back task data of sufficient quality. Correlations between sbMCN modularity and global efficiency and task performance were corrected for 8 comparisons for each task separately using the FDR correction (2 brain metrics [modularity, global efficiency] x 2 sets of sbMCN analyses [early, protracted] x 2 behavioral metrics [SRT task: sequence RT, RT difference; or n-back task: 2-back target accuracy, 2-back d’]).

2.8. Sensitivity analyses

We conducted three supplementary analyses to investigate the robustness of our results. First, we estimated motion during each scan session using resting-state fMRI data in a subset of subjects who had such data to ensure that results were not due to motion in the scanner. Supplementary analyses controlled for the effects of motion, in addition to sex, age in days, and mean cortical thickness. Motion increased across timepoints, specifically at age three. Critically, supplementary results controlling for motion were generally consistent with the main results (see Supplementary Material, Fig. S2 and Tables S3–S4). Second, to ensure that results were not due to spurious weak connections, we thresholded SCN matrices at correlation values of 0.1 and 0.2 and found that results were consistent across thresholds (see Supplementary Material, Fig. S3 and Tables S5–S6). Third, to ensure that results were not due to our choice of atlas, we replicated our analyses using the Desikan-Killiany atlas (Desikan et al., 2006), which includes 64 cortical ROIs (see Supplementary Material, Fig. S4 and Tables S7–S8). The same trajectories of modularity and global efficiency were observed across parcellations. Supplementary analyses additionally examined the effects of atlas on the sbMCN analyses. Replication of sbMCNs with the Desikan-Killiany atlas revealed similar relationships between sbMCN organization and task performance as with the Destrieux atlas, although the significant finding reported in the main text between early development (0–1 year) sbMCNs and RT difference on the SRT task did not reach significance for the Desikan-Killiany atlas (see Supplementary Material, Figure S5).

3. Results

3.1. Task behavior

Performance on the SRT task was assessed using sequence RT (run 1: mean = 679.8 ms, SD = 85.7 ms; run 2: mean = 647.9 ms, SD = 75.7 ms) and RT difference between sequence and random blocks (run 1: mean = 21.7 ms, SD = 44.4 ms; run 2: mean = 31.5 ms, SD = 42.7 ms). These measures were analyzed to examine motor learning between the first and second runs of the SRT task. Subjects became significantly faster on sequence blocks between run 1 and run 2 (t(26) = 4.169, p-adjusted < 0.001; Fig. 4a). However, the RT difference between the random and sequence conditions did not change across the runs (t(26) = −0.898, p-adjusted = 0.377; Fig. 4b).

Fig. 4.

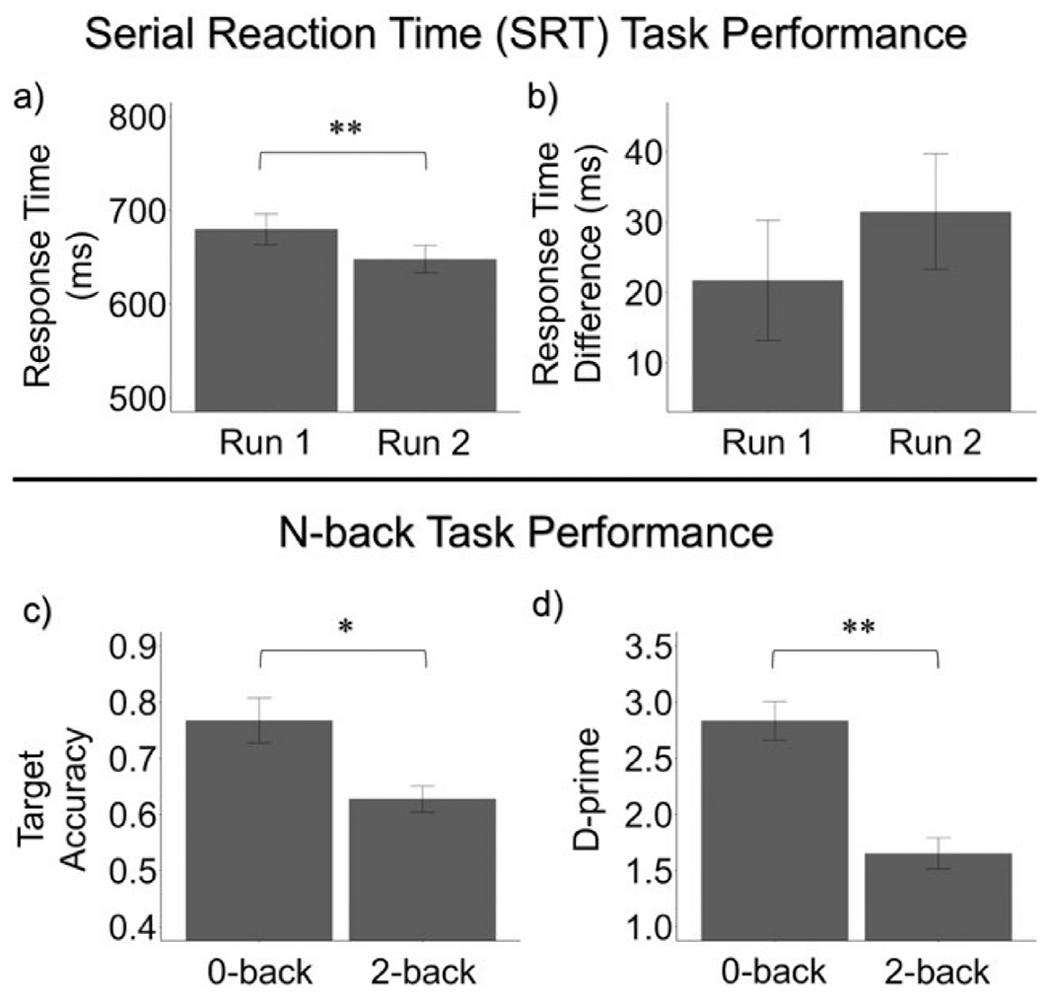
Task Performance on the SRT and n-back tasks. For the SRT task, a) sequence RT significantly decreased across runs (t(26) = 4.169, p-adjusted < 0.001), while b) RT difference between random and sequence conditions did not significantly change (t(26) = −0.898, p-adjusted = 0.377). For the n-back task, c) target accuracy (t(24) = 3.480, p-adjusted = 0.002 and d) d’ (t(24) = 6.159, p-adjusted < 0.001) significantly decreased between 0-back and 2-back conditions. Error bars represent standard error. * p-adjusted < 0.05, * * p-adjusted < 0.001.

Task performance on the n-back task was assessed using accuracy of target trials (0-back: mean = 0.767, SD = 0.200; 2-back: mean = 0.627, SD = 0.116) and d’ (0-back: mean = 2.834, SD = 0.863; 2-back: mean = 1.653, SD = 0.693). Accuracy of target trials and d’ were significantly lower for the 2-back condition as compared to the 0-back condition (target accuracy: t(24) = 3.4802, p-adjusted = 0.00193; d’: t(24) = 6.1595, p-adjusted < 0.001; Fig. 4c and d).

3.2. Effects of age on task performance

For the SRT task, age was not significantly correlated with sequence RT on the second run (r = −0.407, p-adjusted = 0.140) or the RT difference on the second run (r = −0.058, p-adjusted = 0.773). For the n-back task, age was not significantly correlated with 2-back target accuracy (r = 0.265, p-adjusted = 0.399) or 2-back d’ (r = −0.128, p-adjusted = 0.719).

3.3. Structural covariance networks

At the group level, qualitatively modularity increased between 0 and 72 months (Fig. 5a; Table 2). Changes across all timepoints were significant after permutation at FDR-corrected p < .05 except between 6 and 9 months. Qualitatively, global efficiency decreased between 0 and 72 months (Fig. 5b; Table 2). Changes across all timepoints were significant after permutation at FDR-corrected p < .05 except between 24 and 36 months. These results were consistent across thresholds (see Supplementary Material, Fig. S3 and Tables S5–S6) and with the Desikan-Killiany atlas (see Supplementary Material, Fig. S4 and Table S7–S8). Modularity and global efficiency of SCNs were negatively correlated across time (non-permuted SCNs: r = −0.754, p = .007).

Fig. 5.

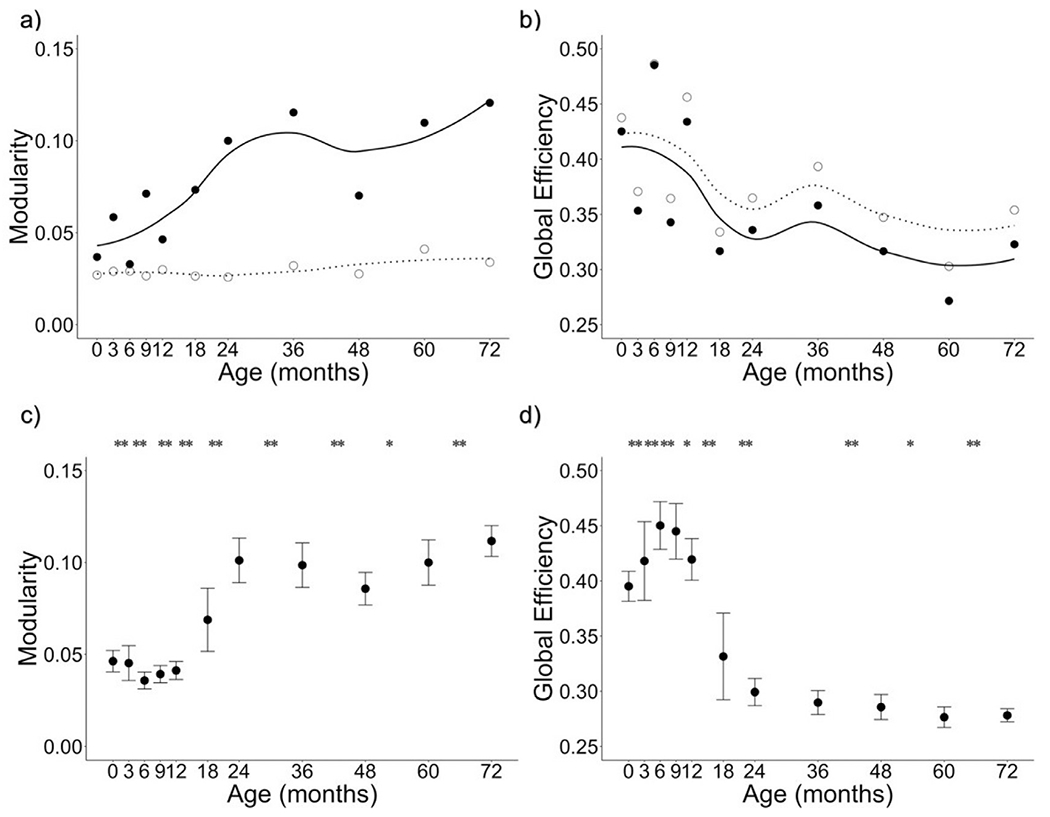
Trajectories of SCN organization from two weeks to six years (0–72 months). a) Modularity of SCNs increased between 0 and 72 months. b) Global efficiency of SCNs decreased between 0 and 72 months. Solid circles represent actual values and solid line represents the loess smoothed fit curve for actual values. Open circles represent the mean of 1000 random networks with the same degree distribution and dashed line represents the loess smoothed fit curve for random values. c) Mean and observed distributions are plotted for modularity of SCNs from permutation tests. d) Mean and observed distributions are plotted for global efficiency of SCNs from permutation tests. Error bars represent the standard deviation of distributions. * indicates significant difference between adjacent timepoints at adjusted p < .05; ** indicates significant difference between adjacent timepoints at adjusted p < .001. Means from non-permuted graphs and statistics from permutation tests are reported in Table 2.

Table 2.

Two-tailed t-tests assessing change in modularity and global efficiency of SCNs across pairs of timepoints. Reported p-values for each graph metric are FDR-corrected for 10 comparisons.

Timepoints (months)		Modularity				Global Efficiency
Time 1	Time 2	Value Time 1	Value Time 2	t-value (dF)	p-adj.	Value Time 1	Value Time 2	t-value (dF)	p-adj.
0	3	0.037	0.058	−19.524 (999)	<0.001	0.425	0.353	10.110 (999)	<0.001
3	6	0.058	0.033	22.617 (999)	<0.001	0.353	0.485	−13.718 (999)	<0.001
6	9	0.033	0.071	0.555 (999)	0.579	0.485	0.343	−30.747 (999)	<0.001
9	12	0.071	0.046	−5.839 (999)	<0.001	0.343	0.434	3.327 (999)	0.001
12	18	0.046	0.073	−68.758 (999)	<0.001	0.434	0.317	81.944 (999)	<0.001
18	24	0.073	0.100	−43.121 (999)	<0.001	0.317	0.336	−15.504 (999)	<0.001
24	36	0.100	0.115	−5.149 (999)	<0.001	0.336	0.358	0.798 (999)	0.425
36	48	0.115	0.070	41.276 (999)	<0.001	0.358	0.317	−18.089 (999)	<0.001
48	60	0.070	0.110	−3.344 (999)	0.001	0.317	0.272	−2.639 (999)	0.009
60	72	0.110	0.121	−5.873 (999)	<0.001	0.272	0.323	−29.939 (999)	<0.001

3.4. Subject-based maturational coupling

Next, we assessed the relationship between network organization of longitudinal cortical thickness maturation within individual subjects and task performance at 8–10 years using sbMCNs. For the SRT task, global efficiency of the early development (0–1 year) sbMCNs was negatively correlated with RT difference of the second run (r = −0.54, p-adjusted = 0.022; Fig. 6). No other correlations between sbMCNs and SRT task performance were significant for either the early development or the protracted development sbMCNs (all p-adjusted values > 0.145). Additionally, there were no significant correlations between sbMCNs and n-back task performance for either the early development or the protracted development sbMCNs (all p-adjusted values > 0.971). Replication of sbMCNs with the Desikan-Killiany atlas revealed a similar relationship between global efficiency of early development sbMCNs and RT difference on the SRT task, although this did not reach significance (p-adjusted = 0.223; see Supplementary Material, Fig. S5).

Fig. 6.

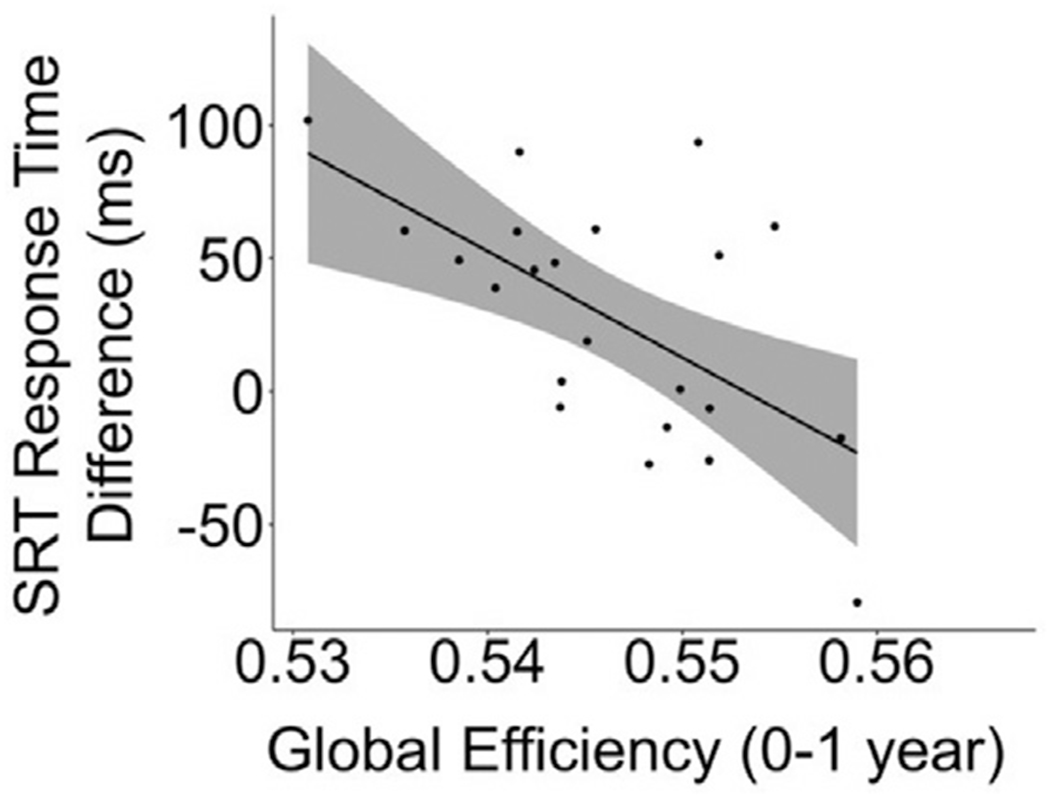
Correlation between sbMCN graph metrics and task performance. There was a negative correlation between global efficiency of early development (0–1 year) sbMCNs and response time difference of the second run of the SRT task (r = −0.606, p-adjusted = 0.022) at 8–10 years. Shading represents 95% confidence intervals, and the trend line represents the line of best fit for this correlation.

4. Discussion

Here, for the first time, we characterized SCN organizational changes between infancy and childhood within a longitudinal sample of subjects and related individual-level network maturation to cognitive outcomes in childhood. At the group level, modularity of SCNs increased and global efficiency decreased between two weeks and six years. We additionally found that decreased global efficiency of sbMCNs during early development (0–1 years) was associated with better motor learning. We did not find a significant correlation between organization of sbMCNs during either early or protracted development and working memory.

Behaviorally, we observed faster motor execution across runs of the SRT task and reduced accuracy and d’ during higher working memory conditions of the n-back task in our sample of children aged 8–10 years. These findings are largely consistent with previous studies examining motor learning (Hodel et al., 2014; Thomas and Nelson, 2001; Thomas et al., 2004) and working memory (Roussotte et al., 2011; Schleepen and Jonkman, 2009; Stollstorff et al., 2010) during childhood. With regard to motor learning on the SRT task, subjects were faster for the sequence condition on the second run as compared to the first run. However, we did not observe the expected increase in RT difference between sequence and random blocks on the second run compared to the first run. While other studies have observed sequence-specific motor learning in children of this age range as operationalized by a significant difference between sequence and random RT on final SRT task runs (Hodel et al., 2014; Thomas and Nelson, 2001; Thomas et al., 2004), there are a few key differences in task design between prior literature and our study that may account for our lack of sequence-specific motor learning. First, we included fewer sequence trials during task runs (384 trials as compared to 420–960; Hodel et al., 2014; Thomas and Nelson, 2001; Thomas et al., 2004). Second, prior work has trained subjects with more practice sessions before task runs (Thomas et al., 2004). It is possible, therefore, that our subjects were still early in the motor learning process. Additionally, we used a fixed-paced version of the SRT task, in which the trial stimuli were presented for constant intervals of time, as opposed to a self-paced version, in which the trial duration is dependent upon the time it takes for a subject to correctly respond (Hodel et al., 2014). Fixed-paced versions have been shown to result in reduced sequence learning effects as compared to self-paced versions in children (Hodel et al., 2014). Generally, for both tasks we excluded approximately 1/3 of subjects for poor performance (less than 50% trials responded to or 50% accuracy on responded trials). This may be due to the fact that the trials were too fast for a large portion of our subjects and as such we observed poorer performance than is typically reported on these tasks in subjects of this age range.

With regard to our findings related to group-level SCN trajectories, extant literature mainly investigates structural network organization in infancy and toddlerhood (e.g., 0–2 years) separately from later in childhood (Fan et al., 2011; Yap et al., 2011; Zhao et al., 2019). Thus, the group level changes in network segregation of SCNs reported here contribute to our understanding of how brain networks reorganize between infancy and childhood. In early infancy, we observed low modularity and high global efficiency. Further, the topology of SCNs were similar to that of random graphs throughout the first year of life. This suggests that SCNs are more randomly organized during infancy, and do not shift to a non-random organization until after the first year of life. Though weak, network structure still exists even in early infancy, consistent with network organization derived from tractography and resting-state fMRI data (De Asis-Cruz et al., 2015; Gao et al., 2011; Yap et al., 2011; Zhao et al., 2019). The increase in modularity we observed between early infancy and six years suggests that cortical networks further differentiate across this time period. In other words, more distinct networks emerge as regions undergoing similar maturation cluster into networks that have similar levels of cortical thickness. This early reconfiguration of brain network organization may underlie the cognitive specialization that emerges over early infancy and early childhood, as has been observed for several cognitive processes, such as perception (Simion et al., 2007) and language (Blasi et al., 2011). Additionally, the Euclidean distance of within-network connections numerically decreased between 0 and 72 months (see Supplementary Material, Figure S7). This provides initial support for the theory that the networks observed at early infancy become more differentiated between infancy and six years, though these distinct networks may emerge from local similarities in cortical maturation and then shift from local to distributed cortical network maturation later in childhood (Zielinski et al., 2010). Further research in larger samples that focuses on the specific nodal composition of networks is needed to better understand how the trajectory of graph metrics reported here fits in with existing literature and the degree to which networks present at birth reorganize across early childhood, as well as how the maturation of modularity may map onto behavioral trajectories of cognitive specialization.

With regard to network integration, we observed that global efficiency of SCNs decreased between birth and six years. Notably, modularity and global efficiency were negatively correlated during this period, suggesting that these trajectories may be in part capturing similar information. This is not surprising, as both increased modularity and decreased global efficiency are characteristics of reduced randomness in terms of network organization. The decrease in global efficiency of SCNs observed here between three and six years is consistent with a study characterizing SCN organization between three and 20 years, which observed a decrease in global efficiency between three and six years, before an increase in later childhood (Nie et al., 2013). In contrast, decreased global efficiency over the first two years is inconsistent with prior literature assessing the maturation of network organization in infancy across neuroimaging modalities, including SCN (Fan et al., 2011), tractography (Huang et al., 2015), and resting-state (Gao et al., 2011) networks. The inconsistent results may be attributed to methodological differences between studies. Specifically, data acquisition parameters may influence graph metric values of tractography networks (Zalesky et al., 2010), and may similarly influence measurement of SCNs. Further, we used weighted matrices to calculate graph metrics while prior studies have used binarized adjacency matrices. Prior research comparing the use of weighted matrices to binarized adjacency matrices from fMRI data revealed higher reliability for weighted networks than binarized networks (Xiang et al., 2020). This is likely because weighted matrices contain more information than binarized matrices, and this could be the case for SCNs as well.

Another difference between our study and previous work is the intensive sampling of data across the first two years of life. In early infancy, synaptogenesis is likely a primary factor driving measures of cortical thickness (Huttenlocher, 1990; Petanjek et al., 2011). Previous work with SCNs may not have had sufficient temporal resolution to observe the impact of this initial burst of synaptic activity on coordinated changes in gray matter thickness. This proliferation of synapses is followed by a rapid synaptic pruning, then a more gradual pruning accompanied by extensive myelination. The timing of the trade-off between proliferation and pruning differs across areas of cortex, but this initial burst in activity is complete between the 2nd and 5th years of life (Petanjek et al., 2011). Thus, processes driving early changes in global efficiency may differ from those driving later changes. Early changes in gray mater (proliferation and pruning) may explain the early shift toward a less random organization (i.e., increases in modularity and decreases in global efficiency). In contrast, the process of myelination, which strengthens long-range connections over the course of several years and continues well into childhood and adolescence (Huang et al., 2015; Lebel and Deoni, 2018), likely allows for more efficient information transfer between networks (i.e., increased global efficiency; Zhao et al., 2019). The protracted process of myelination is likely why network integration is found to increase at six years and beyond in other SCN studies. In the context of cognitive development, the later increases in network integration observed during childhood (Khundrakpam et al., 2013; Nie et al., 2013) may support the emergence of higher order cognition that integrates multiple cognitive processes during this developmental stage (Johnson and Munakata, 2005; Luna et al., 2015).

Contrary to our hypothesis that increased modularity (i.e., increased segregation) of early development sbMCNs would be related to increased motor learning in middle childhood, we instead observed that lower global efficiency (i.e., decreased integration) was associated with better performance on the SRT task in middle childhood. We based our hypothesis on previous neuroimaging work reporting that greater functional network segregation assessed during task performance is related to increased motor task performance in healthy adults (Bassett et al., 2015; Cohen and D’Esposito, 2016). However, these studies assessed the execution of a motor sequence when it was well-learned, and as discussed above our subjects were likely still in the early stages of learning. Our finding is consistent with the finding of decreased functional network integration globally across the brain when learning motor sequences during task performance in adults (Bassett et al., 2015). Subject-based maturational coupling that is more globally efficient during early infancy represents more similar changes in cortical thickness across the whole brain. However, less similar maturation across the brain (i.e., lower global efficiency) may indicate different brain regions that have developed differently in the first year of life allows for later decreased integration and greater learning later in childhood. Additionally, it is intriguing that the global integration that occurs within the first year of life may be important for maturing motor systems and have long-lasting effects. Our finding should be interpreted with the limitations of our small sample size, lack of replication across parcellations, and low levels of learning in our subjects. Thus, further examination in larger samples with better learning outcomes is needed.

We did not observe a relationship between either early or protracted sbMCN organization and working memory. While prior literature has observed that increased functional connectivity strength between regions of different networks (i.e., the thalamus and the salience network) assessed at 1 year relate to working memory ability assessed at 2 years (Alcauter et al., 2014), no extant literature has assessed how early functional or structural network development relates to working memory ability later in childhood. It is possible that the increases in SCN network integration beyond age 6 that are reported in the literature (Khundrakpam et al., 2013; Nie et al., 2013) correspond to the cognitive integration needed for working memory assessed at 8–10 years. Working memory ability at 8–10 years, therefore, may better correspond to network maturation assessed after age 6. While our results indicate that whole-brain measures of subject-based maturational coupling do not predict later working memory ability, our lack of a statistically significant finding could be due to our small sample size and is therefore not conclusive.

While there are certain unique strengths of this study, such as longitudinal data spanning infancy and childhood and densely sampled timepoints to capture early maturation, there are some limitations that should be addressed. Specifically, we are limited by a relatively small sample size, subject dropout for later timepoints, and poor task performance that reduced the number of subjects that could be included in our sbMCN analyses. Future longitudinal studies that cover the age range of infancy and childhood, such as the Baby Connectome Project, will be able to answer similar questions in a larger sample (Howell et al., 2019). Additionally, motion while in the MRI scanner may result in inaccuracies in our cortical thickness measurements (Madan, 2018; Savalia et al., 2017). While the impact of motion on functional connectivity measurements is becoming better understood (Grayson and Fair, 2017; Satterthwaite et al., 2013), it still remains unclear how to best measure motion during structural brain scans (Rosen et al., 2018) and how precisely motion may influence structural covariance and maturational coupling in this and other studies. The structural data collected in this sample between three and six years when some subjects were awake in the scanner may be biased by motion artifacts that result in less accurate estimates of network organization (Grayson and Fair, 2017; Satterthwaite et al., 2013). However, motion is unlikely to account for all of our findings, since as reported in the Supplementary Material we observed similar trajectories for both modularity and global efficiency when controlling for motion. The slight differences in the supplementary analyses are likely due to noisier data after limiting our sample to subjects with available in-scanner motion estimates.

4.1. Conclusion

This study has furthered understanding of the cognitive relevance of early brain network development in several ways. Our finding of high global efficiency, low modularity, and random network configuration in early infancy indicates that initially infants may process information in a global manner that is computationally redundant. The increase in modularity between 0 and 6 years supports the hypothesis that brain networks become specialized for certain cognitive computations throughout early development. Our observation of a decrease in global efficiency between 0 and 6 years, in combination with findings in the literature of increased global efficiency later in childhood (Khundrakpam et al., 2013; Nie et al., 2013), suggests that increases in integration between distinct networks beginning in middle childhood may serve to support complex executive functions such as working memory. These results support current models of brain network development that describe early increases in network segregation, however our subjects may not be old enough to determine whether this early segregation is followed by increases in network integration as hypothesized. Finally, network organization of longitudinal cortical thickness changes observed within individuals corresponded to later cognitive performance such that less integrated whole-brain structural maturation across the first year of life supported later motor learning during childhood. Importantly, this study demonstrates that a child’s early brain developmental trajectory is associated with current cognitive functioning, even many years later. More work is needed to better explicate what shapes early brain development to potentially constrain future cognitive development.

Data and code availability statement

Longitudinal data collection is still ongoing and will be made available upon request after completion of the study. Data for the 8–10 year old timepoint was collected as part of an ongoing National Institutes of Health (NIH) grant and will be made available after completion of the study as per NIH data sharing requirements.