De novo molecular drug design benchmarking

Abstract

De novo molecular design for drug discovery is a growing field. Deep neural networks (DNNs) are becoming more widespread in their use for machine learning models. As more DNN models are proposed for molecular design, benchmarking methods are crucial for the comparision and validation of these models. This review looks at recently proposed benchmarking methods Fréchet ChemNet Distance, GuacaMol and Molecular Sets (MOSES), and provides a commentary on their future potential applications in de novo molecular drug design and possible next steps for further validation of these benchmarking methods.

Deep neural networks (DNNs) used for de novo drug design have different architectures and hyperparameters that impact the final output of suggested drug candidates. Herein we review benchmarking platforms that assess the utility and validity of DNNs.

Introduction

The prevalence and incidence of multidrug-resistant bacteria has increased drastically in recent decades, while new antibiotic development has lagged.¹ Similarly, drug resistance has become rampant in cancer treatment. Today, 90% of chemotherapy failures are due to drug resistant cancer metastasis and invasion.² To find new drug candidates, high-throughput in vitro chemical screening has been used to test large physical libraries of up to 10⁷ compounds for their biological activity.³ However, it has been estimated that 10³⁰ to 10⁶⁰ potential organic compounds exist in chemical space.⁴

De novo molecular design has the capacity to explore all of chemical space efficiently by generating a small number of molecules using search and optimization procedures.⁵ Because of this, de novo drug design has the potential to revolutionize medicinal chemistry and drug discovery. De novo molecular design can be based on a receptor, often using known protein structures to find molecules that fit well in binding pockets. Alternatively, de novo designed molecules can be built “from scratch” from different ligands.⁶

Deep neural networks (DNNs) have existed for a few decades, but their application in de novo molecular design is a more recent development. It was only within the past decade that DNNs have been shown to outperform more traditional machine learning methods and, since 2012, DNN based models have won multiple competitions in categories such as image classifications and molecular activity predictions.⁷

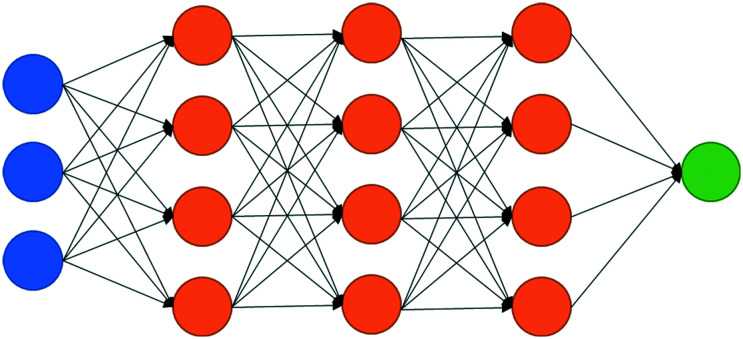
DNNs are often defined as having more than three layers.⁷ The layers of DNNs fit into three categories: an input layer, hidden layers, and an output layer. Each layer is made up of nodes. The input layer will contain as many nodes as there are features. The output layer, if it is a classifier, contains as many nodes as there are classes. The hidden layers can have different numbers of nodes.⁸ Each node will have an activation based on an input signal. This activation will tell a node whether to “fire”, in turn sending an input signal to the next node.^8,9 A basic representation of nodes in a deep neural network can be seen in Fig. 1.

Fig. 1. A basic representation of a deep neural network where the blue circles represent the input layer, the orange circles represent nodes in the hidden layers, and the green circle represents the output layer. Each layer is connected to the next and each node of the previous layer will have an impact on the activation of the nodes in the next layer.

Different DNNs feature different network architectures such as recurrent neural networks (RNNs), fully connected neural networks (FCNNs), and convolutional neural networks (CNNs). Different architectures have different basic structures. The way nodes are connected between input, hidden, and output layers will vary with different architectures.^8,10

All DNN de novo molecular generators go through three steps while producing new molecules. First, molecules are created, then they are scored and, finally, new and better molecules are searched for.^5,11

Molecules are typically created from ligands or fragments.¹² However, methods for molecule construction using in silico chemical reactions have also been published with the goal of increasing the synthetic accessibility of proposed de novo molecules.¹³ Once created, molecules need to be scored by the model.

The way a model scores molecules will depend on whether the model is receptor or ligand based. Models that suggest new molecules to bind to a known 3D structure of a protein will be scored on how well molecules bind to and fit into a protein site.^12,14 These molecular docking scores can be based on molecular force fields, empirical scoring functions, or knowledge-based scoring functions, which are discussed more in depth by Hartenfeller and Schneider.¹²

Ligand based models do not use a protein structure to build new molecules. In order to score molecules, these models can use a reference compound for scoring similarity, with the hypothesis being that similar molecules will have similar pharmacological properties.¹² This is the basis of quantitative structure–activity relationship (QSAR) and quantitative structure–property relationship (QSPR) modelling.¹⁵ Scoring ligand based models can also include methods for predicting physicochemical properties or a combination of these scoring methods.⁵

After scoring molecules, models will look for novel and more effective molecules. This can be done using stochastic optimization methods where a local minimum for the most suitable molecule is found.¹² Models based on the construction of molecules by incrementally adding and scoring ligands have also been developed.¹⁶

The goal of using DNNs for de novo drug design is to create new lead compounds for drug discovery. Ideally, DNNs could be used to propose new compounds in underexplored areas of chemical space. Proposed molecules by DNNs would need to be chemically stable, synthesizable, and bioactive. As well, proposed molecules need to be accepted by medicinal chemists in order to be tested in vivo and in vitro.

As more de novo models for molecular design are proposed, standardized benchmarking procedures are needed to compare the efficacy of these models. Benchmarking models can test de novo methods on many different characteristics such as the novelty of the proposed molecules, validity, fragment similarity, internal diversity, and other criteria. Benchmarking will not only allow new de novo methods to be tested for their efficacy but provide guidance for future improvement of methods.

Recently, benchmarking methods such as Fréchet ChemNet Distance,¹⁷ MOSES,¹⁸ and GuacaMol⁵ have been proposed. They represent a first step towards standardized benchmarking procedures for DNN de novo drug design models. However, as will be discussed in this review, there is a lack of research into the biases these benchmarks can suffer from, including biased scoring functions for novelty that Renz et al.¹⁹ highlights. Investigation into whether models that scored well on benchmarks produced molecules medicinal chemists can actually synthesize and test is another area that should be explored in the future.

This review will give an overview of the methods used by the benchmarking models Fréchet ChemNet Distance,¹⁷ MOSES,¹⁸ and GuacaMol⁵ before discussing where these benchmarks could be improved and where future work is needed to test whether medicinal chemists agree with the scoring outcomes of these benchmarks.

Fréchet ChemNet Distance

Preuer et al.¹⁷ developed Fréchet ChemNet Distance (FCD) as a metric to evaluate generative models. FCD was designed to encompass validity, and chemical and biological meaningfulness into one score. FCD was modelled after Fréchet Inception Distance (FID),²⁰ which is a metric for comparing generative models for images. FCD calculates the distance between the distribution of real-world molecules and the distribution of molecules produced by a generative model. Preuer et al.¹⁷ calculated numerical representations of molecules using the penultimate layer of the neural network ChemNet, a long short-term memory (LSTM) RRN that is based on SMILES representations of molecules. SMILES (simplified molecular input line entry system)²¹ was designed specifically for computers to represent molecules in two dimensions using only letters to represent atoms and special characters to represent different types of bonds. ChemNet was trained to predict the bioactivities of molecules based on approximately 6000 bioassays found in the drug databases ChEMBL,²² Zinc,²³ and PubChem.²⁴

From the activation of the penultimate layer of ChemNet, mean and covariance are calculated for both the distribution of real-world molecules and the distribution of molecules from a generative model. The two distributions are then compared using Fréchet distance,²⁵ also called Wasserstein-2 distance.²⁶ Preuer et al.¹⁷ carried out hyperparameter selection and training using two-thirds of available data, with the last third being saved for testing. They state that large enough data sets are needed for both real and generated molecules to estimate mean and covariance.

Preuer et al.¹⁷ compared FCD to four common metrics for evaluating generative models. The metrics were mean log P, mean druglikeness, mean synthetic accessibility (SA) score, and the internal diversity score with Tanimoto distance. Preuer et al.¹⁷ wanted to show that these metrics have specific flaws and fail to detect biases in generative models. To do this, they manipulated models to produce molecules with either low drug likeness, a high log P, low synthetic accessibility, mode collapse (low internal diversity), or bias toward certain target families for models designed to produce molecules active for a specific target. These manipulated models were compared to real molecules.

FCD was the only evaluation method able to consistently score the manipulated models worse than the real molecules. Preuer et al.¹⁷ also tested their hypothesis that chemical information alone is not enough to test a generative model. To do this they tested what they termed the Fréchet Fingerprint Distance (FFD), which was based on 2048 bit ECFP_4 fingerprints and on purely chemical representation of generated molecules. They found that FCD was able to make stronger distinctions between the manipulated and real sets compared to FFD. This was especially true when looking at biologically relevant information such as when the manipulated model was biased towards a certain target family.

Applications of FCD in the literature

FCD has been incorporated into other benchmarking tools such as GuacaMol and MOSES, which are also discussed in this review. On its own FCD has also been used to compare different models for de novo drug design. Skalic et al.²⁷ used FCD as part of their evaluation and comparison of their shape-based generative model to other generative models such as an adversarial autoencoder (AAE), a character-level recurrent neural network (CharRNN), a variational autoencoder (VAE), and an objective-reinforced generative adversarial network (ORGAN). The shape-based model was found to be comparable to other methods tested.

Grisoni et al.²⁸ also used FCD as part of their evaluation for their new method for SMILES string generation. In their new model, SMILES strings were generated both left-to-right (forwards) and right-to-left (backwards). In their BIMODAL (bidirectional molecule design by alternate learning) model, two RNN's are used. One RNN reads the SMILES strings forward and another backwards. These are then combined for a joint prediction.

For evaluation of their method, Grisoni et al.²⁸ looked at structural novelty defined as “not contained in the training set”, uniqueness defined as the percentage of unique SMILES strings generated, and validity defined as the percentage of chemically valid SMILES strings generated. Grisoni et al.²⁸ also looked at scaffold diversity and novelty using Bemis–Murcko scaffolds.²⁹ Finally, they used FCD to evaluate the chemical and biological relevance of the generated SMILES strings.

For the FCD evaluation, Grisoni et al.²⁸ found the BIMODAL model had a slightly worse FCD score than the traditional forward running RNN when there were 512 hidden units. However, when there were 1024 hidden units, the forward RNN and BIMODAL had comparable scores, with both improving from their 512 scores. This combined with BIMODAL's good scaffold diversity scores made Grisoni et al.²⁸ conclude that the BIMODAL model was worth further investigation.

GuacaMol

GuacaMol⁵ uses a set of benchmarks to assess a model's ability to learn from a data set of molecules and to create new molecules with similar properties. GuacaMol⁵ splits models for de novo molecular design into two categories: distribution-learning and goal-directed. Distribution-learning models aim to generate new molecules based on the chemical distribution of a training set of molecules. Goal-directed models are designed to generate molecules for a specific goal.

GuacaMol⁵ evaluates distribution-learning models based on validity, uniqueness, novelty, FCD, and the Kullback–Leibler (KL) divergence. Validity is an assessment of whether the generated molecules are realistic, at least theoretically. The validity benchmark scores molecules lower for incorrect SMILES syntax or if they have an invalid valence. Uniqueness measures the ability of a model to produce unique molecules. If a model produces a molecule more than once, it is penalized.

For novelty, GuacaMol uses the ChEMBL training set to represent a tiny portion of chemical space. Brown et al.⁵ state that a good model for de novo molecular design should be able to explore a large part of chemical space and would, therefore, be unlikely to reproduce molecules from the training set. Models that overfit receive a low score on this task. However, a bad model could potentially score well on this benchmarking task if that model produces many different simple molecules, such as carbon chains.

The FCD is measured as described previously. Lastly, the KL divergence is a measure of how well a probability distribution approximates another distribution. For GuacaMol, KL divergence is used to measure how diverse the generated molecules are from the training set. Low diversity will lead to a low KL divergence score. All scores are on a scale of 0 to 1.

Since goal-directed models are trying to design one optimized molecule to complete a specific task, generated molecules need to be scored individually. For evaluation, GuacaMol⁵ has goal-directed models produce a set number of high scoring molecules. The models are allowed to iteratively improve their molecules using the scoring function, but the models do not have access to what the scoring function is explicitly calculating. The optimizing function of a model is evaluated by looking at a combination of the structural features (molecular weight, number of aromatic rings, etc.), physicochemical properties, similarity or dissimilarity to other molecules, and presence or absence of substructures, functional groups, or atom types.

For similarity, the model is assessed on its ability to produce molecules that are similar to a target compound. Brown et al.⁵ describe this as a sort of inverse virtual screening because, instead of looking up molecules in a large data base, molecules are generated based on a target molecule. A rediscovery benchmark is also included. This is like the similarity benchmark, except the goal is to rediscover the target molecule and not produce many molecules like it. An isomer benchmark is also included for which the model is tasked with producing isomers from a given molecular formula. This is used to test the flexibility of the model. Lastly, the median molecules benchmark is included to assess a models ability to produce a molecule that is similar to several different molecules. This task is designed to be conflicting, as it is useful for assessing how a model explores chemical space.

GuacaMol⁵ also includes rule sets for assessing the quality of the compounds produced by distribution-learning and goal-directed models. A model that suggests molecules that are potentially unstable, reactive, or too difficult to synthesize will not be used by medicinal chemists. The set of rules used by GuacaMol are designed to determine if suggested molecules could be included in a high-throughput screen. Brown et al.⁵ note that the list of filters they include for assessing compound quality is probably incomplete. However, it is likely that any molecules filtered out by the rule set would not be chosen for synthesis.

Brown et al.⁵ used GuacaMol to evaluate and compare different types of distribution-learning and goal-directed models. For the generative-models, a random sampler was included for a baseline comparison. The random sampler took a set number of molecules from the training set at random for evaluation. The random sampler showed high values for KL divergence and FCD, which were considered to be baselines for good models. The GuacaMol⁵ benchmark results showed that the SMILES LSTM model was the most consistently high-scoring model across benchmarks.

For comparison of goal-directed models, a “Best of Data Set” was used. The “Best of Data Set” used the highest scoring molecules in the data set. These molecules are used to set the bar for the goal-directed models because the purpose of goal-directed models is to return molecules that are better than the original data set. If models do not perform better than the best data from the data set, then they provide no advantage over virtual screening. Of the tested models, the graph genetic algorithm performed the best on all the benchmarks.

Applications of GuacaMol in the literature

Winter et al.³⁰ tested their proposed method for optimizing molecules, molecular swarm optimization (MSO), using GuacaMol. MSO uses a ‘light weight’ heuristic optimization method, particle swarm optimization (PSO), proposed by Hartenfeller et al.³¹ applied to their previously reported continuous chemical representation.³² Winter et al.³⁰ retrained their model using the same subset of ChEMBL originally used for the GuacaMol benchmark. Winter et al.³⁰ found that their method had a higher average score than the baseline models included in GuacaMol.

Kwon et al.³³ proposed an improved VAE method for efficient molecular graph generation. To improve the molecular graph generation, they included three additional learning objectives. These objectives were: approximate graph matching, reinforcement learning, and auxiliary property prediction. Kwon et al.³³ tested their generative model for validity, uniqueness, novelty, KL divergence, and FCD. On the tests for validity, uniqueness, and novelty, the proposed method performed as well as or out-performed the baseline SMILES models, LSTM, VAE, AAE, and ORGAN and the molecular graph generation model GraphMCTS. Their model did not perform well on KL divergence or FCD, which suggests that their model was not able to reproduce the property distribution of the training set. Overall, the graph method was superior to the SMILES string generators at producing chemically valid and diverse molecules but struggled to represent the data-distribution of the training set.

EvoMol³⁴ is another molecular generation model. It sequentially builds molecular graphs using an evolutionary algorithm. This algorithm was developed with the goal to explore both known and unknown chemical space. Leguy et al.³⁴ used the goal-directed benchmarks from GuacaMol to assess EvoMol.

EvoMol performed exceptionally well on the isomer benchmark task in comparison to other molecular generators. EvoMol also outperformed other models on the multi-property objective (MPO) benchmark. Overall, EvoMol performed very well on the GuacaMol benchmark.

Molecular Sets (MOSES)

Molecular Sets (MOSES)¹⁸ is another benchmarking suite for molecular generators. It includes a standardized dataset and evaluation metrics. MOSES compares distribution-learning models using fragment similarity, scaffold similarity, nearest neighbour similarity, internal diversity, and Fréchet ChemNet Distance (FCD). These metrics are used to evaluate how well a generative model approximates an unknown distribution when given a set of training samples from the unknown distribution. MOSES first computes the validity of generated molecules and then only evaluates valid molecules.

Valid molecules are determined using RDKit, which can be used to evaluate molecules for proper atom valency. The authors suggest that, for evaluation, 30 000 molecules should be generated, and molecules labelled valid should make up the generated set for comparison with the reference set.

The benchmarks that compare the generated set to the reference set include novelty. This metric calculates the number of molecules in the generated set that are not present in the reference set. Novelty can be used to evaluate if a model is overfitting. Next, fragment similarity looks at the distribution of BRICS fragments in the generated set compared to the reference set. BRICS is a set of rules for breaking up chemical substructures of biologically active compounds that was developed for medicinal and computational chemists.³⁵ The fragment similarity metric is large if the generated set has similar fragments to the reference set. If the generated set over (or under) represents fragments from the reference set, then the fragment similarity value will be low. Scaffold similarity is another metric; it operates in the same manner as fragment similarity except using Bemis–Murcko scaffolds instead of BRICS fragments. Bemis–Murcko scaffolds is a list of common drug shapes in a graphical representation based on rings, linker atoms, and sidechains.²⁹

MOSES also calculates similarity to a nearest neighbour (SNN) based on Tanimoto similarity between the fingerprint of molecules in the generated set and its nearest neighbour molecule in the reference set. This is used as a precision metric: the lower the score the poorer the precision of the model. MOSES also calculates the FCD for comparison between the generated set and the reference set.

MOSES also looks at various property distributions between the generated and reference sets. The molecular weight distribution shows whether the generated set is biased towards either heavier or lighter molecules. log P and synthetic accessibility (SA) scores are also included. Lastly, the quantitative estimation of drug-likeness (QED) score is included, which evaluates molecules on how likely they are to be viable drug candidates on a scale of 0 to 1. QED is meant to approximate the abstract knowledge held by medicinal chemists on what molecules may be good drug candidates and was proposed by Bickerton et al.³⁶ However, a limitation of QED is that it is only dependent on molecular properties such as molecular weight, octanol–water partition coefficient, number of hydrogen bond donors, and number of hydrogen bond acceptors. Factors such as absorption, distribution, metabolism, excretion, and toxicity (important in vivo and in vitro properties) are not considered.³⁷

Polykovskiy et al.¹⁸ applied MOSES to multiple different models that covered many different approaches to molecular generation. The tested models included character-level neural networks (CharRNN), variational autoencoders (VAE), adversarial autoencoders (AAE), junction tree variational autoencoders (JTN-VAE), LatentGAN, and non-neural baselines. The non-neural baselines included a hidden Markov model (HMM), an n-gram model which collects the frequency of n-grams in a training set and uses the distribution for new strings, and a combinatorial generator that uses BRICS fragments of the training set to randomly assemble new molecules.

Polykovskiy et al.¹⁸ found that the VAE and AAE models had low novelty scores, which is an indication of overfitting. The VAE had the best SNN score, but that was likely due to overfitting. The best FCD, fragment, and scaffold scores were obtained by the CharRNN model. Because of this, the CharRNN was concluded to be the best model tested. This model did not have a problem with overfitting but was still able to represent the distribution of the training set. Polykovskiy et al.¹⁸ conclude that MOSES will allow for fair and comprehensive evaluation of generative models for de novo drug design. They also plan to update MOSES with new baseline models and evaluation metrics in the future.

Applications of MOSES in the literature

In addition to calculating FCD as discussed previously, Skalic et al.²⁷ also used the MOSES benchmark to evaluate their shape-based generative model. Skalic et al.²⁷ compared their shape based model to models tested by Polykovskiy et al.,¹⁸ including the CharRNN, VAE, AAE, ORGAN, and JTN-VAE. It was found that Skalic et al.'s²⁷ model performed similarly to the other models with good validity and uniqueness scores. The shape-based model produced molecules with the highest level of internal diversity, but this seemed to be at the cost of lower compound desirability and increased reactivity.

Boitreaud et al.³⁸ proposed a new graph to selfies VAE. This graph2selfies model was tested using the MOSES benchmarking platform. Graph2selfies performed well on all benchmarks and outperformed the state-of-the-art graph to graph model JTVAE while also being 18 times faster.

Issues with current benchmarking models

One issue with benchmarking platforms, which has been brought up by Renz et al.,¹⁹ is the copy problem. Renz et al.¹⁹ benchmarked a model they called AddCarbon. This generative model creates “new” molecules by taking random molecules from the training set and adding one carbon randomly in the SMILES string. As long as the new SMILES string is valid and is not a molecule already in the training set it is used as a new random sample.

The AddCarbon model was tested using GuacaMol and received a perfect score for novelty, validity, and uniqueness and scored high on KL divergence. The AddCarbon model outperformed all the baseline models except for the LSTM model.

Renz et al.¹⁹ concluded that since their “useless” model scored so well on the GuacaMol benchmark, it calls into question the usefulness of the benchmark. They suggest that better metrics for quantifying novelty would be beneficial.

Renz et al.¹⁹ also looked at the shortcomings of benchmarking goal-directed models. It is difficult to compile all the desirable qualities of a molecule into one score, and molecules generated to optimize a specific score might not be useful. Renz et al.¹⁹ provide a few examples of molecules produced by various goal-directed models that score well on GuacaMol's benchmarks, but have unstable, synthetically unrealistic, or highly uncommon substructures.

There were two main biases explored for goal-directed models: model specific biases and data specific biases. Model specific biases exploit unique features of a model while failing to capture the actual desired characteristics that model is supposed to capture. Data specific biases refers to how models will perform much better on data they have been trained on compared to hold-out data.

Renz et al.¹⁹ showed both model specific biases and data specific biases by comparing an optimization score to a model control score and a data control score. They took a set of data and split it in half. The optimization score was calculated from a classifier trained on split 1 and optimized. The model control score was calculated from a second classifier trained on split 1 but using a different random seed than the optimized score model. Lastly, the data control score was calculated by training a third classifier using split 2 and then using this model to score optimized molecules from split 1. This was done to see if a model trained on different data scores molecules similarly.

In all cases, the optimized score was higher than model control scores, and data control scores were even lower. This showed that model and data specific biases are likely present in optimization. Renz et al.¹⁹ point out that since the goal of de novo design is to explore all of chemical space, data specific biases suggests models are failing.

Another major issue with de novo molecular design benchmarking is the synthesizability of molecules proposed by high scoring models. A model may preform well on benchmarking platforms such as GuacaMol⁵ and MOSES,¹⁸ but if proposed molecules are synthetically inaccessible, they are useless. Gao and Coley³⁹ found that, especially for goal-directed models, a high score on benchmarking does not mean the model will produce synthetically accessible molecules.

Specifically, of the multiple goal-directed models tested by Brown et al.,⁵ the graph genetic algorithm model scored the best. This model was found by Gao and Coley³⁹ to produce no synthesizable molecules when tested by their data-driven computer-aided synthesis planning program. The SMILES genetic algorithm also scored well when tested by GuacaMol,⁵ but did not produce any synthetically accessible molecules when tested by Gao and Coley.³⁹

Since benchmarking methods such as GuacaMol⁵ and MOSES¹⁸ are new, there is not a lot of research evaluating their efficacy. Therefore, it is difficult to determine if medicinal chemists would agree with the scores given by these benchmarks to various de novo molecular generators.

In another study, Bush et al.⁴⁰ evaluated three molecular generators on their ability to produce molecules deemed acceptable by medicinal chemists. To do this, they used three tests.

For the first test, 13 medicinal chemists were asked to suggest 20 molecules to explore the structure–activity relationship based on four hit molecules. These suggested molecules were meant to capture human “ideation”. The four hit molecules were then fed into the molecular generators being tested. The molecular generators were then evaluated on their ability to propose the “ideal” molecules suggested by medicinal chemists.

The second test had medicinal chemists evaluate molecules suggested by the algorithms. For each hit molecule, medicinal chemists were presented with 75 ideas generated algorithmically and 25 ideas designed by medicinal chemists. Molecules were categorized as “like” or “dislike” based on whether the medicinal chemist would consider each molecule for synthesis.

For the last test, molecular generators were evaluated on their ability to generate molecules from six drug patents. One molecule was chosen as a seed molecule, typically the marketed drug, from each patent. The seed molecules were fed to each algorithm. Generated molecules were compared to the patent. Any generated molecules that matched molecules in the patent were refed to the algorithm. This was done in an iterative process meant to mimic design-make-test cycles.

Bush et al.⁴⁰ designed these tests to assist medicinal chemists in picking the best algorithms for generating new molecules. If a molecular generator is supported by medicinal chemists, it will hopefully produce more synthetically accessible molecules with better biochemical and physicochemical properties. Indeed Bush et al.⁴⁰ found that one of the algorithms tested was beneficial. This algorithm could potentially be incorporated into a computational based medicinal chemistry design procedure.

Of the three molecular generators tested by Bush et al.,⁴⁰ none were also tested by Preuer et al.,¹⁷ Brown et al.,⁵ or Polykovskiy et al.¹⁸ In the future it would be interesting to compare results using methods proposed by Bush et al.⁴⁰ to the results of benchmarking models. If GuacaMol⁵ or MOSES¹⁸ are found to score molecular generators similarly to how medicinal chemists score them, this would be evidence that these benchmarks are practical and will be useful for assessing molecular generators developed in the future.

Conclusions

Herein we have discussed multiple benchmarking methods for de novo molecular design, which is a growing field in the realm of drug discovery. As such, there is a need for valid methods for comparing new models.

Preuer et al.¹⁷ proposed the benchmark FCD. They also showed that including both chemical and biological information is important for testing generative models. FCD was incorporated into the benchmarking models GuacaMol and MOSES.

GuacaMol⁵ and MOSES¹⁸ seem to be, overall, more complete benchmarking platforms. Not only do they include datasets for testing, but also multiple different benchmarking metrics for comparing models. GuacaMol evaluates both distribution-learning and goal-directed models, while MOSES focuses primarily on distribution-learning models.

Both GuacaMol and MOSES mention the need for future improvement of their benchmarking platforms. Brown et al.⁵ note that some of their benchmarking tasks were too easily solved by baseline models. This indicates a need for harder benchmarks. Polykovskiy et al.¹⁸ note that in the future they will expand MOSES' repository with new baseline models and evaluation metrics.

The shortcomings of benchmarking techniques pointed out by Renz et al.¹⁹ should be considered for future updates of GuacaMol and MOSES, and for any new benchmarking models proposed in the future.

To validate benchmarking models in the future it would be beneficial to compare how medicinal chemists score molecular generators using methods such as those proposed by Bush et al.⁴⁰ to scores generated by benchmarking models. One of the more difficult areas for benchmarking molecular generators is assessing synthetic accessibility. Generated molecules may score well on benchmarks if they are valid chemical structures that fit well into the desired distribution of molecules. However, if chemists cannot physically make suggested molecules for testing, then they are useless.

In the future, benchmarking suites could help computational medicinal chemists evaluate and improve models for de novo molecular drug design. This is crucial as computational models for drug discovery have the potential to unlock so much of chemical space not currently being explored by other methods such as high-throughput screening. However, further studies are needed to validate the efficacy of benchmarking models such a GuacaMol⁵ and MOSES¹⁸

Author contributions

L. L. Grant was responsible for conceptualization and writing of the original draft. C. S. Sit was responsible for supervision, funding acquisition and writing (reviewing and editing) of the manuscript.

Conflicts of interest

There are no conflicts to declare.