Abstract
The global epidemic caused by novel coronavirus continues to be a crisis in the world and a matter of concern. The way the epidemic has wreaked havoc on the international level has become difficult for the healthcare systems to supply adequately personal protection equipment for medical personnel all over the globe. In this paper, considering the COVID-19 outbreak, a multi-objective, multi-product, and multi-period model for the personal protection equipment demands satisfaction aiming to optimize total cost and shortage, simultaneously, is developed. The model is embedded with instances and validated by both modern and classic multi-objective metaheuristic algorithms. Moreover, the Taguchi method is exploited to set the metaheuristic into their best performances by finding their parameters’ optimum level. Furthermore, fifteen test examples are designed to prove the established PPE supply chain model and tuned algorithms’ applicability. Among the test examples, one is related to a real case study in Iran. Finally, metaheuristics are evaluated by a series of related metrics through different statistical analyses. It can be concluded from the obtained results that solution methods are practical and valuable to achieve the efficient shortage level and cost.
Keywords: Supply chain design, Personal protection equipment, COVID-19, Pandemic, Disaster relief supply chain
1. Introduction
Reportedly, the COVID-19 pandemic became a severe infection with severe consequences, including detrimental respiratory system injuries and even death. Unfortunately, the number of infected cases worldwide is continuously increasing as of April 2021, according to the daily statistics about COVID-19 from World Health Organization (WHO). Evidence from different cases of the COVID-19 shows that it is spreading among people through close contact with an infected person and contaminated surfaces. Thus, societies experience a grave challenge in supplying medical necessities in a few days. Additionally, medical staff and healthcare personnel who have devoted their lives to serving the COVID-19 patients are at the highest risk of contamination [1]. A series of actions and measures have been taken and suggested by policymakers, governments, organizations, and healthcare systems against the COVID-19. These measures can be classified into different groupings, for instance, individuals, organizational, environmental, etc. [2].
One of the leading environmental measures is frequently cleaning and decontamination of surfaces with disinfectants like alcohol. Measuring body temperature, remote working, preventing conferences and meetings, etc., are categorized as organizational measures [2]. Moreover, using Personal Protection Equipment (PPE) like face masks, social distancing, washing hands carefully and regularly, avoiding travel to busy high-risk areas, reduction of gathering like parties, and keeping away from hugging and kissing are some of the measures at individual levels [3], [4].
Among mentioned measures, PPE meets the standard requirements to reduce the infection inhibition and losses caused by contagious viral diseases such as the COVID-19 and helps healthcare systems control the growth of the COVID-19 among their personnel. A group of PPEs is made to control personnel healthcare. The PPEs are gloves, gowns, respiratory protection, eye protection, and testing kits [5].
On the other side, the current stock of PPE might be quickly in shortage for many items like a medical mask or respiratory protection. This crisis is begun by the growing number of COVID-19 cases globally, alongside bulk buying of PPE due to misinformation and fear [1]. Moreover, PPE production has encountered diminished capacity, and increasing daily demand in the hospital must be met to care for contaminated patients [6]. Although it could be recommended numerous avenues to handle PPE demand befittingly, this study aims to propose a mathematical supply chain model in which optimal PPE flow in the network during the COVID-19 pandemic is critical.
Generally, emergency management has been defined in many ways. However, it can be summarized in three main aspects: being prepared before a disaster happens, immediate response to disasters, and reestablishing detrimental damages caused by natural or human-origin disasters [7]. Improper and meager care to injured people by disaster could bring about longstanding health impacts and fatality growth, specifically COVID-19. During a health disaster, adequate and timely supply of necessary commodities such as food, medicine, medical equipment has a tremendous impact on the hectic situation of the public health emergency [8].
In supply chain (SC) theories, the situation mentioned above is called supply chain disruption. Supply chain disruption is an unexpected occasion that disables one or more components in the supply chain and disrupts common goods and commodities distribution within the network [9], [10]. Epidemic outbreaks are named as one of the particular cases of supply chain disruption that is consist of three features as follows: permanent presence and vague disruption level; concurrent disruption significantly spreads in supply chain and occurs over a broad population; it begins on a small scale and immediately dominates numerous geographic areas [11]. Emergency management practices’ performance is intensively associated with relief supply chain design [12].
A set of consecutive activities which help to afford the material, produce goods, move production among the chain, and distribute the final products to their destination is defined as an SC [13]. Correspondingly, managing an SC is a set of applicable plans to handle the production cycle through numerous practices and integrate suppliers, producers, warehouses, and stores to produce and dispense the proper goods. At the same time, it optimizes costs and makes a competitive advantage available for all cooperated partners over the supply chain [14], [15]. So, designing a relief SC is the center of focus, especially during a natural disaster or any uncertain medical emergency like COVID-19. The right step not taken on time becomes the reason for a large number of losses of lives.
Obviously, designing such relief SC networks under particular conditions like pandemic is inevitable to better response time and reliability. Safaei et al. [16] developed an efficient and cost-effective optimization framework to distribute relief items considering dynamic conditions adequately. Reportedly, the Chinese government built new medical facilities less than two weeks after understanding the COVID-19 outbreak in this country [17]. Similarly, the same approach has been implemented in several countries, like Iran, using churches, mosques, stadiums, etc., to be proactive to reach the following advantages:
-
•
Supplying and delivering materials and drugs in the right quantity.
-
•
Providing and planning the right number of nurses and doctors.
-
•
Optimal transportation planning.
-
•
Timely and well-organized responding to the patients.
-
•
Proactive to possible future cases.
-
•
Minimizing the total costs while servicing and covering all potential cases.
-
•
Centralized decision-making.
Hence, this paper develops a multi-objective model including medical supply manufacturers, distributors, medical centers, and world donators to minimize both total costs and unsatisfied demand to provide better distribution of PPEs.
A detailed review of previous related works is conducted and reported in Section 2. The proposed model is formulated in Section 3. Section 4 provides the proposed solution approaches and encoding scheme. We develop applied examples and computational results and also investigate a real case in Section 5. In Section 6, computational outputs are elaborated. Lastly, Section 7 embodies the conclusion is presented, and future directions are proposed.
Table 1.
Overview of relief supply chain literature.
RSCN: Relief supply chain network
PPD: Pre- and post-disaster.
| Author(s) | Description | Period |
Formulation |
Applying Heuristics (Y/N) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Single | Multi | Deterministic | Stochastic | Fuzzy | |||||||
| Wang et al. [18 ] | They considered responses for a disaster in an RSCN (Walmart). | N | |||||||||
| Nagurney and Nagurney [19 ] | They considered PPD relief products delivery. | N | |||||||||
| Mohammadi et al. [20 ] | They developed a model to design an RSCN considering re-response emergency (The United States). | Y | |||||||||
| Sung & Lee (2016) | They designed an RSCN to meet patients’ demands | N | |||||||||
| Zhou et al. [21 ] | They considered resources distribution in post-disaster by optimizing emergency resource allocation and scheduling. | Y | |||||||||
| Jha et al. [22 ] | They designed an RSCN to distribute goods. | Y | |||||||||
| Al Theeb and Murray [23 ] | They designed an RSCN considering VRP. | Y | |||||||||
| Manopiniwes & Irohara (2017) | They considered PPD response in an RSCN. | N | |||||||||
| Li et al. [24 ] | They considered supplies distribution in natural disasters (The United States) | N | |||||||||
| Samani et al. (2018) | They considered blood distribution in RSCNs (Iran). | N | |||||||||
| Cao et al. [25 ] | They considered RSCN in natural disasters (China). | Y | |||||||||
| Safaei et al. [16 ] | They considered logistics operations in RSCN (Iran). | N | |||||||||
| Moreno et al. [26 ] | They designed a location-transportation model to make available relief aids to needy people. (A case study of 2011 based mega-disaster in Brazil). | Y | |||||||||
| Torabi et al. [27 ] | They presented an integrated relief model for the pre-position of the relief item to the planned location for pre-disaster agreements and post-procurement-related decision-making. (Iran). | Y | |||||||||
| Hong and Jeong [28 ] | They proposed a method for disaster planning. | N | |||||||||
| John et al. (2019) | They modeled a humanitarian network in a food RSCN. | N | |||||||||
| Sarma et al. [29 ] | The proposed model was a Facebook disaster map in emergency relief to identify the location of the victims; accordingly, the transportation plan, demand for the relief products are managed (India). | Y | |||||||||
| Ghaffari et al. [7 ] | They considered an emergency-scheduling problem (India). | Y | |||||||||
| Aghajani et al. [30 ] | They proposed a method to select the suppliers for a humanitarian RSCN (Iran). | N | |||||||||
| Yenice and Samanlioglu [31 ] | Earthquake relief network presented to store and distribute relief aid to the people (Turkey) | N | |||||||||
| This Study (2021) | Disaster RSCN for PPEs (Iran) | Y | |||||||||
2. Literature review
Recently, COVID-19 caused millions of death, and also this crisis has influenced global activities. Besides, economic troubles and malfunctions appeared in many sectors, including production, supply chain, logistics [32]. Since the universal supply chain has been dependent on China over the past decades, many large supply chain sectors, including those related to electronics and automotive industries, pharmaceutical manufacturers, airlines, transportation, etc., have been incredibly damaged by the COVID-19 outbreak [33].
As an authentic experience, before WHO’s declaration about COVID-19 widespread presence, a global shortage in supplying PPE was abundantly noticeable. For instance, the storage of N95 masks in the United States reported by Health and Human Services (HHS) was only 12 million, considerably lower than what is expected to be the US needs. Moreover, the US government could not properly use domestic manufacturers to handle the PPE shortage of N95 masks. On the other hand, countries like South Korea made their domestic manufacturers allied to satisfy healthcare PPE demands [34].
Regarding the pandemic disruptions in the SC sector and mitigating severe and harmful impacts on different supply chains, researchers and scholars sought the presence of supply chains that can cope with the unpleasant troubles and problems in this field. As we elaborately discuss recent studies in the supply chain in following, they encompass a variety of subjects such as supply chain design [35], [36], forecasting and planning [37], supply management [38], [39], transportation and logistics management [40], [41].
Nagurney [42] developed a supply chain network using mathematical modeling concentrated on labor availability during the COVID-19 pandemic for industries and businesses. In other researches considering COVID-19 circumstances, she and her collaborators also carried out studies on a variety of subjects, including presenting a model for demand competition on medical supplies and designing supply chain networks for perishable food [42], [43], [44], [45].
Nandi et al. [46] suggested a resilient SC for COVID-19, which is subjected to transparency and sustainability. In this study, localization, agility, and digitization features have been considered in terms of SC. Ivanov [47] utilized simulation research toolkits to study the impacts of the virus on the chain worldwide. This research is divided into two parts. First, they clearly expressed why the epidemic led to a supply chain disruption then provided evidence supporting the practicability of simulation-based studies for predicting epidemic effects.
Goodarzian et al. [48] considered a sustainable chain related to COVID-19 conditions. They suggested a model facilitating medicine distribution to patients while finding the best way to produce and store medicine under perishability constraints. Since the proposed model is NP-hardness for large-size models, the authors decided to solve with hybrid meta-heuristics. In one of the devoting studies for the COVID-19, Abbasi et al. [49] designed an allocation model for a vaccination with both operational constraints (capacity of hospitals, transportation, and storage) and non-operational constraints (exposure risks).
In this work, we formulate an optimization problem for personal protection equipment during the pandemic. Hence, a brief survey on the relief supply chain design is presented, and the more relevant literature on relief supply chain design is accessible in Table 1.
Habibi-Kouchaksaraei et al. [50] implemented a mathematical model for blood donation during disasters like earthquakes, floods. They utilized the goal programming technique to address their model. In some relief supply chain networks, finding the best location for distributing relief goods and telecommunication facilities is indispensable. Mohamadi et al. [51] figured this problem out as an optimization model based on multiple cases in a fuzzy environment. Their proposed model identifies the relevant places for telecommunication towers and shelters and assists decision-makers in amplifying the emergency services.
Shavarani [52] addressed one of the critical issues in disaster settings. When disaster happens, relief centers and gas stations are highly required not only for emergency services by organizations but also for the daily activities of individuals. He suggested mathematical modeling for a multi-level network. Akbarpour et al. [53] considered the same chain for pharmaceutical commodities. The robust optimization model has two objectives: one minimizes the cost of the relief network, and the other maximizes the demand coverage. The formulation also has considered the uncertainty of demand, perishability of commodities, and mobility of facilities.
In one of the recent works of relief SC networks, Li et al. [54] tackled mathematical modeling to distribute injured parties and develop response networks. Ghasemi and Khalili-Damghani [55] presented a hybrid technique including simulation and mathematical modeling in uncertainty conditions for preparedness goals in the relief supply chain. This model cop with decisions regarding the setting up and allocation of distribution centers.
2.1. Research gap
Global COVID-19 outbreaks proved that a well-founded network must overcome unforeseen incidents and handle consequent events associated with the epidemic. One of the most reliable methods and the perfect way by which we can achieve the closest outputs to reality is mathematical modeling. In addition to its superiority in results, it can display a better tool for future prediction.
Literature reviews on COVID-19 supply chain studies and relief SC are presented in the previous section and Table 1 to ensure the developed model is unique in terms of novelty and application. Most of the previous works in the COVID-19 supply chain are focus on subjects comprising labor availability of supply chain, medical supply chain, and allocation model for vaccination. On the other hand, designed relief supply chain literature has paid attention to problems such as blood donation, emergency services, and pharmaceutical distributions.
The proposed bi-objective, multi-period, and multi-product deals with the total cost and unsatisfied demands minimization. No study reported the fair distribution of PPEs among medical centers of a region, considering medical supply manufacturer, distributor, medical center, and world donator. Therefore, there is no similar model for PPE distribution in this context; this model can help prominent associations and organizations to control the COVID-19 pandemic situation.
3. Problem definition and formulation
Generally, there are three primary sources, medical supply manufacturers, humanitarian world aids, and local volunteer aids, to supply and satisfy the PPE demand of the healthcare system, as shown in Fig. 1. These purchased commodities from medical supply manufacturers (MSMs) or globally dispatched medical aids are directly moved to the distributors. Generally, the distributors are authorized institutes or organizations by governments or the ministry of health and medical education. However, local aids are straightly donated to outpatient clinics or hospitals. They are responsible for allocating needed PPE to be occupied and selected hospitals for COVID-19 patients.
Fig. 1.
COVID-19 PPE supply chain network.
One of the pillars of any SC network, especially a relief SC network, is controlling costs or making more profit. According to the literature review, cost minimization is one of the organizations’ essential goals, so most studies in this context have employed a cost minimization objective [56], [57]. Moreover, a relief chain may confront unsatisfied demands, known as a shortage of demands. With this in mind, to model the relief supply chain existence of fairness for demand shortage is essential [58], [59]. Consequently, for the second objective function of this study, we aim to minimize unsatisfied demands.
3.1. Mathematical modeling
In this section, the proposed network is formulated by a mathematical modeling approach.
Indices
| i | MSM center (i1, …, I) |
| j | Distributor (j1,2, …, J) |
| c | COVID-19 PPE (c1,2, …, C) |
| h | Medical center (h1,2, …, H) |
| w | World donator (w1, …, W) |
| t | Time periods (t1, …, T) |
Deterministic parameters
| Occupied space by storing per PPE c (m3) | |
| The maximum amount produced PPE c by MSM i in period t | |
| The capacity of distributors j (m3) | |
| The maximum donation of PPE c by world donator w in period t | |
| The number of donated PPE c by voluntary in period to medical center h | |
| Transportation cost of PPE c from distributors to medical center h | |
| Transportation cost of PPEc from MSM i to distributors j | |
| Transportation cost of PPE c from world donator to distributors j | |
| Inventory holding cost for PPE c charged by distributor j | |
| The procurement cost for PPE c charged by supplier i in period t |
Demand parameters
| The treatment capacity of medical center h | |
| COVID-19 Infection percentage during period t | |
| Population of region | |
| Percentage of needed medical center personnel per COVID-19 patients | |
| Number of COVID-19 patients in treatment in medical center h during period t | |
| The recovery rate of COVID-19 patients in medical center h during period t | |
| Death rate COVID-19 patients in medical center h during period t | |
| Number of working shifts in medical center h in period t | |
| Number of times that PPE c can be reused | |
| Demand for PPE c in medical center h during period t |
Flow Decision Variables
| Number of PPE c shipped from MSM i to distributor j in period | |
| Number of PPE c shipped from world donator w to distributor j in period t | |
| Number of PPE c shipped from distributor j to medical centerh in period t |
Inventory Decision Variables
| The number of PPE c in distributor j in period t | |
| Unsatisfied demand for PPE c in period t |
Assignment Decision Variables
| Is 1 if Distributor j is assigned to medical center h otherwise 0 |
Objective Functions
| (1) |
| (2) |
Eq. (1), as the first objective function, is to minimize the cost of the PPE supply. It includes four parts: the first to third part concentrate on transportation costs between different network components, while the fourth calculates holding cost in distribution spots. The second objective function (Eq. (2)) makes the model distribute the PPE in the network equitably to optimize the maximum amount of unsatisfied demands. Interested readers might refer to the Appendix for linearizing the second objective function (Eqs. (A.1) and (A.2)).
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
Constraint (3) checks the demand flow between the distribution centers and medical centers. is a positive decision variable for the shortage of demand in this flow, provided the transported PPE to the medical center does not match the exact amount of demand. Constraints (4), (5) control the distribution centers’ inventory level and balance the PPE input and output. Constraints (6)–(8) are capacity constraints. Constraint (6) imposes that the total amount of PPE transported from world donators to distribution cannot be unlimited, and it must be less than or equal to the maximum donation by world donators. Constraint (7) denotes that the total amount of PPE moved between the medical manufacturer and distribution centers are limited to each manufacturer’s highest production capacity. Constraint (8) is a space constraint that ensures that distribution centers have sufficient space to conserve PPE packages. Constraint (9) make at least one distribution center to be established. The products might be transported to medical centers from distribution spots only if they are opened, guaranteed by constraint (10). Correspondingly, constraint (11) ensures that there will be PPE transportation flow between distribution spots and medical centers if assigned to each other. Constraint (12) specifies PPE transportation between nodes, inventory variables for distribution centers, and demand shortage in medical centers. Also, constraint (13) ensures the assignment of binary variables.
4. Solution approach
The following section is divided into two subsections: encoding strategy and multi-objective algorithms. The first subsection deals with the utilized encoding scheme known as the random-key method [60], [61]. In the second subsection, four metaheuristics are developed, including some famous and recent algorithms in addition to hybrid ones.
4.1. Encoding strategy
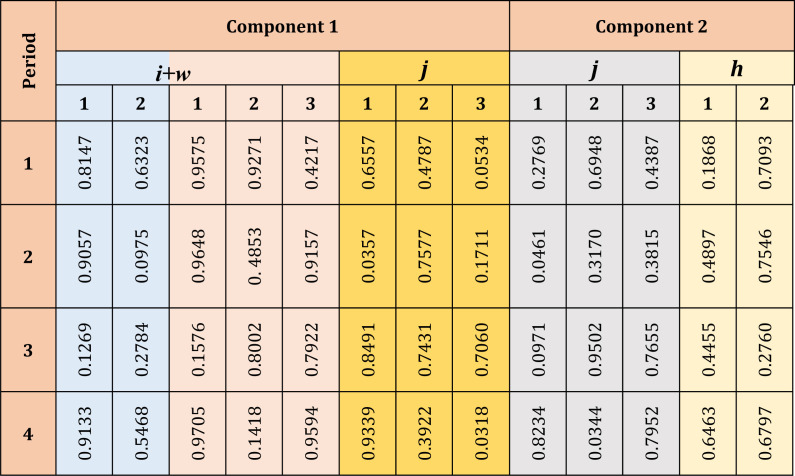
The random-key method is a popular technique to generate the chromosome size for any problem. The generated chromosome will be in the form of a matrix that represents the set of candidate solutions. These chromosomes are then sorted, and priorities are assigned. The matrix obtained after that is known as the priority-based matrix. Initially, the set of candidate solutions are generated in the interval (0, 1) based on the considered problem size. This proposed chromosome matrix, as shown in Fig. 2, is generated by assuming the following data: Medical supply manufacturers (i) 2, Humanitarian world aids (w) 3, Distributors (j) 3, Medical centers (h) 2, and, time period 4.
Fig. 2.
The proposed chromosome structure.
The chromosome matrix designed has two components according to the designed chromosome structure . This chromosome matrix is then converted to the priority-based matrix by assigning the priorities to the random keys, as shown in Fig. 3. Based on these priorities, the flow decisions will be taken. From Fig. 3(a), component one depicts the flow of relief aids from second medical supply manufacturers and humanitarian world aids to the third distributors. This process goes on till one of the capacities is exhausted. When this happens, a second facility is selected, and the procedure is repeated for the other. Similarly, Fig. 3(b) illustrates the flow of received goods from the first medical centers’ first distributors.
Fig. 3.
The assigned priorities for (a) component 1 and (b) component 2.
4.2. Multi-objective algorithms
Generally, these algorithms are to find an optimal solution between two or more conflicting objectives. The weighted sum approach is a famous solution approach in a multi-objective perspective [36], [62], [63], [64]. Under this method, initially, all the objectives are converted to single-objective by assigning some weight, making it easier to apply traditional algorithms. The decision-makers choose the objective function and weight assignments according to the preference of the utility. In contrast, using the Pareto optimal concept achieves a non-dominance solution rather than converting the original problem to a single-objective one [48], [65], [66], [67]. These non-dominance solutions can be determined through comparisons of solutions obtained from the Pareto Front.
The Pareto optimal solution shows good trade-offs between objectives, due to which it is seen as a preferred solution. Pareto fronts are particularly non-dominating solutions that are necessary for this trade-off. Like if we consider two solutions, X and Y. Furthermore, the crowding distance calculation is used to select a good solution from the obtained front.
4.2.1. Multi-Objective Keshtel Algorithm (MOKA)
The MOKA is a well-known metaheuristics algorithm. The algorithm was first introduced and developed by Hajiaghaei-Keshteli and Aminnayeri [68], [69]. In the proposed algorithm, the merging of the population is done based on the sorting using the crowding distance. The procedure is shown in Fig. 4. In this algorithm, Keshtel is referred to as randomly generated solutions, the food source is the solution, and the lake is the feasible region.
Fig. 4.
Crowding distance procedure.
The algorithm follows the six main steps:
-
1.
Landing of the Keshtels in the lake: randomly generated solutions.
-
2.
Finding the lucky Keshtels: finding better solutions in terms of solution quality.
-
3.
Attraction and swirling: local search.
-
4.
Moving Keshtels: to cover the unexplored regions.
-
5.
Startling the Keshtels: replacing the worst solution with new randomly generated solutions.
More explanations can be found in Cheraghalipour et al. [70], and the pseudo-code is presented in Fig. 5.
Fig. 5.
The MOKA pseudo-code.
4.2.2. Multi-objective Simulating Annealing (MOSA)
The process of this algorithm, which its basic version is firstly proposed by Kirkpatrick et al. [71], can be defined as firstly keeping the maximum temperature for the heat bath at which the solid melts. At this temperature, the particles arrange them randomly, and later, the temperature is decreased slowly and carefully. At last, the solid structure is arranged in the optimal lattice structure with minimum energy. Here is the maximum temperature of the heat bath, is the Boltzmann constant, and the accepting rule is known as the Metropolis criteria. The interested readers may refer to Cheraghalipour et al. [70]. The pseudo-code of the MOSA is illustrated in Fig. 6.
Fig. 6.
The MOSA pseudo-code.
4.2.3. Non-dominated Sorting Genetic Algorithm II (NSGA-II)
Genetic Algorithm (GA) is known as one of the most efficient algorithms to solve a wide range of the problem developed by Holland (1975). The multiple objective genetic algorithms MOGA is a particular case when the problem has various objectives. The diversity in the algorithm is maintained using the crowding distance sorting to the set of made solutions [72]. Finally, it converges and returns the optimal Pareto front. To study more, see Deb et al. [73]. Fig. 7 illustrates the pseudo-code of this algorithm.
Fig. 7.
The NSGA-II pseudo-code.
4.2.4. Hybrid Multi-objective Keshtel Algorithm and Simulating Annealing (MOKASA)
The proposed hybrid MOKASA is designed to enrich the search phase of the KA by hybridizing with the SA algorithm intelligently. The generated population in KA gets divided into three parts such as . The the population is known as the best solution and is known as the worst solution. The algorithm has an intense exploration phase and during the exploitation phase the the population is generated randomly using the SA. The better solution witnessed will be accepted or rejected based on the Metropolis criteria. The interested readers may also refer to Chouhan et al. [60]. Fig. 8 illustrates the pseudo-code of this algorithm.
Fig. 8.
Pseudo-code of the MOKASA.
5. Applied examples
Although the number of cases shockingly increases, according to official Iranian statistics provided by the Ministry of Health and Medical Education.1 more than 2,006,964 COVID-19 cases are confirmed, in which 63,884 cases are dead, and 1,684,570 cases are recovered until 8 April 2021. Still, the country has an increasing number of total cases; but the right step was taken at the correct time to ensure the total cases are significantly less as compared to the other countries such as Italy, USA, France, Spain, Germany, UK, Russia, Turkey, etc.2 Countries such as France and Italy, known for their world-class health care facilities, are also failed to do the needful for the country’s people.3
The instances are probed and investigated to validate the model’s pertinence and solution approach in this section. In this regard, we developed fifteen test problems in different sizes (Table 2). The third example is evolved from a real case. Khuzestan province in southern Iran is marked as red zones in Iran with 16,632 Positive cases, 613 deaths, and 15,309 recovered cases until 3 June 2020. In all examples, we assume that the network is designed to handle PPE demands for four time periods, each of which is seven days.
Table 2.
Fifteen test problems with various ranges of dimensions.
| Test # | Indices |
|||||
|---|---|---|---|---|---|---|
| i | w | j | c | h | ||
| Small-Size | 1 | 2 | 2 | 3 | 4 | 2 |
| 2 | 3 | 3 | 4 | 5 | 7 | |
| 3 | 2 | 2 | 5 | 6 | 10 | |
| 4 | 8 | 9 | 7 | 6 | 10 | |
| 5 | 10 | 10 | 8 | 9 | 12 | |
| Medium-Size | 6 | 14 | 13 | 12 | 10 | 14 |
| 7 | 17 | 12 | 16 | 10 | 15 | |
| 8 | 20 | 14 | 18 | 12 | 20 | |
| 9 | 24 | 14 | 22 | 14 | 22 | |
| 10 | 27 | 20 | 30 | 14 | 25 | |
| Large-Size | 11 | 36 | 20 | 48 | 16 | 40 |
| 12 | 40 | 25 | 50 | 16 | 50 | |
| 13 | 60 | 25 | 52 | 18 | 63 | |
| 14 | 56 | 30 | 60 | 20 | 74 | |
| 15 | 70 | 30 | 64 | 20 | 80 | |
In the real-case example, two medical supply manufacturers qualified by the ministry of health and medical education are active in Khuzestan, one in Khorramshahr, and one in Ahvaz. In addition, two international channels, the international Ahvaz airport and Bandar-e-Emam international port exist in Khuzestan to receive international donations. During COVID-19 outbreaks, the government of Iran exclusively appointed medical sciences universities to store and distribute both purchased and global donated PPE. Therefore, in Khuzestan, five medical sciences universities are responsible for supplying necessary PPE for COVID-19 medical centers all over the province. In a similar situation, ten particular medical centers throughout the province are planned to serve the COVID-19 patients. Lastly, the medical centers require a wide range of different PPE; nevertheless, the shortage of apron protection, surgical gloves, face shields, respirator, surgical gowns, and masks are pretty tangible in Khuzestan. Because of the strange situation with which medical centers and related organizations are dealing, the needed data are not provided precisely. As a result, the data are presented in approximate form in Table 3, retrieved from the Statistical Center of Iran,4 and the Ministry of Health and Medical Education. Fig. 9 is a symbolic scheme for medical supply manufacturers, world donators, distributors, and medical centers in Khuzestan province.
Table 3.
Model parameters ranges.
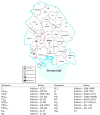 | |||
Fig. 9.
Signal to Noise ratio plot for NSGA-II.
6. Computational results
In the subsequent section, we explore parameter tuning and the behavior of the proposed multi-objective algorithm using the different assessment metrics. To verify the obtained results from the proposed algorithm, statistical techniques have been utilized.
6.1. Performance metrics
After reaching tuned levels for each algorithm, the proposed algorithms are set with these tuned control parameters to find the optimal results. The performance measures for multi-objective problems are somewhat different from single-objective problems. Multiple studies proposed numerous measures to appraise the multi-objective metaheuristics’ performance and help scholars identify intelligent algorithms rather than others. Typically, performance matrices are used to analyze Pareto fronts. Thus, this study utilizes specific metrics to appraise multi-objective metaheuristics added to the next section. The interested reader may also refer to Behnamian and Ghomi [74], Fard et al. [75], and Roghanian and Cheraghalipour [76].
6.1.1. Spread of non-dominated solution (SNS)
SNS calculates the spread of ideal and non-dominance solutions by the following formula:
| (14) |
Here,
6.1.2. Mean ideal distance (MID)
In order to find the gap between Pareto and the ideal solution, we utilize this index, and obviously, the lesser MID is always preferred to achieve better performance.
| (15) |
where represents the entire non-dominated set.
6.1.3. Maximum Spread (MS)
The distance between solutions is calculated by this index concerning the best Pareto front and is given as:
| (16) |
represents the total objective considered, and represent the maximum and minimum of function value in respectively, and represents the maximum and minimum of function value in , respectively.
6.1.4. Hypervolume (HV)
If the points are represented as a solution in the objective space, the solution set’s n-dimensional space (or volume) is referred to as hypervolume. In other words, hypervolume is a metric that measures the volume covered by Pareto set in the feasible space for the objective function. Hypervolume is calculated according to Eq. (17),
| (17) |
where is the set of Pareto solutions, is volume regarding a reference point .
6.1.5. CPU time
An important factor for evaluating an algorithm’s performance is the speed of running the algorithm that achieves optimal solutions. The CPU time for any algorithm is the total computational time for that algorithm. According to this metric, always lesser CPU time is preferred.
6.2. Parameters tuning
Before further proceeding, to avoid useless and time-consuming runs of metaheuristics, parameters are carefully tuned using a popular design of experiment (DOE) method. Among various DOE techniques, Taguchi experimental design method is selected. This method was developed by Taguchi [77]. Taguchi method seeks for maximization of controllable factors as well as minimization of noise effect. In various circumstances, this ratio is considered better in one of these three cases: smaller, nominal, and larger. Since our model is a minimization problem, tuning of parameters is attained by “the smaller is better” for each algorithm (see Eq. (18)).
| (18) |
In this study, the response value is computed based on the division of two separated metrics, namely MID and MS (Eq. (19)).
| (19) |
This response value considers both the convergence rate of solution (MID) and verity of solution (MS) [70]. For a start, the level of each factor for different algorithms should be identified. MOSA has three parameters with three levels. NSGA-II and MOKA have four and five parameters with three levels, respectively. Finally, MOKASA contains seven parameters with three levels. Thus, is recommended as a proper array for NSGA-II, MOKA, and MOKASA in addition to for MOSA. For tuning purposes, test number 10 in Table 2 is applied. Then, the orthogonal arrays are implemented in Minitab software. The obtained plot of is shown in Fig. 9, Fig. 10, Fig. 11, Fig. 12. According to this ratio plot, the level of parameters with the lowest value is preferable. Additionally, tuned values for the tenth test reported in Table 4 are considered for all test problems.
Fig. 10.
Signal to Noise ratio plot for MOSA.
Fig. 11.
Signal to Noise ratio plot for MOKA.
Fig. 12.
Signal to Noise ratio plot for MOKASA.
Table 4.
The algorithms’ parameters and their levels.
| Metaheuristics | Parameter | Parameter Level |
Optimum Level | |||
|---|---|---|---|---|---|---|
| L1 | L2 | L3 | ||||
| NSGA-II | Max | 100 | 200 | 300 | 100 | |
| 100 | 150 | 200 | 150 | |||
| 0.7 | 0.75 | 0.8 | 0.8 | |||
| 0.05 | 0.10 | 0.15 | 0.05 | |||
| MOSA | Max | 100 | 200 | 300 | 200 | |
| 1000 | 1500 | 2000 | 1000 | |||
| 0.88 | 0.90 | 0.99 | 0.90 | |||
| MOKA | Max | 100 | 200 | 300 | 100 | |
| N-Keshtel | 100 | 150 | 200 | 100 | ||
| 10 | 15 | 20 | 15 | |||
| M1 | 0.05 | 0.1 | 0.15 | 0.05 | ||
| M2 | 0.2 | 0.25 | 0.30 | 0.30 | ||
| MOKASA | Max | 100 | 200 | 300 | 200 | |
| N-Keshtel | 100 | 150 | 200 | 100 | ||
| 10 | 15 | 20 | 15 | |||
| M1 | 0.05 | 0.1 | 0.15 | 0.15 | ||
| M2 | 0.2 | 0.25 | 0.30 | 0.25 | ||
| 1000 | 1500 | 2000 | 1500 | |||
| 0.88 | 0.90 | 0.99 | 0.90 | |||
6.3. Comparison among algorithm
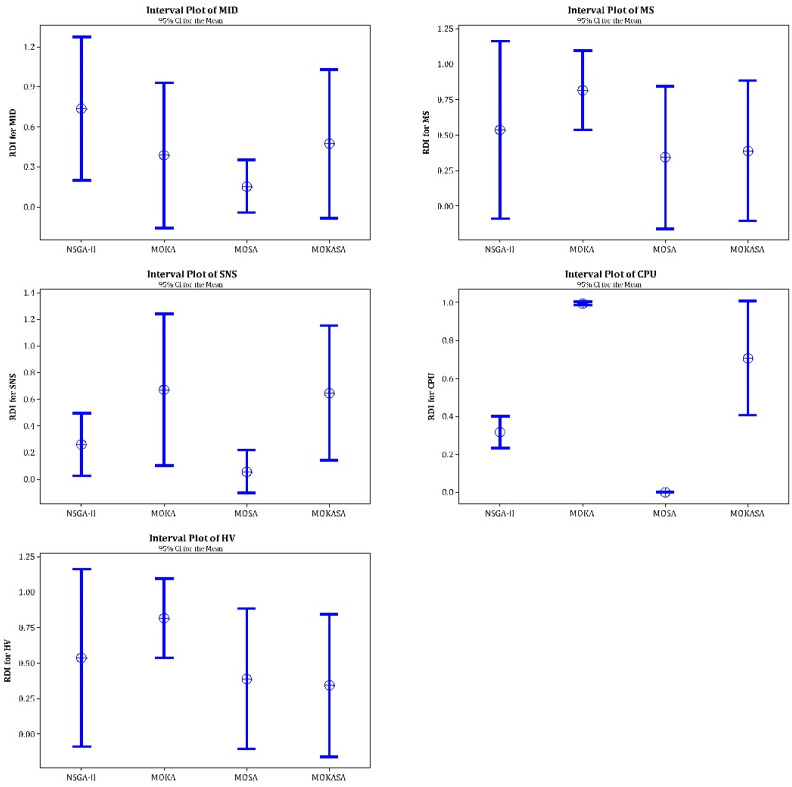
In this section, a comprehensive comparison is presented to check the quality of performance for each algorithm. To this end, we use five performance metrics. In the beginning, we set the parameters with the tuned values obtained in the previous section, then run each test problem 30 times and reported the results of them as the average of all runs. Fig. 13 is related to problems 4, 9, and 14 as representative of different problem sizes.
Fig. 13.
Pareto frontier solutions related to: (a) Problem No. 4 (small-size) (b) Problem No. 9 (medium-size) (c) Problem No. 14 (large-size).
Fig. 13 shows that obtained solutions of metaheuristic algorithms are significantly similar to each other. However, concerning the total cost, MOKASA, in small-size problems, NSGA-II in medium-size problems, and MOKA and MOKASA in large-size problem has better solutions. On the other hand, MOSA remarkably performed rather than other algorithms in demand coverage.
The result of five performance metrics is demonstrated in Table 5. Firstly, we convert all the metrics value to Relative Deviation Index (RDI) by using Eq. (20):
| (20) |
where is the value attained by performance metric, is the best value of performance metric among the applied metaheuristics. The means plot and LSD for each problem size are thoroughly explained in relevant sections.
Table 5.
Metaheuristics evaluation metrics value.
| (a) Small sizes | |||||||||||||||||||||||||
| Test No. |
MID |
MS |
SNS |
CPU Time |
HV |
||||||||||||||||||||
| NSGA-II | MOKA | MOSA | MOKASA | NSGA-II | MOKA | MOSA | MOKASA | NSGA-II | MOKA | MOSA | MOKASA | NSGA-II | MOKA | MOSA | MOKASA | NSGA-II | MOKA | MOSA | MOKASA | ||||||
| Small | 1 | 3.61 | 3.60 | 3.36 | 3.36 | 2.38E+07 | 6.58E+06 | 1.32E+07 | 5.11E+06 | 5.64E+06 | 4.53E+06 | 5.95E+06 | 2.04E+06 | 70.37 | 140.88 | 24.83 | 167.74 | 2.38E+07 | 6.58E+06 | 1.32E+07 | 5.11E+06 | ||||
| 2 | 1.74 | 1.49 | 1.56 | 1.74 | 3.25E+07 | 3.18E+07 | 3.77E+07 | 3.17E+07 | 1.73E+07 | 1.84E+07 | 1.59E+07 | 1.31E+07 | 106.84 | 171.19 | 28.61 | 250.27 | 3.25E+07 | 3.18E+07 | 3.77E+07 | 3.17E+07 | |||||
| 3 | 1.42 | 1.07 | 1.14 | 1.35 | 3.96E+07 | 3.63E+07 | 4.11E+07 | 4.35E+07 | 2.42E+07 | 2.30E+07 | 2.64E+07 | 2.06E+07 | 234.59 | 331.41 | 56.28 | 342.80 | 3.96E+07 | 3.63E+07 | 4.11E+07 | 4.35E+07 | |||||
| 4 | 1.40 | 1.19 | 1.09 | 1.05 | 1.34E+08 | 1.14E+08 | 1.35E+08 | 1.55E+08 | 5.83E+07 | 6.87E+07 | 5.05E+07 | 6.35E+07 | 245.71 | 501.18 | 46.74 | 298.67 | 1.34E+08 | 1.14E+08 | 1.55E+08 | 1.35E+08 | |||||
| 5 | 1.56 | 1.69 | 1.46 | 1.76 | 1.93E+08 | 1.76E+08 | 1.99E+08 | 2.02E+08 | 1.14E+08 | 1.22E+08 | 1.15E+08 | 1.24E+08 | 257.79 | 447.30 | 61.51 | 625.86 | 1.93E+08 | 1.76E+08 | 2.02E+08 | 1.99E+08 | |||||
| Average | 1.95 | 1.81 | 1.72a | 1.85 | 8.48E+07 | 7.30E+07 | 8.52E+07 | 8.75E+07a | 4.39E+07 | 4.72E+07a | 4.28E+07 | 4.47E+07 | 183.06 | 318.39 | 43.59a | 337.07 | 8.48E+07 | 7.30E+07 | 8.98E+07a | 8.29E+07 | |||||
| (b) Medium sizes | |||||||||||||||||||||||||
| Test No. |
MID |
MS |
SNS |
CPU Time |
HV |
||||||||||||||||||||
| NSGA-II | MOKA | MOSA | MOKASA | NSGA-II | MOKA | MOSA | MOKASA | NSGA-II | MOKA | MOSA | MOKASA | NSGA-II | MOKA | MOSA | MOKASA | NSGA-II | MOKA | MOSA | MOKASA | ||||||
| Medium | 6 | 3.50 | 3.49 | 3.33 | 3.57 | 2.04E+08 | 2.13E+08 | 2.25E+08 | 2.14E+08 | 1.37E+08 | 1.39E+08 | 1.39E+08 | 1.31E+08 | 362.46 | 1070.63 | 88.66 | 533.99 | 2.04E+08 | 2.13E+08 | 2.14E+08 | 2.25E+08 | ||||
| 7 | 1.56 | 1.30 | 1.21 | 1.23 | 3.13E+08 | 3.16E+08 | 3.69E+08 | 3.53E+08 | 2.46E+08 | 2.52E+08 | 2.63E+08 | 2.29E+08 | 712.17 | 1478.15 | 177.49 | 779.78 | 3.13E+08 | 3.16E+08 | 3.53E+08 | 3.69E+08 | |||||
| 8 | 2.22 | 2.53 | 2.31 | 2.26 | 3.87E+08 | 3.43E+08 | 4.56E+08 | 4.82E+08 | 2.93E+08 | 2.84E+08 | 2.99E+08 | 2.92E+08 | 657.79 | 1539.59 | 223.29 | 1228.82 | 3.87E+08 | 3.43E+08 | 4.82E+08 | 4.56E+08 | |||||
| 9 | 1.40 | 1.04 | 1.09 | 1.36 | 7.48E+08 | 6.16E+08 | 5.26E+08 | 5.05E+08 | 6.86E+08 | 5.85E+08 | 6.56E+08 | 6.80E+08 | 688.03 | 2351.01 | 179.85 | 2050.09 | 7.48E+08 | 6.16E+08 | 5.05E+08 | 5.26E+08 | |||||
| 10 | 2.58 | 2.37 | 2.44 | 2.43 | 8.51E+08 | 6.63E+08 | 7.35E+08 | 8.31E+08 | 7.41E+08 | 5.64E+08 | 7.90E+08 | 6.19E+08 | 913.72 | 2277.87 | 212.78 | 2313.45 | 8.51E+08 | 6.63E+08 | 8.31E+08 | 7.35E+08 | |||||
| Average | 2.25 | 2.15 | 2.08a | 2.17 | 5.01E+08a | 4.30E+08 | 4.62E+08 | 4.77E+08 | 4.21E+08 | 3.65E+08a | 4.29E+08 | 3.90E+08 | 666.83 | 1743.45 | 176.41a | 1381.23 | 5.01E+08a | 4.30E+08 | 4.77E+08 | 4.62E+08 | |||||
| (c) Large sizes | |||||||||||||||||||||||||
| Test No. |
MID |
MS |
SNS |
CPU Time |
HV |
||||||||||||||||||||
| NSGA-II | MOKA | MOSA | MOKASA | NSGA-II | MOKA | MOSA | MOKASA | NSGA-II | MOKA | MOSA | MOKASA | NSGA-II | MOKA | MOSA | MOKASA | NSGA-II | MOKA | MOSA | MOKASA | ||||||
| Large | 11 | 1.57 | 1.42 | 1.51 | 1.75 | 1.56E+09 | 1.17E+09 | 1.10E+09 | 1.33E+09 | 9.51E+08 | 1.05E+08 | 1.41E+09 | 9.30E+08 | 1261.84 | 3221.06 | 402.03 | 1975.52 | 1.56E+09 | 1.17E+09 | 1.10E+09 | 1.33E+09 | ||||
| 12 | 2.13 | 1.89 | 1.92 | 1.99 | 1.92E+09 | 1.87E+09 | 2.00E+09 | 1.82E+09 | 1.21E+09 | 1.34E+09 | 1.56E+09 | 1.39E+09 | 1493.99 | 3163.65 | 418.55 | 2390.81 | 1.92E+09 | 1.87E+09 | 2.00E+09 | 1.82E+09 | |||||
| 13 | 0.97 | 1.25 | 0.90 | 0.96 | 2.11E+09 | 2.73E+09 | 2.47E+09 | 2.60E+09 | 1.64E+09 | 1.51E+09 | 1.77E+09 | 1.77E+09 | 2674.83 | 7843.67 | 770.52 | 10142.84 | 2.11E+09 | 2.73E+09 | 2.47E+09 | 2.60E+09 | |||||
| 14 | 1.16 | 1.40 | 1.22 | 1.39 | 1.95E+09 | 2.75E+09 | 2.57E+09 | 1.98E+09 | 1.81E+09 | 1.79E+09 | 1.99E+09 | 1.88E+09 | 4560.31 | 10105.33 | 1447.79 | 12570.43 | 1.95E+09 | 2.75E+09 | 2.57E+09 | 1.98E+09 | |||||
| 15 | 2.15 | 1.96 | 1.82 | 1.91 | 1.61E+09 | 1.79E+09 | 1.72E+09 | 1.64E+09 | 1.96E+09 | 1.82E+09 | 1.97E+09 | 1.94E+09 | 9673.44 | 16719.78 | 2015.00 | 18167.51 | 2.66E+09 | 2.80E+09 | 3.29E+09 | 3.44E+09 | |||||
| Average | 1.60 | 1.58 | 1.47a | 1.60 | 1.56E+09 | 1.17E+09 | 1.10E+09 | 1.33E+09a | 1.51E+09 | 1.31E+09 | 1.74E+09a | 1.58E+09 | 3932.88 | 8210.70 | 1010.78a | 9049.42 | 2.04E+09 | 2.26E+09a | 2.29E+09 | 2.23E+09 | |||||
Best performance.
Besides the abovementioned tool, we use two nonparametric statistical tests. Generally, metaheuristic algorithms have stochastic traits, so nonparametric statistical tests are mandatory for a more precise analysis of archived solutions by algorithm and comparison [78]. If the nonparametric statistical test only compares two algorithms, they label as pairwise comparisons. One of the appreciated pairwise nonparametric tests is Wilcoxon signed-rank test which we conduct in our study. As a post hoc test, we implement the Holm test. But, if they compare more than two algorithms, they define as multiple comparisons. The Friedman test is of multiple comparison tests, which is applied here [79]. Table 6 encompasses required definitions of terms associated with statistical tests; however, the detailed information can be found in Derrac et al. [79].
Table 6.
Definition of statistical test terms.
| Terms | Definition |
|---|---|
| The null hypothesis () | Declares that two metaheuristics have no difference. |
| alternative hypothesis () | Declares that two metaheuristics have differences. |
| Statistical significance level () | The probability of mistakenly rejecting . For -value, less than H is rejected. |
| Family-Wise Error Rate (FWER) | The probability of rejecting a correct by at least one comparison test. |
| Post hoc test | The test examines and controls FWER. |
6.3.1. Small-size problems
According to Fig. 14, MOSA is leading in terms of SNS, CPU, and HV, though MOKA and MOKASA are better, respectively, in terms of MID and MS.
Fig. 14.
Comparison of performance metrics for small-size problems.
To implement Wilcoxon signed ranked test, we use HV values for small-size problems and run the test with a statistical significance level () of 0.05 using SPSS software. Table 7 presents the result of the Wilcoxon test. P-values for Wilcoxon tests and Holm tests in each comparison set are less than the significance level () of 0.05.
Table 7.
Wilcoxon signed the ranked test according to HV values for small-size problems.
| Comparison | P-value (Wilcoxon test) | P-value (Holm test) |
|---|---|---|
| NSGA-II versus MOKA | .016 | .022 |
| NSGA-II versus MOSA | .029 | .036 |
| NSGA-II versus MOKASA | .038 | .045 |
| MOKA versus MOSA | .019 | .028 |
| MOKA versus MOKASA | .025 | .030 |
| MOSA versus MOKASA | .009 | .014 |
Finally, we did multiple statistical comparisons using the Friedman test for the small-size problem with a statistical significance level () of 0.05 using SPSS. This test is performed based on all performance metrics, and Table 8 shows the result of the Friedman test. Results state that MOSA has superior performance in all metrics than other algorithms except in HV that MOKA precedes other algorithms. It is worthwhile to mention that p-values in all tests are less than the significance level () of 0.05.
Table 8.
The Friedman ranks performance metrics for small-size problems.
| Meta-heuristics | MID | Rank | MS | Rank | SNS | Rank | CPU | Rank | HV | Rank |
|---|---|---|---|---|---|---|---|---|---|---|
| NSGA-II | 3.20 | 3 | 2.60 | 2 | 2.65 | 2 | 2.45 | 2 | 2.40 | 3 |
| MOSA | 2.01 | 1 | 3.01 | 1 | 3.63 | 1 | 1.31 | 1 | 2.60 | 2 |
| MOKA | 2.20 | 2 | 1.65 | 4 | 1.01 | 4 | 3.10 | 3 | 3.32 | 1 |
| MOKASA | 2.32 | 4 | 2.34 | 3 | 2.42 | 3 | 3.32 | 4 | 2.12 | 4 |
| P-value | .002 | .005 | .011 | .000 | .000 |
6.3.2. Medium-size problems
Fig. 15 displays the means plot and LSD for medium-size problems. It can be concluded that MS, SNS, and CPU means plot and LSD, MOSA outperformed others. In terms of MID and HV, MOKA and MOKASA had better performance in comparison with other algorithms.
Fig. 15.
Comparison of performance metrics for medium-size problems.
The result of the Wilcoxon test is demonstrated in Table 9. Like small-size problems, Wilcoxon signed a ranked test applied using HV values for medium-size problems with a statistical significance level () of 0.05 using SPSS software. P-values for Wilcoxon tests and Holm tests are less than 0.05, so it determined that there is a difference between the two metaheuristics in each set.
Table 9.
Wilcoxon signed the ranked test according to HV values for medium-size problems.
| Comparison | P-value (Wilcoxon test) | P-value (Post-hoc test) |
|---|---|---|
| NSGA-II versus MOKA | .016 | .022 |
| NSGA-II versus MOSA | .036 | .040 |
| NSGA-II versus MOKASA | .015 | .023 |
| MOKA versus MOSA | .014 | .018 |
| MOKA versus MOKASA | .021 | .031 |
| MOSA versus MOKASA | .032 | .035 |
Friedman test for medium-size problems with a significance level () of 0.05 using SPSS was carried out. All performance metrics have participated in this test for multiple comparisons, and Table 10 shows the achieved results. Excluding SNS that MOKA has been surpassed, results assert that MOSA has been at the top in all performance metrics.
Table 10.
The Friedman ranks performance metrics for small-size problems.
| Meta-heuristics | MID | Rank | MS | Rank | SNS | Rank | CPU | Rank | HV | Rank |
|---|---|---|---|---|---|---|---|---|---|---|
| NSGA-II | 2.05 | 2 | 2.43 | 2 | 2.04 | 3 | 2.25 | 2 | 2.12 | 3 |
| MOSA | 1.91 | 1 | 3.22 | 1 | 2.61 | 2 | 1.05 | 1 | 3.40 | 1 |
| MOKA | 2.62 | 4 | 1.78 | 4 | 3.31 | 1 | 2.61 | 3 | 1.52 | 4 |
| MOKASA | 3.42 | 3 | 2.41 | 3 | 1.24 | 4 | 3.38 | 4 | 2.81 | 2 |
| P-value | .008 | .001 | .002 | .000 | .000 |
6.3.3. Large-size problems
Here, the performance of large-size problems is evaluated through previously mentioned metrics. Firstly, the means plot and LSD are presented in Fig. 16. It reveals that MOSA had overcome other algorithms in terms of MS, SNS, CPU, and HV. But, in terms of MID, MOKASA is better than the others.
Fig. 16.
Comparison of performance metrics for large-size problems.
Large-size problems are statistically compared using Wilcoxon signed ranked test. In this test, HV values for large-size problems are considered and run the test with a significance level () of 0.05. The result illustrated in Table 11 for the Wilcoxon test, and Holm test is less than the significance level () of 0.05. As a result, there is a difference between each pair of algorithms. Table 12 shows the results of the Friedman test for the large-size problem with a statistical significance level () of 0.05. It can be comprehended that MOSA has superior performance in all metrics. The obtained -value in all tests is less than 0.05.
Table 11.
Wilcoxon signed the ranked test according to HV values for large-size problems.
| Comparison | P-value (Wilcoxon test) | P-value (Post-hoc test) |
|---|---|---|
| NSGA-II versus MOKA | .007 | .012 |
| NSGA-II versus MOSA | .005 | .015 |
| NSGA-II versus MOKASA | .013 | .023 |
| MOKA versus MOSA | .021 | .032 |
| MOKA versus MOKASA | .018 | .026 |
| MOSA versus MOKASA | .012 | .020 |
Table 12.
The Friedman ranks performance metrics for large-size problems.
| Meta-heuristics | MID | Rank | MS | Rank | SNS | Rank | CPU | Rank | HV | Rank |
|---|---|---|---|---|---|---|---|---|---|---|
| NSGA-II | 3.55 | 4 | 3.35 | 2 | 2.88 | 2 | 2.00 | 2 | 1.22 | 4 |
| MOSA | 2.04 | 2 | 3.65 | 1 | 3.65 | 1 | 1.09 | 1 | 3.83 | 1 |
| MOKA | 1.87 | 1 | 2.87 | 3 | 1.45 | 4 | 3.13 | 3 | 2.11 | 3 |
| MOKASA | 3.45 | 3 | 1.54 | 4 | 2.13 | 3 | 3.88 | 4 | 2.83 | 2 |
| P Value | .011 | .000 | .003 | .000 | .001 |
In conclusion, the analysis of performance metrics for each problem size affirms that MOSA has a better performance compared to other algorithms.
6.4. Sensitivity analyses
Here, we investigate the sensitivity analyses of parameter changes’ effect on the proposed model’s objective function values. In previous sections, MOSA is found as the most superior algorithm. Hence, MOSA is selected as the algorithm used for sensitivity analysis purposes using medium size problem number 9 in Table 2. The first experiment evaluates the impact of storage capacity, distributor capacity, and PPE production capacity on the objective functions. In this experiment, the range of storage capacity, distributor capacity, and PPE production capacity change from the lowest value to the highest value in four test problems. Afterward, test problems are solved using the MOSA algorithm, and the results are reported in Table 13. Fig. 17 exhibits that both objective functions Z1 and Z2 increase as the capacity and storage parameters have positive growth.
Table 13.
The results of sensitivity analysis for the first experiment.
| #Test | |||||
|---|---|---|---|---|---|
| T1 | 1 | 20 | 300 | 2,144,777,892 | 4700 |
| T2 | 1.25 | 28 | 400 | 2,288,917,669 | 4854 |
| T3 | 1.5 | 36 | 500 | 2,403,215,923 | 5907 |
| T4 | 2 | 40 | 600 | 2,625,518,468 | 6988 |
Fig. 17.
Objective functions behavior based on the first experiment.
The second experiment monitors how the treatment capacity of the medical center and population of the region affects the behavior of total cost of supply chain and demand shortage. Similar to the previous experiment, this experiment considers the lowest and highest value of both parameters. For the designed test problems, the achieved outputs of MOSA for the second experiment are presented in Table 14. Furthermore, Fig. 18 emphasizes that the total cost of supply chain and demand shortage are increased while the capacity of the medical center and population of the region significantly raised.
Table 14.
The results of sensitivity analysis for the second experiment.
| #Test | ||||
|---|---|---|---|---|
| T1 | 100 | 1000 | 2,212,085,021 | 4711 |
| T2 | 200 | 5000 | 2,428,290,551 | 5872 |
| T3 | 400 | 10000 | 2,864,609,379 | 7851 |
| T4 | 600 | 20000 | 3,153,300,213 | 9618 |
Fig. 18.
Objective functions behavior based on the second experiment.
The third experiment is founded on the behavior of objective functions influenced by variation of recovery and death rate of patients. We consider a wide range for the death rate, from the lowest to the highest, in four experiments, and utilize the MOSA algorithm to solve these test problems. Table 15 and Fig. 19 point out that total cost and unsatisfied demand in the supply chain network have considerably positive relations.
Table 15.
The results of sensitivity analysis for the third experiment.
| #Test | ||||
|---|---|---|---|---|
| T1 | 0.10 | 0.10 | 2,112,048,000 | 4751 |
| T2 | 0.15 | 0.15 | 2,223,809,174 | 4809 |
| T3 | 0.30 | 0.20 | 2,345,978,529 | 5310 |
| T4 | 0.45 | 0.30 | 2,412,048,000 | 6015 |
Fig. 19.
Objective functions behavior based on the third experiment.
7. Conclusion
A relief SC network for the pandemic situation such as COVID-19 was designed in this paper. We modeled our proposed SC by using a multi-objective mathematical approach. We tried to investigate and analyze the total cost of the PPE SC and shortage throughout the network. Four multi-objective metaheuristic algorithms were applied, including MOKA, MOSA, NSGA-II, and MOKASA, to investigate and endorse the model’s applicability. Afterward, the Taguchi method was used as a tuning assistant in this study to find the best level for the algorithms’ parameters results achieving better performance. Among the fifteen developed test problems, the third test problem is inspired by a real case in Khuzestan province in southern Iran. Then, five evaluation criteria, MID, MS, SNS, HV, and CPU time, were utilized. Considering the evaluation criteria, each algorithm showed different behaviors, but, totally, we can conclude that MOSA showed better performance for the problems we studied in this work.
In this study, we confronted a few limitations which they could be overcome for future researches. Data gathering was the critical limitation in this work. As we earlier alleged, healthcare systems and organizations control the tough situation during the pandemic and try to prevent more casualties; therefore, they could not provide valid data. In future studies, researchers can access more valid data that might bring about closer solutions to reality. Another limitation of this study is that sustainability assumptions should be informed especially environmental and social aspects. In this study, the proposed model has not considered the problem in stochastic and uncertainty settings. Nevertheless, the model might be formulated with uncertainty constraints or parameters.
In general, we suggest the researchers for future studies to design the proposed PPE supply chain model tailored to the specific traits related to other countries’ conditions and constraints, improve the proposed model by considering the vital aspect of sustainability, and formulate stochastic models for the PPE supply chain to satisfy the network’s demand flow.
CRediT authorship contribution statement
Behzad Mosallanezhad: Investigation, Software, Data curation, Formal analysis. Vivek Kumar Chouhan: Conceptualization, Investigation, Formal analysis, Writing – original draft, Visualization. Mohammad Mahdi Paydar: Supervision, Methodology, Validation, Writing – review & editing. Mostafa Hajiaghaei-Keshteli: Supervision, Methodology, Validation, Writing – review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
Appendix. Linearization of the second objective function
In Eq. (2), nonlinearity is discernible, so to overcome this issue, we use Eq. (A.1) instead of Eq. (2) and also add constraint (A.2) to the constraint sets.
| (A.1) |
| (A.2) |
References
- 1.World Health Organization . 27th February 2020, No. WHO/2019-NCov/IPCPPE_use/2020.1. World Health Organization; 2020. Rational use of personal protective equipment for coronavirus disease (COVID-19): interim guidance. [Google Scholar]
- 2.Cirrincione L., Plescia F., Ledda C., Rapisarda V., Martorana D., Moldovan R.E., et al. COVID-19 pandemic: prevention and protection measures to be adopted at the workplace. Sustainability. 2020;12(9):3603. [Google Scholar]
- 3.Sohrabi C., Alsafi Z., O’Neill N., Khan M., Kerwan A., Al-Jabir A., et al. World Health Organization declares global emergency: A review of the 2019 novel coronavirus (COVID-19) Int. J. Surg. 2020;76:71–76. doi: 10.1016/j.ijsu.2020.02.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hosseini S.M., Paydar M.M., Hajiaghaei-Keshteli M. Recovery solutions for ecotourism centers during the Covid-19 pandemic: Utilizing Fuzzy DEMATEL and Fuzzy VIKOR methods. Expert Syst. Appl. 2021 doi: 10.1016/j.eswa.2021.115594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cao Y., Li Q., Chen J., Guo X., Miao C., Yang H., et al. Hospital emergency management plan during the COVID-19 epidemic. Acad. Emerg. Med. 2020;27(4):309–311. doi: 10.1111/acem.13951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Livingston E., Desai A., Berkwits M. Sourcing personal protective equipment during the COVID-19 pandemic. JAMA. 2020 doi: 10.1001/jama.2020.5317. [DOI] [PubMed] [Google Scholar]
- 7.Ghaffari Z., Nasiri M.M., Bozorgi-Amiri A., Rahbari A. Emergency supply chain scheduling problem with multiple resources in disaster relief operations. Transportmetrica A: Transp. Sci. 2020;16(3):930–956. [Google Scholar]
- 8.Jensen L.-M., Hertz S. The coordination roles of relief organisations in humanitarian logistics. Int. J. Logist. Res. Appl. 2016;19(5):465–485. [Google Scholar]
- 9.Haghjoo N., Tavakkoli-Moghaddam R., Shahmoradi-Moghadam H., Rahimi Y. Reliable blood supply chain network design with facility disruption: A real-world application. Eng. Appl. Artif. Intell. 2020;90 [Google Scholar]
- 10.Garvey M.D., Carnovale S. The rippled newsvendor: A new inventory framework for modelling supply chain risk severity in the presence of risk propagation. Int. J. Prod. Econ. 2020 doi: 10.1016/j.ijpe.2020.107752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ivanov D., Dolgui A. Viability of intertwined supply networks: extending the supply chain resilience angles towards survivability. A position paper motivated by COVID-19 outbreak. Int. J. Prod. Res. 2020:1–12. [Google Scholar]
- 12.Hong J.-D., Jeong K.-Y., Feng K. Emergency relief supply chain design and trade-off analysis. J. Humanit. Logist. Supply Chain Manag. 2015 [Google Scholar]
- 13.Escudero L.F., Monge J.F., Morales D.R. On the time-consistent stochastic dominance risk averse measure for tactical supply chain planning under uncertainty. Comput. Oper. Res. 2018;100:270–286. [Google Scholar]
- 14.Fattahi M., Govindan K., Keyvanshokooh E. A multi-stage stochastic program for supply chain network redesign problem with price-dependent uncertain demands. Comput. Oper. Res. 2018;100:314–332. [Google Scholar]
- 15.Abdi A., Abdi A., Fathollahi-Fard A.M., Hajiaghaei-Keshteli M. A set of calibrated metaheuristics to address a closed-loop supply chain network design problem under uncertainty. Int. J. Syst. Sci.: Oper. Logist. 2021;8(1):23–40. [Google Scholar]
- 16.Safaei A.S., Farsad S., Paydar M.M. Emergency logistics planning under supply risk and demand uncertainty. Oper. Res. 2018:1–24. [Google Scholar]
- 17.Ran L., Chen X., Wang Y., Wu W., Zhang L., Tan X. Risk factors of healthcare workers with corona virus disease 2019: A retrospective cohort study in a designated hospital of wuhan in china. Clin. Infect. Dis. 2020 doi: 10.1093/cid/ciaa287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wang X., Wu Y., Liang L., Huang Z. Service outsourcing and disaster response methods in a relief supply chain. Ann. Oper. Res. 2016;240(2):471–487. [Google Scholar]
- 19.A. Nagurney, L.S. Nagurney, A mean–variance disaster relief supply chain network model for risk reduction with stochastic link costs, time targets, and demand uncertainty, in: Paper Presented at the International Conference on Dynamics of Disasters, 2016.
- 20.Mohammadi R., Ghomi S.F., Jolai F. Prepositioning emergency earthquake response supplies: A new multi-objective particle swarm optimization algorithm. Appl. Math. Model. 2016;40(9–10):5183–5199. [Google Scholar]
- 21.Zhou Y., Liu J., Zhang Y., Gan X. A multi-objective evolutionary algorithm for multi-period dynamic emergency resource scheduling problems. Transp. Res. E. 2017;99:77–95. [Google Scholar]
- 22.Jha A., Acharya D., Tiwari M. Humanitarian relief supply chain: a multi-objective model and solution. Sādhanā. 2017;42(7):1167–1174. [Google Scholar]
- 23.Al Theeb N., Murray C. Vehicle routing and resource distribution in post-disaster humanitarian relief operations. Int. Trans. Oper. Res. 2017;24(6):1253–1284. [Google Scholar]
- 24.Li X., Batta R., Kwon C. Effective and equitable supply of gasoline to impacted areas in the aftermath of a natural disaster. Soc.-Econ. Plann. Sci. 2017;57:25–34. [Google Scholar]
- 25.Cao C., Li C., Yang Q., Liu Y., Qu T. A novel multi-objective programming model of relief distribution for sustainable disaster supply chain in large-scale natural disasters. J. Cleaner Prod. 2018;174:1422–1435. [Google Scholar]
- 26.Moreno A., Alem D., Ferreira D., Clark A. An effective two-stage stochastic multi-trip location-transportation model with social concerns in relief supply chains. European J. Oper. Res. 2018;269(3):1050–1071. [Google Scholar]
- 27.Torabi S.A., Shokr I., Tofighi S., Heydari J. Integrated relief pre-positioning and procurement planning in humanitarian supply chains. Transp. Res. E. 2018;113:123–146. [Google Scholar]
- 28.Hong J.-D., Jeong K.-Y. Goal programming and data envelopment analysis approach to disaster relief supply chain design. Int. J. Logist. Syst. Manag. 2019;33(3):291–321. [Google Scholar]
- 29.Sarma D., Das A., Bera U.K., Singh A. International Conference on Information Technology and Applied Mathematics. Springer; Cham: 2019. Uncertain demand allocation with insufficient resource in disaster by using facebook disaster map under limited fund; pp. 567–578. [Google Scholar]
- 30.Aghajani M., Torabi S.A., Heydari J. A novel option contract integrated with supplier selection and inventory pre-positioning for humanitarian relief supply chains. Soc.-Econ. Plann. Sci. 2020 [Google Scholar]
- 31.Yenice Z.D., Samanlioglu F. A multi-objective stochastic model for an earthquake relief network. J. Adv. Transp. 2020;2020 [Google Scholar]
- 32.Barman A., Das R., De P.K. Impact of COVID-19 in food supply chain: Disruptions and recovery strategy. Curr. Res. Behav. Sci. 2021;2 doi: 10.1016/j.crbeha.2021.100017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Belhadi A., Kamble S., Jabbour C.J.C., Gunasekaran A., Ndubisi N.O., Venkatesh M. Manufacturing and service supply chain resilience to the COVID-19 outbreak: Lessons learned from the automobile and airline industries. Technol. Forecast. Soc. Change. 2021;163 doi: 10.1016/j.techfore.2020.120447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Dai T., Zaman M.H., Padula W.V., Davidson P.M. 2021. Supply chain failures amid Covid-19 signal a new pillar for global health preparedness. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Motevalli-Taher F., Paydar M.M. Supply chain design to tackle coronavirus pandemic crisis by tourism management. Appl. Soft Comput. 2021;104 doi: 10.1016/j.asoc.2021.107217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zahedi A., Salehi-Amiri A., Smith N.R., Hajiaghaei-Keshteli M. Utilizing IoT to design a relief supply chain network for the SARS-COV-2 pandemic. Appl. Soft Comput. 2021 doi: 10.1016/j.asoc.2021.107210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nikolopoulos K., Punia S., Schäfers A., Tsinopoulos C., Vasilakis C. Forecasting and planning during a pandemic: COVID-19 growth rates, supply chain disruptions, and governmental decisions. European J. Oper. Res. 2021;290(1):99–115. doi: 10.1016/j.ejor.2020.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Baveja A., Kapoor A., Melamed B. Stopping Covid-19: A pandemic-management service value chain approach. Ann. Oper. Res. 2020;289:173–184. doi: 10.1007/s10479-020-03635-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Iyengar K., Bahl S., Vaishya R., Vaish A. Challenges and solutions in meeting up the urgent requirement of ventilators for COVID-19 patients. Diabetes Metab. Syndr.: Clin. Res. Rev. 2020;14(4):499–501. doi: 10.1016/j.dsx.2020.04.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Chiaramonti D., Maniatis K. Security of supply, strategic storage and Covid19: Which lessons learnt for renewable and recycled carbon fuels, and their future role in decarbonizing transport? Appl. Energy. 2020;271 doi: 10.1016/j.apenergy.2020.115216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kumar M.S., Raut R.D., Narwane V.S., Narkhede B.E. Applications of industry 4.0 to overcome the COVID-19 operational challenges. Diabetes Metab. Syndr.: Clin. Res. Rev. 2020;14(5):1283–1289. doi: 10.1016/j.dsx.2020.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Nagurney A. Optimization of supply chain networks with inclusion of labor: Applications to Covid-19 pandemic disruptions. Int. J. Prod. Econ. 2021;235 doi: 10.1016/j.ijpe.2021.108080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Nagurney A. Supply chain game theory network modeling under labor constraints: Applications to the Covid-19 pandemic. European J. Oper. Res. 2021 doi: 10.1016/j.ejor.2020.12.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Nagurney A. In: Dynamics of Disasters: Impact, Risk, Resilience, and Solutions. Kotsireas I.S., Nagurney A., Pardalos P.M., Tsokas A., editors. Springer International Publishing Switzerland; 2020. Perishable food supply chain networks with labor in the COVID-19 pandemic. [Google Scholar]
- 45.Nagurney A., Salarpour M., Dong J., Dutta P. In: Nonlinear Analysis and Global Optimization. Rassias Themistocles M., Pardalos Panos M., editors. Springer Nature Switzerland AG; 2020. Competition for medical supplies under stochastic demand in the Covid-19 pandemic: A generalized nash equilibrium framework. forthcoming. [Google Scholar]
- 46.Nandi S., Sarkis J., Hervani A.A., Helms M.M. Redesigning supply chains using blockchain-enabled circular economy and COVID-19 experiences. Sustain. Prod. Consum. 2021;27:10–22. doi: 10.1016/j.spc.2020.10.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Ivanov D. Predicting the impacts of epidemic outbreaks on global supply chains: A simulation-based analysis on the coronavirus outbreak (COVID-19/SARS-CoV-2) case. Transp. Res. E. 2020;136 doi: 10.1016/j.tre.2020.101922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Goodarzian F., Abraham A., Fathollahi-Fard A.M. A biobjective home health care logistics considering the working time and route balancing: a self-adaptive social engineering optimizer. J. Comput. Des. Eng. 2021;8(1):452–474. [Google Scholar]
- 49.Abbasi B., Fadaki M., Kokshagina O., Saeed N., Chhetri P. 2020. Modeling vaccine allocations in the COVID-19 pandemic: A case study in australia. Available at SSRN 3744520. [Google Scholar]
- 50.Habibi-Kouchaksaraei M., Paydar M.M., Asadi-Gangraj E. Designing a bi-objective multi-echelon robust blood supply chain in a disaster. Appl. Math. Model. 2018;55:583–599. [Google Scholar]
- 51.Mohamadi A., Yaghoubi S., Pishvaee M.S. Fuzzy multi-objective stochastic programming model for disaster relief logistics considering telecommunication infrastructures: a case study. Oper. Res. 2019;19(1):59–99. [Google Scholar]
- 52.Shavarani S.M. Multi-level facility location–allocation problem for post-disaster humanitarian relief distribution. J. Humanit. Logist. Supply Chain Manag. 2019 [Google Scholar]
- 53.Akbarpour M., Torabi S.A., Ghavamifar A. Designing an integrated pharmaceutical relief chain network under demand uncertainty. Transp. Res. E. 2020;136 [Google Scholar]
- 54.Li Y., Zhang J., Yu G. A scenario-based hybrid robust and stochastic approach for joint planning of relief logistics and casualty distribution considering secondary disasters. Transp. Res. E. 2020;141 [Google Scholar]
- 55.Ghasemi P., Khalili-Damghani K. A robust simulation–optimization approach for pre-disaster multi-period location–allocation–inventory planning. Math. Comput. Simulation. 2021;179:69–95. [Google Scholar]
- 56.Molladavoodi H., Paydar M.M., Safaei A.S. A disaster relief operations management model: a hybrid LP–GA approach. Neural Comput. Appl. 2020;32(4):1173–1194. [Google Scholar]
- 57.Mousavi R., Salehi-Amiri A., Zahedi A., Hajiaghaei-Keshteli M. Designing a supply chain network for blood decomposition by utilizing social and environmental factor. Comput. Ind. Eng. 2021 [Google Scholar]
- 58.Hajiaghaei-Keshteli M., Sajadifar S.M., Haji R. Determination of the economical policy of a three-echelon inventory system with (R, Q) ordering policy and information sharing. Int. J. Adv. Manuf. Technol. 2011;55(5–8):831–841. [Google Scholar]
- 59.Cheraghalipour A., Paydar M.M., Hajiaghaei-Keshteli M. An integrated approach for collection center selection in reverse logistics. Int. J. Eng. 2017;30(7):1005–1016. [Google Scholar]
- 60.Chouhan V.K., Khan S.H., Hajiagheai-Keshteli M., et al. Multi-facility-based improved closed-loop supply chain network for handling uncertain demands. Soft Comput. 2020;24:7125–7147. doi: 10.1007/s00500-020-04868-x. [DOI] [Google Scholar]
- 61.Mosallanezhad B., Hajiaghaei-Keshteli M., Triki C. Shrimp closed-loop supply chain network design. Soft Comput. 2021:1–24. [Google Scholar]
- 62.Nurjanni K.P., Carvalho M.S., Costa L. Green supply chain design: A mathematical modeling approach based on a multi-objective optimization model. Int. J. Prod. Econ. 2017;183:421–432. [Google Scholar]
- 63.Sarvestani H.K., Zadeh A., Seyfi M., Rasti-Barzoki M. Integrated order acceptance and supply chain scheduling problem with supplier selection and due date assignment. Appl. Soft Comput. 2019;75:72–83. [Google Scholar]
- 64.Sarma D., Das A., Bera U.K. Uncertain demand estimation with optimization of time and cost using Facebook disaster map in emergency relief operation. Appl. Soft Comput. 2020;87 [Google Scholar]
- 65.Goodarzian F., Hosseini-Nasab H., Muñuzuri J., Fakhrzad M.B. A multi-objective pharmaceutical supply chain network based on a robust fuzzy model: A comparison of meta-heuristics. Appl. Soft Comput. 2020;92 [Google Scholar]
- 66.Fathollahi-Fard A.M., Ahmadi A., Goodarzian F., Cheikhrouhou N. A bi-objective home healthcare routing and scheduling problem considering patients’ satisfaction in a fuzzy environment. Appl. Soft Comput. 2020;93 doi: 10.1016/j.asoc.2020.106385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Goodarzian F., Taleizadeh A.A., Ghasemi P., Abraham A. An integrated sustainable medical supply chain network during COVID-19. Eng. Appl. Artif. Intell. 2021;100 doi: 10.1016/j.engappai.2021.104188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.M. Hajiaghaei-Keshteli, M. Aminnayeri, Keshtel Algorithm (KA); a new optimization algorithm inspired by Keshtels’ feeding, in: Proceeding in IEEE Conference on Industrial Engineering and Management Systems, 2013, pp. 2249–2253.
- 69.Hajiaghaei-Keshteli M., Aminnayeri M. Solving the integrated scheduling of production and rail transportation problem by Keshtel algorithm. Appl. Soft Comput. 2014;25:184–203. [Google Scholar]
- 70.Cheraghalipour A., Paydar M.M., Hajiaghaei-Keshteli M. A bi-objective optimization for citrus closed-loop supply chain using Pareto-based algorithms. Appl. Soft Comput. 2018;69:33–59. [Google Scholar]
- 71.Kirkpatrick S., Gelatt C.D., Vecchi M.P. Optimization by simulated annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- 72.Golmohamadi S., Tavakkoli-Moghaddam R., Hajiaghaei-Keshteli M. Solving a fuzzy fixed charge solid transportation problem using batch transferring by new approaches in meta-heuristic. Electron. Notes Discrete Math. 2017;58:143–150. [Google Scholar]
- 73.Deb K., Pratap A., Agarwal S., Meyarivan T.A.M.T. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002;6(2):182–197. [Google Scholar]
- 74.Behnamian J., Ghomi S.F. Hybrid flowshop scheduling with machine and resource-dependent processing times. Appl. Math. Model. 2011;35(3):1107–1123. [Google Scholar]
- 75.Fard A.F., Gholian-Jouybari F., Paydar M.M., Hajiaghaei-Keshteli M. A bi-objective stochastic closed-loop supply chain network design problem considering downside risk. Ind. Eng. Manag. Syst. 2017;16(3):342–362. [Google Scholar]
- 76.Roghanian E., Cheraghalipour A. Addressing a set of meta-heuristics to solve a multi-objective model for closed-loop citrus supply chain considering CO2 emissions. J. Cleaner Prod. 2019;239 [Google Scholar]
- 77.Taguchi G. 1986. Introduction to quality engineering: designing quality into products and processes. [Google Scholar]
- 78.Sahebjamnia N., Goodarzian F., Hajiaghaei-Keshteli M. Optimization of multi-period three-echelon citrus supply chain problem. J. Optim. Ind. Eng. 2020;13(1):39–53. [Google Scholar]
- 79.Derrac J., García S., Molina D., Herrera F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011;1(1):3–18. [Google Scholar]