Incorporating European GWAS findings improve polygenic risk prediction accuracy of breast cancer among East Asians

Abstract

Previous GWASs have been largely focused on European (EUR) populations. However, PRSs derived from EUR have been shown to perform worse in non-EURs compared to EURs. In this study, we aim to improve PRS prediction in East Asians (EASs). We introduce a rescaled meta-analysis framework to combine both EUR (N = 122, 175) and EAS (N = 30, 801) GWAS summary statistics. To improve PRS prediction in EASs, we use a scaling factor to up-weight the EAS data, such that the resulting effect size estimates are more relevant to EASs. We then derive PRSs for EAS from the rescaled meta-analysis results of EAS and EUR data. Evaluated in an independent EAS validation dataset, this approach increases the prediction liability-adjusted Nagelkerke’s pseudo R² by 40%, 41%, and 5%, respectively, compared to PRSs derived from an EAS GWAS only, EUR GWAS only, and conventional fixed-effects meta-analysis of EAS and EUR data. The PRS derived from the rescaled meta-analysis approach achieved an area under the receiver operating characteristic curve (AUC) of 0.6059, higher than AUC = 0.5782, 0.5809, 0.6008 for EAS, EUR, and conventional meta-analysis of EAS and EUR. We further compare PRSs constructed by SNPs that have different LD scores and minor allele frequencies (MAFs) between EUR and EAS, and observe that lower LD scores or MAF in EAS correspond to poorer PRS performance (AUC=0.5677, 0.5530 respectively) than higher LD scores or MAF (AUC=0.589, 0.5993 respectively). We finally build a PRS stratified by LD score differences in EUR and EAS using rescaled meta-analysis, and obtain an AUC of 0.6096, with improvement over other strategies investigated.

Introduction

Breast cancer is the most frequently diagnosed cancer and the leading cause of cancer death in females worldwide (Torre et al., 2015) . Although the rate of getting breast cancer has stabilized in some high-income countries, it continues to rise in most Asian and other low and middle-income countries, stressing the need for establishing early risk prediction and management strategies (Denny et al., 2017). Genetic risk factors play an important role in breast cancer predisposition (Nathanson, Wooster, & Weber, 2001). Large scale genome-wide association studies (GWASs) have identified more than 200 loci to be associated with risk of breast cancer (Cai et al., 2014; Michailidou et al., 2015, 2017; Shu et al., 2020; Zheng et al., 2009, 2013). Polygenic risk score (PRS), a weighted aggregation of risk allele counts derived from GWASs, is emerging as a useful tool for breast cancer risk stratification in multiple populations, including Europeans (EURs) and East Asians (EASs) (Khera et al., 2018; Mavaddat et al., 2019; Wen et al., 2016).

The small sample size in GWASs of non-EUR samples and differences of genetic architecture between EUR and other populations make it challenging to develop powerful and well-calibrated PRSs across diverse populations. To date, large-scale breast cancer GWASs were conducted by the Breast Cancer Association Consortium (BCAC), with summary statistics publicly available for ~123,000 (Michailidou et al., 2015) and ~220,000 EUR samples (Michailidou et al., 2017). The largest non-EUR GWAS was conducted by the Asia Breast Cancer Consortium (ABCC), which included more than 40,000 EAS samples (Cai et al., 2014; Shu et al., 2020; Zheng et al., 2009, 2013). From study of 17 anthropometric and blood-panel traits, applying PRSs derived from EUR GWASs directly to non-EUR samples showed poor transferability in general, with approximately ~37%, ~50%, and ~78% lower prediction R² in South Asians, EASs, and Africans, respectively, compared to that in EUR populations (Martin et al., 2019). Therefore, developing polygenic risk prediction models for diverse populations is imperative to translate the GWAS findings to clinical use. This calls for efforts to improve the performance of PRS in non-EUR samples to mitigate the racial disparity.

Given that non-EUR GWASs are usually of insufficient sample size, and that there is extensive genetic sharing across populations (Barbujani, Magagni, Minch, & Cavalli-Sforza, 1997; Gibbs et al., 2015), there are several recent studies that sought to incorporate a large EUR GWAS and a smaller non-EUR GWAS to improve risk prediction in non-EUR populations. Specifically, Coram et al. proposed a cross-population best linear unbiased prediction method based on multi-component linear mixed models, where SNPs were placed in classes defined by GWAS evidence from different ancestries and allelic effects computed in a population-specific fashion (Coram et al., 2015; Coram, Fang, Candille, Assimes, & Tang, 2017); this method requires individual-level training data in the target population. When only GWAS summary statistics are available, Márquez-Luna et al. constructed a trans-ethnic PRS from a weighted linear combination of PRSs from two populations (Márquez-Luna, Loh, Price, & Price, 2017), which could improve the prediction accuracy for type II diabetes in Hispanic/Latinos and South Asians. Grinde et al. found that this approach did not perform well for several anthropometric, blood count, and blood pressure traits in their Hispanic/Latino cohorts (Grinde et al., 2019). Instead, they proposed to construct PRSs by selecting single-nucleotide polymorphisms (SNPs) and their corresponding weights based on different combinations of EUR GWASs, Hispanic/Latino GWASs, or meta-analyses of both. They found that PRSs using an EUR GWAS for SNP selection and a Hispanic/Latino GWAS or meta-analysis for SNP weights performed the best in their empirical studies. These findings suggested that PRS performances could differ by population- and disease-specific genetic architectures. For breast cancer, EUR-based PRSs were reported to perform equally well in Hispanic/Latinos as in EURs but poorly in African Americans (Allman et al., 2015). The performance of EUR- and EAS-based PRSs in EASs remain unclear. This motivates us to evaluate breast cancer PRS predictions in EASs and develop new strategies to construct PRSs targeting non-EUR populations.

Differential linkage disequilibrium (LD) and minor allele frequency (MAF) are major contributors to the poor transferability of PRSs among populations (Wang et al., 2020). In a PRS of the form ∑w_j X_j, where X_j and w_j stand for the standardized genotype and weight for SNP j, respectively, the ideal weight satisfies $w_j^2=h_j^2$, where $h_j^2$ is the disease heritability directly contributed by SNP j (Speed & Balding, 2019). Because the disease heritability contributed by a SNP varies according to local LD (Gazal et al., 2017; Speed, Cai, Johnson, Nejentsev, & Balding, 2017), explicit incorporation of EUR LD information can improve prediction accuracy for EURs (Hu et al., 2017; Marquez-Luna et al., 2019; Vilhjálmsson et al., 2015). In addition, SNPs can serve as better proxies for the underlying “true effects” in populations in which they have high LD scores compared to populations in which they have low LD scores, where the LD score of a SNP is the sum of LD r² measured between this SNP and all other SNPs (Bulik-Sullivan et al., 2015). MAF has been used as an indication of the strength of natural selection, thus the differences in strengths of selection between ancestries might have an impact on PRSs (Wang et al., 2020). This motivates us to examine whether modeling the LD and MAF differences between EURs and EASs could improve effect size estimation and genetic risk prediction in EAS populations.

In this paper, we are primarily interested in 1) evaluating the transferability of EUR GWAS data to breast cancer risk prediction in EASs, 2) improving risk predication for breast cancer in EASs, and 3) exploring effects of LD and MAF differences between EUR and EAS ethnicities in PRS construction. We propose a rescaled meta-analysis framework that upweights EAS signals over EUR signals, yielding effect size estimates closer to the true effect sizes in EASs while taking advantage of the large sample sizes of EUR GWASs. We constructed PRSs using summary statistics from the rescaled meta-analysis of EUR and EAS GWAS data and then evaluated their performances in an independent EAS validation dataset. Our PRS outperforms PRSs derived from the EUR or EAS GWAS alone as well as the conventional meta-analysis of EAS and EUR GWASs. The EUR and EAS GWASs used in the analysis are from the BCAC and ABCC, respectively.

Results

Trade-off between training GWAS sample size and matched genetic ancestry in PRS prediction in EASs

We first constructed PRSs using SNP-level effect sizes from single EUR or EAS GWASs and evaluated their performance in an independent EAS validation dataset. To assess the impact of sample size on PRS performance, we used EUR GWAS from the BCAC published in 2015 (62,533 cases and 60,976 controls) (Michailidou et al., 2015) and EAS GWAS from the ABCC (14,958 cases and 15,843 controls) (Cai et al., 2014; Zheng et al., 2009, 2013) for PRS construction; we used an earlier, smaller EUR GWAS rather than the most recent, much larger GWAS (Michailidou et al., 2017) from the BCAC to illustrate our strategy of combing EAS and EUR data so as to avoid the EAS data being overwhelmed by the EUR data. For each training GWAS dataset, we derived predictors based on the “P+T” method (Materials and methods) and chose parameters that maximize prediction accuracy through cross-validation in an independent EAS validation dataset of 3,853 subjects (1,794 cases and 2,059 controls) (MEGA Shanghai; see Materials and methods and S1 Table).

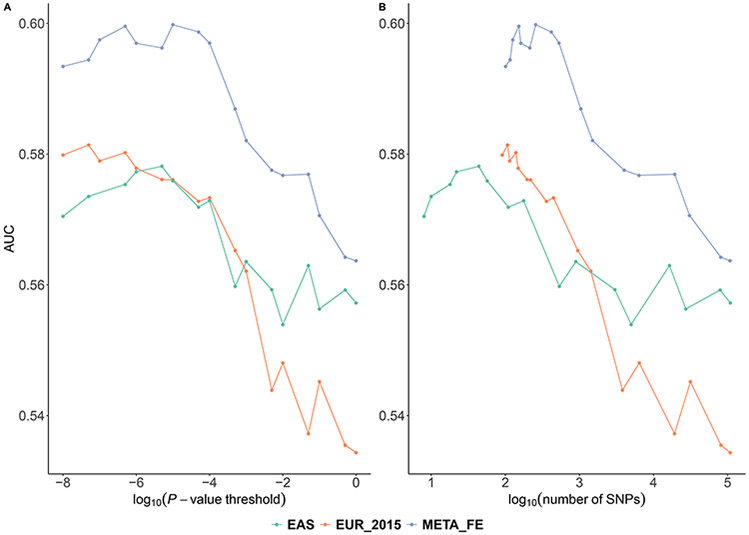
We reported area under the receiver operating characteristics curve (AUC) of the PRSs along with their P-value threshold and number of SNPs included in Fig 1 and Table 1. We found that a single individual sample in the EAS training dataset was substantially more informative about predicting breast cancer risk in the EAS validation dataset compared to that in the EUR training datasets. The best PRS derived from the EAS GWAS yielded an AUC of 0.5782. The best PRS derived from the EUR GWAS, which is ~4 times the sample size of the EAS GWAS, yielded a comparable AUC of 0.5809 in the EAS validation set. These findings are consistent across different P-value thresholds used and numbers of SNPs included in the PRSs (Fig 1), demonstrating the trade-off between higher prediction accuracy conferred by the larger EUR sample size and the matched EAS ancestry. Similar findings for type II diabetes in Latinos have been reported before (Márquez-Luna et al., 2017).

Fig 1. The AUC of PRSs derived from the EAS/EUR GWASs alone and meta-analysis of both.

PRSs are derived from EAS, EUR GWASs and fixed effect meta-analysis of the EAS and EUR (denoted as META_FE). PRSs are evaluated in an independent EAS validation dataset for predicting breast cancer risk. Each PRS was plotted against the (A) P-value threshold and (B) number of SNPs included. The corresponding numerical results were reported in S2 Table.

Table 1.

Prediction AUC, Nagelkerke’s R² and liability adjusted R² in the EAS validation set (adjusted for age and first 2 principal components of genotype)^a.

Modelb	P- thresholdc	N_SNPsd	AUCe	AUC 95% CIf	Nagelkerke’s R2 g	Liability adjusted R2 h	P-value for improvement over reduced modeli
EAS	5 × 10−6	44	0.5782	0.5600-0.5963	0.047	0.0201	9.64 × 10−29
EUR	5 × 10−8	107	0.5809	0.5628-0.5989	0.0465	0.0198	1.99 × 10−28
META_FE	1 × 10−5	257	0.6008	0.5829-0.6188	0.0624	0.0268	1.33 × 10−38
META_2EAS	5 × 10−6	190	0.6049	0.587-0.6228	0.0655	0.0282	1.30 × 10−40
META_3EAS	1 × 10−5	193	0.6059	0.588-0.6238	0.0656	0.0283	1.08 × 10−40
ADD3	NA	265	0.6096	0.5917-0.6274	0.0689	0.0298	7.70 × 10−43

^aWe reported AUC, Nagelkerke’s R² and liability adjusted R² for each of the PRSs in the EAS validation dataset

^bModels that PRSs are based on: EAS: EAS GWAS derived PRS; EUR: EUR GWAS derived PRS; META_FE: conventional fixed-effect meta-analysis; META_2EAS: rescaled meta-analysis that up-weights the EAS summary statistics by a factor of two; META_3EAS: rescaled meta-analysis that up-weights the EAS summary statistics by a factor of three; ADD3: summation of the three best PRSs within each LD category

^cP-value cutoff for including SNPs in model

^dNumber of SNPs in model

^eArea under ROC curve

^f95% confidence interval of AUC

^gNagelkerke’s R² of a full model

^hLiability adjusted Nagelkerke’s R² that accounted for case/control ratio

ⁱP-value from likelihood ratio test compare full model (PRS, covariates including age and first 2 principal components of genotype) with a reduced model (a model with covariates age and first 2 principal components of genotype only)

To explore whether incorporating GWASs from both the EUR and EAS populations can boost prediction performance, we performed a meta-analysis of the EUR and EAS GWASs and used the resulting summary statistics to derive PRSs. We obtained an AUC of 0.6008 in the validation EAS dataset, which was higher than any PRS derived from the EAS or EUR GWASs alone. These results demonstrated that combining information from a higher-powered EUR GWAS and ancestry matched EAS GWAS helped improve breast cancer risk predictions in EASs, which was consistent with previous reports for other traits in EASs (Lam et al., 2019) and Hispanic/Latinos (Grinde et al., 2019).

Upweighting the EAS effect size estimates in meta-analysis improves PRS prediction in EASs

In conventional fixed-effect meta-analysis, the effect size of each SNP is calculated by an inverse variance weighted sum of the effect size estimates from the participating GWASs. When the true effect sizes are equal across the GWASs, this formula is optimal and entails no efficiency loss compared to a joint analysis of the GWASs using individual-level data (Lin & Zeng, 2009). However, this formula may not be optimal when the goal is to provide effect size estimate from EAS and EUR GWASs for constructing PRS in EASs. Instead, we propose to tip the trans-ethnic meta-analysis towards the EAS population by up-scaling EAS effect size estimates by a factor of α in addition to the inverse variance weighting scheme (Materials and methods). This strategy enables us to shrink the meta effect size estimates towards the estimates in the EAS GWAS and increase the power to detect EAS-specific signals. To find a good up-scaling factor α, we conducted a grid search (i.e., α = 1, 2, 3, 4, 5) and then evaluated the AUC of the resulting PRSs using cross-validation (S1 Fig). The conventional fixed-effect meta-analysis is a special case with α = 1.

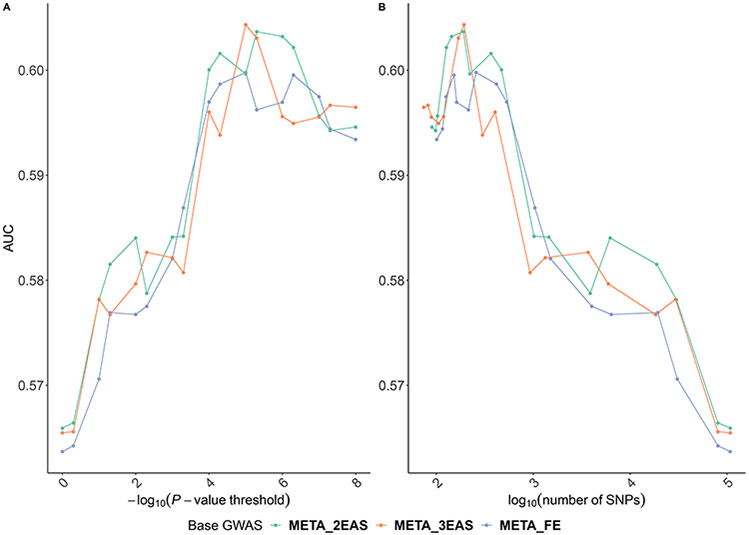
We evaluated these PRSs on the EAS validation dataset and found that up-scaling the EAS GWAS with a factor of two or three in meta-analysis could result in increased predicting accuracy (Fig 2). For example, we obtained an AUC of 0.6059 when using α = 3, compared to an AUC of 0.6008 in conventional fixed-effect meta-analysis (i.e., α = 1). In general, an up-scaling factor of two or three resulted in better prediction performance than conventional fixed-effect meta-analysis across a range of P-value thresholds used and numbers of SNPs included in the PRS in our analysis (Fig 2). We conducted one-sided Delong’s test and did not observe significant difference between the AUCs of PRSs derived from the rescaled meta-analysis (α = 3) and conventional fixed-effect meta-analysis (P-value = 0.14). This is somewhat expected as recent literature on PRS evaluation also showed small AUC differences between PRSs constructed using different methods using the same training dataset (Khera et al., 2018). We note that the difference between the AUCs of PRSs derived from the rescaled meta-analysis (α = 3) and EAS GWAS was statistically significant (P-value = 4.6 × 10⁻⁴), so was the difference between the AUCs of PRSs derived from the rescaled meta-analysis (α = 3) and EUR GWAS (P-value = 1.9 × 10⁻⁴).

Fig 2. The AUC of PRSs derived from rescaled meta-analysis of the EAS and EUR_2015.

PRSs are evaluated in predicting breast cancer risk in the EAS validation dataset. META_FE denotes the conventional fixed-effect meta-analysis; META_2EAS denotes the rescaled meta-analysis that upweights the EAS effect size estimates by a factor of two; and META_3EAS denotes the rescaled meta-analysis that upweights the EAS effect size estimates by a factor of three. Each PRS was plotted against the (A) P-value threshold and (B) number of SNPs. The corresponding numerical results were provided in S2 Table

GWAS effect size heterogeneity is related to LD score differences between ancestries

Wojcik et al. observed inconsistent effect size estimates between populations (Wojcik et al., 2019), which could contribute to reduced transferability of PRSs between populations. The extent of effect size differences between populations differs across the genome. As LD score measures the tagging capacity of a SNP, a natural topic of investigation is whether the extent of LD differences is related to the extent of effect size differences between EURs and EASs.

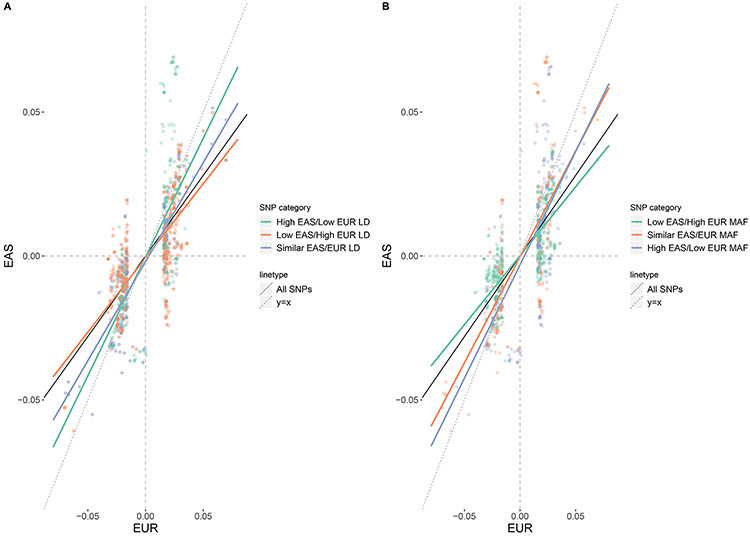
To examine this, we used the difference in EAS and EUR LD score (Bulik-Sullivan et al., 2015): l_diff,j = l_EAS,j − l_EUR,j as an indication of a SNP’s tagging capacity divergence between populations, where l_EAS,j and l_EUR,j are the ancestry-specific LD scores in EASs and EURs, respectively, estimated from the corresponding populations in the 1000 Genomes Project (Auton et al., 2015). We partitioned all available SNPs into three equally sized groups: “low EAS/high EUR LD score” group with l_diff less than its 33% quantile, “similar EAS/EUR LD score” group with l_diff l_diffbetween its 33% and 67% quantiles, and “high EAS/low EUR LD score” group with l_diff l_diff larger than its 67% quantile. To account for the impact of differential GWAS sample sizes on SNPs’ effect size estimates, we calculated “standardized” z-scores by dividing the original z-scores by the square root of GWAS sample size (Wojcik et al., 2019). Then, we compared the standardized z-scores in the EUR and EAS GWASs (denoted as z_EUR and z_EAS, respectively) for SNPs with P-value < 5 × 10⁻⁸ in either the EUR or EAS GWAS (Fig 3A). In general, we observed a reduction of standardized Z scores in EASs compared to EURs regardless of l_diff categories, with an overall slope of 0.64 (z_EAS = 0.64 × z_EUR, 95% confidence interval: 0.61 - 0.67). In addition, we observed that standardized z-scores tended to be even lower in EASs for SNPs with “low EAS/high EUR LD score” (z_EAS = 0.52 × z_EUR, 95% confidence interval: 0.48 - 0.55), and higher in EASs for SNPs with “high EAS/low EUR LD score” (z_EAS = 0.83 × z_EUR, 95% confidence interval: 0.75 - 0.90), suggesting that LD differences are related to observed effect size differences between populations.

Fig 3. Standardized Z-scores of SNPs from EUR and EAS GWAS classified into different LD and MAF groups.

SNPs with P-values < 5 ×10⁻⁸ in either EUR_2015 or the EAS GWAS were included. (A) Low EAS/High EUR LD: SNPs with l_diff less than its 33% quantile; Similar EAS/EUR LD: SNPs with l_diff between its 33% and 67% quantiles; High EAS/Low EUR LD: SNPs with l_diff larger than its 67% quantile. (B) Low EAS/high EUR MAF: SNPs with MAF_diff,j less than its 33% quantile, similar EAS/EUR MAF: SNPs with MAF_diff,j between its 33% and 67% quantiles, and high EAS/low EUR MAF: SNPs with MAF_diff,j larger than its 67% quantile. The black dashed line is the slope of the fitted line of standardized Z score in EAS over standardized Z score in EUR with all SNPs included; the red/blue/green lines are fitted lines of standardized Z score in EAS over standardized Z score in EUR for SNPs in corresponding LD group or MAF group.

Effects of LD differences on genetic risk prediction

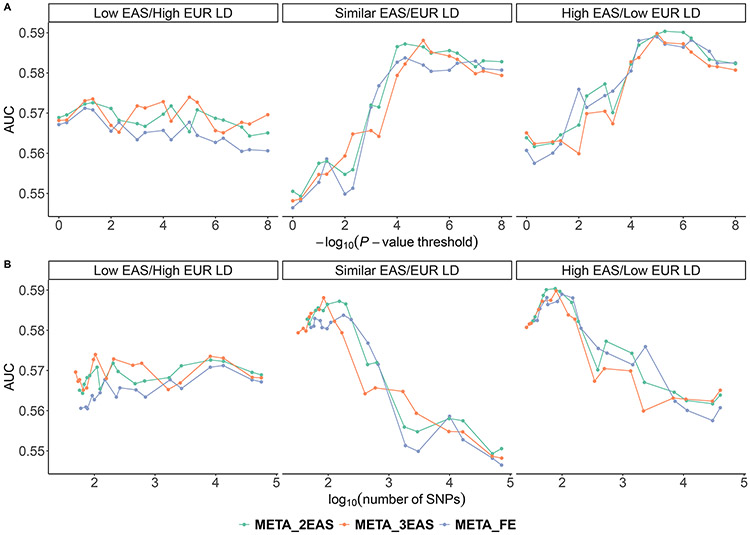
We further investigated the impact of differential tagging capacity due to differential LD levels between populations on PRS performance in EASs. After classifying SNPs into three groups based on l_diff, we constructed group specific PRSs based on both conventional and rescaled meta-analyses and applied the PRSs to the validation EAS dataset. We observed that the performance of PRS in the low EAS/high EUR LD score group is noticeably lower than that in the other two groups. This is true for both the conventional and rescaled meta-analyses (Fig 4). For example, the AUC of the PRS derived from the conventional meta-analysis using SNPs in the low EAS/high EUR LD score group is 0.5677, while the AUC of the PRSs derived using SNPs in the similar EAS/EUR LD score and high EAS/low EUR LD score groups are 0.5837 and 0.5890, respectively. Comparing the rescaled versus conventional meta-analysis, we found that upweighting the EAS effect size estimates with a factor of two or three resulted in a more dramatic increase in prediction accuracy for SNPs in the low EAS/high EUR LD score and similar EAS/EUR LD score groups, while the performance gain in the high EAS/low EUR LD score group appeared to be minimal.

Fig 4.

The AUC of PRSs constructed with SNPs in different l_diff groups. All SNPs were classified into three groups: low EAS/high EUR LD score group with l_diff less than its 33% quantile, similar EAS/EUR LD score group with l_diff between its 33% and 67% quantiles, and high EAS/low LD score group with l_diff larger than its 67% quantile. META_FE denotes the conventional fixed-effect meta-analysis; META_2EAS denotes the rescaled meta-analysis that upweights the EAS effect size estimates by a factor of two; and META_3EAS denotes the rescaled meta-analysis that upweights the EAS effect size estimates by a factor of three. Each PRS was plotted against the (A) P-value threshold and (B) number of SNPs.

As the LD difference is likely a key factor contributing to the poor transferability of EUR-derived PRS to non-EUR populations, we also explored whether taking LD differences among population into account has potential to increase PRS accuracy. We constructed an l_diff-stratified PRS by the summation of the three best PRSs within each l_diff group (referred to as “ADD3”). We observed marginal significant improvement of AUC from ADD3 (AUC = 0.6096) over conventional fixed-effect meta-analysis PRS (AUC = 0.6008, one-sided Delong’s test P-value = 0.05).

Effect of MAF differences on GWAS effect size and genetic risk prediction

As MAF differences between populations might also contribute to GWAS heterogeneity and decreased transferability of PRS, we sought to investigate the effects of MAF empirically. We used a similar approach as in the interrogation of LD differences to partition all available SNPs into three equally sized groups by MAF differences. Specifically, we used the difference in EAS and EUR MAF: MAF_diff,j = MAF_EAS,j − MAF_EUR,j as an indication of a SNP’s MAF divergence between populations, where MAF_EAS,j and MAF_EUR,j are the ancestry-specific MAFs reported by the single population GWASs. We partitioned all available SNPs into three equally sized groups: “low EAS/high EUR MAF” group with MAF_diff,j less than its 33% quantile, “similar EAS/EUR MAF” group with MAF_diff,j between its 33% and 67% quantiles, and “high EAS/low EUR MAF” group with MAF_diff,j larger than its 67% quantile. Then, we compared the standardized z-scores in the EUR and EAS GWASs for SNPs with P-value < 5 × 10⁻⁸ in either the EUR or EAS GWAS similar to what we did previously for LD differences (Fig 3B). We observed that standardized z-scores tended to be lower in EASs for SNPs with “low EAS/high EUR MAF” (z_EAS = 0.48 × z_EUR, 95% confidence interval: 0.44 - 0.51), and higher in EASs for SNPs with “high EAS/low EUR MAF” (z_EAS = 0.78 × z_EUR, 95% confidence interval: 0.64 - 0.83), suggesting that MAF differences are related to observed effect size differences between populations.

We constructed MAF group-specific PRSs based on both conventional and rescaled meta-analyses and applied the PRSs to the validation EAS dataset. We observed that the performance of PRS in the low EAS/high EUR MAF group is noticeably lower than that in the other two groups (Fig S2). This is true for both the conventional and rescaled meta-analyses. For example, the AUC of the PRS derived from the conventional meta-analysis using SNPs in the low EAS/high EUR MAF group is 0.5530, while the AUC of the PRSs derived using SNPs in the similar EAS/EUR MAF and high EAS/low EUR MAF groups are 0.5876 and 0.5993, respectively.

We explored whether integrating MAF and LD difference information would further improve PRS. We stratified SNPs into nine groups cross-tabulated by the three LD score groups and three MAF groups (Fig S3). We observed that the prediction AUC of PRS derived from SNPs in “low EAS/high EUR MAF + high EAS/low EUR LD score” group was the lowest, while the AUC of PRS derived from SNPs in “high EAS/low EUR MAF + high EAS/low EUR LD score” group was the highest. Then, we evaluated the performance of the added score of the best PRSs from the nine groups (referred to as “ADD9”), similar to what we did with ADD3. We found no improvement on AUC for ADD9 (AUC = 0.6084) compared to ADD3 (AUC = 0.6096), indicating that the impact of MAF differences on PRS prediction might overlap with that of LD score differences (the correlation between MAF differences and LD score differences was 0.36).

Evaluation of the PRSs using the prediction Nagelkerke’s pseudo R² and odds-ratio in EASs

We evaluated the candidate PRSs using the prediction Nagelkerke’s pseudo R² and liability-adjusted R² We included the PRSs constructed from the EUR and EAS GWAS alone and the rescaled meta-analyses that upweights the EAS effect size estimates by a factor of two or three. We also included an l_diff-stratified PRS constructed by the summation of the three best PRSs within each l_diff group. We used logistic regression and included age and the first two principal components as covariates. The results were shown in S2 Table. The PRS derived from the rescaled meta-analysis that upweights the EAS effect size estimates by a factor of three increased the prediction Nagelkerke’s pseudo R² (liability-adjusted R²) by 40% (41%), 41% (42%), and 5% (6%), respectively, compared to PRSs derived from the EAS GWAS only, EUR GWAS only, and conventional fixed-effects meta-analysis of both. The l_diff-stratified PRS performed better than the other models, although the improvement was marginal (Table 1).

We assessed the odds ratio (OR) of developing breast cancer in the top 10% individuals with the highest PRSs versus the remaining 90% in the EAS validation dataset. We observed that PRSs derived from the meta-analyses of EAS and EUR GWASs resulted in improved ORs compared to PRSs derived from the EAS GWAS or EUR alone (Table 2). For example, we obtained ORs in the range of 2.31 - 2.50 for PRSs derived from the meta-analyses, while we obtained ORs of 2.23 and 1.73 for PRSs derived from the EAS GWAS or EUR, respectively. We also compared the top 10% individuals with the middle 40%-60% and observed similar results (S2 Table).

Table 2.

OR of developing breast cancer in the top 10% individuals with the highest PRSs versus the remaining 90% in the EAS validation dataset

Modela	OR	OR (95% CI)b	P-value
EAS	2.23	1.78 - 2.80	2.33 × 10−13
EUR	1.73	1.39 - 2.16	3.93 × 10−7
META_FE	2.50	1.99 - 3.14	8.40 × 10−17
META_2EAS	2.31	1.85 - 2.91	1.86 × 10−14
META_3EAS	2.43	1.94 - 3.06	5.34 × 10−16
ADD3	2.50	1.99 - 3.14	8.40 × 10−17

^aMETA_FE denotes the conventional fixed-effect meta-analysis; META_2EAS denotes the rescaled meta-analysis that upweights the EAS effect size estimates by a factor of two; META_3EAS denotes the rescaled meta-analysis that upweights the EAS effect size estimates by a factor of three; ADD3 denotes the l_diff-stratified PRS constructed by the summation of the three best PRSs within each l_diff group.

^bconfidence interval of OR.

Discussion

There has been tremendous progress in discovery of GWAS loci associated with breast cancer, making it feasible to construct PRS for individualized risk stratification. However, there is a lack of well-powered GWAS in non-EUR populations, a challenge that may exacerbate disparity in clinical use. The primary goal of this work is to explore strategies that can improve PRS of non-EUR populations, particularly in EAS. We found that incorporating information from well powered EUR GWAS and explicitly modeling LD and MAF differences are promising to improve PRS for breast cancer risk prediction in EAS. We proposed an approach to construct PRS from a rescaled meta-analysis of EUR and EAS GWAS which upweights the EAS component relative to the conventional inverse-variance based weightings. We observed improvement in PRS prediction accuracy using rescaled meta-analyses. As LD and MAF differences are likely key factors contributing to the poor transferability of EUR-derived PRS to non-EUR populations, we also explored whether taking them into account have potential to increase PRS accuracy. We observed marginal significant improvement of AUC from the l_diff-stratified PRS (“ADD3”) over conventional fixed-effect meta-analysis PRS (“META-FE”, P-value = 0.05) but no further improvement by stratifying on both LD and MAF differences (“ADD9”).

We further dissect why rescaled meta-analysis strategy is able to increase the PRS accuracy of the risk prediction in EAS in this study and in other non-EUR populations in general. We define the true model as y = ∑β_EAS,jx_j for EAS and y = ∑β_EUR,jx_j for EUR. Given the genetic differences between EAS and EUR, β_EAS,j and β_EUR,j are often unequal, and the extent of their differences depends on many factors, including LD, MAF, and environment factors. To construct a powerful PRS for EAS, i.e., ∑w_EAS,jx_j the goal is to assign a weight for the jth SNP w_EAS,j that is close to the true effect size β_EAS,j. When we use weights derived from EAS GWAS as w_EAS,j, the estimates are unbiased but of larger variance due to the smaller sample size. On the other hand, when the weights are derived from EUR GWAS, the estimates have smaller variance but are biased away from the true effect sizes in EAS, leading to poor transferability of EUR-derived PRS to EAS populations. To obtain estimates with a better bias and variance tradeoff, we proposed to combine EAS and EUR data to obtain estimates for use in PRS construction in EAS. Specifically, we proposed a rescaled meta-analysis strategy, with a rescale factor α > 1 to “pull” the estimate towards the true effect size in EAS, i.e. w_EASj = α * w_{inv_EAS,j} β_EASj + w_{inv_EUR,j}β_EURj, where w_{inv_EAS,j} and w_{inv_EUR,j} are the inverse-variance weights in the conventional meta-analysis (Materials and methods). The magnitude of α controls for the extent of “pulling” towards EAS, with α = 0 or α = inf corresponding to the extreme case where only EUR data (α = 0) or only EAS data (α = inf) are used. For α > 1, it upweights EAS in a way that a sample in the EAS GWAS data contributes more than a sample in EUR GWAS to the resulting effect size estimate, thus achieving the effect of pulling toward EAS. The optimal magnitude of α depends on the relative sample size of EAS and EUR, and in general, α increases when EAS sample sizes increases relative to EUR due to a bias-variance tradeoff between the more accurate EAS results and more precise EUR results. When the EAS sample size is much smaller than the EUR sample size, the effect size estimates obtained from the EUR GWAS have much smaller standard errors. In this situation, upweighting the EAS effect size with a larger α may significantly increase the standard errors in the rescaled meta-analyzed compared to that in conventional fixed-effects meta-analysis, offsetting the potential benefit of reduced bias. For example, when we used the latest EUR GWAS data of ~220,000 samples, the optimal α decreases to 1.3, achieving an AUC = 0.6195, compared to AUC = 0.6119 obtained in the traditional meta-analyses. To comprehensively study the relationship between optimal α and relative EUR and EAS sample sizes, we would need access to individual-level training data so that we can conduct a series of GWASs at different sample sizes (e.g., 60k, 120k, 180k, and 220k for EUR and 10k, 20k, and 30k for EAS). For a variety of diseases, more non-EUR samples are being generated, e.g., PAGE (Wojcik et al., 2019) and TOPMed (Taliun et al., 2019), and the reweighting factor is expected to increase when meta-analyzing with EUR data, resulting in increased prediction accuracy for non-EUR samples. Note that we used only a single scaling factor α to controls for the adjustment. Ideally, if we are able to assign a SNP-level scaling factor for every SNP, i.e. w_EASj = α_j * w_{inv_EAS,j}β_EASj + w_{inv_EUR,j}β_EURj where α_j is the scaling factor for the jth SNP, the performance of PRS can be further improved. However, it is challenging to assign scaling factors for each individual risk allele, as it is unknown a priori which alleles have different effect sizes between populations, and to what extent of their differences are. It requires further efforts to model fine-scale genetic difference between populations to assign reasonable SNP-level scaling factors.

We also examined the predictive performance on our validation set using Grinde et al.’s approach that performed well in several anthropometric and blood count traits in Hispanic Americans: select SNPs based on European GWASs and use meta-analysis weight estimates to construct PRS. We find resulting PRS perform worse (AUC = 0.5859) than using conventional meta-analysis GWAS for both SNP selection and weight estimates (AUC = 0.6008). This agrees with previous findings that the best performing PRS for a trait likely depends on the genetic architecture, differences in sample size between populations, and other factors.

We are aware that there are other PRS construction methods besides “P+T”, such as LDpred (Vilhjálmsson et al., 2015) and SBayesR (Lloyd-Jones et al., 2019). Specifically, we applied LDpred using the EAS LD reference panel and presented the results in Table S3. The findings were similar compared to those obtained by “P+T”: PRS derived from conventional fixed-effects meta-analysis performed better than those derived from single population GWASs; PRSs derived from rescaled meta-analysis and the l_diff-stratified PRS performed better than PRS derived from conventional fixed-effect meta-analysis. We observed comparable performance between PRSs constructed using LDpred and “P+T”, which is consistent with existing literature on breast cancer PRS (Khera et al., 2018).

We studied the impact of LD and MAF PRS constructed by taking into account both LD score differences and MAF differences between EAS and EUR did not outperform PRS constructed by taking into account LD score differences alone in EAS. It would be worthy of further exploration on how to better leverage MAF and LD in PRS construction. In addition, we did not explore the impact of functional genomic annotations on trans-ethnic PRS prediction. As previous studies have shown that the use of epigenetic and functional annotations improves heritability estimation and PRS prediction in a single population (Hu et al., 2017; Lloyd-Jones et al., 2019), an interesting topic of investigation is to incorporate those annotations when constructing trans-ethnic PRS to further boosting prediction accuracy.

Our work is based on a target population of EAS, while there are potential opportunities to extend the strategies explored in this study to other ethnicities. For example, the explicit modeling of genetic difference between EUR and African has potential to improve PRS in African and in African Americans. Although our approach has been effective in a relatively homogenous population like EAS, its application remains challenging in admixed populations with complex LD patterns and demographic history like African Americans or Hispanic/Latinos. Since the genomes of admixed individuals are a mosaic of segments with different ancestral origins, a first step would be to get ancestry specific effect size estimates and P-values from training GWASs, which is often not available from publicly available summary statistics. If individual-level training GWAS data is available, recently developed methods like Tractor (Atkinson et al., 2020) could be applied to obtain ancestry specific summary statistics by generating ancestry dosage at each site from local ancestry inference calls and running a local ancestry-aware regression. Similarly, for the validation data, local ancestry haplotype dosage for each person at each variant need to be estimated and weighted by the ancestry specific effect size estimated in the previous step to allow the generation of “ancestry-specific” PRSs. After that, we can experiment with our strategy of globally upweighting the “more informative” ancestry-level PRS. However, local ancestry estimation in both training and validation sets might introduce bias and the anticipated large sample size discrepancies between EUR and African Americans GWAS studies might further complicate the application. We think this question is worthy of further exploration and we believe that the rapid expansion of genomic resources in admixed populations will be critical to improve PRS predictions. Besides genetic factors (e.g., LD and MAF), environmental factors also influence effect size differences among ancestries. We argue that, for admixed populations, it is critical for PRS to be ancestry-aware, especially for clinical use, since each individual admixed genome has unique local ancestry profiles, and without taking local ancestry into account it is hard to maintain desired sensitivity and specificity due to genetic differences among ancestries.

In summary, we proposed an approach to construct breast cancer PRS in EAS derived from a rescaled meta-analysis of EUR and EAS GWAS. Different from conventional inverse-variance based weighting framework, our approach upweights the EAS component over the EUR component. PRS derived from our rescaled meta-analysis outperforms PRS derived from single population GWAS or conventional meta-analysis. This strategy of integrating GWASs across ethnicities when building PRS prediction models could potentially be extended to other non-EUR populations.

Materials and methods

GWAS training data in samples of European ancestry

Two large, publicly available summary statistics datasets based on European ancestry were used in this study. The data were from the Breast Cancer Association Consortium (BCAC) (details see S1 Table). EUR_2015 (Michailidou et al., 2015) includes two subsets, GWAS (N = 32,498) and COGS (N = 89,677). EUR_2017 (Michailidou et al., 2017) is the largest available GWAS study of breast cancer in European ancestry population. This study consisted of three subsets, GWAS, COGS and OncoArray (N = 106,776).

GWAS training data in samples of Asian ancestry

The GWASs in samples of East Asian ancestry were from the Asian Breast Cancer Consortium (ABCC), which includes 14,958 breast cancer cases and 15,843 controls of Asian ancestry (Cai et al., 2014; Zheng et al., 2009, 2013). Samples were from studies conducted in mainland China, South Korea, Japan, Thailand, Malaysia, Singapore, Canada, U.S., Hong Kong, Taiwan and other countries and regions. Details are in S1 Table. We used the meta-analyzed summary statistics data from the study.

Validation data of East Asian ancestry

The validation set of EAS ancestry is from the Shanghai breast cancer genetic study, including 1794 cases and 2059 controls. Samples were all genotyped on MEGA chip (Illumina), with ~80k custom Asian content selected to improve the coverage of low-frequency SNPs in Asian populations. Data were imputed using the Phase 3 release of the 1000 Genomes Project as reference.

Meta-analysis of EUR and EAS

Let β_EAS,j and V_EAS,j be the expectation and its variance of SNP j in EAS GWAS. The corresponding estimates in EUR are β_EUR,j and V_EUR,j. In conventional meta-analysis, we have

$$\widehat{\beta }=\frac{w_{inv\_EAS,j}{\beta }_{EAS,j}+w_{inv\_EUR,j}{\beta }_{EUR,j}}{w_{inv\_EAS,j}+w_{inv\_EUR,j}}$$

where w_{inv_EAS,j} = 1/V_EAS,j and w_{inv_EUR,j} = 1/V_EUR,j are the inverse-variance weights for EAS and EUR, respectively. As our goal is to obtain weights to construct PRS for EAS, we multiply a scaling factor (denoted as, α > 1) for EAS to the inverse variance weight to obtain a rescaled estimate

$$\widehat{\beta }=\frac{\alpha \ast w_{inv\_EAS,j}{\beta }_{EAS,j}+w_{inv\_EUR,j}{\beta }_{EUR,j}}{\alpha \ast w_{inv\_EAS,j}+w_{inv\_EUR,j}}$$

with variance

$$\widehat{v}={\left(\frac{\alpha \ast w_{inv\_EAS,j}}{\alpha \ast w_{inv\_EAS,j}+w_{inv\_EUR,j}}\right)}^2{V}_{EAS,j}+{\left(\frac{w_{inv\_EUR,j}}{\alpha \ast w_{inv\_EAS,j}+w_{inv\_EUR,j}}\right)}^2{V}_{EUR,j}$$

To select the scaling factor, we tried a grid of α = 1, 2, 3, 4, 5 to derive the resulting summary statistics. Then we selected the scale factor to use along with P-value threshold that achieved a high prediction accuracy by cross-validation in the EAS validation set.

“P+T”

The P+T method refers to the calculation of PRS using informed LD-pruning and P-value thresholding. In this study, we use the implementation of the P+T method in the software package PRSice-2 (Euesden, Lewis, & O’Reilly, 2015) with the default threshold of r² = 0.2 for clumping correlated markers and clumping windows of 250 kb. We examined varying strengths of LD among SNPs by repeating the procedures and changing threshold for clumping correlated markers (r² = 0.1, 0.2, 0.4, 0.6, 0.8) and the sizes of clumping windows (250 kb, 500 kb), and found results to be similar. For any pair of SNPs that have a physical distance smaller than the clumping window or r² greater than the selected threshold, the less significant SNP is removed. PRS is computed by summing risk alleles weighted by effect sizes derived from input summary statistics. The P-value threshold are selected using validation data to optimize prediction accuracy. We constructed PRS for EAS using selected SNPs and effect size estimates $PRS={\sum }_{j=1}^J{w}_{EAS,j}{x}_j$, which w_EAS,j is the weight for the jth SNP.

LDpred

LDpred is a method that uses the GWAS summary statistics and LD information from the external LD reference sample to infer the posterior mean effect size of each SNP, conditioning on the SNP effect estimates of other correlated SNPs. This method assumes a point-normal prior on the distribution of SNP effects such that only a fraction of SNPs have non-zero estimated effects. These fractions of causal SNPs (denoted as f) were used in the validation set: 1 (i.e., all SNPs), 0.3, 0.1, 0.03, 0.01, 0.003, and 0.001, with an LD radius of 400 (i.e., M/3000, M is the number of SNPs, around 1.2 million Hapmap SNPs is included in the current analysis) to obtain local LD information, as suggested by the authors.

Assessment of PRSs

Our analysis used genotypes and phenotypes in independent validation data of East Asian ancestry from training GWAS. We reported area under the ROC curve (AUC) in a logistic regression model using the disease as outcome. When using model with only PRS as the predictor, we report the in-sample fit using all individuals in the validation set. When using models with PRS, age and first 2 genotype PCs, we use the 10-fold cross-validation procedure. To compare AUCs from different training GWAS data, we conducted one-sided Delong’s test for paired AUC curves using “roc.test” implemented in R package pROC.

We also include average Nagelkerke’s pseudo R² liability-scale pseudo R² for the models (Lee, Goddard, Wray, & Visscher, 2012) and the likelihood ratio test P-value. Nested models are considered to provide performance estimates of PRSs: the full model (PRS + covariates including age and first two PCs of genotype) and the reduced model (covariates only). Nagelkelke’s pseudo R² was calculated comparing the full model with the reduced model with the covariates alone, thus yielding an estimate of how well the variable (PRS here) explains the data. R packages “rcompanion” (see Web Resources) was used in the analysis. Since Nagelkelke’s R² suffers from bias when case/control proportion is different, we included liability-scale R² that accounted for an ascertained case/control ratio (Lee et al., 2012).

To assess the relationship of PRS with breast cancer case/control status, individuals in the validation set were binned into 10 deciles according to the PRS, and the percentage of cases within each bin was determined. We calculated odds ratio (OR) comparing top 10% of the individuals with the remaining 90% of the samples as reference group, as well as OR comparing top 10% of individuals with individuals in the 40^th-60^th percentiles.

Supplementary Material

SUP TABLES

S1 Table. Studies contributing to the current analysis (Shu et al., 2020)

S2 Table. Odds ratio (OR) comparing those with high PRS (10%) with the middle (40%-60%) of the population (adjusted for age and first 2 principal components of genotype). We reported ORs of breast cancer for the top 10% PRS relative to 40%-60% of population. Models: EAS: EAS GWAS derived PRS; EUR: EUR GWAS derived PRS; META_FE: conventional fixed-effect meta-analysis; META_2EAS: rescaled meta-analysis that up-weight the EAS summary statistics by a factor of two; META_3EAS: rescaled meta-analysis that up-weight the EAS summary statistics by a factor of three; ADD3: summation of the three best PRS within each LD category. OR: odds ratio; OR (95% CI): 95% confidence internal for OR; P-value: logistic regression association test P-values.

S3 Table. The AUCs of PRSs derived from the EAS/EUR GWASs alone, conventional fixed-effects meta-analysis of both, and rescaled meta-analysis of both using LDpred. PRSs are derived from EAS, EUR GWASs, fixed effect meta-analysis of the EAS and EUR (denoted as META_FE), META_2EAS denotes the rescaled meta-analysis that upweights the EAS effect size estimates by a factor of two; and META_3EAS denotes the rescaled meta-analysis that upweights the EAS effect size estimates by a factor of three. PRSs are evaluated in an independent EAS validation dataset for predicting breast cancer risk. AUC was determined using a logistic regression model adjusted for age and the first two principal components of ancestry. LDpred algorithm was used to derive the scores and the tuning parameter f reflects the proportion of polymorphisms assumed to be causal for the disease.

SUP FIGURES

S1 Fig. The AUC of PRSs derived from rescaled meta-analysis EAS and EUR GWASs in predicting breast cancer risk in EAS samples. The PRSs were computed on a validation sample of EAS ancestry (MEGA Shanghai, see Materials and methods) using summary statistics from 1) conventional fixed-effect meta-analysis (denoted as META_FE), 2) rescaled meta-analysis that up-weights the EAS summary statistics by a factor of two (denoted as META_2EAS), 3) rescaled meta-analysis that up-weights the EAS summary statistics by a factor of three (denoted as META_3EAS), 4) rescaled meta-analysis that up-weights the EAS summary statistics by a factor of four (denoted as META_4EAS) and 5) rescaled meta-analysis that up-weights the EAS summary statistics by a factor of five (denoted as META_5EAS). Each PRS was plotted against (A) P-value threshold and (B) number of SNPs.

S2 Fig. The AUC of PRSs constructed with SNPs in different MAF difference groups. All SNPs were classified into three MAF difference groups (low EAS/high EUR MAF score group with MAF_diff less than its 33% quantile, similar EAS/EUR MAF score group with MAF_diff between its 33% and 67% quantiles, and high EAS/low MAF score group with MAF_diff larger than its 67% quantile). META_FE denotes the conventional fixed-effect meta-analysis; META_2EAS denotes the rescaled meta-analysis that upweights the EAS effect size estimates by a factor of two; and META_3EAS denotes the rescaled meta-analysis that upweights the EAS effect size estimates by a factor of three. Each PRS was plotted against the P-value threshold.

S3 Fig. The AUC of PRSs constructed with SNPs in different MAF and LD difference groups. All SNPs were classified into nine groups by cross-tabulation of three MAF difference groups (low EAS/high EUR MAF score group with MAF_diff less than its 33% quantile, similar EAS/EUR MAF score group with MAF_diff between its 33% and 67% quantiles, and high EAS/low MAF score group with MAF_diff larger than its 67% quantile) and three LD difference groups (low EAS/high EUR LD score group with l_diff less than its 33% quantile, similar EAS/EUR LD score group with l_diff between its 33% and 67% quantiles, and high EAS/low LD score group with l_diff larger than its 67% quantile). META_FE denotes the conventional fixed-effect meta-analysis; META_2EAS denotes the rescaled meta-analysis that upweights the EAS effect size estimates by a factor of two; and META_3EAS denotes the rescaled meta-analysis that upweights the EAS effect size estimates by a factor of three. Each PRS was plotted against the P-value threshold.

Data Availability Statement

Access to the ABCC data could be requested by submission of an inquiry to Dr. Wei Zheng (wei.zheng@vanderbilt.edu). Request of access to the BCAC data could be submitted directly to BCAC (http://bcac.ccge.medschl.cam.ac.uk/).