Reservoir computing with biocompatible organic electrochemical networks for brain-inspired biosignal classification

Biocompatible artificial neural networks allow the monitoring and recognition of malign patterns in biosignals.

Abstract

Early detection of malign patterns in patients’ biological signals can save millions of lives. Despite the steady improvement of artificial intelligence–based techniques, the practical clinical application of these methods is mostly constrained to an offline evaluation of the patients’ data. Previous studies have identified organic electrochemical devices as ideal candidates for biosignal monitoring. However, their use for pattern recognition in real time was never demonstrated. Here, we produce and characterize brain-inspired networks composed of organic electrochemical transistors and use them for time-series predictions and classification tasks using the reservoir computing approach. To show their potential use for biofluid monitoring and biosignal analysis, we classify four classes of arrhythmic heartbeats with an accuracy of 88%. The results of this study introduce a previously unexplored paradigm for biocompatible computational platforms and may enable development of ultralow–power consumption hardware-based artificial neural networks capable of interacting with body fluids and biological tissues.

INTRODUCTION

Artificial intelligence (AI) is quickly progressing and will greatly influence our future life. One particular area where AI is a powerful tool is medicine and health care (1, 2). For instance, AI-based methods have achieved superhuman performance in the recognition of malign patterns present in biometric data and biosignals [e.g., electrocardiograms (ECG) (3) and electroencephalograms (EEG) (4)] or x-ray imaging (5). These results are based on artificial neural networks (ANNs), algorithms that mimic the parallel architecture principles of the brain for recognizing and classifying patterns (6).

However, real-world clinical implementation is so far limited to an “offline” analysis of the patients’ data using software-implemented neural networks. A highly attractive vision is the active monitoring and detection of malign patterns in vivo through computational platforms attachable to or even implantable into the body. The stringent constraints for weight, volume, and heat dissipation limit the use of traditional AI-dedicated hardware in biological systems (7). In addition, the electrolytic environment and the mechanical mismatch with soft biological tissues further hamper their integration.

Recently, much effort has been dedicated to the development of biocompatible organic materials for electronics (8, 9). In particular, organic electrochemical transistors (OECTs) were demonstrated for biosignal detection (10–14) owing to their response to local changes of ion concentrations, as well as their low power consumption and possible biocompatibility. However, their use for active recognition of alteration of biosignal and, more in general, information processing is, to date, lacking. Fundamental advances have been reported in the fields of hardware-based ANNs (15–18). Moreover, in 2020, Yao et al. (19) reported on purely hardware-based convolutional ANNs using memristor devices, and Liu et al. (20) showed efficient neural signal processing using memristor arrays. Although these results demonstrate the huge potential of physical ANNs, their use in biological environments is still challenging. Training each neuron requires a precise control over the individual units of the network. For these reasons, the computational approach of reservoir computing (RC) stands out as a potential brain-inspired framework to produce hardware neural networks and perform on-chip computation (21). Neural networks used for RC consist of a reservoir of randomly ordered nonlinear neurons, whose connections are not subject to training. Natschläger et al. (22) have introduced the liquid state machine as a variant of RC and have shown that the group of disordered, recurrent connected neurons behaves similarly to a cortical column in a biological neural system. Moreover, memory and computation units are inseparable (23), hence circumventing the Von Neumann bottleneck. This concept belongs to the class of computational paradigms known as natural or intrinsic computation (24). Software-implemented RC was proven to be excellent at recognizing harmful EEG or ECG patterns (25) and, since only the output layer of RC networks requires training (linear regression), RC is easier to implement on hardware than traditional neural networks (16, 26–28).

Up to now, the only work on using a combination of OECTs and RC for computation was reported by Pecqueur et al. (29): They showed that an array of traditional OECTs in global gate configurations can be used to distinguish sinusoidal and square waveforms using RC. Their work nicely demonstrates the usefulness of the global gate condition, although the reservoir does not seem to improve the separability of the two classes chosen for the test. Such global connectivity, in which the OECTs are immersed in the same ion-conductive electrolyte, mediates the time-dependent interactions between all the devices and allows mimicking the homeostatic regulation present in cortical systems. This condition, key for our system and hardly achievable with traditional inorganic semiconductor technology, was thoroughly investigated by Gkoupidenis and colleagues: They demonstrated the global control of the weight of the artificial synapses via modulation of the gate voltage and ion concentration (30) and that soft connections between all the devices produce global oscillations reminiscent of the synchronized brain oscillations (31).

In this work, we build nonlinear, dendritic networks of OECTs and use them for information processing on biosignals, demonstrating real-time classification in a biocompatible, hardware neural network. We produce dendritic fibers composed of the organic mixed ionic-electronic conductor poly(3,4-ethylenedioxythiophene) (PEDOT) doped with hexafluorophosphate (PF₆). We use these fibers, similar in nature to OECTs, to produce (semi)random networks as reservoir (Fig. 1A): The networks interact directly with the surrounding electrolytic solution and respond to local ionic displacement by nonlinearly projecting the input electrical signals onto the output layer. The information is stored into ionic state and harvested to perform information processing. The networks are grown via AC electropolymerization (32). Although the growth is intrinsically stochastic, we can control the branching degree and directionality. By using this technique with multiple metal pads, we grow semiconductive dendritic networks with tunable resistance and response time. The inherent coupling of fibers within the reservoir through the electrolyte creates a strong nonlinear transformation of the input signals, ideal for brain-inspired approaches of computation, such as RC. When electrically excited, the networks show strong nonlinearities. We characterize the origin of the nonlinear behavior and find that, to ensure the nonlinear coupling, the network must feature a balance between the connections that bridge the input to the output layer (excitatory fibers) and fibers that branch out of the input layer but terminate before connecting to the output (inhibitory fibers), as shown in Fig. 1B. The former mainly carry the signals, while the latter alter the conductivity of neighboring fibers, therefore being responsible for the nonlinear effects of the networks. Recurrent connectivity, balanced between excitation and inhibition (E/I balance), is a key principle of our hardware similar to the cortical computational system (33). Moreover, the intertwined relationship between the hardware (PEDOT:PF₆ network), the environment (the electrolytic solution), and its time-dependent changes (ion displacement) is reminiscent of the intrinsic computation typical of biological systems.

Fig. 1. Nonlinear behavior of the networks.

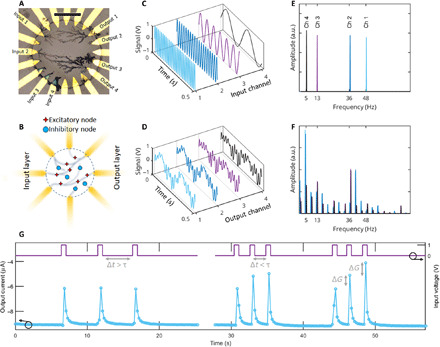
(A) Optical microscope picture of a network, with four input channels and four output channels labeled (scale bar, 100 μm). (B) Sketch of a network with E/I balance with highlighted excitatory and inhibitory nodes. (C) Input signals injected to the four labeled channels and (D) readout of the reservoir states measured at the four output channels. (E) and (F) report the Fourier transforms of (C) and (D), proof that the transfer function of the network is nonlinear: A multitude of new frequencies appear, proving the nonlinear projection performed by the reservoir. (G) Short-term memory featured by the network, key in RC. ΔG is the change in conductance and τ is the response time of the fiber.

Last, the structural complexity of the networks, the large set of input and output neurons, and the E/I balance allow us to go far beyond what was already achieved with RC in combination with OECTs. We test our system on a variety of computational tasks, including time-series prediction and classification. As we envision our system as an implant, each experiment is performed in a phosphate-buffered saline (PBS), an aqueous salt solution with an osmolarity and ion concentrations that match those of the human body. Attempting to classify four different classes of arrhythmic beats from the MIT-BIH dataset (34), we achieve an accuracy of 88%.

Nonlinear projection of the inputs

The networks are produced by AC electropolymerization as described in (32) and Methods: Starting with a 20-electrode circular configuration, we bridge multiple metal pads through semiconductive networks (Fig. 1A). The single-device operational principle of patterned OECTs and our PEDOT:PF₆ fibers is analogous. However, significant differences arise when producing multichannel networks because the random arrangement of the fibers and branches leads to the existence of multiple time constants that mediate each fiber-fiber coupling via the liquid electrolyte (30, 31).

The stochastic mechanism of the growth grants a degree of randomness to the network, as well as the formation of fibers with different resistance and response time to external stimuli. The organic networks can be grown randomly or semirandomly, without the need of following accurate patterns or configurations. It was shown that the device-to-device variability is a requirement that simultaneously grants a richer reservoir as well as a high fault tolerance during the fabrication process (29), which lends well to the fabrication method we use here. This ultimately enables not only a facile and low-cost fabrication process but also complex nonlinear voltage-dependent and frequency-dependent reservoirs, as well as giving the networks high degree of interconnectivity and recurrency, which are desirable features in neuromorphic engineering.

Once the network is produced, time-dependent electrical signals are applied to a set of electrodes (input layer) and injected into the network immersed in PBS. The potential at another set of electrodes (reservoir) is read out. As shown in Fig. 1, the network projects the input signals onto the reservoir nonlinearly by mapping different randomly weighted sums of the input signal through the network’s nonlinearity: When sine waveforms are injected (Fig. 1C), the output signal (Fig. 1D) is a nonlinear superposition of the inputs. To prove this, we analyze the Fourier transform spectra (Fig. 1, E and F) and observe new frequencies arising in the outputs. The nonlinear projection of the input is required for computation because it increases the separability of the classes in the output domain (35). The network in dry ambient is purely resistive and hence linear: Such reservoirs lack any computational power. However, when PBS immerses the networks, the fibers and their mutual interactions give rise to a rich variety of nonlinearities. Figure S1 (A and B) proves that the nonlinear behavior is mediated by the ion drift in solution, which responds to the time-varying local electric field to change the ionic states of the reservoir. At the same time, the electrolyte behaves linearly, as expected at the small fields and low ion concentration that we operate at (fig. S1C). The existence of multiple time constants due to the random branching grants the networks complex dynamics. However, we can break down the processes into three main mechanisms leading to the desired nonlinear trajectories: First, if a potential V_i is applied to an inhibitory fiber and a potential V_e is applied to an excitatory fiber, a classical three-terminal transistor configuration is reproduced. PEDOT:PSS-based OECTs have been thoroughly studied and characterized, and their transfer characteristics can be modeled (36) according to

$$i=\mathrm{\mu }\frac{\mathit{Wt}}{L}C·\{\begin{array}{cc}{V}_e(V_{\mathit{th}}-V_i+\frac{V_e}{2}),& \text{for} V_i-V_e<V_{\mathit{th}}\\ -\frac{1}{2}{(V_{\mathit{th}}-V_i)}^2,& \text{for} V_i-V_e>V_{\mathit{th}}\end{array}$$ (1)

where V_th is threshold voltage, μ is the hole mobility, C is the volumetric capacitance, and W, L, and t are the geometrical width, length, and thickness of the channel, respectively. If the OECT operates close to saturation, the output characteristics become weakly nonlinear. Stronger nonlinearities arise in the sub-threshold regimes. The second effect is a fiber-fiber cross-talk that stems from the interaction between two excitatory fibers: Differently from the previous situation, both fibers are carrying the signal and “gating” each other simultaneously. If V₁ and V₂ are the potentials applied to the two fibers, then the currents I₁ and I₂ can be modeled, assuming two parallel and identical fibers, as

$$I_1=\mathrm{\mu }\frac{\mathit{Wt}}{L}C(2V_{\mathit{th}}-V_2+V_1)\frac{V_1}{2}$$ (2)

and

$$I_2=\mathrm{\mu }\frac{\mathit{Wt}}{L}C(2V_{\mathit{th}}-V_1+V_2)\frac{V_2}{2}$$ (3)

Hence, Eqs. 2 and 3 resemble Eq. 1. The two parallel fibers behave like a transistor that requires higher voltage to reach saturation because of the linear voltage drop across both the channel and the gate. The complete mathematical derivation of Eqs. 2 and 3 is in note S1. Moreover, this is proven in fig. S2, where two parallel fibers are grown and their conductance is measured while both are biased, showing the nonlinear cross-talk between them according to Eqs. 2 and 3 and note S1. This example is key to show that a typical transistor geometry (gate and channel) is not necessary to have a nonlinear projection of the input. Rather, a multitude of fibers can achieve the same results while granting a larger number of readouts.

Last, it is worth noting that even a single fiber features nonlinear output characteristics when immersed in an electrolyte. This is caused by the ionic transport in the bulk solution that occurs in parallel with the electronic transport through the channel. As a consequence, ions accumulate at the electrodes and compensate the PF₆ anions in the semiconductor at the interface. This leads to a voltage dependency of the fiber’s resistance, as proven through electrical impedance spectroscopy in fig. S3. The equations and considerations reported are valid for a steady-state condition and neglect the non-instantaneous ion accumulation at the liquid/fiber interface, producing a marked frequency dependency and further enriching the reservoir’s dynamics. In particular, the time-dependent interaction between fibers translates into a short-term memory effect. Memory is a key feature in RC networks as it ensures that the reservoir state of one time instance not only depends on the current input signal but also is affected by immediate past reservoir states. This effect is proven in Fig. 1G: Here, pulses applied to an inhibitory fiber change the conductance of the neighboring excitatory fiber. If the temporal offset of the pulses is larger than the ionic relaxation time τ, the reservoir will always react toward the same state. On the contrary, a different response is expected if the excitations are repeated with an offset smaller than τ, where a continuous change of the fiber’s conductance is observed. An analogous effect was shown to demonstrate paired pulse facilitation of traditional PEDOT-based devices (37). After proving a sufficient complexity and nonlinearity of the networks and identifying three distinct sources of nonlinearity, we capitalize on the use of this system for information processing.

Reservoir design

Because of the nonconscious design of the reservoirs, and the indistinguishable memory and computing units, RC is usually regarded as a brain-inspired approach. On top of this, our networks mimic another well-established condition present in the brain, i.e., an E/I balance: Although almost any OECT network morphology leads to nonlinear transformation of the inputs, two situations result in linear networks incapable of solving any computational task: (i) if no fiber bridges the input layer with the output (totality of inhibitory fibers) and (ii) if the network is fully interconnected (totality of excitatory fibers). This is similar to the brain, in which efficient and accurate input processing is possible only if a precise balance between inhibitory and excitatory neurons (E/I balance) is maintained, as observed experimentally (38) and theoretically (39).

When applying sinusoidal excitations to a completely inhibitory network, the reservoir relies on the ionic transport. Here, the high resistance and the linear behavior of the electrolyte (fig. S1C) prevent the use of the networks (Fig. 2A). After producing some excitatory fibers (Fig. 2B), a nonlinear mapping is obtained. Last, by growing more and bridging the leftover inhibitory fibers, a completely excitatory network is formed (Fig. 2C): Here, the input is projected onto the output nodes almost linearly because the signal propagates down the fibers, producing minimal ion displacement. An in-depth analysis of the optimal E/I balance for the OECT networks is missing and will be investigated theoretically and experimentally in a separate study. Besides, we can tune the properties of the individual fibers: The ionic transient time, as observed for OECTs, is directly proportional to the resistance of the solution and the channel capacitance (40). The capacitance of the fibers is proportional to their volume, and it is controlled by varying the growing parameters when making the network, according to necessity: For example, highly capacitive (thicker) fibers were found to be suitable for a slow time-series prediction and can be made by electropolymerizing at low frequency. Faster dynamics are needed when trying to sample heartbeats, hence requiring smaller capacitance.

Fig. 2. E/I balance of the network at different stages of the network growth.

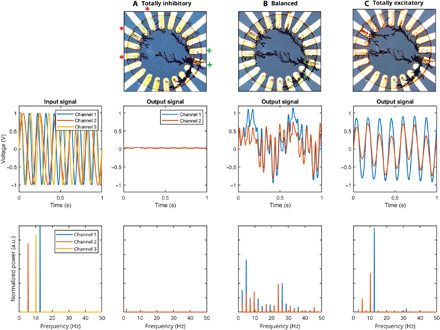
Output signals read out with a network grown to be (A) totally inhibitory, (B) E/I balanced, and (C) totally excitatory. The input channels are marked with a red “*,” and the outputs are read out at the electrodes marked with a green “+.” As proven by the respective Fourier transforms (bottom row), only a balanced network is able to project the input nonlinearly onto the output layer.

RESULTS

The process of collecting inputs, mapping them nonlinearly, and extracting previously unknown knowledge is known as computation or information processing. This is a purely physical phenomenon widely harnessed by means of the electromagnetic laws and Boolean logic in digital computers, but, in principle, applicable to any physical closed system. The machine learning approach we use is a single-node RC. Our networks are particularly suitable for RC because of the random configuration of the fibers, their global connectivity, the nonlinear behavior, and the short-term memory effect. Here, we use PEDOT:PF₆ networks submerged in an electrolytic environment to carry out information processing. The network projects the input signals nonlinearly into a new domain where the linear classification becomes more likely (fig. S5). Eighty percent of the input data are labeled with the target class. This is used to train the network by finding the best linear transformation, which is used to test the remaining 20% of the data. Accuracy A is defined as

$$A(\%)=\frac{\text{Correctly classified entries}}{\text{Total number of entries}}·100$$ (4)

During the testing phase, we use a winner-takes-all approach. Our system can be used in two configurations, shown in fig. S4: a first one, in which the input signals are applied to the metal electrodes, and a second one, where one or more metal lines of the input layers are biased with a DC voltage while the input signal is directly applied to the solution. The former is suited for systems where a multitude of inputs need to be processed simultaneously (e.g., neural and sensory inputs), while the latter can be used to study single inputs that cause large ion displacements, such as muscular or cardiac signals. As a preliminary test, we evaluate vastly different classification tasks to assess the usefulness of the system in a wide variety of applications. First, we perform a classification task using the Iris dataset (41), a classic dataset with four attributes for three species of flowers. By encoding the dataset entry into a DC (see Methods) voltage, we obtain A = 70% (fig. S6A). Since a DC voltage does not make use of the time-dependent interaction between fibers, we encode the dataset entry into a frequency value, and we apply them to the input layer with sine waves of amplitude 1 V. In this way, we achieve 96.7% accuracy (see fig. S6B and Methods). In addition, we use the network for a time-series prediction using stock data (42) with an accuracy of 97% (fig. S6C).

Stimulated by these promising results in classification and time-series prediction, we attempt the classification of biological signals. Given the interaction of the networks with the ions and their biocompatibility, a very attractive application of the PEDOT:PF₆ networks would be in a biological environment for the in vivo detection of malign patterns. Here, we classify heartbeats of four different categories, using the MIT-BIH (34) Arrhythmia Database. The MIT-BIH dataset includes the ECG signals for 48 different subjects, and it is recommended by the American Association of Medical Instrumentation (AAMI) as the heartbeats are classified into four main groups defined by AAMI (details in Methods). The heartbeats are injected into the reservoir with an average rate of 60 heartbeats per minute.

A first experiment led to an accuracy of 80%, which already shows an improvement of 20% with respect to the same classification tasks performed with the input vectors. To improve the accuracy, we implemented an analog feedback loop delay line with a delay time of 260 ms. Using RC in combination with a delay line (Fig. 3A) is a typical method to increase the numbers of nodes. In turn, increasing the dimensionality in ANNs is known to increase the model variance, thus better fitting more complex data. The delay has the practical effect of storing the reservoir state in the long term and creates recurrency in the nodes, a key aspect in artificial and biological neural networks. The delay line works effectively provided that the delay is longer than the response time of the reservoir τ_r (27). For our system, τ_r ≈ 100 ms, limited by the ionic motion. The circuit designed for the delay line is reported in fig. S7. With the use of the delay line, the accuracy significantly increases. Figure 3B shows the results of the classification: A regular heartbeat (class N) is correctly distinguished by an arrhythmic one 91% of the time (9% false positive), while false negatives happen in 13% of the cases. Overall, each class is recognized with a good accuracy, ranging from a minimum of 85% for class F to a maximum of 92% for class A. Overall, an excellent total accuracy of 88% is obtained. See Table 1 for the definition of the classes.

Fig. 3. Heartbeat classification using PEDOT networks.

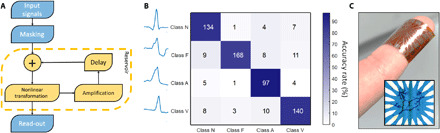
(A) Schematics of the steps used for carrying out information processing with the networks. The use of the delay line is optional. (B) Confusion plot of the measurement performed with the delay line to classify heartbeats: A = 88%. (C) Reservoir patterned and grown onto a conformable substrate of polyimide. In the inset, a magnification of the network grown on polyimide (photo credit: Matteo Cucchi, Technische Universität Dresden). The different surface does not affect the growth or the lithographic process.

Table 1. The classes of the MIT-BIH dataset can be lumped into four main classes according to the AAMI.

Category	Classes
A	Atrial premature beat (A), aberrated atrial premature beat (a), nodal (junctional) premature beat (J), supraventricular premature beat (S)
F	Fusion of ventricular and normal beat (F)
N	Normal beat (N), left and right bundle branch block beats (L,R), atrial escape beat (e), nodal (junctional) escape beat (j)
V	Premature ventricular contraction (V), ventricular escape beat (E)

Above, we demonstrated that PEDOT:PF₆ networks can be used to monitor electrical biological signals. Their use can be extended to the analysis of biofluids. For example, fig. S8 shows the response of a network immersed in blood before and after a meal. Hence, polymer-based reservoirs might be used in the future for real-time monitoring of blood parameters.

We envision this system as a potential implantable computational platform for in vivo detection and classification of biosignals to be used, for instance, in the aftermath of “open” surgeries. In general, PEDOT was demonstrated to be a biocompatible and cytocompatible material (43–45). In addition, the in-liquid operation of the networks creates an intrinsic affinity between the computing reservoir and the biological environment, and the high capacitance of the fibers ensures their response to small ionic displacement. Moreover, the higher temperature is expected to speed up the network’s response because of the larger diffusivity of the ions. However, a number of challenges must be overcome to this end. In our work, while the projection in the linearly separable space is carried out by the reservoir, the linear regression is calculated afterward on software. It is, however, possible to combine the linear regression with the reservoir to have a fully integrated circuit and achieve classification on hardware. This can be achieved by using a crossbar array of adjustable memristive devices capable of solving matrix multiplication through Ohm’s law. Examples are abundant [see, for example, (39, 46, 47)]; electrochemical nonvolatile organic devices are PEDOT-based devices that could be used in combination with our PEDOT networks (37) for the linear regression.

Another key aspect for implantable electronics is the conformable nature of the substrate as well as its weight, realizable by patterning the network on a polymeric conformable substrate: We achieve this by producing reservoirs on a flexible polyimide substrate as shown in Fig. 3C. Last, we must ensure a low power consumption of the networks to prevent the tissue from overheating and to allow the implant to be supplied by small and light-wave thin-film batteries: The power consumption of the networks is approximately 200 nW per output channel used; for comparison, the power consumption of electronic RC systems [e.g., (28)] often exceeds 1 W, and other implantable systems, such as modern pacemakers, consume around 30 μW. Although including more output channels increases the power consumption, it leads to improved classification results because of the higher dimensional domain of the output layer. Ultimately, the geometrical size of the networks needs to be designed to have the optimal solution: Increasing the size could limit the cross-talk between two fibers lying far apart. On the other hand, miniaturizing the system will increase the speed of the system, allowing for the computation of faster signals (currently limited at around 200 Hz), e.g., for speech recognition. However, miniaturization can introduce redundant output signals coming from the high-density integration of the output pads: Two neighboring output electrodes might provide an almost equivalent signal, hence a redundant information that does not improve the separation. As a final note, a collection of reservoirs, connected in series or parallel, may improve the classification accuracy rate and potentially lead to hierarchically organized RC.

DISCUSSION

In this work, we produced biocompatible hardware-based ANNs based on OECTs, which we use for computation and classification tasks using the RC approach. The dendritic, semirandom configuration of the networks immersed in aqueous electrolyte produces a reservoir that shows a rich variety of responses to time-dependent electrical excitations. The ionic states of the reservoir are harvested and used for information processing in the framework of RC. We demonstrated that the organic networks are particularly suitable for such purpose owing to complex nonlinear dynamics, which we characterize in detail, and features typical of biological cortical systems (e.g., recurrency, short-term memory, and E/I balance). Since these devices operate in an electrolytic environment and PEDOT is a biocompatible material, we envision the networks as lightweight, noninvasive implants, capable of monitoring biosignals, and perform “online” computation without the aid of energy-consuming software. We prove the usefulness of the organic networks on a diverse set of computational tasks such as a flower classification using the Iris dataset (accuracy of 96%), time-series prediction (97%), and biofluids monitoring. Owing to these excellent results, we attempt a classification of arrhythmic heartbeats: We achieve an accuracy of 88%.

METHODS

Glass and polyimide substrates were prepared by evaporating 3 nm of Cr and 50 nm of Au, followed by lithographic patterning using the positive resist AZ 1518 (microchemicals), standard etchant gold, and chromium. Last, an insulation layer (negative photoresist SU8) was spin-coated and patterned. The networks were grown starting from a 20-electrode configuration by means of AC electropolymerization: The central area is immersed in a precursor solution containing the monomer EDOT, as in (32). We used tetrabutylammonium hexafluorophosphate (TBAPF₆) as electrolyte. TBAPF₆ features a large electrochemical window and grants conductive properties to the resulting polymer, similarly to the commonly used PSS. As long as the fibers can be electrochemically doped and dedoped, the choice of the dopant is not crucial. Note that the electrolytic solution used for the network fabrication is different from the one used for the measurements throughout this work, which is PBS, an aqueous salt solution with an osmolarity and ion concentrations that match those of the human body.

A sine or square wave signal of amplitude 2 V and arbitrary frequency is applied between two (or more) electrodes. As a result, dendritic fibers grow following the lines of the electric field. For the computational tasks, dataset entries were preprocessed (see below) and used as inputs for the reservoir. Simultaneously, the output signals (across a load resistor of 100 kilohms) were read out using an analog data acquisition system (Measurement computing USB-1208HS-4AO). Eighty percent of the output data are used for the training: The data are arranged in a matrix X and the linear regression consists of finding the matrix Y such that

$$X*Y=T$$ (5)

where T is the target matrix composed of the known outputs. The remaining 20% of the data are multiplied by Y and, by using a winner-takes-all approach, the resulting class is determined.

Iris dataset entries were normalized to have zero mean. Afterward, the entries were encoded into frequency, using a sine wave of amplitude 1 V. For the heartbeat classification, individual heartbeats have been extracted from the MIT-BIH dataset, the most used database for this kind of classification. They were then divided into the four main categories of arrhythmia specified by the AAMI, as shown in Table 1. Last, the data were resampled, normalized to have zero baseline and 1 V peak, and fed into the network with a pace of 60 heartbeats per minute. A total of 3000 heartbeats (750 per class) were randomly selected from the dataset and used for the classification task.

The delayed-feedback line used for the heartbeat classification consisted of three main blocks: (i) a nonlinear element, (ii) a low-pass filter, and (iii) a delay unit. The nonlinear element is, as described above, the OECT-based network. One output fiber of the network is then connected to a transimpedance amplifier to convert the current output to a voltage and to provide gain. This is afterward passed through a first-order low-pass filter implemented via an RC network, whose output is then fed to the delay line. The delay line itself is implemented fully analog, as an eight-stage LC-ladder network. Additional amplifiers and buffers complete the circuit to isolate the different stages (fig. S7). The characterization of the short-term memory and of the crosstalk between two parallel fibers were carried out with two SMUs Keithley 2600 interfaced to a computer using the software SweepMe! (www.sweep-me.net).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/34/eabh0693/DC1