Guanidine-II aptamer conformations and ligand binding modes through the lens of molecular simulation

Abstract

Regulation of gene expression via riboswitches is a widespread mechanism in bacteria. Here, we investigate ligand binding of a member of the guanidine sensing riboswitch family, the guanidine-II riboswitch (Gd-II). It consists of two stem–loops forming a dimer upon ligand binding. Using extensive molecular dynamics simulations we have identified conformational states corresponding to ligand-bound and unbound states in a monomeric stem–loop of Gd-II and studied the selectivity of this binding. To characterize these states and ligand-dependent conformational changes we applied a combination of dimensionality reduction, clustering, and feature selection methods. In absence of a ligand, the shape of the binding pocket alternates between the conformation observed in presence of guanidinium and a collapsed conformation, which is associated with a deformation of the dimerization interface. Furthermore, the structural features responsible for the ability to discriminate against closely related analogs of guanidine are resolved. Based on these insights, we propose a mechanism that couples ligand binding to aptamer dimerization in the Gd-II system, demonstrating the value of computational methods in the field of nucleic acids research.

INTRODUCTION

Riboswitches reside in the 5′-UTRs of bacterial mRNAs and regulate gene expression upon interaction with small molecular ligands (1). Ligand binding to the aptamer domain triggers changes in the so-called expression platform, that then modulates translation initiation or transcription termination. Riboswitches are often characterized by relatively short sequences that do not require the presence of regulatory proteins, thus offering a promising general strategy for gene expression control in industrial, scientific, and future medical applications. Although the general principles are relatively well understood, mechanistic details of how ligand binding to the riboswitch exerts control on gene expression is often hard to address due to the inherent flexibility and complex dynamics of these structured RNAs.

Here, we investigate the guanidine-II riboswitch (Gd-II) that selectively recognizes guanidinium cations (Figure 1). So far, three other guanidine-sensing riboswitches (Gd-I, Gd-III and Gd-IV) are known. After first being predicted by computational screening methods in the early 2000s (2–4), guanidinium was only recently identified as the true ligand of these riboswitches (5–7). Subsequently, crystal structures of all three classes have been reported (8–12). Recently a fourth guanidinium riboswitch class was identified (13). All Gd-riboswitches induce the expression of genes that enable the export or degradation of guanidine in response to increased levels of guanidine inside the cell (5). The surprising finding that many bacteria encode guanidine-responsive riboswitches is intriguing, since so far no physiological role of guanidine is known. However, the discovery of wide-spread guanidine-responsive regulation is remarkable and indicates the existence of a so far unrecognized guanidine metabolism present in many bacteria (14).

Figure 1.

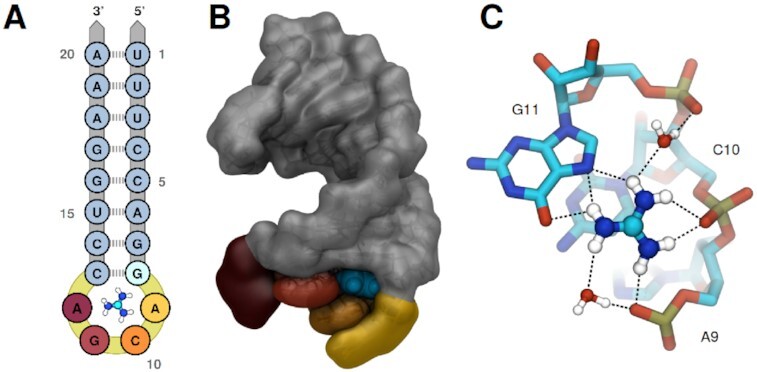
The hairpin motif of the Gd-II aptamer. (A) Sequence and secondary structure. The highly conserved residues A9, C10, G11 and A12, which form the binding pocket and dimerization interface are colored gold, orange, red and dark red, respectively. The guanidinium ligand is sketched inside the binding pocket, with carbon, nitrogen and hydrogen atoms colored cyan, blue and white, respectively. (B) The aptamer as extracted from the 5NDI crystal structure. From the spatial orientation of the aptamer shown here all future reference to the front, back, top or down part of the stem–loop is derived. Coloring follows A, guanidinium is represented in cyan. (C) Close-up view of guanidinium inside the binding pocket. Carbon, nitrogen, oxygen, phosphor and hydrogen atoms are colored in cyan, blue, red, gold and white, respectively. Prospective hydrogen-bonds are indicated by dashed lines.

The structure of the Gd-II riboswitch in presence of guanidinium, as resolved by X-ray crystallography, consists of two stem–loops (see Figure 1B) connected by a linker of variable length (7–40 nucleotides, not shown) (6,15). Each of the stem–loops incorporates a single ligand in a highly conserved ACGA loop, thus acting as the aptameric part of the riboswitch. The two stem–loops dimerize via an interface formed by the ACGA residues and a CG base-pair. This structural arrangement explains the experimentally observed positive cooperative effect of ligand binding to the hairpin–linker–hairpin sequence. If guanidinium is present, the chance of two connected aptamers to rearrange into the ligand bound, dimeric state are high due to their spatial proximity. This dimerization probability is decreased for unconnected stem–loops, where ligand binding is observed only at relatively high guanidinium concentrations (6).

In each of the two stem–loops, guanidinium is tightly bound inside a binding cavity via a combination of ionic interactions and the formation of a coplanar hydrogen-bond network between five of the six amine hydrogens of guanidinium and the surrounding A9–C10–G11 residues (see Figure 1C). The remaining amine hydrogen is exposed towards a small opening, facing towards the pocket entrance of the second aptamer in the dimer state. This opening allows for the recognition of guanidine analogs carrying small modifications at one nitrogen, such as methylguanidine, aminoguanidine and 1-ethylguanidine with only slightly reduced binding affinities (6). Analogs with bulkier modifications, in particular arginine and its precursors, are discriminated against, most likely due to steric clashes. The adjacent pocket entrances and the insensitivity towards single-site modifications was recently exploited for the design of an artificial, high-affinity ligand for the Gd-II aptamer. By linking two guanidine groups with an aliphatic linker spanning the ∼6 Å gap, the binding affinity could be increased 10-fold compared to guanidinium (16).

While sterical effects explain the ability of the Gd-II aptamer to discriminate against bulky guanidinium analogs inside the cell, it is not known how the riboswitch is able to favor guanidinium over urea and selectively bind the former even in the presence of high concentrations of urea, as shown by experiment (6). Despite the structural similarity the two molecules differ in important aspects: First, the substitution of an amine group by an oxygen results in two hydrogen donors being exchanged by a hydrogen-acceptor. Second, urea is uncharged, while guanidinium is positively charged, the charge being delocalised over the whole molecule (17).

The questions which interactions govern the ligand binding to the Gd-II aptamer, how this is intertwined with dimerization of the two hairpins, and which factors lead to the ability to discriminate between guanidinium and urea call for an investigation by molecular simulations.

Molecular dynamics (MD) simulations are an invaluable tool to study the structure and dynamics of biomolecules on a molecular level. In recent years, the simulation models (force fields) for nucleic acid systems have seen many new developments regarding the crucial treatment of base stacking, base pairing and ionic interactions, including extensive reparametrizations against experimental data (18–22). In this work, we have used MD simulations and mathematical analysis methods to identify conformational states of the Gd-II binding pocket and to characterize ligand-bound and ligand-unbound states. We can investigate the interplay between the presence/absence of different ligands and conformational transitions in a single Gd-II aptamer which affect the stability of the dimerization interface. Moreover we can provide a structural basis for the discrimination between guanidinium and urea as ligands.

MATERIALS AND METHODS

System and simulation details

Starting structures for the Gd-II aptamer were generated using chain A of the 5NDI crystal structure (8). For simulations without ligand, guanidinium was removed from the binding pocket. To investigate how the Gd-II aptamer is able to efficiently discriminate against urea, which is very similar to guanidinium from a structural point of view, we set up simulations where guanidinium was exchanged with urea in different orientations inside the binding pocket. Replacing one of the amine groups by oxygen yielded three starting structures, with different orientations of the urea oxygen inside the binding pocket. From each starting structure (no ligand, with guanidinium, with urea in three orientations), three independent classical MD simulations were prepared following a standardized equilibration protocol (Supplementary Table S1). Production simulations were run for 2 μs each (30 μs in total). If not noted otherwise, analysis was performed on snapshots every 10 ps for all trajectories resulting in a dataset of 3× 10⁶ structures.

For all simulations, the GROMACS 2018.1 software package (23) was used in combination with an AMBER based force field from here on denoted as DESRES. The DESRES force field was specifically designed for nucleic acid simulations and published by the D.E. Shaw research group (18). It was employed as implemented by Giovanni Bussi, Stefano Piana and Sandro Bottaro at https://github.com/srnas/ff/tree/desres in combination with TIP4PD, a reparametrized version of the TIP4P water model (24). Guanidinium parameters were implemented as published by Wernesson et al. (17). For comparison, we carried out additional simulations with the AMBER ff14SB force field as implemented in the Amber 14 package (25,26), in combination with the TIP3P water model (27). Moreover, additional simulations with a guanidinium parameter set derived from the arginine group of the DESRES force field were carried out (for details see SI). All data shown in the main manuscript were obtained with the DESRES force field and the guanidium parameters by Wernesson et al. (17), the additional data with ff14SB are shown in the SI and referred to from the respective parts of the results section.

The electrostatic interaction were calculated by using the particle mesh Ewald method (PME) (28,29), with a real space and van der Waals cutoff distance of both 1 nm. All MD simulations were performed using an integration timestep of 2 fs in the NPT ensemble at 300 K and 1 bar. The velocity-rescale algorithm (30) was used for temperature coupling and the Parrinello-Rahman algorithm (31) with a damping constant of 2.0 ps for pressure coupling.

Analysis workflow for aptamer conformations

For the analysis of the large, high-dimensional data sets from the MD simulations of the aptamer-ligand systems we have established the following workflow (also sketched in Supplementary Figure S1): First, we have identified a set of internal distances, so-called collective variables (CVs), which is well suited to describe the important conformational changes of the binding pocket. This, still quite high dimensional, CV space was further reduced with principal component analysis (PCA) (32,33) in order to identify the most important states and features. This can be understood as projecting the high-dimensional conformation space of the aptamer into a two-dimensional plane, where the different aptamer structures are separated according to their structural variance. In the so obtained 2D conformational landscape, we have identified the characteristic states with a clustering algorithm, extracted representative structures and determined relevant features for each of the studied systems.

Collective variable selection

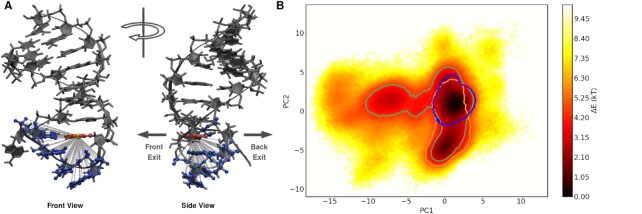
To reduce the amount of data while retaining the relevant information that is necessary to describe and monitor the motion of the binding pocket, a set of internal collective variables (CVs) was selected (34–36). As CVs we have chosen the 85 internal distances between the heavy atoms of residues A9, C10, G11 and C13 to the center of mass (COM) of the non-hydrogen atoms of nucleobase G8 (see Figure 2). This reference position was chosen since nucleobase G8 is close to the binding pocket and we found that the G8–C13 base pair remains rigid and structurally stable throughout all simulations (see Supplementary Figure S2). To demonstrate that these 85 internal distances are able to capture the behaviour of the binding pocket, a larger set of CVs consisting of the 1955 pairwise distances between all non-hydrogen atoms of the residues surrounding the binding pocket and all non-hydrogen atoms of residue G8 was analysed (Supplementary Figure S3). Comparison of the results obtained with the two CV sets shows that the COM of nucleobase G8 suffices as a reference point. The orientation of the different edges of the central G8 remain fixed throughout the simulations. Supplementary Figure S2B, C also shows that the adjacent residues in the stem loop remain paired and structurally stable, corroborating the decision to omit all residues not in close proximity to the binding pocket from the employed CV set.

Figure 2.

(A) Front and side view of Gb-II riboswitch with 85 selected internal distances (dashed lines) used as CVs for dimensionality reduction with PCA. These include all distances between the non-hydrogen atoms of residues A9, C10, G11 and C13 (blue) to the center of mass (gold) of the nucleobase atoms of residue G8 (red). Atoms of the aptamer not used for CV selection are represented in dark grey. Arrows indicate the direction of a possible front and back exit out of the binding pocket. (B) Projection of the structures from MD simulations of all systems onto the first two PCs; displayed as estimate of the free-energy difference (ΔE = −ln ρ, where ρ is a probability density). Contour lines: regions visited by simulations with guanidinium (blue), urea (green) and without ligand (gold). Contour lines were drawn with a ΔE = 6 kT to the deepest minimum of the respective separate projection of each system.

Dimensionality reduction with PCA

To distinguish the dominant conformational states of the binding pocket, the 85-dimensional CV space was projected to two dimensions by PCA. This method, given a high-dimensional data set with many correlated input variables, identifies a smaller and linearly uncorrelated subset containing most of the variability of the original data. Projection of the input data onto the first few principal components usually retains most information about the studied system. For PCA the PyEMMA package version 2.5.4 (17) was used. The instantaneous correlation matrix between input CVs and PCs was calculated as implemented in the feature_PC_correlation tool in PyEMMA.

Clustering with HDBSCAN

After obtaining the two-dimensional projection of the internal distances describing the binding pocket, we identified conformationally homogeneous states with the help of density based clustering – using the hierarchical density-based spatial clustering of applications with noise (HDBSCAN) algorithm (37). This clustering algorithm is able to identify clusters of varying density and shape while requiring few input parameters (and being quite robust to their selection). First, a dendrogram based on the population density of the input feature space is constructed. Subsequently, the trees of the dendrogram are cut at different heights, scoring the degree of membership of each structure to the corresponding cluster. Structures that do not fall into any of the identified clusters are considered noise. The prime parameter HDBSCAN requires is a minimum cluster size (here set to 5× 10⁴ structures). Clusters populated by fewer structures are not considered. The minimum number of clusters to expect was set to two. We used the HDBSCAN python implementation (version 0.8.19) (37).

While HDBSCAN allows for efficient clustering of the input data, it does not provide cluster centers (centroids) by design. To retrieve reference structures for each cluster, the conformation closest to the geometric center was chosen (with the additional condition that the reference structures should originate from the simulations most dominant in the cluster, e.g. the reference structure for the bound-like state should stem from a simulation with a guanidinium ligand present). Since this process of choosing a reference structure for a cluster is by no means unambiguous, we have compared the result to two alternative procedures based on root mean square deviations (RMSD) (38) in Cartesian space and based on the internal distance CVs (see SI). The resulting cluster representatives were found to be very similar as demonstrated in Supplementary Figure S4.

Metadynamics

Metadynamics simulations (39) were run using the PLUMED package (40,41). In metadynamics, Gaussian potentials are added onto a set of predefined CVs for configurations already visited, thereby efficiently guiding the studied system to regions of conformational space not visited before. As a biasing collective variable we chose the distance between the ligand carbon atom and the reference center of mass as previously defined for the CV selection. Gaussians with a height of 0.2 nm and a sigma of 0.1 nm were deposited every picosecond. Simulations were stopped as soon as the distance between the respective ligand and the reference COM was larger than 2 nm, which corresponds to conformations where the ligand is definitely outside of the binding pocket. 50 independent metadynamics simulations were started for each of the three urea systems, and 150 simulations for the guanidinium system.

RESULTS

A two-dimensional map of aptamer conformations

To identify and characterize the conformational states of the Gd-II aptamer, the structures from the 30 μs classical MD simulations were projected into a two-dimensional conformational landscape obtained from PCA analysis of the 85 internal distances describing the ligand binding pocket (Figure 2). The PCA projection exhibits three clearly distinguishable basins, corresponding to three distinct conformational states, which are connected by broad and shallow transition regions. To identify the areas in PCA space which are visited by the different simulated systems, structures in PCA space were traced back to the corresponding simulations. In Figure 2B contour lines indicate the regions accessible to simulations with guanidinium (blue), urea (green) or without ligand (gold). Separate projections of the three systems are shown in Supplementary Figure S5. While simulations with guanidinium exclusively populate the most dominant basin, simulations without ligand overlap in part with the guanidinium simulations, but also visit the second largest basin. Simulations with urea are not restricted to any specific area of the PCA landscape. Apart from the two dominant basins mentioned before, they also populate the third basin and less dense regions not visited by the other two systems

We found that the first two PCs account for 64.7% of the conformational variance of the binding pocket, which indicates that two dimensions are well suited to characterize the system. Analysis of the correlation between the input CVs and the first two PCs can be used to identify which internal distances are responsible for the separation of the three identified states described above (Figure 3A, B). The first PC separates the two deep basins from the more shallow basin populated solely by structures with a urea ligand. The internal distances that are most highly correlated to PC1 are the ones between the nucleobase atoms of residue A9 and the reference point in nucleobase G8 as well as the the ones between the phosphate atoms of residue C10 to the reference point (Figure 3A, C). PC2 separates the two deep basins, and is sensitive to the position of nucleobase and phosphate atoms of residue G11, as well as sugar atoms of residue C10 (Figure 3B, C). By projecting the input data onto the two most highly correlated distances (indicated by cyan and golden triangles in Figure 3A, B), the three previously identified states states are also obtained, and the overall distribution of conformations mirrors the PCA landscape (Supplementary Figure S6). This corroborates that these distances are good representatives to distinguish the conformational states of the binding pocket. Note that the two distances are not unique in that they are well suited to describe the conformational states of the binding pocket. Internal distances to neighboring atoms could have been chosen just as well (as can nicely be seen from their high correlations to PC1 and PC2 in Figure 3A, B). To obtain an uncorrelated measure of feature importance for the CVs a more sophisticated analysis would be needed. This is not necessary for the present system, where due to the rigid nature of the nucleobases and the sugar-rings a high degree of correlation is to be expected and does not hamper the further analysis.

Figure 3.

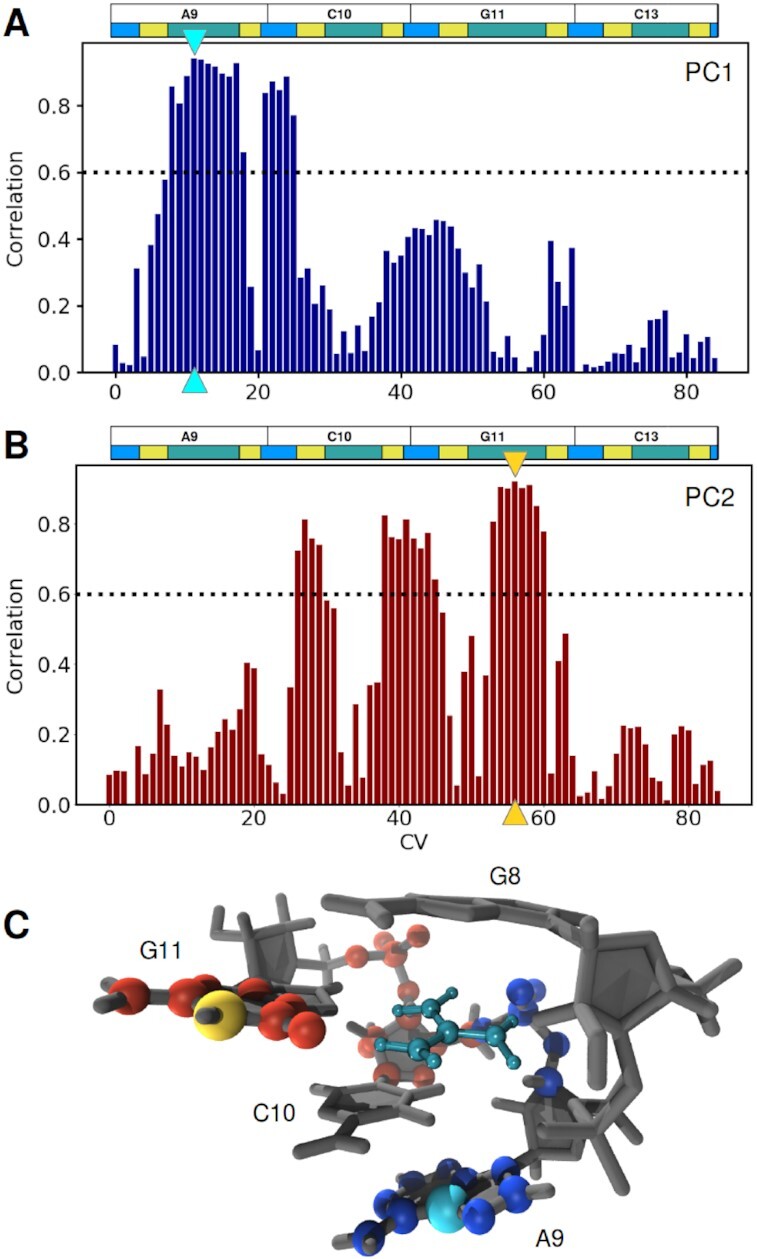
(A, B) Correlation between input CVs and the first and second PCs. The CVs with the highest correlation for each PC are marked by cyan and golden triangles for PC1 and PC2, respectively. The black dotted line indicates a correlation threshold of 0.6, above which a CV was regarded as relevant for the corresponding PC. Colored horizontal boxes illustrate RNA sequence behind the distances each CV stands for; green, yellow and blue correspond to distances involving nucleobase, sugar and phosphate atoms, respectively. (C) Structural representation of atoms corresponding to the internal distances considered highly relevant for PC1 (blue and cyan) and PC2 (red and gold), as described in A. The distances which have the highest correlation to PC1 and PC2, atom C5 of residue A9 to the reference COM and atom N1 of residue G11 the reference COM, are highlighted in cyan and gold, respectively (in line with the triangles highlighting the corresponding CVs in A).

Identification of conformational states

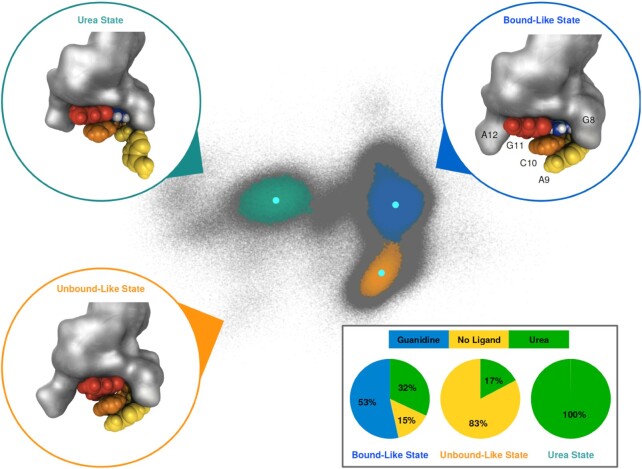
Clustering of the PCA landscape using the HDBSCAN algorithm yielded three distinct clusters (Figure 4) which correspond to the three basins identified before. These three clusters encompass 75.6% of the simulation structures, the remaining 24.4% of the structures (gray points) were not further assigned to clusters. Composition analysis revealed characteristic shares of the simulated systems for each cluster (Figure 4, inset). The smallest cluster (colored in green, 162357 structures, 5.4% of all data points) consists of structures almost exclusively originating from simulations with urea. The midsize cluster (colored in orange, 440201 structures, 14.7% of all data points) contains structures predominantly from simulations without ligand, and a smaller share from simulations with urea. The largest cluster (colored in blue, 1 663 972 structures, 55.5% of all data points) consists of structures originating from all three systems, about half from guanidinium simulations and smaller shares from urea and ligand free simulations. Please note that the number of structures originating from urea simulations is three times higher than that from the other two systems, due to the variation in the initial urea orientation (see Materials and Methods section). To check for the existence of sub-clusters hidden in the combined PCA projections, individual HDBSCAN clustering was carried out on the separate PCA projections of the three systems. This analysis yielded essentially the same clusters as the joint clustering of the complete structure pool (Supplementary Figure S5).

Figure 4.

Identification of conformational states using the HDBSCAN clustering algorithm on the PCA projection of internal distance data of the three studied systems. Structures in the PCA landscape belonging to the three identified clusters are colored blue (‘bound-like state’), orange (‘unbound-like state’) and green (‘urea state’). Structures not assigned to any of the clusters are depicted in gray and considered noise. Representative structures for each cluster are shown in circles colored according to the corresponding cluster. Residues A9, C10 and G11 are colored yellow, orange and red, respectively. Other nucleic residues are depicted in grey surface representation, guanidinium and urea in according to the coloring scheme introduced in Figure 1C. The location of the reference structures in PCA space is shown with cyan spots inside each corresponding cluster. Pie charts highlighting the composition of the three systems for each of the three states are shown in the lower right panel.

The unassigned (gray) data points originate predominantly from urea simulations (68.6%) and to a smaller fraction from ligand-free (23.9%) and guanidinium simulations (7.5%). The ratio urea/ligand-free reflects that there are three times as many urea data points. By comparison, the small guanidinium fraction points towards a more compact and structurally uniform cluster.

Given the clear pattern of which conformational states of the aptamer binding pocket are visited by which of the systems, the states will from here on be referred to as ‘bound-like state’, ‘unbound-like state’ and ‘urea state’. However, it is important to realize that the denotation of these states is slightly deceptive, e.g. structures in the bound-like state do not necessarily have a ligand bound inside the binding pocket. In other words, while simulations without ligand are predominantly found in the unbound-like state, they also populate the bound-like state to a smaller extent. Urea simulations repeatedly visit all three states, with the urea state exclusively populated by structures from these simulations. The guanidinium simulations are restricted to the bound-like state, with few data points in the surrounding gray area, i.e. this system appears to be structurally the most uniform.

Characterization of conformational states

Figure 4 shows structures that are representative of the three states (for details, see Materials and Methods). A comparison of these three representative conformations is in line with the correlation analysis between the internal distances and the PCs. The bound-like and unbound-like state show significant difference in the position of nucleobase G11 (colored in red), while the defining feature of the urea state is the position of residue A9 and the connected backbone atoms (colored in yellow). Note that up to this point, the characterization of the aptamer conformations has been entirely derived from internal distances of the binding pocket, i.e. the presence or absence of a ligand has not been explicitly taken into account. In the following we will describe the three states in more details and also investigate the relationship between aptamer conformation and the presence of guanidinium or urea as well as the potential impact of solvent molecules in proximity to the binding pocket.

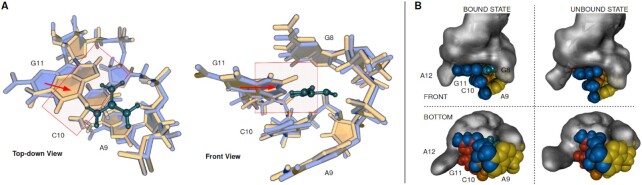
In the bound-like state, residues G8, A9, C10 and G11 form a cavity which allows for incorporation of a guanidinium-shaped ligand (Figure 5A). This conformation is in a good agreement with the 5NDI crystal structure of the Gd-II dimer with guanidinium (see Supplementary Figure S7A). In particular the atom positions of residues A9, C10 and G11 in the bound-like state, which are involved in the dimerization interface, match the ones in the experimental structure. We further confirmed this structural similarity by projecting all structurally distinct chains of the crystal structures 5NDI and 5VJ9 (Gd-II dimer, guanidinium bound)) into the PCA space (Supplementary Figure S8C), finding that all conformations fall into the region of the bound-like state.

Figure 5.

Structural analysis of the reference conformations of the bound- and unbound-like state. (A) Overlay of the two structures in top-down (left) and front side (right) view. Coloring according to the clusters of origin, blue for the bound-like state and gold for the unbound-like state. The guanidinium ligand is part of the bound-like structure, and shown in dark cyan. The direction of the largest conformational change between the two structures, the collapse of nucleobase G11 into the binding pocket, is indicated with red arrows. Red boxes sketch the volume where the structure from the unbound-like state collides with the guanidinium ligand from the bound-like structure. (B) Shape of the dimerization interface in the bound-like (left side) and unbound-like (right side) state. Atoms involved in both, ligand binding and dimerization are depicted in blue, atoms from residues A8, C10 and G11 in yellow, orange and red, respectively. Other RNA atoms are drawn in gray molecular surface representation. The upper half and lower half show the conformations in front and bottom-up view, respectively.

In the unbound-like state, the nucleobase of residue G11 is collapsed into the interior of the binding pocket (Figure 5A). Superposition with the bound-like state illustrates that nucleobase G11 in the unbound-like state collides with the position that would be occupied by the ligand. A second, important consequence of the collapse of this nucleobase into the binding cavity is a deformation of the dimerization interface as illustrated in Figure 5B and Supplementary Figure S7B which shows a superposition of the representative of the unbound-like state with the crystal structure.

The most dominant conformational feature defining the urea state is a shift of nucleobase A9 away from the pocket, thus twisting the connected backbone into a position distinct from the other two states (Figure 4). Otherwise, the reference structure of the urea states resembles the conformation of the ligand-bound state. Monitoring the orientation of the urea oxygen inside the binding pocket revealed that the urea state is predominantly populated by conformations, where the oxygen is positioned inside the binding pocket (Supplementary Figure S9). Conformations where the oxygen is solvent exposed towards the front side of the binding pocket are projected into the bound-like state.

Ligand influence on aptamer conformation

Guanidinium simulations

The binding pocket conformation in all simulations with guanidinium bound to the aptamer stays close to the starting structure for the entire length of the simulations (2 μs each). The guanidinium cation remains tightly bound inside the pocket. Examination of the distance previously identified as most sensible for discriminating between the unbound-like and bound-like state shows a short-lived conformational change in the first 30 ns in one of the three simulations (Supplementary Figure S10A, orange). Apart from that, the binding pocket exhibits no indication of larger conformational changes.

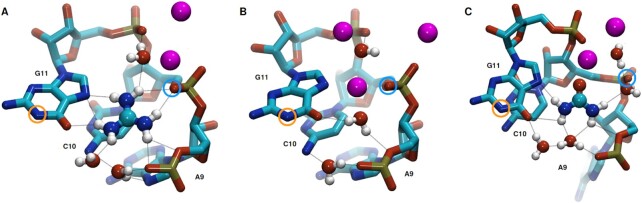
Guanidinium bound inside the pocket is typically solvent exposed in two directions as illustrated in Figure 6A. Two water molecules are located at the front side of the binding pocket. One molecule is forming hydrogen-bonds to residues A9 and C10, the other water molecule is coordinated to the one amine group of guanidinium that is not directly hydrogen bonding to the aptamer. At the back of the binding pocket, a water molecule is coordinated to a phosphate oxygen of residue G11 and an amine group of guanidinium. A sodium ion is coordinated between this water molecule and the C10-phosphate oxygen atoms. Finally, a second sodium ion is located at the rear side of the aptamer, further neutralizing the negative charge density of the phosphate backbone. The coordination of multiple sodium ions to the back of the binding pocket is persistent over time, as shown by the number of sodium ions in close proximity to the O2P atom of residue C10 (Supplementary Figure S10A, upper panel). However, the ions are not fixed in this position, but are replaced on a regular basis (Supplementary Figure S10A, middle and lower panels). While solvent contacts via the front entrance of the aptamer could already be predicted from analysis of the X-ray structure, solvent contacts through the ‘back-side’ of the pocket were not expected due to the position of the G11-phosphate atoms. In the crystal structure, the phosphate group of residue C10 is located slightly closer to the pocket core, shielding the entire rear side of the binding cavity (Supplementary Figure S7A).

Figure 6.

Binding pocket of the reference structures for (A) bound-like, (B) unbound-like and (C) urea states. Coloring follows the scheme introduced in Figure 1C, nucleic hydrogens are not shown to improve clarity. Sodium atoms are depicted in pink, water molecules in red (oxygen) and white (hydrogen). Prospective hydrogen-bonds are drawn as black dotted lines. Orange and blue circles highlight atom N1 of residue G11 and atom O2P of residue C10, respectively.

Simulations without ligand

The starting conformation for these simulations was derived from the ligand-bound crystal structure, i.e. resembles the bound-like state. In all simulations a first collapse of this structure into the more compact ligand-unbound state occurred already during equilibration. This initial conformational change is followed by multiple transitions between the bound-like and unbound-like state, as can be seen for example by monitoring the distance from atom N1 of residue G11 to the reference COM (orange line in (Supplementary Figure S10B). This agrees well with the distribution of structures for this system in PCA space, where both states are populated (see Figure 2), and analysis of the relative fluctuation of each atom of the aptamer (Supplementary Figure S2B, C). Investigation of the relative populations of both states revealed that in all simulations without ligand the binding pocket is twice as likely to adopt the unbound-like conformation (Supplementary Figure S11).

Closer inspection of solvent atoms inside and in close proximity to the binding cavity in the reference structure reveals a characteristic pattern of solvent coordination for the ligand-unbound state (Figure 6B). The center of the pocket is occupied by a sodium ion and a water molecule. The former is located between the phosphate group of residue C10 and the nucleobase G11, compensating for the missing charge of guanidinium, while the latter is forming hydrogen-bonds, compensating for the missing ligand. Two more sodium ions are coordinated to the phosphate groups of residue G11 and C10, and two water molecules are involved in forming additional hydrogen-bonds between the pocket residues. The incorporation of an additional sodium ion compared to simulations with guanidinium is persistent over time, as the number of sodium ions in the vicinity of the binding pocket reveals (ions within a distance closer than 0.65 nm to the O2P atom of residue C10; Supplementary Figure S10B, upper panel). On average 2.4 ions are found in simulations without ligand, while it is 1.7 ions for simulations with guanidinium. As with the guanidinium simulations, the identity of the sodium ion closest to the binding pocket changes repeatedly (Supplementary Figure S10B, middle panel), but less frequently. This exchange of the sodium ion incorporated inside the binding cavity is observed only when the aptamer is in the bound-like state, and not from the more compact unbound-like state. This can be demonstrated by correlating the switch between the bound-like and unbound-like states with the identity and distance of the sodium ion closest to the C10-O2P atom (Supplementary Figure S10B, middle and lower panels, indicated by green dotted lines).

To confirm that the transition between the two states is not an artifact of the force field, corresponding simulations of the aptamer without ligand were set up using the ff14SB force field. The conformational space visited in these simulations agrees well with the corresponding conformations obtained with the DESRES force field (Supplementary Figure S8A, B). Both, bound-like and the unbound-like states are visited and multiple transitions between them were observed. Furthermore, to validate the employed guanidinium model by Wernerson et al. (17), a second guanidinium model derived from arginine parameters in the ff14SB force field was tested. Conformational behaviour, shape of the binding pocket as well as the binding pattern of guanidinium agree very well between simulations with the two models (Supplementary Figure S12A, B).

Urea simulations

In simulations where the guanidinium ligand is substituted by urea, an orientation-dependent decrease in conformational stability of the binding pocket is observed, and spontaneous unbinding events occur in three out of nine simulations. Ligand unbinding can be identified by monitoring either the distance between the urea carbon atom and the pocket, or changes in the solvent shell of urea (Supplementary Figure S13A, B). The three exit events are evenly distributed between simulations from the three different starting configurations.

As long as urea is incorporated inside the binding pocket, conformational stability of the pocket residues is largely dependent on the orientation of the urea oxygen. Conformations visited by the Gd-II aptamer in presence of urea can be well categorized by the distance between the oxygen and the front entrance and highlighted in PCA space (Supplementary Figure S9).

Conformations where the oxygen is positioned inside or close to the back of the binding pocket are not maintained for extended periods of time, and exhibit a rather volatile behaviour. The C10-phosphate atoms are twisted away from the binding pocket, and the nucleobase A9 is frequently flipped away and back again from its initial position (Supplementary Figure S10C). This conformational change corresponds to the area in PCA space defined as the urea state, and can nicely be seen in Supplementary Figure S9, green scatter. In the reference structure of the urea state, two water molecules are coordinated to both, front and back side of the pocket (Supplementary Figure S10C). Two sodium ions are located close to the backbone phosphates at the rear entrance of the binding pocket, one of them directly bridging the the backward facing urea oxygen and the O2P atom of residue G11. These sodium ions are very loosely coordinated to the binding pocked and are frequently exchanged (Supplementary Figure S10D). If the urea oxygen faces the front entrance of the pocket, either because of its initial placement or after rotation inside the pocket, the conformation of the aptamer resembles the guanidinium bound conformation, and populates the region in PCA space associated with the bound-like state (Supplementary Figure S9, blue scatter). All spontaneous unbinding events occur from this configuration with the urea oxygen facing towards the front side pocket entrance, even if the the simulation was visiting conformations distinct from the bound-like state prior to unbinding (Supplementary Figure S13C). In the events where spontaneous unbinding occurs, the binding pocket without urea exhibits repeated transitions between bound-like and unbound-like regions of PCA space as previously observed in simulations without ligand (Supplementary Figure S10C and Supplementary Figure S5B). Calculating the relative populations of both states for simulations after spontaneous urea unbinding occurred revealed a two-to-one ratio in favor of the unbound-like state (Supplementary Figure S11), agreeing well with the results obtained from simulations without ligand. This is a further confirmation that the behaviour of the binding pocket after urea unbinding matches the behavior of the system that that was set up without a ligand—which in turn confirms that these ligand-free simulations did not produce a completely artificial conformational ensemble.

Direction of ligand unbinding

In the free simulations, no spontaneous guanidinium unbinding events were observed, while urea repeatedly left the binding pocket via the front exit. To investigate the possibility of multiple unbinding pathways, we set up a preliminary set of metadynamics simulations with a biasing potential along the distance between the ligand carbon atom and the reference COM in the binding pocket. For both ligands unbinding events were observed in the direction of both solvent exposed sides of the pocket (Table 1). However, it is important to note that the metadynamics simulations employed here only use a single, not optimised collective variable. This choice can strongly impact the unbinding event, and easily push the system in regions of phase space that are physically not relevant. We decided to use these metadynamics simulations only to get a first impression whether unbinding via both pocket exits are in principle possible. A full exploration of both pathways and their respective free energy barriers with different methods will be conducted in a follow up study.

Table 1.

Unbinding of guanidinium and urea from the Gd-II aptamer

System	Simulation method	Orientationa	Front exit (%)	Back exit
Guanidiniumb	Unbiased MD	-	0	0
Ureac	Unbiased MD	Front	100	0
Ureac	Unbiased MD	Left	100	0
Ureac	Unbiased MD	Right	100	0
Guanidinium	Metadynamics	-	42	58
Urea	Metadynamics	Front	14	86
Urea	Metadynamics	Left	48	52
Urea	Metadynamics	Right	32	68

^aLabel according to the orientation of the urea oxygen in the three different starting structures.

^bNo unbinding event in three trajectories observed.

^cOne single unbinding event in three trajectories observed.

DISCUSSION

The Gd-II aptamer is a two-state system

MD simulations of the Gd-II aptamer with and without a guanidinium ligand show that the guanidinium binding pocket essentially adopts two major conformational states. The bound-like state resembles the conformation reported in X-ray structures of the Gd-II dimer with guanidinium tightly bound inside the pocket. The second conformation, referred to as the unbound-like state, is characterized by the collapse of nucleobase G11, one of the residues involved in formation of the binding cavity, into the pocket interior, which is only possible in absence of a ligand. In the absence of guanidinium, the missing positive charge and hydrogen-bonds are substituted by incorporation of ions and water molecules into the binding pocket. Consequently, the unbound-like state can be understood as the sodium-bound equivalent to the guanidinium-bound aptamer, where due to the small size of sodium the binding cavity contracts. This sodium-bound conformation, however, appears to be less stable than the guanidinium-bound one. This is indicated by multiple binding-unbinding events of the incorporated sodium ion as well as repeated transitions between the unbound- and bound-like states observed in simulations without ligand. These findings support the idea of a ‘breathing’ apo-form of the binding pocket that is characterized by an equilibrium between bound-like and unbound-like state, with the first one being more strongly populated. Importantly, this ‘breathing’ apo-form is also found in the urea simulations after urea has naturally exited the binding pocket, confirming that this form is not an artifact caused by alchemically deleting the guanidinium ligand from the starting structure.

So far, it is not known how the processes of ligand binding and dimerization are intertwined. Our results suggest that the aptamer is able to form a stable, guanidinium bound monomer, where the eventual binding interface is already preformed. We also observe that the arrangement of atoms involved in the dimerization interface is affected by the conformational change accompanying the collapse of the binding pocket in the apo-form. Although a bound-like conformation is occasionally visited by the apo-form, the binding interface is not lastingly maintained without guanidinium stabilizing the pocket. This is in line with the experimentally observed breakup of the dimer in absence of guanidinium (6). They conclude that while transient interactions between two aptamers occur if they are already in close proximity, formation of a stable dimer is presumably happening only upon ligand incorporation in at least one of the aptamers. The coupling of ligand binding and dimerization also provides an explanation why the crystal structure for the Gd-II stem–loop dimer in absence of guanidinium could only be solved in presence of high concentrations of (NH₄)₂SO₄. Due to their larger size and hydrogen-bonding capacity, ammonium ions might better mimic guanidinium compared to sodium, resulting in a conformation where the binding interface is less severely altered. This allows dimerization and crystallization into a crystal structure that resembles the guanidinium-bound one (8), with ammonia incorporated in the binding pocket.

Urea is a poor substitute for guanidinium

Despite the structural resemblance, replacing guanidinium by urea resulted in a lower structural stability of the pocket, and even spontaneous urea unbinding events were observed. The key features identified that give rise to the aptamer’s ability to discriminate against urea are the orientation of the urea oxygen inside the binding pocket, the different hydrogen-bonding patterns between the respective ligand and the aptamer and the charge difference between guanidinium and urea.

If the urea oxygen is positioned inside the pocket, the structure of the binding cavity is destabilized. In particular, nucleobase A9 frequently shifts away from its initial position into the solvent. Exchanging an amine group inside the binding pocket with an oxygen is unfavorable due to electrostatic repulsion from the negatively charged phosphate groups of the RNA backbone located close to the backside of the binding cavity. This repulsion is amplified by the missing positive charge of the ligand. The adverse impact of electrostatic interactions onto the binding affinity of urea is only increased by the missing hydrogen-bonds inside the binding pocket. A stable conformation of the binding pocket can only be recovered after the urea oxygen changes its orientation and faces towards the front opening. In this configuration, urea mimics the shape of guanidinium inside the binding pocket very well, the four amine hydrogens are exhaustively hydrogen-bonded to adjacent RNA atoms and a water molecule. Yet, multiple spontaneous unbinding events of urea were observed from this configuration. While the amine group of guanidinium at the pocket entrance forms a hydrogen bond to an oxygen of nucleobase G11, the urea oxygen atom gets solvated by an additional water molecule after a slight opening up of the binding pocket or a shift of the urea molecule towards the solvent. This can possibly be viewed as initiation of an unbinding event.

Ligand binding and unbinding

Although binding and unbinding of guanidinium to and from the Gd-II aptamer exceeds the timescales available for MD simulations, a combination of experimental results, enhanced sampling simulations and the observation of unbinding events of urea and sodium ions from the aptamer can provide clues regarding the mechanism of ligand binding.

Firstly, exchange of the sodium ion that is incorporated in absence of guanidinium was only observed from the more open, bound-like conformation. Similar behavior can be expected for other small, positively charges ions. This provides evidence that ligand binding might occur during the observed breathing process, when the expanded binding pocket of the bound-like state is formed.

Secondly, as the reference structure of the bound-like state reveals, guanidinium inside the binding pocket is solvent exposed in two directions. This gives rise to the possible existence of two distinct binding/unbinding pathways. Notably, all spontaneous unbinding events observed for urea occur to the front-exit of the binding pocket. Subsequent metadynamics simulations with guanidinium and urea showed, that in principle unbinding events in the direction of both pocket entrances can occur. Note though, that the respective free-energy barriers were not determined, i.e. the verdict on the binding/unbinding via the rear exit is still out. Building on the experimental results with different guanidinium analogs, ligand binding via the front side of the binding pocket is presumably the more relevant mechanism. For example, an artificially designed divalent ligand is reported to bind to the aptamer with high affinity – with the aliphatic linker that connects the two guanidinium moieties traversing through the front openings of the two binding pockets (16).

CONCLUSION

In this work, we have combined molecular simulations with dimensionality reduction methods to characterize the conformational states of the monomeric Gd-II aptamer. From the ligand-dependence of the conformations of the binding pocket—including the shape and stability of the interface that is presented to a second aptamer—we propose a mechanism that couples ligand binding to dimerization (Figure 7).

Figure 7.

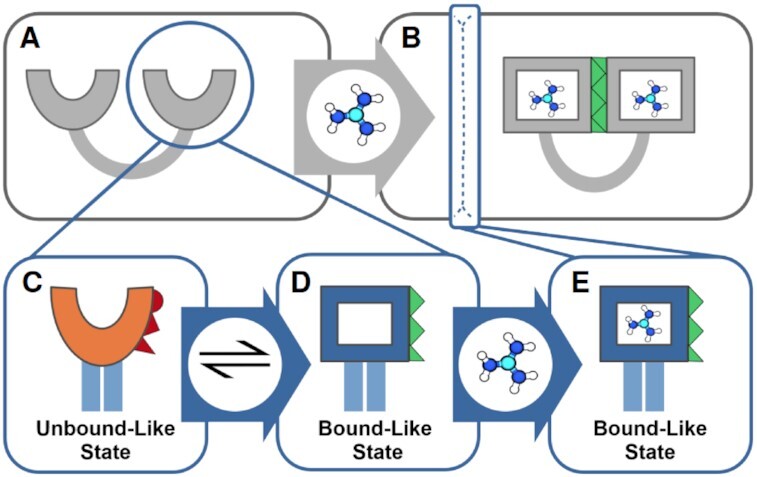
Proposed mechanism of ligand binding to the Gd-II riboswitch. Insights originating from this work are shown in blue boxes. (A) In absence of guanidinium, the two stem–loops are split apart. (B) In presence of guanidinium, the two stem–loops bind a guanidinium each and dimerize by a loop-loop interaction along a stable dimerization interface (green). Our work shows, that the apo-state of the riboswitch is characterized by two alternating conformations of the binding pocket: a collapsed state (C), where the binding interface (red) is substantially deformed and an open state (D), where the binding interface is recovered (green), and guanidinium can be bound. (E) Our results indicate that the aptamer with bound guanidinium is also stable as a monomer. This suggests that ligand binding in the Gd-II stem–loop does not require a pairing of the two stem loops prior to the binding, but rather functions as the initiation event for subsequent dimerization of the stem–loops.

The conformation of the aptamer in presence of guanidinium remains stable for the entire length of the simulations and resembles the experimentally observed, ligand-bound conformation in the dimer. Removal or unbinding of the ligand from the binding cavity results in a two-state system. Here, the binding pocket repeatedly switches between a collapsed conformation and one very similar to the bound-like state. In the collapsed conformation, a sodium ion occupies the binding pocket, resulting in a contraction of key residues involved in the formation of the binding cavity. The same residues also play a crucial role in the formation of the dimerization interface in the experimentally observed structure. Therefor, a consequence of the contraction of the binding pocket is a conversion of the binding interface, which presumably results in the experimentally shown destabilization and disassembling of the dimer in absence of guanidinium. Furthermore, we have observed significant differences in binding stability for simulations where urea is incorporated as a ligand instead of guanidinium. This is in line with the experimental observation that the Gd-II riboswitch is able to discriminate with a high selectivity between the two molecules. Metadynamics simulations building on the previously identified conformational states of the aptamer revealed the possible existence of two distinct binding/unbinding pathways for both, guanidinium as well as urea. However, they have also highlighted the importance of accompanying the metadynamics approach with additional methods such as transition path sampling, to derive the underlying mechanisms and accurate energy barriers for these unbinding pathways.

Our results are a valuable basis for future in-depth investigation of the binding and unbinding processes of the ligand, the dimerization mechanism of the two aptamers as well as the design and development of novel guanidinium analogs, potentially establishing the Gd-II riboswitch as an important tool in future biomolecular and pharmaceutical research and application.

DATA AVAILABILITY

Simulation data and run input files are available via GitHub at https://ag-peter.github.io/gmw4nhr/.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Baden-Württemberg through the bwHPC project; German Research Foundation (DFG) [INST no. 35/1134-1 FUGG]; Konstanz Research School Chemical Biology (KoRS-CB); Zukunftskolleg of the University of Konstanz; Carl Zeiss Foundation. Funding for open access charge: University of Konstanz.

Conflict of interest statement. None declared.