Resonant quantum principal component analysis

An energy-tunable ancillary qubit efficiently probes the principal components of a low-rank matrix.

Abstract

Principal component analysis (PCA) has been widely adopted to reduce the dimension of data while preserving the information. The quantum version of PCA (qPCA) can be used to analyze an unknown low-rank density matrix by rapidly revealing the principal components of it, i.e., the eigenvectors of the density matrix with the largest eigenvalues. However, because of the substantial resource requirement, its experimental implementation remains challenging. Here, we develop a resonant analysis algorithm with minimal resource for ancillary qubits, in which only one frequency-scanning probe qubit is required to extract the principal components. In the experiment, we demonstrate the distillation of the first principal component of a 4 × 4 density matrix, with an efficiency of 86.0% and a fidelity of 0.90. This work shows the speedup ability of quantum algorithm in dimension reduction of data and thus could be used as part of quantum artificial intelligence algorithms in the future.

INTRODUCTION

In many optimization and machine learning applications, principal component analysis (PCA) plays an important role in the process of feature extraction and dimension reduction because of its ability to preserve the information of the data (1, 2). It is achieved by projecting the data point onto a new low-dimensional basis spanned by the vectors called principal components, which are the eigenvectors of the dataset’s covariance matrix. To reduce the dimension, one can select only the eigenvectors with large eigenvalues as principal components and discard the ones with eigenvalues below a given threshold. In this way, the variance of the projected data is maximized, while the data are mapped into the low-dimensional space. The process of computing the principal components, i.e., the largest eigenvectors of the covariance matrix, involves the diagonalization of a Hermitian matrix and can be speed-up by adopting quantum algorithms. It was shown that the quantum version of PCA (qPCA) (3, 4) is exponentially more efficient than classical methods if the covariance matrix is low rank and is stored in the form of a quantum state. In combination with recent advances in other linear algebra–based quantum algorithms such as solving linear systems (5–8), data analysis (9, 10), quantum random accessed memory (11, 12), and learning algorithms (13–25), this could lead to more applications of quantum machine learning.

The problem of qPCA reduces to the question of how to distill the principal components of an unknown low-rank density matrix ρ = ∑_iλ_i∣λ_i〉〈λ_i∣, where 〈λ_i ∣ λ_j〉 = δ_ij. If many copies of ρ are given in the quantum form, then one can use them to construct the unitary operator e^−iρt (3, 26) and then adopts the quantum phase estimation algorithm (PEA) (27) for the analysis. With the ability of accessing log(ϵ⁻¹) ancillary qubits and applying e^−i2kρt conditioned on the state of kth ancillary qubit, PEA can reveal the information of eigenvalues and eigenstates to the accuracy ϵ within time O(poly(ϵ⁻¹)). On an ideal quantum processor, PEA achieves a good level of precision of eigenvalues (2^−m) given a large number m of the ancillary qubit adopted. However, the demonstration of qPCA remains technically challenging and elusive because of the high requirements for both the number of qubits and the precision of quantum operations. Furthermore, how far one can reveal the information of the principal components in a coherence-limited physical system is still an open question.

In this work, we propose a resonance-based quantum PCA (RqPCA) algorithm to avoid the high requirements of PEA-type methods. Instead of a large PEA ancillary register, our RqPCA adopts an energy-tunable probe qubit to locate and distill the principal components of the unknown matrix. This scalable scheme only needs one ancillary qubit and also simpler quantum operations, which makes it capable to be demonstrated experimentally with current technology. In the experiment, we use a prototype hybrid spin system in diamond under ambient conditions and measure the eigenvalues of principal components with a precision of 2⁻¹⁰. We find that the decoherence of the ancillary qubit becomes the dominant source limiting both the distillation efficiency and the accuracy of the result. To suppress this effect, we further develop the RqPCA algorithm to combine with the dynamical decoupling strategy, enabling the high-fidelity and high-efficient principal component distillation. The first principal component is then distilled from the mixed state ρ with a fidelity of 0.90 and the distillation efficiency of 86%.

RESULTS AND DISCUSSION

The basic idea of our scheme is illustrated in Fig. 1. We start with an ancillary qubit conditionally coupled to an n-dimension quantum register with the overall Hamiltonian H = ∣1〉〈1∣⊗ ρ. Its time evolution generates exactly the conditional evolution operator e^−iρt, which is the core of qPCA. Then, a tunable energy offset was introduced, leading to the Hamiltonian $H_{\text{int}}=\mid 1\rangle \langle 1\mid \otimes \mathrm{\rho }+\frac{\mathrm{\omega }}{2}{\mathrm{\sigma }}_z\otimes I_n$ where σ_x,y,z is the Pauli operator of the probe qubit and I_n is the identity matrix with dimension n. The energy spectrum of this system is shown in Fig. 1A, where ∣λ_n〉 is the eigenstate corresponding to the largest eigenvalue, i.e., the principal component of interest. If a small external field drives the ancillary qubit with strength c, then the transition between eigenstates ∣1〉∣λ_i〉 and ∣0〉∣λ_j〉 will be excited when i = j and ∣ω − λ_i∣ is small. The ancillary qubit thus probes the transition occurring condition ω ≈ λ_i by monitoring its state change.

Fig. 1. Schematics of resonant quantum PCA algorithm.

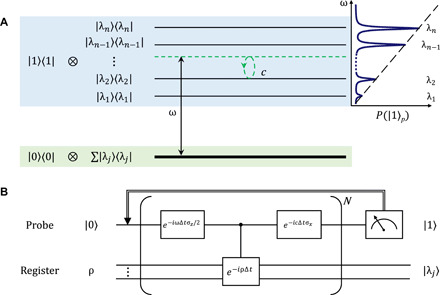
(A) The energy structure of the coupled probe-register system with H = ∣1〉〈1∣ ⊗ ρ. ∣λ_i〉 is the ith eigenstate of ρ, and λ_i ∈ [0,1] is the corresponding eigenvalue. After introducing the probe qubit’s Hamiltonian, the energy of lowest level moves to the green dashed line. Once the scanning frequency ω ≈ λ_i, the Rabi oscillations of the probe qubit is induced. (B) The quantum circuit of RqPCA using the Suzuki-Trotter decomposition (NΔt = τ). The projective measurement of the probe qubit in the state ∣1〉 indicates success of the algorithm, with principal component being distilled in the register.

Given the copy of quantum state of interest ρ, we initialize the probe qubit on the state ∣0〉 and have the initial state ρ_ini = ∣0〉〈0∣⊗ ρ. Then, the system is evolved under the Hamiltonian

$$\begin{array}{cc}\hfill {\mathcal{H}}_{\text{Rq}}(\mathrm{\omega })& =\frac{\mathrm{\omega }}{2}{\mathrm{\sigma }}_z\otimes I_n+c{\mathrm{\sigma }}_x\otimes I_n+\mid 1\rangle \langle 1\mid \otimes \mathrm{\rho }\hfill \\ & ={\displaystyle \sum _i}\frac{\mathrm{\omega }-{\mathrm{\lambda }}_i}{2}{\mathrm{\sigma }}_z\otimes \mid {\mathrm{\lambda }}_i\rangle \langle {\mathrm{\lambda }}_i\mid +\mathit{c}{\mathrm{\sigma }}_x\otimes I_n+{\mathit{I}}_2\otimes {\displaystyle \sum _i}\frac{{\mathrm{\lambda }}_i}{2}\mid {\mathrm{\lambda }}_i\rangle \langle {\mathrm{\lambda }}_i\mid \hfill \end{array}$$ (1)

for a certain time τ. Once the frequency ω matches one specific eigenvalue λ_i of ρ, the probe qubit will flip from ∣0〉 to ∣1〉 with the probability

$$P_i(\mathrm{\omega })={\mathrm{\lambda }}_i{D}_i^2{\text{sin}}^2\left(\frac{c\mathrm{\tau }}{D_i}\right),i=1,2,\dots ,n$$ (2)

where $D_i=\sqrt{\frac{{(2c)}^2}{{(2c)}^2+{(\mathrm{\omega }-{\mathrm{\lambda }}_i)}^2}}$. The transition probability P_i(ω) approaches its optimal value λ_i in the resonant condition, i.e., ω − λ_i ≪ c and $\mathrm{\tau }\approx \frac{\mathrm{\pi }}{2c}$. By scanning the frequency ω and recording the readout probability being in state ∣1〉, one can obtain a typical resonance spectrum, as shown in Fig. 1A, where the position of each resonance peak tells the specific eigenvalue.

After having the probability distribution information, one can quickly locate the eigenstate of interest, e.g., the first principal component ∣λ_n〉 corresponding to the largest eigenvalue λ_n. In the resonant condition of ω − λ_n ≪ c, only the transition from ∣0〉∣λ_n〉 to ∣1〉∣λ_n〉 is excited, while all other components ∣0〉∣λ_j〉(j ≠ n) remain in the subspace of ∣0〉. After a projective measurement of the probe qubit, the readout of state ∣1〉 indicates that the quantum register is projected into ∣λ_n〉. If the probe is still in ∣0〉, which means that no transition was excited, then one can return to the start of the algorithm and rerun the circuit. The probability of success in a single run equals to P_n(ω) and is close to λ_n in the optimal case, which is the population of the first principal component in the initial state ρ. The efficiency of principal component distillation, defined as how many populations of principal component are captured, equals to $D_i^2=\frac{{(2c)}^2}{{(2c)}^2+{(\mathrm{\omega }-{\mathrm{\lambda }}_i)}^2}$.

The evolution of Hamiltonian ℋ_Rq(ω) can be implemented through the Suzuki-Trotter decomposition (Fig. 1B) (28). The controlled operation of e^−iρΔt can be implemented with extra copies of ρ (3, 26). In comparison with the conventional qPCA algorithm, RqPCA minimizes the number of ancillary qubits required in quantum phase estimation at the cost of increasing quantum circuit repetitions for the frequency scanning. To further optimize our method, we adopt the adaptive implementation which greatly reduces the repetition times by focusing the area around the eigenvalues of interest. On the other hand, the length of the quantum circuit of RqPCA has the similar scaling property as conventional qPCA, with potential complexity advantage benefit from the lower number of qubits. Therefore, this method is more applicable to current intermediate-scale quantum computers.

We experimentally demonstrate this algorithm on a nitrogen-vacancy defect (NV) center electron spin associated with the nitrogen nuclear spin (N) and a nearby carbon nuclear spin (C). The electron spin (∣0〉 : m_S = 0, ∣1〉 : m_S = + 1) is chosen as the probe qubit, and two nuclear spins (¹⁴N, m_I = { + 1,0}; ¹³C, m_I = {+ 1/2, − 1/2}) are used as the quantum register to store the density matrix ρ for analysis. In this hybrid spin system, electron spins offer fast, versatile, and high-fidelity readout and control (29–37), and nuclear spins provide additional qubits for the quantum register with long coherence time (38–42). The Hamiltonian of the NV-C-N system driven in an external microwave field is described by

$${\mathcal{H}}_{\text{NV}}=\frac{\mathrm{\delta }}{2}{\mathrm{\sigma }}_z^e+\frac{{\mathrm{\Omega }}_{\text{MW}}}{2}{\mathrm{\sigma }}_x^e+{\mid 1\rangle }_e\langle 1\mid \otimes (A_{\parallel }^C{I}_z^C+A_{\parallel }^N{I}_z^N)$$ (3)

in the rotating frame of microwave frequency, where Ω_MW is the amplitude of the microwave control field and $A_{\parallel }^C$ and $A_{\parallel }^N$ denote the hyperfine coupling strengths between the electron spin and the two nuclear spins, respectively (see Materials and Methods).

The density matrix of interest in this experiment is $\mathrm{\rho }=0.15{\mathrm{\sigma }}_z^1+0.09{\mathrm{\sigma }}_x^1-0.03{\mathrm{\sigma }}_z^2+{\mathit{I}}_4/4$. Because it is not a product state, a combination of nuclear spin rotation, nonlocal controlled operation, and a controllable laser-induced dephasing process is required to prepare initial state ρ_ini = ∣0〉〈0∣⊗ ρ. The initialization fidelity reaches the value of up to 95%. For a given ω, the corresponding evolution Hamiltonian ℋ_Rq(ω) can be constructed from the Hamiltonian of the NV system through a local transformation and mapping (see Materials and Methods). Figure 2A shows the experimental diagram proceeding in three steps. The evolution time is setting as τ = π/2c so that the transition probability is optimized. Last, the electron spin state is optically readout to get the transition possibility for different ω, from which the eigenvalues are obtained directly.

Fig. 2. The resonant spectra obtained from an adaptive implementation of RqPCA.

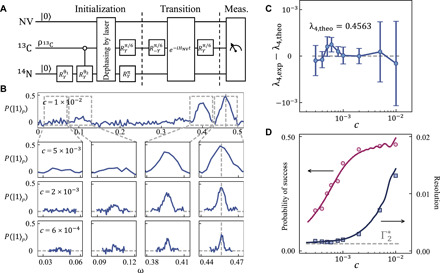
(A) The schematic circuit of resonant quantum PCA. The electron in NV serves as probe qubit, while the nuclear spins are used to store the information of the matrix ρ (see Materials and Methods for details.) (B) The transition spectra are obtained through an adaptive implementation of the method. The resonant peaks appear when ω is close to one of the eigenvalues λ_j of ρ. (C) The deviations of the experimentally measured eigenvalues of the first principal component ∣λ₄〉, compared to the theoretical expectations. The experimental eigenvalue and its uncertainty are obtained through a Gaussian spectrum fitting of the transition spectrum in (B). Results of different driving strength c are compared with the same times of circuit repetitions. (D) The probability of success and the resolution of λ₄, with respect to different driving strength c. The dots refer to the experimental results, and the solid lines denote the modeled result taking into account the dephasing of the electron spin. The dashed line marks the lower bound of the resolution ${\mathrm{\Gamma }}_2^{*}=\sqrt{\text{ln} 2}/(\mathrm{\pi }{T}_{2\mathit{e}}^{*}{f}_{\text{map}})$ due to the dephasing of the probe qubit (see Materials and Methods).

Figure 2B shows the transition spectrum obtained through an adaptive implementation of the method. A considerable large driving strength is firstly applied to quickly estimate the eigenvalues in a broad frequency range. After this, the driving strength and the scanning range are tuned adaptively according to the resonance peak information obtained in the previous step. In four adaptive steps, the spectral linewidth (resolution) approaches to a lower bound, while the number of sampling points keeps low. In combination with the adaptive method, RqPCA can thus greatly reduce the frequency scanning repetition times. However, the enhancement of the resolution is at the cost of longer experiment length and therefore losing the probability of success because of the decoherence effect in realistic experiments (Fig. 2D). Thus, the uncertainty of the peak position decreases initially with the reduction in spectral linewidth but lately increases because of the lower success probability (Fig. 2C). In the experiment, the observed peak position has a maximal deviation of 3 × 10⁻⁴ to the theoretical eigenvalue due to the external magnetic field instability (see Materials and Methods). The resulting eigenvalue precision is 2⁻¹⁰, equivalent to perfect PEA implementation with 10 ancillary qubits in the conventional qPCA algorithm.

To better understand the above results, we numerically simulated the dephasing of electron spin using independently measured decoherence quantities. We find good agreement between the modeled results (solid lines in Fig. 2D) and the experimental results (dots) of both the uncertainties of the eigenvalue and success probabilities. The success probability reduces because the electron spin loses its coherence during its flip to ∣1〉, because of the dephasing process. Thus, the resolution of the eigenvalue is limited by the dephasing rate of the electron spin. To suppress the dephasing and increase the success probability, we extend the current scheme to an approach that naturally combines with the dynamical decoupling technique (43). The single evolution period is split into two half periods with the first π pulse applied at the middle and the second π pulse used at the end (Fig. 3A). The resonant spectra with this modification (red, denoted as ECHO method below) and the native method (blue) when c = 6 × 10⁻⁴ are shown in Fig. 3B. While using the ECHO method, the probability of success is increased greatly, leading to the higher efficiency of principal component distillation in later steps. Figure 3C shows how the likelihood of success and the resolution of the eigenvalue vary with different c. When c is small, the possibility of success adopting the ECHO method is always much higher than the one in the native way. In contrast, the resolution of both methods approaches to a lower bound that comes from the dephasing of the electron spin.

Fig. 3. RqPCA with ECHO pulses to suppress the decoherence of the probe qubit.

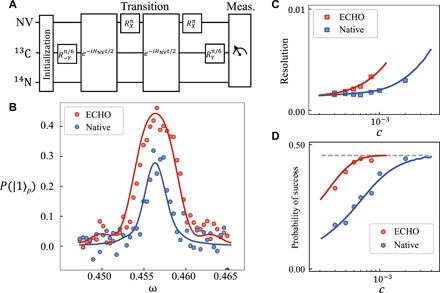
(A) Schematic diagram of the ECHO pulses used to suppress the decoherence effect (see Materials and Methods for details). (B) The resonant spectra with ECHO (red) and the native method (blue) when c = 6 × 10⁻⁴. (C and D) The resolution of the eigenvalue and the probability of success with respect to driving strength c. The probability of success has an upper bound (dashed horizontal line) that equals to the population of the first principal component in ρ. Here, dots are the experimental results, and solid lines are theoretically simulated results with modeled decoherence.

To reveal the first principal component ∣λ₄〉, we tune the resonance frequency ω to be the largest eigenvalue λ₄ measured in previous steps, so only the first principal component will be on resonant. After applying the circuit of RqPCA, if the probe qubit is measured as ∣1〉, then the other qubits will collapse to the first principal component of ρ, i.e., ∣λ₄〉. To better understand how well the principal component is distilled, we measured both the state before and after the RqPCA using state tomography (see Materials and Methods). The first column of Fig. 4 shows the measured initial state represented in terms of four eigenstates of ρ. A mixture of four eigenstates is observed in the subspace of probe being in ∣0〉, while almost no population is in the subspace of ∣1〉. The same measurements are performed after RqPCA, and the results using native and ECHO methods are shown in the second and third columns, respectively. After running the circuit, the state in the subspace of ∣1〉 is close to the principal component ∣λ₄〉, when the state in the subspace of ∣0〉 remains a mixture of different eigenstates. It is noted that although both methods (ECHO and native) can distill the principal component ∣λ₄〉 from the background of the mixed eigenstates in ρ, the efficiencies of distillation are different. While adopting the ECHO method, 86.0% of the population of ∣λ₄〉 transits to the subspace of ∣1〉, which indicates a high efficiency of principal component distillation. At the same time, very few populations of other components (∣λ_1,2,3〉) appear in the subspace of ∣1〉, leading to a distillation fidelity of 0.90. In the case of the native method, both the efficiency (48.1%) and the fidelity (0.73) are much lower because of the electron spin’s dephasing effect.

Fig. 4. The principal component distillation.

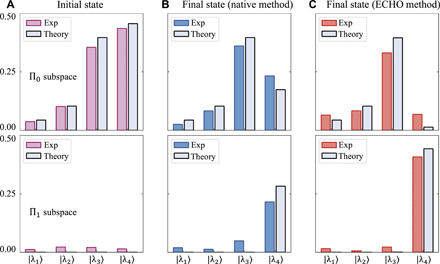
(A) The initial state before RqPCA obtained by state tomography. (B and C) The states after applying the native and ECHO methods of RqPCA, respectively, with the same parameters: c = 6 × 10⁻⁴ and ω = 0.4566 determined from Fig. 3B. Here, the subspace ∏_k is spanned by the eigenbasis of ρ (∣λ_1,2,3,4〉) while the probe (electron spin) is in the state ∣k〉(k = 0,1). The bars denote the populations of the basis states ∣λ_1,2,3,4〉 in the experimentally measured states.

The resonance-based PCA algorithm in our work adopts an energy-tunable ancillary qubit to locate and distill the principal components of an unknown matrix. Compared to the PEA-type methods, which have high requirements for the size and controllability of the quantum processor, our method only needs one ancillary qubit and simpler operations, making it more applicable with current technology. In the experiments, the first principal component of the density matrix is distilled with high efficiency and high fidelity. This method can be easily applied to resolve other eigenstate finding problems such as molecular energy simulation in quantum chemistry (44). If combined with a faithful demonstration of density matrix exponentiation, our method could serve as an essential part of a variety of quantum machine learning implementations. Furthermore, the ability to combine with decoherence-suppressed technique makes the method applicable to the intermediate-scale noisy quantum computers nowadays.

MATERIALS AND METHODS

Experimental setup and spin system

The experiment was carried out on a home-built confocal microscope under ambient conditions. A continuous wave laser at 532 nm is used for optical pumping and readout of the NV spin and is gated with two acoustic-optic modulators. The laser beam was focused by an oil objective, while the fluorescence signal was collected by the same objective. An active temperature control to within 5 mK was used to increase the magnetic field stability. The microwave signal used to control the electron spin was generated by an arbitrary waveform generator (AWG; crs1w000b, CIQTEK) in combination with a microwave generator through the in-phase and quadrature (I/Q) modulation. The radio-frequency signal used to control the nuclear spins was also generated by the same AWG.

We used a NV center containing one coupled ¹³C nuclear spin ($A_{\parallel }^C\simeq 12.8 \text{MHz}$) and an intrinsic ¹⁴N nuclear spin ($A_{\parallel }^N\simeq -2.16 \text{MHz}$) in a [100]-oriented diamond. To improve the photon collection efficiency, a solid immersion lens was fabricated on the NV centers. An external magnetic field of 380 G was applied to remove the degeneracy between the electronic states m_S = + 1 and m_S = − 1. The dephasing time of the whole spin system is measured as $T_{2,\mathrm{e}}^{*}\sim$ 5.8 μs, $T_{2,\mathrm{C}}^{*}\sim$ 2.0 ms, and $T_{2,\mathrm{N}}^{*}\sim$ 5.0 ms. In comparison to the evolution time of the whole circuit, only the dephasing of electron spin is dominant for the effect of decoherence.

Hamiltonian mapping

By applying a rotation of angle θ′ on the ¹³C nuclear spin, the Hamiltonian ℋ_NV is transformed into

$$\mathcal{H}=\frac{\mathrm{\delta }}{2}{\mathrm{\sigma }}_z^e+\frac{{\mathrm{\Omega }}_{\text{MW}}}{2}{\mathrm{\sigma }}_x^e+{\mid 1\rangle }_e\langle 1\mid \otimes (\mathrm{\alpha }{I}_z^C+\mathrm{\beta }{I}_x^C+A_{\parallel }^N{I}_z^N)$$ (4)

where $\mathrm{\alpha }=A_{\parallel }^C\text{cos} {\mathrm{\theta }}^{\prime },\mathrm{\beta }=A_{\parallel }^C\text{sin} {\mathrm{\theta }}^{\prime }$. By setting δ = f_map(ω − 1/4) and Ω_MV = 2f_mapc with a mapping factor f_map = 2π × 36.25 MHz, the Hamiltonian of NV is mapped to the evolution Hamiltonian ℋ_Rq(ω) with a difference of constant term that can be neglected.

State preparation

Because of dynamical optical pumping (45), the spin system starts from an initial state ρ₀ = ∣0〉_e〈0∣ ⊗ ρ_C ⊗ ∣ 0〉_N〈0∣, with ${\mathrm{\rho }}_{\mathrm{C}}=\left(\begin{array}{cc}0.85& 0\\ 0& 0.15\end{array}\right)$. The spin rotation R_Y(θ₁) ≔ e^{−iσ_yθ₁/2} on the nitrogen nuclear spin and a nonlocal C^CROT^N(θ₂) gate then distribute populations among nuclear spin state subspace. Here, C^CROT^N(θ₂) denotes the spin rotation of nitrogen nuclear spin ${\mathrm{R}}_Y^{\mathrm{N}}({\mathrm{\theta }}_2)$ conditioned on the carbon nuclear spin being in state ∣0〉. This is realized by a conditional phase gate on the electron spin, in combination with local controls (39). As can be seen in Fig. 5, the electron spin transition spectrum associated with nitrogen state ∣1〉_N changed to the one associated with nitrogen state ∣0〉_N after the C^CROT^N(π) gate, while it did not change when the carbon nuclear spin state is in the state ∣0〉_C. The resulting state is

$$0.85{\mid 0\rangle }_{\mathrm{C}}\langle 0\mid \otimes \left(\begin{array}{cc}{\mathrm{\alpha }}_1^2& {\mathrm{\alpha }}_1{\mathrm{\beta }}_1\\ {\mathrm{\alpha }}_1{\mathrm{\beta }}_1& {\mathrm{\beta }}_1^2\end{array}\right)+0.15{\mid 1\rangle }_{\mathrm{C}}\langle 1\mid \otimes \left(\begin{array}{cc}{\mathrm{\alpha }}_2^2& {\mathrm{\alpha }}_2{\mathrm{\beta }}_2\\ {\mathrm{\alpha }}_2{\mathrm{\beta }}_2& {\mathrm{\beta }}_2^2\end{array}\right)$$ (5)

where ${\mathrm{\alpha }}_1=\text{cos} \left(\frac{{\mathrm{\theta }}_1+{\mathrm{\theta }}_2}{2}\right)$, ${\mathrm{\beta }}_1=\text{sin} \left(\frac{{\mathrm{\theta }}_1+{\mathrm{\theta }}_2}{2}\right)$, ${\mathrm{\alpha }}_2=\text{cos} \left(\frac{{\mathrm{\theta }}_1}{2}\right)$, and ${\mathrm{\beta }}_2=\text{sin} \left(\frac{{\mathrm{\theta }}_1}{2}\right)$. After this, a laser-induced dephasing process is introduced to eliminate the off-diagonal matrix terms. As shown in Fig. 5, at a laser power of 190 μW, a fast dephasing time ($T_{2,\text{laser}}^{*}\sim 0.6 \mathrm{\mu }$s) of nitrogen nuclear spin was observed, accomplished by a repolarization to the state ∣0〉_N〈0∣ with a decay rate of T_{1, laser} ∼ 2.1 μs. On the basis of these results, we choose a laser pulse length of 1.4 μs to completely dephase the coherence and θ₁ = 0.58π and θ₂ = 0.31π to account for the finite repolarization. The quantum state turns into

$$0.85{\mid 0\rangle }_{\mathrm{C}}\langle 0\mid \otimes \left(\begin{array}{cc}0.53& 0\\ 0& 0.47\end{array}\right)+0.15{\mid 1\rangle }_{\mathrm{C}}\langle 1\mid \otimes \left(\begin{array}{cc}0.70& 0\\ 0& 0.30\end{array}\right)$$ (6)

Fig. 5. Initial state preparation.

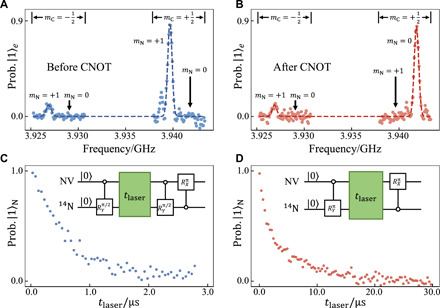
(A and B) The pulsed optically detected magnetic resonance (ODMR) spectrum of laser initialized state ρ₀ and the state after applying the CNOT operation. (C) The decay of ¹⁴N nuclear spin’s coherence under the green laser illumination. The pulse sequence is shown in the inset, including the preparation of the coherent state $({\mid 0\rangle }_{\mathrm{N}}+{\mid 1\rangle }_{\mathrm{N}})/\sqrt{2}$, the laser-induced dephasing, and the map to the electron spin for optical readout. (D) The repolarization of ¹⁴N nuclear spin from the state ∣1〉_N to the state ∣0〉_N under laser illumination.

Last, a single-qubit rotation ${\mathrm{R}}_Y^{\mathrm{C}}\left(\frac{\mathrm{\pi }}{6}\right)$ on the carbon nuclear spin and a ${\mathrm{R}}_Y^{\mathrm{N}}(\mathrm{\pi })$ pulse on the nitrogen nuclear spin were applied; the system was prepared into the state ρ with fidelity 95%. Figure 6 shows the density matrix obtained by the state tomography.

Fig. 6. Experimental measured results of the initial state ρ_ini.

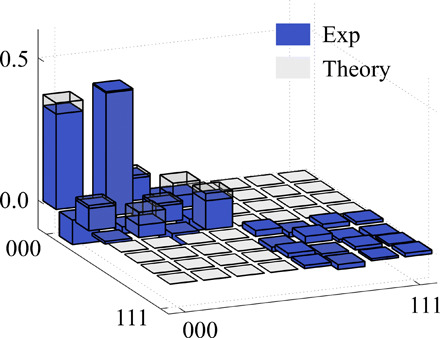
Only the diagonal blocks relevant for our analysis are shown here.

Error analysis

To understand the deviation between experimental and theoretical eigenvalues, we notice that the external magnetic field slowly drifts during the experiments. Suppose B₀ changes δB during the experiments, then the Hamiltonian ℋ becomes

$${\mathcal{H}}_{\text{drift}}=\frac{(\mathrm{\delta }-{\mathrm{\gamma }}_e{\mathrm{\delta }}_B)}{2}{\mathrm{\sigma }}_z^e+\frac{{\mathrm{\Omega }}_{\text{MW}}}{2}{\mathrm{\sigma }}_x^e+{\mid 1\mathrm{\rangle }}_e\mathrm{\langle }1\mid \otimes (\mathrm{\alpha }{I}_z^C+\mathrm{\beta }{I}_x^C+A_{\parallel }^N{I}_z^N)$$ (7)

According to the linear mapping between ℋ and ℋ_Rq(ω), the effective ω in ℋ_Rq(ω) changes to

$${\mathrm{\omega }}_{\text{eff}}=\mathrm{\omega }-\mathrm{\delta }\mathrm{\omega }=\mathrm{\omega }-{\mathrm{\gamma }}_e{\mathrm{\delta }}_B/f_{\text{map}}$$ (8)

The change of external magnetic field δ_B thus causes the deviation of ω in the experiments. By estimating the instability of magnetic field via recording the electron spin’s resonance frequency in 14 hours, we find that δ_B satisfies a Gaussian distribution and the standard deviation (SD) is 12.4 kHz, which corresponds to δω = 3.4 × 10⁻⁴, consistent with the eigenvalue inaccuracy observed in the experiment.

Dynamical decoupling–combined component analysis

Here, we consider the effect of dephasing of the electron spin while using a general sequence in the form of ${(\frac{\mathrm{\tau }}{2M}-\mathrm{\pi }-\frac{\mathrm{\tau }}{2M}-\mathrm{\pi })}^M$, where τ = π/2c. The native and ECHO methods correspond to the case of M = 0 and M = 1, respectively. The dephasing is considered by adding an additional term δ_fσ_z/2 into the total Hamiltonian ℋ_Rq(ω), with δ_f satisfying a Gaussian distribution with the SD determined by $T_{2,e}^{*}$. For the native case, this model returns to a pulsed spin resonance with a spectral width $\sqrt{\text{ln} 2}/(\mathrm{\pi }{T}_{2,e}^{*})$ (46).

A more general consideration of the dephasing is performed through the numerical simulation. Figure 7 shows the spectra and the extracted features of resolution and amplitude, from M = 0 to M = 8. One can see that when the driving strength c is very weak, increasing the number 2M of π pulses can continuously improve the amplitude of peak to the upper bound, with almost no broadening of peak width.

Fig. 7. Numerical simulation for dynamical decoupling–combined PCA.

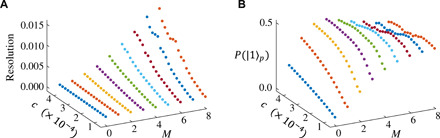
(A) Resolution obtained from resonant spectra for different driving strength c and the order of echo M. (B) The probability of success obtained from resonant spectra for different c and M.

Performance of RqPCA

Compared to the qPCA using PEA, RqPCA minimizes the number of ancillary qubits needed at the cost of increasing quantum circuit repetitions for the frequency scanning. RqPCA only requires one tunable ancillary qubit when PEA-type methods usually need a large ancillary register consisting of tens of qubits, e.g., 10 qubits to achieve the same accuracy as our work. Both methods need the ability to apply the conditional evolution operator e^−iρt with the help of multiple copies of ρ and require the evolution time τ = O(ϵ⁻¹) to achieve the accuracy ϵ of the eigenvalues. Following the smaller scale of the quantum circuit in RqPCA, the number and complexity of multiqubit quantum operations are also reduced, enabling the high-fidelity and high-efficient experimental implementation. Although the RqPCA requires more quantum circuit repetitions to obtain the resonant spectrum, the adaptive implementation used in this work can greatly reduce the repetition times by only focusing the area around the eigenvalues of interest. In the worst case, the repetition time needed to obtain the resonant spectrum scales as O(ϵ⁻¹), which also scale polynomially with the desired accuracy of the eigenvalues.

In RqPCA, the distillation efficiency $D_i^2$ is determined by the accuracy of eigenvalue measurement. To improve it, the evolving time of the system τ needs to be increased to accumulate more information on the density matrix of interest. The infidelity of the distilled principal eigenvectors comes from unwanted excitations, which brings in the information of other eigenvectors. This cross-excitation emerges when another eigenvalue is close to the interested one. This can be suppressed by reducing the driving strength c, which causes a trade-off between the distillation efficiency and the fidelity. For a very coherent quantum system, both the distillation efficiency and the fidelity can be very high.