Automatic classification of white regions in liver biopsies by supervised machine learning

Summary

Automated assessment of histological features of non-alcoholic fatty liver disease (NAFLD) may reduce human variability and provide continuous rather than semiquantitative measurement of these features. As part of a larger effort, we perform automatic classification of steatosis, the cardinal feature of NAFLD, and other regions that manifest as white in images of hematoxylin and eosin–stained liver biopsy sections. These regions include macrosteatosis, central veins, portal veins, portal arteries, sinusoids and bile ducts. Digital images of hematoxylin and eosin–stained slides of 47 liver biopsies from patients with normal liver histology (n = 20) and NAFLD (n = 27) were obtained at 20× magnification. The images were analyzed using supervised machine learning classifiers created from annotations provided by two expert pathologists. The classification algorithm performs with 89% overall accuracy. It identified macrosteatosis, bile ducts, portal veins and sinusoids with high precision and recall (≥82%). Identification of central veins and portal arteries was less robust but still good. The accuracy of the classifier in identifying macrosteatosis is the best reported. The accurate automated identification of macrosteatosis achieved with this algorithm has useful clinical and research-related applications. The accurate detection of liver microscopic anatomical landmarks may facilitate important subsequent tasks, such as localization of other histological lesions according to liver microscopic anatomy.

1. Introduction

Non-alcoholic fatty liver disease (NAFLD) is the most common liver disease in children and adults in the United States [1,2]. NAFLD has a spectrum that starts with a mild phenotype simple steatosis where only steatosis is present, and ends with a severe phenotype non-alcoholic steatohepatitis where steatosis is present with hepatic necro-inflammation and fibrosis [3]. Accurate distinction of mild from severe phenotypes of the disease is essential because simple steatosis rarely progresses, whereas non-alcoholic steatohepatitis can progress to cirrhosis, liver failure, and hepatocellular carcinoma [4-7]. Phenotyping of NAFLD is currently based on a pathologist’s evaluation of the “gold standard” diagnostic test, liver biopsy [3].

The state-of-the-art scoring system of liver biopsies performed for NAFLD is based on manual pathologist assessment and semi-quantification of four key histological features: steatosis grade, lobular inflammation, fibrosis stage and degree of hepatocyte ballooning [8]. It is therefore critical that these features of injury are reliably and reproducibly recognized.

Our group and others [8-15] have demonstrated that there is intra- and inter-observer variability in pathologists’ assessment of NAFLD histological features and assignment of a final disease diagnosis / phenotype. Automation of this assessment may reduce variability, increase accuracy, and offer a continuous rather than semi-quantitative grading of these histological features of NAFLD.

The overall aim of our ongoing project is to test the hypothesis that decision support systems for pathologists, which include computational methods for quantification of the key histological features of NAFLD, will lead to continuous, more accurate and less variable scores and ultimately better phenotyping and improved patient outcome. Key liver biopsy features—including macrosteatosis, central veins (CV), portal veins (PV), portal arteries (PA), sinusoids (SN) and bile ducts (BD)—oftentimes contain a white region, or manifest entirely as white regions, in liver biopsies when stained with a hematoxylin-eosin (H&E) stain as shown in Fig. 1. In this paper, we present an important subtask of our project—the accurate categorization of the white regions in liver biopsy images.

Fig. 1.

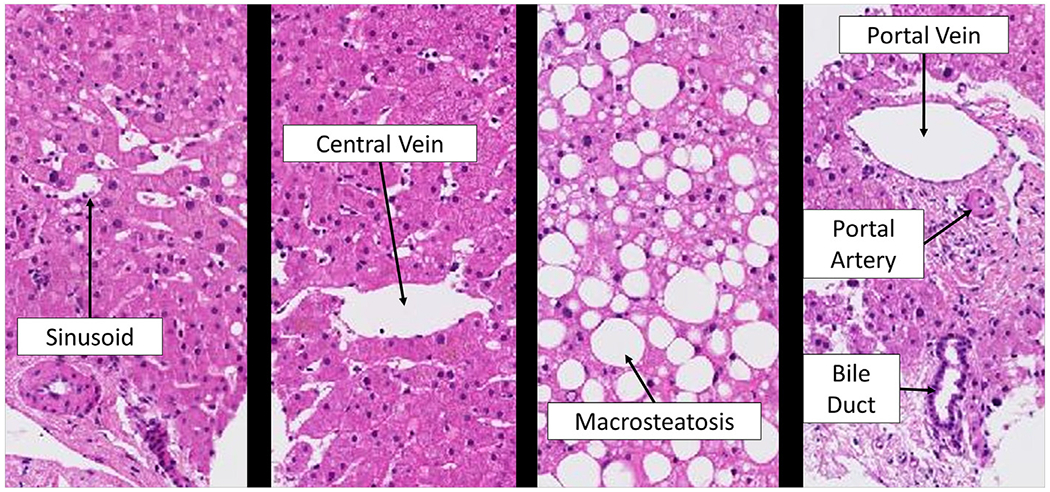
White regions in liver biopsies.

2. Materials and methods

This research protocol was reviewed and approved by the Internal Review Board of the Medical College of Wisconsin. A dataset consisting of 59 unique liver biopsy scans is included in our dataset and represents patients with a full range of different diagnosis and steatosis grades. Of our 59 patients, pathologist steatosis grading was available from two different pathologists for 47 patients (20 with normal liver histology and 27 with NAFLD of varying severity). Using a custom-built, Web-based Java Applet, our study pathologists manually annotated biopsy images and categorized 1969 different white regions.

Supplementary Table 1 provides counts for the total number of annotations for each feature type in our dataset, and Supplementary Fig. 1 shows the count of patients in our study by steatosis grade. There is overall good agreement between pathologists on the grade for each patient with D.E.K. having a slightly lower threshold for calling small degrees of steatosis as grade 1 than R.K. (Supplementary Fig. 1).

We carried out the following steps to classify white regions (Fig. 2):

Fig. 2.

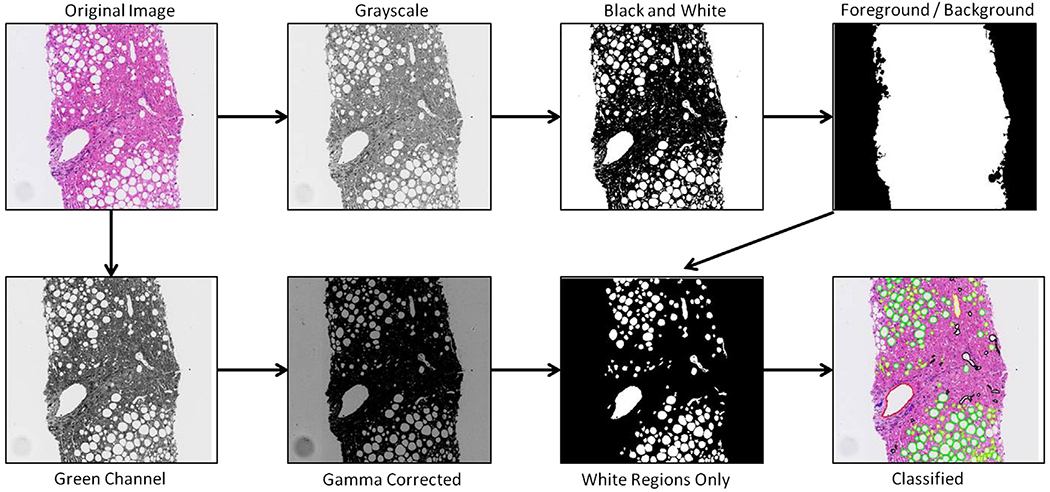
Flow chart pictorially showing the steps taken to classify white regions.

1. Obtain Image: liver biopsy samples are obtained and stained with a H&E stain. They are then scanned at 20× magnification using a NanoZoomer scanner (Hamamatsu) and stored as RGB images with 8 bits per color channel.

2. Convert RGB image to gray scale: 2 separate 8-bit gray scale images are created. The first is used to distinguish between tissue sample and background. The second is created with higher contrast and used for identifying white regions within the tissue sample.

3. Conversion to black and white image: Otsu’s method [16] is used to determine a global threshold value from our first gray scale image. This threshold is then applied to convert the image to black and white.

4. Identify biopsy (image foreground versus background): a region growing algorithm is used to separate image foreground from image background. Any small artifacts outside of the primary biopsy tissue region are removed from the image foreground based on their small size.

5. Image Adjustment: the gray scale image created from the green channel is smoothed using a 3×3 average filter. The image is then darkened significantly using a gamma correction factor of 6 to increase contrast.

6. Identify White Regions of Interest: all foreground pixels are divided into 2 classes using k-means clustering. Once assigned a class, adjacent pixels of the same class are grouped into either a white region or non-white region based on 4-neighborhood connectivity. White regions that are smaller than a chosen threshold are considered noise and eliminated for further analysis.

7. Feature vector representation: each white region is assigned a feature vector representation to be used in a classifier.

8. Supervised learning and classification: white regions that have been annotated by pathologists are used as training data for a supervised machine learning classifier. The models learned from annotated data are applied to entire images to classify all white regions.

Using the annotations provided by pathologists, a feature vector (a list of attributes specific to each white region) is created. One goal of this research is to compare the use of morphological features (as had been done in previous, non-machine learning based studies) with the use of additional region properties. For that reason, feature vectors are created using only the morphological properties of the white region itself for comparison with other feature vectors that contain additional information about the texture and statistical properties of the white region and surrounding pixels.

For attributes related to a white region’s surrounding pixels, features are extracted from two different surrounding regions (Fig. 3). The first is the bounding box enclosing the region (Fig. 3C). Any features based on the bounding box are also inclusive of the white region itself. The second region type is the “band” of pixels surrounding the white region (Fig. 3D). Texture and statistical features are then extracted for pixels that fall just within this band. Features based on the surrounding band are motivated by the fact that many of our white regions, such as bile ducts and portal veins, have color regions surrounding the white region that are unique to that specific type of liver anatomy.

Fig. 3.

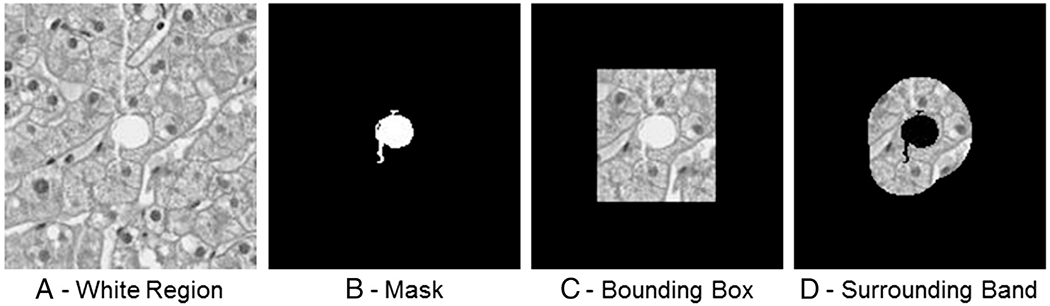
A, A white region located at center. B, The mask applied to reveal just the white region. C, The rectangular bounding box around the white region. D, The surrounding band of pixels around the white region. Features are extracted from the regions visible in C and D for attributes related to the white region’s surrounding pixels.

Texture and statistical features are created based on gray images with scale representation created using a Gaussian blur at varying sigma (σ) levels [17]. Scale representation is based on the fact that objects in the world appear in different ways depending on the scale of observation. All texture and statistical-based features are extracted for both the gray scale bounding box at a given sigma level, and the associated surrounding bands (Fig. 4).

Fig. 4.

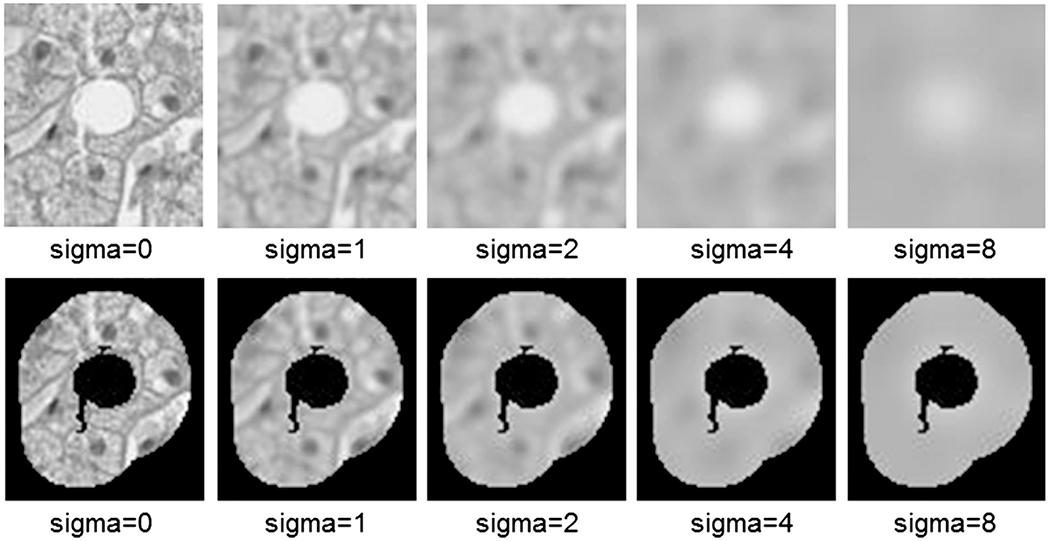
Scale representation of a white region at the given sigma levels.

The list below details the feature vectors used for analysis of white regions. Each white region is assigned three different feature vectors. The first includes just the morphological features below. The second contains all the features below; however, scaled representation was only used at sigma = 0. In other words, texture and statistical properties are only based on the original image with no blurring. The third is all features with scale representation occurring at sigma levels of 0, 1, 2, 4 and 8.

• Morphological Features: features based on the shape and size characteristics of the white region. Includes measures such as area, perimeter, eccentricity, axis lengths, etc.

• Texture: texture and histogram statistics are computed for the gray scale bounding box and surrounding pixel band at each sigma level. The features include measures such as mean intensity, statistical moments, entropy, etc.

• Gray level Co-Occurrence Matrix: the gray level co-occurrence matrix (GLCM) is computed for pixels in the surrounding band of each white region. GLCM’s are a measure of how often two different (or identical) pixel intensities occur next to each other in an image. For the GLCM, 8-bit gray scale images are converted to 3-bit images resulting in an 8 × 8 matrix. The GLCM matrix is created symmetrically. In other words, an occurrence of pixel intensity 2 to the left of intensity 1 is the same occurrence as a pixel intensity 1 to the left of intensity 2. This reduces our feature set from 64 to 36 for a 8 × 8 matrix. The GLCM itself is only used as a feature at sigma = 0.

• GLCM Statistics: at each scale level, GLCM statistics such as contrast and energy are used as features for both the horizontal and vertical GLCM.

• N-jet: for each sigma level in our scale representation we compute the first and second derivatives with respect to x and y, otherwise known as the 2-jet [18]. For the 2-jet at each sigma level, the four rotationally invariant descriptors below are generated: gradient magnitude, Laplacian, determinant of Hessian, rescaled level curve curvature. For each of the 4 descriptors, statistical measures are then taken for each pixel either within the white region itself or in its surrounding band.

• Nuclei Density: nuclei density is a measure of the number of cell nuclei in a given radius. Though not discussed in detail herein, a method was developed as part of this research to threshold cell nuclei from stained biopsy sections for quantification.

All supervised machine learning tasks in this work are carried out with support vector machine. Various different classifiers including naive Bayes, logistic regression, decision trees, and neural networks were considered, but support vector machines routinely performed better or equivalent to other classifiers.

Supervised machine learning is carried out using the open-source Waikato Environment for Knowledge Analysis (Weka) data mining software (Weka Machine Learning Project, 2011). Weka’s implementation of sequential minimal optimization algorithm for training a support vector classifier using polynomial or RBF kernels [19] is used in learning experiments. This classifier is used with a linear kernel first order polynomial.

3. Results

The models shown here all use the feature vectors described in the previous section with the dataset. The result are based on the annotations provide by R.K., D.E.K., and a combined data set.

Three different types of feature vectors are created for comparison: the first is based on just the morphology of a white region (12 features), the second includes morphology as well as texture and statistical attributes from surrounding pixels (157 total features), and the last includes morphology as well as the texture and statistical attributes of surrounding pixels occurring at different scales (413 total features).

Table 1 gives the overall test-set accuracy of models using these feature vectors averaged over 10 folds. Evaluation of white region classification was carried out using a 10-fold cross-validation experiment, where in each experiment 10% of our data are withheld to serve as testing data and the remaining 90% is used for training a model.

Table 1.

Overall accuracy and P-value of models created using R.K.’s annotations, D.E.K.’s annotations, and the combination of both R.K. and D.E.K.’s annotations

Model	Overall Accuracy			P-value
	Pathologist (R.K.)	Pathologist (D.E.K.)	Combined
Morphology	76.4%	64.6%	70.9%
+ Texture at sigma = 0	92.1%	84.0%	87.2%	<.0001
+ Scaled representation	93.5%	84.5%	89.3%	.0025

NOTE. P values are for combined models being compared with the row above.

As Table 1 shows, accuracy is improved by using more advanced and robust features that include not only information about the shape and size of a region but also information about the texture and statistical properties of surrounding pixels. In addition, examining texture and statistical features at different scales further improves model performance.

Table 2 shows the confusion matrix for each feature type in the model. Table 3 shows the precision and recall rates, as well as areas under the receiver operating characteristic (ROC) curve for each individual feature type. Precision is a measure of the preciseness of predictions. In other words, if the model predicts a region is of type X, then the precision for region type X is the percentage of times the model is correct. Recall is a measure of the percentage of the time a given feature type is correctly identified. The area under the ROC curve measures discrimination, that is, the probability the model will rank a randomly chosen region of type X, higher than a randomly chosen region that is not of type X.

Table 2.

Confusion matrix for classified white regions

Actual	Predicted
	Bile duct	Central vein	Macrosteatosis	Other	Portal artery	Portal vein	Sinusoid
Bile duct	51	0	1	0	6	4	0
Central vein	0	72	8	2	2	13	17
Macrosteatosis	0	4	1072	4	1	3	16
Other	0	6	4	43	0	4	11
Portal artery	3	7	0	0	32	10	2
Portal vein	2	6	5	0	7	184	4
Sinusoid	0	12	30	1	0	5	305

NOTE. Classification performed using data from combined two-pathologists dataset created with support vector machine with a linear kernel.

Table 3.

Precision rate, recall rate, and ROC area under the curve for models created using R.K.’s annotations, D.E.K.’s annotations, and their combined annotations

Feature	Pathologist (R.K.)			Pathologist (D.E.K.)			Combined model
	Precision	Recall	ROC area	Precision	Recall	ROC area	Precision	Recall	ROC area
Bile duct	0.92	0.87	0.98	1.00	0.56	0.93	0.911	0.82	0.99
Central vein	0.64	0.79	0.92	0.67	0.64	0.83	0.615	0.63	0.83
Macrosteatosis	0.98	0.99	0.98	0.92	0.94	0.96	0.957	0.98	0.97
Other	1.00	0.86	0.99	0.76	0.69	0.90	0.860	0.63	0.94
Portal artery	0.85	0.77	0.97	0.67	0.18	0.94	0.667	0.59	0.96
Portal vein	0.91	0.77	0.97	0.81	0.88	0.97	0.825	0.84	0.97
Sinusoid	0.90	0.89	0.96	0.80	0.79	0.92	0.859	0.86	0.94

Examining the results, macrosteatosis shows very strong precision and recall rates across all models. BD, PV, and SN all show strong precision and recall rates as well. CV and PA do not perform as well but both still have relatively high ROC areas.

Models initially trained using the annotations provided by R.K. had an overall accuracy of 93.5% and achieved the best overall model results. The model achieved 84.5% accuracy using the annotations provided by D.E.K. and 89.3% when combining the 2 pathologists’ annotations.

With a model and approach for white region classification, a method now exists for identifying all the macrosteatosis in a biopsy section. With that, a simple computation can be performed taking the total surface area of the steatosis versus the surface area of the biopsy section to compute a continuous measure of the overall percentage of steatosis in a biopsy sample. To obtain this percentage of steatosis, a different model was created for each patient using only training data from other patients, otherwise known as a leave-one-sample out approach.

To gauge the effectiveness of this approach and its ability to generalize, percentage steatosis grades were computed and correlated with steatosis grades provided by our two study pathologists. Fig. 5 shows the results of correlating the computed percentage steatosis with the average of the two study pathologists grades. Note that cases where the average pathologist grade ends in .5 indicates the pathologists disagreed by one grade level. The charts show a good relationship, with a spearman rank correlation of 90.8%, between average pathologist grade and overall percentage steatosis. This correlation drops to 83.3% or 88.6% when using just the scores provided by R.K. or D.E.K., respectively. This is in fact a desired result as the ability to correlate more closely with the average of the two pathologist grades, than to either pathologist individually, suggests cases where pathologists disagreed are truly on the border between two grade levels. The continuous nature of the percentage steatosis metric allows this to be captured.

Fig. 5.

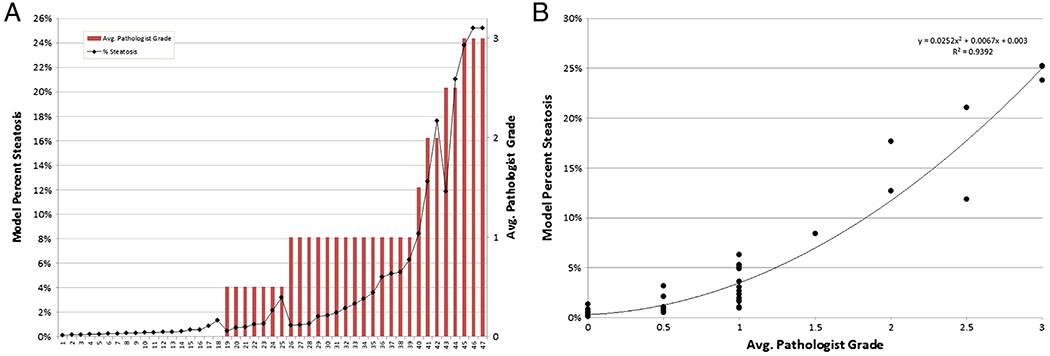
Correlation (A) and relationships (B) of computed percentage steatosis with the average of the two study pathologists’ grades.

4. Discussion

The results of this work demonstrate that automated classification of white regions in digital liver biopsy images is feasible and highly accurate. Our classifier has the best reported accuracy in the literature for detecting and quantifying steatosis, and the first to accurately identify multiple hepatic anatomy landmarks in images of liver biopsy. No bias was used when selecting the biopsy samples and images included in our study. This demonstrates the classifier’s robustness to typical variations in the appearance of the tissue sample, which can be caused by the strength and concentration of the H&E stain used on the tissue sample, as well as any other noise or artifacts introduced in the biopsy slide preparation process or image acquisition.

Mimicking steps followed by human pathologists, our classifier learns based on features related to a white region’s morphology, as well as the scaled representation of texture features of the immediate surrounding areas.

Accurate classification of all white regions has several direct and significant implications.

First, it provides a direct road map to quantify steatosis in a biopsy image. Once all steatotic regions have been identified, a calculation can be carried out dividing the total area of steatotic regions by the total area of the biopsy sample to arrive at a continuous measure of the overall percentage steatosis. This metric can then be correlated with expert pathologist’s semiquantitative grading of hepatic steatosis. Automatic quantification of steatosis can aid in diagnosing and assessing the severity of NAFLD, determining donor liver suitability for transplantation, or response of NAFLD to interventions in clinical trials. Extending the application of this classifier to clinical practice will depend on validation of its performance in additional cohorts and availability of digital scanners in pathology practices in order to create the digital images from the glass liver biopsy slides.

The second direct implication is the identification of white regions that are liver anatomical landmarks to be used in subsequent tasks. Two of the key histological features associated with NAFLD are inflammation and fibrosis. Determining their presence as well as their location in a biopsy sample is important. Therefore, if we have a method for identifying PV, PA, and BD, all of which only occur in the portal triad area, or for CV which resides in the lobule, we have a method to determine if nearby inflammation or fibrosis should be excluded or included from further quantitative analysis.

Previous research has been done in the areas of quantification of hepatic steatosis, fibrosis, and hypertrophy. Fibrosis does not manifest as white in H&E-stained biopsy images, and its quantification is not closely related to the white region classification task, the subject of this paper.

The majority of other studies on white region classification have focused on the specific task of classifying white regions as either steatosis, or not-steatosis [20-27]. The primary challenge in the automated quantification of steatosis is to correctly identify all fatty cells, while being careful to not include other white features such as CV, PV, BD and others that are similar in appearance [20]. This research differs from past research on white regions classification in four ways:

1. Past researchers have set out to identify either just steatosis or central veins [21] in liver biopsy images. In contrast, this work aims to classify all types of white regions. This is the first research identifying BD, PA, PV, and SN.

2. Previous studies have relied on semi-quantitiative analysis or an interactive step [22,23]. In some cases, that work has relied on specific stains designed to simplify the identification of steatosis [24]. Our method is purely automated and does not rely on a stain with the singular purpose of identifying steatosis.

3. With the exception of the study by Foley et al [21] to identify CV, all other studies have relied on handcrafted rules or thresholds chosen by computational analysis or trial and error to identify white regions [20,24-27]. These computations have been found to generally correlate to a pathologist’s semiquantitative measure; however, because they lack labeled regions, their accuracy is unknown. This research uses a supervised machine learning approach that allows the overall accuracy of the classifier to be quantified directly rather than by surrogate measures.

4. All previous methods for identifying steatosis have been based purely on the morphology of white regions. This research examined and utilized other attributes of a white region, such as the texture and statistical properties of adjacent regions, as beneficial attributes in classification.