SIAMESE VERIFICATION FRAMEWORK FOR AUTISM IDENTIFICATION DURING INFANCY USING CORTICAL PATH SIGNATURE FEATURES

Abstract

Autism spectrum disorder (ASD) is a complex neurodevelopmental disability, which is lack of biologic diagnostic markers. Therefore, exploring the ASD Identification directly from brain imaging data has been an important topic. In this work, we propose the Siamese verification model to identify ASD using 6 and 12 months cortical features. Rather than directly classifying a testing subject is ASD or not, we determine whether it has the same or different label with the reference subject who has been successfully diagnosed. Then, based on the comparison to all the reference subjects, we can predict the label of the testing subject. The advantage of modeling the classification problem as a verification framework is that it can greatly enlarge the training data size and enable us to train a more accurate and reliable model in an end-to-end manner. In addition, to further improve the classification performance, we introduce the path signature (PS) features, which can capture the dynamic longitudinal information of the brain development for the ASD Identification. Experiments showed that our proposed method reaches the best result, i.e., 87% accuracy, 83% sensitivity and 90% specificity comparing to the state-of-the-art methods.

1. INTRODUCTION

Autism spectrum disorder (ASD) is a complex neurodevelopmental disability that can cause significant difficulties in social-related function and communication as well as repetitive and restricted behaviors. According to the Disease Control and Prevention (CDC) Report in 2018, about 1 in 59 children has been identified with ASD in U.S. [1]. However, due to the unknown pathological reason and lacking of biologic diagnostic markers, ASD might not be recognized until elder age when the required social deficits and behavioral patterns are identified [2]. This will miss the best opportunity of treatment intervention. Recent research demonstrates that early brain changes could be observable in structural brain MR imaging before autistic behaviors first emerge [3], which motivated the study to explore patterns in infant brain imaging data for facilitating the earlier ASD diagnosis.

Literally, through the combination of machine learning methods and brain imaging data, many methods have shown promising results for the ASD/non-ASD classification. Among them, the deep learning based algorithms have been introduced into ASD classification recently [3][4][5][6][7]. Deep convolutional neural networks (CNNs) and its variants are powerful image-based feature extraction and classification methods, but require large number of training data. In [5][6][7], they converted MRI data as either a set of meaningful patches [5][6] or a set of intrinsic connectivity networks [7] to enlarge the training data size. In [3][4], the high-level feature vectors are extracted to reveal essential brain properties, but they are difficult to expand the size because every subject is an unique sample. Due to the limited number of participants, a very basic deep learning method, such as the two-stack autoencoder (AE) module is chosen for feature learning and then, the support vector machine (SVM) is adopted to use the learned features for the final classification. Therefore, in the ASD research, an end-to-end method which has the potential ability for adapting the large scale dataset is highly needed to automatically extract representative features for the robust and accurate classification.

In this work, we study the 6 and 12 months infant brain MR images with their cortical morphological features for the ASD Identification. Rather than using a classification model, we propose to adopt the verification framework that identifies a pair of subjects as belonging to the same class or not. This strategy significantly increases the training data size and also enables us to better explore the high-level representation for the ASD classification in an end-to-end manner. In the training process, the model learns the similarity metric from all subject pairs, whose number is much larger than the training subject number. In the testing process, we firstly compute the similarity between the testing subject and all training subjects, and then its label is determined by the majority voting. Specifically, we propose a Siamese fully-connected (FC) neural network model to learn the pair-wise similarity metric. Moreover, considering the ASD can be better identified with the longitudinal information, instead of using the static features at each time point, we propose to leverage the longitudinal information by generating the path signature (PS) based feature to effectively characterize the longitudinal brain development. To the best of our knowledge, it is the first time utilizing the verification model for ASD classification. In our experiments, we achieve 87% accuracy, 83% sensitivity and 90% specificity.

2. MATERIALS

The T1w and T2w brain MR images were gathered in the National Database of Autism Research (NDAR). All images were acquired at around 6 and 12 months of age on Siemens 3T scanners. Subjects were naturally sleeping with their heads secured in a vacuum-fixation device and ear protected. T1w MR images were acquired with 160 sagittal slices using parameters: TR/TE=2400/3.16ms and voxel resolution = 1 × 1 × 1 mm³. T2w MR images were obtained with 160 sagittal slices using parameters: TR/TE = 3200/499 ms and voxel resolution = 1 × 1 × 1 mm³.

All infant MR images are then preprocessed following an established infant specific computational pipeline [8]. We obtain the regions of interest (ROIs) based on an infant dedicated cortical surface atlas [9], which includes 70 anatomically meaningful ROIs following the Freesurfer parcellation protocol. Each subject is aligned to the atlas to get the ROI-based features. For each ROI, we obtain two representative morphological features, i.e., cortical surface area and cortical thickness. In addition, we compute the total brain volume. Accordingly, for each subject at two longitudinal time points (6 and 12 months), we have a 283-dimensional feature vector that includes 140 6-month ROI cortical features, 140 12-month ROI features, 2 total volume features, and the gender.

3. METHOD

Given cortical features of N subjects at 6 and 12 months, our goal is to predict whether the subject will have ASD or not. We will present the dual-path verification model and PS feature extraction method in details.

3.1. Siamese verification model

Verification and classification have subtle differences and they are well studied in various applications, like face, handwriting, and fingerprint. In general, classification is to classify the input into different class labels (identities), while verification is to classify a pair of inputs whether belonging to the same class or not [10]. Additionally, Siamese architecture enforces two paths having the same structure and parameters, which enables the pair-wise input and expands the training data size. Hence, for our binary classification problem, the verification model can decide whether two subjects are from the same class or not. If the label of one input is given, the label of the other input can be derived accordingly.

Given N subjects (including both ASD and NC) with both 6 and 12 months features, we can group any two different subjects as one training pair, T_ij = {n_i, n_j}. Their label is binary, indicating two subjects belonging to the same (defined as 1) or different (defined as 0) classes. In this way, we can have [(N − 1) × N]/2 training pairs all together, which is much larger than the number of original subjects.

The training and testing frameworks of Siamese verification model are shown in Fig. 1. We propose to use two fully connected (FC) layers because of their simplicity and effectiveness in feature combination and dimensional reduction. We ensure that two paths are identical and share the same set of weights, which is known as Siamese architecture [10]. Finally the similarity function is defined as the cosine similarity $\mathcal{D}$, which has been successfully applied in image searching and face verification,

$$\mathcal{D}\left(x_i,x_j\right)=\frac{x_i\cdot x_j}{\Vert x_i\Vert *\Vert x_j\Vert }$$ (1)

where x_i and x_j are computed FC features of subject n_i and n_j. The distance between two features is small if they belong to the same classes and large otherwise.

Fig. 1.

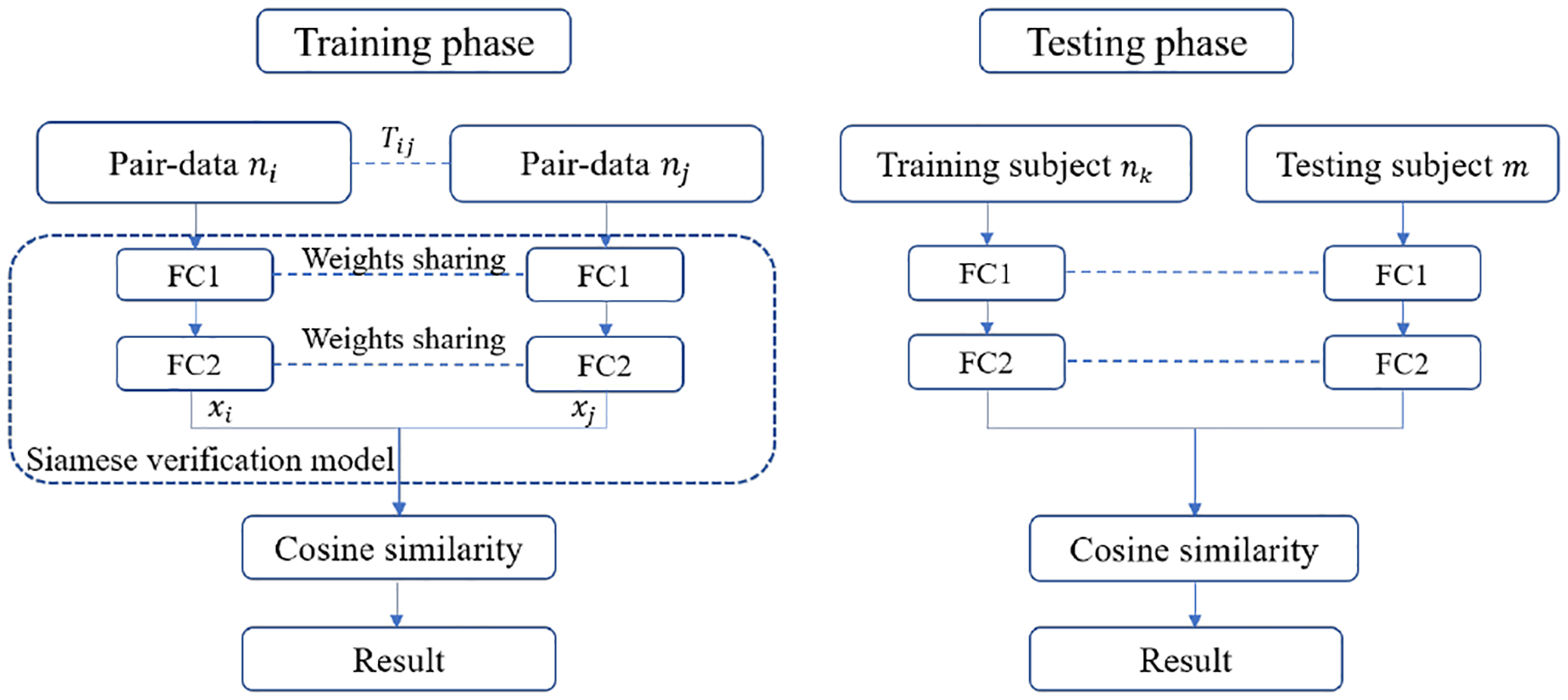
Illustration of Siamese verification model for the training and testing modes.

In the testing process, we compute the similarity distance between the testing subject m_t and each training subject n_k and obtain the result. The final label is obtained by the majority voting based on the results of all training data.

3.2. Path signature based longitudinal features

By modeling the classification problem as a verification framework, we enlarged the training data size. To better leverage the longitudinal information, we propose to extract path signature features to capture the dynamic longitudinal brain development.

The rough path theory was originally proposed to solve differential equations driven by highly oscillatory signals. The core object of the rough paths theory is the path signature (PS) [11], which has been recently used as a trajectory descriptor and applied to many different research fields such as the handwriting recognition [12], and hand gesture recognition [13]. The key advantage is that it is a top-down effective description of the trajectory/path in terms of its effects as a graded tensor series element. It has various advantages, such as the universality, the time-parameterization invariance and fixed dimensional descriptor of time series of variable length/missing data/unequally time spaced. Therefore, we propose to extract the path signature (PS) based feature of cortical longitudinal properties. ¹

3.2.1. Preliminary of Path Signature

We briefly introduce the mathematical definition and geometric interpretation of path signature (PS), which is mainly referred to [14]. Assume a path $P:\left[t_1,t_2\right]\to {ℝ}^d$, where [t₁, t₂] is a time interval. The features of t are denoted by ($P_t^1,\dots ,P_t^d$), where each $P^i:\left[t_1,t_2\right]\to ℝ$ is a real-value path. For an integer k ≥ 1 and the collection of indices i₁, …, i_k ∈ {1, …, d}, the k-fold iterated integral of the path along indices i₁, …, i_k can be defined as:

$$S{(P)}_{t_1,t_2}^{i_1,\dots ,i_k}={\int }_{t_1<a_k<t_2}\dots {\int }_{t_1<a_1<a_2}d{P}_{a_1}^{i_1}\dots d{P}_{a_k}^{i_k}$$ (2)

where t₁ < a₁ < a₂ < … < a_k < t₂.

The signature of path P, denoted by $S{(P)}_{t_1,t_2}$, is the collection (infinite series) of all the iterated integrals of P:

$$S{(P)}_{t_1,t_2}=\left(1,S{(P)}_{t_1,t_2}^1,S{(P)}_{t_1,t_2}^2,\dots ,S{(P)}_{t_1,t_2}^d,S{(P)}_{t_1,t_2}^{1,1},\dots ,S{(P)}_{t_1,t_2}^{1,d},\dots ,S{(P)}_{t_1,t_2}^{d,d},\dots ,S{(P)}_{t_1,t_2}^{1,\dots ,1},\dots ,S{(P)}_{t_1,t_2}^{i_1,\dots ,i_k},\dots ,S{(P)}_{t_1,t_2}^{d,\dots ,d},\dots \right)$$ (3)

The k-th level PS is the collection (finite series) of all the k-fold iterated integral of path P. The 1-st and 2-nd level represents path displacement and the signed area enclosed by the path respectively. By increasing level k, higher levels of path information can be extracted, but the dimensionality of iterated integrals grows rapidly as well. In practice, we often truncate the $S{(P)}_{t_1,t_2}$ at level m to ensure the dimensionality of the PS feature in a reasonable range.

3.2.2. Longitudinal feature set

We propose to compute the PS feature along the longitudinal direction. We can define a path P: [t₁, t₂] that starts at 6-month t₁ and ends at 12-month t₂. Hence, the PS cortical feature can be computed according to eq.3, where ($P_{t_1}^1,\dots ,P_{t_1}^d$) and ($P_{t_2}^1,\dots ,P_{t_2}^d$) are ROI-based thickness and area and the truncated level is k = 3. Similarly, we can compute the PS feature of total volume and we set its truncate level as k = 1, which is essentially the volume change. Therefore, the input feature is consisted of five parts, i.e., the cortical feature, cortical PS feature, total volume, volume PS feature and gender, as shown in Fig. 2.

Fig. 2.

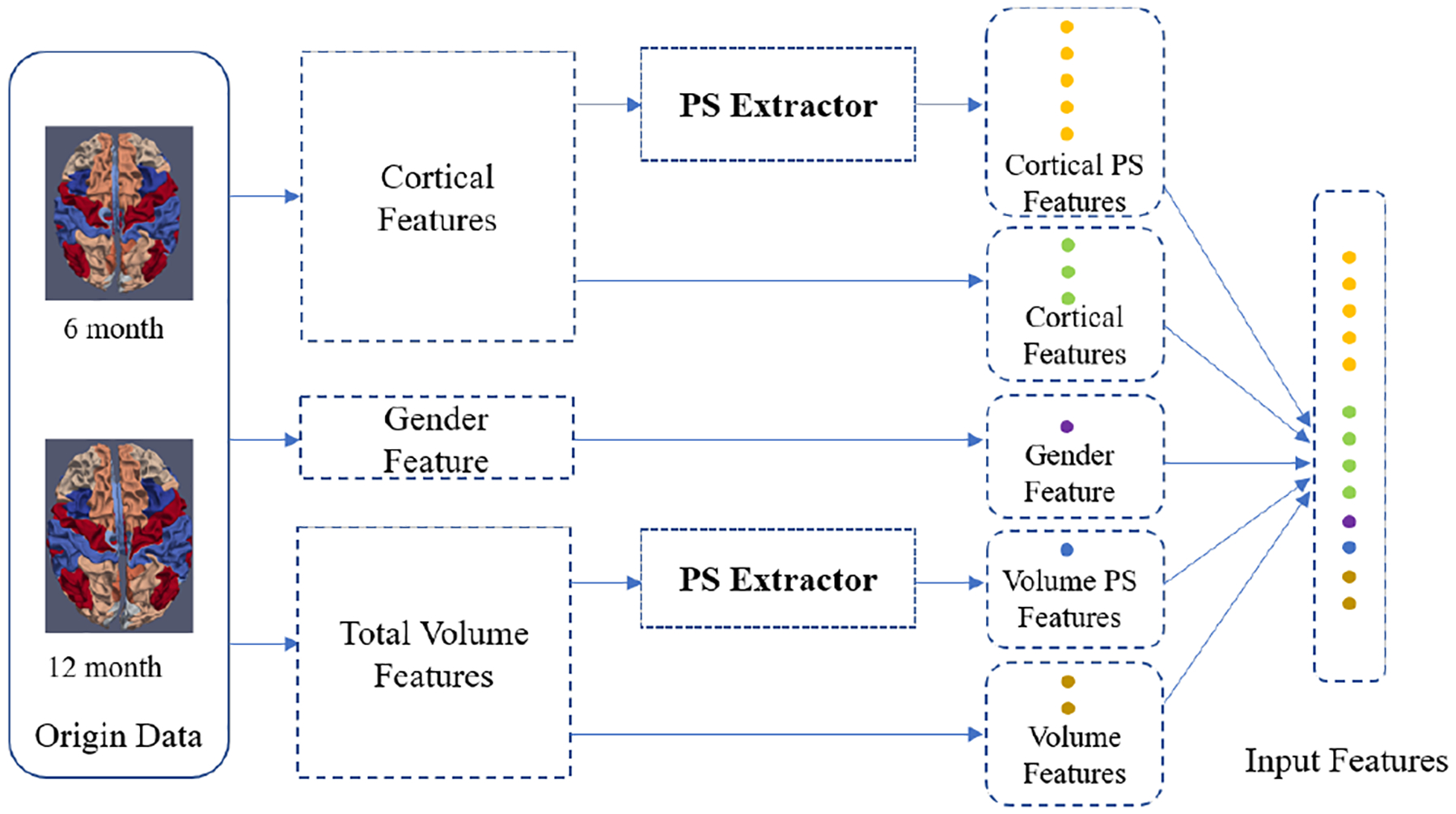
Input features with PS feature extraction.

4. EXPERIMENTAL RESULTS

4.1. Dataset and implementation

We use 60 subjects (30 ASD and 30 normal subjects randomly selected from NDAR dataset) with their longitudinal brain MRimages at 6 and 12 months of age. In this work, we utilize cortical thickness and area features of 70 brain regions.

We evaluate the method with 10-fold cross-validation strategy. In each fold, we ensure to have the equal number of ASD and normal subjects. For the verification model, we group any two different subjects as one training pair. If both samples in the pair are autistic or normal, the label is 1; otherwise the corresponding label of the pair is 0. As a result, we have 1,431 training pairs in every fold to train the model. During training phase, we set the epoch as 20 and learning rate as 0.0005 with Adam optimization. During testing phase, given the trained model, we compute the similarity between the testing subject and all the training subjects. So that each testing sample has 54 pair-wise results and its final label (ASD/Normal) are determined by majority voting.

4.2. Ablation study

We do some ablation experiments to explore the effectiveness of the verification framework and new PS features. The comparison results with six statistical indexes are shown in Table 1. Firstly, we train the classifier using the fully-connected (FC) layers with original features as the input and use the traditional classification model, referred as V-1 in Table 1. Based on that, we only change the classifier into the Siamese verification model, referred as V-2. Then, we keep the FC classifier but change the input as new PS based features, referred as V-3. Comparing the results of V-2 to V-1, we can see the verification model has led to a superior performance over the traditional classification model. Comparing V-3 and V-1, we can see the longitudinal information has led to better performance. The combination of these two reaches the best performance in the last row.

Table 1.

Ablation study. M-1: accuracy; M-2: sensitivity; M-3: specificity; M-4: positive predictive value (PPV); M-5: negative predictive value (NPV); M-6: F1-score. V-1: Original data with FC classifier; V-2:Original data with proposed verification model; V-3: PS features with FC classifier.

Methods	M-1	M-2	M-3	M-4	M-5	M-6
V-1	0.67	0.8	0.53	0.63	0.73	0.71
V-2	0.73	0.70	0.77	0.75	0.72	0.72
V-3	0.72	0.63	0.80	0.76	0.69	0.69
Our method	0.87	0.83	0.90	0.90	0.84	0.86

4.3. Comparison with the other methods

We also compare our method with several widely used classification methods, like Logistic Regression (LR), Random Forest (RF), and Support Vector Machine (SVM). Also, we implement a recent most related work [3], which studied the 6 and 12 months ASD problem with cortical features using the three-layer auto-encoder (AE) for feature extraction and SVM for classification. Comparison results are shown in Table 2. In terms of the accuracy, our proposed method reached the best result. For the sensitivity, our method is comparable with [3] which means we can detect ASD with the same accuracy. But considering the specificity, our method is much better which indicates less mistakes in the normal subject classification. Hence, in general, our proposed method is much more accurate and reliable.

Table 2.

Experimental comparison. M-1 to M-6 definition is the same with Table 1.

Methods	M-1	M-2	M-3	M-4	M-5	M-6
RF	0.62	0.60	0.63	0.62	0.61	0.61
SVM	0.63	0.43	0.83	0.72	0.60	0.54
LR	0.63	0.63	0.63	0.63	0.63	0.63
AE+SVM [3]	0.72	0.83	0.60	0.68	0.78	0.75
Our method	0.87	0.83	0.90	0.90	0.84	0.86

5. CONCLUSIONS

We have proposed Siamese verification model with PS based cortical features for infant ASD Identification using 6 and 12 months MRI data. The model adopts fully connected layers as the main block. The Siamese architecture enforces two same paths and ensures pair-wise inputs. In this way, the training data size is expanded and the similarity between two classes can be learnt effectively. Additionally, we leverage path signature algorithm to characterize the longitudinal brain features. We compared the proposed method with several state-of-the-art frameworks and our method achieved the best result. In the future, we will further improve the similarity model in the verification model and test the spatial path signature features.