Neurally driven synthesis of learned, complex vocalizations

SUMMARY

Brain Machine Interfaces (BMIs) hold promise to restore impaired motor function and serve as powerful tools to study learned motor skill. While limb-based motor prosthetic systems have leveraged nonhuman primates as an important animal model,^1–4 speech prostheses lack a similar animal model and are more limited in terms of neural interface technology, brain coverage, and behavioral study design.^5–7 Songbirds are an attractive model for learned complex vocal behavior. Birdsong shares a number of unique similarities with human speech,^8–10 and its study has yielded general insight into multiple mechanisms and circuits behind learning, execution, and maintenance of vocal motor skill.^11–18 In addition, the biomechanics of song production bear similarity to those of humans and some nonhuman primates.^19–23 Here, we demonstrate a vocal synthesizer for birdsong, realized by mapping neural population activity recorded from electrode arrays implanted in the premotor nucleus HVC onto low-dimensional compressed representations of song, using simple computational methods that are implementable in real time. Using a generative biomechanical model of the vocal organ (syrinx) as the low-dimensional target for these mappings allows for the synthesis of vocalizations that match the bird’s own song. These results provide proof of concept that high-dimensional, complex natural behaviors can be directly synthesized from ongoing neural activity. This may inspire similar approaches to prosthetics in other species by exploiting knowledge of the peripheral systems and the temporal structure of their output.

In brief

Songbirds, like humans, need to control a sophisticated vocal organ to produce rich vocal sequences. Arneodo et. al. use knowledge of the biomechanics of the vocal organ and the structure of the vocal sequence to synthesize birdsong from recorded premotor neural activity.

Graphical Abstract

RESULTS AND DISCUSSION

We describe two methods for synthesizing realistic vocal signals from neural activity recorded in a premotor nucleus of zebra finches (Taeniopygia guttata). Each method exploits a different trait of the vocal-motor process. First, we leverage understanding of the biomechanics of birdsong production. We employ a biomechanical model of the vocal organ that captures much of the spectro-temporal complexity of song in a low-dimensional parameter space.²⁴ This dimensionality reduction, compared to the full time-frequency representation of song, enables training of a shallow feedforward neural network (FFNN) that maps neural activity onto the model parameters. As a second synthesis method, we capitalize on predictive components in the temporal covariance between neural activity and song, which can be learned by a recurrent, long-short-term memory neural network (LSTM)²⁵ trained directly on frequency domain representations (spectrograms) of the vocal output.

Neuronal input for each synthesis comes from the sensorymotor nucleus HVC, where neurons generate high-level commands that drive the production of learned song. Adult male zebra finches (Taeniopygia guttata) sing individually stereotyped motifs comprising a sequence of 3–10 syllables. Activity in multiple HVC neuronal subtypes is modulated during singing: projection neurons targeting area X and RA (HVC_x/RA) evince short, precise, sparse activity bursts during the motif,^{15,17,26–30} while inhibitory interneurons (HVC_I) display more tonic activity during singing.^14,29,31,32 To obtain ensemble HVC activity and vocal output, we implanted 16- or 32-channel Si probes in male, adult (>120-day-old) zebra finches and recorded extracellular voltages simultaneously while each bird sang (n = 4 birds, 70–120 vocal motifs per session). Neural recordings were sorted automatically using Kilosort and manually curated to exclude noise.³³ Non-noise clusters were classified as single- or multi-unit activity (SUA or MUA) based on the number of refractory period violations and putatively as projection or interneurons based on the sparseness of the activity during singing. The recordings were dominated by MUA clusters (n = 88) and HVC interneurons (HVC_I; n = 29), with relatively few putative projection neurons (HVC_x/RA; n = 15). Example song-aligned neural activity histograms are shown in Figure 1A. Example rasters with the numbers of clusters per bird are shown in Figure S1.

Figure 1. A neural-network-based decoder to synthesize birdsong from premotor neural activity.

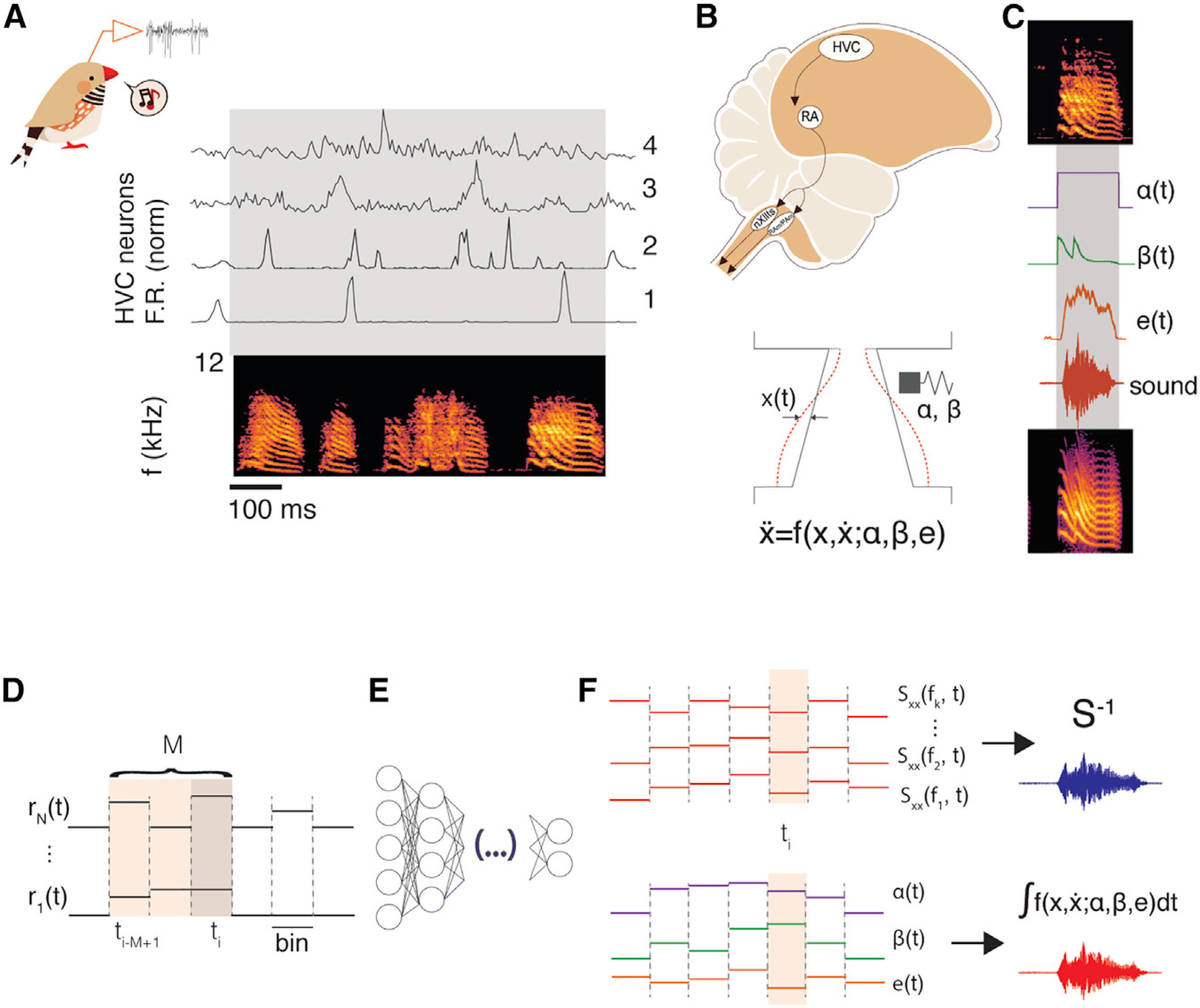
(A) Neural activity is collected from awake-singing animals. Sorted, extracellularly recorded single- and multi-units show different degrees of singing-related sparseness, robustness, and spiking precision (4 example clusters; top traces: normalized mean firing rate over 70 repetitions of the bird’s motif; below: spectrogram of the motif; see also Figure S1).

(B) Downstream of HVC, the posterior motor pathway leads into nuclei that control the muscles driving the sound production (nXII and RAm/PAm).³⁴ Syringeal and respiratory muscles act coordinately to modulate the flow of air through sets of labia and produce sound.³⁵ The complex labial motion is captured by the equations of a nonlinear oscillator;²³ parameters that define acoustic properties of the sounds are surrogates of the activities of syringeal and respiratory muscles.³⁶

(C) To reproduce a particular vocalization (top) from the biomechanical model, we fit the parameters (middle {α(t), β(t), e(t)}) such that, upon integration, the synthetic song (bottom) matches the pitch and spectral richness.

(D) The input of the neural network is an array with the values of a set of neural features (spike counts of sorted units/multi-units) over a window of M previous time steps.

(E) The hidden layer(s) of the network are composed either by a densely connected layer (FFNN) or two layers of LSTM cells.

(F) When training or reconstructing directly the spectral features of the song, the output of the network is a vector of powers across a range of frequency bands at a given time; the generated spectral slices are then inverted to produce synthetic song (top). When training or reconstructing via the biomechanical model, the output of the network at a given time is a 3-dimensional vector of parameters (as illustrated in C); the equations of the model are then integrated with these values to produce synthetic song (bottom). Illustrations were taken from Arneodo.³⁷

Biomechanically meaningful compression enhances neurally driven synthesis

Synthesizing a complex motor sequence from neural activity requires mapping between two high-dimensional representations. To reduce the dimensionality of the problem, we leveraged a biomechanical model of the avian vocal organ that transforms neural activity to vocal output. The model accounts for the syrinx and the vocal tract.^24,27,38 The syrinx contains labial folds that oscillate when induced by the sub-syringeal air sac pressure and modulate the airflow to produce sound (Figure 1B).³⁵ The dynamics of the labia can be modeled after the motion equations of a nonlinear oscillator, in which the features of the sounds produced are determined by two time-varying parameters,^23,24,36 representing physiological motor instructions (the sub-syringeal pressure and the activity of the muscles that tense the labia).²⁴ In its simplest form, the syrinx model is computable in real time to produce synthetic vocalizations.³⁸ We model the vocal tract (the trachea, the oropharyngeal-esophageal cavity, and the beak) as a passive acoustic filter that determines species-specific spectral traits, such as the timbre.^24,27,39

To synthesize song from neural activity via the biomechanical model, we first fit the parameters of the model to produce a synthetic version of each vocalization.^24,27,38 We searched for the parameters that produce, upon integration of the equations of the model, the closest match in pitch, spectral richness, and amplitude of the target vocalization. This effectively compresses each segment of a bird’s own song (BOS) into a time series in a 3D parameter space, which generates a corresponding segment of synthetic song (SYN) (Figure 1C).^36,38 For each session, we randomly select 60% of the motifs for training, split each motif into 5-ms bins, and train a one-hidden-layer FFNN to predict the biomechanical model parameters corresponding to each bin independently from the neural activity in a 50-ms, immediately preceding time window. The neural activity was represented by the average firing rate of each cluster, split into 1-ms bins. To avoid introducing temporal correlations, we randomized the order in which each pair of neural activity window and target model parameters was presented to the network. After training, we predict the values of the biomechanical model parameters corresponding to a test set of neural activity and integrate the differential equations of the model to produce each bin of neurally driven synthetic song. This yields synthetic vocalizations that sound similar to the bird’s own. An example motif from each bird is illustrated in Figure 2 (and Audio S1, S2, S3, and S4).

Figure 2. Song synthesized from premotor neural activity via a biomechanical model of the vocal organ is similar to the recorded bird’s own song.

Spectrogram of one or two instances of a bird’s motif (BOS; upper) and corresponding song generated by inferring the biomechanical model parameters from neural activity using a shallow FFNN and integrating the model, for four different birds (z007, z017, z020, and z028, respectively; see also Audio S1, S2, S3, and S4, respectively, and Figures S2 and S4).

In contrast, implementing a FFNN to directly predict the spectro-temporal features of a song results in a low-quality synthesis. We trained a similar network as before but with the spectral components of the song, as represented by the power across 64 frequency bands, as the targets. Examples of songs synthesized in this way for each bird (Figure 3; Audio S1, S2, S3, and S4) show how the FFNN fails to produce well-defined harmonic stacks that are typical of the zebra finch song and to faithfully reproduce vocal onsets and offsets.

Figure 3. Direct spectrogram synthesis from neural activity.

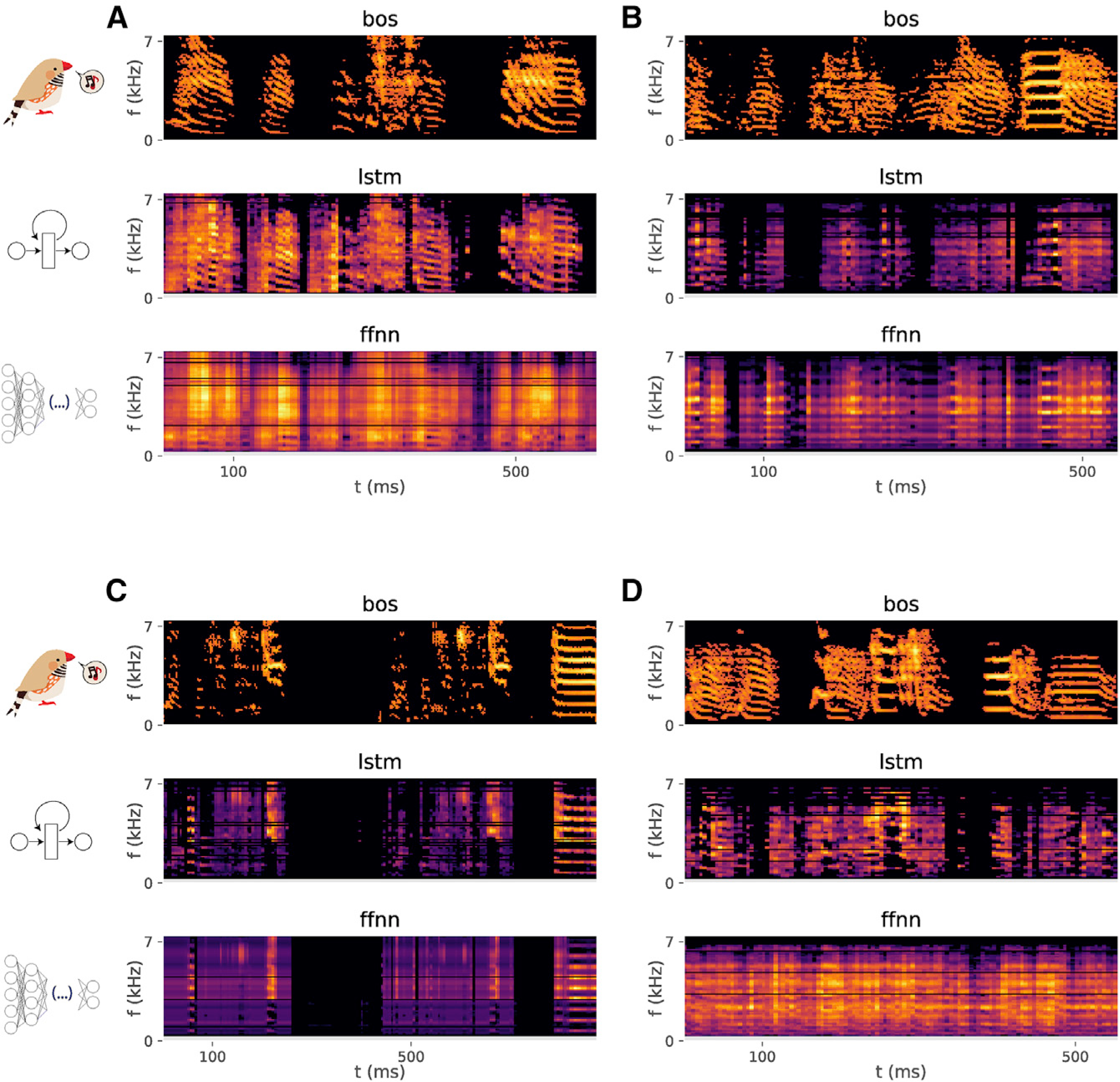
Spectrogram of a bird’s motif (BOS; upper), song generated by inferring the spectrogram directly from neural activity, after training an LSTM (middle), and song generated by feeding neural activity and spectrograms to a FFNN of similar architecture to the one used for Figure 2 (bird z007, z017, z020, and z028, respectively, for each panel. See also Audio S1, S2, S3, and S4, respectively, and Figure S4).

The differing capacities for the FFNN to predict model parameters compared to spectro-temporal coefficients (Figures 2, 3, and 4) suggest that reducing the dimensionality of the behavior enhances prediction. To confirm, we trained the FFNN to reproduce a different “compression” of the behavior, namely the first 3 principal components (PCs) of the spectrogram. The performance at predicting the values of the 3 PCs from the neural activity is similar to that at predicting the biomechanical model parameters (Figure S4A). The advantage of the latter is in their generative capacity to produce songs more similar to the BOS.

Figure 4. Performance comparisons aggregated for all birds.

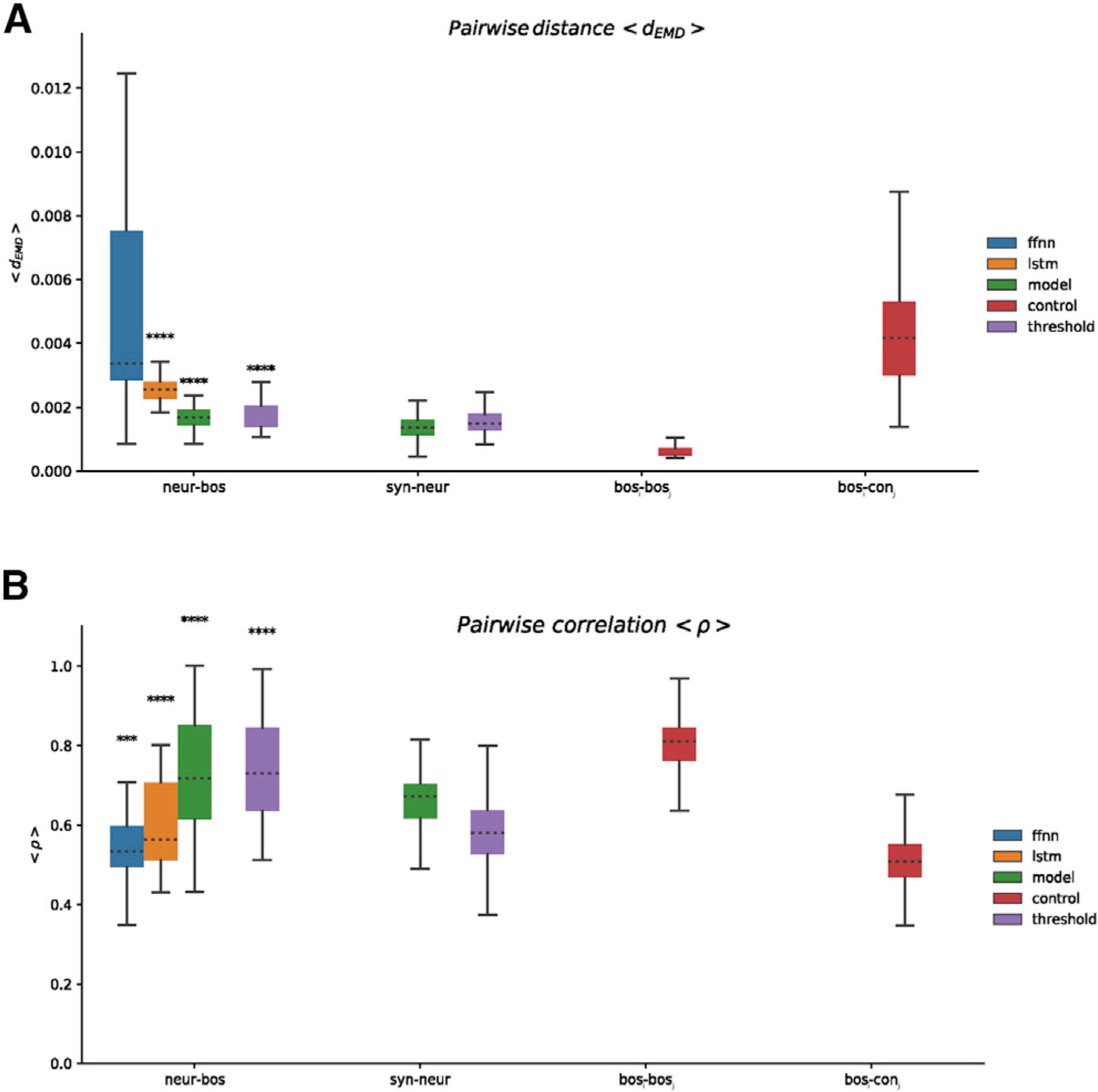
(A) Boxplots showing time-averaged earth mover’s distance (< d_EMD >; lower = better). Neur-bos, distance between each pair of synthesized or target spectrograms in the test set. Ffnn and lstm indicate training directly with spectrogram via a FFNN and LSTM using sorted spikes, model indicates training or synthesis via the biomechanical model of the vocal organ using sorted spikes, and threshold indicates the same training or testing as in model, albeit using supra-threshold activity instead of sorted spikes. Syn-neur indicates the distance between the synthetic instance of each motif in the testing set (the one produced when fitting the parameters of the biomechanical model for a given motif) and the one synthesized from neural activity. Bos_i-bos_j indicates distance between each pair of motifs of BOS. Bos_i-con_j indicates distance between pairs of bos and songs from a pool of conspecific birds.

(B) Boxplots showing time-averaged spectral correlation (< ρ >; higher = better); same pairs as in (A) (***p < 0.001; ****p < 0.0001; Mann-Whitney U test, one sided against bos_i-con_j). Performance for each bird is shown in Figure S3.

The biophysical model can be integrated in real time to produce synthetic vocalizations online.³⁸ This motivated us to skip the spike-sorting step and use a representation of the neural activity that requires cheaper computation and no manual curation. Instead of representing the neural activity with clustered spikes, we trained the FFNN to predict the biomechanical model parameters directly from supra-threshold events in each electrode signal.^1,3,40–42 The results (Figures 4, S2, and S3) suggest that it is plausible to replace the spike sorting by a computationally cheaper representation of the neural activity without significant deterioration of the synthesis.

Exploiting temporal structure

The failure of the FFNN to accurately predict the spectral coefficients of a bird’s motif may reflect the inability of this model to capture more complex temporal dynamics across response clusters that precede specific vocalizations. To capture these dynamics, we trained an LSTM²⁵ to predict the spectral components of the song (64 frequency bands) directly from the preceding 50 ms of neural activity, using the same input and output data as described in the previous section. Unlike the FFNN, the LSTM yields a neurally driven song synthesis that sounds similar to the intended bird’s own song (Figure 3; Audio S1, S2, S3, and S4).

Because zebra finch songs are highly stereotyped across renditions from the same singer, we wondered whether the LSTM might be capturing a trivial correspondence between two synchronized signals (the neuronal activity and the song). To rule out this possibility, we independently shuffled the spectral coefficients in each time slice of the spectrograms. This created a novel stereotyped “song,” in which the explicit relationship between neural activity and any given acoustic feature varied across time, but the temporal correlation between the average neural activity and the waveform envelope was unchanged. After normalizing the durations of all instances of the motif in a bird’s own song through dynamic time warping,⁴³ we permuted the coefficients within each spectral time slice using the same pseudo-random mask for each motif. The quality of the LSTM synthesis dropped significantly for the pseudo-random stereotyped songs (Figure S4C), indicating a non-trivial relationship between temporal dynamics of HVC population responses and the spectro-temporal characteristics of natural song.

To assess the relative similarity of all our syntheses to BOS quantitatively, we compared the spectrograms of each synthesized and target motif pair using two different metrics. We computed the mean distance between spectrograms as the earth mover’s distance (d_EMD)⁴⁴ between each pair of corresponding spectral slices, averaged across time. Intuitively, d_EMD measures the work required to transform one distribution of spectral power onto another and is sensitive to differences in spectral richness (harmonic stacks versus pure tones or broadband energy distribution) and vocalization onset or offset timing. Figure 4A displays a summary of pairwise mean distances < d_EMD > aggregated for all birds (Figure S3 shows data grouped by bird). We show the distance between each motif of BOS and the corresponding synthesis achieved with each different strategy. For reference, we compute the distance between all pairs of motifs of BOS (bos_i – bos_j) and the distances between pairs of BOS and conspecific birds’ motifs (bos_i – con_j). We also computed the mean spectral correlation < ρ > between each synthetic motif and its target across the span of each motif. Results are presented in the same manner in Figures 4B and S3. Consistent with the intuition from Figures 2 and 3, both measures show that an FFNN trained to directly predict the spectrogram yields poorer song synthesis compared to the LSTM and the biomechanical model-aided network, even when trained with supra-threshold neural events.

We show that it is possible to synthesize a rich vocal behavior from neural ensemble activity recorded in singing songbirds, a well-established animal model for vocal communication. Similarity of the synthesis with respect to the bird’s intended vocalization is significantly enhanced by either compressing behavior into a low-dimensional parameter space or by exploiting the spectro-temporal correlation structure of song by the synthesis algorithm. Our results provide insight into how BMIs for complex behavior may be enhanced through detailed understanding of the underlying biomechanics of motor control and the statistical structure of the target behavior.

Introducing a biomechanical model of the vocal organ enables dimensionality reduction and generativity. Compressing the behavior into a few dimensions enables the use of cheap computations that can be implemented in real time³⁸ with relatively small training sets. As a compressive model, the “latent” space provided by the time-varying parameters of the biomechanical model is attractive in that it is a proxy for muscular and respiratory activities.²⁴ In principle, however, other low-dimensional representations of behavior should also be reconstructable from neural activity. Indeed, the 3 strongest PCs of the spectrogram can be predicted by a simple feedforward network almost as well as the parameters of the biomechanical model (Figures S4A and S4B), although these PCs yield poorer synthetic song (Figure S4A) compared to the biomechanical model (Figures 4A and S4B). As a generative model, song synthesized by the biomechanical model is similar to the BOS (Figure 2) and can evoke responses in neural circuits that are highly selective to the BOS.^27,45–47 It remains to be tested whether the biomechanical model-generated song will be sufficient for sensory feedback in closed-loop experiments where neurally driven synthesis replaces BOS³⁸ and whether the synthetic vocalizations can drive naturalistic responses in females, given the species’ ability to differentiate songs based on fine differences in spectro-temporal structure.^39,48,49 Perhaps more detailed models are necessary to fulfill certain functions (BOS replacement and successful courtship). It is also likely that a similar approach can be translated to other species and motor behaviors that admit a low-dimensional, generative representation. This could be the case when the biomechanics are sufficiently understood^{6,22,41,50–56} or when there are enough examples of the behavior to enable data-driven dimensionality reductions.^6,7,57

The limited repertoire of male zebra finches might suggest that a direct synthesis could be achieved by relatively simple means. Yet the FFNN trained to predict spectral coefficients, which, because of its loss function, is close to a regularized nonlinear regression, yielded poor-quality songs compared to all other methods (Figures 4 and S3). The reason for this is not entirely clear, but it may reflect the neuronal subtype compositions of our datasets. Unfortunately, the relatively low yield of well-isolated single units in our recordings (Figure S1) prevents us from examining the contributions of HVC interneurons and projection neurons directly. Most clusters in our datasets were MUA, which are likely dominated by interneuron activity.²⁹ Although the precise function of HVC interneuron activity is not fully understood, it plays a prominent role in multiple models of HVC^29,31,32 sequence generation, and fluctuations in the average firing rates of interneurons are closely timed to bursting in projection neurons.¹⁵ While one should not interpret our results to support the presence of an explicit “motor code” in HVC ensemble activity, employing a recurrent network that captures the temporal structure of our neural population activity, rather than a FFNN, nonetheless yields synthetic songs that are much closer matches to the birds own song.

We have demonstrated a BMI for a complex communication signal, using computation blocks that are implementable in real time in an established animal model for production and learning of complex vocal behavior. The strength of our approach lies in the ability to find a low-dimensional parameterization of the behavior in a manner that it can be driven with the activities recorded from relatively small samples (by tens) of neurons. Doing so with recordings from the superficially located nucleus HVC enables accessibility by less invasive micro-electrode arrays, capable of resolving not only LFP, which has been shown suitable for BMI,⁴¹ but also SUA and MUA.^{1,3,40–42,58,59} This provides a novel tool for probing the neural circuits underlying the production, acquisition, and maintenance of vocal communication signals and unlocks access to new models and experiments directed at understanding how neuronal activity is transformed into natural action and how peripheral effectors shape the neural basis of action.^22,54 Our approach also provides a proving ground for vocal prosthetic strategies. While birdsong differs in important ways from human speech, the two vocal systems have many similarities, including features of the sequential organization and strategies for their acquisition,^60,61 analogies in neuronal organization and function,^10,12 genetic bases,⁹ and physical mechanisms of sound production.^19,23 The experimental accessibility, relatively advanced understanding of the neural and peripheral systems, and status as a well-developed model for vocal production and learning make songbirds an attractive animal model to advance speech BMI, much like the nonhuman primate model for motor BMI.

STAR★METHODS

RESOURCE AVAILABILITY

Lead contact

Further information and requests for resources should be directed and will be fulfilled by the lead contact, Timothy Q. Gentner (tgentner@ucsd.edu).

Materials availability

Printable hardware and electronic designs developed for this work are available in the following github repository: https://github.com/singingfinch/bernardo.

Data and code availability

Data generated in this study have been deposited to https://doi.org/10.6084/m9.figshare.14502198.

Code for data acquisition, processing pipeline and analysis developed for this work is available in the following github repositories: https://github.com/zekearneodo/swissknife; https://github.com/kaichensh/curr_bio_2021.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Subjects

Electrophysiology data was collected from n = 4 adult (> 120 dph) male zebra finches.⁶² Birds were individually housed for the entire duration of the experiment and kept on a 14:10h light:dark cycle. The birds were not used in any other experiments.

Ethical note

All procedures were approved by the Institutional Animal Care and Use Committee of the University of California (protocol number S15027).

METHOD DETAILS

Neural and audio recordings

We used 4-shank, 16/32 site Si-Probes (Neuronexus A4×2-tet-5mm-150–200-121 -PEDOT coated, bird z007-; Buzsaki32 -pedot coated, bird z028-; A4×1-tet-3mm-150–121 -birds z017 & z020-). We mounted the probes on an in-house designed, printable microdrive and implanted them targeting nucleus HVC. Audio was registered with a microphone (Earthworks M30) connected to a preamplifier (ART Tube MP). Extracellular voltages and pre-amplified audio were amplified and digitized at 30kHz using an Intan RHD2000 acquisition system, Open ephys and custom software. Ref and gnd were shorted together via a 0 Ohm resistor on the headstage (Intan RHD2132/RHD2116).

Electrode implant

Animals were anesthetized with a gaseous mixture of Isoflurane/oxygen (1%–2.5%, 0.7 lpm) and placed in a stereotaxic frame. Analgesia was provided by means of a 2mg/kg dose of carprofen (Rimadyl) administered I.M. The scalp was partially removed and the upper layer of the skull over the y-sinus was uncovered. The probe was attached to the shaft of a microdrive of our design (https://github.com/singingfinch/bernardo/tree/master/hardware/printable_microdrive) which was printed in-house using a B9 Creator printer and the BR-9 resin. A craniotomy site was open 2400 μm lateral to the y-sinus (right/left hemispheres). The dura was removed, and the electrode array was lowered to a 300–500 μm depth. The opening was then covered with artificial dura (DOWSIL 3–4680 Silicone Gel Kit) and the microdrive was cemented to the skull using dental cement (C&B Metabond). A reference wire was made with a 0.5 mm segment of platinum-iridium wire (0.002”) soldered to a silver wire lead and inserted between the dura and the skull in through a craniotomy roughly 3mm medial (contralateral to the hemisphere where the electrode was inserted) and 1.5 mm anterior to the y-sinus. The reference electrode was cemented to the skull and the silver lead was soldered to the ref and gnd leads of the Neuronexus probe. Most of the open area, including the electrode and the microdrive, was covered with a chamber designed and 3D printed in house, which was cemented to the skull. The skin incision was sutured and glued to the chamber with superglue. The mass of the probe, microdrive and protective chamber was 1.2–1.4g. Upon returning to a single-housing cage, a weight reliever mechanism was set up: an end of a segment of thin nylon wire (fishing line) was attached to an ad hoc pin in the chamber; the other end routed through a set of pulleys and attached to a counterweight mass of ~1g.⁶³

Dataset preparation

Song detection

A template matching filter written in python was used to find putative instances of the motif, and then curated manually to rule out false positives.

Spike sorting

Spikes were detected and sorted using Kilosort; details of the procedure can be found in Pachitariu et al.³³ The number of clusters was initialized to 32/64 (twice the number of channels of the probe) and the algorithm was allowed to automatically merge similar clusters. In post hoc curation, we removed the clusters that were visibly noise (as per the waveform) and labeled units as putatively SUA/MUA depending on whether the fraction of refractory period (2ms) violations was below/above 3% respectively.

Single Unit type classification

SUA clusters were classified as putatively representing sparse firing projection neurons or tonically firing interneurons, based on their base firing rate and their bursting behavior. We labeled a SUA cluster a putative projection neuron if its mean, spontaneous firing rate was below 5Hz and it produced at most 4 bursts with a frequency of 100 Hz or higher during the motif.³²

Supra-threshold event detection

We wrote scripts in Python to detect spiking events in each channel. First, the RMS of each channel was estimated using a running window, over a period of time that ranged from minutes to an hour. Then, events that deviated in absolute value more than a number of RMS (2.5–5.5) were detected using the package peakutils (min_distance = 0.5ms).

Neural activity features

With all clusters spike-sorted or supra-threshold events, we extracted spike counts within each motif and collapsed them into 1ms (30 samples at 30,000 samples/second) time bins.

Spectral features

When training the networks with spectral features, the target at each time step was a vector containing a spectrogram slice (in log power scale). We generated the spectral slices using the spectrogram function of the signal module in the scipy package.⁶⁴ We used 5ms windows (150 samples) and kept the 64 first bands above 300 Hz.

Biomechanical model of the vocal organ

Model

A model of the zebra finch vocal organ has been previously introduced and it is explained in detail in Perl et al.³⁶ and Arneodo et al.³⁸ This model considers mainly a sound source and a vocal tract that further shapes the acoustics of the vocalizations.

The source (syrinx) comprises two sets of tissues or labia that can oscillate induced by the sub-syringeal pressure and modulate the airflow to produce sound.³⁵ The motion of the labia is represented as a surface wave propagating in the direction of the airflow, that can be described in terms of the lateral displacement of the midpoint of the tissue.²³ Its mathematical form is the motion equation of a nonlinear oscillator in which two parameters that determine the acoustic features of the solutions are controlled by the bird: the sub-syringeal air sac pressure and the stiffness of the restitution (through the activity of syringeal muscles). In order to integrate the model in real time, a set of equations was found that is computationally less expensive yet capable of displaying topologically equivalent sets of solutions as the parameters are varied:⁶⁵

$$\{\begin{array}{l}\frac{dx}{dt}=y\hfill \\ \frac{dy}{dt}={\gamma }^2\alpha +{\gamma }^2\beta x+{\gamma }^2{x}^2-{\gamma }^2{x}^3-\gamma xy-\gamma x^{2}y\hfill \end{array}$$

where x represents the departure of the midpoint position of the oscillating labia, γ is a time scaling factor, and the parameters α and β are functions of the air sac pressure and the activity of the ventral syringeal muscle, respectively.

The upper vocal tract further shapes the sound produced by the source, determining spectral properties such as the timbre. We used a model for the vocal that includes a tube, accounting for the trachea, followed by a Helmholtz resonator, accounting for the oropharyngeal-esophageal cavity (OEC)^66,67 (see Figure 1A in Arneodo et al.³⁸). The pressure at the input of the tube that represents the trachea is P_i(t) = ax(t) – r x(t – τ), where ax(t) is the contribution to the fluctuations by the modulated airflow, r is the reflection coefficient at the opposing end of the tube of length L and τ = 2L/c, with c the sound velocity. The pressure fluctuations at the output of the trachea force the air at the glottis, approximated by the neck of the Helmholtz resonator that represents the OEC. The mass of air at the glottis, forced into the cavity, is subject to a restitution force exerted by the larger mass of air in it.

In acoustics, it is common to write an analog electric computational model to describe a system of filters. The acoustic pressure is represented by an electric potential and the volume flow by the electric current.⁶⁸ In this framework, short constrictions are inductors, and cavities (smaller than the wavelengths) are well represented by capacitors. The equations for the equivalent circuit of the post-tracheal part of the vocal tract, (see Figure 1B in Arneodo et al.³⁸) read:

$$\{\begin{array}{l}\frac{di}{dt}={\Omega }_1,\hfill \\ \frac{d{\Omega }_1}{dt}=-\frac{1}{L_g{C}_h}{i}_1-R_h\left(\frac{1}{L_b}+\frac{1}{L_g}\right){\Omega }_1+\hfill \\ +i_3\left(\frac{1}{L_g{C}_h}-\frac{R_b{R}_h}{L_b{L}_g}\right)+\frac{1}{L_g}\frac{d{V}_{ext}}{dt}+\frac{R_h}{L_g{L}_b}{V}_{ext},\hfill \\ \frac{d{i}_3}{dt}=-\frac{L_g}{L_b}{\Omega }_1-\frac{R_b}{L_b}{i}_3+\frac{1}{L_b}{V}_{ext},\hfill \end{array}$$

where the electric components relate to geometric parameters of acoustic elements, and are described in detail in Perl et al.³⁶ and Arneodo et al.³⁸ The pressure fluctuations at the glottal end of the trachea relate linearly to the electric tension V_ext driving the circuit. Following the same scheme, the electrical potential at the resistor standing for the beak V_b = i₃R_b is the analog of the pressure fluctuations at the output of the beak. In our model, this quantity is the sound radiated by the vocal organ.

Parameter fitting

In order to fit the parameter series that will lead to reconstruction of the song, we perform a procedure similar to that previously described.^27,36 Timescale parameter is set to a value of 23,500; α is set to −0.15 during vocalization and 0.15 otherwise, and β is set in order to minimize the distance in the (pitch, spectral content) space between the synthesized and the recorded song segments;³⁶ the envelope (e(t) in the main text) is obtained by rectifying and smoothing the recorded waveform; the parameters of the vocal tract were fixed, in the same values as in Perl et al.³⁶ In order to extract the pitch of the song, we follow a modification of the automatic procedure presented in Boari et al.,⁶⁹ and we add a layer of manual curation. When integrating the model, we apply the extracted envelope (e(t)) as an extra multiplicative factor when computing ax(t), since it recovers the amplitude fluctuations that were discarded when reducing the model to its normal form and driving it with the bi-valued parameter α. The parameters accounting for the geometry of the vocal tract are constants and are set to the same values as in Perl et al.²⁴

Neural network training

Neural network -based decoders were implemented in python 3.6, using Tensorflow 2.0 and Keras. They were run on Ubuntu 16.04 and 18.04 PCs equipped with NVidia GPUs (Tesla k40c, Titan Xp, and Titan X Pascal). CUDA version was 10.2.

LSTM network architecture

The network has 2 layers of LSTM cells, with Nx5 cells in the first layer and N in the second, where N is the number of clusters in the neural data. The output layer has as many relu units as the target space (64 for the spectrogram bands). The input of the network is a Nx50 array that contains the spike count of each cluster, in each of 50, 1ms bins preceding the output bin. The output of the network is a 1×64 array containing the spectral bands corresponding to a 5ms bin. Both LSTM layers utilized 20% dropout and 0.001 L2 regularization during training to prevent overfitting.⁷⁰

Feed-forward Network architecture

The network has 1 dense hidden layer of Nx25 relu units, where N is the number of clusters in the neural data. The output layer has as many relu units as the target space (p = 64 for the spectrogram bands, p = 3 for the biomechanical model parameters). The input of the network is a Nx50 vector that contains the spike count of each cluster, in each of 50, 1ms bins preceding the output bin. The output of the network is a 1xP array containing the spectral bands (p = 64) or the biomechanical model parameters (p = 3) corresponding to a 5ms bin. The hidden layer utilized 20% dropout and 0.001 L2 regularization during training

Training procedure

We utilized a gradient-based optimizer (Adam/rmsprop⁷¹) and mean square error (MSE) as a loss function for LSTM/FFNN. We used 40% of all the motifs for testing and the rest motifs for training. We made 3 passes using non-overlapping motifs as a testing set, in order to have as many decoded examples as the number of motifs in the session. In each pass, all of the neural-activity/decoder-target pairs (one per bin) were fed in random order to the network, both when training and decoding. We reserved 10% of the training set as a validation subset for early stopping, where the training session would be stopped if validation loss failed to decrease within 5/10 training epochs. Figure 4 shows the results of this motif -based training averaged across all birds. As an alternative training method, we masked a fraction of each motif (roughly 3.3%), trained on the complement, then generated the song corresponding to the masked fraction. We repeated this piece-wise procedure tiling the whole motif, and generated entire motifs using segments of data that were novel to the decoder. Figure S3 shows the results of both the motif-wise and piece-wise training for individual birds.

Song waveform generation

Spectrogram inversion

We used LSEE-STFTM algorithm to invert spectrograms back to audio waves,⁷² as implemented in the librosa python package.⁷³ The algorithm iteratively estimates a signal from the short-time Fourier transform magnitude (STFTM), through minimizing the mean square error between the short-time Fourier transform (STFT) and the estimated STFT, and subsequently performs STFT on the estimated signal, the magnitude of which will be passed on to the next iteration.

Within each iteration, a signal was approximated using the equation below:

$$x(n)=\frac{{\sum }_{m=-\infty }^{\infty }w(mS-n)y_w(mS,n)}{{{\sum }_{m=-\infty }^{\infty }w}^2(mS-n)}$$

where x(n) denotes the estimated signal; w(n) denotes the analysis window used in STFT. The variable S is a positive integer, representing the sampling rate of the STFT. Here, y_w(mS, n) is the target signal corresponding to Y_w(mS, n), which denotes the target STFTM, in our case spectrogram powers. To calculate in each iteration, we used a sinusoidal window:⁷²

$$w_s(n)=\frac{2w_r(n)}{\sqrt{4a^2+2b^2}}\left[a+bcos\left(\frac{2\pi n}{L}+\varphi \right)\right]$$

where L represents the length of the window. Here, w_r(n) is a rectangular window with an amplitude of $\sqrt{S/L}$ within 0≤ n < L and zero anywhere outside. A modified Hamming window can be obtained by setting a = .54, b = − .46, $\varphi =\frac{\pi }{L}$. After obtaining an x(n) value within each iteration, the STFT of x(n) was calculated, which was used in place of Y_w(mS, n) in the next iteration. The squared error between the target STFTM and the estimated STFTM is proven to decrease in each iteration of the algorithm.

Biomechanical model integration

Once the model parameters are predicted by the decoder, they are re-sampled and fed to an ordinary differential equation integrator. Resampling to 30 Khz is performed (with cubic interpolation). A fourth order runge-kutta ODE integrator (custom coded) integrates then the equations of the model with a time step of (900 KHz)⁻¹.

Synthesis through principal components

PC decomposition was made using the PCA module in the scikit-learn package.⁷⁴ We obtained the principal component decomposition of all the spectrograms of all the motifs sung by each bird during the length of the experiment. 512 frequency bins were used for the spectrograms, which were concatenated and projected onto the N principal components T_{N =} SW_N, where S is the 512-dimension spectrum time series and W_N the transformation matrix (the matrix of the L eigenvectors of SS^T with the largest eigenvalues) via the pca.fit and pca.fit_transform methods. For reconstruction from principal components, the inverse transformation was applied by means of the pca.inverse_transform method.

Spectrum shuffle mask

Time warping

We adopted a simplified version of Dynamic Time Warping (DTW⁷⁵) specific to zebra finch songs. Instead of segmenting the song into different syllables and matching each syllable to different syllable templates, we took advantage of the stereotypical nature of zebra finch songs and directly computed minimal distance matrices (D) between each song-level spectrogram and a spectrogram template. Starting at the first slice of each spectrogram,

$$D(i,j)=d(i,j)+min\left\{D(i-1,j)iff{w}_j(l-1)\ne w_j(l-2),D(i-1,j-1),D(i-1,j-2)\right\}$$

Where i indexes the time frames of the input pattern, j indexes the time frames of a single template, l indexes the ordered steps along a specific path. d(i, j) is the local distance between slice i and slice j. w_j(l) denotes the specific step at l in the space of j. Once a distance matrix D was calculated, we determined an optimal path with the lowest cumulative distance between the input and the template, and proceeded to stretch, delete or keep each input slice, depending on the path.

Masking

We applied a random yet consistent shuffling mask, P, to our entire warped spectrogram repertoire so that spectral consistency across time is disrupted while the temporal pattern within each motif remains. For the i-th spectrogram slice in each warped song, we shuffled all 64 spectral elements using the same shuffling pattern P_i. Treating all spectrograms with the same shuffling mask P enabled us to determine whether our model is decoding the spectral information within birdsongs or recreating the same pattern regardless of spectral consistency across time. In our shuffling training session, we used the shuffled spectrograms as output.

Reordering mask

After training, we tested our model on novel neural data, the target of which were also shuffled spectrograms. In order to visually compare our model’s performance with and without shuffling, we reordered the reconstructed shuffled spectrograms. We achieved this by applying a reordering mask, R, that traces and reverses all the shuffling done through the aforementioned shuffling mask P. For any spectrogram S, R(P(S)) = S.

QUANTIFICATION AND STATISTICAL ANALYSIS

Performance Evaluation

Root Mean Square Error (RMSE)

We used RMSE between each pair of original and predicted spectrogram magnitude as a metric to evaluate the performance of our models.

Spectral correlation

To obtain the spectral correlation across time for a pair of spectrograms, we first computed the pearson correlation coefficient between each corresponding pair of spectral slices that conform the two spectrograms (via the function pearsonr from the stats module of the scipy python package⁶⁴). Then, we obtained the time-averaged value across the span of the motif.

Earth mover’s distance

To obtain the distance across time for a pair of spectrograms, we computed the earth mover’s distance (d_EMD) or Wasserstein metric between each pair of spectral slices that conform the two spectrograms (via the function wasserstein_distance from the stats module of the scipy python package⁶⁴). Prior comparison, each spectral slice was normalized such that the total area under the slice be 1; for silences, a value of 1 was assigned to the first bin of the spectrogram. Then, we obtained the time-averaged value across the span of the motif.

Spectrogram Normalization

In order to account for variations among motifs from different birds, we normalized spectrograms for each bird so that the collection of original spectrograms for each bird had a maximum power of 1 and minimum power of 0:

$${\widehat{p}}_i=\frac{p_i-p_{max}}{p_{max}-p_{min}}$$

Where p_i is the power of a point on either an original spectrogram or a predicted spectrogram before normalization, while $\widehat{p_{\iota }}$ is the normalized power of the corresponding point. p_max denotes the maximum power of the entire set of original spectrograms, while p_min represents the minimum power of the entire set of original spectrograms. With such normalization, we were able to account for variations among motifs from different birds while keeping the variations within motifs from the same bird.

Pairwise performance comparisons

We performed comparisons among and between different sets of songbirds (displayed in Figure 4 boxplots for instance). BOS-BOS: comparisons provide a baseline of the variability of the bird’s own motifs during the session: comparison across each pair of motifs. neur-bos: comparison across each pair of natural motifs and it’s corresponding one decoded from neural activity.

In order to provide an extra control reference, we also computed spectrogram comparisons against a set of 47 motifs from conspecific birds (other zebra finches; about half of them from our colony and half from other colonies). This produced the sets: BOS-CON: comparisons across each BOS motif and all of the conspecific (CON) motifs.

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Bacterial and virus strains
Biological samples
Chemicals, peptides, and recombinant proteins
Critical commercial assays
Deposited data
Original data	This paper, Figshare	https://doi.org/10.6084/m9.figshare.14502198
Experimental models: Cell lines
Experimental models: Organisms/strains
Oligonucleotides
Recombinant DNA
Software and algorithms
Code for acquisition, pipeline, analysis written in C/Python.	This paper	https://github.com/zekearneodo/swissknife
Code for analysis written in Python.	This paper	https://github.com/kaichensh/curr_bio_2021
Other
Printable Microdrive and signal conditioning hardware designs.	This paper	https://github.com/singingfinch/bernardo
LIFE SCIENCE TABLE WITH EXAMPLES FOR AUTHOR REFERENCE
REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Rabbit monoclonal anti-Snail	Cell Signaling Technology	Cat#3879S; RRID: AB_2255011
Mouse monoclonal anti-Tubulin (clone DM1A)	Sigma-Aldrich	Cat#T9026; RRID: AB_477593
Rabbit polyclonal anti-BMAL1	This paper	N/A
Bacterial and virus strains
pAAV-hSyn-DIO-hM3D(Gq)-mCherry	Krashes et al., 2011	Addgene AAV5; 44361-AAV5
AAV5-EF1a-DIO-hChR2(H134R)-EYFP	Hope Center Viral Vectors Core	N/A
Cowpox virus Brighton Red	BEI Resources	NR-88
Zika-SMGC-1, GENBANK: KX266255	Isolated from patient (Wang et al., 2016)	N/A
Staphylococcus aureus	ATCC	ATCC 29213
Streptococcus pyogenes: M1 serotype strain: strain SF370; M1 GAS	ATCC	ATCC 700294
Biological samples
Healthy adult BA9 brain tissue	University of Maryland Brain & Tissue Bank; http://medschool.umaryland.edu/btbank/	Cat#UMB1455
Human hippocampal brain blocks	New York Brain Bank	http://nybb.hs.columbia.edu/
Patient-derived xenografts (PDX)	Children's Oncology Group Cell Culture and Xenograft Repository	http://cogcell.org/
Chemicals, peptides, and recombinant proteins
MK-2206 AKT inhibitor	Selleck Chemicals	S1078; CAS: 1032350–13–2
SB-505124	Sigma-Aldrich	S4696; CAS: 694433–59–5 (free base)
Picrotoxin	Sigma-Aldrich	P1675; CAS: 124–87–8
Human TGF-β	R&D	240-B; GenPept: P01137
Activated S6K1	Millipore	Cat#14–486
GST-BMAL1	Novus	Cat#H00000406-P01
Critical commercial assays
EasyTag EXPRESS 35S Protein Labeling Kit	PerkinElmer	NEG772014MC
CaspaseGlo 3/7	Promega	G8090
TruSeq ChIP Sample Prep Kit	Illumina	IP-202–1012
Deposited data
Raw and analyzed data	This paper	GEO: GSE63473
B-RAF RBD (apo) structure	This paper	PDB: 5J17
Human reference genome NCBI build 37, GRCh37	Genome Reference Consortium	http://www.ncbi.nlm.nih.gov/projects/genome/assembly/grc/human/
Nanog STILT inference	This paper; Mendeley Data	http://dx.doi.org/10.17632/wx6s4mj7s8.2
Affinity-based mass spectrometry performed with 57 genes	This paper; Mendeley Data	Table S8; http://dx.doi.org/10.17632/5hvpvspw82.1
Experimental models: Cell lines
Hamster: CHO cells	ATCC	CRL-11268
D. melanogaster: Cell line S2: S2-DRSC	Laboratory of Norbert Perrimon	FlyBase: FBtc0000181
Human: Passage 40 H9 ES cells	MSKCC stem cell core facility	N/A
Human: HUES 8 hESC line (NIH approval number NIHhESC-09–0021)	HSCI iPS Core	hES Cell Line: HUES-8
Experimental models: Organisms/strains
C. elegans: Strain BC4011: srl-1(s2500) II; dpy-18(e364) III; unc-46(e177)rol-3(s1040) V.	Caenorhabditis Genetics Center	WB Strain: BC4011; WormBase: WBVar00241916
D. melanogaster: RNAi of Sxl: y[1] sc[*] v[1]; P{TRiP.HMS00609}attP2	Bloomington Drosophila Stock Center	BDSC:34393; FlyBase: FBtp0064874
S. cerevisiae: Strain background: W303	ATCC	ATTC: 208353
Mouse: R6/2: B6CBA-Tg(HDexon1)62Gpb/3J	The Jackson Laboratory	JAX: 006494
Mouse: OXTRfl/fl: B6.129(SJL)-Oxtrtm1.1Wsy/J	The Jackson Laboratory	RRID: IMSR_JAX:008471
Zebrafish: Tg(Shha:GFP)t10: t10Tg	Neumann and Nuesslein-Volhard, 2000	ZFIN: ZDB-GENO-060207–1
Arabidopsis: 35S::PIF4-YFP, BZR1-CFP	Wang et al., 2012	N/A
Arabidopsis: JYB1021.2: pS24(AT5G58010)::cS24:GFP(-G):NOS #1	NASC	NASC ID: N70450
Oligonucleotides
siRNA targeting sequence: PIP5K I alpha #1: ACACAGUACUCAGUUGAUA	This paper	N/A
Primers for XX, see Table SX	This paper	N/A
Primer: GFP/YFP/CFP Forward: GCACGACTTCTTCAAGTCCGCCATGCC	This paper	N/A
Morpholino: MO-pax2a GGTCTGCTTTGCAGTGAATATCCAT	Gene Tools	ZFIN: ZDB-MRPHLNO-061106–5
ACTB (hs01060665_g1)	Life Technologies	Cat#4331182
RNA sequence: hnRNPA1_ligand: UAGGGACUUAGGGUUCUCUCUAGGGACUUAGGGUUCUCUCUAGGGA	This paper	N/A
Recombinant DNA
pLVX-Tight-Puro (TetOn)	Clonetech	Cat#632162
Plasmid: GFP-Nito	This paper	N/A
cDNA GH111110	Drosophila Genomics Resource Center	DGRC:5666; FlyBase:FBcl0130415
AAV2/1-hsyn-GCaMP6- WPRE	Chen et al., 2013	N/A
Mouse raptor: pLKO mouse shRNA 1 raptor	Thoreen et al., 2009	Addgene Plasmid #21339
Software and algorithms
ImageJ	Schneider et al., 2012	https://imagej.nih.gov/ij/
Bowtie2	Langmead and Salzberg, 2012	http://bowtie-bio.sourceforge.net/bowtie2/index.shtml
Samtools	Li et al., 2009	http://samtools.sourceforge.net/
Weighted Maximal Information Component Analysis v0.9	Rau et al., 2013	https://github.com/ChristophRau/wMICA
ICS algorithm	This paper; Mendeley Data	http://dx.doi.org/10.17632/5hvpvspw82.1
Other
Sequence data, analyses, and resources related to the ultra-deep sequencing of the AML31 tumor, relapse, and matched normal	This paper	http://aml31.genome.wustl.edu
Resource website for the AML31 publication	This paper	https://github.com/chrisamiller/aml31SuppSite
PHYSICAL SCIENCE TABLE WITH EXAMPLES FOR AUTHOR REFERENCE
REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, peptides, and recombinant proteins
QD605 streptavidin conjugated quantum dot	Thermo Fisher Scientific	Cat#Q10101MP
Platinum black	Sigma-Aldrich	Cat#205915
Sodium formate BioUltra, ≥99.0% (NT)	Sigma-Aldrich	Cat#71359
Chloramphenicol	Sigma-Aldrich	Cat#C0378
Carbon dioxide (13C, 99%) (<2% 18O)	Cambridge Isotope Laboratories	CLM-185–5
Poly(vinylidene fluoride-co-hexafluoropropylene)	Sigma-Aldrich	427179
PTFE Hydrophilic Membrane Filters, 0.22 μm, 90 mm	Scientificfilters.com/Tisch Scientific	SF13842
Critical commercial assays
Folic Acid (FA) ELISA kit	Alpha Diagnostic International	Cat# 0365–0B9
TMT10plex Isobaric Label Reagent Set	Thermo Fisher	A37725
Surface Plasmon Resonance CM5 kit	GE Healthcare	Cat#29104988
NanoBRET Target Engagement K-5 kit	Promega	Cat#N2500
Deposited data
B-RAF RBD (apo) structure	This paper	PDB: 5J17
Structure of compound 5	This paper; Cambridge Crystallographic Data Center	CCDC: 2016466
Code for constraints-based modeling and analysis of autotrophic E. coli	This paper	https://gitlab.com/elad.noor/sloppy/tree/master/rubisco
Software and algorithms
Gaussian09	Frish et al., 2013	https://gaussian.com
Python version 2.7	Python Software Foundation	https://www.python.org
ChemDraw Professional 18.0	PerkinElmer	https://www.perkinelmer.com/category/chemdraw
Weighted Maximal Information Component Analysis v0.9	Rau et al., 2013	https://github.com/ChristophRau/wMICA
Other
DASGIP MX4/4 Gas Mixing Module for 4 Vessels with a Mass Flow Controller	Eppendorf	Cat#76DGMX44
Agilent 1200 series HPLC	Agilent Technologies	https://www.agilent.com/en/products/liquid-chromatography
PHI Quantera II XPS	ULVAC-PHI, Inc.	https://www.ulvac-phi.com/en/products/xps/phi-quantera-ii/

Highlights.

• Songbirds sing rich, complex, learned songs

• A model of their vocal organ can synthesize song with few control parameters

• This allows neurally driven song synthesis via a simple neural network

• Brain machine interfaces can be enhanced by understanding the biomechanics