A cryptography-based approach for movement decoding

Abstract

Brain decoders use neural recordings to infer the activity or intent of a user. To train a decoder, one generally needs to infer the measured variables of interest (covariates) from simultaneously measured neural activity. However, there are cases for which obtaining supervised data is difficult or impossible. Here, we describe an approach for movement decoding that doesn’t require access to simultaneously measured neural activity and motor outputs. We use the statistics of movement—much like cryptographers use the statistics of language—to find a mapping between neural activity and motor variables, and then align the distribution of decoder outputs with the typical distribution of motor outputs by minimizing their Kullback-Leibler divergence. By using datasets collected from the motor cortex of three non-human primates performing either a reaching task or an isometric force-production task, we show that the performance of such a distribution-alignment decoding algorithm is comparable with the performance of supervised approaches. Distribution-alignment decoding promises to broaden the set of potential applications of brain decoding.

Introduction

The aim of brain decoding is to infer the relationship between neural activity and a covariate of interest. Thus by measuring neural activity, we can predict what someone is viewing[1, 2], what word they are thinking about[3, 4], or even their movements[5, 6]. Decoding approaches can also be used to elucidate the link between external factors (stimuli) and the brain, which is essential for understanding how the brain encodes information. In all of these settings, training data are collected by simultaneously recording brain activity along with the covariates that we wish to predict.

In many situations, obtaining simultaneous recordings of both neural activity and the covariates of interest is challenging, expensive, or impossible[7]. This includes settings where complex task variables are difficult to track[8], as well as in motor decoding settings where the user is paralyzed and thus cannot generate motor outputs. In these situations, we seek an alternative to applying a supervised approach to learn a mapping between neural activity and the underlying covariates that we wish to predict[9].

To train a decoder without simultaneous measurements of neural activity and covariates, we looked to cryptography for inspiration. When code breakers crack a cypher, they leverage prior information about the distribution of both individual characters and their joint statistics[10, 11]. For example, the probability of observing a written ‘E’ is much higher than the probability of observing a ‘Z’. Using such information, Alan Turing and his Bletchley Park team cracked the World War II German Enigma code by exploiting the distribution of words known to appear in encrypted messages from their enemies. The key idea underlying this type of code-breaking strategy is to learn a mapping from the encrypted to decrypted text that produces a distribution with structure similar to what we expect based upon prior knowledge. Here, we ask if the same concept could be used to learn a mapping from neural activity to motor outputs.

We will highlight this concept with a movement example, where the aim is to decode the 2D velocity of a user’s hand from recorded neural activity (Fig. 1). In this example, the goal of the decoder is to produce an output that is matched to the distribution of the desired movement (e.g., reaching, drinking, or shaking an object) (Fig. 1a). If the decoder is tuned correctly, the distribution of the decoded movement variables should roughly match the distribution of the kinematics of the actual movement (Fig. 1b, aligned movement in green). If the decoder is not tuned correctly, then its output should produce a different distribution (misaligned movement in red). Thus, we can effectively train a decoder that relates brain activity to motor variables by simply asking whether decoder outputs match the distribution of the intended movement.

Figure 1. Decoding structured movements with distribution alignment.

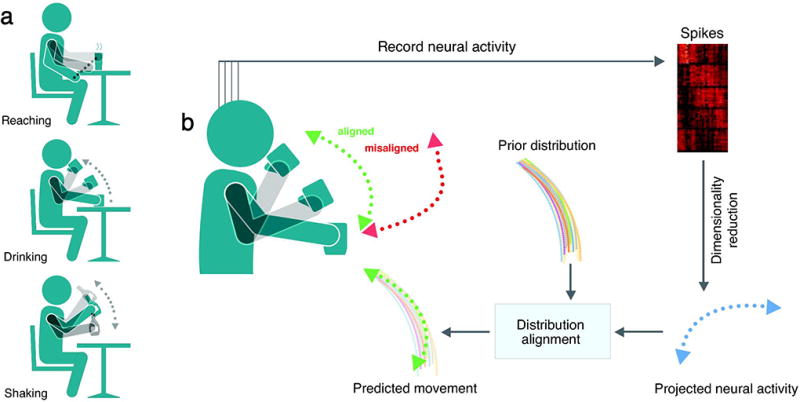
(a) Many tasks, such as reaching, eating, and shaking, produce highly structured, yet varied, movement distributions. (b) The firing rates of neurons in motor cortex (M1) are mapped into a low-dimensional (2–3 dimensions) space using dimensionality reduction. DAD then finds an affine mapping that aligns the projected neural activity with the prior distribution of kinematics. After aligning the neural data with the prior movement distribution, we produce a decoded movement that is similar to the true movement distribution (aligned, green). When neural activity is decoded incorrectly, this produces a divergent distribution (misaligned, red); the distance between the distribution of predicted movements and the distribution of prior movements can be quantified through the Kullback-Liebler (KL)-divergence. The proposed method, distribution alignment decoding (DAD), aims to find a decoded movement distribution that minimizes the KL-divergence between the decoder output and the prior distribution over the movement.

Just as in cryptography, where breaking a cypher is easier when the underlying signal has clear statistical structure[10], distribution alignment requires that the decoded distribution of movements also be highly structured. Fortunately, there is evidence that natural movements, such as eating, walking, and dancing, exhibit a great deal of structure and regularity[12, 13, 14, 15]. The existence of structure in natural movements suggests that deviations from a typical movement distribution could be statistically detected. By aligning the distribution of predicted movements with a prior over natural movements, we can relate neural activity to movement without the need to measure them simultaneously.

Here we introduce an approach for movement decoding called distribution alignment decoding (DAD), which finds a low-dimensional mapping of neural activities that matches the distribution of movements. DAD learns a decoder that minimizes the deviation between the distribution of projected (low-dimensional) neural activities and kinematics (see Methods). We applied DAD to neural datasets collected from the primary motor cortex (M1) of three non-human primates (NHPs) performing either a reaching task or an isometric force production task. When compared with supervised decoders that have access to both neural and behavioral training data, DAD provided comparable performance with standard methods. Additionally, we found that DAD can be used to in an across-subject setting by using one subject’s movement data to decode the neural activity from a different subject. We thus show how cryptography-inspired ideas can be used to solve the movement decoding problem.

Results

To test our idea for alignment-based decoding, we used recordings from populations of neurons in the arm area of M1 of two NHPs (Subjects M and C) while they performed a center-out reaching task (Fig. 2a,b), as well as recordings from the hand area of M1 from one NHP (Subject J) during an isometric wrist force production task (Fig. 2a,c). To produce datasets with meaningful structure, we sub-sampled the data to remove certain target directions (see Fig. 2d for details on this choice). This generated a non-isotropic movement distribution that we could align with the equally non-isotropic distribution of neural activities to test the performance of DAD.

Figure 2. KL-divergence minimization for aligning low-dimensional distributions.

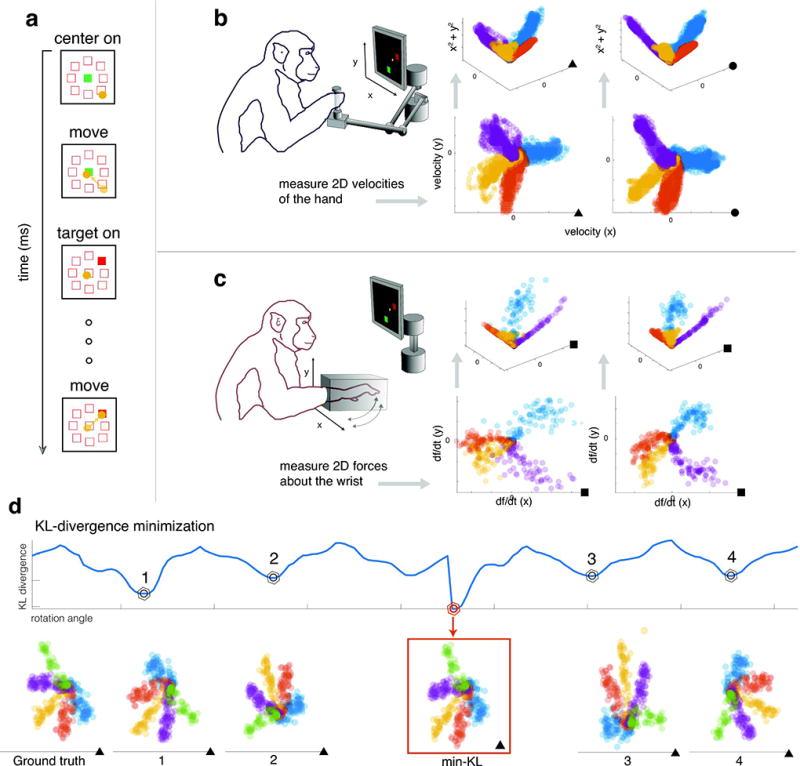
(a) The setup of the delayed center-out motor task. The task consists of 5 phases: a target appears at the center, the subject moves the cursor to the center, one of eight targets around the center will turn on, the subject must wait for a delay period to plan their movement, and finally they move a cursor towards the illuminated target. (b) A schematic of a monkey performing a reaching task by moving a 2D manipulandum towards the target. To the right, we show the kinematics (bottom) and 3D movement data when augmented with speed as a covariate (top). The kinematics data is shown with the target directions displayed as different colors. The resulting lifted 3D data lies on a conical shape in three dimensions. (c) A schematic of the force production task. Again, the datasets are conical in shape in 3D but the force distributions exhibit significant curvature compared to the reaching data. (d) Here we demonstrate the idea behind distribution alignment on artificially rotated kinematics data from Subject M. The KL-divergence is displayed as a function of the rotation angle used for alignment in 2D. The correct solution (ground truth), min-KL predicted solution, and four non-optimal rotations/reflections are displayed. Note that since the reflections of this task are roughly equivalent, the first local minimum (labeled as 1) of the KL-divergence is a ipped-version of the correct solution. Kinematics data from Subject M, C, and J are denoted by filled triangles, circles, and squares, respectively.

Our approach relies on the fact that we can find a low-dimensional embedding of neural activity that can be aligned to a distribution of known motor variables. If there is indeed a linear mapping between neural activity and motor variables, then we expect to see task-related structure in projected neural data. However, neural data can be quite noisy and thus may not reveal the covariates of interest[16]. Instead, if we filter the data to select a subset of the data (e.g., before or after the start of a trial or go cue), we can more clearly resolve task structure present (Fig. 3). The challenge is finding that key window of time when the task structure is apparent and can be revealed through dimensionality reduction. To tackle this challenge, we developed a model selection method (Fig. 3) that searches over a set of parameters used to subsample and smooth the data to select a model that produces factors that match the known movement distribution (see Methods). This approach can be used to produce an unsupervised estimate of the best model parameters and can be further augmented when supervised data exists. Our model selection approach provides a straightforward way to learn a low-dimensional representation of the neural data that most closely matches the known distribution of desired motor outputs.

Figure 3. Finding task-related structure in low-dimensional embeddings of neural data.

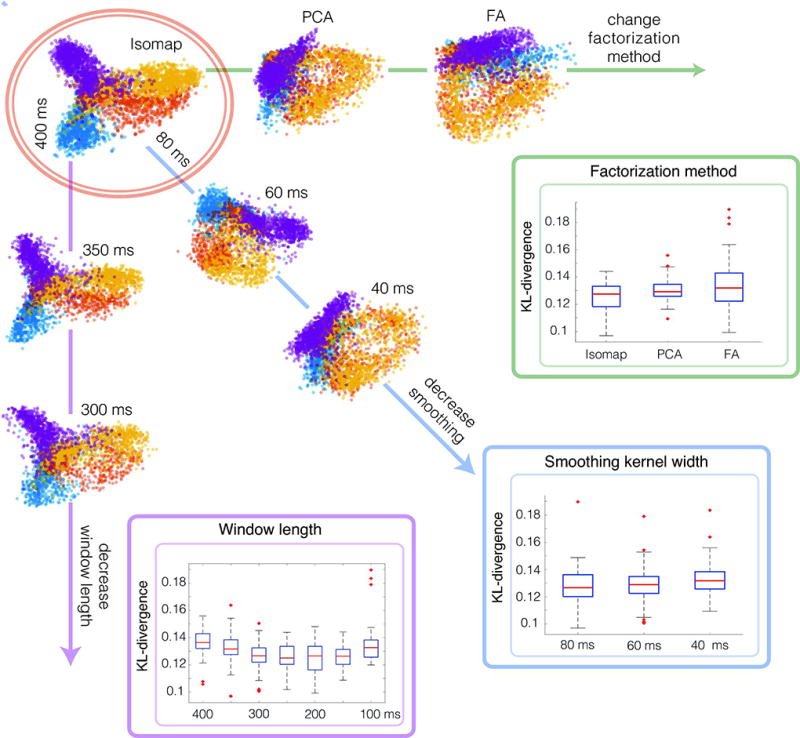
We explore the impact of data processing parameters on our ability to find task-relevant structure in low-dimensional embeddings of the neural firing rates. High-lighted at the top left in orange, we show an exemplar solution of DAD. Then along each axis, we show the result of DAD as we vary the parameter of interest while holding the other parameters fixed. For all three parameters, we display the distribution of KL-divergences obtained using DAD.

We applied our model selection algorithm to neural and behavioral datasets from all three subjects (Fig. 4). In all cases, we found examples where our model selection approach effectively pulls out task structure from neural datasets. This is true for our fully unsupervised model selection approach (smoothKL), which uses the Kullback Leibler (KL)-divergence of each model fit to find the best model with minimum KL-divergence, as well as a supervised variant (maxR²), which selects the model that produces the maximum decoding performance on a training set. Our results suggest that for simple behaviors like a center-out task, we can apply our model selection method to reveal task structure from both movement (Subject M, C) as well as isometric force production (Subject J) datasets, with no modifications to our method.

Figure 4. Distribution alignment decoding across different motor tasks.

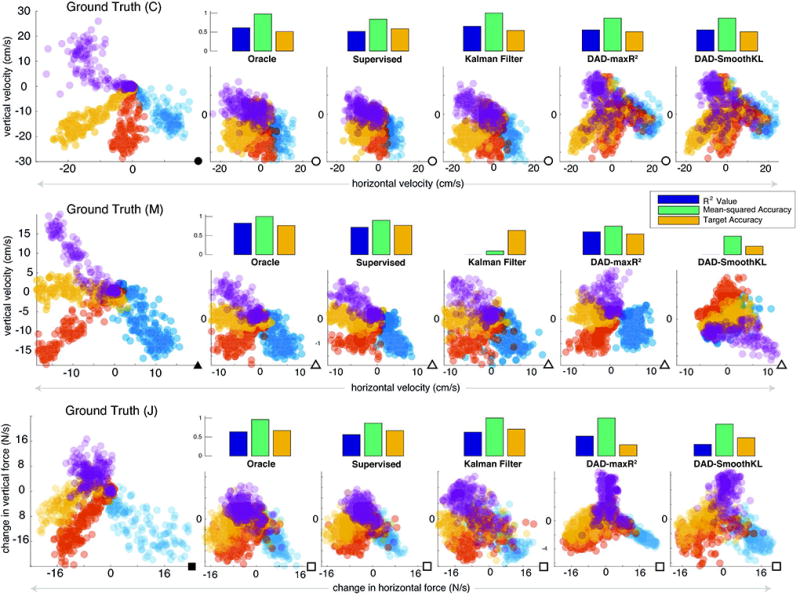
Along the top two rows, we show examples of reaching datasets from Subject C (top) and Subject M (middle). In the bottom row, we show the an isometric force production dataset from Subject J. In each row, from left to right (colored according to the target), we show the test data, the results from the Oracle, a Supervised decoder, a Kalman Filter, and for DAD: a supervised maximum R² model and unsupervised minimum-KL model. Above each solution, we display the R², the Mean-squared Accuracy, and the Target Accuracy (percentage of correct targets estimated). Kinematics data from Subject M, C, and J are denoted by filled triangles, circles, and squares, respectively. Projected neural data from Subject M, C, and J are denoted by open triangles, circles, and squares, respectively.

To put the performance of DAD into context, we compared with standard supervised approaches, including a standard supervised linear decoder (Eqn. 2) and a Kalman Filter. For interpretation purposes we also plotted an effective upper bound on possible performance, the Oracle decoder. This decoder, which in practice is impossible to ever construct, trains and predicts on the same dataset and thus sets a strict upper bound on the performance of a linear decoder. We compared DAD to supervised approaches (Fig. 4, Fig. 5) and found DAD to be competitive with both supervised methods we tested. In the case of Subject M, we observed that the Kalman Filter was unstable and therefore produced poor decoding performance (as measured by the R² and Mean-Squared Accuracy) when compared with a linear supervised and Oracle decoder. When the signal-to-noise is low and resolving the trajectory of movements is difficult, we found that DAD can still decode the reach direction with high reliability. Through combining model selection and distribution alignment, we obtain performance similar to a supervised linear decoder without requiring simultaneously recorded motor variables and neural activity.

Figure 5. Decoding neural data using kinematics from another subject.

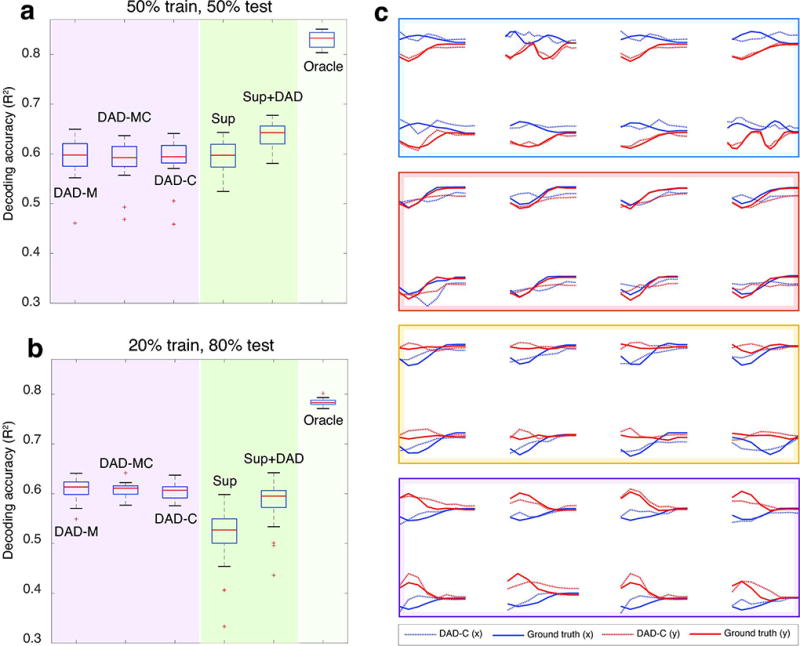
In (a–b), we show the results from three different decoding settings where we vary the training kinematics: DAD-M (train and test on M), DAD-MC (train on M,C and test on M), and DAD-C (train on C and test on M). Performance comparisons for supervised approaches (in shaded green regions) and DAD (in shaded purple regions) are shown for different amounts of training and test data. Each boxplot shows the R² values obtained over 20 trials; the median is displayed as a red line in each box, the edges of the box represent the 25% and 75% percentile, the whiskers indicate the range of the data not considered an outlier, and the outliers are displayed in red (+). In (a) we show the R² values obtained when we use 50% of the total data for training and 50% for test for Subject M and C, respectively. In (b), we display the R² values obtained when we use 20% of the total data for training and 80% for test. Both (a,b) compare the performance of DAD, with a supervised linear decoder (Sup), the average between the predictions of Sup and DAD-M (Sup+DAD), and the Oracle. In (c), we show the R² values obtained for DAD-C (dashed, R²=0.612), when overlaid on the true kinematics of individual reaches (solid). The horizontal and vertical velocities are displayed in blue and red, respectively. Eight randomly selected reaches are organized into colored boxes according to their corresponding target.

Since we do not rely on simultaneously measured neural and motor data in DAD, we can apply this approach to decode the neural data from one subject using motor data from another subject (Fig. 5a,b). As Subject M’s neural data provided the highest signal-to-noise ratio, we applied DAD to neural data from Subject M and tested different movement distributions for training: DAD-M (movement data from M), DAD-MC (movement data from both M and C), and DAD-C (movement data from C only). Our results suggest that DAD is relatively insensitive to the choice of movement distribution used for training, as all three distributions produce similar R² values (Fig. 5b). We further confirmed this through examining the decoding performance of DAD across individual reaches and across different targets (Fig. 5c). When provided with enough training data, we found that DAD performs similarly to supervised methods. However, when only a small amount of training data is provided (Fig. 5b), DAD tends to outperform supervised approaches as it only relies on movement data for alignment and thus has weaker dependence on the size of the training set. We note that in our comparisons, the supervised method is allowed to use training kinematics and neural data to build a decoder and then is tested on held out neural data. In contrast, DAD-M is given the same training kinematics and uses the neural test data to solve the alignment problem, thus making it an inherently offline method (see Methods). Our results demonstrate that it is possible to meaningfully decode movements even when no previous movement data has been recorded from a subject.

To further explore the stability of our method, we used DAD to decode Subject J’s neural activity over subsequent recording sessions (Fig. 6). In our experiments, the aim was to decode the change in 2D forces applied to the wrist while it is held fixed. When DAD is trained using data collected from the first day of recording (D1), we could successfully decode data from a second day of recording (D2) without changing any model parameters. Additionally, we found that when DAD was applied to neural datasets from either D1 or D2, we could use training kinematics from all datasets (D1–D4) to obtain similar results. Our results suggest that DAD can be used to decode data across multiple time points without having to modify the model parameters.

Figure 6. Aligning motor outputs across multiple days of recordings.

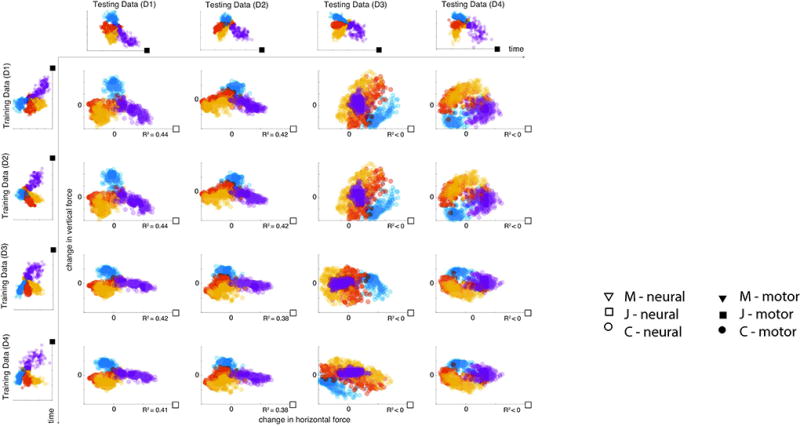
In this example, we apply DAD to datasets collected from Subject J over multiple recording sessions. Each subplot displays the decoded estimate of the change in applied forces obtained by DAD (colors indicate different targets). In each row, we show the effect of varying the testing data for a fixed training set (from left to right, D1, …, D4). In each column, we show the effect of varying the training data for a fixed testing set (from top to bottom, D1, …, D4). Kinematics and projected neural data from Subject J are marked with filled and open squares, respectively.

It is not only important to know how well DAD performs, but also how expected experimental innovations will affect its performance[17]. To characterize DAD’s performance as the size of the recorded population grows, we created a synthetic data set by simulating the firing rates of a population of neurons with tuning curves drawn from a distribution of parameters designed to match the real datasets (see Methods). We compared the performance of DAD with that of the Oracle decoder which has access to both the neural activity and kinematics of the test set. Our results demonstrate that as the number of neurons increases, the performance (R²) improves. For this model, DAD performs as well as the Oracle for populations with roughly 1,000 neurons. This model appears to align nicely with our results on real data; for populations of 100–200 neurons, the average R² is around 0.6–0.8 (R²=0.62 and R²=0.78 for d = 128 and 256 neurons, respectively). Our analysis suggests that with recordings from even larger populations, distribution alignment will become more accurate, approaching the optimal linear decoder’s (Oracle) performance.

Discussion

We have introduced DAD, a cryptography-inspired approach for brain decoding. In the context of motor decoding, we showed how DAD can be used to learn a decoder by minimizing the KL-divergence between the distribution of typical motor outputs and a projected low-dimensional distribution of neural activity. Thus, instead of requiring access to simultaneous recordings of neural activity and motor outputs, our approach relies on the structure of movement and the fact that this structure is preserved in low-dimensional projections of motor cortical activity to solve the decoding problem. We presented evidence that the algorithm works well on simulated data, as well as multiple datasets collected from the motor cortex of three NHPs.

One assumption that is integral to our current approach is that the variables of interest, e.g. the low-dimensional velocities or forces, appear in the set of the first few components of a dimensionality reduction algorithm. This seems a reasonable assumption, as cosine tuning is one of the most frequently described properties of motor cortex activity [18]. However, this assumption is not true for many datasets[16], to which our current instantiation of DAD can not be applied. If motor cortex primarily deals with movement vectors, why do they not consistently show up in the first principal components? Variables such as response timing, attention, motor preparation, and other factors are likely to play a role in whether dimensionality reduction methods find directions that resemble the motor outputs of interest. If task-relevant structure is in the top 20 principal components, instead of the top three, then a natural extension of DAD could be to solve the alignment problem in these higher dimensional spaces. If extended to higher dimensions, DAD could potentially find task-relevant structure across a wider range of datasets.

Our approach assumes that projected neural activity depends linearly on the distribution of movements. However, this assumption often does not hold in practice[19]. This is likely why we observe that the fine-scale structure of the predicted kinematics within each target direction can be warped (Fig. 3a). An exciting line of future research would be to extend our approach to incorporate further non-linearities. One possibility would be to explore the use of mixture models[20] to model the low-dimensional structure of the data, instead of using a single subspace model with PCA or factor analysis. Kernel methods[21] could also be used to lift the neural data to a higher-dimensional space where the neural activity depends linearly on the kinematics. With approaches that address the non-linearity of the data, the underlying structure of movement contained in the neural data can be preserved, thus leading to an improvement in the performance of the decoder.

To guarantee a unique solution for the problem of distribution alignment, the distribution of movements must be anisotropic (no rotational or reflection symmetry). However, in many laboratory tasks such as center-out-reaching tasks, this assumption is often violated. Here, we circumvent this problem by sub-sampling the dataset. This introduces asymmetries into the motor task and, in turn, guarantees the uniqueness of the resulting solution. While requiring nonisotropic movements is clearly a drawback of our approach, natural movement tasks[22, 23] (Fig. 1a) are more likely to produce non-isotropic distributions. Moreover, in the case of isotropic distributions where multiple alignments exist, we can use prior knowledge of the decoder or feedback from the user, to rule out incorrect alignments. Since natural movements typically exhibit asymmetries, we expect that our approach can be applied to decode motor variables in a wide range of tasks.

Our results demonstrate that DAD can achieve comparable performance to that of a linear decoder. While a linear decoding scheme is by no means state-of-the-art, demonstrating that DAD can do as well as a decoder with full access to simultaneously recorded neural and behavioral data, still represents an important advance. State-of-the-art decoders use additional information about neural activity and the task structure to improve the decoder’s performance. For instance, temporal dynamics [24], modeling non-linearity in neural firing rates [19, 25], target information[6], smooth temporal structure[24], and the drift of neural properties[26] can all be used to improve the performance of the supervised decoding scheme we presented. While we did not include such additions in our current implementation of supervised decoders (or for DAD), we expect that by doing so, their performance would also improve.

Another important line of research in movement decoding has focused on closed-loop systems, where the user and machine can co-adapt to use neural activity to drive a cursor or prosthetic limb[27, 28, 29]. In contrast to the offline setting we consider here, closed-loop systems require the user to adapt or modify their neural representation to drive a fixed decoder. As many existing closed-loop decoding algorithms[27, 28, 29] rely on initializing the decoder with a Kalman Filter, DAD could provide an alternative approach for initializing and re-aligning the decoder. Extending DAD to a closed-loop setting could help reduce the amount of labeled training data needed to initialize and calibrate closed-loop decoders.

We solved the decoding problem by exploiting the known structure of movements to learn a decoder, thus demonstrating one way in which cryptography might be applied to brain decoding. The cryptography approach we used here is rudimentary, but we imagine that more sophisticated code-breaking strategies could be used in this and other brain decoding scenarios beyond that of movement. For example, one could imagine decoding what someone is listening to using cryptography approaches. Thus, ideas from cryptography and distribution alignment promise to enable a broad range of approaches into brain decoding and new insights into how to crack the neural code.

Methods

0.1 Data collection

Neural and behavioral data were collected from three rhesus macaque monkeys. At the time of data collection, Subject M, Subject C, and Subject J, were 5, 6, and 7 years old, respectively. All surgical and experimental procedures were approved by the Northwestern University Animal Care and Use Committee, and were consistent with the National Institutes of Health Guide for the Care and Use of Laboratory Animals.

In the first experiment (Subject M and C), the subjects performed a standard delayed center-out reaching movement paradigm. The subjects were seated in a primate chair and grasped a handle of a custom 2D planar manipulandum that controlled a computer cursor on a screen. The subject began each trial by moving to a 2×2 cm target in the center of the workspace. The subject was then required to hold for 500 – 1500 ms before another 2 cm target was randomly displayed in one of eight outer positions regularly spaced at a radial distance of 8 cm. For Subject M, this is followed by another variable delay period of 500 – 1500 ms to plan the movement before an auditory ‘go’ cue. The subjects were required to reach to the target within 1000 – 1300 ms and hold within it for 500 ms to receive an auditory success tone and a liquid reward.

In the second experiment (Subject J), the subject performed an isometric version of the center-out task. The hand was placed in a box attached to a 6-axis force-torque sensor (JR3, Inc, Woodland, CA), and the subject applied torque about the wrist to move a cursor on a screen. The x and y positions of the cursor were linearly related to the applied horizontal and vertical forces. The subject began each trial by keeping the hand relaxed so that the cursor rested within a start target on the screen. After staying in that target for 200 – 1000 ms, a second target appeared and the subject was required to apply force to reach it within a period of 2000 ms. There was no delay period in this task, therefore the subject could go to the target as soon as it appeared. The subject was then required to hold within this target for 500 ms to receive an auditory success tone and liquid reward.

After the subjects received extensive training in each task, we surgically implanted a 100-electrode array with 1.5 mm shaft length (Blackrock Microsystems, Salt Lake City) in the primary motor cortex (M1) of each subject. We placed the subjects under isoflurane anesthesia and opened a small craniotomy above the motor cortex. We localized primary motor cortex using both visual landmarks and intracortical microstimulation to identify the arm region in Subjects M and C, and the hand region in Subject J. The arrays were then inserted pneumatically. During the behavioral experiments, we acquired neural data using a Blackrock Microsystems Cerebus system. The cortical signals were amplified and band-pass filtered (250 to 5000 Hz). To record the spiking activity of single neural units, we identified threshold crossings of 5.5 to 6 times the root-mean square (RMS) noise on each of the 96 recording channels and recorded spike times and brief waveform snippets surrounding the threshold crossings. For the first experiment, we recorded kinematic data from the robot handle at 1000 Hz using encoders in the manipulandum. For the second experiment, we recorded force data from the force-torque sensor at 2000 Hz. After each session, we sorted the neural waveform data using Offline Sorter (Plexon, Inc, Dallas, TX) to identify single neurons and discarded all waveforms believed to be multi-unit activity.

0.2 Data preparation

After sorting the spike data, we estimated the firing rate of each neuron by binning the spike trains into non-overlapping windows of equal size (50 ms bin width for Subject C, J; optimized bin width of 180–240 ms for Subject M). In all datasets, we select neural responses in small window around the ‘go’ cue: this window is specified by the delay after the go cue (N_d) and then number of samples (N_s) to acquire until the end of the trial). After selecting a subset of data samples (N_go + N_d : N_go + N_d + N_s), we apply a box car filter of length B_smooth to temporally smooth the firing rates in time. For this smoothing step, we don’t assume that we know the trial boundaries and thus some spillover between trials can occur, though we haven’t found an issue with this in practice. In many cases, we found that these preprocessing parameters (N_d, N_s, B_smooth) can be automatically selected by finding the set of parameters that produce decoded outputs with minimum divergence to the training distribution.

For all of our experiments, we sub-sampled the neural and behavioral datasets by removing directions of movement or force-production to produce datasets that were non-isotropic (asymmetric and non-reflective). In Figure 4, we use the same movement distribution for all three subjects (remove targets at 90, 45, 0, 180 degrees). However, we find that DAD is relatively insensitive to the specific pattern of reaches used, as long as the pattern have sufficient isometry to avoid incorrect matches due to rotational symmetries. In each experiment, we selected the entire movement and neural data to use only the trials in the selected directions. This approach is necessary to produce non-isotropic movement distributions that can be aligned with DAD.

When applying DAD to motor datasets, we normalize the data by removing the mean and whitening the covariance of the data. To later retrieve the scaling of the signal to compute the Mean-Squared Accuracy (MSA) in Fig. 4, we rescaled the aligned neural data to have ℓ₂-norm equal to the training kinematics dataset. Thus we deal with the scale ambiguity by solving the alignment problem on normalized data and then rescaling back according to the training data.

0.3 Problem setup

Before diving into the details of our decoding approach, we first need to define the variables for our decoding problem. Let y_i ∈ ℝ^d denote the firing rate of d neurons at the i^th point in time (sample). The time-varying neural activity of a population of d neurons can be represented as a matrix Y of size d × T by stacking the neural activity vectors {y₁, y₂, …, y_T} into the columns of Y. The aim of movement decoding is to make use of the measured firing rates of a population to estimate the intended velocity vector ṽ_i ∈ ℝ² at the i^th point in time, where each entry of ṽ_i corresponds to the Cartesian velocities of movement in the xy-plane. Ultimately, our objective will be to map the neural activities to the space of decoded movements.

A large body of work has demonstrated that the relationship between the instantaneous velocity vector ṽ_i and the neural activity signal y_i in the motor cortex area M1 is approximately linear[30, 31, 32]. More recently, studies have shown that neurons are also tuned to to the squared sum (norm) of the 2D velocities[33]. Thus the kinematics and their norm, at the i^th point in time, can be decoded as v_i = Hy_i, where H is a 3 × d matrix and v_i ∈ ℝ³ includes the norm of the kinematics as its third dimension.

In general, the right matrix for decoding (H) is unknown and must be estimated from neural and kinematics recordings. Here we assume that this linear model is time-invariant, and thus we can also write this model in matrix form as

$$\mathbf{V}=\mathbf{\text{HY}},$$ (1)

where V is a 3 × T matrix that contains the kinematics associated with the observed neural activities. When we have access to simultaneous recordings of kinematics V and the neural activity Y, this information can be used to estimate the matrix H (Eqn. 1). One way of solving this problem is to find a regularized least-squares estimate which minimizes the following loss function

$$\underset{\mathbf{H}}{\text{min}}\frac{1}{T}{\Vert \mathbf{V}-\mathbf{\text{HY}}\Vert }_F^2+\lambda {\Vert \mathbf{H}\Vert }_F^2,$$ (2)

where ${\Vert \mathbf{A}\Vert }_F^2≔{\sum }_{\mathit{\text{ij}}}{\mathbf{A}}_{\mathit{\text{ij}}}^2$ is the Fröbenius norm and λ ≥ 0 is a user specified regularization parameter. This loss function defines the interplay between an error term and a term favoring simpler solutions.

0.4 Overview of distribution alignment decoding (DAD) approach

In contrast to the standard paradigm described above, we now consider the setting where we acquire N samples of the kinematics V ∈ ℝ^3×N separately from neural activity. Take for instance the case where we have recorded the kinematics from multiple users doing the same task and then, at a later time, we collect neural activity Y ∈ ℝ^d×T from a new user performing the same task. Since the kinematics V and neural activity Y are recorded at different times and are potentially of unequal dimension, determining the linear model H cannot be done by solving Eqn. 1. Even if the datasets contain the same number of samples (i.e. N = T), finding correspondence between the columns of V and the columns of Y is a NP hard problem[34].

Rather than tackling the problem of finding correspondence, we can leverage the fact that the underlying distributions of samples in both spaces have similar structures to find a linear mapping that aligns the two. A natural framing of this problem is to find the best linear embedding of the neural data which minimizes the KL-divergence between the predicted distribution of kinematics (q) and the prior distribution of recorded kinematics (p). More formally, assume that the set of samples {v₁, v₂, …, v_N} are drawn from a distribution p and that the predicted kinematics vectors v̂_i = Hy_i are drawn from a distribution q. To estimate H, our goal is to find a solution to the following optimization problem:

$${\mathbf{H}}^{\ast }=\underset{\mathbf{H}\in {ℝ}^{d\times 3}}{\text{arg min}}\text{ KL}(p\Vert q)≔\underset{\mathbf{H}\in {ℝ}^{d\times 3}}{\text{arg min }}{𝔼}_p\left[\text{log }\right(\frac{p(\mathbf{x})}{q(\mathbf{x})}\left)\right],$$ (3)

where the random variable x ∈ ℝ³ is drawn from the distribution p. By minimizing the KL-divergence, our approach essentially finds an affine transformation which maximizes the similarity between the distribution of transformed neural activity and prior distribution of kinematics.

In general, solving the problem in Eqn. 3 is intractable, due to the fact that the KL-divergence can be a non-convex and non-differentiable function of H. However, we can exploit the fact that, without substantial loss of information, Y can be projected into a lower-dimensional space where solving this problem is possible. We denote the resulting projected neural activities and the corresponding (low-d) decoder as Y_ℓ and H_ℓ, respectively. When the mapping between Y and V is linear, the problem of distribution alignment can be reduced to finding the best linear transformation H_ℓ such that the KL-divergence between the distribution of observed kinematics p and predicted kinematics q is minimized. In a lower-dimensional space, the alignment between the distributions of neural data and kinematics is feasible. To solve our low-dimensional alignment problem, we use the KL-divergence as a metric for alignment.

0.5 Step 1. Dimensionality reduction

The first step of our approach is to reduce the dimensionality of the data in order to reduce the complexity of our alignment procedure. To do this, we used a Matlab toolbox[35] to apply numerous off-the-shelf methods for dimensionality reduction, including principal components analysis (PCA), factor analysis (FA), Isomap[36], stochastic neighborhood embedding (SNE) [37], and Probabilistic PCA [38] to the data. We also included exponential PCA[39] in our list of methods to try initially. To quickly assess the low-dimensional structure of the data, we designed a module to preprocess and apply a variety of dimensionality reduction techniques to the data. Using this Matlab module, a user can quickly visually inspect the results of different methods to confirm that the task structure is indeed visible in the data. Note that this step can be done in a completely unsupervised way. We also describe a model selection procedure which can be used to perform an automatic search for low-dimensional representations that have task-related structure. Thus by searching for the embedding that produces the smallest KL-divergence with our training distribution, our methods can be used to find a low-dimensional representation of the data that contains task-related structure.

0.6 Step 2. Distribution alignment

After reducing the dimensionality of the neural data, the next step of DAD is to align the projected neural data with the prior distribution over the movement. To do this, we implemented a custom global search method which finds a rotation, scaling, and translation of the projected neural data which minimizes their KL-divergence. Our method consists of three main ingredients: (i) an efficient method for estimating the KL-divergence between two datasets, (ii) a 3D search routine that uses random sampling and refinement to explore the search space, and (iii) a fine-scale 2D alignment procedure that uses a more accurate measurement of the KL-divergence to measure the goodness of fit.

To measure the KL-divergence between the distributions p (target) and q (source) in Eqn. 3, we adopt a non-parametric approach that allows us to obtain an accurate estimate of these distributions without making any restrictive assumption on the form of either distribution. In particular, we rely on the popular k-nearest neighbors (KNN) density estimation algorithm[40, 41], which estimates a distribution using only distances between the samples and their k^th nearest neighbor. To make this concrete, we define the distance between a vector x and a matrix A as ρ_k(x, A) = ‖x − a_k‖₂, where a_k is the k^th nearest neighbor to x contained in the columns of A. The value of the empirical distribution p at v_i is then estimated using the following consistent estimator[40]:

$$p({\mathbf{v}}_i)\propto \frac{k}{N{\rho }_k^3({\mathbf{v}}_i,\mathbf{V})}.$$

We partition the 3D space and then compute this quantity for every grid point. After computing the 3D density, we normalize to obtain a proper probability distribution over the space of grid points. Note that the intuition behind this approach is that in regions where we have higher density of samples, the k-nearest distance ρ_k(v_i, V) will be small and thus, the probability of generating a sample at this location is large.

To estimate the distribution of the predicted kinematics V̂ = H_ℓY_ℓ from the projected neural activities Y_ℓ, we again use the same nearest neighbor approach. Assuming that we have an estimate for H_ℓ and Y_ℓ, the empirical distribution of the predicted dynamics is given by $q({\mathbf{v}}_i)\propto \frac{k}{T{\rho }_k^3({\mathbf{v}}_i,\hat{\mathbf{V}})}$. As with p, we compute this quantity for all D grid points and then normalize to produce a probability distribution of these points.

To obtain the results described in this paper, we set the number of nearest neighbors (k) to 5 in our 3D searches and to 3 for 2D. We found that once the number of time points is sufficiently large (T > 300), these values of k produce stable alignments.

Once we compute the empirical distributions p and q over a fixed 3D grid {s₁, …, s_D}, we can use the following formula to estimate the KL-divergence:

$$\text{KL}(p\Vert q)\approxeq \frac{1}{D}\sum _{i=1}^{D}p({\mathbf{s}}_i)\text{ log }\left(\frac{p({\mathbf{s}}_i)}{q({\mathbf{s}}_i)}\right).$$

After estimating the probability distributions p and q, the next step is to find the best H_ℓ that minimizes their divergence. Even for this relatively low-dimensional problem, we found that global search methods and other non-convex optimization methods failed to find a stable solution. We thus implemented a global search method that estimates the 3D rotation and translation that minimizes the KL-divergence between the aligned embedding and training kinematics. This method iteratively refines its estimate of the rotation, translation, and scaling of the data to minimize the KL-divergence between the transformed neural data and the prior distribution over movements. After finding the best 3D rotation and translation, we then project the data into 2D and solve a fine-scale alignment of the data in two dimensions. Our results suggest that our search method can efficiently align two low-dimensional distributions, even in light of numerous local minima in the solution landscape.

0.7 Model selection

For many of the datasets we studied, selecting the right set of parameters to prepare the data can be critical for finding a low-dimensional factorization that contains task-related structure. Thus we developed a model selection procedure for doing this automatically. Our approach performs an exhaustive search over the parameters used to process the data, solves the alignment problem for all of the possible options, and then selects the model that provides either small KL-divergence (in unsupervised case) or small decoding/target error (in semi-supervised case). The parameters that we use in our optimization procedure include: how long we wait after the ’go’ cue before starting to sample data (N_d), the number of samples to select (N_s), the width used to temporally smooth the neural firing rates (B_smooth), and in some cases, the bin size. Our model selection approach provides an automated way to find task-related structure in firing rates from neural populations.

To optimize the parameters in our model, our goal is to select the value of each parameter that produces the best aligned models on average, as measured by their final KL-divergence. We start by running DAD on all possible sets of input parameters that the user wishes to search over (using a grid search). To compute the model with the smallest KL-divergence, our aim is to minimize the following expression:

$$\underset{0<i\le \ell }{\text{min}}d(q,p_i),$$

where θ_i = [θ_i1, θ_i2, θ_i3, …, θ_ik] denotes a vector containing of the parameters that we wish to optimize, d(q, p_i) denotes the KL-divergence between the prior q and the distribution p_i of the projected neural dataset obtained with the i^th model (θ_i), and ℓ is the number of model parameters.

The KL-divergence provides a good measure of whether a model will be accurate. However, we find that selecting the model with absolute smallest divergence is not always the best strategy, as this solution often does not generalize. We found that we can get a more stable solution by smoothing the KL-divergence as a function of model parameters, which rules out the outliers (smoothKL). The divergences can be smoothed by resampling the data (bootstrapping), running the method and then taking the average of their resulting divergences. In practice, we simply smooth the KL-divergences by applying spatial smoothing to the samples, which has the effect of reducing the effect of spurious minima in our search procedure.

When some supervised data is provided (e.g., the hand position or the target information), we can reliably pick a model that rules out incorrect alignments in high noise regimes. The maximum R² (maxR²) model returns the solution that produces the best R² on a training set. Likewise, we can also learn a model that produces the best target prediction performance on a training set (maxTarg). We provide an implementation of these and other model selection criterion online (github.com/KordingLab/DAD).

0.8 Dimensionality of neural representations of movement

When examining the neural representations of movement through dimensionality reduction, in two of the three subjects (M,J), we found neural representations of movement (M) and force production (J), give rise to projections that can be well approximated by a cone in 3D. This structure makes sense in light of studies that suggest neurons in M1 are tuned to the 2D task (kinematics or force) as well as the speed[33]. Indeed, when we lift the 2D motor variables measured from Subject M (Fig. 2b) and Subject J (Fig. 2c) to 3D by adding speed as the third covariate, we obtain a conical shaped distribution that matches the observed 3D projections of neural data that we observed. In the case of Subject C, we found task-related structure present in two-dimensional projections but did not find consistent three-dimensional structure that could be used for alignment. Thus we projected the neural data directly into 2D and performed alignment in this space to decode Subject C’s neural activity. In all datasets, we align both the 2D and 3D embeddings of neural data and select the result that has minimum KL-divergence.

0.9 Synthetic model

When simulating neural activity, the firing rate of the n^th neuron at the t^th time point is given by

$$f_{n,t}=\text{exp}[{\alpha }_n+{\beta }_t\text{ cos}({\theta }^n-{\theta }^t)],$$

where θⁿ is the preferred direction of the n^th neuron, θ^t = tan⁻¹(υ_x,t/υ_y,t) is the direction of the movement at the t^th time point, υ_x,t is the velocity in the x-direction at time t, υ_y,t is the velocity in the y-direction at time t, and α_n and β_n are scalars which shift and modulate the firing rate, respectively. To generate spikes for a population of size N, we generate Poisson random variables according to the firing rates {f₁, …, f_N}. In our simulations (Fig. 4), we set the baseline α_n = 2, for all neurons (∀n) and set the modulation term ${\beta }_t=\overline{\upsilon }\sqrt{{\upsilon }_{x,t}^2+{\upsilon }_{y,t}^2}$ where $\overline{\upsilon }=\frac{1}{T}{\sum }_{i=1}^T\sqrt{{\upsilon }_{x,i}^2+{\upsilon }_{y,i}^2}$.

0.10 Performance evaluations

In our performance comparisons against supervised approaches (Fig. 4, Fig. 5), we split the full neural (Y) and motor (V) datasets into a test and train set to create four non-overlapping datasets, Y_te, Y_tr, V_te, and V_tr. In the case of the supervised methods, we use a standard protocol: the decoders are given access to ordered training data (V_tr, Y_tr) to learn a mapping H based upon these data and then use this to predict an estimate V̂_te from neural data Y_te. To train the regularized linear decoder (Sup), we used regularization to avoid overfitting (see Eqn. 2) and learned the regularization parameter with 10-fold cross validation. When comparing the methods, we computed the: R₂, the Mean-squared Accuracy which is computed as 2|x − y|〈x, y〉/(‖x‖ + ‖y‖), and the Target Accuracy which reports the percentage of reach directions correctly decoded. Our implementations of the supervised linear decoder and Kalman Filter are provided in our online github repository (github.com/KordingLab/DAD).

To predict V̂_te from neural data Y_te, we give DAD access to V_tr and Y_te and allow the method to align the test data onto the training kinematics. Note that in many cases, V_tr and Y_te can either be collected from different subjects or on different days. For decoding, we only need a kinematics dataset that will be sufficient for alignment. When performing model selection with a supervised metric (maxR², maxTarg), we use the same set of training samples as the supervised methods to obtain our model estimate.

0.11 Data availability

The authors declare that all data supporting the findings of this study are available within the paper, as well as at http://github.com/KordingLab/DAD.

0.12 Code availability

The authors declare that all of the code required to run the method and the scripts required to create the figures are available at http://github.com/KordingLab/DAD.

Figure 7. How distribution alignment scales with the number of recorded neurons.

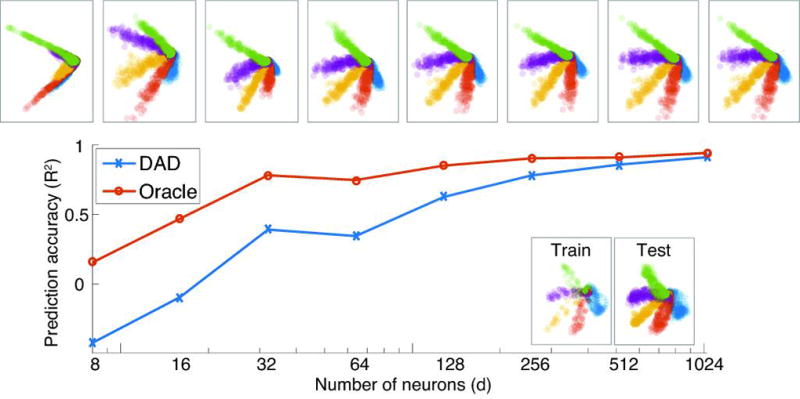
To understand the limits of DAD, we visualize the performance of DAD on synthetic data as we increase the number of neurons in our model. As we increase the size of the neural population, we plot the trimmed mean of the R² values (the top and bottom 10% of trials are removed) obtained for DAD and the Oracle, averaged over 100 trials. We show examples of alignments obtained as we increase the number of neurons in our synthetic model (above), as well as examples of training and test kinematics (at the bottom).