Using focal cooling to link neural dynamics and behavior

Abstract

Establishing a causal link between neural function and behavioral output has remained a challenging problem. Commonly used perturbation techniques enable unprecedented control over intrinsic activity patterns and can effectively identify crucial circuit elements important for specific behaviors. However, these approaches may severely disrupt activity, precluding an investigation into the behavioral relevance of moment-to-moment neural dynamics within a specified brain region. Here we discuss the application of mild focal cooling to slow down intrinsic neural circuit activity while preserving its overall structure. Using network modeling and examples from multiple species, we highlight the power and versatility of focal cooling for understanding how neural dynamics control behavior and argue for its wider adoption within the systems neuroscience community.

Banerjee et al. demonstrate the power and versatility of focally cooling neural circuits as a means of testing the link between brain dynamics and behavior, supporting this view using examples from multiple species as well as network simulations.

The need for cooling

Neuroscientists have long attempted to link brain function to behavior by studying the effects of focal perturbations to neural activity. Even as early as the 1870s, electrical stimulation of motor cortical areas was shown to drive specific muscle movements (Fritsch and Hitzig, 1870). Conversely, lesion studies have been instrumental in understanding the behavioral relevance of specific brain regions (Broca, 1861). More recent developments, such as optogenetics (Fenno et al., 2011) and pharmacogenetics (Sternson and Roth, 2014), have allowed specific neuronal cell types to be selectively manipulated to infer their contribution to brain function. These approaches continue to be enormously important for modern neuroscience, and methodological advances enable the perturbation of neural activity with ever-increasing levels of control (Deubner et al., 2019).

One potential disadvantage of standard perturbation approaches, however, is that they can disrupt the behavior they were designed to investigate. Often these methods result in fundamental changes to ongoing intrinsic neural dynamics (Bernard, 2020; Li et al., 2019; Panzeri et al., 2017; Wolff and Olveczky, 2018; Yoshihara and Yoshihara, 2018), preventing a more nuanced analysis of the relationship between neural dynamics and behavior. Neural population activity can be conceptualized as a single point in a multidimensional space, where each dimension corresponds to the firing rate of one neuron. Each point in this space represents the instantaneous “state” of the joint population activity. For illustration, we depict this in a dimensionality-reduced state space (Cunningham and Yu, 2014). Over time, the point moves around to create a neural trajectory (Figure 1A). There exists a moment-by-moment mapping between this ensemble neural activity and behavior, with trial-by-trial variability in neural dynamics during repetition of the same behavior determining the range of possible trajectories. Using this framework, we illustrate that standard methods for manipulating neural systems can strongly perturb both network dynamics and the resulting behavior (Figure 1B) by showing a neural trajectory abruptly deviating from its canonical path (Jazayeri and Afraz, 2017; Shenoy and Kao, 2021).

Figure 1. Two Approaches for Perturbing Neural Activity and Behavior.

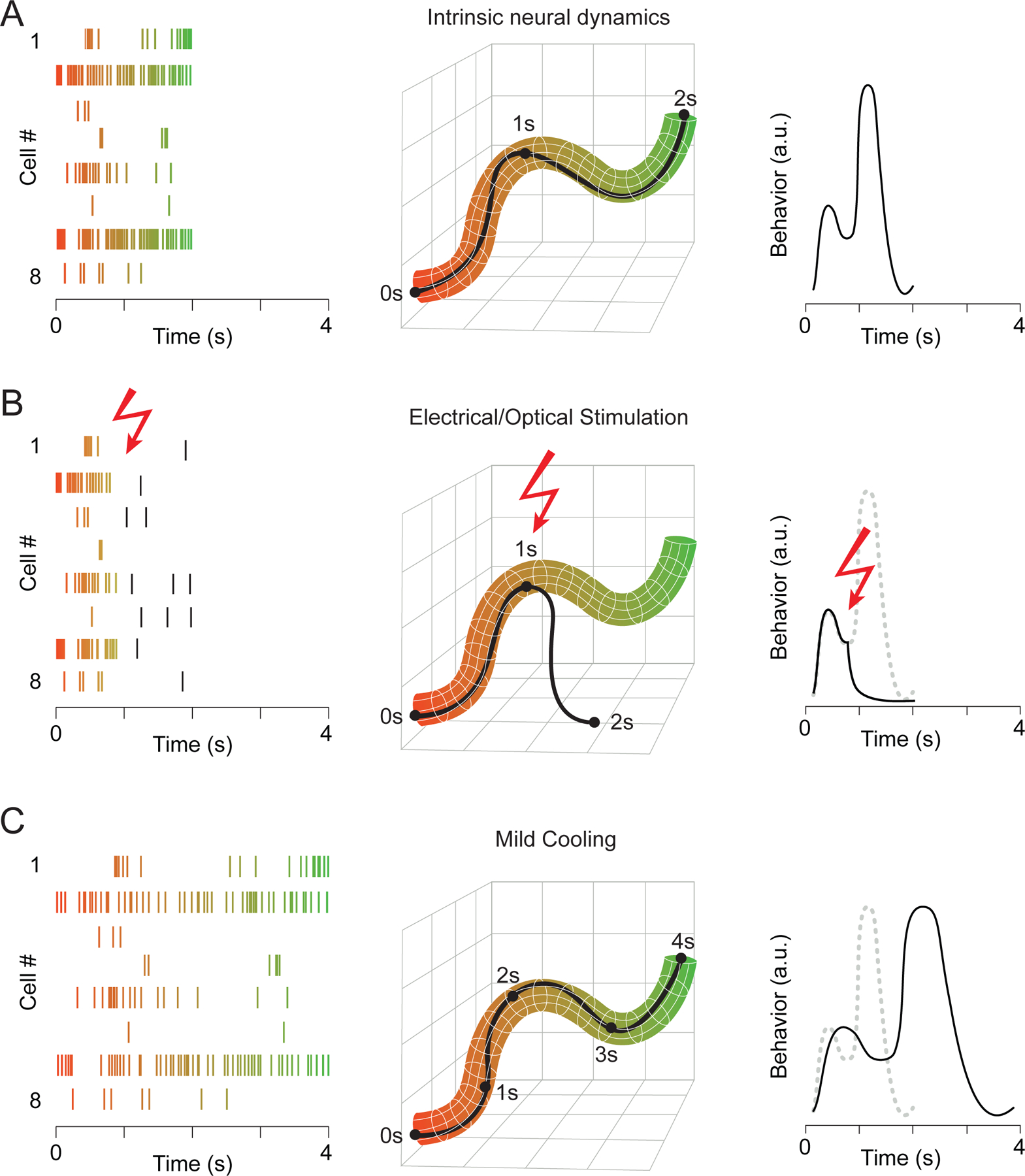
(A) Spike raster plot of eight simultaneously recorded neurons (left). The proportion of the trial is color-coded, transitioning from orange to green throughout its duration. Dimensionality-reduced neural activity plotted in state-space (middle). The black line describes the example trial at left. Since individual trials are not identical in this network, the standard network structure is determined by the correlated population activity, and its thickness reflects trial-by-trial variability. In this case, a causal relationship exists between the joint spiking activity of the network and a measurable behavioral output (right).

(B) Neural activity from (A) is interrupted in the middle of the trial, which causes the network to deviate from the normal activity patterns, leading to a concomitant behavioral disruption.

(C) A manipulation that changes the temporal dynamics of neural activity while preserving the overall structure of the population activity can maintain but temporally distort behavioral output.

To better understand the exact causal mapping between neural activity and behavior, we require a method that can avoid some of the difficulties of pushing dynamic systems from their operating regimes in extreme ways, like large-scale silencing. Instead, if we can simply affect the speed of neural activity without disrupting its overall structure, then behavior may be preserved, albeit at a different time scale (Figure 1C). If neural activity of a particular brain area controls behavioral output, then changing the speed of neural dynamics should lead to a concomitant change in behavior. Here we explore the idea that mild cooling can be used as a highly effective perturbation technique; we build an intuition about the effects of cooling on neural circuit activity by providing examples from various systems; and we point out the advantages and limitations of using focal cooling compared to other existing approaches.

Cooling an isolated neural circuit

Before examining how focal cooling can accurately assess the behavioral relevance of identified brain regions embedded within a larger neural network, we will first discuss the impact of temperature changes on a single, isolated neural circuit: the stomatogastric ganglion (STG). The STG contains approximately 30 neurons that can generate rhythmic behavior even after being dissected away from the rest of the nervous system, including a cyclic pyloric rhythm that regulates stomach musculature (Marder et al., 1998). Three cell types within this rhythm-generating circuit (PD, LP, and PY) are sequentially active, as revealed by intracellular recordings and visualized by plotting the joint activity of these three cell types in state space (Figure 2) (Tang et al., 2010). Using this preparation, temperature can be manipulated by simply superfusing the ganglion with cooled or warmed saline solutions. As with other invertebrate central pattern generators (Calabrese and Arbas, 1984; Katz et al., 2004), the pyloric rhythm is robust over a wide temperature range (Robertson and Money, 2012). For instance, lowering the temperature from 23°C to 15°C causes the rhythmic cycles to slow their tempo while maintaining the relative network timing (Figure 2A). In fact, when we linearly stretch voltage traces recorded at 23°C to match the timescale of those recorded at 15°C, some minor changes become apparent (e.g., slight increase in spikes per burst at the warmer temperature), but the phase relationship of neural activity across neurons remains strikingly similar (Figure 2B). Therefore, cooling can slow down neural dynamics without disrupting them. Importantly, similar temperature sensitivity of the pyloric rhythm can be seen in vivo despite the presence of a considerably more complex network and neurochemical environment (Soofi et al., 2014). Taken together, these results demonstrate that cooling a simple neural circuit can selectively alter the speed of neural activity while preserving its overall structure.

Figure 2. Temperature-induced Manipulation of Neural Dynamics in an Isolated Circuit.

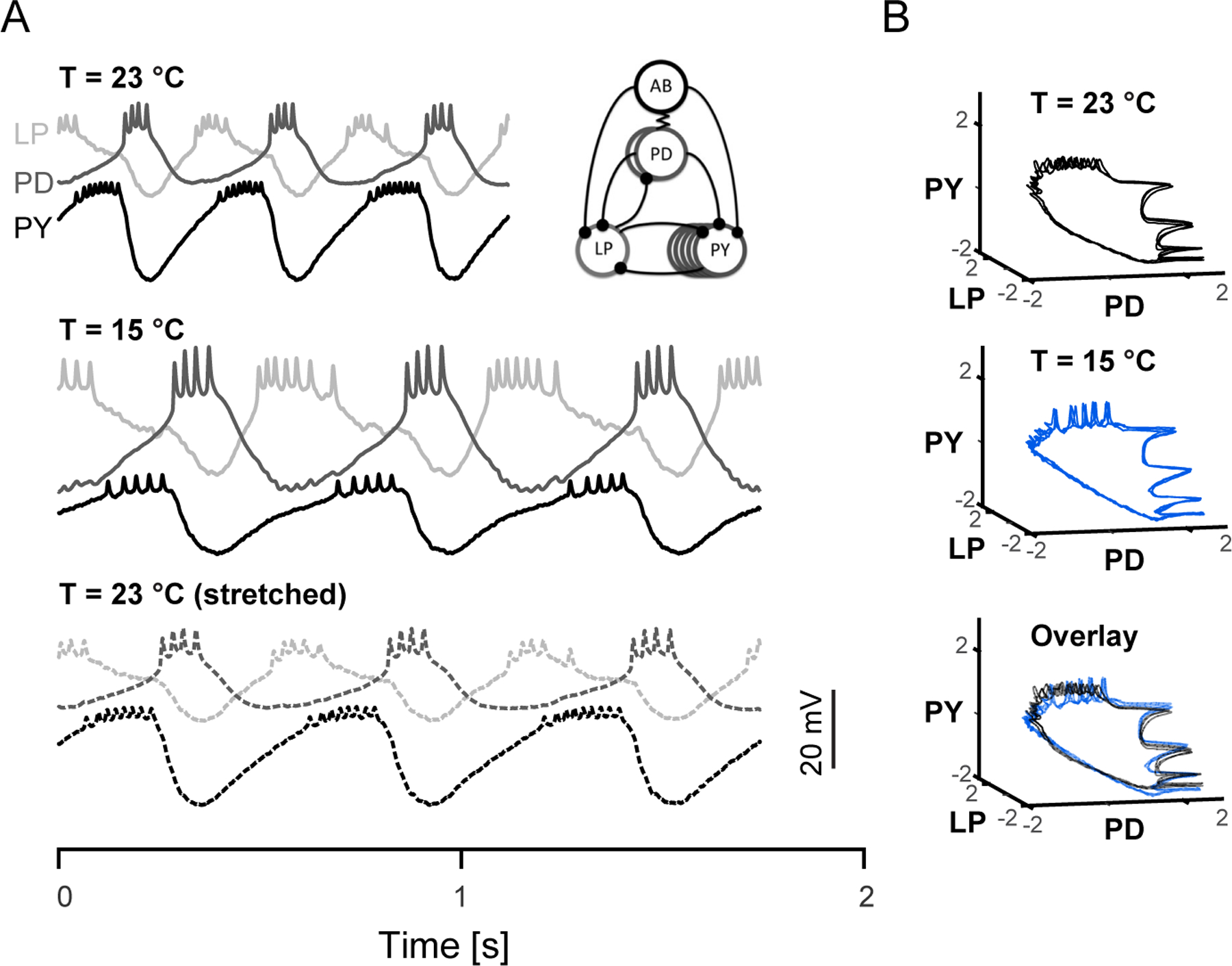
(A) Simultaneous intracellular recordings from three interconnected neurons (LP, PD and PY) from the crab somatogastric ganglion. Activity recorded from three complete pyloric rhythm cycles are plotted at 23°C (top) and 15°C (middle). Artificially stretched traces at 23°C (bottom) closely match profile of 15°C traces. Inset: simplified diagram of pyloric circuit. Replotted data from (Tang et al., 2010).

(B) Data from (A) depicted in a state-space plot (z-scored) forms a simple 3D trajectory at 23°C (top) and 15°C (middle). Both trajectories (23°C black, 15°C blue) occupy similar space when plotted together (bottom).

Biophysical substrates of cooling

Before examining how focal cooling can be used as a tool to identify behaviorally relevant dynamics, we examine the cellular and synaptic mechanisms leading to temperature-driven network changes. Brain function is broadly temperature dependent, including both pre- and postsynaptic cellular processes (Kalmbach and Waters, 2012; Volgushev et al., 2000a; Volgushev et al., 2000b). For instance, Strong cooling (ΔT: ~ −30°C) can block spiking (Coomber et al., 2011; Lomber, 1999; Michalski et al., 1993), likely due to a strong depolarization of neurons leading to sodium channel inactivation (Jasper et al., 1970). As a result, this manipulation has provided systems neuroscientists with a means of rapidly and reversibly inactivating brain regions. At more moderate cooling levels (ΔT: < −10°C), however, cellular processes remain largely intact but are slowed. For instance, cooling can slow down spontaneous membrane potential oscillations, as in the case of the inferior olivary nucleus, where the frequency of large amplitude rhythms generated by a confluence of voltage-gated conductances (Lampl and Yarom, 1997) can be halved by lowering the temperature by approximately 5°C (Figure 3).

Figure 3. Biophysical Mechanisms of Cooling.

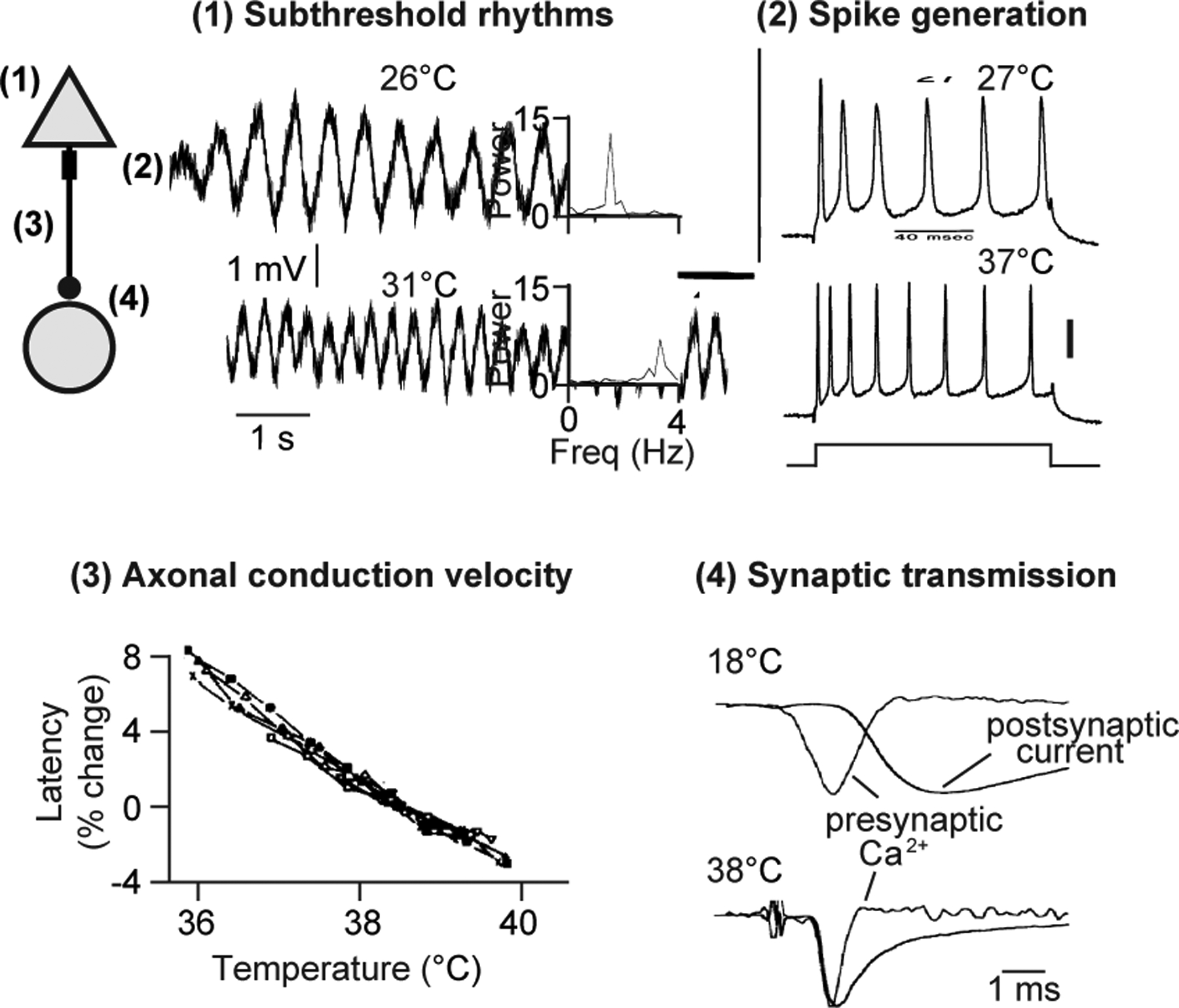
At left, a schematic of a synaptically connected pair of neurons with numbers indicating four sites at which temperature-sensitive processes are occurring as illustrated in the accompanying examples: (1) Frequency of subthreshold membrane potentials from a guinea pig inferior olivary neuron decreases with cooling, as indicated with power spectra at right. Adapted from (Lampl and Yarom, 1997).

(2) Evoked spikes of a guinea pig CA1 pyramidal neuron are slower and wider at lower temperatures (Injected current: 120 ms, 0.85 nA). Scale bar: 20 mV. Adapted from (Thompson et al., 1985).

(3) Relationship between brain temperature and conduction latency in 8 unmyelinated axons from the Dutch belted rabbit. Adapted from (Swadlow et al., 1981).

(4) Difference in timing between presynaptic calcium current and postsynaptic current (i.e., synaptic delay) at two different temperatures. Adapted from (Sabatini and Regehr, 1996).

Distinct aspects of neural circuit function are often variably affected by temperature. Such a dependency is quantified as the Q₁₀ coefficient, or the rate of change of the time constant underlying a linearly varying biological process resulting from altering the temperature by 10°C. For instance, the aforementioned olivary rhythm changes considerably over a small temperature range with a Q₁₀ of ~4. Other cellular processes are also highly temperature sensitive, such as synaptic transmission (Hodgkin and Katz, 1949; Sabatini and Regehr, 1996; Volgushev et al., 2000a). The time between an action potential arriving at the axon terminal and the onset of the postsynaptic current (i.e., synaptic delay) can be ~100 μs at mammalian body temperatures but expand by nearly an order of magnitude when cooled (Figure 3), likely due to kinetics of presynaptic calcium channels involved in neurotransmitter release (Nobile et al., 1990). Mild cooling can also widen action potentials and lower the rate of repetitive firing (Figure 3) (Thompson et al., 1985; Volgushev et al., 2000b) (AP width Q₁₀: ~ 2, AP rate Q₁₀: ~ 2). Some other processes are considerably less dependent on temperature, including axonal conduction velocity (Figure 3), which changes by approximately 3%/°C (Swadlow et al., 1981), or a Q₁₀ of 1.3.

Given the heterogeneous Q₁₀ values that exist within neural circuits, it is surprising that nervous system function can remain robust across a range of temperatures (Hamaguchi et al., 2016; Tang et al., 2010). For instance, the STG maintains a rhythmicity from approximately 0.7 to 2.9 Hz, with a network-level Q₁₀ of 2.3, despite being the product of multiple conductances that each exhibit different relationships with temperature, including synaptic currents (Q₁₀ = 2.3), input conductance (Q₁₀ = 1.6), and voltage-gated currents, such as I_A (Q₁₀ = 3) (Tang et al., 2010). Such temperature robustness could reflect evolutionary adaptations that enable animals to withstand environmental temperature variations (Donahue et al., 2009) and may also be crucial for maintaining network function during physiologically challenging conditions (Hoffstaetter et al., 2018).

It should be noted that increasing brain temperature can also affect neural function. These effects are especially relevant for modern neuroscience, given that substantial heating can result from commonly employed methods, such as 2-photon imaging (Podgorski and Ranganathan, 2016) and optogenetic light delivery protocols (Owen et al., 2019). Importantly, heating can result in devastating side effects, such as seizure generation (Kasahara et al., 2018) or lasting tissue damage (Yarmolenko et al., 2011), while mild focal cooling appears to avoid such complications (Ibayashi et al., 2021). Additionally, the relationship between heating and cellular function may be considerably more complex than that observed with cooling (Owen et al., 2019), which may lead to difficulties in interpretation for studies in which focal heating is used. Therefore, we maintain a focus on mild cooling for the remainder of this manuscript.

Control of neural dynamics and behavior in the songbird

We now explore how focal cooling can be used to pinpoint the link between neural dynamics and behavior. For our first example, we will focus on the song control pathway of the zebra finch. Male zebra finches vocally imitate their courtship song; once learned, the structure of the song is highly stereotyped with timing that varies by less than 3% across renditions (Egger et al., 2020; Glaze and Troyer, 2006; Sossinka and Böhner, 1980). Song production is controlled by a series of nuclei located throughout the brain (Nottebohm et al., 1982; Nottebohm et al., 1976). Premotor neurons within a forebrain nucleus, HVC (proper name) (Figure 4A), collectively display a sequence of activity during song production (Egger et al., 2020; Lynch et al., 2016; Picardo et al., 2016), with each neuron producing a high-frequency burst of action potentials at a single time point during the song (Figure 4B) (Hahnloser et al., 2002; Kozhevnikov and Fee, 2007). Remarkably, small variations in burst timing of premotor neurons precisely mirror the small variations in overall song duration (Figure 4C). Hence, the population activity of HVC premotor neurons forms a sequential pattern that unfolds at slightly different speeds across song renditions, corresponding to minute changes in behavioral timing under normal conditions.

Figure 4. Change to Neural Dynamics and Behavior from Cooling Zebra Finch HVC.

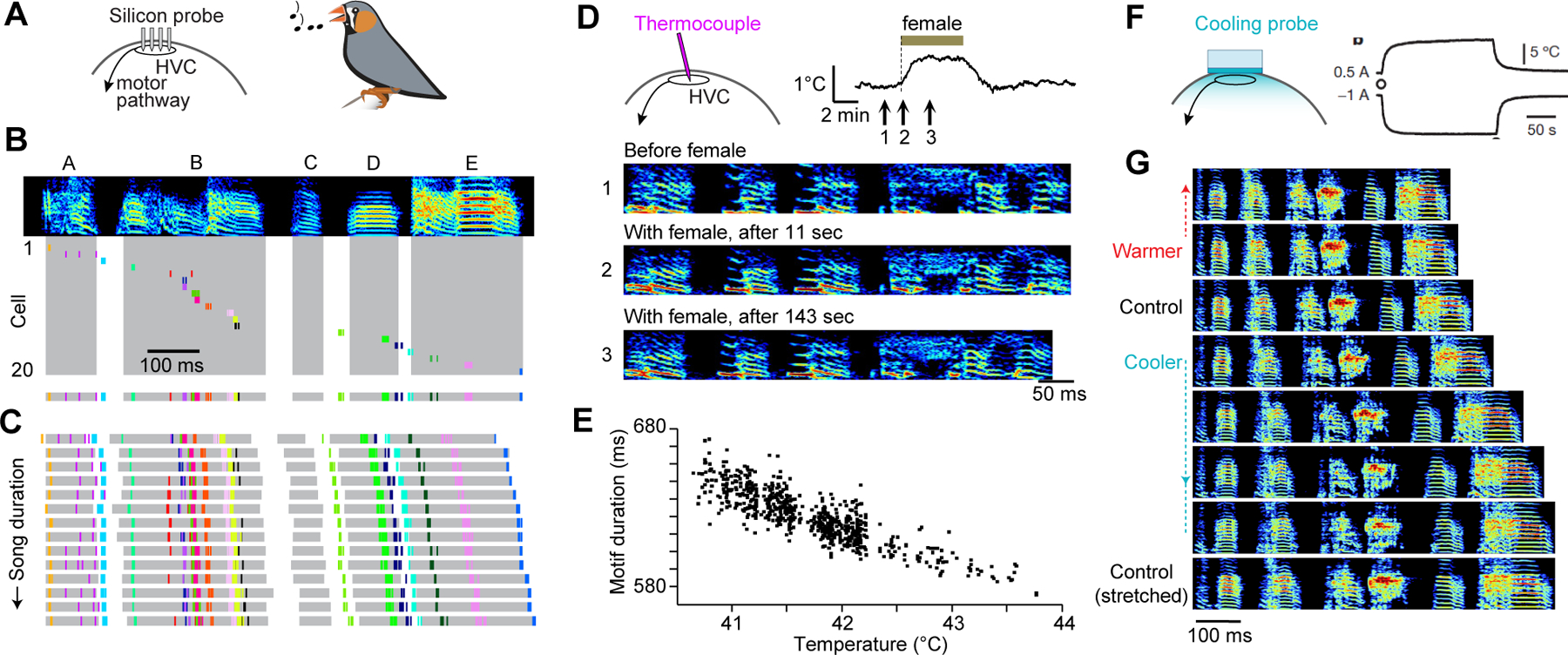
(A) Schematic of recording array in the forebrain nucleus HVC of the zebra finch.

(B) Spectrogram of a zebra finch song motif consisting of syllables A through E (top). Spike times of 20 simultaneously recorded HVC premotor neurons in which activity from each neuron separated vertically (middle) or collapsed into a single row (bottom). Syllables shaded in grey. Sonograms here and below display frequencies from 0.5 to 8.0 kHz. Adapted from (Egger et al., 2020).

(C) Spike times of the same neurons as in (B) and syllable durations during 14 song renditions, sorted by increasing duration. Adapted from (Egger et al., 2020).

(D) Context-dependent increase in brain temperature upon exposure to a female (top). Numbers correspond to spectrograms from a male zebra finch singing in isolation (undirected song) or to a female (directed song) (bottom). Adapted from (Aronov and Fee, 2012).

(E) In the context of naturally occurring brain temperature variability, song motif duration is inversely proportional to HVC temperature. Adapted from (Aronov and Fee, 2012).

(F) HVC temperature can be selectively controlled using a chronically implanted Peltier device. Measuring temperature levels 0.5 mm below the surface of the cooling probe demonstrates that applied current (0.5A and −1.0A) leads to heating and cooling, respectively. Adapted from (Long and Fee, 2008).

(G) Representative sonograms at a range of different experimentally determined HVC temperatures. For reference, a spectrogram of a control song linearly stretched to duration of motif produced at coldest temperature (below). Adapted from (Long and Fee, 2008).

Several factors determine the speed of neural dynamics and thereby song production; for instance, undirected song – performed in isolation – had long been shown to be slower than singing in the presence of a female (Sossinka and Böhner, 1980). Aronov and Fee (Aronov and Fee, 2012) tested the hypothesis that this context-specific change in timing could be explained by rapid changes in brain temperature (Figure 4D). To measure this, they inserted a thermocouple in either HVC or in a forebrain location outside the song system. Brain temperature in both locations increased by up to 1°C (leading to a ~ 3% increase in song speed) in less than a minute following the presentation of a female bird (Figure 4D). Song duration was shown to strongly vary as a result of natural changes in brain temperature (Figure 4E), consistent with the idea that brain temperature can alter the speed with which the network traverses its premotor neural trajectory.

Because the presence of a female increases temperature across the male bird’s entire brain non-specifically, the change in song tempo cannot be causally attributed to any of the individual nuclei within the song control pathway (Aronov and Fee, 2012). Such whole brain temperature changes affecting song timing have long been described in ectothermic animals; in field crickets, for instance, the chirp rate is so sensitive to ambient temperature that the inter-chirp interval can be used as an accurate “thermometer” (i.e., Dolbear’s law) (Dolbear, 1897). Subsequent studies have used focal temperature manipulations – administered to specific parts of the nervous system – to pinpoint song production circuitry in both insects (Pires and Hoy, 1992) and frogs (Yamaguchi et al., 2008). To address the relative contributions of various nuclei to zebra finch singing behavior, a head-mounted Peltier probe was used to selectively manipulate the temperature of HVC (Figure 4F). Cooling HVC led to a monotonic change in song length (Figure 4G), while cooling a downstream region – the robust nucleus of arcopallium – showed no such effect (Long and Fee, 2008). This result demonstrates that song production continues even when HVC temperatures are lowered to levels significantly less than what is naturally observed in zebra finches and other songbirds (Goldin et al., 2013; Zhang et al., 2017). Indeed, the behavioral impact of cooling HVC alone matched that of widespread natural temperature variations (~ 3%/°C, Q₁₀: ~ 1.3), suggesting that HVC is largely orchestrating the temporal structure for song production. Furthermore, recent work has indicated that the timing of HVC activity sequences is largely determined by the kinetics of axonal conduction within HVC (Egger et al., 2020). Consistent with this view, axonal transmission exhibits a similar temperature sensitivity with singing behavior (Long and Fee, 2008; Swadlow et al., 1981). Because slowing down the natural premotor dynamics in HVC leads to a dilation of song timing, the songbird provides a clear example of using cooling to link neural activity to a complex learned behavior (Figure 4G).

Cooling alters speed of neural dynamics in a recurrent neural network model

Using cooling to manipulate neural dynamics in songbirds has demonstrated that this tool can be used to study neural control of behavior. One caveat is that the neurons within the zebra finch HVC are highly specialized, responding in a sparse and precise manner during song production, while brain regions in other systems may have more complex temporal activity patterns. To explore the generality of cooling in neural circuits, we developed a toy model (800 neurons) where the network activity at every moment controls a simple ‘behavioral’ output (Figure 5A). In this example, behavior is represented by two distinct rhythms chosen to independently assess the impact of activity perturbations at these two timescales. Neurons in the recurrent network produced a variety of complex firing rate patterns (Figure 5B), and a simplified version of network activity can be visualized by plotting the first two principal components of network activity.

Figure 5. Manipulations in a Recurrent Neural Network.

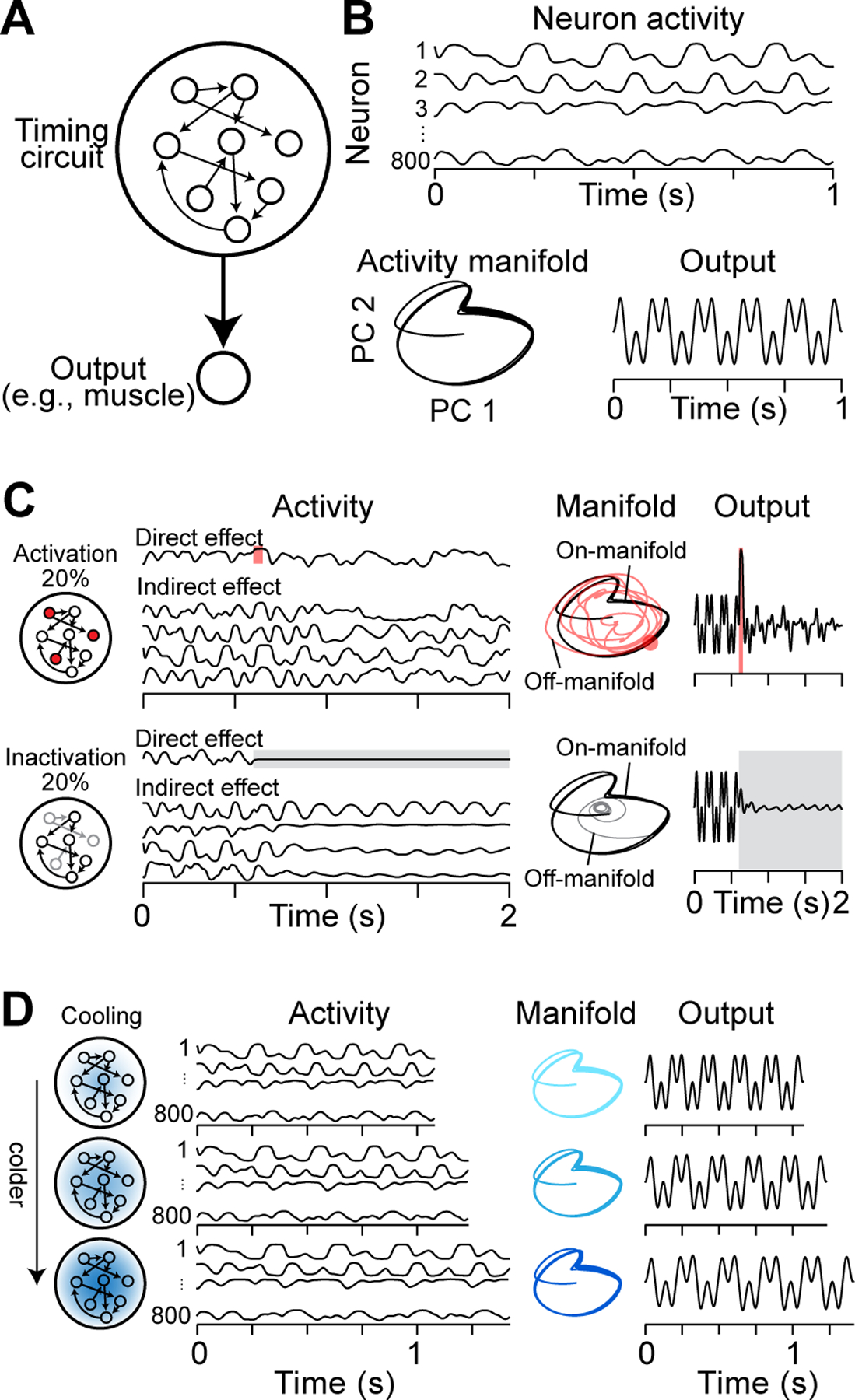
(A) Schematic of our timing circuit model which consists of N = 800 rate-based neurons forming an all-to-all recurrent neural network with random synaptic weights drawn from a normal distribution scaled by a factor $g/\sqrt{N}$ with g set to 1.5 (Sussillo and Abbott, 2009). Additionally, all neurons synapse onto a single output unit. Recurrent and output weights are updated using the FORCE algorithm (Sussillo and Abbott, 2009) to learn a desired output pattern (Laje and Buonomano, 2013).

(B) Activity of 4 example neurons after learning (top). Network activity structure visualized using the first two principal components (PC; bottom left) and a learned output signal (bottom right).

(C) Simulated large-scale manipulations and their effects on neuronal activity (left), network dynamics (center), and output (right). Shown here are responses to activation (top row, shaded red area) and persistent (bottom row, shaded grey area) inactivation of 20% of neurons within the simulated network.

(D) Simulated cooling manipulation through three monotonically increasing levels of focal cooling. Mild cooling was modeled by augmenting network dynamics by a factor Q: $\tau \frac{d\overrightarrow{x}}{dt}=-\overrightarrow{x}$. Here, τ = 10ms, W_rec is the recurrent weight matrix, and $\overrightarrow{x}$ and $\overrightarrow{r}$ are vectors of length N describing the internal dynamics and firing rates of each neuron. Temperature dependence of Q was modeled using Q₁₀ = 2. Note that this simplified rate model does not account for axonal conduction delays (Egger et al., 2020; Swadlow et al., 1981).

Both activation and inactivation of a fraction of neurons in our recurrent neural network model resulted in changes to the activity patterns of all neurons. As a result, the trajectory of the neural population deviated significantly from its intrinsic activity pattern and resulted in qualitative changes in behavioral output (Figure 5C). In contrast, cooling the network (i.e., changing the timescales of biophysical properties of the model neurons) left activity patterns of individual neurons largely intact (Figure 5D). Since cooling-induced changes were consistent between neurons, the resultant neural activity maintained the same structure – albeit at a different speed – and consequently behavioral output was slowed down equally for both the fast and the slow rhythms. This result generalizes to other choices of ‘behavioral’ output and is conceptually similar to the stretching of zebra finch song at all timescales upon cooling HVC (Figure 4). In summary, modeling suggests that cooling can manipulate the timing of neural dynamics in recurrent neural networks, extending its utility to neural circuits with complex and diverse activity profiles. In the next section, we highlight some examples of how focal cooling can be used to infer behaviorally relevant neural dynamics in cortical circuits.

Using cooling to infer the organization of hierarchical neural networks

In the zebra finch model system, it is now widely accepted the timing of singing behavior appears to be primarily controlled by a single defined brain region, but see (Andalman et al., 2011; Goldin et al., 2013; Hamaguchi et al., 2016). However, a hierarchical relationship may exist in other systems in which different circuits can be spatially segregated and control different aspects of behavioral timing. For example, in the midshipman fish – a species that forms a variety of vocal behaviors (Figure 6A) – the duration of the vocal display and the production of each vocal element appears to be controlled in distinct brain regions (Figure 6B) (Bass, 2014; Chagnaud et al., 2011). To understand how focal cooling can disentangle the relationship between neural dynamics and behavior in such a scenario, we again turn to a simplified model. We consider two timing circuits: The first (‘Circuit 1’) represents a recurrent neural network (i.e., Figure 5), which is trained to produce a simple tonic signal that sets the duration of the behavior without directly specifying the rhythm. The second (‘Circuit 2’) acts as a pattern generator; specifically, a single neuron that produces high-frequency bursts at characteristic intervals in response to an input signal (e.g., a current injection). The timing circuits are arranged hierarchically, with the output of Circuit 1 providing input to the pattern generating Circuit 2 (Figure 6C). If the output of Circuit 1 is ‘On’, Circuit 2 can produce burst spiking at its own characteristic frequency.

Figure 6. Use of Cooling to Infer Hierarchical Organization of Timing Circuits.

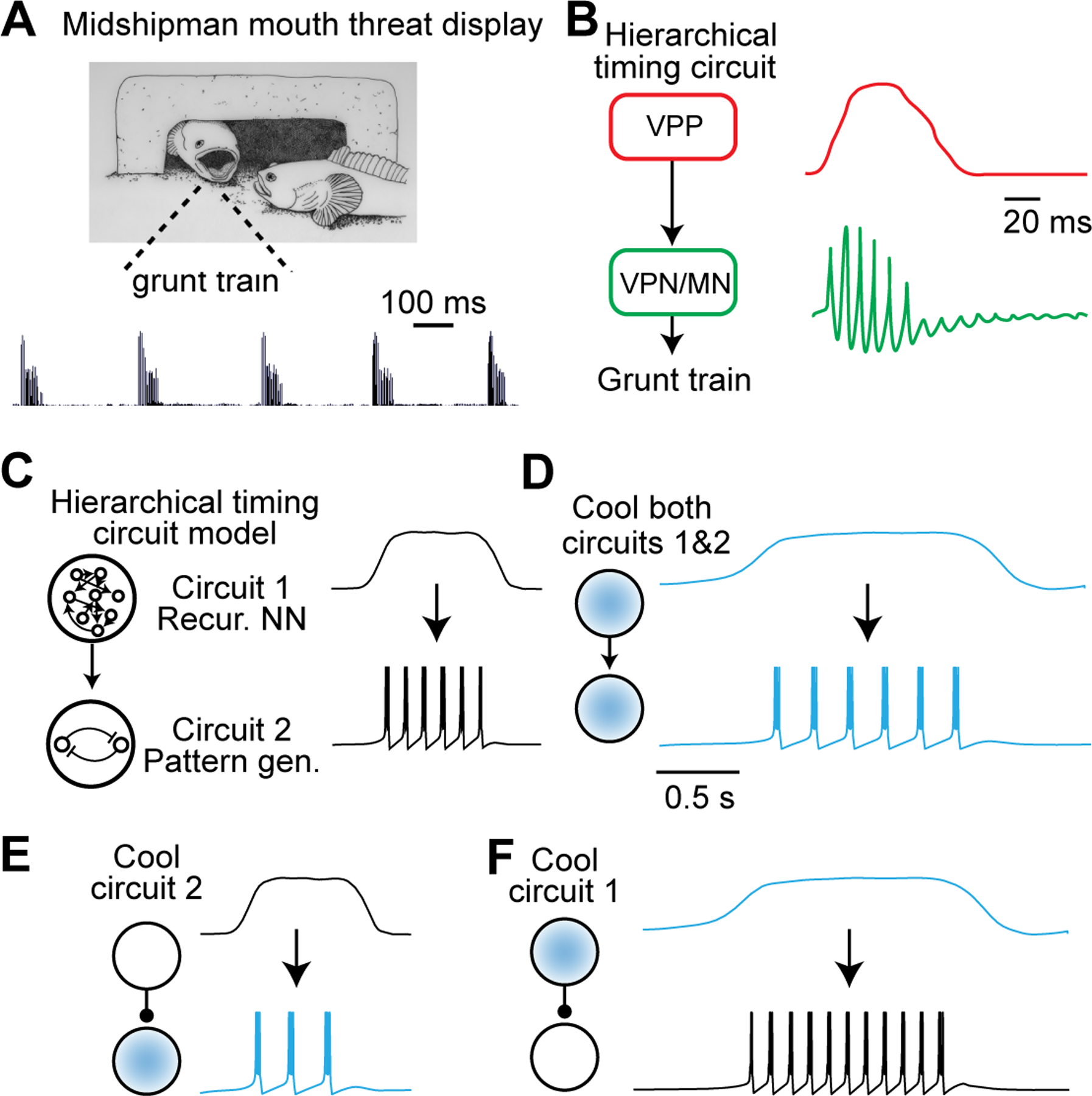
(A) Picture of a male plainfin midshipman fish and accompanying sound waveform indicating a grunt train. Adapted from (Brantley and Bass, 1994).

(B) Simplified diagram of part of the vocal control circuit in the male plainfin midshipman fish. VPP: vocal prepacemaker nucleus; VPN: vocal pacemaker nucleus; MN: vocal motoneurons. Right: Cartoon of intracellular membrane potential at different timescales in VPP (top) and VPN neurons (bottom). Adapted from (Chagnaud et al., 2011).

(C) Simple model of a hierarchically organized timing circuit. A recurrent neural network (top) produces an output that switches between a low and a persistent high level, which serves as input drive to a pattern-generating circuit (bottom) that produces bursts during the time the input is at a high level. For simplicity, we modeled the pattern-generating circuit (Izhikevich, 2003) with parameters a = 0.02, b = 0.2, c = −50mV and d = 2.0. Temperature dependence was modeled by scaling the time derivatives of the membrane potential v and the internal state variable u by a factor Q with Q₁₀ = 2.

(D)–(F) Cooling both the recurrent neural network (upstream circuit) and the pattern generator (downstream) leads to a decrease in interburst interval and an expansion of the burst epoch (D). Cooling either the upstream or downstream network individually can selectively affect one of these two variables (i.e., interburst interval or burst epoch) without changing the other (E and F).

Cooling both timing circuits to the same degree results in coordinated stretching of both signals at all timescales (Figure 6D): The bursting neuron produces the same number of bursts after cooling but at a lower frequency, at longer intervals, and for a longer overall duration. In contrast, cooling Circuit 2 alone does not affect the overall duration of the bursting episode, but instead causes bursts to be produced at longer intervals, resulting in a smaller total number of bursts (Figure 6E). Cooling Circuit 1 alone stretches the activity patterns of individual recurrent neural network units (similar to Figure 5) resulting in a longer tonic output signal (Figure 6F, blue trace). Because the burst generating mechanism is not affected, elongating the behavioral duration leads to an increased total number of bursts (Figure 6F). Our simple model shows that focal cooling can decouple behavioral timescales by slowing neural dynamics in one circuit at a time and simultaneously monitoring behavioral output. It may therefore be possible to infer the position of the cooled circuit within a hierarchical network structure.

Recent experiments with Alston’s singing mice (Scotinomys teguina) – a highly vocal rodent native to the cloud forests of Central America – provide a compelling example of the application of focal cooling for characterizing hierarchically organized networks (Okobi et al., 2019). The advertisement song of the singing mice consists of a highly stereotyped series of notes, each associated with an exhalation, that evolve over many seconds (Campbell et al., 2010). To elucidate the neural circuit mechanisms that are relevant for these vocal performances, we used intracortical microstimulation to identify cortical sites whose activation led to reliable flexion of vocally relevant musculature (Figure 7A). Our search pinpointed an area in anterolateral motor cortex corresponding to a region identified in other rodents as relevant for orofacial motor control (Komiyama et al., 2010; Mercer Lindsay et al., 2019), which we subsequently refer to as the Orofacial Motor Cortex (OMC). Electrical stimulation of OMC during singing led to either truncation or reversible pauses, suggesting an important role for OMC in song production. However, electrical microstimulation may activate neural circuits nonspecifically (Histed et al., 2009) by impacting population activity in antidromically-activated upstream regions as well as a variety of downstream areas. Moreover, the truncation of the song precludes any further characterization of motor control, complicating further interpretation (Otchy et al., 2015).

Figure 7. Temporal and Spatial Segregation of Function Revealed by Cooling.

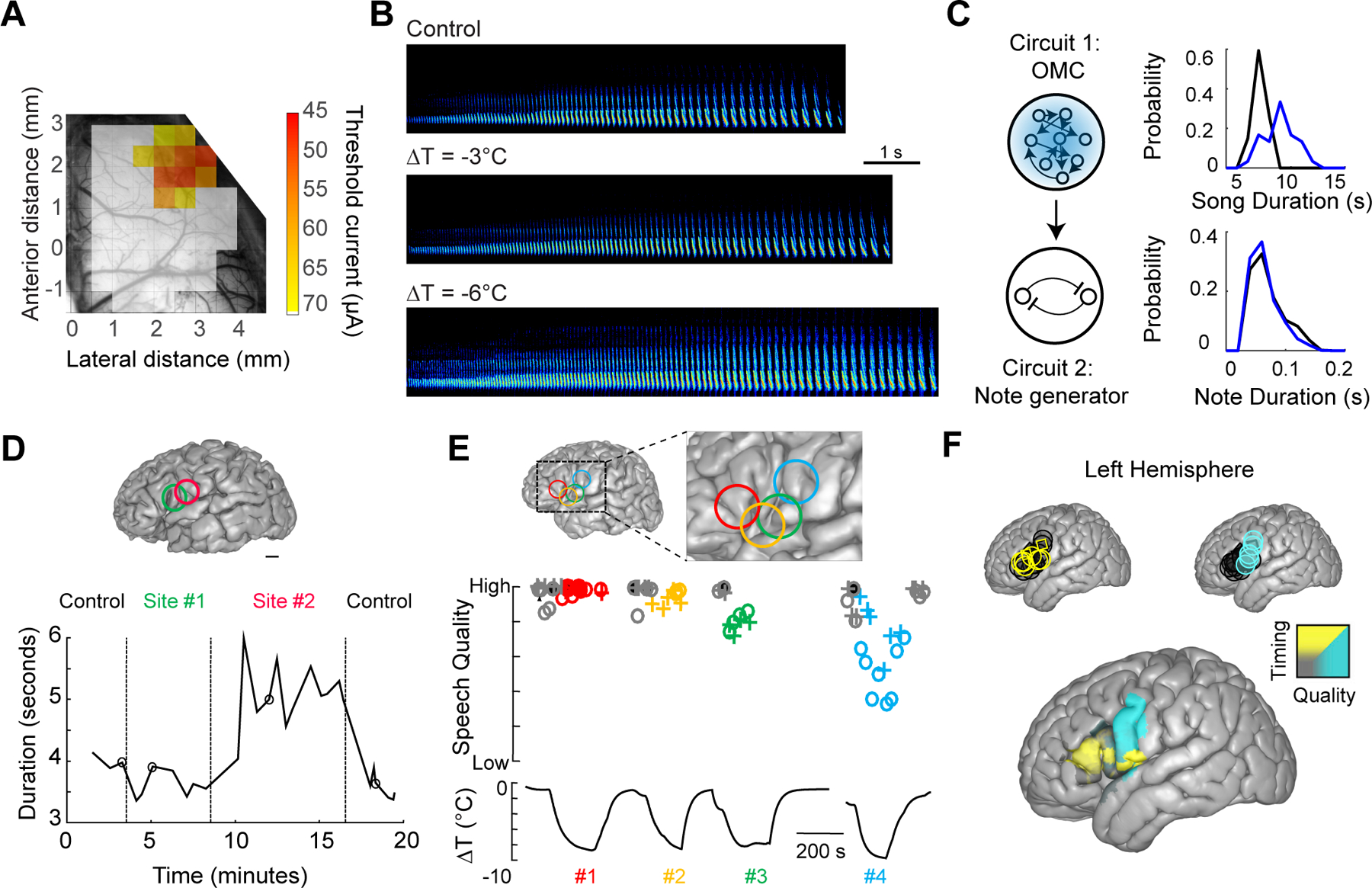
(A) Anatomical location of the orofacial motor cortex (OMC) in the singing mouse (S. teguina) as determined by intracortical microstimulation. Adapted from (Okobi et al., 2019).

(B) Spectrograms of example S. teguina songs during control and cooling sessions. Adapted from (Okobi et al., 2019).

(C) A schematic depicting a hierarchical song control network in S. teguina with an upstream OMC region coupled with a subcortical note generating circuit. Cooling OMC increases song duration without modifying note duration, supporting this model of a separation of timescales. Modified from (Okobi et al., 2019).

(D) Intraoperative mild cooling of human cortical surface can affect speech timing. Surface rendering of brain structure indicating two cooling sites. The duration of the speech task (i.e., ‘Monday, Tuesday, Wednesday, Thursday, Friday’) is significantly expanded when Site #2 is cooled with no effect of cooling Site #1 nearby. Adapted from (Long et al., 2016).

(E) Intraoperative cooling can affect speech quality. Brain surface rending with four cooling sites (top). While cooling each site, participants were asked to recite the days of the week (‘o’ symbols) or a string of numbers (‘+’ symbols) (middle). The estimated temperature change at each site (bottom). Site #4 had a strong relationship between temperature and speech quality. Adapted from (Long et al., 2016).

(F) Brain regions that affect speech quality and timing are spatially segregated in the human brain. Significant timing (upper left, yellow) and quality sites (upper right, blue) are provided as well as a higher spatial resolution map of cooling-induced changes. Adapted from (Long et al., 2016).

To further test OMC’s role in vocal behavior, we applied our cooling method during the production of the advertisement song. OMC cooling did not eliminate singing behavior, but it clearly changed song structure (Figure 7B), lengthening song duration without stretching out individual notes (Figure 7C). This evidence is consistent with our hierarchical model of behavioral control (Figure 6F) and reminiscent of the organization of song control in midshipman fish (Figures 6A and B). Unlike HVC in songbirds, which dictates the fine temporal structure of notes, OMC does not appear to be the song pattern generator but instead regulates activity in a downstream circuit that directly dictates note patterning (Figure 7C). Therefore, mild cooling of a brain region can be an effective circuit manipulation to infer its role within a hierarchically organized network.

Using cooling to manipulate cognitive variables

Thus far, we have considered the application of cooling to behaviorally relevant brain regions acting either as direct pattern generators (e.g., crab STG or zebra finch HVC) or as a higher-order control region in the motor hierarchy (e.g., singing mouse OMC). Can cooling also be used to gain insight into higher level functions that are less directly related to motor output? In recent years, mild focal cooling has also been used to localize important dynamics underlying a range of processes including those related to cognition. In the hippocampus, for instance, theta rhythms have been proposed to support cognitive processes such as memory formation and spatial navigation (Buzsaki and Tingley, 2018). Recently, a cooling probe was inserted into the medial septum to lower the frequency of hippocampal theta rhythms by approximately 10% (Petersen and Buzsaki, 2020). Spike sequences expanded as a function of temperature, but the relative phase of these events with respect to the theta cycle was maintained. From this work, cooling emerges as a potentially transformative means of manipulating neural oscillations (e.g., Figure 3), which are pervasive across the brain and have been proposed to have central roles in cognitive and behavioral neuroscience (Buzsaki, 2006) but have been notoriously difficult to experimentally manipulate with other methods.

In another study, bilaterally cooling the medial prefrontal cortex delayed behavioral responses in a motor timing task, a result that was not observed when a similar cooling manipulation was performed in the motor cortex (Xu et al., 2014). Population dynamics in the striatum and the accompanying decision-making processes were also slowed through focal temperature changes without affecting other aspects of motor timing (Monteiro et al., 2020), highlighting a role for the striatum as an important population clock for estimating elapsed time (Gouvea et al., 2015). Similarly, cooling may also be effective in testing evidence accumulation models in the brain; focal cooling is expected to slow down the rate of accumulated spikes per unit time and may thereby lead to longer reaction times in behavioral tasks (Brunton et al., 2013; Jazayeri and Shadlen, 2015; Roitman and Shadlen, 2002). These examples demonstrate the generality of focal cooling as a strategy for testing specific hypotheses about neural circuit function.

Given the utility of focal cooling in model systems, we have recently taken the first steps towards applying this perturbation approach towards investigating the link between brain function and behavior in human participants. Although cooling was previously employed as a therapeutic approach for addressing conditions such as hypoxia or epilepsy (Csernyus et al., 2020), the application of focal cooling to understand brain function has been considerably more limited. Recently, however, focal cooling has been adapted in a clinical setting (Bakken et al., 2003; Katlowitz et al., 2017; Long et al., 2016), enabling neurosurgeons to localize regions relevant for speech production during intercranial procedures targeted to remove tumors or epileptic tissue. Such awake functional mapping is typically performed through electrical stimulation (Ojemann et al., 1989; Penfield and Boldrey, 1937), which has the potential side-effect of seizure initiation (Piccioni and Fanzio, 2008). In contrast, mild cooling (ΔT = −6 to −8°C at a depth of 2 mm, or approximately cortical Layer 5) is a reversible and safe (Ibayashi et al., 2021) means of changing the processing speed of neural circuits in a spatially specific manner. In previous work, mild focal cooling was used while participants performed overlearned speech sequences (Figure 7 D and E), either counting (‘21’, ‘22’, ‘23’, ‘24’, ‘25’) or reciting the days of the week (‘Monday’, ‘Tuesday’, ‘Wednesday’, ‘Thursday’, ‘Friday’). Cooling the inferior frontal gyrus – including what is traditionally considered Broca’s region – led to a slowing down of speech sequences (Figure 7 D and F), while the same manipulation in the primary motor cortex resulted in a measurable decrease in speech quality. Uncovering this functional dissociation would not have been possible with electrical stimulation, a perturbation that often leads to speech arrest, where the patient is temporarily unable to produce words (Ojemann et al., 1989).

Technical considerations and Outlook

Given the utility of focal cooling for probing the relationship between neural dynamics and behavior, it is also important to discuss the limitations of this technique. First, surface cooling is spatially more restricted compared to cooling of deep structures with a typical length constant of ~1.5 mm (Aronov and Fee, 2011; Long and Fee, 2008). For brain regions smaller than the spatial length scale of cooling, the amount of cooling is likely to be homogenous across the entire structure. However, for laminar structures such as the cerebral cortex, placing a cooling device on the cortical surface will lead to strong yet nonuniform cooling, exponentially decaying from superficial to deeper layers. In such cases, a careful consideration of the spatial extent of temperature spread is necessary to interpret the results of focal cooling. Second, cooling deeper targets requires the implantation of a penetrating cooling probe (typically < 0.5 mm), which may damage important neural tissue and can lead to nonselective cooling of neighboring structures (Aubert et al., 2004; Hamaguchi et al., 2016; Long and Fee, 2008; Petersen and Buzsaki, 2020). Third, cooling is considerably slower than optogenetic or electrical stimulation (~1 ms); neural tissue typically takes 2–5 minutes to reach a steady-state temperature, which eliminates the possibility of selectively targeting behavioral epochs that unfold on a faster time scale (e.g., grasping as part of a more elaborate food retrieval task) (Guo et al., 2015). Fourth, unlike many genetically encoded methods for manipulating neural circuits, focal cooling does not yet feature cell type specificity. That said, membrane-bound actuators such as ferritin may offer the possibility of cell-autonomous temperature changes through DC magnetic fields (i.e., the magneto-caloric effect) (Barbic, 2019), although the extent to which this manipulation can preserve network structure remains unclear. Fifth, the utility of focal cooling – like most perturbations – is limited to cases in which intrinsic behavioral variability is small. As a result, cooling may be most effective in highly trained behavioral paradigms that require stereotyped motor readouts such as saccades, specific arm movements, or licking (Gouvea et al., 2015; Shenoy et al., 2013; Sparks and Barton, 1993; Svoboda and Li, 2018) since intrinsic variability of motor output after training is restricted in such tasks.

Despite these limitations, focal cooling has important strengths that warrant its wider adoption. First, as demonstrated above, cooling allows the experimenter to parametrically vary the speed of population activity without disrupting its structure. Thus, in contrast to methods that add or subtract large numbers of spikes, cooling maintains population activity on the manifold of endogenous patterns. Additionally, because the biophysical mechanisms of spike generation and conduction are largely conserved (e.g., Figure 3), the effect of mild cooling on neuronal dynamics may generalize across different circuits as well as different species. Furthermore, the application of this technique does not require specific genetic lines or viral tools, thereby expanding its utility to most model systems that are not traditionally used in the laboratory. By embracing this diversity, focal cooling presents an opportunity to lead the field towards important new insights concerning the link between brain function and behavior.