The effect of consanguinity on coalescence times on the X chromosome

Abstract

Consanguineous unions increase the frequency at which identical genomic segments are inherited along separate paths of descent, decreasing coalescence times for pairs of alleles drawn from an individual who is the offspring of a consanguineous pair. For an autosomal locus, it has recently been shown that the mean time to the most recent common ancestor (T_MRCA) for two alleles in the same individual and the mean T_MRCA for two alleles in two separate individuals both decrease with increasing consanguinity in a population. Here, we extend this analysis to the X chromosome, considering X-chromosomal coalescence times under a coalescent model with diploid, male–female mating pairs. We examine four possible first-cousin mating schemes that are equivalent in their effects on autosomes, but that have differing effects on the X chromosome: patrilateral-parallel, patrilateral-cross, matrilateral-parallel, and matrilateral-cross. In each mating model, we calculate mean T_MRCA for X-chromosomal alleles sampled either within or between individuals. We describe a consanguinity effect on X-chromosomal T_MRCA that differs from the autosomal pattern under matrilateral but not under patrilateral first-cousin mating. For matrilateral first cousins, the effect of consanguinity in reducing T_MRCA is stronger on the X chromosome than on the autosomes, with an increased effect of parallel-cousin mating compared to cross-cousin mating. The theoretical computations support the utility of the model in understanding patterns of genomic sharing on the X chromosome.

1. Introduction

In consanguineous unions, parents are closely related, producing offspring who inherit identical genomic segments along both parental lines. Consanguinity is common in human populations; couples related at a level of second cousins or closer, together with their offspring, might represent as much as 10% of the global population (Bittles and Black, 2010).

Different forms of consanguinity vary in frequency across human populations, often as a result of cultural norms concerning preferred mate choices (Bittles, 2012). For example, first-cousin marriages can follow four distinct patterns, as classified by the sexes of the two sibling parents. These patterns are named from the perspective of the male in the consanguineous marriage: (1) patrilateral-parallel, a male marries his father’s brother’s daughter; (2) patrilateral-cross, he marries his father’s sister’s daughter; (3) matrilateral-parallel, he marries his mother’s sister’s daughter; and (4) matrilateral-cross, he marries his mother’s brother’s daughter. The “parallel” marriage patterns refer to same-sex sibling parents and the “cross” patterns refer to opposite-sex sibling parents.

The inheritance of a genomic segment via both parents due to consanguineous unions has consequences for genomic phenomena such as runs of homozygosity (ROH)—long homozygous segments in diploid individuals—and sharing between individuals of long identical-by-descent (IBD) segments. In particular, it is well-known that due to pairing of IBD segments within individuals, consanguinity increases the frequency and length of ROH (e.g. McQuillan et al., 2008; Kirin et al., 2010; Pemberton et al., 2012; Kang et al., 2016; Ceballos et al., 2018).

Recently, we have argued that consanguinity also increases the frequency and length of IBD segments shared between pairs of individuals (Severson et al., 2019). In a model of coalescence in a diploid population, the mean time to the most recent common ancestor (T_MRCA) for a pair of alleles in separate individuals was seen to decrease with increasing consanguinity. Because genomic sharing increases with decreasing T_MRCA, the reduction in T_MRCA in turn increases genomic sharing. The interpretation of Severson et al. (2019), established in further detail by Severson et al. (2021), is that consanguinity decreases effective population size, increasing genomic sharing both for within-individual ROH and for between-individual IBD segments.

When studying the autosomal genome, the four forms of first-cousin mating—patrilateral-parallel, patrilateral-cross, matrilateral-parallel, and matrilateral-cross—are indistinguishable in their effects, as males and females each contribute a copy of the autosomal genome in each generation. For the X chromosome, however, owing to the fact that the X chromosome is not transmitted from fathers to sons, the consanguineous pairs in these four types of unions have different levels of relatedness (Jacquard, 1974; Lange, 2002). Hence, populations with different forms of first-cousin mating potentially have different patterns for T_MRCA, ROH, and IBD sharing.

Here, we extend our autosomal model of monogamous diploid mating pairs to consider X-chromosomal inheritance. We focus our analysis on the four types of first-cousin mating. The results reveal effects of different types of consanguinity on autosomal and X-chromosomal T_MRCA.

2. Autosomal results

We extend the framework from Severson et al. (2019), which considers a diploid population of N monogamous mating pairs (Figure 1). This framework, which allows for a variety of forms of consanguinity, in turn generalizes a sib mating model from Campbell (2015).

Figure 1:

A diploid mating model for two successive generations. (A) Each generation has N monogamous mating pairs, a fraction c₀ of which are sib mating pairs, shaded (N = 5, c₀ = 0.2). (B) The sibs in each sib mating pair in the offspring generation (shaded pair in the offspring generation) share a parental pair from the previous generation. (C) Non-sib mating pairs are associated with two mating pairs from the previous generation. Note that a pair of parents chosen in the parental generation might itself be a sib pair (shaded pair in the parental generation). Small squares, males; small circles, females; large circles, mating pairs. The figure is modified from Severson et al. (2019).

We build on Severson et al. (2019) by explicitly including the sex of the individuals. For autosomal loci, this change adds states to our Markov chain, states that are needed for our computations with the X chromosome. The addition of the three new states produces results that reduce to those of Severson et al. (2019). We review these results, and we then examine the effect of consanguinity on X-chromosomal coalescence times.

The models of Campbell (2015) and Severson et al. (2019) consider alleles in three possible states: within an individual, in two individuals in a mating pair, and in two individuals in separate mating pairs. In incorporating sex, we decompose the three states into six (Figure 2). Enumerating these possible states, state 1 is two alleles in a male and state 2 is two alleles in a female. State 3 is two alleles in two different individuals in the same mating pair. States 4, 5, and 6 describe two alleles in two individuals in different mating pairs, where the two individuals are two males, a male and a female, and two females, respectively.

Figure 2:

Six possible states for two sampled alleles at autosomal loci. Males are squares; females are circles. State 1: within a male (red). State 2: within a female (blue). State 3: in two individuals in a mating pair (green). State 4: in two males in different mating pairs (yellow). State 5: in a male and a female in different mating pairs (orange). State 6: in two females in different mating pairs (purple).

We define six random variables to denote coalescence times of two alleles in our six states (Figure 2). T_m is T_MRCA for two alleles in the same male (state 1) and T_f is T_MRCA for two alleles in the same female (state 2). As in Severson et al. (2019), U is T_MRCA for two alleles in two individuals in the same mating pair (state 3). Finally, V_mm is T_MRCA for two males in separate mating pairs (state 4), V_mf is T_MRCA for a male and a female in separate mating pairs (state 5), and V_ff is T_MRCA for two females in separate mating pairs (state 6). We calculate the means $\mathbb{E}\left[T_m\right]$, $\mathbb{E}\left[T_f\right]$, $\mathbb{E}[U]$, $\mathbb{E}\left[V_{mm}\right]$, $\mathbb{E}\left[V_{mf}\right]$, and $\mathbb{E}\left[V_{ff}\right]$ for autosomal and X-chromosomal loci under sib and first-cousin mating. States 1 and 2 are “lumped” into one state by Severson et al. (2019), as are states 4, 5, and 6.

2.1. Siblings

We follow Campbell (2015) and Severson et al. (2019) to derive equations for mean coalescence times. In each generation, a constant fraction c₀ of the N mating pairs are sib mating pairs. Chance consanguinity is excluded, so that the remaining N(1 − c₀) pairs are not sib mating pairs.

Beginning with T_m and T_f, two alleles within the same male (state 1) or female (state 2) must have been inherited from a single mating pair (state 3) one generation back. We have

$$\mathbb{E}\left[T_m\right]=\mathbb{E}\left[T_f\right]=\mathbb{E}[U]+1.$$ (1)

For two alleles in separate individuals in a mating pair (state 3), the mating pair is a sib mating pair with probability c₀. Conditional on the individuals in the mating pair being sibs, the sampled alleles can be inherited from the previous generation in four ways. First, they could coalesce in the previous generation, an event that occurs with probability $\frac{1}{4}$. Next, they could both be inherited from the father and not coalesce, an event that has probability $\frac{1}{8}$, giving coalescence time $\mathbb{E}\left[T_m\right]+1$. Similarly, they could both be inherited from the mother and not coalesce, with probability $\frac{1}{8}$ and coalescence time $\mathbb{E}\left[T_f\right]+1$. Finally, they could be inherited from two individuals in a mating pair in the previous generation, with probability $\frac{1}{2}$ and coalescence time $\mathbb{E}[U]+1$.

The event that the mating pair is not a sib mating pair has probability 1 − c₀. Conditional on this event, the alleles have three possibilities. They arise from two males in separate mating pairs with probability $\frac{1}{4}$, giving coalescence time $\mathbb{E}\left[V_{mm}\right]+1$. They are inherited from a male and a female in separate mating pairs with probability $\frac{1}{2}$, giving coalescence time $\mathbb{E}\left[V_{mf}\right]+1$. Lastly, with probability $\frac{1}{4}$, they are inherited from two females in separate mating pairs, giving coalescence time $\mathbb{E}\left[V_{ff}\right]+1$. Combining the cases, we have

$$\begin{gathered} \mathbb{E}[U]=c_0\left[\frac{1}{4}+\frac{1}{8}\left(\mathbb{E}\left[T_m\right]+1\right)+\frac{1}{8}\left(\mathbb{E}\left[T_f\right]+1\right)+\frac{1}{2}(\mathbb{E}[U]+1)\right] \\ +\left(1-c_0\right)\left[\frac{1}{4}\left(\mathbb{E}\left[V_{mm}\right]+1\right)+\frac{1}{2}\left(\mathbb{E}\left[V_{mf}\right]+1\right)+\frac{1}{4}\left(\mathbb{E}\left[V_{ff}\right]+1\right)\right]. \end{gathered}$$ (2)

In considering autosomal loci, coalescence patterns for alleles in two individuals in different mating pairs are the same irrespective of the sexes of the individuals. Hence, equations for $\mathbb{E}\left[V_{mm}\right]$, $\mathbb{E}\left[V_{mf}\right]$, and $\mathbb{E}\left[V_{ff}\right]$ are the same. Because we draw a parental pair uniformly with replacement for each individual in the current generation, the probability that, by chance, two individuals in separate mating pairs are siblings is $\frac{1}{N}$. Conditional on the event that we randomly sample two siblings, as in Eq. 2, the alleles have four possibilities: they coalesce, they come from the father in the previous generation and do not coalesce, they come from the mother in the previous generation and do not coalesce, or they come from separate individuals in the previous generation. The probabilities and coalescence times for these events follow from sib mating in Eq. 2.

The event that the two individuals are not siblings occurs with probability $1-\frac{1}{N}$. Three events are then possible: the two alleles come from two males in separate mating pairs, from a male and a female, or from two females. The probabilities and coalescence times for these events follow from non-sib mating in Eq. 2. We have

$$\begin{gathered} \mathbb{E}\left[V_{mm}\right]=\mathbb{E}\left[V_{mf}\right]=\mathbb{E}\left[V_{ff}\right]=\frac{1}{N}\left[\frac{1}{4}+\frac{1}{8}\left(\mathbb{E}\left[T_m\right]+1\right)+\frac{1}{8}\left(\mathbb{E}\left[T_f\right]+1\right)+\frac{1}{2}(\mathbb{E}[U]+1)\right] \\ +\left(1-\frac{1}{N}\right)\left[\frac{1}{4}\left(\mathbb{E}\left[V_{mm}\right]+1\right)+\frac{1}{2}\left(\mathbb{E}\left[V_{mf}\right]+1\right)+\frac{1}{4}\left(\mathbb{E}\left[V_{ff}\right]+1\right)\right]. \end{gathered}$$ (3)

Eqs. 1–3 form a linear system of equations in six variables, with solution

$$\mathbb{E}\left[T_m\right]=\mathbb{E}\left[T_f\right]=4N\left(1-c_0\right)+6$$ (4)

$$\mathbb{E}[U]=4N\left(1-c_0\right)+5$$ (5)

$$\mathbb{E}\left[V_{mm}\right]=\mathbb{E}\left[V_{mf}\right]=\mathbb{E}\left[V_{ff}\right]=4N\left(1-\frac{3}{4}{c}_0\right)+4.$$ (6)

We reduce the model to a model without sexes by collapsing states 1 and 2 into a single state for two alleles from a single individual (male or female), and by collapsing states 4, 5, and 6 into a single state for two alleles from individuals of unspecified sex in different mating pairs. Using T to represent T_MRCA for two alleles sampled in the combined states 1 and 2, Eq. 4 gives

$$\mathbb{E}[T]=4N\left(1-c_0\right)+6.$$ (7)

We can use V to represent T_MRCA for the collapsed state for states 4, 5, and 6. Eq. 6 can be collapsed into

$$\mathbb{E}[V]=4N\left(1-\frac{3}{4}{c}_0\right)+4.$$ (8)

Eqs. 7, 5, and 8 are equivalent to Eqs. 4, 5, and 6, respectively, of Severson et al. (2019). Breaking the three states of Severson et al. (2019) into six by consideration of the sexes of individuals provides further detail, but it does not change the quantitative results.

2.2. First cousins

Severson et al. (2019) considered first-cousin mating, assuming a constant fraction c₁ in each generation for the fraction of first-cousin mating pairs in a population, and again assuming that no chance consanguinity occurs. Rephrasing their results for mean autosomal coalescence times with a decomposition of states by sex, the derivation otherwise follows Severson et al. (2019), and the quantitative results are the same. The four types of cousin mating give the same recursions. For completeness, we include the derivation in Appendix A. We obtain

$$\mathbb{E}\left[T_m\right]=\mathbb{E}\left[T_f\right]=4N\left(1-\frac{1}{4}{c}_1\right)+10$$ (9)

$$\mathbb{E}[U]=4N\left(1-\frac{1}{4}{c}_1\right)+9$$ (10)

$$\mathbb{E}\left[V_{mm}\right]=\mathbb{E}\left[V_{mf}\right]=\mathbb{E}\left[V_{ff}\right]=4N\left(1-\frac{3}{16}{c}_1\right)+7.$$ (11)

Severson et al. (2019) noted that $\mathbb{E}\left[V_{mm}\right]=\mathbb{E}\left[V_{mf}\right]=\mathbb{E}\left[V_{ff}\right]$ exceeds $\mathbb{E}\left[T_m\right]=\mathbb{E}\left[T_f\right]$ for nonzero c₁ and sufficiently large N. They also observed that in comparison with a non-consanguineous diploid population of size 2N, the mean coalescence times are reduced by linear factors, $1-\frac{1}{4}{c}_1$ in Eqs. 9 and 10, and $1-\frac{3}{16}{c}_1$ in Eq. 11.

2.3. Double first cousins

We can similarly examine double-first-cousin mating, a case not considered by Severson et al. (2019). We use the six states, with a fraction c₁ of double-first-cousin mating pairs in each generation. The two types of bilateral cousin mating give the same recursions. The derivation appears in Appendix B. We obtain

$$\mathbb{E}\left[T_m\right]=\mathbb{E}\left[T_f\right]=4N\left(1-\frac{1}{2}{c}_1\right)+10$$ (12)

$$\mathbb{E}[U]=4N\left(1-\frac{1}{2}{c}_1\right)+9$$ (13)

$$\mathbb{E}\left[V_{mm}\right]=\mathbb{E}\left[V_{mf}\right]=\mathbb{E}\left[V_{ff}\right]=4N\left(1-\frac{3}{8}{c}_1\right)+7.$$ (14)

The reduction factors due to consanguinity in comparison with a non-consanguineous population are $1-\frac{1}{2}{c}_1$ for Eqs. 12 and 13, and $1-\frac{3}{8}{c}_1$ for Eq. 14.

3. X-chromosomal results

We now derive new results for the X chromosome, comparing them to autosomal results. As before, we consider N mating pairs in each generation; the number of alleles in the population in each generation is 3N, 2N in females and N in males. Because two sampled X-chromosomal alleles cannot be in the same male, we remove state 1.

3.1. Siblings

For sib mating, as before, let c₀ be the fraction of sib mating pairs each generation. Chance sib mating is forbidden. In the event that two X chromosomes are present within a female, in the previous generation they must have been in a mating pair, and the mean coalescence time, $\mathbb{E}\left[T_f\right]$, remains the same as for autosomes:

$$\mathbb{E}\left[T_f\right]=\mathbb{E}[U]+1.$$ (15)

For two X chromosomes within a mating pair (state 3), the individuals are siblings with probability c₀. Given that they are siblings, three possibilities exist for how two sampled alleles were inherited. First, with probability $\frac{1}{4}$, the alleles coalesce in the mother in the previous generation. Second, with probability $\frac{1}{4}$, they trace to the mother and do not coalesce, giving mean coalescence time $\mathbb{E}\left[T_f\right]+1$. Third, with probability $\frac{1}{2}$, they derive separately from the mother and father, giving mean coalescence time $\mathbb{E}[U]+1$.

Suppose now that the individuals in the mating pair are not siblings, an event with probability 1 − c₀. The X chromosome in the male is inherited from his mother, and the X chromosome in the female has probability $\frac{1}{2}$ of being inherited from her mother and probability $\frac{1}{2}$ of being inherited from her father. These events give coalescence times $\mathbb{E}\left[V_{ff}\right]+1$ and $\mathbb{E}\left[V_{mf}\right]+1$, respectively. Combining cases, we obtain

$$\begin{gathered} \mathbb{E}[U]=c_0\left[\frac{1}{4}+\frac{1}{4}\left(\mathbb{E}\left[T_f\right]+1\right)+\frac{1}{2}(\mathbb{E}[U]+1)\right] \\ +\left(1-c_0\right)\left[\frac{1}{2}\left(\mathbb{E}\left[V_{mf}\right]+1\right)+\frac{1}{2}\left(\mathbb{E}\left[V_{ff}\right]+1\right)\right]. \end{gathered}$$ (16)

Because X chromosomes are not inherited from father to son, states 4–6 no longer produce identical recursions, as they did for autosomes. In all three states, the probability continues to be $\frac{1}{N}$ that two alleles in separate individuals in separate mating pairs are in siblings. For V_mm, given that the two males are siblings, with probability $\frac{1}{2}$, the two alleles coalesce in one generation (in their mother). With probability $\frac{1}{2}$, they derive from the mother and do not coalesce, giving coalescence time $\mathbb{E}\left[T_f\right]+1$. If the two males are not siblings, an event with probability $1-\frac{1}{N}$, then the X chromosomes trace to non-sib mothers, and the expected coalescence time is $\mathbb{E}\left[V_{ff}\right]+1$. Combining these terms, we have

$$\mathbb{E}\left[V_{mm}\right]=\frac{1}{N}\left[\frac{1}{2}+\frac{1}{2}\left(\mathbb{E}\left[T_f\right]+1\right)\right]+\left(1-\frac{1}{N}\right)\left(\mathbb{E}\left[V_{ff}\right]+1\right).$$ (17)

For V_mf, if the male and female in separate mating pairs are siblings, then probabilities and coalescence times follow from Eq. 16. If the male and female are not siblings, then with probability $\frac{1}{2}$, the alleles have been inherited from a male and a female in separate mating pairs, and with probability $\frac{1}{2}$, they have been inherited from two females in separate mating pairs. The coalescence times follow similarly from Eq. 16. Combining terms, we get

$$\begin{gathered} \mathbb{E}\left[V_{mf}\right]=\frac{1}{N}\left[\frac{1}{4}+\frac{1}{4}\left(\mathbb{E}\left[T_f\right]+1\right)+\frac{1}{2}(\mathbb{E}[U]+1)\right] \\ +\left(1-\frac{1}{N}\right)\left[\frac{1}{2}\left(\mathbb{E}\left[V_{mf}\right]+1\right)+\frac{1}{2}\left(\mathbb{E}\left[V_{ff}\right]+1\right)\right]. \end{gathered}$$ (18)

For V_ff, if the two females are siblings, then two sampled alleles coalesce in one generation in the father with probability $\frac{1}{4}$ and in the mother with probability $\frac{1}{8}$, giving total coalescence probability $\frac{3}{8}$. With probability $\frac{1}{8}$, the alleles derive from the mother and do not coalesce, giving coalescence time $\mathbb{E}\left[T_f\right]+1$. With probability $\frac{1}{2}$, one allele derives from the mother and the other derives from the father, giving coalescence time $\mathbb{E}[U]+1$. If the alleles do not come from siblings, then coalescence times and probabilities follow the pattern of autosomes, and the transition probabilities and coalescence times follow the non-sibling portion of Eq. 2. Combining terms, we have

$$\begin{gathered} \mathbb{E}\left[V_{ff}\right]=\frac{1}{N}\left[\frac{3}{8}+\frac{1}{8}\left(\mathbb{E}\left[T_f\right]+1\right)+\frac{1}{2}(\mathbb{E}[U]+1)\right] \\ +\left(1-\frac{1}{N}\right)\left[\frac{1}{4}\left(\mathbb{E}\left[V_{mm}\right]+1\right)+\frac{1}{2}\left(\mathbb{E}\left[V_{mf}\right]+1\right)+\frac{1}{4}\left(\mathbb{E}\left[V_{ff}\right]+1\right)\right]. \end{gathered}$$ (19)

Solving the system of five equations associated with the five states, Eqs. 15–19, we obtain

$$\mathbb{E}\left[T_f\right]=\frac{36N^3\left(1-c_0\right)+56N^2\left(1-\frac{1}{28}{c}_0\right)-6N\left(1-c_0\right)-6}{12N^2\left(1-\frac{1}{4}{c}_0\right)-N\left(1-c_0\right)-1}$$ (20)

$$\mathbb{E}[U]=\frac{36N^3\left(1-c_0\right)+44N^2\left(1+\frac{1}{44}{c}_0\right)-5N\left(1-c_0\right)-5}{12N^2\left(1-\frac{1}{4}{c}_0\right)-N\left(1-c_0\right)-1}$$ (21)

$$\mathbb{E}\left[V_{mm}\right]=\frac{36N^3\left(1-\frac{3}{4}{c}_0\right)+23N^2\left(1+\frac{9}{23}{c}_0\right)-9N}{12N^2\left(1-\frac{1}{4}{c}_0\right)-N\left(1-c_0\right)-1}$$ (22)

$$\mathbb{E}\left[V_{mf}\right]=\frac{36N^3\left(1-\frac{3}{4}{c}_0\right)+35N^2\left(1-\frac{3}{35}{c}_0\right)-N\left(1-5c_0\right)-5}{12N^2\left(1-\frac{1}{4}{c}_0\right)-N\left(1-c_0\right)-1}$$ (23)

$$\mathbb{E}\left[V_{ff}\right]=\frac{36N^3\left(1-\frac{3}{4}{c}_0\right)+29N^2\left(1+\frac{3}{29}{c}_0\right)-7N\left(1-\frac{3}{7}{c}_0\right)-3}{12N^2\left(1-\frac{1}{4}{c}_0\right)-N\left(1-c_0\right)-1}.$$ (24)

In examining these equations, we immediately notice that the highest-order terms and coefficients are the same for Eqs. 20 and 21 and for Eqs. 22–24. For large N,

$$\frac{\mathbb{E}\left[T_f\right]}{3N}=\frac{\mathbb{E}[U]}{3N}\approx \frac{1-c_0}{1-\frac{1}{4}{c}_0}$$ (25)

$$\frac{\mathbb{E}\left[V_{mm}\right]}{3N}=\frac{\mathbb{E}\left[V_{mf}\right]}{3N}=\frac{\mathbb{E}\left[V_{ff}\right]}{3N}\approx \frac{1-\frac{3}{4}{c}_0}{1-\frac{1}{4}{c}_0}.$$ (26)

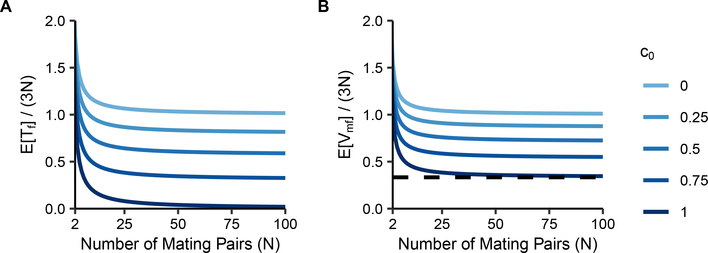
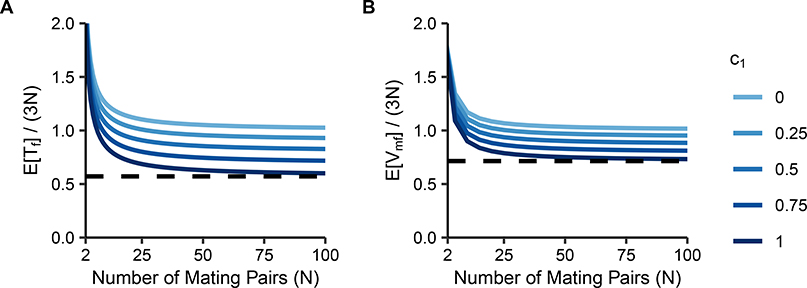
Eqs. 20 and 23 divided by 3N, the number of X chromosomes present each generation, are plotted in Figure 3. As N increases, $\mathbb{E}\left[T_f\right]/(3N)$ and $\mathbb{E}\left[V_{mf}\right]/(3N)$ both quickly approach their large-N limits. The limits, Eqs. 25 and 26, give reduction factors due to consanguinity. Note that $\mathbb{E}\left[V_{mf}\right]-\mathbb{E}\left[T_f\right]\approx 3N{c}_0/\left(4-c_0\right)$, so for c₀ > 0, $\mathbb{E}\left[V_{mf}\right]/(3N)>\mathbb{E}\left[T_f\right]/(3N)$ in the large-N limit. When we take the limit as N → 1 of $\mathbb{E}\left[V_{mf}\right]/(3N)$, we observe that for c₀ = 1, the limit is $\frac{1}{3}$, so that consanguinity can reduce the mean coalescence time to $\frac{1}{3}$ of the value it attains without consanguinity.

Figure 3:

Normalized mean coalescence times on the X chromosome under a sib-mating model. Coalescence times are plotted as a function of the number of mating pairs (N) and the proportion of mating pairs that are sib mating pairs (c₀). (A) $\mathbb{E}\left[T_f\right]/(3N)$, Eq. 20. (B) $\mathbb{E}\left[V_{mf}\right]/(3N)$, Eq. 23. The dashed line at $\frac{1}{3}$ represents the minimal mean coalescence time under consanguinity, achieved at c₀ = 1.

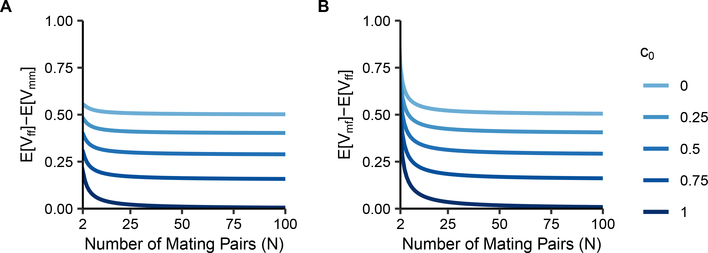
Although Eqs. 22–24 have the same large-N approximation, they differ slightly. It is straightforward to verify from the equations that if N ≥ 2 and 0 ≤ c₀ ≤ 1, then $\mathbb{E}\left[V_{mm}\right]<\mathbb{E}\left[V_{ff}\right]<\mathbb{E}\left[V_{mf}\right]$. The pairwise differences among the three equations appear in Figure 4, where we can observe this result.

Figure 4:

Differences between mean coalescence times of two X chromosomes sampled in separate individuals under sib mating. Differences are plotted as a function of the number of mating pairs (N) and the sib mating proportion (c₀). (A) $\mathbb{E}\left[V_{ff}\right]-\mathbb{E}\left[V_{mm}\right]$. (B) $\mathbb{E}\left[V_{mf}\right]-\mathbb{E}\left[V_{ff}\right]$. The panels visualize Eqs. 22–24.

The sequence $\mathbb{E}\left[V_{mm}\right]<\mathbb{E}\left[V_{ff}\right]<\mathbb{E}\left[V_{mf}\right]$ can be explained by coalescence probabilities in a single generation. In each of states 4–6, when we sample parental mating pairs from the previous generation, two individuals are siblings with probability $\frac{1}{N}$. The coalescence probability in the previous generation for two alleles sampled in these siblings is $\frac{1}{2}$ for two males, $\frac{1}{4}$ for a male and a female, and $\frac{3}{8}$ for two females. The lower single-generation probability of coalescence for state 5, or $\frac{1}{4}$, contributes to $\mathbb{E}\left[V_{mf}\right]$ having the largest mean coalescence time among the three quantities. The higher single-generation coalescence probability of $\frac{1}{2}$ for state 4 contributes to $\mathbb{E}\left[V_{mm}\right]$ having the lowest coalescence time, and the intermediate $\frac{3}{8}$ for state 6 places $\mathbb{E}\left[V_{ff}\right]$ between the other two values.

With the X-chromosomal mean coalescence times established for sib mating, we can compare them to corresponding autosomal values. Both for autosomes and for the X chromosome, the leading term in the mean coalescence time is a product of the number of alleles in the population, 4N or 3N, and a reduction factor due to consanguinity. For within-individual coalescence times (Eqs. 7 and 25), the autosomes have reduction factor 1−c₀ and the X chromosome has reduction factor $\left(1-c_0\right)/\left(1-\frac{1}{4}{c}_0\right)$. For 0 < c₀ < 1, $1-c_0<\left(1-c_0\right)/\left(1-\frac{1}{4}{c}_0\right)$ and the autosomes have a smaller reduction factor. The reduction factor due to consanguinity has a stronger effect on the autosomal within-individual coalescence time than on the X-chromosomal value.

For the between-individual coalescence times for individuals in different mating pairs (Eqs. 8 and 26), the reduction factors are $1-\frac{3}{4}{c}_0$ for autosomes and $\left(1-\frac{3}{4}{c}_0\right)/\left(1-\frac{1}{4}{c}_0\right)$ for the X chromosome, so that again, the effect of consanguinity is stronger on the autosomes than on the X chromosome. Thus, both for pairs of alleles within individuals and for pairs of alleles in separate mating pairs, under sib mating, consanguinity reduces expected time to coalescence by a greater degree in the autosomal case compared to the X-chromosomal case.

3.2. First cousins

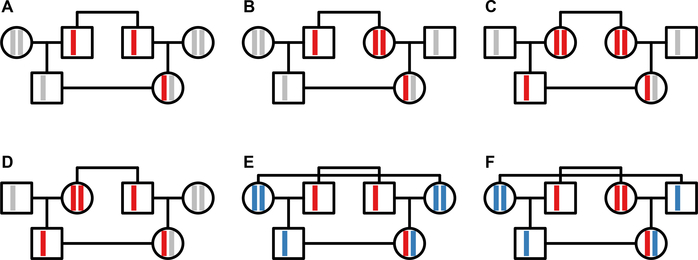
We move next to first-cousin mating. Whereas the four types of cousin mating have the same effect on autosomal coalescence times, for the X chromosome, their effects differ. We consider all four types of first-cousin mating, in addition to two double-first-cousin mating schemes: bilateral-parallel cousins, where a male mates with a female who is both his father’s brother’s daughter and his mother’s sister’s daughter, and bilateral-cross cousins, where a male mates with a female who is both his father’s sister’s daughter and his mother’s brother’s daughter (Figure 5).

Figure 5:

X chromosomes in first-cousin mating schemes. (A) Patrilateral-parallel. (B) Patrilateral-cross. (C) Matrilateral-parallel. (D) Matrilateral-cross. (E) Bilateral-parallel. (F) Bilateral-cross. X chromosomes are depicted in red for the sib parents and their offspring in the unilateral mating regimes. The two sets of X chromosomes in the two mating pairs are depicted in red and blue in the bilateral mating regimes, colored identically to associated X chromosomes in the offspring.

In each scheme, we continue to consider N mating pairs, a fraction c₁ of which are consanguineous pairs of a specified cousin mating type. We continue to disallow chance consanguinity, and we permit only a single consanguinity regime at a time. As before, we exclude state 1, as two X chromosomes cannot be in the same male.

The mean coalescence time for two alleles in state 2 is the same irrespective of the type of consanguinity, and it follows from Eq. 15 for all of the cases. For states 4, 5, and 6, two individuals in separate mating pairs are siblings with probability $\frac{1}{N}$. Because chance first-cousin mating is not allowed, equations associated with these states follow from our X-chromosomal sib-mating model (Eqs. 17–19). Only for state 3 does the recursion differ across cases.

3.2.1. Patrilateral-parallel

For patrilateral-parallel cousin mating, it never occurs that X-chromosomal alleles are shared identically by descent in the consanguineous pair, as the male in the pair does not receive an X chromosome from his father (Figure 5A). Hence, the fact that their fathers are brothers does not reduce coalescence times of X-chromosomal loci in a consanguineous pair compared with a non-consanguineous pair, and we can disregard c₁.

The X chromosome in the male of the mating pair has probability $\frac{1}{2}$ of coming from a male two generations back, and probability $\frac{1}{2}$ of coming from a female two generations back. The X chromosome in the female of the mating pair has probability $\frac{1}{4}$ of coming from a male two generations back and probability $\frac{3}{4}$ of coming from a female two generations back. Combining these cases for the positions of the alleles two generations back, with probability $\frac{1}{8}$, the alleles in two individuals in a mating pair come from two males, producing coalescence time $\mathbb{E}\left[V_{mm}\right]+2$. They come from a male and a female with probability $\frac{1}{2}$, producing coalescence time $\mathbb{E}\left[V_{mf}\right]+2$. They come from two females with probability $\frac{3}{8}$, producing coalescence time $\mathbb{E}\left[V_{ff}\right]+2$. We have

$$\mathbb{E}[U]=\frac{1}{8}\left(\mathbb{E}\left[V_{mm}\right]+2\right)+\frac{1}{2}\left(\mathbb{E}\left[V_{mf}\right]+2\right)+\frac{3}{8}\left(\mathbb{E}\left[V_{ff}\right]+2\right).$$ (27)

When we solve the linear system of equations formed by Eqs. 15, 27, and 17–19, we have

$$\mathbb{E}\left[T_f\right]=\frac{144N^3+368N^2-16N-40}{48N^2-N-5}$$ (28)

$$\mathbb{E}[U]=\frac{144N^3+320N^2-15N-35}{48N^2-N-5}$$ (29)

$$\mathbb{E}\left[V_{mm}\right]=\frac{144N^3+191N^2-65N}{48N^2-N-5}$$ (30)

$$\mathbb{E}\left[V_{mf}\right]=\frac{144N^3+239N^2+15N-35}{48N^2-N-5}$$ (31)

$$\mathbb{E}\left[V_{ff}\right]=\frac{144N^3+215N^2-33N-20}{48N^2-N-5}.$$ (32)

As N →∞, these equations have limit 3N. The limiting mean coalescence time for each state depends only on the number of mating pairs N and not on the consanguinity rate c₁. For patrilateral-parallel first-cousin mating, consanguinity has no effect on the mean coalescence time of X-chromosomal alleles.

3.2.2. Patrilateral-cross

Patrilateral-cross first-cousin mating (Figure 5B) is similar to patrilateral-parallel first-cousin mating in that a pair of X-chromosomal alleles in the two individuals of a consanguineous pair cannot both derive from the sibling parents. As a result, if we proceed through the possible cases for where X chromosomes in a consanguineous pair could be located two generations in the past, we obtain exactly the same cases that underlie Eq. 27; for state 3, the mean coalescence time follows Eq. 27, and the consanguinity fraction c₁ has no effect on this coalescence time.

The resulting system of equations is the same as for patrilateral-parallel first-cousin mating, and therefore has the same solution. For each state, the mean coalescence time approaches 3N as N →∞. As was seen with our patrilateral-parallel solution, consanguinity has no effect on coalescence times of X-chromosomal alleles under patrilateral-cross first-cousin mating.

3.2.3. Matrilateral-parallel

In matrilateral-parallel first-cousin mating, the male in a mating pair mates with his mother’s sister’s daughter (Figure 5C). For two alleles sampled in state 3, the probability that the X chromosome in the male of a consanguineous pair originates from the sib parent is 1, and the corresponding probability is $\frac{1}{2}$ for the female. Hence, c₁/2 is the probability that a mating pair is consanguineous and both alleles chosen from the two individuals in the mating pair are from the sib parents. Given that the alleles trace to the sib parents, they coalesce two generations back with probability $\frac{3}{8}$. The event that the alleles come from a shared female ancestor two generations back and do not coalesce has probability $\frac{1}{8}$ and gives coalescence time $\mathbb{E}\left[T_f\right]+2$. The event that the two alleles come from separate individuals in a mating pair two generations back has probability $\frac{1}{2}$ and gives coalescence time $\mathbb{E}\left[U\right]+2$. The event that the two alleles are sampled from a consanguineous pair but do not trace to the sib parents has probability c₁/2. In this case, two generations back, the alleles trace to a male and a female with probability $\frac{1}{2}$ (giving coalescence time E[V_mf] + 2), or they trace to two females with probability $\frac{1}{2}$ (giving coalescence time E[V_ff] + 2). The event that the two alleles are sampled from a non-consanguineous pair has probability 1 − c₁. In this case, the alleles follow the same pattern as in Eq. 27. Combining the cases, we have

$$\begin{gathered} \mathbb{E}[U]=\frac{c_1}{2}\left[\frac{3}{8}\times 2+\frac{1}{8}\left(\mathbb{E}\left[T_f\right]+2\right)+\frac{1}{2}(\mathbb{E}[U]+2)\right] \\ +\frac{c_1}{2}\left[\frac{1}{2}\left(\mathbb{E}\left[V_{mf}\right]+2\right)+\frac{1}{2}(\mathbb{E}[V_{ff}]+2)\right] \\ +(1-c_1)\left[\frac{1}{8}\left(\mathbb{E}\left[V_{mm}\right]+2\right)+\frac{1}{2}\left(\mathbb{E}\left[V_{mf}\right]+2\right)+\frac{3}{8}\left(\mathbb{E}\left[V_{ff}\right]+2\right)\right]. \end{gathered}$$ (33)

Eqs. 15, 33, and 17–19 form a linear system, with solution

$$\mathbb{E}\left[T_f\right]=\frac{144N^3\left(1-\frac{1}{2}{c}_1\right)+368N^2\left(1-\frac{1}{92}{c}_1\right)-16N\left(1-\frac{1}{4}{c}_1\right)-40}{48N^2\left(1+\frac{1}{16}{c}_1\right)-N\left(1+c_1\right)-5}$$ (34)

$$\mathbb{E}[U]=\frac{144N^3\left(1-\frac{1}{2}{c}_1\right)+320N^2\left(1-\frac{7}{320}{c}_1\right)-15N\left(1-\frac{1}{3}{c}_1\right)-35}{48N^2\left(1+\frac{1}{16}{c}_1\right)-N\left(1+c_1\right)-5}$$ (35)

$$\mathbb{E}\left[V_{mm}\right]=\frac{144N^3\left(1-\frac{5}{16}{c}_1\right)+191N^2\left(1+\frac{11}{191}{c}_1\right)-65N}{48N^2\left(1+\frac{1}{16}{c}_1\right)-N\left(1+c_1\right)-5}$$ (36)

$$\mathbb{E}\left[V_{mf}\right]=\frac{144N^3\left(1-\frac{5}{16}{c}_1\right)+239N^2\left(1-\frac{13}{239}{c}_1\right)+15N\left(1+\frac{1}{3}{c}_1\right)-35}{48N^2\left(1+\frac{1}{16}{c}_1\right)-N\left(1+c_1\right)-5}$$ (37)

$$\mathbb{E}\left[V_{ff}\right]=\frac{144N^3\left(1-\frac{5}{16}{c}_1\right)+215N^2\left(1-\frac{1}{215}{c}_1\right)-33N\left(1-\frac{2}{33}{c}_1\right)-20}{48N^2\left(1+\frac{1}{16}{c}_1\right)-N\left(1+c_1\right)-5}.$$ (38)

The highest-order terms are the same for Eqs. 34 and 35 and for Eqs. 36–38. The N → ∞ limits give

$$\underset{N\to \infty }{\lim }\frac{\mathbb{E}\left[T_f\right]}{3N}=\underset{N\to \infty }{\lim }\frac{\mathbb{E}[U]}{3N}=\frac{1-\frac{1}{2}{c}_1}{1+\frac{1}{16}{c}_1}$$ (39)

$$\underset{N\to \infty }{\lim }\frac{\mathbb{E}\left[V_{mm}\right]}{3N}=\underset{N\to \infty }{\lim }\frac{\mathbb{E}\left[V_{mf}\right]}{3N}=\underset{N\to \infty }{\lim }\frac{\mathbb{E}\left[V_{ff}\right]}{3N}=\frac{1-\frac{5}{16}{c}_1}{1+\frac{1}{16}{c}_1}.$$ (40)

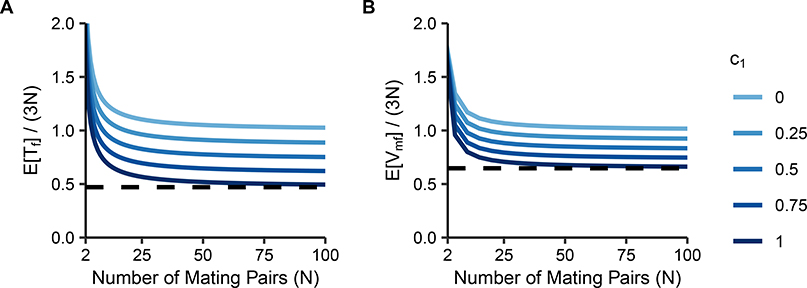
Eqs. 34 and 37 normalized by 3N are plotted in Figure 6. As N increases, $\mathbb{E}\left[T_f\right]$ and $\mathbb{E}\left[V_{mf}\right]$ both quickly approach their limits, a product of the number of X chromosomes in the population and the reduction factor due to consanguinity. We have $\mathbb{E}\left[V_{mf}\right]-\mathbb{E}\left[T_f\right]\approx 9N{c}_1/\left(16+c_1\right)$, so if 0 < c₁ ≤ 1, then $\mathbb{E}\left[V_{mf}\right]>\mathbb{E}\left[T_f\right]$ in the large-N limit. The lower bound on the limiting reduction factor for $\mathbb{E}\left[T_f\right]/(3N)$ due to consanguinity, achieved when c₁ = 1, is $\frac{8}{17}$. For $\mathbb{E}\left[V_{mf}\right]/(3N)$, the lower bound is $\frac{11}{17}$.

Figure 6:

Normalized mean coalescence times on the X chromosome under matrilateral-parallel first-cousin mating. Coalescence times are plotted as a function of the number of mating pairs (N) and the proportion of mating pairs that are matrilateral-parallel pairs (c₁). (A) $\mathbb{E}\left[T_f\right]/(3N)$, Eq. 34. (B) $\mathbb{E}\left[V_{mf}\right]/(3N)$, Eq. 37. The dashed lines represent the maximal reduction due to consanguinity, obtained by setting c₁ = 1: $\frac{8}{17}$ in (A) and $\frac{11}{17}$ in (B).

3.2.4. Matrilateral-cross

Next, we consider matrilateral-cross first-cousin mating, in which a male mates with his mother’s brother’s daughter (Figure 5D). We consider two alleles sampled in state 3. As seen in the matrilateral-parallel case, the probability is c₁/2 that a mating pair represents first cousins and that we sample the sib parent alleles. In this case, because a male is the sib parent of the female in the mating pair, the alleles have three possible origins. First, the two sampled alleles coalesce in two generations with probability $\frac{1}{4}$. Second, with probability $\frac{1}{4}$, the alleles derive from the shared grandmother but do not coalesce, giving coalescence time $\mathbb{E}\left[T_f\right]+2$. Third, with probability $\frac{1}{2}$, the two alleles come separately from the male and female in the grandparental mating pair, giving coalescence time $\mathbb{E}\left[U\right]+2$. As was seen for matrilateral-parallel consanguinity, the event that the two alleles are sampled from a consanguineous pair but do not trace to the sib parents has probability c₁/2. In this scenario, two generations back, with probability $\frac{1}{4}$ the alleles trace to two males (giving coalescence time E[V_mm] + 2), with probability $\frac{1}{2}$ they trace to a male and a female (coalescence time E[V_mf] + 2), or with probability $\frac{1}{4}$ they trace to two females (coalescence time E[V_ff] + 2). As was seen with matrilateral-parallel cousins, if the mating pair is not a first-cousin pair (which happens with probability 1 − c₁), then the transition probabilities and coalescence times follow from Eq. 27. Combining cases, we have

$$\begin{gathered} \mathbb{E}[U]=\frac{c_1}{2}\left[\frac{1}{4}\times 2+\frac{1}{4}\left(\mathbb{E}\left[T_f\right]+2\right)+\frac{1}{2}(\mathbb{E}[U]+2)\right] \\ +\frac{c_1}{2}\left[\frac{1}{4}\left(\mathbb{E}\left[V_{mm}\right]+2\right)+\frac{1}{2}(\mathbb{E}[V_{mf}]+2)+\frac{1}{4}(\mathbb{E}[V_{ff}]+2)\right] \\ +\left(1-c_1\right)\left[\frac{1}{8}\left(\mathbb{E}\left[V_{mm}\right]+2\right)+\frac{1}{2}\left(\mathbb{E}\left[V_{mf}\right]+2\right)+\frac{3}{8}\left(\mathbb{E}\left[V_{ff}\right]+2\right)\right]. \end{gathered}$$ (41)

Eqs. 15, 41, and 17–19 form a linear system with solution

$$\mathbb{E}\left[T_f\right]=\frac{144N^3\left(1-\frac{1}{2}{c}_1\right)+368N^2\left(1-\frac{1}{92}{c}_1\right)-16N\left(1-\frac{3}{4}{c}_1\right)-40}{48N^2\left(1-\frac{1}{8}{c}_1\right)-N\left(1-2c_1\right)-5}$$ (42)

$$\mathbb{E}[U]=\frac{144N^3\left(1-\frac{1}{2}{c}_1\right)+320N^2\left(1+\frac{1}{160}{c}_1\right)-15N\left(1-\frac{2}{3}{c}_1\right)-35}{48N^2\left(1-\frac{1}{8}{c}_1\right)-N\left(1-2c_1\right)-5}$$ (43)

$$\mathbb{E}\left[V_{mm}\right]=\frac{144N^3\left(1-\frac{3}{8}{c}_1\right)+191N^2\left(1+\frac{18}{191}{c}_1\right)-65N}{48N^2\left(1-\frac{1}{8}{c}_1\right)-N\left(1-2c_1\right)-5}$$ (44)

$$\mathbb{E}\left[V_{mf}\right]=\frac{144N^3\left(1-\frac{3}{8}{c}_1\right)+239N^2\left(1-\frac{6}{239}{c}_1\right)+15N\left(1+\frac{2}{3}{c}_1\right)-35}{48N^2\left(1-\frac{1}{8}{c}_1\right)-N\left(1-2c_1\right)-5}$$ (45)

$$\mathbb{E}\left[V_{ff}\right]=\frac{144N^3\left(1-\frac{3}{8}{c}_1\right)+215N^2\left(1+\frac{6}{215}{c}_1\right)-33N\left(1-\frac{2}{11}{c}_1\right)-20}{48N^2\left(1-\frac{1}{8}{c}_1\right)-N\left(1-2c_1\right)-5}.$$ (46)

The highest-order terms agree for Eqs. 42 and 43 and for Eqs. 44–46. The N → ∞ limits give

$$\underset{N\to \infty }{\lim }\frac{\mathbb{E}\left[T_f\right]}{3N}=\underset{N\to \infty }{\lim }\frac{\mathbb{E}[U]}{3N}=\frac{1-\frac{1}{2}{c}_1}{1-\frac{1}{8}{c}_1}$$ (47)

$$\underset{N\to \infty }{\lim }\frac{\mathbb{E}\left[V_{mm}\right]}{3N}=\underset{N\to \infty }{\lim }\frac{\mathbb{E}\left[V_{mf}\right]}{3N}=\underset{N\to \infty }{\lim }\frac{\mathbb{E}\left[V_{ff}\right]}{3N}=\frac{1-\frac{3}{8}{c}_1}{1-\frac{1}{8}{c}_1}.$$ (48)

Figure 7 plots Eqs. 42 and 45 divided by 3N. As N increases, $\mathbb{E}\left[T_f\right]/(3N)$ and $\mathbb{E}\left[V_{mf}\right]/(3N)$ quickly approach their limits. $\mathbb{E}\left[V_{mf}\right]-\mathbb{E}\left[T_f\right]\approx 3N{c}_1/\left(8-c_1\right)$, so for 0 < c ≤ 1, $\mathbb{E}\left[V_{mf}\right]>\mathbb{E}\left[T_f\right]$ in the large-N limit. The lower bound on the large-N reduction factor for $\mathbb{E}\left[T_f\right]/(3N)$ is $\frac{4}{7}$ achieved at c₁ = 1. For $\mathbb{E}\left[V_{mf}\right]/(3N)$, the bound is $\frac{5}{7}$.

Figure 7:

Normalized mean coalescence times on the X chromosome under matrilateral-cross first-cousin mating. Coalescence times are plotted as a function of the number of mating pairs (N) and the proportion of mating pairs that are matrilateral-cross pairs (c₁): (A) $\mathbb{E}\left[T_f\right]/(3N)$, Eq. 42. (B) $\mathbb{E}\left[V_{mf}\right]/(3N)$, Eq. 45. The dashed lines represent the maximal reduction due to consanguinity, obtained by setting $c_1=1:\frac{4}{7}$ in (A) and $\frac{5}{7}$ in (B).

3.3. Double first cousins

3.3.1. Bilateral-parallel

In bilateral-parallel cousin mating, the male in a pair mates with a female who is his mother’s sister’s daughter and his father’s brother’s daughter (Figure 5E). The bilateral-parallel case contains both matrilateral-parallel and patrilateral-parallel cousin mating. Hence, for two alleles sampled in state 3, as in the matrilateral-parallel case, the event that the individuals are first cousins and the two alleles are sampled from the sib parents has probability c₁/2 to trace to the female sib parents and probability 0 to trace to the male sib parents. The patrilateral-parallel line of descent does not contribute to the possibility of identity by descent, so that the bilateral-parallel case behaves like the matrilateral parallel case. The equation associated with state 3 follows from Eq. 33. All equations for the bilateral-parallel case mirror the matrilateral-parallel case, and the same conclusions follow.

3.3.2. Bilateral-cross

In bilateral-cross cousin mating, the male in a pair mates with a female who is simultaneously his father’s sister’s daughter and his mother’s brother’s daughter (Figure 5F). The matrilateral-cross component of the bilateral-cross pedigree contributes to allele sharing in the mating pair, but the patrilateral-cross line of descent does not contribute to allele sharing in the mating pair. Coalescence times follow from the matrilateral-cross case.

3.4. Comparison of cousin-mating schemes

The six cousin mating regimes, four unilateral and two bilateral, produce three patterns in their effects on X-chromosomal coalescence times. The patrilateral-parallel and patrilateral-cross cases are mathematically identical; for short, we refer to this pair simply as patrilateral. The matrilateral-parallel and bilateral-parallel cases are identical, as are the matrilateral-cross and bilateral-cross cases; we refer to these pairs as matrilateral-parallel and matrilateral-cross, respectively. Reduction factors for the various cases are summarized in Table 1.

Table 1:

Large-N reduction factors of pairwise coalescence times due to various types of consanguinity.

	Autosomal			X-chromosomal
	Siblings	First cousins	Double first cousins	Siblings	First cousins
					Patrilateral-parallel, Patrilateral-cross	Matrilateral-parallel, Bilateral-parallel	Matrilateral-cross, Bilateral-cross
Kinship coefficient	$\frac{1}{4}$	$\frac{1}{16}$	$\frac{1}{8}$	$\frac{1}{2}$	0	$\frac{3}{16}$	$\frac{1}{8}$
Tm, Tf, U	1 −c0	$1-\frac{1}{4}{c}_1$	$1-\frac{1}{2}{c}_1$	$\frac{1-c_0}{1-\frac{1}{4}{c}_0}$	1	$\frac{1-\frac{1}{2}{c}_1}{1+\frac{1}{16}{c}_1}$	$\frac{1-\frac{1}{2}{c}_1}{1-\frac{1}{8}{c}_1}$
Vmm, Vmf, Vff	$1-\frac{3}{4}{c}_0$	$1-\frac{3}{16}{c}_1$	$1-\frac{3}{8}{c}_1$	$\frac{1-\frac{3}{4}{c}_0}{1-\frac{1}{4}{c}_0}$	1	$\frac{1-\frac{5}{16}{c}_1}{1+\frac{1}{16}{c}_1}$	$\frac{1-\frac{3}{8}{c}_1}{1-\frac{1}{8}{c}_1}$

These reduction factors give multipliers for the mean T_MRCA for a non-consanguineous population of 2N individuals: 4N for autosomes and 3N for X chromosomes. The kinship coefficient for a mating pair refers to the probability that two alleles sampled from the two individuals of the pair are identical by descent. Kinship coefficients are computed separately for autosomal loci and X-chromosomal loci. Note that T_m is used only in the autosomal case; for the X chromosome, two alleles cannot be in the same male.

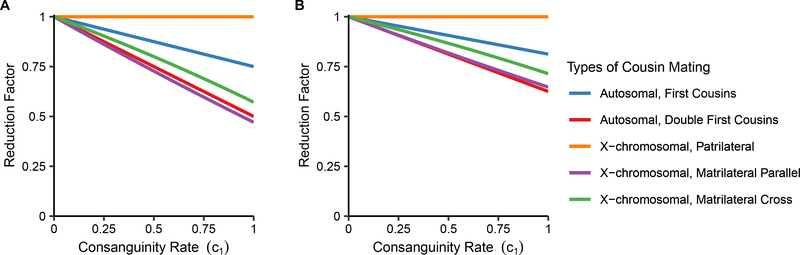
As noted in Sections 3.2.1 and 3.2.2, consanguinity has no effect on patrilateral cousin mating because the male in the first-cousin mating pair never inherits an X chromosome from the sib parent (his father). We can, however, compare reduction factors due to consanguinity for the matrilateral-parallel and matrilateral-cross cases. For $\mathbb{E}\left[T_f\right]$ and $\mathbb{E}[U]$, the reduction factor for matrilateral-parallel cousin mating is $\left(1-\frac{1}{2}{c}_1\right)/\left(1+\frac{1}{16}{c}_1\right)$ (Eq. 39). The reduction factor for matrilateral-cross cousin mating is $\left(1-\frac{1}{2}{c}_1\right)/\left(1-\frac{1}{8}{c}_1\right)$ (Eq. 47).

To place the various X-chromosomal reduction factors in rank order, we observe that for $\mathbb{E}\left[T_f\right]$ and $\mathbb{E}[U]$, $\left(1-\frac{1}{2}{c}_1\right)/\left(1+\frac{1}{16}{c}_1\right)<\left(1-\frac{1}{2}{c}_1\right)/\left(1-\frac{1}{8}{c}_1\right)<1$ for 0 < c₁ ≤ 1. The matrilateral-parallel case has the strongest reduction factor, followed by the matrilateral-cross case, followed by the patrilateral case, which has no reduction at all. For $\mathbb{E}\left[V_{mm}\right]$, $\mathbb{E}\left[V_{mf}\right]$, and $\mathbb{E}\left[V_{ff}\right]$, we can see that $\left(1-\frac{5}{16}{c}_1\right)/\left(1+\frac{1}{16}{c}_1\right)<\left(1-\frac{3}{8}{c}_1\right)/\left(1-\frac{1}{8}{c}_1\right)<1$ for 0 < c₁ ≤ 1. As is true for $\mathbb{E}\left[T_f\right]$ and $\mathbb{E}[U]$, the matrilateral-parallel case has the strongest reduction factor, followed by the matrilateral-cross case, followed by the patrilateral case (Figure 8).

Figure 8:

Reduction factors for mean autosomal and X-chromosomal pairwise coalescence times under various types of unilateral and bilateral first-cousin mating, plotted as a function of the consanguinity rate (c₁). (A) Reduction factors for $\mathbb{E}\left[T_m\right]$, $\mathbb{E}\left[T_f\right]$, and $\mathbb{E}[U]$ ($\mathbb{E}\left[T_m\right]$ for autosomes only). (B) Reduction factors for $\mathbb{E}\left[V_{mm}\right]$, $\mathbb{E}\left[V_{mf}\right]$, and $\mathbb{E}\left[V_{ff}\right]$. See Table 1 for formulae.

Additionally, $\left(1-\frac{1}{2}{c}_1\right)/\left(1-\frac{1}{8}{c}_1\right)<1-\frac{1}{4}{c}_1$ for 0 < c₁ ≤ 1, so that the reduction in $\mathbb{E}\left[T_f\right]$ and $\mathbb{E}[U]$ for the matrilateral-cross case is stronger than for the autosomal case. Similarly, $\left(1-\frac{3}{8}{c}_1\right)/\left(1-\frac{1}{8}{c}_1\right)<1-\frac{3}{16}{c}_1$, so that the same is true for $\mathbb{E}\left[V_{mm}\right]$, $\mathbb{E}\left[V_{mf}\right]$, and $\mathbb{E}\left[V_{ff}\right]$.

The reduction factors in Table 1 indicate that consanguinity has no effect on coalescence times for X-chromosomal loci under patrilateral cousin mating, and in increasing order of strength, the effect of consanguinity is greater on autosomal loci under first cousin mating, on X-chromosomal loci under matrilateral-cross mating, and on X-chromosomal loci under matrilateral-parallel mating.

When we also consider the autosomal double-first-cousin case, we see that $\left(1-\frac{1}{2}{c}_1\right)/\left(1+\frac{1}{16}{c}_1\right)<1-\frac{1}{2}{c}_1$ for 0 < c₁ ≤ 1, so that the reduction in $\mathbb{E}\left[T_f\right]$ and $\mathbb{E}[U]$ for the X-chromosomal matrilateral-parallel case is stronger than for the autosomal bilateral case. We also see that $1-\frac{1}{2}{c}_1<\left(1-\frac{1}{2}{c}_1\right)/\left(1-\frac{1}{8}{c}_1\right)$ 0 < c₁ ≤ 1, so that the reduction in $\mathbb{E}\left[T_f\right]$ and $\mathbb{E}[U]$ is greater for the autosomal bilateral case than for the X-chromosomal matrilateral-cross case. For $\mathbb{E}\left[T_f\right]$ and $\mathbb{E}[U]$, the strengths of reduction in increasing order are matrilateral-cross, autosomal bilateral, and matrilateral-parallel (Figure 8A).

We next examine the reduction factors for $\mathbb{E}\left[V_{mm}\right]$, $\mathbb{E}\left[V_{mf}\right]$, and $\mathbb{E}\left[V_{ff}\right]$ for double-first-cousin mating. We see that $1-\frac{3}{8}{c}_1<\left(1-\frac{5}{16}{c}_1\right)/\left(1+\frac{1}{16}{c}_1\right)$ for 0 < c1 ≤ 1, so that the reduction in $\mathbb{E}\left[V_{mm}\right]$, $\mathbb{E}\left[V_{mf}\right]$, and $\mathbb{E}\left[V_{ff}\right]$ for the autosomal double-first-cousin case is stronger than for the X-chromosomal matrilateral-parallel case. For $\mathbb{E}\left[V_{mm}\right]$, $\mathbb{E}\left[V_{mf}\right]$, and $\mathbb{E}\left[V_{ff}\right]$, the effect of consanguinity in increasing order is matrilateral-cross, matrilateral-parallel, and autosomal bilateral (Figure 8B). Whereas the unilateral cases have the same rank order for the strength of reduction for within-individual states ($\mathbb{E}\left[T_f\right]$ and $\mathbb{E}[U]$) and between-individual states ($\mathbb{E}\left[V_{mm}\right]$, $\mathbb{E}\left[V_{mf}\right]$, and $\mathbb{E}\left[V_{ff}\right]$), these rank orders differ for the autosomal bilateral case.

4. Discussion

We have explored the effect of consanguinity on mean pairwise coalescence times on the X chromosome. We extended the model of Severson et al. (2019) to the X chromosome, comparing X-chromosomal and autosomal theoretical results. We found that patrilateral first-cousin mating has no effect on X-chromosomal coalescence; however, matrilateral first-cousin mating—and especially matrilateral-parallel mating—decreases X-chromosomal mean pairwise coalescence times relative to autosomal coalescence times (Table 1).

In a coalescent model with first-cousin mating in a population of N diploid mating pairs, we have observed that in a large population, mean pairwise T_MRCA is the product of the mean coalescence time in the absence of consanguinity, 4N for autosomes and 3N for X chromosomes, and a reduction factor due to consanguinity (Table 1). Four types of unilateral first-cousin mating, which are equivalent for autosomal loci, differ in their effects on the X chromosome (Eqs. 9–11, 39 and 40, 47 and 48).

In all four types of unilateral first-cousin mating, mean coalescence time for two alleles in the same individual is reduced by consanguinity to a greater extent than mean coalescence time for two alleles in two individuals in separate mating pairs (Table 1). This effect for the X chromosome accords with similar autosomal results (Severson et al., 2019). Because the X chromosome is never inherited from father to son, patrilateral-parallel and patrilateral-cross consanguinity do not affect X-chromosomal coalescence times. Matrilateral consanguinity, however, induces a stronger reduction in X-chromosomal coalescence times compared to autosomal coalescence times.

For bilateral consanguinity, corresponding to double-first-cousin matings, coalescence times follow the relationship of the mothers in the consanguineous pair: bilateral-parallel consanguinity has the same coalescence time as matrilateral-parallel consanguinity, and bilateral-cross consanguinity has the same coalescence time as matrilateral-cross consanguinity. Interestingly, however, whereas bilateral-parallel X-chromosomal coalescence times have a stronger reduction than that of bilateral autosomal coalescence times when considering within-individual coalescence ($\mathbb{E}\left[T_m\right]$ and $\mathbb{E}\left[T_f\right]$), this order is reversed for between-individual coalescence ($\mathbb{E}\left[V_{mm}\right]$, $\mathbb{E}\left[V_{mf}\right]$, and $\mathbb{E}\left[V_{ff}\right]$).

Genomic sharing around a site is inversely related to coalescence time at that site (Palamara et al., 2012; Carmi et al., 2014; Browning and Browning, 2015); specifically, ROH lengths are inversely related to within-individual coalescence times, and IBD lengths are inversely related to between-individual coalescence times. Thus, the model predicts that reduced coalescence times on the X chromosome—owing to both smaller population size and to a stronger effect of matrilateral consanguinity in reducing those times—give rise to longer ROH and IBD sharing on the X chromosome than on the autosomes. Further, the smaller mean within-individual coalescence times ($\mathbb{E}\left[T_m\right]$ and $\mathbb{E}\left[T_f\right]$) than between-individual coalescence times ($\mathbb{E}\left[V_{mm}\right]$, $\mathbb{E}\left[V_{mf}\right]$, and $\mathbb{E}\left[V_{ff}\right]$) predict greater ROH sharing within individuals than IBD sharing between individuals. The smaller X-chromosomal population size compared to autosomal population size, together with the greater reduction from matrilateral consanguinity of X-chromosomal within- and between-individual T_MRCA compared to autosomal within- and between-individual T_MRCA, predicts greater ROH and IBD sharing on the X chromosome relative to autosomes.

Recent analyses have explored a variety of population-genetic features of the difference between the X chromosome and autosomes, tracing both to a difference in population size and also to effects of differing inheritance patterns. Such studies have included analyses focused on computations of nucleotide diversity (Arbiza et al., 2014), coalescence times (Ramachandran et al., 2008), and genomic sharing (Buffalo et al., 2016), and on various consequences of sex-biased demography (Wilkins and Marlowe, 2006; Bustamante and Ramachandran, 2009; Goldberg and Rosenberg, 2015; Webster and Wilson Sayres, 2016). Our model adds to this work in its focus on effects of specific consanguinity models.

We note that our models are limited in that we have studied the effect of different types of first-cousin consanguinity separately, and we have not considered a population with a mixture of the various types. In actual populations, while one of the four types of unilateral consanguinity might be culturally preferred (Bittles, 2012), the appropriate model suited to a specific population might involve a superposition of two or more types. The separation-of-time-scales coalescent approach of Severson et al. (2021) successfully examined a superposition of consanguinity at different levels of relatedness; we expect that this method will be useful for superimposing multiple forms of first-cousin consanguinity. The separation-of-time-scales approach also has the benefit of producing asymptotic coalescence time distributions extending beyond mean coalescence times.

A second limitation is that our model formulation considers only the most recent shared ancestral pair for a consanguineous pair; that ancestral pair could itself be consanguineous, so that consanguineous pairs in the current generation might possess additional, more distant, shared ancestors. The approximation that this more distant consanguinity is ignored in computing mean coalescence times is likely to be more problematic in cases in which multiple shared lines of descent are most probable, such as for small N or for large c₁ (Severson et al., 2021).

This year marks the centennial of the pioneering studies of Sewall Wright (1921) on the effects of mating models on features of pointwise genotypic sharing—studies that have been central to the large volume of subsequent work on genetic consequences of consanguinity, inbreeding, and relatedness (Hill, 1996). In recent years, the study of consanguinity and its connections to runs of homozygosity and identity by descent has been much advanced by new models and genomic tools for data analysis (Bittles, 2012; Browning and Browning, 2012; Thompson, 2013; Romeo and Bittles, 2014; Cussens and Sheehan, 2016; Ceballos et al., 2018). By exploring coalescent models that incorporate each of the various types of first-cousin consanguinity, we have determined the effects of first-cousin consanguinity in shaping X-chromosomal coalescence times, and by extension, genomic sharing. In addition to providing new coalescent theory for populations with consanguinity, the study further enhances the understanding of the effects of sex-biased processes on genomes, the factors that contribute to differences in genetic variation between X chromosomes and autosomes, and the determinants of patterns of genomic sharing.

Appendix A: Autosomal first cousins

We consider the two-sex autosomal model with a fraction, c₁, of first-cousin mating pairs. Each generation, N is the number of mating pairs. We forbid chance sib mating, chance first-cousin mating, and double-first-cousin mating. As in the autosomal sib mating case, alleles within an individual (states 1 and 2) must have come from a single mating pair one generation back. Hence $\mathbb{E}\left[T_m\right]$ and $\mathbb{E}\left[T_f\right]$ follow Eq. 1 from the sib mating case.

$\mathbb{E}[U]$ again represents the mean coalescence time for two alleles in two individuals in a mating pair (state 3). Two individuals in a mating pair are first cousins with probability c₁. Given that a mating pair represents first cousins, the probability that the sampled alleles both come from the sib parent is $\frac{1}{4}$. The sampled alleles then have four possible cases. First, the alleles coalesce two generations back with probability $\frac{1}{4}$. They both derive from the shared grandfather with probability $\frac{1}{8}$, giving coalescence time $\mathbb{E}\left[T_m\right]+2$. They both derive from the shared grandmother with probability $\frac{1}{8}$, giving coalescence time $\mathbb{E}\left[T_f\right]+2$. With probability $\frac{1}{2}$, they derive separately from the two grandparents, coalescing with time $\mathbb{E}[U]+2$.

If the sampled alleles are either not from a first-cousin mating pair or not from the sib parents of a first-cousin mating pair—an event with probability $1-\frac{1}{4}{c}_1$— then the two alleles must be in state 4, 5, or 6 two generations back, and the transition probabilities follow the non-sib mating portion of Eq. 2. Combining cases, we have

$$\begin{gathered} \mathbb{E}[U]=\frac{c_1}{4}\left[\frac{1}{4}\times 2+\frac{1}{8}\left(\mathbb{E}\left[T_m\right]+2\right)+\frac{1}{8}\left(\mathbb{E}\left[T_f\right]+2\right)+\frac{1}{2}(\mathbb{E}[U]+2)\right] \\ +\left(1-\frac{1}{4}{c}_1\right)\left[\frac{1}{4}\left(\mathbb{E}\left[V_{mm}\right]+2\right)+\frac{1}{2}\left(\mathbb{E}\left[V_{mf}\right]+2\right)+\frac{1}{4}\left(\mathbb{E}\left[V_{ff}\right]+2\right)\right]. \end{gathered}$$ (A1)

For two alleles in separate mating pairs, because parental mating pairs are chosen at random from the previous generation, the probability that the two individuals are siblings by chance is $\frac{1}{N}$. Eq. 3 continues to apply. Solving the linear system containing Eq. 1, A1, and 3, we obtain Eqs. 9–11. When sex is ignored, Eqs. 9–11 reduce to Eqs. 8–10 from Severson et al. (2019).

Appendix B: Autosomal double first cousins

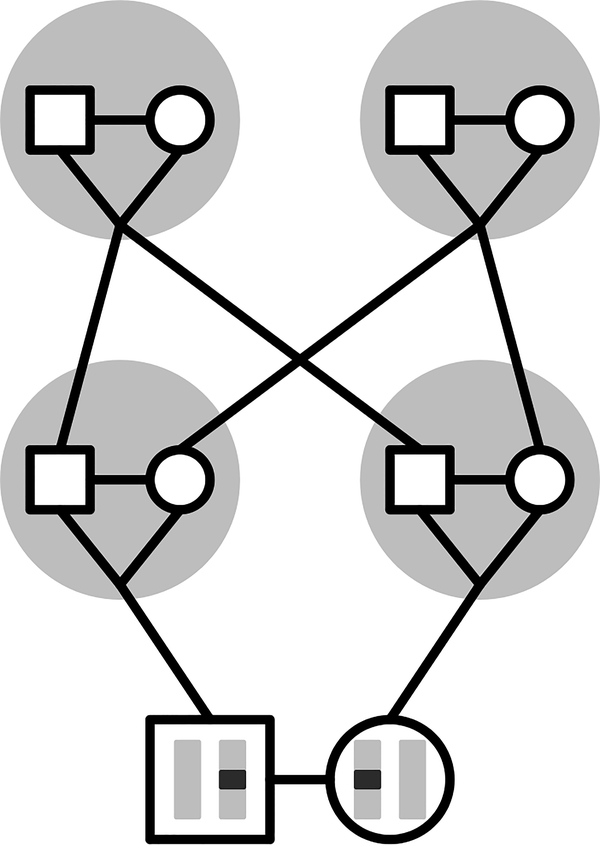
We extend the first-cousin mating model of Appendix A to double first cousins. If two individuals are double first cousins, then each parent of one individual is a sibling of a parent of the other individual, and the individuals share two grandparental mating pairs (Figure B1). This scenario can occur with children of two brother-sister pairs or with children of two brothers and two sisters. For autosomes, the two categories are mathematically equivalent.

Each generation, the fraction of double-first-cousin mating pairs is a constant value c₁. Chance sib mating, first-cousin mating, and double-first-cousin mating are forbidden among non-consanguineous mating pairs. If two alleles are present within one individual, then they must have been present in two individuals in a mating pair in the previous generation. $\mathbb{E}\left[T_m\right]$ and $\mathbb{E}\left[T_f\right]$ have the same recursions as before (Eq. 1).

For $\mathbb{E}[U]$, if two alleles are in two individuals of a mating pair, then with probability c₁, those individuals are double first cousins. The probability that two alleles in the double first cousins are inherited from one specific grandparental pair is $\frac{1}{4}$, and the probability that two alleles are inherited from the same grandparental pair is $\frac{1}{2}$. If the two alleles are inherited from a grandparental pair, then two generations ago they have four options. They coalesce with probability $\frac{1}{4}$, giving a coalescence time of 2. With probability $\frac{1}{8}$, they are inherited from the grandfather with mean coalescence time $\mathbb{E}\left[T_m\right]+2$. With probability $\frac{1}{8}$, they are inherited from the grandmother with mean coalescence time $\mathbb{E}\left[T_f\right]+2$. Finally, with probability $\frac{1}{2}$ they are two alleles in the two individuals in a grandparental mating pair, giving mean coalescence time $\mathbb{E}[U]+2$. If the individuals are not double first cousins (and because chance sib mating, first-cousin mating, and double-first-cousin mating are forbidden), then the two alleles have probability $\frac{1}{4}$ of being in two males in separate mating pairs two generations ago, probability $\frac{1}{2}$ of being

Figure B1:

Double first cousins. If two individuals in a mating pair are double first cousins, then each parent of the female is a sibling of one of the parents of the male, and the male and female share two grandparental mating pairs.

Figure B2:

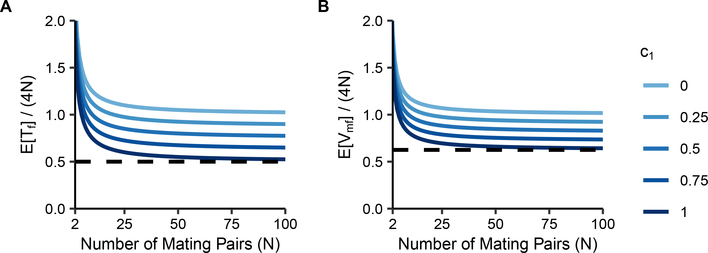
Normalized mean coalescence times for autosomal double-first-cousin mating. Coalescence times are plotted as a function of the number of mating pairs (N) and the proportion of mating pairs that are double-first-cousin pairs (c₁). (A) $\mathbb{E}\left[T_f\right]/(4N)$, Eq. 12. (B) $\mathbb{E}\left[V_{mf}\right]/(4N)$, Eq. 14. The dashed lines represent the maximal reduction due to consanguinity, c = 1: $\frac{1}{2}$ in (A) and $\frac{5}{8}$ in (B).

in a male and a female in separate mating pairs two generations ago, and probability $\frac{1}{4}$ of being in two females in separate mating pairs two generations ago. These cases have mean coalescence times $\mathbb{E}\left[V_{mm}\right]+2$, $\mathbb{E}\left[V_{mf}\right]+2$, and $\mathbb{E}\left[V_{ff}\right]+2$, respectively. Combining cases gives

$$\begin{gathered} \mathbb{E}[U]=\frac{c_1}{2}\left[\frac{1}{4}\times 2+\frac{1}{8}\left(\mathbb{E}\left[T_m\right]+2\right)+\frac{1}{8}\left(\mathbb{E}\left[T_f\right]+2\right)+\frac{1}{2}(\mathbb{E}[U]+2)\right] \\ +\left(1-\frac{1}{2}{c}_1\right)\left[\frac{1}{4}\left(\mathbb{E}\left[V_{mm}\right]+2\right)+\frac{1}{2}\left(\mathbb{E}\left[V_{mf}\right]+2\right)+\frac{1}{4}\left(\mathbb{E}\left[V_{ff}\right]+2\right)\right]. \end{gathered}$$ (B1)

$\mathbb{E}\left[V_{mm}\right]$, $\mathbb{E}\left[V_{mf}\right]$, and $\mathbb{E}\left[V_{ff}\right]$ also have the same recursions as before; because parental mating pairs are chosen uniformly at random with replacement from the N possible pairs, if two alleles are in two individuals in separate mating pairs, then the individuals share the same parental mating pair with probability $\frac{1}{N}$, giving rise to Eq. 3. Eqs. 1, B1, and 3 form a system of equations, the solution to which is given in Eqs. 12–14.

Eqs. 12–14 have a similar form to the solutions for first cousin mating, the difference being that c₁/4 is replaced by c₁/2 in Eqs. 12 and 13 and $\frac{3}{16}{c}_1$ by $\frac{3}{8}{c}_1$ in Eq. 14; the kinship coefficient for double first cousins $\left(\frac{1}{8}\right)$ is twice that of first cousins $\left(\frac{1}{16}\right)$. Next, $\mathbb{E}\left[V_{mf}\right]-\mathbb{E}\left[T_m\right]=N{c}_1/2-3$. Hence, if $c_1>\frac{6}{N}$ (or the number of consanguineous mating pairs Nc₁ exceeds 6), then the mean coalescence time for two alleles in different mating pairs ($\mathbb{E}\left[V_{mm}\right]$, $\mathbb{E}\left[V_{mf}\right]$, and $\mathbb{E}\left[V_{ff}\right]$) exceeds the mean coalescence time for two alleles within an individual ($\mathbb{E}\left[T_m\right]$ and $\mathbb{E}\left[T_f\right]$). For c₁ near 0, the mean coalescence times are near 4N, and as c₁ approaches 1, $\mathbb{E}\left[T_m\right]\approx 2N$ and $\mathbb{E}\left[V_{mf}\right]\approx \frac{5}{2}N$.

Eqs. 12 and 14 normalized by 4N are plotted in Figure B2. The means are bounded below by the maximal reduction due to consanguinity $\frac{1}{2}$ for $\mathbb{E}\left[T_m\right]$ and $\frac{5}{8}$ for $\mathbb{E}\left[V_{mf}\right]$. As the number of mating pairs, N, increases, the mean coalescence times approach the product of 4N, the mean coalescence time for a non-consanguineous diploid population of size 2N, and the reduction factor due to consanguinity, $1-\frac{1}{2}{c}_1$ for Eq. 12 and 1 $1-\frac{3}{8}{c}_1$ for Eq. 14.