Abstract
Improving quality of care in diabetes requires a good understanding of variations in diabetes outcomes and related interventions. However, little is known about the impact of diabetes interventions on outcome measures at the subpopulation-level. In this study, we developed methods that combine causal inference techniques with subset scanning techniques to study the heterogeneous effects of treatments on binary health outcomes. We analyzed a diabetes dataset consisting of 70,000 initial inpatient encounters to investigate the anomalous patterns associated with the impact of 4 anti-diabetic medication classes on 30-day readmission in diabetes. We discovered anomalous subpopulations where the likelihood of readmission was up to 1.8 times higher than that of the overall population suggesting subpopulation-level heterogeneity. Identifying such subpopulations may lead to a better understanding of the heterogeneous effects of treatments and improve targeted intervention planning.
Introduction
Thirty-day hospital readmission is an important outcome measure for assessing the quality of care given to diabetes patients. Reducing readmission rates among diabetes patients could improve care and reduce care-related costs1. However, although diabetes patients have an increased risk of readmission, little research has been done on this subject1. Some of the key barriers to understanding the risk factors of readmissions in diabetes are complicated by the natural variations in diabetes outcomes and related interventions. For example, care providers may use different treatments for their patients, and patients may respond differently to the same treatments. To improve the quality of care in diabetes care, there is a need for robust approaches for investigating variations at the subpopulation level. This is particularly useful since methods that analyze individual patients may fail to identify subtle patterns that are discernable when groups of patients are considered collectively, while methods that generate aggregate statistics for entire populations may fail to detect small-scale patterns2.
Traditional approaches to investigating subpopulation-level heterogeneity have relied on manual stratification of covariate profiles. For example, an outcome such as mortality can be stratified by age, gender, and ethnicity to identify high-risk subpopulations. However, this is limited to analyzing only a few features beyond which it becomes computationally infeasible. Furthermore, these approaches lack a data-driven knowledge discovery aspect as investigators must suggest a priori which features they would like to stratify across, and may also inadvertently lead to data manipulation as investigators attempt to produce desired p-values (‘p-hacking’). Machine learning approaches have also been used to investigate heterogeneity. Techniques such as LASSO regression can be used to select important covariates, while decision tree regression can be used to recursively partition data. However, these approaches are either subject to several modeling assumptions and limitations or lack adequate interpretability3. Fortunately, recent advancements in the anomalous pattern detection literature enable the scalable and unsupervised discovery of specific subpopulations (subsets) that are anomalous. These subset scanning methods focus on identifying anomalous subsets of records in a multidimensional array that differ from expected behavior. Herein, anomalousness is quantified using a scoring function that is typically a log-likelihood ratio statistic2. The scoring function is maximized over the exponentially-many combinations of feature values to identify the subset with the highest score. This function must satisfy the linear time subset scanning (LTSS) property so that the search can be done in linear rather than exponential time2.
Some of the key subset scanning techniques include Bias-Scan4, treatment effect subset scanning (TESS)3, and anomalous patterns of care (APC) Scan5. Bias-Scan focuses on the discovery of the subpopulation with the most divergence between the true outcomes and the predicted probabilities of a binary classifier. TESS discovers heterogeneous treatment effects by identifying the subpopulation in a randomized controlled trial that is most significantly impacted by the studied treatment. APC Scan extends TESS to enable anomalous pattern detection in observation data by incorporating multiple treatments and propensity score weighting to account for observable differences between treated and untreated patients. While these techniques can be applied in health and research informatics domains, certain limitations have to be addressed to improve their utility. For example, Bias-Scan is primarily used for the assessment of bias in predictive binary classifiers and although it analyzes binary outcomes, it has not been adopted for use in the assessment of heterogeneous effects of treatments. On the other hand, TESS and APC Scan are primarily designed for scalar outcomes and are currently limited to the discovery of heterogeneous effects of single interventions in randomized controlled trials (i.e., TESS) or multiple interventions with the assumption of temporal independence between the interventions (i.e., APC).
The overarching goal of our research is to extend and generalize the application of anomalous pattern detection techniques from subset scanning literature to enable the efficient discovery of anomalous patterns in large-scale observational health data such as electronic health records. The objectives of this study were threefold. First, we proposed an approach for selecting the least biased propensity score (PS) model among multiple PS models to overcome treatment selection bias in observational studies. Second, we developed algorithms combining causal inference and anomalous pattern detection techniques to discover the heterogeneous effects of interventions on binary outcomes. Third, we demonstrated the application of the developed techniques to discover anomalous patterns associated with the impact of diabetes medications on 30-day hospital readmission in diabetes care.
Methods
Propensity score based bias smoothing
Causal inference and anomalous pattern detection on observational studies require smoothing of the treatment assignment bias that accounts for observable differences (bias) between treated and untreated groups. Propensity score models, which are often used for such tasks, model the probability of receiving a treatment (ps) conditioned on observed baseline covariates, i.e., ps(X) = p(Z = 1|X), where X is a set of covariates for a given sample, and Z is a particular treatment assigned.
Once the propensity score for each sample in a study is computed, several propensity-based smoothing techniques could be applied6. These include the following: (a) Inverse Propensity of Treatment Weighting (IPTW) that uses weights based on propensity scores to generate synthetic samples such that the distribution of covariates is independent of the treatment; (b) Propensity Score Matching that matched sets of treated and untreated subjects who share a similar value of the propensity score; (c) Stratification on the Propensity Score that stratifies subjects into mutually exclusive subsets (e.g. quintiles) based on their propensity scores.; and (d) Covariate Adjustment Using the Propensity Score in which the outcome variable is regressed on an indicator variable denoting treatment status and the propensity score.
Among these approaches, we selected IPTW due to its effectiveness compared to the others as it does not require matching or stratification that might result in discarding unmatched samples or suboptimal stratification. IPTW uses weights based on propensity scores to generate synthetic samples such that the distribution of covariates is independent of the treatment. These weights include: Average Treatment Effects (wATE ); Stabilized Average Treatment Effects (wATE_stab) and Average Treatment Effect on the Treated (wATT), which could be computed as follows:
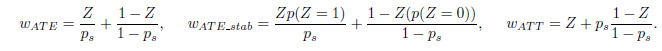
Balance diagnosis and evaluation of positivity violation
Propensity score-based bias smoothing could be achieved using different binary classification algorithms, such as logistic regression and random forest. Thus, it is important to evaluate the balance of the treatment bias achieved by the propensity model. To this end, existing balance diagnosis methods could be grouped into two: graphical and quantitative methods.
Graphical methods provide visualizations to qualitatively evaluate the balance between treated and untreated subsets. Examples of graphical balance diagnosis methods include the Propensity Score Distribution, Covariate Balance Love Plot, Covariate Balance Slope Plot, and Covariate Balance Box Plot as shown in Fig. 1. Propensity score distribution presents the probability density of treated and untreated groups across propensity score. Overlapping between the two density functions suggests balancing where a horizontal deviation of these distributions signals the lack of balancing and hence positivity assumption violations. Covariate Balance Love Plot provides the absolute standard mean difference for each covariate between the treated and untreated group, before and after weighting is applied. A smaller deviation (< 0.1) signals good balancing. The Covariate Balance Slope Plot is another visualization of the absolute mean differences and an alternative to the Covariate Balance Love Plot. Finally, the Covariate Balance Box Plot shows the mean propensity score for the treated and untreated groups, where good balance is depicted from similar mean propensity scores of the two groups.
Figure 1:
Examples of graphical methods to assess the balance of observed covariates in treated and comparison groups using propensity scores and inverse probability of treatment weighting.
Quantitative methods provide quantifiable values regarding the balancing by the propensity score-based weights, which could then also help to evaluate positivity assumption violations7. Examples of quantitative methods include the standardised difference (sd)7, the Kolmogorov-Smirnov test statistic (ks)8, and overlapping index (oi)9. Given a covariate profile, x, which becomes xt for treated group and xc for the comparison group, these quantitative values could be obtained as follows:
where 
and 
represent mean of treated (xt) and comparison (xc) groups, respectively; sxt and sxc represent the standard deviation of xt and xc, respectively. Similarly, pstx and pscx represent the propensity score for xt and xc, respectively.
Unified Performance Index
The quantitative approaches used to diagnose both the imbalance of the treated and comparison groups as well as positivity assumption violations are often used separately, yet it is important to have a unified evaluation framework that takes into consideration the different quantitative evaluation techniques. To this end, we introduced the Unified Performance Index (UPI) that takes into account the overlapping index, mean stabilized ATE weights, KS statistic, and mean of the weighted standardized mean difference. Better balancing and lesser positivity assumption violation diagnosis correspond to a higher UPI score. The UPI maximizes the overlapping index oi, minimizes the absolute mean standardized differences for covariates sd, minimizes the KS test statistic ks and minimizes the deviation of mean stabilized ATE weights wATE_stab from unit value. Thus, UPI is formulated to reflect these proportionality characteristics as follows:
Here, oi has a domain of [0, 1] such that oi = 0 indicates that the propensity score distributions among the treated and untreated groups are completely separated. Conversely oi = 1 indicates that the two distributions the same. The sd has a domain of [0, 1] such that sd = 0 implies that there is no difference in the mean or prevalence of variables between the treated and untreated groups. ks also has a domain of [0, 1] such that ks = 0 if the cumulative distributions of propensity scores among the treated and untreated groups are identical, and ks = 1 if the distributions are completely distinct. Lastly, wATE_stab has a domain of [−∞, +∞] such that mean stabilized weights that are further from one are indicative of higher degrees of the violation of the positivity assumption.
Subset scanning for anomalous pattern detection
In subset scanning literature, the pattern detection problem can be framed as a search over all subsets in a multidimensional array that spans any combination of feature values to identify the most anomalous subset, i.e. the subset with the most evidence of divergence from expected behavior. Scanning is achieved by maximizing a scoring function, F (S), over all subsets to identify the highest-scoring subset, S∗ = arg maxSF (S). This approach can, therefore, be used to reveal hidden anomalous subsets that may not be obvious when inspecting individual features manually. The scoring functions exploit a mathematical property, the Linear Time Subset Scanning (LTSS) property2, which proves that the values of a given discrete/discretized feature can be ordered optimally using a priority function such that scanning is done without requiring an exhaustive search and is guaranteed to be completed in linear time (O(n)) rather than in exponential time (O(2n)).
As previously highlighted, several subset scanning techniques have been developed. In this study, we specifically extend the Bias-Scan methodology. The goal of Bias-Scan is to discover the subpopulation with the most divergence between the true outcomes and the predicted probabilities of a binary classifier4. Given tabular data with discrete/discretized covariates, a binary outcome, yi, and predictions generated by a binary classifier, 
, Bias-Scan maximizes a Bernoulli likelihood ratio scoring statistic, scorebias(S), that quantifies bias in a given subgroup. The algorithm identifies the subgroup that has the most evidence of having the expected odds differing from the predicted odds. Here, the null hypothesis is that prediction odds are correct across all subgroups, 
; while the alternative hypothesis assumes a constant multiplicative increase in the prediction odds for some given subgroup, 
. The scoring function in Bias-Scan is:
Consequently, subsets in which records have larger numbers of yi = 1 but smaller corresponding pi will have higher scores. To detect the anomalous subgroups, Bias-Scan uses the Multi-Dimensional Subset Scanning (MDSS) algorithm10. Given a multi-dimensional array of discrete/discretized features, MDSS optimizes Bias-Scan’s likelihood ratio statistic over all subsets of values of each feature conditioned on the current subset of all other features in the multi-dimensional array. To do so efficiently and exactly, MDSS satisfies the LTSS property2 with a priority function computed as the ratio of the observed odds and the expected odds. This priority function3 ranks the values of a given feature and then select the highest-scoring subset as the subset consisting of the “top-k” priority values for some k ∈ [1, . . . , J ]. MDSS iterates over all features in the multidimensional array until convergence to a local maximum is found. The global maximum is subsequently optimized using multiple random restarts.
Anomalous subgroup detection for binary outcomes
Our study combines propensity score techniques with the Bias-Scan to discover anomalous patterns associated with medication classes used in diabetes care. Here, we specifically proposed three algorithms: Conditional Automated Stratification Scan (CASS), Matched Conditional Automated Stratification Scan (mCASS), and Weighted Conditional Automated Stratification Scan (wCASS). These algorithms analyze tabular data with discrete/discretized covariate profiles X, a single binary treatment Z ∈ {0, 1}, and a single binary outcome Y ∈ {0, 1}. The key steps in the algorithms are described in Table 1 and discussed in detail below.
Table 1:
Algorithms for anomalous subgroup detection for binary outcomes
| Conditional Automated Stratification Scan (CASS) | Matched Conditional Automated Stratification Scan (mCASS) | Weighted Conditional Automated Stratification Scan (wCASS) |
|---|---|---|
| ||
| ||
|
) using Data|Z=1
, as the average outcome among the identified nearest neighbors1 Conditional Automated Stratification Scan (CASS)
The CASS algorithm represents our simplest extension of the Bias-Scan methodology to enable the estimation of heterogeneous effects of interventions on a binary outcome. In CASS, the anomalousness of any given subpopulation S of treated subjects is quantified as E[Yi(1) = 1|Xi ∈ S] > E[Yi(0) = 1] for under-risked subpopulations (i.e. lower than expected outcomes), and E[Yi(1) = 1|Xi ∈ S] > E[Yi(0) = 1] for over-risked subpopulations (i.e. higher than expected outcomes). Here, Yi(1) denotes the occurrence the an outcome for a treated subject, 
is the probability of the outcome in the subpopulation S, and 
is the marginal probability of occurrence of the outcome among the comparison group subjects. Therefore, CASS assumes that the counterfactual outcome for each treated subject is E[Y (0) = 1] and that the average unit-level causal effect of the treatment for each treated subject is Y (1)i − E[Y (0) = 1]. CASS then searches for a specific most anomalous subpopulation S∗ as the subpopulation in which the probability of the outcome conditioned on belonging to this subpopulation has the most evidence of being divergent from the marginal probability of the outcome among all the comparison group subjects. Procedurally, the key steps in CASS are described in Table 1.
2 Matched Conditional Automated Stratification Scan (mCASS)
The mCASS algorithm combines propensity score matching with Bias-Scan to discover heterogeneous treatment effects across subpopulations. In mCASS, the counterfactual outcome for each treated subject is determined by propensity score matching between pairs of treated and comparison group subjects who have similar propensity scores. Consequently, in mCASS, the average treatment effect is estimated as the average of the differences between the actual versus counterfactual outcome within each pair. While several propensity score matching techniques can be used in mCASS, we specifically use the nearest neighbor caliper matching6. In this approach, matching is done on the logit of the propensity scores using calipers of width 0.2 standard deviation of the logit of the propensity score as a threshold for matching6. The key steps in mCASS are described in Table 1.
3 Weighted Conditional Automated Stratification Scan (wCASS)
The wCASS algorithm uses the IPTW derived from propensity scores. Specifically we use the previously described average treatment effect on the treated (ATT) weights, wATT. When using wCASS, the anomalousness of a subpopulation S is quantified as E[wiYi(1)|Xi ∈ S] < E[wiYi(0)] for under-risked subpopulations and as E[Yi(1)|Xi ∈
S] > E[Yi(0)] for over-risked subpopulations. Here, wiYi(1) denotes the weighted outcome for a treated subject, 
is the weighted probability of the outcome in the subpopulation S, and 
is the weighted marginal probability of occurrence of the outcome among the comparison group subjects. Procedurally, wCASS works as described in Table 1.
Randomization Testing
All the 3 algorithms, CASS, mCASS, and wCASS use randomization testing to estimate the statistical significance of the detected anomalous subgroups. To do so, we draw 1000 bootstrapped random subpopulations and compute the subset score for each subpopulation drawn, and then compare each score to the score for the detected anomalous subpopulation. We compute the empirical p-value as 
where r is the number of scores greater than or equal to that actual score and n is the total randomization scores for bootstrapped samples.
Experiment and Results
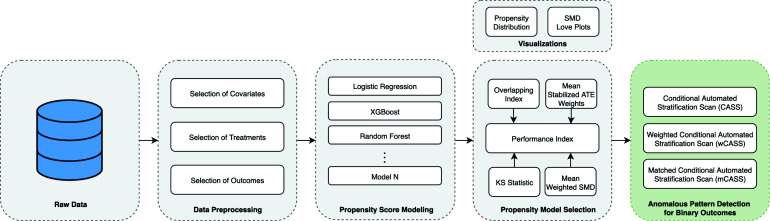
To validate the algorithms we developed, we used a case study whose goal was to detect the anomalous patterns associated with the impact of medications on 30-day hospital readmission in diabetes. Figure 2 illustrates the pipeline used in the study.
Figure 2:
Pipeline for anomalous pattern detection associated with binary Outcomes in healthcare
The Diabetes Cohort and Dataset
We used a de-identified diabetes dataset extracted from the Health Facts database (Cerner Corporation, Kansas City, MO). The study population consisted of 69,990 patients with inclusion criteria defined as follows: (1) having an initial inpatient encounter (a hospitalization), (2) having a diagnosis of diabetes made at the initial encounter, (3) the length of stay at least 1 day and at most 14 days, (4) laboratory tests were performed during the encounter, and (5) medications were administered during the encounter11. The data preprocessing is described in more detail by Strack et al.11 who also made it publicly available as supplementary material accessible at http://dx.doi.org/10. 1155/2014/781670. We conducted additional preprocessing to generate a final dataset that consisted of a binary outcome (Readmission within 30 days), 10 discrete/discretized covariates (race, gender, age group, admission type, discharge disposition, admission source, primary diagnosis, secondary diagnosis, tertiary diagnosis, and HbA1C), and 4 intervention drug classes (Biguanides, Insulin, Sulfonylureas, and Thiazolidinediones). These preprocessing steps included dropping features with a large proportion of missing values, remapping categorical features e.g., age groups and race, mapping specific ICD9-CM codes to more general ICD9-CM codes, mapping treatment interventions to binary pharmacological classes, and mapping the readmission outcome to a binary variable. Table 2 describes the features and the distribution of the feature values in the final dataset.
Table 2:
Distribution of feature values in the final dataset
|
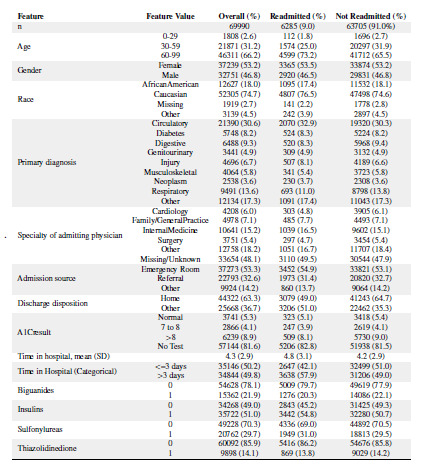
Propensity Score Modeling
For each of the 4 treatment classes (biguanides, insulins, sulfonylureas, and thiazolidinediones) in the final dataset, we trained 3 propensity score models for predicting the likelihood of a patient subject receiving the treatment given his/her covariate profile. The predictor variables in each model consisted of race, gender, age, discharge disposition, admission source, time in hospital (continuous), primary diagnosis, hbA1C result, and the medical specialty of the admitting physician. Each response variable was a binary treatment class. These variables are described in Table 2. The trained propensity score models included a logistic regression model, a gradient boosting decision tree model (XGBoost), and a random forest model. Table 3 describes the modeling performance results. We note that, based on the UPI score, XGBoost consistently performed well across the treatment classes considered. Logistic regression also performs relatively well, while the random forest model performed worst across all the treatments despite having relatively better Area Under Curve results for training and test sets. The overlapping indexes for the propensity scores generated from the random forest model were lower than those of the other two models. These findings confirm a known observation that the best propensity score models are not necessarily those that are good at prediction, but those that provide better overlapping between the propensity scores of the treated versus untreated subjects.
Table 3:
Propensity Score Modeling Performance Results
|
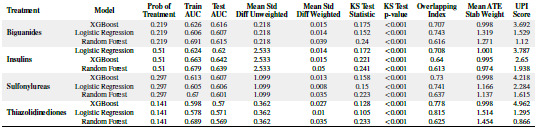
Characteristics of the most anomalous subpopulations discovered
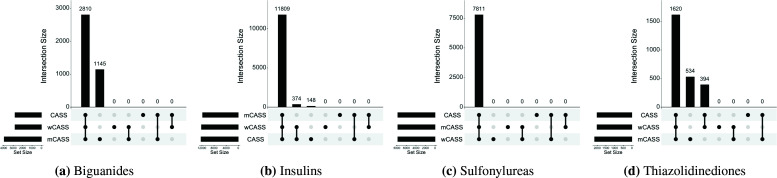
Table 4 shows the anomalous pattern detection results for the different treatments analyzed and algorithms used. Each algorithm was able to identify heterogeneous treatment effects by discovering the most anomalous subgroup conditioned on patients receiving a given treatment. This heterogeneity is described in terms of risk difference, relative risk, and odds ratio in the overall population of treated subjects versus the most anomalous subpopulation identified. We observe that for each treatment, the discovered anomalous subpopulations are relatively similar in sizes across the CASS, mCASS, and wCASS algorithms. We also observe that for each treatment, the algorithms resulted in similar measures of effect across the identified anomalous subpopulations. This observation could be explained by the high degrees of overlaps in the subpopulations identified by the different algorithms as illustrated in Figure 1.
Table 4:
Anomalous Pattern Detection Results
|
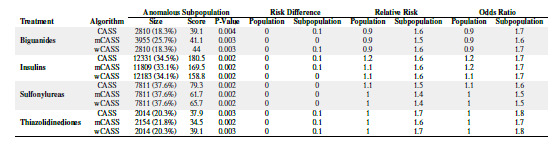
Interestingly, the subgroups with the largest measures of effect pertained to the use of thiazolidinediones, suggesting a stronger heterogeneous treatment effect of this class of drugs on 30-day hospital readmission. By way of example, the subsets discovered by CASS and wCASS for thiazolidinediones were identical and suggests that patients who use thiazolidinediones and are aged 60 years or older; and are Caucasian or African American or have their race information missing; and have a primary diagnosis that is not musculoskeletal; and were admitted by specialists who are not cardiologists; and had HbA1C >8 or had no HbA1C test conducted at the time of admission; and were discharged to destinations other than their homes, were 1.8 times more likely to be readmitted within 30 days than the average non-treated population. This subpopulation had a 30-day readmission rate that differed the most from the expected 30-day readmission rate determined as the global mean among untreated subjects.
Discussion
This study aimed at developing and demonstrating the application of techniques for assessing the causal heterogeneous effects of binary interventions on binary outcomes in observational health data such as electronic health records. To this end, the study proposed a unified performance index (UPI) for choosing the best propensity score model among multiple propensity score models and describes how algorithms from the causal inference and anomalous pattern detection literature could be leveraged to discover anomalous patterns of care. Furthermore, the demonstrates how the developed algorithms can be used to detect the heterogeneous treatment effects captured in electronic health records.
We discovered highly similar subpopulations among which the use of anti-diabetic medication classes (biguanides, insulins, sulfonylureas, and thiazolidinediones) was associated with an increased likelihood of being readmitted within 30 days after the index inpatient admission. Interestingly, thiazolidinedione therapy has previously been associated with a higher risk of hospital readmissions on average12–14. The findings from our study suggest that certain subpopulations may be differentially affected by this class of drugs as well as other commonly used classes of anti-diabetic medication. However, we take cognizance of the fact that our approach should be viewed as a method for generating hypotheses about the specific subpopulations that are most likely to be impacted by the interventions. How such heterogeneity occurs or is realized is beyond the scope of the current approach and further investigations are warranted to confirm the generated hypotheses.
Current literature has primarily focused on studying the average treatment effect of interventions on binary outcomes6, or on studying heterogeneous treatment effects of single interventions in clinical trials3. These approaches are, however, done separately. To the best of our knowledge, our study is the first to leverage and extend both causal inference and subset scanning techniques to study the effect of interventions on binary health outcomes. The techniques we have developed can provide researchers, care providers, and other stakeholders with the ability to identify positive or adverse clinical practices and subsequently institute better care delivery plans based on the identified insights. They can also be used as a basis for risk analysis and recommendation of follow-up interventions to improve care experiences and outcomes for individual patients, especially in differential service delivery and targeted intervention planning settings. Furthermore, they can enable payers to identify drivers of poor outcomes and unnecessary costs across patient subpopulations.
Whereas we took the necessary steps to ensure robustness in our study, several limitations can be observed. First, as would be expected, feature selection and engineering can affect propensity scoring modeling and the anomalous pattern detection, subsequently bias findings. We minimized this by testing our approach on a diabetes dataset validated by Strack et al.11 while maintaining the features and feature values used in the aforementioned study. Second, the UPI score is currently unbounded and ranges from zero to infinity with higher scores implying better performance. However, a monotonic function that maps the UPI score to [0,1] can be applied without loss of generality. As part of our future work, we intend to refine, test, and compare different formulations of the UPI across different propensity score models trained on several publicly available datasets. Third, the subset scanning approach applied in this study can be misconstrued as conducting multiple hypotheses testings. However, we consider this and use parametric bootstrapped randomization tests to determine the statistical validity of anomalous subpopulations discovered by our algorithms. Fourth, the results of the subset scanning process can be complex and difficult to interpret even for persons with domain expertise. As part of our future work, we intend to incorporate into our pipeline a penalized version of Bias-Scan that uses a penalty function to minimizes the complexity and maximize the size of the identified subpopulations15. Lastly, our current approach can only analyze binary interventions and binary outcomes. We, however, acknowledge that there are different healthcare outcomes that can be binary (e.g. mortality), discrete (e.g. number of days spent in hospitals), continuous (e.g. blood glucose levels). At the same time, the intervention space in healthcare is often complex and can range from single interventions given only once (e.g. single dose medications or vaccinations), to multiple interventions used simultaneously (e.g. drug combinations in regimens), to sequential interventions (e.g. temporally dependent drug regimens, clinical pathways). As part of our future work, we plan to develop techniques for discovering anomalous patterns associated with these different types of interventions and outcomes in healthcare data. Additionally, we intend to compare our approach to state-of-the-art subgroup analysis techniques and to generate meaningful clinical insights, perspectives, and interpretations of the discovered anomalous subpopulation through counterfactual analyses of modifiable risk factors that could serve as a baseline for targeted intervention planning.
Conclusion
We studied 30-day readmission in diabetes using methods that combine techniques from causal inference and anomalous pattern detection literature to study the heterogeneous effects of treatments. This study shows that a unified performance index can be used to select the best propensity score models among multiple models. It also shows that techniques such as propensity score matching and inverse probability of treatment weighting could be leveraged to study the impact of binary treatment on binary outcomes at the subpopulation-level and in a disciplined statistical approach. Furthermore, the study shows that for a given treatment, the studied algorithms result in the identification of subpopulations that are highly similar in terms of common covariate characteristics. Lastly, the study demonstrates that for certain subpopulations, the likelihood of 30-day hospital readmission among index diabetes encounter may be differentially impacted by the use of some anti-diabetic medication classes and that these differential effects may not be discernible at the overall populations. Future work includes delineating the merits and demerits of our algorithms, penalizing complexity while maximizing subset sizes for easier interpretability, and generalizing the approaches for application across disparate intervention and outcome data types.
Figure 3:
Overlaps between anomalous subpopulations identified by CASS, mCASS, and wCASS
References
- [1].Rubin Daniel J. Correction to: hospital readmission of patients with diabetes. Current diabetes reports. 2018;18(4):21. doi: 10.1007/s11892-018-0989-1. [DOI] [PubMed] [Google Scholar]
- [2].Neill Daniel B. Fast subset scan for spatial pattern detection. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2012;74(2):337–360. [Google Scholar]
- [3].McFowland Edward, III, Somanchi Sriram, Neill Daniel B. Efficient discovery of heterogeneous treatment effects in randomized experiments via anomalous pattern detection. arXiv preprint arXiv:1803.09159. 2018 [Google Scholar]
- [4].Zhang Zhe, Neill Daniel B. Identifying significant predictive bias in classifiers. arXiv preprint arXiv:1611.08292. 2016 [Google Scholar]
- [5].Somanchi Edward, McFowland Sriram, III, Neill Daniel B. Detecting anomalous patterns of care using health insurance claims. Presented at Conference on Information Systems and Technology. 2017 [Google Scholar]
- [6].Austin Peter C, Stuart Elizabeth A. Estimating the effect of treatment on binary outcomes using full matching on the propensity score. Statistical methods in medical research. 2017;26(6):2505–2525. doi: 10.1177/0962280215601134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Austin Peter C, Stuart Elizabeth A. Moving towards best practice when using inverse probability of treatment weighting (iptw) using the propensity score to estimate causal treatment effects in observational studies. Statistics in medicine. 2015;34(28):3661–3679. doi: 10.1002/sim.6607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Sekhon Jasjeet S. Alternative balance metrics for bias reduction in matching methods for causal inference. Survey Research Center, University of California, Berkeley. 2007 [Google Scholar]
- [9].Pastore Massimiliano, Calcagn`ı Antonio. Measuring distribution similarities between samples: A distribution-free overlapping index. Frontiers in psychology. 2019;10:1089. doi: 10.3389/fpsyg.2019.01089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Neill Daniel B, McFowland Edward, III, Zheng Huanian. Fast subset scan for multivariate event detection. Statistics in medicine. 2013;32(13):2185–2208. doi: 10.1002/sim.5675. [DOI] [PubMed] [Google Scholar]
- [11].Strack Beata, DeShazo Jonathan P, Gennings Chris, Olmo Juan L, Ventura Sebastian, Cios Krzysztof J, Clore John N. Impact of hba1c measurement on hospital readmission rates: analysis of 70,000 clinical database patient records. BioMed research international. 2014;2014 doi: 10.1155/2014/781670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Masoudi Frederick A, Inzucchi Silvio E, Wang Yongfei, Havranek Edward P, Foody JoAnne M, Krumholz Harlan M. Thiazolidinediones, metformin, and outcomes in older patients with diabetes and heart failure: an observational study. Circulation. 2005;111(5):583–590. doi: 10.1161/01.CIR.0000154542.13412.B1. [DOI] [PubMed] [Google Scholar]
- [13].Hsiao Fei-Yuan, Tsai Yi-Wen, Wen Yu-Wen, Chen Pei-Fen, Chou Hao-Yu, Chen Chen-Huan, Kuo Ken N, Huang Weng-Foung. Relationship between cumulative dose of thiazolidinediones and clinical outcomes in type 2 diabetic patients with history of heart failure: a population-based cohort study in taiwan. Pharmacoepidemiology and drug safety. 2010;19(8):786–791. doi: 10.1002/pds.1999. [DOI] [PubMed] [Google Scholar]
- [14].Inzucchi Silvio E, Masoudi Frederick A, Wang Yongfei, Kosiborod Mikhail, Foody Joanne M, Setaro John F, Havranek Edward P, Krumholz Harlan M. Insulin-sensitizing antihyperglycemic drugs and mortality after acute myocardial infarction: insights from the national heart care project. Diabetes Care. 2005;28(7):1680–1689. doi: 10.2337/diacare.28.7.1680. [DOI] [PubMed] [Google Scholar]
- [15].Speakman Skyler, Somanchi Sriram, McFowland Edward, III, Neill Daniel B. Penalized fast subset scanning. Journal of Computational and Graphical Statistics. 2016;25(2):382–404. [Google Scholar]