Developing High Performance Secure Multi-Party Computation Protocols in Healthcare: A Case Study of Patient Risk Stratification

Abstract

We demonstrate that secure multi-party computation (MPC) using garbled circuits is viable technology for solving clinical use cases that require cross-institution data exchange and collaboration. We describe two MPC protocols, based on Yao's garbled circuits and tested using large and realistically synthesized datasets. Linking records using private set intersection (PSI), we compute two metrics often used in patient risk stratification: high utilizer identification (PSI-HU) and comorbidity index calculation (PSI-CI). Cuckoo hashing enables our protocols to achieve extremely fast run times, with answers to clinically meaningful questions produced in minutes instead of hours. Also, our protocols are provably secure against any computationally bounded adversary in a semi-honest setting, the de-facto mode for cross-institution data analytics. Finally, these protocols eliminate the need for an implicitly trusted third-party "honest broker" to mediate the information linkage and exchange.

Introduction

Patient risk stratification is an important task in population health management. The idea is to assign patients in a population to segments based on how much care they are expected to require. With these strata in mind, a health system can allocate resources appropriately to reduce overall cost while improving overall quality of care. Indeed, a recent study¹ found that 5% of the Medicare patients incur nearly half of the program's entire budget. Risk stratification promises not only to reduce this disproportionately high cost, but also to provide more effective and customized care for the patients who need it most.

Given its potential benefits, it is not surprising that risk stratification (or simply identifying high-risk patients) is an active area of research². Two features from clinical records are often leveraged for this classification task^3,4,5: comorbidity (the presence of multiple chronic diseases) and past high utilization of healthcare resources (especially expensive emergency department (ED) visits and inpatient hospital stays). Applying these features is complicated when a patient is being seen by multiple healthcare providers who have independent patient data repositories, which lead to siloed perceptions of comorbid conditions and resource utilization.

Such data fragmentation could potentially create significant challenges in quantitative assessment. For example, Brannon et al.³ complain that an individual healthcare institution is unlikely to identify high utilizers accurately because the ED visits for such patients may be registered at multiple providers and obtaining all ED visits may be impossible due to the difficulty in information exchange among different healthcare providers and matters of patient privacy. Such concerns have been confirmed via a city-wide project carried out in Houston⁶, where evidence have shown that high utilizers are indeed visiting multiple healthcare institutions to seek emergency care.

Similarly, complete and accurate data collection is essential to carry out analyses about comorbidity. Several studies^7,8,9 indicate a given hospital's electronic health record (EHR) is unlikely to include all pre-admission comorbidities, since some comorbidities reside within other hospitals' EHR systems. Mitigating such a situation requires cross-institution linkage to capture a complete picture of comorbidities. One study¹⁰ conducted in Italy has attempted to validate a novel comorbidity score using a multisource approach, leveraging cross-hospital linkages enabled by a national beneficiary identifier. More often, however, cross-institution linkage may be challenging for a variety of reasons. For example, Quan et al.¹¹ report underestimation of comorbidity due to the unavailability of reliable unique identifiers. Lichtensztajn¹² comments on additional burdens in multi-site comorbidity studies, including legal, resource, and procedural barriers to cross-institution record linkage.

At present, the most common method is performing privacy preserving record linkage (PPRL) via a trusted honest broker¹³. Such a method has been used to assemble a city-wide data set from six different institutions to identify high utilizers in Chicago⁴, where linkages are established via matching hash tokens. However, such centralized data aggregation has drawbacks. It requires the participation of a trusted third party and the transmittal of data by all participating institutions to a central data store. This is inherently time consuming and demands considerable resources, along with a complicated multi-institution policy arrangement. Moreover, its centralized approach has security implications¹⁴.

To address these shortcomings, we propose using secure multi-party computation (MPC) approach. Long viewed as a purely theoretical topic and impractical to apply in practice, MPC has recently emerged as a viable alternative thanks to advances in cryptography. Here we apply Yao's protocol¹⁵, based on garbled circuits and oblivious transfer, which we accelerate using state-of-the-art Cuckoo hashing technique to optimize performance. Due to the complicated computation such as comorbidity index involving both logical and arithmetic operations, circuit-based MPC is much more efficient than fully homomorphic encryption schemes¹⁶. Here, we demonstrate our approach can reach extraordinary speed when studying patient risk stratification in a cross-institution setting. Some prior works^17,18 focused on cross-institution cohort characterization using circuit-based MPC only addressed the fundamental task of secure patient matching – which is a generic application of private set intersection (PSI), devoid of any context for clinical implications and applications.

Other investigators pursuing techniques for privacy-preserving data analytics for healthcare have experimented with deploying MPC in a few healthcare applications. Shi et al¹⁹ demonstrated the viability of performing logistic regression using garbled circuits for EHR data. Several cases also achieve privacy-preserving genomics comparison for similar patient query or disease diagnoses²⁰. In addition, cryptographers and privacy experts come together at the annual iDASH Workshop to showcase the latest findings in privacy-preserving analytics – including MPC. These approaches are domain specific, and they only run efficiently in their initial context. On the other hand, they do not readily generalize to additional use cases. Researchers are also identifying tools and techniques to support SQL queries over MPC applied to clinical data research network^21,22. These systems support a broader class of workloads, although their generality may leave room for significant reduction in query runtime. Our investigation here attempts to achieve both generalizability and high performance at the same time by implementing two building blocks each can be optimized with great efficiency and flexibility to address common use cases in clinical data research. The first building block is a component that performs secure patient matching, and the second is an analytics component that securely computes functions specific to the analytics task at hand, for example calculating comorbidity index.

Background

In this section, we review high utilizers and comorbidity index – two metrics that are essential in patient risk stratification, and we also introduce the key technical components used in our method.

High utilizers refer to a group of patients who disproportionately consume healthcare resources. In general, providers categorize high utilizers in high-risk strata both because of their own health conditions but also the high expenses they typically incur. Although there has no formally agreed-upon definition, we adopt a commonly used criterion that high utilizers have ever visited an ED four or more times within a year^3,4. Because not including ED visits from other healthcare organizations could potentially render true high utilizers undetected, jointly screening high utilizers across institutions will produce more accurate risk stratification.

Comorbidity refers to the presence of multiple chronic diseases within a single patient. Assessing comorbidity has significant implications for mortality, healthcare utilization, and patient outcomes. The most prevalent comorbidity measurement is the Charlson comorbidity index²³. In this measurement, several chronic conditions are assigned scores ranging from 1 to 6 according to disease severity. The scores are then aggregated into a single value to measure overall comorbidity. The most common approach leverages algorithms based on ICD (International Classification of Disease) codes^24,25 from the hospital administrative databases. The corresponding scores for each disease are aggregated into a final index value, which is used to represent the patient's overall health status. During patient risk stratification, patients with higher comorbidity index score are put into higher risk strata. Because missing comorbid conditions inevitably lower the overall score, computing comorbidity index across institutions promises more accurate risk stratification.

Secure multi-party computation (MPC) is a cryptographic technique that allows multiple parties to compute a function jointly without revealing anything beyond the output. First introduced by Andrew Yao¹⁵ within the context of Millionaires' Problem, MPC was later generalized by Goldreich, Micali and Wigderson to the multi-party setting²⁶. To use an MPC protocol, we need to first represent the function to compute as a Boolean circuit or arithmetic circuit²⁷. Until recently, MPC was not considered practical due to the heavy computation and the large amount of communication required to evaluate even modest functions (simple circuits). In the past decade, the exploitation of hardware acceleration and a series of algorithmic optimizations including free-XOR, half-gates, and OT-extension have improved the efficiency of the garble circuits by several orders of magnitude^28,29,30. Various specific applications of MPC have been considered practical to use in the real world. In the area of privacy-preserving machine learning³¹, MPC has been used between multiple parties who want to train a model based on their combined dataset without exposing any party's data. Also, MPC can achieve the distribution of highly secret information, such as the private key for digital signature³².

Private set intersection (PSI) is an important application of secure multi-party computation. It allows two parties to compute the intersection of their sets without revealing any elements that are not in the intersection or indeed without exposing any information beyond the intersection. PSI has found a number of practical applications. For example, an instant message (IM) service provider can use PSI to explore a clients' personal network without being able to learn any of the clients' cell phone contacts. Banks can take advantage of PSI to detect malicious mortgage fraud without sharing their clients' data. In healthcare, the most common PSI application is to identify the common patients from different healthcare provider's databases. There exist different PSI protocols that are realized by various techniques, including naïve hash-based PSI, public-key-based PSI, circuit-based PSI and OT-based PSI. Current state-of-the-art PSI protocols are based on Oblivious PRF (OPRF)³³ and Cuckoo hashing³⁴.

Cuckoo hashing³⁵ is a hash scheme that avoids hash collision of input values in a hash table. The initialization phase requires the preparation of n hash functions h₁, h₂, … , h_n and m empty bins B[1, … ,m]. To insert an input x into the hash table, first hash x using all hash functions. Then check if any bin of B[h₁(x)], … , B[h_n(x)] is empty. If so, insert the item x into that bin, otherwise evict one of the occupying items x' in any bin listed above and insert x instead. Then re-enter x' the same way as x. Recursively try to insert and evict items based on the hash values until finally all items are accessible through one of the hash tables or an infinite loop is detected.

Method

Our protocol is a combination of Yao's garbled circuits and state-of-the-art PSI protocols. Although the problem to solve in our setting is similar to PSI, there are significant differences. In PSI, we only need to find the common elements. For our task, we need first to find the common elements (i.e., patients visit both healthcare institutions) as in PSI, but we then must compute a function defined for the specific clinical use case we are trying to address (i.e., Unifying data from different institutions for their common patients to identify those who have high Charlson index scores or have visited an ED for at least 4 times within a year). Our protocol consists of following steps:

Algorithm 1. Cross-institution patient risk stratification MPC protocol.

Algorithm 1 above outlines the protocol to perform the task of patient risk stratification in a cross-institution setting. The inputs include two private datasets from two institutions A and B. The dataset has two parts, the first part is patient data which is used by PSI to link patients; the second part is a payload from the institution's EHR tailored to serve as input to the specific use case's function. (In the two use cases discussed here, these two functions' outputs could be used to perform enhanced risk stratification across two institutions). Two protocol components, High Utilizer (HU) and Charlson Index (CI), introduced below, are used to identify high utilizers or to compute the Charlson comorbidity index. The inputs also include three public hash functions h₁, h₂, h₃ that both institutions have agreed upon in advance.

Prior to executing PSI protocol to link common patients, A and B prepare their inputs using three public hash functions. Assuming A initiates the MPC request, and B responds to the request, A uses Cuckoo hashing to obtain table T, and B uses ordinary bin-and-ball hashing to obtain table T’. Assuming A's patient data set has p patients, the size of T and T’ are both set to m (m = 1.5p). Such choices of 1.5p and three hash functions³⁶ are made to ensure the Cuckoo hashing schema only has a failure rate of about 1/2⁴⁰ to enter an infinite loop. Using h₁, h₂, h₃, Institution A hashes all its patient records to a Cuckoo hash table T of size m. Here, Cuckoo hashing guarantees each location will have at most one item, and since m = 1.5p, one third of T will be empty. Institution B, using the same set of hash functions, hashes all its patient records and obtain a set of bins T₁',..., T_m’. The PSI protocol checks if the patient in T matches any patients at the same location in T’, which is carried out inside garbled circuits by performing bit-wise comparison between the items in T and T’.

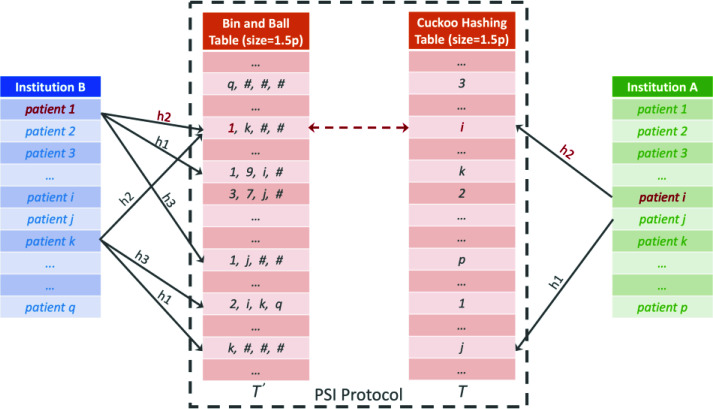
Figure 1 illustrates PSI process using a concrete example. Assuming the i^th patient from institution A and first patient from institution B (patient 1 highlighted in red) are indeed the same person, i.e., this patient visits providers at both institutions. A uses the Cuckoo hashing to obtain a table T, and B uses bin-and-ball hashing to obtain table T’ of the same size. Notice in this example, the i^th patient's position in the Cuckoo hash table is obtained using the second hash function h₂. This indicates the i^th patient from institution A was evicted once from the position generated by h₁, whereas the j^th patient from A has not been evicted since first being hashed by h₁. The same patient's record also exists at institution B (as patient 1), and, because all three hashes are used, one of the items from the bin at the same bin location (also generated by h₂) is guaranteed to match the corresponding entry in A's Cuckoo hash table, as indicated by the red arrow.

Figure 1.

Cuckoo hashing-based PSI protocol.

One caveat here is B's bin sizes may leak private information to A. For instance, an empty bin for B may reveal to A its own patient in the same table location never visit any providers from institution B. To mitigate this risk, all the bins are padded to have the maximum size of B's bins. In the above figure, this is illustrated using "#" to pad each bin to have maximum size of four, assuming the largest bins has four patients mapped in it. This ensures our protocol reveals nothing about either institution's patient records other than which patients match.

The use-case protocol components CI and HU are customized to evaluate specific functions. In CI, additional use-case payload is included to record the comorbid conditions for each patient. The CI circuit component is designed to calculate the dot product of a weight vector of 17 disease categories and each patient's disease vector jointly obtained from two institutions. The 17 weights of values of 1, 2, 3 or 6 are defined in the Charlson comorbidity index. Using garbled circuits, the disease data payloads for the same patient from two different institutions will be unified together using Boolean union operator. Similarly, using the HU circuit components, the ED visit payloads for the same patient are added together. To keep the size of the payload small, we ignore multiple ED visits to the same provider in the same month. Given this, we scan each (sliding window) 12-month period's combined ED episode to see if the total number of ED visits is ever greater than or equal to four times. If it is, the patient is identified as a high utilizer.

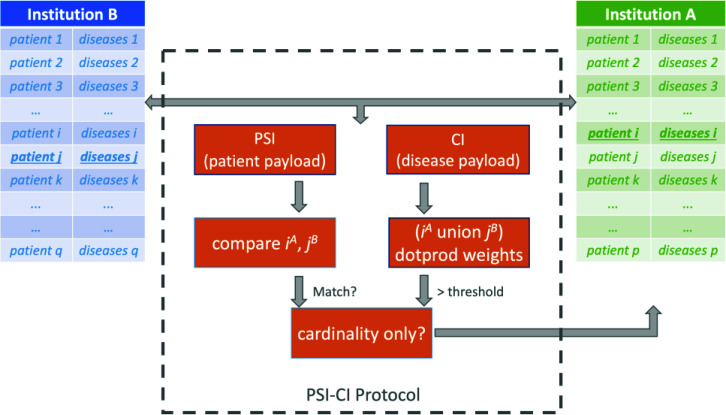
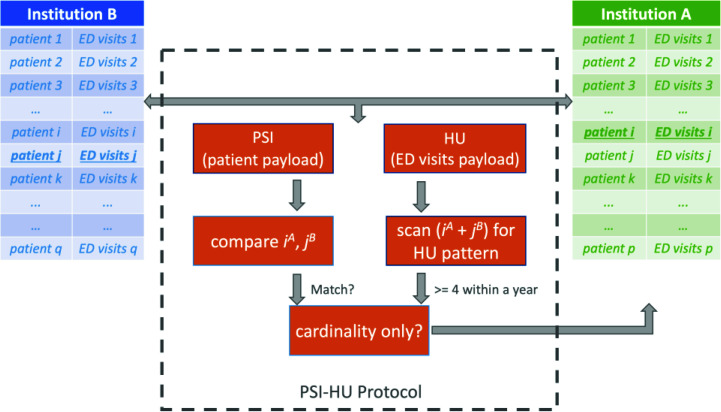
Figures 2 and 3 illustrate our two protocols PSI-CI and PSI-HU, respectively. Note each protocol has a PSI component as well as a data analytics component. The PSI component applies on patient data payload and the analytics component (e.g. CI and HU) applies on the use case specific payload. Figure 2 and 3 illustrate the point in time when the protocol performs computation on the i^th patient from A and j^th patient from B. In addition, each protocol has a regular mode as well as a cardinality-only mode, where only the total number of patients who meet the defined criteria will be the output, instead of a record for each identified patient. By convention, we append a suffix "CA" when this mode is invoked (e.g., PSI-CI-CA and PSI-HU-CA). Using different thresholds, for example a Charlson index score of 9 for high mortality risk and 2 for low mortality risk, the PSI-CI-CA protocol can calculate the size of each risk strata. Similarly, using 6 for super-utilizer, 4 for high-utilizer and 1 for average utilizer, the PSI-HU-CA can characterize the patient risk strata in terms of resource spending. The regular versions of PSI-CI and PSI-HU are used to when the requesting institution needs to identify the individual patients.

Figure 2.

Illustration of Charlson comorbidity index protocol PSI-CI.

Figure 3.

Illustration of high utilizer identification protocol PSI-HU.

In Figures 2 and 3, the protocols only return results to the requesting party A. Under properly arranged data sharing agreements, the outputs can also be shared with the responding party B. In addition, the protocols can be tuned to also output the actual values of Charlson index itself, or the exact total number of ED visits during the 12-month high utilization period. Such patient level results offer finer details in the risk stratification analysis. Furthermore, PSI-CI and PSI-HU could be combined together to derive strata to reflect both disease severity and healthcare resource spending.

Our protocols reveal no additional information about either institution's patient records beyond the mutually agreed-upon outputs. The protocols are secure in the semi-honest setting with static corruption. In a semi-honest setting, we assume the parties involved are curious but not malicious. The parties may try to infer additional information, but they will not intentionally break the protocol or intentionally mislead the computation to produce incorrect results. Semi-honest mode is the de-facto threat model in cross-institution clinical data analytics since full trust cannot be granted to parties outside the covered entities. However, reputational and legal costs should discourage overtly malicious behavior by the parties.

The security of our protocols is promised by the underlying two-party computation protocol, which is the classical Yao's garbled circuits. The protocols return accurate results under these assumptions. To implement the protocol, we use the EMP-toolkit³⁷, which provides a suite of tools for executing two-party and multi-party computation protocols efficiently. This toolkit includes state-of-the-art protocol and implementation optimizations. We use AES-based hash function to compute the Cuckoo hash table for improved efficiency.

We implement our computation in EMP functions, where all operations are overloaded to execute cryptography operations instead of computation in clear. To avoid any side-channel leakage, all computation has to be oblivious, that is, the behavior of the computation cannot depend on the payload data. Usually, this will reduce the efficiency of the computation since we need to incur the worst-case running time regardless of the computation. To alleviate this slowdown, we perform the optimization as follows: for each bin from T and T’, we first perform PSI to see whether there are matching patients, if yes then compute the use case function only once using the matched patients' payloads, otherwise merely compute the same function using the first patient's payloads from each bin. This optimization significantly reduces the number of comparisons while keeping the correctness and security.

Data Preparation.

In order to simulate a real-world multi-institution setting, we use Synthea³⁸ to create a large-scale, realistically synthesized dataset. The Synthea platform deploys publicly available health statistics and clinical practice guidelines to simulate large scale electronic healthcare data, including modeled interactions between patients, providers, payers, etc. over the lifespan of synthetic patients. Synthea applies public census and health data to generate patient population with realistic demographics and leverages expert-curated disease packages to model disease progression throughout the patient's lifetime. The synthetic data produced by Synthea has no privacy or security restrictions.

We use Synthea to generate a Chicago city-wide database consisting of approximately 2.7 million patients and ~141 million encounters. Records of 1.3 million ED visits over three years are processed to test the performance of our protocols. To simulate patients arriving at EDs in different institutions for different visits, we took the longitudes and latitudes for the ED departments from seven large academic hospitals in Chicago. After measuring the distance from those ED departments to the synthesized patients' addresses at ED visits, an ED is chosen randomly from the two closest EDs. The encounter records are then split into seven data sets, each representing the institution's own ED encounter data sets during the 3 year period. Datasets for two institutions that are geologically very close are chosen to test the performance of our protocols. These two datasets contain 120,666 and 109,072 patients respectively. Using these two datasets, we generate patient payloads for both PSI-CI and PSI-HU in order to allow direct performance comparison between them as shown in the next section.

To prepare the patient (PSI) payload, each patient is represented by a 64-bit integer. Although the synthetic data contains an SSN field that is an excellent choice for cross-institution patient matching and it only takes 32-bit to represent, we consider the factor that participating institutions of MPC may want to avoid using SSN directly due to its sensitive nature, even though only AES encrypted bits of SSN leaves the institutional boundary during the protocol execution. Moreover, SSN values are not reliably available in practice. The 64-bit integer is obtained using the first 64 bits of the SHA256 hashes generated from patients' name, SSN, birthday. The combination of such demographics data fields ensures the hash tokens can uniquely identify patients while allowing patient payload to be reasonably lightweight. The chance of a single collision occurs in our data is thus approximately 120,000/2³² = 0.003%, where 1/232 is derived from the birthday paradox.

To construct the use case payload for the PSI-HU protocol, we encode patients' presence at ED each month. This results in a Boolean vector of length 36 for the last three years for each patient. (This renders additional visits to the same institution within the same month invisible. Using additional bits would allow for a more accurate accounting, at the expense of greater memory needs.) For the PSI-CI protocol, we use a Boolean vector of length 17 to encode the presence of each disease. Here we used the 17 comorbid conditions in the modified index²⁴ instead of the 19 conditions in the original index²³. At the time of this writing, Synthea only contains 10 conditions with the highest morbidity in the US, and many conditions required in Charlson index calculations – such as chronic pulmonary disease, rheumatologic disease, peptic ulcer disease – are not currently included as Synthea disease modules. Therefore, instead of using the disease output from the Synthea, we impute the distribution of 17 conditions from published disease percentage statistics¹¹. Further details can be seen at our demo website (see footnote of this page).

Results

Table 1 below shows the main performance results for our protocols. Four main categories - running time, circuit size, network traffic and memory – are evaluated for PSI-CI and PSI-HU. Here we test both the full and cardinality-only versions for each protocol. Using large-scale realistic datasets, the protocols complete in around 3 minutes and 7 minutes, respectively. The memory usages are 2.9 GB for PSI-CI and 3.5 GB for PSI-HU, acceptable on even basic consumer systems. PSI-HU requires slightly more memory since its payload is larger (36 bits versus 17 bits for the use case payload). Network communication depends only on the size of the circuit, which primarily depends on the complexity of the use case specific function. Hence, the high utilizer protocol PSI-HU also requires more network resources than the PSI-CI protocol because the HU circuit function is more complicated. Additional overhead in running time, circuit size, and communication cost are present in the cardinality-only protocols because of the additional counter components required in the circuits.

Table 1. Performance testing results for our secure computation protocols, max padding size is 11.

Protocol	Running Time (Seconds)	Circuit Size (Number of AND Gates)	Network Traffic (GB)	Memory (GB)
PSI-CI	193	163,608,000	5.7	2.9
PSI-CI-CA	203	173,751,634	6.0	2.9
PSI-HU	422	378,098,088	12.7	3.5
PSI-HU-CA	432	388,241,722	13.0	3.5

In order to prevent information leak, all the bins in institution B's bin-and-ball table are padded to the maximum size, as described above. The maximum bin size is determined by B's patient data payload and hashing functions. Larger patient datasets require larger padding sizes. Using our hashing functions and data sets where institution A has 120,666 patients and B has 109,072 patients, the maximum padding size is 11. For the above experiments, we use simulated average network delay and bandwidth of 96 ms (roundtrip) and 50 MB/s in a WAN setting. We adopt these simulation parameters from another study³³ that uses such settings to evaluate a PSI system. Our experiments were performed on a system with an Intel i7-8750H 2.2 GHz CPU and 16 GB memory. The software for the presented protocols, including the synthetic dataset and programs to reproduce our results, can be found on GitHub^†.

Discussion

In this paper, we demonstrate the practicability and flexibility of state-of-the-art MPC approaches for real-world clinical use cases. Our approach meets requirements for real-world deployment, as it is performant using affordable computing resources. Our most complex protocol completes in only a little over seven minutes, running over a large dataset. Compared to two early stage circuit-based clinical informatics applications for the simpler tasks of PSI¹⁷ and joint cohort discovery¹⁸, our results achieved improvements of an order of magnitude. Table 2 captures the performance of our most complex protocol and the published results from these two earlier garbled circuits systems. Our performance advantage is obtained in spite of using patient data sets that are more than 10 times larger, having higher precision patient payloads, adding analytics workload, and being simulated in WAN setting.

Table 2. Comparison between our highly optimized protocol and two previous circuit-based MPC systems.

	Running Time	Data Size	Patient Payload	Use Case	Network	Security
PSI-HU-CA	432 seconds	121K,109K	64-bit	36-bit add, scan	WAN	128 bits (AES)
Dong et al. 18	~2 hours	10K, 10K	36-bit	N/A	LAN	128 bits (AES)
Chen et al. 17	~3 hours	10K, 10K	36-bit	N/A	LAN	80 bits

Our performance improvement is largely due to our use of Cuckoo hashing. With Cuckoo hashing, the number of required patient comparisons is drastically reduced. In the previous work, naïve patient-by-patient comparisons between the two data sets implies a complexity of O(N²), where N is the number of patients at an institution. In our work, the complexity is O(1.5σN), where N is the maximum padding size. The maximum padding size σ grow roughly logarithmically as the dataset grows. Using Cuckoo hashing, we cut the running time by a factor of 2N/3σ. In our experiments, the patient comparison takes place 1,799,688 times, whereas in the naïve method of pairwise comparison that needs to take place 109702×120666 times, therefore using our Cuckoo hashing scheme the patient comparison workload is reduced by a factor of 7355 compared to naïve methods used in those two previous works. Obviously, our performance here is aided somewhat by simplifying the patient linkage (PPRL) step to PSI. To be practical, this would require the existence of unique identifiers for patients used by both institutions. As discussed above, universal identifiers are rarely available. However, deterministic linkage implementations like the one suggested by Kho and associates¹³ are amenable to optimization by Cuckoo hashing, as they require perfect matching of at least one of several concatenations of hashed PHI elements. In their initial implementation, they suggest four such concatenations, which would require four pairs of hash tables under our approach and raise the complexity to O(4×1.5σN), which is still O(N). But we must concede that methods for linking patients will be constrained under our optimization.

On the other hand, because all computable functions can be expressed as a Boolean circuit, our approach can be adapted flexibly to other clinical use cases beyond patient risk stratification. As shown in the results section, it only takes a few gigabytes memory per site to run a secure protocol on a relatively large dataset. This suggests our approach is ready to handle protocols using payloads about one order of magnitude larger, while still running on very affordable hardware. It is also worth noting the disease cohorts often seen in pre-clinical trial studies are much smaller – typically on the order of hundreds or thousands of patients. This indicates our approach is ready to provide circuit-based MPC solutions to many real-world multi-site clinical studies.

The security of our protocol is based on the underlying premise of Yao's garbled circuits, which is provably secure in a semi-honest setting. From a correctness perspective, it returns correct results all the time. The only caveat is that, as established by Demmler et al.³⁶, building a Cuckoo hash table with three hash functions along with the factor of 1.5 has a failure rate of about 1/2⁴⁰. A failure occurs when a patient cannot fit into the Cuckoo hash table. In this extremely unlikely event (approximately 1 in a trillion), the protocol could easily re-generate the Cuckoo hash table with a new set of hash functions. Such an event has no apparent security or privacy implications.

For future work, we plan to develop new protocols to incorporate heterogeneous data domains to handle complex scenarios that not only involve traditional clinical data, but also data from genomics, mobile health, and social determinants of health. Since our protocols are memory efficient, this leaves a lot of room for expanding payloads to represent more complex clinical data elements, such as medications and lab tests. EMP-toolkit boasts support for MPC involving multiple parties, so we plan to study its application to more complex multi-site clinical scenarios.

As the clinical data model becomes more sophisticated, it will inevitably require more memory friendly payload designs. So such space optimization promises to be another avenue for research.

Finally, we plan to compare our protocol to existing trusted third-party approaches. Abel and associates¹³ report matching patients among seven institutions takes significant computational time. We would like to perform controlled experiments to compare our circuit-based approach directly with such standard PPRL systems. We note our protocol is provably secure in a semi-honest setting, whereas the centralized third-party approach has demonstrated security vulnerabilities in the same setting¹⁴.

Conclusion

Having demonstrated their performance with measures important for patient risk stratification, we assert the protocols developed based on garbled circuits are ready for real world deployment in clinical informatics. In the context of discussing the adoption of blockchain, Kuo and Ohno-Machado³⁹ argue there are two ways for cutting-edge secure computing technology to make a real-world impact. First, sustained trust with policy and regulatory bodies must be built. Second, early adopters must be encouraged, so they may serve to allay the fears of institutions to adopt who feel hesitant. Breakthroughs in cryptography have made circuit-based MPC a completely viable technology for healthcare. Well-defined clinical use cases and provably secure processing of patient data should help build trust with governing bodies in healthcare and may help streamline review processes. The time to champion the adoption of circuit-based MPC protocols in real-world multi-site clinical analytics is upon us.