The airborne contagiousness of respiratory viruses: A comparative analysis and implications for mitigation

Graphical abstract

Abstract

The infectious emission rate is a fundamental input parameter for airborne transmission risk assessment, but data are limited due to reliance on estimates from chance superspreading events. This study assesses the strength of a predictive estimation approach developed by the authors for SARS-CoV-2 and uses novel estimates to compare the contagiousness of respiratory pathogens. We applied the approach to SARS-CoV-1, SARS-CoV-2, MERS, measles virus, adenovirus, rhinovirus, coxsackievirus, seasonal influenza virus and Mycobacterium tuberculosis (TB) and compared quanta emission rate (ER_q) estimates to literature values. We calculated infection risk in a prototypical classroom and barracks to assess the relative ability of ventilation to mitigate airborne transmission. Our median standing and speaking ER_q estimate for SARS-CoV-2 (2.7 quanta h⁻¹) is similar to active, untreated TB (3.1 quanta h⁻¹), higher than seasonal influenza (0.17 quanta h⁻¹), and lower than measles virus (15 quanta h⁻¹). We calculated event reproduction numbers above 1 for SARS-CoV-2, measles virus, and untreated TB in both the classroom and barracks for an activity level of standing and speaking at low, medium and high ventilation rates of 2.3, 6.6 and 14 L per second per person (L s^–1 p^–1), respectively. Our predictive ER_q estimates are consistent with the range of values reported over decades of research. In congregate settings, current ventilation standards are unlikely to control the spread of viruses with upper quartile ER_q values above 10 quanta h⁻¹, such as SARS-CoV-2, indicating the need for additional control measures.

1. Introduction

The COVID-19 pandemic has renewed attention to airborne contagion in shared indoor atmospheres. Airborne transmission of respiratory tract infection results from the inhalation of virus- or bacteria-laden droplet nuclei, defined as the evaporated residua of respiratory droplets expired during breathing, vocalizing, coughing, and sneezing. Modeling by Balachandar et al. (2020) indicated that all expired respiratory droplets below 100 μm in diameter will evaporate to droplet nuclei of non-volatile biological material within a second of expiration and after less than 1 m of travel, even at 98% ambient air humidity. As such, there is an urgent need to quantify the emission rate of droplets below 100 μm to facilitate airborne infection risk assessment. Buonanno et al. (2020a) developed a novel predictive estimation approach for the quanta emission rate as a function of respiratory activity and activity level. The quantal dose–response concept for airborne contagion was originally developed by Wells (1955) with the understanding that infection by inhalation is a probabilistic process involving myriad random variables with substantial heterogeneity. Using a Poisson model, a quantum equals the unknown amount of pathogenic airborne droplet nuclei that will cause sustained infection in 63% of exposed susceptibles. As cautioned by Nardell (2016), “quantum,” the dose traditionally back calculated from the end result of infections in a group of susceptibles, should not be confused with “infectious particles,” that originate from the infected source and can be measured in units of RNA copies or plaque forming units (PFUs). The predictive estimation approach bridges the gap between these two concepts, with a quantum representing a human infectious dose for 63% of susceptibles (HID₆₃) by droplet nuclei inhalation that can be approximately related to a viral or bacillary load in the emitting subject through experimental analysis, as was achieved for seasonal influenza virus by Bueno de Mesquita et al. (2020).

The aim of this work is threefold: (i) to assess the strength of the predictive estimation approach for the airborne emission rate of common respiratory pathogens by comparing estimates to back-calculated values reported in literature, (ii) to use the estimates to compare the contagiousness of the modeled pathogens through the airborne route, and (iii) to assess the ability of modern standards of ventilation to prevent their epidemic spread.

2. Materials and methods

The predictive estimation approach for the quanta emission rate (ER_q) is presented as Eq. (1) for respiratory viruses (Buonanno et al., 2020b), but can also be applied to bacterial pathogens as described subsequently in this section:

$${\mathrm{E}\mathrm{R}}_{\mathrm{q}}=c_{\mathrm{v}}\times c_i\times IR\times V_{\mathrm{d}}=c_{\mathrm{v}}\times \frac{1}{{\mathrm{c}}_{\mathrm{R}\mathrm{N}\mathrm{A}}\times {\mathrm{c}}_{\mathrm{P}\mathrm{F}\mathrm{U}}}\times IR\times V_{\mathrm{d}}$$ (1)

where c _v is the viral load in sputum (RNA copies mL⁻¹), c_i (quanta RNA copies⁻¹) is a conversion factor defined as the ratio between one quantum and the infectious dose expressed in viral RNA copies, IR is the inhalation rate (m³  h⁻¹), and V _d is the droplet volume concentration expelled by the infectious person (mL m⁻³). The conversion factor, c_i, can be calculated as the inverse of the product of the number of RNA copies per plaque-forming unit (PFU) (c_RNA) and the number of PFU approximating the human infective dose (HID₆₃) by droplet nuclei inhalation (one quantum) (c_PFU, PFU quanta^–1). Where viral load is provided in units of PFU mL⁻¹, or the median tissue culture infectious dose (TCID₅₀) mL⁻¹, the C_RNA term becomes unnecessary. For unit conversions, approximately four-fifths of a quantum is a TCID₅₀ (Wells, 1955), and a PFU is commonly approximated as seven-tenths of a TCID₅₀. The droplet volume concentration V _d is a function of the expiratory activities and was derived from the total volume emitted by a loud-speaking person provided by Stadnytskyi et al. (2020). Representative values for the inhalation rate (0.49 m³ h⁻¹ for resting, 0.54 m³ h⁻¹ for standing, and 1.38 m³ h⁻¹ for light exercise) were obtained from Adams (1993).

While inhalation rate and droplet volume concentrations are known to vary between individuals based on age, body mass, and natural physiological heterogeneity, we hold them constant for each of three evaluated expiratory activities to simplify the calculation and limit variation to the viral load. With this assumption the product $\mathit{IR}\times V_{\mathrm{d}}$ becomes a constant droplet volume emission rate in mL h⁻¹ as follows: 9.8 × 10^–4 for resting, oral breathing; 4.9 × 10^×3 for standing, speaking; and 8.3 × 10^–2 for light activity, speaking loudly. Derived from a laser light scattering study (Stadnytskyi et al., 2020), the droplet emission rates span the size range of expiratory droplets produced by speaking. The high sensitivity of light scattering better quantifies droplets in the range of 10–100 μm which can be missed by aerodynamic particle sizer (APS) measurements.

To apply the predictive approach, we used Eq. (1) and a lognormal distribution of viral load to create a lognormal distribution of ER_q defined by an associated probability density function. We compiled viral load and infectious dose data for the following eight (8) viruses: severe acute respiratory syndrome (SARS) coronavirus (CoV) 1 and 2, Middle East respiratory syndrome (MERS) coronavirus, measles virus, seasonal influenza virus, rhinovirus, coxsackievirus, and adenovirus. We did not include respiratory syncytial virus (RSV) in our evaluation because transmission between infants is generally a greater concern than between adults and this is beyond our current scope (Kulkarni et al., 2016). We did not include smallpox (variola) virus, chickenpox (varicella) virus, parainfluenza viruses, mumps and rubella viruses and others due to lack of data on viral load in the respiratory tract and/or infectivity by droplet nuclei inhalation.

While the focus of this paper is respiratory viruses, we did apply the predictive approach to Mycobacterium tuberculosis (TB) as it is the most well-studied agent of airborne contagion. For TB we separately used bacillary loads representative of both untreated active cases and cases after two weeks of treatment, and an estimate of infectious dose in colony forming units (CFUs). We also considered Bordetella pertussis, which is an airborne-transmitted pathogen causing whooping cough (Warfel et al., 2012) that may have an infectious dose below 100 CFU (Weyrich et al., 2014). However, data collected by Brotons et al. (2016) found infected individuals over the age of 15 to have significantly lower bacillary loads (log₁₀ median of 1.7 CFU mL⁻¹) versus infected children and infants (e.g. log₁₀ median of 4.9 CFU mL⁻¹ for ages 2 to age below 6 months). Thus, as with RSV, we omitted its inclusion herein, but note that the low bacillary loads for adults indicate quanta emissions without coughing may be low.

Parameters selected for each virus and for TB are summarized in Table 1 . A narrative with referencing for all parameter values and rationales for inclusion is provided in the Supplementary data text. Where sputum viral load data were unavailable or considered otherwise non-representative, we used nasal swab or nasal wash data as a substitute.

Table 1.

Viral/bacillary load and infectivity input data.

Pathogen	log10 cv mean (st.dev)	Conversion Factor (ci)
Adenovirus	3.2 (0.95) TCID50 mL−1	0.50 quanta TCID50–1
Coxsackievirus	3.4 (1.1) TCID50 mL−1	0.025 quanta TCID50–1
Influenza	6.7 (0.84) RNA copies mL−1	7.1 × 10−6 quanta RNA copies−1
Measles	3.5 (1.6) TCID50 mL−1	1.0 quanta TCID50–1
MERS	6.7 (1.6) RNA copies mL−1	2.3 × 10−6 quanta RNA copies−1
Rhinovirus	3.6 (0.83) TCID50 mL−1	0.053 quanta TCID50–1
SARS-CoV-1	6.1 (1.3) RNA copies mL−1	6.8 × 10−6 quanta RNA copies−1
SARS-CoV-2	5.6 (1.2) RNA copies mL−1	1.4 × 10−3 quanta RNA copies−1
TB (Untreated)	5.5 (1.3) CFU mL−1	2.0 × 10−3 quanta CFU−1
TB (On Treatment)	4.0 (1.4) CFU mL−1

Over the course of 2021, novel strains of SARS-CoV-2 have emerged that preliminary epidemiological data suggest are more transmissible than those circulating at the beginning of the pandemic. A more contagious strain would have higher ER_q values through a higher median viral load and/or a lower infectious dose. For the B1.1.7 (Alpha) variant, the median and 65th percentile viral load values estimated by Kidd et al. (2021) of approximately log₁₀ 5.2 and log₁₀ 6.2 copies mL⁻¹, respectively, are generally consistent with our viral load distribution values of log₁₀ 5.6 and log₁₀ 6.1 copies mL⁻¹, respectively. Based on this the increased transmissivity of B1.1.7 (Alpha) may relate to a lower infectious dose, but clearly further data are necessary. For B.1.617 (Delta) variant infections, Li et al. (2021) found viral loads to be approximately 1000 times higher on the first day of positive testing than those of the original 2020 strains in mainland China. As approximately 81% of oropharyngeal swab samples contained Delta variant viral loads above log₁₀ 5.8 copies mL⁻¹ (Li et al., 2021), the increased transmissivity of the Delta variant appears at least in part related to viral loads higher than those used to generate our estimates. We note that the predictive estimation approach lends itself to efficient updating of the emission distributions as new variants emerge and associated data sets are published. Our calculations used the thermodynamic equilibrium dose–response model of Gale (2020), which suggests a very low median infectious dose of only 1 to 2 PFU due to the relative absence of a protective effect in the mucus barrier. Thus, our ER_q estimates already reflect the high contagiousness of SARS-CoV-2 through the airborne route even though they are based on the earlier viral load distributions described in the Supplementary data text.

To quantify the ability of ventilation to mitigate the risk of airborne transmission, we calculated the individual risk (R) of an exposed person (Buonanno et al., 2020b) and event reproduction numbers (R_event) for a typical classroom studied by Wells (1943) and for a military barracks studied by Couch et al. (1970). R_event is defined as the expected number of new infections arising from a single infectious individual at an event (Tupper et al., 2020). We performed the calculations using low, medium, and high ventilation rates of 2.3 L per second per person (L s^–1p^–1), 6.6 L s^–1p^-1, and 14 L s^–1p^–1, respectively, and assuming one infectious occupant and a fully susceptible population. Our low and medium ventilation rates correspond to the mean values estimated for low and high ventilation dormitories in Zhu et al. (2020), and our high ventilation rate corresponds to the value estimated by Wells for the control classrooms in his air disinfection experiments (Wells, 1943). Based on the room volumes these ventilation rates are equivalent to 1.3, 3.8 and 8.0 air changes per hr for the classroom, and 0.70, 2.0 and 4.3 air changes per hr for the barracks, respectively. For reference, the ANSI/ASHRAE 62.1 combined outdoor air rate values for acceptable indoor air quality for these two spaces are approximately 6.3 L s^–1p^–1 and 3.7 L s^–1p^–1 for classrooms and barracks sleeping areas, respectively (ASHRAE, 2019). These values, as well as the low and medium ventilation rates used in our models, are below the World Health Organization’s (WHO) recommended minimum ventilation rate of 10 L s^–1p^–1 in non-residential settings in the context of the COVID-19 pandemic (World Health Organization WHO, 2021). We also note that even the high ventilation rate of 14 L s^–1p^–1 results in well below the 12 air changes per hour minimum WHO recommendation for an airborne precaution room (Atkinson et al., 2009). A summary of the modeling approach and parameter assumptions are provided in the Supplementary data text.

The infection risk equations and quanta emission rate distributions documented in this paper are implemented in a spreadsheet tool named the Airborne Infection Risk Calculator (AIRC) Version 3.0, posted in the public domain (Mikszewski et al., 2021). For SARS-CoV-2, AIRC Version 3.0 will generally produce higher risk estimates using the default emission rates than earlier versions of the tool, owing to the higher standard deviation of the viral load distribution used herein.

3. Results and discussion

3.1. Quanta emission rates

The median ER_q estimates from the predictive estimation approach are ranked from high to low as follows: measles virus, adenovirus, TB (untreated), SARS-CoV-2, rhinovirus, coxsackievirus, seasonal influenza, TB (on treatment), MERS, and SARS-CoV-1. Table 2 provides the 5th percentile, 50th percentile (median), and 95th percentile ER_q estimates for each virus for the three emission profiles evaluated herein (resting, oral breathing; standing, speaking; light activity, speaking loudly). Based on the assumed lognormal distribution for the viral load, the ER_q estimates also follow a lognormal distribution, with the log₁₀ mean value equal to the log₁₀ of the reported median value in Table 2, and the log₁₀ standard deviation equal to that of the viral load in Table 1. For example, the log₁₀ ER_q distribution for SARS-CoV-2 for standing and speaking has a mean of 0.43 (the log₁₀ of 2.7) and a standard deviation of 1.2. Plots of the lognormal distributions for the standing and speaking activity level are provided in Fig. 1 . Published ER_q values in literature are presented in Table 3 for comparison.

Table 2.

Predictive ER_q (quanta h⁻¹) statistics as a function of the expiratory activity and activity level provided as 50th percentile (5th percentile, 95th percentile).

Pathogen	Resting, oral breathing	Standing, speaking	Light activity, speaking loudly
SARS-CoV-1	0.0084 (6.1E-5, 1.2)	0.042 (3.1E-4, 5.8)	0.71 (0.0052, 98)
MERS	0.011 (2.6E-5, 4.7)	0.056 (1.3E-4, 24)	0.96 (0.0022, 410)
TB (On Treatment)	0.020 (1.0E-4, 4.0)	0.098 (4.9E-4, 20)	1.7 (0.0085, 340)
Influenza	0.035 (0.0015, 0.84)	0.17 (0.0071, 4.1)	3.0 (0.12, 72)
Coxsackievirus	0.062 (9.6E-4, 4.0)	0.31 (0.0048, 20)	5.2 (0.081, 340)
Rhinovirus	0.21 (0.0091, 4.9)	1.0 (0.043, 23)	18 (0.78, 420)
SARS-CoV-2	0.55 (0.0058, 52)	2.7 (0.029, 250)	46 (0.49, 4,300)
TB (Untreated)	0.62 (0.0045, 85)	3.1 (0.023, 430)	52 (0.38, 7,200)
Adenovirus	0.78 (0.021, 28)	3.9 (0.11, 140)	66 (1.8, 2,400)
Measles	3.1 (0.0072, 1,300)	15 (0.035, 6,400)	260 (0.61, 1.1E+5)

Fig. 1.

Predictive ER_q distributions for the standing and speaking activity level. Boxes span the interquartile ranges, with whiskers extending from the 5th–95th percentile values and the median denoted by the vertical line in each box.

Table 3.

Predictive ER_q comparisons with literature values.

Virus & Setting	Reference	ERq(quanta h−1)	Standing, speaking (percentile)	Light activity, speaking loudly (percentile)
SARS-CoV-1: Taipei Hospital	Liao et al. (2005)	29	98th	89th
SARS-CoV-2: Wuhan Apartment	Bazant and Bush (2021)	15	73rd	35th
SARS-CoV-2: Cruise Ship	Bazant and Bush (2021)	15	73rd	35th
SARS-CoV-2: Wuhan Bus #1	Prentiss et al. (2020)	36	83rd	46th
SARS-CoV-2: Ningbo Bus	Bazant and Bush (2021)	45	85th	50th
SARS-CoV-2: Restaurant	Buonanno et al. (2020b)	61	87th	54th
SARS-CoV-2: Wuhan Bus #2	Prentiss et al. (2020)	62	87th	54th
SARS-CoV-2: School, Germany	Kriegel et al. (2020)	116	91st	63rd
SARS-CoV-2: Courtroom	Vernez et al. (2021)	130	92nd	65th
SARS-CoV-2: Buddhist Bus	Prentiss et al. (2020)	133	92nd	65th
SARS-CoV-2: School, Israel	Kriegel et al. (2020)	139	92nd	66th
SARS-CoV-2: Meeting	Kriegel et al. (2020)	139	92nd	66th
SARS-CoV-2: Fitness Center	Prentiss et al. (2020)	152	93rd	67th
SARS-CoV-2: Abattoir	Kriegel et al. (2020)	232	95th	72nd
SARS-CoV-2: Call Center	Prentiss et al. (2020)	683	98th	84th
SARS-CoV-2: Chorus, USA	Miller et al. (2021)	970	98th	87th
SARS-CoV-2: Chorus, Germany	Kriegel et al. (2020)	4213	–	95th
Measles: Classroom	Wells, 1955, Riley et al., 1962	18	52nd	23rd
Measles: Elementary and secondary schools	Riley (1980)	60 (min.)	65th	35th
		600 (median)	84th	59th
		5600 (max.)	95th	80th
Measles: Secondary school	Azimi et al. (2020)	2765	92nd	74th
Measles: Pediatrician’s office	Remington et al. (1985)	8640	96th	83rd
Influenza: Human transmission trials in quarantine rooms	Bueno de Mesquita et al. (2020)	0.11	41st	4th
Influenza: Transmission experiments among ferrets	Zhou et al. (2018)	7.95	98th	69th
Influenza: Airliner during delay with inoperable ventilation	Moser et al., 1979, Rudnick and Milton, 2003	79	–	95th
Rhinovirus: Transmission trials using card playing games	Dick et al., 1987, Rudnick and Milton, 2003	3.1	72nd	18th

The three evaluated coronaviruses have similar viral load distributions, but the significant difference in infectivity results in ER_q estimates for SARS-CoV-2 that are over an order of magnitude higher than SARS-CoV-1 and MERS. Recent estimates of ER_q back calculated from SARS-CoV-2 superspreading events are presented in Table 3, including data from pre-prints that are subject to revision, and approximately span the 35th-95th percentile for the light activity, speaking loudly distribution. The result of most percentile values above the median for SARS-CoV-2 is expected, as it is overdispersed with a minority of cases responsible for most secondary transmission (Endo et al., 2020).

Previous ER_q estimates for measles virus are significantly different based on calculations made before and after the introduction of the vaccine in the early 1960s. Riley et al. (1962) reported the emission rate of the average child with measles to be 18 quanta h⁻¹ based on the earlier work of Wells, 1943, Wells, 1955, which is very similar to our median estimate for standing and speaking. The pattern of the spread of measles in schools studied by Wells in the pre-vaccine era was consistent with past epidemiology showing outbreaks to begin when the density of susceptibles reached 30%–40%, and wane when the density decreased to 15%–20% (Wells, 1943, Wells, 1955). Conversely, the post-vaccine era estimates are based on superspreading events with back calculated emission rates reaching over 1000 quanta h⁻¹ (Riley, 1980, Remington et al., 1985, Azimi et al., 2020). This discrepancy is potentially explained by the impact of the density of susceptibles on the threshold emission rate needed to reproduce infection. Wells (1955) noted a contact rate, or probability of infection, of 11% for measles over a three-day infectious period in a well-ventilated classroom, from which the 18 quanta h⁻¹ estimate was derived. The initial density of susceptibles in the class was approximately 33%. If this density of susceptibles were reduced to 5% through vaccination, to generate an equivalent number of secondary cases on average, the contact rate would need to increase to approximately 75%. This corresponds to an emission rate over 200 quanta h⁻¹, more consistent with the post-vaccine estimates of Riley (1980). Community transmission of measles in the post-vaccine era appears limited to individuals with high viral load, and thus high ER_q, capable of picking out the few remaining susceptibles in a group (Langmuir, 1980).

The median estimated ER_q for seasonal influenza for standing, speaking (0.17 quanta h⁻¹) is consistent with the recent estimate of 0.11 quanta h⁻¹ calculated from a human transmission trial (Bueno de Mesquita et al., 2020). The 79 quanta h⁻¹ estimate for a superspreading event on a grounded airliner (Moser et al., 1979, Rudnick and Milton, 2003) is approximately equal to the 95th percentile value for the light activity, speaking loudly activity level (Table 3). Supporting the extreme nature of the airliner case study, Bischoff et al. (2013) measured the maximum emission rate from 61 influenza patients to be approximately 1.2 × 10⁶ RNA copies h⁻¹, equal to 8.7 quanta h⁻¹ using the conversion factor in Table 1. We therefore conclude that ER_q values above 10 quanta h⁻¹ may be quite uncommon for seasonal influenza, limiting the potential for explosive outbreaks of short duration. However, our estimates are for breathing and vocalizing, and severely symptomatic cases with high frequency of cough may generate significantly higher emissions, as with the airliner case study.

The median estimated ER_q for rhinovirus of 1.0 quanta h⁻¹ for standing and speaking is consistent with the mean value of 3.1 quanta h⁻¹ calculated based on the range of values (0.6–7.8) estimated by Rudnick and Milton (2003).

The median ER_q estimated for adenovirus of 3.9 quanta h⁻¹ for standing and speaking is second only to measles. No literature values are available for comparison, but a high emission rate is consistent with explosive outbreaks observed at US military basis during the late 1990s and early 2000s when the adenovirus vaccine was temporarily unavailable. Russell et al. (2006) described one such military outbreak where over the course of a 4-week period a 98% attack rate was observed among 180 susceptible persons. Echavarria et al. (2000) identified a correlation between adenovirus PCR results on air filters and the number of hospitalizations within military companies and found that companies with one ventilation unit per floor and wing had lower attack rates (11%) than those with one ventilator supplying air for multiple floors (18–21%). While resumption of adenovirus vaccination largely eliminated these types of outbreaks on US military bases, China has not yet included adenovirus in its military vaccination program. Guo et al. (2020) described a recent outbreak of adenovirus type 7 at a boot camp in China that lasted 30 days, resulting in 375 cases and 109 hospitalizations.

The estimated ER_q values for coxsackievirus fall between those of influenza and rhinovirus, with a median of 0.31 quanta h⁻¹ for standing and speaking. Airborne transmission of coxsackievirus A₂₁ was conclusively demonstrated in a cross-infection experiment conducted in a military barracks with physical separation of occupants and well-mixed air (Couch et al., 1970). We modeled the mean emission rate for each of 10 infected subjects in this experiment to be between 1.3 quanta h⁻¹ and 3.6 quanta h⁻¹, consistent with the predictive calculations at the 72nd percentile to 83rd percentile range of the standing and speaking distribution. A description of the experiment and our modeling approach is provided in the Supplementary data text.

The closest model for the contagiousness of SARS-CoV-2 may be provided by an untreated, active case of TB, as we estimated a median ER_q of 3.1 quanta h⁻¹ for standing and speaking, approximately 15% higher than that of SARS-CoV-2. The office outbreak from an untreated case modeled by Nardell et al. (1991) (13 quanta h⁻¹) corresponds to the 68th percentile of the standing, speaking distribution, while the modeled emission rate from an explosive outbreak of multi-drug resistant (MDR) TB aboard a long-haul flight (108 quanta h⁻¹; Ko et al., 2004) corresponds to the 88th percentile value.

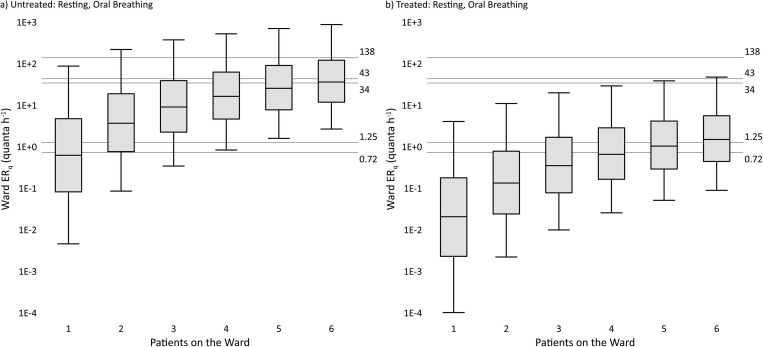
To compare our estimates to the human-to-guinea pig transmission trials of Riley et al. (1959, 1962) and the similar studies in the MDR-TB and HIV era (Escombe et al., 2007, Escombe et al., 2008, Dharmadhikari et al., 2012), we created ER_q distributions for up to six infected individuals from the resting, oral breathing activity level for both untreated and treated TB. This was done by adding together up to six random samples from the respective lognormal distributions 100,000 times. The simulated distributions are presented on Fig. 2 a (untreated) and 2b (treated), representing the predicted cumulative ER_q produced on a TB ward with up to six occupied beds, consistent with the five to six bed occupancy of the seminal works (note that while the Escombe et al. (2007) study used an eight-bed ward, mean bed occupancy was 66%, or 5.3 beds). Fig. 2a shows that the untreated predictive estimates for a five to six-patient ward are consistent with the recent MDR-TB and HIV-era transmission trials, whereas Fig. 2b shows that the treated predictive estimates for a five to six-patient ward are more consistent with the original experiments of Riley et al., 1959, Riley et al., 1962. The highest two ER_q estimates from individual TB patients in the guinea pig studies, 60 quanta h⁻¹ (Riley et al., 1962) and 226 quanta h⁻¹ (Escombe et al., 2008), approximately correspond to the 94th and 98th percentile values, respectively, of the resting, oral breathing distribution for untreated TB.

Fig. 2.

Predictive cumulative ER_q distributions for a tuberculosis (TB) ward with up to six patients based on the resting, oral breathing expiration and bacillary load (see Supplementary data text) representative of active, untreated TB (Fig. 2a) and after two weeks of treatment (Fig. 2b). Boxes span the interquartile ranges, with whiskers extending from the 5th–95th percentile values and the median denoted by the horizontal line in each box. Labeled gridlines present the cumulative ER_q estimates from seminal human-to-guinea pig transmission trials as follows: 0.72 quanta h⁻¹ from a six-bed ward (after Riley et al., 1959), 1.25 quanta h⁻¹ from a five-bed ward (after Riley et al., 1962), 34 quanta h⁻¹ from a six-bed ward with patients wearing masks (after Dharmadhikari et al., 2012), 43 quanta h⁻¹ from an eight-bed ward with 66% occupancy (after Escombe et al., 2007, calculated as the mean reported individual patient ER_q of 8.2 quanta h⁻¹ times the mean bed occupancy of 5.3 beds), and 138 quanta h⁻¹ from a six-bed ward with no mask use (after Dharmadhikari et al., 2012).

3.2. Classroom and barracks modeling scenarios

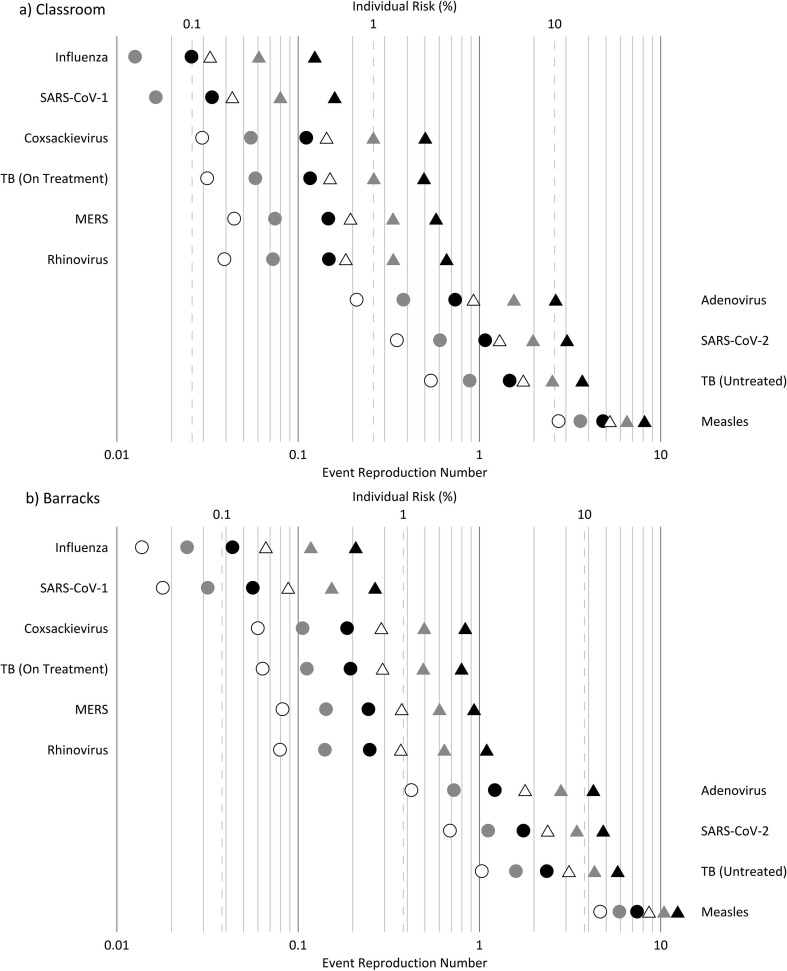
Results of the two modeling scenarios described in the Supplementary data text are presented in Fig. 3 a and Supplementary data Table S1 for the classroom, and Fig. 3b and Supplementary data Table S2 for the barracks. With respect to the individual risk (R) in both settings at the standing and speaking expiration, the results indicate: (i) the low ventilation rate (2.3 L s^–1p^–1) is only able to keep R below 1% for seasonal influenza and SARS-CoV-1, 2) the high ventilation rate (14 L s^–1p^–1) is needed to keep R approximately at or below 1% for rhinovirus, MERS, coxsackievirus, and TB (on treatment), and (iii) even at the high ventilation rate, R is above 1% for adenovirus, TB (untreated), and SARS-CoV-2, and above 10% for measles. With respect to the expected number of infections resulting from the exposures at standing and speaking: (i) at the high ventilation rate, R_event is above 1 in both settings for TB (untreated), SARS-CoV-2, and measles, with adenovirus also above 1 in the barracks, and (ii) R_event approaches or exceeds 1 in the barracks at the low ventilation rate for rhinovirus, MERS, coxsackievirus, and TB (on treatment). Illustrating the potential for high attack rates of SARS-CoV-2 in congregate housing, R_event is above 1 in the barracks at the resting, oral breathing expiration at both the medium and low ventilation rates. The four pathogens with calculated R_event values above 1 at the high ventilation rate have upper quartile ER_q estimates above 10 quanta h⁻¹ for standing and speaking (Fig. 1).

Fig. 3.

Individual risk (R, %) and event reproduction numbers (R_event) for the (a) classroom and (b) barracks modeling scenarios. Circles depict results for resting, oral breathing and triangles depict results for standing, speaking. White, gray, and black symbol fill corresponds to the high, medium, and low ventilation rates, respectively.

Of the pathogens evaluated, the modeling results suggest airborne transmission risk to be greatest for adenovirus, TB (untreated), SARS-CoV-2, and measles, for all of which even a high ventilation rate of 14 L s^–1p^–1 may be insufficient to maintain event reproduction numbers below one in a fully susceptible population, depending on indoor occupant activities. To maintain safe operation of classrooms during the on-going COVID-19 pandemic, interventions such as improving natural or mechanical ventilation combined with minimizing the amplitude of vocalization should be pursued, as conceptualized by Stabile et al. (2021). For the less contagious pathogens, secondary transmission becomes a significant concern in congregate living settings like the barracks where ventilation is poor (e.g. 2.3 L s^–1p^–1 or less). However, the modeling results indicate that improved ventilation in such settings can effectively reduce reproductive numbers of endemic rhinovirus and seasonal influenza, consistent with real-world studies in university dormitories (Sun et al., 2011, Zhu et al., 2020). Lastly, our finding of high contagiousness of SARS-CoV-2 via the airborne route reinforces the need for airborne precaution rooms and N95 or FFP3 respirators to protect health care workers. This conclusion is supported by mounting evidence of the inadequate protection provided by surgical masks, even in the absence of aerosol generating procedures (Ferris et al., 2021, Goldberg et al., 2021).

3.3. Limitations

Our mass balance analysis should be interpreted as a proof of concept and is limited by the paucity of data on viral load and infectious dose by natural inhalation in the real world. Where sputum data were unavailable, the use of nasal swab data may bias ER_q estimates low due to dilution in transport medium, although this may be offset by laboratory-derived infectious dose estimates that are lower than those required by breathing ambient air in the real world. Uncertainty also arises from virus-specific nuances, with one example for measles being the potential expiration of cell-associated virus derived from epithelial damage in the upper respiratory tract (Ludlow et al., 2013). The relative proportion of virions and bacteria in sputum versus expired droplets requires further study (Patterson and Wood, 2019). Droplet volume emissions from coughing and sneezing require better quantification so that comparisons can be made to emissions from vocalization, and refinement of the predictive approach is necessary to incorporate variation in droplet volume emissions between individuals (Edwards et al., 2021). We expect on-going advancements in exhaled breath sampling (e.g. Patterson et al., 2020) to help validate and improve the predictive approach.

The main limitation of our infection risk modeling approach is the assumption of a homogeneous concentration of droplet nuclei within the room, instead of a plume with the highest concentration closest to the emitting source. Additional mechanisms decreasing the viral concentration, such as particle deposition and inactivation in ambient air, are held constant in the model, but should be evaluated for more detailed site-specific analysis, also considering that the airborne inactivation rate varies significantly between pathogens and based on environmental factors such as relative humidity.

4. Conclusions

The ER_q estimates we produced for a range of respiratory viruses and for TB are in good agreement with the range of values back calculated from experimental studies and superspreading events in literature, although further work is necessary to compare droplet volume emissions from symptomatic cases with those of speaking loudly at varying activity levels. The predictive estimation approach advances methods of prospective risk assessment for airborne transmission of disease. Our calculations suggest measles virus to be the most contagious of those evaluated, but the median estimates for SARS-CoV-2, adenovirus, and untreated, active TB are within the same order of magnitude. Our risk modeling scenarios for a classroom and barracks show that even a high ventilation rate of 14 L s^–1p^–1 will likely fail to prevent the spread of adenovirus, TB (untreated), SARS-CoV-2 and measles in a fully susceptible population, indicating that additional engineering controls such as advanced ventilation design or air disinfection are necessary to supplement public health measures. Conversely, a ventilation rate of 14 L s^–1p^–1 is more likely to prevent sustained airborne transmission of rhinovirus, SARS-CoV-1, MERS, coxsackievirus, TB (on treatment) and seasonal influenza. For SARS-CoV-2, our results highlight the importance of masking for both source control and personal respiratory protection and reinforce the need for airborne precaution and/or isolation rooms in health care or cohabitation settings treating COVID-19 patients.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article:

Supplementary data, text

(i) Information regarding the selected viral load and infectivity parameters for the predictive estimation approach; (ii) retrospective estimation of the quanta emission rate for coxsackievirus; (iii) documentation of the prospective modeling scenarios for a classroom and barracks, including two results summary tables.

Supplementary data, Table 1

Event reproduction numbers (Revent) for the classroom modeled under high ventilation, medium ventilation, and low ventilation conditions, also including the mean Revent and individual risk (R) of all classroom scenarios.

Supplementary data, Table 2

Event reproduction numbers (Revent) for the barracks modeled under high ventilation, medium ventilation, and low ventilation conditions, also including the mean Revent and individual risk (R) of all barracks scenarios.