Materials for emergent silicon-integrated optical computing

Abstract

Progress in computing architectures is approaching a paradigm shift: traditional computing based on digital complementary metal-oxide semiconductor technology is nearing physical limits in terms of miniaturization, speed, and, especially, power consumption. Consequently, alternative approaches are under investigation. One of the most promising is based on a “brain-like” or neuromorphic computation scheme. Another approach is quantum computing using photons. Both of these approaches can be realized using silicon photonics, and at the heart of both technologies is an efficient, ultra-low power broad band optical modulator. As silicon modulators suffer from relatively high power consumption, materials other than silicon itself have to be considered for the modulator. In this Perspective, we present our view on such materials. We focus on oxides showing a strong linear electro-optic effect that can also be integrated with Si, thus capitalizing on new materials to enable the devices and circuit architectures that exploit shifting computational machine learning paradigms, while leveraging current manufacturing infrastructure. This is expected to result in a new generation of computers that consume less power and possess a larger bandwidth.

OPTICAL COMPUTING WITH INTEGRATED SI PHOTONICS

The early conceptualization of “a-machine” by Alan Turing in 1936¹ (also called the Turing machine) proved the existence of fundamental limitations on the power of mechanical computation albeit with powerful mathematical models and algorithms using a processing unit [e.g., CPU (Central Processing Unit)] as is done today. Instead, modern computers utilize random-access memory instead of an infinite memory tape divided into discrete cells. John von Neumann in his “First draft of a report on the EDVAC” in 1945² articulated what is called the first general purpose computing architecture based on memory, processing units, and networks (interconnects). Fascinatingly, von Neumann utilizes synapses, neurons, and neural networks in this 1945 explanation of his von Neumann architecture and then predicts his own limitations, now called the von Neumann bottleneck, by stating that “the main bottleneck of an automatic very high speed computing device lies: At the memory.” Brain-inspired neuromorphic computing, conceptually, had preceded the von Neumann computing architecture.³ However, it was slow in adoption due to technical challenges in both hardware implementation and algorithmic development.⁴ In the 1980s, optical neural network studies became a very active area of study in achieving massively parallel brain-like computing at the speed of light.^5–11 However, the pioneer himself, Psaltis, declared that he was abandoning optical neuromorphic computing in 1990 because of two reasons: (1) lack of practical devices that can be integrated and (2) insufficient knowledge of complex neural networks. Fast forward to 2021, three decades later, when we are now witnessing three major changes occurring. First, machine reinforcement learning algorithms utilizing deep neural networks have advanced to learning complex dynamical systems from observation, such that a learned artificial machine with a few overnights of training and self-play can beat the human world champion of 33 years in the game of Go.^12,13 While the advances in machine learning algorithms benefit both electronic and photonic computing, photonic neuromorphic computing avoids two approaches in today's electronic computing we mention next—(a) applying the new algorithms brute forcedly onto von Neumann computing platforms (e.g., data centers with GPUs and DRAMs) with the von Neumann bottleneck and (b) the slow-down of Moore's law. Second, the rate of increase in integration density of silicon photonics (optical Moore's law) is now twice as fast as that of electronic integration density (electronic Moore's law). Thus, we now find silicon photonic integrated circuits with ten thousand photonic components on a die manufactured on 300-mm silicon photonic wafers from a number of foundries. Third, while Moore's law is barely maintaining its trend of continuing increases in transistor density going from 5, 4, 3 nm, and possibly down to 2 nm and below, the slowing down of this trend is evident. Dennard's law,^14,15 which governs energy efficiency, has already stalled in 2005. Hence, electronics alone cannot sustain the exponential increases of data processing, especially with von Neumann computing architectures requiring data movements across the von Neumann bottlenecks. The natural conclusion from these three major changes point at photonic neuromorphic computing as the key solution to future computing.

Recognizing this natural conclusion, there recently have been remarkable advances in silicon photonics for future computing, in particular, via neuromorphic computing. Broadly, there are two main approaches of such brain-inspired computing. The first is focused efforts toward realizing such silicon photonics for in-plane photonic processing that includes an arbitrary matrix operation (e.g., matrix multiplication, correlation, fast Fourier transform, convolution, etc.). The second is the investigation of silicon photonic planes for surface normal photonic information processing. The first approach offers, theoretically, complete sets of arbitrary mathematical operations with, in principle, lossless elements such as Mach–Zehnder (2 × 2) interferometers (MZIs) to implement unitary matrices.^16,17 We must, however, consider the requirements for the need to incorporate on the order of N² [i.e., $\mathcal{O}$ (N²)] MZIs cascaded in an order of N [i.e., $\mathcal{O}$ (N)] number of stages to realize N × N fully reconfigurable unitary matrices as in deep learning.¹⁸ The second approach also has the same requirements but uses more easily populated $\mathcal{O}$ (N²) optical elements such as spatial-light-modulators (SLMs) utilizing phase-change materials or meta-materials¹⁹ on each plane, despite the same requirements for $\mathcal{O}$ (N) cascaded planes for fully reconfigurable matrices that could suffer diffraction and scattering losses at each layer. Our article will focus on the first method, in particular, the technologies behind reconfigurable MZIs as a building block. We should also note that recent advances in photonic tensor train decomposition successfully demonstrated tensor decomposition of 1024 × 1024 synaptic tensor interconnections with 582-fold reduction in the number of MZIs and 171.8-dB lower total insertion loss assuming 0.2 dB loss at each MZI.^20–22

Silicon photonics is an emergent technology aiming to revolutionize information processing by switching from electrons to photons while still being fully compatible with traditional complementary metal-oxide semiconductor (CMOS) technology. Silicon (Si) is an indirect gap semiconductor and, as such, appears a poor choice for optical applications, which come naturally to III–V semiconductors such as GaAs. Si also absorbs rather strongly for wavelengths shorter than 1000 nm. However, Si is essentially transparent above 1300 nm and can be machined into practically any shape with extremely high precision and with minimal surface roughness. These two properties make Si extremely attractive for fabricating waveguides operating at the telecom wavelength of 1550 nm, making a natural connection between the optical fiber and the Si chip. Si photonics has many applications; for an overview of the recent work and opportunities for integrated photonics in neuromorphic computing, see Stark et al.²³ One of the key elements of this emergent technology is the integrated electro-optical modulator (MZI or ring resonator) used as nonvolatile optical weights. An artist's rendition of a quantum electro-optic network based on the MZI is shown in Fig. 1.

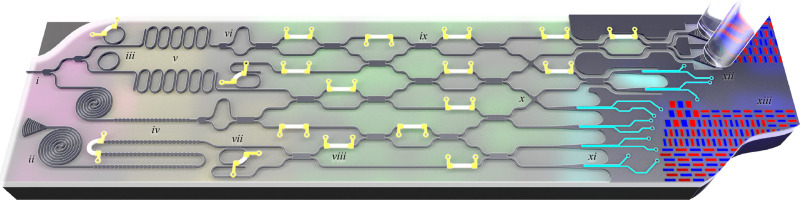
FIG. 1.

Mock-up of a quantum photonic device, showing how various components might fit together, and what those components might look like. Regions of the chip are color coded. From left to right: photon sources (magenta), pump-removal filters (yellow), passive and active optics (green), single-photon detectors (cyan), and control and feedback electronics (blue). Labels indicate: (i) the pump input and splitter, (ii) spiral waveguide photon-pair source, (iii) ring resonator photon-pair source, (iv) Bragg reflector pump removal filter, (v) coupled-resonator optical waveguide (CROW) pump removal filter, (vi) asymmetric Mach–Zehnder interferometer (MZI) wavelength-division multiplexer (WDM), (vii) ring resonator WDM, (viii) thermal phase tuner, (ix) multi-mode interference waveguide coupler (MMI), (x) waveguide crossing, (xi) superconducting nanowire single-photon detector (SNSPD), (xii) grating-based fiber-to-chip coupler, and (xiii) control and logic electronics. From Silverstone et al., IEEE J. Sel. Top. Quantum Electron. 22, 6 (2016). Copyright 2016 Author(s), licensed under a Creative Commons Attribution (CC BY) License.

In what follows, we will focus on the recent work on integrating LiNbO₃ (LNO) and BaTiO₃ (BTO) with Si photonics to make such integrated electro-optical modulators for applications in neuromorphic computing. For an overview of the recent work, extolling opportunities and advantages for integrated photonics in quantum computing, quantum information science, and close to demonstrating quantum supremacy over classical computers, see Refs. 24–26. We first briefly introduce artificial neural networks, the linear electro-optic effect before discussing advances in the integration of transition metal oxides LNO and BTO on Si (001), and integration of light sources on the Si platform. Our goal is to provide a compact assessment of the status of the field. Our article is only focused on the last few years of this line of research and is a combination of a brief overview with results from our own research.

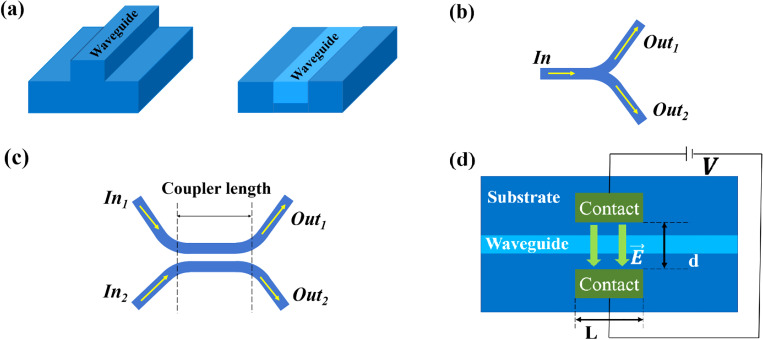
Let us consider the basic elements of hardware implementation and the fundamental reasons for their use and the advantages they offer. Surprisingly, to enable optical neuromorphic and quantum computing, one needs only four basic elements: a waveguide (straight and curved), a beam splitter (Y-junction), a directional coupler, and a waveguide phase shifter. Only the last one is an active device that requires power, and the rest in the ideal case are lossless and require no power at all to operate. We show the schematics of these elements in Fig. 2. In Fig. 2(a), we show so-called rib and embedded, straight waveguides. The mode confinement is achieved through the difference in the refractive index of the rib and surrounding air or between the waveguide and the embedding material with a lower index. In Fig. 2(b), we show a Y-junction where the original waveguide splits into two identical waveguides of the same type. The directional coupler is shown in Fig. 2(c), and a top view of a waveguide phase shifter/modulator is shown in Fig. 2(d). The passive devices based on a rib waveguide can be simply etched in Si using standard fabrication methods, while the embedded waveguide requires a somewhat more involved fabrication process. The waveguide modulator, described in more detail below, is the nontrivial active element and is the protagonist of this story.

FIG. 2.

(a) Schematics of a rib and embedded waveguide, (b) symmetric 50/50 Y-junction, and (c) directional coupler. (d) A top view of a waveguide phase shifter with an EO active waveguide. Contacts provide the electric field that changes the refractive index in the waveguide via a linear EO effect, which results in additional phase $\frac{2\pi }{\lambda }r\frac{V}{d}L$, where λ is the wavelength of light, V is voltage, r is the EO coefficient, L is the length of the electrodes, and d is their separation. The waveguide dimensions vary with the wavelength and the waveguide material; but at 1.55 μm on a standard silicon-on-insulator (SOI) wafer (220 nm silicon on 2 μm SiO₂), the single mode waveguide is 450–550 nm wide.

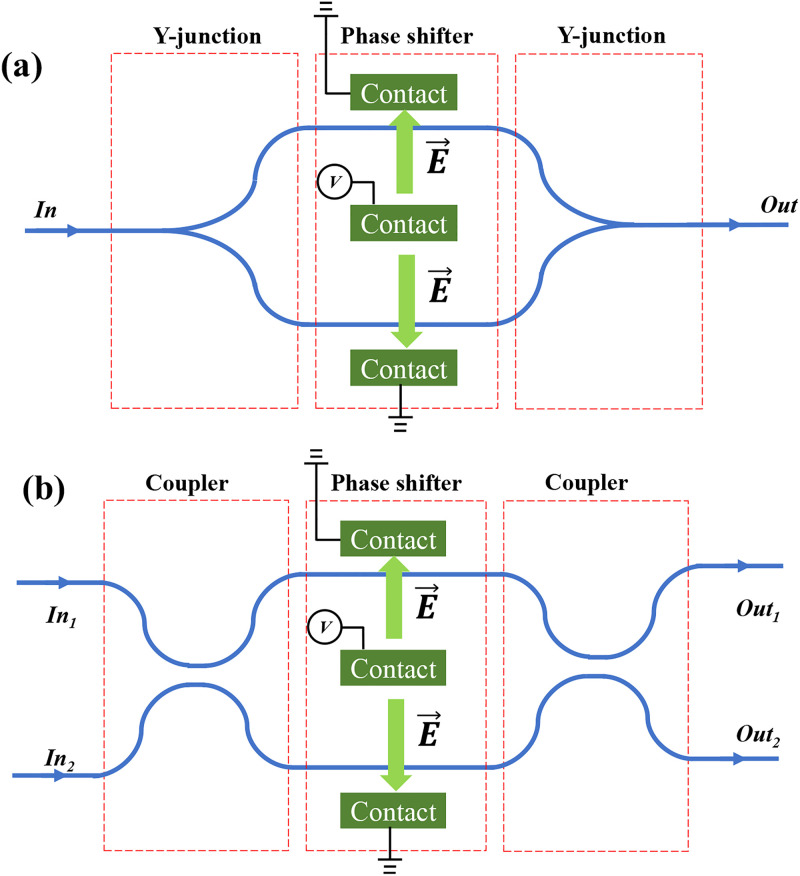
In Fig. 3, we show how, by assembling these four elements, one can build two active optical devices known as scalar and vector MZIs. Both devices comprise three parts. In the case of a scalar MZI, they are a beam splitter (Y-junction), a phase shifter or phase shifters in one or two parallel waveguides, and a beam combiner (a reverse Y-junction). For the vector MZI, the Y-junctions are substituted with directional couplers. To describe the propagation of the guided mode [most often transverse electric (TE) mode], it is convenient to use the transfer-matrix formalism, sometimes known as the beam propagation method.²⁷ The 2 × 2 transfer matrix relates the output signal to the input signal representing the amplitudes of the electric field of the guided waves. The transfer matrices for the four elements are listed in Table I.

FIG. 3.

(a) Scalar MZI comprises three parts, a beam splitter, a phase shifter, and a beam combiner. The overall effect on the incoming signal is multiplication by $\cos (\phi )$. (b) Vector MZI is a four-port device where the phase shifter is sandwiched between two directional couplers.

TABLE I.

Transfer matrices for simple optical devices.

Device	Figure	Type	Transfer matrix
Y-junction splitter	2(b)	Passive	${\displaystyle M_Y=\left(\begin{array}{c}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right)}$
Y-junction combiner		Passive	${\displaystyle M_Y^T=\left(\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)=\frac{1}{\sqrt{2}}}$
Phase shifter/modulator	2(d)	Active	${\displaystyle M_{shifter}\left(\begin{array}{cc}{e}^{i\phi }& 0\\ 0& e^{-i\phi }\end{array}\right)}$
Directional coupler	2(c)	Passive	${\displaystyle M_{coupler}=\left(\begin{array}{cc}\frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right)}$
Scalar MZI	3(a)	Active	$\begin{array}{rl}{M}_{MZIS}=M_Y^T{M}_{shifter}{M}_Y& =\left(\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right)\left(\begin{array}{cc}{e}^{i\phi }& 0\\ 0& e^{-i\phi }\end{array}\right)\left(\begin{array}{c}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right)=\cos (\phi )\end{array}$
Vector MZI	3(b)	Active	$\begin{array}{rl}{M}_{MZIV}=M_{coupler}{M}_{shifter}{M}_{coupler}& =\frac{1}{2}\left(\begin{array}{cc}1& -1\\ 1& 1\end{array}\right)\left(\begin{array}{cc}{e}^{i\phi }& 0\\ 0& e^{-i\phi }\end{array}\right)\left(\begin{array}{cc}1& -1\\ 1& 1\end{array}\right)\\ & =\left(\begin{array}{cc}\mathrm{i}\sin (\phi )& -\cos (\phi )\\ \cos (\phi )& -\mathrm{i}\sin (\phi )\end{array}\right)\end{array}$

Consider a signal being split 50/50 (in terms of optical power) by a Y-junction that we call a splitter. If we focus just on the signal amplitude (i.e., electric field), which is a scalar, this splitting can be described by a 2 × 1 transfer matrix,

$$M_Y=\left(\begin{array}{c}{\displaystyle \frac{1}{\sqrt{2}}}\\ {\displaystyle \frac{1}{\sqrt{2}}}\end{array}\right).$$

The power (a square of the output) is simply divided evenly between the two outgoing ports. If, on the other hand, we send the signal in reverse, say through the upper port [Out 1 in Fig. 2(b)], the result will be simply as follows:

$$\left(\begin{array}{cc}{\displaystyle \frac{1}{\sqrt{2}}}& {\displaystyle \frac{1}{\sqrt{2}}}\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)={\displaystyle \frac{1}{\sqrt{2}}.}$$

The transfer matrix of a combiner is, therefore, a transposed matrix of the splitter. The output power is only a half of what has been sent in, with the rest of the energy being radiated out of the waveguide.

The waveguide modulator, a four-port “device,” has one or two phase shifters, as shown in Fig. 2(d), in its arms. The shifters can induce a relative delay between the signals propagating through the arms, resulting in a relative phase shift $\phi$. The transfer matrix for such a device is as follows:

$$M_{shifter}=\left(\begin{array}{cc}{e}^{i\phi }& 0\\ 0& e^{-i\phi }\end{array}\right).$$

If we combine a splitter, a shifter, and a combiner, the corresponding transfer matrices need to be multiplied to obtain the transfer matrix of the scalar MZI (Table I). The effect of this device, as shown in Fig. 3(a), on the incoming signal is simply a multiplication by $\cos (\phi )$,

$$M_{MZIS}=M_Y^T{M}_{shifter}{M}_Y=\left(\begin{array}{cc}{\displaystyle \frac{1}{\sqrt{2}}}& {\displaystyle \frac{1}{\sqrt{2}}}\end{array}\right)\left(\begin{array}{cc}{e}^{i\phi }& 0\\ 0& e^{-i\phi }\end{array}\right)\left(\begin{array}{c}{\displaystyle \frac{1}{\sqrt{2}}}\\ {\displaystyle \frac{1}{\sqrt{2}}}\end{array}\right)=\cos (\phi ).$$

The transmitted power then will be given by $\cos {(\phi )}^2$, so if one can control the phase shift as we describe later, then this can be used as a nonlinear weight in neuromorphic computing.²⁸

We next consider a directional coupler as shown in Fig. 2(c), originally introduced in fiber optics. It consists of two waveguides that are brought sufficiently close together for the evanescent wave of one waveguide to leak out into the other. This results in two waveguides being coupled, and the transfer matrix for a lossless 50/50 directional coupler is presented in Table I.

We can now compute the transfer matrix (Table I) for the so-called vector MZI as shown in Fig. 3(b). Note that this is a unitary U(2) matrix. Each component of the output signal vector $\left(\begin{array}{c}Ou{t}_1\\ Ou{t}_2\end{array}\right)$ is a linear combination of the input signals In₁, In_2. However, the norm of the signal vector is conserved. And it is precisely this property that makes a vector MZI an ideal device for quantum computation.²⁹

The last but not least point we would like to consider is the mechanism that introduces the phase shift $\phi$ in a phase shifter. In principle, one can just use two waveguides of different lengths. The length difference ΔL will produce a phase delay of $\frac{2\pi }{\lambda }n\mathrm{\Delta }L$, (λ is the wavelength of light and n is the refractive index of the guided wave), but then, that would be a fixed value. In what follows, we will use a waveguide modulator, where a waveguide (or its segment) exhibits a linear EO or Pockels effect, i.e., the refractive index can be changed by applying an electric field. In this case, the phase shift is proportional to $\frac{2\pi }{\lambda }r\frac{V}{d}L$, where r is the Pockels or EO coefficient, V is the applied or drive voltage, d is the separation between the electrodes, and L is the length of the contact [Fig. 2(d)]. The figure of merit commonly used for these modulators is the ratio of the drive voltage to the bandwidth. Ignoring the loss and geometric factors, we can write³⁰

$${\displaystyle \frac{V}{\mathrm{\Delta }f}\sim \left({\displaystyle \frac{{\epsilon }_{eff}\mathrm{\Delta }}{n^{3}r}}\right).}$$

Here, ${\epsilon }_{eff=}\left(\frac{{\epsilon }_0}{2}\right)\left(1+\frac{{\epsilon }_s}{{\epsilon }_0}\right)$, where in the case of the embedded waveguide ${\epsilon }_s$ is the dielectric constant of the substrate, $\mathrm{\Delta }=1-\frac{N_0}{N_m}$, where $N_0$ is the effective index of the guided mode, $N_m=\sqrt{{\epsilon }_{eff}}$, and n and r are the refractive index and the EO coefficient, respectively. For any neuromorphic computing device, we want to keep the voltage low and the modulation to be broadband, and therefore, a large EO coefficient is a must. For applications in silicon photonics, integrability with Si is another important consideration, which points us toward LNO and BTO. Other materials have been integrated with Si photonics; for a recent review, see Rahim et al.³¹ As we shall see, inorganic ferroelectrics offer many advantages and are the focus of this Perspective.

Neuromorphic computing encompasses a wide variety of application domains from visual recognition to classification, forecasting and decision-making. These are all information acquisition/processing/inference tasks, but they are also diverse. Nature has produced different optimal solutions for these tasks, many of them organism-specific. There are also different models of how the brain processes information, which leads to competition between diverse ways of planning, designing, and building brain-inspired chips. One goal is a 3D integrated and selectively trainable neuronal network (NNs) using novel integrated electro-photonic synaptic interconnects integrated on Si. Like biological neuronal networks, these new artificially intelligent neuromorphic chips can learn and adapt to various inputs and outputs by means of modulation, reconfiguration, and storage of internal states.

Classical artificial and trainable NNs consist of computational neuronal units (layers) that transform or map input vectors from some finite dimensional Hilbert space to an output Hilbert space via one or more tensor layers. It is considered a “deep” network if at least one of these tensor layers is “hidden,” meaning that it allows for intermediate (latent) variable calculation and memory (storage).^32,33 Each layer is comprised of a number of artificial neurons mathematically representing a 3D matrix (order-3 tensor) of parameters that multi-linearly transforms the output from the previous layer. Multi-linear parametric transforms or cascadic feature mapping allows approximating the output as a multivariate polynomial of the input, possibly in very high dimensions. To allow for non-linear analytic function transforms, nonlinear activation functions, such as a sigmoid or a rectified linear unit, can be added between the cascadic network layers.

An optimal non-linear and high dimensional approximation or the model is learned, directly from input–output data, by the neuronal network. Training or teaching a neural network to learn the “best” model consists of running repeated iterations of twin passes: a forward pass, or propagation parametric mapping step, from input to output, followed by a backward pass, or propagation parameter update and tuning step from output to input. In the forward propagation step, the current instance of the parametric map of the neural network is used to make a prediction of the output based on the input, which is then compared to the actual output using an accuracy (or loss) metric. Using the gradient of this loss metric, and with respect to all the current parameters, akin to a corrective force vector, a stochastic gradient descent technique is used to update the tensorial parameters of the model. Effectively, the deep neural network architecture allows nonlinearities to compound at each layer, permitting the approximation of highly nonlinear function models.³⁴

A major disadvantage of NNs is that typically there is a huge number of tensorial parameters that need to be trained (by iterative updates in each backward pass). However, the hidden layers of reservoir computing (RC) architectures do not need to be trained. These hidden layers consist of randomly connected (recurrent) neural units. The only part of the system that is trained is the output layer parameters; the input and the tensorial parameters of the neural nodes within the reservoir are kept fixed. This leads to a simpler NN design and training process and is more efficient in practice than what is required for traditional deep neural networks.³⁵ Indeed, given this and their demonstrable learning ability of dynamical systems, recurrent (or recursive) layers form an initial choice for the reservoir pool for neuromorphic chips, which flourish in applications that include learning neuromorphic behavior, such as natural language speech recognition,³⁶ and modeling of neuromorphic dynamical systems as described above.³⁷

RC is also a computational framework suited for temporal/sequential stream data processing.³⁸ This computing system consists of a reservoir for mapping inputs into a high-dimensional space and a readout for pattern analysis from the high-dimensional states in the reservoir. The reservoir is fixed, and only the readout is trained with a simple method such as linear regression and classification. The major advantage of reservoir computing compared to other NNs is its fast learning, which reduces training cost.

A few different types of reservoirs are currently recognized. A first type is derived from several recurrent neural network (RNN) models, including Liquid State Machine (LSM),³⁹ Echo State Networks (ESNs),⁴⁰ and Backpropagation Decorrelation (BPDC)⁴¹ (herein referred to as “RNN-reservoirs”). Proposed LSMs generally have reservoirs built using the Leaky Integrate and Fire (LIF) neurons⁴² with a dynamic synapse model. On the other hand, ESNs have been proposed to have reservoirs built from analog sigmoidal neurons. Spiking neuron (SN) models are more complex than sigmoidal neurons and are computationally more powerful.^43–45 The readout layer for these SN models can approximate any continuous function over a compact set in an n-D space of input values. A second type replaces the RNN with a single node modeled as a delayed differential equation (DDE) (herein referred to as “delayed reservoirs”).⁴⁶ Several studies show that the reservoir can be successfully implemented as a single time-delayed dynamical node characterized by complex dynamics, for example, by an electronic implementation of the chaotic time-delayed Mackey–Glass equation⁴⁷ or by a multi-stable time-delayed optoelectronic oscillator.⁴⁸

Taken together, all these observations point to the potential of time-delayed, multi-stable integrated neuromorphic computer (MINC) devices with adjustable connectivity and reconfigurability within and across neuronal motifs. Progressive designs of trainable MINC devices combine optoelectronic hardware and firmware and possess the programmable granularity of synaptic variability and adjustable network connectivity at very low power.

Knowledge is needed to assess whether model systems properly represent neurological brain functions. Current approaches are limited by resolution, inefficient and insufficient data collection, analysis bottlenecks, and the use and dissemination of brain structure-functional data. The field of computational neuroscience is developing very rapidly, as new mathematical models emerge and capture our new knowledge and understanding of cognition and decision making.^49,50

LINEAR ELECTRO-OPTIC (POCKELS) EFFECT

Let us now discuss the physics that enables the fabrication of ultra-compact, low-power, and ultra-fast electro-optic modulators that will enable the computational revolution we have discussed. The linear electro-optic (EO), or Pockels, effect describes the change of the refractive index of a crystal under an applied electric field. Being linear in the applied field, it exists only in non-centrosymmetric crystals. Originally introduced in the context of a change in the indices of refraction that define the optical indicatrix as follows:⁵¹

$$\mathrm{\Delta }\left({\displaystyle \frac{1}{n_{ij}^2}}\right)=\mathrm{\Delta }{({ϵ}_{ij})}^{-1}=\sum _{\gamma }{r}_{ij\gamma }{E}_{\gamma },$$ (1)

it can also be written as the first-order change to the dielectric tensor induced by an applied electric field $E_{\gamma }$,⁵²

$$d{ϵ}_{ij}=-\sum _k{r}_{ij\gamma }{ϵ}_{ii}{ϵ}_{jj}d{E}_{\gamma }(\omega ).$$ (2)

In piezoelectric crystals such as BTO, one needs to take into account the lattice response to the electric field that in turn affects the dielectric tensor. Therefore, we expand the full differential of the dielectric tensor into purely electronic, ionic, and piezoelectric contributions,

$$\begin{array}{rl}{\left[{\displaystyle \frac{d{\epsilon }_{ij}(R,{\eta }_0,E)}{d{E}_{\gamma }}}\right]}_{R_{0,{\eta }_o}E=0}& ={\left[{\displaystyle \frac{\mathrm{\partial }{\epsilon }_{ij}(R_0,{\eta }_0,E)}{\mathrm{\partial }{E}_{\gamma }}}\right]}_{E=0}+4\pi \sum _{k,\alpha }{\left[{\displaystyle \frac{\mathrm{\partial }{\chi }_{ij}^{(1)}(R,{\eta }_0)}{\mathrm{\partial }{\tau }_{k\alpha }}}\right]}_{R_0}{\tau }_{k\alpha }^{E_{\gamma }}\\ & & +4\pi \sum _{\mu ,\nu =1}^3{\left[{\displaystyle \frac{\mathrm{\partial }{\chi }_{ij}^{(1)}(R_o,\eta )}{\mathrm{\partial }{\eta }_{\mu \nu }}}\right]}_{{\eta }_o}{\eta }_{\mu \nu }^{E_{\gamma }}.\end{array}$$ (3)

Here, $E_{\gamma }$ is the electric field component in the direction γ, R is the ionic coordinates, ${\eta }_{\mu \nu }$ is the (μ,ν) element of the strain tensor describing the distortion due to the electric field, the naught refers to values at equilibrium, ${\chi }_{ij}^{(1)}$ is the electronic susceptibility, and ${\tau }_{\kappa \alpha }$ is the displacement of atom κ in the α direction. The superscript “$E_{\gamma }$” denotes a derivative being taken with respect to that variable.

The first term on the right-hand side (RHS) of Eq. (3) represents the purely electronic contribution and comes from the interaction of the field with the valence electrons, assuming the ions to be clamped at their equilibrium positions. It is related to the second-harmonic generation (SHG) effect and can be written in terms of ${\chi }^{(2)}$.

The second term on the RHS of Eq. (3) is the ionic response of the crystal and describes the effect of the movement of the ions, assuming the lattice is held fixed (clamped). The derivative of the electronic susceptibility ${\chi }_{ij}^{(1)}$ with respect to the ionic displacement is essentially the Raman susceptibility.⁵³ It is useful to express the derivative of the ionic displacement with respect to the electric field in terms of the mode polarity, a product of the Born effective charge $Z_{k^{\mathrm{\prime }}\gamma \beta }^{\ast }$ and the phonon eigendisplacements $u_m(k^{\mathrm{\prime }}\beta )$.⁵³ Thus, the ionic contribution to the EO tensor is a sum over the mode-dependent product of the mode polarity, the Raman susceptibility, and the inverse square of the phonon frequencies,

$$4\pi \sum _m{\displaystyle \frac{1}{{\omega }_m^2}\left(\sum _{k\alpha }{\displaystyle \frac{\mathrm{\partial }{\chi }_{ij}^{(1)}(R)}{\mathrm{\partial }{\tau }_{k\alpha }}{u}_m(k\alpha )}\right)\left(\sum _{k^{\mathrm{\prime }}\beta }{Z}_{k^{\mathrm{\prime }}\gamma \beta }^{\ast }{u}_m(k^{\mathrm{\prime }}\beta )\right).}$$ (4)

The ionic term often dominates the clamped Pockels response in perovskites, including unstrained and strained BTO,^53,54 strained SrTiO₃ (STO),⁵⁵ and strained PbTiO₃ (PTO).⁵⁶ This form offers a simple physical picture of what drives a strong EO effect in the intermediate frequency range when optical phonons can be engaged; one needs strong electron—phonon coupling (the Raman susceptibility) and soft modes (a small denominator ${\omega }_m^2$).

The last term on the RHS of Eq. (3) represents the converse piezoelectric effect. It is the low-frequency response involving acoustic phonons. If the frequency of the applied electric field is too high, the crystal will be “clamped” and the lattice vectors will not change; but if the applied field frequency is low enough, the full “unclamped” response is achieved. The piezoelectric response can be written in terms of the piezoelectric strain coefficients $d_{\gamma \mu \nu }$ and elasto-optic coefficients $p_{ij\mu \nu }$.⁵³ In some situations, this term can be the dominant contribution to the Pockels tensor,⁵⁶ but typically its magnitude is approximately 10% the ionic contribution.^55–58

Altogether, the unclamped Pockels tensor (for a low-frequency external field) in the principal axes of the crystal is given by

$$r_{ij\gamma }^{\sigma }=-{{\displaystyle \frac{8\pi }{n_i^2{n}_j^2}{\chi }_{ijl}^{(2)}}|}_{l=\gamma }+-{\displaystyle \frac{4\pi }{\sqrt{{\mathrm{\Omega }}_0}{n}_i^2{n}_j^2}{\sum }_m{\displaystyle \frac{{\alpha }_{ij}^m{p}_{m,\gamma }}{{\omega }_m^2}}+{\sum }_{\mu ,\nu =1}^3{p}_{ij\mu \nu }{d}_{\gamma \mu \nu },}$$ (5)

where n is the index of refraction, ${\chi }^{(2)}$ is the non-linear susceptibility, ${\mathrm{\Omega }}_0$ is the volume of the unit cell, ${\alpha }_{ij}^m=\sqrt{{\mathrm{\Omega }}_0}{\sum }_{\kappa ,\beta }{u}_m(\kappa \beta )\times \mathrm{\partial }{\chi }_{ij}^{(1)}/\mathrm{\partial }{\tau }_{\kappa \beta }$ is the Raman susceptibility, $p_{m,\gamma }={\sum }_{\kappa ,\beta }{Z}_{\kappa ,\gamma \beta }^{\ast }{u}_m(\kappa \beta )$ is the mode polarity, $u_m$ is the eigendisplacement of mode m, and ${\omega }_m$ is the frequency of phonon mode m. The first two terms of Eq. (5) are the clamped Pockels tensor, commonly denoted $r_{ij\gamma }^{\eta }$.

INTEGRATION OF LINBO₃ AND BATIO₃ ON SI

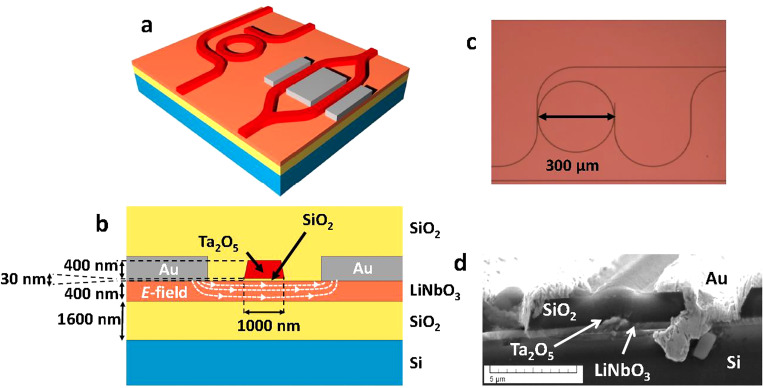
Lithium niobate (LiNbO₃) or LNO is an almost ideal material for applications in integrated Si photonics. It is transparent in a very wide spectral range from 0.35 to 5 μm and optical gain can be achieved in crystals doped with Er or other rare earth elements.⁵⁹ Most importantly, LNO shows strong second-order nonlinearity via the EO effect. This enables the control of the refractive index, second harmonic generation, mixing optical signals at different wavelengths for parametric amplification, wavelength conversion, and generation of entangled photon pairs.⁶⁰ It is the perfect material for EO modulators as it allows pure phase modulation with no variation in absorption. Hybrid Si-LNO resonators on Si have been introduced by Lee and co-workers who fabricated them on a silicon-on-insulator platform using a standard 0.18 μm CMOS process.⁶¹ However, the efficiency of the EO effect was not very high. A more promising way to integrate LNO on Si has been discussed by Rabie et al.⁶² A thin layer of LNO was integrated on Si via wafer bonding with SiO₂ bottom cladding and rib structures made of Ta₂O₅ deposited on LNO to form ridge waveguides. This approach avoids both the need to etch LNO and high bending losses. They demonstrated micro-ring optical resonators and Mach–Zehnder optical modulators. A quality factor of ∼7.2 × 10⁴ was measured in the micro-resonators, and a half-wave voltage-length product of 4 V cm and an extinction ratio of 20 dB were measured in the modulators. We show their devices in Fig. 4.

FIG. 4.

(a) Schematics of the demonstrated microring resonators and Mach–Zehnder modulators are shown. The top SiO₂ cladding layer and the ultrathin SiO₂ diffusion barrier shown in (b) are omitted here for simplification. The dimensions are not in scale. (b) Cross section of the waveguide structure at one arm of the modulator with typical dimensions. The different layers are Si (substrate), SiO₂ (claddings and diffusion barrier regions), LiNbO₃ (core and active region), Ta₂O₅ (loaded rib), and Au (metallic contact). Shown also is a simplistic RF electric-field profile in the LiNbO₃ active region; (c) top-view high-magnification optical microscope image of a fabricated ring-resonator with input and output bent bus waveguides; (d) SEM image of a cross section of a fabricated waveguide. Reproduced with permission from Rabiei et al., Opt. Express 21, 25573–25581 (2013). Copyright 2013, Optical Society of America.

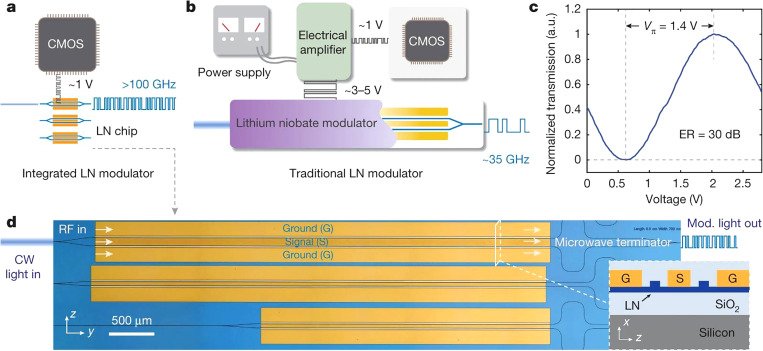
After these feasibility studies, three questions still need to be addressed before deeming the technology viable. To that end, one needs to simultaneously achieve low switching voltage, high bandwidth, and low optical loss. Recently, Wang and co-authors⁶³ demonstrated a monolithically integrated LNO modulator supporting high bandwidth with a switching voltage of just 1.4 V, which is a CMOS-compatible drive voltage. The modulator supported data rates up to 210 gigabits per second and showed an on-chip optical loss of less than 0.5 dB. The modulator operated in a traveling wave Mach–Zehnder interferometer configuration. We show their device in Fig. 5. The interferometer is based on a 50:50 Y-junction that forms two LNO waveguides running through the dielectric gaps of a ground-signal-ground coplanar microwave strip [Fig. 5(d)]. For a 20 mm device, a V_π voltage of 1.4 V has been recorded. The same device showed a high 3-dB bandwidth of more than 45 GHz. The devices were fabricated from a commercial x-cut LNO-on-insulator wafer, where a 600-nm device layer is placed on a SiO₂/Si substrate. These NanoLN wafers are created via a two-step process. First, the LNO crystal is sliced using the same SmartCut technology as employed in the fabrication of regular SOI wafers, and then these free standing LNO membranes are bonded to a SiO₂ layer deposited on a carrier insulating wafer.⁶⁴ Usually, it is an LNO substrate but can also be Si or other insulator.

FIG. 5.

Nanophotonic LN modulators compatible with CMOS drive voltages. (a) and (b) Schematic comparison of the data-transmitting setups for integrated (a) and traditional (b) LN modulators. The nanophotonic LN modulator (a) supports direct CMOS driving with high bandwidths (>100 GHz), while traditional modulators (b) require large and power-consuming electrical driver amplifiers and have limited bandwidths (approximately 35 GHz). (c) Normalized optical transmission of a 20-mm device as a function of the applied voltage, showing a low half-wave voltage of 1.4 V. The measured extinction ratio is 30 dB. (d) Microscope image of the fabricated chip consisting of three Mach–Zehnder modulators with various microwave signal linewidths and device lengths. The thin-film configuration allows for maximum field overlap and velocity matching between microwave and optics. Inset shows the cross-sectional schematic of the nanophotonic LN modulator. Mod, modulated; RF, radiofrequency. Reproduced with permission from Wang et al., Nature 562, 101–104 (2018). Copyright 2018, Springer Nature.

A slightly different approach to using LNO in MZ modulators has been recently proposed by He et al.⁶⁵ They used a hybrid LNO/Si approach, but the EO effect still occurred in the LNO waveguides fabricated by dry etching the x-cut LNO membrane. They reported an insertion loss as low as 2.5 dB, EO bandwidth of at least 70 GHz, and modulation rates up to 112 Gbit s⁻¹.

Barium titanate (BaTiO₃) or BTO is optically transparent and has high refractive indices (n_o = 2.437 and n_e = 2.365) at the 1550-nm optical wavelength that is critical for dense wavelength division multiplexing, allowing one to leverage the capabilities and the cost advantage of Er-doped fiber amplifiers and low attenuation in the optical fiber. Integration of EO active films with Si chips would pave the way toward power-efficient, ultra-compact integrated devices, such as interconnects, modulators, tuning elements, and bi-stable switches. Bulk BTO has a giant Pockels responses at 1550 nm (r₄₂= 1,300 pm/V),⁵⁷ and EO devices featuring BTO integrated on MgO operating at a wavelength of 632 nm have been reported,⁶⁶ indicating that BTO maintains a strong EO response in the visible spectrum.

Over 20 years ago, McKee and co-workers discovered a way to epitaxially integrate STO on Si (001) and then BTO on Ge (001)⁶⁷ using molecular beam epitaxy (MBE). The key element of their approach to integration of the perovskite STO on Si was to use a Sr sub-monolayer template⁶⁸ followed by a SrO buffer that prevented oxidation of the Si substrate;⁶⁹ the formation of the amorphous oxide SiO₂ during the STO growth would have completely eliminated any hope of crystalline epitaxy. Following this work, Droopad et al. have developed an industrial process of depositing STO on 8″ Si (001) using MBE.⁷⁰ This approach, known as the “Motorola process,” is at the heart of all current methods of growing epitaxial BTO on Si (001). At the beginning of the Motorola process, the low-temperature Sr-assisted desorption of native SiO₂⁷¹ is followed by growth of a thin STO buffer, which serves as the pseudo-substrate is used for the subsequent epitaxy of BTO. It was later shown that while the initial layers of BTO are oriented with the c-axis normal to the film's surface for thicknesses over 25 nm, the film transitions to being a-axis oriented with the long axis parallel to the surface.⁷²

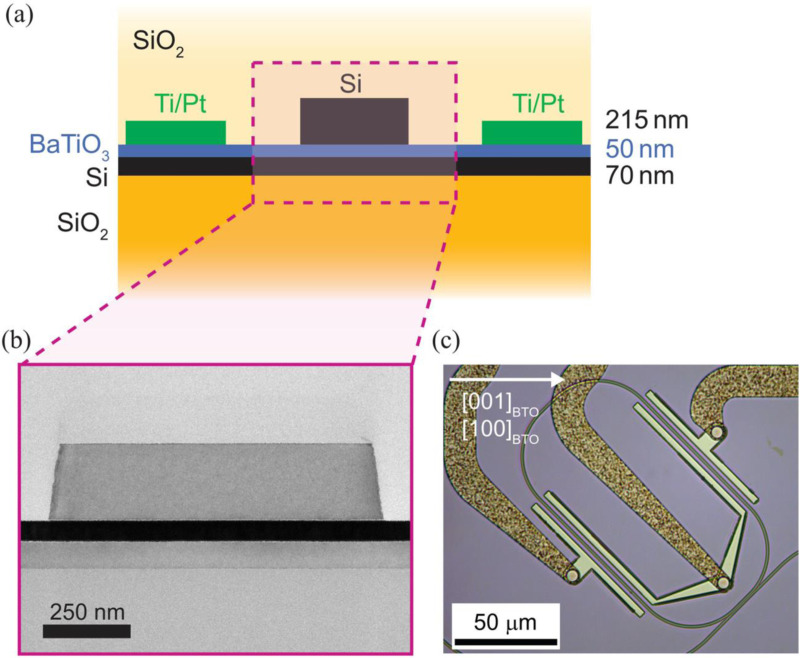
In 2013, Abel and co-workers reported a large effective Pockels coefficient of 148 pm V⁻¹ extracted from a 130 nm BTO film epitaxially integrated on Si (001) via a 4 nm-thick STO buffer by MBE.⁷³ It was believed that the majority of BTO was a-oriented meaning the long c-axis of tetragonal 4 mm BTO is oriented parallel to the film surface. As the Si substrate is cubic, there are two possible orthogonal orientations of the c-axis, corresponding to two possible domains. The population ratio of these domains was assumed to be 50:50. The x-ray diffractometry and high resolution scanning electron microscopy confirmed both assumptions. The use of electrodes that allowed for different orientations of the electric field with respect to the crystal axes clearly indicated the tensor nature of the EO effect. Though the individual tensor components were found significantly smaller than in bulk BTO (r₄₂ was estimated to be only 105 pm V⁻¹), the effective Pockels coefficient was still five times larger than that of bulk LNO. Three years later, the same group reported a racetrack resonator and a Mach–Zehnder modulator using a hybrid Si-BTO technology based on BTO epitaxially grown on Si.⁷⁴ The half-way etched Si waveguides were fabricated by depositing a 220 nm-thick layer of hydrogenated amorphous Si (a-Si:H) by plasma-enhanced chemical vapor deposition (PECVD) on a 50 nm thick BTO integrated on Si. In Fig. 6, we show the resulting racetrack resonator. While the propagation losses were relatively high (47 and 98 dB/cm for the TE and TM modes, respectively), the bend loss of less than 0.1 dB per 90° for a bending radius of <5 μm was quite promising.

FIG. 6.

(a) Schematics of an active HE-type BaTiO₃ slotted waveguide structure. The thickness of the titanium/platinum electrodes is 150 nm. (b) STEM cross section of the slotted-waveguide core. The upper silicon layer of this particular structure (HE stands for half-way etched) is crystalline silicon, but it is typically replaced by a-Si:H to remove the interfacial SrTiO₃ layer and thus lower the propagation losses. (c) Optical microscopy image of a fully processed, active racetrack resonator with electrodes oriented at 45° relative to the main crystalline axes of the BaTiO₃ layer (indicated by the white arrow). Reproduced with permission from Abel et al., J. Lightwave Technol. 34, 1688 (2016). Copyright 2016, Optical Society of America.

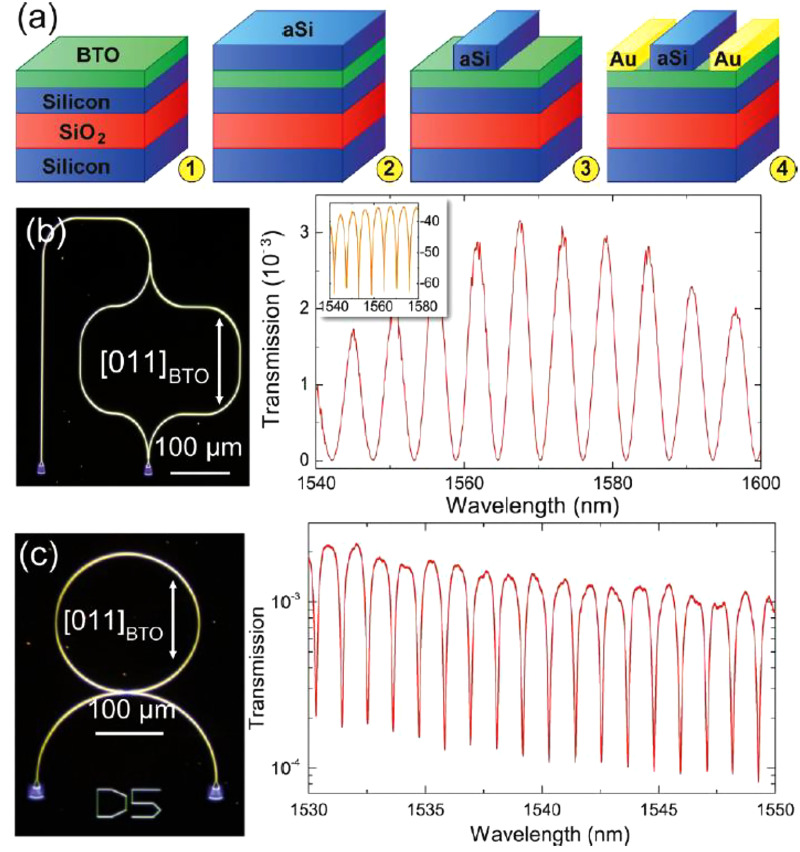
Xiong and co-workers extracted an even larger effective electro-optic coefficient of 213 ± 49 pm/V in the Si-integrated BTO thin films using a Mach−Zehnder interferometric device.⁷⁵ An 8 nm (20 unit cell) STO buffer was grown on the undoped device layer of the SOI substrate, and an 80 nm-thick layer of BTO was grown on that buffer. At a wavelength of 1550 nm, compared to silicon, BTO has a lower refractive index (n_BTO = 2.38, n_Si= 3.47), hence, conventional rib and strip waveguides prevent optical confinement in the BTO layer. Xiong et al. designed a horizontal slot waveguide consisting of a thin BTO layer sandwiched between two high-index silicon layers.

The device layer of the SOI substrate served as the lower Si layer, and a layer of amorphous undoped silicon (a-Si) of same thickness served as the upper Si layer. Plasma-deposited amorphous Si supports low-loss optical transmission at 1550 nm. The actual waveguide was lithographically patterned into a-Si. With this approach, they fabricated electrically driven Mach−Zehnder interferometers and micro-racetrack resonators that enable electro-optic modulation up to 4.9 GHz. The devices and fabrication schematic are shown in Fig. 7. Loaded optical Q factors of 7000 were extracted from fitting the resonance dip with a Lorentzian curve. A propagation loss of 44 dB/cm was determined using the relation α = 10 log10 e⋅2πn_g/Q_intλ (where Q_int is the intrinsic quality factor, λ is the wavelength, and n_g is the group index).

FIG. 7.

Si-integrated BTO waveguide devices. (a) Fabrication flow for the integrated BTO modulators. (a1) Epitaxial growth of an 80 nm thick film of BTO on STO/SOI. (a2) PECVD of 110 nm thick amorphous silicon on BTO. (a3) Nanolithography and patterning of a-Si waveguides. (a4) Lithography and patterning of the Ti/Au electrodes. (b) Optical micrograph of a BTO on SOI MZI. The straight segment of the MZI arm is aligned to BTO lattice's [011] direction. The optical transmission is shown in both linear (right) and log scale (inset). The extinction ratio of the MZI is 25 dB. (c) Optical micrograph of a microring resonator slot waveguide. BTO lattice's [011] direction is shown as a reference. The radius of the ring shown is 100 μm, and the typical loaded optical Q-factor is 7000. The optical transmission is shown on the right. Reproduced with permission from ACS Nano Lett. 14, 14195 (2014). Copyright 2014, American Chemical Society.

It soon became clear that high optical propagation losses in the range of 40−600 dB/cm limit the performance of BTO-Si EO devices when compared with state-of-the-art silicon photonic devices (<2 dB/cm). Eltes and co-workers were able to identify the origin of these high propagation losses and demonstrate a path to fabricate low-loss BTO−Si waveguides (see Fig. 8) with propagation losses of only 6 dB/cm (see Fig. 8).⁷⁶ They identified the thin STO buffer used for the epitaxial deposition of BTO on silicon as the main source of absorption. During the fabrication of slot-waveguide structures, the BTO/STO layer stack is exposed to hydrogen and it is the hydrogen incorporated in the STO layer that causes absorption. It was found that a low-temperature anneal at 350 °C in oxygen for 60 min was sufficient to remove hydrogen and significantly reduce propagation losses in waveguides significantly. This eliminated the showstopper for incorporating functional and highly nonlinear BTO films into silicon photonic structures.⁷⁶ Si waveguides were fabricated by wafer bonding the original wafer with integrated BTO onto another SOI wafer using a 5 nm Al₂O₃ adhesion layer deposited by atomic layer deposition (ALD). The original Si was then largely removed by grinding and selective etching leaving behind only the device Si layer. This Si was then used to fabricate the waveguides using electron beam lithography (EBL), and losses as low as 6 dB/cm have been reported for slot waveguides.⁷⁶

FIG. 8.

STEM images of a BaTiO₃−Si slot waveguide. (a) BF-STEM image showing the full waveguide cross section. The cladding is platinum from sample preparation. (b) HAADF-STEM image showing the Al₂O₃ interface after wafer bonding. (c) HAADF-STEM image showing the SrTiO₃ seed layer. Reproduced with permission from Eltes et al. from ACS Photonics 3, 1698 (2016). Copyright 2016, American Chemical Society.

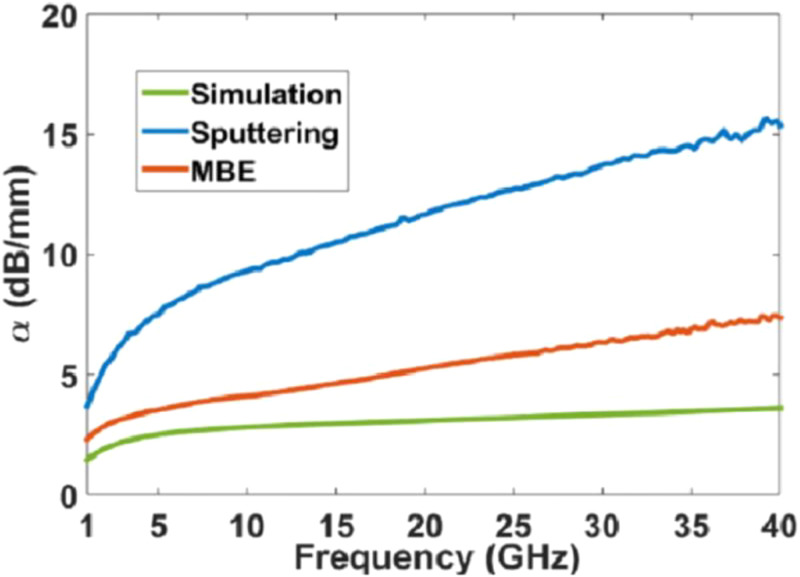
For high-speed applications, the design of the RF electrodes depends critically on the relative permittivity of the BTO film. In bulk single domain clamped crystals, it varies between 56 and 2200 for the directions parallel and perpendicular to the optical axis.⁷⁷ For BTO thin films deposited on a silicon-on-insulator (SOI) substrate, values between 800 and 1600 have been estimated at 20 GHz.⁷⁷ To do the measurement, the BTO layer was covered by a 500 nm-thick PECVD SiO₂ layer, and Al coplanar waveguides (CPW) were fabricated atop it (Al thickness was 750 nm). The permittivity was extracted using a multi-line method. The measured permittivity has been used to properly design the RF electrodes for high-speed modulation and modulation bandwidths up to 40 GHz have been demonstrated. The bandwidth was limited by the microwave propagation losses and, in this case, different losses have been measured depending on the BTO growth process. Coplanar strip line (CPS) electrodes in the traveling wave configuration used in the study allowed for the measurement of dielectric losses as shown in Fig. 9.⁷⁷

FIG. 9.

Simulated and experimental microwave propagation losses of the CPS electrode as a function of RF frequency. In the simulation, only conductor losses were included. Reproduced with permission from Opt. Mater. Express 7, 12 (2017). Copyright 2017, Optical Society of America.

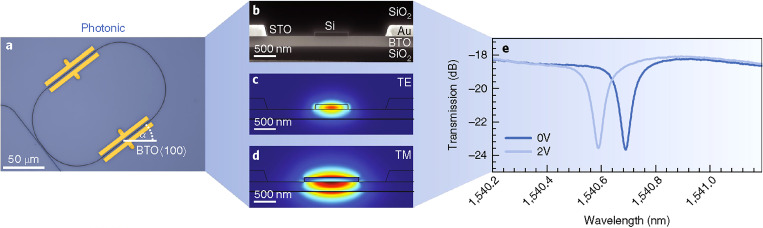
Abel and co-workers tested the anisotropy and frequency behavior of the EO response of Si-integrated racetrack resonators with differently oriented straight sections relative to the BTO crystalline axes [Fig. 10(a)].⁷⁸ The structures have a relatively small footprint (∼100 × 100 μm²), which allowed the fabrication of devices of different orientation to probe the angular dependence of the EO response and confirm its tensor nature. A constant EO response up to 30 GHz was measured in a ring modulator with Q = 9 × 10³ with data rates of 40 Gbit s⁻¹.

FIG. 10.

Layout of the photonic device. (a) False-color optical microscopy image of a photonic ring resonator before fabrication of contact pads. Angle α indicates the orientation of the straight section relative to the BTO ⟨100⟩ axis (pseudo-cubic notation). Waveguides are shown in black, the BTO surface in blue, and the electrodes in yellow. (b) Scanning electron microscopy (SEM) cross-sectional image of the photonic devices between the electrodes. (c) and (d) Simulated mode profiles of the photonic TE (c) and TM (d) modes, respectively (see Methods). The colors indicate the electric field strength, ranging from blue (low) to red (high). (e) Exemplary transmission spectra of a photonic racetrack resonator for two different bias voltages. The EO response is calculated based on the shift of the resonance wavelength. Reproduced with permission from Nat. Mater. 18, 42 (2019). Copyright 2019, Springer Nature.

The fabrication process combined monolithic integration and direct wafer bonding. First, 80- to 225-nm-thick BTO layers were grown by MBE on SOI substrates. Epitaxy to Si was achieved with a 4-nm-thick MBE-grown STO buffer. Then, the BTO layer was transferred onto another silicon wafer covered with SiO₂ via direct wafer bonding and substrate back etching using Al₂O₃ as the bonding interface. The 5- to 10-nm thick Al₂O₃ layer deposited on both the host and the donor wafer via atomic layer deposition guarantees a high bonding strength, provided the surface roughness for both wafers was below 0.4 nm. Finally, the donor wafer was removed via grinding and etching, producing the Si/STO/BTO/Al₂O₃/SiO₂/Si wafer stack. Most of these steps are fully compatible with a standard CMOS process.

The two largest non-vanishing coefficients of the Pockels tensor in the BTO layer in the photonic structures were found to be r₄₂ = 923 ± 215 and r₃₃ = 342 ± 93 pm V⁻¹. As the Pockels effect is linear, domains with opposing ferroelectric orientations induce an opposite phase shift. This results in a vanishing EO response for films with a 50:50 distribution of ferroelectric domains. The EO response saturates with increasing bias once all domains are polarized in the same direction. The measured coercive field E_c of 2 × 10⁵V m⁻¹ is in good agreement with that for BTO films on silicon of similar thickness. The EO response measured in TE photonic waveguides suggested a V_πL product of 0.45 V cm, making the device competitive with state-of-the-art integrated Si and InP EO phase shifters.

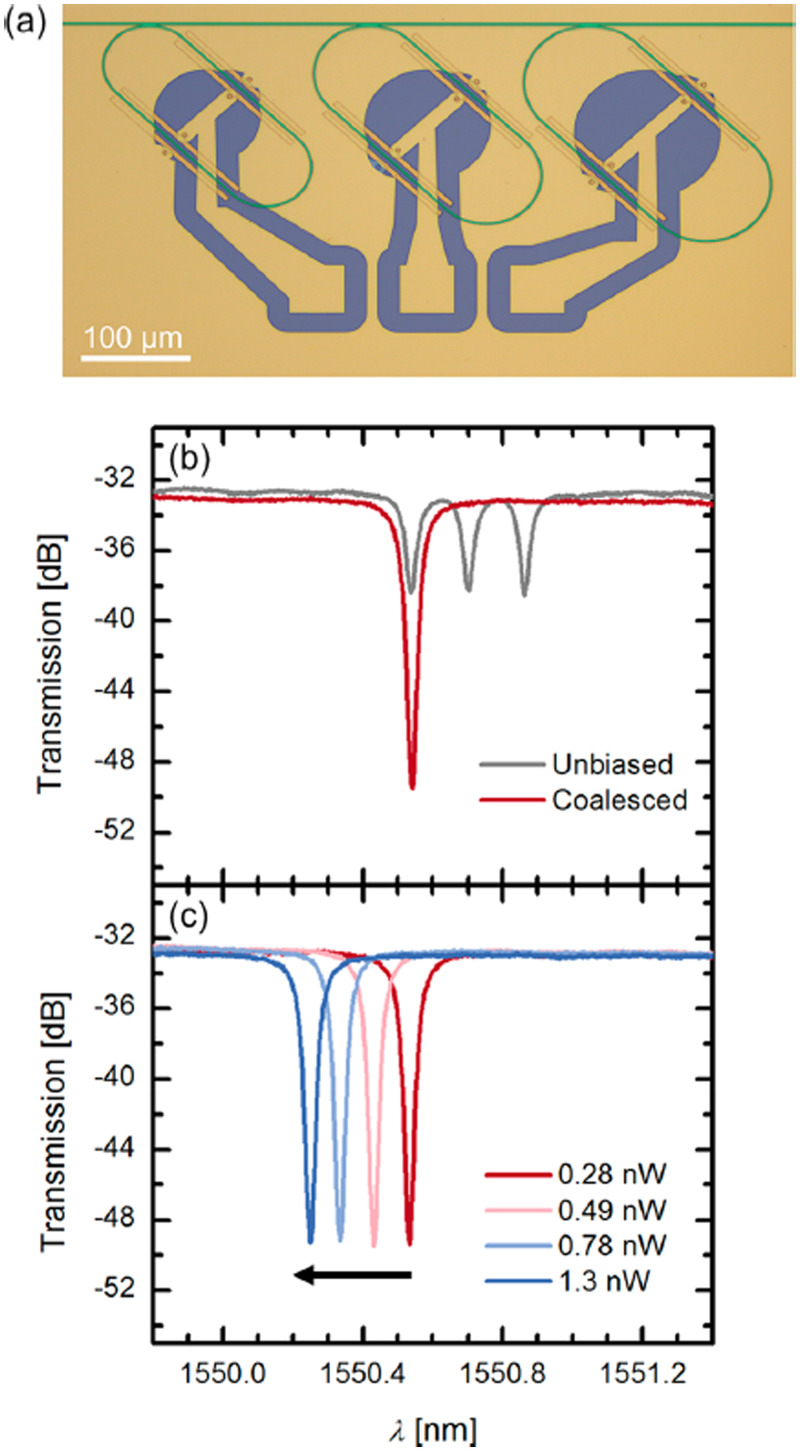
Importantly, silicon is not the only material one can use to make waveguides on Si-integrated BTO. Ortmann et al. have demonstrated ultra-low-power refractive index tuning in a hybrid BTO−silicon nitride (Si₃N₄ or SiN) platform integrated on silicon.⁷⁹ The tuning was achieved using the EO effect in BTO films of sub-100 nm thickness. The extrapolated power consumption for tuning a free spectral range (FSR) in racetrack resonator devices is only 106 nW/FSR, several orders of magnitude less than many previous reports. SiN potentially offers certain advantages over silicon-based devices, combining ultra-low-power refractive index tuning in BTO with the low optical losses available in SiN. Also, there are no mobile charge carriers in highly insulating SiN that can impact electro-optic performance. Perhaps, most importantly, due to different material absorption, the optical wavelength range available in BTO−SiN would allow operation in the visible range.

The 80 nm thick single crystal BTO films were grown by MBE on SOI substrates and transferred to thermally oxidized silicon wafers via wafer bonding. The device silicon layer of the donor wafer was removed by dry chemical etching. PECVD was used to deposit 150 nm of SiN on the BTO layer. Waveguides were formed by patterning SiN using e-beam lithography and reactive ion etching. Side electrodes, vias, cladding, and metal pads for contacting the devices were fabricated with tungsten deposition, SiO₂ deposition, and dry chemical etching. Hybrid BTO−SiN racetrack resonators were fabricated that demonstrated the ability to electrically tune the effective refractive index on the order of 10⁻³. One potential application of this hybrid device is to compensate thermal refractive index variations over a temperature range of 20 °C. Tunable multi-resonator optical filters could also be used to compensate for fabrication imperfections. In Fig. 11(a), we show such a multi-resonator tunable filter featuring three racetrack resonators coupled to a straight waveguide. Differences in resonator cavity lengths result in three distinct resonances. The individual resonances can be coalesced into a single resonance whose extinction ratio is equal to the sum of the extinction ratios of the individual resonances [Fig. 11(b)]. Most recently, the need for Si integrated cryogenic EO modulators has arisen, since in addition to radioastronomy, particle physics, and terahertz sensing, cryogenic photonics has potential applications in quantum computing and Si offers a convenient platform for this along with a vast, well-developed fabrication infrastructure.^25,80

FIG. 11.

(a) False-color optical micrograph of a multiresonator tunable filter, showing the SiN strip waveguides (green), metal electrodes (yellow), and regions of SiO₂ cladding not covered with metal (blue). (b) Unbiased (gray) and biased (red) spectra of the multiresonator filter, demonstrating the ability to coalesce individual resonances into a single resonance. (c) Coalesced resonance shifted by an external electric field. The arrow indicates the tuning direction, and the legend indicates the total tuning power. Reproduced with permission from Ortmann et al., ACS Photonics 6, 2677 (2019). Copyright 2019, American Chemical Society.

Eltes and co-workers used two waveguide designs fabricated on single crystalline BaTiO₃ layers bonded to SiO₂-buffered silicon substrates. In the first design, SiN-based waveguides allowed for a study of the purely BTO intrinsic response in the absence of mobile charge carriers that could complicate the analyses.⁸⁰ In the second design, Si waveguides were used to demonstrate high-speed data modulation. The enhanced efficiency originates from a larger optical-mode overlap with the BTO layer (41%) than with SiN waveguides (18%). The low propagation losses in the SiN device (5.6 dB/cm) were not affected by the presence of BTO throughout the temperature range. They have reported a strong temperature dependence of the effective Pockels coefficient r_eff in the range from 340 to 4 K in Si-integrated BTO.⁸⁰ Initially, upon cooling r_eff increases as the film approached the tetragonal-to-orthorhombic transition around 240 K, but then declines continuously reaching an effective Pockels coefficient of 200 pm V⁻¹ at 4 K. The fabricated devices showed an electro-optic bandwidth of 30 GHz, ultralow-power tuning that is 10⁹ times more efficient than thermal tuning and high-speed data modulation at 20 Gbps.

So far, we have discussed BTO deposited by MBE. Even though MBE produces some of the highest quality BTO films, it is not at all the only deposition method; atomic layer deposition (ALD),^81–83 PLD,^84,85 RF sputtering,⁸⁶ solgel deposition,^87–89 and CVD⁹⁰ can all grow thin BTO films on the STO/Si pseudo-substrate, and all these BTO films do show an EO response. Recently, Kormondy and co-workers analyzed BTO thin films with thickness ranging from 70 to 100 nm deposited by several different methods on STO-buffered Si (001) having a range of morphology morphology and structural quality.⁹¹ Indeed, it was found that even highly porous, polycrystalline BTO films had a linear EO response and could be appropriate for some low-cost applications. This study demonstrated a strong link between structural and electro-optic properties of BTO thin films and showed that although obtaining dense and highly tetragonal films is critical to obtain large Pockels coefficients needed in high-speed BTO/Si photonic modulators discussed above, fabricating layers with large grain sizes is the crucial parameter to maximize the memory window as needed for non-volatile optical storage.⁹² Tetragonality is very important because among all BTO polymorphs, it is the tetragonal 4 mm phase that exhibits the giant linear EO effect.

POSSIBILITY OF BTO WAVEGUIDES

Barium titanate waveguides present an intriguing approach since the electric field could be applied directly to the BTO faces and more of the BTO cross section in the light propagation direction would be used. The absence of low roughness wet etch processes for BTO has so far resulted in the need to fabricate the waveguides in silicon or silicon nitride. This obviously limits the extent to which the high EO coefficient of BTO can be used, as only a portion of light associated with the evanescent wave travels through BTO. One possible approach to BTO waveguides is selected area deposition in which growth of the BTO for the waveguide is restricted to a predefined region.⁹³ Only certain regions of the surface are active for growth and other regions are passivated against growth. After BTO growth, the passivating material is removed and a free-standing waveguide remains. Two potential routes are offered here that exploit the templating nature of a crystalline substrate as the BTO crystal film grows at the free surface. For example, a thick layer of SiO₂ can be deposited on several nm of STO (001) on Si (001), and the desired structure can be etched exposing STO (001)/Si (001) underneath. Such a strategy has already been successfully implemented by Ponath et al. on (001) germanium.⁹⁴ It is possible to grow crystalline BTO directly on Ge (001). Ponath et al. reported the selective area in finestra growth of highly crystalline BaTiO₃ within photolithographically defined openings of a sacrificial SiO₂ layer on a Ge (001) wafer by molecular beam epitaxy. After BTO deposition, the sacrificial SiO₂ was etched away, revealing isolated nanoscale gate stacks circumventing the need to etch the titanate thin film; a similar approach could be applied to a STO (001)/Si (001) surface. Coffey et al. used an STO (001) substrate and patterned 50 nm-thick polystyrene films using UV light to cross-link certain regions of the polystyrene.⁹³ The uncrosslinked regions were simply dissolved away with toluene and crystalline BTO films were grown on the exposed STO (001) surfaces using atomic layer deposition at 225 °C. The cross-linked polystyrene was subsequently etched in an O₂ plasma and the films were annealed to improve crystallinity. As chemical solution deposition also relies on surface phase epitaxy, it may also be a viable route to selective area deposition on STO (001) templated Si (001).⁸⁸ Realizing the necessary BTO transmittance⁸⁷ and EO properties⁹¹ will likely require post-growth annealing at elevated temperatures, and any area selective approach needs to allow for this annealing step.

ISOLATION

The use of SOI wafers limits conductive losses, but direct wafer bonding is still used to achieve better isolation of BTO; the device Si layer of the original wafer is sometimes used to form waveguides. Elimination of Si in the proximity of the BTO layer offers additional advantages with respect to isolation and opens avenues to design devices with purely BTO waveguides. This can be achieved with the epitaxial oxide-on-glass technology recently developed by Ortmann and co-workers.⁹⁵

They have demonstrated the fabrication of epitaxial, ultra-thin STO on thick SiO₂ without the need for complicated wafer-bonding processes. The resulting Transition Metal Oxide (TMO)-on-glass layer stack is analogous to traditional SOI wafers, where the crystalline device silicon layer of SOI has been replaced by a crystalline functional TMO layer. Fabrication starts with a ultra-thin-body SOI on which crystalline STO is grown epitaxially by molecular beam epitaxy. Figure 12(a) shows epitaxial STO on a 4 nm-thick device Si layer of the SOI wafer. The device silicon layer is subsequently fully oxidized by ex situ high-temperature dry O₂ annealing, as confirmed by x-ray photoelectron spectroscopy, x-ray reflectivity, and high-resolution electron microscopy. STO maintained its epitaxial registry to the carrier silicon substrate after annealing, and no evidence for degradation of the STO crystalline quality as a result of the TMO-on-glass fabrication process is observed. The ease of fabricating the TMO-on-glass platform [see Fig. 12(b)] without the need for wafer bonding will enable rapid progress in the development of state-of-the-art TMO-based electronic and photonic devices.

FIG. 12.

Cross-sectional HREM images of (a) as-grown sample and (b) sample after O₂ annealing. The HREM images confirm complete oxidation of the device silicon layer after O₂ annealing. Reproduced with permission from ACS Appl. Nano Mater. 2, 7793 (2019). Copyright 2019, American Chemical Society.

A detailed investigation of dry oxidation of Si (001) beneath a thin epitaxial STO layer was performed by Guo et al. using furnace annealing in flowing oxygen.⁹⁶ A 10-nm thick STO buffer was epitaxially grown by MBE on Si with no SiO₂ interlayer. For such a structure, an annealing temperature of 800 °C was found to be the limiting temperature to avoid silicate formation and disruption of the interface structure. The effect of annealing time on the thickness of the SiO₂ layer was investigated. In situ XPS and RHEED were used to ensure that the STO quality was not degraded by the annealing process. The authors demonstrated that the underlying Si can be safely oxidized at a relatively high temperature (800 °C) with the STO crystallinity not significantly degraded. The SiO₂ thickness was measured by ellipsometry and compared with a Deal-Grove-like oxidation model, and a good agreement was found between the data and the model. Therefore, one can use this model to predict the temperature and time needed to obtain the desired SiO₂ thickness for Si that is covered by a thin layer of STO. This additional knob for controlling the layer structure enabled the Ortmann study⁹⁵ and paves the way to integrate BTO on this STO/glass/Si pseudo-substrate, especially for applications requiring complete decoupling between the TMO and Si.

Until now, devices relying on the co-integration of silicon and epitaxial perovskites such as BTO have been limited to basic, planar geometries due to practical issues with their fabrication. Another interesting approach was recently developed by Ortmann et al.⁹⁷ They reported a method to produce high-quality TMO/Si(001)/TMO/Si(001) heterostructures without wafer bonding, resulting in the straightforward three-dimensional integration of EO oxides and active Si(001) layers into a technologically relevant platform that is needed for on-chip hardware implementations of neuromorphic computing based on optical signals. Without going into detailed structural and chemical characterization of these heterostructures, we shall discuss the main steps needed for their fabrication.

The epitaxial growth of silicon on many common perovskite TMO materials is fundamentally problematic due to a tendency for spontaneous silicon oxidation and amorphization upon deposition due to oxygen scavenging. Oxidation of deposited silicon may occur even if deposition is carried out in ultra-high vacuum (UHV) conditions, owing to the relatively low energy cost of creating oxygen vacancies in many TMOs compared to the formation energy of oxidized silicon. The ease of creating oxygen vacancies can be traced to the oxide bandgap, suggesting epitaxial silicon deposition may only be possible on TMO materials that have a large bandgap. Indeed, the deposition of elemental silicon has previously been demonstrated on single crystalline LaAlO₃ (LAO) substrates,⁹⁸ a material with a bandgap of approximately 5.6 eV, nearly 2.5 eV larger than that of STO and BTO. The compatibility of Si(001) deposition with wide-bandgap TMOs suggests that three-dimensionally integrated, epitaxial Si(001)/TMO/Si(001) structures may be experimentally realizable so long as every TMO layer is terminated with an oxygen scavenging barrier made from a wide-bandgap oxide, such as LAO. In Fig. 13, we show that a silicon layer deposited on LAO, which in turn is grown on STO-buffered Si is of suitable quality to support the epitaxial deposition of another STO layer.⁹⁷ Cross-sectional high-angle annular dark field (HAADF) and medium-angle annular dark field (MAADF) STEM images reveal a highly ordered, apparently single crystalline epitaxial STO film deposited atop the silicon film. No regions of polycrystalline or disordered STO are observed in electron microscopy imaging of the top STO film and only the (00l) orientation of STO is observed in XRD. This approach indicates a possibility of combining CMOS quality electronics with layers of EO active oxides and layers of lesser quality Si that, however, are good enough to support manufacturing of waveguides as well as simple thin-film transistor (TFT)-level logical circuits.

FIG. 13.

Cross-sectional STEM of epitaxial STO on deposited silicon. (a) HAADF and (b) MAADF STEM images of the interface between the deposited silicon film and the top epitaxial STO film. A thin amorphous layer can be observed between the STO and silicon films, likely silicon oxidized during STO growth Reproduced with permission from Ortmann et al., ACS Appl. Nano Mater. 4, 2153 (2021). Copyright 2021, American Chemical Society.

INTEGRATION OF IR LIGHT SOURCES ON SI

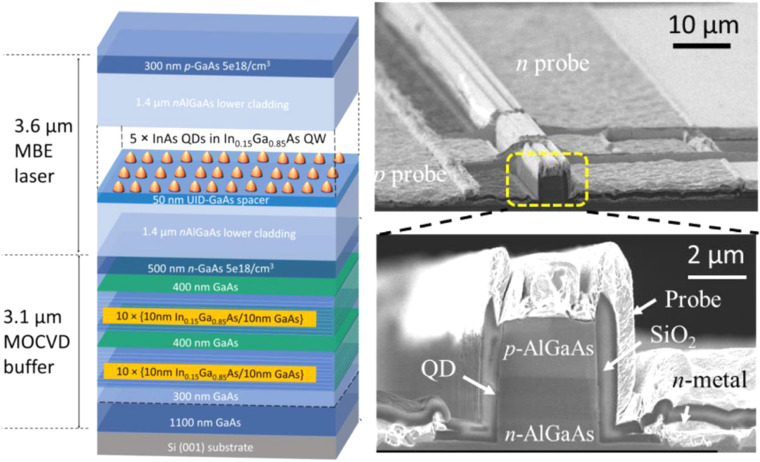
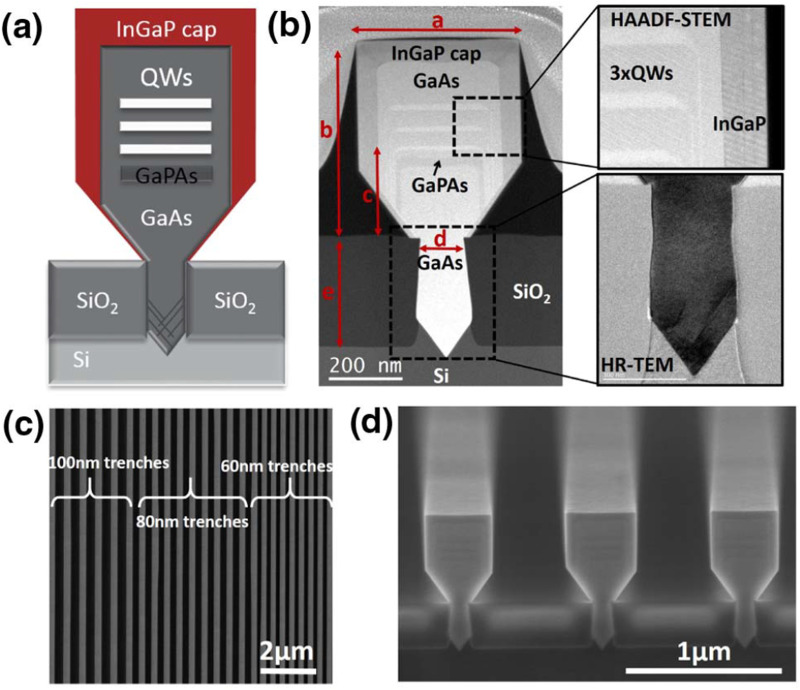
Photon sources—integrated onto the silicon platform—are needed in future manifestations of quantum (Fig. 1) and neuromorphic RC computing devices. There has been tremendous progress in developing IR light sources on Si. Since Si is an indirect bandgap semiconductor, it will not be a good optical IR emitter and a direct bandgap semiconductor, such as a III–V semiconductor, is required for IR emission. III–V semiconductor lasers can be integrated on Si by bonding^99,100 and by direct III–V epitaxial growth.^101–107 There are three major challenges in direct III–V semiconductor growth on Si: (i) defects due to the surface symmetry, (ii) defects due to the mismatch in lattice parameters, and (iii) thermal expansion mismatch. The surfaces of both Si and III–V semiconductors are inherently twofold symmetric rather than fourfold symmetric as a result of sp³ covalent bonding. A single atomic step on a Si(001) surface results in surface dimers rotating by 90° on the surface.¹⁰⁸ Growth of a III–V semiconductor on such a surface will result in antiphase domains and boundaries, regions on the surface where the in-plane orientations of III–V crystals are 90° with respect to each other. Although vicinal (∼4°–6°) Si(001) surfaces can be used to create biatomic (double height) steps, resulting in all dimers being aligned in the same direction,¹⁰⁸ vicinal surfaces are often not desired for other reasons. However, recently, there has been tremendous improvement in the quality of III–V semiconductor epitaxial growth using on-axis Si(001) substrates. One critical breakthrough was the ability to grow anti-phase boundary-free and defect-free nearly lattice-matched GaP on Si(001) without intentional miscut via metal organic vapor phase epitaxy (MOVPE).¹⁰⁹ The process involves epitaxial growth of Si and annealing at high temperature (975 °C) in a hydrogen environment (950 mbar) to create biatomic steps prior to a low temperature flux-modulated nucleation followed by high temperature GaP growth.¹⁰⁹ A similar annealing of Si(001) in hydrogen prior to GaAs epitaxy has also been used to create antiphase domain-free GaAs epitaxial layers.¹¹⁰ These antiphase boundary-free epitaxial GaP and GaAs layers serve as template layers for further III–V semiconductor growth and have been successfully used to grow low-threshold (34.6 A/cm² per layer) 1.3 μm InAs/GaAs quantum dot lasers^111,112 (see Fig. 14).¹¹² The quantum dots are formed by utilizing the Stranski–Krastanov growth mode that results from the large lattice mismatch (∼7%) between InAs and GaAs. The advantage of quantum dot lasers is that they are much more tolerant to threading dislocations compared to quantum well lasers as individual threading dislocations only affect one to a few quantum dots, making them have lower thresholds and better reliability.^113,114

FIG. 14.

Schematic of a MOCVD grown buffer structure and full stack of a standard quantum dot laser structure grown by MBE. The SEM images show the cross section of an as-cleaved laser. From Wan et al., IEEE J. Sel. Top. Quantum Electron. 22, 6 (2016). Copyright 2016 Author(s), licensed under a Creative Commons Attribution (CC BY) License.

The second major challenge is the lattice mismatch. GaAs has an ∼4% and InP has an ∼8% larger lattice parameter than Si, which will induce crystalline defects, such as dislocations and stacking faults, in the epitaxial layers. Annealing,¹¹⁵ strain relaxed Ge/Ge_xSi_1−x/Si(001) buffer layers,¹¹⁶ superlattices for dislocation filtering,^101,117 and selective area growth and aspect ratio trapping^118,119 have all been used to reduce the number of threading dislocations reaching the active layer. By combining aspect ratio trapping, V-grooved trench etching to yield (111) Si surfaces,^120,121 epitaxial lateral overgrowth antiphase domain-free GaAs thin films can be grown on-axis Si(001) using metal organic chemical vapor deposition (MOCVD).¹²² Figure 15 shows a TEM image of GaAs grown on V-grooved Si(001) showing how stacking faults on the {111}planes are trapped by the SiO₂ dielectric layer.¹²² Molecular beam epitaxial (MBE) growth of 1.3 μm InAs/InGaAs quantum dot lasers has also been successfully demonstrated on these layers.¹⁰³ By continual reduction of the dislocation density in the active region, the laser lifetime keeps improving.¹²³

FIG. 15.

TEM images showing (a) coalesced GaAs epitaxial layer grown on V-grooved Si and (b) the stacking fault trapping by a “tiara”-like structure formed by the Si undercuts under the SiO₂. Reprinted with permission from Appl. Phys. Lett. 106, 072105 (2015). Copyright 2015 AIP Publishing LLC.

Dislocations are induced due to the thermal expansion mismatch during cooldown after growth. Selvidge et al.¹²⁴ proposed the introduction of thin mechanically hardened layers above and below the active layers to locally inhibit threading dislocation glide and displace misfit dislocation away from quantum dots during the post-growth cooldown, reducing the threading dislocation density by one order of magnitude. This approach has resulted in improved designs of strained dislocation filter layers and thermal treatment during and after buffer layer growth.¹²⁵

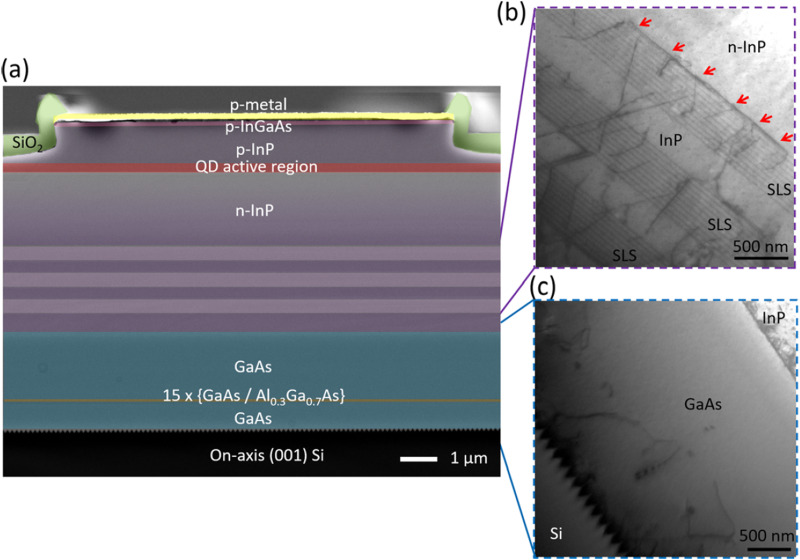
The fabrication of 1.5 μm lasers on Si is more challenging as these are based on materials with larger lattice parameters closer to InP rather than GaAs, making them lattice mismatched to both Si and GaAs. Furthermore, as the mismatch of ∼3% between InAs and InP is smaller than ∼7% mismatch between InAs and GaAs, making quantum dot formation using Stranski–Krastanov growth more challenging and is strongly dependent on the encapsulating layers.^126,127 Recently, using the V-grooved Si approach, Zhu et al. have grown and fabricated 1.5 μm quantum dot lasers that operated in pulsed mode with a threshold current density of 1.6 kA/cm²¹²⁸ as well as 1.5 μm InGaAs/InAlGaAs multi-quantum well lasers on Si(001) with threshold currents of 3.3 kA/cm² also under pulsed operation.¹²⁹ The large lattice mismatched growth results in a high density of threading dislocations in InP despite the strained layer superlattice dislocation filters, as can be seen in Fig. 16.¹²⁸ An exciting alternative approach to growing full layers is to use selective area growth for forming microridges¹³⁰ and nanoridge lasers^{105–107,131–133} (Fig. 17).¹³¹ So far these have only achieved lasing through optical excitation. Further work is required to achieve lasing by electrical injection.

FIG. 16.

(a) Color-enhanced cross-sectional SEM image of the 1.5 μm quantum dot epitaxial laser structure. Cross-sectional TEM images of (b) three stacks of 10-period InGaAs/InP strain layer superlattices (SLSs) with dislocation filtering effects identified by red arrows, (c) 2.2-nm-thick GaAs intermediate buffer on a nanopatterned V-grooved on-axis (001) Si substrate. Reprinted with permission from, Appl. Phys. Lett. 113, 221103 (2018). Copyright 2018 AIP Publishing LLC.

FIG. 17.

(a) Sketch of a GaAs nano-ridge laser stack. The inclined lines at trench bottom indicate how planar defects and threading dislocations are trapped inside the trench. (b) HAADF-STEM images of the GaAs nano-ridge waveguide. The upper one shows zoomed-in QWs, barriers, and the passivation layer, while the lower high-resolution (HR) TEM shows that defects are trapped in the V-shaped trench. (c) SEM image of the nano-ridge array with trench width from 60 to 100 nm. (d) Tilted cross section SEM image of three 80-nm trench ridges. Reproduced with permission from Shi et al., Optica 4, 1468 (2017). Copyright 2017, Optical Society of America.

FUTURE OUTLOOK

It seems obvious to us that the future of computing lies in the optical domain. The parallel nature of optics is ideal for both neuromorphic and quantum computation, and the fact that the computing itself can be done at a low energy cost offers an ultralow power, ultrafast implementation (the energy cost is associated mainly with the control of the optical flow and training the optical fabric). However, at the moment, pure optical systems are not ready for commercial implementation, and electro optics offers a reasonable compromise. In addition, silicon photonics by virtue of its relation with silicon manufacturing is ideally suited for large-scale manufacturing of low-cost electro-optic computing systems on a chip. If such chip-scale electro-optic computing systems are already equipped with the on-chip light sources and detectors, they would be extremely useful in the so-called edge-computing, like that needed for autonomous vehicles, space exploration, robotic surgery, or autonomous weapons systems with battlefield awareness.

Besides electronics to control these systems, three elements are needed to make this vision a reality: chip-scale waveguides to establish an optical network, on-chip light sources and detectors, and energy-efficient high-frequency modulators. The first part is already in existence. We have described the current progress in on-chip light sources and a particular flavor of electro-optical modulators. It should be noted that there are many different types of modulators available for implementation in silicon photonics. Plasma dispersion phase modulators are commercially available and operate at a speed of 100 GB/s with the sub-volt drive signal consuming fJ/bit in a μm size footprint. Also, many emergent materials besides ferroelectrics are being considered such as organics, SiGe alloys, III–Vs, and 2D materials.³¹ However, we believe that for the purposes of neuromorphic and quantum computing, ferroelectrics offer many significant advantages. More mature Si-integrated LiNbO₃ modulators have demonstrated to operate at 100 GHz, with ∼7 dB loss when the waveguide was fabricated in Si, and a 2.5 dB loss has been reported in a 5 mm phase shifter that has been reported to provide a 70 GHz bandwidth. However, we believe that BTO that can be monolithically integrated on Si, with its giant Pockels coefficient, high thermal stability, and large transparency window, holds truly tremendous promise. The Pockels coefficient allows significant reduction in size and operating voltage. This translates in higher packing density and reduction in power, making these devices very attractive for integrated photonic circuits or PICs. Furthermore, co-integration of IR light sources with ferroelectric EO modulators is a very promising direction of research with potential applications in edge computing.

The work has just begun, and the device-level data are being obtained from the hybrid devices, where the waveguide is fabricated of Si or SiN on the top of the perovskite film. The relatively high losses ∼10 dB are stemming from hydrogen impurities introduced during deposition of Si and SiN to fabricate the waveguides. The next step is to fabricate BTO waveguides or waveguide segments to harness the full potential of this extraordinary material. Much more needs to be learned at the materials’ level, as the electromechanical conditions alter the phase morphology of the BTO films integrated on Si. This will be particularly important at cryogenic temperatures needed in quantum computing. So, the story of BTO in optical computing has just begun.

DATA AVAILABILITY

Data sharing is not applicable to this article as no new data were created or analyzed in this study.