Cross-paradigm connectivity: reliability, stability, and utility

Abstract

While functional neuroimaging studies typically focus on a particular paradigm to investigate network connectivity, the human brain appears to possess an intrinsic “trait” architecture that is independent of any given paradigm. We have previously proposed the use of “cross-paradigm connectivity (CPC)” to quantify shared connectivity patterns across multiple paradigms and have demonstrated the utility of such measures in clinical studies. Here, using generalizability theory and connectome fingerprinting, we examined the reliability, stability, and individual identifiability of CPC in a group of highly-sampled healthy traveling subjects who received fMRI scans with a battery of five paradigms across multiple sites and days. Compared with single-paradigm connectivity matrices, the CPC matrices showed higher reliability in connectivity diversity, lower reliability in connectivity strength, higher stability, and higher individual identification accuracy. All of these assessments increased as a function of number of paradigms included in the CPC analysis. In comparisons involving different paradigm combinations and different brain atlases, we observed significantly higher reliability, stability, and identifiability for CPC matrices constructed from task-only data (versus those from both task and rest data), and higher identifiability but lower stability for CPC matrices constructed from the Power atlas (versus those from the AAL atlas). Moreover, we showed that multi-paradigm CPC matrices likely reflect the brain’s “trait” structure that cannot be fully achieved from single-paradigm data, even with multiple runs. The present results provide evidence for the feasibility and utility of CPC in the study of functional “trait” networks and offer some methodological implications for future CPC studies.

Introduction

Cognitive neuroscience employs a variety of psychological paradigms to investigate functional connectomic basis of the human mind. Each paradigm may target a specific functional domain and elicit the activation of domain-specific brain networks. For instance, a resting-state paradigm may activate the brain’s default-mode network but deactivate cognitive control systems (Buckner et al. 2008; Raichle et al. 2001). In contrast, a working memory task would render the frontoparietal network strongly activated (McCarthy et al. 1994; Owen et al. 2005), with decreased activity of the default-mode network (Buckner et al. 2008). Although breaking down the complex functions of the brain into discrete domain-related phenotypes has facilitated identification of neural architectures underlying functionally distinct domains, this strategy may be less sensitive to identifying commonalities in network architecture across paradigms.

Recent studies have observed that the human brain possesses an intrinsic “trait-like” functional architecture that is independent of the employed paradigm, and brain networks observed during different paradigms are shaped primarily by this “trait” architecture and secondarily by paradigm-specific features (Cole et al. 2014; Geerligs et al. 2015; Krienen et al. 2014). Based on these findings, we have previously proposed a measure termed “cross-paradigm connectivity” (CPC (Cao et al. 2018a; Cao et al. 2019b)), which essentially quantifies the state-independent functional connectivity for a given individual across multiple paradigms. Specifically, the CPC matrices are computed based on the principal component analysis (PCA) of the functional connectivity matrices derived from different fMRI paradigms. The first principal component (PC) extracted from these multi-paradigm functional connectivity matrices represents the connectivity pattern that explains the majority of variance shared across the paradigms and thus likely reflects a “trait” architecture of the human brain. Using this strategy, our prior work has shown the power of CPC matrices in the prediction and characterization of psychotic disorders (Cao et al. 2018a; Cao et al. 2019b), suggesting CPC as a promising approach to study inter-subject differences, at least in clinical populations.

Although CPC has shown potential to track individual connectivity traits associated with behavior and risk for mental illness, at least four practical questions remain to be addressed regarding this approach. First, as a common concern in neuroimaging research, the reliability of the CPC matrices has not been established. A series of studies has demonstrated good reliability or generalizability of functional connectivity matrices derived from a single paradigm, including resting state (Braun et al. 2012; Cao et al. 2018b; Cao et al. 2014; Wang et al. 2011) and active tasks (Cao et al. 2018b; Cao et al. 2014). However, whether the high reliability in a single-paradigm context would translate to the multi-paradigm CPC matrices is unclear, a question that would affect the application of such an approach in longitudinal studies, such as those related to clinical trials or neurodevelopment. In addition, as previously shown in the single-paradigm functional connectivity studies, the choice of data processing pipeline such as atlas and the choice of fMRI paradigm both significantly influence reliability outcomes (Cao et al. 2018b; Cao et al. 2014; Wang et al. 2011; Welton et al. 2015). This raises the possibility that CPC reliability may also be affected by these factors. In theory, the CPC matrices derived from a PCA approach can be performed on any number of paradigms (larger than one) as well as different types of paradigms (resting state, various active tasks). Whether the paradigm number and paradigm type would influence the resulting CPC matrices and their reliabilities is unknown.

Another important consideration for the CPC matrices is stability. Specifically, while the reliability analysis quantifies how consistent the measures of CPC matrices are in a repeated-measures setting (Shavelson and Webb 1991; Shrout and Fleiss 1979), the stability analysis estimates whether the CPC matrices derived from different numbers and/or types of paradigms reflect the same architecture (Cole et al. 2014; Geerligs et al. 2015). This is of important practical significance because if the stability increases with an increase in number of paradigms, a CPC analysis with more fMRI paradigms included would then make the resulting network structure more stable and thus closer to representing the brain’s “trait” organization; otherwise, the number of included paradigms may have little influence on the generation of the “trait” network and therefore may be less important in the computation and interpretation of CPC results.

The third question relates to the similarity between the CPC matrices and the matrices computed from a single paradigm using the same PCA approach, in order to inform whether CPC matrices and highly-sampled single-paradigm matrices share the same network architecture. Specifically, while the CPC metric is typically generated from multiple fMRI paradigms, it is unclear whether a PCA analysis on a single paradigm with multiple sessions would resemble that derived from multiple paradigms. In other words, it is an open question whether CPC indeed reflects a shared network architecture across different paradigms that cannot be achieved by a single paradigm, or simply increases signal-to-noise ratio (SNR) when collapsing data from multiple sessions. The answer to this question has important practical value since many neuroimaging studies may not have acquired multi-paradigm data but have a single paradigm (e.g. resting state) scanned across multiple sessions (Laumann et al. 2015; Poldrack et al. 2015; Zuo et al. 2014). If the multi-paradigm and single-paradigm (with repeated sessions) results are comparable, the brain’s “trait” network can simply be acquired from highly-sampled resting-state data.

Finally, we aim to demonstrate the superiority of CPC in studying individual variability compared with single-paradigm functional connectivity, as an empirical example of the utility of such approach in neuroscience research. Our prior work has demonstrated CPC alterations in individuals at clinical risk for psychotic disorders, a finding that is undetectable solely using resting-state whole-brain functional connectivity data, suggesting the superiority of CPC in distinguishing risk for progression of illness among at-risk individuals (Cao et al. 2018a). However, whether such superiority translates to healthy subjects is unclear. Given the hypothesis that CPC likely reflects a state-independent “trait” architecture of the human brain, it is possible that these “trait” measures would detect individual differences to a better extent than single-paradigm connectivity measures that contain mixed signals of both “trait” and “state”. If so, the CPC metrics would show potential as biomarkers for cognitive and behavioral predictions.

Here, we examined the above questions using a traveling-subject sample as previously reported (Cao et al. 2018). In this unique sample, eight healthy participants were scanned twice at each of the eight study sites, using a battery of five fMRI paradigms. This sample allows us to directly quantify multi-site reliability, stability, and individual identifiability for the CPC matrices constructed from the five paradigms. Moreover, to investigate potential influences of the employed paradigms on these measures, we also computed CPC based on all possible two-, three-, and four-combinations of these paradigms and compared the above measures between different combinations.

Methods and materials

Subjects

The studied sample included eight healthy traveling subjects (age 26.9 ± 4.3 years, 4 males) recruited from eight study sites across the United States and Canada: Emory University, Harvard University, University of Calgary, University of California Los Angeles, University of California San Diego, University of North Carolina Chapel Hill, Yale University, and Zucker Hillside Hospital. The sample details have been described previously in (Cao et al. 2018b). Specifically, eight participants (one for each site) traveled to each of the eight sites in a counterbalanced order. At each site, they were scanned twice on two consecutive days with a battery of five fMRI paradigms, generating a total of 128 sessions (8 subjects x 8 sites x 2 days) for each paradigm. The fMRI paradigms included an eyes-open resting state paradigm, a verbal working memory task, an episodic memory encoding task, an episodic memory retrieval task, and an emotional face matching task. Details on these paradigms were given in (Cao et al. 2018b). Of note, for each of the working memory, episodic memory and face matching tasks, one session was unusable due to technical artifacts, and one session for the episodic memory paradigms did not complete successfully, leaving a total of 126 sessions available for all five paradigms.

All participants received the Structured Clinical Interview for Diagnostic and Statistical Manual of Mental Disorders (DSM-IV-TR (First et al. 2002)) and Structured Interview for Psychosis-risk Syndromes (McGlashan et al. 2001), and were excluded if they met the criteria for psychiatric disorders or psychosis prodromal syndromes. Other exclusion criteria included a history of neurological or psychiatric disorders, substance dependency in the last six months, IQ < 70 (assessed by the Wechsler Abbreviated Scale of Intelligence (Wechsler 1999)) and the presence of a first-degree relative with mental illness. The whole study was performed in accordance with the protocols and guidelines approved by the institutional review boards at each study site. All subjects provided written informed consent for the study protocols.

Data acquisition and preprocessing

All data were acquired from eight 3 T MR scanners (Siemens Trio, GE HDx, and GE Discovery) located at eight study sites using gradient-recalled-echo echo-planar imaging (GRE-EPI) sequences with identical parameters. Specifically, the following parameters were used for all paradigms: TE = 30 ms, 77 degree flip angle, 30 4-mm slices, 1 mm gap, and 220 mm FOV. The working memory and face matching tasks used TR = 2.5 s while the other paradigms used TR = 2 s. The total time points for the five paradigms were between 132 and 250 (154 for resting state, 184 for working memory, 250 for episodic memory encoding, 219 for episodic memory retrieval, 132 for face matching). Since the time series for working memory and episodic memory tasks were much longer than that for resting state, we only used the first 154 time points in these tasks in order to avoid potential confounds caused by differences in amount of data between paradigms. In addition, we also acquired high-resolution T1-weighted images for all participants with the following sequences: 1) Siemens scanners: magnetization-prepared rapid acquisition gradient-echo (MPRAGE) sequence with 256 mm x 240 mm x 176 mm FOV, TR/TE 2300/2.91 ms, 9 degree flip angle; 2) GE scanners: spoiled gradient recalled-echo (SPGR) sequence with 260 mm FOV, TR/TE 7.0/minimum full ms, 8 degree flip angle.

Data preprocessing followed standard procedures implemented in the Statistical Parametric Mapping software (SPM8, http://www.fil.ion.ucl.ac.uk/spm/software/spm8/). In brief, all fMRI images were slice-time corrected, realigned for head motion, registered to the individual T1-weighted structural images, and spatially normalized to the Montreal Neurological Institute (MNI) template. Finally, the normalized images were spatially smoothed with an 8 mm full-width at half-maximum (FWHM) Gaussian kernel.

Network construction

Following previously published work (Cao et al. 2018b; Cao et al. 2014), we used two brain atlases to construct connectome-wide networks: a structure-based AAL atlas with 90 nodes (Tzourio-Mazoyer et al. 2002) and an expanded function-based Power atlas with 270 nodes (Cao et al. 2018a; Cao et al. 2017; Cao et al. 2018b; Power et al. 2011). These atlases represent different node definition strategies and meanwhile cover both cortex and subcortex. Details on network construction were described previously (Cao et al. 2018b). In brief, the mean time series for each node in both atlases were extracted from the preprocessed images. The extracted time series were further corrected for task coactivations (for task data), white matter and cerebrospinal fluid signals, the 24 head motion parameters (i.e. the 6 rigid-body parameters generated from the realignment step, their first derivatives, and the squares of these 12 parameters (Power et al. 2014; Satterthwaite et al. 2013)), and the frame-wise displacement. The corrected time series were then temporally filtered (task data: 0.008 Hz high pass, rest data: 0.008–0.1 Hz band pass) to account for scanner and physiological noises. Pearson correlations were performed to generate a 90 × 90 (AAL atlas) or 270 × 270 (Power atlas) pairwise connectivity matrix for each session during each paradigm (i.e. each atlas has 126 × 5 matrices in total).

Principal component analysis and cross-paradigm connectivity

CPC were built upon the connectivity matrices derived from the five paradigms using PCA, following our previously published procedure (Cao et al. 2018a). Specifically, for each atlas, the connectivity matrices of the five paradigms at the same session were vectorized, mean centered, and decomposed into a set of principal components (PCs) using singular value decomposition (SVD). The first PCs generated from the analysis represented the CPC and were thus extracted (one for each session, 126 in total). In addition, for comparison purposes, we also performed PCA on each of the two-, three-, and four-combinations of the paradigms, yielding a total of 126 × 26 CPC matrices (10 for two-combination, 10 for three-combination, 5 for four-combination and 1 for all five paradigms). These generated CPC matrices were further used for the assessment of reliability, stability, and utility.

Reliability analysis

To assess multi-site reliability of CPC matrices, we calculated two metrics characterizing the key structure of the matrices: node strength and node diversity. Node strength is the average connectivity between a given node and all other nodes in the network, reflecting how strongly the node is connected to others; while node diversity is the connectivity variance between a given node and all other nodes, reflecting the variability of the connectivity pattern for that node in the network (Bullmore and Bassett 2011; Cao et al. 2019a). Note that the definitions in the current study are based on the CPC matrices rather than original connectivity matrices, which may reflect the strength and variability of the weighted linear combinations of the original connectivity matrices. The multi-site reliability of node strength and node diversity were subsequently quantified using generalizability theory (Cao et al. 2018b; Shavelson and Webb 1991). Specifically, the total variance in each of the outcome measures (σ² _psd) was decomposed into a participant-related variance σ² _P, a site-related variance σ² _s,a day-related variance σ² _d, their two-way interactions σ² _ps, σ² _pd, σ² _sd, and their three-way interaction as well as random error σ² _psd,e (Shavelson and Webb 1991). The variance decomposition was performed using a three-way analysis of variance (ANOVA) model with participant, site and day included as random factors.

$${\sigma }_{psd}^2={\sigma }_p^2+{\sigma }_s^2+{\sigma }_d^2+{\sigma }_{ps}^2+{\sigma }_{pd}^2+{\sigma }_{sd}^2+{\sigma }_{psd,e}^2$$

Reliabilities of node strength and node diversity were then quantified by the D-coefficient (ϕ), which measures the proportion of participant-related variance over the total variance, thereby evaluating the absolute agreement of the target measure (analogous to ICC(2,1) in classical test theory (Shavelson and Webb 1991)). The formula is given as follows:

$$\text{Φ=}\frac{{\sigma }^{2}p}{{\sigma }^{2}p+\frac{{\sigma }^{2}s}{n\left(s\right)}+\frac{{\sigma }^{2}d}{n\left(d\right)}+\frac{{\sigma }^{2}ps}{n\left(s\right)}+\frac{{\sigma }^{2}pd}{n\left(d\right)}+\frac{{\sigma }^{2}sd}{n\left(s\right)*n\left(d\right)}+\frac{{\sigma }^{2}psd,e}{n\left(s\right)*n\left(d\right)}}$$

where n(i) represents the number of levels in factor i, and p, s, and d refer to participant, site, and day, respectively. Depending on how to define the number of levels, the D-coefficient can be calculated in two different situations, namely, the generalizability study (G-study) and the decision study (D-study). The D-coefficients in the G-study are estimated based on the facets and their levels in the studied sample (here n(s) = 8, n(d) = 2)(Cao et al. 2018b; Forsyth et al. 2014; Shavelson and Webb 1991). In contrast, investigators define the number of facets and levels in the D-study in terms of research interest (Cao et al. 2018b; Noble et al. 2016; Shavelson and Webb 1991). Since “nested” designs are commonly used in neuroimaging research whereby each participant is scanned only one time at one site, the expected site- and day-related variance would be higher than those in a “crossed” design as used in this study (Lakes and Hoyt 2009). We thereby also computed the D-coefficients based on n(s) = 1 and n(d) = 1, which corresponds to the expected multi-site reliability in a “nested” design with distinct subjects between sites and days. In this work, we report reliability measures from both G- and D-studies.

Stability analysis

To assess stability of the CPC matrices and to directly compare the stability between different numbers and types of paradigms, we used a correlation-based method similar to that in (Cole et al. 2014). Specifically, if two matrices are structurally similar, they should be highly correlated element-wise. Here, we quantified the similarity of the CPC matrices constructed from different paradigm combinations by computing their Pearson correlation coefficients for each of the 126 sessions. In addition, for comparison purposes, we also assessed the similarities between the single-paradigm connectivity matrices derived from each of the five paradigms and these CPC matrices using the same method. This resulted in a 31 × 31 pair-wise correlation matrix for each session, with each element in the matrix representing the Pearson correlation coefficient between two different connectivity or CPC matrices (5 single-paradigm connectivity matrices and 26 CPC matrices as described above). The stability of a given connectivity or CPC matrix was subsequently measured as the average of the correlation coefficients across all 31 matrices (i.e. row or column mean).

Utility analysis and individual identification

To compare CPC matrices with multi-session single-paradigm connectivity matrices, the same correlation-based approach as described above was used. To condense single-paradigm connectivity data from multiple sessions and meanwhile equate the amount of data with that used in multi-paradigm CPC, we performed a similar PCA analysis on five randomly-chosen sessions for each of the five paradigms and each of the eight subjects. This randomization was repeated for 16 times which generated a total of 16 first-PC matrices for each paradigm and subject, each representing the cross-session shared variance for a single paradigm. The derived 16 matrices were further averaged to acquire a single-paradigm PC matrix. Similarly, the multi-paradigm CPC matrices and original connectivity matrices for each paradigm and each subject were also averaged across the 16 sessions, thereby assuring the same amount of data being compared. Subsequently, we compared the similarities of the derived single-paradigm PC matrices with ones acquired from multiple paradigms using Pearson correlations. In case that CPC simply increases SNR, a close similarity between single-paradigm PC matrices and multi-paradigm PC matrices would be observed, which should be more similar than that between single-paradigm PC matrices and single-paradigm connectivity matrices. Otherwise, it is more likely that the CPC matrices capture shared connectivity patterns across different paradigms and thus a multi-paradigm design is indeed required in such a situation.

We investigated the ability of CPC matrices in individual identification using the recently developed “connectome fingerprinting” approach (Finn et al. 2015; Kaufmann et al. 2017). This approach was originally employed to identify individuals across different paradigms, where the identification accuracy was measured based on the comparison of functional connectivity matrices derived from one paradigm with those from another. Here, since we aim to directly compare the outcome identification accuracies between paradigms, we slightly modified this approach by calculating the identification accuracy based on the comparison of matrices across different sites and days. Specifically, in an iterative process, one subject’s CPC or functional connectivity matrix at one scan site and one scan date was selected, and the similarity of this preselected matrix with all subjects’ matrices from a different site and date was calculated based on Pearson correlation coefficients. Individual identification was determined by finding the one among all tested matrices that had the highest similarity to the preselected matrix. If the individual was successfully identified, a value of 1 was assigned to this attempt, and otherwise a value of 0 was assigned. This procedure was repeated with every subject being the target subject once across all sites and days. Following previous procedures (Finn et al. 2015; Kaufmann et al. 2017), the accuracy of connectome fingerprinting for a given individual was calculated as the number of successful identifications divided by the total number of iterations for that individual. The accuracy values were generated for each subject at each paradigm and paradigm combinations.

Statistics

For the derived reliability, stability, and utility measures, we used mixed-effect models to investigate potential contributing factors to these outcome measures. Specifically, we asked: 1) whether the use of different brain atlases would influence results; 2) how the outcomes would change with the increase of number of paradigms in the CPC construction; and 3) whether different types of paradigm (i.e. resting state and active tasks) would affect the resulting measures. To answer these questions, brain atlas, number of paradigms, and paradigm type were modeled as fixed-effect variables, while subject was modeled as random-effect variable with random intercept considered for each subject (details see Results). Statistical analyses were performed on SPSS 26.

Results

Cross-paradigm connectivity

We first examined the extracted first PC matrices to ensure that these matrices indeed reflected the majority of variance in the connectivity matrices shared across different paradigms. We found that for both AAL and Power atlases, the first PC matrices in general explained ~ 80% of total variance across paradigms. Specifically, depending on the paradigm combination, 76.0–89.1% of total variance were captured in the first PC matrices using the AAL atlas, while 66.9–83.8% were captured using the Power atlas (Fig. 1A). Notably, when resting state was included in the PCA analysis, the variance explained by the first PC was between 66.9% and 83.2% for both atlases, compared to that between 73.2% and 89.1% when using task data only. In addition, the first PC matrices explained 76.2–89.1%, 69.8–83.9%, 67.7–81.3% and 66.9–76.0% of total variance for two-paradigm, three-paradigm, four-paradigm and five-paradigm combinations, respectively. To test whether different factors had significant influences on the explained cross-paradigm variance, we used a mixed-effect model where atlas (AAL vs Power), paradigm type (including rest vs only task) and number of paradigms (two to five) were entered as fixed-effect variables and subject as a random-effect variable. Significant main effects were shown for all three fixed-effect factors (P < 0.001 for atlas, paradigm type and number of paradigms). In particular, the percent of variance explained in the PC matrices derived from the AAL atlas and from task data only was significantly higher than that in PC matrices derived from the Power atlas and from data with resting state included (Fig. 1B). Moreover, the percent of variance significantly dropped with the increase of number of paradigms. These findings indicate that the performance of CPC in explaining multi-paradigm variance depends on factors such as atlas, number of paradigms and whether resting state data are included or not.

Fig. 1.

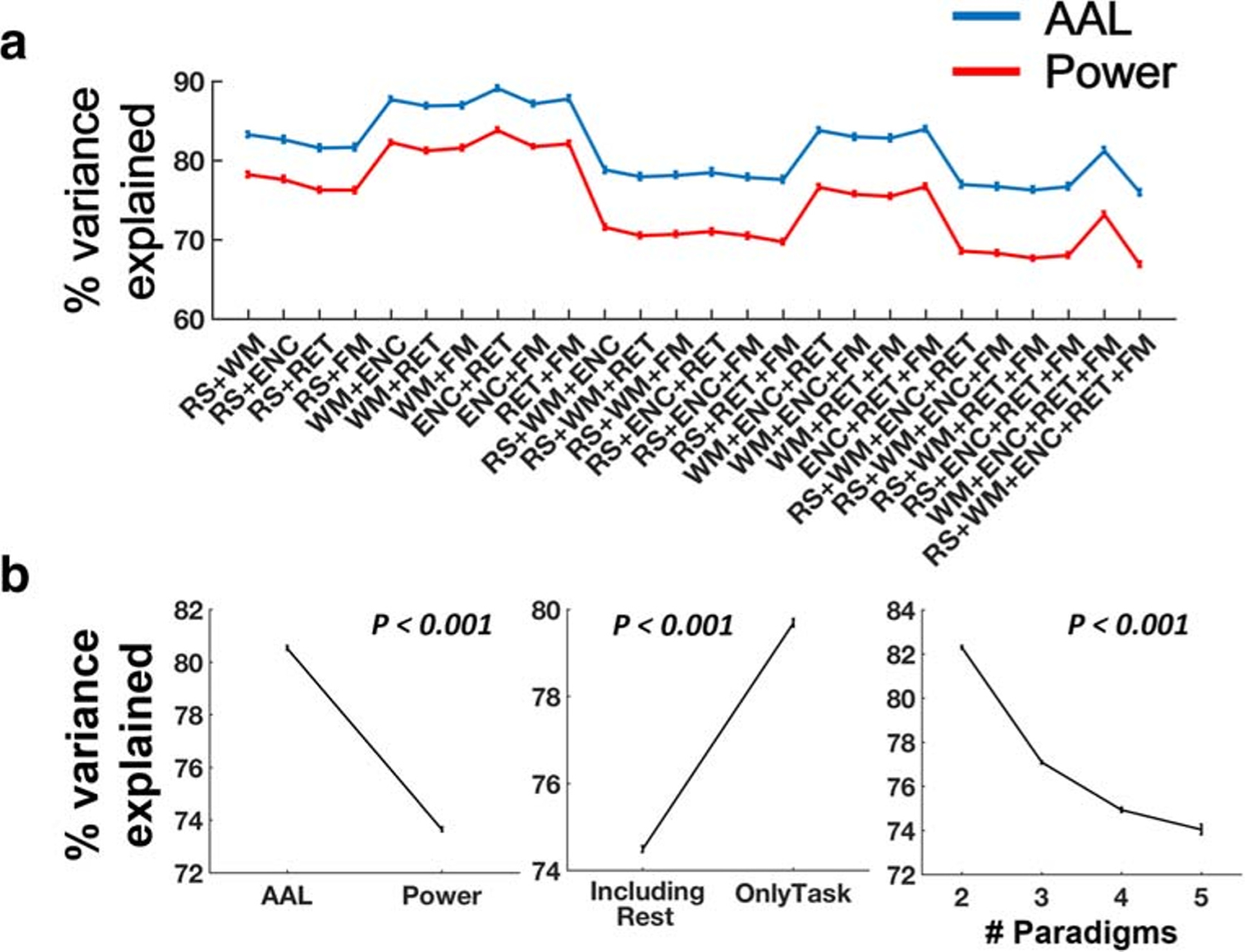
Percent of variance explained by CPC (the first PC in the PCA analysis). (A) For all possible combinations of the fMRI paradigms used in the data, the first PC explained ~ 80% of total variance across paradigms. (B) Significantly higher percent of variance was explained by the first PC when the analysis was performed on the AAL atlas (vs Power atlas), only task data (vs rest data) and a small number of paradigms. Error bars indicate standard errors

Reliability of cross-paradigm connectivity

Consistent with our prior work (Cao et al. 2018b), the G-study revealed high reliability for both node strength and node diversity across all paradigm combinations and atlases (overall range between 0.68 and 0.90, Fig. 2A and B, Tables S1 & S2). Specifically, node diversity with the AAL atlas showed the highest reliability (ranging between 0.74 and 0.90), while node strength with the AAL atlas showed the lowest reliability (ranging between 0.68 and 0.85). Reliabilities for two-, three-, four- and five-paradigm combinations ranged between 0.68 and 0.90, between 0.77 and 0.90, between 0.81 and 0.89, and between 0.84 and 0.88, respectively. With the increase of number of paradigms included in the CPC, a gradually enhanced reliability was clearly shown for both metrics and both atlases.

Fig. 2.

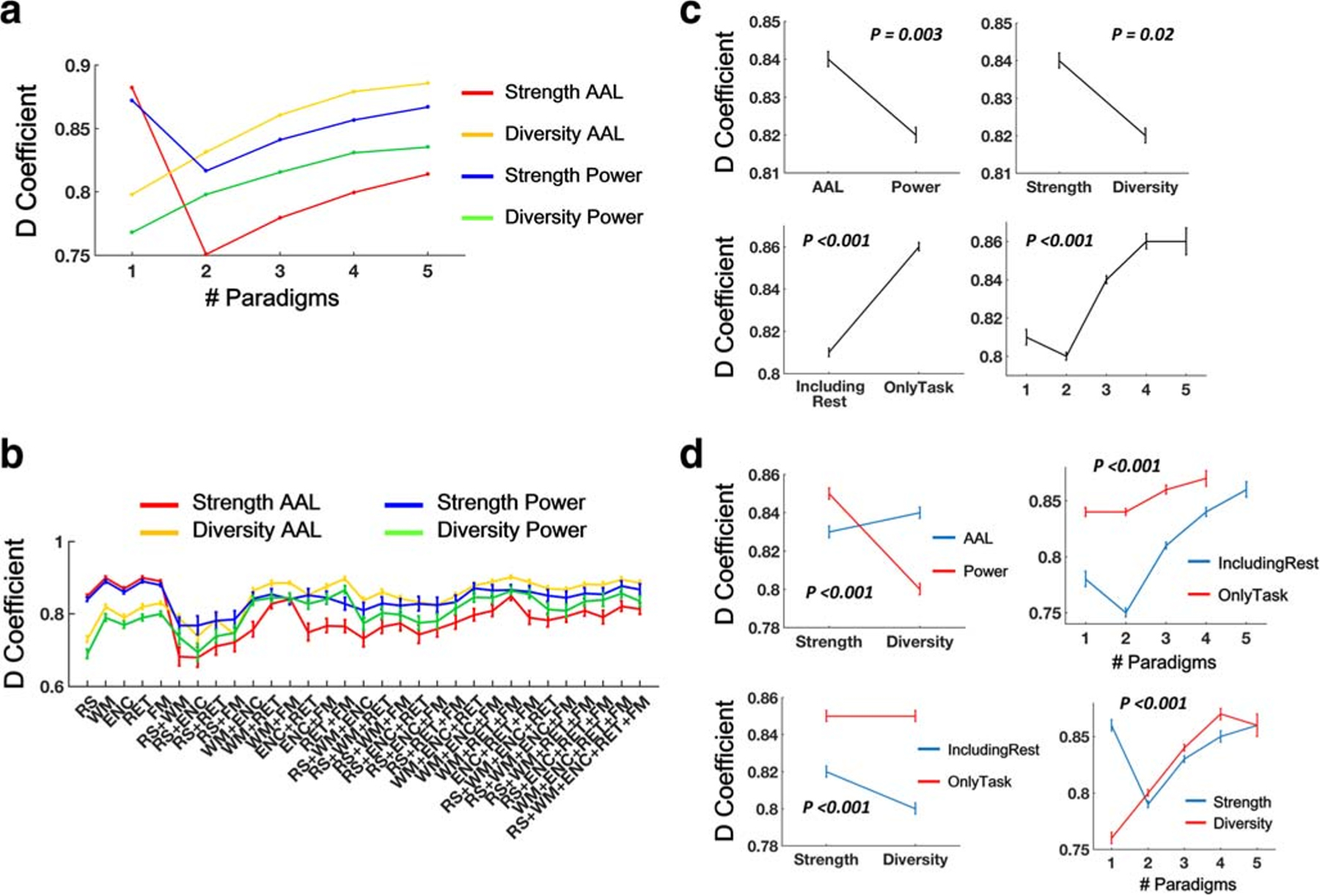
Measures of CPC matrices showed high reliability (D-coefficients) in the G-study. Note that reliability measures for functional connectivity matrices during each of the five paradigms were also included (as number of paradigm = 1) to facilitate direct comparisons with those of the CPC matrices. These single-paradigm reliabilities were reported previously in (Cao et al. 2018b). (A) Reliability of node strength and node diversity as a function of number of paradigms. (B) Reliability of node strength and node diversity across different paradigm combinations. (C) The matrices derived from the AAL atlas, task data, and larger number of paradigms had higher reliability compared with the Power atlas, rest data, and small number of paradigms. (D) Interactive effects were shown for metric x atlas, metric x paradigm type, metric x number of paradigms, and number of paradigms x paradigm type on the reliability measures. Error bars indicate standard errors

Similar patterns were also present for the reliability measures in the D-study, albeit with lower values (Figs. 3A and B). In particular, the overall range for the D-coefficients was between 0.24 and 0.50, regardless of atlas, metric and paradigm combination. Again, the highest reliability was shown for node diversity with the AAL atlas (range between 0.29 and 0.50), while the lowest reliability was found for node strength with the AAL atlas (range between 0.24 and 0.39). Reliability increased as a function of number of paradigms included in the CPC, ranging from between 0.24 and 0.47 for two-paradigm combinations to between 0.38 and 0.49 for five-paradigm combinations.

Fig. 3.

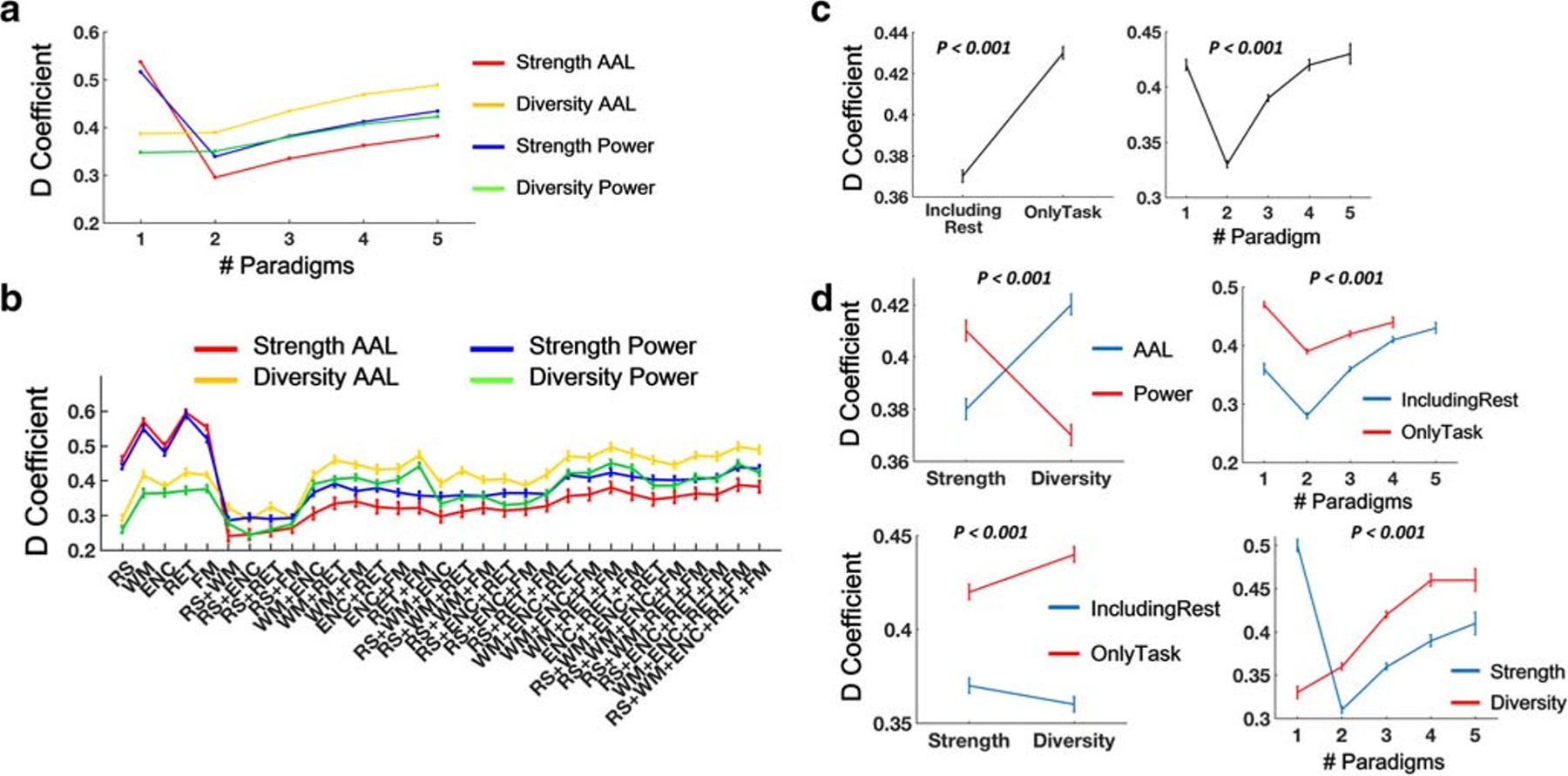
Reliability (D-coefficients) for measures of CPC matrices in the D-study. Note that reliability measures for functional connectivity matrices during each of the five paradigms were also included (as number of paradigm = 1) to facilitate direct comparisons with those of the CPC matrices. These single-paradigm reliabilities were reported previously in (Cao et al. 2018b). (A) Reliability of node strength and node diversity as a function of number of paradigms. (B) Reliability of node strength and node diversity across different paradigm combinations. (C) The matrices derived from only task data and larger number of paradigms had higher reliability compared with rest data and small number of paradigms. (D) Interactive effects were shown for metric x atlas, metric x paradigm type, metric x number of paradigms, and number of paradigms x paradigm type on the reliability measures. Error bars indicate standard errors

To directly compare these cross-paradigm reliability measures with the ones derived from single paradigms, we extracted the D-coefficients for node strength and node diversity from our previously reported work (Cao et al. 2018b). Interestingly, we found that the two examined metrics showed the opposite effects in terms of single-paradigm and multi-paradigm reliabilities (Figs. 2A, B, 3A, B). Specifically, the reliability for node diversity continuously increased with the increase of number of paradigms, while the reliability for node strength dramatically dropped from single to multiple paradigms, regardless of brain atlas. This discrepancy suggests a reliability trade-off between strength and diversity, where CPC would increase the reliability of network diversity at the cost of lower reliability of network strength.

We performed a four-way ANOVA analysis on the outcome reliability measures where atlas (AAL vs Power), examined metric (strength vs diversity), number of paradigms (one to five) and paradigm type (including rest, with 16 combinations vs only task, with 15 combinations) were modeled as fixed-effect factors. Two-way interactions between these variables were also included in the model since the findings strongly suggest an interactive effect. We found significant main effects for connectiviy metric, number of paradigms and paradigm type in both G- and D-studies (P < 0.02, Figs. 2C and 3C), and a significant main effect for atlas in the G-study (P = 0.003, Fig. 2C). In particular, significantly higher reliability was detected for the CPC constructed from only task data compared to those from data including resting state. Moreover, two-paradigm combinations had significantly lower reliability than other three-, four-, and five-paradigm combinations (P_Bonferroni < 0.001), and three-paradigm combinations had significantly lower reliability than four-paradigm combination in the G-study (P_Bonferroni = 0.001). In the D-study, significant effects were shown for all pairwise comparisons except for that between four- and five-paradigm combinations (P_Bonferroni < 0.001). For both G- and D-studies, significant interactive effects were shown for metric x atlas, metric x paradigm type, metric x number of paradigms, and number of paradigms x paradigm type (all P < 0.001, Figs. 2D and 3D). Specifically, node strength was less reliable than node diversity with the AAL atlas but more reliable than node diversity with the Power atlas. Similar pattern was also present in terms of paradigm type, with higher reliability of node strength using data including resting state but higher reliability of node diversity using data including only task paradigms. In addition, as expected, significant interactive effect on metric x number of paradigms indicates that CPC would enhance the reliability of node diversity but reduce the reliability of node strength, at least for the maximal number of paradigms that can be acquired in the current sample.

Since the D-study generally yielded lower overall reliability than the G-study, we further investigated the D-coefficients in the D-study for each single node in the CPC matrices, in order to inform the most reliable nodes in a cross-paradigm research (Tables S3 & S4). Using the CPC built upon all five paradigms, we found that regions with the highest reliability (top 20% ranked by D-coefficient values of all nodes) were largely distributed in the brain’s default-mode system, sensorimotor system, and frontoparietal system, regardless of atlas and metric (Fig. 4). In addition, the subcortical and cerebellar system also showed high reliability in terms of node strength, while the salience system showed high reliability in terms of node diversity. Figure 4 illustrated the top 20% most reliable nodes separated for each atlas and each metric, with nodes in the Power atlas assigned to the established systems (sensorimotor, visual, auditory, default-mode, cingulo-opercular, frontoparietal, salience, attention, subcortico-cerebellar) according to (Power et al. 2011).

Fig. 4.

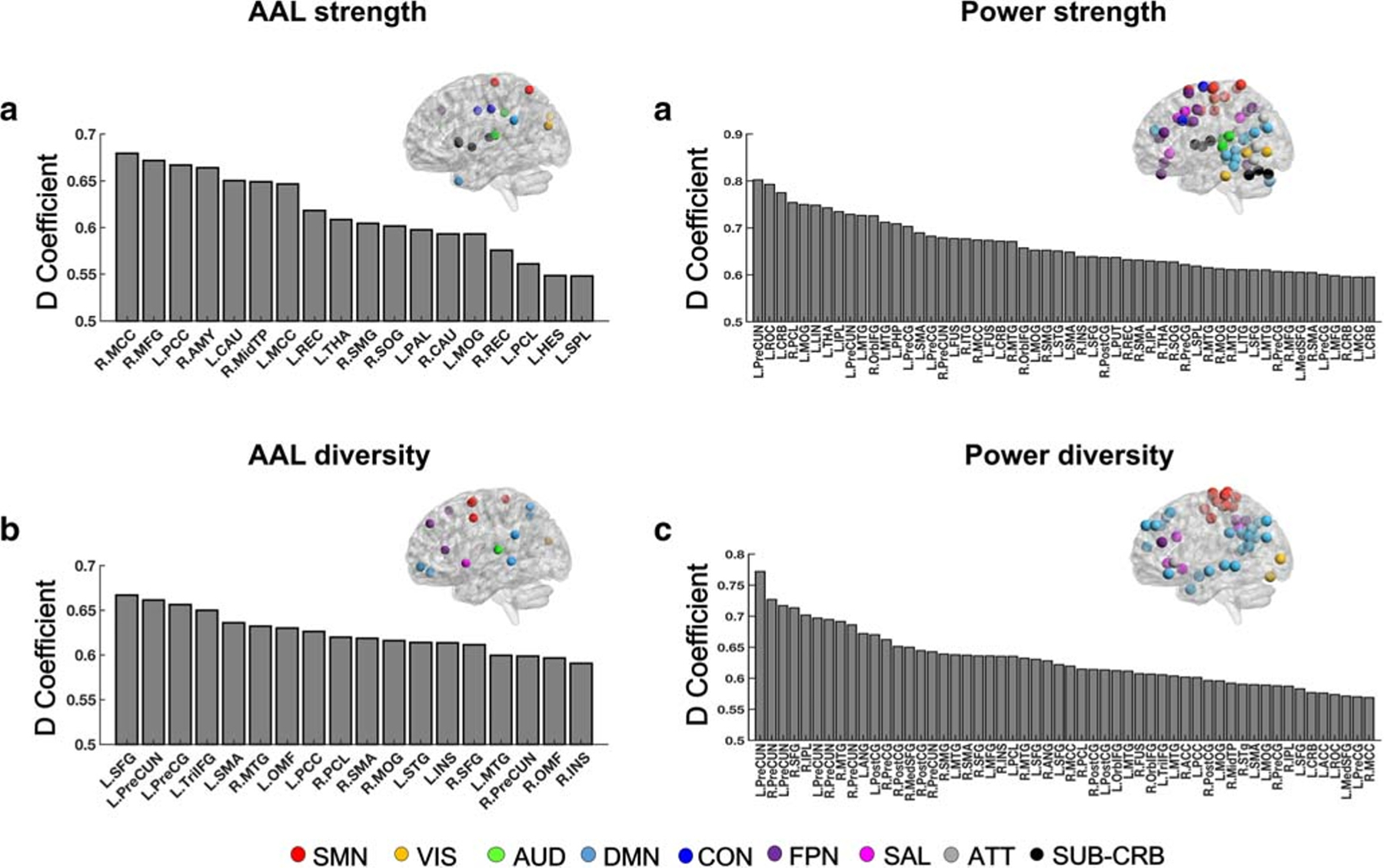
Top 20% of most reliable nodes for the CPC matrices constructed from all five paradigms in the D-study (A: node strength with AAL atlas; B: node diversity with AAL atlas; C: node strength with Power atlas; D: node diversity with Power atlas). For (C) and (D), nodes were allocated to the established networks according to (Power et al. 2011). For (A) and (B), nodes were assigned to the most representative Power network as described in (Cao et al. 2019a). SM = sensorimotor; VIS = visual; AUD = auditory; DMN = default-mode; CON = cingulo-opercular; FPN = frontoparietal; SAL = salience; ATT = attentional; SUB-CRB = subcortico-cerebellar

Considering the small sample size in the present study, we additionally calculated the largest possible null hypothesis values that can be tested for each derived reliability estimates, as an assessment of their performance. The calculation was performed using the R package ICC.Sample.Size (https://cran.r-project.org/web/packages/ICC.Sample.Size/index.html), at statistical power = 0.8, sample size = 8, rater number = 16, and alpha = 0.05 (two-tailed). The results were shown in Table S1 and Table S2. In general, the largest possible null hypothesis values were very close to the derived reliability values at an adequate statistical power (0.8), suggesting that the present sample, albeit small, may still have reasonable power to detect a small effect.

To examine whether head motion would be related to connectivity metrics (node strength and node diversity) in the CPC analysis, which in turn influence the reliability measures, we calculated the correlations between the mean frame-wise displacements across all five paradigms and the mean CPC metrics derived from all five paradigms. The results did not show any significant correlations between head motion and CPC metrics (node strength: P = 0.93 and P = 0.96 for the AAL and Power atlas, respectively; node diversity: P = 0.11 and P = 0.66 for the AAL and Power atlas, respectively). These findings suggest that measures of node strength and node diversity in the CPC analysis are unlikely to be affected by head motion.

Stability of cross-paradigm connectivity

The overall correlation coefficients between different paradigms and paradigm combinations ranged from 0.61 to 0.99 for the AAL atlas (Fig. 5A), and from 0.49 to 0.99 for the Power atlas (Fig. 5B). In general, with the increase of number of paradigms, the CPC matrices became more and more similar to each other, and thus more stable. In particular, the mean pairwise one-paradigm correlations were 0.76 and 0.67 for the AAL atlas and Power atlas, respectively. These numbers increased to 0.89 and 0.83 for the two-paradigm combinations, 0.96 and 0.92 for the three-paradigm combinations, and 0.98 and 0.97 for the four-paradigm combinations. Accordingly, the stability for different paradigms and paradigm combinations increased from 0.78 (for single-paradigm resting state) to 0.95 (for all 5-paradigm combination) with the AAL atlas and from 0.72 to 0.93 with the Power atlas (Fig. 5C, Table S5).

Fig. 5.

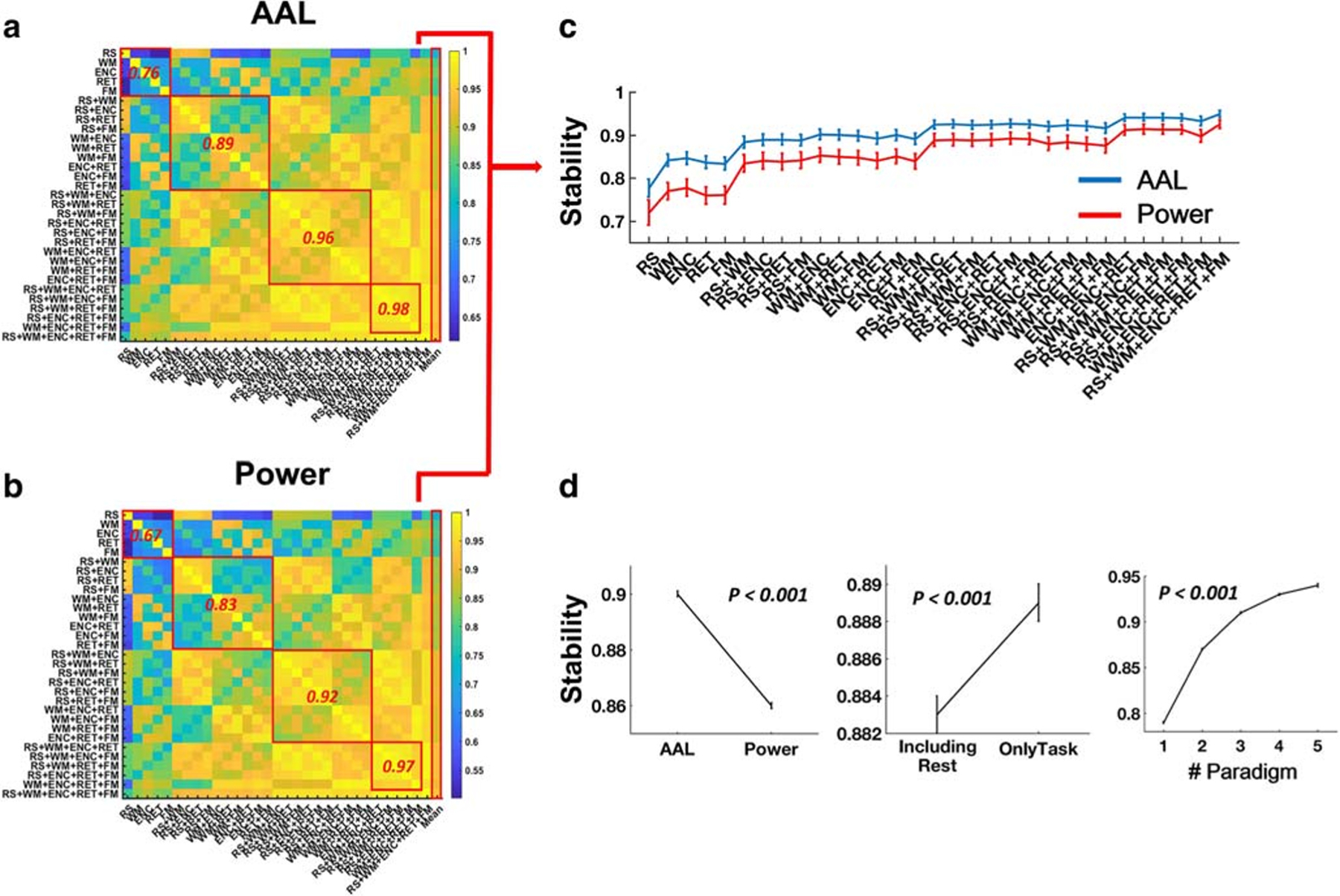
Pairwise similarities of CPC matrices constructed from different paradigm combinations assessed by Pearson correlations (A: AAL atlas; B: Power atlas). The mean pairwise similarities within five single paradigms as well as within two-, three-, and four-paradigm combinations were given in red. The right-most columns indicated the mean similarities (stability) for each paradigm or paradigm combination across all other paradigm or paradigm combinations, which were shown in details in (C). (D) Significant effects were shown for atlas, paradigm type and number of paradigms on the matrical stability. Error bars indicate standard errors

Further statistics using atlas, number of paradigms and paradigm type as fixed-effect factors demonstrated significant main effects for all of these factors. In particular, the AAL atlas, the data without resting-state included, and more paradigms were associated with higher stability of CPC (P < 0.001, Fig. 5D).

Utility of cross-paradigm connectivity

We first investigated whether the single-paradigm PC matrices would be more similar to the multi-paradigm PC matrices, or would more resemble the single-paradigm connectivity matrices. We found that the similarity between multi-paradigm and single-paradigm PC matrices ranged from 0.86 to 0.98, depending on paradigm, atlas, and subject. Similar similarities were also detected between multi-paradigm PC matrices and single-paradigm connectivity matrices (ranging from 0.90 to 0.98). In stark contrast, the similarity between single-paradigm PC matrices and single-paradigm connectivity matrices were ~ 1 (> 0.99) for all paradigms, atlases, and subjects (Fig. 6). The statistical comparison showed a significantly higher similarity between single-paradigm PC and single-paradigm connectivity matrices compared with other pairs (P < 0.001). This finding provides direct evidence that single-paradigm PC matrices are more similar to single-paradigm connectivity matrices than multi-paradigm PC matrices, and thus unlikely to reflect the same network architecture as the CPC.

Fig. 6.

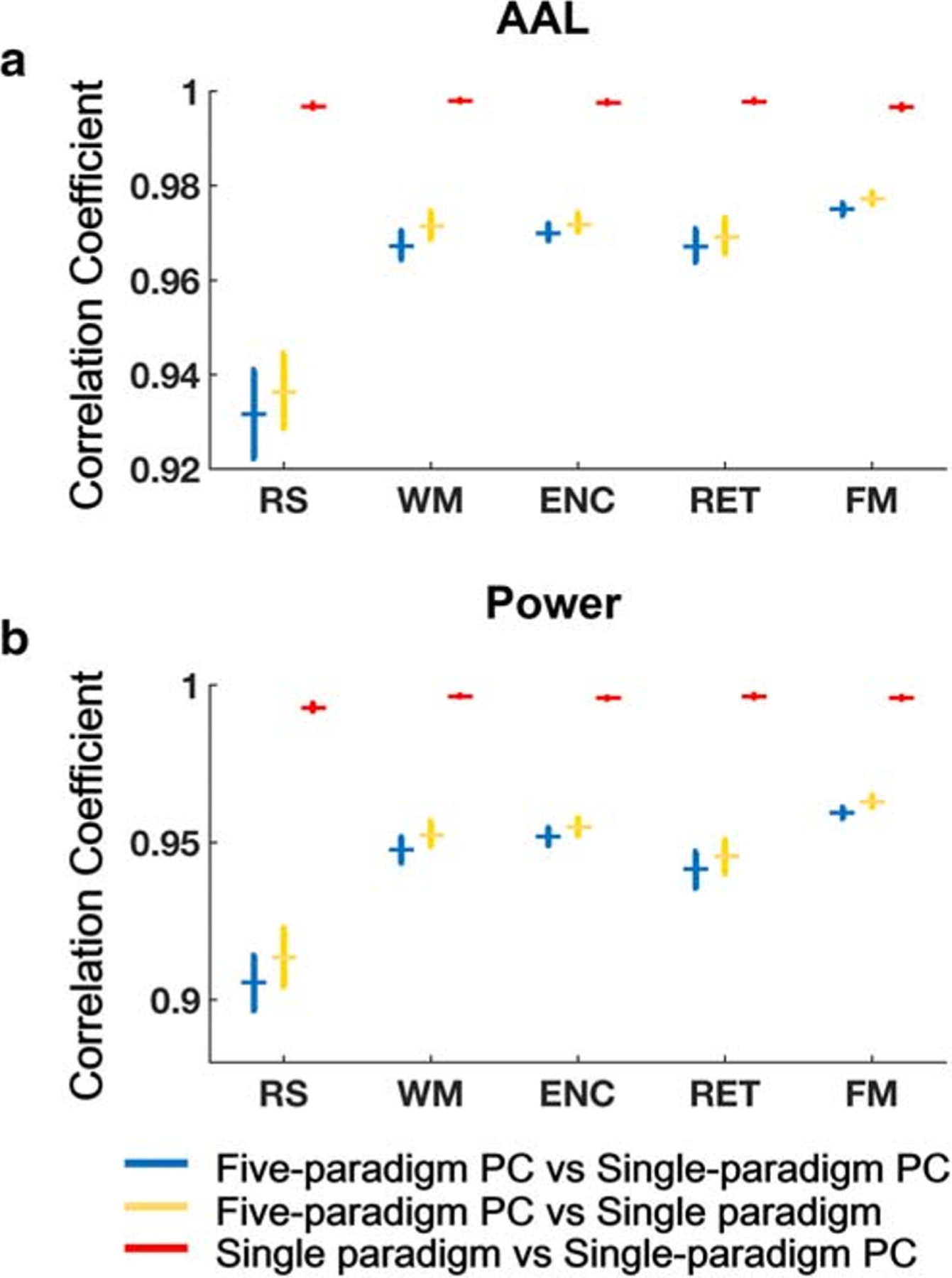
Similarities between multi-paradigm PC matrices, single-paradigm PC matrices, and single-paradigm connectivity matrices (A: AAL atlas; B: Power atlas). Matrices built upon single paradigm and single-paradigm PCA were almost identical (r ~ 1), both of which were much less similar to that built upon multi-paradigm PCA. Error bars indicate standard errors

The connectome fingerprinting analysis showed that the overall accuracy ranged between 0.35 and 0.97 for the AAL atlas, and between 0.68 and 1 for the Power atlas. Specifically, accuracies for single-paradigm connectivity ranged between 0.35 and 0.95 for the AAL atlas, and between 0.69 and 1 for the Power atlas. For the AAL atlas, two-, three-, four-, and five-paradigm CPC fingerprinting accuracies were between 0.41 and 0.95, between 0.53 and 0.97, between 0.55 and 0.97, and between 0.60 and 0.97, respectively. The minimal accuracies for two-, three-, four-, and five-paradigm CPC using the Power atlas were 0.68, 0.74, 0.77 and 0.80, respectively, while the maximal accuracies all reached 1 (Fig. 7A, Table S6). All derived accuracies were significantly higher than the chance level, as demonstrated from 10,000 permutations.

Fig. 7.

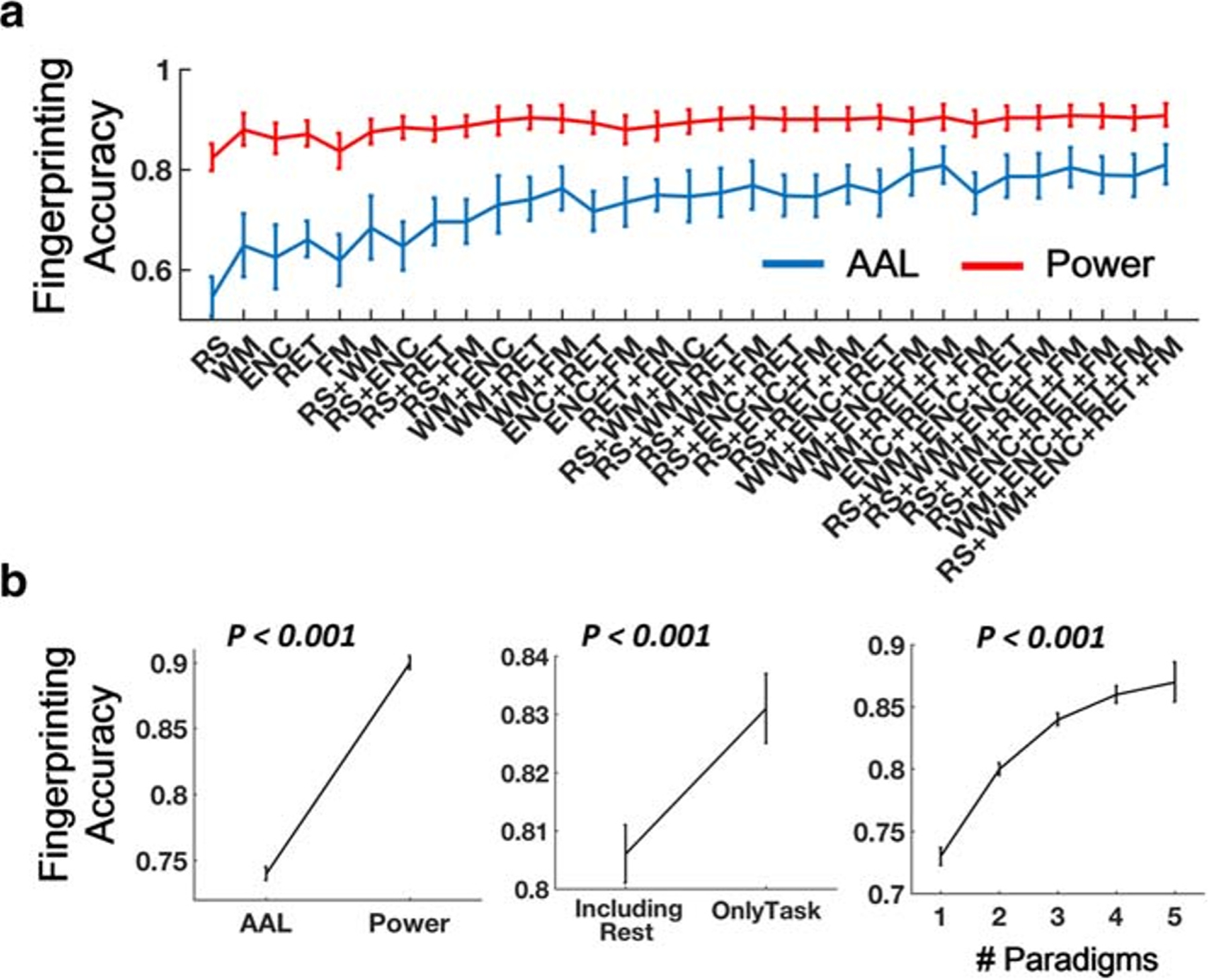
(A) Accuracy of connectome fingerprinting using CPC matrices across different paradigm combinations. Note that fingerprinting accuracies for functional connectivity matrices during each of the five paradigms were also included (as number of paradigm = 1) to facilitate direct comparisons with that of the CPC matrices. All derived accuracies were significantly higher than the chance level (~ 0.125), as calculated from 10,000 permutations. (B) Significantly higher accuracies were shown for matrices using Power atlas, only task data, and larger number of paradigms. Error bars indicate standard errors

Similar as steps described above, we also performed a mixed-effect model to investigate the contributions of different factors to connectome fingerprinting accuracy. With atlas, number of paradigms and paradigm type modeled as fixed-effect variables and subject as random-effect variable, we found significant effects for atlas, number of paradigms, and paradigm type (P < 0.001, Fig. 7B). In particular, CPC fingerprinting accuracies were significantly higher for the Power atlas and for including only task data compared with the AAL atlas and including rest data. In addition, the accuracy also became higher when the number of paradigms increased. These findings suggest that an optimal processing pipeline and fMRI paradigm would reduce the false positive and false negative rates in connectome fingerprinting.

Discussion

In this study, we computed individual CPC patterns using our previously proposed approach (Cao et al. 2018a) in a sample of traveling subjects scanned with five fMRI paradigms, and assessed the reliability, stability, and utility of these derived CPC patterns. Our results demonstrated that the CPC matrices were reasonably reliable, stable, and were capable of distinguishing individuals from one another, at least in the current sample with the employed paradigms. Moreover, factors such as the choice of brain atlas, the number of paradigms, and type of paradigms significantly influenced the outcomes. Overall, these findings suggest PCA-based CPC analysis as a promising approach to study human brain “traits” in neuroimaging research, although the choices of brain atlas and fMRI paradigm are worthy of consideration in future studies.

Consistent with our prior work using the same sample (Cao et al. 2018b), we observed good to excellent reliability for CPC node strength and node diversity in the G-study, and relatively lower reliability for these measures in the D-study when generalized into the context of single-site and single-day (N_site = 1, N_day = 1). Interestingly, while node strength was more reliable than node diversity using single-paradigm data, the pattern was partly flipped for multi-paradigm CPC matrices, suggesting node diversity as a promising target measure in longitudinal and/or multi-center studies using the CPC approach. When comparing reliability measures from single-paradigm connectivity matrices with those from multi-paradigm CPC matrices, we found an increase from single- to multi-paradigm in terms of node diversity but a decrease in terms of node strength, suggesting that the use of multi-paradigm data has a mixed effect on the derived connectivity matrices. On the one hand, the PCA analysis would extract the most consistent variance across multiple paradigms and thus render the node diversity (which per se is a measure of connectivity variance) more reliable; on the other hand, since functional connectivity strength differs between different paradigms, the inclusion of multiple paradigms would make the resulting node strength more heterogeneous and thus less reliable than that from a single paradigm. However, this reliability loss tends to be greatly compensated by the increase of number of paradigms, suggesting that acquiring high reliability of node strength in the CPC context may need a sufficient number of paradigms.

We found that the most reliable nodes in the CPC matrices were predominantly distributed in the default-mode network, sensorimotor network, and frontoparietal network. This finding is highly parallel to our prior finding that the default-mode and sensorimotor systems are consistently reliable during both resting state and active tasks (Cao et al. 2018b). It has been well known that the default-mode network is a brain system that is strongly activated when individuals are at rest but deactivated during goal-directed tasks (Buckner et al. 2008; Raichle et al. 2001). The robust rest-related activation and task-related deactivation may account for the high reliability of its connectivity patterns. Similarly, the sensorimotor system is required when subjects perform motor response during active tasks, and it may also be involved in the sensation of environmental changes during resting state. In addition, the frontoparietal network is the key cognitive control system in the human brain which serves as a “control hub” that coordinates and regulates the function of other systems in order to reach the task goals (Cole et al. 2014; Cole et al. 2013; Dosenbach et al. 2007). It is also robustly activated across a variety of cognitive and emotional tasks (Dosenbach et al. 2007; Iidaka et al. 2006; Lindquist and Barrett 2012; Owen et al. 2005). As a result, the functionality of these systems makes them plausible to be reliable during a multi-paradigm CPC analysis.

With larger number of paradigms included, the derived CPC matrices became more and more similar to each other, suggesting that increasing number of paradigms would enhance CPC stability. Two possible reasons may account for this. First, when the number of paradigms increases, more shared “paradigm-independent” variance was extracted, and the corresponding CPC matrices would more resemble the “trait” matrices for each individual. These “trait” matrices are naturally more stable than the “state” matrices, which are mixed signals of brain’s trait structure, state dynamic, and random noise (Geerligs et al. 2015). Second, when condensing data from multiple paradigms, the random noise becomes attenuated. As a consequence, this process simultaneously increases SNR, which would make the resulting matrices more stable. However, given the fact that single-paradigm PC matrices are much more similar to single-paradigm functional connectivity matrices than to multi-paradigm CPC matrices, the second interpretation is unlikely to be the case to account for increased stability. Together, our results suggest that use of more paradigms would make the derived CPC matrices closer to the brain’s “trait” architecture, the pattern of which is unachievable from single-paradigm matrices, even with multiple sessions.

Since the CPC matrices most likely reflects the “trait” architecture of the brain system that is unattainable by single-paradigm fMRI, the utility of such “trait” patterns becomes critically important. Using the “connectome fingerprinting” approach, we demonstrated that the CPC matrices were able to identify individuals among the healthy population, the accuracy of which outperformed that using single-paradigm functional connectivity matrices, suggesting the superiority of CPC in estimating inter-subject variability and in subject identification. Notably, the identification accuracy became higher with the increase of number of paradigms, suggesting that closer to the functional “trait” network would render the CPC matrices more distinct and identifiable. Since human functional connectome is highly individualized and predictive of a variety of demographic, cognitive, and behavioral variables such as age (Dosenbach et al. 2010), gender (Zhang et al. 2018), intelligence (Finn et al. 2015), attentional ability (Rosenberg et al. 2016), and personality traits (Dubois et al. 2018; Hsu et al. 2018; Jiang et al. 2018), these findings suggest the potential of CPC as a novel and possibly better individual predictor in cognitive and behavioral research. Moreover, clinical studies also revealed that the patterns of functional connectome are highly predictive of symptom severity in multiple brain disorders such as schizophrenia (Cao et al. 2018a), Alzheimer’s disease (Lin et al. 2018), autism (Plitt et al. 2015), and stroke (Watson et al. 2018), which further suggests the broader utility of CPC in both healthy and clinical populations.

Several factors significantly affected the outcomes of the CPC matrices. Specifically, compared with the Power atlas, the AAL atlas was associated with higher reliability of node diversity, lower reliability of node strength, higher stability, and lower identification accuracy. Compared with data including only task paradigms, data including rest paradigm were associated with lower reliability, lower stability, as well as lower identification accuracy. These findings may have interesting implications for future CPC studies. One possible explanation for the effect of brain atlas is the different number of nodes between the two examined atlases. As previously shown, networks constructed from the larger size Power atlas are generally more reliable than the smaller size AAL atlas (Cao et al. 2018b; Cao et al. 2014). In addition, a relatively high-resolution parcellation is related to higher individual variability, and thus boosts identification accuracy (Finn et al. 2015). However, larger network size may also be associated with higher chance of spurious connections and noise, which may relatively reduce stability. Another explanation is the different definitions of the two atlases. Since the Power atlas is functionally defined based on both resting-state and task data, it may by nature more accurately represent functionally separated units in the human brain that in turn increases the reliability of its connectivity strength. In contrast, the function of the structurally defined AAL atlas tends to be more heterogeneous, thereby increasing the reliability of connectivity diversity. These results suggest that the choice of brain atlas may depend on research purposes in the CPC studies. Besides the brain atlas effect, the lower performance of CPC matrices with data including resting state may be attributed to several reasons. First, compared to the conditions when subjects are actively involved in goal-directed tasks, a resting state design lacks the component to constrain the subjects’ attention and thoughts. This naturally makes the connectivity differences between resting state and active tasks larger than those between different task conditions. As a consequence, the CPC matrices constructed from both rest and task data would capture less shared variance than those constructed from only task data, and thus less stable. Second, the lower reliability with data including resting state well corresponds to previous work showing that task-based brain networks are more reliable than resting-state brain networks (Cao et al. 2018b; Deuker et al. 2009b). Compared to task paradigms which require considerably more attentional effort, resting state involves the random engagement of internal thoughts such as introspection, future envisioning and autobiographical memory retrieval (Buckner et al. 2008), and thus by nature is more vulnerable to state-related within-subject factors such as mood, tiredness, diurnal variations, and scan environment. These discrepancies would also contribute to their differences in connectome fingerprinting accuracy, where the connectome during tasks outperformed that during rest. Notably, the same finding has been reported before in (Finn et al. 2017). As discussed by the authors, “Rest has become the default state for probing individual differences, chiefly because it is easy to acquire and a supposed neutral backdrop… However, mounting evidence suggests that rest may not be the optimal state for studying individual differences.” This argument seems to be supported by our own data based on CPC fingerprinting.

Besides the CPC approach, a recent study has proposed a method assessing “general functional connectivity (GFC)” based on the concatenation of time series across multiple fMRI paradigms (Elliott et al. 2019). Interestingly, the results from the GFC method seem to be highly similar to those reported in the current study using a CPC approach. In particular, both studies have shown that the inclusion of multiple paradigms would significantly increase the reliability of derived connectivity metrics, and that a combination of multi-paradigm data would achieve better individual predictability compared with resting-state data alone. While future studies are encouraged to compare the performance of these two approaches quantitatively, both studies have clearly pointed to the important value of leveraging multi-paradigm fMRI data in studying individual brain networks.

We would like to note several limitations for our study. First, we acknowledge that the sample size in this study is relatively small, which may to a certain degree constrain the power to quantify the desired measures of CPC matrices. Despite the fact that this fMRI sample is one of the largest to date with subjects repeatedly sampled from multiple sites, days, and paradigms, future studies with larger sample size assessing the performance of CPC matrices are still warranted. Second, while we explicitly tested the effect of brain atlas on the outcome measures, many other factors during fMRI data processing may as well influence our findings, such as preprocessing parameters (Braun et al. 2012), filter frequency (Braun et al. 2012; Deuker et al. 2009a), noise correction strategy (Braun et al. 2012; Cao et al. 2018b; Liao et al. 2013), connectivity metrics (Fiecas et al. 2013; Liang et al. 2012), among others. Since variabilities in these factors were not examined in this study, we would like to emphasize that our findings are based on a preselected data processing pipeline and may not necessarily generalize to other pipelines. In a similar way, our results are also generated from a typical set of fMRI experiments evaluating memory, emotion and resting functions of the brain, and CPC matrices computed from other paradigms may show (presumably slight) differences from this battery. Third, an interesting yet unexplored question is whether lower reliability of node strength in multi-paradigm CPC would be completely compensated for using a larger number of fMRI paradigms. If this is the case, multi-paradigm studies with large number of paradigms would certainly be beneficial in investigating individual traits.

To sum up, using a traveling-subject multi-paradigm fMRI dataset, our study provides the first evidence for the reliability, stability, and utility of CPC in neuroimaging research. The findings in the present data encourage the use of CPC approach to study brain functional “traits” related to individual cognition, behavior, and neuropathology, and offer some useful insights into the choices of brain atlas and fMRI paradigm. While these findings still merit further replication, they suggest that a shift toward the collection of large batteries of paradigms is preferred to understand individual differences in cognitive and clinical neuroscience, in addition to resting-state data where the vast majority of current research has been focused on.