Abstract
Against the COVID-19 pandemic, non-pharmaceutical interventions have been widely applied and vaccinations have taken off. The upcoming question is how the interplay between vaccinations and social measures will shape infections and hospitalizations. Hence, we extend the Susceptible-Exposed-Infectious-Removed (SEIR) model including these elements. We calibrate it to data of Luxembourg, Austria and Sweden until 15 December 2020. Sweden results having the highest fraction of undetected, Luxembourg of infected and all three being far from herd immunity in December. We quantify the level of social interaction, showing that a level around 1/3 of before the pandemic was still required in December to keep the effective reproduction number below 1, for all three countries. Aiming to vaccinate the whole population within 1 year at constant rate would require on average 1,700 fully vaccinated people/day in Luxembourg, 24,000 in Austria and 28,000 in Sweden, and could lead to herd immunity only by mid summer. Herd immunity might not be reached in 2021 if too slow vaccines rollout speeds are employed. The model thus estimates which vaccination rates are too low to allow reaching herd immunity in 2021, depending on social interactions. Vaccination will considerably, but not immediately, help to curb the infection; thus limiting social interactions remains crucial for the months to come.
Keywords: SEIR model, Cross-country comparison, Bayesian inference, Markov Chain Monte Carlo, Healthcare system
1. Introduction
In December 2019, a novel strain of coronavirus SARS-CoV-2 (severe acute respiratory syndrome coronavirus 2) was first reported in Wuhan, China. In severe cases, it causes an acute respiratory distress syndrome (ARDS), which can lead to respiratory failure, septic shock, multi-organ failure and death (Mohanty et al., 2020). By mid December 2020, worldwide 72 million confirmed cases and 1,6 million dead people had been identified to be infected with SARS-CoV-2.
To help mitigating the coronavirus disease 2019 (COVID-19) pandemic, mathematical modelling has become a major tool in understanding its diffusion (Currie et al., 2020). As COVID-19 is currently widely spread across the globe, short- and medium-term modelling forecasts assess the need for containment strategies. For these purposes, one of the most employed models is the Susceptible-Exposed-Infectious-Removed (SEIR) model, for which numerous extensions have been recently developed. Extensions including compartments for hospitals and deaths have been developed among others for Italian regions (Reno et al., 2020) and Sweden (Sjoedin et al., 2020). An extension to investigate the crucial role of asymptomatic cases was developed in Emery et al. (2020). One including a time-varying transmission rate was presented in Cazelles et al. (2021) for France and Ireland. A network-based version of the SEIR model focused on Italian regions (Gatto et al., 2020) showed that the effects of the employed measures have been decisive in preventing much worst outcomes. An extension including asymptomatic cases showed that the timing of social distancing is crucial (Gevertz et al., 2021). Various synergies of different mitigation strategies can lead to similar suppression of the infection, with different consequences (Proverbio et al., 2021). Models were developed to investigate the effectiveness of specific non-pharmaceutical interventions employed as lockdown-like measures and universal masking (Yang et al., 2021) or social distancing and travel restrictions (Parino et al., 2021). Different measures have different economical consequences, and the epidemiological and economical aspects of the pandemic strongly influence each others (Burzynski et al., 2021).
In this study, we extend the SEIR model including a social interaction parameter, the presence of undetected cases, vaccination and the disease progression through hospitals, ICU, recovery and death. The aim is to understand the different phases of the pandemic which occurred in countries employing different policies, and to investigate how the interplay between vaccination strategies and social interactions might lead towards herd immunity throughout 2021. We focus on the epidemic dynamics of three countries: Luxembourg, having the highest fraction of detected COVID-19 cases per 100,000 inhabitants in Europe in December 2020; Sweden, following different intervention strategies, not imposing a full lockdown and considered having attempted to reach herd immunity early on; Austria, showing dynamics comparable to Luxembourg. We calibrate the model separately to publicly available data of each country, and employ it to compare the epidemic dynamics during infection waves within and between countries.
The model is further used to investigate dynamical trends associated with vaccination. As several vaccines became available at the end of 2020, systematic vaccination campaigns have taken off in a number of countries in the first months of 2021. They are of extreme importance, not only to protect the most vulnerable people, but also to contribute to eradicate the virus in the population through herd immunity (Rashid et al., 2012). Herd immunity is achieved when a certain fraction of the total population is immune to the infectious disease (through natural infection or vaccination), so that the infectious agent can no longer generate large outbreaks (Fontanet and Cauchemez, 2020). Much remains to be learned about immunity to SARS-CoV-2 (Poland et al., 2020) and there exist additional challenges to mass vaccination, associated to supplying the vaccines and to the logistic of their deployment. A key question in the current COVID-19 pandemic is thus how and when herd immunity could be achieved (Fontanet and Cauchemez, 2020).
To tackle this question, we use our model to investigate the potential impact of various vaccination strategies and their synergy with social measures for the considered countries. We investigate when herd immunity might be reached depending on vaccines rollout speeds in plausible scenarios. The desirable objective would be to achieve herd immunity primarily by mass vaccination, while avoiding the saturation of healthcare systems and having as few cases and deaths as possible. In fact, the alternative to achieve herd immunity primary by infection has been shown to pose severe risks of overwhelming the health care system and to lead to high numbers of deaths (Brett and Rohani, 2020).
With our study, we are aligned to a long standing tradition of using mathematical models in the design of mass immunization programs (Nokes and Anderson, 1988). Recently, some works presented results based on simple models and conceptual scenarios (Good and Hawkes, 2020, Anderson et al., 2020, Saad-Roy et al., 2021, Deng et al., 2021). Attainability of herd immunity by vaccination in the UK is investigated in Moore et al. (2021). Instead, the presented model is calibrated on data from multiple countries and includes compartments for disease progression and undetected cases and has the scope to systematically investigate the interplay of vaccination strategies and plausible social interaction scenarios in the pursuit of herd immunity. This model was also employed during the ongoing pandemic to investigate the impact of reductions of social interaction and to generate projections to inform policy-making.
2. Methods
2.1. Mathematical model
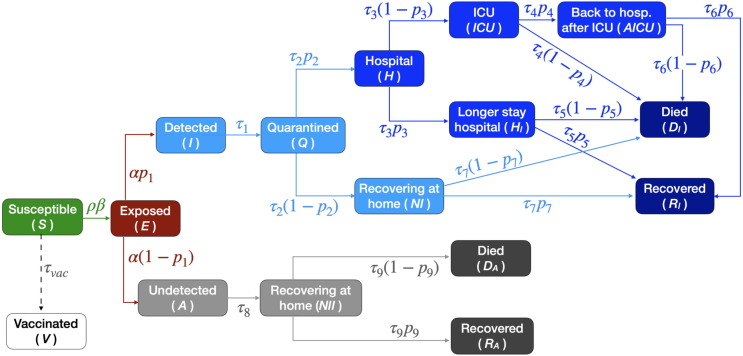
We develop a mathematical model of the transmission of COVID-19 within a country’s population, extending the standard Susceptible-Exposed-Infectious-Removed (SEIR) model (Kermack et al., 1927) to include: 1) undetected cases; 2) varying social interaction; 3) the progression of severe cases through hospitalization, intensive care and eventually death or recovery and 4) vaccination. The model, Fig. 1 , is implemented through a set of ordinary differential equations (Eqs. (A.2) in Appendix). The total population N of the considered country is streamed at time t into 16 compartmental variables, Table A.1. An important fraction of infected people is usually not detected (Li et al., 2020), so we introduce a separation between detected and undetected cases. One branch (detected cases) can lead to quarantine and possibly to hospital and/or ICU. The other (undetected cases, either because they are asymptomatic (Emery et al., 2020) or simply due to lack of testing) continues spreading the infection until recovery or death. The probability of an infected individual to be detected is indicated as and assumes different values for each country and wave of infections, Table B.2 and Table H.6.
Fig. 1.
Scheme of the mathematical model. The model construction is described in Section 2.1. Each compartment is associated to a variable, see Appendix Table A.1 and Eqs. (A.2). Each variable represents the fraction of individuals in that state at a given time. Arrows represent flow of individuals between states, with associated probabilities and rates reported in Table B.2. Their values for each country and wave are summarized in Table H.6. Vaccination is assumed to occur at a constant rate, to have efficacy and to be administered to susceptible individuals only. These assumptions lead to the projections involving vaccination to be optimistic, see Sections 2.1 and 4.
Most model parameters represent either probabilities of going to one compartment or another, or rates describing how fast individuals flow through compartments (i is an index over parameters, their values are listed in Table B.2). Probability parameters determine which fraction of population goes to one branch, which to the other. Rates, representing the inverse of the average length of stay in a compartment, capture how fast (on average) individuals flow from one pool to the next. The only parameter not representing a rate or probability is the social interaction parameter , which tunes the average contact rate . It represents the fraction of social interactions taking place at any given time, with respect to the one pre-pandemic. Thus, a value of means the same level of social interaction as in the beginning of 2020. This parameter incorporates non-pharmaceutical interventions and changes in population behaviour similarly affecting the dynamics. It changes whenever new measures or major updates in social interactions take place (lockdown, schools opening/closure, summer vacation, etc.).
Mathematical models are necessarily simplifications of reality. They balance complexity, including the factors crucial to answer the investigated questions and to learn useful real-world lessons, with simplicity, as they need to be simple enough to be numerically and/or computationally tractable. Hence, the present model relies on a number of assumptions.
As other SEIR models, the present model is deterministic and mean-field, so it does not describe the stochastic aspects of the epidemic, e.g. super-spreading events, but concentrates instead on its average evolution. Alternative approaches to ODE-based models have been developed, e.g. agent-based models (Tracy et al., 2018), recently applied e.g. to Luxembourg (Thompson and Wattam, 2021), Switzerland (Shattock et al., 2021) or Australia (Chang et al., 2020). Deviations from mean-field effects are expected to play an important role in periods of low infections numbers, where e.g. one or few super-spreading events can make the difference between starting or not a wave of infections (Althouse et al., 2020). However, with high case numbers we expect a deterministic description to be sufficiently accurate, especially when it comes to the progression of infected individuals into more severe stages as hospitalisation, ICU and death.
The model does not include an age structure. As COVID-19 case fatality rates, hospitalization and ICU admission rates vary with age, the values of our parameters represent an average over age groups. Instead of capturing the age-dependent risk of disease progression, the present model fits and simulates aggregated hospitals and ICUs occupations and deaths. This allows to compare simulated scenarios for the evolution of aggregated quantities under different assumptions, for which age structure is not crucial. Moreover, not considering explicitly the age structure reduces the number of parameters to fit, thus improving calibration and reducing fitting uncertainties. In addition, while in principle the effective reproduction number can be derived analytically in age-structured SEIR-like models (Hethcote, 2009, Cao and Zhou, 2012, Diekmann et al., 2010), the absence of age structure here contributes to make its derivation much more tractable in practice. Nonetheless, the current assumption could lead our estimates to represent a pessimistic case, since previous computational studies have shown that including age-dependent contacts in an agent based model can reduce the threshold for reaching herd immunity (Britton et al., 2020).
The other factor contributing to make analytically tractable is the way we implement vaccination. Vaccination is also modelled in a simplified manner, namely as individuals flowing at a constant rate out of the susceptible compartment (see also Appendix D). This implies four assumptions. First, we assume that vaccination proceeds at a constant rate. In reality, the rate depends among other factors on vaccines availability; hence, the vaccination rate in the model is intended as an average, reference value. Second, we use the terms “vaccination” and “vaccinated people” referring to individuals who have been fully vaccinated (not those with half coverage from two-doses vaccines). This should be considered when comparing real numbers to the vaccination rollout speeds employed in this paper. Third, we assume 100 vaccine efficacy in preventing an individual from getting infected, developing symptoms and infecting others. This is an optimistic approximation. Fourth, we assume that only susceptible individuals are vaccinated, while in reality also recovered individuals are. While the number of recovered individuals is in the countries and scenarios investigated here considerably lower than the number of susceptible, to some extent supporting this approximation, removing this assumption would somewhat increase the vaccination rates needed to obtain the same results with respect to our estimates. Overall, these assumptions make our vaccination simulations an optimistic limit. However, the absence of age-structure makes our estimates of the herd immunity threshold a pessimistic limit, so the two effects might compensate to some extent, which is difficult to quantify. The impact of the assumptions mentioned here is discussed in more detail in Section 4.
2.2. Model calibration and fit to public data
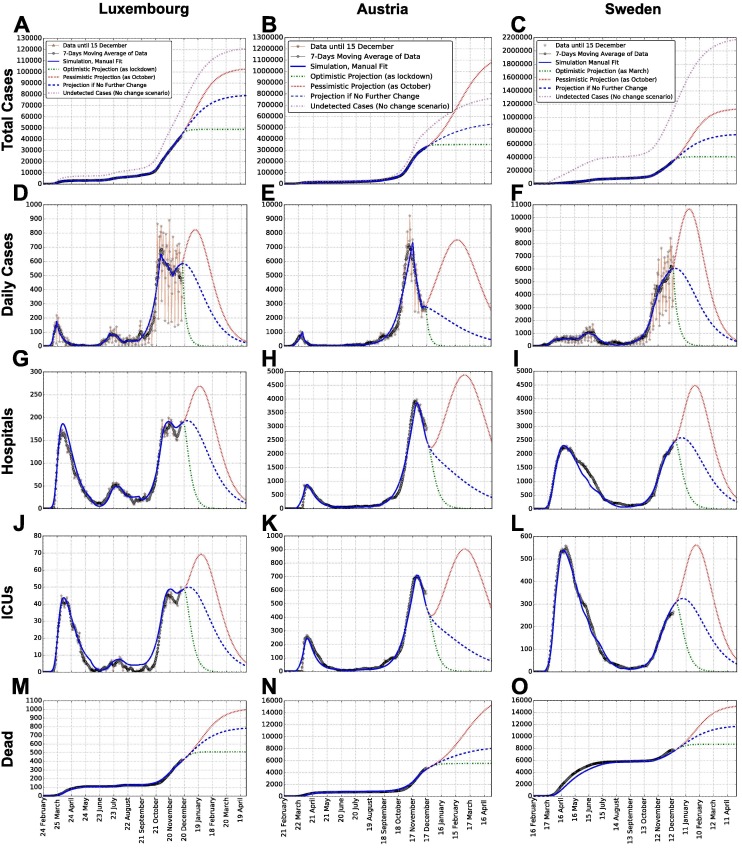
The model is fitted to publicly available time-series data (from February to 15 December 2020), independently for each wave and country. Detailed methodology, data and dates are discussed in the Appendices. These data are displayed in Fig. 2 for total detected cases (A, B, C) and corresponding daily new cases (D, E, F), hospital occupation (G, H, I), ICU occupation (J, K, L) and deaths (M, N, O). Subsequent waves of infections have occurred; we refer to them as 1st and 2nd wave for Austria and Sweden, respectively for those starting in February and September. Luxembourg had an additional wave during July (see Fig. 2 D). So, we refer to it as 2nd wave, and to the rise in September as 3rd wave.
Fig. 2.
Data, model simulations and projections of total cases, daily cases, hospital and ICU occupation and dead, for each country. Reported are: total cases (A, B, C), daily new cases (D, E, F), hospital occupation (G, H, I), ICU occupation (J, K, L) and deaths (M, N, O). Such values are respectively estimated from Appendix Eqs. I.2–I.6, for each country (see columns). In addition to model simulation, raw data are shown (red stars), together with their weekly moving average (gray dots). Panels A, B, C also report (in violet) the cumulative number of estimated undetected cases, obtained as the sum of undetected cases being either infectious, recovering, recovered or dead, see Appendices. Entries of panel A’s legend hold for each panel, except the one for undetected cases, displayed only in panels A, B and C. Projections for several months after the last data point illustrate the potential simulated scenarios explained in the main text.
For each country and epidemic wave, we initially manually calibrate a set of parameters that allow the simulations to fit the data while incorporating literature knowledge (see Appendix H). In the rest of the paper, we will refer to this parameter set as “manual fit” or “manual calibration”. In particular, these parameters are obtained from non-country-specific literature (Rees et al., 2020, Liu et al., 2020, Wu et al., 2020), or from country-specific literature or data (Böhning et al., 2020, Snoeck et al., 2020, Folkhalsomyndigheten 1, Folkhalsomyndigheten 2), or from assumptions. Details are provided in Appendix H: rates and probabilities used are listed in Appendix Table H.6; social interaction parameter values and their changes over time are displayed in Fig. 3 (main text) and listed in Appendix Table F.3 (Luxembourg), Table F.4 (Austria) and Table F.5 (Sweden). Values of the social interaction parameter employed for a given time-period (between two changes in measures) are obtained by best fitting the simulation of new cases to the moving average of the corresponding data. This method already returns good agreement between simulations and data from several time-series data (cf. Fig. 2), thus supporting our choice of parameters.
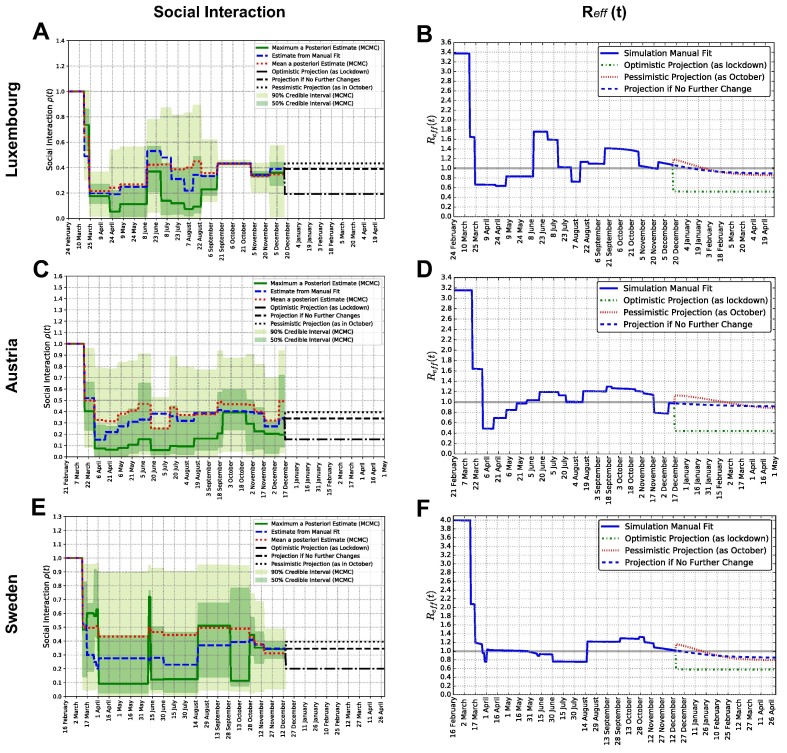
Fig. 3.
Social interaction parameterand effective reproduction numberfor each country. Panels A, C, E: social interaction parameter , manual and Bayesian estimates for Luxembourg, Austria and Sweden. Dates of change and parameter values are reported in Appendix Table F.3 for Luxembourg, Table F.4 for Austria and Table F.5 for Sweden. Panels B, D, F: effective reproduction number , computed from Appendix Eq. C.2, corresponding to the values of the social interaction parameter for Luxembourg, Austria and Sweden, from their manually calibrated parameter sets.
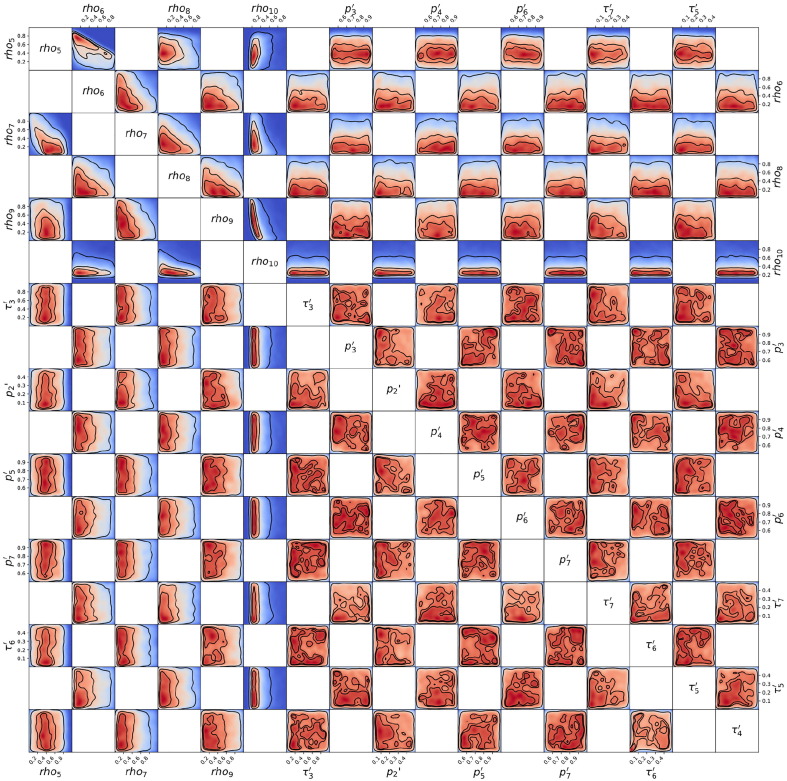
We further cross-validate the calibration of our model by Bayesian inference and Markov Chain Monte Carlo (MCMC) methods (cf. Appendix I). Such methods have been widely applied in the framework of the pandemic to infer epidemiological parameters from SEIR-based or other models, e.g. for Spain (Castro et al., 2020), Germany (Dehning et al., 2020) and in a comparison of 11 countries, including Austria and Sweden (Bryant and Elofsson, 2020). Most of these studies did not include hospitalisations, ICU, deaths and undetected cases and all of them focus on one country, except (Bryant and Elofsson, 2020) which focuses on the basic reproduction number. The set of MCMC simulations is performed to obtain an estimate of the parameters and to quantify their uncertainties. The choice of prior probability distributions for the parameters is specified in Appendix I.2; chains are verified to converge in Appendix I.5. The values of the manual fit are usually included within the Bayesian credible intervals and are thus consistent (cf. Appendix Fig. J.3). We observe high degeneracy between parameters, with combinations (e.g. ratios) of parameters being often better constrained than individual ones (cf. Appendix, Fig. J.4, Fig. J.5, Fig. J.6, Fig. J.7, Fig. J.8, Fig. J.9, Fig. J.10 and corresponding sections). The MCMC is extremely useful to estimate the uncertainty that affects our estimate of parameters and their potential ranges of values, but it does not provide a unique parameter set due to poor identifiability, common to SEIR models (Roda et al., 2020). In fact, the two parameter sets obtained respectively from the maxima of the posteriors (maximum a posteriori estimate) and from the means of the posteriors are rather different from each other due to asymmetric posteriors. Moreover, certain parameters are poorly constrained by the data, resulting in rather flat posterior probability distributions. For the simulations, we thus employ the manually calibrated parameter set, which is unique, consistent with the results of the MCMC, and incorporates domain knowledge from literature as explained in Appendix H.
Fig. J.3.
Posterior probability distributions from MCMC for each parameter, compared with priors and with manual fits, for each country and wave. Luxembourg (A: 1st wave, B: 2nd wave, C: 3rd wave), Austria (D: 1st wave, E: 2nd wave) and Sweden (F: 1st wave, G: 2nd wave). For each parameter, prior probability distributions are reported as gray areas, while the posteriors are reported by means of their (blue) and (cyan) credible intervals, with their maxima reported as large blue dots and their means as red squares. The parameter values for the manual fit (Table H.6 for probabilities and rates, Table F.3, Table F.4, Table F.5 for ) are reported as green small circles.
Fig. J.4.
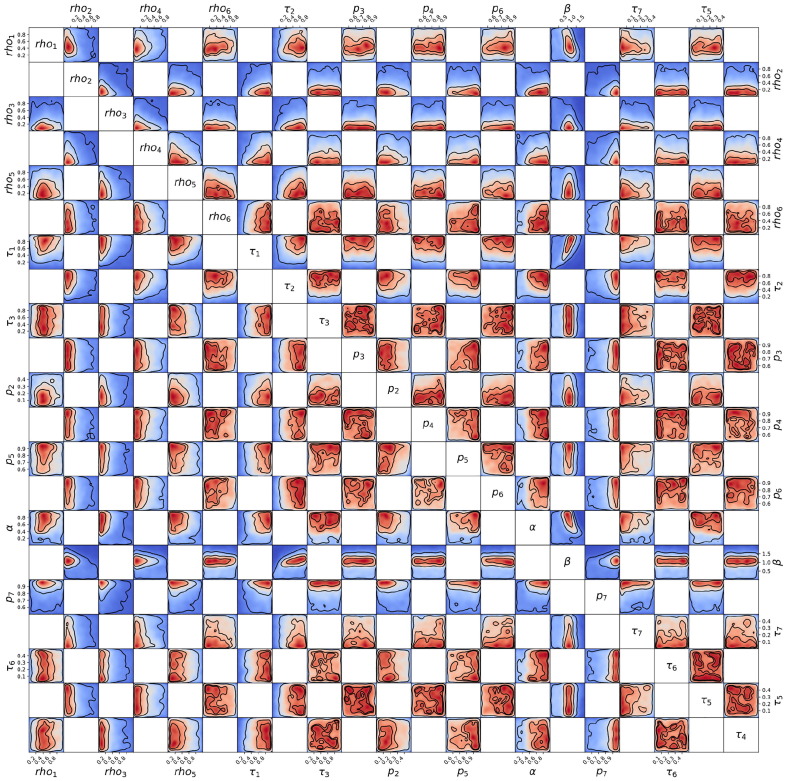
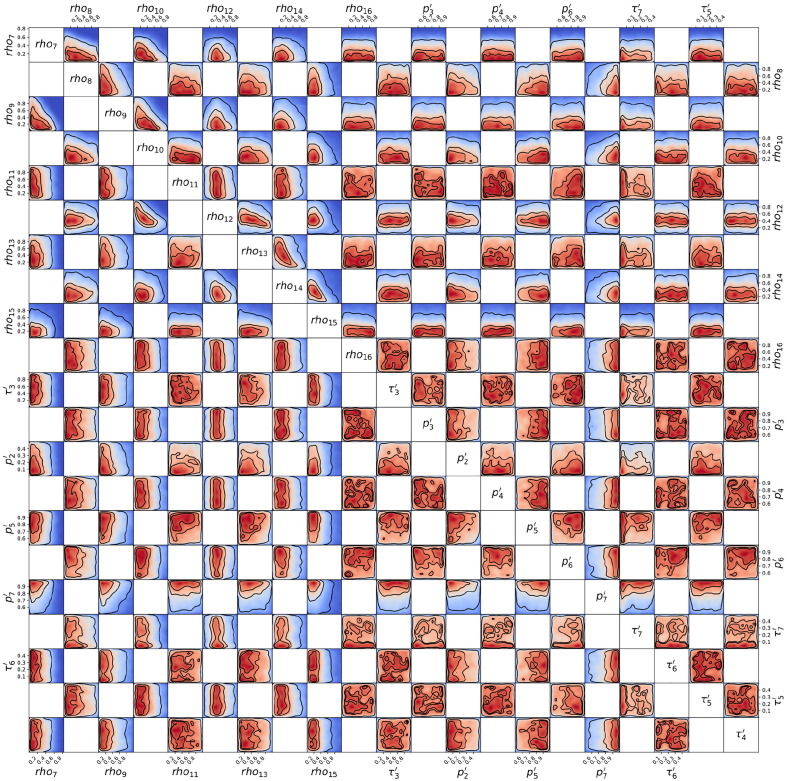
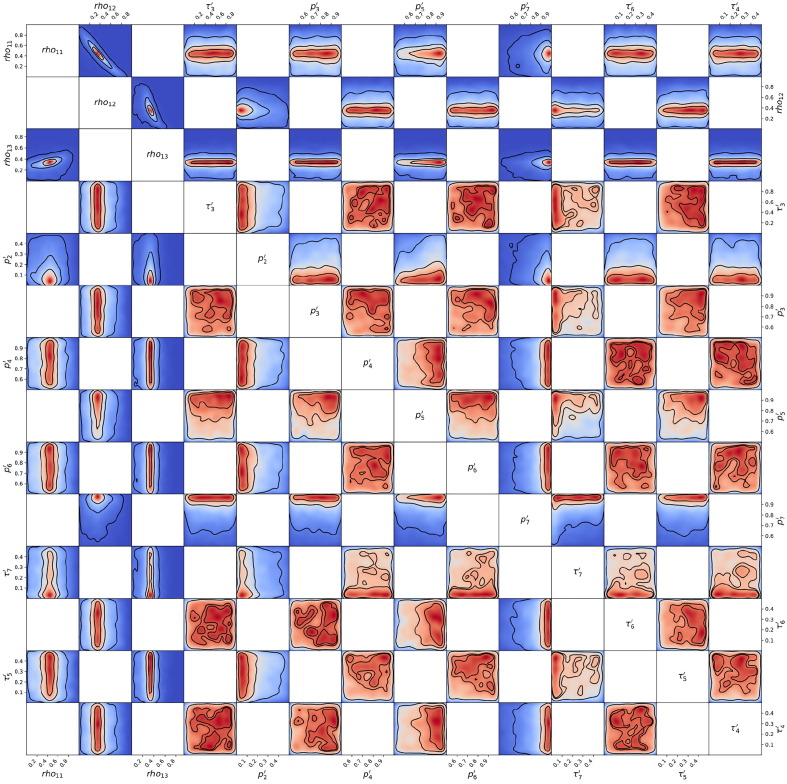
Posterior probability distribution from MCMC projected over each pair of parameters, for the 1st wave of Luxembourg. On each square, the 2D projection of the posterior probability distribution estimated (cf. Appendix I) corresponds to the 1D projections of Fig. J.3. For visual clarity, the parameters’ names and scales are reported only at the margins of the figure and on the diagonal, but they apply to all subplots. As the figure is symmetric along the diagonal, each projection is only reported once (hence the white squares). The heatmap colors represent posterior probability values: red equals high and blue low probability. Dark blue represents a probability close to 0. The three black contours reported in each panel represent and Bayesian credible regions. Correlations, anti-correlations and more complex degeneracy between parameter pairs are visible.
Fig. J.5.
Posterior probability distribution from MCMC projected over each couple of parameters, for the 2nd wave of Luxembourg. This figure is constructed in the same way described in the caption of Fig. J.4.
Fig. J.6.
Posterior probability distribution from MCMC projected over each couple of parameters, for the 3rd wave of Luxembourg. This figure is constructed in the same way described in the caption of Fig. J.4.
Fig. J.7.
Posterior probability distribution from MCMC projected over each couple of parameters, for the 1st wave of Austria. This figure is constructed in the same way described in the caption of Fig. J.4.
Fig. J.8.
Posterior probability distribution from MCMC projected over each couple of parameters, for the 2nd wave of Austria. This figure is constructed in the same way described in the caption of Fig. J.4.
Fig. J.9.
Posterior probability distribution from MCMC projected over each couple of parameters, for the 1st wave of Sweden. This figure is constructed in the same way described in the caption of Fig. J.4.
Fig. J.10.
Posterior probability distribution from MCMC projected over each couple of parameters, for the 2nd wave of Sweden. This figure is constructed in the same way described in the caption of Fig. J.4.
3. Results
3.1. The model accounts for undetected cases and projects potential scenarios
The model (Fig. 1) is developed and calibrated so that it fits available time-series data from considered countries (cf. Section 2.1). To improve the identification of the model parameters, we cross-validate the manual calibration, used in model simulations, with a Bayesian fit (cf. Appendix H, Appendix I, Appendix J and Fig. J.3). Data evolution and model simulations are reported in Fig. 2.
The model also accounts for undetected cases, through a dedicated compartment. In particular, the probability of being detected is estimated for each country and wave from available prevalence data, see Appendix Table H.6. These undetected cases are reported in panels A, B and C of Fig. 2 as cumulative numbers. Over time, this number (violet dashed curve) is approximately between one and two times the number of detected cases for Luxembourg and Austria, while it is up to three to four times for Sweden. The percentage of undetected is in all three countries higher than that of detected, which is in line with estimates like Bicher et al., 2021. Nevertheless, for Austria and Sweden the sum of detected cases and the estimated number of undetected cases until December remains more than an order of magnitude smaller than the population of the country, while for Luxembourg it is higher. In fact, our model shows that, until 15 December 2020, the percentage of population having been infected by SARS-CoV-2 in Luxembourg is about 18.3% (7.2% detected and 11.1% undetected); in Austria 9% (3.7% detected and 5.3% undetected) and in Sweden 14.5% (3.5% detected and 11% undetected). For all three countries, this made herd immunity still far from being reached in December 2020.
On top of reproducing the historical development, the model is employed to simulate potential future scenarios of the epidemic in each country. In Fig. 2 (dashed lines), we simulate the possible progression of the epidemic in the early months of 2021 until spring. Three scenarios are considered: one corresponds to no changes in social interaction w.r.t. mid December; an optimistic scenario where social interaction becomes as low as during the lockdown in March; a pessimistic scenario where it becomes as high as in October. These three scenarios are meant to represent an average outcome and two extreme, but plausible cases. While instructive, projections might be accurate for few weeks, but less so on longer time periods as small changes in e.g. social interaction and corresponding parameter can lead to large changes in the simulated outcome. Consequently, their goal is mainly to investigate potential scenarios that might unfold from the current situation (Castro et al., 2020) and compare them between each other.
3.2. Social interactions drive epidemic dynamics
The parameter tunes social interactions, and changes when new measures or major behavioural changes occur. It is thus implemented as a piece-wise constant function of time. Its value changes at specific dates when modifications in non-pharmaceutical measures took place. A mean constant value is estimated from fitting model simulations to data, and assumed over the subsequent period of time. The evolution of is reported in Fig. 3 for Luxembourg, Austria and Sweden, respectively in panels A, C and E. Measures, dates and values are summarized in Appendix Table F.3 (Luxembourg), Table F.4 (Austria) and Table F.5 (Sweden). When interpreting the results for , it should be recalled that it lumps both population-wide non-pharmaceutical interventions and targeted ones. This choice contributes to make the calculation of analytically tractable, dramatically reduces the number of free parameters, reduces their estimated uncertainties and does not require additional data stratified over population groups. In turn, this description does not capture the effects of heterogeneous measures across population groups (e.g. working sector, etc.). This aspect was instead investigated for Luxembourg in Burzynski et al. (2021). As a result, corresponds to an estimate of the average social interaction across all groups of the population.
Panels in Fig. 3 show values of from both manual calibration and Bayesian inference, which are both proportional to daily cases number. Manually calibrated social interaction values are consistent with the Bayesian estimates, falling within the or credible intervals (respectively, dark green or light green bands). This supports the validity of manually calibrated values, which yield very good model fit to data of detected cases, see Fig. 2, panels A, B, C. This identifies social interaction as an essential model parameter, in turn underlying the importance of social interaction management for epidemic control.
Directly proportional to and to the susceptible population fraction is the effective reproduction number . Its time evolution (analytical derivation in Appendix C, see Eq. C.2) for each country is displayed in Fig. 3, panels B, D and F. Step-wise changes in arise from changes of , while gradual changes are instead due to depletion of the pool of susceptible individuals. The value of at the pandemic beginning provides the basic reproduction number . We estimate for Luxembourg, for Austria and for Sweden. Such values are consistent with those of independent studies. In general, estimates of from Western Europe vary between 2 ad 6 (Yuan et al., 2020, Ke et al., 2021, Locatelli et al., 2021), depending on country, study, method and associated uncertainties. Bryant and Elofsson, 2020 estimates for Austria and 2.89 for Sweden, with posterior probability distributions extending from 2 to 4 (see Fig.2 therein). In Luxembourg, Thompson and Wattam, 2021, provide a value of with their baseline SEIR model. Our full estimates of is also consistent with that reported in the official Luxembourg government website (https:275//covid19.public.lu/fr/graph.html, last accessed on 26/07/2021), estimated with independent methods. There, is estimated to be around 3.3.
From Fig. 3 we can evince the value of at the last data-point, namely 15 December 2020, which is for Luxembourg, for Austria and for Sweden, all very close to . The percentage of social interaction (w.r.t. before the pandemic and corresponding measures) needed at that date to have was similar across countries: 36 in Luxembourg and 34 in both Austria and Sweden.
3.3. Parameter fitting reveals probability of hospitalization decreases between waves
The social interaction parameter changes a limited number of times to represent changes in non-pharmaceutical interventions or population behaviour. To fit the first waves of Luxembourg and Austria, all other parameters are constant (though slightly different between the two countries), as the time evolution of daily new cases, hospital and ICU occupation are alike, although scaled and delayed. However, the same parameters from the first wave overestimate the hospital progression during the second wave.
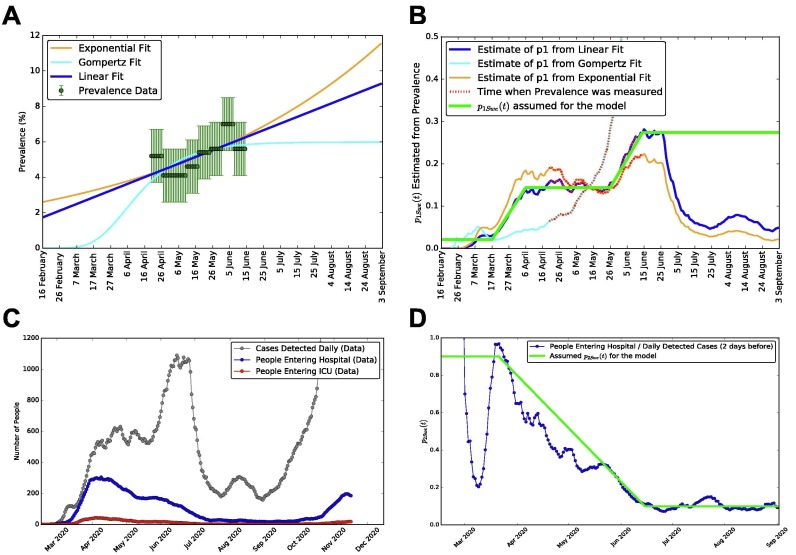
Fig. 4 reports the parameter fold-changes (FCs) between one wave and the subsequent. There, we display the changes observed by different fitting methods, to discuss how stable such results are. In the manually calibrated parameter sets (green circles) the probability of being hospitalized when detected positive, , needs to be decreased between each wave and the subsequent, both in Luxembourg and Austria (among other parameter changes). The same trend in the parameter , which decreases considerably, is also observed in the maximum a posteriori estimate (blue dots) from the Bayesian estimate both between the 2nd and 3rd waves of Luxembourg (panel B), and between the 1st and 2nd waves of Austria (panel C). Only from the 1st to 2nd wave of Luxembourg the Bayesian estimate shows a slight decrease for the maximum of the estimate, but conversely a slight increase in the mean (red squares). Notice that different parameters appear on the horizontal axes of different panels. For Sweden, instead of a step-wise change, we assume a continuous decrease in from 0.9 in March 2020 to 0.1 from June 2020 onward. This is based on data of new daily cases and hospital admissions; further analysis is reported in Appendix G and Fig. G.2 (panel D). These findings underline that, overall, the probability of being hospitalized when detected () decreased for subsequent waves of each investigated country. This likely reflects the improvement and up-scaling of testing strategies over time, leading to an increased capacity to detect asymptomatic or non-severe cases. In fact, represents the probability of being hospitalized if tested positive. So, more effective or widespread testing combined with similar severity of the disease would result in a decrease of . Supporting this interpretation is the fact that in Luxembourg and Sweden we estimated , the probability of being detected positive if infected, to be higher (or constant at most) at subsequent times (see Appendix Table H.6 and corresponding sections).
Fig. 4.
Fold-changes (FC) of the estimates of each parameter, between a wave and the subsequent, for each country.A: 2nd wave versus 1st wave, Luxembourg. B: 3rd wave versus 2nd wave, Luxembourg. C: 2nd wave versus 1st wave, Austria. D: 2nd wave versus 1st wave, Sweden. The values for the parameters employed are displayed in Appendix Fig. J.3 for both manual and Bayesian fit, and summarized in Table H.6 for the manually calibrated parameter set. The vertical axes indicate , with for each parameter, generically indicated as . A value of 0 corresponds to no change, 1 to doubling from the previous wave to the next, to halving from the previous wave to the next, and so on. The green small dots depict the fold changes for the manually calibrated parameter sets. Errors on the means were computed by the standard error of the mean, but are too small to be noticeable in the figure.
Fig. G.2.
Derivation of the time-dependent probabilities of detectionand hospitalization, for Sweden.A: prevalence data for Sweden from Folkhalsomyndigheten 1, Folkhalsomyndigheten 2, with three alternative fits: a linear, a Gompertz and an exponential (for comparison). B: number of detected cases over total cases on time, inferred from prevalence, for the three fits to prevalence of panel A. The final functional form for (the probability of being detected if infected) is in green. C: data for daily new detected cases, people entering hospital and people entering ICU (not to be confused with the numbers of people occupying hospitals and ICUs displayed in Fig. 2 of the main text). D: in blue the ratio of people entering hospitals divided by new daily detected cases two days earlier, which we employ to build the piece-wise linear function (in green). This is assumed for , i.e. the probability of being hospitalized when detected positive.
The MCMC estimates do not fully reflect the changes in some parameters that we performed between one wave and the next in the manually calibrated parameter set (see Fig. 4 and Appendix Table H.6). These discrepancies could indicate that, due to the large uncertainty in parameter identification in our Bayesian inference, multiple parameter sets could provide equally good fit between model and data (see Appendices I and J for further discussion about system identifiability). Supposedly, means provide more robust information than maxima, which are representative of the posterior distribution only when the posterior has a clear peak and is not almost flat. This results in some of the FCs obtained from the maxima (large blue dots) having extreme values, in particular those associated with and , i.e. the rates involved in the patient progression through hospital and ICU.
3.4. Social interactions strongly impact infection in early 2021, along with vaccination
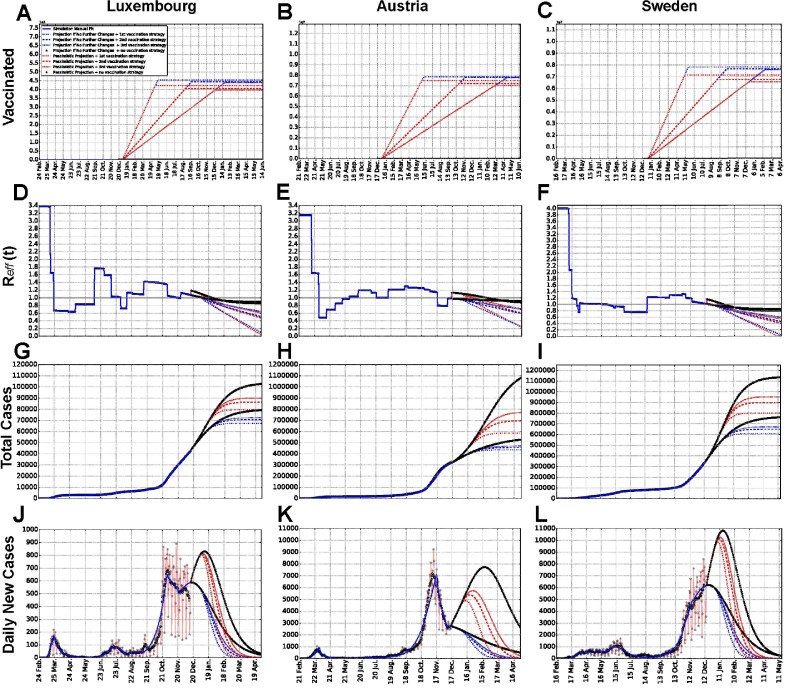
The model includes fully protective vaccination and investigates the interplay between its dynamics and social interaction Three potential vaccination strategies (corresponding to three vaccines rollout speeds) are simulated, starting from 1 January 2021: vaccinating all the country population within the first 6 months of 2021, within 1 year, or within 1.5 years. These would correspond to fast, average and slow rollout, respectively, and represent potential timelines that countries might attempt to implement.
For comparison, we consider the baseline case where no vaccination is performed. The results are displayed in Fig. 5 . Panels A, B, C report people fully vaccinated over time for various scenarios, panels D, E, F display , panels G, H, I the number of total detected cases and panels J, K and L show the number of new daily detected cases. Dashed curves represent the four different vaccines rollout strategies. To investigate the interplay between social measures and vaccination strategies, we simulate combinations of the two. We consider two alternative values of social interactions: a value corresponding to the pessimistic scenario of Fig. 2 (going back to the levels of October 2020, shown in red), and a value corresponding to the average scenario (no change in social interaction w.r.t. December 2020, shown in blue). The optimistic scenario for social interaction is not included, because it corresponds to full lockdown, unlikely to happen for several months consecutively.
Fig. 5.
Simulations of different vaccination strategies: projections of number of fully vaccinated people,, total detected cases and daily new cases for each country. Panels A, B and C show the number of fully vaccinated people as a function of time. Panels D, E and F show . Panels G, H and I show the number of total detected cases. Panels J, K and L show the number of new daily detected cases. Luxembourg (A, D, G, J), Austria (B, E, H, K) and Sweden (C, F, I, L) are reported. Projections for several months after the last data point illustrate potential simulated scenarios, for three alternative vaccination strategies and for no vaccination, both in the case of the “pessimistic” scenario (red, corresponding to social interaction as high as in October) and the “no change” scenario (blue, corresponding to no change in the social interaction) from Fig. 2 and Fig. 3. For each social interaction scenario, we show the curves for no vaccination and for three alternative vaccination strategies (each corresponding to a different vaccines rollout speed), which correspond to vaccinating all the population of a country in, respectively, 6 months, 1 year or 1.5 years, starting from 1 January 2021. Scientific notation is used in panels A, B and C, such that 1e5 in panel A and 1e7 in panels B and C stand respectively for one hundred thousand and ten million people. Assumptions on vaccination are summarised and discussed in Sections 2.1 and 4.
Panels A, B and C in Fig. 5 show that, for high social interaction levels, a smaller number of people will need vaccination, since more people already got infected naturally. Slower vaccination strategies will also result in less people to be vaccinated as more people will by then have acquired immunity naturally. These observations are consistent across considered countries.
Panels D, E and F report the simultaneous effects of social interaction and shrinking of the pool of susceptible, due to both infection and vaccination, on . In each country, for any vaccination strategy as well as for no vaccination, the pessimistic scenario (red) starts with a higher than the “no change” scenario (blue). However, the situation is eventually inverted due to larger shrinking of the susceptible pool associated with higher social interactions. This suggests that the interplay between social interactions and vaccination is non-trivial; it is deeper investigated in the next section.
Panels G, H and I illustrate the changes in dynamics of total detected cases for the same scenarios and strategies. We observe that the faster the vaccines rollout, the fewer total detected cases are reached asymptotically. Any vaccination strategy considered leads to considerable reduction of the detected cases number w.r.t. no vaccination. This discrepancy is larger than the difference in cases between the three strategies. For all three countries, the number of total cases is impacted more, or with similar magnitude, by the different social interaction scenarios (compare red and blue groups) than by vaccination (different dashed curves for the same group color). The corresponding new daily cases plots are displayed in panels J, K and L.
Thus, we can conclude based on this analysis that, at least until spring 2021, social interaction measures are expected to still play an important and dominant role.
3.5. Vaccinating whole population in a year, herd immunity not before mid summer
Expanding what considered above, we tackle the following question: when might herd immunity be reached, depending on combinations of social interaction and vaccination strategies? In mean field SEIR-like models with homogeneous mixing of the individuals, the population fraction needing to be immune, in order to reach herd immunity in the absence of measures, is estimated as (Fontanet and Cauchemez, 2020). To answer the above question, we compute this quantity for the three countries. Using the values of previously estimated, we obtain: for Luxembourg, for Austria and for Sweden, with the pool of susceptible left given by the remaining population. When additional complexities are included in the model, the formula above might not perfectly hold. Hence, we confirmed its results by numerically analysing the model outputs, as described in Appendix E. Briefly, the procedure involves finding the fraction of susceptible, in the measures-free model, that corresponds to the maximum of the infectious curve, which corresponds to herd immunity by definition. The herd immunity thresholds estimated computationally in our model are for Luxembourg and for Austria, for Sweden. These values are similar to the ones obtained analytically and potentially more representative; so, they will be employed in the remaining of the analysis. As reference, Manaus (Brazil) registered a 76% of infected population and a catastrophic losses of lives, before the epidemic naturally slowed down, without relevant interventions (from antibody tests performed in October 2020 (Buss et al., 2021)). Hence, similar values for the herd immunity threshold might occur in reality, and there is consensus (De la Sen and Alonso-Quesada, 2011, Fontanet and Cauchemez, 2020) in aiming for herd immunity primarily by vaccination, instead of natural infection, as the latter could yield symptoms of various severity, occupation of health care facilities and, in a fraction of cases, death. Nevertheless, Manaus also witnessed a major surge in cases in early 2021 (Sabino et al., 2021), leaving open the question if herd immunity against COVID-19 can be reached in real settings.
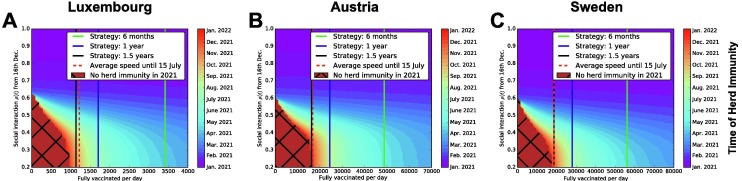
Fig. 6 addresses specifically how we could aim at herd immunity primarily by vaccination, displaying the time at which herd immunity might be reached for all possible social interaction values and vaccines rollout speed. Average social interaction values are assumed to apply from 16 December 2020 onward; the constant number of fully vaccinated people per day is assumed to apply from 1 January 2021, and it should be intended as an average value over time. By requiring the percentage of people still susceptible to be less or equal than , we identify when herd immunity would be reached for each combination of parameters. Herd immunity can be either reached purely by natural infection (by moving along the vertical axis), or purely by vaccination (by moving along the horizontal axes), or by a combination of the two. The three vertical lines in the panels of Fig. 6 show the number of full vaccinations/day required to vaccinate the country’s whole population respectively within 6 months, 1 year or 1.5 years. The corresponding vaccination rates are derived in Appendix D. A vaccines rollout strategy aiming to fully vaccinate the whole country’s population in a year would require approximately 1,700 full vaccinations/day in Luxembourg, 24,000 in Austria and 28,000 in Sweden, and could potentially lead to achieve herd immunity during July 2021 in Luxembourg and during August 2021 in Austria and Sweden. In all three countries, herd immunity cannot be achieved within 2021 with the typical levels of social interactions that were observed so far, without vaccination nor with too low vaccination rates.
Fig. 6.
Systematic investigation of the interplay between vaccination strategies and social interaction scenarios, to estimate the time by which herd immunity might be reached. Luxembourg (A), Austria (B) and Sweden (C). Panels A, B and C: indicative dates at which herd immunity might be reached, depending on combinations of social interaction parameter and number of fully vaccinated people/day. The black grid indicates the combinations of social interaction and vaccination speed that would not allow to achieve herd immunity before 2022. In all panels, vertical lines indicate the three alternative vaccination strategies described in the main text. Depending on measures and population behaviour, estimated levels of social interaction since the beginning of the pandemic have been mostly between and (i.e. to of social interactions w.r.t. before the pandemic). Assumptions of vaccination, like 100% efficacy, are summarised and discussed in Section 2.1 and Section 4. The red dashed line represents an estimate of the number of fully vaccinated people per day for each country, averaged over time from 27 December , 2020 to 15 July , 2021.
For Luxembourg, all three vaccination strategies considered in this study might well obtain herd immunity within 2021; for Austria and Sweden the 1.5 years strategy is only borderline sufficient to reach herd immunity by the end of 2021, while the other two are enough for each country. It remains to be seen if the actual availability of vaccines will make possible any of these example strategies; in the end of this section and in the discussion we compare them with real vaccines rollout speeds recorded until July 2021. If herd immunity had to be reached purely by vaccination (or at low levels of social interaction), the 6 months strategy would take approximately until April 2021 for Luxembourg, and May for Austria and Sweden, and the 1 year strategy until July 2021 for Luxembourg and August for Austria and Sweden. Higher values of social interactions might anticipate it, but with undesired consequences on the healthcare. Several factors not included in the model might influence these estimates, making herd immunity more difficult or easier to achieve, e.g. reinfections and age structure of the population, discussed at the end of the paper.
As COVID-19 is an ongoing situation, we further estimate the vaccine rollout speeds taking place in reality and which can be compared with the three reference strategies of Fig. 6. Based on the model’s assumptions, we hence consider the number of individuals fully vaccinated, averaged over time. In Luxembourg, 248995 people have been fully vaccinated in 200 days, from 27 December 2020 until 15 July 2021; in Austria 3937701 and in Sweden 3716260. In Luxembourg, this corresponds to around 42% of the total resident population being fully vaccinated, in Austria 44% and in Sweden 36.3%. These numbers would correspond to an average of 1245 fully vaccinated people/day in Luxembourg, 19689 people/day in Austria and 18581 people/day in Sweden. We display these estimates in each panel of Fig. 6 as a dashed red vertical line.
4. Discussion
This work consists of two main analysis. First, we calibrated our model to fit time series data of quantities of epidemiological interest, for three countries. By doing so, we tackled the problem of identifiability of complex model parameters, we demonstrated the valuable use of mean field models to describe epidemiological trends in different countries and we obtained a reliable baseline model. Next, we used the knowledge about the epidemiological situation to infer the impact of vaccination campaigns in the pursuit of herd immunity. This provides data-based estimations of the interplay between social measures and vaccination rollouts.
To obtain a reliable dynamical model, we estimated its parameters. Complex epidemiological models might suffer from poor identifiability of their parameters (Roda et al., 2020) often associated with data quality, quantity and fitting methods. To address this and provide consistent estimates, the parameter set was initially manually calibrated and then cross-validated by Bayesian inference, which elucidates parameters uncertainties. Out of such analysis, three remarks are particularly relevant. First: the uncertainties associated to each parameter are non-negligible, and sometimes rather large (e.g. Fig. J.3), possibly due to a large number of parameters. Second: several parameter combinations are better constrained than the corresponding individual parameters (e.g. Fig. J.4 and subsequent). Third: the manual calibration is compatible with the Bayesian estimate (Fig. J.3), but its set of parameters correspond to one possible choice and shouldn’t be considered fully exhaustive. These characteristics are common to any epidemiological model. Here, we carefully investigate them, and where possible we incorporate domain knowledge from literature.
The main parameter controlling the model behaviour is the social interactions parameter , which represents both measures applied by policy-makers and population behaviour. This confirms the well-established fact (e.g. Vrugt et al., 2020) that social interactions are a major driver of epidemic dynamics and of the reproduction number . Changes in are also driven by the depletion of the pool of susceptible that only starts having noticeable effects in fall 2020. So far the effect of on is more pronounced for Luxembourg, where a larger fraction of total population has been infected, than for Austria and Sweden. However, its impact is predicted to become visibly more relevant with subsequent months across 2021 as more people get infected. This is evident from the stronger gradual bending of the curves in winter and spring 2021, especially for the pessimistic scenario, in Fig. 3.
For the model to fit the data, other parameters can be kept constant within single waves in Luxembourg and Austria. However, their value change between waves. This aspect can be explained by reduced probabilities of being hospitalized, as we tested with the manually calibrated parameter set. For Luxembourg (see Fig. 4 and Appendix Table H.6), decreases from in the 1st wave to in the 2nd to in the 3rd. For Austria, from in the 1st to in the 2nd. These changes where also supported by similar changes in the maxima of the Bayesian estimates for 3rd versus 2nd wave in Luxembourg and 2nd versus 1st wave in Austria. This is most likely driven by testing strategies which improved over time, and it might also reflect changes in treatment capacities, in the influenced age categories, and in other factors. For Sweden, considering a different set of parameter values is not enough to fit its data with the same model structure. Instead, time-dependent probabilities of being detected and hospitalized when tested positive, dramatically decreasing from March to June 2020, need to be introduced within the first wave. This does not reflect a rise in infections, but rather a major change in testing strategy and a better prognosis linked to younger patients (Kavaliunas et al., 2020, Ludvigsson, 2020).
The model also allows to estimate the fraction of undetected cases from prevalence data. Luxembourg and Austria display (see Fig. 2) similar fractions of undetected, while Sweden has more, accumulated mostly during the first wave. Until December 15, in Luxembourg about 18.3% (7.2% detected and 11.1% undetected) of the population had SARS-CoV-2; in Austria 9% (3.7% detected and 5.3% undetected) while in Sweden 14.5% (3.5% detected and 11% undetected). Despite the different policies, Sweden was actually not only far from herd immunity, but also further than Luxembourg as of December 2020.
Once calibrated, the model allows to inspect future scenarios to inform data-driven decisions. The epidemic time evolution is simulated in three alternative scenarios for each country (Fig. 2): no change in social interaction w.r.t. mid December 2020; social interaction as low as during lockdown/March 2020 (optimistic); social interaction as high as in October (pessimistic). Infection curves for the three scenarios are well separated from each other, indicating that they could be further reduced by decreases of social interactions (by measures or changes in population behaviour) to values close to those during the first lockdown. In Luxembourg and Austria, the level of social interactions of December 2020 seems to be sufficient to maintain a sub-linear growth of number of total cases in the subsequent months. However, for any of the three countries, an increase of the social interaction parameter to the levels of October would likely trigger a considerable rebound of the infection curve. This would be associated with a rebound in hospital and ICU occupations, thus calling for the maximum caution by population and policymakers alike. In addition, the number of deaths is proportional to the area under the daily infections curve. Thus, keeping daily cases contained to avoid hospitals and ICU saturation does not fully prevent a steady growth of the cumulative number of dead, in particular in the pessimistic scenario.
After calibration, we extended the model with a vaccination compartment and we quantified how long it would take to reach herd immunity. First, we considered the same scenarios as above (cf. Fig. 5). The difference between the detected cases curves of the two considered social interaction scenarios is larger than the difference between the different vaccination strategies. This indicates that during the vaccination process, reduced social interactions are still going to be crucial to keep the number of cases under control, to avoid saturation of hospitals and ICUs and to reduce the number of deaths.
Considering herd immunity by vaccination only (Fig. 6) the strategy of vaccinating everyone in 6 months, alone, would have provided herd immunity by April 2021 for Luxembourg and May 2021 for Austria and Sweden. Slower strategies will lead to herd immunity later on, depending on social interaction values. With an average value of social interactions compared to March-December 2020, aiming to vaccinate the whole population within 1 year at a constant rate could lead to herd immunity by mid summer 2021, in particular by July in Luxembourg and August in Austria and Sweden. Vaccines rollout slower than approximately 1,000 full vaccinations/day in Luxembourg, 16,000 in Austria and 18,000 in Sweden would not allow to reach herd immunity within 2021 in the country, except with high levels of social interaction, which would come with their undesired consequences.
We also compared the simulated strategies to an estimate of the average number of fully vaccinated people per day recorded until 15 July 2021 (cf. Section 3.5). So far and for all three countries, the estimated average vaccine rollout speed has been very close to the simulated scenario labelled “Strategy: 1.5 years”, which was the slowest of the three considered and aimed at vaccinating all of the country’s population within 1.5 years (Fig. 6). This estimate overlaps with the 1.5 years strategy for Sweden, it is slightly faster for Austria and a bit faster for Luxembourg. Simulations indicate that, if vaccination would continue with this same average value in the coming months, and for moderate values of social interaction (below or around 0.4), Luxembourg would still not obtain herd immunity until beginning of the autumn, Austria and Sweden not until end of the year. We can thus conclude that, despite the current advancement status of the vaccination campaign in these three countries, herd immunity has not been reached so far as of 15 July 2021 and thus keeping social interaction contained within a reasonable extent is still crucial until a larger fraction of the population will be fully vaccinated.
What just discussed depends on the interplay with the social interaction . Having would be roughly consistent with the estimates for most of 2020 and possibly until spring 2021. Nevertheless, with the widespread relaxation of measures starting from end of spring and beginning of summer 2021, higher values of might occur. Moreover, variants with increased infectiousness such as Alpha (B.1.1.7) and Delta (B.1.617) have become widespread. The increased infectiousness of such variants can be modeled as an additional factor v (greater than 1) multiplying , thus the increased infectiousness of the variants would have a similar effect as a higher . Together with actual vaccine efficacy and its variability w.r.t. different virus variants, these factors modify the potential to reach herd immunity. Additional research would be needed to further investigate this. Moreover, it still remain to be seen if herd immunity against COVID-19 will be eventually obtained because the disease might anyway become endemic, depending on circulation within groups of not vaccinated people or due to fading immunity, insufficient vaccine efficacy or insufficient overall number of people getting vaccinated. Overall, while vaccination is extremely helpful in protecting the vulnerable, limiting social interactions will still play a major role until the vaccination effects become dominant by far.
As any modelling effort, the current model comes with limitations. To begin with, it does not include an age structure. Age distribution can influence hospital admission rates and fatality rates, and has been suggested to play a role in lowering the herd immunity fraction potentially down to 30–50 (Britton et al., 2020, Ragonnet et al., 2020, Thompson and Wattam, 2021). The age distribution should be considered when designing vaccination campaigns, as literature studies agree that vaccinating the elderly first would reduce the hospital burden and death toll (Bubar et al., 2021, Jahn et al., 2021, MacIntyre et al., 2021). As a consequence, our model was primarily used to investigate the aggregated dynamics and to project reasonable scenarios with homogeneous interventions in pursuit of overall herd immunity, but it does not cover the design of age-dependent measures.
As for standard SEIR-like models, we assumed that recovered people are immune and cannot be reinfected. It has been shown that individuals who were infected with SARS-CoV-2 develop some level of immunity to the disease for a certain time (Poland et al., 2020), but the duration is not yet clear. Cases of reinfection by SARS-CoV-2 have been reported but there is still low statistics and consensus (Fontanet and Cauchemez, 2020, Tillett et al., 2021, Edridge et al., 2020, Simmonds et al., 2020). On our considered time scale (up to end 2021), reinfection is likely to play a negligible role, but might become relevant over years, potentially challenging herd immunity. The model simulations are to be considered reasonable for time periods that do not exceed considerably the duration of the acquired immunity.
Similarly, the quality and duration of immunity by vaccination is still unclear. Despite their higher or lower efficacy, none of the available vaccine protect at (Polack et al., 2020, Baden et al., 2021) and it is not yet assessed to what extent current vaccines prevent individuals not only from developing the disease, but also to be infectious (as assumed in the model). Moreover, evolving variant strains of the virus might present increased resistance to vaccines (Kennedy and Read, 2020). These effects could contribute to challenge herd immunity (Anderson et al., 2020), contrasting the effect of age distribution. Conceptual models (Saad-Roy et al., 2021) have been developed to investigate the interplay between naturally achieved individual immunity, immunity by vaccination and waning immunity, but much still need to be done with more supporting data. Finally, the evolving impact of new variants — e.g. escaping antibodies (Starr et al., 2021) or causing longer infections (Kissler et al., 2021) – is not fully clear and thus not considered in the model. However, it can be easily incorporated after changing the appropriate parameters once additional evidence is collected. Finally the case of Manaus, Brazil, which was though to have obtained herd immunity by October 2020 (Buss et al., 2021), but witnessed a major surge in cases in early 2021 (Sabino et al., 2021) leave open the question if it will be possible to reach herd immunity against COVID-19 in reality.
5. Conclusions
Our comprehensive model describes the past epidemic dynamics and make reasonable projections. Despite some modelling assumptions, its basic structure allows to control the calibration uncertainties and to investigate and compare different scenarios. In particular, we estimated that herd immunity could be within reach in 2021, but rather towards the last part of the year (beginning of fall for Luxembourg and end of the year for Austria and Sweden) or longer, depending on how fast countries continue to vaccinate their population. As discussed above, the current projections for herd immunity are to be considered optimistic. Hence, the challenge over this year will be for governments and populations to obtain and use COVID-19 vaccines efficiently, while still containing social interaction. Limiting social interactions will still be a major driver to control the pandemic in the coming months, until vaccination effects become strongly dominant in curbing the pandemic.
6. Data availability
This study employs publicly available data-sets, provided by sources external to the authors. Each data-set employed is referenced and extensively described in Appendices F.1, F.2 and F.3. To foster reproducibility, a copy of the time-series data employed for model fitting is provided along with the code, both are made publicly available on GitHub at https://github.com/StefanoMagni/Model_COVID19_Dynamics_Luxembourg_Austria_Sweden.
7. Code availability
The code implementing model, analysis and simulations is publicly available on GitHub at https://github.com/StefanoMagni/Model_COVID19_Dynamics_Luxembourg_Austria_Sweden.
8. Funding
FK’s is supported by the Luxembourg National Research Fund (FNR) PRIDE DTU PARK-QC [Grant No.: PRIDE17/12244779/PARK-QC]. DP’s and SM’s work is supported by the FNR PRIDE DTU CriTiCS [grant reference: 10907093]. A.H.’s work is partially supported by the Foundation Cancer Luxembourg. JG is partly supported by the 111 Project on Computational Intelligence and Intelligent Control [reference: B18024]. AA is supported by the FNR [project code: 13684479]. AS is supported by the FNR [project: C14/BM/7975668/CaSCAD] and by the National Biomedical Computation Resource (NBCR) [Grant No.: NIH P41 GM103426] from the National Institutes of Health.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors thank the Research Luxembourg – COVID-19 Task Force for mutual collaborations. The findings in this paper do not necessarily represent the views of the Task Force. Any errors or omissions are the authors’ responsibility. The authors are also grateful to Matías Nicolás Bossa for useful discussions and to the editors and the anonymous reviewers for the precious feedback.
Appendix A. Mathematical model
In this Appendix we illustrate the model, the considered data from Luxembourg, Austria and Sweden, a computational approach to estimate herd immunity and the procedures to provide an estimate of the parameters and their uncertainties.
In this study, we developed a mathematical model of the transmission of COVID-19 within a population, building upon the standard SEIR model (Kermack et al., 1927). Our extension of the SEIR model is described by Fig. 1 in the main text. The total population N of the modelled country at time t is divided into 16 compartments. First, we introduce a separation between detected and undetected cases; in fact, a non-negligible fraction of infected people is usually not detected (Li et al., 2020), e.g. for lack of testing or because asymptomatic. Next, we include compartments to model the progression of the disease to more severe states, requiring hospitalisation, intensive care (ICU) or leading to death. Finally, we include compartments for recovered people. The model variables are summarized in Table A.1 and represent the number of individuals in different stages, normalized by the total population of the considered country.
Susceptible (S) and exposed (E) compartments are in common with the standard SEIR model. An exposed person might be detected (via a PCR test), thus entering the “infectious and detected” (II) compartment, and subsequently the “quarantined” (Q) compartment, from where the person cannot infect others any further. At this point, a person might (or not) become “hospitalized” (H), and then either simply “require longer hospitalization” (Hl) or require “intensive care treatment” (ICU). If the health improves, the individual can return to “regular hospital treatment after ICU” (AICU). At any of these hospitalization stages, the person can “die in hospitals or ICUs” (), or “recover from hospital or ICUs” (). People who are either recovered or dead are the equivalent of the removed compartment of a standard SEIR model, and thus do not get reinfected a second time in the model. Most detected people are not hospitalized, so they recover at home (NI), or alternatively they can die at home (). Finally, the fraction of people who got infected but do not get detected are represented by the infectious and undetected compartment (A). Being unaware of their state, they can continue to spread the infection without constraints. These people spend some time recovering outside hospitals (), and eventually they end up either recovered undetected (), or dead undetected (). The total number of undetected cases in Fig. 2 of the main text is obtained as the sum of the variables .
We assume conservation of the total population N (people can die, thus entering the dedicated compartments, but there is no removal of individuals from the system, and we neglect birth), such that for each country:
| (1) |
where the variables have been normalized by N to represent the fraction of the total population being in the corresponding state. The dynamics of our model is described by the following system of ordinary differential equations:
| (A.2a) |
| (A.2b) |
| (A.2c) |
| (A.2d) |
| (A.2e) |
| (A.2f) |
| (A.2g) |
| (A.2h) |
| (A.2i) |
| (A.2j) |
| (A.2k) |
| (A.2l) |
| (A.2m) |
| (A.2n) |
| (A.2o) |
| (A.2p) |
| (A.2q) |
We initialise every simulation with the initial conditions detailed in Table A.1 . For any simulation in this work (except those involving vaccination, see Appendix D) to numerically solve the set of ordinary differential equations we employ the python (version 3.6.1) solver odeint from the package scipy (version 1.5.2), which uses the LSODA method for numerical integration.
Table A.1.
Variables employed in the model and their initial conditions. The 16 variables represent the fraction of population of a country being in each of the compartments. The initial conditions are the standard ones usually employed for SEIR-like models, with all the population susceptible except one person already exposed to the virus. They are the same for every simulation and country, except for the country’s population being individuals for Luxembourg, for Austria and for Sweden.
| Variable | Representing fraction of people | Value at days |
|---|---|---|
| S(t) | Susceptible | 1–1/N |
| E(t) | Exposed | 1/N |
| I(t) | Infectious (Detected) | 0 |
| Q(t) | Quarantined | 0 |
| H(t) | Hospitalized | 0 |
| Hl(t) | Hospitalized – Longer | 0 |
| ICU(t) | in ICU | 0 |
| AICU(t) | Hospitalized after ICU | 0 |
| NI(t) | Recovering at Home (Detected) | 0 |
| DI,hos(t) | Dead in hospitals (Detected) | 0 |
| DI,hom(t) | Dead at home (Detected) | 0 |
| RI(t) | Recovered (Detected) | 0 |
| A(t) | Infectious (Undetected) | 0 |
| NII(t) | Recovering at Home (Undetected) | 0 |
| DA(t) | Dead at home (Undetected) | 0 |
| RA(t) | Recovered (Undetected) | 0 |
Appendix B. Model parameters
The parameters of the model and their interpretation are detailed in Table B.2 . The parameters can be divided in three categories, based on what type of physical quantity they describe: rates, probabilities and social interaction.
Table B.2.
Parameters of the model. The parameters of the model with their description and unit of measure. For each country and wave, the following assumptions have been made: . This is motivated by the fact that these parameters are relative to the undetected branch, and thus cannot be inferred from data. Thus, we assumed that undetected cases would evolve with the same parameter values as detected cases not entering hospitals/ICUs. represents the number of times that the social interaction parameter changes: for Luxembourg and Sweden and for Austria. The values of the manual fit of all the rates and probabilities for each country and wave are summarized in Table H.6. The values and dates of change for the social interaction parameter are reported in Table F.3 for Luxembourg, in Table F.4 for Austria and in Table F.5 for Sweden.
| Parameter | Description | Units |
|---|---|---|
| social interaction | adim. | |
| β | average contact rate | days−1 |
| α | (mean incubation period)−1 | days−1 |
| (mean time in I)−1 | days−1 | |
| (mean time in Q)−1 | days−1 | |
| (mean time in H)−1 | days−1 | |
| (mean time in ICU)−1 | days−1 | |
| (mean time in Hl)−1 | days−1 | |
| (mean time in AICU)−1 | days−1 | |
| (mean time in NI)−1 | days−1 | |
| (mean time in A)−1 | days−1 | |
| (mean time in NII)−1 | days−1 | |
| probability of | adim. | |
| probability of | adim. | |
| probability of | adim. | |
| probability of | adim. | |
| probability of | adim. | |
| probability of | adim. | |
| probability of | adim. | |
| probability of | adim. | |
When individuals can move from one compartment to one of two different compartments, the probability controls which fraction of people will go to one compartment, the remaining fraction going to the other. Their value is bounded between 0 and 1. The parameters are indexed with .
The parameters and represent rates. The parameters are indexed with . Each rate represents the inverse of the average time that takes for an individual to move from one compartment to the next. Of particular relevance are the rates and , which have the same meaning as the corresponding parameters of a standard SEIR model: represents the inverse of the mean incubation period of the disease, and represents the average contact rate.
The average contact rate is then multiplied by the additional parameter , in order to model any measure or change in people’s behaviour that can lead to a change (decrease or increase) in the average contact rate. Thus, is a constant and it represents the “natural” average contact rate, while represents an effective average contact rate which considers the measures or social behaviours in place. We assume for any country, before any measure was implemented at the beginning of the pandemic in February 2020. Afterwards, we assume to be a piece-wise constant function of time, where each value is indicated by , with for Luxembourg and Sweden and for Austria. We assume that changes in occur whenever a major new measure is implemented or lifted by the authorities of a country, or in case of a major happening (e.g. schools starting in September in Luxembourg). The dates employed for every country, and which measures where taken/lifted on that date, are summarized in Table F.3 for Luxembourg, Table F.4 for Austria and Table F.5 for Sweden.
Appendix C. Analytical derivation of the effective reproduction number
To obtain from the current model we used the next generation matrix method (Diekmann et al., 2010, van den Driessche, 2017, Blackwood and Childs, 2018). From the next generation matrix, we find its eigenvalues and 0. In our case, is given by:
| (C.1) |
From , we can deduce , given by
| (C.2) |
By substituting the values of the parameters for each country and scenario, we obtain the curves depicted in Fig. 3 of the main text, panels B, D, F.
Appendix D. Incorporating vaccination in the model
To include vaccination, we add one additional compartment representing the fraction of vaccinated population. We assume that a fixed number of people will be vaccinated every day. Thus, the equation for the number of people vaccinated reads:
| (D.1) |
with being the parameter representing how many people will be vaccinated per day. Correspondingly, the equation for the susceptible compartment becomes:
| (D.2) |
since we assume that only people who did not already naturally develop antibodies by being infected will be vaccinated.
In order to simulate three potential vaccination strategies, i.e. 3 vaccines rollout speeds, at which countries might manage to perform vaccination, we fix the parameter to three values that, if all the population would still be susceptible, would lead to vaccinating all the population of a country within respectively 6 months, 1 year and 1.5 years. These are typical timescales potentially envisaged by different countries. Thus, we consider the three values and (recall that model variables are normalized by the total country population N, so they sum up to 1). These three values of correspond, respectively, to perform approximately 3415, 1707 and 1138 full vaccinations/day in Luxembourg, 48773, 24386 and 16258 full vaccinations/day in Austria and 56055, 28027 and 18685 full vaccinations/day in Sweden. Luxembourg numbers are an order of magnitude smaller than those for Austria and Sweden, proportionally to their total populations. It is in fact reasonable that vaccination capability would scale with country population (for European countries with comparable standards of living), i.e. that the more populated a country, the higher its capacity to perform vaccinations. Thus e.g. performing 56055 full vaccinations/day in Sweden might be as challenging as performing 3415 full vaccinations/day in Luxembourg.
When numerically integrating the system of ordinary differential equations from Eq. (A.2) with the addition of vaccination (Eqs. (D.1) and (D.2)), we consider an additional constraint to prevent the variable to decrease below 0, which would happen otherwise due to Eq. (D.2). Interrupting the odeint routine when the condition is met is not possible; hence, in all the simulations involving vaccination, we instead perform numerical integration by means of the forward Euler method with if . We used an integration time-step and verified beforehand that further decreasing it would not lead to any significant change in the integration result, while significantly increasing computation time.
Appendix E. Herd immunity
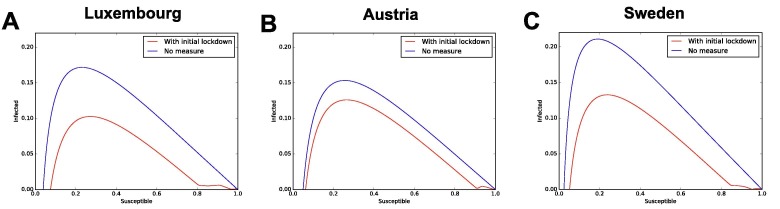
Section 3.5 of the main text described how to analytically derive the fraction of susceptibles who needs to be fully immune in order to reach herd immunity; we complement that analysis with numerical inspection of the model. Herd immunity by definition occurs when the pandemic is not spreading anymore within a population, without the need of any measure. Hence, is given by 1 minus the fraction of S that yields the maximum of infectious I, when no measure is in place (after the maximum, the epidemic curve decreases on its own with no need of measures). This is a typical approach to numerically estimate the herd immunity threshold in SEIR-like models. Hence, we simulate the time evolution of the baseline model and we plot the results on the phase plane I vs S, obtaining the curve . We then identify the value of S such that the curve reaches its maximum. is the fraction of susceptible when the number of I naturally starts to decrease, corresponding by definition to , i.e. herd immunity. The phase planes are shown in Appendix Fig. E.1 , panel A for Luxembourg, B for Austria and C for Sweden. To fully investigate the complexity of the model, we consider both the baseline model (no measures from the beginning, blue curve) and the next-to-baseline case (all measures lifted after the last available data point, red curve).
Fig. E.1.
Phase plane for numerical estimation of the herd immunity threshold. In each panel, the maximum of the curve represents the value of the fraction of susceptible people that would yield herd immunity. Panel A for Luxembourg, panel B for Austria and panel C for Sweden.
For both blue and red curves, the maxima occur at around for Luxembourg and for Austria and for Sweden. Since , we obtain that the computationally estimated values of the herd immunity threshold are and , respectively. We compare them with the analytic values from the formula , i.e. and (cf. Section 3.5): the values are extremely close, with small differences of and . The threshold values estimated computationally are higher than their counterpart for all countries, possibly due to the additional complexities of our model w.r.t. a standard SEIR model. We thus employ these computationally obtained ones, both because they account for any additional model complexity and in order to provide a more conservative estimate of when herd immunity might be reached.
Appendix F. Data and analyzed countries
We consider three different countries: Luxembourg, Austria and Sweden. The model structure described above is maintained unchanged across the three countries. For consistency, we change the value of the total country population N and the parameter values so that the model fits the data of the corresponding country. We use data of total detected cases, hospitalized people, people in ICUs and dead people. We gathered these data from https://www.acaps.org/covid19-government-measures-dataset, a public independent database recognised by the WHO (last accessed on 03/12/2020) as well as from the public repositories listed below. Moreover, for each country we allow the social interaction parameter to change when major changes in measures took place. We list below also the sources of information for the changes in measures.
F.1. Luxembourg
For Luxembourg, we obtained the dates at which major changes in policy took place in Luxembourg from https://covid19.public.lu/fr/mesures-sanitaires-en-vigueur.html (last accessed 15/12/2020), and summarize them in Table F.3 . The time-series data of total cases, hospitalised people, people in ICU and dead people for Luxembourg are publicly available on Fig. 2 of the main text, along with their 7-days moving average. The moving average smooths detection and intrinsic noise and filters out the effects of considerable weekend under-testing, consistently observed and confirmed by the considerably lower number of total tests performed over weekend days. The moving average is centered on the day of interest to not induce shifts of the features (like the peaks) of the time-series.
Table F.3.
Changes in the piece-wise constant social interaction parameter of the model for Luxembourg.
| Starting Date | Measure or change in social activities | Manual Calibration | Which Wave | |
|---|---|---|---|---|
| – | No restrictions | 1 | – | |
| 16.03 | Lockdown | 0.4902 | 1st | |
| 23.03 | Measures fully effective | 0.1984 | 1st | |
| 20.04 | Opening construction sector | 0.1918 | 1st | |
| 04.05 | Opening high schools | 0.2507 | 1st | |
| 10.06 | Relaxation of measures | 0.5298 | 2nd | |
| 29.06 | End of classes splitting | 0.4804 | 2nd | |
| 13.07 | School holidays | 0.3101 | 2nd | |
| 31.07 | Start holidays | 0.2203 | 2nd | |
| 12.08 | Change mobility (Google mobility data) | 0.3457 | 2nd | |
| 23.08 | End holidays of construction sector | 0.3351 | 2nd | |
| 14.09 | Opening schools | 0.4333 | 3rd | |
| 01.11 | Restrictions, including curfew (11 p.m.) | 0.341 | 3rd | |
| 26.11 | Stricter measures, HORESCA closure | 0.39 | 3rd |
According to the public data mentioned above, the first positive case was detected in Luxembourg on February 29, 2020. Considering the lag between being susceptible, being exposed and being detected, we initialize the model at its initial conditions reported in Table A.1 with time on February 24. Data about the COVID-19 prevalence in the population were obtained from the CON-VINCE study (Snoeck et al., 2020).
Each country in this study is modelled as a closed system, which might be a limitation for Luxembourg, due to the small size of the country and the high cross-border mobility. The publicly available data employed for Luxembourg and mentioned in this section only include cases that are detected and resident in Luxembourg. For considerations about cross-border workers in Luxembourg and interplay with economical features, refer to Burzynski et al., 2021. Our model was used to regularly monitor the progression of the epidemic in Luxembourg and to produce short- and mid-term projections during the crisis. It aimed to promptly deliver preliminary results and then increasingly more refined results and projections as available data increased over time. Hence, some of our parameters have been updated multiple times throughout the course of the crisis, to incorporate new knowledge. In this manuscript, our model is reporter in its state in December 2020, but it has been, overall, a continuously evolving tool.
F.2. Austria
We obtained the dates at which major changes in policy took place in Austria from https://de.wikipedia.org/wiki/COVID-19-Pandemie_in_Österreich (collection of various sources, last accessed on 15/12/2020). Table F.4 summarizes dates and associated policies. The time-series data of total cases, hospitalised people, people in ICU and dead people for Austria come from https://covid19-dashboard.ages.at/dashboard_Hosp.html (last accessed on 15/12/2020). They are reported in Fig. 2 of the main text, where we also report their 7-days moving average.
Table F.4.
Changes in the piece-wise constant social interaction parameter of the model for Austria.
| Starting Date | Measure or change in social activities | Manual Calibration | Which Wave | |
|---|---|---|---|---|
| – | No restrictions | 1 | – | |
| 16.03 | Closure schools/universities, limitations in shops/restaurants | 0.52 | 1st | |
| 30.03 | Wearing masks | 0.155 | 1st | |
| 14.04 | Opening small shops | 0.22 | 1st | |
| 01.05 | Opening malls and hairdressers | 0.27 | 1st | |
| 15.05 | Opening certain school classes | 0.31 | 1st | |
| 29.05 | Opening additional schools | 0.33 | 2nd | |
| 15.06 | Mask obligation in public area, no mask in shops/schools | 0.38 | 2nd | |
| 11.07 | School holidays | 0.36 | 2nd | |
| 21.07 | Mask obligation everywhere | 0.32 | 2nd | |
| 13.08 | Increase of infections due to people returning from holidays | 0.385 | 2nd | |
| 14.09 | Opening schools | 0.415 | 2nd | |
| 21.09 | Extended mask obligation/ 10 people invitations | 0.405 | 2nd | |
| 25.09 | Curfew (10 p.m.) Salzburg, Voralberg and Tirol | 0.395 | 2nd | |
| 23.10 | Private gatherings limited to 6 people inside, 12 outside | 0.385 | 2nd | |
| 03.11 | Lockdown | 0.27 | 2nd | |
| 07.12 | Relief of lockdown | 0.34 | 2nd |
According to the data mentioned above, the first positive case was detected in Austria on February 26, 2020. Considering the lag between being susceptible, being exposed and being detected, we initialize the model at its initial conditions reported in Table A.1 on February 21. Similar starting dates for modelling the epidemic in Austria have been used elsewhere, e.g. February 22 in Bryant and Elofsson, 2020 (see Table 1 therein). Data about COVID-19 prevalence were obtained from https://www.sora.at/nc/news-presse/news/news-einzelansicht/news/COVID-19-praevalenz-1006.html (last accessed on 15/12/2020).
F.3. Sweden
We obtained the dates at which major changes in policy took place in Sweden from Ludvigsson, 2020 until August and from https://www.krisinformation.se/en/news (last accessed on 15/12/2020) later on, and we summarize them in Table F.5 . The time-series data of total cases, hospitalised people, people in ICU and dead people for Sweden are available on https://www.folkhalsomyndigheten.se/smittskydd-beredskap/utbrott/aktuella-utbrott/covid-19/statistik-och-analyser/bekraftade-fall-i-sverige/, https://www.icuregswe.org/en/data-results/covid-19-in-swedish-intensive-care/, https://c19.se (last accessed on 15/12/2020). They are displayed in Fig. 2 in main text, where we also report their 7-days moving average.
Table F.5.
Changes in the piece-wise constant social interaction parameter of the model for Sweden.
| Starting Date | Measure or change in social activities | Manual Calibration | Which Wave | |
|---|---|---|---|---|
| - | No restrictions | 1 | - | |
| 11.03 | Gatherings of more than 500 people forbidden | 0.52 | 1st | |
| 16.03 | Home office, school above 17 initiate distance learning | 0.3 | 1st | |
| 27.03 | Gatherings of more than 50 people forbidden | 0.25 | 1st | |
| 30.03 | Visits to the elderly care are banned | 0.2 | 1st | |
| 02.04 | Certain students aged 17 allowed back to classroom | 0.277 | 1st | |
| 10.06 | Starting holidays | 0.265 | 1st | |
| 13.06 | Ease of travel restriction | 0.28 | 1st | |
| 01.07 | Further ease of travel restriction | 0.23 | 1st | |
| 17.08 | Opening of schools for children | 0.37 | 1st | |
| 01.10 | Visit ban lifted | 0.395 | 1st | |
| 27.10 | Stricter guidelines in Skåne | 0.41 | 2nd | |
| 03.11 | Stricter guidelines in Jönköping, Halland, Örebro | 0.375 | 2nd | |
| 16.11 | Stricter guidelines in Gävleborg, Västernorrland | 0.345 | 2nd |
Swedish policy has been analysed e.g. in Larsson et al., 2021, Kavaliunas et al., 2020, Rees et al., 2020. While the very first case detected was on 31st January, no other case was detected until February 26. It is likely that the first case was isolated and did not infect others, otherwise most likely a second case would have been detected earlier; in addition, the first case was reported from a woman who had traveled to Wuhan and was isolated upon detection. On the other hand, following the second detected case on February 26, 9 more cases were detected in the next 2 days. To account for potential further lag in the uncertain starting time of the epidemic in Sweden, we initialise the model at its initial conditions reported in Table A.1 on February 16. Similar starting dates for modelling the epidemic in Sweden have been used elsewhere, with Bryant and Elofsson, 2020 starting their modelling on February 18 (see Table A.1 therein).
Appendix G. To fit Sweden, the model needs time-dependent probabilities of detection and hospitalisation, unlike for Luxembourg or Austria
Extending our model to Sweden is to gain insight on a country which applied different policies than Luxembourg and Austria (which adopted similar policies). To fit Swedish data with the same model structure as the other countries, it was not sufficient to consider a different set of parameter values. Instead, it was necessary to introduce time-dependent probabilities of being detected and of being hospitalized , within an epidemic wave.
The parameter corresponds to the probability of an infected individual being detected. To obtain an estimate of this parameter for Sweden, we considered prevalence data estimated weekly through antibody tests for 8 consecutive weeks between mid April and mid June 2020, obtained from (Folkhalsomyndigheten 1, Folkhalsomyndigheten 2) and shown in Fig. G.2 panel A. The prevalence went from about to , growing over the course of these two months, likely resulting from more infections. Due to the large error bars, multiple functional forms could be considered a reasonable fit, so we chose the simplest, a linear fit.
Prevalence represents the total percentage of the country’s population that is estimated to have contracted the virus, including detected and undetected individuals. We obtain an estimate of as the ratio between the measured detected cases and the total cases estimated from the prevalence. We do so in Fig. G.2, panel B, which reports the number of detected cases divided by the number of total cases inferred based on prevalence, as a function of time, for the three fits to prevalence of panel A. In green, we report our final assumption for the functional form for , i.e. the probability of being detected if infected, which is time-dependent for Sweden. We assumed to be piece-wise linear, approximately following the behaviour of the linear fit to prevalence, and saturating after the last available data point (to avoid introducing further assumptions).
Furthermore, we incorporated an additional information: during the early phases of the pandemic in Sweden, the majority of the detected cases were people needing hospitalization. This can be seen from Fig. G.2, panel C, which shows data for daily new detected cases, people entering hospital and people entering ICU (not to be confused with the number of people currently occupying hospitals and ICUs). The data of people entering hospital and ICU are publicly available on Socialstyrelsen and https://www.icuregswe.org/en/data-results/COVID-19-in-swedish-intensive-care/. In March and April, the daily number of people entering hospital was more than half of the daily number of detected cases. This ratio is shown in panel D (in blue, the ratio of people entering hospitals divided by new daily detected cases two days earlier). This is used to build the piece-wise linear function (in green), which was assumed as a proxy for , i.e. the probability of being hospitalized when detected positive. This is between approximately and during March and April, as can be seen in both panels C and D, meaning that, during the early weeks/months of the epidemic, Sweden mostly detected those people that required hospital treatment. This clearly changed in May and June, likely due to the change in testing strategy ordered by the government on May the 3rd (Ludvigsson, 2020). As observed in Kavaliunas et al., 2020, the peak recorded at the end of June reflects an extension of the testing strategy to everyone with COVID-19 symptoms and to contact tracing.
Appendix H. Manual calibration of model parameters
We determine the values of the model parameters that provide a good fit to the available data, while having reasonable values w.r.t. the literature. In this section we explain the initial manual calibration, later on we will cross-validate it with Markov Chain Monte Carlo methods in Appendix I.
The following methodology was applied similarly for Luxembourg and Austria, while to Sweden with some differences described in Appendices G and F.3. We recall that most of the parameters have values due to their interpretation as rates or probabilities. Rates are in fact defined as the inverse of the average time individuals spend in a compartment; hence, a rate smaller than 1 means an average time in that compartment of 1 day or more, which is a reasonable value given the interpretations of the compartments, e.g. hospital and ICU, where people are very likely staying on average for at least 1 day or more.
The only exception is , for which we considered values between 0 and 2 (minimum average time of half a day). We initially set and following literature values (Liu et al., 2020, Wu et al., 2020). When possible, we chose for the other parameters a tentative initial value based on domain knowledge. For example, observed average length of stay in hospitals or ICUs (Rees et al., 2020) are typically several days, leading to correspondingly low initial values of the rates for exiting these compartments. For the remaining parameters, e.g. those concerning non–hospitalized individuals, an initial educated guess was made based on the information available and what seemed reasonable at the time.
Next, we manually tuned the parameter values in order for the simulated model output to fit the available data. It must be stressed that, due to the model structure, individuals can only flow in one direction in the model, i.e. from being initially in the susceptible compartment, to eventually end up in either one of the recovered or dead compartments. Due to this structure, several of the parameters only influence the variables appearing downstream in the flow, not upstream. For instance, while and influence all compartments, the probabilities of being hospitalised or the probability of entering ICU do not influence the total detected cases. Thus, we start the manual fit by fixing those parameters that influence the total detected cases, so that the simulated curve fits the moving average of the available data. Unlike all the others, the parameter changes value every time that a new measure is implemented. Each value is thus fixed in order to improve the model fit to the data of total detected cases (averaged over a week) until the next change, before moving to the next value. Eventually, parameters downstream in the flow of individuals are also changed in order for the model to fit the data of the corresponding boxes. In particular, first parameters impacting total cases, then parameters impacting hospitalisations, than parameters impacting ICU and eventually those impacting death. The procedure was repeated until a satisfactory fit was achieved. The final values of parameters from our manual fit, for each country and wave of infection, are reported in Table H.6 .
Table H.6.
Parameter values for manual calibration of each wave and country. All rates ( and each ) are expressed in , the other parameters are dimensionless. The symbol “–” means the parameter is not changed w.r.t. the value to its left in the table. The quantities and are depicted in Fig. G.2 and their derivation is described in the corresponding section.
| Parameter | Manual fit Luxembourg |
Manual fit Austria |
Manual fit Sweden |
||||
|---|---|---|---|---|---|---|---|
| 1st wave | 2nd | 3rd | 1st wave | 2nd | 1st wave | 2nd | |
| 1.287 | – | – | 1.287 | – | 1.287 | – | |
| 0.4433 | – | – | 0.4433 | – | 0.4433 | – | |
| 0.6808 | – | – | 0.6808 | – | 0.6808 | – | |
| 0.5979 | – | – | 0.5979 | – | 0.5979 | – | |
| 0.5246 | – | – | 0.5246 | 0.5246 | 0.5246 | 0.5246 | |
| 0.0513 | 0.1050 | 0.106 | 0.0991 | 0.0948 | 0.1875 | 0.0933 | |
| 0.0617 | 0.1514 | 0.1605 | 0.1047 | 0.1240 | 0.2383 | 0.1247 | |
| 0.0853 | 0.1514 | 0.1590 | 0.1073 | 0.0856 | 0.1093 | 0.0838 | |
| 0.1084 | 0.1084 | – | 0.1084 | 0.1084 | 0.1084 | 0.1084 | |
| 0.31 | 0.41 | – | 0.41245 | – | 0.27389 | ||
| 0.1534 | 0.08 | 0.042 | 0.162 | 0.065 | 0.1 | ||
| 0.7906 | 0.86 | 0.78 | 0.72 | 0.82 | 0.72 | 0.88 | |
| 0.7906 | 0.9048 | 0.8868 | 0.6972 | 0.8345 | 0.6667 | 0.8965 | |
| 0.8717 | 0.9814 | 0.8692 | 0.8499 | 0.9275 | 0.9021 | 0.9820 | |
| 0.9072 | 0.9816 | 0.8868 | 0.8292 | 0.8946 | 0.7866 | 0.9731 | |
| 0.9876 | 0.9979 | 0.997 | 0.99 | 0.992 | 0.99 | 0.992 | |
We performed this procedure for Luxembourg and for the first wave, which we conventionally assume to end with the minimum of the moving average of new daily cases occurring on June 4. Fitting the cases of the second wave with the parameter set from the first wave lead to a significant over-prediction of the number of people in hospital and ICU for the second wave, with respect to what is observed in the data. Thus, some of the parameter values need to be changed in order for the model to fit the data of the second wave. Similarly for the third wave. For both, we repeat the procedure of manual parameter calibration described above starting from the values of the parameters for the previous wave, and incorporating any further domain knowledge about average length of stay in hospitals and so on that become available in the meantime.
Most parameters were initially tuned for Luxembourg, and then employed for Austria and Sweden with the necessary changes to achieve a reasonably good fit to the data, or where literature was available reporting a country-specific estimate, as it is the case for the probability of being detected , inferred from country-specific prevalence studies as detailed below. While this procedure is repeated for Austria with only changes in parameter values, it is not sufficient to fit Sweden. For Sweden, we further need to derive time-dependent probabilities of detection and of hospitalizations , as described in detail in Appendix G. These two functions are reported in Fig. G.2 .
Similarly to Luxembourg, we assume the 1st wave to end with the minimum of the moving average of new daily cases on June 12 for Austria and on August 31 for Sweden. We further assume the 3rd wave in Luxembourg to start from the re-opening of schools on September 15 . We do not split Austria or Sweden data in a third wave as only the data for Luxembourg show clearly three waves of infections, see Fig. 2 in main text. The final values of parameters from our manual fit, for each country and wave of infection, are reported in Table H.6.
A key parameter for each country is the probability of being detected if infected, which has been derived from prevalence studies. For Luxembourg we consider this probability to be in the first wave thanks to the CON-VINCE study (Snoeck et al., 2020), and we assume it to be for the second and third wave based on internal communication. These numbers correspond to values for total cases over detected cases of respectively 1/0.31 = 3.2 and 1/0.4 = 2.5, which are close to the value 2.3 reported as an approximated estimate for several countries by Böhning et al., 2020. For Austria, has been as well derived from prevalence data https://www.sora.at/nc/news-presse/news/news-einzelansicht/news/covid-19-praevalenz-1006.html (last accessed on 15/12/2020). For Sweden, we describe how we obtain and in Appendix G. This estimate is also based on the prevalence data from Folkhalsomyndigheten 1, Folkhalsomyndigheten 2 displayed in Fig. G.2, panel A. As shown in Fig. G.2, panel B, we assume a time-dependent which increases from an estimated value of in March to an estimated value of from June onward.
Appendix I. Bayesian inference for cross-validation of parameters and evaluation of uncertainties
The parameter sets obtained by manual calibration are used in the manuscript to illustrate a number of qualitative and quantitative results. Nevertheless, the next question naturally arising is “how unique is each of these parameter sets, given the available data?”. We thus want to investigate to what extent the available data constrain the parameters of the model, and to which extent these parameter values can change, i.e. to quantify the uncertainties in the estimation of these parameters, given the data. A Bayesian framework provides a natural perspective to explore this uncertainty. For this purpose, we apply Bayesian Inference, and in particular Markov Chain Monte Carlo (MCMC) methods to I) quantify the uncertainty (via credible intervals) of the estimates of each parameter given the data, and to II) assess uncertainties on combinations of parameters (credible regions), often better identifiable than the corresponding individual parameters. In order to apply Bayesian inference and MCMC methods, we employ the dedicated python library pymcmcstat (Miles, 2019), version 1.9.0.
I.1. Sum of square residuals for the likelihood function
To perform Bayesian inference by MCMC, we need to construct a likelihood function of parameter values given the available data and to provide prior probability distributions for each parameter, which allows us to incorporate our prior knowledge. The vector of parameters, which will be specific for each country and wave, is here indicated as .
The pymcmcstat package employs for the Likelihood function the sum of square residuals (SSR), such that the minimum of the SSR corresponds to the maximum of the Likelihood. This choice of the likelihood function corresponds to assuming that deviations of data from the model are due to Gaussian errors, which is the simplest assumption to make without additional knowledge of the potential sources of errors.
The SSR for Luxembourg is:
| (I.1) |
where is the array of parameters, indicates the number of days from the beginning of the epidemic (assumed for that country), and are respectively the first and last day of the wave under investigation (1st wave, 2nd wave or, for Luxembourg, 3rd wave), C is the cumulative total number of detected cases, H is the number of people in hospital, ICU is the number of people in ICU, and are respectively the number of people dead in hospital (including ICU) or outside hospital ( includes also nursing houses). The same SSR was employed for Austria and Sweden (with the corresponding data and model variables), except that the two compartments for deaths were merged into one compartment due to lack of more fine-grained data.
The quantities in Eq. (I.1) derived from the model, omitting the dependencies on time and parameters for ease of notation, in terms of the model variables (Table A.1) are given by:
| (I.2) |
| (I.3) |
| (I.4) |
| (I.5) |
| (I.6) |
The sum of square residuals Eq. (I.1) attributes the same weight to all time-series data. While this choice is the simplest, it is worth noticing that it is not unique and more complex weighting approaches could represent valid choices as well.
I.2. Prior probability distributions
For each country and wave, we assume flat prior probability distributions on each parameter over a reasonable parameter space. The reasons in doing so are mainly two. First, flat priors are the simplest choice which does not require any additional knowledge – except the intervals over which these priors should be extended. Second, flat priors are the less informative choice we can make, without introducing bias toward a particular parameter set. This allows to cross-validate the manually calibrated parameter set, as the result only depend on the public time-series data and on a reasonable limitation of the available parameter space by means of the priors.
The social interaction parameter ranges from 0 to 1. Each rate parameter ranges from to , except for beta that ranges from to . Each probability parameter is from 0 to or to 1 depending what the probability represents. We opt for these somewhat reduced parameter spaces rather than the full intervals from 0 to 1 because, without loss of generality (we do not expect probabilities of dying being above 0.5, i.e. , and so on), they are less demanding in terms of time and computational resources needed for the MCMC chains to converge. Similarly, we further restricted the priors between 0 and 0.5 for those rates associated to an average length of stay which is known to be considerably larger than a day, e.g. for the rate of exiting ICU. These flat prior probability distributions are reported for each country and wave as the light gray area in Fig. J.3 , where we observe that the posterior probability distributions are indeed narrower than the priors. The posteriors are depicted via their and credible intervals, respectively in blue and cyan.
I.3. Markov Chain Monte Carlo (MCMC) method
After defining the likelihood function and the priors, we calculated the posterior probability distribution over the parameter space (for each country and wave separately) by means of Markov Chain Monte Carlo (MCMC) methods available via the dedicated python library pymcmcstat.
Among the different Metropolis based sampling techniques, we employ the Delayed Rejection Adaptive Metropolis (DRAM) algorithm. It is a combination of the Delayed-Rejection (DR) algorithm, which delays rejection by sampling from a narrower distribution, and the Adaptive-Metropolis (AM) algorithm, which adapts the covariance matrix of the proposal Gaussian distribution at specified intervals.
To increase the speed of our sampling, we run 8 chains in parallel. Each chain is initialized at random initial conditions extracted from the flat prior distribution for each parameter. The multiple chains will also be useful to assess convergence of the chains (see next section). Each chain is run for 500000 iterations to ensure chain convergence (measured by the method described in the next sections). The first half of each chain is automatically discarded as burn-in (default settings of the package), while the second half is employed to determine the posterior probability distributions.
I.4. Thinning of the chains only for visualization
We did not employ the thinning of chains (only considering one sample every several) as it is not usually appropriate when the goal is precision of estimates from an MCMC sample (Link and Eaton, 2012). Nevertheless, thinning can be useful for other reasons, such as memory or time constraints in post-chain processing. It was thus used to generate the figures with estimates of the posteriors, e.g. Fig. J.4. To generate these figures, we thinned the chains keeping only every 100th sample. For the posteriors, rather than thinning we monitored the convergence of the MCMC estimates by comparing the outputs of multiple independent chains (Link and Eaton, 2012). We thus considered the variation among these independent chains to implement the Gelman-Rubin diagnostic (Gelman and Rubin, 1992, Brooks and Gelman, 1998).
I.5. Ensuring convergence of MCMC chains through Gelman-Rubin diagnostic
By visual inspection of the posterior probability distributions derived by each independent chain (a simple approach also performed in Mbuvha and Marwala, 2020), it seems that all the chains have converged to about the same distribution (with the exception of very few parameters where one or few chains lead to slightly different posteriors). We nevertheless further used a more quantitative approach.
There are many diagnostics available for assessing chain convergence. As suggested by Link and Eaton, 2012, a robust approach is to use the Gelman-Rubin diagnostic (Gelman and Rubin, 1992, Brooks and Gelman, 1998), which requires several sets of chains for comparison. The Gelman-Rubin approach essentially performs an analysis of the variances within each chain set and between each chain set. The same diagnostic was used for the same purpose in the framework of MCMC convergence in modelling COVID-19 in e.g. Bryant and Elofsson, 2020, Dehning et al., 2020. The Gelman-Rubin diagnostics for the full chains returns values of R, the so-called “Potential Scale Reduction Factor (PSRF)”, that are extremely close to 1 for most parameters, which indicates that the chains have converged (Gelman and Rubin, 1992, Brooks and Gelman, 1998).
Appendix J. Results from the MCMC
In order to confirm the viability of the choice of parameter values from the manual calibration, we show in the Results section of the main text that the simulations generated by our model fit the available data for these countries. Additionally, we show in Appendix J.1 that the manually calibrated sets are consistent with the Markov Chain Monte Carlo estimates. This, in turn, shows that the available data constrain the parameters only to some extent, leaving considerable uncertainties. When possible, we had informed our manually calibrated parameter set with values obtained from literature or from domain knowledge, e.g. length of stay of patients in ICUs and hospitals. Instead, the MCMC was let free to reproduce the raw time-series data. This induces larger uncertainties and yields some degeneracy between parameters, with combinations (e.g. ratios) of parameters being better constrained by the data than individual parameters (see Appendix J.2).
J.1. Manually calibrated parameter sets are compatible with Bayesian inference estimate, which underlines wide uncertainties in parameter values
The parameter sets from the manual calibration of the model discussed in Appendix H are summarized in Tables H.6, Table F.3, Table F.4, Table F.5 and are employed through the manuscript. Fig. J.3 shows the Bayesian estimates of these parameters given the time series data, obtained by MCMC (credible intervals) and employed to cross-validate them.
Posteriors are indicated by their (blue) and (cyan) credible intervals, and are usually considerably narrower than the corresponding assumed flat prior distributions (from Appendix I.2). Nevertheless, this is not the case for some parameters, for which the posteriors are almost flat and as wide as the priors. This means that some parameters are not well identified by the available data and model structure. Fig. J.3 reports the point-estimates from the MCMC, i.e. mean and maximum a posteriori estimate of the posterior of each parameter. For rather symmetric distributions the two values tend to correspond, while they differ considerably for very skewed distributions. Moreover, for almost flat posterior distributions (like e.g. those for most of the parameters with ) the maximum is not very representative of the distribution.
Fig. J.3 shows that, for all countries and waves, the values of the manual fit (green) are mostly very close to either the maximum or the mean a posteriori estimate. It is usually within the credible interval of the posterior, or at least inside the credible interval, with only a couple of exceptions. Thus, our manually calibrated sets of parameters are fully consistent with the Bayesian estimate based on MCMC. However, credible intervals are relatively wide, which indicates that the estimated uncertainties of these parameters, based on the data alone, are rather large. In particular, at a qualitative level, the values of the social interaction parameter are in general better constrained than the other parameters, with the probabilities being slightly better constrained than the rates . These are in general poorly identified, except for and which are affected by smaller uncertainties w.r.t. other rates. In turn, the probability (out of “recovery at home”) is extremely well constrained (to values close to 1) in most of the waves and countries.
J.2. Quantifying uncertainties on estimates of parameters by MCMC: wide uncertainties and degeneracy in parameter estimations
The domain of the posterior probability distribution obtained via the MCMC, Appendix I, has the same number of dimensions as the number of parameters considered, i.e. 19 for the 1st wave of Luxembourg. When we are interested in one parameter at a time, we project the chains on one dimension (which, if we had an analytic form for the posterior, would be done by integrating over all parameters except the one of interest, thus obtaining the marginal posterior distribution for that parameter). This is how the 1D posteriors in Fig. J.3 were obtained.
The next question is: are the wide uncertainties affecting some parameters an effect of having projected to a lower dimensional space, or are certain parameters poorly identified? We anticipate that both types of situations arise, depending on the parameter.
To investigate this, we project the posterior distribution over two parameters at a time, for each couple of parameters in Fig. J.4 for the MCMC run of the 1st Wave of Luxembourg, and in Fig. J.5, Fig. J.6, Fig. J.7, Fig. J.8, Fig. J.9, Fig. J.10 for the other waves and countries. While certain parameter pairs are very well constrained, others are not; certain parameter pairs appear to be correlated or anti-correlated. We hence observe a degree of degeneracy between parameters: there is not a unique combination of parameters that allows a good fit of the model to the data, but many of them.
Moreover, certain combinations (e.g. ratios) of parameters are better constrained than the individual parameters. Consider e.g. the parameters and , which come from the standard SEIR model.
Their credible intervals are displayed in Fig. J.3. The joint posterior over the two parameters (close to the center of Fig. J.4 for Luxembourg, Fig. J.7 for Austria and Fig. J.9 for Sweden) is narrow and rotated toward the diagonal direction, showing anti-correlation between the estimates of the two parameters. This means that low values of can only be considered together with high values of , and the other way around. These patterns occur for other parameters as well, and they are conserved to some extent across countries. So, they are likely specific to the model’s structure and parameters rather than to the country. Other interesting patterns are visible, e.g. anti-correlation between each and the subsegiquent in time in the 2nd and 3rd waves of Luxembourg, the 2nd wave of Sweden and to some extent in the 1st and 2nd waves of Austria. This can easily be understood in terms of the model: lowering the social interaction one time-period and increasing it the next, or doing the converse, can both lead to a similarly good agreement with data. While certain couples of parameters seem to be well constrained, other parameters have projected posteriors that are still close to flat, resulting in squares that are predominantly red in Fig. J.4 e subsequent. This effect is weaker for certain waves and countries (3rd wave of Luxembourg and the 2nd wave of Sweden), but stronger for others (1st wave of Sweden, where parameters seem to be very poorly identified). This could be related to the dimension of the domain of the posterior (the higher the number of parameters, the less constrained), as the 3rd wave of Luxembourg and the 2nd wave of Sweden both have indeed “only” 14 parameters each, while the 1st wave of Sweden has 26 of them.
References
- Althouse B., Wenger E., Miller J., Scarpino S., Allard A., HÃbert-Dufresne L., Hu H. Superspreading events in the transmission dynamics of SARS-CoV-2: Opportunities for interventions and control. PLOS Biol. 2020;18 doi: 10.1371/journal.pbio.3000897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson R.M., Vegvari C., Truscott J., Collyer B.S. Challenges in creating herd immunity to SARS-CoV-2 infection by mass vaccination. The Lancet. 2020;396(10263):1614–1616. doi: 10.1016/S0140-6736(20)32318-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baden L.R., El Sahly H.M., Essink B., Kotloff K., Frey S., Novak R., Diemert D., Spector S.A., Rouphael N., Creech C.B., McGettigan J., Khetan S., Segall N., Solis J., Brosz A., Fierro C., Schwartz H., Neuzil K., Corey L., Gilbert P., Janes H., Follmann D., Marovich M., Mascola J., Polakowski L., Ledgerwood J., Graham B.S., Bennett H., Pajon R., Knightly C., Leav B., Deng W., Zhou H., Han S., Ivarsson M., Miller J., Zaks T. Efficacy and Safety of the mRNA-1273 SARS-CoV-2 Vaccine. New Engl. J. Med. 2021;384:403–416. doi: 10.1056/NEJMoa2035389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bicher M., Rippinger C., Schneckenreither G., Weibrecht N., Urach C., Zechmeister M., Brunmeir D., Huf W., Popper N. Model based estimation of the sars-cov-2 immunization level in austria and consequences for herd immunity effects. medRxiv. 2021 doi: 10.1101/2021.03.10.21253251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blackwood J.C., Childs L.M. An introduction to compartmental modeling for the budding infectious disease modeler. Lett. Biomath. 2018;5(1):195–221. doi: 10.1080/23737867.2018.1509026. [DOI] [Google Scholar]
- Böhning D., Rocchetti I., Maruotti A., Holling H. Estimating the undetected infections in the covid-19 outbreak by harnessing capture-recapture methods. Int. J. Infect. Dis. 2020;97:197–201. doi: 10.1016/j.ijid.2020.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brett T.S., Rohani P. Transmission dynamics reveal the impracticality of COVID-19 herd immunity strategies. Proc. Natl. Acad. Sci. USA. 2020;117(41):25897–25903. doi: 10.1073/pnas.2008087117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Britton T., Ball F., Trapman P. A mathematical model reveals the influence of population heterogeneity on herd immunity to SARS-CoV-2. Science. 2020;369(6505):846–849. doi: 10.1126/science.abc6810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brooks S., Gelman A. General Methods for Monitoring Convergence of Iterative Simulations. J. Comput. Graphi. Stat. 1998;7:434–455. doi: 10.1080/10618600.1998.10474787. [DOI] [Google Scholar]
- Bryant P., Elofsson A. Estimating the impact of mobility patterns on COVID-19 infection rates in 11 European countries. PeerJ. 2020;8:e9879. doi: 10.7717/peerj.9879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bubar K.M., Reinholt K., Kissler S.M., Lipsitch M., Cobey S., Grad Y.H., Daniel B. Model-informed COVID-19 vaccine prioritization strategies by age and serostatus. Science. 2021;26:916–921. doi: 10.1126/science.abe6959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burzynski M., Machado J., Aalto A., Beine M.A.R., Goncalves J., Haas T., Kemp F., Magni S., Mombaerts L., Picard P.M., Proverbio D., Skupin A., Docquier F. COVID-19 Crisis Management in Luxembourg: Insights from an Epidemionomic Approach. Economics & Human Biology. 2021;43(101051) doi: 10.1016/j.ehb.2021.101051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buss L.F., Prete C.A., Jr., Abrahim C., Mendrone A., Jr., Salomon T., de Almeida-Neto C., França R., Belotti M.C., Carvalho M., Costa A.G., Crispim M., Ferreira S.C., Fraiji N.A., Gurzenda S., Whittaker C., Kamaura L.T., Takecian P.L., da Silva Peixoto P., Oikawa M.K., Nishiya A.S., Sabino E.C. Three-quarters attack rate of SARS-CoV-2 in the Brazilian Amazon during a largely unmitigated epidemic. Science (New York, N.Y.) 2021;371(6526):288–292. doi: 10.1126/science.abe9728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao H., Zhou Y. The discrete age-structured seit model with application to tuberculosis transmission in china. Math. Comput. Mod. 2012;55(3):385–395. doi: 10.1016/j.mcm.2011.08.017. [DOI] [Google Scholar]
- Castro M., Ares S., Cuesta J.A., Manrubia S. The turning point and end of an expanding epidemic cannot be precisely forecast. Proc. Natl. Acad. Sci. 2020;117(42):26190–26196. doi: 10.1073/pnas.2007868117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang S., Harding N., Zachreson C., Cliff O., Prokopenko M. Modelling transmission and control of the COVID-19 pandemic in Australia. Nat. Commun. 2020;11 doi: 10.1038/s41467-020-19393-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cazelles B., Champagne C., Nguyen-Van-Yen B., Comiskey C., Vergu E., Roche B. A mechanistic and data-driven reconstruction of the time-varying reproduction number: Application to the COVID-19 epidemic. PLOS Computational Biology. 2021;17(7):e1009211. doi: 10.1371/journal.pcbi.1009211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Currie C.S., Fowler J.W., Kotiadis K., Monks T., Onggo B.S., Robertson D.A., Tako A.A. How simulation modelling can help reduce the impact of COVID-19. J. Simul. 2020;14(2):83–97. doi: 10.1080/17477778.2020.1751570. [DOI] [Google Scholar]
- Dehning J., Zierenberg J., Spitzner F.P., Wibral M., Neto J.P., Wilczek M., Priesemann V. Inferring change points in the spread of COVID-19 reveals the effectiveness of interventions. Science. 2020;369(6500) doi: 10.1126/science.abb9789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De la Sen M., Alonso-Quesada S. Vaccination strategies based on feedback control techniques for a general seir-epidemic model. Appl. Math. Comput. 2011;218(7):3888–3904. doi: 10.1016/j.amc.2011.09.036. [DOI] [Google Scholar]
- Deng J., Tang S., Shu H. Joint impacts of media, vaccination and treatment on an epidemic Filippov model with application to COVID-19. J. Theor. Biol. 2021 doi: 10.1016/j.jtbi.2021.110698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diekmann O., Heesterbeek J.A.P., Roberts M.G. The construction of next-generation matrices for compartmental epidemic models. J. Roy. Soc. Interface. 2010;7(47):873–885. doi: 10.1098/rsif.2009.0386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edridge A.W.D., Kaczorowska J., Hoste A.C.R., Bakker M., Klein M., Loens K., Jebbink M.F., Matser A., Kinsella C.M., Rueda P., Ieven M., Goossens H., Prins M., Sastre P., Deijs M., van der Hoek L. Seasonal coronavirus protective immunity is short-lasting. Nat. Med. 2020;26(11):1691–1693. doi: 10.1038/s41591-020-1083-1. [DOI] [PubMed] [Google Scholar]
- Emery J., Russell T., Liu Y., Hellewell J., Pearson C., Knight G., Eggo R., Kucharski A., Funk S., Flasche S., Houben R. The contribution of asymptomatic SARS-CoV-2 infections to transmission on the diamond princess cruise ship. eLife. 2020;9 doi: 10.7554/eLife.58699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Folkhalsomyndigheten, Påvisning av antikroppar efter genomgången covid-19 i blodprov från öppenvården (delrapport 1) (2020)
- Folkhalsomyndigheten, Påvisning av antikroppar efter genomgången covid-19 hos blodgivare (delrapport 2), 2020
- Fontanet A., Cauchemez S. COVID-19 herd immunity: where are we? Nat. Rev. Immunol. 2020;20 doi: 10.1038/s41577-020-00451-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gatto M., Bertuzzo E., Mari L., Miccoli S., Carraro L., Casagrandi R., Rinaldo A. Spread and dynamics of the COVID-19 epidemic in Italy: Effects of emergency containment measures. Proc. Natl. Acad. Sci. USA. 2020;117(19):10484–10491. doi: 10.1073/pnas.2004978117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman A., Rubin D.B. Inference from iterative simulation using multiple sequences. Statist. Sci. 1992;7(4):457–472. doi: 10.1214/ss/1177011136. [DOI] [Google Scholar]
- Gevertz J.L., Greene J.M., Sanchez-Tapia C.H., Sontag E.D. A novel covid-19 epidemiological model with explicit susceptible and asymptomatic isolation compartments reveals unexpected consequences of timing social distancing. J. Theor. Biol. 2021;510 doi: 10.1016/j.jtbi.2020.110539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Good M.F., Hawkes M.T. The Interaction of Natural and Vaccine-Induced Immunity with Social Distancing Predicts the Evolution of the COVID-19 Pandemic. mBio. 2020;11(5) doi: 10.1128/mBio.02617-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hethcote H.W. Age-structured epidemiology models and expressions for R_0. Mathematical Understanding of Infectious Disease Dynamics. 2009:91–128. doi: 10.1142/9789812834836_0003. [DOI] [Google Scholar]
- Jahn B., Sroczynski G., Bicher M., Rippinger C., Mhlberger N., Santamaria J., Urach C., Schomaker M., Stojkov I., Schmid D., Weiss G., Wiedermann U., Redlberger-Fritz M., Druml C., Kretzschmar M., Paulke-Korinek M., Ostermann H., Czasch C., Endel G., Bock W., Popper N., Siebert U. Targeted COVID-19 Vaccination (TAV-COVID) Considering Limited Vaccination Capacities - An Agent-Based Modeling Evaluation. Vaccines. 2021;9(5) doi: 10.3390/vaccines9050434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kavaliunas A., Ocaya P., Mumper J., Lindfeldt I., Kyhlstedt M. Swedish policy analysis for covid-19. Health Policy Techn. 2020;9(4):598–612. doi: 10.1016/j.hlpt.2020.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ke R., Romero-Severson E., Sanche S., Hengartner N. Estimating the reproductive number r0 of sars-cov-2 in the united states and eight european countries and implications for vaccination. J. Theor. Biol. 2021;517 doi: 10.1016/j.jtbi.2021.110621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy D., Read A. Monitor for COVID-19 vaccine resistance evolution during clinical trials. PLOS Biol. 2020;18 doi: 10.1371/journal.pbio.3001000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kermack W.O., McKendrick A.G., Walker G.T. A contribution to the mathematical theory of epidemics. Proc. Roy. Soc. A-Math. Phy. 1927;115(772):700–721. doi: 10.1098/rspa.1927.0118. [DOI] [Google Scholar]
- Kissler, S., Fauver, J.R., Mack, C., Tai, C.G., Breban, M.I., 2021. Densely sampled viral trajectories suggest longer duration of acute infection with b.1.1.7 variant relative to non-b.1.1.7 SARS-CoV-2. https://nrs.harvard.edu/URN-3:HUL.INSTREPOS:37366884.
- Larsson E., Brattström O., Agvald-Öhman C., Grip J., Jalde F., Strålin K., Nauclér P., Oldner A., Konrad D., Persson B., Eriksson L., Mårtensson J., Group F. Characteristics and outcomes of patients with COVID-19 admitted to ICU in a tertiary hospital in Stockholm, Sweden. Acta Anaesth. Scand. 2021 doi: 10.1111/aas.13694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R., Pei S., Chen B., Song Y., Zhang T., Yang W., Shaman J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2) Science. 2020;368(6490):489–493. doi: 10.1126/science.abb3221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Link W.A., Eaton M.J. On thinning of chains in MCMC. Methods Ecol. Evol. 2012;3(1):112–115. doi: 10.1111/j.2041-210X.2011.00131.x. [DOI] [Google Scholar]
- Liu Y., Gayle A.A., Wilder-Smith A., Rocklöv J. The reproductive number of COVID-19 is higher compared to SARS coronavirus. J. Travel Med. 2020 doi: 10.1093/jtm/taaa021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Locatelli I., Traechsel B., Rousson V. Estimating the basic reproduction number for covid-19 in western europe. PLoS ONE. 2021:e0248731. doi: 10.1371/journal.pone.0248731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ludvigsson J.F. The first eight months of Sweden COVID-19 strategy and the key actions and actors that were involved. Acta Paediatr. 2020;109(12):2459–2471. doi: 10.1111/apa.15582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacIntyre, C.R., Costantino, V., Trent, M., 2021. Modelling of COVID-19 vaccination strategies and herd immunity, in scenarios of limited and full vaccine supply in NSW, Australia. Vaccine. 10.1016/j.vaccine.2021.04.042 [DOI] [PMC free article] [PubMed]
- Mbuvha R., Marwala T. Bayesian inference of COVID-19 spreading rates in South Africa. PLoS ONE. 2020;15 doi: 10.1371/journal.pone.0237126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miles P.R. pymcmcstat: a python package for bayesian inference using Delayed Rejection Adaptive Metropolis. J. Open Source Softw. 2019;4(38):1417. doi: 10.21105/joss.01417. [DOI] [Google Scholar]
- Mohanty S., Satapathy A., Naidu M. Severe acute respiratory syndrome coronavirus-2 (SARS-CoV-2) and coronavirus disease 19 (COVID-19) – anatomic pathology perspective on current knowledge. Diagn. Pathol. 2020;151:103. doi: 10.1186/s13000-020-01017-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore S., Hill E., Dyson L., Tildesley M., Keeling M. Modelling optimal vaccination strategy for SARS-CoV-2 in the UK. PLOS Comput. Biol. 2021;17 doi: 10.1371/journal.pcbi.1008849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nokes D., Anderson R. The use of mathematical models in epidemiological study of infectious diseases and in the design of mass immunization programmes. Epidemiol. Infect. 1988;101:1–20. doi: 10.1017/S0950268800029186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parino F., Zino L., Porfiri M., Rizzo A. Modelling and predicting the effect of social distancing and travel restrictions on COVID-19 spreading. J. Ro. Soc. Interface. 2021;18:20200875. doi: 10.1098/rsif.2020.0875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polack F.P., Thomas S.J., Kitchin N., Absalon J., Gurtman A., Lockhart S., Perez J.L., Pareez Marc G., Moreira E.D., Zerbini C., Bailey R., Swanson K.A., Roychoudhury S., Koury K., Li P., Kalina W.V., Cooper D., Frenck R.W., Hammitt L.L., Treci A., Nell H., Schaefer A., Aanal S., Tresnan D.B., Mather S., Dormitzer P.R., Aahin U., Jansen K.U., Gruber W.C. Safety and Efficacy of the BNT162b2 mRNA Covid-19 Vaccine. New Engl. J. Med. 2020;383(27):2603–2615. doi: 10.1056/NEJMoa2034577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poland G.A., Ovsyannikova I.G., Kennedy R.B. SARS-CoV-2 immunity: review and applications to phase 3 vaccine candidates. Lancet. 2020;396:1595–1606. doi: 10.1016/S0140-6736(20)32137-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Proverbio D., Kemp F., Magni S., Husch A., Aalto A., Mombaerts L., Skupin A., Gonçalves J., Ameijeiras-Alonso J., Ley C. Dynamical SPQEIR model assesses the effectiveness of non-pharmaceutical interventions against COVID-19 epidemic outbreaks. PLOS ONE. 2021;16(5):1–21. doi: 10.1371/journal.pone.0252019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ragonnet, R., Briffoteaux, G., Williams, B.M., Savulescu, J., Segal, M., Abayawardana, M., Eggo, R.M., Tuyttens, D., Melab, N., Marais, B.J., McBryde, E.S., Trauer, J.M., 2020. Optimising social mixing strategies achieving COVID-19 herd immunity while minimising mortality in six European countries. medRxiv. 10.1101/2020.08.25.20182162. [DOI]
- Rashid H., Khandaker G., Booy R. Vaccination and herd immunity: What more do we know? Curr. Opin. Infect. Dis. 2012;25:243–249. doi: 10.1097/QCO.0b013e328352f727. [DOI] [PubMed] [Google Scholar]
- Rees E., Nightingale E., Jafari Y., Waterlow N., Clifford S., Pearson C., Group C., Jombart T., Procter S., Knight G. COVID-19 length of hospital stay: A systematic review and data synthesis. BMC Med. 2020;18:270. doi: 10.1186/s12916-020-01726-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reno C., Lenzi J., Navarra A., Barelli E., Gori D., Lanza A., Valentini R., Tang B., Fantini M.P. Forecasting COVID-19-Associated Hospitalizations under Different Levels of Social Distancing in Lombardy and Emilia-Romagna, Northern Italy: Results from an Extended SEIR Compartmental Model. J. Clin. Med. 2020;9:1492. doi: 10.3390/jcm9051492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roda W.C., Varughese M.B., Han D., Li M.Y. Why is it difficult to accurately predict the covid-19 epidemic? Infec. Dis. Model. 2020;5:271–281. doi: 10.1016/j.idm.2020.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saad-Roy C., Levin S., Metcalf C.J., Grenfell B. Trajectory of individual immunity and vaccination required for SARS-CoV-2 community immunity: a conceptual investigation. J. Roy. Soc. Interface. 2021;18:20200683. doi: 10.1098/rsif.2020.0683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabino E., Buss L., Carvalho M., Prete Junior C., Crispim M., Fraiji N., Pereira R., Parag K., Peixoto P., Kraemer M., Oikawa M., Salomon T., Cucunub Z.M., Castro M., Santos A., Nascimento V., Pereira H., Ferguson N., Pybus O., Faria N. Resurgence of COVID-19 in Manaus, Brazil, despite high seroprevalence. the Lancet. 2021;397:452–455. doi: 10.1016/S0140-6736(21)00183-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shattock A.J., Le Rutte E.A., Dünner R.P., Sen S., Kelly S.L., Chitnis N., Penny M.A. Impact of vaccination and non-pharmaceutical interventions on SARS-CoV-2 dynamics in Switzerland. medRxiv. 2021 doi: 10.1101/2021.04.14.21255503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simmonds P., Williams S., Harvala H. Understanding the outcomes of COVID-19–does the current model of an acute respiratory infection really fit? J. Gen. Virol. 2020 doi: 10.1099/jgv.0.001545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sjoedin H., Johansson A.F., Brannstrom A., Farooq Z., Kriit H.K., Wilder-Smith A., Astrom C., Thunberg J., Soderquist M., Rocklov J. COVID-19 healthcare demand and mortality in Sweden in response to non-pharmaceutical mitigation and suppression scenarios. Int. J. Epidemiol. 2020 doi: 10.1093/ije/dyaa121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snoeck C.J., Vaillant M., Abdelrahman T., Satagopam V.P., Turner J.D., Beaumont K., Gomes C.P.C., Fritz J.V., Schröder V.E., Kaysen A., Pavelka L., Stute L., Ramos Meyers G., Pauly L., Hansen M., Pauly C., Aguayo G.A., Perquin M., Hanff A.-M., Ghosh S., Gantenbein M., Huiart L., Ollert M., Krüger R. Prevalence of SARS-CoV-2 infection in the Luxembourgish population: the CON-VINCE study. medRxiv. 2020 doi: 10.1101/2020.05.11.20092916. [DOI] [Google Scholar]
- Socialstyrelsen, Utvecklingenöver tid, nyinskrivningar, avlidna och smittade på särskilt boende, 2020.
- Starr T.N., Greaney A.J., Addetia A., Hannon W.W., Choudhary M.C., Dingens A.S., Li J.Z., Bloom J.D. Prospective mapping of viral mutations that escape antibodies used to treat COVID-19. Science. 2021;371(6531):850–854. doi: 10.1126/science.abf9302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson J., Wattam S. Estimating the impact of interventions against COVID-19: from lockdown to vaccination. medRxiv. 2021 doi: 10.1101/2021.03.21.21254049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tillett R.L., Sevinsky J.R., Hartley P.D., Kerwin H., Crawford N., Gorzalski A., Laverdure C., Verma S.C., Rossetto C.C., Jackson D., Farrell M.J., Van Hooser S., Pandori M. Genomic evidence for reinfection with SARS-CoV-2: a case study. Lancet Infec. Dis. 2021;21(1):52–58. doi: 10.1016/S1473-3099(20)30764-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tracy, M., Cerd, M., Keyes, K.M., 2018. Agent-Based Modeling in Public Health: Current Applications and Future Directions, Annu. Rev. Publ. Health 39 (1) 77–94, pMID: 29328870. 10.1146/annurev-publhealth-040617-014317. [DOI] [PMC free article] [PubMed]
- van den Driessche P. Reproduction numbers of infectious disease models. Infect. Dis. Model. 2017;29(2):288–303. doi: 10.1016/j.idm.2017.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vrugt M.T., Bickmann J., Wittkowski R. Effects of social distancing and isolation on epidemic spreading modeled via dynamical density functional theory. Nat. Commun. 2020;11:5576. doi: 10.1038/s41467-020-19024-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu J.T., Leung K., Leung G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020;395(10225):689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang W., Shaff J., Shaman J. Effectiveness of non-pharmaceutical interventions to contain COVID-19: a case study of the 2020 spring pandemic wave in New York City. J. Roy. Soc. Interface. 2021;18:20200822. doi: 10.1098/rsif.2020.0822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan J., Li M., Gang L., Lu Z.K. Monitoring transmissibility and mortality of covid-19 in europe. Int. J. Infect. Dis. 2020;95:311–315. doi: 10.1016/j.ijid.2020.03.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
This study employs publicly available data-sets, provided by sources external to the authors. Each data-set employed is referenced and extensively described in Appendices F.1, F.2 and F.3. To foster reproducibility, a copy of the time-series data employed for model fitting is provided along with the code, both are made publicly available on GitHub at https://github.com/StefanoMagni/Model_COVID19_Dynamics_Luxembourg_Austria_Sweden.