Large Hall and Nernst responses from thermally induced spin chirality in a spin-trimer ferromagnet

Significance

The scalar spin chirality (SSC) produced by noncoplanar spins is a cornerstone of the foundation of skyrmionics and the physics of geometrically frustrated magnets; this quantity translates the topology of the magnetic structure to the language of directly measurable responses in transport properties. In this work, we not only report the gigantic Hall and Nernst effects emerging from thermally induced SSC in a conducting ferromagnet, but also find arguments for the relevance of the momentum space description of the generated Berry phase. Furthermore, we demonstrate that the idea of fluctuating SSC is not limited to magnets with conduction electrons strongly Hund’s-rule–coupled to local magnetic moments but is valid for a broader group of itinerant magnets with triangular-like lattice geometry.

Abstract

The long-range order of noncoplanar magnetic textures with scalar spin chirality (SSC) can couple to conduction electrons to produce an additional (termed geometrical or topological) Hall effect. One such example is the Hall effect in the skyrmion lattice state with quantized SSC. An alternative route to attain a finite SSC is via the spin canting caused by thermal fluctuations in the vicinity of the ferromagnetic ordering transition. Here, we report that for a highly conducting ferromagnet with a two-dimensional array of spin trimers, the thermally generated SSC can give rise to a gigantic geometrical Hall conductivity even larger than the intrinsic anomalous Hall conductivity of the ground state. We also demonstrate that the SSC induced by thermal fluctuations leads to a strong response in the Nernst effect. A comparison of the sign and magnitude of fluctuation–Nernst and Hall responses in fundamental units indicates the need for a momentum–space picture to model these thermally induced signals.

Scalar spin chirality (SSC) is defined as a mixed product of three noncoplanarly configured neighboring spins: χ _ijk = S _i · ( S _j × S _k ) in proportion to the solid angle subtended by them. Via the coupling between local moments and conduction electrons moving in the magnetic background, the latter accumulate a Berry phase proportional to the SSC and thus experience an additional, fictitious magnetic field (emergent magnetic field). If the total SSC does not vanish after summation over the bulk volume, it leads to responses in off-diagonal transport properties (1, 2) such as Hall and Nernst effects. These transverse responses from the SSC are termed here geometrical Hall and Nernst effects, while the latter has been less explored. This scenario for the emergent magnetic field has been well established for materials hosting long-range noncoplanar magnetic order or topologically nontrivial spin textures (3, 4), such as magnetic skyrmions (5, 6).

Recent theoretical models (7 –10) predict that, in the presence of Dzyaloshinskii–Moriya interactions (11, 12) (DMI), finite SSC can also be realized by canting of thermally fluctuating spins in the region close to the transition between paramagnetic and ferromagnetic states. Besides the geometrical Hall effect via the emergent magnetic field, it has also been predicted that fluctuating SSC can act as a source of additional skew scattering (13, 14). The entire experimental evidence presented so far for SSC in the fluctuating regime was, however, focused on the Hall resistivity in materials with strong Hund’s-rule coupling between hopping carriers and local magnetic ions (15 –21).

Here, we report evidence for the emergence of SSC driven by thermal fluctuations accompanying the magnetic ordering transition in a weakly coupled ferromagnet, with a magnetic structure in which the local magnetic moments are arranged in arrays of atomic trimers. Our arguments are based on the observation of the geometrical Hall and Nernst conductivities, whose absolute magnitudes around the magnetic transition temperature are gigantic, comparable to or even larger than those of the anomalous Hall and Nernst conductivities of the ferromagnetic ground state. The growth of the SSC can be well modeled in terms of a nonvanishing thermal average of the SSC, well defined on the spin-trimer sites.

The target compound of this study is Nd₃Ru₄Al₁₂, a ferromagnet with Curie temperature T _C = 40 K (22). It crystallizes in the centrosymmetric P6₃/mmc (#194) hexagonal structure (23) shown in Fig. 1A . An important feature of the magnetic sublattice is a specific arrangement of Nd³⁺ ions carrying localized magnetic moments. They form two-dimensional planes perpendicular to the c-axis, separated by interlayer spacing of 4.81 Å. These arrays are constructed of two types of corner-sharing trimers with relatively short and long interatomic distances (triangle edge lengths) of 3.73 Å and 5.12 Å, respectively. This constitutes a breathing kagomé lattice, sketched in Fig. 1B . Below T _C , the magnetic moments align along the c direction as determined by neutron diffraction and confirmed by significant magnetic anisotropy with c direction being the easy axis (24). Although the overall crystal structure is centrosymmetric, the inversion center relating two trimers lies between the layers, which thus opens a window for nonzero intratrimer DMI. Previously, the presence of spin-chiral features was reported in Dy- and Gd-based isostructural analogs of Nd₃Ru₄Al₁₂; static ordering with SSC was found in Dy₃Ru₄Al₁₂ (25), and the emergence of a skyrmion phase has been evidenced in Gd₃Ru₄Al₁₂ (26). These findings motivated us to search for the SSC driven by thermal fluctuations in this class of materials. The spin-trimer unit endowed with such a DMI can provide an ideal arena to explore the impact of fluctuation SSC.

Fig. 1.

Breathing kagomé lattice and anomalous Hall effect in Nd₃Ru₄Al₁₂. (A) Unit cell with Nd trimers marked with blue and red colors. (B) Arrangement of Nd³⁺ ions forming a breathing kagomé lattice. (C) Temperature dependence of $-{\stackrel{\sim }{\sigma }}_{xy}$ and $-{\sigma }_{xy}^{\hspace{0.17em}M}$ at B = 1 T. The shaded area stands for the SSC-related Hall conductivity ${\sigma }_{xy}^{\hspace{0.17em}\chi }$ = ${\stackrel{\sim }{\sigma }}_{xy}$ − ${\sigma }_{xy}^{\hspace{0.17em}M}$ . (D) Magnetic field dependence of the anomalous Hall conductivity ${\stackrel{\sim }{\sigma }}_{xy}$ _, (red) and the Karplus–Luttinger term ${\sigma }_{xy}^{\hspace{0.17em}M}$ (blue) for various temperatures. As ${\sigma }_{xy}^{\hspace{0.17em}M}/M=\text{const}.$ is used in the analysis, the right y-axis scale, which uses units of net magnetization M, also refers to the blue curves.

Results and Discussion

Hall Effect.

As the Hall effect has been proven to be a sensitive probe of spin-chiral textures (1, 27), we start our analysis from this vantage point. In ferromagnetic metals, the Hall conductivity ${\sigma }_{xy}$ , besides the ordinary term ${\sigma }_{xy}^O$ attributed to the orbital motion of electrons, has a contribution from the anomalous Hall effect (2), expected to be proportional to the net magnetization M. We isolated the anomalous Hall conductivity ${\stackrel{\sim }{\sigma }}_{xy}$ ( Materials and Methods ) and plotted it as a function of temperature and magnetic field in panels C and D of Fig. 1. At temperatures far enough below T _C , ${\stackrel{\sim }{\sigma }}_{xy}\left(B\right)$ almost perfectly reproduces the shape of the magnetization M(B). When temperature is increased, however, the anomalous Hall conductivity no longer follows the magnetization. The largest discrepancy is observed in the vicinity of T _C . Here, ${\stackrel{\sim }{\sigma }}_{xy}$ shows strong enhancement in the low field region when T approaches T _C from below or above. This kind of behavior of the anomalous Hall conductivity is not expected for conventional ferromagnets. Conventionally, ${\stackrel{\sim }{\sigma }}_{xy}$ is related to magnetization and diagonal conductivity ${\sigma }_{xx}\approx \frac{1}{{\rho }_{xx}}$ via

$${\stackrel{\sim }{\sigma }}_{xy}=S_{\text{A}}M{\left({\sigma }_{xx}\right)}^p,$$ [1]

where S _A is the anomalous Hall coefficient and the exponent p varies from 0 to 1.6, depending on the underlying mechanism (28, 29). Considering that σ _xx in the present compound is of the order of 10⁴ ⋅ Ω⁻¹ ⋅ cm⁻¹ around T _C (see SI Appendix for details), we anticipate the dominance of the intrinsic (30) contribution to ${\stackrel{\sim }{\sigma }}_{xy}$ with the above exponent p = 0; namely, ${\stackrel{\sim }{\sigma }}_{xy}$ should be independent of the scattering time due to the dissipationless character of the intrinsic anomalous Hall current. Even when taking into account the possible influence of the skew scattering mechanism (p = 1), which is expected to become significant only when σ _xx >10⁶ ⋅ Ω⁻¹ ⋅ cm⁻¹ (2), Eq. 1 fails to capture the enhancement of the anomalous Hall effect in the vicinity of the Curie temperature. Both magnetization and longitudinal conductivity monotonically increase as temperature is decreased, which leaves no possibility for ${\stackrel{\sim }{\sigma }}_{xy}$ to attain a maximum along the way. A plausible explanation for these observations is that the thermal fluctuations accompanying the phase transition carry finite SSC, contributing an additional geometrical-Hall term, ${\sigma }_{xy}^{\chi }$ , to the anomalous Hall conductivity (31).

To extract the SSC-induced Hall effect, we have quantified the magnetization-dependent intrinsic ${\sigma }_{xy}^M$ using Eq. 1 with p = 0 (i.e., setting ${\sigma }_{xy}^M/M$ constant and independent of temperature). The lowest temperature data (T = 2 K), in which fluctuations are expected to be frozen out, is used as a reference point in this analysis. For comparison, we have added the calculated ${\sigma }_{xy}^M\left(T\right)$ and ${\sigma }_{xy}^M\left(B\right)$ curves to panels C and D in Fig. 1, respectively. The largest impact of ${\sigma }_{xy}^{\chi }$ is clearly observed in the temperature region directly surrounding the magnetic transition. Note also that the peak magnitude of ${\sigma }_{xy}^{\chi }$ at B = 1 T (∼60 Ω⁻¹ ⋅ cm⁻¹) is even larger than the ground-state ${\sigma }_{xy}^M$ (∼50 Ω⁻¹ ⋅ cm⁻¹).

Geometrical Hall Effect Compared with SSC Model.

An intuitive description of the features observed in the Hall effect is sketched in Fig. 2A . The spins associated with a trimer of Nd ions in the breathing kagomé plane fluctuate around the net magnetization direction. When they are canted and form a noncoplanar “umbrella” configuration by thermal agitation, this corresponds to a finite SSC ${\chi }_{ijk}={\mathit{S}}_i\cdot \left({\mathit{S}}_j\times {\mathit{S}}_k\right)$ on the individual trimer with spins ${\mathit{S}}_i,$ ${\mathit{S}}_j,$ ${\mathit{S}}_k$ (see Fig. 2A ). In extending this notion from a single trimer to the entire lattice, the (breathing-)kagomé geometry of the present Nd³⁺ sublattice is essential to avoid cancellation of the effects of fluctuation SSC: Even if the total SSC vanishes when summing over the entire kagomé lattice, ${\chi }^{\text{tot}}={\displaystyle {\sum }_{\langle ijk\rangle }{\chi }_{ijk}}=0,$ the inequality of neighboring plaquettes (hexagons, small and large triangles) leads to unequal impacts on the conduction electrons (32, 33). Therefore, in general, the contributions $\sim {\chi }_{ijk}$ to the Hall effect do not cancel mutually, and it is reasonable to consider the SSC of different plaquettes separately. For Nd₃Ru₄Al₁₂, we expect that the small trimers, shaded red in Fig. 2A , yield the strongest contributions to the Hall signal. A thermally induced average SSC $\langle \chi \rangle$ on these small trimers therefore controls the overall SSC-induced Hall effect. In contrast, the lattice geometry does not play a comparably significant role in determining the average of SSC from large-scale spin structures with a finite topological winding number ${\chi }^{\text{tot}}\ne 0$ (such as skyrmions). This was discussed in refs. 8 –10, in which the authors considered simple triangular or square lattices in which neighboring plaquettes are equivalent.

Fig. 2.

Fluctuation-driven SSC and related Hall effect. (A) Schematic drawing of a solid angle subtended by three noncoplanar spins giving rise to finite SSC. (B) Thermal average of the SSC $\langle \chi \rangle$ of an isolated spin trimer as a function of the normalized magnetization. The circles denote data obtained by Monte Carlo simulations with couplings D/|J| = 0.5. A magnetic field with the strength H/|J| up to 2 is applied along the c-axis. Calculations at different temperatures in the range T/|J| from 0.28 to 1.82 are shown in different shades of red color. (C) SSC-related Hall conductivity $-{\sigma }_{xy}^{\hspace{0.17em}\chi }$ plotted as a function of m = M/M _max. The dashed line marking the envelope of the calculated $\langle \chi \rangle$ curve has been superimposed on the experimental Hall data.

In anticipation that the leading term of ${\sigma }_{xy}^{\chi }$ is enhanced in the vicinity of T _C in proportion to $\langle \chi \rangle$ , we have conducted detailed Monte Carlo simulations. Our theoretical description of the magnetic fluctuations starts from the spin-Hamiltonian of a single trimer with symmetric exchange interaction J, antisymmetric Dzyaloshinskii–Moriya interaction D, and a Zeeman term in response to the applied magnetic field:

$$E=-J\sum _{⟨i,j⟩}{\mathit{S}}_i\cdot {\mathit{S}}_j-D\sum _{⟨i,j⟩}\hat{\mathit{z}}\cdot \left({\mathit{S}}_i\times {\mathit{S}}_j\right)-\sum _i\mathit{B}\cdot {\mathit{S}}_i.$$ [2]

The thermal average SSC $\langle \chi \rangle$ on the trimer is defined as $\langle \chi \rangle =\frac{1}{Z}{\displaystyle \int }{\chi }_{123}\hspace{1em}{e}^{-\beta E}d{\mathit{S}}_{1}d{\mathit{S}}_{2}d{\mathit{S}}_3$ , where $Z$ is the partition function and $\beta =1/\left(k_{B}T\right)$ . Notice that for this particular type of DMI, the sign of the SSC depends on both the sign of the DMI and on the magnetic field—in contrast to the bulk or interfacial DMI in refs. 8 –10. Consequently, the lowest-order term in a high-temperature expansion $e^{-\beta E}=1-\beta E+\frac{1}{2}{\left(\beta E\right)}^2+\mathcal{O}\left[{\left(\beta E\right)}^3\right]$ with the correct symmetries is proportional to $DB{\beta }^2$ , and it is indeed nonvanishing; see the SI Appendix for details. Fig. 2B shows the thermal average of the SSC of independent spin trimers as a function of the normalized magnetization m = $M/M_{\text{max}}$ . The dashed line indicates the envelope of $\langle \chi \rangle \left(m\right)$ at different temperatures and fields. Here, it is noted that the D/J ratio, while not being determined experimentally, affects only the absolute value of the averaged chirality and does not change the shape of the ${\chi }^{\mathrm{tot}}\left(m\right)$ plot, as shown in SI Appendix, Fig. S3B . Fig. 2C shows the experimental ${\sigma }_{xy}^{\chi }$ plotted as a function of $m$ , where M _max = 6.8 µ _B/f.u. (Bohr magneton per formula unit) is the ground-state magnetization at which the SSC-related term is suppressed to zero. The experimental curves reproduce the shape of the calculated thermal average $\langle \chi \rangle \left(m\right)$ , confirming its close relation to ${\sigma }_{xy}^{\chi }$ . We have also considered more complex models, which involve other symmetry-allowed interactions, such as uniaxial anisotropies of second and fourth order, anisotropic exchange interactions, compass anisotropy terms, and intertrimer interactions, but they do not qualitatively alter the results and contribute subleading corrections. The details are shown in the SI Appendix .

The Hall resistivity in colossal magnetoresistance manganites has been found to follow a similar dome-shaped scaling with M/M _max (17, 18). In these materials with negligibly small ground-state anomalous Hall effect due to the vanishing orbital moment on the magnetic Mn sites, it has been proposed that ρ _yx is related to temperature and magnetic field only implicitly through M(T,B). However, the electrical resistivity of manganites around T _C exceeds the Mott–Ioffe–Regel limit, signaling the hopping transport regime. This is in contrast to the present case of Nd₃Ru₄Al₁₂, in which transport remains coherent in the whole temperature range. Also, the relevant coupling scheme between conduction electron and local spin/moment differs between these two cases. While the conducting charge carrier spins in manganites are strongly locked to the magnetic moments via Hund’s-rule coupling, Nd₃Ru₄Al₁₂ should be described using a weak coupling scheme; the conduction Ru-4d state is spin-polarized via the influence of local Nd moments. The fact that both classes of compounds show similar scaling suggests that this behavior is generic for systems with fluctuating SSC regardless of metallicity or the coupling limit. It can be noticed that the ${\sigma }_{xy}^{\chi }\left(m\right)$ curves for T = 40 and 45 K (i.e., in the closest vicinity of T _C ) deviate slightly from the general trend. This could be an artifact originating from the experimental uncertainty ( Materials and Methods ). However, one cannot entirely neglect the theoretically predicted (13, 14) scenario in which the Hall signal is additionally amplified by SSC-induced skew scattering, which is not captured by our approach based solely on SSC. Another interesting possibility is that cooperative effects, including critical fluctuations, play an essential role near T _C — a profound problem that deserves further investigation but is beyond the scope of the present paper.

Nernst Effect.

Having evidenced the impact of thermal fluctuation–induced SSC on the Hall effect in Nd₃Ru₄Al₁₂, we now explore the related response in off-diagonal thermoelectric transport (Nernst effect). Previously, the Nernst response has been reported for some systems hosting noncoplanar static spin textures (34 –37), such as 2-in-2-out order on the pyrocholore-lattice and topological skyrmions/hedgehogs, with finite ${\chi }^{\text{tot}}$ . Here, we explore the Nernst effect as well, produced by the thermally induced SSC in the present compound. The off-diagonal thermoelectric conductivity (Nernst conductivity) is expressed as ${\alpha }_{xy}={\sigma }_{xx}{S}_{xy}+{\sigma }_{xy}{S}_{xx}$ , where the experimental observables S _xx and S _xy are the Seebeck and Nernst coefficients, respectively. The field dependence of ${\alpha }_{xy}$ is shown in Fig. 3A at various temperatures, including the region around the ferromagnetic phase transition.

Fig. 3.

Nernst effect in Nd₃Ru₄Al₁₂ and its components, including a fluctuation-driven signal. (A) Nernst conductivity α _xy (red color, left axis) plotted together with magnetization M (blue color, right axis) as a function of magnetic field for various temperatures. (B) Temperature dependence of the quantity ${{\alpha }_{xy}/\left(TM\right)|}_{B\to +0}$ providing an estimate for the magnetization-proportional anomalous term ( ${\alpha }_{xy}^{\hspace{0.17em}M}$ ). The dashed black line represents a polynomial fit to the data at the lowest temperatures and above T = 50 K. A strong deviation from the main trend (shaded region) is visible close to the Curie temperature. (C) Nernst component ${\alpha }_{xy}^{\hspace{0.17em}\chi }$ from SSC fluctuations, deduced as a function of magnetic field at various temperatures.

In magnetic materials with SSC, the total Nernst signal comprises three contributions:

$${\alpha }_{xy}={\alpha }_{xy}^O+{\alpha }_{xy}^M+{\alpha }_{xy}^{\chi }.$$ [3]

The first one, ${\alpha }_{xy}^O$ , is the ordinary Nernst effect component corresponding to orbital motion of electrons in a field, the second ${\alpha }_{xy}^M$ is the M-dependent anomalous Nernst effect, and, finally, ${\alpha }_{xy}^{\chi }$ represents the contribution from SSC. We argue that the presence of three components, following Eq. 3 , is apparent already from the raw data. Like the Hall effect, ${\alpha }_{xy}\left(B\right)$ follows the hysteresis of the magnetization M(B) at the lowest temperature T = 9.8 K, and a roughly linear slope is observed at higher fields. We assign the former, hysteretic part to ${\alpha }_{xy}^M$ and the latter, field-linear signal to the ordinary Nernst effect. As temperature is increased toward T _C , the strong step-like feature in the low-field region is weakened and almost disappears for the curve at T = 31.2 K. At this temperature, a weak kink of opposite sign appears in ${\alpha }_{xy}$ around zero field; in contrast, the magnetization maintains its step-like behavior in the low-field region. This kink is the SSC-related Nernst signal ${\alpha }_{xy}^{\chi }$ , discussed in more detail in the following paragraph. As the temperature is increased further, the positive, magnetization-dependent signal at low fields is gradually restored, signaling the suppression of ${\alpha }_{xy}^{\chi }$ .

A useful quantity to discuss the anomalous and SSC-related conductivity is the ratio $-{\alpha }_{xy}/\left(TM\right)$ determined in the B→+0 limit, which is expected to be dominated by ${\alpha }_{xy}^M$ and ${\alpha }_{xy}^{\chi }$ (unlike these, the normal Nernst signal does not change abruptly around zero field). At high temperatures, $-{{\alpha }_{xy}/\left(TM\right)|}_{B\to +0}$ is positive and, within the experimental resolution, independent of T. This indicates that the magnetization-driven Nernst effect dominates over its ordinary and SSC-related counterparts in this temperature range; in the regime of moderate disorder, ${\alpha }_{xy}^M/T\sim M$ is expected for the spin-orbit coupling–driven Nernst signal (38, 39). Moving below T = 100 K, $-{{\alpha }_{xy}/\left(TM\right)|}_{B\to +0}$ starts to increase, followed by an abrupt drop and sign change below T _C . Further temperature decrease restores the dominance of the positive term in Fig. 3B , which eventually becomes temperature independent below 12 K. Such a nonmonotonic behavior of $-{{\alpha }_{xy}/\left(TM\right)|}_{B\to +0}$ , with a pronounced minimum in the vicinity of the magnetic transition, indicates the presence of an additional SSC-driven component ${\alpha }_{xy}^{\chi }$ with opposite sign to ${\alpha }_{xy}^M$ . We find that the SSC-related contribution clearly discerns itself from the background ${\alpha }_{xy}^M+{\alpha }_{xy}^O$ , as shown by the red shaded area in Fig. 3B . Importantly, ${\alpha }_{xy}^{\chi }$ is different in sign from ${\alpha }_{xy}^M$ , but its extremal value (after removal of the entropy factor T) is comparable in peak magnitude to ${\alpha }_{xy}^M/T$ of the fully ordered state. Due to its large contribution to the total Nernst conductivity, it is possible to separate ${\alpha }_{xy}^{\chi }$ from the background (black dashed line in Fig. 3B ) according to Eq. 3 , with the final result shown in Fig. 3C . Details of the subtraction procedure are discussed in Materials and Methods .

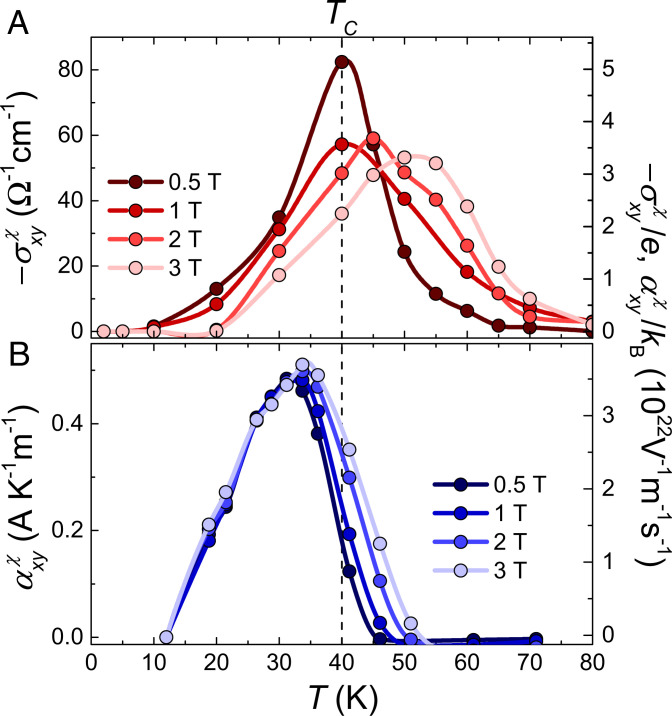
Having observed the emergence of the SSC-related Hall and Nernst signals in the vicinity of the ferromagnetic transition in Nd₃Ru₄Al₁₂, we may now compare their main features. Temperature dependence of $-{\sigma }_{xy}^{\chi }$ and ${\alpha }_{xy}^{\chi }$ for various magnetic fields is plotted in panels A and B of Fig. 4, respectively. While the signs of both quantities are opposite, they share similar overall behavior, with a broad maximum situated in the vicinity of T _C . Both maxima are observed to move to higher temperatures with increasing magnetic field, in accord with the scenario based on the thermal fluctuation–induced SSC. One can notice that the peak in ${\alpha }_{xy}^{\chi }\left(T\right)$ is shifted by several Kelvin toward lower temperatures as compared with ${\sigma }_{xy}^{\chi }\left(T\right)$ . Indeed, it is well established that ${\sigma }_{xy}$ driven by k -space Berry curvature is a property of the Fermi sea, while the corresponding thermoelectric response ${\alpha }_{xy}$ is defined by quasiparticles very close to the Fermi surface (2). A shift of the peak of ${\alpha }_{xy}^{\chi }$ to lower temperatures should occur in real materials when SSC around T _C is strong enough to drive the formation of k -space–emergent monopoles with energy separation larger than k_B T (40, 41). The conventional real space model anticipates that ${\sigma }_{xy}^{\chi }$ and ${\alpha }_{xy}^{\chi }$ follow the sign of their ordinary analogs, through which they are connected to the emergent field (35). This is not the case for Nd₃Ru₄Al₁₂, where ${\sigma }_{xy}^O$ and ${\alpha }_{xy}^O$ are both positive, while the sign of SSC-related conductivities changes from negative for ${\sigma }_{xy}^{\chi }$ to positive for ${\alpha }_{xy}^{\chi }$ . Therefore, an approach based on spatially homogeneous emergent magnetic field appears not suitable here.

Fig. 4.

Comparison between fluctuation-driven SSC contributions to Hall (A) and Nernst conductivities (B) at various magnetic fields. Right ordinates display $-{\sigma }_{xy}^{\hspace{0.17em}\chi }/e$ and ${\alpha }_{xy}^{\hspace{0.17em}\chi }/k_B$ , where e is the fundamental charge and k _B is the Boltzmann constant. The scaling illustrates the comparable magnitude of the two observables in reduced units.

Normalizing the SSC-driven signals (i.e., dividing ${\sigma }_{xy}^{\chi }\left(T\right)$ by the fundamental charge and ${\alpha }_{xy}^{\chi }\left(T\right)$ by the Boltzmann constant) allows for a comparison of their absolute magnitudes. The extrema attained by ${\sigma }_{xy}^{\chi }/e$ and ${\alpha }_{xy}^{\chi }/k_B$ , shown on the right ordinate scales of Figs. 4 A and B , are surprisingly close to each other, demonstrating an even impact of χ on both Hall and Nernst conductivities. Recently, it has been proposed (40, 42, 43) that the ratio of anomalous contributions to Nernst and Hall conductivities being a sizeable fraction of $k_B/e$ suggests a genuinely topological character of the underlying mechanism, driven by sources and sinks of k -space Berry curvature (such as Weyl nodes) near the Fermi surface (44, 45). Conversely, our observation indicates that even the thermally induced SSC from subnanometric spin trimers in this itinerant system ( ${\sigma }_{xx}$ ∼10⁴ ⋅ Ω⁻¹ ⋅ cm⁻¹, see SI Appendix, Fig. S1A ) shall be considered in terms of Berry curvature generation in k -space, comparable to the case of the intrinsic anomalous Hall effect from spin-orbit coupling in collinear ferromagnets (2) or noncollinear antiferromagnets (46).

For a broader perspective, it is useful to compare the magnitude of the Nernst response to other materials with SSC. Since there have been no preceding reports on the Nernst effect caused by fluctuating SSC, we can only refer to systems in which the static scenario is relevant. The maximum value of ${\alpha }_{xy}^{\chi }/T\approx$ 1.6 ⋅ 10⁻² ⋅ AK^{− 2} ⋅ m⁻¹ observed in Nd₃Ru₄Al₁₂ is comparable to those of $\approx$ 4 ⋅ 10⁻² ⋅ AK^{− 2} ⋅ m⁻¹ in Gd₂PdSi₃ (37) and $\approx$ 2.1 ⋅ 10⁻² ⋅ AK^{− 2} ⋅ m⁻¹ in MnGe (35), indicating that the Nernst conductivity from fluctuating SSC can be as large as the signal caused by long-range topologically nontrivial magnetic structures.

Conclusions

To conclude, we have examined the off-diagonal transport and thermoelectric properties of ferromagnetic Nd₃Ru₄Al₁₂ to prove the emergence and impact of SSC on the spin-trimer unit as induced by thermal fluctuations in the vicinity of the Curie temperature. We provide evidence for a thermal-fluctuation induced, large Hall signal in a highly conducting magnet with weak coupling between local moments and itinerant electrons. We corroborate that the mechanism of thermally induced SSC is relevant to a novel class of materials with magnetic structure based on subnanometric trimers. Our work also demonstrates that the fluctuation-induced SSC generates momentum space Berry curvature leading to a large Nernst response with a magnitude comparable to that observed for long-range ordered (i.e., static) topological spin textures.

Materials and Methods

Sample Preparation.

Single crystals of Nd₃Ru₄Al₁₂ were grown using the Czochralski method in a tetra-arc furnace under Ar atmosphere. Single-crystalline samples were chosen for the measurements. Crystals were oriented using the Laue method and cut to the required dimensions.

Magnetization and Transport Measurements.

Magnetization and resistivity were measured using a physical properties measurement system (PPMS) developed by Quantum Design. The vibrating-sample magnetometry option was used for magnetization measurements. Resistivity and Hall effect were measured using the PPMS with a standard four-probe technique, in which the current was applied along the a-axis. Thin gold wires serving as electrical contacts were attached to the sample surface with silver paint. The magnetic field was applied along the crystallographic c-axis (i.e., perpendicular to the current direction). In order to calibrate the longitudinal resistivity ρ _xx , we have measured an elongated sample, thus minimizing the geometrical uncertainty related to the finite size of electrical contacts. The normal Hall effect was subtracted from the measured Hall resistivity ${\rho }_{yx}$ , as described in the SI Appendix , to yield the anomalous term ${\stackrel{\sim }{\rho }}_{yx}={\rho }_{yx}-{\rho }_{yx}^O$ . From this, we obtain the anomalous Hall conductivity ${\stackrel{\sim }{\sigma }}_{xy}={\stackrel{\sim }{\rho }}_{yx}/\left[{\left({\rho }_{xx}\right)}^2+{\left({\rho }_{yx}\right)}^2\right]$ (where ρ _xx is the longitudinal resistivity). For the anomalous Hall effect, discussion of ${\stackrel{\sim }{\sigma }}_{xy}$ is preferred to ${\stackrel{\sim }{\rho }}_{yx}$ because it minimizes the impact of temperature-dependent scattering rates. We corrected demagnetization effects by calculating the internal magnetic field B = μ ₀ (H-NM) with the demagnetization factor N determined from the sample geometry.

In Fig. 2C , the divergence of ${\sigma }_{xy}^{\chi }\left(m\right)$ curves at T = 40 and 45 K from the general trend could be an artifact originating from the experimental uncertainty. Both the magnetization and Hall resistivity show a steep T dependence in this range. Even a minute temperature mismatch between the relevant experiments performed with different setups may account for the deviation directly or through imperfect subtraction of the M-proportional Hall conductivity.

Monte Carlo Simulations.

Monte Carlo simulations were performed using the Metropolis algorithm with local single-spin updates. A quasi–two-dimensional 10 × 10 × 1 superlattice was constructed, which contains 200 decoupled spin trimers. Our simulations were performed by classical spin lattice model, modeling the Nd³⁺ ion as Heisenberg spins coupled by a ferromagnetic nearest-neighbor exchange J and a nearest-neighbor Dzyaloshinskii–Moriya interaction D, which arises from the broken inversion symmetry within the ab-plane. The SSC χ was averaged over 3 ⋅ 10⁶ single spin updates after thermalizing by 3 ⋅ 10⁵ single spin updates.

Nernst Effect Measurements.

In the Nernst effect measurements, the heat current was applied along the a-axis with the one-heater two-thermometer method in a custom setup using the PPMS cryostat. Magnetic fields up to 9 T were applied along the c-axis. For details of the measurement setup and procedure, see ref. 37. The sign of the Nernst signal is determined in accordance with the vortex convention (47).

The Nernst response obeys the Mott rule, ${\alpha }_{xy}=-\frac{{\pi }^2}{3}\frac{{\left({\mathrm{k}}_{\mathrm{B}}\right)}^{2}T}{e}{\frac{\partial {\sigma }_{xy}}{\partial E}|}_{E_F}$ , where k_B and e are Boltzmann constant and electron charge, respectively. If the Hall conductivity can be decomposed into three additive components, then a separate Mott-type relation should connect Hall and Nernst conductivities for each component, assuming elastic scattering processes for the relaxation.

While we can neglect the scattering-rate dependence of ${\sigma }_{xy}^M$ as a hallmark of the intrinsic mechanism and set ${\sigma }_{xy}^M/M$ independent of temperature, the behavior of ${\alpha }_{xy}^M$ is more difficult to predict (29); a similarly simplified approach with setting ${\alpha }_{xy}^M/M$ independent of temperature cannot be used for our Nernst effect (see Fig. 3B and SI Appendix for details). The high- and low-temperature regimes of $-{{\alpha }_{xy}/\left(TM\right)|}_{B\to +0}$ in Fig. 3B are both dominated by ${\alpha }_{xy}^M$ , as stated in Nernst Effect in the main text. To separate the SSC contribution, we smoothly connect ${\alpha }_{xy}^M\left(T\right)$ observed at high and low T, estimating its value in the temperature region with strong magnetic fluctuations (dashed line in Fig. 3B ). In the next step, we separate the SSC-related contribution from the remaining signal ${\alpha }_{xy}$ − $\hspace{1em}{\alpha }_{xy}^M$ = $\hspace{1em}{\alpha }_{xy}^O$ + ${\alpha }_{xy}^{\chi }$ (further details are shown in the SI Appendix ).

The crystal structure in Fig. 1 was drawn using the software package Vesta (48).

Data Availability

All study data are included in the article and/or SI Appendix .

Change History

November 12, 2021: Figure 3 has been updated; please see accompanying Correction for details.