A dynamical study of SARS-COV-2: A study of third wave

Abstract

The coronavirus still an epidemic in most countries of the world and put the people in danger with so many infected cases and death. Considering the third wave of corona virus infection and to determine the peak of the infection curve, we suggest a new mathematical model with reported cases from March 06, 2021, till April 30, 2021. The model provides an accurate fitting to the suggested data, and the basic reproduction number calculated to be ${\mathcal{R}}_0=1.2044$. We study the stability of the model and show that the model is locally as well as globally asymptotically stable when ${\mathcal{R}}_0<1$, for the disease free case. The parameters that are sensitive to the basic reproduction number, their effect on the model variables are shown graphically. We can observe that the suggested parameters can decrease efficiently the infection cases of the third wave in Pakistan. Further, our model suggests that the infection peak is to be May 06, 2021. The present results determine that the model can be useful in order to predict other countries data.

Introduction

Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) is the virus that responsible for the COVID-19 (coronavirus disease 2019) disease and its epidemics. Currently, Pakistan facing the third wave of coronavirus infection with many cases of death and infection. It is observed that this COVID wave is more dangerous than the previous wave 1 and 2. The death percentage comprised to the first and second wave is 2% while the infection and the death cases were found less in the first and second wave. The mortality rate due to infection was 1% in total reported cases in the country in COVID-19 waves 1 and 2 while in this wave third, it is found to be 2%. The number of infected cases in Pakistan from the beginning of infections is reported to be 854,240 with 18 797 deaths and 752,712 were recovered. There is observed an increasing trend of infection in the country since March 06, 2021, and daily hundreds of infections cases are reporting. This increasing trend of infection is an alarming situation for the country, where there are fewer facilities of hospitals (with an available number of beds and ventilators) and other emergency equipment for coronavirus infected people. With the less equipment’s and low space of hospital beds and ventilators, almost the countries hospitals are full. If the people of Pakistan did not follow the SOPs, then the situation will be like our neighbor country India. To get the situation to be worse, a strict lockdown and the implementations of the SOPs suggested by the World Health Organization (WHO) should be followed.

The coronavirus infection has been studied from a different perspective from the researcher’s point of view. One of the perspectives is to study the infection through a mathematical model. In this regard, many researchers of the world formulated mathematical models to study this infection and to determine the peak of the infection curve. Further, to predict the disease eliminations using the model sensitive parameters. Some mathematical models that considered the modeling of the novel coronavirus are suggested, see for details the references therein [1], [2], [3], [4], [5], [6], [7]. For example, using the early reported cases in China through a mathematical model is suggested in [1]. Using the data from Spain and Italy, an SEIR model has been suggested by the authors in [2]. An SEIR-based model to predict the dynamics of the COVID-19 model is studied in [3]. The forced SEIR model for Italian infected data is suggested in [4]. Using South African infected cases and the impact of social distancing through a mathematical model is considered in [5]. A comparative analysis of the COVID-19 models has been analyzed in [6]. A mathematical model for the prediction of Mexican data is suggested in [7]. The authors in [8] studied the real data of Saudi Arabia and obtained the dynamic results using a novel mathematical model. The modeling of coronavirus and its control has been studied in [9]. The modeling and controls measures to address the infected cases in Pakistan through effective mathematical modeling are suggested in [10]. The COVID-19 model based on the lockdown prediction is suggested in [11]. The literature on the COVID-19 is a lot where the authors studied the disease controls and its eliminations using useful mathematical models, we refer the readers to see [12], [13], [14], and the references therein. Some recent updates regarding the modeling of the coronavirus, the authors constructed a mathematical model based on the fuzzy fractional derivative and obtained the results [15]. The role of vaccination to reduce the number of infections due to COVID-19 has been studied through a mathematical model in [16]. The fuzzy approach to study the COVID-19 has been discussed in [17]. The authors in [18] considered different fractional operators for study of the coronavirus infection model. The coronavirus model with quarantine has been discussed in [19]. Piecewise differential and integral operators and its applications have been discussed in [20].

The purpose of this present work is to study the third wave of coronavirus infection in Pakistan through a new mathematical model. We consider the third wave of reported cases of Pakistan and obtain the results for the model. We predict the infection and its peak by using real data. Comprehensive details on the literature related to coronavirus infection have been done above. The model and its analysis in the given paper are as follows: Section “Model formulation” explores the mathematical modeling of the novel coronavirus and its related results. Section “Stability results” shows the stability analysis of the model and the endemic equilibria. Sections “Estimations of the parameters”, “Numerical solution” and “Conclusion”, shows the estimations of system parameters, numerical solutions, and conclusions respectively.

Model formulation

The infection of COVID-19 which is in the third phase/wave in Pakistan, that bringing a lot of infection and death cases. Due to not taking seriously this infection by the people of Pakistan, the situation is going from bad to worse. The government of Pakistan in line with WHO suggested detailed guidelines that how to prevent themselves and protect other people. Therefore, the government and the health agencies are looking for the peak of the infection to estimate the disease elimination stage. In this regard, we consider a new mathematical model with suggested cases from wave 3, which is currently underway that started from March 6, 2021. We consider the cases from March 6 2021 till April 30, 2021, and use them in our analysis. Before, we start the modeling process, we denote the human’s populations into six classes; that is, the healthy individuals that can attract the disease COVID-19 is given by $S\left(t\right)$, those attract the disease but are not yet infectious are given by $E\left(t\right)$, infected after completing the incubation period is shown by $I$, those who not showing symptoms but infect other healthy people and may spread the infection further to other healthy people, is shown by $A$ (asymptomatic infected), the individuals that are recovered from infection is given by $R$, and those died from this infections are accumulated to dead class, given by $D\left(t\right)$. So, we write $N\left(t\right)=S\left(t\right)+E\left(t\right)+I\left(t\right)+A\left(t\right)+R\left(t\right)+D\left(t\right)$. The evolutionary differential equations that describe the dynamics of coronavirus infection in Pakistan is shown by the following evolutionary differential equations:

$$\left\{\begin{array}{c}\frac{dS}{dt}=\Pi -\psi (I+\tau A)\frac{S}{N-D}-\mu S,\hfill \\ \hfill \\ \frac{dE}{dt}=\psi (I+\tau A)\frac{S}{N-D}-(\delta +\mu +{\mu }_0)E,\hfill \\ \hfill \\ \frac{dI}{dt}=\delta (1-\omega )E-(\mu +{\mu }_1+{\gamma }_1)I,\hfill \\ \hfill \\ \frac{dA}{dt}=\delta \omega E-(\mu +{\mu }_2+{\gamma }_2)A,\hfill \\ \hfill \\ \frac{dR}{dt}={\gamma }_{1}I+{\gamma }_{2}A-\mu R,\hfill \\ \hfill \\ \frac{dD}{dt}={\mu }_{0}E+{\mu }_{1}I+{\mu }_{2}A,\hfill \end{array}\right)$$ (1)

with non-negative initial conditions. In above model (1), the healthy individuals are recruited through the parameter $\Pi$. The healthy individuals that attract the SARS-COV-2infection after interacting with the infected people at the rate of $\psi$. The parameter $\tau$ denotes the transmissibility multiple of asymptomatic infection. The individuals die naturally at a rate $\mu$. After successful completion of the incubation period, the exposed individuals are infected at the rate of $\delta (1-\omega )$, while $\omega \delta$ contributes to the generations of symptomatic cases. We assumed that the during the test of individuals the asymptomatic infections observed for the people and its recovery is shown by ${\gamma }_2$, while the recovery from symptomatic infection is given by ${\gamma }_1$. We consider the disease death at exposed, infected class and asymptomatic class respectively given by ${\mu }_0,{\mu }_1$ and ${\mu }_2$. In the absence of the last equation, the model takes the following form:

$$\left\{\begin{array}{c}\frac{dS}{dt}=\Pi -\psi (I+\tau A)\frac{S}{N}-\mu S,\hfill \\ \hfill \\ \frac{dE}{dt}=\psi (I+\tau A)\frac{S}{N}-(\delta +\mu +{\mu }_0)E,\hfill \\ \hfill \\ \frac{dI}{dt}=\delta (1-\omega )E-(\mu +{\mu }_1+{\gamma }_1)I,\hfill \\ \hfill \\ \frac{dA}{dt}=\delta \omega E-(\mu +{\mu }_2+{\gamma }_2)A,\hfill \\ \hfill \\ \frac{dR}{dt}={\gamma }_{1}I+{\gamma }_{2}A-\mu R.\hfill \end{array}\right)$$ (2)

The total dynamics of system (2) can be obtained by adding all its equations:

$$\frac{dN}{dt}=\Pi -\mu N-{\mu }_{0}E-{\mu }_{1}I-{\mu }_{2}A\le \Pi -\mu N.$$ (3)

So,

$$\frac{dN}{dt}\le \Pi -\mu N,$$ (4)

and hence

$$N\left(t\right)\le \frac{\Pi }{\mu }\mathrm{whenever}t⟶\infty .$$ (5)

The biological feasible region for the model (2) is,

$$\Gamma =\left\{(S,E,I,A,R)\in {\mathbb{R}}_{+}^5:N\left(t\right)\le \frac{\Pi }{\mu }\right\}.$$ (6)

Equilibria

We determine the equilibria of the model (2) by equating the right side of the system and getting the equilibrium for the disease free case, denoting by $D_0$ and is given by

$$D_0=\left(S^0,0,0,0,0\right)=\left(\frac{\Pi }{\mu },0,0,0,0\right).$$

Further, to obtain the expression for the basic reproduction number ${\mathcal{R}}_0$, we follows [21] and have the following results:

$$F=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill \psi \hfill & \hfill \tau \psi \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),V=\left(\begin{array}{ccc}\hfill k_1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\delta (1-\omega )\hfill & \hfill k_2\hfill & \hfill 0\hfill \\ \hfill -\delta \omega \hfill & \hfill 0\hfill & \hfill k_3\hfill \end{array}\right),$$ (7)

where $k_1=(\delta +\mu +{\mu }_0)$, $k_2=(\mu +{\mu }_1+{\gamma }_1)$ and $k_3=(\mu +{\mu }_2+{\gamma }_2)$. The following ${\mathcal{R}}_0$ is obtained using the spectral radius of $\rho \left(F{V}^{-1}\right)$:

$${\mathcal{R}}_0=\frac{\delta \psi \left(k_2\tau \omega +k_3(1-\omega )\right)}{k_1{k}_2{k}_3},=\underset{{\mathcal{R}}_1}{\underbrace{\frac{\delta \tau \psi \omega }{k_1{k}_3}}}+\underset{{\mathcal{R}}_2}{\underbrace{\frac{\delta \psi (1-\omega )}{k_1{k}_2}}}.$$

Stability results

We explore the stability of the model (2) at $D_0$. We suggest the following results:

Theorem 1

The model (2) at $D_0$ is locally asymptotically stable if ${\mathcal{R}}_0<1$ .

Proof

We have the following Jacobian at $D_0$,

$$J\left(D_0\right)=\left(\begin{array}{ccccc}\hfill -\mu \hfill & \hfill 0\hfill & \hfill -\psi \hfill & \hfill -\tau \psi \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -k_1\hfill & \hfill \psi \hfill & \hfill \tau \psi \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \delta (1-\omega )\hfill & \hfill -k_2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \delta \omega \hfill & \hfill 0\hfill & \hfill -k_3\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\gamma }_1\hfill & \hfill {\gamma }_2\hfill & \hfill -\mu \hfill \end{array}\right).$$

It is obvious that the two roots $-\mu ,-\mu$ have negative real parts, while the cubic equations given below can determines the remaining roots with negative real parts satisfying the conditions come from Routh–Hurtwiz criteria, $m_j>0$ for $j=1,2,3$ and $m_1{m}_2>m_3$.

$${\lambda }^3+m_1{\lambda }^2+m_2\lambda +m_3=0,$$ (8)

where

$$m_1=k_1+k_2+k_3,$$

$$m_2=k_1{k}_3(1-{\mathcal{R}}_1)+k_1{k}_2(1-{\mathcal{R}}_2)+k_3{k}_2,$$

$$m_3=k_1{k}_2{k}_3(1-{\mathcal{R}}_0),$$

and

$$m_1{m}_2-m_3=k_1\left(k_1+k_2+k_3\right)\left(k_3(1-{\mathcal{R}}_1)+k_2(1-{\mathcal{R}}_2)\right)+k_2\left(k_2+k_3\right)k_3+k_1{k}_2{k}_3{\mathcal{R}}_0>0.$$

So, the above conditions hold and hence the model (2) is locally asymptotically stable for the case $D_0$ when ${\mathcal{R}}_0<1$. □

The following theorem describes the global asymptotical stability of the system (2). We establish the global stability of the model (2) at $D_0$ as follows:

Theorem 2

The DFE $D_0$ of SAR-COV2 model (2) is globally asymptotically stable if ${\mathcal{R}}_0\le 1$ .

Proof

Let, we define the Lyapunov function given by

$$\mathcal{L}\left(t\right)={\pi }_1\left(S\left(t\right)-S^0-S^{0}log\left(\frac{S\left(t\right)}{S^0}\right)\right)+{\pi }_{2}E\left(t\right)+{\pi }_{3}I\left(t\right)+{\pi }_{4}A\left(t\right),$$ (9)

where ${\pi }_l>0$ for $l=1,2,3,4$, should be determined at a later stage. Differentiating $\mathcal{L}$ gives

$${\mathcal{L}}^{\prime }\left(t\right)={\pi }_1\left(1-\frac{S^0}{S}\right)S^{\prime }+{\pi }_2{E}^{\prime }+{\pi }_3{I}^{\prime }+{\pi }_4{A}^{\prime }.$$ (10)

Consider model (2) with some arrangement, we get the following,

$${\mathcal{L}}^{\prime }\left(t\right)={\pi }_1[\Pi -\psi (I+\tau A)\frac{S}{N}-\mu S]\left(1-\frac{S^0}{S}\right)+{\pi }_2[\psi (I+\tau A)\frac{S}{N}-k_{1}E]+{\pi }_3[\delta (1-\omega )E-k_{2}I]+{\pi }_4[\delta \omega E-k_{3}A],=-\mu {\pi }_1\left(\frac{{(S-S^0)}^2}{S}\right)+(\psi {\pi }_1-{\pi }_3{k}_2)I+(\psi \tau {\pi }_1-{\pi }_4{k}_3)A+({\pi }_4\delta \omega +\delta (1-\omega ){\pi }_3-{\pi }_2{k}_1)E.$$ (11)

Now, we can select these ${\pi }_l$ for $l=1,\dots ,4$ as follows: ${\pi }_1={\pi }_2=k_2{k}_3$,  ${\pi }_3=\psi k_3$, ${\pi }_4=\tau \psi k_2$. So, we have finally,

$${\mathcal{L}}^{\prime }\left(t\right)\le -\mu k_2{k}_3\left(\frac{{(S-S^0)}^2}{S}\right)-k_2{k}_3{k}_1\left[1-{\mathcal{R}}_0\right]E.$$ (12)

When ${\mathcal{R}}_0\le 1$, then ${\mathcal{L}}^{\prime }\left(t\right)$ is negative and hence the SARS-COV-2model (2) is globally asymptotically stable at $D_0$. □

Endemic equilibria

We obtain the endemic equilibria of the system (2) denoted by $D_1=(S^{\ast },E^{\ast },I^{\ast },A^{\ast },R^{\ast })$, given by

$$\left\{\begin{array}{c}{S}^{\ast }=\frac{\Pi }{{\lambda }^{\ast }+\mu }\hfill \\ \hfill \\ E^{\ast }=\frac{{\lambda }^{\ast }{S}^{\ast }}{k_1}\hfill \\ \hfill \\ I^{\ast }=\frac{\delta (1-\omega )E^{\ast }}{k_2}\hfill \\ \hfill \\ A^{\ast }=\frac{\delta \omega E^{\ast }}{k_3},\hfill \\ \hfill \\ R^{\ast }=\frac{{\gamma }_2{A}^{\ast }+{\gamma }_1{I}^{\ast }}{\mu }.\hfill \end{array}\right)$$

Using the above in the following:

$${\lambda }^{\ast }=\frac{\psi (I^{\ast }+\tau A^{\ast })}{N^{\ast }},$$ (13)

we arrive at,

$$j_1{I}^{\ast }+j_2=0,$$

where

$$j_1=\delta k_3(1-\omega )\left({\gamma }_1+\mu \right)+k_2\left(\delta \omega \left({\gamma }_2+\mu \right)+k_3\mu \right),$$

$$j_2=k_1{k}_2{k}_3\mu (1-{\mathcal{R}}_0).$$

Here, $j_1$ is positive and the existence of the positive equilibria depends on the value of ${\mathcal{R}}_0$, when ${\mathcal{R}}_0<1$, then we can obtain $I^{\ast }=-j_2/j_1$, and hence no positive equilibria. So, to have a positive endemic equilibria when ${\mathcal{R}}_0>1$, then there exists a unique endemic equilibrium for the model (2).

Estimations of the parameters

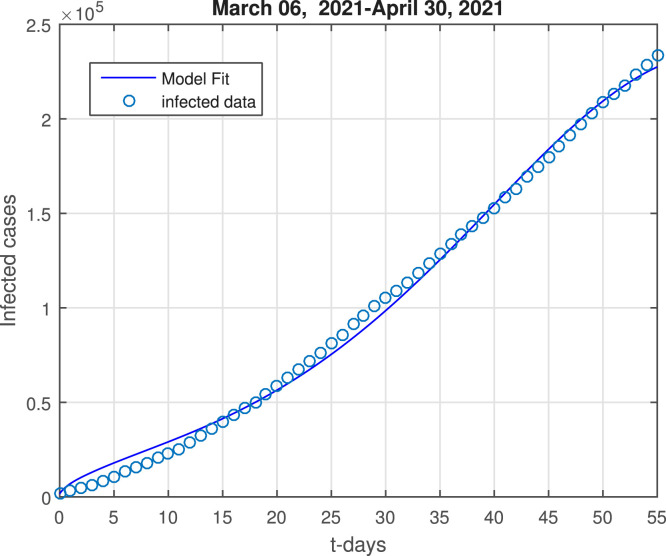
To obtain the realistic parameters and to predict the disease peak of the third wave in Pakistan, we need to use the real cases reported from March 06, 2021, till April 30, 2021. These cases have been obtained from the world-meter, see the details [22]. The total corona cases reported until now are 841 636 with 18 429 deaths while 738,727 people have been recovered. Now to parameterized the model (2), we need first to calculate some of the values of the parameters of the model, such as the natural death and the recruitment rate of the populations. So, we consider the total population of Pakistan at 2021, is to be $N\left(0\right)=220000000$, and so the parameter $\Pi$ which represents the recruitment rate of the susceptible population, and $d$ is the natural death rate are shown respectively by $\Pi \approx 8903$ per day and $\mu =1/(67.7\times 365)$, where $\mu =1/(67.7)$ describes the average life span in Pakistan. The remaining parameters involved in the system are fitted to the model and have been given in Table 1. Using the nonlinear least square curve fitting technique, we obtain the desired fitting in Fig. 1 with the estimated basic reproduction number ${\mathcal{R}}_0\approx 1.2044$. It can be seen that the reported cases are fitted accurately to the model and hence the obtained parameters values can be useful to study the model solution graphically.

Table 1.

Estimated parameters.

Symbol	Definition	Value/per day	Source
$\Pi$	Recruitment rate	$\mu \times N\left(0\right)$	Estimated
$d$	Natural mortality rate	$\frac{1}{67.7\times 365}$	[23]
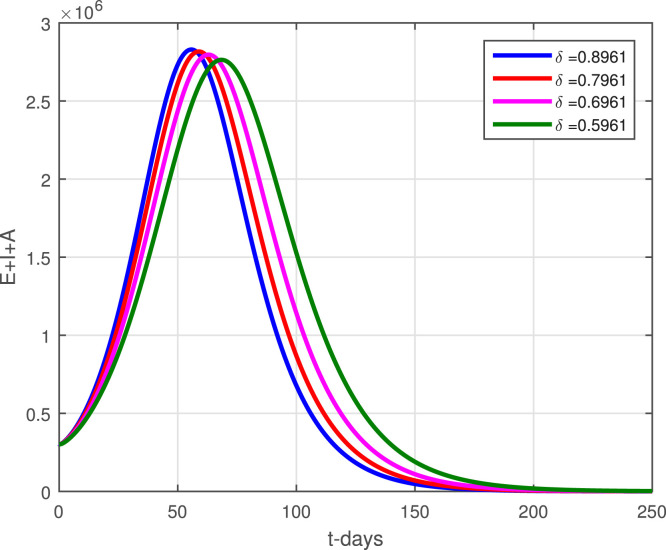
$\delta$	Incubation period	0.8961	Fitted
${\mu }_0$	Death due to disease at E	0.0126	Fitted
$\omega$	Proportion of infected cases	0.9692	Fitted
${\mu }_1$	Death due to infection of symptomatic people	0.0010	Fitted
${\gamma }_1$	Recovery of symptomatic people	0.1456	Fitted
${\mu }_2$	Disease death of asymptomatic people	0.0069	Fitted
$\psi$	Disease contact rate	0.9549	Fitted
$\tau$	Transmissibility multiple for asymptomatic people	0.9635	Fitted
${\gamma }_2$	Recovery of asymptomatic people	0.8666	Fitted

Fig. 1.

Reported cases from third wave in Pakistan, March 06, 2021–April 30, 2021 versus model fit.

Numerical solution

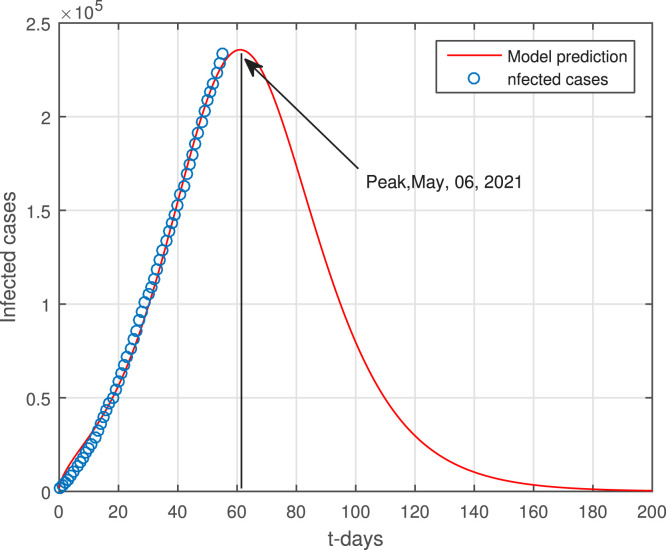
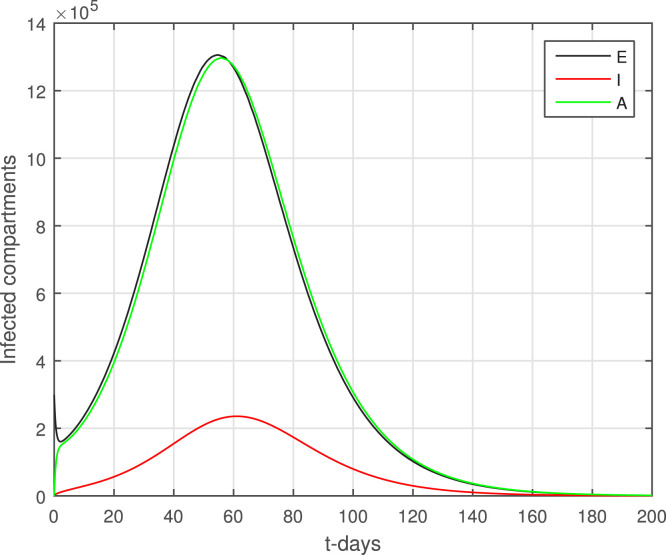
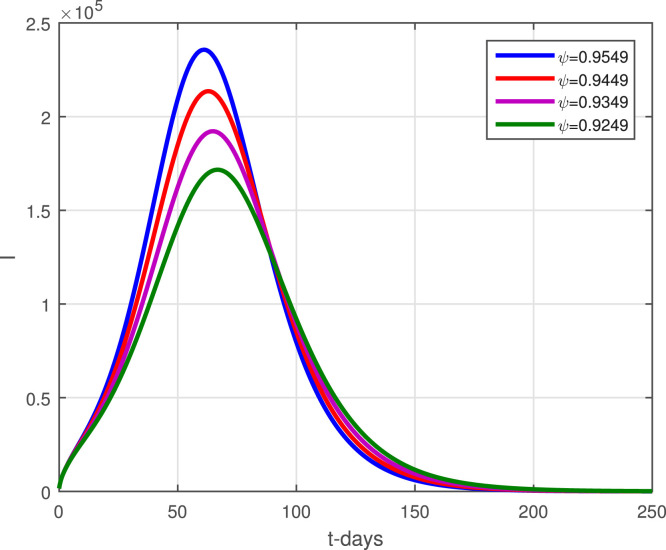
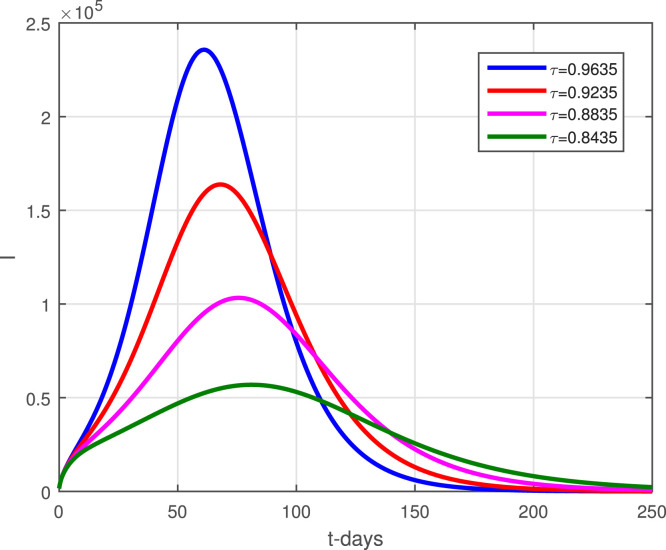
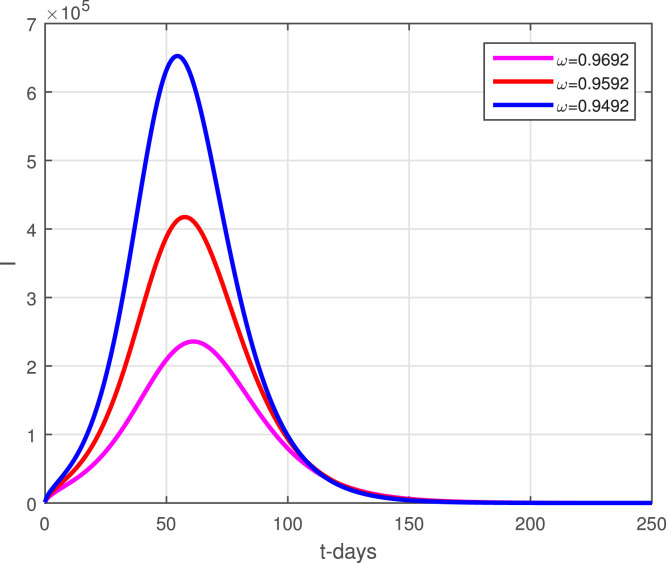
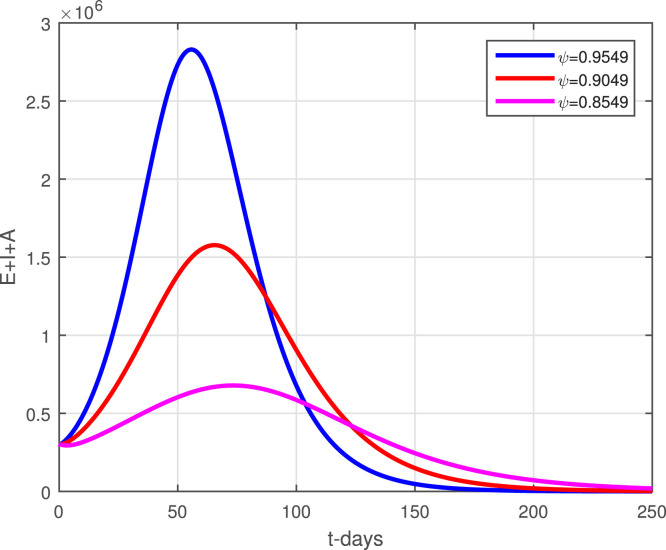
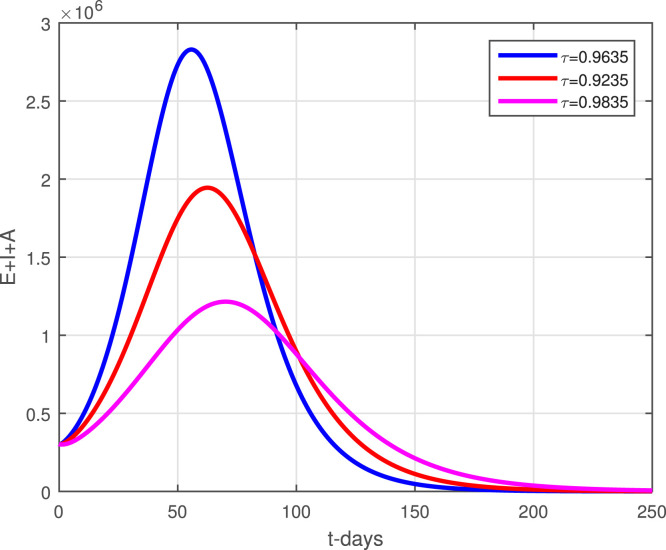
The model (2) with the newly reported cases of coronavirus in Pakistan are considered here to obtain the numerical solution. Taking the time unit in days where the numerical values of the parameters obtained through data fitting has been shown in Table 1 are considered to obtain the simulation results. The initial conditions used in graphical results are : $S\left(0\right)=219698286$, $E\left(0\right)=300000$, $I\left(0\right)=1714$, $A\left(0\right)=R\left(0\right)=D\left(0\right)=0$. Fig. 2 determines the predictions of the peak of the curve and it is shown that the peak may occur on May 6, 2021. The lockdown and using the social distances and other necessary actions suggested by the World Health Organization (WHO) can decrease the infection of coronavirus cases in Pakistan by following strict action from the government. The district government should take strict actions against those people who do not follow the SOPs and should be punished and jailed. It has been observed that in many parts of the country, the SOPs have been violated during the religious gathering, Aftar parties, etc., this should be discouraged and a proper check-in balance from the district government should be implemented. Fig. 3 shows that the infective compartments vanishing for t $=$ 200. Fig. 4 shows the effective contact rate $\psi$ using its different values. It can be seen that social distancing and the SOPs can reduce the infection spread. The impact of parameter $\tau$ that generating the asymptomatic infections has been shown graphically in Fig. 5. With the decreasing of the value of $\tau$, a decrease in the infective individuals is observed. Fig. 6 shows the impact of $\delta$ on the infected populations, decreasing the value of $\delta$, the infected population are decreasing. The parameter $\omega$ and its effect on the infected population have been shown in Fig. 7. It can be seen that by reducing the value of $\omega$, the infection decreasing. Fig. 8, Fig. 9, Fig. 10 describe the impact of the parameters $\psi$, $\delta$ and $\tau$. With the decreasing of these parameters values, a decreasing trend in the infected compartments is suggested.

Fig. 2.

Model predictions to determine peak of the infection curve.

Fig. 3.

Dynamics of infective compartments.

Fig. 4.

Impact of $\psi$ on infected individuals.

Fig. 5.

Impact of $\tau$ on infected individuals.

Fig. 6.

Impact of $\delta$ on infected individuals.

Fig. 7.

Impact of $\omega$ on infected individuals.

Fig. 8.

Impact of $\psi$ on infected compartments.

Fig. 9.

Impact of $\delta$ on the infected compartments.

Fig. 10.

Impact of $\tau$ on infected individuals.

Conclusion

The third wave of coronavirus in Pakistan has been modeled through a mathematical model. We taking into consideration the infected cases from March 06, 2021 till April 30, 2021. We obtained that the model is locally as well as globally asymptotically stable at ${\mathcal{R}}_0<1$. Further, using the infected reported cases, we determined that the basic reproduction number ${\mathcal{R}}_0\approx 1.2044$. The realistic parameters values obtained through the least square curve fitting method have been used to obtained the numerical results graphically. We simulated the parameters that can effectively decrease the infection and shown it graphically. We observed from the graphical results that the infection can be minimized effectively if the SOPs are follows effectively. We observed from the data and its comparison, and found that the cases in Pakistan can be decreased from May 06, 2021 as shown by the results from our model. This peak is important for any country and determine the maximum populations infected at a particular day. The results obtained in this paper for the Pakistani data can be useful for the health authorities and the decision-making process.

CRediT authorship contribution statement

Xiao-Ping Li: Funding acquisition, Resources, Software, Validation, Writing - review & editing. Ye Wang: Resources, Software, Validation , Writing - review & editing. Muhammad Altaf Khan: Funding acquisition, Resources, Software, Validation, Writing - original draft, Validation, Formal analysis. Mohammad Y. Alshahrani: Validation, Visualization, Writing - review & editing. Taseer Muhammad: Validation, Visualization, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.