Habitat selection by the Spiny-tailed lizard (Uromastyx aegyptia): A view from spatial analysis

Abstract

Many factors affect the habitat selection for animal species, which in turn may greatly affect their distribution in different ecosystems. Understanding the processes that affect habitat selection is also critical for guiding and managing conservation initiatives. Our study aimed to assess the habitat selection by free-ranging Spiny-tailed lizard (Uromastyx aegyptia) by analyzing a geospatial data connecting its burrow parameters to different habitat characteristics within selected sites in Hail region, Saudi Arabia. We examined evidence and patterns of significant spatial clustering for (366) active burrows by linking their parameters (burrow entrance size, burrow entrance width and burrow entrance height), their reference geographical locations and, two habitat characteristics defined by soil type and vegetation cover. The objective of the analysis was to increase the understanding on the burrows aggregation process in the space and, to describe its possible relation to other spatial habitat configurations. Analysis of distances based on the Nearest Neighbor Index (NNI) and hotspots detection in Nearest neighbor hierarchical clustering (Nnh) suggested twelve (12) spatial clusters located within the study area. In addition, a spatial ordinary least square (OLS) and Poisson regression models revealed significant effects of soil type and vegetation cover on burrow parameters (OLS, p < 0.05; Poisson, p < 0.001), which indicate a strong association between burrows parameters and habitats characteristics. Findings from the study also suggest that other factors such as elevations, highways, and human settlement concentration spots could possibly play a major role in defining burrow spatial aggregation and furthermore have a significant impact on habitat selection.

1. Introduction

Animal species select their habitats from different spatial scales based on numerous environmental factors (Mackey and Lindenmayer, 2001, Rodríguez et al., 2007). Therefore, there is a great need to consider the habitat requirements of the species to establish successful management strategies that help prevent species extinction (Morrison et al., 2006). Such information will provide fundamental bases for restore species, identify important ecosystems and protected areas (Sato et al., 2014). However, this information is not always available and knowledge on how species select their habitats is limited for several species (IUCN, 2014).

Research on habitat selection is important for understanding the animal biological strategies they adapted to meet their needs. Additionally, information on pattern of habitat use or selection are critical for conservation and management purposes (Scott et al., 2002, Guisan and Thuiller, 2005). Understanding this behavioral process requires observation of both of the habits of animals in their natural habitats (e.g. burrow parameters) and how they make use of their surrounding environments. For this purpose, many statistical methods, including combination models, were developed to quantify habitat selection (see Manly et al., 2002, Fauchald and Tveraa, 2003, Strickland and McDonald, 2006, Freitas et al., 2008). Generally, these methods use resource selection function, which compare resource attributes in areas where animals are observed and areas where animals are known to be available. Here, we try to incorporate the spatial dimension for habitat selection and how this analysis may possibly yield a useful result that can be implemented in conservation strategies. It is also important to note that spatial data analysis is mainly concern about the data that are spatially located with consideration to their explicit importance in their spatial arrangement.

The key species used in this study, the spiny-tailed lizards of the genus Uromastyx, is spreading across North Africa, Arabia, and the Middle East deserts (Wilms et al., 2012, Tamar et al., 2018). Wilms and Böhme (2007) identified 15 sub-species known to inhabit the open free range of the Arabian Peninsula. The spiny-tailed lizards (Uromastyx aegyptia) had experienced the greatest decline in population size (Wilms et al., 2012). This decline in population could be attributed to several factors (local and global). For instance, there is a high demand from locals because it is edible in their cultures. Changing in land-use policies is an example of the global factors thought to affect the population size of Spiny-tailed lizards negatively. Moreover, excessive hunting has resulted in a significant decrease in their wild population (Wilms et al., 2012). The conservation status, however, clearly appears very unequal across its entire range (Cox et al., 2012).

In our study we used the spatial data analysis to infer habitat selection and demonstrates how this model analysis can: (1) identify habitat characteristics that reflect the burrows aggregation within the study area and, best explaining their differences in parameters; (2) evaluate the significant response to different habitat characteristics (i.e. soil type and vegetation cover) and; (3) how habitat selection can possibly be predicted through variations in burrow parameters. The overall aim of this study is to provide the decision-makers and conservation managers with the essential information required to implement a long-term conservation action plan and to assist in the creation of legislation designed to conserve the species across its natural range.

2. Materials and methods

2.1. Study area and data collection

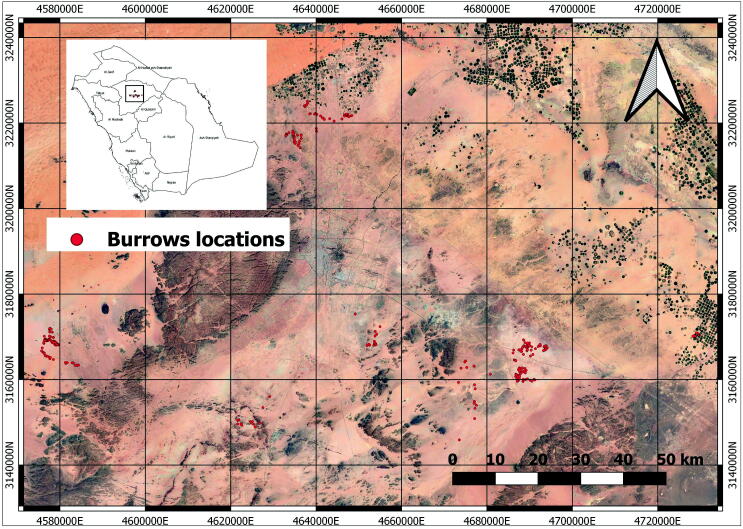
The study was conducted in Hail region, Saudi Arabia (Fig. 1), during the spring and summer of 2013, 2014, 2017, 2018, and 2019. A total of 366 active burrows were identified and recorded in each site locations. A sample route was made at each site by driving a four-wheel car at a speed of 20–30km/h. The detected active burrows were photographed, and their locations were recorded using a handheld GPS device. A burrow was considered active either the spiny-tailed lizard was directly observed, or its fresh marks/tracks were found at the entrance of the burrow. For each active burrow, the following parameters (burrow entrance width, burrow entrance height, soil type, and vegetation cover) were reported (Wilms et al., 2009, Wilms et al., 2010). The soil type was classified into three groups (coarse sand CS, fine gravel FG, and medium gravel MG). At the same time, the following categories of vegetation cover were measured around entrances (vegetation cover 0 < 25% (1), 25 < 50% cover (2), 50 < 75% cover (3) and > 75% cover (4)) within a radius of five meters. After that, the size of each burrow entrance was measured using the equation below:

$$(\mathrm{A})=\pi \ast \mathrm{W}/2\ast \mathrm{H}/2$$

Where: A = size of the burrow entrance in cm², W = entrance width in cm, H = entrance height in cm (see Wilms et al., 2010).

Fig. 1.

Study areas and burrows locations in Hail region, Saudi Arabia.

2.2. Spatial data analysis

2.2.1. Assessing spatial dependence for burrow parameters

The spatial nature of each data value was evaluated by creating a spatial weight matrix based on data value locations. Since several methods for creating spatial weights exist (Anselin and Rey, 2014), the Queen’s Contiguity method was implemented in this analysis. Based on spatial weight matrix, hypothesis of spatial randomness in burrow parameter values was tested using global and local Moran’s I statistical tests. Global Moran's I (Moran, 1950) is widely used to examine the existence of spatial autocorrelation. As suggested by Moran (1948), the model will describe the statistics between a variable and its spatial lag, assuming that random and independent variations exist. Its values vary between −1 and 1. The meaning “1>” signifies perfect positive spatial autocorrelation, while “−1<” indicates perfect negative spatial autocorrelation, and “0” implies perfect spatial randomness (Tu and Xia, 2008). Local spatial autocorrelation was quantified using Local Indicators of Spatial Association (LISA), which calculates the degree of spatial autocorrelation at each particular position by utilizing local Moran's I (Anselin, 2010). LISA may also be used to determine the effect of specific locations on global statistical significance and classify ”outliers“ (see Levine, 2013).

Whilst the global Moran’s I was used to test whether burrows are clustering in across data values in space, local Moran’s I was used to detect locations of spatial patterns (hot and cold spots) and identify significant clusters. Anselin (2010) defined the local Moran statistics as an analysis of local clusters and outliers in space. The local cluster map describes the High and Low-Low spatial clusters where the outliers are labeled in Low-High and High-Low values. As mentioned, positive and negative global Moran’s I statistic indicates a clustering process where similar and dissimilar values are close to each other respectively.

2.2.2. Examining other habitat physical characteristics and processes

We discussed other physical factor such as possible effects of elevation, highways, and human settlement concentration spots as driving factors in habitat selection. In the last part, we also discussed the effect of habitat fragmentation as a possible ecological driver and process could shape the species habitat selection in different ways.

2.3. Data analysis

Spatial data analyses were performed using the functions implemented in GeoDa® (Anselin et al., 2006), CrimeStat IV® (Levine, 2013), QGIS v.3.16.1 (QGIS, 2020) and ArcGIS® Desktop v.10.1 (ESRI, 2011). Other spatial data used in this study were downloaded from DIVA-GIS (https://www.diva-gis.org/), including cities, villages, highways, and elevation values. To achieve our objective, we evaluated our dataset using the following methods that combine both burrow parameter and habitat characteristics: 1) we examined the First-order properties (general spatial distribution) by assessing the variation in burrow parameter values without regards to the location of each sample (test of global Moran's I), 2) Second-order properties (sub-regional patterns) by identifying clusters in Local Moran cluster map, 3) explaining the variation by performing regression analysis using – ordinary least squares OLS and Poisson to examine the spatial relationship and factors behind the observed spatial pattern and, 4) Distance analysis by running the Nearest Neighbor Index (NNI) and detection of hotspots in Nearest Neighbor Hierarchical Clustering (Nnh). Data analysis were performed using the burrow entrance size calculated from the parameters as response, soil type and vegetation cover as explanatory variables.

2.3.1. Model testing

2.3.1.1. Statistical test of robustness of the model

The statistical tests involved testing validity of ordinary least squares (OLS) standard assumptions and spatial dependence in regression residuals. The linear regression analysis is used to find a (linear) relationship between a dependent variable, 'burrow entrance size' and two explanatory (independent) variables: soil type and vegetation cover.

2.3.1.2. Analysis of Poisson regression

Assuming errors are distributed independently, discreetly, and following a Poisson distribution, the Poisson regression was used here to describe the actual distribution of probabilities. Assuming that the mean and variance of the errors are equal, the Maximum Likelihood Estimator (MLE) was used to evaluate Poisson regression using the method implemented in CrimeStat IV.

2.3.1.3. Distance analysis: Nearest Neighbor Index (NNI)

The nearest neighbor index (Clark and Evans, 1954) attempts to compare the distances between nearest points and distances that would be predicted on the basis of chance. This model calculates the distance to the nearest other point (nearest neighbor) with an average of all other points, theoretically, and for each point. If the NNI is less than 1.0, this indicates that the observed average distance is smaller than the mean random distance (i.e., points are closer to each other than would be predicted by chance) and thus suggesting clustering evidence. The function for this analysis was also performed in CrimeStat IV.

2.3.1.4. Hotspot analysis: nearest neighbor hierarchical clustering (Nnh)

The nearest neighbor hierarchical clustering analysis (Nnh) attempts to classify the spatially similar points into groups according to a specific criterion (i.e., burrow parameters in this case). The (Nnh) function routine implemented in CrimeStat works by repeating clustering until all points are either clustered into a single cluster or the clustering fails.

3. Results

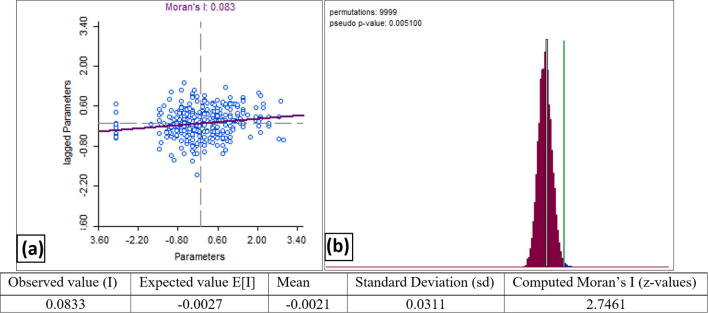
Burrow parameters were plotted in the horizontal (X) axis where their spatially lagged parts in the vertical (Y) axis as shown in Moran scatter plot (Fig. 2a). As shown in the figure, in the top of the plot which is (0.083) is indicated the linear slop that corresponds to global Moran's I value. Again, the scatter plot reveals some outliers which can be found at the high end of the slop line.

Fig. 2.

(a) Moran scatter plot and (b) reference distribution for Moran’s I.

3.1. Assessing significance by reference distribution

By running the randomization option with the number of permutations of (9999) in the Fig. 2a, a pseudo p-value have been generated (p = 0.005) indicating a rejection to our null hypothesis that there is no difference in burrow parameters (Fig. 2b). Right side to the reference distribution, the green line is showing the actual statistics of the data at (0.0.083).

3.2. Significance map

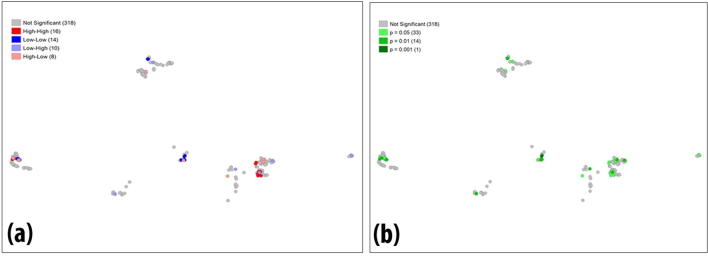
By running the model for (999) permutations and p-value (0.05) for both cluster maps (Fig. 3a), a new map (Fig. 3b) has identified groups of significances ranging from light to dark green corresponding to more spatial associations (dark green) where the p-value is (0.001).

Fig. 3.

LISA (a) cluster and (b) significant maps (Significance level is shown as *P < 0.05, **P < 0.01).

3.3. Regression analysis

3.3.1. Ordinary least squares (OLS) and Poisson regression

Results explained in (Table 1) showing that both soil type and vegetation cover have a significant effect on the parameters of the burrows (P < 0.05). Test of Poisson regression for the model also indicated a strong correlation (Table 1). Test with Maximum Likelihood Estimator (MLE) for both models can be found in (Table 2) respectively.

Table 1.

Regression analysis and Model diagnostics.

Regression analysis
	Predictor	df	Coefficient	St. Err.	Tolerance	t-value	p	Model	*Model p-value
Burrow parameters	Intercept	1	34.280	3.402	–	10.077	0.001	OLS	0.002
	Soil type	1	7.464	1.789	0.957	4.173	0.001
	Vegetation cover	1	11.726	1.680	0.957	6.980	0.001
	Intercept	1	3.645	0.020	–	189.948	0.001	Poisson	0.000
	Soil type	1	0.128	0.009	0.957	14.234	0.001
	Vegetation cover	1	0.194	0.008	0.957	22.682	0.001
Model diagnostics
Test			df	value	Prob.		Type of diagnostic
jarque-bera			2	30.300	0.000		Normality of errors
breusch-pagan test			2	3.577	0.1672		Heteroscedasticity
koenker-bassett test			2	2.100	0.34990
Moran's I (error)			0.072	2.445	0.0145		Spatial dependence
Lagrange Multiplier (lag)			1	6.155	0.0131
Robust LM (lag)			1	7.660	0.0056
Lagrange Multiplier (error)			1	5.350	0.0207
Robust LM (error)			1	6.855	0.0088
Lagrange Multiplier (SARMA)			2	13.010	0.0015

^*see (Table 2).

Table 2.

OLS and Poisson regression models: both tested with Maximum Likelihood Estimator (MLE).

OLS regression model		Poisson regression model
Test	Value	Test	Value
Squared multiple R	0.1735	Likelihood statistics:
Adjusted squared multiple R	0.1695	Log-likelihood	−3916.836
F test of model	40.801	Per case	−10.0175
P-value of model	0.002	AIC	7841.671
Mean absolute deviation:	18.670	Per case	20.055
1st (highest) quartile	30.003	BIC/SC	7857.546
2nd quartile	9.048	Per case	20.096
3rd quartile	8.596	Deviance	5686.654
4th (lowest) quartile	26.774	P-value of Deviance	0.0001
Mean squared predicted error:	607.326	Pearson Chi-Square	4409.026
1st (highest) quartile	1180.847	P-value of Chi-Square	0.000
2nd quartile	118.590	Model error estimates:
3rd quartile	118.640	Mean absolute deviation	19.218
4th (lowest) quartile	999.111	1st (highest) quartile	30.565
		2nd quartile	10.049
		3rd quartile	8.529
		4th (lowest) quartile	27.473
		Mean squared predicted error:	643.043
		1st (highest) quartile	1219.597
		2nd quartile	143.889
		3rd quartile	128.498
		4th (lowest) quartile	1067.074
		Dispersion tests
		Adjusted deviance	14.694
		P-value of Deviance	0.000
		Adjusted Pearson Chi-Square	11.393
		P-value of Chi-Square	0.000
		Dispersion multiplier	10.363
		Z	6.562
		P-value of Z	n.s
		Inverse dispersion multiplier	0.096

3.3.2. Model diagnostics

Regression diagnostics test for both models as explained in (Table 1) showing the p-values for Jarque-Bera and indicating there is no problem with the normality of errors in selected model. Diagnostics for heteroscedasticity, as explained by Breusch-Pagan and Koenker-Bassett tests, are showing larger values than 0.05. Diagnostics test for spatial dependence of the model was performed using Moran’s I score which was significant (0.0725) and indicating strong spatial autocorrelation of the residuals.

3.4. Distance and hotspot analyses

Analysis result of nearest neighbor index as described in (Table 3) indicates a NNI index of (0.0977). Results of Nearest Neighbor Hierarchical Clustering (Nnh) as shown also in (Table 3) indicate (12) clusters found among the areas of study. The results were transferred in QGIS to illustrate those cluster positions (Fig. 4a). We also reported the burrow clustering based on the soil type and vegetation cover within the study area (Fig. 4b&c).

Table 3.

Nearest Neighbor Index (NNI) and Nearest Neighbor Hierarchical Clustering (Nnh) analysis.

Nearest Neighbor Index (NNI)		Nearest Neighbor Hierarchical Clustering (Nnh)
Test	Value	Test	Value
Mean Nearest Neighbor Distance	249.70 m	Likelihood of grouping pair of points by chance	0.500 (50.000%)
Standard Dev of Nearest:		Z-value for confidence interval	0.000
Neighbor Distance	609.31 m	Standard Deviations	1.0
Minimum Distance	2.43 m	Clusters found	12
Maximum Distance	136471.90 m
Mean Random Distance	2555.74 m
Mean Dispersed Distance	5492.44 m
Nearest Neighbor Index	0.0977
Standard Error	69.83 m
Test Statistic (Z)	−33.023
p-value (one tail)	0.000
p-value (two tail)	0.000

Fig. 4.

Clusters as revealed by (a) Nearest Neighbor Hierarchical Clustering (Nnh) method and, the burrow clustering based on (b) soil type and (c) vegetation cover as determined by nearest neighbor analysis.

4. Discussion

Numerous factors contribute to the loss of the species, including habitat destruction, grazing, hunting, and degradation (Sodhi et al., 2009). Rapid increase in human population, urban sprawl and the transition to marginal agricultural and grazing land have been known to change the natural ecosystems and have contributed to the extinction of many species across the globe (Sala et al., 2000, Cardillo et al., 2004). Reptiles are among the most threatened species; nevertheless, limited scientific interest has been given reptile species, particularly in the field of conservation (Böhm et al., 2013, Gibbon et al., 2000). This can be due to that reptiles are considered elusive and inhabit different and difficult habitat types. In the Arabian Peninsula the reptiles were from the least studied species until recently where more species had been described (Sindaco et al., 2013, Sindaco et al., 2014, Šmíd et al., 2013, Badiane et al., 2014, Metallinou et al., 2015, Carranza et al., 2018).

Addressing data gaps is essential to reverse species loss for conservation managers, decision-makers, and management strategies (Morrison et al., 2006). Research in conservation planning in areas where there are still threatening processes working on wild species is therefore highly needed.

This study addressed the question on how animal species choose their habitat based on surrounding environment. We investigated whether burrow parameters and its location preferences vary depending on habitat characteristics, particularly, soil type and vegetation cover at different sites in Hail region, Saudi Arabia. We used three different types of cluster statistics: global, local and distance to scrutinize our hypothesis regarding burrow clustering patterns. Furthermore, we incorporated a spatial dependency analysis by testing the spatial regression using OLS and Poisson regression models.

4.1. Cluster statistics

4.1.1. Global Moran’s I and LISA

Global statistics can define whether spatial structure exists, but cannot identify which cluster it is, nor can it decide whether the clusters differ from one location to another. Earlier spatial pattern tests (like Moran’s I) were global in nature, and provided one statistic, such as a global autocorrelation coefficient, that summarized spatial pattern over the entire sampling sites. Moran’s I can give a global statistic indicating there is clustering going on within the study area but, cannot explain exactly where or how. This pattern can explain the emerged outliers in the scatter plot shown in (Fig. 2).

To investigate deeper, we run local cluster statistics by testing the Local Indicators of Spatial Association (LISA). Local cluster statistics such like LISA (Anselin, 2010) tends to quantify spatial autocorrelation and clustering within the small areas that together comprise the whole study area. It can also reveal the presence of significant spatial clusters or outliers and a testing for regional clustering. Results obtained in (Fig. 3a&b) indicated significant clustering going on at different sites within the study area and supporting our hypothesis.

4.1.2. NNI and Nnh

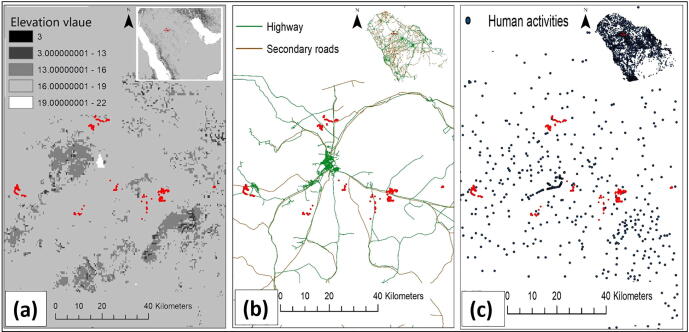
Cluster analysis is a classification method that group objects based on their properties. It recognizes the similarities between observations to group related observations together. As an example, hierarchical clustering method can categorize all observations into groups, and then aligning the groups based on how similar they are. The nearest neighbor distance is also used as an indicator of dissimilarity in the hierarchical clustering (Bailey and Gatrell, 1995). A comparison of the distances between two points (or group of points) and the average distance of all points is the closest neighbor measure, when the distance fulfills a prior criterion (i.e. probabilities of threshold distance) observes are linked into a new class. This process is repeated until all points in a first-order cluster have been assigned. The results of the nearest neighbor index analysis (NNI) and the nearest neighbor hierarchical clustering (Nnh) show strong clustering evidence, suggesting 12 possible clusters within the study area. Here we will drive two potential reasons for such form of clustering pattern observed in our study area based on physical characteristics and human activities within the study area. Physical features such as elevation variations may play a significant deterministic role in habitat selection (Fischer and Lindenmayer 2005). As shown in (Fig. 5a), burrows were located at two different elevation levels, indicating that lower elevation could allow more aggregation and better habitat characteristics (combined with the 'Nnh' results). This can be described in terms of other related elevation variables such as temperature and relative humidity (Wilms et al., 2009, Wilms et al., 2010).

Fig. 5.

A map showing the burrow locations within the study area and across (a) different elevation values, (b) roads and highways and (c) towns and villages.

4.2. Spatial dependency analysis

Based on the results of OLS and Poisson tested models, the burrow parameters can be explained by the soil type and vegetation cover. However, the two explanatory variables used in the model cannot explain the outliers shown in (Fig. 2) (i.e. Moran scatter plot), indicating that other biotic or abiotic factors may shape habitat selection or burrow preference for the spiny-tailed lizards (Jablonski, 2008, Peñalver-Alcázar et al., 2016).

4.3. Habitat fragmentation

As ecological driver and influential factor, habitat fragmentation is a process involving the splitting and discontinuity of preferred habitat for many species (Fahrig, 2003, Rogan and Lacher, 2018). This process is mainly driven by human activities (Barnosky et al., 2012, Elias, 2013). As illustrated in (Fig. 5b&c) combined with Fig. 3a&b, we assumed that the expansion of human activities, roads, cities, villages and highways may have a significant effect on a species' natural habitat (Brehme et al., 2013). Changes in habitat due to fragmentation may shift the range of species by dividing the natural ecosystems into small isolated patches, therefore, we expected these isolate patches to have a potential effect on our species selection for habitat. We suggest a fragmentation-based study that includes genetic information about the animal to better examine this hypothesis and, to highlight the dispersal mechanism and testing the gene flow between and among different sites.

5. Conclusion

In this study we addressed two ecological questions: 1) Where are the hotspots with higher-than-expected proportion of burrows within the study area? and, 2) What is/are the factor(s) contributing to higher-than-expected aggregation. In order to ensure the survival of our key species, further studies are needed to evaluate more variables that might influence Spiny-tailed lizards' habitat selection/preference. Key suggested studies that incorporate genetic investigation, capture-recapture and population assessment could further highlight the current situation of the species within its range. Since the survival of our species depends on their patchy habitats, a solid action plan for long-term conservation is urgently needed. These measures may include: 1) Annual surveys to get the latest information on status and distribution. 2) Inclusion of land use management into land use planning. 3) Conservation needs to understand that spiny-tailed lizards can only thrive in the socio-economic climate of human societies where they share wild terrestrial ecosystems.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.