A novel analytical approach to the prediction of respiratory diaphragm motion based on external torso volume change

Abstract

An analytical approach to predict respiratory diaphragm motion should have advantages over a correlation-based method, which cannot adapt to breathing pattern changes without re-calibration for a changing correlation and/or linear coefficient. To quantitatively calculate the diaphragm motion, a new expandable ‘piston’ respiratory (EPR) model was proposed and tested using 4DCT torso images of 14 patients. The EPR model allows two orthogonal lung motions (with a few volumetric constraints): (1) the lungs expand (ΔV_EXP) with the same anterior height variation as the thoracic surface, and (2) the lungs extend (ΔV_EXT) with the same inferior distance as the volumetrically equivalent ‘piston’ diaphragm. A volume conservation rule (VCR) established previously (Li et al 2009 Phys. Med. Biol. 54 1963–78) was applied to link the external torso volume change (TVC) to internal lung volume change (LVC) via lung air volume change (AVC). As the diaphragm moves inferiorly, the vacant space above the diaphragm inside the rib cage should be filled by lung tissue with a volume equal to ΔV_EXT (=LVC – ΔV_EXP), while the volume of non-lung tissues in the thoracic cavity should conserve. It was found that ΔV_EXP accounted for 3–24% of the LVC in these patients. The volumetric shape of the rib cage, characterized by the variation of cavity volume per slice over the piston motion range, deviated from a hollow cylinder by −1.1% to 6.0%, and correction was made iteratively if the variation is >3%. The predictions based on the LVC and TVC (with a conversion factor) were compared with measured diaphragm displacements (averaged from six pivot points), showing excellent agreements (0.2 ± 0.7 mm and 0.2 ± 1.2 mm, respectively), which are within clinically acceptable tolerance. Assuming motion synchronization between the piston and points of interest along the diaphragm, point motion was estimated but at higher uncertainty (~10% ± 4%). This analytical approach provides a patient-independent technique to calculate the patient-specific diaphragm motion, using the anatomical and respiratory volumetric constraints.

1. Introduction

Four-dimensional radiation therapy (4DRT) is an emerging field of clinical research, aiming to compensate for the target motion so to spare the maximum amount of normal tissue and/or to permit dose escalation to the target, aiming to improve the therapeutic ratio (Shirato et al 2000, Schweikard et al 2000 and 2004, Keall et al 2001 and 2006, Jaffray et al 2007, Li et al 2008). Such clinical objective could be ultimately achieved by target motion tracking (Keall 2004, Keall et al 2005, D’Souza et al 2005) with 100% duty cycle, provided that a real-time monitoring technique is available. Currently, the only clinically viable, real-time imaging of respiratory target motion is x-ray fluoroscopy, which requires implanted fiducials to visualize and quantify the motion (Shirato et al 2000, Schweikard et al 2000, Seppenwoolde et al 2002), as well as delivers an extraneous radiation dose to patients. Using implanted fiducials with the megavoltage treatment beam may eliminate the additional radiation (Wiersma et al 2008), depending upon anatomical sites. Owing to the lack of suitable real-time motion monitoring techniques in the clinic, alternative approaches (Keall et al 2006), such as respiratory gating using respiratory surrogate (Jiang 2006), has become a clinically viable option with substantially reduced duty cycle, as well as grossly approximated target localization (Korreman et al 2008).

Characterization of target motion without implanted fiducials has become clinically possible through 4D computed tomography (4DCT) imaging (Vedam et al 2003a, Low et al 2003, Keall et al 2004, Rietzel et al 2005b). Patient-specific motion models can be derived from 4DCT to provide a pre-defined target motion trajectory (Keall et al 2005, Rietzel et al 2005a, Zhang et al 2007). In a 4DCT simulation, breathing irregularity may occur, reducing the fidelity of the respiratory model. Amplitude-based 4DCT reconstruction is more preferable with higher tolerance of the irregularity than phase-based reconstruction (Lu et al 2006) and dual respiratory surrogates seem necessary (Mutaf et al 2007, Li et al 2009). From the 4DCT simulation to daily treatments, breathing patterns may change, reducing the reliability of the respiratory model. Therefore, it is questionable to assume that a patient breathes in exactly the same pattern over the course of multi-fractional treatment (Chi et al 2006, Yan et al 2006, Killoran et al 2008, Korreman et al 2008). Although these breathing irregularities and pattern variations could be eased by respiratory coaching (Kubo and Wang 2002, Neicu et al 2006), they cannot be eliminated. Some reports showed no significant difference with or without respiratory coaching (Vedam et al 2001, Mageras and Yorke 2004). Hence, it has become a focus of clinical research to fill in the gap between the 4D simulation and 4D treatment.

Respiratory surrogates based on point fiducial height, tension change or airflow variation have been used for retrospective 4DCT image reconstruction, as well as for real-time target motion tracking in 4DRT treatment delivery (Keall et al 2006, Jaffray et al 2007, Li et al 2008). The most widely employed methodology in the clinic is correlation-based prediction using fiducial surrogates, such as the real-time position management (RPM) system. The diaphragm motion can be projected (predicted) by assuming a linear external–internal response, which requires patient-based calibration (or quality assurance, QA) to determine the correlation, linear coefficient and possible phase shift (Vedam et al 2001 and 2003b, Schweikard et al 2004, Gierga et al 2005, Ionascu et al 2007). Owing to variations in marker placement location, patient abdominal pressure, as well as patient breathing pattern, the use of fiducials has limitations (Mageras and Yorke 2004), including low inter-fractional reproducibility (Hoisak et al 2004, Chi et al 2006, Yan et al 2006, Killoran et al 2008, Korreman et al 2008). Although the tidal volume measured by spirometry has shown a superior correlation with the diaphragm motion compared with the fiducial-based correlation (Hoisak et al 2004), significant baseline drift, potential air leakage and inconvenience limit the use of spirometry in the clinic (Low et al 2003, Lu et al 2005b, Ha et al 2008).

Recently, a volumetric approach was reported to predict tidal volume, by establishing a volume conservation rule (VCR), in which the external torso volume change (TVC) reflected the lung air volume change (AVC) with a one-to-one ratio (uncertainty <±3%) during quiet respiration (Li et al 2009). One distinct advantage of the analytical approach over the correlation approaches was that the external–internal one-to-one relationship is patient independent, eliminating the need for patient-based calibration and the dependence of breathing patterns.

In this paper, we extended the volumetric approach to predict the diaphragm displacement during free breathing. A novel expandable ‘piston’ respiratory (EPR) model was proposed with assumptions that (1) the diaphragm moves like a ‘piston’ inside the rib cage, (2) the lungs expand anteriorially with the same height variation as the thoracic surface, and (3) the lungs extend inferiorly the same distance as allowed by the lung extension volume. 4DCT torso images of 14 patients were acquired, and both the EPR model and the VCR rule were applied in this study. The predicted and measured diaphragm displacements were compared with excellent agreements. The motion of points of interest along the diaphragm was further estimated with the assumption of motion synchronization, but with higher uncertainty.

2. Methods and materials

2.1. A volume conservation rule linking external–internal volumetric changes

The VCR rule, which was previously reported (Li et al 2009), indicates that the external TVC (ΔV_Torso) equals to the lung AVC (ΔV_Air) during quiet respiration. Based on this rule, the external TVC predicts the internal AVC:

$$\mathrm{\Delta }{V}_{\text{Torso}}\cong \mathrm{\Delta }{V}_{\text{Air}},$$ (1)

and the relationship between the AVC and lung volume change (LVC, or ΔV_Lung) is established by lung density correction between a respiratory stage X and reference stage 0 (full exhalation):

$$\mathrm{\Delta }{V}_{\text{Lung}}=\mathrm{\Delta }{V}_{\text{Air}}+\left(\mathrm{C}{\mathrm{T}}_{\text{Lung}}^X\cdot V_{\text{Lung}}^X-\mathrm{C}{\mathrm{T}}_{\text{Lung}}^0\cdot V_{\text{Lung}}^0\right),(X=1,2,\dots ,12),$$ (2)

where CT_Lung and V_Lung are the CT number and volume of the lung, respectively.

In this study, the quantity of interest is the LVC, which can be estimated from the AVC using a conversion factor (k), which is respiratory stage dependent. However, the variation is small (<5%), so a stage-averaged conversion factor (〈k〉) is introduced:

$$\langle k\rangle =\frac{1}{10}\cdot \sum _{X=2}^{11}\left(1+\frac{{\text{CT}}_{\text{Lung}}^X\cdot V_{\text{Lung}}^X-{\text{CT}}_{\text{Lung}}^0\cdot V_{\text{Lung}}^0}{\mathrm{\Delta }{V}_{\text{Air}}}\right).$$ (3)

All respiratory stages are used except the two (or three) stages at or near full exhalation. A patient-averaged conversion factor ($\overline{\langle k\rangle }=1.11\pm 0.03$, from table 1) is used to estimate the LVC:

$$\mathrm{\Delta }{V}_{\text{Lung}}\approx \overline{\langle k\rangle }\cdot \mathrm{\Delta }{V}_{\text{Air}}\cong \overline{\langle k\rangle }\cdot \mathrm{\Delta }{V}_{\text{Torso}}.$$ (4)

The calculated LVC is slightly underestimated (~2%) for stages near full inhalation, while slightly overestimated (~2%) for stages near full exhalation. Two methods can be used to calculate the LVC: one is based on 4DCT image segmentation, while the other is based on the TVC using equation (4), and the results are compared.

Table 1.

Characterization of patient-specific, respiration-related features. The breathing pattern is quantified using two volume ratios: the external ((tVC/TVC)^Max) and the internal ((ΔV_EXP/ΔV_Lung)^Max). The stage-averaged conversion factor $(\langle \overline{k}\rangle =1.11\pm 0.03)$ is approximately a constant for all patients. From the reference ‘piston’ position (0 mm) to a displacement (ΔZ = 15 mm), the volume variation (α = (V₁₅−V₀)/V_7.5) smaller than 3% is considered a cylindrical rib cage, while three patients (#6, #9 and #11) have conically shaped rib cages (>3%). For up to 30 mm motion range, an approximate linear volume increase was found (R² = 0.95). Equation (11) or (12) was used for calculating diaphragm displacement, depending on the volumetric shape.

Patient	Gender	Breathing pattern descriptors		〈LVC/AVC〉		Volume of the rib cage (cm3/slice)			(V15–V0)/V7.5 (%)
		(tVC/TVC)Max (%)	(ΔVEXp/ΔVLung) Max (%)	〈k〉	σk	0 (mm)	7.5 (mm)	15.0 (mm)
1	M	10.0	6.7	1.13	0.04	59.09	59.50	59.99	1.5
2	M	19.9	8.1	1.15	0.07	61.87	62.01	61.89	0.0
3	M	31.4	12.3	1.08	0.04	69.61	70.32	70.93	1.9
4	F	8.9	7.3	1.12	0.08	46.13	46.74	46.61	1.0
5	F	10.3	5.6	1.11	0.03	41.79	42.27	42.23	1.0
6	M	2.7	2.8	1.14	0.07	63.41	65.99	67.34	6.0
7	M	8.3	6.0	1.11	0.07	49.98	50.63	51.31	2.6
8	F	16.7	7.1	1.10	0.05	42.08	42.77	43.02	2.2
9	M	17.5	10.3	1.09	0.05	70.21	72.03	73.06	4.0
10	F	14.0	15.3	1.07	0.05	38.58	38.54	38.16	−1.1
11	M	6.2	2.9	1.13	0.05	64.86	67.47	68.39	5.2
12	M	45.8	24.1	1.14	0.08	57.30	57.80	57.93	1.1
13	M	16.1	9.4	1.16	0.19	51.85	52.37	52.99	2.2
14	M	23.1	8.3	1.06	0.04	41.06	41.48	42.03	2.4
Average		16.5	9.0	1.11	0.07	54.13	54.99	55.42	0.02
St. Dev.		11.3	5.5	0.03	0.04	11.06	11.56	11.88	0.02

2.2. Amplitude-based 4DCT imaging and image segmentation

Fourteen patients’ torso 4DCT images are acquired using a 16-slice CT scanner (Philips Medical, Bothell, WA) with both the bellows and spirometry as respiratory surrogates. Special efforts are made to minimize residual motion artifacts in the 4DCT images, including (1) entire torso scan (~464 slices) with 1.5 mm slice thickness, (2) dual surrogates for measuring the pseudotidal volume, (3) redundant (25) scans with low (40) mAs for each abutting section in cine mode, (4) amplitude-based retrospective sorting in 12-stage bins and (5) nearly quietcent breathing during image acquisition as the patients are pre-instructed to maintain normal breathing. Details of the 4DCT imaging conditions can be found in previous publications (Lu et al 2006, Li et al 2009).

A customized treatment planning system is used for image analysis. The volumes of external torso and internal lung are calculated based on a voxel-counting algorithm using different thresholds (⩽ −350 HU for lung and all HU for body) within body contour, which is segmented using an edge-tracing algorithm with a threshold of −350 HU and 2x erosion-dilation smoothing. The torso is defined anatomically from the clavicles to pubic bone. The lung range is defined from the first to the last slices that contained segmented lungs. The diaphragm range is defined from the first superior slice, in which the apex of the diaphragm is segmented (location 1 in figure 1(B)), to the inferior ends of the lungs (location 2 or 3 in figure 1(B)). The right and left lungs are processed separately. The full-exhalation stage CT is used as the reference for calculating the LVCs and diaphragm displacements.

Figure 1.

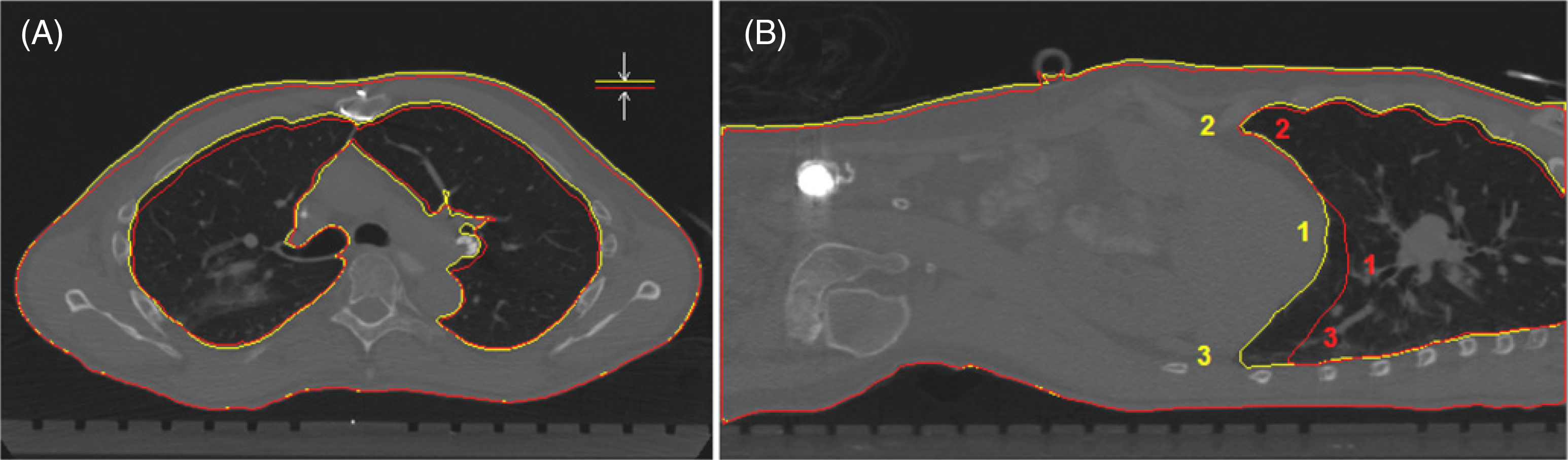
Demonstration of the similarity between thoracic surface height variation and anterior lung height variation. Torso and lung contours in full-exhalation (red) and full-inhalation (yellow) stage CTs of a patient in supine position. (A) The axial view also shows that lateral width variations of the lung and body are small. (B) The sagittal view illustrates the unevenness of diaphragm motion, as well as three locations (1, 2 and 3) that are used for calculating the position and displacement of the averaged diaphragm and individual points.

To calculate the thoracic cavity volume, excluding all tissues (lung and non-lung) inside the rib cage, a semi-automatic segmentation procedure is utilized. Non-lung tissues are temporarily assigned with the lung CT number at the interface with the rib cage using a paint brush, topologically isolating the chest wall from the interior. Then the thoracic cavity is automatically segmented, as shown in figure 3. The thoracic cavity volume per slice is calculated and averaged over three consecutive slices.

Figure 3.

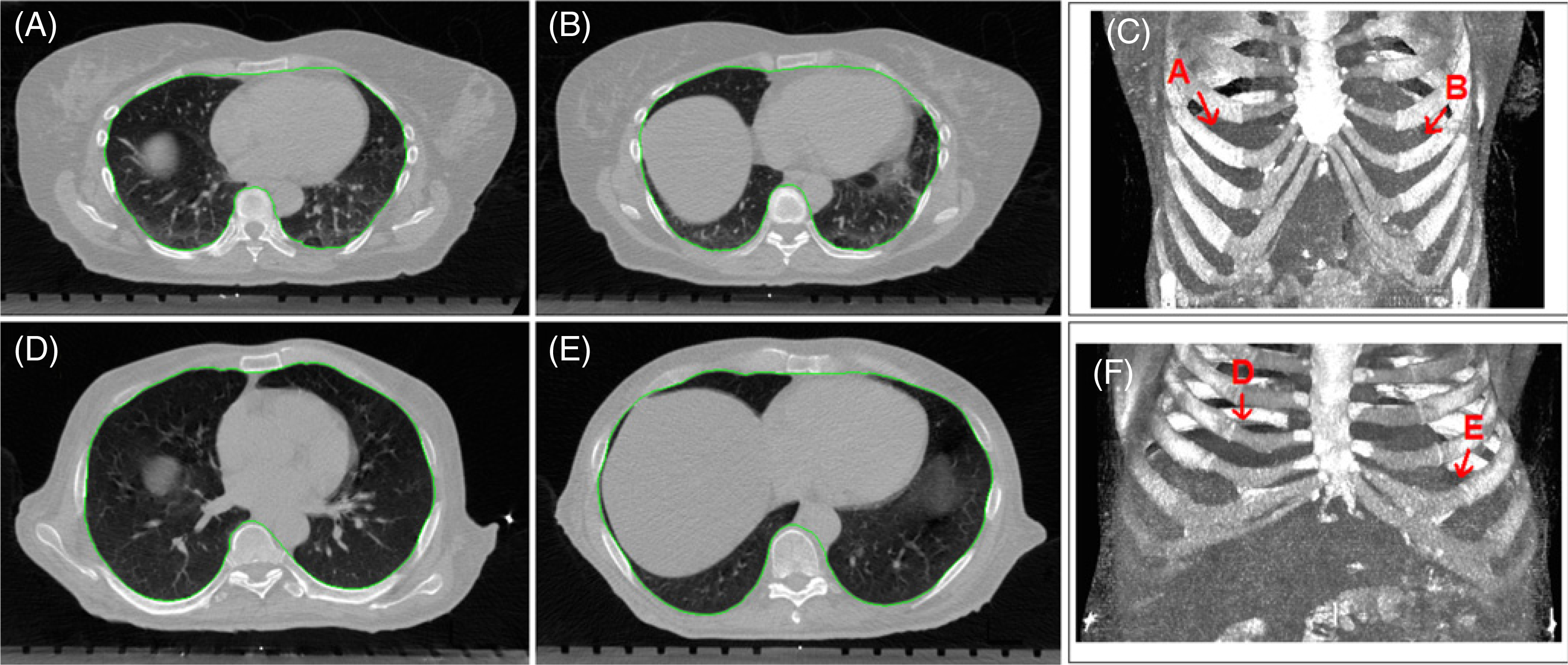
Two examples of cylindrical and conical rib cages and segmentation (green) of thoracic cavity inside the rib cages. The top-row images (A)–(C) show a cylindrical rib cage (patient #8) and the bottom-row images (D)–(F) show a conical rib cage (patient #9). The axial images (A), (B), (D) and (E) are at the top of the diaphragm interfaced with the right or left lungs, and the volumetric images (C) and (F) show the rib cage and the position of apex of the left and right diaphragms.

2.3. An expandable ‘piston’ respiratory (EPR) model for predicting diaphragm motion

The EPR model is proposed for predicting diaphragm displacement within the rib cage, as shown in figure 2. Two major orthogonal lung motions are allowed: (1) posterior–anterior (PA) expansion and (2) superior–inferior (SI) extension.

Figure 2.

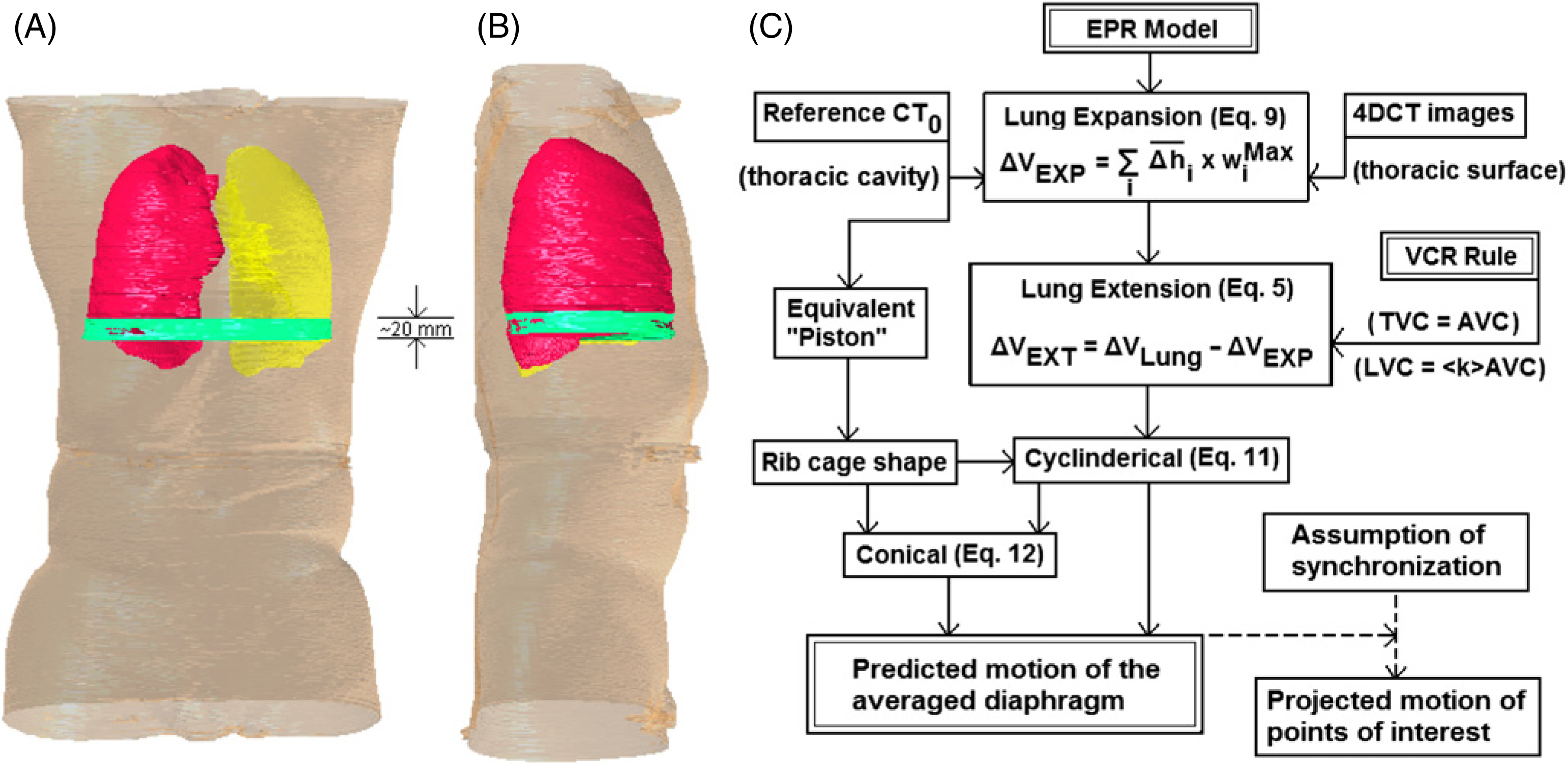
Illustration and description of the expandable piston respiratory (EPR) model. (A) and (B): the piston (equivalent diaphragm) motion range (green) of 1.5–3.0 cm in the superior–inferior (SI) direction is overlaid to the full-exhalation stage CT (right lung in red and left lung in yellow) in frontal and sagittal views. A cylindrical volumetric shape within the piston motion range (green) is shown. (C): the flow chart for calculating the diaphragm motion using the EPR model and the VCR rule, together with patient-specific data inputs (or volumetric constraints). With the assumption of motion synchronization, the motion of points of interest at or near the diaphragm can be projected.

For lung expansion, it is assumed that the well-known thoracic skin height variation during respiration can be directly translated into the lung height variation in the PA direction. In other words, the tissue anterior to the lungs is assumed to have a constant thickness on average, as shown in figure 1(A). Laterally, although there is a slight lung width change due to respiration, it causes negligible volume variation (estimated as 5–10% of the PA volume variation). The lung expansion volume (ΔV_EXP) can then be calculated based on the reference CT and external thoracic surface variation. The lung extension volume (ΔV_EXT) is obtained by subtracting the ΔV_EXP from the LVC (ΔV_Lung) at a certain respiratory stage (X):

$$\mathrm{\Delta }{V}_{\text{EXT}}^X=\mathrm{\Delta }{V}_{\text{Lung}}^X-\mathrm{\Delta }{V}_{\text{EXP}}^X,(X=1,2,\dots ,12).$$ (5)

For lung extension, it is assumed that the piston position can be estimated by the average of six pivot points (one superior apex and two inferior nadirs on each lateral side) of the diaphragm, as shown in figure 1(B). The SI displacement (~1–3 cm) of the diaphragm generates a vacant space within the rib cage with a volume that should be equal to the ΔV_EXT. Therefore, the vertical (SI) extent of the empty space should predict the diaphragm displacement:

$$\mathrm{\Delta }{V}_{\text{EXT}}^X=V_{\text{Cavity}}^{\text{Cylinder}}\cdot \mathrm{\Delta }{Z}^X,(X=12,\dots ,12),$$ (6)

where $V_{\text{Cavity}}^{\text{Cylinder}}$ is cylindrical cavity volume per slice, and ΔZ^X is the piston displacement at stage X. It is worthwhile to mention that only lung tissue should be used to fill the empty cavity while the volume of non-lung tissues conserves. More details are discussed in the following sections.

2.4. Lung expansion and extension volume calculation

Based on the observation of 14 torso 4DCT images, as shown in figure 1, it was assumed that the averaged lung expansion in the PA direction is the same as the averaged thoracic surface elevation in any lung-containing slice of the 4DCT images. In any respiratory stage (X), the average height variation $\left(\overline{\mathrm{\Delta }{h}_i}\right)$ of the thoracic surface in a slice (i) can be calculated by the body area variation (ΔA_i) divided by the maximum external thoracic width (L_i^Max), namely,

$${\left(\overline{\mathrm{\Delta }{h}_i}\right)}^X={\left(\frac{\mathrm{\Delta }{A}_i}{L_i^{\mathrm{Max}}}\right)}^X,(X=1,2,\dots ,12).$$ (7)

The lung expansion volume (ΔV_i) can be estimated from the maximum width of the lungs (w_i^Max = w_iR^Max + w_iL^Max) multiplied by the height variation $\left(\overline{\mathrm{\Delta }{h}_i}\right)$ and the slice thickness (t):

$${\left(\mathrm{\Delta }{V}_i\right)}^X={\left(\overline{\mathrm{\Delta }{h}_i}\right)}^X\cdot w_i^{\text{Max}}\cdot t,(X=1,2,\dots ,12).$$ (8)

So, the overall lung expansion volume (ΔV_EXP) is the sum of all lung-containing slices (N) in reference to the full-exhalation CT image:

$$\mathrm{\Delta }{V}_{EXP}^X=\sum _i^N{\left(\mathrm{\Delta }{V}_i\right)}^X=\sum _i^N{\left(\overline{\mathrm{\Delta }{h}_i}\right)}^X\cdot w_i^{\text{Max}}\cdot t,(X=1,2,\dots ,12).$$ (9)

Then, the lung extension volume (ΔV_EXT) can be calculated using equation (5).

2.5. Equivalent diaphragm position and volumetric shape of the rib cage

The diaphragm position can be determined quantitatively in the reference CT using a volume-weighted average (⟨Z⟩) of the diaphragm, which is equivalent of the inferior edge of the lungs. Such an average defines the piston position with a volume-equivalent, inferiorly flat lung within the rib cage:

$${\langle Z\rangle }^0={\left(\frac{{\sum }_{n=1}^N{V}_i\times Z_i}{{\sum }_{n=1}^N{V}_i}\right)}^0,$$ (10)

where i, N, V_i and Z_i are the slice index, number of slices, lung volume and SI position, respectively. The left and right diaphragms were processed separately, and then averaged.

The diaphragm may move ΔZ(~10–30 mm, from table 2) inferiorly during respiration. The volumetric shape of the rib cage (‘cylindrical’ or ‘conical’) within this motion range from ⟨Z⟩ to ⟨Z⟩+ΔZ is critical, since the volume of vacant space is a function of the thoracic cavity, as shown in figure 3. To determine the volumetric shape of the cavity, a plot of cavity volume per slice versus slice position is generated, providing volume change rate (α = ΔV/V_middle within the motion range). A cylindrical rib cage has small α (<3%), while a conical rib cage has large α (⩾3%), which necessitates a correction (see section 2.7).

Table 2.

Comparison of the predicted and measured diaphragm motions in the respiratory cycle. The motion ranges (ΔZ_M^Max and ΔZ_P^Max), stage-averaged difference (〈dΔZ〉, equation (15)), the standard deviation (σ_ΔZp−ΔZm) and relative standard deviation (σ/ΔZ_P^Max) are listed. Two methods of calculation are employed using the LVC (equation (2)) or the TVC (equation (4)) with the patient-averaged conversion factor ($\overline{\langle k\rangle }=1.11\pm 0.03$, from table 1). Close agreements between the predicted and the measured diaphragm motions are found for both the methods.

Patient	Measured ΔZMMax (mm)	Prediction using ΔVLung (mm)				Prediction using 〈kΔ ΔVTorso (mm)
		Predicted ΔZPMax (mm)	〈dΔZ〉	σ ΔZp−ΔZm	(σ/ΔZPMax) (%)	Predicted ΔZPMax (mm)	〈dΔZ〉	σ ΔZp−ΔZm	(σ/ΔZPMax) (%)
1	15.25	14.56	−1.38	1.02	7.0	13.06	−1.86	1.12	8.5
2	15.50	15.37	0.09	0.74	4.8	15.49	0.52	0.88	5.7
3	15.50	14.47	0.40	1.82	12.6	14.39	−0.87	1.99	13.8
4	8.50	8.90	0.21	0.48	5.4	10.86	1.47	0.72	6.6
5	18.00	18.25	−0.44	0.64	3.5	19.94	0.22	1.22	6.1
6	10.75	11.42	0.76	0.71	6.2	11.89	1.57	0.76	6.4
7	15.25	15.39	−0.27	0.55	3.6	14.78	0.19	0.66	4.4
8	13.75	13.83	0.95	0.47	3.4	12.57	0.35	0.94	7.4
9	29.00	29.62	0.36	2.97	10.0	32.95	1.30	1.92	5.8
10	13.25	13.49	−0.01	0.41	3.0	13.78	−0.24	0.51	3.7
11	15.75	15.15	0.34	0.90	5.9	13.81	−1.95	1.08	7.8
12	13.00	10.41	−0.87	1.30	12.5	10.22	−0.68	1.45	14.2
13	10.50	13.07	0.99	0.87	6.6	13.97	1.39	1.17	8.4
14	8.50	9.61	0.99	0.77	8.0	9.38	0.77	0.64	6.8
Average	14.46	14.54	0.2	1.0	6.6	14.79	0.2	1.1	7.6
St. Dev.	5.07	5.04	0.7	0.7	3.2	5.83	1.2	0.5	3.1

2.6. Volume conservation for non-lung tissues inside the thoracic cavity

Both the respiratory and cardiac motions make non-lung tissues in the thoracic cavity move and deform in a manner constrained by the conservative volume. In other words, the volume of non-lung tissues is a constant regardless the respiratory stage, assuming that (1) there is a dynamic equilibrium of the blood flow in and out the thoracic cavity, (2) the patients are not swallowing anything, including air, and (3) their esophagus is empty or no food passes and no reflux during scanning. In addition, the shape of the rib cage in the diaphragm region is assumed to have little change during quiet respiration. Therefore, in the EPR model, the empty space generated by the SI motion of the ‘piston’ inside the rib cage should be filled with lung tissue only.

2.7. Diaphragm displacement prediction with the rib-cage volume constraint

In the case of a cylindrical rib cage, the equation for calculating diaphragm displacement can be obtained by combining equations (5) and (6). At a stage X, it can be expressed as

$$\mathrm{\Delta }{Z}_{\text{Predicted}}^X=\left(\frac{\mathrm{\Delta }{V}_{\text{EXT}}^X}{V_{\text{Cavity}}^{\text{Cylinder}}}\right)\cdot t,(X=1,2,\dots ,12),$$ (11)

where ΔV_EXT, $V_{\text{Cavity}}^{\text{Cylinder}}$ and t are the lung extension volume, the cylindrical cavity volume per slice inside the vacant space and the slice thickness, respectively.

In the case of a conical rib cage, a numerical iterative approach is applied with the initial value taken from the above equation. As the cavity volume changes with the piston displacement, a linear volume increase rate per displacement (α′) is used to project the average cavity volume. The iterative equation $\left(\mathrm{\Delta }{Z}^{J+1}=f\left(\mathrm{\Delta }{Z}^J\right)\right)$ can be expressed as

$${\mathrm{\Delta }{Z}_{\text{Predicted}}^X|}_{j+1}=\left(\frac{\mathrm{\Delta }{V}_{\text{EXT}}^X}{\mathrm{\Delta }{V}_{\text{Inserted}}^{\text{Cylinder}}+{0.5\cdot {\alpha }^{\prime }\cdot \mathrm{\Delta }{Z}_{\text{Predicted}}^X|}_j}\right)\cdot t,(X=1,2,\dots ,12).$$ (12)

The denominator represents the adaptive volume of the conical rib cage at the piston position. The stopping criterion was set as (ΔZ^J+1 – ΔZ^J) < 0.1 mm.

2.8. Comparison of predicted and measured diaphragm displacements

Six points (three on each lateral side) are used to calculate the average diaphragm position and its displacement, as shown in figure 1(B). This average position represents key anatomical locations in the right–left and anterior–posterior sides, accounting for some deformation. The measured displacement (ΔZ_Measured) is the position difference in the SI direction (Z) between a stage (X) and the reference stage (0):

$$\mathrm{\Delta }{Z}_{\text{Measured}}^X={\left(\frac{1}{6}\cdot \sum _{j=1}^3\left(z_j^R+z_j^L\right)\right)}^X-{\left(\frac{1}{6}\cdot \sum _{j=1}^3\left(z_j^R+z_j^L\right)\right)}^0,(X=1,2,\dots ,12).$$ (13)

The residual differences between the predicted and the measured at any respiratory stage are

$$\text{d}{(\mathrm{\Delta }Z)}^X=\mathrm{\Delta }{Z}_{\text{Predicted}}^X-\mathrm{\Delta }{Z}_{\text{Measured}}^X,(X=1,2,\dots ,12).$$ (14)

The stage-averaged diaphragm displacement (〈dΔZ〉) with standard deviation can also be used to evaluate the ‘goodness of fit’ of the two motion curves for a patient:

$$\langle \text{d}\mathrm{\Delta }Z\rangle =\frac{1}{12}\cdot \sum _{X=1}^{12}\text{d}{(\mathrm{\Delta }Z)}^X.$$ (15)

2.9. Comparison of predicted and measured point motion at the diaphragm

Based on the predicted diaphragm motion, the motion of any point of interest at or near the diaphragm can also be predicted, assuming that the point moves in synchronization with the diaphragm and has a measurable motion range (Δz^Max). The point displacement at any stage (X) in the respiratory cycle can be calculated as

$$\mathrm{\Delta }{z}_{\text{Predicted}}^X=\beta \cdot \mathrm{\Delta }{Z}_{\text{Predicted}}^X=\left(\frac{\mathrm{\Delta }{z}^{\mathrm{Max}}}{\mathrm{\Delta }{Z}^{\mathrm{Max}}}\right)\cdot \mathrm{\Delta }{Z}_{\text{Predicted}}^X,(X=1,2,\dots ,12),$$ (16)

where β = Δz^Max/ΔZ^Max is the linear coefficient, and ΔZ^Max is the motion range of the diaphragm. The discrepancy between the predicted and the measured at any respiratory stage is

$$\text{d}{(\mathrm{\Delta }z)}^X=\mathrm{\Delta }{z}_{\text{Predicted}}^X-\mathrm{\Delta }{z}_{\text{Measured}}^X,(X=1,2,\dots ,12).$$ (17)

Similarly, the stage-averaged point motion discrepancy (〈dΔZ〉) can be defined as

$$\langle \text{d}\mathrm{\Delta }z\rangle =\frac{1}{12}\cdot \sum _{X=1}^{12}\text{d}{(\mathrm{\Delta }z)}^X.$$ (18)

3. Results

3.1. Compensating for lung expansion volume in the posterior–anterior direction

The height variation of a patient’s thorax on the skin between two respiratory stages is roughly the same as that of the anterior lung surface, as shown in figure 1. The change in lung area in the anterior direction accounts for the primary difference in the axial images, while in the lateral direction it is negligible (<5–10% of the anterior variation). Table 1 shows the ratio of the maximum ΔV_EXP over the maximum V_Lung, indicating the contribution of the lung expansion to the tidal volume. This is a more precise descriptor of the breathing pattern than the estimation based on external volumes (tVC/TVC) (Li et al 2009). The thoracic respiratory expansion among the 14 patients is diverse, ranging from 3% to 24%. In other words, the lung extension consumes 76–97% of the tidal volume.

3.2. Cylindrically or conically shaped rib cages among patients

The reference diaphragm position is calculated using a volume-weighted average, which provides a volumetrically equivalent reference ‘piston’ position for the full-exhalation CT, as shown in figure 2. Table 1 shows three thoracic cavity volumes at the reference piston position and within the common motion range. This volume variation serves as an indicator of the shape of the rib cage within the motion range. Three patients (6, 9 and 11) show 6.0%, 4.0% and 5.2% volume increase, suggesting a conical rib cage, while the remaining patients have an approximately cylindrical rib cage (α < 3%). For the conically shaped rib cages, the increase in the volume as a function of displacement is linear (R² > 0.95). Figure 3 shows a representative cylindrical and conical rib cage, in axial as well as 3D views.

3.3. Comparison between the predicted and the measured diaphragm motion

Figure 2(C) illustrates the procedure for calculating the diaphragm displacement based on the EPR model, together with the VCR rule. Table 2 shows the comparison between the measured and two predicted diaphragm displacements. The maximum displacements (from 8.5 to 29 mm) are in excellent agreement. The stage-averaged residual errors among patients are 0.2 ± 0.7 mm and 0.2 ± 1.1 mm, based on the LVC and TVC, respectively. The relative errors are 6.6 ± 3.2% and 7.6 ± 3.1%, respectively. Figure 4 shows four examples of the predicted and measured diaphragm motion trajectories as a function of respiratory stage. These curves are similar to one another in both shape and amplitude. Figure 5 shows two examples of improved calculation using the conical shape correction. The residual error distributions of the LVC-based and TVC-based calculations are shown in figure 6: the latter is slightly broadened due to the uncertainties in both the VCR rule and the approximation of the conversion factor.

Figure 4.

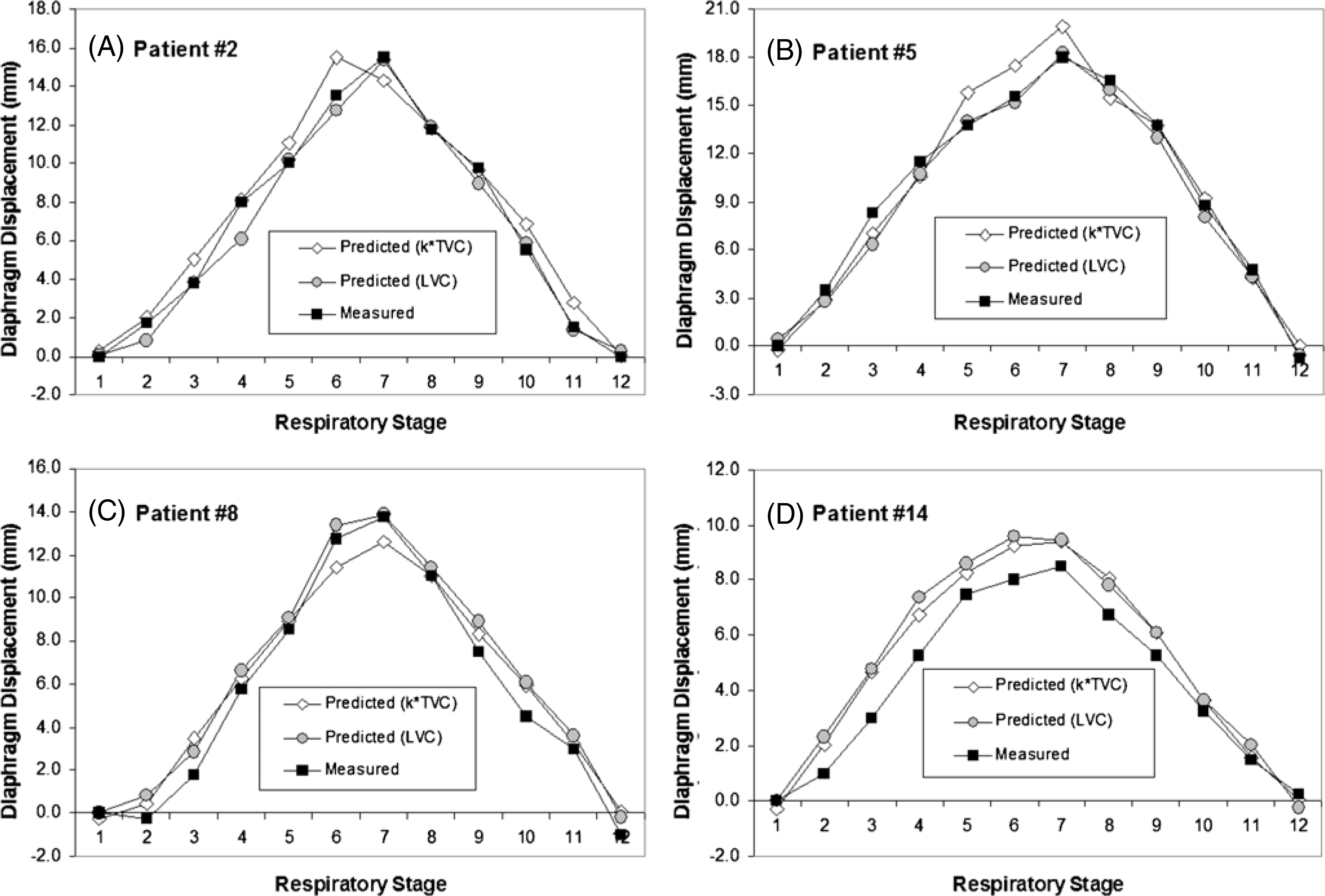
Four examples of the diaphragm motion trajectories measured from 4DCT and predicted using the TVC and the LVC. The prediction based on the LVC is superior to that based on the TVC in most cases.

Figure 5.

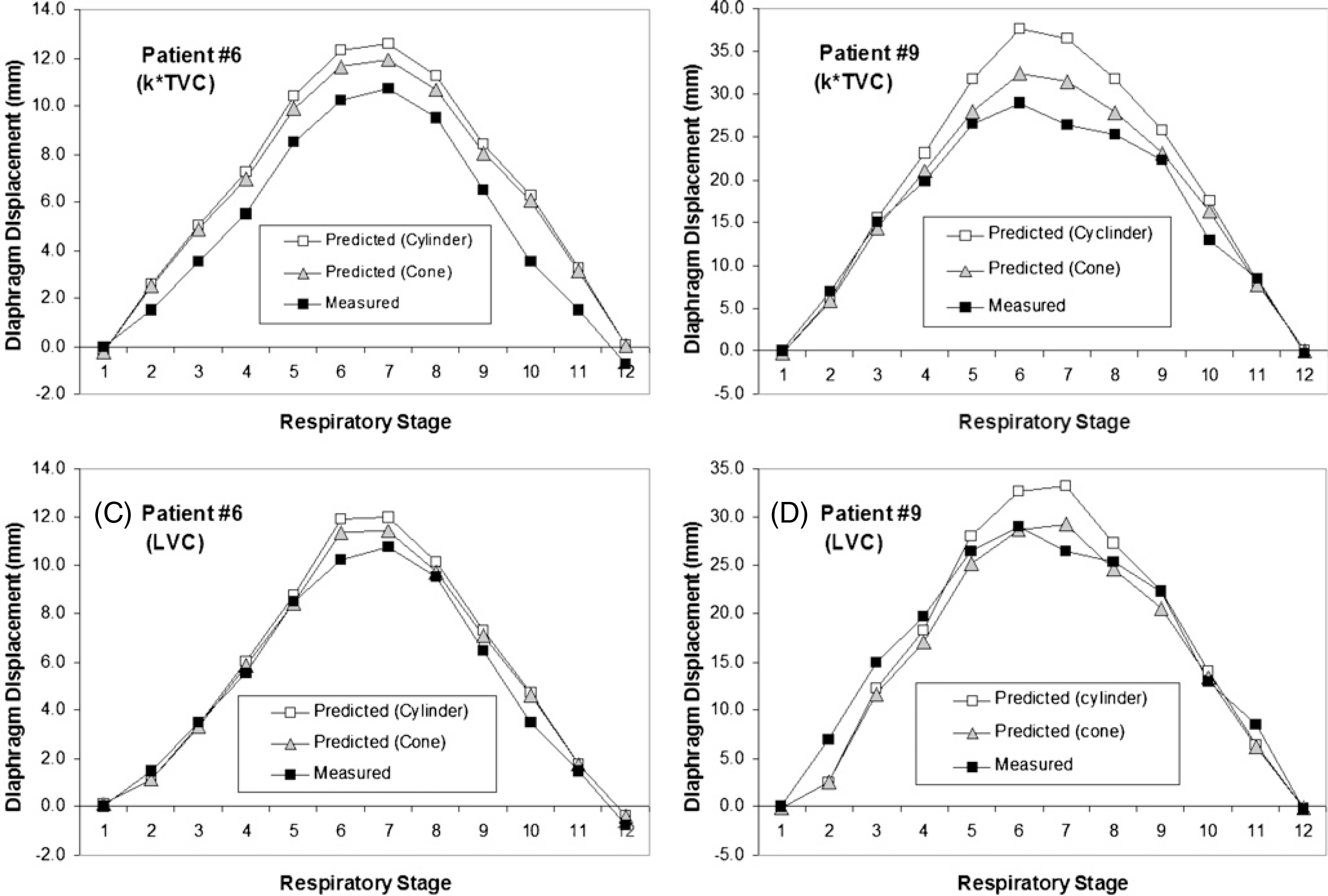
Two examples of correlation of the cone-shape rib cage in the diaphragm displacement calculation within the respiratory cycle. After the volumetric shape correction, the predicted diaphragm motion is improved using the LVC and the TVC methods in comparison with the measured curve.

Figure 6.

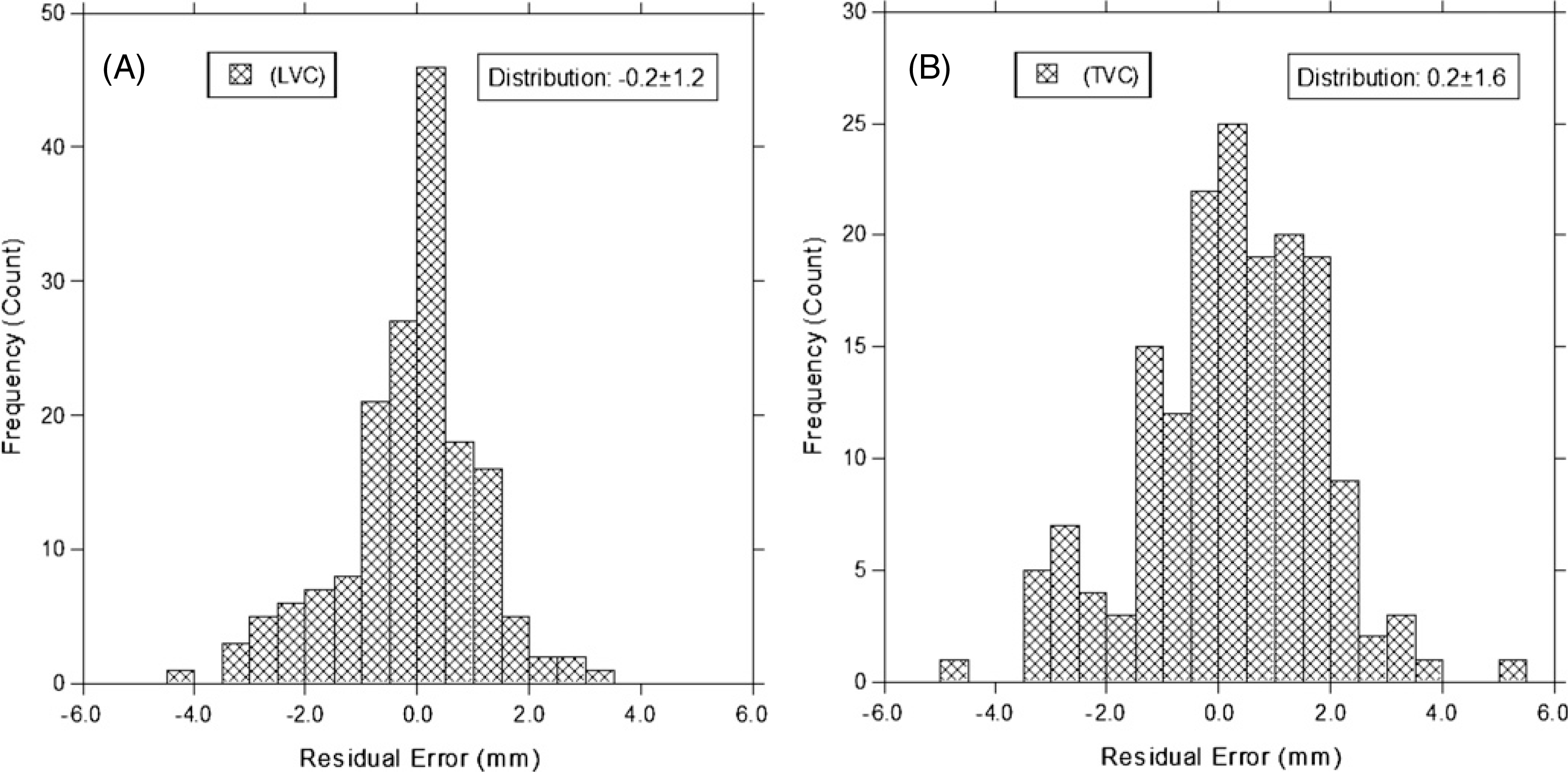
Residual error histograms (between the prediction and the measurement) for the LVC method (−0.2 ± 1.2 mm) and the TVC (0.2 ± 1.6 mm) method. The data of all respiratory stages in all patients are used in these two plots.

3.4. Motion prediction of points of interest with known motion range

The motion ranges and residual errors for six locations (figure 1(B)) at the diaphragm are shown in table 3. A diverse diaphragm motion range was shown in these six locations, ranging from 1.5 mm (location 2) to 63 mm (location 3) with an average close to those at location 1. Four out of 84 points shows a stage-averaged residual error larger than 2.0 mm, while 12 points have a standard deviation larger than 3 mm. However, the residual error for the points at the apex of the diaphragm (location 1) is ~0.0 ± 0.7 mm among all patients. At location 2, 27 out of the 28 points have a stage-averaged discrepancy within 2.0 mm. The larger motion range (up to 63 mm) for points at location 3 has larger discrepancy, relatively about 10% ± 4%. For some patients, the points at location 2 or 3 appear to have phase shift (violating the synchronization assumption), resulting in the observed high discrepancy.

Table 3.

Comparison of the predicted and measured displacements for six points along the diaphragm. The points (1–3 in figure 1(B)) in the right and left sides have heterogeneous motion range (Δz^Max). The patient-specific diaphragm motions (table 2 and figures 4 and 5) are utilized to predict the motion of these points using equation (16), assuming motion synchronization. The stage-averaged difference (dΔz), equation (18)) and standard deviations (σ) between the predicted and the measured are shown. Out of the 84 points, 4 points (5%) have the stage-averaged discrepancy >2.0 mm, and 12 points (14%) have a standard deviation >3 mm.

Patient	Three points at right (R) lung/diaphragm									Three points at left (L) lung/diaphragm
	Point #1(R)			Point #2(R)			Point #3(R)			Point #1(L)			Point #2(L)			Point #3(L)
	ΔzMax	〈dΔZ〉	σ	ΔzMax	〈dΔZ〉	σ	ΔzMax	〈dΔZ〉	σ	ΔzMax	〈dΔZ〉	σ	ΔzMax	〈dΔZ〉	σ	ΔzMax	〈dΔZ〉	σ
1	15.0	−1.2	1.3	10.5	−0.4	1.2	24.0	−2.1	3.6	19.5	0.8	2.1	15.0	−1.9	3.1	25.5	−0.6	4.2
2	15.0	1.2	1.5	1.5	0.2	0.9	34.5	−2.1	3.0	16.5	0.7	1.9	7.5	1.0	2.0	19.5	1.3	1.5
3	18.0	−0.2	2.2	3.0	0.6	1.7	39.0	−1.6	5.9	15.0	0.1	2.2	7.5	0.0	1.7	24.0	0.6	5.9
4	15.0	0.9	1.7	6.0	0.4	1.5	21.0	−1.5	2.3	6.0	−0.6	0.8	6.0	0.9	0.8	9.0	0.0	1.4
5	24.0	−0.6	1.9	16.5	−1.0	1.4	28.5	−1.7	2.9	16.5	−1.9	1.3	9.0	−0.6	0.9	19.5	−1.7	1.6
6	12.0	0.3	0.7	4.5	0.4	1.7	22.5	−0.2	1.8	10.5	0.6	1.0	10.5	0.2	0.9	12.0	0.3	1.6
7	16.5	1.1	2.1	6.0	0.1	1.1	28.5	0.4	1.4	15.0	−0.1	0.9	12.0	1.5	1.6	16.5	1.1	1.5
8	15.0	−0.8	1.7	10.5	0.1	2.2	24.0	0.9	2.4	13.5	0.3	0.9	13.5	1.5	1.6	15.0	0.2	1.3
9	22.5	−0.7	1.4	4.5	0.3	2.1	63.0	−2.0	5.7	28.5	−0.8	1.2	9.0	−0.7	0.7	52.5	−3.7	4.3
10	13.5	−0.4	0.9	10.5	−0.1	1.1	15.0	−0.5	0.8	16.5	−0.5	0.9	13.5	−0.6	1.1	12.0	−0.2	0.8
11	19.5	−0.3	1.9	18.0	−0.6	3.2	22.5	−0.7	2.3	13.5	−0.3	2.2	19.5	−0.1	3.0	13.5	0.6	2.0
12	12.0	−0.2	1.4	10.5	2.6	5.5	36.0	0.2	3.3	12.0	−0.6	0.9	9.0	0.3	4.5	31.5	1.6	4.0
13	12.0	−0.1	0.9	6.0	−0.5	1.2	12.0	−0.5	1.2	10.5	0.2	1.1	13.5	0.2	1.4	15.0	−0.7	1.8
14	7.5	0.5	0.8	1.5	−0.2	0.4	10.5	0.3	1.1	9.0	0.1	0.9	7.5	1.1	1.2	15.0	0.0	1.3
Average	15.5	0.0	1.5	7.8	0.1	1.8	27.2	−0.8	2.7	14.5	−0.1	1.3	10.9	0.2	1.8	20.0	−0.1	2.4
St. Dev.	4.4	0.7	0.5	5.1	0.8	1.3	13.3	1.0	1.6	5.4	0.7	0.5	3.7	1.0	1.1	11.1	1.3	1.5

4. Discussion

4.1. Accuracy of the diaphragm displacement prediction

As demonstrated in both table 2 and figure 6, the uncertainty in the prediction of diaphragm motion based on the TVC is ⟨σ⟩ = 1.1 mm, ranging from 0.5 to 2.0 mm, over the 14 patients studied. Relatively, it is about 7%. This accuracy is within a clinically acceptable tolerance, as the uncertainty is below that of the current image-guided patient setup (<±3 mm). The cumulative accuracy is attributed to all steps in the volumetric prediction process, including 4DCT imaging, image segmentation, volume calculation, the VCR rule, as well as the EPR model.

Residual motion artifacts in the 4DCT were observed around the diaphragm and in abutting sections at the abdomen (Li et al 2009), due to patient’s breathing irregularity despite the use of dual-surrogates (Mutaf et al 2007), multi-scans in cine mode (Pan 2005), as well as amplitude-based sorting with 12 bins (Lu et al 2006). The torso segmentation showed an uncertainty of <±1 cm³ and the inclusion of foreign objects (tubes and bellows) resulted in an uncertainty of <±10 cm³ (Li et al 2009). However, these uncertainties are small (~2–3%) provided that the tidal volume is approximately 500 cm³.

The VCR rule, which links the TVC to the LVC via the AVC, was estimated to have an uncertainty of about 2–3%, depending upon the pressure variation within the lungs and the gastrointestinal tract (Li et al 2009). The conversion factor $\overline{\langle k\rangle }$ averaged over all respiratory stages and all patients shows σ ≈ 6% (in table 1), contributing primarily to the difference between the LVC-based and TVC-based calculations and the broadening of the residual error distribution, as shown in figure 6.

The EPR model is an approximation of the actual respiratory motion relying on five major assumptions: (1) the anterior expansion of the lungs can be estimated using average skin height variations, (2) the thoracic region of interest can be estimated using the equivalent piston motion range, (3) the non-lung tissues in the thoracic cavity conserve volume, (4) the diaphragm position can be represented by six key points at three locations on the right and left diaphragm domes, and (5) the thoracic cavity volume remains constant in the diaphragm motion range and can be calculated from the reference CT image. The shape of the patient-specific rib cage, whether cylindrical or conical, has been accounted for in the diaphragm displacement calculation. The average relative uncertainty of the results, as shown in both table 2 and figure 6, is within 8% for all patients, and the overall discrepancy of the predicted diaphragm motion is ~2 mm, which is clinically acceptable.

Based on the error propagation theory, the general cubic-root relationship from volume to distance possesses high error tolerance in volume measurements, producing a more accurate calculation in distance. Here, the prediction from the LVC to the diaphragm displacement appears to be error forgiving, resulting in the surprisingly high accuracy of the motion prediction.

4.2. Point motion estimation based on the predicted diaphragm motion

This study shows preliminary results for a linear projection of the motion from the average diaphragm to points of interest along the diaphragm, assuming that the two internal motions are synchronized. A mild phase shift was observed in a few cases, where the point motion was lagged or advanced to the average, resulting in a relatively large error. Although some results in table 3 have a standard deviation larger than 3 mm, their motion ranges are significantly larger than that of the diaphragm itself (averaged). As a matter of fact, more than half of the points at location 3 (as shown figure 1(B)) have range of motion larger than 30 mm (up to 63 mm for patient #9 who has a dramatic tidal volume of ~1700 cm³). For points at location 1, however, the patient-averaged residual errors are 0.0 ± 1.5 mm and −0.1 ± 1.3 mm on the right and left lateral sides, respectively. The top of the diaphragm is readily identifiable in 4DCT and AP fluoroscopic images, but the locations 2 and 3 are only identifiable in 4DCT images. The different motion ranges among locations 1, 2 and 3 suggest different muscle engagements in different areas of the diaphragm, causing deformable motion. For points with small motion range less than 15 mm, the discrepancy is less than 2 mm, while for points with large motion range between 15 mm and 63 mm, the averaged relative uncertainty is about 10%.

The assumption of motion synchronization is equivalent to linear motion correlation without phase shift. The motion range is measured from 4DCT, serving as patient-based calibration for the linear coefficient. Fundamentally, this estimation of point motion relies on the assumed correlation, similar to the existing fiducial-based approaches. So, it reflects the disadvantage of the correlation-based approach, including possible greater uncertainty of the prediction due to breathing irregularity and breathing pattern variation. The synchronization assumption, although reasonable, might not hold true for all points along the highly deformable diaphragm. In fact, phase shifts are present in some of the points, resulting in high uncertainty (table 3).

It is expected that similar results may apply to other locations in the vicinity of the diaphragm, such as the lower lobes of the lungs and a superior portion of the liver. Point motion becomes more difficult to predict in regions distal to the diaphragm (Mageras et al 2001, Ozhasoglu and Murphy 2002) as it is affected by other factors, including local anatomical structures (bronchi and blood vessels), as well as unrelated motions (cardiac and digestive motions) (Seppenwoolde et al 2002). Thus, the assumption of motion synchronization is expected to fail, so that different approaches should be considered. This is an on-going investigation, in which the predicted diaphragm motion will be utilized as an input for predicting the target motion.

4.3. The analytical (volumetric) approach versus correlation-based approaches

Many studies have reported a correlation between external fiducial and internal organ motions (Vedam et al 2003b, Hoisak et al 2004, Mageras and Yorke 2004, Lu et al 2005b, Keall et al 2006). The respiratory response of these point- or line-based fiducials was location dependent and could contain a phase shift, due to anatomical deformation. An ideal PRM reflector placement was reported to be in the mid-point between the umbilicus and the xyphoid (Vedam et al 2003b), although other places were also used, as well as multiple fiducial locations on patient’s lower thorax or upper abdomen (Yan et al 2006, Baroni et al 2007). Even if the marker locations could be reproduced among fractions, the change in a patient’s breathing pattern could likely alter the abdominal height variation (Mageras and Yorke 2004). Therefore, the point-based correlation may be disrupted, resulting in an unreliable prediction. In contrast, the volumetric approach eliminates the dependence on fiducial location and is free from phase shift (Li et al 2009), since the volumetric response of entire torso (both thorax and abdomen) accounts for tissue motion as well as deformation. The EPR model can adapt to the variation of lung expansion and extension, predicting the diaphragm motion in rhythm with the patient-specific breathing pattern as it progresses and/or changes.

Vedam et al (2003b) found a strong correlation between the RPM signal and the diaphragm motion observed under x-ray fluoroscopy. Five patients were observed over multiple treatment sessions. The first session was used to ‘calibrate’ a linear model, which was used to predict the diaphragm motion (σ = 1 mm) in the subsequent sessions. By comparison, the volumetric approach predicted diaphragm motion trajectory with a similar range of uncertainty (⟨σ⟩ = 1.0–1.1) with a clinically acceptable tolerance of ~2 mm. This accuracy was limited by the precision of the ground truth: the 4DCT images have slice thickness (1.5 mm) and possible residual motion artifacts at the diaphragm and the mid-abdominal region (Li et al 2009). However, the volumetric method predicts the diaphragm motion analytically, while the correlation methods predict the relative motion, which requires patient-based calibration to determine the correlation, linear coefficient and potential phase shift. Furthermore, inter-fractional breathing baseline shifts may diminish the benefit of respiratory gating (Korreman et al 2008). Therefore, the advantages of the volumetric approach are that it provides quantitative motion prediction (1) without the need of patient-based calibration and (2) without the influence of breathing pattern variation.

4.4. Potential clinical implications of diaphragm displacement prediction

It is possible to adapt an optical-based surface imaging (OSI) technique to provide real-time torso surface information for this volumetric method to predict internal diaphragm motion. Up to this time, optical surface imaging has only been mostly used for the patient setup (Djajaputra and Li 2005, Bert et al 2006) and respiratory gating based on external–internal correlation (Schoffel et al 2007). As discussed above, the correlation-based approach (either RPM or OSI) requires patient-based QA using internal fiducials and x-ray radiographic imaging (Jiang 2006), which may not be practical in the clinics. Even if patient-based QA is performed, the respiratory pattern may vary during the multi-fractional treatment course, jeopardizing the usefulness of the correlation-based respiratory gating techniques (Korreman et al 2008). This study has established a novel volumetric technique to predict the motion of the diaphragm analytically, which is fundamentally different from the correlation-based predictions. It is an on-going study on the feasibility of using the OSI to provide the TVC from the external torso surface in real time and feed the EPR model and VCR rule for diaphragm motion prediction (as shown in figure 2(C)). Modifications of existing OSI systems seem necessary for this proposed clinical application.

5. Conclusion

This study proposed and evaluated an expandable ‘piston’ respiratory (EPR) model for predicting the diaphragm motion. The expansion and extension of lungs were taken into account separately, and various volumetric constraints were applied based on the external torso surface variation, the full-exhalation stage CT anatomy, and the previously reported volume conservation rule (VCR). The stage-averaged discrepancy between the predicted and measured diaphragm motions was within 2 mm for all patients studied. The motion of points of interest along the diaphragm could be estimated assuming a synchronized motion, but at higher uncertainties (~10% ± 4%). Further investigations are necessary to translate the diaphragm motion to the target motion for clinical 4DRT applications.