Estimation of the critical external heat leading to the failure of lithium-ion batteries

Abstract

A detailed experimental investigation on the critical external heat leading to the failure of lithium-ion (Li-ion) batteries was conducted using an Accelerating Rate Calorimeter (ARC) at the National Institute for Occupational Safety and Health (NIOSH). Several types of commercial Li-ion batteries were selected for the study, including an iron phosphate Li-ion battery (LFP), a lithium-titanate battery (LTO), and a lithium-nickel-manganese-cobalt-oxide battery (NMC). Each battery was placed in a specially designed sealed steel canister and heated in the ARC. Battery voltage throughout the test was monitored and used to indicate the time to a battery failure. Three thermocouples, one attached to the battery surface, one measuring air temperature inside the canister, and one attached to the canister’s internal surface, were used to record temperature changes during the heating tests. Different thermal behaviors were observed for the various battery types. An analytical model was developed to estimate the total external heat received by the battery using the measured temperatures. Experimental data ranked the batteries tested in terms of the heat to failure as: LFP 26650 (11 kJ) > LFP 18650 (4.3 kJ) > NMC 18650 MH1 (3.6 kJ) ≈ LTO 18650 (3.6 kJ) > NMC 18650 HG2 (3 kJ). Total heat normalized to the battery nominal energy capacity was also calculated and ranked as: LTO 18650 ≈ LFP 26650 ≈ LFP 18650 > NMC 18650 MH1 ≈ NMC 18650 HG2. The test and analysis method developed can be extended to other types of batteries with a cylindrical shape. Results from this work provide insights to the thermal safety of Li-ion batteries and can help enhance battery thermal design and management.

1. Introduction

The thermal safety of lithium-ion (Li-ion) cells has been an increasing concern due to their ever-growing number of applications, from consumer electronic products to large electrical vehicles. Li-ion battery-powered electric vehicles (BEVs) are also an important alternative to diesel-powered devices in the mining industry. The potential use of Li-ion BEVs in gassy underground mines poses unique fire and explosion hazards [1]. Methane-air mixtures are found in coal, salt, copper, uranium and other types of mines, and the energy released during Li-ion battery failure and thermal runaway can be a potential ignition source for such mixtures [2, 3]. A more reliable Li-ion battery and its safe use can help reduce the risks of fire and explosion accidents in underground mines.

Many studies have been performed to investigate the thermal stability of Li-ion batteries. When the external heat applied to a battery exceeds its operating limit, chemicals inside the battery will start to react. Generally, a Li-ion battery will undergo several chemical transformation processes under heat abuse [4–6]: solid electrolyte interphase (SEI) layer decomposition, which has been reported to start at a temperature as low as 69 °C [7], anode material and electrolyte reaction, cathode material and electrolyte reaction, electrolyte decomposition, and anode material and binder reaction. Exothermal chemical reactions will release energy and heat the battery further until thermal runaway occurs.

Abraham et al. [8] conducted Accelerating Rate Calorimetry tests on 18650-type Li-ion batteries and found that self-heating started at 84 °C. Wang et al. [9] studied the combustion behavior of 50 Ah LiFePO4/graphite batteries from external radiation and found that the thermal runaway occurs when battery surface temperature reaches 126.7 ± 2.2 °C. Jhu et al. [10] reported the thermal instability properties (initial exothermic temperature, self-heating rate, maximum temperature, etc.) of LiCoO₂ and Li(Ni_1/3Co_1/3Mn_1/3)O₂ of batteries using an adiabatic calorimetry test method. FM Global studied the flammability of Li-ion batteries in bulk storage and the effectiveness of a sprinkler fire suppression system [11]. Quintiere described a calorimetry technique to measure the energetics of a Li-ion battery in thermal runaway [12] and was able to investigate the dynamics of a battery’s thermal performance, including the time events, temperature, mass loss, and energies. The thermal runaway of a cylindrical Li-ion battery was experimentally studied using an Accelerating Rate Calorimeter [13]. Three stages of reactions were identified, and pressure and temperature change were used to indicate each stage. Thermal modeling of cylindrical Li-ion batteries has also been conducted to investigate their heat transfer characteristics and thermal behaviors under various conditions, i.e., charging, discharging and heat abuse [14–15].

Fire calorimeter tests were performed in several studies to investigate the heat release rate and total heat released from a burning Li-ion battery. Chen [16] investigated the thermal hazards of cylindrical 18650 LiCoO₂ and 18650 LiFePO₄ batteries under different states of charge (SOC), and found that the total heat release from a combusting battery increases with SOC. Larsson et al. [17] studied the LFP 26650 battery burning characteristics and calculated the normalized total heat release per energy capacity, estimated at 30 kJ/Wh for a pack of nine batteries. Chen et al. [18] studied the heat release of different configurations of battery packs and found that the total heat released from fires varied linearly with the number of cells.

Much of the previous work on the thermal stability of Li-ion batteries has been focused on the effects of temperature on the internal chemical reactions and their subsequent consequences. Battery temperature, as a convenient parameter, does provide important information on the battery thermal safety. However, the battery thermal safety is also a function of the heating mode and heat duration. From the perspective of energy balance, the amount of external heat that will lead to the abnormal battery behaviors is also important information that has rarely been reported in the literature. Total heat received by the battery is a combined parameter of the heating power, duration and heating mode. Thus, it could be a good representative of the battery thermal stability. In this paper, experimental investigations were performed to look at the critical external heat that leads to the failure of several types of Li-ion batteries using Accelerating Rate Calorimeter. The amount of time for the battery voltage to drop to zero was taken as the time to battery failure. Temperature measurements were recorded for the battery surface and external heat sources. An analytical model for the evaluation of the heat transfer between the heat source and the battery was developed and used to estimate the critical amount of external heat that leads to the failure of the battery. Normalized heat to failure using battery electrical energy capacity was also calculated and compared to assess the thermal performance of the batteries tested. The results from this paper provide new information on battery thermal behaviors and can be used to improve the thermal design of a Li-ion battery under heat abuse.

2. Experiments

2.1. Selected batteries

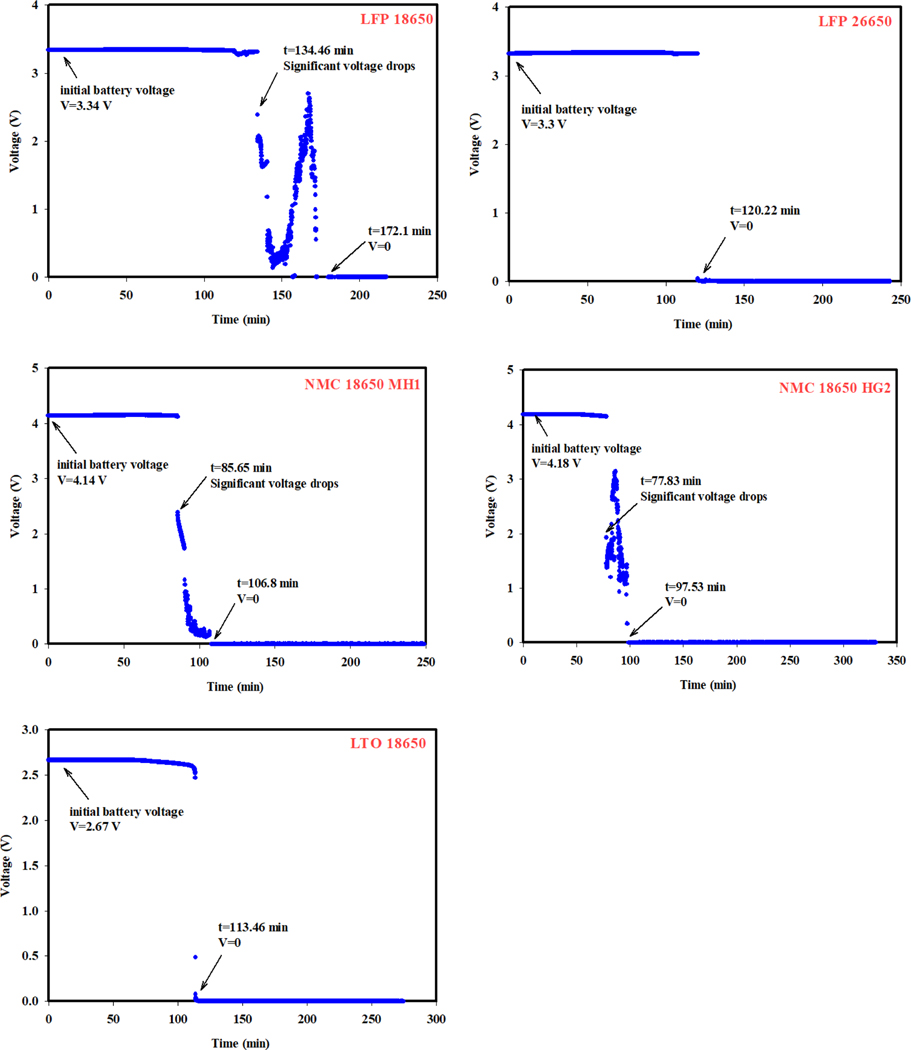
Five types of commonly used commercial Li-ion batteries were selected for the study: iron phosphate lithium-ion (LFP) batteries with two sizes, 18650 and 26650 (18650 means the cylinder is 18 mm in diameter and 65 mm in length; 26650 means the cylinder is 26 mm in diameter and 65 mm in length), two types of lithium-nickel-manganese-cobalt-oxide (NMC) 18650 batteries which use lithium-nickel-manganese-cobalt as a cathode and graphite as an anode (the proportion of the metal oxide mixtures in the cathode of the two NMC batteries is not open information), and lithium-titanate (LTO) 18650 batteries which use lithium titanate for an anode and lithium manganese oxide as a cathode. The LFP battery uses a lithium ferro-phosphate (LiFePO4) cathode and a graphite anode. The two types of NMC batteries have different rated capacities and were noted as NMC 18650 MH1 and NMC 18650 HG2. Among the batteries selected, LFP batteries is primarily used for stationary storage due to its stability, NMC batteries are viewed as the ideal material for electric cars with its high capacity, LTO batteries are widely used in mobile medical devices [19]. Table 1 lists the pretest parameters of the tested batteries. Prior to testing, the batteries were conditioned with three charge-discharge cycles and then charged to 100% state of change (SOC) using an Arbin Multi-channel Potentiostat/Galvanostat (MSTAT) system following battery manufacturer-specific parameters.

Table 1.

Parameters of the tested batteries

Battery type	Weight (g)	Measured/Rated capacity (Ah)	Measured/Nominal voltage (V)	Measured/nominal energy capacity (Wh)
LFP 18650	41.8	1.605/1.5	3.34/3.2	5.36/4.8
LFP 26650	84.1	3.048/3.2	3.32/3.2	10.12/10.24
LTO 18650	38.6	1.278/1.3	2.67/2.4	3.41/3.12
NMC 18650 MH1	45.7	3.076/3.2	4.14/3.7	12.73/11.84
NMC 18650 HG2	46.9	2.985/3.0	4.18/3.6	12.48/10.8

2.2. Accelerating Rate Calorimeter

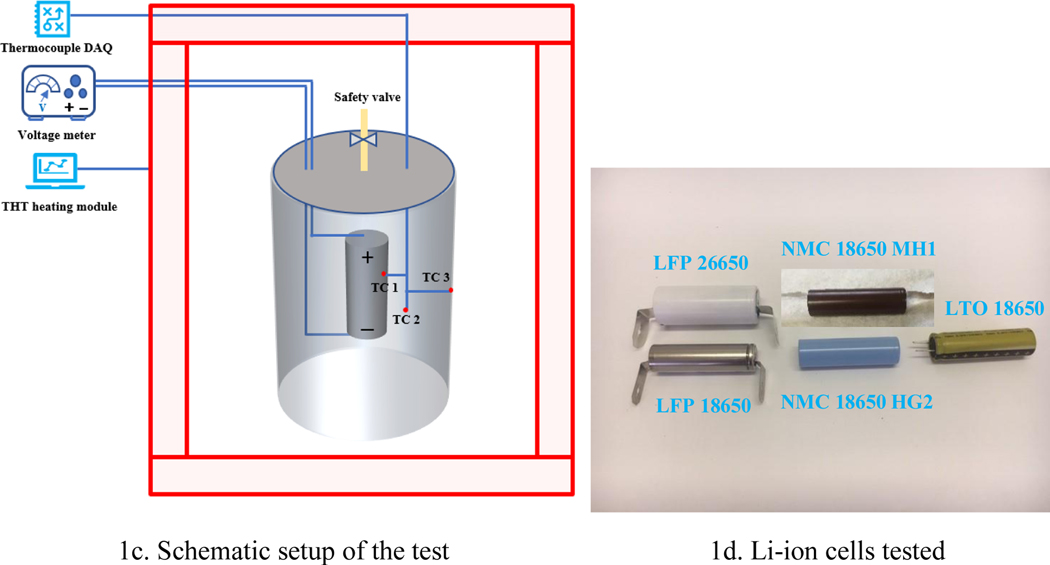
Figure 1a shows the EV+ Accelerating Rate Calorimeter (ARC, Thermal Hazard Technology (THT), Bletchley, UK) that was used to conduct the battery thermal tests. The ARC is cylindrical with a diameter of 40 cm and a depth of 44 cm. Several heaters were installed within the ARC to provide a maximum temperature of 305°C with a measuring sensitivity of 0.05 °C/min. Thermocouples embedded in the ARC lid, walls, and bottom recorded the temperature of the ARC. During the tests, the heating power of the ARC is set to 70% of its maximum, which is 7 kW per its using requirements. Calibrations were conducted on a regular basis to ensure there is no temperature drift during tests. The heating power of the ARC was kept the same for all the tests.

Figure 1.

Lab photo and schematic setup of the battery thermal test

2.3. Holding canister

Inside the ARC, a specially designed cylindrical steel canister was used to contain the battery, shown in the Figure 1b. The canister was made of black steel with a 9.7-cm diameter and 17.4-cm height. The side-wall thickness was approximately 0.3 cm. The inside surface of the canister was painted with flat black stove paint so that the heat transfer process from the canister wall to the battery could be treated as black body radiation. Multiple holes were drilled on the canister cap for compression fittings to facilitate temperature and voltage measurements inside the canister. Canister seal integrity was checked prior to ARC tests using a manometer and a pneumatic hand pump. The canister was positioned in the center of the ARC.

2.4. Temperature and voltage measurement

For each test, one Li-ion battery was positioned in the center of the canister. The external plastic cover of the battery was removed, this is to avoid that when the battery is heated in the ARC, the external plastic cover will be melted and forming a layer of protection, thus influencing the heat transfer to the battery. The outside metal surface was painted using flat black stove paint so that the emissivity of the battery surface can be taken as one and the calculation of the radiative heat transfer can be simplified. Wire leads were attached to both ends of the battery for voltage measurements. Three N-type thermocouples with a bead diameter of 0.5 mm, one attached to the battery surface (TC 1), one inside the canister measuring the air temperature (TC 2), and one attached to the canister inside wall (TC 3) were used to record the temperature data. For the two thermocouples attached to the battery and the canister wall, cares were taken to make sure they did not fall during the ARC heating. The ARC temperature was raised to a constant value to provide steady-state heating. Temperature and voltage data were recorded until the battery went into thermal runaway. Room temperature was approximately 20 °C. Each battery test was repeated twice to ensure test repeatability, and uncertainty analyses were performed in section 3.6. The schematic setup of the experiments is shown in Figure 1c.

3. Results and Discussion

3.1. Detection of battery failure

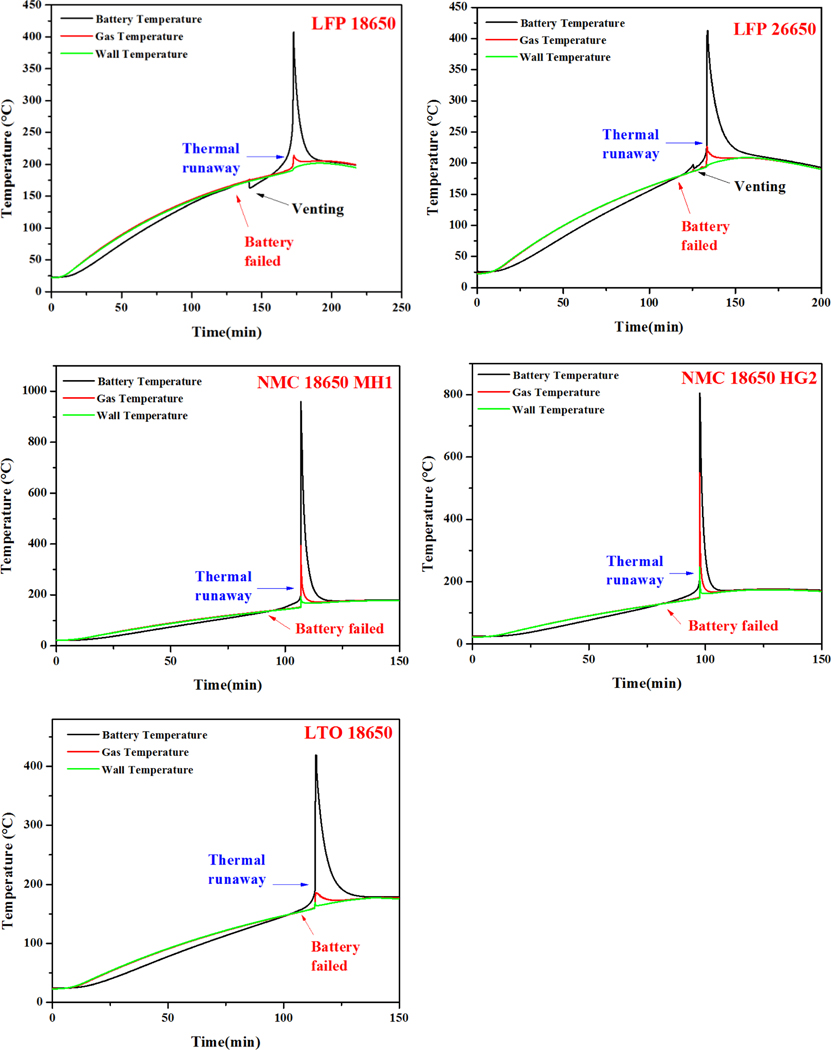
Figure 2 shows the time plot of battery voltage. In the case of the LFP 18650 battery, the initial battery voltage started at 3.34 V and, after about 2 hours of heating in the ARC, a significant drop in voltage was observed. After that, the battery voltage went through a turbulent period till resting at 0 V. In the case of LFP 26650 battery, a sudden drop to 0 V was observed. The voltage change patterns of NMC 18650 MH1 and HG2 were similar to that of LFP 18650, while the LTO 18650 was similar to that of LFP 26650. Hereafter, battery failure is defined when a significant voltage drop is observed and the time to the battery failure is used for battery heat transfer analysis.

Figure 2.

Battery voltage changes in thermal tests

3.2. Temperature measurement

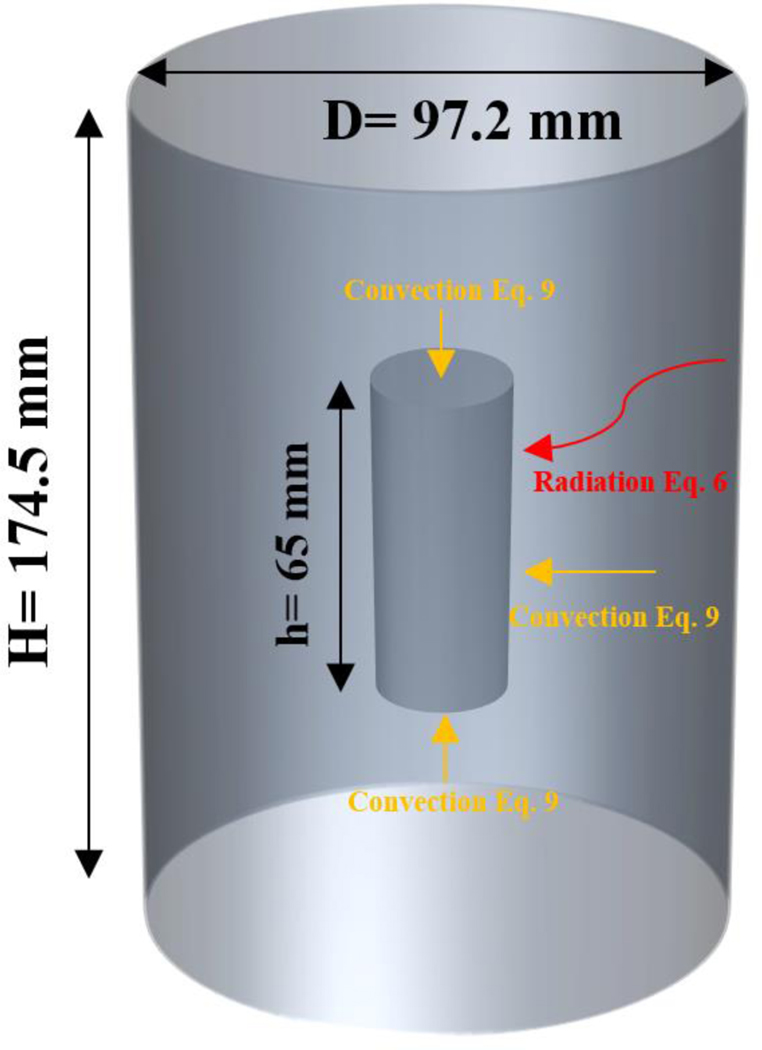
Battery surface temperature, gas temperature inside the canister, and canister interior wall temperature for each battery test were plotted against time and shown in Figure 3 The battery inside the canister was heated by hot wall radiation and gas convection. Generally, a battery will go through several thermal stages during an ARC test. First, the battery temperature increases as the canister wall temperature and interior gas temperature increase. In this stage, the battery keeps absorbing heat from its surroundings, both in the form of wall radiation and natural convection. After the battery temperature reaches a certain point, chemicals inside the battery start to react and the battery temperature quickly rises and exceeds the canister and gas temperature due to the exothermic processes. At this stage, the battery will no longer absorb heat from the surroundings but, instead, it will release energy in the form of vented gases. Battery temperature will reach its peak value when thermal runaway occurs, after which the test is terminated, and the cooling starts.

Figure 3.

Battery surface, gas, and wall temperatures during ARC tests

Various thermal behaviors were observed for different types of batteries during the heating in the ARC. For example, the LFP batteries vented at about 180 °C with a slight drop in temperature. After venting, chemical reactions inside the battery kept releasing heat, and the battery temperature increased until thermal runaway occurred. Battery thermal runaway peak temperature for the NMC MH1 battery reached around 1,000 °C and was much higher than the peak thermal runaway temperatures of the other types of batteries. The battery failure happened around the time when battery temperature exceeded the wall and gas temperatures. In this study, in order to estimate the amount of external heat that was absorbed by the battery until its failure, the temperature data were used to do a heat transfer analysis for the period from the start of the test to the battery failure. The time to battery failure, time to battery thermal runaway, temperature at battery failure, and peak temperature at battery thermal runaway for each battery type are summarized in Table 2.

Table 2.

Timing and temperatures for each battery type

Battery type	Time to failure (min)	Time to thermal runaway (min)	Temperature at failure (°C)	Thermal runaway peak temperature (°C)
LFP 18650	134.46	172.8	168	408
LFP 26650	120.22	134.1	183	412
LTO 18650	113.46	114	150	419
NMC 18650 MH1	85.65	106.8	125	960
NMC 18650 HG2	77.83	97.6	124	805

3.3. Heat transfer to the battery

One of the most important parameters of interest to battery safety design and storage is the total heat received by the battery through its surface from the surrounding environment. In this section, an analytical model is provided to understand the contribution from the different modes of heat transfer and to estimate the total heat transfer to the battery causing battery failure and potential thermal runaway.

For each test, the ARC was first turned on and a uniform heating was imposed on the entire canister. As shown in Figure 3, the gas temperature inside the canister nearly coincided with the canister internal wall temperature. Battery surface temperature also increased following the heating from the canister wall and gas. Since the experimental setup is a closed system, forced convection does not exist. Thermal conductivity of air at the tested temperatures is low, and conductive heat transfer to the battery surface is negligible. Therefore, the heat transfer to the battery from the surroundings is primarily controlled by canister wall radiation and natural convection from the gas. Other heat transfer mechanisms, such as the latent heat of the battery, conductive heat transfer within the battery, and the heat generation due to chemical reactions, can be important to analysis of the thermal behavior of the battery at different stages [19–21]. However, the current analysis focuses on the early stage before the thermal runaway occurs. Thus these heat transfer mechanisms inside the battery are neglected. Figure 4 illustrates the geometries of the battery inside the canister.

Figure 4.

Radiation and convection heat transfer to the battery

In order to formulate the analytical model, several assumptions will have to be made. Specifically, 1) the battery surface and the canister surface have uniform temperature throughout the tests [22], 2) the battery is held in the geometrical center of the canister. Once the battery is positioned inside the canister, it will not be moved during the test, and 3) the surfaces of the battery and the canister are painted black such that the emission of the surface is from a black body, and the incident heat transfer onto a surface either for the battery or the canister is completely being absorbed.

3.4. Radiative heat transfer

Considering the one-zone enclosure filled with air, the analysis of radiative heat transfer to the battery exterior surfaces requires the evaluation of surface–surface exchange factors. Mathematically, the surface–surface exchange factors between the battery surface and the canister surface, s_is_j, can be evaluated from the following integration [23–25]:

$$s_i{s}_j=\frac{1}{\sigma T_w^4}\underset{A_i}{\int }\underset{A_j}{\int }{\int }_0^{\infty }\frac{e_{\lambda b}\left(T_w\right)e^{-a_{\lambda }\left(T_g\right)s}\cos {\theta }_i\cos {\theta }_j}{\pi S^2}d\lambda d{A}_{j}d{A}_i$$ (1)

where T_w is the interior surface temperature of the canister with an area of A_i, T_g is the gas medium temperature, S is the line-of-sight distance between the two integration area elements, dA_i and dA_j, θ_i and θ_j are the angles between the line-of-sight and the unit normal vector of the two differential area elements, σ is the Stefan-Boltzmann constant, e_λb is the blackbody emissive power, and a_λ is the local absorption coefficient. Using the neural network formulation provided in [24], Eq. (1) can be expressed as:

$$s_i{s}_j=A_i{F}_{i-j}\left(1-{\alpha }_{i-j}\left(T_g,T_w,P_g{L}_{m,a},X_{C{O}_2},f_v{L}_{m,a}\right)\right)$$ (2)

where F_i-j is the view factor from canister surface A_i to battery surface A_j, α_i-j is the geometric absorptance between two areas, P_g is the absorbing gas partial pressure, X_CO2 is mole fraction of CO₂, f_v is the soot volume fraction, and L_m,a is the averaged mean beam length.

In the current geometric setting, a battery surface can only view a certain part of the canister (i.e., the top and bottom surface of the battery can view two canister surfaces, the side surface of the battery can view three canister surfaces). For that, the incident heat flux due to the canister wall emission will be:

$${\dot{q}}_{w,i}^{\prime \prime }=\sigma T_{w,j}^4\left(1-\sum _{j=1}^N{F}_{ji}{\alpha }_{ij}\left(T_{w,j},T_g,P_g{L}_{ij},X_{C{O}_2},f_v{L}_{ij}\right)\right)$$ (3)

Since the gas medium bounded between the battery surface and the canister surface is absorbing and emitting radiation, the incident heat flux due to the gas medium will be:

$${\dot{q}}_{g,i}^{\prime \prime }=\sigma T_g^4\sum _{j=1}^N{F}_{ji}{\alpha }_{ij}\left(T_g,T_g,P_g{L}_{ij},X_{C{O}_2},f_v{L}_{ij}\right)$$ (4)

The total radiative heat transfer on the battery surface will be the sum of the wall emission and the gas emission:

$${\dot{q}}_{rad,i}^{\prime \prime }={\dot{q}}_{w,i}^{\prime \prime }+{\dot{q}}_{g,i}^{\prime \prime }$$ (5)

Equations 3–5 are the general governing equations to estimate the total radiation heat transfer on the battery surface due to both emission from the canister wall and the gas medium. From Figure 3, it can be seen that the emitting surface temperature of the canister wall and the temperature of the gas medium were very close (less than 5% difference). The energy being absorbed by the gas due to emission from the canister surface will be made up by the emission from the gas itself [24]. Therefore, the radiation effect due to the participating gas medium is negligible. It is worth noting that the effect of the participating medium for the analysis of radiative heat transfer will become significant when the emitting surface and the gas medium temperatures are significantly different. With this simplification, the net radiative heat transfer to the battery from the canister wall can be simplified as:

$${\dot{q}}_{rad}=A_b\left({\dot{q}}_{w,i}^{\prime \prime }+{\dot{q}}_{g,i}^{\prime \prime }\right)=\sigma A_b\left(T_w^4-T_b^4\right)$$ (6)

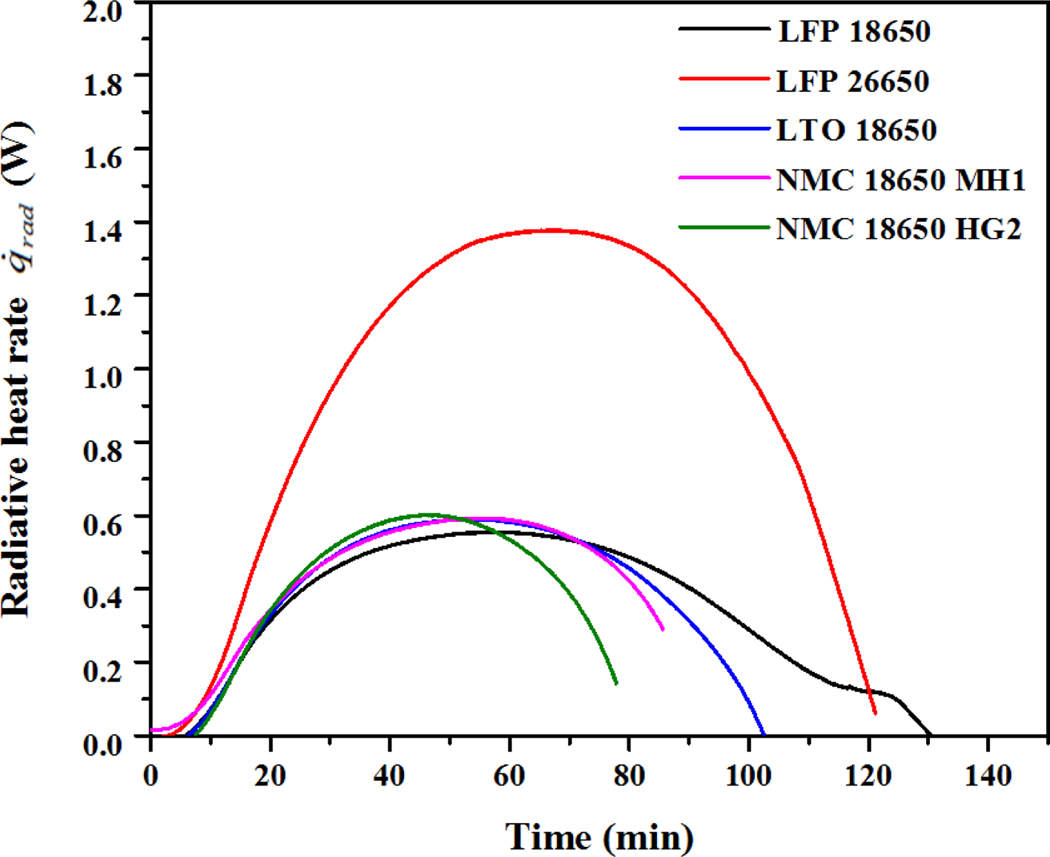
where T_w and T_b are the canister wall and battery surface temperature respectively. A_b is the battery surface area. The net heat exchange for the battery surface due to thermal radiation, ${\dot{q}}_{rad}$, is plotted in Figure 5 against the time. The data were only displayed from the start of the test to the battery failure. It can be observed that the radiation heat received for LFP 26650 was much higher than other types of batteries, partly because the size of the LFP 26650 is larger than other types of batteries, and thus it has a larger total heat capacity. For the same amount of heat absorbed by the battery, the surface temperature rise would be lower for LFP 26650.

Figure 5.

Radiative heat transfer from the wall to the battery surface

It is worth noticing that the peak radiative heat transfer rate occurred at around half of the time to failure for the battery thermal tests instead of at the end of the time to failure. This observation partly explains that heat transfer rate to the battery alone cannot determine the battery status, and that the total heat to the battery should be considered.

3.5. Natural convection

Gas inside the sealed canister is also a heat source for the battery during thermal tests. The gas will first be heated by the canister wall, and heat will then be transferred from the gas to the battery. As can be seen from the temperature distributions in Figure 3, the gas temperature was close to the canister wall temperature but higher than the battery temperature before chemical reactions occurred inside the battery. Using the measured temperatures, convection heat transfer from the hot gas to the battery can be calculated using the following equation:

$${\dot{q}}_{conv}=h_c{A}_b\left(T_g-T_b\right)$$ (7)

where ${\dot{q}}_{conv}$ is the convective heat transfer rate (in W), h_c is the convective heat transfer coefficient (W/m²K), and T_g is the gas temperature (K). The convection heat transfer process is driven by the temperature difference between the battery surface and the gas medium. As discussed above, only natural convection was considered here. The natural convection coefficient, h_c, can be expressed in the following correlation [26]:

$$h_c=f{\left(\frac{\left|T_g-T_b\right|}{L}\right)}^n$$ (8)

Where f and n are the coefficients in Table 3 based on the heat transfer conditions, and L is the characteristic length of the battery.

Table 3.

Coefficients used in Equation 8 [26].

Geometry	Condition	f (W mn-2 K-n-1)	n
Horizontal plate	Width > 0.152 m upper surface Tb>Tg or lower surface Tb<Tg	1.36	0.25
	Width > 0.152 m upper surface Tb<Tg or lower surface Tb>Tg	0.68	0.25
	Width < 0.152 m upper surface Tb>Tg or lower surface Tb<Tg	0.83	0.33
	Width < 0.152 m upper surface Tb<Tg or lower surface Tb>Tg	0.42	0.33
Vertical plate	Height > 0.152 m	1.49	0.25
	Height < 0.152 m	0.94	0.35

$$\begin{array}{c}{\dot{q}}_{conv}=\frac{f}{L^n}{\left|T_g-T_b\right|}^n{A}_b\left(T_g-T_b\right)=\{\begin{array}{ll}\frac{0.83}{L^{0.33}}{A}_{b_{-}top}{\left(T_g-T_b\right)}^{1.33}& topsurface\\ \frac{0.42}{L^{0.33}}{A}_{b_{-}bottom}{\left(T_g-T_b\right)}^{1.33}& bottomsurface\\ \frac{0.94}{L^{0.35}}{A}_{b_{-}side}{\left(T_g-T_b\right)}^{1.35}& sidesurface\end{array}\end{array}$$ (9)

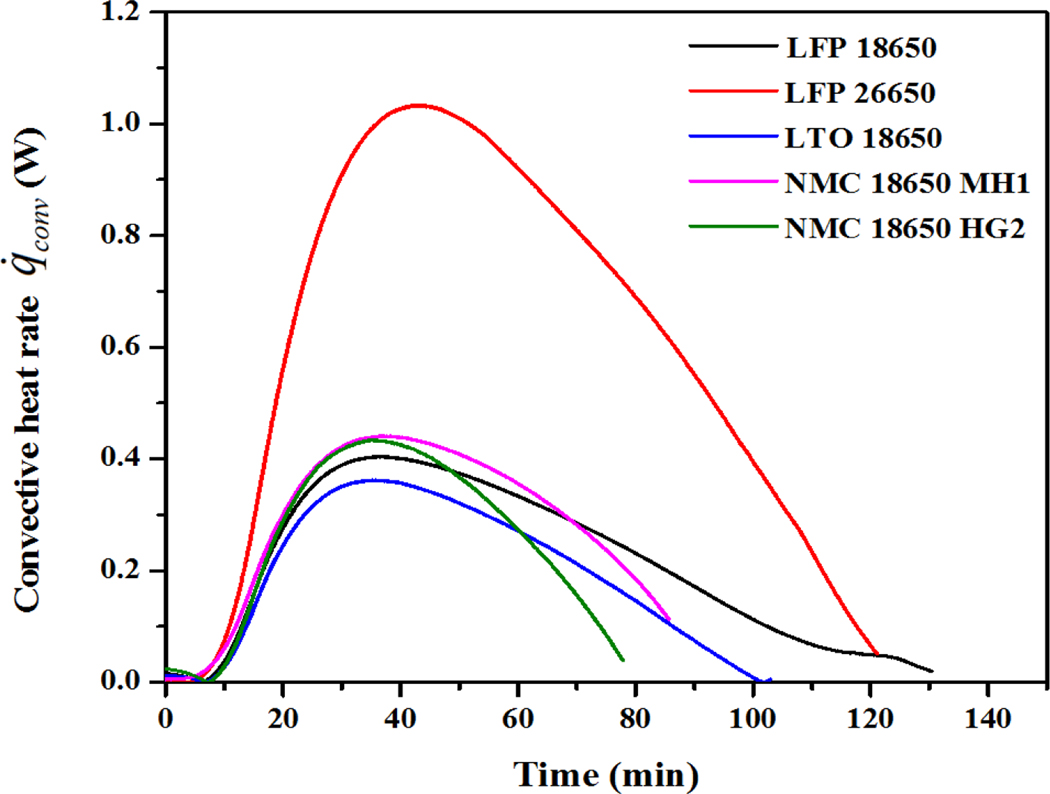
The convective heat transfer rate was calculated for each battery surface (top, bottom, and vertical) using Equation 9, where A_{b_top}, A_{b_bottom}, and A_{b_side} refer to the areas of battery top, bottom, and vertical side surfaces. The calculated total ${\dot{q}}_{conv}$ for the entire battery surface is shown in Figure 6.

Figure 6.

Convective heat transfer to the battery surface

Similar to the radiative heat transfer, the peak convective heat rate did not occur at the end of the time to failure, indicating again that the receiving heat transfer rate to the battery needs to be combined with the total heat received to evaluate the battery thermal status.

3.6. Total heat and uncertainty analysis

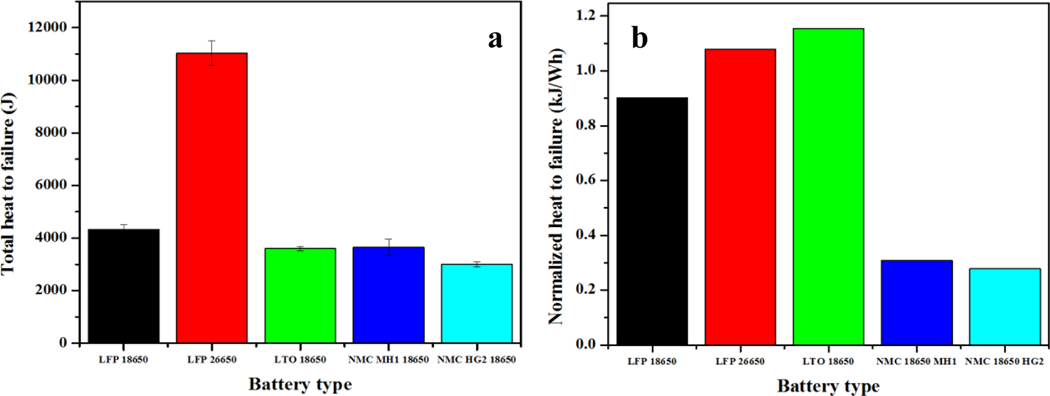
Radiative and convective heat transferred from the wall and the hot gas to the battery at the battery failure can be calculated by integrating the radiative and convective heat flux on Figs. 5 and 6 against time. Calculated total heats to failure for different batteries are plotted in Figure 7a. Data show that the LFP 26650 required the most external heat (around 11 kJ) for its failure, indicating that its thermal stability is the best out of all batteries tested. Four other types of batteries with the same size of 18650 displayed different thermal stability performances under external heat. The LFP 18650 needed a little over 4 kJ to fail the battery, which is the highest/safest among the four 18650 batteries. The NMC 18650 HG2 needed only 3 kJ to fail, which indicates that this battery type is the most vulnerable/unstable to external heat.

Figure 7.

(a) Total heat to failure for batteries of different types, (b) Normalized heat to failure by battery nominal energy capacity

Total heats to failure were also normalized by the battery nominal electrical energy capacity (kJ/Wh) listed in Table 1. Normalized data are shown in Figure 7b. Distinctions can be observed from the figure for the two NMC batteries compared to the other three types of batteries. The normalized heats to failure for LFP 18650, LFP 26650, and LTO 18650 were between 0.9 and 1.1 kJ/Wh regardless of the battery size and chemistry, while for the NMC batteries, the normalized heats to failure were much smaller, between 0.2 and 0.3 kJ/Wh. A few observations can be made from the comparison: (1) although the total heat to failure for LFP 26650 is the highest among the tested batteries, it does not necessarily indicate it is the most stable type of battery considering unit energy capacity; both the total heat to failure and the normalized heat need to be considered to evaluate the thermal stability of Li-ion batteries, and (2) NMC batteries have the highest energy capacity, but they are generally less thermally stable than the other types of batteries tested, as can be seen from both the total heats to failure and the normalized heats to failure. Further evidence can be found in Figure 3 and Table 2, as NMC batteries had the lowest temperatures at failure and the highest thermal runaway peak temperatures. The times to failure were also the shortest among the tested batteries.

The uncertainty of the data reported comes from two sources, namely, the uncertainty of the temperature measurement and the uncertainty of repeating tests. The uncertainty of temperature measurement is mainly due to the thermocouple accuracy and sensitivity. The N type thermocouple used in the study has an uncertainty of 0.75% according to its manufacturer, which will result in the calculated radiation uncertainty using Equation 6 up to 3.03%. The uncertainty for the convection calculation is the same as the temperature measurement uncertainty of 0.75%. The uncertainty of repeating tests is described as the standard deviation of the total heats calculated. For each type of battery tested, LFP 18650 has a 2.02% standard deviation, LFP 26650 has 2.4%, LTO has 0.4%, NMC 18650 MH1 has 6.4%, and NMC 18650 HG2 has 1.6%. The combined uncertainty for each battery type can be calculated using the following formula [27]:

$$u_c(y)=\sqrt{\sum _{i=1}^n{\left[c_{i}u\left(x_i\right)\right]}^2}$$ (10)

where u_c(y) is the combined uncertainty, c_i is the sensitivity coefficient, and u(x_i) is the standard uncertainty. Table 4 shows the uncertainty for each category and the combined uncertainty for each battery type, which are also shown in Figure 7a as the error bar.

Table 4.

Estimated uncertainty of measurements

Battery type	Uncertainty of repeating test, %	Uncertainty of radiation from temperature measurement, %	Uncertainty of convection from temperature measurement, %	Combined uncertainty, %
LFP 18650	2.0	3.03	0.75	3.72
LFP 26650	2.4			3.94
LTO 18650	0.4			3.15
NMC 18650 MH1	6.4			7.12
NMC 18650 HG2	1.6			3.51

4. Conclusions

As a part of NIOSH’s continual efforts to develop workplace solutions to minimize the occurrence of mine disasters, such as those potentially originating from Lithium-ion battery fires, experimental investigations were performed using the Accelerating Rate Calorimeter to study the thermal performances of different types of Li-ion batteries with a focus on the amount of external heat needed to cause battery failure. The test method can be easily extended to other types of batteries with a cylindrical shape. An analytical model was developed to estimate the total external heat applied to the battery at failure using the experimental data. The results ranked the batteries tested in terms of the heat to failure as: LFP 26650 (11 kJ) > LFP 18650 (4.3 kJ) > NMC 18650 MH1 (3.6 kJ) ≈ LTO 18650 (3.6 kJ) > NMC 18650 HG2 (3 kJ). However, total heats normalized to the battery nominal energy capacity gave a different rank: LFP 26650 (1.1 kJ/Wh) ≈ LFP 18650 (0.9 kJ/Wh) ≈ LTO (1.15 kJ/Wh) 18650 > NMC 18650 MH1 (0.31 kJ/Wh) ≈ NMC 18650 HG2 (0.28 kJ/Wh). The results from this work provide insights into the thermal stability of Li-ion batteries and indicate that the evaluation of thermal stability for a Li-ion battery should consider both total heat to failure and the normalized heat to failure. Information provided here can be used for developing a sensor or indicator of a battery failure and warning of further dangers, such as thermal runaway. Further Li-ion battery thermal studies are needed to examine if the results are applicable to batteries under other forms of abuses, such as overcharging.

Highlights:

1. An experimental method was developed to study the thermal safety of Li-ion batteries.

2. Radiative, convective and total heat transfer to the battery is calculated using temperature.

3. Batteries tested were ranked based on the heat and normalized heat to failure