White matter hyperintensities segmentation using the ensemble U-Net with multi-scale highlighting foregrounds

Abstract

White matter hyperintensities (WMHs) are abnormal signals within the white matter region on the human brain MRI and have been associated with aging processes, cognitive decline, and dementia. In the current study, we proposed a U-Net with multi-scale highlighting foregrounds (HF) for WMHs segmentation. Our method, U-Net with HF, is designed to improve the detection of the WMH voxels with partial volume effects. We evaluated the segmentation performance of the proposed approach using the Challenge training dataset. Then we assessed the clinical utility of the WMH volumes that were automatically computed using our method and the Alzheimer’s Disease Neuroimaging Initiative database. We demonstrated that the U-Net with HF significantly improved the detection of the WMH voxels at the boundary of the WMHs or in small WMH clusters quantitatively and qualitatively. Up to date, the proposed method has achieved the best overall evaluation scores, the highest dice similarity index, and the best F1-score among 39 methods submitted on the WMH Segmentation Challenge that was initially hosted by MICCAI 2017 and is continuously accepting new challengers. The evaluation of the clinical utility showed that the WMH volume that was automatically computed using U-Net with HF was significantly associated with cognitive performance and improves the classification between cognitive normal and Alzheimer’s disease subjects and between patients with mild cognitive impairment and those with Alzheimer’s disease. The implementation of our proposed method is publicly available using Dockerhub (https://hub.docker.com/r/wmhchallenge/pgs).

1. Introduction

White matter hyperintensities (WMHs) appear as abnormal hyper-signals within the white matter region on the human brain MRI including T2-weighted (T2w), proton density (PD), and fluid-attenuated inversion recovery (FLAIR) imaging. These atypical signals mostly result from aging processes such as demyelination and axonal loss, both as a result of cerebral small vessel diseases (Prins and Scheltens, 2015). They are frequently observed in the elderly and tend to increase in size and number with age (Habes et al., 2016), while at the same time being associated with several potential vascular risk factors, particularly hypertension (Abraham et al., 2016).

Based on quantitative analyses of WMHs (Barber et al., 1999; Dubois et al., 2014; Habes et al., 2016; Lee et al., 2016; Prins and Scheltens, 2015), previous studies showed that the presence and severity of WMHs are associated with dementia (Dubois et al., 2014) and increase risk of conditions such as Alzheimer’s disease (Habes et al., 2016; Lee et al., 2016), vascular dementia, and dementia with Lewy bodies (Barber et al., 1999). These studies suggest that the quantitative characterization of WMHs plays an important role in various clinical research into neurological disorders.

Manual delineation of WMHs provides ground-truth for volumetric quantification of WMHs. However, it is a laborious, tedious, and time-consuming task and requires a high level of expertise to avoid unacceptable levels of intra- and inter-rater variability. Besides, this becomes more problematic with the size of a dataset, encouraging automated segmentation.

A number of methods have been proposed to segment WMHs automatically. Jeon et al. (2011) attempted WMHs segmentation based on the Markov random field and an intensity thresholding method. Other studies have developed k-nearest neighbors-based clustering approaches (Griffanti et al., 2016; Jiang et al., 2018; Steenwijk et al., 2013). These methods used various features (e.g., spatial information, intensity information, and texture) from T1w and FLAIR images as the input of the clustering algorithm. Dadar et al. (2017) evaluated various classifiers such as logistic regression, support vector machines, decision trees, and random forests. They observed that the random forest achieved the best performance. Recently, convolutional neural networks (CNN), a class of deep neural networks, have rapidly become a primary method in medical image segmentation and shown remarkable performance (Litjens et al., 2017). For the segmentation of WMHs, Moeskops et al. (2018) proposed a CNN model based on multi-scale patches extracted from T1w, T1w inversion-recovery, and FLAIR images. Rachmadi et al. (2018) added global spatial information to the patch that was used as an input to a CNN to improve the segmentation of WMHs.

The use of different evaluation metrics (e.g., Dice, Jaccard, Hausdorff indices), as well as evaluations against manually WMHs delineations by different experts, makes it difficult to compare the performance of segmentation methods from various studies systematically. To address these issues, the WMH Segmentation Challenge 2017 was held for a standardized comparison of the automatic segmentation of WMHs (Kuijf et al., 2019) in conjunction with the 20th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI) (Descoteaux et al., 2017). The Challenge provided a public platform to standardize the evaluation of WMHs segmentation methods based on a unified dataset of MRI, evaluation metrics, and expert labeling. Twenty teams proposed new methods and performed training and testing on the dataset provided. By using an ensemble approach, which is a good way to reduce over-fitting of deep learning algorithms, with the U-Net which is a deep encoder-decoder architecture and has skip connections concatenating the feature maps in the encoder to the feature maps in the decoder, Li et al. (2018) achieved the best performance.

Partial volume effects (PVE) on MRI images due to limited spatial resolution is associated with the problem where one pixel/voxel represents a signal of a mixture of different brain tissues. This effect becomes strong at voxels of the boundary between structures having different tissue characteristics or between a lesion and the surrounding brain tissue. Unidentification of the voxel with PVE may result in underestimating the segmentation of the target lesion, in particular for small lesions and lesions of boundaries.

Such a problem may not be inevitable for deep neural network approaches. Indeed, we tested a standard U-Net method on WMH segmentation and observed the unsuccessful classification of voxels placed at both the edges of WMHs or small WMHs. The predicted probability of foreground is low for the WMH voxels with strong PVE due to their features uncertainty, and the networks tend to fail to identify those partial volume WMHs (PV-WMHs). In general, the volume of the PV-WMHs is relatively small compared to the volume of the overall WMHs. Thus the PV-WMHs contribute little to the network loss, resulting in the network insufficiently learn the PV-WMHs.

We propose the network to be trained using a multi-scale approach of highlighting foregrounds (HF). In the standard U-Net, the training is accomplished by minimizing the Dice loss at the output layer, which is computed by comparing the posterior probability map with the ground truth label. To emphasize the label voxels on WMH boundaries, which would likely lie on PV-WMH voxels, we propose to compute and minimize the Dice losses at the particular intermediate decoder layers by comparing their output probability maps with the corresponding labels generated using the proposed HF method. The HF approach downsamples the ground truth labels sequentially by applying 2 × 2 max-pooling with stride 2, resizing the labels to the size of each of the decoder layers. The approach emphasizes the influence of the voxels lying on the lesion boundaries or consisting of small lesions on the training of a network.

We used the labels generated using the proposed HF method to train auxiliary classifiers in the intermediate decoder layers. Training by inserting auxiliary classifiers in the intermediate layers is known as deep supervision. In natural image classification, GoogLeNet (Szegedy et al., 2015) is based on this method. However, this study did not systematically evaluate the use of auxiliary classifiers. Independently, Lee et al. (2015) proposed deeply-supervised networks that were combined with auxiliary classifiers at all intermediate layers for image classification. They showed that the deep supervision method improved the convergence rate of networks by alleviating the vanishing or exploding gradient problem. It also improved the discriminative ability of the features learned by directly driving the low- and mid-level features in intermediate layers to very high-level features (i.e., target output). Wang et al. (2015) applied the deep supervision method to deeper convolutional networks. They proposed to add auxiliary classifiers after certain intermediate layers for better classification performance in the deeper convolutional networks. Chen et al. (2016a) used the deep supervision framework for neuronal structure segmentation on electron microscopy images. Their method added deconvolutional layers to the intermediate encoder layers to train auxiliary classifiers and fused the outputs. Several variants of the deeply-supervised networks were further introduced to segment brain tissue (Chen et al., 2018), liver, whole heart and great vessel (Dou et al., 2017), and retinal vessels (Lin et al., 2018). Zhu et al. (2017) proposed to use a U-Net with deep supervision for prostate segmentation in MR images. These previous works (Chen et al., 2018; Chen et al., 2016a; Dou et al., 2017; Lin et al., 2018; Zhu et al., 2017) reported that deep supervision could improve segmentation accuracy.

Though the proposed method is similar to these previous works (Chen et al., 2018; Chen et al., 2016a; Dou et al., 2017; Lin et al., 2018; Zhu et al., 2017), our approach has several differences in the processing. We generate label images at different resolutions from the ground truth labeling while emphasizing the foreground voxels using the proposed highlight foreground (HF) method. The generated multi-scale label image is used for the network to learn the features focusing on the foreground area at different resolutions. On the other hand, these previous works used the ground truth labels without modification at the original image resolution. During training, they upsampled feature maps to the original image resolution in order to generate the output. Instead, the proposed method computes the loss functions without the need for the upsampling of network outputs, mitigating GPU memory usage.

The MICCAI WMH Segmentation Challenge continues to host further studies since its initial opening. Of the 39 methods submitted the challenge as of March 1st, 2020, our team that proposed the ensemble U-Net with multi-scale HF currently achieves the best performance. In the following sections, we outline the methods we used to achieve state-of-the-art performance on this task. We first outline the U-Net with HFs model. Then, we show that the proposed method significantly improved the WMHs segmentation performance compared to the standard U-Net. In the results section, we evaluate the proposed method in comparison to other methods and assess the influence of the multi-scale HFs and the effect according to their organization. Finally, using the Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset, we investigate the potential clinical utility of the HF method by automatically segmenting WMHs and associating the WMH volumes with cognitive performance scores that are used for the diagnosis of mild cognitive impairment and Alzheimer’s Disease (i.e., Mini-Mental State Examination (MMSE), Alzheimer’s Disease Assessment Scale-Cognitive Subscale (ADAS-Cog), and Clinical Dementia Rating Scale sum (CDR sum)).

2. Materials and methods

2.1. Challenge dataset and pre-processing

We validated our method based on the dataset and evaluation framework in WMH Segmentation Challenge 2017 because this provides a standardized assessment of the segmentation performance of WMHs (Kuijf et al., 2019). The challenge organization provided a training dataset and a test dataset consisting of 170 subjects in total. Details of the datasets are given in Table 1. The training dataset included 60 subjects and was publicly available and downloadable after registration at https://wmh.isi.uu.nl/data/. We used this dataset to train our network and investigate the effect of the HF method. The test dataset including the rest of the 110 subjects was only available for evaluating predictions when submitted to the challenge.

Table 1.

The overview of the characteristics of the WMH Segmentation Challenge 2017 dataset.

Institute	Scanner	T1 voxel size(TR/TE(/TI))	FLAIR voxel size(TR/TE/TI)	Train	Test
UMC Utrecht	3T Philips Achieva	1.00 × 1.00 × 1.00 mm3(7.9/4.5 ms)	0.96 × 0.95 × 3.00 mm3(11,000/125/2800 ms)	20	30
NUHS Singapore	3T Siemens TrioTim	1.00 × 1.00 × 1.00 mm3(2300/1.9/900 ms)	1.00 × 1.00 × 3.00 mm3(9000/82/2500 ms)	20	30
VU Amsterdam	3T GE Signa HDxt	0.94 × 0.94 × 1.00 mm3(7.8/3.0 ms)	0.98 × 0.98 × 1.20 mm3(8000/126/2340 ms)	20	30
	1.5T GE Signa HDxt	0.98 × 0.98 × 1.50 mm3(12.3/5.2 ms)	1.21 × 1.21 × 1.30 mm3(6500/117/1987 ms)	0	10
	3T Philips Ungenuity	0.87 × 0.87 × 1.00 mm3(9.9/4.6 ms)	1.04 × 1.04 × 0.56 mm3(4800/279/1650 ms)	0	10

^*Abbreviations: TR: repetition time; TE: echo time; TI: inversion time.

Each subject included the brain MR images before and after pre-processing for T1w and FLAIR images and a manual delineation of WMHs. The images were acquired from five different MR scanners in three different institutes. The images acquired in the three MR scanners (i.e., 3T Philips Achieva, 3T Siemens TrioTim, and 3T GE Signa HDxt) were used for both training and testing. The images acquired in the other two MR scanners (i.e., 1.5T GE Signa HDxt and 3T Philips Ingenuity) were used only for testing. All the 3D FLAIR images from VU Amsterdam institute were resampled into the axial direction with 3mm slice thickness. The WMHs were labeled on the FLAIR images by two experts, based on Standards for ReportIng Vascular changes on nEuroimaging (STRIVE) criteria (Wardlaw et al., 2013). The organizers provided the pre-processed data like 1) T1w images that were registered to the FLAIR images using the Elastix toolbox (Klein et al., 2009); 2) the T1w and FLAIR images that underwent correction for the intensity non-uniformity using SPM12 (Ashburner and Friston, 2000).

We further pre-processed these data for training or testing our method. First, to reduce false positives, we removed non-brain tissue, using ROBEX (Iglesias et al., 2011). Second, we performed intensity normalization to match the intensity distribution among the training data. For each image, we calculated means and variances using intensities ranging from 2nd to 98th percentiles in the brain region. We then normalized the intensities within the brain in each image using z-score transformation. Finally, to equalize the size of the input data to the network, the axial slices in each 3D image were cropped or padded to a size of 200 × 200. We used 2D slices to train our 2D CNN model.

2.2. Network architecture

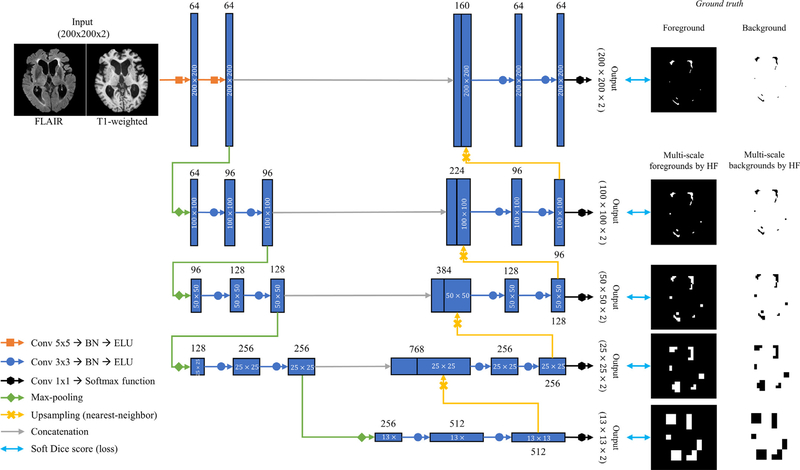
In the current study, we propose to combine multi-scale HFs with a U-Net architecture (Ronneberger et al., 2015). The main idea of the U-Net is the skip connections between the encoder and decoder to allow the network to reuse the feature maps in the encoder. This generally helps the network to predict dense segmentation results and alleviates the vanishing gradient problem. Variants of the U-Net have been used in diverse medical image segmentation problems and have demonstrated outstanding performance (Çiçek et al., 2016; Drozdzal et al., 2018; Guerrero et al., 2018). In the original Challenge in 2017, Four among the top teams, including the top team (Li et al., 2018), exploited the U-Net architecture (Kuijf et al., 2019). Here, we advance a 2D U-Net for WMHs segmentation (Fig. 1) with two novel components: use of different details of the network architecture and inclusion of the multi-scale HFs.

Fig. 1.

The workflow of the proposed U-Net with multi-scale highlighting foregrounds.

2.2.1. Details of the network configuration

As seen in Fig. 1, the modified network is based on the encoder-decoder structure. In the encoder during both training and testing, the axial slices of FLAIR and T1w modalities are fed into the network as a two-channel input (i.e., the input size is 200 × 200 × 2). We chose the axial slice for the 2D input data because the best image resolution was found on the FLAIR axial slice. In our network, we adopt the following configurations as suggested in recent works: 1) Instead of 3 × 3 kernel convolutions in the standard U-Net, we use 5 × 5 kernel convolutions in the first two layers for handling different transformations as in Li et al. (2018); 2) Batch normalization is added to the 18 convolutional layers each, which accelerates the training process and improve the network performance by reducing internal covariate shift (Ioffe and Szegedy, 2015). 3) Finally, we use an exponential linear unit (ELU) (Clevert et al., 2015) as the activation function for non-linearity capacity instead of a rectified linear unit (ReLU) in the standard U-Net. ReLU is neither activated nor updated at a negative value, while ELU does not only have all the strengths of ReLU but also is activated and updated at negative values, improving the learning characteristics (Clevert et al., 2015). The encoder contains four 2 × 2 max-pooling layers with a stride 2 after every two convolution layers for downsampling (Fig. 1). Upsampling layers based on nearest-neighbor interpolation are applied after every two convolutional layers in the decoder (Fig. 1). Prior to downsampling, the feature maps in the encoder are concatenated to the feature maps right after upsampling in the decoder. At the output convolutional layers, a 1 × 1 convolution with softmax function is used to convert the feature maps into the label space with the depth of two (i.e., two classes; WMHs and non-WMHs).

2.2.2. Multi-scale highlighting foregrounds

We add modified label images by the multi-scale HF approach to the intermediate layers in the decoder in our network (Fig. 1). The intermediate output convolutional layers convert the feature maps into the multi-scale segmentation probability maps (black arrows in Fig. 1). The multi-scale HFs max-pool the label image (Fig. 2). Given the foreground pixels in one label image, the label image max-pooled by HF is defined as follow:

$$l_k^{HF}=f_{MP}\left(l_{k-1}^{HF}\right)(k=1,2,\dots ,n),$$ (1)

Fig. 2.

Illustration of the multi-scale highlighting foregrounds.

Where f_MP is a 2 × 2 max-pooling operator with stride 2 and $l_k^{HF}$ is the label image max-pooled, which generated by applying f_MP k times and $l_0^{HF}$ is the original foreground image (i.e., ground truth label). The background image, $l_k^{BG}$, is defined as follow:

$$l_k^{BG}=1-l_k^{HF}(k=0,1,2,\dots ,n),$$ (2)

Where $l_0^{BG}$ is the original background image and $l_k^{BG}$ is a background of inverting $l_k^{HF}$.

The foreground/background images by multi-scale HFs are used to generate losses through comparison with the corresponding outputs. We used a soft Dice score as a loss function. Let $L^c=\left(l_0^c,l_1^c,\dots ,l_M^c\right)$ be ground truth label image $\left(l_0^c\right)$ and M represents different scales for multi-scale HF. The c represents the type either HF or BG. Then, let $S^c=\left(s_0^c,s_1^c,\dots ,s_M^c\right)$ be the segmentation resulting from the network. $s_0^c$ and $\left(s_1^c,\dots ,s_M^c\right)$ is the output segmentation at the size of the original label image $l_0^c$ and multi-scale label images $\left(l_1^c,\dots ,l_M^c\right)$ each. The Multi-scale Loss Functions (MLF) can be written as

$$\text{MLF}=\sum _{\text{c}=1}^{\text{C}}\sum _{\text{m}=0}^{\text{M}}{\text{w}}_{\text{m}}\frac{2\left({\text{l}}_{\text{m}}^{\text{co}}{\text{s}}_{\text{m}}^{\text{c}}\right)+ϵ}{{\text{l}}_{\text{m}}^{\text{c}}+{\text{s}}_{\text{m}}^{\text{c}}+ϵ},$$ (3)

where C is the foreground or background, ° is the element-wise product, w_m is the weight for mth scale loss function, and ϵ is a smoothing constant to prevent MLF from division by 0, which we set as 0.00001 for current network training. The sum of all of w_m is one. We evaluated various sets of w_m and found the best segmentation performance when w_m was the same for all of the losses as described in the following section.

3. Experiments

3.1. Evaluation metrics and ranking system

We used the five evaluation metrics that the WMH challenge adopted to compare the methods that participating teams developed quantitatively (details in Table 3). Let ML be the WMHs manually labeled by expert and AL be the WMHs automatically labeled by the proposed approach. The five evaluation metrics are as follow: (1) the Dice similarity coefficient (DSC) as the overlap index between ML and AL, (2) a modified Hausdorff distance (95th percentile; H95) as the overall distance between ML and AL boundaries, (3) the absolute percentage volume difference (AVD) between the total WMHs of ML and AL, (4) recall as the sensitivity in detecting individual lesions, and (5) F1-score as the average of precision and recall in detecting individual lesions. The challenge organization defined the individual lesions in both recall and F1 as 3D connected components within an image. All five measurements are positive real-valued and the closer the measured values of DSC, recall, and F1 approach one, the higher the similarity between ML and AL. On the contrary, the closer the measured values of H95 and AVD are to zero, the higher the similarity between ML and AL. Table 3 details the definition of these five metrics. These metrics for our testing results were computed by the challenge organization.

Table 3.

List of evaluation metrics and their definitions. The organization of the challenge defined individual lesions for recall and F1 as 3D connected components. N means the number of 3D connected components. $\widehat{d}(X,Y)$ means $\underset{x\in X}{\max }\underset{y\in Y}{\min }d(x,y)$, where d(x, y) is the distance between x and y points. V_ML and V_AL mean the WMH volume computed by manual segmentation and our method, respectively.

	DSC	H95	AVD	Recall	F1
Equation	$\frac{2TP}{FP+FN+2TP}$	$\max \{\widehat{d}(X,Y),\widehat{d}(Y,X)\}$	$\frac{\left|V_{ML}-V_{AL}\right|}{V_{ML}}$	$\frac{N_{TP}}{N_{TP}+N_{FN}}$	$\frac{2N_{TP}}{2N_{TP}+N_{FN}+N_{FP}}$

^*Abbreviations – DSC: the Dice Similarity Coefficient; H95: a modified Hausdorff distance (95th percentile); AVD: the absolute percentage volume difference; Recall: the sensitivity for detecting individual lesions; F1: F1-score for individual lesions; TP: true positive; FN: false negative; FP: false positive.

The challenge organization proposed a system for ranking the overall performance of participating teams. This system consisted of four steps. First, the mean of each metric was computed over all test data for each team’s method. Second, for each evaluation metric, the organization sorted all of the teams from best to worst. Next, the best and worst teams received a rank score of zero and one, respectively, for that metric. Other teams were assigned a rank score between zero and one following their results within the range of that metric. Finally, the five rank scores were averaged into the overall rank score indicating the overall performance of that team. The overall rank score was used to determine the ranking of each team on the result board on the challenge homepage (https://wmh.isi.uu.nl/results/).

3.2. Implementation details

The proposed network and experimental networks were implemented in Python using Tensorflow (Abadi et al., 2016). The networks were trained on four NVIDIA Titan-Xp GPUs with 12GB RAM. The hyperparameters of the networks were set as follows: mini-batch size=30, optimizer=Adam (Kingma and Ba, 2014), learning rate=0.0002, the number of epochs=1000, and He initialization (He et al., 2015). Early stopping based on a validation dataset was used to avoid overfitting in training data. The performance of all networks converged within 1000 epochs. Data augmentation was applied during training to enhance robustness in the face of limited training data. To this end, flipping of axial-sliced images to each axis and various affine transforms including translation, rotation, scaling, and shearing were randomly applied. The details of the parameters of data augmentation were as follows: the probability of flipping each axis=0.5, the range of translation ratio=(−0.1, 0.1), the range of rotation=(−15°, 15°), the range of scaling ratio=(0.9, 1.1), the range of shearing=(−18°, 18°). The networks were trained on an 1:3 ratio of original data to augmented data at each epoch.

To achieve robust segmentation results, we applied an ensemble method and a flip averaging to the proposed method. In a training step, we performed 5-fold cross-validation where each fold (n=12) images were randomly and equally sampled from each site dataset in the whole training dataset (n=60). Then, validating each fold, we trained the proposed network using the other four folds (n=48), resulting in 5 networks trained separately. In a testing step, we first flipped each individual image with respect to the x-axis, y-axis, and xy-axis, which generated 3 flipped images per individual. Then, each of the four images was used as input to a network generated from 5-fold cross-validation. The flip averaging was the major voting of four outputs from an original input and three inputs flipped to the x-axis, y-axis, and xy-axis in a network. As a result, the final output was the major voting of five outputs generated from the flip averaging of each network.

3.3. The evaluation of the importance of multi-scale highlighting foregrounds

To investigate the importance of multi-scale HF in WMHs segmentation, we evaluated our model with various parameters of multi-scale HF, which included 1) the type of pooling for HF, and 2) the weights of losses at output layers. We performed this evaluation through a cross-scanner validation using the training datasets (60 subjects) of WMHs segmentation challenge. The dataset for the evaluation was split into a training dataset (1st and 2nd sites: 40 subjects) and a validation dataset (3rd site: 20 subjects). Our evaluation results are based on the raw network output (i.e., without ensembling and flip averaging).

The type of pooling for HF: We compared the network using the proposed max-pooled label images with the corresponding average-pooling version. We downsampled the ground truth label image into the lower resolutions at the intermediate output layers by repeatedly using a 2 × 2 average pooling operation with stride 2. We then generated their hard labels by thresholding the downsampled soft labels at 0.5. The network for this experiment was equipped with either four max-pooled or four average-pooled label images and the same loss weights at all of the output layers. To avoid cherry-picking results by random seed, we performed a cross-scanner validation (3-fold cross validation) with 5 runs of random initialization (resulting in 15 trained networks for each tested method) for the original U-Net, U-Net with HF, and U-Net with average-pooled labels (AVG). Each fold represented each scanner dataset: i.e., the UMC dataset, NUHS dataset, or VU dataset. We treated the results of each fold as an individual sample. We performed paired t-tests for the comparison among the tested methods and calculated 95% confidence interval (CI) according to the paired sample test.

The weights of losses about all of the output layers: In this experiment, we investigated the impact of the set of w_m in Eq. (3). The network with four max-pooled label images was used for this experiment. Three sets of w_m were tested: 1) $w_0=\frac{5}{15}$, $w_1=\frac{4}{15}$,$w_2=\frac{3}{15}$, $w_3=\frac{2}{15}$, and $w_4=\frac{1}{15}$; 2) $w_0=\frac{3}{15}$, $w_1=\frac{3}{15}$, $w_2=\frac{3}{15}$, $w_3=\frac{3}{15}$, and $w_4=\frac{3}{15}$; 3) Finally, $w_0=\frac{1}{15}$, $w_1=\frac{2}{15}$, $w_2=\frac{3}{15}$, $w_3=\frac{4}{15}$, and $w_4=\frac{5}{15}$; For this experiments, we trained three networks (only one run for each fold; a total of three runs) and averaged the results on a patient-level to investigate statistical differences.

3.4. Clinical utility evaluation

The aim here was to assess the clinical utility of the proposed method by evaluating whether the proposed HF-based automated volumetry is a biomarker of the dementia severity (i.g., cognitive performance decline) or a diagnostic measurement of dementia. Accordingly, we analyzed the association of the WMH volumes with cognitive performance scores or with the diagnosis among cognitively normal (CN), mild cognitive impairment (MCI), and early Alzheimer’s Disease (AD). Also, to analyze the effect of WMH volume on subject diagnosis (CN, MCI, and AD), we compared classification performances using logistic regression under three different conditions (WMH volume only, clinical variables only, and WMH volume and clinical variables combined).

3.4.1. ADNI dataset and preprocessing

We employed the datasets from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (http://adni.loni.usc.edu). We randomly selected 243 ADNI subjects who completed cognitive evaluations and MRI scans at their baseline visits. The data include 73 CN, 115 MCI, and 55 AD subjects at baseline diagnosis. We used Mini-Mental State Examination (MMSE), Alzheimer’s Disease Assessment Scale-Cognitive Subscale (ADAS-Cog), and Clinical Dementia Rating Scale sum (CDR sum) as cognitive performance evaluations that followed a standardized protocol (Petersen et al., 2010). The score ranges of MMSE, ADAS-Cog, and CDR sum were 0–30, 0–70, and 0–18, respectively. A higher ADAS-Cog or a CDR sum score indicates lower cognitive performance. On the other hand, a lower MMSE means lower cognitive performance. Each individual MRI scan consisted of a set of a T1w image and FLAIR image acquired axial-plane. Table 2 details demographic and clinical information.

Table 2.

The overview of the characteristics of 243 ADNI subjects.

Characteristic	Total, Mean (SD)	Diagnosis at baseline, Mean (SD)
		Cognitively normal	MCI	AD
Sample, No.	243	73	115	55
Age, y	73 (7.5)	75 (6.5)	71 (7.9)	76 (7.1)
CV risk	1.7 (1.0)	1.7 (1.1)	1.7 (1.0)	1.6 (1.0)
Education, y	16 (2.7)	16 (2.5)	17 (2.7)	16 (2.7)
Male, No. (%)	123 (51)	36 (49.3)	56 (48.7)	31 (56.4)
ApoE4 genotype, 0/1/2	114/100/29	48/23/2	50/49/16	16/28/11
Race
White	218	63	105	50
Other	25	10	10	5
MMSE score	27 (2.8)	29 (1.3)	28 (2.1)	23 (2.1)
ADAS-Cog score	11 (6.8)	6 (3.1)	10 (4.8)	20 (5.8)
CDR sum	1.75 (1.99)	0.12 (0.53)	1.4 (1.1)	4.6 (1.7)
WMHs, cm3	9.94 (11.74)	9.13 (14.33)	8.72 (9.04)	13.58 (12.41)

We pre-processed all images through the same steps that are described in Section 2.1. Challenge dataset and pre-processing for consistent data processing. We did not perform the cropping or padding of the images to 200 × 200 axial planes because inputting an arbitrary size image is accepted in fully convolutional networks at test time.

3.4.2. Statistical analysis

We used a general linear model (GLM) to assess whether WMH volumes computed using our method were associated with the cognitive performance scores or the diagnosis of subjects. We included each type of the cognitive scores or the diagnosis (i.e., CN, MCI, and AD) as a dependent variable and the WMHs volume as an independent variable. In the GLM, we also included age, cardiovascular risk, education, gender, ApoE4 genotype, and race as covariates to collect for their confounding effects. The cardiovascular risk score ranged from 0 to 5 by counting the following diseases or characteristics individually: hypertension, stroke, smoking, diabetes mellitus, and cardiovascular disease. To mitigate the possible issue of the skewed distribution of the cognitive scores and WMH volumes, we applied the square root transformation to MMSE and CDR sum, and the log-transformation to WMH volumes as suggested in Carmichael et al. (2010). Then, all the transformed values and ADAS-Cog were normalized using the z-score transformation. All the statistical tests were implemented using Matlab 2019b.

3.4.3. Classification analysis

We assessed whether alterations in WMH volume were used to classify an unseen individual into CN, MCI, or AD. To this end, we used logistic regression as a classifier and performed the classification under three different conditions where input features varied: 1) WMH volume only; 2) clinical variables only (age, cardiovascular risk, education, gender, ApoE4 genotype, and race; these are mentioned in Section 3.4.2), and 3) WMH volume and clinical variables combined. The classification was evaluated using a leave-one-out strategy. We calculated the receiver operating characteristic (ROC) curves from the classification resulting in from each of the three conditions and compared their area under the curve (AUC) values. Classification analysis was processed using Matlab 2019b.

4. Results

In this section, we compare our results with the results of the top 2nd–5th algorithms listed in the WMH Segmentation Challenge as of April 30, 2020. We also show the influence of multi-scale HF on the proposed network’ys performance. Finally, the results of the clinical analysis are presented.

4.1. Results of the WMH segmentation challenge

As of March 1st 2020, the following four teams, as well as our team, were listed as the top five in the challenge leaderboard: 1) sysu_media_2– deep 2D multi-scale stacked U-Net and ensemble learning; 2) sysu_media– fully convolutional ensemble neural networks (Li et al., 2018); 3) anonymous_20200413 – brain atlas guided attention U-Net; and 4) coroflo– multi-dimensional convolutional gated recurrent units and ensemble learning. More description of each method is available on the challenge website.

Table 4 shows the results of the top five teams about five metrics (i.e., DSC, H95, AVD, recall, and F1). Bold text indicates the best performance among all algorithms for the given metric. Our method pgs achieved the best overall performance.

Table 4.

Comparison of our method with other methods in the MICCAI WMH segmentation challenge. Bold fonts indicate the best result among all teams.

	Team	Rank	DSC	H95 (mm)	AVD (%)	Recall	F1
1	pgs (ours)	0.0185	0.81	5.63	18.58	0.82	0.79
2	sysu_media_2	0.0187	0.80	5.76	28.73	0.87	0.76
3	sysu_media	0.0288	0.80	6.30	21.88	0.84	0.76
4	anonymous_20200413	0.0314	0.79	6.17	22.99	0.83	0.77
5	coroflo	0.0493	0.79	5.46	22.53	0.76	0.77

^*Abbreviations – DSC: the Dice Similarity Coefficient; H95: a modified Hausdorff distance (95th percentile); AVD: the absolute percentage volume difference; Recall: the sensitivity for detecting individual lesions; F1: F1-score for individual lesions.

The results of our method are detailed in Table 5. Part of the test dataset (n=90) was from three sites (Utrecht, Singapore, and AMS GE3T) that matched the sites from which the training datasets were acquired. Whereas the other 20 subjects were from AMS GE1.5T and AMS PETMR which were completely unseen. However, the proposed method demonstrated similar performance in this unseen dataset relative to the three-site dataset.

Table 5.

Results about five metrics of the proposed method in the test dataset of the challenge.

	DSC	H95 (mm)	AVD (%)	Recall	F1
Utrecht (n=30)	0.81	6.76	18.62	0.81	0.75
Singapore (n=30)	0.84	4.71	15.69	0.83	0.80
AMS GE3T (n=30)	0.80	3.74	22.03	0.83	0.82
AMS GE1.5T (n=10)	0.74	9.30	22.09	0.75	0.77
AMS PETMR (n=10)	0.80	7.00	13.25	0.82	0.81
Weighted average	0.81	5.63	18.58	0.82	0.79
rank [0...1]	0.000	0.004	0.003	0.086	0.000

4.2. The influence of the multi-scale highlighting foregrounds and other parameters on segmentation accuracy

We evaluated the segmentation accuracy of the proposed network under different configurations of the multi-scale HF. Table 6 shows the segmentation results and 95% confidence intervals for 15 multiple runs of original U-Net, U-Net with HF, and U-Net with AVG. The U-Net with HF achieved the best performance across all metrics compared to the other two methods. Table 7 shows the effect of the weights of losses at all the output layers on segmentation accuracy. The network with equal weights among all the five output layers outperformed the networks using other arrangements of the weights.

Table 6.

The segmentation results and 95% confidence intervals for the 15 multiple runs of original U-Net, U-Net with HF, and U-Net with average-pooled labels (AVG). Bold fonts indicate the best result.

		DSC	HD95 (mm)	AVD (%)	recall	F1-score
Original U-Net	Mean±SD	0.8033±0.0204*	6.2509±1.6870*	18.8337±6.086*	0.7261±0.0538*	0.7273±0.0466*
	95% CI	[0.0060, 0.0089]	[−0.7435, −0.3917]	[−2.8959, −1.2721]	[0.0212, 0.0440]	[0.0228, 0.0298]
Original + AVG	Mean±SD	0.8037±0.0191*	6.9537±2.5907*	17.6740± 6.4449	0.7373±0.0552*	0.7340±0.0513*
	95% CI	[0.0055, 0.0085]	[−1.7264, −0.8143]	[−2.0247, −0.1762]	[0.0086, 0.0341]	[0.0126, 0.0266]
Original + HF	Mean±SD	0.8107±0.0203	5.6833±1.8080	16.7497±6.9472	0.7587±0.0456	0.7536±0.0436

^*p-value corrected by FDR < 0.05 between U-Net with HF and other (paired t-test).

Abbreviation – SD: standard deviation; CI: confidence interval.

Table 7.

Influence of various weighting among all the output layer losses on the segmentation accuracy. Bold fonts indicate the best result.

	DSC	H95 (mm)	AVD (%)	Recall	F1
Original + HF (all 0.2)	0.8139±0.0878	5.0383±4.3894	15.893±24.845	0.7725±0.1033	0.7575±0.0903
Original + HF (1/15 → 5/15)	0.8095±0.0952	5.4751±4.9443	17.890±29.337	0.7707±0.1055	0.7523±0.0956
Original + HF(5/15 → 1/15)	0.8093±0.0912	6.1427±5.7800	16.709±18.847	0.7496±0.1020	0.7595±0.0746

4.3. Clinical utility of the proposed segmentation approach

WMH volumes computed using our method were significantly associated with cognitive scores and group diagnosis of the ANDI subjects (Table 8; MMSE, CDR sum, and group diagnosis: Bonferroni correction p-value < 0.05; ADAS-Cog: FDR correction p-value < 0.05). In other words, the bigger WMH was, the more was cognitive decline and the more severe was the diagnosis of a patient observed. Furthermore, our linear model showed that a 1-standard deviation (SD) increase in WMH volume corresponded 0.133 and 0.165 SD increases in ADAS-Cog and CDR sum scores, respectively, and a 0.176 SD decrease in MMSE score.

Table 8.

Summary of the results of the general linear model using WMH volumes and covariates as independent variables and cognitive scores and group diagnosis as dependent variables.

	Cognitive scores
	MMSE		ADAS-Cog		CDR sum		Group(CN/MCI/AD)
	β	p-value	β	p-value	β	p-value	β	p-value
WMH volume	−0.176	< 0.001**	0.133	0.017*	0.165	0.009**	0.131	0.008**
Age	–	–	–	–	–	–	–	–
CV risk	–	–	–	–	–	–	–	–
Education	0.062	< 0.001**	−0.061	0.001**	−0.047	0.031*	–	–
Gender	–	–	–	–	–	–	–	–
ApoE4 genotype	−0.296	< 0.001**	0.184	< 0.001**	0.421	< 0.001**	0.299	< 0.001**
Race	–	–	–	–	–	–	–	–

^*p-value corrected by FDR < 0.05.

^**p-value corrected by Bonferroni method < 0.05.

Even though feeding WMH volume alone to the classifier did not achieve a better classification compared to using clinical variables only (Fig. 3), We observed that combining WMH volume with clinical variables resulted in the best classification performances between CN and AD (AUC=0.75) and between MCI and AD (AUC=0.67). In the classification of CN vs. MCI, the classification performance was not improved by combining WMH volume and clinical variables (AUC=0.58) compared to using clinical variables only (AUC=0.59).

Fig. 3.

The receiver operating characteristic (ROC) curves for logistic regression about two types of the classification (CN vs AD and MCI vs AD).

5. Discussion

We proposed a new U-Net variant with multi-scale highlighting foregrounds (HF) in this paper. Our network framework was designed to improve the detection of the WMH voxels involving a degree of partial volume effects. We added the multi-scale label images that were max-pooled by HF to a U-Net for WMHs segmentation. The proposed method has been placed at the top rank for the overall score in the MICCAI WMH Segmentation Challenge. The WMH volume computed using our automated approach was significantly associated with cognitive performance scores (MMSE, ADAS-Cog, and CDR-sum) and the dementia diagnosis (CN, MCI, and AD). Furthermore, the automated WMH volumetry improved the classification of unseen subjects into CN, MCI, or AD.

5.1. Comparison to other methods evaluated in the WMH segmentation challenge

Our method has achieved the best overall evaluation scores, the highest dice similarity index, and the best F1-score in the MICCAI WMH Segmentation Challenge among all the listed 39 methods. Our method has also achieved the top 5 for other evaluation metrics (Hausdorff distance 95: 2nd, average volume difference: 3rd, and recall: 5th). Given that the Dice similarity index represents the overlap between the automated and manual segmentation and the Hausdorff distance represents their boundary gap, our achievement of high accuracy in these two indices demonstrates that the proposed method successfully detects the WMH voxels that are located either at the boundary of the WMH or in small WMH volumes and consequently exposed to PVE. Indeed, a visual inspection of individual segmentations shows the superior segmentation of such partial volume voxels in the proposed U-Net with multi-scale HF compared to the standard U-Net (Fig. 4). In Fig. 4, the proposed method more accurately segmented WMHs on the boundary of manual WMHs (Subject 1) as well as small clusters of WMHs (Subjects 2–4) compared to the standard U-Net. Despite a relatively low recall (5th rank, meaning relatively more false-negative voxels detected), we achieved the best F1-score which is the harmonic mean of recall and precision. This suggests two things. First, our method yielded a higher true-positive rate and a lower false-positive rate than other methods. Second, our method may have difficulty in detecting some WMH voxels even though it detects the small cluster and the border of WMHs better than other approaches.

Fig. 4.

Segmentation results in the training dataset. From top to bottom are axial slices of four different subjects. From left to right are FLAIR image, ground truth, the results from the standard U-Net, and the results from the proposed U-Net with multi-scale HF method. Yellow voxels indicate WMHs segmented using each method. Color boxes show our approach’s improvement of false-positives (orange border) or false-negatives (green border) observed in the standard U-Net.

5.2. Configuration of the multi-scale highlighting foregrounds

The segmentation performance was the best when setting equal all the weights of different scale HFs suggesting that the feature maps generated from all scales are equally important for deep learning of WMHs segmentation. Our method achieved statistically significant improvements in all metrics compared to the original U-Net, and significant improvements in all metrics excepted average volume difference compared to the U-Net with AVG (Table 6). Although U-Net with AVG tends to have better performance in all metrics than the original U-Net, these differences did not reach the statistical significance. These results indicate that the superior performance of U-Net with HF did not merely result from a lucky random seed. The significant improvements in Dice score and F1-score by our method suggest that the proposed method can more accurately detect WMH clusters that are hard to detect by other methods, such as small WMHs involving large partial volume effects.

Based on these results, therefore, we confirm that the proposed HF approach is highly advantageous to WMHs segmentation and likely to segmentation of brain lesions which have similar characteristics (size, shape, or intensity), such as multiple sclerosis (Weeda et al., 2019), microbleeds (Seghier et al., 2011), and perivascular space (Ballerini et al., 2018). Since our method uses multi-scale label images emphasizing foreground voxels (i.e., unbalanced data), it can be used in combination with various loss functions (boundary loss, (Kervadec et al., 2019); focal loss, (Lin et al., 2017); Tversky loss, (Salehi et al., 2017); and focal Tversk loss, (Abraham and Khan, 2019)) to overcome the problem of unbalanced data. It may be worth trying to combine the above-mentioned loss functions and HF in various ways and compare the results to find a loss function that fits well with HF. Additionally, our method can also simply be applied to various networks based on the encoder-decoder structure such as U-Net variants or other variants of deep supervision methods.

5.3. Clinical evaluation

Previous studies showed that the increase in WMHs volume relates to cognitive decline (Barber et al., 1999; Dubois et al., 2014; Habes et al., 2016; Lee et al., 2016; Prins and Scheltens, 2015). On the basis of findings in these studies, we evaluated the clinical utility of the proposed approach by investigating whether automated WMH volumetry can predict cognitive performance declines or the diagnosis of a subject (CN, MCI, and AD). Our results demonstrate that the automatically computed WMH volume is significantly associated with cognitive performance in the direction we hypothesized (Table 8).

Furthermore, we hypothesized that feeding the automatically computed WMH volumes to a classifier individually can diagnose subjects. The results of this experiment showed that classification performance for CN vs. AD and MCI vs. AD can be improved using the combined feature-set of WMH volumes and clinical variables. These results are consistent with previous findings that WMHs provide an imaging marker for AD (Habes et al., 2016; Lee et al., 2016; Prins and Scheltens, 2015).

6. Conclusions

In the current study, we proposed a U-Net with multi-scale highlighting foregrounds (HF). Our various evaluations show that the proposed method improves detecting WMH voxels with partial volume effects as intended. However, it still remains challenging for our model to retain both high precision and recall. Attention-based models (Chen et al., 2016b; Woo et al., 2018) that effectively learn important characteristics of a target structure for segmentation can potentially be a way to solve this issue. To improve WMHs segmentation, integrating an attention-based model into deep neural networks is thus suggested in the future. Our clinical evaluation demonstrates the clinical utility of our method. Yet, the individual diagnosis of unseen subjects using WMH volumes alone is below the clinical standard. In a further study, other information of WMHs such as the location or distribution of WMH volumes and the longitudinal trajectory of WMH volume changes would be incorporated for the improvement of individual diagnosis. The implementation of our proposed method is available at Dockerhub (Merkel (2014); https://hub.docker.com/r/wmhchallenge/pgs).

Data and code availability statements

The data that support the findings of this study are openly available in 2017 MICCAI WMH Segmentation Challenge homepage at https://wmh.isi.uu.nl/data/, reference number (Kuijf, 2019). Our code also is openly available at https://hub.docker.com/r/wmhchallenge/pgs.