A 2D FSI mathematical model of blood flow to analyze the hyper-viscous effects in atherosclerotic COVID patients

Abstract

Recent researches on COVID 19 has been extended to analyze the various morphological and anatomical changes in a patient's body due to the invasion of the virus. These latest studies have concluded that there happens a high rise in the viscosity of the blood in a COVID 19 patient, supported by the extensive analysis of the clinical data. In the present paper, a mathematical model in the form of a differential equation system has been proposed to disclose the various changes that occur in the flow across the stenosis of an arterial segment. The consequences of the hyperviscosity of blood on the blood flow characteristics in a stenosed artery are analyzed by solving the model using a finite element method (FEM) solver. A laminar flow coupled with solid mechanics through the Fluid-Structure Interaction (FSI) interface has been studied using an Arbitrary Lagrangian-Eulerian (ALE) method. For the first time, the mathematical model was used to analyze the hyper-viscous flow condition in COVID 19 patients. The present research is mainly based on the numerous clinical reports enlisting the various morphological, hematological, and rheological changes in the blood.

Nomenclature:

$\overrightarrow{\mathit{u}}$

Velocity vector $(m/s)$

$\mathit{t}$

Time variable ($s$)

$\mathit{p}$

Fluid pressure ($Pa$)

$\mathit{D}\left(\overrightarrow{\mathit{u}}\right)$

Starin rate $\left(s^{-1}\right)$

$\overrightarrow{\mathit{s}}$

Displacement vector

$\mathit{A},\mathit{B}$

Lame’ constants ($Pa$)

${\mathit{E}}_{\mathit{Y}}$

Young's modulus ($N/m^2$)

Greek Letters

$\mathit{\rho }$

Blood density ($Kg/m^3)$

${\mathit{\rho }}_{\mathit{w}}$

Arterial wall density ($Kg/m^3)$

μ

Blood viscosity ($Pas$)

$\mathit{\gamma }$

Poisson ratio

$\mathit{\Omega }$

Fluid flow domain

$\partial \mathit{\Omega }$

Fluid domain boundary

${\mathit{\Gamma }}^{\mathit{d}}$

Dirichlet boundary

${\mathit{\Gamma }}^{\mathit{d}}$

Neumann boundary

${\mathit{\Gamma }}^{\mathit{out}}$

Outlet boundary

${\mathit{\Gamma }}_{\mathit{N}}$

Solid domain boundary towards media tunica

${\mathit{\Gamma }}_{\mathit{D}}$

Inlet and outlet for the solid domain

$\mathit{\tau }$

Time variable

${\mathit{\Omega }}_{\mathit{s}}$

Solid domain

${\mathit{\Omega }}_0$

Reference computational domain

${\mathit{\Omega }}_{{\mathfrak{R}}_{\mathit{t}}}$

Moving computational domain

Other symbols

$\Vert .{\Vert }_2$

2-norm or Euclidean norm

Inner product

${\mathit{W}}^{\mathit{p},\mathit{q}},{\mathit{H}}^1$

Sobolev spaces

${\mathit{L}}^{\mathit{p}}$

Lebesgue space

${\mathit{C}}^{\mathit{p},\mathit{q}}$

Holder space

${\mathbb{R}}^{\mathit{N}}$

n-dimensional real vector space

$\mathit{g},\mathit{h},{\mathit{s}}_0,{\mathit{s}}_1,$

${\mathit{u}}_0,{\mathit{p}}_0,\mathit{\alpha },\mathit{\beta }$ Given functions

1. Introduction

Rapidly spreading disease, COVID 19, not only affects the respiratory system of the patient but also has a severe impact on the morphological, hematological, and rheological properties of the blood [[1], [2], [3]]. An understanding of these changes in the blood properties can aid in the disease diagnosis and can aid in decision-making. The major morphological changes encountered in the blood of COVID 19 patients are abnormal neutrophils, lymphocytes with abundant blue cytoplasm, and activation of abnormally shaped monocytes [1,4]. The most prevalent hematological findings are thrombocytopenia [5], lymphocytopenia [6,7], neutrophilia [8,9]. The clinical reports on hematological parameters have revealed that the alterations in these parameters can be the strongest determinants of undesirable treatment outcomes, such as (Intensive Care Unit) ICU admission or even death. Eventually, the most prominent changes that increase the severity of the disease in a patient who is already at risk of atherosclerosis or aneurysms are the rheological changes. These rheological changes comprise the factors namely viscosity, shear rate, and shear stress [10]. The rationale behind these alterations can be reduced deformation and the increased aggregation of red blood cells, and abnormal red blood cell morphology [[11], [12], [13]]. The aberrant changes in red blood cells result in rising in the viscosity values of the blood in COVID 19 patients [3,14].

In the case of a COVID infected patient, it has been noticed that the (Red Blood Cells) RBCs undergo rheological changes such as deformability, aggregation, and abnormal morphology [15]. The decreased deformability of RBCs is recorded due to the RBC membrane distortion [16]. The reason for the increased RBC aggregation has not been made clear yet. As a consequence of these changes in RBC structure, the blood viscosity is noticed to have higher values when compared to the non-COVID individuals with stenosis. Numerous clinical and therapeutic studies have proved the hyper-viscous property of the blood of COVID-infected patients [3,14,17]. These previously published articles are utilized as a source of the data for the present study.

Viscosity, a prominent property of any fluid which plays an important role in the rheology of the fluid. The same argument holds for blood as well. In the preservation of vascular homeostasis, viscosity plays a vital part. And it is the factor that is utilized in the measurement of the wall shear stress (WSS) imparted by the blood on the vessel wall [18]. Wall shear stress is a flow characteristic that affects the orientation of the endothelial layer of the inner vessel wall [19]. The magnitude of WSS decides the disorientation of the endothelial layer leading to the pathogenic environment in the arteries. Hence, viscosity alterations result in a change in flow characteristics leading to pathogenesis. Blood, by default, has a self-adjusting viscosity depending on the flow dimensions. The alterations in the viscosity of blood impart non-Newtonian nature to the flow [20]. But for the present study, to interpret the changes that happen in flow characteristics due to the increase in the viscosity, the Newtonian flow of blood is considered.

The arterial wall is a complex structure composed of several chemical components as a three-layer framework. The layers are [21]:

• •Tunica Intima, the inner layer with the endothelial lining
• •Tunica media, the elastic and muscular middle layer
• •Adventitia, the outer layer

Each of these layers performs its functions in different aspects of maintaining blood vessel homeostasis. Among the three layers, intima plays a significant role in blood flow. It regulates the oscillations caused due to the flow of the fluid in the lumen of the artery [22]. Hence, for the present study, the intimal layer has been considered to study the hyper-viscous effects of the blood in COVID patients. The governing equations of the fluid flow and the structure model are coupled using the Fluid-Structure Interaction (FSI) model through Arbitrary Lagrangian-Eulerian (ALE) formulation. A note on the ALE formulation has been discussed in the later sections of the manuscript.

The study of stenosis and the spread of COVID infection are studied, by modeling mathematically, as two separate subjects. But the clinical reports on the rheology of COVID infected person builds a connection between these two subjects. The rise in viscosity seen in the infected person's blood creates modifications in the flow characteristics across the stenosis lump, as viscosity is a prominent feature deciding the flowing nature. The study in this direction has not been made using mathematical models. Thus, the theme of our work is to investigate the flow characteristics across a stenosed artery using the clinically proved rheological parameter values.

The objective of the present work is to consider the hyper-viscous effects of blood in an atherosclerotic artery and to investigate the various abnormalities caused due to the increased viscosity in COVID patients. Various alterations exhibited by the rise in the viscosity on the flow characteristics are investigated. Initially, an arterial segment with pre-existing stenosis is constructed computationally. Following the mesh construction, the simulations are run for normal and hyper-viscous values. To completely understand the hyper-viscous effects in COVID patients, the following sections are considered. In section 2 of the manuscript, the methodology adopted to study the hyper-viscous effects of blood is presented. The mathematical model framed for the present study is mathematically analyzed for the existence of the solution, with the aid of various principles of functional analysis and fluid dynamics. The energy inequalities for the fluid and the solid models are investigated to access the break-free dependence of the solution on the given data. Also, as the model formulated is solved using a Finite Element Method (FEM) solver, the mesh details are also presented in the following sub-sections. In section 3, we project the simulation results obtained using an FSI model. Detailed discussion about the results obtained is presented in this section of the manuscript. In the final section, we investigate the future developments that can be made to the framed mathematical model.

2. Methodology

Blood flow in the arterial system is modeled using the standard Navier Stokes equation coupled with the continuity equation. The mathematical model is framed by accounting for the following assumptions:

• As the present study interprets the various alterations in flow characteristics, treating blood as Newtonian is suitable. Blood viscosity, shear rate, shear stress, and flow geometry dimensions are closely related parameters. The viscosity of blood varies with the shear rate; whereas the shear rate is a function of the diameter of the flow path [23]. In the present study, the geometry is designed as a representative of a non-pathologized coronary artery model which encounters a shear rate greater than $100s^{-1}$. Thus, the Newtonian property is adopted for the study [24,25]. Even though the present investigation deals with the pathologized arterial segment with stenosis lump, the Newtonian nature is chosen as the steady-state simulation is considered [26].

• •Blood flow is incompressible. The flow is assumed to be laminar.
• •The arterial wall is made up of only one layer, intima. This assumption is supported by the fact that the blood flow is considerably affected by the intimal layer when compared to the other two layers [27].
• •As the nature of blood is assumed to be Newtonian, the stationary study consideration has been made for the present investigation. Transient analysis demands the non-Newtonian property of the blood.
• •The only force driving the blood flow in the arterial domain considered is the pressure gradient. No external forces are considered for the present study.
• •Atherosclerotic plaque is already developed in the patient under study.

2.1. Lumenal flow is modeled as

$$\mathit{\rho }\frac{\partial \mathit{u}}{\partial \mathit{t}}+\mathit{\rho }\left(\mathit{u}.\nabla \right)\mathit{u}+\nabla \mathit{p}-2\nabla .\left(\mathit{\mu }\mathit{D}\left(\mathit{u}\right)\right)=0,\text{in}\text{Ω},t\in \left(0,T\right)$$ (1)

$$\nabla .\mathbf{u}=0,\text{in}\text{Ω},t\in \left(0,T\right)$$ (2)

$$\mathit{u}={\mathit{u}}_0,\text{in}\text{Ω},t=0$$ (3)

Let $\mu$ be a bounded function that is strictly positive, for two constants ${\mu }_0>0$ and ${\mu }_1>0$ we have $\forall t\in \left(0,T\right),{\mu }_0\le \mu \le {\mu }_1$ almost everywhere in $\text{Ω}$.

Boundary conditions (BCs):

$$\mathit{u}=\mathit{g}\text{on}{\text{Γ}}^d,t\in \left(0,T\right)$$ (4)

$$-\mathit{pn}+2\mathit{\mu }\mathit{D}\left(\mathit{u}\right).\mathit{n}=\mathit{h}\text{on}{\text{Γ}}^n,t\in \left(0,T\right)$$ (5)

where ${\text{Γ}}^d$ and ${\text{Γ}}^n$ are the portions of $\partial \text{Ω}$ at which the Dirichlet and Neumann BCs are applied, such that. ${\text{Γ}}^d\cup {\text{Γ}}^n=\partial \text{Ω}.$

Now, the model formulated is analyzed mathematically for the existence of the solution by converting it to the weak form. Weak formulations are key tools to analyze mathematical models, so that the notions of linear algebra may be transferred to tackle problems in other domains, such as partial differential equations. Various principles of Functional Analysis are utilized in the upcoming subsection to mathematically analyze the model fabricated. These principles are enlisted in the form of Table 1 .

Table 1.

Principles of functional analysis and fluid dynamics.

Sl.No.	Principle	Statement	Reference
1	Cauchy- Schwarz Inequality	For any n-dimensional vectors v and w, . Also, only when v is a scalar multiple of w and conversely.	[28]
2	Sobolev Embedding Theorem	For a bounded domain $\text{Ω}$, and $1\le q<\infty$, ${\mathit{W}}_0^{1,\mathit{q}}\left(\mathbf{\Omega }\right)\subseteq \{\begin{array}{l}{\mathit{L}}^{\frac{\mathit{nq}}{\mathit{n}-\mathit{q}}}\left(\mathbf{\Omega }\right),q<n\hfill \\ {\complement }^{0,\mathit{\alpha }}\left(\mathbf{\Omega }\right),\alpha =1-\frac{\mathit{n}}{\mathit{q}},q>n\hfill \\ i.e.inparticular\subseteq {\complement }^0\left(\Omega \right)\hfill \end{array}$ Also, these embeddings are continuous.	[29]
3	Poincare Inequality	For $f:{\mathbb{R}}^{\mathbb{N}}\to \mathbb{R}$ of $H^1\left(\text{Ω}\right)$, a Sobolev space, with f vanishing on a strictly positive measure subset of the boundary. Then, for a positive constant $C_p$ depending on the domain and the subset considered, ${||\mathbf{f}||}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}\le {\mathit{C}}_{\mathit{p}}{||\mathbf{\nabla }\mathbf{f}||}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}$	[30]
4	Korn Inequality	For a domain $\text{Ω}$ with smooth boundary, $1\le i,j\le n,\sum _{\mathit{i},\mathit{j}}{\left|\left|\frac{1}{2}\left(\frac{\partial {\mathit{v}}_{\mathit{i}}}{\partial {\mathit{x}}_{\mathit{j}}}+\frac{\partial {\mathit{v}}_{\mathit{j}}}{\partial {\mathit{x}}_{\mathit{i}}}\right)\right|\right|}_{0,\mathbf{\Omega }}^2+{\left|\left|\overrightarrow{\mathit{v}}\right|\right|}_{0,\mathbf{\Omega }}^2\ge \mathit{C}{\left|\left|\overrightarrow{\mathbf{v}}\right|\right|}_{1,\mathbf{\Omega }}^2,\forall \overrightarrow{\mathit{v}}\in \mathit{E}$ $\mathit{E}=\left\{\overrightarrow{\mathit{w}}\in {\left({\mathit{L}}^2\left(\mathbf{\Omega }\right)\right)}^2:\frac{1}{2}\left(\frac{\partial {\mathit{w}}_{\mathit{i}}}{\partial {\mathit{x}}_{\mathit{j}}}+\frac{\partial {\mathit{w}}_{\mathit{j}}}{\partial {\mathit{x}}_{\mathit{i}}}\right)\in {\mathit{L}}^2\left(\mathbf{\Omega }\right),\forall \mathit{i},\mathit{j}\right\}$ where C is a constant.	[31]
5	Green formula	For $\mathit{b}:\mathbf{\Omega }\to {\mathbb{R}}^2$ is a ${\complement }^1$ vector field. $\left(\nabla \mathit{u},\mathit{bv}\right)=-\left(\mathit{ub},\nabla \mathit{v}\right)-(\mathit{u},\mathit{v}\nabla .\mathit{b})$ where $(.,.)$ is the $L_2$ inner product.	[32]
6	Gronwall's lemma	If f is a non-negative integrable function in the interval (0,t) and for two functions g and $\varphi$ in the interval, with g non-decreasing. For g and $\varphi$ being continuous, the following condition holds: If $\mathit{\varphi }\left(\mathit{t}\right)\le \mathit{g}\left(\mathit{t}\right)+\underset{0}{\overset{\mathit{t}}{\int }}\mathit{f}\left(\mathit{\tau }\right)\mathit{\varphi }\left(\mathit{\tau }\right)\mathit{d}\mathit{\tau },\forall \mathit{t}\mathbf{\in }\left(0,\mathit{t}\right),$ then $\mathit{\varphi }\left(\mathit{t}\right)\le \mathit{g}\left(\mathit{t}\right)\mathit{exp}\underset{0}{\overset{\mathit{t}}{\int }}\mathit{f}\left(\mathit{\tau }\right)\mathit{d}\mathit{\tau },\forall \mathit{t}\mathbf{\in }\left(0,\mathit{t}\right).$	[33]
7	ALE Transport Theorem	Let ${\mathit{W}}_0\subset {\mathbf{\Omega }}_0,{\mathit{W}}^{{\mathfrak{R}}_{\mathit{t}}}\subset {\mathbf{\Omega }}_{\mathit{t}}$ be its image under the mapping ${\mathfrak{R}}_{\mathit{t}}$. Also, for $\mathit{f}:(0,\mathit{t})\times {\mathbf{\Omega }}_{\mathit{t}}\to \mathbb{R}$ be continuously differentiable concerning both variables. Then, $\frac{\mathit{d}}{\mathit{dt}}\underset{{\mathit{W}}^{{\mathfrak{R}}_{\mathit{t}}}}{\int }\mathit{f}=\underset{{\mathit{W}}^{{\mathfrak{R}}_{\mathit{t}}}}{\int }\left(\frac{{\mathit{D}}^{\mathfrak{R}}}{\mathit{Dt}}\mathit{f}+\mathit{f}\nabla .\mathbf{w}\right)=\underset{{\mathit{W}}^{{\mathfrak{R}}_{\mathit{t}}}}{\int }(\frac{\partial \mathit{f}}{\partial \mathit{t}}+\nabla .\left(\mathit{fw}\right))=\underset{{\mathit{W}}^{{\mathfrak{R}}_{\mathit{t}}}}{\int }\frac{\partial \mathit{f}}{\partial \mathit{t}}+\underset{\partial {\mathit{W}}^{{\mathfrak{R}}_{\mathit{t}}}}{\int }\mathit{fw}.\mathit{n}$ where ${\mathbf{\Omega }}_0$ is the reference configuration, ${\mathbf{\Omega }}_{\mathit{t}}$ is the domain varying with time.	[34]

2.2. Weak form of the Navier Stokes equation

Consider a vector function $v\in V$, where $V$ is a functional space referred to as test function space.

Now, we perform the following operations:

• •Taking the scalar product of Navier Stokes equation with the vector function $v$
• •Integrating over $\text{Ω}$, the domain geometry

As a result, we get

$$\mathit{\rho }\left(\frac{\partial \mathit{u}}{\partial \mathit{t}},\mathit{v}\right)+\mathit{\rho }\left(\left(\mathit{u}.\nabla \right)\mathit{u},\mathit{v}\right)+2\underset{\mathbf{\Omega }}{\int }\mathit{\mu }\mathit{D}\left(\mathit{u}\right):\mathit{D}\left(\mathit{v}\right)-\left(\mathit{p},\nabla .\mathbf{v}\right)=\underset{\partial \mathbf{\Omega }}{\int }\mathit{v}.\mathbf{(}2\mathit{\mu }\mathit{D}\left(\mathit{u}\right).\mathit{n}-\mathit{pn}\mathit{)}$$ (6)

Performing a similar operation on the continuity equation by considering the vector function $q$ from the functional space $Q$, we get

$$\left(\nabla .\mathbf{u},\mathbf{q}\right)=0$$ (7)

Thus, the resulting system is

$$\begin{array}{l}\mathit{\rho }\left(\frac{\partial \mathit{u}}{\partial \mathit{t}},\mathit{v}\right)+\mathit{\rho }\left(\left(\mathit{u}.\nabla \right)\mathit{u},\mathit{v}\right)+2\underset{\mathbf{\Omega }}{\int }\mathit{\mu }\mathit{D}\left(\mathit{u}\right):\mathit{D}\left(\mathit{v}\right)-\left(\mathit{p},\nabla .\mathbf{v}\right)=\underset{{\mathbf{\Gamma }}^{\mathit{d}}}{\int }\mathit{v}.\left(2\mathit{\mu }\mathit{D}\left(\mathit{u}\right).\mathit{n}-\mathit{pn}\right)+\underset{{\mathbf{\Gamma }}^{\mathit{n}}}{\int }\mathit{v}.\mathit{h}\\ \text{and}\left(\nabla .\mathbf{u},\mathbf{q}\right)=0\end{array}$$ (8)

We notice that the Neumann limit contribution is now data, whereas the Dirichlet boundary contribution can be deleted by selecting the testing range $V$ correctly.

Let $\mathit{V}=\left\{\mathit{v}\mathbf{\in }{\mathit{H}}^1\left(\mathbf{\Omega }\right),\mathit{v}|{\mathbf{\Gamma }}^{\mathit{d}}=0\right\}$, $\mathit{Q}=\left\{\mathit{q}\mathbf{\in }{\mathit{L}}^2\left(\mathbf{\Omega }\right),\mathit{with}\underset{\mathbf{\Omega }}{\int }\mathit{q}=0\mathit{if}{\mathbf{\Gamma }}^{\mathit{d}}=\partial \mathbf{\Omega }\right\}$

And if we seek at each $t\in \left(0,T\right)$, the velocity in ${\mathit{V}}_{\mathit{g}}=\left\{\mathit{u}\mathbf{\in }{\mathit{H}}^1\left(\mathbf{\Omega }\right),\mathit{u}|{\mathbf{\Gamma }}^{\mathit{d}}=\mathit{g}\right\}$ and pressure in $Q$.

Now let us find, $\forall t\in \left(0,T\right),u\left(t\right)\in V_g$ and $p\left(t\right)\in Q$ such that.

SYSTEM 1:$\mathit{\rho }\left(\frac{\mathbf{\partial }\mathbf{u}}{\mathbf{\partial }\mathbf{t}}\mathbf{,}\mathbf{v}\right)\mathbf{+}\mathit{a}\left(\mathbf{u}\mathbf{,}\mathbf{v}\right)\mathbf{+}\mathit{c}\left(\mathbf{u}\mathbf{,}\mathbf{u}\mathbf{,}\mathbf{v}\right)\mathbf{+}\mathit{b}\left(\mathbf{v}\mathbf{,}\mathbf{p}\right)\mathbf{=}{\mathbf{\int }}_{{\mathbf{\Gamma }}^{\mathbf{n}}}\mathit{v}\mathbf{.}\mathit{h}\mathbf{,}\mathbf{\forall }\mathit{v}\mathbf{\in }\mathit{V}\mathit{b}\mathbf{(}\mathit{u}\mathbf{,}\mathit{q}\mathbf{)}\mathbf{=}\mathbf{0}\mathbf{,}\mathbf{\forall }\mathit{q}\mathbf{\in }\mathit{Q}where\mathit{a}\left(\mathit{u},\mathit{v}\right)=2\underset{\mathbf{\Omega }}{\int }\mathit{\mu }\mathit{D}\left(\mathit{u}\right):\mathit{D}\left(\mathit{v}\right)$,

$$\mathit{c}\left(\mathit{w},\mathit{u},\mathit{v}\right)=\mathit{\rho }\underset{\mathbf{\Omega }}{\int }\left(\left(\mathit{w}.\nabla \right)\mathit{u}.\mathit{v}\right),$$

$$\mathit{b}\left(\mathit{v},\mathit{p}\right)=-\underset{\mathbf{\Omega }}{\int }\mathit{p}\nabla .\mathbf{v}$$

In the case of the homogeneous Dirichlet problem, when ${\text{Γ}}^d=\partial \text{Ω}$ and $g=0,$ we get

$$\mathit{V}={\mathit{H}}_0^1\left(\mathbf{\Omega }\right),\mathit{Q}={\mathit{L}}_0^2\left(\mathbf{\Omega }\right)=\left\{\mathit{q}\mathbf{\in }{\mathit{L}}^2\left(\mathbf{\Omega }\right),\underset{\mathbf{\Omega }}{\int }\mathit{q}=0\right\}$$ (9)

and the weak form becomes.

• $\forall t\in \left(0,T\right)$, to find $u\left(t\right)\in V$ and $p\left(t\right)\in Q$ such that

SYSTEM 2:

$$\mathit{\rho }\left(\frac{\partial \mathit{u}}{\partial \mathit{t}},\mathit{v}\right)+\mathit{a}\left(\mathit{u},\mathit{v}\right)+\mathit{c}\left(\mathit{u},\mathit{u},\mathit{v}\right)+\mathit{b}\left(\mathit{v},\mathit{p}\right)=0,\forall \mathit{v}\mathbf{\in }\mathit{V},$$

$$\mathit{b}\left(\mathit{u},\mathit{q}\right)=0,\forall \mathit{q}\mathbf{\in }\mathit{Q}$$

Proposition 1

The bilinear and the trilinear forms$\mathit{a}:\mathit{V}\times \mathit{V}\to \mathbb{R},\mathit{c}:\mathit{V}\times \mathit{V}\times \mathit{V}\to \mathbb{R},\mathit{b}:\mathit{V}\times \mathit{Q}\to \mathbb{R}$are continuous with respect to their arguments. In addition, the bilinear form$\mathit{a}(.,.)$is coercive.

Proof

The continuity of the bilinear forms a and b can be proved by the application of the principles of functional analysis (entry 1 from Table 1).

For the tri-linear form c, we consider the Sobolev Fractional Theorem, we get

$${\mathit{H}}^1\left(\text{Ω}\right)\to {\mathit{L}}^6\left(\text{Ω}\right)$$

$$\Rightarrow {\mathit{H}}^1\left(\text{Ω}\right)\to {\mathit{L}}^4\left(\text{Ω}\right)$$

Itfollowsthat, $\forall u,v,v\in V$$\mathit{c}\left(\mathit{w},\mathit{u},\mathit{v}\right)\le {\mathit{C}}_1{||\mathbf{w}||}_{{\mathit{H}}^1\left(\mathbf{\Omega }\right)}{||\mathbf{u}||}_{{\mathit{H}}^1\left(\mathbf{\Omega }\right)}{||\mathbf{v}||}_{{\mathit{H}}^1\left(\mathbf{\Omega }\right)}$, ${\mathit{C}}_1\mathbf{\in }{\mathrm{ℝ}}^{+}$ , implies that c is continuous.

The coercivity of 'a' can be derived from Poincare inequality- a multidimensional caseandtheKorninequality. Hencethelemma.

Define ${\mathit{V}}_{\mathit{div}}=\left\{\mathit{u}\mathbf{\in }\mathit{V}:\nabla .\mathit{u}=0\mathit{a}.\mathit{e}.\mathit{in}\mathbf{\Omega }\right\}$

Theorem 1

If u is a weak solution of the variational formulation (system 2), then it satisfies

$$\mathit{\rho }\left(\frac{\partial \mathit{u}}{\partial \mathit{t}},\mathit{v}\right)+\mathit{a}\left(\mathit{u},\mathit{v}\right)+\mathit{c}\left(\mathit{u},\mathit{u},\mathit{v}\right)=0,\forall \mathit{v}\mathbf{\in }{\mathit{V}}_{\mathit{div}},\mathit{t}\in \left(0,\mathit{T}\right)$$ (10)

Conversely, if, $\forall \mathit{t}\in \left(0,\mathit{T}\right),\mathit{u}\left(\mathit{t}\right)\mathbf{\in }{\mathit{V}}_{\mathit{div}}$is a solution of equation (3) and $\frac{\partial \mathit{u}}{\partial \mathit{t}}\in {\mathit{L}}^2\left(\text{Ω}\right)$ then $\exists$ a unique $\mathit{p}\mathbf{\in }\mathit{Q}$ such that $(\mathit{u},\mathit{p})$ satisfies (2).

Proof: If u is the solution of the system (2) then it is an element of the set $V_{div}$ and hence it fulfills (10), since $V_{div}\subset V.$

Inverse implication: For $\text{Ω}$ being a domain of ${\mathbb{R}}^{\mathbb{N}}$ and let $L\in V^{\text{'}}$. Then $\mathit{L}\left(\mathit{v}\right)=0,\forall \mathit{v}\mathbf{\in }{\mathit{V}}_{\mathit{div}}$ iff there exists a function p in $L^2\left(\text{Ω}\right)$ satisfying the equation $\mathit{L}\left(\mathit{v}\right)=\left(\mathit{p},\nabla .\mathit{v}\right),\forall \mathit{v}\mathbf{\in }\mathit{V}$.

The application L is defined as

$$\mathit{L}\left(\mathit{v}\right)=\mathit{\rho }\left(\frac{\partial \mathit{u}}{\partial \mathit{t}},\mathit{v}\right)+\mathit{a}\left(\mathit{u},\mathit{v}\right)+\mathit{c}\left(\mathit{u},\mathit{u},\mathit{v}\right),\forall \mathit{v}\mathbf{\in }\mathit{V}$$ (11)

Then, $\mathit{L}\left(\mathit{v}\right)$ features to $V^{\prime }$as it is a linear continuous functional defined on V. This proves the converse part of the theorem.

We take the energy inequality for the weak interpretation (system 2) as a measurable dependent on the solution from the data.

Lemma 2

If u is a solution of(2)then$\mathit{c}(\mathit{u},\mathit{u},\mathit{u})$=0.

Proof: We have

$$\mathit{c}\left(\mathit{u},\mathit{u},\mathit{u}\right)=\underset{\mathbf{\Omega }}{\int }\left(\mathit{u}.\nabla \right)\mathit{u}.\mathit{u}$$

$$=\underset{\mathbf{\Omega }}{\int }1/2\nabla {\left(\left|\mathit{u}\right|\right)}^2.\mathit{u}$$

=$-1/2\underset{\mathbf{\Omega }}{\int }{\left(\left|\mathit{u}\right|\right)}^2\nabla .\mathit{u}$ + $1/2\underset{\partial \mathbf{\Omega }}{\int }{\left(\left|\mathit{u}\right|\right)}^2\mathit{u}.\mathit{n}$, by Green formula

As $\mathit{u}=0$ on $\partial \text{Ω},$

$$\mathit{c}\left(\mathit{u},\mathit{u},\mathit{u}\right)=-1/2\underset{\mathbf{\Omega }}{\int }{\left(\left|\mathit{u}\right|\right)}^2\nabla .\mathit{u}$$

$$=-\frac{1}{2}\left[\underset{\mathbf{\Omega }}{\int }{\left(\left|\mathit{u}\right|\right)}^2\nabla .\mathit{u}+\frac{\mathit{c}}{2}\underset{\mathbf{\Omega }}{\int }\left(\nabla .\mathbf{u}\right)\right],$$

where $\mathit{c}=\underset{\mathbf{\Omega }}{\int }{\left(\left|\mathit{u}\right|\right)}^2$

$$=-\frac{1}{2}\underset{\mathbf{\Omega }}{\int }({\left|\mathit{u}\right|}^2-\mathbf{c})\nabla .\mathit{u}$$

$$=-\frac{1}{2}\mathit{b}\left(\mathit{u},\left({\left|\mathit{u}\right|}^2-\mathit{c}\right)\right)=0,$$

As $\left({\left|\mathit{u}\right|}^2-\mathit{c}\right)\in \mathit{Q}$ and $\mathit{b}\left(\mathit{u},\mathit{q}\right)=0,\forall \mathit{q}\mathbf{\in }\mathit{Q}.$Hence the Proof.

The energy inequalities are given by.

Theorem 2

Let$\mathit{u}\left(\mathit{t}\right)\mathbf{\in }{\mathit{V}}_{\mathit{div}}$be a solution of system (2), $\forall \mathit{t}\mathbf{\in }\mathit{I}.$ Then the following inequalities hold

$$\left|\right|\mathit{u}\left(\mathit{t}\right)|{|}_{{\mathit{L}}^2\left(\text{Ω}\right)}^2+{\mathit{C}}_1\underset{0}{\overset{\mathit{t}}{\int }}||\nabla \mathit{u}(\mathit{\tau }\left)\right|{|}_{{\mathit{L}}^2\left(\text{Ω}\right)}^2\mathit{d}\mathit{\tau }\le {\mathit{e}}^{\mathit{t}}{\left(\left|\right|{\mathit{u}}_0|{|}_{{\mathit{L}}^2\left(\text{Ω}\right)}^2\right)}^{}$$ (12)

where ${\mathit{C}}_1=4{\mathit{\mu }}_0{\mathit{C}}_{\mathit{k}}$, and

$$\left|\right|\mathit{u}\left(\mathit{t}\right)|{|}_{{\mathit{L}}^2\left(\text{Ω}\right)}^2+{\mathit{C}}_2\underset{0}{\overset{\mathit{t}}{\int }}||\nabla \mathit{u}(\mathit{\tau }\left)\right|{|}_{{\mathit{L}}^2\left(\text{Ω}\right)}^2\mathit{d}\mathit{\tau }\le \left|\right|{\mathit{u}}_0|{|}_{{\mathit{L}}^2\left(\text{Ω}\right)}^2$$ (13)

where ${\mathit{C}}_2=2{\mathit{\mu }}_0{\mathit{C}}_{\mathit{k}}$, ${\mathit{C}}_{\mathit{k}}$ is the constant in a consequence of Korn inequality.

Proof: Consider $v=u\left(t\right)$ in the momentum equation of (10).

Thus,

$$\frac{1}{2}\frac{d}{dt}{\left|\right|\mathit{u}\left(\mathit{t}\right)\left|\right|}_{{\mathit{L}}^2\left(\text{Ω}\right)}^2+\mathit{c}\left(\mathit{u},\mathit{u},\mathit{u}\right)+\mathit{b}\left(\mathit{u},\mathit{p}\right)+\mathit{a}\left(\mathit{u},\mathit{u}\right)=0.$$ (14)

The second term of the above expression vanishes from the previously established property of the tri-linear form.

We get,

$$\frac{1}{2}\frac{\mathit{d}}{\mathit{dt}}{\left|\right|\mathit{u}\left(\mathit{t}\right)\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2+\mathit{b}\left(\mathit{u},\mathit{p}\right)+\mathit{a}\left(\mathit{u},\mathit{u}\right)=0.$$ (15)

The second term of the above expression vanishes by the definition of Q.

The resulting expression is,

$$\frac{1}{2}\frac{\mathit{d}}{\mathit{dt}}{\left|\right|\mathit{u}\left(\mathit{t}\right)\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2+\mathit{a}\left(\mathit{u},\mathit{u}\right)=0.$$ (16)

As a consequence of Korn inequality, we have

$$\mathit{a}\left(\mathit{u},\mathit{u}\right)=2\underset{\mathbf{\Omega }}{\int }\mathit{\mu }\mathit{D}\left(\mathit{u}\right):\mathit{D}\left(\mathit{v}\right)\ge 2{\mathit{\mu }}_0{\mathit{C}}_{\mathit{k}}{\left|\right|\nabla \mathit{u}\left(\mathit{t}\right)\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2$$ (17)

Then,

$$\frac{\mathit{d}}{\mathit{dt}}{\left|\right|\mathit{u}\left(\mathit{t}\right)\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2+4{\mathit{\mu }}_0{\mathit{C}}_{\mathit{k}}{\left|\right|\nabla \mathit{u}\left(\mathit{t}\right)\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2\le 0\le 2\mathit{\epsilon }{\left|\right|\mathit{u}\left(\mathit{t}\right)\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2$$ (18)

for any $\mathit{\epsilon }>0.$

Choosing $\mathit{\epsilon }=0.5,$

$$\frac{\mathit{d}}{\mathit{dt}}{\left|\right|\mathit{u}\left(\mathit{t}\right)\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2+4{\mathit{\mu }}_0{\mathit{C}}_{\mathit{k}}{\left|\right|\nabla \mathit{u}\left(\mathit{t}\right)\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2\le 0\le {\left|\right|\mathit{u}\left(\mathit{t}\right)\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2$$ (19)

Integrating between 0 and t, we get

$${\left|\right|\mathit{u}\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2+4{\mathit{\mu }}_0{\mathit{C}}_{\mathit{k}}\underset{0}{\overset{\mathit{t}}{\int }}{\left|\right|\nabla \mathit{u}\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2\mathit{d}\mathit{\tau }\le \underset{0}{\overset{\mathit{t}}{\int }}{\left|\right|\mathit{u}\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2\mathit{d}\mathit{\tau }+{\left|\right|{\mathit{u}}_0\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2$$ (20)

By Gronwall’s lemma, if $\mathit{\varphi }\left(\mathit{t}\right)\le \mathit{g}\left(\mathit{t}\right)+\underset{0}{\overset{\mathit{t}}{\int }}\mathit{f}\left(\mathit{\tau }\right)\mathit{\varphi }\left(\mathit{\tau }\right)\mathit{d}\mathit{\tau },\forall \mathit{t}\mathbf{\in }\left(0,\mathit{t}\right),$ then $\mathit{\varphi }\left(\mathit{t}\right)\le \mathit{g}\left(\mathit{t}\right)\mathit{exp}\underset{0}{\overset{\mathit{t}}{\int }}\mathit{f}\left(\mathit{\tau }\right)\mathit{d}\mathit{\tau },\forall \mathit{t}\mathbf{\in }\left(0,\mathit{t}\right).$

Considering ${\left|\right|\mathit{u}\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2+4{\mathit{\mu }}_0{\mathit{C}}_{\mathit{k}}\underset{0}{\overset{\mathit{t}}{\int }}{\left|\right|\nabla \mathit{u}\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2\mathit{d}\mathit{\tau }$ as $\mathit{\varphi }\left(\mathit{t}\right)$,

We get

$${\left|\right|\mathit{u}\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2+4{\mathit{\mu }}_0{\mathit{C}}_{\mathit{k}}\underset{0}{\overset{\mathit{t}}{\int }}{\left|\right|\nabla \mathit{u}\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2\mathit{d}\mathit{\tau }\le {\left|\right|{\mathit{u}}_0\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2\mathit{exp}\left(\mathit{t}\right)$$ (21)

This proves the first energy inequality.

Considering the inequality (18),

$$\frac{\mathit{d}}{\mathit{dt}}{\left|\right|\mathit{u}\left(\mathit{t}\right)\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2+4{\mathit{\mu }}_0{\mathit{C}}_{\mathit{k}}{\left|\right|\nabla \mathit{u}\left(\mathit{t}\right)\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2\le 0\le 2\mathit{\epsilon }{\left|\right|\mathit{u}\left(\mathit{t}\right)\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2$$ (22)

By applying Poincare inequality for the last term, we get

$$\frac{\mathit{d}}{\mathit{dt}}{\left|\right|\mathit{u}\left(\mathit{t}\right)\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2+4{\mathit{\mu }}_0{\mathit{C}}_{\mathit{k}}{\left|\right|\nabla \mathit{u}\left(\mathit{t}\right)\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2\le 0\le 2\mathit{\epsilon }{\left|\right|\mathit{u}\left(\mathit{t}\right)\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2\le 2\mathit{\epsilon }{\mathit{C}}_{\mathit{p}}^2{\left|\right|\nabla \mathit{u}\left(\mathit{t}\right)\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2$$ (23)

Now integrating between 0 and t, and let $\mathit{\epsilon }=\frac{{\mathit{\mu }}_0{\mathit{C}}_{\mathit{k}}}{{\mathit{C}}_{\mathit{p}}^2}$, we get

$${\left|\right|\mathit{u}\left(\mathit{t}\right)\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2+4{\mathit{\mu }}_0{\mathit{C}}_{\mathit{k}}\underset{0}{\overset{\mathit{t}}{\int }}{\left|\right|\nabla \mathit{u}\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2\mathit{d}\mathit{\tau }\le \frac{2{\mathit{\mu }}_0{\mathit{C}}_{\mathit{k}}{\mathit{C}}_{\mathit{p}}^2}{{\mathit{C}}_{\mathit{p}}^2}\underset{0}{\overset{\mathit{t}}{\int }}{\left|\right|\nabla \mathit{u}\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2\mathit{d}\mathit{\tau }+{\left|\right|{\mathit{u}}_0\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2$$ (24)

$${\left|\right|\mathit{u}\left(\mathit{t}\right)\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2+2{\mathit{\mu }}_0{\mathit{C}}_{\mathit{k}}\underset{0}{\overset{\mathit{t}}{\int }}{\left|\right|\nabla \mathit{u}\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2\mathit{d}\mathit{\tau }\le {\left|\right|{\mathit{u}}_0\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2$$ (25)

where $C_p$ is the constant from Poincare inequality.

2.3. The coupled fluid-structure problem

In large bloodstream arteries in which the vessel wall might change in a radius of up to 10% because of bloodstream strength, this aspect is especially crucial. We will first provide a framework for the Navier Stokes equations in motion domains which are particularly useful for the analysis and the development of numerical solutions.

As the inlet and the outlet limits are hypothetical fictional limits, they can alter over time but stay flat and stable along the vessel's axis. This shows plainly how unworkable is the Eulerian technique. The Lagrangian technique is therefore used. The above limits are conveyed in this technique along the fluid pathways which lead to a larger distortion over large time intervals.

The arbitrary Lagrangian-Eulerian (ALE) approach is the best-suited method to study such complex problems. According to the ALE approach, even if the wall is moving, the inlet and outlet boundaries are kept at the same spatial location along the vessel axis. The ALE formulation is governed by the following mappings:

$${\mathfrak{R}}_{\mathit{t}}:{\mathbf{\Omega }}_0\to {\mathbf{\Omega }}_{{\mathfrak{R}}_{\mathit{t}}},\mathit{Y}\to \mathit{y}\left(\mathit{t},\mathit{Y}\right)={\mathfrak{R}}_{\mathit{t}}\left(\mathit{Y}\right)$$ (26)

$${\mathbf{\Omega }}_{{\mathfrak{R}}_{\mathit{t}}}\equiv {\mathfrak{R}}_{\mathit{t}}\left({\mathbf{\Omega }}_0\right)={\mathbf{\Omega }}_{\mathit{t}},\forall \mathit{t}\mathrm{\epsilon }(0,\mathit{t})$$ (27)

The ALE mapping should be continuous and bijective in $\overline{{\text{Ω}}_0}$.

The domain velocity field is defined as $\check{\vartheta }\left(\mathit{t},\mathit{Y}\right)=\frac{\partial }{\partial \mathit{t}}\mathit{y}(\mathit{t},\mathit{Y})$

Which, in the spatial coordinates is expressed as. $\vartheta \left(\mathit{t},\mathit{y}\right)=\check{\vartheta }\left(\mathit{t},{\mathfrak{R}}_{\mathit{t}}^{-1}\left(\mathit{y}\right)\right).$

The ALE derivative of a function $\mathit{f}:(0,\mathit{t})\times {\mathbf{\Omega }}_{\mathit{t}}\to \mathbb{R}$ is given by

$$\frac{{\mathit{D}}^{\mathfrak{R}}}{\mathit{Dt}}\mathit{f}=\frac{\partial \mathit{f}}{\partial \mathit{t}}+\vartheta .\nabla \mathit{f}$$ (28)

By the application of the ALE derivative on the Navier Stokes equation, we get.

SYSTEM 3:

$$\frac{{\mathit{D}}^{\mathfrak{R}}}{\mathit{Dt}}\mathit{u}+\left[\left(\mathit{u}-\vartheta \right).\nabla \right]\mathit{u}+\nabla \mathit{p}-2\nabla .\left(\mathit{\mu }\mathit{D}\left(\mathit{u}\right)\right)=0$$

$$\nabla .\mathit{u}=0$$

in ${\text{Ω}}_t$ and $\forall t\in \left(0,t\right)$.

System (3) coupled with the generalized string model [35], with s as the displacement vector, under null external stresses,

$$\frac{{\partial }^2\mathit{s}}{\partial {\mathit{t}}^2}-\mathit{a}\frac{{\partial }^2\mathit{s}}{\partial {\mathit{z}}^2}+\mathit{bs}-{\mathit{c}}^2\frac{{\partial }^3\mathit{s}}{\partial \mathit{t}\partial {\mathit{z}}^2}=0\text{in the reference configuration.}$$ (29)

with, for $t=0$

$$\mathit{u}={\mathit{u}}_0,\mathit{x}\mathbf{\in }{\mathbf{\Omega }}_0,\mathit{s}={\mathit{s}}_0,\dot{\mathit{s}}={\mathit{s}}_1\text{in the reference configuration}$$ (30)

Boundary conditions for $t\in \left(0,t\right)$.

$$\left[2\mathit{\mu }\mathit{D}\left(\mathit{u}\right)-\Delta \mathit{pI}\right].\mathit{n}=0\text{, on the outlet, }\Delta \mathit{p}=\mathit{p}-{\mathit{p}}_0$$ (31)

$\mathit{u}=\mathit{g},\text{on the inlet}$ (32)

$\mathit{s}=\mathit{\alpha }\text{at}\mathit{z}=0$ (33)

$$\mathit{s}=\mathit{\beta }\text{at}\mathit{z}=\mathit{L}$$ (34)

and the interface condition

$$\tilde{\mathit{u}}=\mathit{u}\circ {\mathfrak{R}}_{\mathit{t}}=\frac{\partial \mathit{s}}{\partial \mathit{t}}{\mathit{e}}_{\mathit{r}}\text{on the interface for}t\in \left(0,t\right)$$ (35)

Here $u_0,\alpha ,\beta ,g$ are given functions.

Energy inequality for the coupled problem:

Considering the homogeneous boundary conditions, the coupled problem satisfies the equation:

$$\frac{\mathit{d}}{\mathit{dt}}\left[\frac{\mathit{w}}{2}{||\mathit{u}\left(\mathit{t}\right)||}_{{\mathit{L}}^2\left({\mathbf{\Omega }}_{\mathit{t}}\right)}+{\mathit{H}}_{\mathit{s}}\left(\mathit{t}\right)\right]+2\mathit{w}\underset{{\mathbf{\Omega }}_{\mathit{t}}}{\int }\mathit{\mu }\mathit{D}\left(\mathit{u}\right):\mathit{D}\left(\mathit{u}\right)+\mathit{c}{{\left|\left|\frac{{\mathbf{\partial }}^{\mathbf{2}}\mathbf{s}}{\mathbf{\partial }\mathbf{t}\mathbf{\partial }{\mathbf{z}}^{}}\right|\right|}^2}_{{\mathit{L}}^2\left({\mathbf{\Gamma }}_0^{\mathit{w}}\right)}+\frac{\mathit{w}}{2}\underset{{\mathbf{\Gamma }}_{\mathit{t}}^{\mathit{out}}}{\int }{\left|\mathit{u}\right|}^2\mathit{u}.\mathit{n}=\text{0}$$ (36)

where ${\mathit{H}}_{\mathit{s}}\left(\mathit{t}\right)=\frac{1}{2}\left({{||\frac{\mathbf{\partial }\mathbf{s}}{\mathbf{\partial }\mathbf{t}}||}^2}_{{\mathit{L}}^2\left({\mathbf{\Gamma }}_0^{\mathit{w}}\right)}+\mathit{\alpha }{{||\frac{\mathbf{\partial }\mathbf{s}}{\mathbf{\partial }\mathbf{z}}||}^2}_{{\mathit{L}}^2\left({\mathbf{\Gamma }}_0^{\mathit{w}}\right)}+\mathit{b}{{||\mathbf{s}||}^2}_{{\mathit{L}}^2\left({\mathbf{\Gamma }}_0^{\mathit{w}}\right)}\right)$ and $\mathit{w}=\frac{\mathit{\rho }}{{\mathit{\rho }}_{\mathit{w}}{\mathit{h}}_0}$.

As there is always flow from the outlet boundary of the domain, $\underset{{\mathbf{\Gamma }}_{\mathit{t}}^{\mathit{out}}}{\int }{\left|\mathit{u}\right|}^2\mathit{u}.\mathit{n}\ge 0,\forall \mathit{t}\mathbf{\in }\left(0,\mathit{T}\right).$

$$\frac{\mathit{w}}{2}{||\mathit{u}\left(\mathit{t}\right)||}_{{\mathit{L}}^2\left({\mathbf{\Omega }}_{\mathit{t}}\right)}+{\mathit{H}}_{\mathit{s}}\left(\mathit{t}\right)+{\mathit{\mu }}_0{\mathit{C}}_{\mathit{k}}\mathit{w}\underset{0}{\overset{\mathit{t}}{\int }}{\left|\right|\nabla \mathit{u}\left|\right|}_{{\mathit{L}}^2\left(\mathbf{\Omega }\right)}^2\mathit{d}\mathit{\tau }+\mathit{c}\underset{0}{\overset{\mathit{t}}{\int }}{{||\frac{{\mathbf{\partial }}^{\mathbf{2}}\mathbf{s}}{\mathbf{\partial }\mathbf{t}\mathbf{\partial }{\mathbf{z}}^{}}||}^2}_{{\mathit{L}}^2\left({\mathbf{\Gamma }}_0^{\mathit{w}}\right)}\mathit{d}\mathit{\tau }\le \frac{\mathit{w}}{2}{||{\mathit{u}}_0\left(\mathit{t}\right)||}_{{\mathit{L}}^2\left({\mathbf{\Omega }}_{\mathit{t}}\right)}+{\mathit{H}}_{\mathit{s}}\left({\mathit{t}}_0\right),\mathit{t}\mathbf{\in }\left(0,\mathit{T}\right)$$ (37)

The above inequality can be proved by using the ALE transport theorem, the Poincare inequality, and Korn inequality.

For the present study, we consider a simplified form of the generalized string model to govern the structure model. The model we employ here is the Saint Venant- Kirchhoff model.

The model is given as:

For $\mathit{s}={({\mathit{s}}_1,{\mathit{s}}_2)}^{\mathit{T}}:{\mathbf{\Omega }}_{\mathit{s}}\to {\mathbb{R}}^2$,

$${\mathit{\rho }}_{\mathit{w}}\frac{{\partial }^2\mathit{s}}{\partial {\mathit{t}}^2}-\nabla .\left(\left({\mathit{I}}_2+\nabla \mathit{s}\right)\sum \left(\mathit{s}\right)\right)=0,{\mathbf{\Omega }}_{\mathit{s}}\times \left(0,\mathit{T}\right)$$ (38)

$$\mathit{s}=0,\text{on}{\mathbf{\Gamma }}_{\mathit{D}}\times \left(0,\mathit{T}\right)$$ (39)

$$\left(\left({\mathit{I}}_2+\nabla \mathit{s}\right)\sum \right)\mathit{n}=0,\text{on}{\mathbf{\Gamma }}_{\mathit{N}}\times \left(0,\mathit{T}\right)$$ (40)

$$\mathit{s}\left(\mathit{x},0\right)={\mathit{s}}_0\left(\mathit{x}\right),\text{in}{\mathbf{\Omega }}_{\mathit{s}}$$ (41)

$$\frac{{\partial }^{}\mathit{s}}{\partial \mathit{t}}=\dot{{\mathit{s}}_0}\left(\mathit{x}\right),\text{in}{\mathbf{\Omega }}_{\mathit{s}}$$ (42)

where ${\mathbf{\Omega }}_{\mathit{s}}$ is the intimal domain, ${\mathbf{\Gamma }}_{\mathit{D}}$ are the inlet and outlet corresponding to the solid domain, ${\mathbf{\Gamma }}_{\mathit{N}}$ is the boundary towards the tunica media. Here $\sum$ is given by $\mathit{A}\mathit{tr}\left[\frac{1}{2}(\nabla \mathit{s}+{\left(\nabla \mathit{s}\right)}^{\mathit{T}}+{\left(\nabla \mathit{s}\right)}^{\mathit{T}}\nabla \mathit{s}\right]{\mathit{I}}_2+2\mathit{B}\left[\frac{1}{2}(\nabla \mathit{s}+{\left(\nabla \mathit{s}\right)}^{\mathit{T}}+{\left(\nabla \mathit{s}\right)}^{\mathit{T}}\nabla \mathit{s}\right],$ where $\mathit{A}=\frac{\mathit{\gamma }{\mathit{E}}_{\mathit{Y}}}{\left(1-2\mathit{\gamma }\right)(1+\mathit{\gamma })},\mathit{B}=\frac{{\mathit{E}}_{\mathit{Y}}}{2(1+\mathit{\gamma })}$ (Lame’ constants); ${\mathit{E}}_{\mathit{Y}}$ representing Young's modulus and $\mathit{\gamma }$ is the Poisson ratio.

2.4. Geometry and mesh details

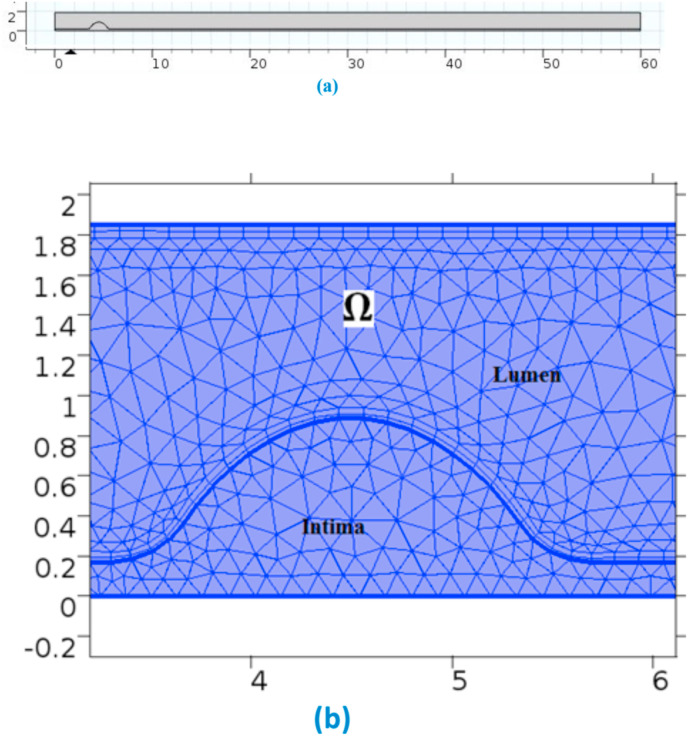
The computationally designed geometry has the measurements: total length of 60 mm, complete width of the artery is 1.85 mm, the thickness of the intimal layer is 0.1702 mm, as seen from Fig. 1 (a). The geometrical dimensions and the degree of stenosis allow a large stress situation as the study considers a coronary arterial model with 45% stenosis. The reduction in the path diameter results in the high-stress condition. Physics-controlled meshing has been done over the domain by incorporating suitable domain discretizations. A Mesh independence test has been done for the selection of a suitable meshing configuration. The meshes are varied from extremely coarser to finer. Peak velocity is noted for each simulation case. It has been seen that the change in peak velocity is less than 1% during the transformation from Fine to Finer meshing. Thus, fine meshing has been made over the domain of interest, as seen from Fig. 1(b).

Fig. 1.

(a)-Geometry of the domain & (b)-Meshing near the stenosis.

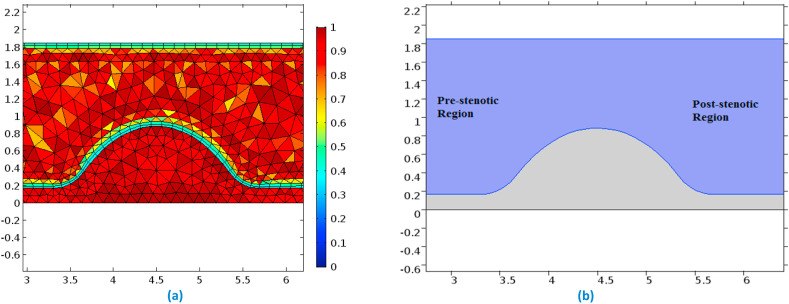
The mesh element details are enlisted in Table 2 . Fig. 2 (a) represents the mesh element quality at the region of stenosis and Fig. 2(b) displays the pre- and the post-stenotic regions of the arterial segment.

Table 2.

Mesh details.

Sl.No.	Mesh descriptions	Values
1	Triangular elements	66,522
2	Quadrilateral elements	4660
3	Edge elements	3273
4	Vertex elements	10
5	Minimum element quality	0.3333
6	Average element quality	0.903
7	Element area ratio	0.04572
8	Mesh area	111 $m{m}^2$
9	Maximum growth rate	2.329
10	Average growth rate	1.272

Fig. 2.

(a)-Mesh quality near the stenosis & (b)-Pre and Post stenotic regions displayed explicitly.

2.5. Numerical and physical parameters

The values of the various numerical and the physical parameters used in the model framed are listed in Table 3 .

Table 3.

Numerical and physical parameter values.

Parameters	Values	References
BLOOD (FLUID)
Density	1060 kg/m3	[14,[36], [37], [38]]
Viscosity (Normal)	0.0015 Pa s
Hyper-viscosity	0.0042 Pa s
ARTERIAL WALL (STRUCTURE)
Lame Parameter, A	$20\times 6.20\times {10}^6$	[39]
Lame Parameter, B	$6.20\times {10}^6$
Density	960 kg/m3
BOUNDARY CONDITIONS
Initial Pressure	10,000 Pa	[37,38]
Inlet velocity	1.18 m/s
Outlet pressure	9332.57 Pa

3. Results and discussion

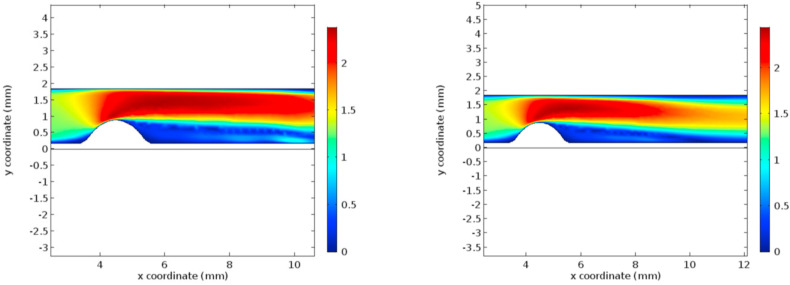
The condition of hyper-viscosity has been simulated using a Finite Element Method (FEM) solver using the coupled fluid-structure system. Initially, the results are obtained for the normal viscosity condition. Later the results are recorded for the hyper-viscous condition. The flow characteristics under investigation are velocity profiles, pressure profiles, wall shear stress, and Von Mises stress, as these are the properties governing the rupture of the currently existing plaque and the formation of new atherosclerotic plaques [[40], [41], [42], [43]]. Figs. 3 and 4 represent the velocity profiles and the velocity streamlines for the two cases under study. Due to the low viscosity, the first graphs of Figs. 3 and 4 include a low-velocity profile in the post stenosis region. It can be seen from graphs that the velocity in both the cases, the velocity profile remains to be same until 10 mm coordinate along the flow channel. But in the post stenotic region, the velocity seems to increase in the hyper-viscous case. Noticeable alterations are seen in the recirculation zones in both cases. The increased velocity in the hyper-viscous case results in the increase in cellular components and plasma proteins in the blood leading to endothelium damage resulting in thrombosis (increased fibrinogen concentration) [44].

Fig. 3.

Velocity profiles for normal and hyper-viscous cases respectively.

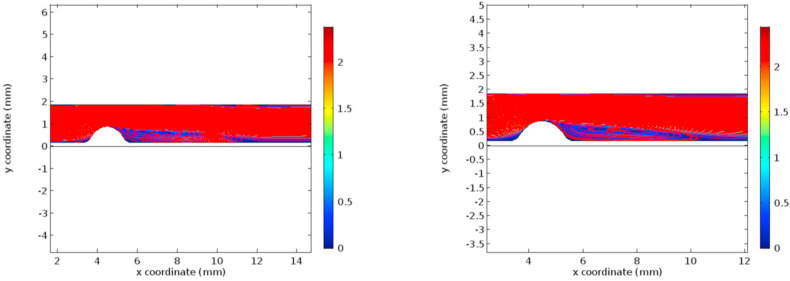
Fig. 4.

Velocity streamlines for normal and hyper-viscous cases respectively.

The recirculation regions clearly support the high-velocity profile for the hyper-viscous case. The increased velocity causes high resistance to the flow in the microcirculatory system. The condition of increased viscosity is termed “Hyper-viscosity syndrome” [45], which requires plasma exchange treatment. Thus, it is evident that the increased viscosity doesn't affect the formation of new plaques in the post stenotic regions as mentioned in the previously published articles [46].

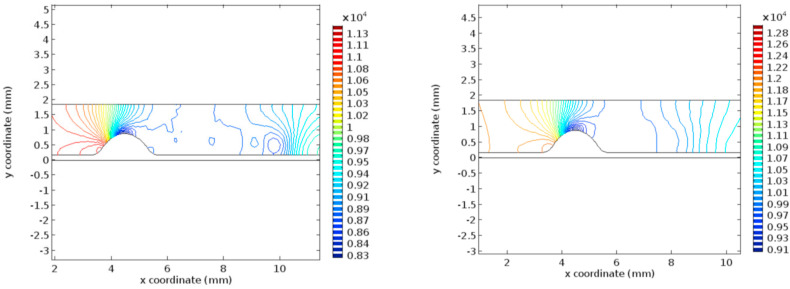
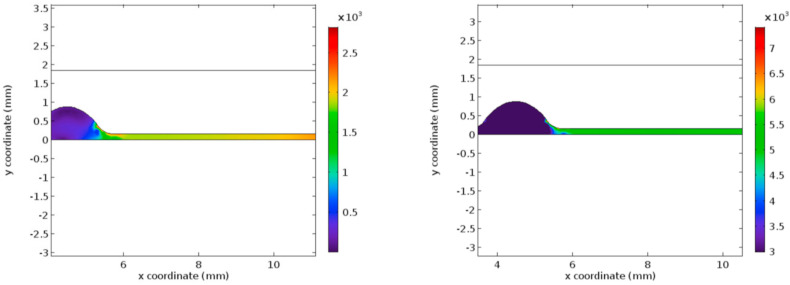
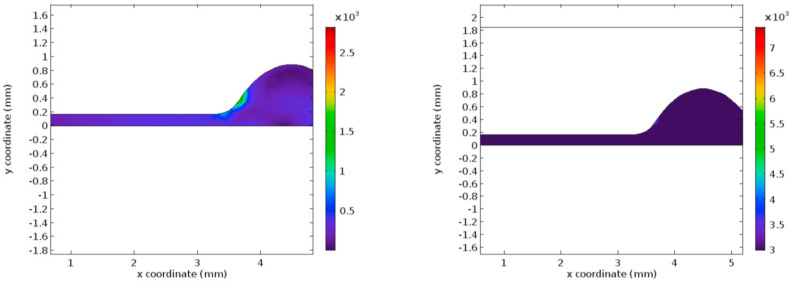
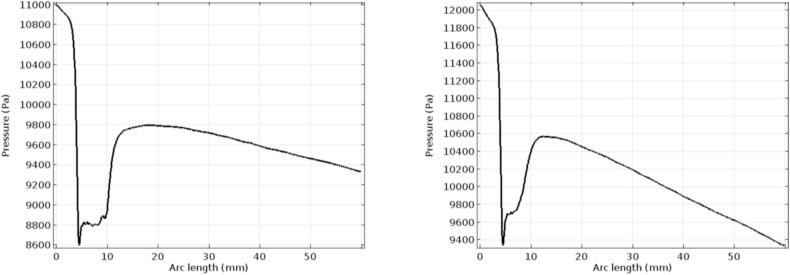
Fig. 5 represents the pressure profile for the normal and the hyper-viscous cases under study. These graphs indicate that the pressure recovery happens at a faster rate for the normal viscous case whereas the recovery begins only after few millimeters of the flow channel in the post-stenotic region. Apart from the delay in the pressure recovery, the magnitude of pressure is not affected by the increasing viscosity significantly. Figs. 6 and 7 represent the Von Mises stress magnitudes in the pre- and the post-stenotic regions of the arterial segment under study. It is the stress which indicates the capacity of a material to yield or break. Hence in the pre-stenotic region, as seen from Fig. 7, the Von Mises stress in the intimal region caused due to the flow of blood in the lumen of the artery is uniform and does not show any significant rise or fall in the value. From Fig. 6 it can be perceived that Von Mises stress shows a greater rise in the value in the post-stenotic region. The stress near the stenosis peak in the post stenotic region is 1500 Pa–2000 Pa and 4000 Pa–6000 Pa for the normal viscosity and hyperviscosity cases respectively. The pattern seems to increase along the arterial wall away from the stenosis in the post-stenotic region. The highest Von Mises stress value reduces the risk of plaque rupture [47]. The peak Von Mises stress values for the two cases considered are 3000 Pa and 10,000 Pa respectively.

Fig. 5.

Pressure profiles for normal and hyper-viscous cases respectively.

Fig. 6.

Von Mises Stress for normal and hyper-viscous cases respectively (post stenotic case).

Fig. 7.

Von Mises Stress for normal and hyper-viscous cases respectively (pre-stenotic case).

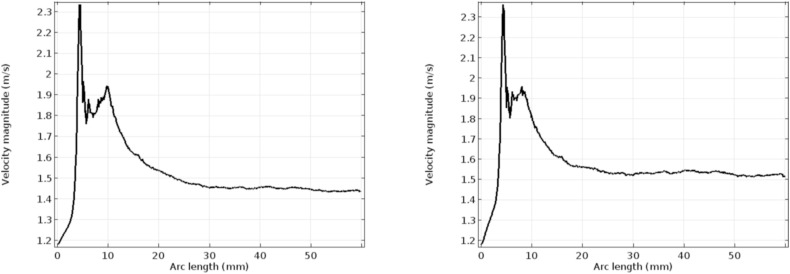
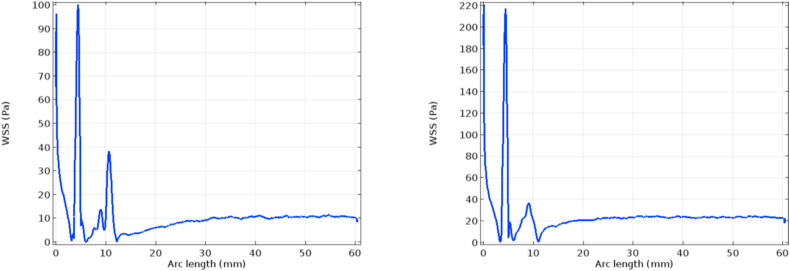
Figs. 8 and 9 depict the velocity and pressure graphs along the axis of the flow channel. These graphs follow Bernoulli's pressure-velocity relationship given by $\frac{1}{2}\mathit{\rho }{\mathit{v}}^2+\mathit{p}=0$ [48]. The peak velocity reached in the case of the hyper-viscous condition is higher than that of the normal viscosity case, as described in the previous paragraph. In the post-stenotic region, the velocity attained is 1.45 m/s and 1.7 m/s respectively [49]. Plots in Fig. 10 indicate the wall shear stress along with the lumen-intima interfaces with stenosis. The considerable difference is seen in the graphs in Fig. 10. At the inlet of the channel, a high WSS value is seen in the case of the hyper-viscous scenario when compared to the normal viscosity. This is due to the fact that the WSS is the product of solution viscosity and shear rate. Also, it has been seen from the simulation graphs that the shear rate for the normal viscous rate is 66,000/s and the value for the other case is found to be 59,000/s. Due to the increased viscosity in the latter case, the WSS values reach a peak.

Fig. 8.

Axial velocity for normal and hyper-viscous cases respectively.

Fig. 9.

Axial pressure for normal and hyper-viscous cases respectively.

Fig. 10.

WSS profile along the lumen-intima interface for normal and hyper-viscous cases respectively.

The summary of the results obtained is presented in the form of a table below(see Table 4 ).

Table 4.

Comparison for normal and COVID 19 infected blood flow parameters.

Flow parameters	Normal case (Stenosis + Non-COVID)	Hyper-viscous case (Stenosis + COVID)
Axial velocity	Normal	Higher
Axial pressure	Normal	Lower
Number of recirculation zones (Post-stenotic)	2	1
Pressure recovery rate (Post-stenotic)	Faster	Slower
Wall shear stress (Post-stenotic)	Normal	Higher
Von Mises stress (Post-stenotic)	Lower	Higher

From the above discussions made on the various flow characteristics, it can be seen that for the geometry considered, the effect of increased viscosity among the COVID patients seems to be imperceptible. They do not show any signs of development of new plaques downstream of the flow in the post-stenotic regions. The effect can be considerably seen in the microcirculatory systems (namely in arterioles, venules, and capillaries), as the microcirculation is greatly affected by the thrombosis caused due to the increased viscosity.

4. Limitations

The assumptions made while framing the mathematical model for the present study, it is seen that the blood flow in arteries was treated as the stationary study subject. But the heart works in a periodic way. The geometry considered is similar to the coronary arterial system; this system of arteries being largely affected by the time dependency of the blood flow is to be studied under a time-dependent study case.

Also, to completely explore the effect of the elevated viscosity levels, microcirculation is to be taken into consideration. Finally, the blood traveling the entire vascular system of the human body is non-Newtonian in nature [50]. The non-Newtonian nature of blood can be considered for future studies.

5. Conclusions

In the present study a mathematical model to govern the blood flow using the FSI model. The effect of elevated viscosity on the stenosed artery has been investigated by analyzing the flow characteristics of blood. The following observations are made at the end of the investigation:

• •Velocity rise can be seen in the hyper-viscous case.
• •Pressure recovery delay is seen in the post stenotic region in the case of hyper-viscous case.
• •Recirculation zones are minimized in the hyper-viscous case.
• •Due to the elevated viscosity, the WSS graphs show a high peak in the hyper-viscous case at the tip of the stenosis.
• •The WSS values in the neck of the stenosis in the post-stenotic region are seen less in the hyper-viscous case.
• •Microcirculation can be better studied by the elevated viscosity when compared to the flow in the large dimension arteries.
• •Due to the elevated velocity caused by the high viscosity the blood is forced to travel towards the micro-arteries at a greater rate. This results in the increased concentration of the plasma proteins and the cellular entities leading to the condition of thrombosis.

Credit author statement

Conceptualization- S. Shankar Narayan, Sunanda Saha; Formal analysis- S. Shankar Narayan, Sunanda Saha; Investigation- S. Shankar Narayan, Sunanda Saha, Anuradha Bhattacharjee; Methodology- S. Shankar Narayan, Sunanda Saha; Supervision- Sunanda Saha, Anuradha Bhattacharjee; Validation- S. Shankar Narayan, Sunanda Saha, Anuradha Bhattacharjee; Visualization- S. Shankar Narayan, Sunanda Saha, Anuradha Bhattacharjee; Roles/Writing - original draft- S. Shankar Narayan; Writing - review & editing- S. Shankar Narayan.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.