Phylogenomic Subsampling and the Search for Phylogenetically Reliable Loci

Abstract

Phylogenomic subsampling is a procedure by which small sets of loci are selected from large genome-scale data sets and used for phylogenetic inference. This step is often motivated by either computational limitations associated with the use of complex inference methods or as a means of testing the robustness of phylogenetic results by discarding loci that are deemed potentially misleading. Although many alternative methods of phylogenomic subsampling have been proposed, little effort has gone into comparing their behavior across different data sets. Here, I calculate multiple gene properties for a range of phylogenomic data sets spanning animal, fungal, and plant clades, uncovering a remarkable predictability in their patterns of covariance. I also show how these patterns provide a means for ordering loci by both their rate of evolution and their relative phylogenetic usefulness. This method of retrieving phylogenetically useful loci is found to be among the top performing when compared with alternative subsampling protocols. Relatively common approaches such as minimizing potential sources of systematic bias or increasing the clock-likeness of the data are found to fare worse than selecting loci at random. Likewise, the general utility of rate-based subsampling is found to be limited: loci evolving at both low and high rates are among the least effective, and even those evolving at optimal rates can still widely differ in usefulness. This study shows that many common subsampling approaches introduce unintended effects in off-target gene properties and proposes an alternative multivariate method that simultaneously optimizes phylogenetic signal while controlling for known sources of bias.

Introduction

During the last decades, molecular data sets composed of thousands of genes have become common. Although a few phylogenetic questions have remained uncertain even in the face of such large data sets (King and Rokas 2017; Smith et al. 2020), phylogenomics has greatly improved our understanding of the structure of the tree of life (Dunn et al. 2008; Spang et al. 2015; Burki et al. 2020), the timing of origin of major clades (dos Reis et al. 2012), and the changes in genomic architecture associated with key evolutionary transitions (Paps and Holland 2018; Fernández and Gabaldón 2020). At the same time, the analysis of phylogenomic data sets has posed numerous novel challenges. These range from a high prevalence of genes whose evolutionary histories deviate from that of the group of species under study (such as results from events of paralogy, incomplete lineage sorting, and hybridization, among others), to an accumulation of nonphylogenetic signals as a product of heterogeneities in evolutionary processes. Although many of these issues can be alleviated by implementing more complex models of molecular evolution, computational limitations often preclude their use with entire phylogenomic data sets (Simion et al. 2020).

Phylogenomic subsampling is a common procedure to alleviate these issues (Meyer et al. 2011; Chen et al. 2015; Edwards 2016; Simmons et al. 2016; Molloy and Warnow 2018; Mongiardino Koch 2019). By focusing on a small fraction of genes that are considered more reliable, contentious, or unstable nodes can be tested, and the effects of potentially confounding factors such as missing data and saturation can be disentangled (Fernández et al. 2014; Sharma et al. 2014; Borowiec et al. 2015; Kocot et al. 2017; Mongiardino Koch et al. 2018; Stiller et al. 2020). Smaller data sets are also amenable to analysis using more complex and computationally demanding approaches, including inference under site heterogenous and multispecies coalescent models (Whelan et al. 2015; Thawornwattana et al. 2018; Ballesteros et al. 2019; Marlétaz et al. 2019). Phylogenomic subsampling can therefore reduce heterogeneities in the data set and improve model fit, producing results that are often preferred. The same logic applies to divergence-time estimation, where subsampling can be used to both alleviate computational burden and produce more accurate results (Dornburg et al. 2014; Smith et al. 2018; Carruthers et al. 2020; Mongiardino Koch and Thompson 2021).

Given these benefits, multiple subsampling protocols have been proposed. Although sharing a common goal of retrieving phylogenetically reliable loci (throughout, used interchangeably with genes), they have often employed—and sought to optimize—entirely different criteria. These can either be a measure of information quantity, such as the length of the alignment or its proportion of missing data/occupancy (e.g., Hosner et al. 2016; Foley et al. 2019), or a variable reflecting information quality. Among the latter, common approaches include the selection of loci with high levels of phylogenetic signal (e.g., Salichos and Rokas 2013) and the removal of those potentially affected by systematic biases (e.g., Nesnidal et al. 2010). However, multiple sources of bias are known (KapLi et al. 2021) and different proxies for signal have been employed (Salichos and Rokas 2013; Salichos et al. 2014; Arcila et al. 2017; Philippe et al. 2019; Vankan et al. 2020), and the downstream consequences of choosing among these are largely unknown. This is further complicated by the fact that sources of bias and proxies for signal can be strongly correlated (Mongiardino Koch and Thompson 2021), such that the optimization of either dimension individually modifies the other in potentially unintended ways. As a consequence, it remains unclear if these alternatives (retaining “good” genes vs. discarding “bad” ones) converge on a similar pool of reliable loci, and if not, whether one systematically outperforms the other. It is also uncertain whether subsampling approaches favored when dealing with notoriously complicated phylogenetic questions are useful for data sets that lack any obvious sign of issues.

Ultimately, levels of both signal and noise are manifestations of underlying differences in rates of evolution. Rate-based subsampling is therefore also common, but there seems to be little consensus on how it should be implemented: studies have variously supported the use of molecular data that evolve at fast, intermediate, or slow rates, as well as the generation of partitions with homogenous rates (e.g., Cummins and McInerney 2011; Rota-Stabelli et al. 2011; Fernández et al. 2014; Sharma et al. 2014, 2015; Telford et al. 2014; Streicher et al. 2018; Rangel and Fournier 2019; Evangelista et al. 2021; Li et al. 2021). These studies have also relied on different types of rate estimates—including tree- and alignment-based metrics of substitution rates, measures of character similarity and compatibility, and proportions of variable/informative sites—as well as different units of measurement (sites or loci). Furthermore, the discovery of appropriate rates of evolution can be complicated by heterogeneities among sites and lineages that are often not accounted for (Dornburg et al. 2019). An alternative method involves using some notion of the relationships among the taxa under study (including topology and branch lengths in units of time) to predict the likely behavior of data evolving under differing rates (Townsend 2007; Townsend et al. 2012; Su and Townsend 2015). This approach, termed phylogenetic informativeness (PI), can be used to quantify the expected probabilities of sites contributing toward correctly or incorrectly resolving a given quartet, guiding the discovery of particularly useful genes (e.g., Alda et al. 2019; Bellot et al. 2020).

Although many studies have optimized just one of these properties, others have devised complicated subsampling schemes intended to find loci that satisfy a number of requisites. In the majority of cases, this is performed by iteratively removing data based on a number of rules (e.g., Fernández et al. 2014; Sharma et al. 2015; Whelan et al. 2015). To some extent, this approach can be used to test the effect of individual gene properties on phylogenetic reconstruction, as well as progressively narrow in on a small set of loci that satisfy multiple criteria. However, the final results depend on the order in which properties are evaluated and the thresholds enforced, decisions that are difficult to justify (if not entirely arbitrary). A handful of studies (Borowiec et al. 2015; Kocot et al. 2017; Mongiardino Koch and Thompson 2021) have therefore selected loci that simultaneously satisfy a number of conditions. In the case of Mongiardino Koch and Thompson (2021), subsampling was not performed directly on the variables measured but on principal component (PC) axes derived from these. This approach produced axes capturing differences in rate of evolution and overall phylogenetic usefulness along which loci could be sorted. Whether major axes of variation in other phylogenomic data sets can be interpreted in similar ways remains unknown.

Several recent studies have explored a number of these gene properties in an attempt to discover reliable predictors of the phylogenetic performance of loci (Aguileta et al. 2008; Doyle et al. 2015; Shen et al. 2016; Brown and Thomson 2017; Kuang et al. 2018; Burbrink et al. 2020; Vankan et al. 2020; Evangelista et al. 2021). Their recommendations have often differed, raising the possibility that a universal predictor might not exist. They have also invariably focused on correlating alternative properties with measures of topological distance or clade support, without actually evaluating the performance of subsampled data sets composed of multiple loci (i.e., the trees they support). In this study, I calculate numerous gene properties across 18 phylogenomic data sets, representing diverse clades whose evolutionary histories began anytime between the Middle Cambrian and the Late Cretaceous (table 1). With these data, I explore the existence of universal patterns of covariance between gene properties and test whether such patterns capture useful information regarding the evolutionary history of loci. I then analyze the success of alternative subsampling strategies in finding phylogenetically reliable data sets of small sizes.

Table 1.

Phylogenomic Data Sets Employed.

Data Set	Age (Ma)	Number of Taxa	Number of Loci	Occupancy (%)	Mean Locus Length
Actinopterygii (Hughes et al. 2018)	376.3	302	1,035	81.2	167.1
Araneae (Fernández et al. 2018)	366.1	160	1,114	64.2	218.8
Aspergillacea (Steenwyk et al. 2019)	117.4	81	1,660	97.5	633.8
Blattodea (Evangelista et al. 2019)	206.7	45	2,556	82.1	374.4
Echinoidea (Mongiardino Koch and Thompson 2021)	265.0	34	2,356	71.6	257.1
Gnathostomata (Irisarri et al. 2017)	457.6	100	4,543	81.6	430.4
Heliozelidae (Milla et al. 2020)	84.0	38	1,040	92.2	271.4
Hemipteroids (Johnson et al. 2018)	420.3	171	2,225	90.6	771.0
Hexapoda (Misof et al. 2014)	479.1	134	1,467	94.7	869.5
Hymenoptera (Peters et al. 2017)	281.0	169	2,665	84.8	647.6
Lepidoptera (Kawahara et al. 2019)	299.5	186	2,021	88.8	359.4
Monilophytes (Shen, Jin, et al. 2018)	321.1	69	2,357	89.5	284.3
Myriapoda (Fernández et al. 2016)	504.4	40	1,942	82.2	297.1
Opiliones (Fernández et al. 2017b)	414.2	54	1,288	63.2	265.7
Phasmatodea (Simon et al. 2019)	121.8	38	1,022	88.6	772.3
Pseudoscorpiones (Benavides et al. 2019)	337.5	41	2,110	63.2	376.1
Saccharomycotina (Shen, Opulente, et al. 2018)	404.0	332	2,348	88.1	464.6
Scorpiones (Sharma et al. 2018)	381.3	30	1,462	86.6	226.3

Note.—Age constitutes the inferred date of the last common ancestor of the ingroup (in million years, My) as estimated by the same study. Number of taxa corresponds only to ingroup taxa, number of loci to those for which all properties could be estimated (see Materials and Methods); these and other numbers can differ from those reported in the original studies.

Results

Data set sampling purposefully avoided notoriously difficult phylogenetic questions, focusing instead on more typical data sets. These do not suffer from any evident source of bias, and thus there is no clearly preferable approach to subsample them, or any expectation that a single method would work well for all of them. All matrices were coded as amino acids and were modified only by removing loci with less than 50% occupancy (further details can be found in Materials and Methods). Time-calibrated species trees were also obtained from the corresponding studies. Gene trees were inferred using ParGenes v. 1.0.1 (Morel et al. 2019) under optimal models, and 100 replicates of nonparametric bootstrap (BS) were used to calculate node support. Site-wise rates of evolution were estimated using the empirical Bayes method implemented in Rate4Site (Mayrose et al. 2004). All other analyses were performed in the R statistical environment (R Core Team 2019) using custom scripts. This included the estimation of 15 gene properties: 1) alignment length; 2) proportion of missing data; 3) level of occupancy; 4) proportion of variable sites; 5) total tree length (i.e., sum of all branches); 6) level of treeness (i.e., the fraction of tree length on internal branches; Lanyon 1988); 7) average pair-wise patristic distance between terminals, a proxy for sensitivity to long-branch attraction (Struck 2014); 8) clock-likeness, calculated using the variance of root-to-tip distances; 9) level of saturation, estimated as one minus the regression slope of patristic distances on p-distances (Nosenko et al. 2013); 10) compositional heterogeneity, measured by the relative composition frequency variability (RCFV; Phillips and Penny 2003; Zhong et al. 2011); 11) average BS support; 12) Robinson–Foulds (RF) similarity to the species tree supported by each study (Robinson and Foulds 1981); two estimates of evolutionary rates, including 13) the total tree length divided by the number of terminals (Telford et al. 2014) and 14) the harmonic mean of site rates; and 15) the area under the penalized PI profile (iPIpen). For this last one, site rates were used to calculate a PI profile (an estimate of the utility of a locus for inferring relationships at different timescales) for the entire time spanned between root and tips using PhyInformR (Dornburg et al. 2016). To account for the accumulation of phylogenetic noise (i.e., homoplastic site patterns arising in fast-evolving sites), which is not directly accounted for by the method, informativeness values for times older than that of the peak were penalized following the method described in Bellot et al. (2020). This was done by multiplying their values by the ratio between their current height and that of the PI peak. The area under this curve is a proxy for the signal in the data to resolve nodes spanning the entire depth of the tree and was estimated using spline interpolation with the package MESS (Ekstrom 2020). All properties were measured at the level of genes. Metrics were defined such that positive attributes (such as RF similarity) should be maximized, whereas negative attributes (such as level of saturation) should be minimized. More information on these metrics can be found in supplementary table S1, Supplementary Material online.

Across all data sets, proxies for phylogenetic signal (average BS, RF similarity, and iPIpen) correlate most strongly with the length, rate of evolution (estimated as the harmonic mean of site rates), and proportion of variable sites of loci, increasing with all three (supplementary fig. S1, Supplementary Material online). Other properties previously suggested as strong predictors of signal, such as clock-likeness and compositional heterogeneity (Doyle et al. 2015; Shen et al. 2016; Kuang et al. 2018; Vankan et al. 2020; Evangelista et al. 2021), show less predictable relationships that can range from strongly positive to strongly negative (supplementary fig. S1, Supplementary Material online). Some variables (e.g., saturation, treeness) have stronger effects on some proxies than others, which further complicates extracting meaningful patterns. More importantly perhaps, 97.1% of all pair-wise correlations among the 15 properties are significant across more than half of the data sets (including those between signal proxies and all predictors; supplementary fig. S2, Supplementary Material online). There is also no evidence that any of these gene properties significantly depends on the absolute age of clades (all P values > 0.2).

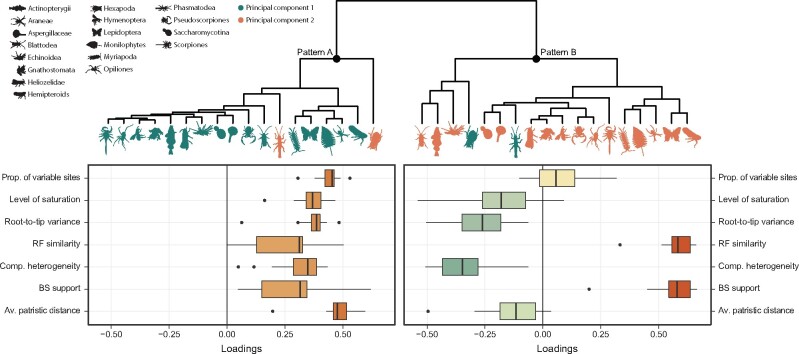
In order to explore whether gene properties share common patterns of covariance across data sets, I followed the approach of Mongiardino Koch and Thompson (2021), focusing on a subset of seven variables: two proxies for signal (average BS and RF similarity), four sources of bias (average pair-wise patristic distance, level of saturation, compositional heterogeneity and root-to-tip variance, the latter representing deviations from clock-likeness), and the proportion of variable sites. A principal component analysis (PCA) of these data sets resulted in two major axes explaining an average of 51.7% and 24.5% of total variance. Hierarchical and k-means clustering of the loadings of these first two PCs support the hypothesis that these axes are capturing similar aspects of molecular evolution across data sets (fig. 1 and supplementary fig. S3, Supplementary Material online). Both techniques resulted in a split of PCs into two main groups: one that includes PCs along which all properties increase/decrease (a pattern generally captured by PC 1), and another group of PCs along which sources of bias change in the opposite direction than proxies for signal (a pattern generally retrieved as PC 2). Two data sets (Hexapoda and Phasmatodea) have PCs whose groupings are reversed relative to others.

Fig. 1.

Gene properties covary in predictable ways, revealing underlying patterns of evolution that are shared by all phylogenomic data sets. The dendrogram shows that the eigenvectors of PC axes can be clustered into two major groups, labeled as patterns A and B. While pattern A is generally captured by PC 1 (green icons) and pattern B by PC 2 (orange icons), the hexapod and phasmatodean data sets are inverted. The histograms on the bottom she the distribution of loadings across variables. Results using k-means clustering are shown in supplementary figure S3, Supplementary Material online.

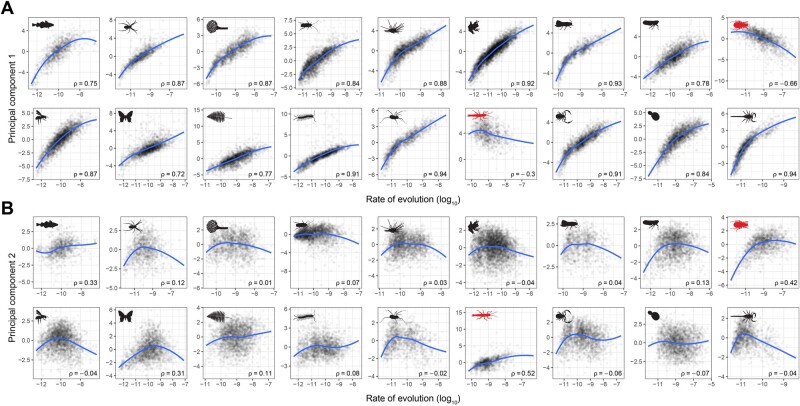
To understand what underlying factors could be generating these patterns, the scores of loci along both PCs were correlated with estimates of evolutionary rates (using the log-transformed harmonic mean of site rates). This analysis confirmed that the variability generally captured along PC 1 reflects differences in rates of evolution (fig. 2). On the other hand, PC 2 constitutes a dimension that is largely uncorrelated with evolutionary rates, but that often shows a more or less conspicuous peak at intermediate rates. Once again, the hexapod and phasmatodean data sets deviate from these patterns by exhibiting the lowest levels of correlation between rates and PC 1, as well as the highest level of correlation between rates and PC 2 (in absolute terms). These results are insensitive to the choice of an alternative, tree-based method to estimate evolutionary rates (i.e., the total tree length divided by the number of terminals, see supplementary fig. S4, Supplementary Material online).

Fig. 2.

Rate of evolution is the primary factor driving differences in gene properties. Scores of loci along PCs 1 (A) and 2 (B) were correlated against the log-transformed harmonic means of site rates. Blue lines correspond to LOESS regressions, and Spearman’s rank correlation coefficients (ρ) are shown in each plot. Clade icons are as in figure 1; the deviating hexapod and phasmatodean data sets are highlighted in red. Results using a tree-based estimate of evolutionary rates are shown in supplementary figure S4, Supplementary Material online.

The phylogenetic behavior of loci selected by both PC axes was then compared against other common subsampling strategies. For this, phylogenomic data sets were sorted according to a number of criteria and reduced to sizes of both 50 and 250 loci, selecting those that scored the highest or the lowest, depending on the strategy. A total of 23 subsampled matrices of both sizes were built from each data set. These included matrices that maximized gene length, occupancy, proportion of variable sites, average BS, RF similarity, iPIpen, and treeness, as well as matrices that minimized saturation, compositional heterogeneity, and root-to-tip variance. Data sets were also built from the fastest and slowest evolving loci, those showing intermediate rates (i.e., those whose rates were closest to the median rate of the entire data set), as well as those that scored highest and lowest along PC axes 1 and 2. Sorting was also done with SortaDate (Smith et al. 2018), a common pipeline for phylogenomic subsampling based on three gene properties. However, this method ordered loci in ways that were nearly identical to those achieved by using just one variable, whichever was selected as the first sorting step (see supplementary fig. S5, Supplementary Material online). Since all three variables were already being assessed, this method was not employed. Finally, five data sets were generated by sampling genes at random.

Phylogenetic inference using subsampled data sets was performed using IQ-TREE 1.6.3 (Nguyen et al. 2015) under the LG+F + G model, and node support was estimated using 1,000 replicates of ultrafast bootstrap (UFBoot; Hoang et al. 2018). Characterizing the performance of these data sets is complicated by the fact that the underlying phylogenies are unknown (in fact some of the trees used here have already been challenged to some degree; see Meusemann et al. 2020; Szucsich et al. 2020; Tihelka et al. 2020). Although large phylogenomic data sets generally produce fully resolved and supported topologies, model violations can favor incorrect trees (Delsuc et al. 2005; KapLi et al. 2021). Although this necessarily means that topologies supported by full phylogenomic data sets are only imperfect proxies with which to evaluate phylogenetic accuracy, it is also true that the proportion of nodes sensitive to model choice in any given analysis is small. Optimal subsampled data sets should be able to recapitulate this general tree structure, although not necessarily every detail; in other words, high topological similarity should still be favored, although the highest value does not guarantee the best results. At the same time, genes differ in their levels of phylogenetic signal, and an adequate subsampling scheme should be able to recover genes with above-average performance. Considering this, subsampling schemes were ranked in descending order of RF similarity to the tree found by the original studies, breaking ties using the average UFBoot values. The values for the five replicates of random subsampling were averaged to obtain a single estimate of their performance. Subsampling strategies ranking systematically better than randomly chosen loci were considered valid. Given difficulties establishing the identity of PC axes for Hexapoda and Phasmatodea, the results of these data sets were not included with the rest and are shown separately in supplementary figure S6, Supplementary Material online.

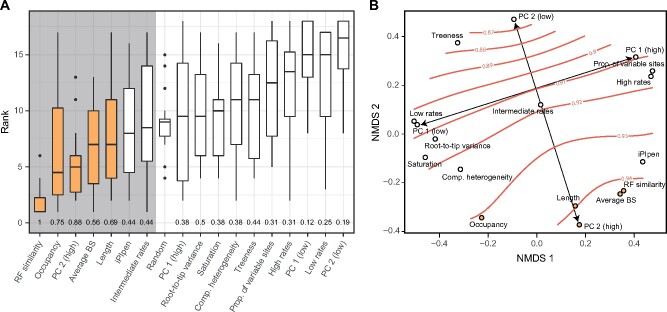
When subsampling to 250 loci, only five methods outperformed randomly chosen loci across more than half of the data sets (fig. 3A). These include matrices designed to maximize RF similarity, average BS, occupancy, and length, as well as those with loci that rank highest along PC 2. Two additional approaches—iPIpen and intermediate rates—have median ranks above that of randomly chosen loci, although ranking below more often than not. Of these, RF similarity and PC 2 (high) are the most consistent (i.e., have the lowest variance); other approaches behave well on average, but can occasionally perform poorly. As expected, differences in performance between strategies are even larger when subsampling to 50 loci (supplementary fig. S7, Supplementary Material online); however, the same set of methods is favored, with the further addition of loci with the highest proportions of variable sites. Very common approaches, including rate-based subsampling (saving the marginally good behavior shown by loci with intermediate rates) and the direct minimization of systematic biases (including saturation and among-lineage compositional and rate heterogeneities), perform systematically worse than randomly chosen loci at both subsampling levels (fig. 3A and supplementary fig. S6, Supplementary Material online).

Fig. 3.

Comparison of the performance of alternative subsampling strategies. (A) Distribution of ranks attained by different strategies (lower ranks represent better results). Two criteria for selecting adequate strategies are highlighted: those whose median ranks are lower than randomly chosen loci (grey background), and those that outperform these in more than half of the data sets (yellow bars). The proportion of times a given strategy ranks better than random loci is shown at the bottom. Results correspond to matrices of 250 loci; those for 50 loci are shown in supplementary figure S7, Supplementary Material online. (B) NMDS of pair-wise distances between strategies, representing the average frequency with which they share loci (smaller distances represent higher probabilities of targeting the same loci). Average RF similarity (orange lines) is overlayed as a smooth surface. PC 2 defines an axis that traverses the RF similarity gradient, whereas PC 1 (and other rate proxies) sample genes along a perpendicular axis that follows an isocline.

To further explore these patterns, I calculated the fraction of shared loci between matrices built using different subsampling strategies. This value was turned into a pair-wise distance metric and averaged across data sets, producing an estimate of the expected frequency with which strategies select the same genes. Nonmetric multidimensional scaling (NMDS) was used to project these distances into a 2D space on which the average topological similarity was overlain (fig. 3B). In line with previous results (figs. 1 and 2), this confirms that: 1) PCs built from the gene property data sets represent axes of evolutionary rate and phylogenetic usefulness; 2) rate and usefulness are perpendicular axes, such that rate-based subsampling does not optimize usefulness; and 3) directly minimizing sources of bias performs poorly because it has the unintended consequence of targeting slow-evolving loci that are largely uninformative.

Discussion

Quantifying and predicting which loci contribute toward recovering correct topologies has become central to phylogenomic inference (Meyer et al. 2011; Salichos and Rokas 2013; Doyle et al. 2015; Edwards 2016; Shen et al. 2016, 2017; Arcila et al. 2017; Brown and Thomson 2017; Molloy and Warnow 2018; Smith et al. 2018; Dornburg et al. 2019). This step can be used to explore phylogenetic conflicts, test specific hypotheses of relationships, measure the impact of different sources of bias, and allow for a better modeling of evolutionary processes. For the many phylogenetic questions that still remain unanswered, the preferred topology can entirely depend on assessments of the phylogenetic information contained within different loci (e.g., Simon et al. 2018; Lozano-Fernandez et al. 2019; Marlétaz et al. 2019; Smith et al. 2020). This has led to a plethora of recommendations on what constitutes a reliable gene and which proxies can be used to enrich data sets in them. Many of these were supported by searching for strong predictors of the topological distance to a preferred topology (Doyle et al. 2015; Burbrink et al. 2020; Vankan et al. 2020). However, extracting the individual effects of potential predictors is complicated by the pervasive levels of correlation that these exhibit (Shen et al. 2016; Kocot et al. 2017; Mongiardino Koch and Thompson 2021). Subsampling based on any individual property in the presence of such strong correlations can also have unintended effects: for example, increasing occupancy can reduce overall levels of phylogenetic signal, and targeting longer genes can increase compositional heterogeneity (supplementary figs. S1 and S2, Supplementary Material online).

Instead of focusing on correlating pairs of variables, I propose that a better understanding of the information content of loci can be gained by searching for regularities in the patterns of covariance between multiple properties and exploring the underlying factors that might produce them. Across a sample of 18 diverse phylogenomic data sets, I find that most of the variability captured across multiple gene properties happens along two major axes. These axes show remarkably similar patterns of covariance that can be readily interpreted as representing differences in evolutionary rate and phylogenetic usefulness (figs. 1 and 2 and supplementary figs. S4 and S6, Supplementary Material online). In the case of the latter, highly useful loci exhibit a consistent set of properties that include not only high values of node support and topological similarity but also low levels of saturation and reduced compositional and rate heterogeneities (i.e., simultaneously high signal and low biases). They also seem not to be among the fastest or slowest evolving genes, implying the existence of an optimal rate as predicted by theory (Yang 1998; Townsend 2007; Susko and Roger 2012; Klopfstein et al. 2017; Dornburg et al. 2019). Data sets with high levels of rate variation have reduced variation in phylogenetic usefulness and vice versa (supplementary fig. S8, Supplementary Material online), which is also expected if usefulness peaks at a particular (optimal) rate.

Many common subsampling strategies are justified in either phylogenetic theory or in the aforementioned correlation with measures of topological distance at the gene level. However, the behavior of multilocus subsampled data sets obtained by filtering genes based on such correlates has been seldom explored. Phylogenetically useful loci should also possess other properties besides low topological distances to a target tree, such as displaying a minimum of nonphylogenetic signals that can provide hidden support for incorrect topologies (Gatesy and Springer 2014), a problem that can become exacerbated in smaller data sets (Tilic et al. 2020). When the performance of subsampling strategies is evaluated, it becomes clear that many common approaches do not perform well on average. Such is the case of rate-based subsampling: matrices composed of the slowest or fastest evolving loci are among the worst that can be generated from phylogenomic data sets (fig. 3 and supplementary fig. S6, Supplementary Material online). Even targeting loci with intermediate rates, or those whose sites evolve at a pace that maximizes PI, does not drastically improve results relative to selecting loci at random (although iPIpen does succeed when subsampling to very small sizes, and also seems to select many genes in common with better-performing strategies; fig. 3 and supplementary fig. S7, Supplementary Material online). Different lines of evidence show that this inefficacy is a consequence of evolutionary rate being a dimension that is perpendicular to phylogenetic usefulness (figs. 1 and 3B). At first glance, this might seem to conflict with the existence of optimal rates for inference, but peaks in usefulness are evident in figure 2 and supplementary figure S4, Supplementary Material online. Another explanation could be that a direct link between rates and usefulness only exists at the level of sites (Dornburg et al. 2019), as different distributions of site rates can potentially average to identical gene rates. This not only implies that gene rates should be avoided for subsampling, but they might even constitute abstractions with weak ties to evolutionary processes. The results presented here confirm that gene rates are not a useful subsampling approach, but they also show that they do capture relevant differences in evolutionary history. Multiple proxies for gene rates converge on similar values, and genes with comparable rates share many common features, defining the major axis of variance in gene properties across most data sets. The problem does not seem to lie in gene rates being inappropriate, but rather that they constitute just one of several criteria that a phylogenetically useful locus should possess. Loci evolving at optimal gene rates exhibit large variabilities in usefulness (supplementary fig. S9, Supplementary Material online), which makes rate-based subsampling inefficient even when optimal gene rates can be discovered. Although this might be caused by differences in the underlying distributions of site rates, it likely also reflects compositional and rate heterogeneities that are not accommodated by approaches based on rates or informativeness (Dornburg et al. 2019).

Another common method to reduce the size of phylogenomic data sets is to discard loci that seem most affected by potential sources of bias (Nesnidal et al. 2010; Borowiec et al. 2015; Whelan et al. 2015; Kocot et al. 2017; Mongiardino Koch et al. 2018; Marlétaz et al. 2019), including high levels of saturation and heterogeneities in both composition and evolutionary rates. However, selecting the loci least affected by these issues does not result in phylogenetically accurate data sets (fig. 3A). These results are in strong conflict with many previous analyses that supported the use of clock-like, unsaturated, and compositionally homogenous genes (Doyle et al. 2015; Kuang et al. 2018; Lozano-Fernandez et al. 2019; Vankan et al. 2020; Evangelista et al. 2021). Although all three of these properties clearly represent severe issues for phylogenetic inference (Delsuc et al. 2005; KapLi et al. 2021), directly minimizing them enriches the data set in conserved and slow-evolving loci that do not contain enough phylogenetic information (fig. 3B). This unintended consequence highlights the fact that selecting genes based on any individual attribute can produce strong and undesired shifts in the distributions of other variables. This does not mean that these confounding factors should not be targeted, only that it should be done in a manner that ensures appropriate levels of information content or phylogenetic usefulness are retained. Clock-like genes are also routinely favored for estimating divergence times (Smith et al. 2018; Carruthers et al. 2020); it is therefore important to note that sampling the most clock-like genes can deplete phylogenetic signal and bias rate estimates.

Only five approaches are found to systematically outperform random loci selection at both levels of subsampling (fig. 3 and supplementary fig. S6, Supplementary Material online). These include two proxies for phylogenetic signal (RF similarity and average BS), two measures of amount of information (alignment length and occupancy), and the phylogenetic usefulness axis obtained using PCA. The finding that maximizing RF similarity is consistently recovered as the best approach was expected, as the ranking of strategies is to a large degree also determined by this metric. This circularity complicates an objective evaluation of this approach, which would require simulations under a known topology (to some degree, this is true for other conclusions drawn here). However, maximizing average BS support, a different proxy for signal that does not suffer from this problem, results in the sampling of a very similar set of loci (fig. 3B), providing indirect evidence of the suitability of subsampling based on topological similarity. At the same time, given that sampling of genes selected for their RF similarity recovers the topologies most similar to those of targeted trees, this strategy provides an effective way of replicating results with smaller data sets, but should not be interpreted as a test of phylogenetic results. Although longer genes were previously found to recover better topologies (Aguileta et al. 2008; Betancur-R et al. 2014; Shen et al. 2016; Brown and Thomson 2017), occupancy had been considered less of a concern for data sets composed of hundreds of loci (Philippe et al. 2004; Roure et al. 2013; Streicher et al. 2016; Molloy and Warnow 2018). Results shown here suggest that maximizing both of these are among the best-performing subsampling strategies on average, but also exhibit a relatively inconsistent behavior, occasionally ranking among the worst. Their use should be accompanied by some assessment of how they are impacting overall levels of signal.

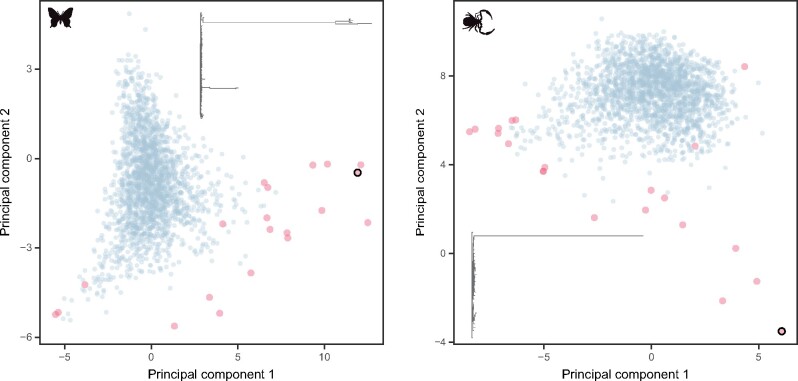
Finally, maximizing phylogenetic usefulness through the use of PCA provides a direct way to optimize levels of phylogenetic signal while also controlling for sources of bias. This is done simultaneously and without the need to arbitrarily order variables or establish thresholds. By drawing information from multiple properties, the approach is able to discover patterns that are unique to each data set, weighting factors in proportion to their relative contributions. This also provides a useful avenue for filtering outlier genes, as shown in the Materials and Methods and figure 4. The method, named genesortR, is implemented as an R script available at https://github.com/mongiardino/genesortR. For all but two of the data sets analyzed, the interpretation of the second PC dimension as a usefulness axis was straightforward; for the remaining ones (Phasmatodea and Hexapoda), a more careful study revealed usefulness was captured along PC 1 (supplementary fig. S6, Supplementary Material online). In the specific case of the hexapod data set, both PC axes seemed to correlate relatively strongly with rate estimates (fig. 2), which is consistent with the idea that resolving the phylogeny of ancient clades requires highly conserved, slow-evolving genes. Taken to an extreme, this could potentially induce the collapse of rate and usefulness into a single dimension, at which point the method here described would become impractical, as it would converge on sampling slow-evolving loci. Therefore, this approach may not be universally applicable, and might not help resolve phylogenies outside the range of conditions explored, including clades that are older, evolve faster, or contain recalcitrant nodes characterized by extreme levels of phylogenetic conflict. Under such conditions, it is possible that better estimates of phylogeny will be returned using methods that are here found to be inappropriate for average phylogenetic questions, such as minimizing evolutionary rates or sources of systematic bias. Even so, it is likely that progress in our understanding of contentious relationships that have defied resolution will happen as we improve our ability to decode the evolutionary processes ingrained along the different axes that describe the information content of loci.

Fig. 4.

Detection of outlier genes using multiple gene properties in two exemplary data sets, Lepidoptera (left) and Pseudoscorpiones (right). Plots show the PC axes built from the entire data sets, with the genes considered outliers shown in red. The topology of the largest outlier (highlighted with a black border) is plotted.

Materials and Methods

Data sets chosen for this study had to fulfill a number of criteria. First, I only used data sets built from full genomes and/or transcriptomes, as these are likely to exhibit a wider range of values across different properties—such as rates—than data sets built using methods of targeted enrichment (e.g., ultraconserved elements, anchored hybrid enrichment). For standardization, all data sets were coded as amino acids, although the methods employed are applicable to other data types. Studies also had to infer a time-calibrated topology, establishing a timescale of diversification that could be used to estimate rates of evolution in number of substitutions per unit of time. These topologies were inferred and calibrated using entirely different methodologies, but represent in every case the best estimate of relationships as supported by the authors. Taxon sampling within the ingroup had to be reasonably thorough to allow for accurate estimates of site and gene properties, such as evolutionary rates (Hugall and Lee 2007). Finally, data sets with notoriously contentious relationships, such as lophotrochozoans (Kocot et al. 2017), chelicerates (Sharma et al. 2014), and metazoans (King and Rokas 2017), were avoided. Instead, an effort was made to focus on data sets showing more typical levels of phylogenetic signal and noise. The 18 data sets sampled (table 1) were only modified by filtering loci with values of occupancy below 50%.

Gene trees were inferred using ParGenes v. 1.0.1 (Morel et al. 2019) that automated model selection with ModelTest-NG (Darriba et al. 2020) and phylogenetic inference with RAxML-NG (Kozlov et al. 2019) for each multiple sequence alignment. The optimal model was considered to be the one minimizing the Bayesian Information Criterion; support values were estimated with 100 replicates of nonparametric BS. Rates of evolution for all sites in each data sets were estimated using the empirical Bayes method implemented in Rate4Site (Mayrose et al. 2004) using the time-calibrated tree pruned to include only terminals present in each locus. Given that outgroups often represent poorly sampled clades that can be distantly related to the ingroup (e.g., in the case of Echinoidea extending the age of the tree root by 200 My; Mongiardino Koch and Thompson 2021), and thus have a strong effect on estimated rates, they were removed from both trees and alignments. Branch length optimization was disabled and all other options were left as default. For some loci, the inference of gene trees or the estimation of site rates failed; these loci were dropped from further analyses, resulting in the final numbers shown in table 1.

A group of 15 properties was calculated for each locus in R using custom scripts (see Results). Scripts relied on functions from packages adephylo (Jombart et al. 2010), ape (Paradis and Schliep 2019), MESS (Ekstrom 2020), phangorn (Schliep 2011), PhyInformR (Dornburg et al. 2016), phytools (Revell 2012), and the tidyverse (Wickham 2017). As with site rates, outgroups were removed before estimating these. Correlations among all gene properties, and between these and the absolute age of clades, were visualized using package corrplot (Wei and Simko 2017) and P values were corrected using Benjamini and Hochberg (1995) correction for multiple comparisons. Following Mongiardino Koch and Thompson (2021), a subset of seven gene properties was subject to PCA. Among these are two widely employed proxies for phylogenetic signal: the RF similarity to the species tree (i.e., the complement of the RF distance; Robinson and Foulds 1981), generally taken to be an estimate of topological accuracy, and the average BS support (Salichos and Rokas 2013; Doyle et al. 2015; Shen et al. 2016; Vankan et al. 2020). Four other variables are known to induce systematic errors in tree reconstruction (Delsuc et al. 2005; Nesnidal et al. 2010; Nosenko et al. 2013; Struck 2014; Kocot et al. 2017; KapLi et al. 2021): the variance of root-to-tip distances (i.e., the degree of deviation from a strict clock-like behavior), the average pair-wise patristic distance between terminals (indicative of susceptibility to long-branch attraction), the level of saturation (estimated as one minus the regression slope of patristic distances on p-distances), and the compositional heterogeneity (measured by the RCFV scores). The last variable included was the proportion of variable sites, a metric generally interpreted to represent information content (Aguileta et al. 2008; Mclean et al. 2019), and that is strongly correlated with estimates of rates and tree length in the data sets employed (supplementary fig. S2, Supplementary Material online). All of these properties have been used individually for phylogenomic subsampling (see supplementary table S1, Supplementary Material online). This approach suffers from some degree of circularity given the use of topological similarity in the selection of genes, but this should bias results minimally as this is just one of the several attributes employed. In case the species tree for the lineages sampled is highly uncertain, an option is available to run the analysis without using RF similarities as input for the PCA. Alternatively, uncertain nodes can be collapsed in the tree used to measure topological distances; taken further this would converge on the approach used by Philippe et al. (2019) to focus only on the recovery of a handful of uncontroversial monophyletic groups. A few different sets of variables were explored, as well as alternative metrics for some of them (such as different tree distances); these changes did not improve the proportion of variance captured by the first two PCs and were not further explored. It should be noted, however, that a thorough optimization of the variables included was not performed, and this is likely to have some effect on results.

PCA is susceptible to outlier data points (i.e., observations that strongly deviate from the general structure of correlation between variables), as these contribute a large fraction of total variance and can attract the first components. Although this can be seen as a limitation of the method, it also provides an opportunity to detect and filter out outlier genes. These can arise from both analytical and biological processes (e.g., errors in orthology inference or alignment, strong selective pressures, etc.), and have a strong impact on tree reconstruction (Brown and Thomson 2017; Shen et al. 2017; Walker et al. 2018). To remove outlier genes, I measured the Mahalanobis distance of all observations to the origin of the PC space (employing all seven dimensions) and removed the top 1% with the greatest distances (fig. 4). These represent alignments with highly unlikely combinations of gene properties given the structure of correlation of the entire data set. PCA was then repeated on the remaining observations. Compared with other methods devised to remove outlier data from phylogenomic data sets (e.g., de Vienne et al. 2012; Mai and Mirarab 2018), this approach benefits from not only considering tree topology, but doing so alongside other gene properties. The removal of outlier genes not only helps correctly identify the major axes of variance among “regular” observations (i.e., ensures that PCs capture true differences in rate and usefulness) but also provides an extra step of sanitation, likely to be especially important before data sets are reduced in size. Future work would likely benefit from a more sophisticated approach to outlier detection, such as is offered by robust PCA methods (Todorov and Filzmoser 2009).

Both hierarchical and k-means clustering were used to discover groupings of similar PC axes that could potentially represent similar underlying factors. Given that PC orientation is arbitrary, clustering was done using eigenvectors as well as their opposites (fig. 1 has the mirrored half of the dendrogram removed). Hierarchical clustering was performed using Euclidean distances and complete linkage (fig. 1); k-means clustering used 10,000 random starting configurations (supplementary fig. S3, Supplementary Material online). The identity of these axes was first established by correlating the scores of the first two PCs against different estimates of gene-wise evolutionary rates: the total tree length divided by the number of terminals (Telford et al. 2014; Howard et al. 2020), and the harmonic mean of site rates. For all data sets except Hexapoda and Phasmatodea, the Spearman rank correlation coefficients (ρ) between both estimates of rate and PC 1 were larger than 0.7 and more than twice the values of ρ between rate estimates and PC 2 (fig. 2 and supplementary fig. S4, Supplementary Material online). This was taken to represent strong evidence that PC 1 was (in general) capturing rate variation. Correlations between PC 1 and tree-based rates were much higher (average ρ = 0.94) than between PC 1 and sequence-based rates (average ρ  =  0.86). This seems to confirm that averaged site rates are an inaccurate proxy for gene-wise evolutionary rates (Dornburg et al. 2019). The relationship between gene rates and phylogenetic usefulness (supplementary fig. S9, Supplementary Material online) was also studied by binning loci into 25 categories based on their rates and calculating the mean and variance of usefulness (i.e., PC 2 scores) within each. A linear regression between these two metrics was assessed after excluding outliers, identified as those whose residuals were significantly larger than expected using a chi-square test in package outliers (Komsta 2011).

Phylogenomic data sets were sorted based on 13 different properties (gene length, occupancy, proportion of variable sites, average BS, RF similarity, iPIpen, treeness, saturation, RCFV, root-to-tip variance [clock-likeness], sequence-based evolutionary rate, and PCs 1 and 2) and subsampled to sizes of 50 and 250. These numbers were chosen because they represent common data sizes used for computationally intensive methods such as total-evidence dating (Lee 2016; Brennan et al. 2021; Mongiardino Koch and Thompson 2021) and inference under complex site heterogenous models (Ballesteros et al. 2019; Marlétaz et al. 2019), respectively. Subsampled data sets were composed of either the highest or lowest scoring loci, depending on the variable used for sorting. In the case of rates and PC axes, both the highest and lowest scoring loci were used. An extra subsampling strategy targeting intermediate rates (defined as those loci with sequence-based rates closest to the median value for the entire data set) was also used. Five extra matrices were built by selecting loci at random, for a total of 23 matrices per phylogenomic data set and subsampling size. It should be noted that some low occupancy taxa had no data in the subsampled matrices and had to be removed. In conditions of extremely uneven occupancy, these protocols should be paired with additional steps to ensure key taxa are represented in the final data sets. Tree inference was performed in IQ-TREE 1.6.3 (Nguyen et al. 2015) under the LG + F + G model, and 1,000 replicates of ultrafast bootstrap (UFBoot; Hoang et al. 2018) were used to estimate node support values.

The performance of subsampling strategies was evaluated using two metrics: the RF similarity to the tree supported by the original studies (i.e., the same used to estimate topological similarity for individual loci), and the average UFBoot support. The values obtained for the five replicates of randomly sampled loci were averaged. Subsampling strategies were then ranked based on RF similarity scores with ties broken using average support values, such that strategies that result in more accurate and well-supported trees receive lower ranks. Two criteria were used to establish which subsampling approaches are useful: 1) strategies that attain a median rank that is lower than that of randomly sampled data across data sets; and more strictly, 2) strategies that attain a lower rank than randomly sampled data for more than half of data sets (fig. 3 and supplementary fig. S7, Supplementary Material online). Given the nonstandard behavior of the hexapod and phasmatodean data sets, results from these were not combined with those of other data sets, and are reported separately in supplementary figure S6, Supplementary Material online. It should be noted that subsampling was always performed by selecting entire genes and that results for some strategies might differ from those obtained by selecting sites (e.g., when using rates). Retaining the gene structure of the data sets is not only necessary for some types of phylogenetic inference such as summary coalescent methods but also provides access to a much larger pool of properties, including all of those estimated on gene trees. A focus on loci can also help discover outlier data (fig. 4) and reveal important evolutionary processes, such as compositional and rate heterogeneities (or at least aid in their discovery). The relative performance of strategies was also evaluated at the level of the entire tree topology, and some of the methods used (e.g., iPIpen) might be more suitable for finding optimal loci to resolve specific nodes or time intervals.

Finally, the dissimilarities between pairs of 250-loci matrices obtained through different subsampling strategies (i.e., the proportion of loci not shared) were calculated and averaged across data sets. The resulting distance matrix was decomposed into a 2D space using NMDS. This relied on package vegan (Oksanen et al. 2020) and employed 10,000 iterations from random starts. Stress was evaluated using a Shepard diagram (i.e., a plot of observed distances vs. ordination distances), and a nonmetric estimate of goodness-of-fit returned an R-squared value of 0.99. The averaged RF similarity across data sets was overlain onto this plot as a smooth surface, which was fitted using penalized regression splines.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.