Preparation and growth mechanism of micro spherical ammonium dinitramide crystal based on ultrasound-assisted solvent-antisolvent method

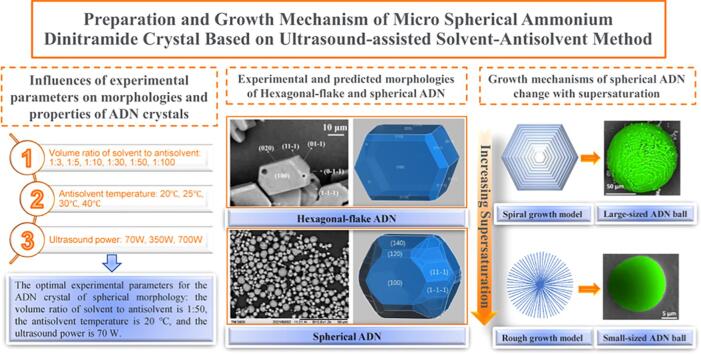
Graphical abstract

Highlights

• •Preparation technology of spherical ammonium dinitramide (ADN) crystals.
• •An ultrasound-assisted solvent-antisolvent method.
• •Influences of experimental parameters on morphology and particle size of ADN.
• •Predicted ADN crystal morphologies by growth and equilibrium morphology methods.
• •Growth mechanisms of spherical ADN crystal change with supersaturation.

Abstract

Micro-sized spherical ammonium dinitramide (ADN) crystals are successfully prepared by a facile ultrasound-assisted solvent-antisolvent recrystallization method without introducing any additives. The influences of the volume ratio of solvent to antisolvent, the antisolvent temperature and the ultrasound power on the micro-morphologies and properties of ADN crystals are studied systematically. The changes of morphology, particle size, crystal structure and melting point of the ADN crystals are characterized through scanning electron microscopy (SEM), laser particle size analyzer (LPSA), X-ray diffraction (XRD) and differential scanning calorimetry (DSC), respectively. The results show that the optimal experimental parameters for the ADN crystal of spherical morphology are as follows: the volume ratio of solvent to antisolvent is 1:50, the antisolvent temperature is 20 ℃, and the ultrasound power is 70 W. The predicted hexagonal-flake and spherical morphologies for the ADN are close to the experimental morphologies. The growth mechanism of the spherical ADN crystal changes with supersaturation of the ADN solution. As the degree of supersaturation increases, the growth models of the spherical ADN change from the spiral growth to the rough growth, and the morphologies of ADN change from the large-sized ADN ball to the small-sized ADN ball.

1. Introduction

The ammonium dinitramide (ADN, NH₄N(NO₂)₂), which firstly was synthesized by Zilinsky Institute in Moscow in 1970s, is a promising and environment-friendly strong oxidizer to replace ammonium perchlorate (AP) in solid propellants because of its high oxygen balance of 25.8%, low characteristic signal, high burning rate [1] and high specific impulse [2], [3]. However, the raw ADN in the needle crystals has many fatal flaws in the solid propellant application, such as strong hygroscopy at the critical relative humidity of 55.2% at 25.0 ℃, low loading density, and poor mechanical properties [1]. It has been proved that the spherical ADN has higher mechanical properties than the flaky ADN in propellant [4]. Therefore, many researchers have focused on developing the spherical ADN.

The three traditional technologies have been developed to prepare spherical ADN: prilling tower process, emulsion crystallization and spray crystallization. In 2000, Highsmith, et al. reshaped the ADN by the prilling tower method [5]. In the same year, Ulrich Teipel, et al. prepared spherical ADN of the particle size from 10 μm to 600 μm by the emulsification crystallization method [6]. Whereafter, the spray crystallization was introduced to prepare spherical ADN with an average diameter of 106 μm by Heintz and Fuhr in 2005[7] and Johansson, et al. in 2006[8]. However, the common problem for the three methods is that the molten ADN is needed to be made. The molten ADN has been demonstrated to be hazardous, and the impact sensitivity threshold of the molten ADN (<0.25 J) is lower than that of solid ADN (4 J), and similar to the one of nitroglycerin (<0.25 J) [9]. Recently, Jean-Edouard Berthe, et al. produced the spherical ADN nanocrystallisation of the particle diameter around 32 and 34 nm by developing a new technology of spray flash evaporation (SFE) in 2018[2]. However, the nano-scale spherical ADN is too small to disperse uniformly in actual propellants. Thereupon, the traditional solution crystallization process is considered to be employed in the reshaping of ADN. Micron-scale lamellar ADN has been obtained through combining experiments and simulation by changing different solutions in our lab, and the introduction of NaF could induce the formation of polyhedral ADN [10].

Solvent-antisolvent crystallization method is a simple, safe, time-saving, effective and scalable technique in reducing crystal size and controlling morphology and purity under room temperature and pressure [11], which requires that solute has a good solubility in solvent and a poor solubility in antisolvent, as well as good compatibility between solvent and antisolvent, and could generate high supersaturation and leading to fast nucleation [12]. Compared to cooling or evaporative crystallization, it requires less energy input. Raj et al. demonstrated the particle size and morphology of nano-sized 1,3,5-trinitro-1,3,5-triazacyclohexane (RDX) and 1,3,5,7-tetranito-1,3,5,7-tetraaza cyclooctane (HMX) could be tuned by changing the solvent with the evaporation-assisted solvent-antisolvent interaction method [13]. This method has been applied for many high energetic materials (HEMs), such as RDX, HMX, hexanitrohexaazaisowurtzitane (CL-20)[14], 2-methyl-1,3,5-trinitrobenzene (TNT)[12], triaminotrinitrobenzene (TATB)[15], hexanitrostilbene (HNS)[16]. As a consequence, the solvent-antisolvent method is taken into consideration to control the ADN nucleation process in this research.

The purpose of this research is to find a safe and facile way of preparing micron-sized spherical ADN. To obtain the optimal experimental parameters for preparation of the spherical ADN crystal, the morphology and particle size of ADN are explored based on solution crystallization in the solvent-antisolvent method through changing the volume ratio of solvent to antisolvent, the antisolvent temperature, and the ultrasound power.

2. Experiment and simulation

2.1. Materials

Raw ADN was provided by Xi’an Modern Chemistry Research Institute, China. The solvent absolute ethanol (EN) and ethyl acetate (EA), and antisolvent dichloromethane (DCM) were purchased from Beijing Tong Guang Fine Chemicals Company, China.

2.2. Recrystallization process of ADN

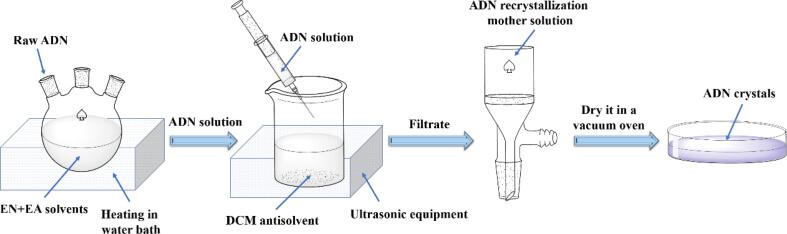
A general recrystallization process of ADN using solvent-antisolvent method was depicted in Scheme 1. The raw ADN was dissolved in the mixed solvent composed of EN and EA to gain the ADN solution. Then the ADN solution and antisolvent were mixed. Maintain it for 2 h, and filtrate, then dry it in a vacuum oven at 50 ℃ to obtain ADN crystals. Change the experimental conditions to prepare different ADN crystals by controlling the variable parameters.

Scheme 1.

Preparation process of ADN recrystallization.

2.3. Characterization

The morphology and mean volume particle size of ADN crystals were characterized by TM3000 scanning electron microscopy (SEM, HITACHI, Japan) and Hydro 2000MU laser particle size analyzer (LPSA, Malvern, UK). And the high magnification SEM images were captured by Regulus 8230 SEM (HITACHI, Japan). The aspect ratios of ADN were calculated using Image J software from SEM images. Crystal structure of ADN crystals was analyzed by powder X-ray diffraction (XRD, Rigaku, Japan) using Cu Kα radiation as an X-ray source (λ = 1.54178 Å) at room temperature. The voltage and current applied were 40 kV and 15 mA, respectively. The crystals were scanned at 2θ from 2° to 60° at a scanning rate of 6°/min. The melting points of ADN were tested by differential scanning calorimetry (DSC, Netzsch, Germany) with a heating rate of 10 ℃/min from 30 ℃ to 100 ℃ under the nitrogen gas flow of 20 mL/min.

2.4. Morphology prediction

Unit cell model of the ADN is constructed according to its cell parameters (CCDC number 854801, monoclinic system, P2₁/c space group, a = 6.914 Å, b = 11.787 Å, c = 5.614 Å, α = γ = 90°, β = 100.40°) [17]. The ADN crystal morphology in a vacuum is simulated by running Morphology module in Materials Studio (MS) software. Both the growth morphology and equilibrium morphology of ADN crystals are predicted by Growth morphology and Equilibrium morphology methods with the Dreiding force field and the current charge at ultra-fine quality, respectively.

3. Results and discussion

3.1. Effects of experimental parameters on morphology and size of ADN crystals

By a series of controllable experiments, it is found that the ultrasound-assisted solvent-antisolvent recrystallization method provides a facile means to tailor the morphology and size of ADN crystals by varying experimental parameters, such as the volume ratio of solvent to antisolvent, the antisolvent temperature, and the ultrasound power.

3.1.1. Volume ratio of solvent to antisolvent

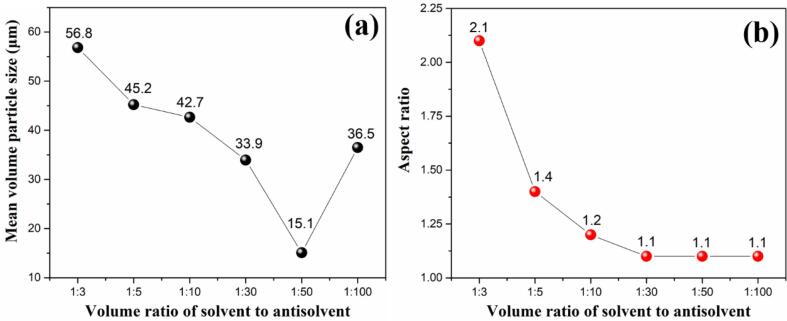
The volume ratios of solvent to antisolvent are varied from 1:3 to 1:100 systematically, meanwhile keeping other experimental conditions unchanged. The morphologies of ADN are shown in Fig. 1, and the corresponding mean volume particle size and aspect ratio are shown in Fig. 2. It is very interesting that the ADN crystal morphology could be tuned by varying the volume ratio of solvent to antisolvent exhibited in Fig. 1. When the volume ratios of solvent to antisolvent are 1:3 and 1:5, the ADN crystals present hexagonal-flake; when the ratio is 1:10, the ADN crystals present the mixture of hexagonal-flake and sphere; when the ratio is 1:30, the ADN is spherical with the different particle size distributions, but there are phenomena of beads-like and dendritic growth; when the ratios are 1:50 and 1:100, the ADN crystals grow as spherical shape with good dispersibility.

Fig. 1.

SEM images of ADN crystals at different volume ratios of solvent to antisolvent.

Fig. 2.

Mean volume particle size (a) and aspect ratio (b) of ADN crystals at different volume ratios of solvent to antisolvent.

From Fig. 2 (a), with the increase of volume ratios of solvent to antisolvent from 1:3 to 1:100, the mean volume particle size of ADN mainly decreases, and reaches the smallest value of 15.1 μm when the volume ratio of solvent to antisolvent is 1:50. However, for the 1:100 ratio of the solvent to antisolvent, the particle size rise to 36.5 μm. Particle aspect ratio is defined by the ratio of its length to width, which is the mean value of 100 particles shown in SEM images in this research. As the antisolvent increases, the aspect ratio of ADN crystal gradually decreases and then tends to remain unchanged. When volume ratio of solvent to antisolvent is 1:30 and the greater, its aspect ratio is stable at 1.1. On the base of above analysis, 1:50 should be the optimum volume ratio of solvent to antisolvent for tailoring spherical ADN crystal.

3.1.2. Antisolvent temperature

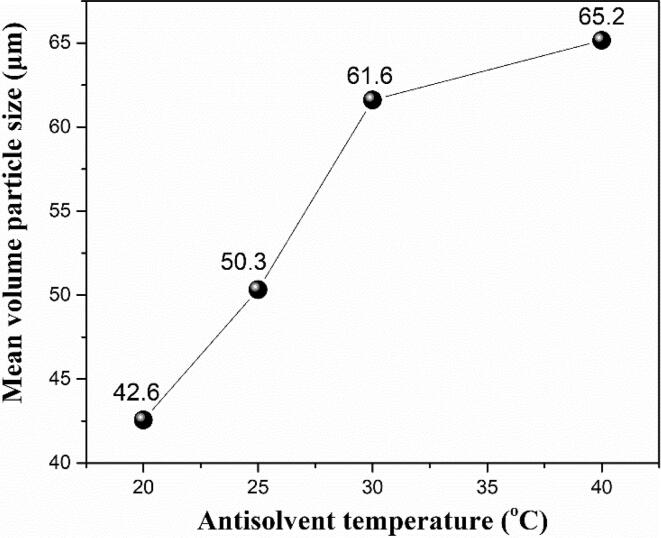
The antisolvent temperature was set at 20, 25, 30 and 40 ℃, respectively. Fig. 3 and Fig. 4 show the SEM images and mean volume particle size of ADN crystals at different antisolvent temperatures. Combining Fig. 3 and Fig. 4, the spherical ADN crystals can be formed at different antisolvent temperatures. The lower antisolvent temperature means the smaller crystal size. When the temperature is low, the crystallization process is mainly an interfacial interaction. When the temperature rises, the diffusion becomes dominant effect.

Fig. 3.

SEM images of ADN crystals at different antisolvent temperatures.

Fig. 4.

Mean volume particle size of ADN crystals at different antisolvent temperatures.

From the perspective of solution supersaturation, the temperature plays an important role in the dissolution of solutes, and it directly affects the supersaturation degree of solution. In solvent-antisolvent crystallization, the degree of supersaturation can be defined as the difference between the concentration of the solute before and after adding the antisolvent, and the ratio of supersaturation can be simplified as

$$\mathit{S}=\frac{\mathit{C}}{{\mathit{C}}^{*}}$$ (1)

where C is the actual concentration, g/mL; C* is the equilibrium concentration reached when the antisolvent is added, g/mL [18]. The nucleation rate (J, the nuclei number of per unit volume in unit time) and growth rate (R) of crystal can be expressed by the following equations,

$$\mathit{J}=\mathit{Aexp}\left[\frac{{-\mathit{W}}^{*}}{\mathit{kT}}\right]$$ (2)

where A is the pre-exponential kinetic parameter (~10³⁰ for solution), W* is the nucleation work, k is the Boltzmann constant (k = 1.380649$\times$10^-23 J/K), and T is the absolute temperature [19].

$${\mathit{R}=\mathit{k}}_{\mathit{G}}{(\mathit{lnS})}^{\mathit{n}}$$ (3)

where n is the growth order, which depends on the different growth mechanisms, and $k_G$ is an overall growth constant coefficient [18].

From Eq. (2), the higher the temperature, the faster the nucleation rate. However, the higher the antisolvent temperature, the lower the supersaturation, the slower the growth rate according to Eq. (3). In higher antisolvent temperature, ADN crystal nuclei form quickly and grow up into large-sized crystals slowly. Therefore, the lower the antisolvent temperature, the smaller the mean particle size of ADN. That is to say, when the antisolvent temperature is 20 ℃, the mean particle size of ADN is the smallest.

3.1.3. Ultrasound power

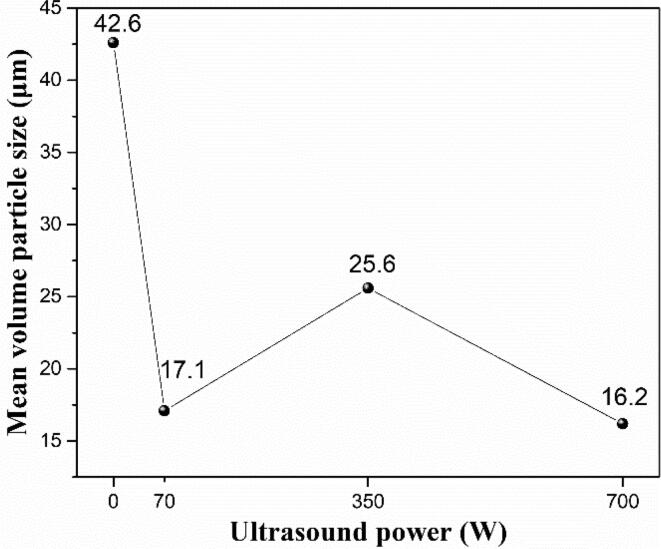
The ultrasound for the solution is applied to study its effects on morphology and particle size of the ADN crystal during the crystallization process, which is set at low (70 W), medium (350 W) and high (700 W) levels, respectively. The SEM images and particle size of the precipitated ADN crystals are shown in Fig. 5 and Fig. 6. It is amazing that all the ADN crystals under the different ultrasound powers have a regular spherical morphology, good dispersion without the agglomeration and the relatively uniform size around 16–26 μm. Compared without the ultrasound (0 W), the average particle size of the ADN crystal is reduced. Because the ultrasound crystallization is a non-invasive method to obtain uniform morphology and particle size by controlling the point of nucleation and the number of nuclei. The cavitation of the ultrasound can form a nucleation center at a lower degree of supersaturation, which lead to narrowing the width of the metastable zone and reducing the size distribution of the crystal growth, so that the morphology of crystal is regular and uniform [14]. From the above results, the ultrasound for the solution with different powers all can bring similar control effects for ADN crystal, so the best choice of power parameters is the lowest power of 70 W in consideration of energy saving.

Fig. 5.

SEM images of ADN crystals at different ultrasound powers.

Fig. 6.

Mean volume particle size of ADN crystals at different ultrasound powers.

3.1.4. Predicted and experimental ADN morphologies

The external morphology of the crystalline can be predicted from its internal crystal structure by the morphology module in MS software. The Bravais-Friedel Donnay-Harker (BFDH) method is a geometrical calculation method that a list of possible growth faces and their relative growth rates are generated by using the crystal lattice and symmetry. The growth morphology method could predict the shape of the crystal more accurately than the BFDH method because it takes the energetics of the system into account based on the attachment energy (AE)[20]. The equilibrium morphology of the crystal only depends on the specific free energies of the different {hkl} forms of the crystal according to Gibbs-Wulff’s theorem [21].

The morphology of the above regular hexagonal-flake ADN crystals is simulated by MS software with the Dreiding force field, according to Growth morphology model, and the experimental morphologies of hexagonal-flake ADN crystals are obtained under the conditions of Fig. 1 (a₁, a₂) and (b₁, b₂). The comparison between the predicted and experimental morphologies of hexagonal-flake ADN are shown in Fig. 7, and the calculated morphologically important faces of hexagonal-flake ADN are listed in Table 1.

Fig. 7.

SEM images of hexagonal-flake ADN faces (a, b) and morphology simulated (c) by using MS software with the Growth morphology model.

Table 1.

The morphologically important faces of ADN by Growth morphology model.

hkl	Mul	dhkl (Å)	Eatt(tot) (kcal/mol)	Eatt(vdW) (kcal/mol)	Eatt(elect) (kcal/mol)	Eatt(H-bond) (kcal/mol)	Total facet area (%)
(1 0 0)	2	6.80	−18.34	−9.49	0.00	−8.85	33.69
(0 2 0)	2	5.89	−21.28	−12.28	0.00	−8.62	26.40
(1 1 0)	4	5.89	−24.74	−9.52	0.00	−15.22	6.39
(0 1 1)	4	5.00	−28.29	−11.02	0.00	−17.27	27.73
(1 1-1)	4	4.39	−32.90	−16.88	0.00	−16.02	5.79

From Fig. 7 (c) and Table 1, there are five morphologically important faces for the predicted hexagonal-flake ADN according to the Growth morphology method, i.e. (1 0 0), (0 2 0), (1 1 0), (0 1 1), (11–1). In comparison with the predicted morphology, the prepared hexagonal-flaky ADN crystals shown in Fig. 7 (a) and (b) exhibit the large (1 0 0) faces with the slowest growth rate, followed by (0 2 0) faces. The (11–1), (01–1), (1–1–1), (0–1–1) and their symmetric faces are represented in the final crystal morphology, whereas the (1 1 0), (1–10) and their symmetric faces disappear owing to their faster growth rate. This is because the change of supersaturation affects the relative growth rates of these crystal faces, resulting in the modification of the final morphology of ADN crystals in actual experiments. As a consequence, the (1 0 0) faces have the highest surface area and become the dominated faces in the final hexagonal-flake ADN crystal morphology.

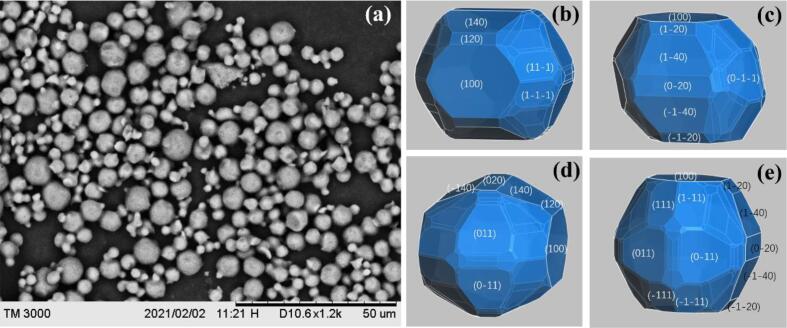
The morphologies of the spherical ADN crystals are simulated by MS software with the Dreiding force field according to the Equilibrium morphology model. The experimental morphologies of spherical ADN crystals could be obtained under the conditions of Fig. 1 (d₁, d₂), (e₁, e₂) and (f₁, f₂). Fig. 8 and Table 2 are the experimental and calculated results for the spherical ADN, the predicted athermal equilibrium morphology of ADN shows the polyhedral quasi-spherical morphology, which is composed of 75 faces (Table S1). The 15 important faces where the total facet area of each face accounts more than 1% are listed in Table 2, and their total facet area is 86.9%. The (1 4 0) and (1 0 0) faces are the dominated faces with slower growth rates. The comparison of the predicted and experimental morphologies in Fig. 8 (a) of spherical ADN shows that the boundary of each crystal face of the spherical ADN crystal obtained by the experiment has become very blurred, and it is completely close to or becomes a smooth spherical shape. It means that under the experimental conditions, the increase in supersaturation makes the growth rate of each crystal face at the ADN crystal close, and finally the smooth spherical crystals are formed.

Fig. 8.

SEM image of spherical ADN (a) and the predicted morphologies (b, c, d, e) at different views by the Equilibrium morphology method.

Table 2.

The morphologically important faces of ADN by Equilibrium morphology model.

hkl	Mul	dhkl (Å)	Esurf(tot) (kcal/mol)	Esurf(vdW) (kcal/mol)	Esurf(elect) (kcal/mol)	Esurf(H-bond) (kcal/mol)	Total facet area (%)
(1 4 0)	4	2.70	0.14	0.08	0.00	0.06	17.05
(1 0 0)	2	6.80	0.14	0.07	0.00	0.07	16.86
(0 1 1)	4	5.00	0.16	0.07	0.00	0.10	12.09
(1 1-1)	4	4.39	0.17	0.09	0.00	0.08	7.22
(1 1 1)	4	3.75	0.16	0.09	0.00	0.07	5.49
(0 2 0)	2	5.89	0.14	0.09	0.00	0.06	5.35
(1 2 0)	4	4.45	0.15	0.08	0.00	0.08	4.55
(1 2-1)	4	3.69	0.16	0.08	0.00	0.08	3.87
(3 6 2)	4	1.25	0.16	0.08	0.00	0.07	2.82
(1 2 1)	4	3.28	0.16	0.08	0.00	0.08	2.71
(4 9-4)	4	0.88	0.16	0.08	0.00	0.08	2.09
(4 9-3)	4	0.95	0.16	0.08	0.00	0.08	1.95
(3 7-2)	4	1.27	0.16	0.08	0.00	0.08	1.81
(4 7 4)	4	0.85	0.16	0.08	0.00	0.08	1.77
(4 9-5)	4	0.80	0.17	0.08	0.00	0.09	1.27
Total							86.90

The predicted and experimental aspect ratios of hexagonal-flake and spherical ADN are summarized in Table S2. The predicted aspect ratios of the hexagonal-flake ADN and the spherical ADN are 2.0 and 1.4, respectively, close to the experimentally obtained aspect ratios. The above results indicate that the predicted crystal morphologies of hexagonal-flake and spherical ADN are close to the experimental morphologies.

3.2. Effects of experimental parameters on crystal structure of ADN crystals

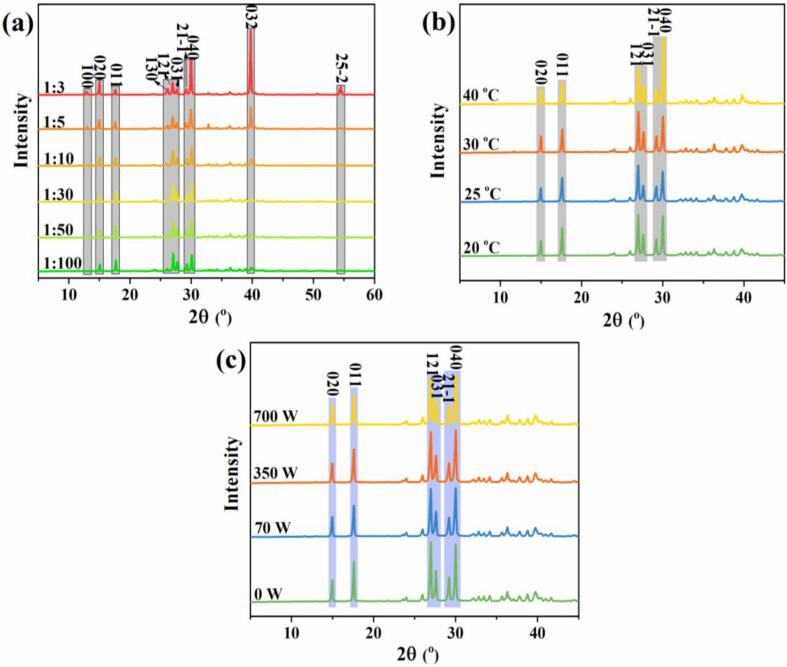
Fig. 9 shows the XRD patterns of the ADN crystals at different volume ratios of solvent to antisolvent (a), antisolvent temperatures (b) and ultrasound powers (c). In Fig. 9 (a), when the ratios of solvent to antisolvent are 1:3 and1:5, the hexagonal-flake ADN crystals expose 10 crystal faces, i.e. (1 0 0), (0 2 0), (0 1 1), (1 3 0), (1 2 1), (0 3 1), (21–1), (0 4 0), (0 3 2) and (25–2) faces, and (0 3 2), (0 4 0) and (0 2 0) crystal faces have relatively high peak intensities. With the increase of antisolvent, i.e., when the ratio is within the range of 1:10–1:100, (25–2) and (1 0 0) crystal faces have completely disappeared, the relative peak intensities of (0 3 2), (1 3 0) and (0 4 0) crystal faces gradually weaken. Combined with SEM images in Fig. 1, the spherical ADN mainly shows six crystal faces (0 2 0), (0 1 1), (1 2 1), (0 3 1), (21–1) and (0 4 0). From the foregoing, the appearance of the hexagonal-flake ADN crystal is caused by the (0 3 2) crystal plane. It means that the higher supersaturation can obviously inhibit the growth of (0 3 2) crystal plane, form spherical crystal that is the lower volume ratio of the solvent to antisolvent. Perceptibly, most of the faces diffracted in XRD patterns don’t exposure the actual steady-state morphology of SEM images. The reason is that most of the crystal faces initially present on ADN crystal, then grow into the edges or the vertices, even disappeared in the final ADN morphology [22].

Fig. 9.

XRD patterns of ADN crystals at different volume ratios of solvent to antisolvent (a), antisolvent temperatures (b) and ultrasound powers (c).

As shown in Fig. 9 (b), all XRD patterns of the ADN crystals at different antisolvent temperatures show mainly six crystal faces of (0 2 0), (0 1 1), (1 2 1), (0 3 1), (21–1) and (0 4 0). The higher the temperature, the greater the peak intensity difference between (1 2 1) and (0 4 0) crystal faces, and the more irregular the spherical morphology of ADN crystal combining the SEM images in Fig. 3. In Fig. 9 (c), the ADN under different ultrasound powers have the same six main crystal faces of (0 2 0), (0 1 1), (1 2 1), (0 3 1), (21–1) and (0 4 0), which are similar to the spherical ADN crystals without ultrasound (0 W). It can be seen that the changes of volume ratio of solvent to antisolvent have important influences on the structures of ADN crystals, and the antisolvent temperature and the ultrasound power do not change the structure of the ADN crystals.

3.3. Effects of experimental parameters on melting point of ADN crystals

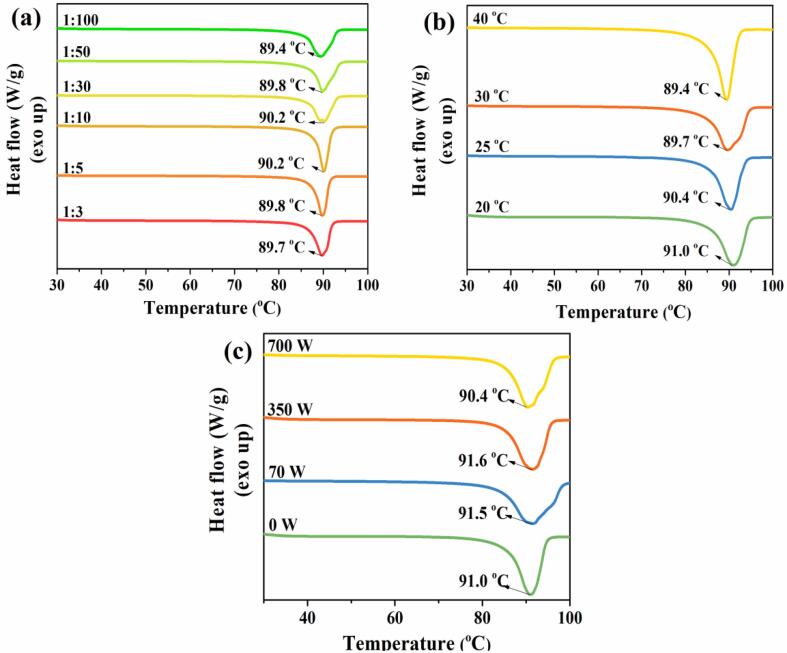
Fig. 10 shows the DSC curves of ADN crystals at different volume ratios of solvent to antisolvent (a), antisolvent temperatures (b) and ultrasound powers (c). In Fig. 10 (a), the highest melting point value of ADN is 90.2 ℃ when the volume ratios of solvent to antisolvent are 1:10 and 1:30, and its lowest value is 89.4 ℃ when the volume ratio of solvent to antisolvent is 1:100. The difference between the highest and the lowest melting point is 0.8 ℃. This shows that the change of the volume ratio of solvent to antisolvent has little effect on the melting point of the ADN crystals. From Fig. 10 (b), the melting point of the ADN crystals decreases from 91.0 ℃ to 89.4 ℃ while the antisolvent temperature increases from 20 ℃ to 40 ℃. It means that the lower antisolvent temperature is favorable to the crystallization of ADN with a higher melting point. In Fig. 10 (c), the ADN crystals at the 70 W and 350 W powers have closer melting points (91.5 and 91.6 ℃). At the high power 700 W, the melting point of the ADN crystal reduces to 90.4 ℃. This indicates that the ultrasound condition with the low and medium power is beneficial to the increase of the melting point of ADN comparing to that of ADN without applying ultrasound (91.0 ℃), while excessively high ultrasound power causes the melting point to decrease again.

Fig. 10.

DSC curves of ADN crystals at different volume ratios of solvent to antisolvent (a), antisolvent temperatures (b) and ultrasound powers (c).

3.4. Growth mechanisms of supersaturation-dependent spherical ADN crystals

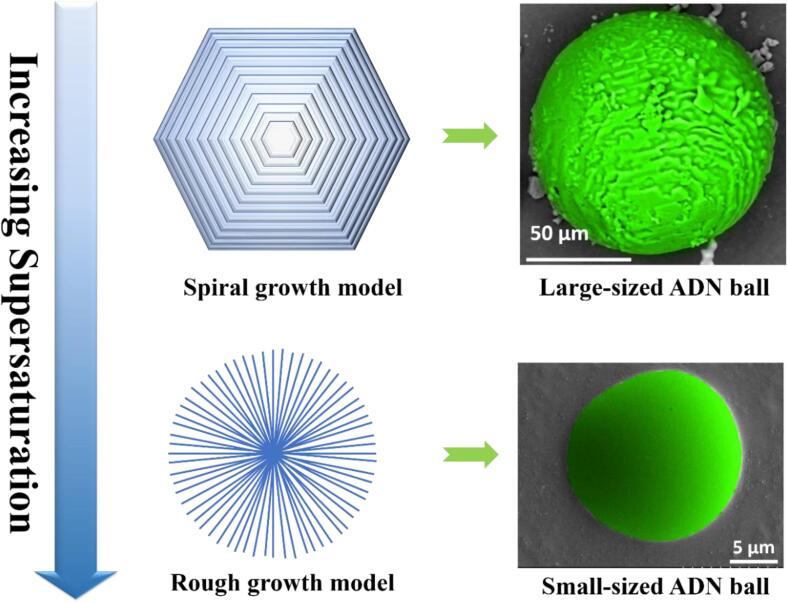
In Section 3.1, there are mainly two different spherical ADN dimensions, namely, the small-sized spherical ADN with a diameter of about 3–20 μm, and the large-sized spherical ADN with a diameter of about 30–100 μm. The different dimensional spherical ADN crystals mean the different crystal growth processes.

As shown in Fig. 11, lots of small-sized ADN balls appear with or without external ultrasound under the experimental conditions of Fig. 1 (d₁, e₁, f₁), Fig. 3 (a₁, b₁, c₁, d₁) and Fig. 5 (a₁, b₁, c₁, d₁). When the ultrasound is not applied, the mixture of the large-sized ADN balls and small-sized ADN balls is caused by the uneven mixing; relatively uniform small-sized spherical crystals are produced when the local supersaturation is high, and the large-sized balls are produced when the local supersaturation is low. When the ultrasound is applied, the small-sized ADN spheres with uniform particle size will be produced, without the formation of large-sized ADN spheres as described above. A high-resolution SEM in Fig. 11 (b) is used to magnify and observe the surface morphology of such small-sized ADN balls. Such kind of small ADN balls has a very smooth surface morphology. This may be due to the fact that ADN solutions have high supersaturation at partial growth sites, the interface between the ADN crystal nucleus and solution become rough, and growth mechanism is in accord with the rough growth model. When ADN solution is mixed with antisolvent, the ADN solute quickly nucleates and grows up into a smooth small-sized ball under a large degree of supersaturation.

Fig. 11.

SEM images of small-sized ADN balls by rough growth.

Additionally, many large-sized ADN balls are produced without external force (ultrasonic) displayed in Fig. 1 (d₁) and Fig. 3 (a₁, b₁, c₁ and d₁). The growth process of such large-sized ADN balls can be observed as shown in Fig. 12. Fig. 12 (a₂, b₂, and c₂) is the enlarged views of the red dotted frame in Fig. 12 (a₁, b₁, and c₁). The yellow hexagon box in Fig. 12 (a₂, b₂, and c₂) means the source of the hexagonal dislocation of the large-sized spherical ADN crystal. Clearly, the hexagonal layered growth pattern remains on the surface of the spherical ADN crystal. This may be due to the local low supersaturation. When the solution and the antisolvent are mixed under the condition of no external force (no ultrasound), it is easy to cause uneven mixing, resulting in the spherical morphology from the collection of the layered ADN crystals. In a short time, the local solute is not diluted by enough antisolvent to nucleate. At this time, the interface between ADN nucleus and solution is smooth, and crystal growth mechanism conforms to the screw dislocation growth model or BCF (Buston-Cabresa-Frank) theoretical model [23]. That is, the solute first nucleates and grows into a hexagonal step source, and then the remaining solute grows around spiral dislocation line circling the step source. Due to the presence of the screw dislocation, the crystal growth rate is greatly accelerated, finally grows into a large-sized ADN ball.

Fig. 12.

SEM images of large-sized ADN balls from the hexagonal dislocation source by spiral growth.

It is concluded that in Fig. 13 the crystal growth mechanism and interface roughness vary with the change of the supersaturation [23]. At low supersaturation, the ADN crystal grows up into large-sized balls according to the spiral growth model; at high supersaturation, the ADN crystal becomes into small-sized balls by the rough growth.

Fig. 13.

Growth mechanisms of spherical ADN change with supersaturation.

4. Conclusions

Through controlling the experimental parameters of the crystallization process, the ADN crystals of the different morphologies were obtained by the ultrasound-assisted solvent-antisolvent method, especially, the micro-sized spherical ADN crystal is successfully prepared, the optimal experimental parameters for the spherical ADN crystal are as follows: the volume ratio of solvent to antisolvent is 1:50, the antisolvent temperature is 20 ℃, and the ultrasound power is 70 W. The volume ratio of solvent to antisolvent is the most important factor in the controlling the morphology and particle size of ADN crystals. As the antisolvent temperature increases, the spherical ADN crystal size gradually increases. Noticeably, the ultrasound is a non-invasive way, which is helpful to obtain the spherical ADN crystals of the more uniform morphology and particle size. XRD patterns show the six main growth crystal faces for the spherical ADN crystal. DSC results show the ultrasound with low and medium powers can raise the melting point of the spherical ADN crystal. In the predicted hexagonal-flake and spherical ADN morphologies by Growth morphology and Equilibrium morphology methods are close to the experimental morphologies. The growth mechanisms of spherical ADN are studied, with the degree of supersaturation increasing, growth models of the spherical ADN crystal transfer from the spiral growth model to the rough growth model, and the morphologies of ADN transform from the large-sized ADN balls in the small-sized ADN balls.

CRediT authorship contribution statement

Jingjing Li: Methodology, Conceptualization, Software, Investigation, Validation, Data curation, Writing - original draft, Writing - review & editing. Rongjie Yang: Conceptualization, Writing - review & editing, Supervision, Resources, Project administration, Funding acquisition. Tao Zeng: Software, Writing - review & editing. Jinghui Hu: Conceptualization, Writing - review & editing. Weiqiang Tang: Methodology, Writing - review & editing. Zhenhui Liu: Methodology, Investigation. Li Gong: Methodology, Formal analysis, Investigation.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: