Learning to estimate the fiber orientation distribution function from diffusion-weighted MRI

Abstract

Estimation of white matter fiber orientation distribution function (fODF) is the essential first step for reliable brain tractography and connectivity analysis. Most of the existing fODF estimation methods rely on sub-optimal physical models of the diffusion signal or mathematical simplifications, which can impact the estimation accuracy. In this paper, we propose a data-driven method that avoids some of these pitfalls. Our proposed method is based on a multilayer perceptron that learns to map the diffusion-weighted measurements, interpolated onto a fixed spherical grid in the q space, to the target fODF. Importantly, we also propose methods for synthesizing reliable simulated training data. We show that the model can be effectively trained with simulated or real training data. Our phantom experiments show that the proposed method results in more accurate fODF estimation and tractography than several competing methods including the multi-tensor model, Bayesian estimation, spherical deconvolution, and two other machine learning techniques. On real data, we compare our method with other techniques in terms of accuracy of estimating the ground-truth fODF. The results show that our method is more accurate than other methods, and that it performs better than the competing methods when applied to under-sampled diffusion measurements. We also compare our method with the Sparse Fascicle Model in terms of expert ratings of the accuracy of reconstruction of several commissural, projection, association, and cerebellar tracts. The results show that the tracts reconstructed with the proposed method are rated significantly higher by three independent experts. Our study demonstrates the potential of data-driven methods for improving the accuracy and robustness of fODF estimation.

1. Introduction

1.1. Background and motivation

Estimation of the orientation of major brain white matter fiber bundles from diffusion-weighted magnetic resonance imaging (DW - MRI) measurements is a long-standing and important problem. A simple model that can account for anisotropic diffusion is the diffusion tensor imaging (DTI) model (Basser et al., 1994). This model is still used in practice because it can estimate the direction of the major fiber in each imaging voxel and it can quantify the degree of anisotropy. Furthermore, compared with some of the more elaborate models, its parameters can be estimated robustly from a smaller number of measurements.

Despite its advantages, the DTI model is too simplistic for representing more complex fiber configurations. Often, axon fibers within an imaging voxel display complex configurations such as bending, fanning, and crossing. In such voxels, the DTI model fails to estimate the true fiber configuration, which can significantly impact the accuracy of downstream processing steps such as tractography and connectivity analysis.

To overcome the limitations of the DTI model, many methods have been put forward in the past two decades. Some of these methods extend the DTI model by considering a multi-compartment model, whereby the measured diffusion signal is assumed to be the sum of the diffusion signals caused by individual compartments. The most straightforward extension of the standard DTI model leads to the multi-tensor model, where each compartment has the same parameterization as that of the DTI model. The number of parameters of the multi-tensor model grows with the number of tensors, making the model fitting more difficult and less robust. Some studies have introduced mathematical tricks or physical assumptions to reduce the number of unknown parameters or simplify the estimation of the parameters of a multi-tensor model (Chen et al., 2004; Tuch, 2002).

There are a wide range of parametric methods that can be regarded as variations of the multi-tensor model. For example, in the ball-and-sticks model each tensor has only one non-zero eigen-value, allowing the diffusion of water molecules only in one direction (Behrens et al., 2003). The “ball” compartment in this model represents isotropic Gaussian diffusion and is a common feature of many multi-compartment models. Some studies fall between the simplistic stick model and the full tensor parameterization, such as the model proposed in Anderson (2005), where an axially-symmetric tensor is used to represent each fascicle. The composite hindered and restricted water diffusion (CHARMED) model includes two types of compartments: a compartment with restricted diffusion in the form of an impermeable cylinder is used to represent the intra-cellular compartment, and an anisotropic diffusion tensor is used to model the signal from an extra-cellular compartment (Assaf and Basser, 2005). Another notable mention is DIAMOND (Scherrer et al., 2016) that, unlike most other models, accounts for compartment heterogeneity by modeling each compartment with a peak-shaped matrix-variate distribution. Specifically, it assumes that each compartment can be modeled with a symmetric positive definite tensor that follows a matrix Gamma distribution. The expected value of the distribution represents the overall diffusivity of a compartment and the “concentration” of the distribution represents the compartment’s degree of heterogeneity. Parameters of multi-compartment models are usually estimated using non-convex optimization algorithms.

Another class of methods aim at estimating a fiber orientation distribution function (fODF). An fODF can be regarded as a probability distribution on the sphere, where the value of fODF for each direction indicates the probability that a major fiber points in that direction. Some of these methods such as QBall Imaging, Tuch (2004), and Diffusion Spectrum Imaging (DSI), Wedeen et al. (2005), first estimate an intermediate probability distribution called the diffusion orientation distribution function (dODF). Methods based on spherical deconvolution, on the other hand, directly estimate an fODF (Dell’Acqua et al., 2010; Tournier et al., 2004). They estimate the response function for a single fiber, and model the diffusion signal as the convolution of the fODF with this response function. The fODF is then naturally recovered using a mathematical deconvolution algorithm.

All methods discussed above have certain important limitations (Seunarine and Alexander, 2014). Multi-compartment models are limited in their ability to model bending and fanning fiber configurations in a voxel, which can be very important for tractography and connectivity analysis. Furthermore, determination of the correct number of compartments is a difficult discrete optimization problem and the proper choice of a method for solving this problem is not clear (Jeurissen et al., 2013). On the other hand, some of the methods that estimate an fODF are sensitive to noise and prone to predicting false fibers, while others such as DSI require a very large number of measurements that can lead to unrealistic scan times. Some works have proposed unifying frameworks that use ideas from both parametric and non-parametric classes of methods in order to overcome the limitations of each class (Schultz et al., 2010).

In recent years, several data-driven and machine learning methods have been proposed for estimating various diffusion parameters from DW-MRI measurements. These methods can take advantage of recent advancements in machine learning and computational hardware to learn models that map the diffusion signal to the diffusion parameters of interest. In addition, because these methods are model-free, they avoid imposing sub-optimal assumptions that are an essential component of the methods described above (Golkov et al., 2016). Several recent studies have shown that machine learning methods, and in particular deep learning methods, have the potential to accurately estimate scalar diffusion measures from DW-MRI data (Aliotta et al., 2019; Gibbons et al., 2019; Golkov et al., 2016). However, estimation of fiber orientation that is necessary for tractography and connectivity mapping has received much less attention. In this paper, we propose a deep learning model for direct estimation of an fODF from DW-MRI measurements. We also propose methodologies for training this model. We develop methods that allow for synthesizing reliable training data in-silico. Through extensive evaluations, we demonstrate that the model can be effectively trained using either real DW-MRI data or simulated data.

1.2. Related works

Here, we briefly review some of the studies that have employed machine learning techniques in estimating diffusion parameters from DW-MRI measurements. A successful line of work, pioneered by Golkov et al. (2016) have aimed at estimating scalar diffusion parameters. Examples of parameters that have been estimated in these studies include mean diffusivity (Aliotta et al., 2019), fractional anisotropy (FA) and generalized FA (Aliotta et al., 2019; Gibbons et al., 2019), diffusion kurtosis measures (Golkov et al., 2016), neurite orientation dispersion index (Gibbons et al., 2019; Golkov et al., 2016), and volume fraction of different compartments (Ye et al., 2019). Overall, these works have shown that deep learning methods have the potential to accurately estimate such scalar diffusion parameters using a fraction of the measurements that are typically needed by the classical data-fitting and optimization-based methods.

Some studies have developed machine learning methods for tractography. Standard tractography techniques are known to produce inaccurate results, usually containing many false positive streamlines (Maier-Hein et al., 2017). Errors of standard tractography methods may be caused by many factors such as errors in local fiber orientation estimation and failure to include the spatial context of the streamline/bundle being tracked. Machine learning methods have the potential to reduce these sources of error by avoiding to rely on sub-optimal mathematical models of the diffusion signal and by learning to incorporate the local and non-local information more effectively. Some of the machine learning models that have been successfully applied for tractography include random forests (Neher et al., 2017; 2015), convolutional neural networks (CNNs) (Wasserthal et al., 2018), multi-layer perceptrons (Jörgens et al., 2018), and different forms of recurrent neural networks such as gated recurrent units (Benou and Raviv, 2019). A recent review of these techniques can be found in Poulin et al. (2019).

More related to the work presented in this paper, however, are studies that have aimed at estimating the fODF or the number and orientations of major compartments in a voxel. Support vector regression (SVR) (Schultz, 2012) and CNNs (Koppers et al., 2017b) have been used for estimating the number of compartments in a voxel. Deep learning models such as CNNs (Koppers et al., 2017a; Koppers and Merhof, 2016; Lin et al., 2019) and multilayer perceptrons (MLPs) (Nath et al., 2019a; 2019b) have been used for estimating fODFs from diffusion signal. One study proposed a method that combined unsupervised machine learning with standard optimization-based methods for fODF estimation (Patel et al., 2018). Specifically, the authors proposed learning an fODF prior using deep autoencoders, and used that prior to regularize standard methods such as spherical deconvolution. Another work used a deep learning model to estimate the fODF in an iterative hard thresholding framework (Ye and Prince, 2017).

In this paper, we propose to learn a direct mapping between the diffusion measurements in the q-space and the target fODF. We formulate the model as a single-shell HARDI technique. To make the model independent of a specific gradient table and applicable to scans with different diffusion gradient directions, we represent the diffusion measurement and the target fODF on fixed hemi-spherical grids. We use an MLP as the base model to learn the mapping between the diffusion signal and the fODF. Our approach is different from previous studies discussed above. The method of Koppers and Merhof (2016), for example, is based on cyclic shifting of the diffusion signal to artificially create a 2D input for a CNN. Nath et al. (2019b) employ an MLP, but they use histologically-determined fiber orientation distributions for training. Such data is hard to obtain for a large human cohort, risking the generalizability of the trained model due to limited availability of the training data. An important contribution of this work is that we propose novel methods for simulating reliable training data. We present methods for training the model using either simulated or real DW-MRI data. We compare our proposed method, trained with either simulated or real data, with several classical as well as machine learning-based techniques. Because the contribution of this work is an fODF estimation method, our evaluations and comparisons are mostly in terms of the accuracy of fODF estimation. Nonetheless, we also present evaluations in terms of the accuracy of the generated tractograms. We demonstrate that the proposed method has significant merits compared with other techniques in terms of the accuracy and robustness of fODF estimation.

2. Materials and methods

2.1. Proposed model

The method that we propose in this paper is based on learning a direct mapping between the diffusion measurements and the fODF. Fig. 1 shows our method schematically. We use the diffusion measurements in their native q space, rather than representing them in some basis such as spherical harmonics. Nonetheless, because the gradient tables vary across subjects and scans, we define a fixed hemi-spherical grid and interpolate the diffusion measurements onto this grid. Similarly, we consider a fixed hemi-spherical grid for fODF prediction. We denote these hemi-spherical grids with their sets of unit vectors $U_s={\left\{u_s^i\right\}}_{i=1}^{n_s}$ and $U_f={\left\{u_f^i\right\}}_{i=1}^{n_f}$, respectively.

Fig. 1.

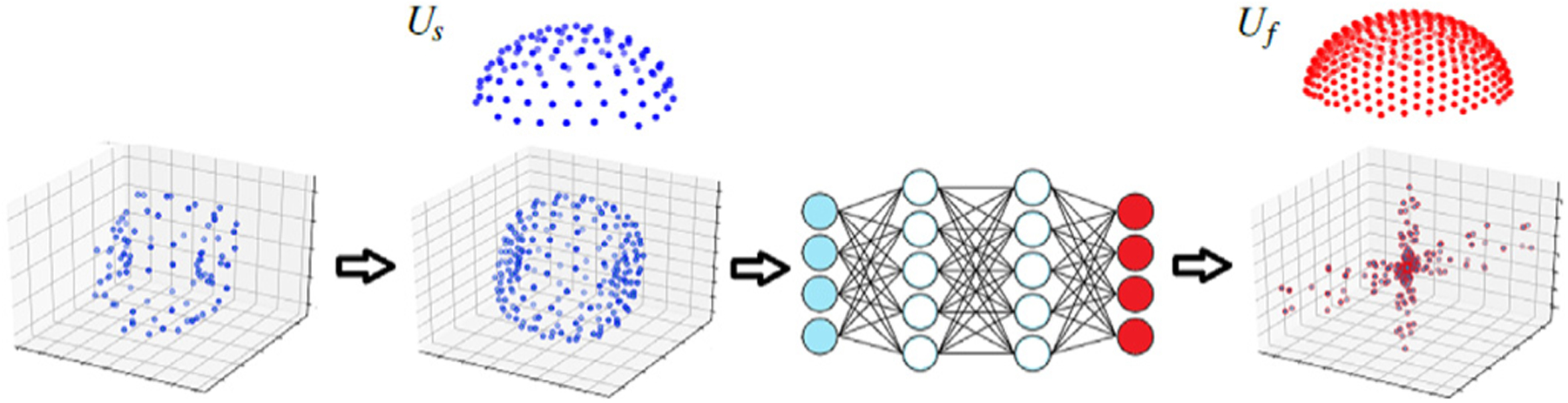
A schematic representation of the main steps of the proposed method. The raw diffusion signal measured with an arbitrary gradient table is re-sampled onto a fixed hemi-spherical grid, U_s. This will form the input to the MLP, which predicts the fODF directly on the target hemi-spherical grid, U_f. In this schematic, we have shown the example interpolated signal and the predicted fODF using their symmetric representation on the full sphere for better illustration.

The choice of the number of vectors in U_s and U_f presents a trade-off between computational load and angular resolution. For U_s, we empirically found that approximately 100 vectors were sufficient. Therefore, in all experiments reported in this paper we set n_s = 100. For U_f we used n_f = 362, leading to a resolution of 7.2°. In some experiments we increased n_f up to 2500, corresponding to a resolution of 2.8°, but did not observe significant improvements in fODF estimation accuracy. We present a quantitative assessment of the effect of grid size/resolution in Section 3.

We used the Fibonacci spiral sphere method (González, 2010) to construct the spheres. We found this method to generate more uniformly distributed grids than other available methods. One way to assess how uniformly-distributed a spherical grid is would be in terms of the distance between neighboring points. For example, with the Fibonacci spiral sphere method the distance between the nearest neighbors for spheres with 100 and 362 points are 13.7 ± 0.28 and 7.2 ± 0.09, respectively. With the latitude–longitude method (Kantsiper and Weiss, 1997), on the other hand, these values are 13.8 ± 0.89 and 7.21 ± 0.24, respectively. Smaller standard deviations with the Fibonacci spiral method indicate a more uniform distribution. González (2010) used a different criterion, based on the estimation of areas on the sphere, to compare different spherical grids. They also found that the Fibonacci spiral method generated more uniform grids.

Our method assumes single-shell HARDI measurements. As mentioned above, our method requires interpolation of diffusion weighted measurements on U_s. Consider a set of diffusion measurements in a voxel, ${\left\{s\left(q_j,b^{*}\right)\right\}}_{j=1}^m$, where b* is the diffusion strength (b-value) and q_j is the unit vector indicating the gradient direction for the jth measurement. We interpolate the signal s that has been measured on ${\left\{q^j\right\}}_{j=1}^m$ onto $U_s={\left\{u_s^i\right\}}_{i=1}^{n_s}$ as follows:

$$s\left(u_s^i\right)=\sum _{{\Omega }_{ij}}{w}_{ij}s\left(q_j\right)/s_0,w_{ij}\propto \frac{1}{\alpha \left(u_s^i,q_j\right)+ϵ},$$ (1)

where $\alpha \left(u_s^i,q_j\right)$ is the angle between the two vectors and ϵ = 0.1 rad is introduced to avoid division by zero. The weights w_ij are normalized to sum to one. s₀ is the signal measured with b = 0 and Ω_ij is the set of indices of the K closest q_j to $u_s^i$. Note that since we are considering a hemi-spherical grid in the q-space, in determining the K closest q_j to $u_s^i$ we do consider the measurements that fall on the other side of the sphere. Similarly, the angles α are computed modulo-π; for example an α = 175 degrees translates to α = 5 degrees. We set K = 5, which we found to lead to good results using cross-validation experiments on simulated data with known ground truth.

The vector of interpolated diffusion signals, $s\left(u_S^i\right)$, is used by an MLP to directly predict the fODF on the target grid, U_f. Our MLP has six hidden layers with {300, 300, 300, 400, 500, 600} neurons in each layer. The input and output layers have n_s and n_f neurons, respectively. All hidden layers used a rectified linear unit, ReLU, activation.

2.2. Training data

2.2.1. Simulated data

In the experiments reported in this paper, we used simulated or real diffusion measurements to train our model. To generate simulated data, we first simulated 1–3 random tensors. The tensors were axially symmetric with axial diffusivity in the range λ_‖ ∈ [0.0018, 0.0025] mm²s⁻¹ and radial diffusivity in the range λ_⊥ ∈ [0.00035, 0.00050] mm²s⁻¹. The orientation of each tensor was randomly and independently initialized on the surface of the unit sphere. Picking a uniformly-distributed random point on the unit sphere is not possible by choosing uniformly-distributed spherical coordinates θ ∈ [0, 2π) and ϕ ∈ [0, π], as this will result in an oversampling of the poles (i.e., parts of the sphere with ϕ close to either 0 or π). One correct way, used in this work, is to simulate three independent zero-mean Gaussian random variables x, y, and z and then form the unit vector u = υ/‖υ‖, where υ = [x, y, z] (Marsaglia, 1972). If more than one tensors were considered and the main axes of any pair of tensors were less than 30° apart, that simulation was discarded. A multi-tensor model was then used to simulate a signal as follows:

$$s(q)/s_0=f_{\text{csf}}\text{ exp}\left(-b{d}_{\text{csf}}\right)+\sum _{k=1}^K{f}_k\text{ exp }\left(-b{q}^T{D}_{k}q\right)$$ (2)

where f_csf is the occupancy fraction of the cerebrospinal fluid (CSF) compartment, d_csf = 0.003 mm²s⁻¹, and f_k is the occupancy fraction of the k^th tensor, D_k. These fractions were also set at random. Specifically, f_csf was uniformly randomly selected between a minimum of 0.0 and a maximum of 0.50, 0.40, and 0.20 for voxels with one, two, and three simulated tensors, respectively. The occupancy fractions of the tensors were selected such that they summed to 1 − f_csf, with a minimum fraction, f_k, of 0.20 and 0.15 for voxels with two and three simulated tensors, respectively. The above computation was performed for all q in the gradient table.

Rician noise was added to the signal to obtain a signal-to-noise ratio (SNR) in the range 15–30 dB. This range was selected based on the SNR values reported and used for simulation in previous studies (e.g., Tournier et al., 2007, Dell’Acqua et al., 2010). Here, SNR is defined as $10\text{ log}\frac{\text{ signal power }}{\text{ noise power }}.$ For each simulated voxel, we selected an SNR value from the uniform distribution υ [15, 30] and added Rician noise to the simulated signal to obtain the selected SNR. The noise distribution in MRI follows a Rician or non–central chi–square distribution (Canales-Rodríguez et al., 2015). These distributions are strictly valid only under restrictive assumptions including that the noise in different coils be uncorrelated and have equal variance. Nonetheless, experimental measurements have shown that the noise in real data closely follows these distributions (Dietrich et al., 2008; Sotiropoulos et al., 2013). In many prior DWI studies and software, a Rician model has been used to simulate signal noise (for example, Caruyer et al., 2014; Close et al., 2009; Garyfallidis et al., 2014; Hosey et al., 2005). The simulated noisy signal was then interpolated onto U_s using Eq. (1) to form the simulated input.

The directions of the major axes of the tensors, i.e., the directions of the eigenvectors corresponding to λ_∥, were then used to synthesize the simulated fODF. This was done using the following equation:

$$\text{fODF}\left(u_f^i\right)=\sum _k|⟨u_f^i,u_k⟩{}^p{f}_k^{*}|$$ (3)

In this equation, u_k denotes the direction of the major eigenvector of the k^th fascicle and 〈.,.〉 denotes inner product. The coefficients $f_k^{*}$ are proportional to the fractions of the tensors, f_k, but they are scaled such that the fODF sums to one. This normalization is necessary to ensure that the fODF is a probability distribution.

The power p in Eq. (3) controls how smooth/pointy the synthesized fODF is. Our preliminary experiments showed that making the simulated fODFs too smooth by choosing a very small p would lead to poor tractography results. With very smooth fODFs, the number of false positive streamlines in tractography would increase substantially because the true peaks are smoothed out. On the other hand, increasing p to very large values would lead to fODFs that have only a few non-zero elements. Our experiments show that training of our MLP with such fODFs becomes highly unstable. This is probably because two tensors that are only a few degrees apart would have very similar diffusion signals but the fODFs would be completely different. This is easy to imagine by considering the extreme case when p is very large. In our setting, when p ≫ 20, the synthesized fODFs would have only one non-zero element for each tensor and all other fODF values would be near zero. In this case, if a tensor is rotated by an angle on the order of the angular resolution of U_f, the diffusion signal would change little while the two fODFs would be as different from each other in terms of the ℓ₂ distance as when the two tensors are at 90° angle. Therefore, increasing p to very large values would create ambiguous and confusing training data.

In order to decide on the proper range of values for p, we resorted to quantitative measures of fiber orientation dispersion. Specifically, we used the Orientation Dispersion Index (ODI) as proposed in the NODDI model (Zhang et al., 2012). To estimate ODI, one fits a Watson distribution to the fODF and computes ODI as:

$$\text{ODI}=\frac{2}{\pi }\text{arctan}(1/\kappa ),$$ (4)

where κ is the concentration parameter of the fitted distribution. We used the procedure proposed by Riffert et al. (2014) to compute ODI. The range of ODI values for white matter is well below 0.5, typically below 0.2 for white matter voxels with fractional anisotropy of above 0.40 (Fukutomi et al., 2019; Zhang et al., 2012). Histological measurements have shown that typical white matter bundles have ODI in the range [0.08,0.13], although there are white matter bundles with ODI as low as 0.02 and as high as 0.40 (Schilling et al., 2016). Fig. 2(a) shows a plot of ODI versus p for fODFs estimated using Eq. (3). Based on this figure and reported values of ODI mentioned above, we decided to consider a range of p = [2, 18] in our simulations, resulting in ODIs in the range [0.03, 0.30]. Example fODFs generated with different values of p are shown in Fig. 2(b).

Fig. 2.

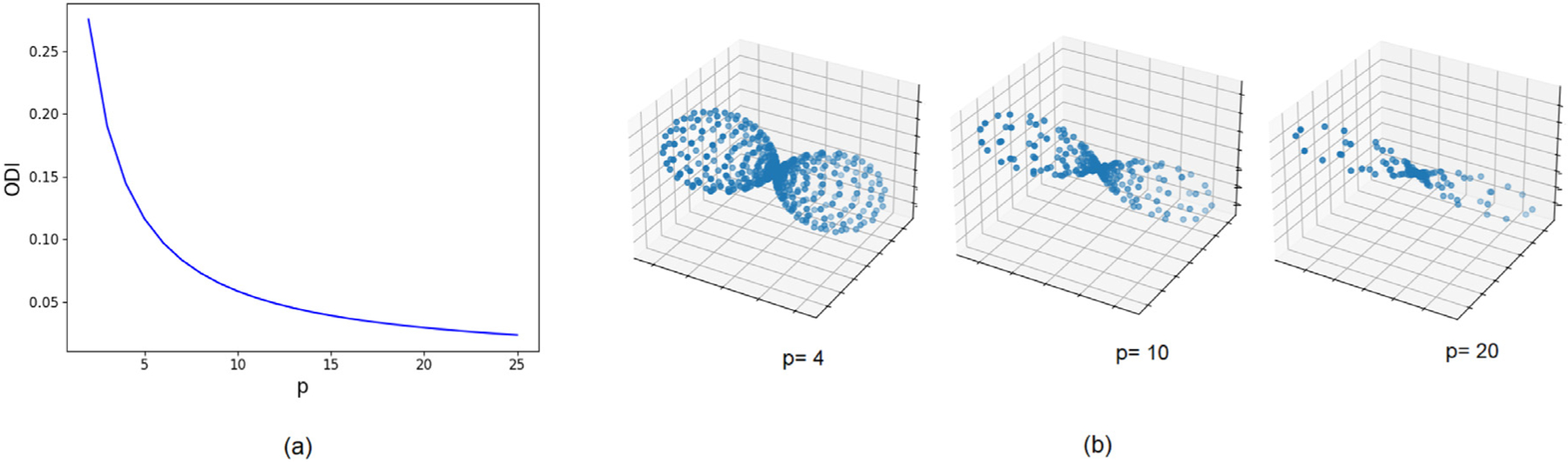
(a) Plot of the Orientation Dispersion Index (ODI) versus the parameter p used to generate fODFs in Eq. (3). (b) Example single-fiber fODFs generated with different values of p.

In our experiments with simulated data, we generated three million voxels with one, two, and three tensors each using the above-described method, for a total of nine million data points.

2.2.2. Real data

For training with real data, we used the DW-MRI data from the developing Human Connectome Project (dHCP) dataset (Bastiani et al., 2019). Each scan in this dataset includes 20 non-DW measurements (i.e., b = 0) and 280 DW measurements with b values of 400 (n = 64), 1000 (n = 88), and 2600 (n = 128). In the absence of an fODF ground truth for this dataset, we applied the Multi-Shell Multi-Tissue Constrained Spherical Deconvolution (MSMT-CSD) (Jeurissen et al., 2014), which is a well-known and widely-used technique, on the full multi-shell data to obtain a reference fODF. We used this fODF as reference for training our proposed method as well as for evaluation. In order to evaluate our proposed fODF estimation method and compare it with other single-shell techniques, we applied them on the measurements in either b = 1000 or b = 2600 shell and compared the estimated fODFs with the reference fODF estimated by MSMT-CSD using the full multi-shell data. We used the white matter voxels of 140 subjects, for a total of 10 million voxels, for training. We then tested our method and other methods on data from other subjects that had not been included in training.

2.3. Training

We implemented the MLP in TensorFlow under Python. The loss function used to optimize the MLP was the following:

$$\text{loss}(f)=\Vert f-f_g\Vert {}^2+{\lambda }_s{L}_s(f),$$ (5)

where f and f_g denote the predicted and target fODFs, respectively. The regularization term L_s(f) encourages smoothness, and is implemented as a matrix-vector product. Specifically, L_s(f) penalizes the difference between the estimated fODF at each direction and the weighted average of the fODF at its 3 nearest neighbors. We empirically set λ_s = 10⁻⁴.

Model weights were initialized using the method proposed by He et al. (2015). Training was performed with batches of size 1000. Adam (Kingma and Ba, 2014) was used for optimization with an initial learning rate of 10⁻², which was reduced by 0.90 after every two passes through the training data if the loss did not decrease on the validation set.

2.4. Evaluation criteria and compared methods

The purpose of the proposed method is fODF estimation. Therefore, in our experiments, when a ground truth or reference fODF was available, we evaluated the estimated fODF by computing the Jensen-Shannon divergence (JSD) between the estimated fODF and ground truth. Given two probability distributions p₁ (x) and p₂ (x) defined on a probability space $\mathcal{X}$, JSD between them is defined as $\text{JSD}\left(p_1\Vert p_2\right)=\frac{1}{2}\left(D\left(p_1\Vert p_2\right)+D\left(p_2\Vert p_1\right)\right)$, where $D\left(p_1\Vert p_2\right)=\sum _{x\in \mathcal{X}}{p}_1(x)\text{ log }\left(p_1(x)/p_2(x)\right)$ is the Kullback–Leibler divergence from p₂(x) to p₁(x) (Murphy, 2012). Several prior studies have used JSD for comparing fODFs (Chiang et al., 2008; Elhabian et al., 2014). We also computed the angle between the largest peak in the estimated and ground truth fODFs. A more general metric that takes crossing fibers into account is the weighted average angular error (WAAE) proposed by Schultz (2012). WAAE is defined as $\text{WAAE}={\sum }_i{w}_i{\text{min}}_j\text{ arccos}\left(|u_i^{\text{gt}},u_j^{\text{est}}|\right)$, where u^gt and u^est are direction vectors of the peaks of the ground truth and estimated fODFs and w_i is the magnitude of the ith ground truth peak. Hence, WAAE considers all peaks and assigns larger weights to the errors in estimating the orientation of larger ground truth fODF peaks.

In some of our experiments we also compared different fODF estimation methods based on the resulting tractograms. Tractography is a less direct way of comparing fODF estimation methods because the tractography algorithm can mask or confound the differences between the fODF estimation methods. In order to have a fair comparison, we used the same fiber tracking algorithm with the same settings for all fODF estimation methods. Specifically, we used the EuDX fiber tracking algorithm (Garyfallidis, 2013). This choice is motivated by the fact that this algorithm has been designed to be more faithful to the voxel-wise fODF reconstruction results rather than correcting or enhancing the tracts by imposing global priors (Garyfallidis, 2013). Admittedly, this may give rise to more spurious tracks and may not yield the same high-quality tractography results as those obtained with methods that impose global anatomical priors. However, it can better amplify the differences between different fODF estimation methods. Moreover, this tracking algorithm has been designed to work well with different fODF estimation methods and hence it is not biased towards or against any fODF estimation technique (Garyfallidis, 2013). Starting from a seed point, this algorithm predicts the next track point via Euler’s method with a step size that should be smaller than the voxel size. The propagation direction at the current tracking point is computed using trilinear interpolation of the closest peaks of the 8 neighboring voxel centers. If the direction of the closest fODF peak in a neighboring voxel is very different from the current tracking direction, that neighbor is ignored. The algorithm involves several stopping criteria; tracking stops if the contribution from neighboring voxels is below a threshold (boundary points) or if anisotropy is below a threshold (gray matter or cerebrospinal fluid voxels). In all of our experiments with this tractography method, we set the step size to half the voxel size. Moreover, the fODFs estimated by all methods are normalized to sum to one in each voxel.

We compared our method with the following:

• Sparse Fascicle Model (SFM) (Rokem et al., 2015).

• Constrained Spherical Deconvolution (CSD) (Tournier et al., 2007).

• Orientation Probability Density Function (OPDF) (Tristán-Vega et al. (2009), Tristan-Vega et al. (2010)).

• Constant Solid Angle Q-Ball model (CSA) (Aganj et al., 2010).

• Multi-tensor model fitting. For determining the number of fibers in each voxel we used the bootstrap method outlined by Scherrer et al. (2013).

• Bayesian model fitting proposed by Behrens et al. (2003).

• • The deep learning method proposed by Koppers and Merhof (2016). In this method, the diffusion signal in each voxel is first interpolated onto a pre-defined spherical grid using spherical harmonic interpolation. Then, this 1D signal is converted into a 2D signal, much like an image patch, via cyclic shifting. A CNN is then trained to estimate the fiber orientations from this signal. The fODF is estimated on a fixed grid (Koppers and Merhof, 2016). In this paper we refer to this model as CNN-2D because the input to the CNN is a 2D signal.

• The deep learning method proposed by Lin et al. (2019). This method exploits the spatial structure of fODF by including the data from neighboring voxels. Specifically, for estimating the fODF in a voxel, the diffusion signals from a 3 × 3 × 3-voxel neighborhood centered on that voxel are included. The diffusion signal in each voxel is represented using spherical harmonic coefficients. A lightweight CNN with two convolutional layers and two fully-connected layers is used to map the input 3D patch to the spherical harmonic coefficients of the fODF. In the rest of this paper we refer to this model as CNN-3D because the input to the model are 3D patches.

3. Results and discussion

3.1. Evaluation with phantom data

For evaluation with simulated data, we used the HARDI-2013 phantoms (Caruyer et al., 2014). For one of the phantoms in this dataset the ground truth fiber orientations in each voxel were given. Most voxels contained one or two fibers, but some include more than two fibers. The DWI measurements consisted of 64 gradient directions at b = 3000. We trained our model, CNN-2D, and CNN-3D using simulated training data generated as described in Section 2.2.1. Our model and CNN-2D work on data from individual voxels, whereas CNN-3D uses data from the 3 × 3 × 3-voxel neighborhood of a voxel. Therefore, training of CNN-3D requires knowledge of the fODF in the neighboring voxels. For this purpose, we used phantoms similar to those used in Scherrer et al. (2013). We then applied these trained models as well as other non-machine-learning methods on the phantom data to reconstruct the fODF in each voxel. To compare different methods, we computed the WAAE between the peaks of the fODF estimated by each method with the ground truth fiber orientations. Note that for this phantom we cannot compute JSD because we do not have the ground truth fODFs, but only the fiber orientations.

Table 1 shows values of WAAE for this experiment. The proposed method, CNN-2D, and SFM achieved lower error than other methods. Statistical significance t-tests showed that the proposed method was significantly (p < 0.01) more accurate than all other methods except for CNN-2D and SFM. The proposed method, CNN-2D, and SFM were not statistically different. CNN-3D performed worse than other methods. In our opinion, this was because the fiber orientations in the local voxel neighborhoods were different in the training and test phantoms. Learning the spatial fODF patterns is a potential advantage of CNN-3D, but it requires that the spatial fODF patterns in the training and test data be similar. In this experiment, we did not have access to other phantoms that had the same spatial fODF structure as those in the test phantom.

Table 1.

WAAE for different fODF estimation methods on the HARDI-2013 phantom. The WAAE for the proposed method was significantly lower than all other methods except for SFM and CNN-2D.

Method	WAAE (degrees)
SFM	10.0 ± 1.2
CSD	11.0 ± 2.0
OPDF	11.6 ± 2.1
CSA	11.2 ± 1.7
Multi-tensor fitting	11.3 ± 2.3
Bayesian model fitting	11.8 ± 1.0
CNN-2D	10.3 ± 1.0
CNN-3D	16.1 ± 2.2
Proposed method	9.6 ± 1.5

Another phantom in the HARDI-2013 dataset included 20 pairs of seed and target tractography regions of interest (ROIs) with different numbers of seed voxels. An illustration is shown in Fig. 3(a). We used this phantom to compare different methods in terms of accuracy of tractography. For this phantom, too, the diffusion measurements consisted of one b = 0 scan and 64 diffusion-weighted scans at b = 3000. We trained our model, CNN-2D and CNN-3D using simulated data generated as explained above. We then applied all methods to compute the fODF in each voxel, followed by tractography using EuDX algorithm. For each seed-target ROI pair we computed the ratio of the number of streamlines that ended up in the target ROI to the number of streamlines that were launched from the corresponding seed ROI. We refer to this ratio as tractography accuracy.

Fig. 3.

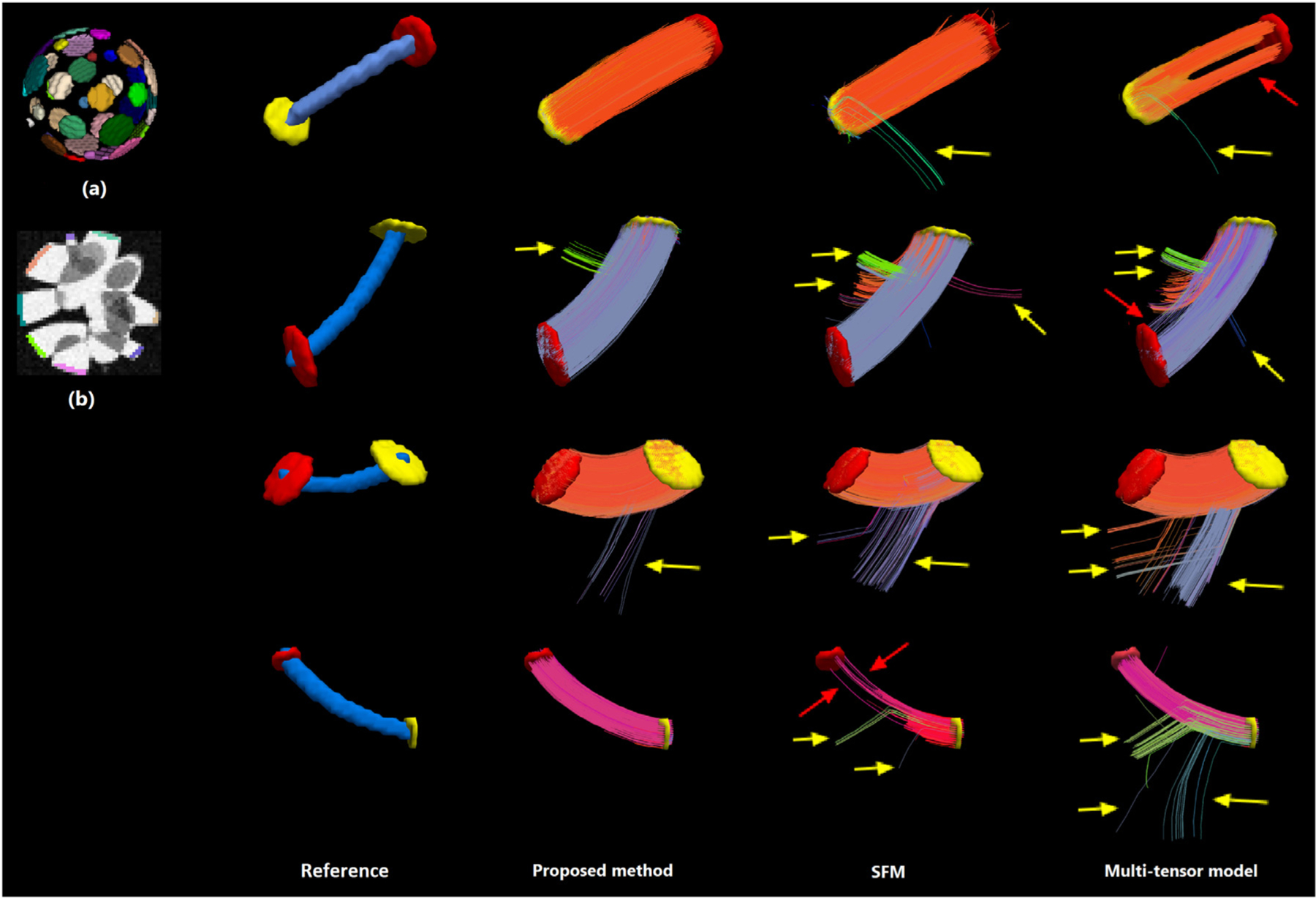
A comparison of the tract bundles reconstructed with SFM, multi-tensor model, and the proposed method on the HARDI-2013 phantom. Part (a) of the figure shows how the seed and target ROIs are distributed in 3D. Part (b) shows a slice through the FA image of the phantom in gray-scale with some of the ROIs marked in color. On the right side of the figure, we have shown four seed-target ROI pairs and the bundles reconstructed using the fODFs estimated with the proposed method, SFM, and the multi-tensor method. In each of these four rows, the seed ROI is shown with a yellow disk and the target ROI is shown with a red disk. In the Reference column, the blue cylinder shows the dilated center-line of the true bundle connecting the seed to the target. On the bundles reconstructed with different methods, yellow arrows indicate streamlines diverging from the correct tract path, and red arrows indicate missing streamlines.

Table 2 shows the mean, standard deviation, and the range of the computed tractography accuracy for different methods. Our method and SFM achieved higher average accuracy than the other methods. Fig. 3 shows example tracts from this phantom. Overall, we observed that our proposed method, SFM, CSD, and CNN-2D resulted in smaller numbers of prematurely-terminated fibers, and that our proposed method and SFM resulted in smaller numbers of diverging streamlines than the other methods. We ran paired t-tests to compare our proposed method with each of the other eight methods. Paired t-tests, with seed-target pairs as test units, allowed us to achieve high statistical power despite the high variance in tractography accuracy between seed-target pairs, as shown in Table 2. The tests showed that the tractography accuracy achieved with our method was significantly (p < 0.01) higher than all other methods except for SFM.

Table 2.

Comparison of the proposed method with several other methods in terms of the mean, standard deviation, and range of tractography accuracy on the 20 seed-target ROI pairs of the HARDI-2013 phantom. The tractography accuracy achieved by our method was significantly higher than the accuracy achieved by all other techniques, except for SFM.

Method	accuracy
SFM	0.55 ± 0.30,	[0.00, 0.93]
CSD	0.50 ± 0.23,	[0.06, 0.93]
OPDF	0.48 ± 0.19,	[0.03, 0.85]
CSA	0.50 ± 0.18,	[0.01, 0.90]
Multi-tensor fitting	0.42 ± 0.29,	[0.03, 0.84]
Bayesian model fitting	0.42 ± 0.25,	[0.06, 0.76]
CNN-2D	0.51 ± 0.18,	[0.00, 0.86]
CNN-3D	0.44 ± 0.22,	[0.06, 0.76]
Proposed method	0.56 ± 0.23,	[0.04, 0.97]

3.2. Evaluation on real data

In the experiments reported in this section, we used DW-MRI scans from the dHCP dataset. To train our method, we used either real data, generated from 140 dHCP subjects, or simulated data. The methods of generating these training datasets have been explained in Section 2.2. We used the same training data to train CNN-2D and CNN-3D. We then applied our method and all other competing single-shell methods on data from 20 subjects from the dHCP dataset that had not been used in the training stage. We performed this experiment twice; once using the measurements in the b = 1000 shell and once using the measurements in the b = 2600 shell. Similar to training data, to generate ground truth fODFs on test subjects we applied MSMT-CSD on the full multi-shell data (b = 400, 1000, and 2600).

Table 3 shows the results of this experiment. For the machine learning methods we have presented two sets of results, one for models trained with simulated data and the other for models trained with real data. The results show a clear advantage of the machine learning methods, especially when they are trained with real data. This is the case for both b = 1000 and b = 2600 shells. In terms of JSD, which is a measure of closeness of fODFs, the machine learning methods are much better than CSD, SFM, OPDF, and CSA, demonstrating that these machine learning methods can learn to predict the fODF from the training data. Also in terms of orientation error of the largest peak and WAAE, machine learning methods were better than CSD, SFM, OPDF, CSA, Multi-tensor fitting, and Bayesian model fitting. These differences were statistically significant (p < 0.01) for the experiment with b = 1000 shell as well as experiment with b = 2600 shell. For statistical significance tests, we used paired t-tests with subjects as units. These statistical significance tests showed that our method was significantly better (p < 0.01) than the six non-machine-learning methods in terms of the three metrics shown in this table. This was the case for the model trained with simulated data and the model trained with real data. Compared with CNN-2D and CNN-3D, our model achieved significantly lower error in estimating the orientation of the largest peak and significantly lower WAAE (p < 0.01). Our method also achieved significantly lower JSD than CNN-2D.

Table 3.

Comparison of different fODF reconstruction methods in terms of orientation error of the largest peak, WAAE, and JSD. The machine learning methods were trained twice, once with the simulated data and another time with real DWI data with ground truth fODFs estimated with MSMT-CSD. Because multi-tensor fitting and Bayesian model fitting methods do not estimate fODF, we cannot compute JSD for these two methods. Our method achieved significantly better results in terms of all three metrics than non-learning methods and CNN-2D. Our method was also significantly better than CNN-3D in term of orientation error of the largest peak and WAAE. The patterns of differences between methods, including the advantages of our proposed method over other techniques, are largely consistent across the two shells.

b value		Method	Orientation error of the largest peak	WAAE (degrees)	JSD
1000		SFM	15.0 ± 1.0	16.4 ± 1.1	0.113 ± 0.019
		CSD	15.2 ± 1.3	16.4 ± 1.4	0.071 ± 0.013
		OPDF	15.7 ± 1.6	17.0 ± 1.9	0.122 ± 0.023
		CSA	15.3 ± 1.3	16.5 ± 1.5	0.092 ± 0.018
		Multi-tensor fitting	16.1 ± 1.8	19.3 ± 2.1	-
		Bayesian model fitting	15.5 ± 1.6	16.0 ± 1.7	-
	Trained on simulated data	CNN-2D	14.2 ± 1.2	15.2 ± 1.2	0.048 ± 0.004
		CNN-3D	14.3 ± 0.9	15.4 ± 1.0	0.044 ± 0.004
		Proposed method	13.5 ± 1.1	13.8 ± 0.9	0.041 ± 0.004
	Trained on real data	CNN-2D	12.5 ± 0.7	14.7 ± 1.3	0.032 ± 0.003
		CNN-3D	12.0 ± 0.7	14.4 ± 1.0	0.030 ± 0.004
		Proposed method	10.4 ± 0.9	12.9 ± 1.1	0.028 ± 0.003
2600		SFM	14.2 ± 1.1	15.1 ± 1.1	0.104 ± 0.017
		CSD	14.4 ± 1.0	15.4 ± 1.3	0.068 ± 0.011
		OPDF	15.0 ± 1.5	16.1 ± 1.2	0.110 ± 0.017
		CSA	14.6 ± 1.3	16.0 ± 1.4	0.076 ± 0.015
		Multi-tensor fitting	15.8 ± 2.0	17.0 ± 1.8	-
		Bayesian model fitting	15.1 ± 1.7	15.5 ± 1.5	-
	Trained on simulated data	CNN-2D	13.4 ± 1.2	14.0 ± 1.0	0.044 ± 0.005
		CNN-3D	13.2 ± 0.7	14.1 ± 1.1	0.043 ± 0.005
		Proposed method	12.5 ± 0.8	12.8 ± 0.8	0.040 ± 0.004
	Trained on real data	CNN-2D	11.9 ± 0.8	13.5 ± 1.1	0.028 ± 0.005
		CNN-3D	11.7 ± 0.8	13.1 ± 0.8	0.027 ± 0.003
		Proposed method	9.5 ± 0.8	12.1 ± 0.8	0.027 ± 0.004

Fig. 4 shows example fODFs predicted by the proposed method and competing techniques. In this figure, for each case we have shown the T2 image and corresponding color fractional anisotropy (CFA) image. The location of a region of interest (ROI) has been marked on the T2 image in order to aid in understanding the location of the displayed fODF. The size of each ROI is 10 × 10 voxels. We have displayed the estimated fODFs for the ROI. For each example, we have displayed the reference fODF (estimated using measurements in all three shells by MSMT-CSD), the fODF predicted by the proposed method, and the fODFs estimated with SFM and CNN-3D. We chose SFM because, overall, it was better than the other non-learning methods. We also chose CNN-3D because it was better than CNN-2D.

Fig. 4.

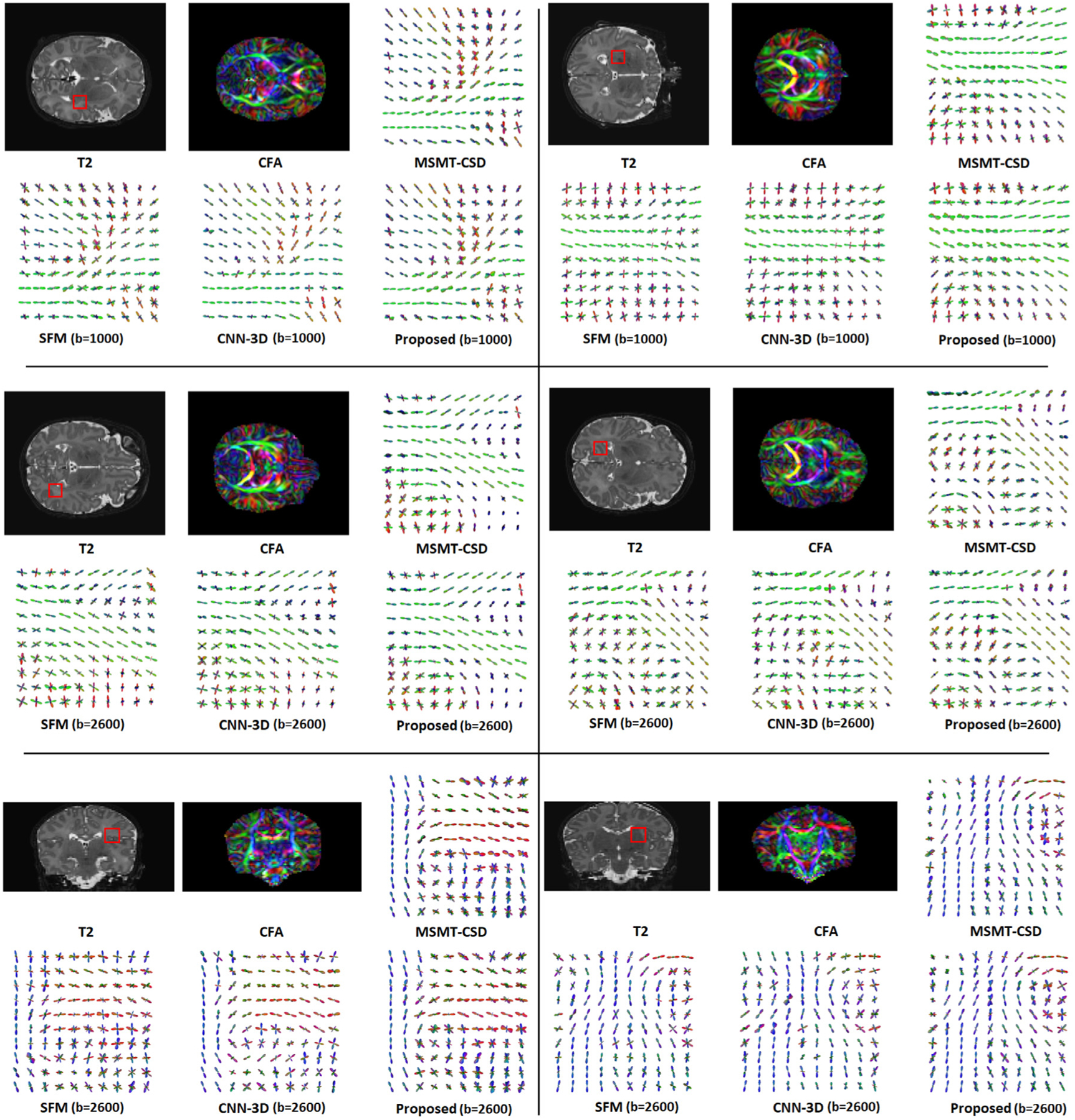
Illustration of the fODFs estimated by the proposed method and two competing techniques. For each of the six displayed cases, the top row shows the T2 image, the CFA image, and the reference fODF estimated with MSMT-CSD using measurements in all three shells. A red square on the T2 image shows the location of the ROI that is selected for displaying the fODFs. In the bottom row for each case we have displayed the fODFs estimated by SFM, CNN-3D, and our proposed method. These single-shell methods were applied on the measurements in either b = 1000 shell of b = 2600 shell. This has been indicated next to the names of these methods.

A potential advantage of machine learning-based methods over non-learning methods is their ability to learn the mapping between under-sampled or noisy data with the desired output. This potential is highly desirable as it can reduce the scan times and improve the fODF reconstruction accuracy in applications such as fetal DW-MRI where data is inherently limited (Marami et al., 2017). In order to assess this potential, we compared different methods on subsets of 60 and 40 DWI measurements for 20 subjects in the dHCP dataset. We performed this experiment, separately, with the b = 1000 shell and the b = 2600 shell. In the experiment with the b = 2600 shell, instead of all 128 measurements in that shell, only 60 and 40 measurements from that shell were used for each subject. For example to select the 60 measurements out of 128, we created a spherical grid of size 60 using the Fibonacci spiral sphere method and selected the measurements with the diffusion gradient direction that were closest to each of the points on that grid for each subject. We similarly selected 40 measurements out of 128 for each subject. We selected 60 and 40 measurements out of the 88 measurements in the b = 1000 shell in the same way.

Table 4 shows the results of this experiment. For this experiment, we dropped the multi-tensor fitting, Bayesian model fitting, and OPFD methods because they performed worse than other methods in the above experiments (Table 3). The advantage of the machine learning methods is clear from this table. They were significantly (p < 0.01) more accurate than SFM, CSD, and CSA in terms of the three metrics reported in this table. This was the case for both b = 1000 and b = 2600 shells. Our proposed method was significantly (p < 0.01) better than CNN-2D and CNN-3D in estimating the orientation of the largest peak and also in terms of WAAE. In terms of JSD, our method was significantly (p < 0.01) better than CNN-2D and significantly (p < 0.01) better than CNN-3D with n_data = 40.

Table 4.

Results of experiments to investigate the performance of different fODF estimation methods with down-sampled data.

b value		ndata = 60			ndata = 40
	Method	Orientation error of the largest peak	WAAE (degrees)	JSD	Orientation error of the largest peak	WAAE (degrees)	JSD
1000	SFM	15.7 ± 1.0	17.0 ± 1.3	0.122 ± 0.020	18.2 ± 1.1	19.1 ± 1.3	0.148 ± 0.027
	CSD	16.0 ± 0.9	17.1 ± 1.2	0.083 ± 0.021	18.6 ± 1.3	19.4 ± 1.6	0.125 ± 0.026
	CSA	16.2 ± 1.2	17.4 ± 1.5	0.098 ± 0.026	18.8 ± 1.6	19.5 ± 1.7	0.129 ± 0.029
	CNN-2D	14.1 ± 1.1	15.6 ± 1.4	0.050 ± 0.006	16.1 ± 1.7	16.4 ± 1.5	0.112 ± 0.017
	CNN-3D	13.5 ± 0.9	14.5 ± 1.0	0.038 ± 0.004	16.2 ± 1.3	16.9 ± 1.6	0.106 ± 0.015
	Proposed method	11.8 ± 0.7	13.1 ± 0.8	0.040 ± 0.004	14.2 ± 1.0	14.5 ± 1.1	0.082 ± 0.019
2600	SFM	14.8 ± 1.1	15.9 ± 0.9	0.108 ± 0.021	17.0 ± 0.9	17.8 ± 1.1	0.126 ± 0.024
	CSD	15.2 ± 0.8	16.1 ± 1.0	0.076 ± 0.018	17.3 ± 1.2	17.8 ± 1.3	0.104 ± 0.023
	CSA	15.1 ± 1.5	16.3 ± 1.4	0.090 ± 0.022	17.5 ± 1.5	18.6 ± 1.5	0.115 ± 0.027
	CNN-2D	13.6 ± 1.0	14.9 ± 1.3	0.045 ± 0.005	15.5 ± 1.3	15.7 ± 1.3	0.89 ± 0.018
	CNN-3D	12.4 ± 0.7	12.8 ± 0.9	0.034 ± 0.005	15.2 ± 1.4	16.0 ± 1.3	0.074 ± 0.014
	Proposed method	11.2 ± 0.8	12.0 ± 0.7	0.033 ± 0.004	13.2 ± 0.8	13.9 ± 1.1	0.070 ± 0.016

We further evaluated our method in terms of expert quality rating of the resulting tractography on real human brain data. This is a less direct and more challenging evaluation method because of the imper-fections of the tractography algorithms (Maier-Hein et al., 2017) and subjective nature of expert assessments (Schilling et al., 2020). We applied our method and SFM on the b = 1000 shell data of 20 subjects from the dHCP dataset to estimate fODFs in each voxel, and generated whole-brain tractograms using the EuDX algorithm. The tractograms were evaluated by three expert neuroanatomists (LV, CJ, and FM), separately and independently. Given the limited availability of the experts and the time required to carefully rate each tractogram in detail, in this experiment we only compared our method with SFM. SFM performed slightly better than CSD, CSA, and OPDF in the experiments reported in Tables 3 and 4 above with real data. SFM also performed better than other methods including the two machine learning methods (CNN-2D and CNN-3D) in experiments with phantom data presented in Tables 1 and 2. In particular, on the tractography experiment with phantom data, presented in Table 2, SFM performed better than all other competing methods.

The tractograms generated by our method and SFM for each subject were named “result_01” and “result_02” at random and were presented to the experts. The experts were told that the naming was random, but they were blind to the naming of the tractograms. The experts decided to exclude three of the subjects from evaluation. This was because those three brains were highly oblique with respect to the standard planes. This made it less reliable to identify the tracts bilaterally and accurately assess them. On the remaining 17 subjects, the experts evaluated each of the two tractograms for each subject separately by assessing the accuracy of reconstruction of eight tracts including commissural (corpus callosum and anterior commissure), projection (frontopontine fibers, corticospinal tract, and fornix), association (inferior fronto-occipital fasciculus and uncinate fasciculus), and cerebellar (middle cerebellar pedunculus) tracts. Each of the experts graded these eight tracts based on tract integrity (i.e., reconstruction of all components of the tract) and bilateral presence. A grade of 3 was assigned if all components of the given tract were present bilaterally. A grade of 2 was given if at least one component of the tract was absent, regardless of the side of the brain. A grade of 1 was assigned if the tract was missing in both hemispheres of the brain.

Tables S1–S3 in the Supplementary Materials of the paper show the detailed scores provided by the three experts. We used Cohen’s kappa (κ) statistic (Cohen, 1960) to assess the agreement between pairs of experts. This coefficient ranges between −1 and 1. Negative values of κ indicate accidental agreement, whereas values in the intervals 0.1 – 0.2, 0.2 – 0.4, 0.4 – 0.6, 0.6 – 0.8, and 0.8 – 1.0 indicate slight, fair, moderate, substantial, and near–perfect agreement, respectively. The mean ± standard deviation, across the eight tracts, of κ between the three experts, evaluated pairwise, was 0.62 ± 0.13, 0.56 ± 0.16, and 0.57 ± 0.16. This indicates moderate to substantial agreement between the experts. For each subject and method, we summed the scores given by each of the three experts on the eight tracts to obtain one total score in the range [8, 24] for the entire tractogram. Table 5 shows the mean and standard deviation of the total scores received by our method and SFM on the 17 subjects from each of the three experts. As can be seen from this table, all three experts gave higher scores to the tractograms produced by our method compared with SFM. For statistical significance test, we compared our method and SFM in terms of the grades given by each of the three experts, separately, using the Wilcoxon signed-rank test (Berenson et al., 2012). At p = 0.01, the total score received by our method was significantly higher than the score received by SFM for all three experts. Table S4 in the Supplementary Materials shows the results of statistical significance tests for individual tracts. The score received by our method was significantly higher than SFM’s score on 6, 7, and 5 tracts for the three experts. Fig. 5 shows example tracts reconstructed using fODFs estimated with the proposed method and SFM.

Table 5.

Comparison of the proposed method and SFM in terms of the tractography score given by three independent experts. The values shown are the mean ± standard deviation of the total scores on 17 subjects. The score received by our method was significantly higher than the score received by SFM for all three experts.

Method	Expert 1	Expert 2	Expert 3
SFM	15.6 ± 2.30	15.6 ± 1.19	18.4 ± 1.24
Proposed method	21.4 ± 2.19	22.1 ± 1.67	22.6 ± 0.77

Fig. 5.

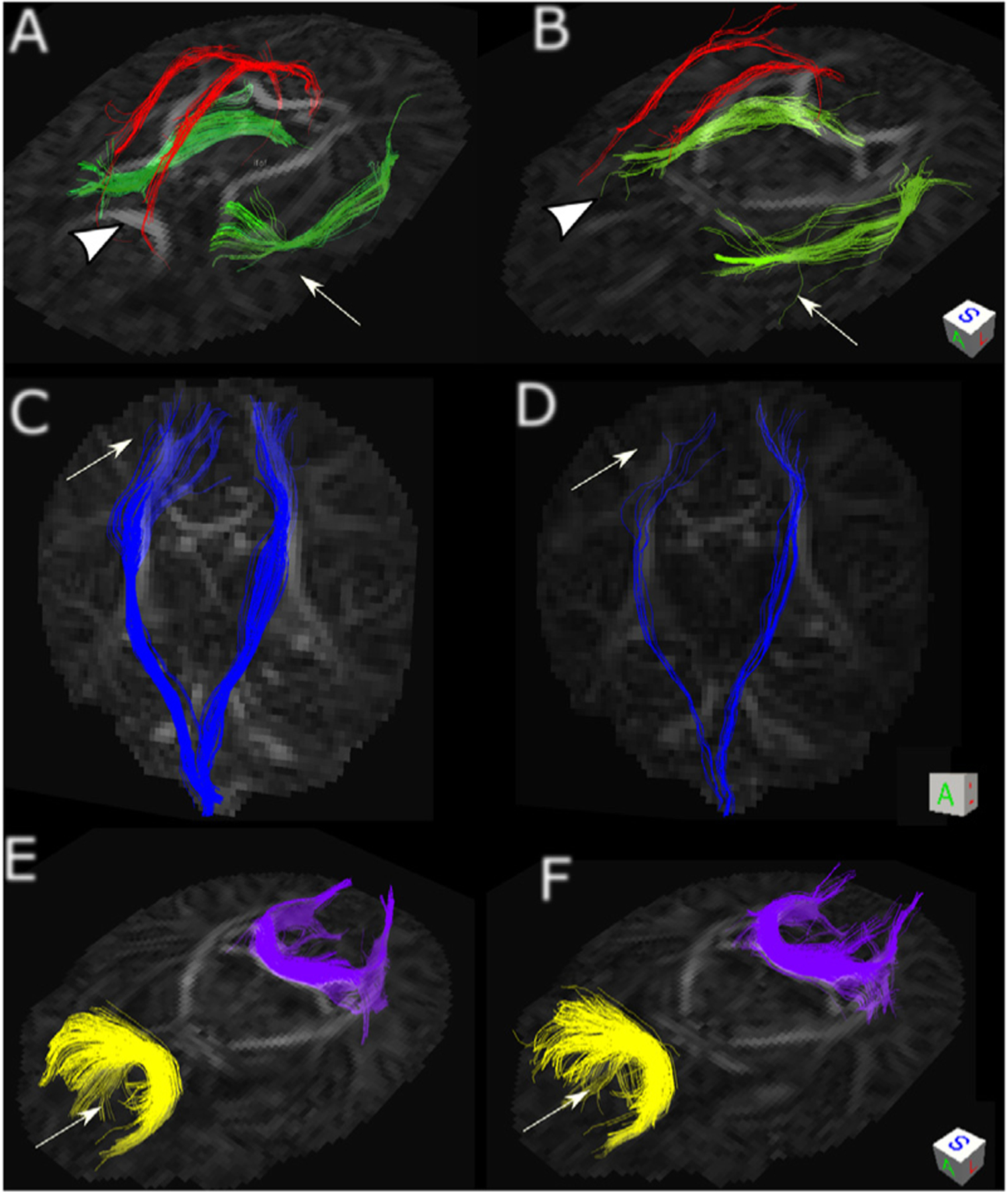
Examples fiber tracts dissected from the whole-brain connectomes reconstructed using fODFs estimated with our method (A,C,E) and with SFM (B,D,F). We note that tractography is only an indirect way of assessing fODF estimation methods, and since tractography algorithms are known to have high rates of type I errors (Maier-Hein et al., 2017), they may not show the full range of differences between fODF estimation methods. Knowing this fact, we used the same fiber tracking algorithm (Garyfallidis, 2013) to evaluate the relative impact of our method and SFM on fiber tracking. (A,B) show the cingulum in red and the inferior fronto-occipital fasciculus (IFOF) in green. Compared to (A), the cingulum fibers were terminated early in (B) (arrowhead). (A) shows better delineation of the IFOF with less spurious tracts compared to (B) (arrow). (C,D) show the corticospinal tracts (CST) in blue. Compared to (D), our method (C) showed much better delineation of the CST including better delineation of CST projections into the cortex, whereas the tracts were terminated immaturely in an area of crossing fibers in (D) (arrow). (E,F) show the forceps major (purple) and forceps minor (yellow). For both of these tracts, our method (E) resulted in less spurious fibers than SFM (F) (arrow).

There are several design choices and hyper-parameters that may influence the performance of our proposed method. Here we address some of these aspects. One of these is the model size, which is determined by the number of layers (i.e., the network depth) and the size of each layer (i.e., the number of neurons in each layer). As mentioned in Section 2.1, the MLP used in all of the experiments reported above had six hidden layers with {300, 300, 300, 400, 500, 600} neurons in each layer. This amounts to approximately 1.18 million parameters. Table 6 shows a comparison with several different model sizes. In this experiment, we varied the network depth (number of layers) as well as the width (number of neurons in each layer). We trained each model with real data, generated as explained in Section 2.2.2. We then applied the model on 20 test subjects from the dHCP dataset and computed WAAE, JSD, and the amount of time needed to compute the fODF for the entire brain. The computation time depends on many factors such as the hardware. Since we were only interested in comparing the relative values for different model sizes, we used the same NVIDIA GeForce GTX 1080 GPU for all models. One single GPU was used for training/testing in all experiments. The results show that models with 2 or 4 hidden layers are not deep enough to learn the complex mapping between the diffusion signal and the fODF. Increasing the depth to 10 hidden layers did not significantly improve the estimation accuracy compared with models with 6 hidden layers. With sufficient model depth, the effect of the number of neurons per layer seems to play only a minor role. This can be seen by comparing the three models with 6 hidden layers. They had 0.63, 1.18, and 1.82 million trainable parameters, but they achieved similar estimation accuracy levels.

Table 6.

Effect of the model size on performance of the proposed fODF estimation method. Model size shows the size of the hidden layers. n_layer is the number of hidden layers. n_param is the number of model parameters in millions.

Model size	n layer	nparam (×106)	WAAE (degrees)	JSD	time (s)
{300, 500}	2	0.52	16.0 ± 1.3	0.068 ± 0.015	5.0 ± 0.21
{300, 400, 500, 600}	4	1.01	14.8 ± 1.1	0.047 ± 0.003	5.7 ± 0.23
{200, 200, 200, 300, 300, 400}	6	0.63	13.1 ± 1.2	0.033 ± 0.003	5.4 ± 0.24
{300, 300, 300, 400, 500, 600}*	6	1.18	12.9 ± 1.1	0.028 ± 0.003	6.9 ± 0.28
{300, 400, 500, 600, 600, 700}	6	1.82	12.8 ± 0.9	0.028 ± 0.003	7.6 ± 0.27
{200, 300, 300, 400, 500, 600, 600, 700}	8	1.98	12.8 ± 0.9	0.026 ± 0.003	8.0 ± 0.24
{200, 250, 300, 350, 400, 450, 500, 550, 600, 650}	10	2.14	12.8 ± 0.8	0.026 ± 0.003	8.3 ± 0.27

Another design choice in our proposed method is the size of the grids in the signal and fODF spaces. Increasing the grid resolution may lead to a higher prediction accuracy at the expense of larger number of model parameters in the first and last layers. The choice of the grid in the q-space, U_s, may affect the approximation error incurred during signal interpolation. The choice of the grid in the fODF space, U_f, can affect the accuracy of extracting the orientation of the peak(s). An alternative to representation/interpolation on grids is representation in spherical harmonics bases. This is the representation used by CNN-2D and CNN-3D. We compared these alternatives in an experiment with 20 dHCP test subjects. We first trained our own model, shown in Fig. 1, with finer grids in both signal and fODF spaces. We then trained our model by replacing the grids with representation in spherical harmonics. As suggested in previous works (Koppers et al., 2017a; Koppers and Merhof, 2016; Lin et al., 2019), we used spherical harmonics order of 4 to represent the diffusion signal and order of 8 to represent the fODF. In order to compute the WAAE and JSD, we had to convert the estimated spherical harmonic coefficients back to spatial coordinates. For this purpose, we used two different hemi-spherical grids with 362 and 2500 points.

Results of this experiment are presented in Table 7. Overall, the results show only a small improvement in fODF estimation accuracy with increasing grid size/resolution. Increasing the grid resolution had a slightly larger impact when spherical harmonic representations were used. With the network architecture shown in Fig. 1, increasing the size of the fODF grid (n_f) increases the number of model parameters. For example, increasing n_f from 362 to 2500 adds 1.25 million new parameters to be learned. With spherical harmonics, on the other hand, the size of the output layer (i.e., the number of spherical harmonics coefficients) remains the same regardless of n_f. Therefore, one can use an arbitrarily large grid size for reconstructing the fODF without changing the number of model parameters. Nonetheless, results shown in Table 7 indicate that representing the MLP’s input and output in spherical harmonics bases does not improve the fODF estimation accuracy. One reason for this may be due to the inevitable approximation errors when the signal and fODF are projected from their native space onto spherical harmonics bases. The proposed method, too, includes some inevitable approximation error due to interpolating the diffusion signal on a fixed grid (Eq. (1)). However, inspecting the first five rows of Table 7 seems to indicate that the size of U_s has a very small impact on this error.

Table 7.

Results of a set of experiments with 20 subjects from dHCP dataset to determine the effect of grid size on the fODF estimation accuracy. The first five rows show the results for the model shown in Fig. 1. The bottom two rows show the results for a model where the input and output of the MLP were represented with their spherical harmonics coefficients. The output of this model was then converted to fODF on a hemi-spherical grid with n_f points. Therefore, in the last two rows, n_f shows the size of the hemi-spherical grid used to compute WAAE and JSD.

Model	WAAE (degrees)	JSD
ns = 100, nf = 362	12.9 ± 1.1	0.028 ± 0.003
ns = 180, nf = 362	12.9 ± 1.1	0.027 ± 0.003
ns = 180, nf = 1000	12.7 ± 0.9	0.026 ± 0.004
ns = 360, nf = 1000	12.7 ± 1.0	0.026 ± 0.003
ns = 360, nf = 2500	12.6 ± 0.9	0.025 ± 0.003
Spherical harmonics (nf = 362)	13.4 ± 1.3	0.033 ± 0.004
Spherical harmonics (nf = 2500)	13.0 ± 1.2	0.032 ± 0.003

Future studies can improve and expand this work in various directions. In terms of the machine learning methodology, various different deep learning architectures can be investigated. Our decision to use an MLP model was motivated by the very high representational capacity of MLPs and their ease of implementation on GPUs, allowing for fast training on huge datasets and fast computation at test time. We also experimented with support vector regression models, but their training on large datasets was extremely slow. Therefore, we had to substantially reduce the amount of training data and the test accuracy was much lower than the MLP model. Therefore, we think that the deep learning models have a better potential to be successful in this application. Nonetheless, we cannot claim that the MLP used in this work is the best choice. Recent studies have reported very successful application of other deep learning models for solving various regression problems (Lathuilière et al., 2018; 2019; Wu et al., 2020). These models may be explored in future works.

Our methods of generating the training data may also be improved. In this work, we tried to use models that were sufficiently accurate but also easy to implement and run to simulate diffusion data for millions of voxels. In general, mathematical models of complex biophysical phe-nomena cannot be perfect (Box, 1976). Nonetheless, more realistic training data may lead to significantly more robust methods and more accurate models. In our work, in addition to the multi-tensor model shown in Eq. (2), we also used the CHARMED model (Assaf and Basser, 2005) that included restricted as well as hindered compartments, but did not achieve better results. Nonetheless, other more accurate signal generation and noise models may improve the accuracy of the method proposed in this work.

There are other aspects of our diffusion-weighted signal simulation approach that may need further exploration. For example, as we mentioned in Section 2.2.1, we did not consider voxels with crossing fibers closer than 30 degrees. This decision was partly motivated by experimental observations. Specifically, removing those simulations from our training data resulted in models that were more accurate at test time. In addition to this empirical observation, we think there are other reasons that justify this choice. Even though crossing fibers in the brain white matter can certainly be closer than 30 degrees, studies have shown that current diffusion MRI measurements and reconstruction methods may be inherently limited in resolving such fibers. For example, Schilling et al. (2016, 2018) evaluated standard reconstruction methods using histological ground truth. They found that many standard reconstruction methods including CSD failed to resolve fibers that were closer than 60 degree apart. The number of diffusion measurements in the dHCP dataset that we used in our work is larger than the number of measurements used in those works, but the inherent limitations remain. Overall, we found that including crossing fibers that are too close together in the training set would impose an unrealistic demand on our method. Nonetheless, this aspect can also be explored further in future works.

4. Conclusion

This paper presented a data-driven approach to estimating the fODF directly from DW-MRI measurements in each voxel. The proposed method exploits the representational capacity of deep neural networks to learn the complex relation between the DW-MRI signal and the fiber orientation distribution that gives rise to that signal, without imposing any mathematical models or physical assumptions. We also proposed methods of training the model using simulated and real data. Our experiments showed that this approach could lead to significantly more accurate estimation of the fODF and better tractography results than several competing methods including methods based on nonlinear optimization, Bayesian estimation, spherical deconvolution, and machine learning. These results show the significant potential of deep learning methods for improving the accuracy of fODF estimation from DW-MRI measurements.

Data availability

The simulated data used in this study we produced by an in-house script. This script is publicly available at https://github.com/bchimagine.

The real human scan data used in this study consisted of a subset of the developing Human Connectome Project (dHCP) dataset. This dataset is publicly available at: http://www.developingconnectome.org/project/data-release-user-guide/.